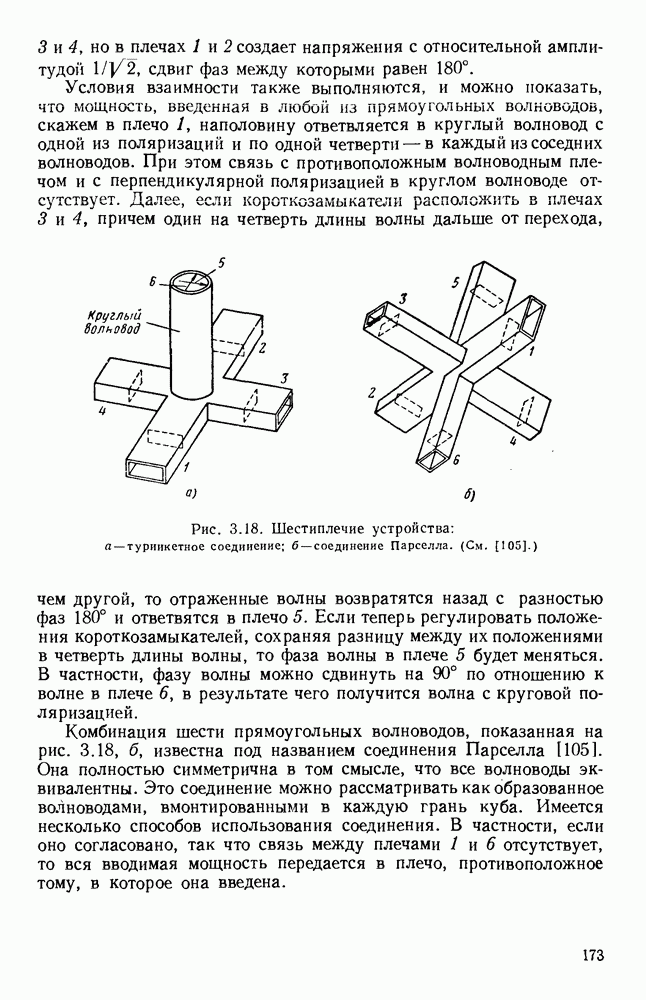
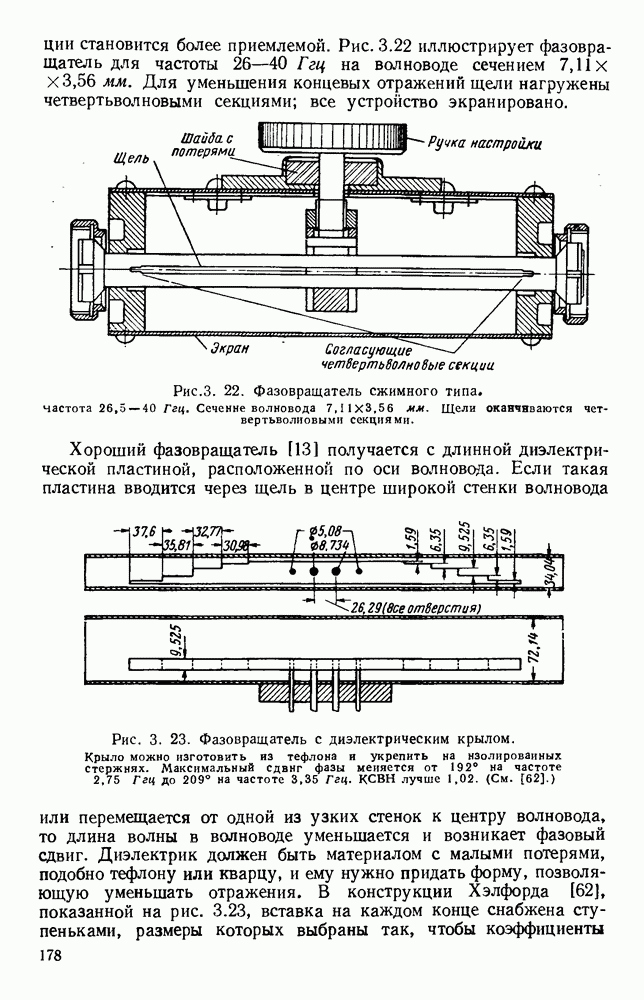
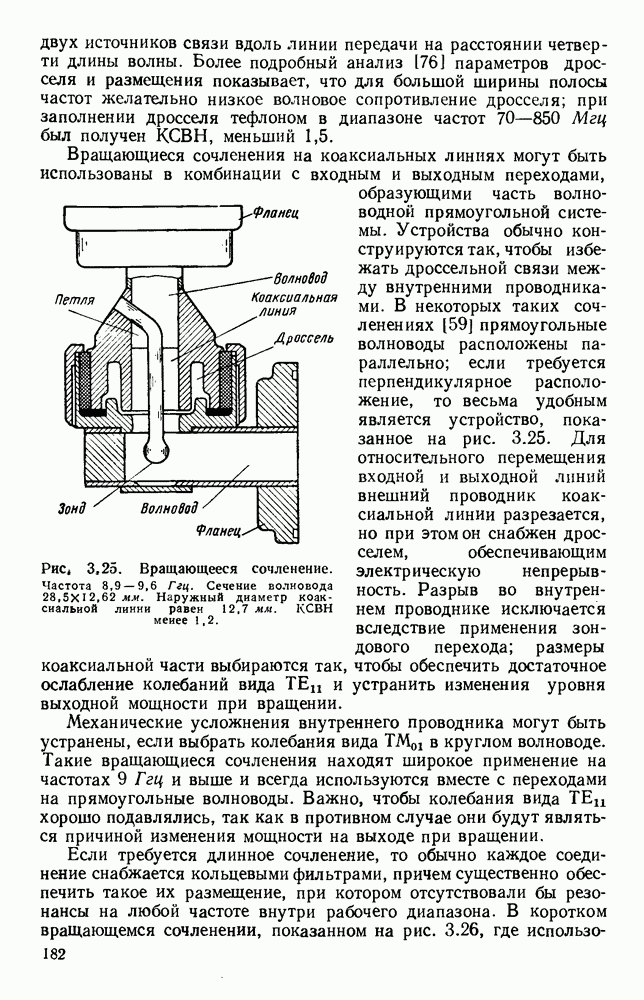
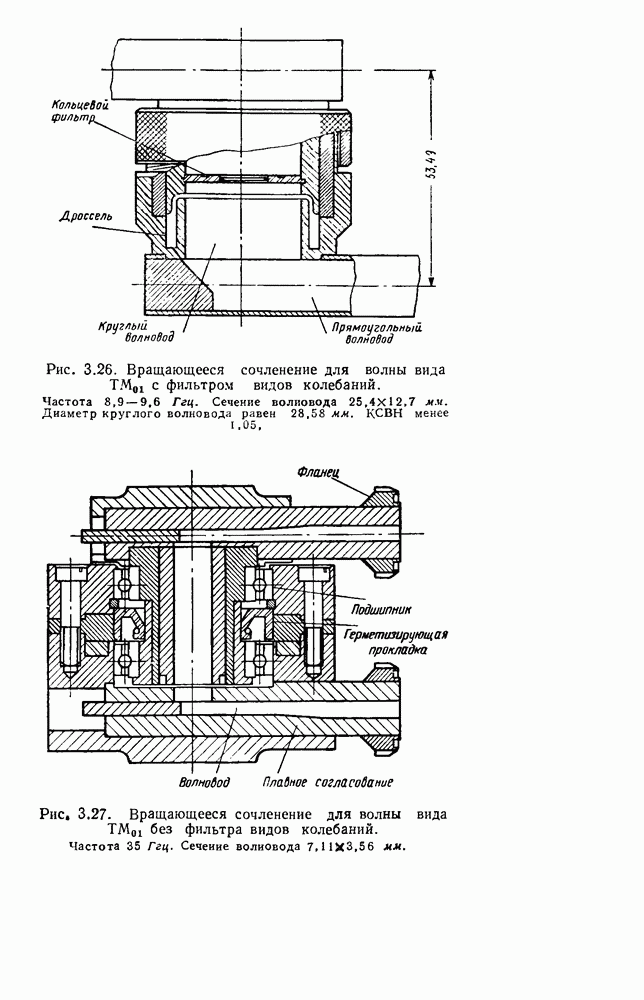
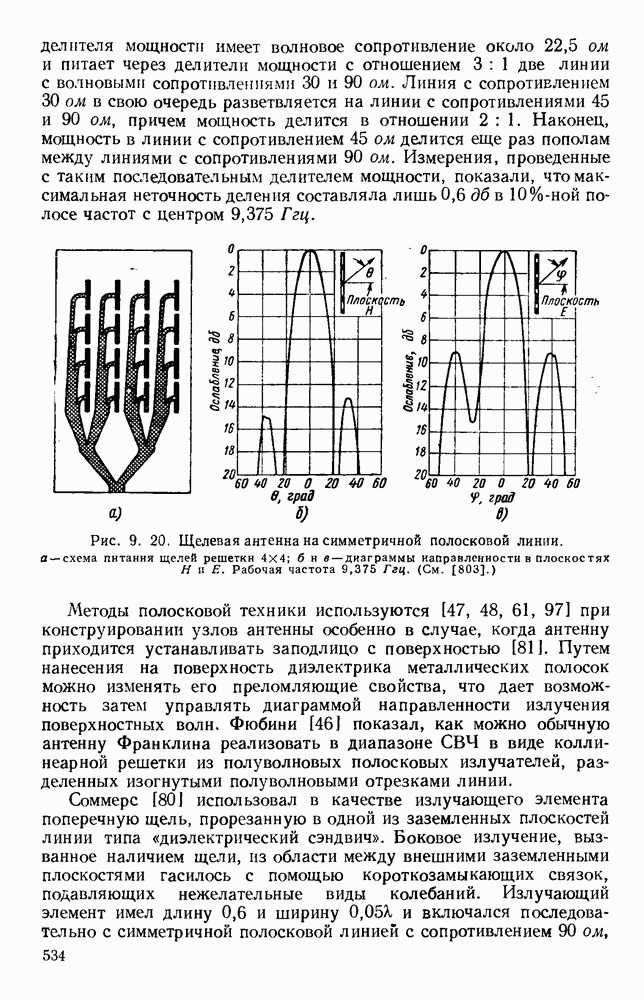
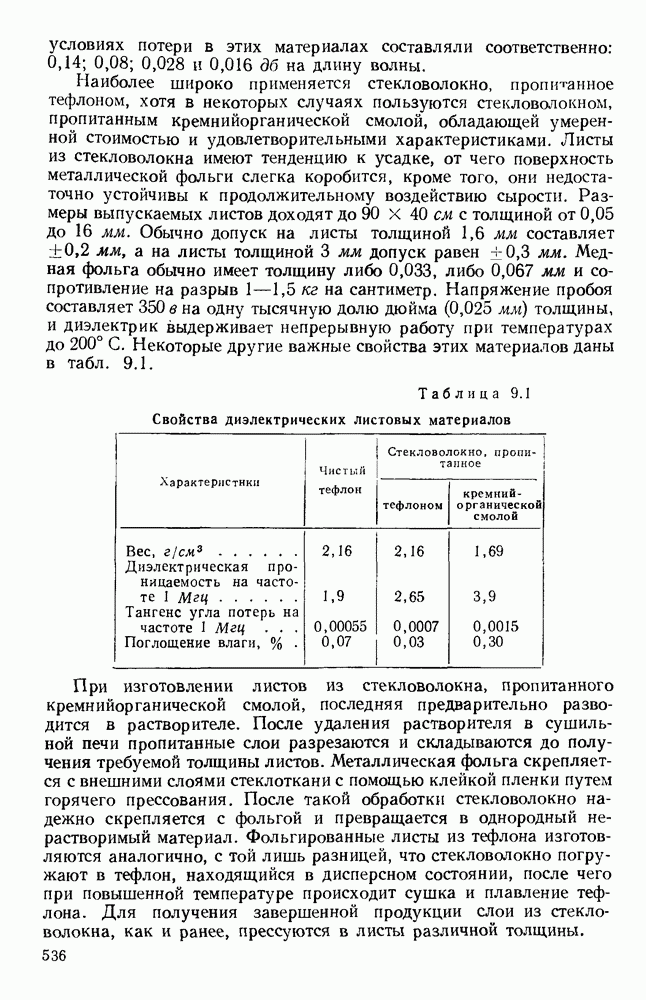
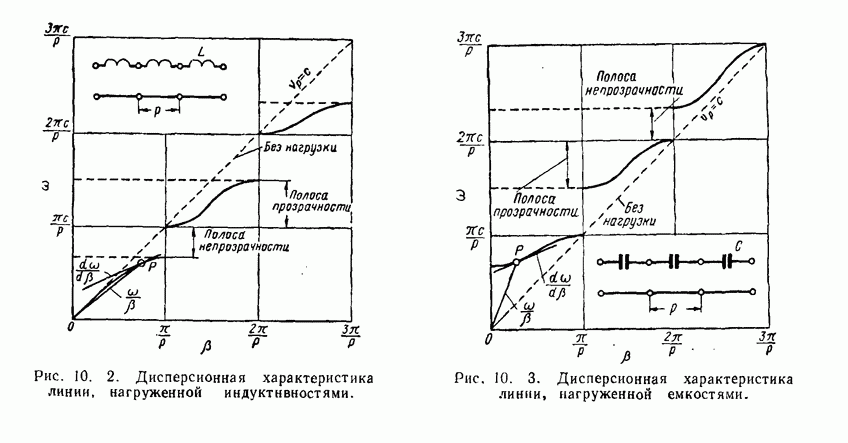
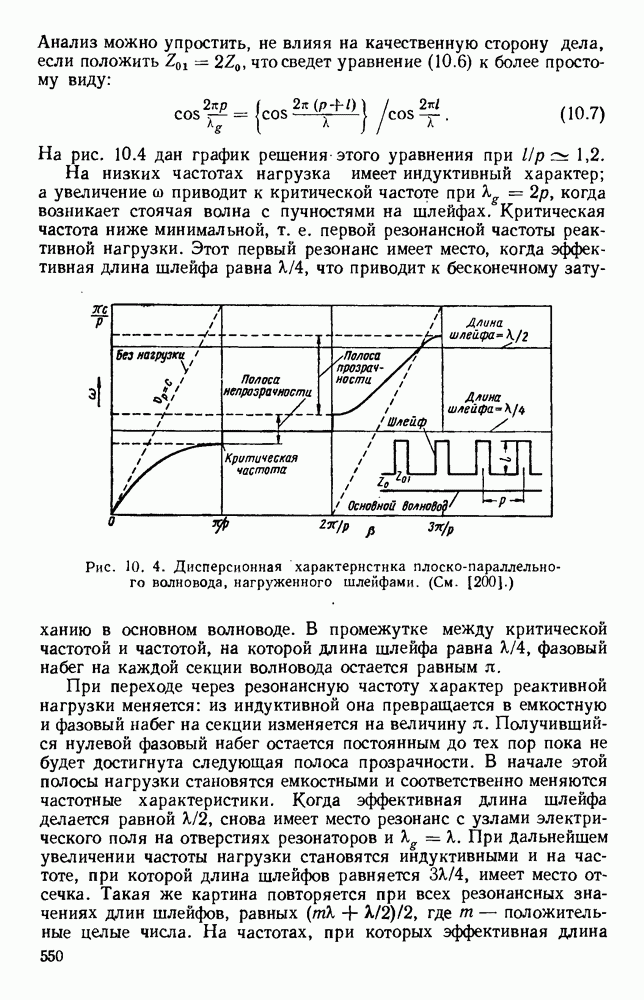
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
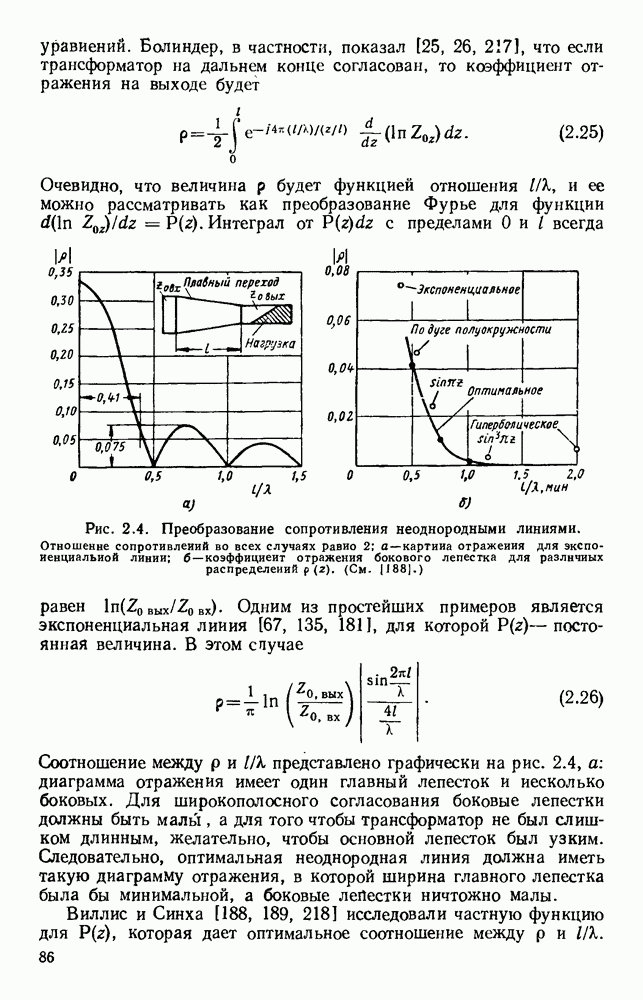
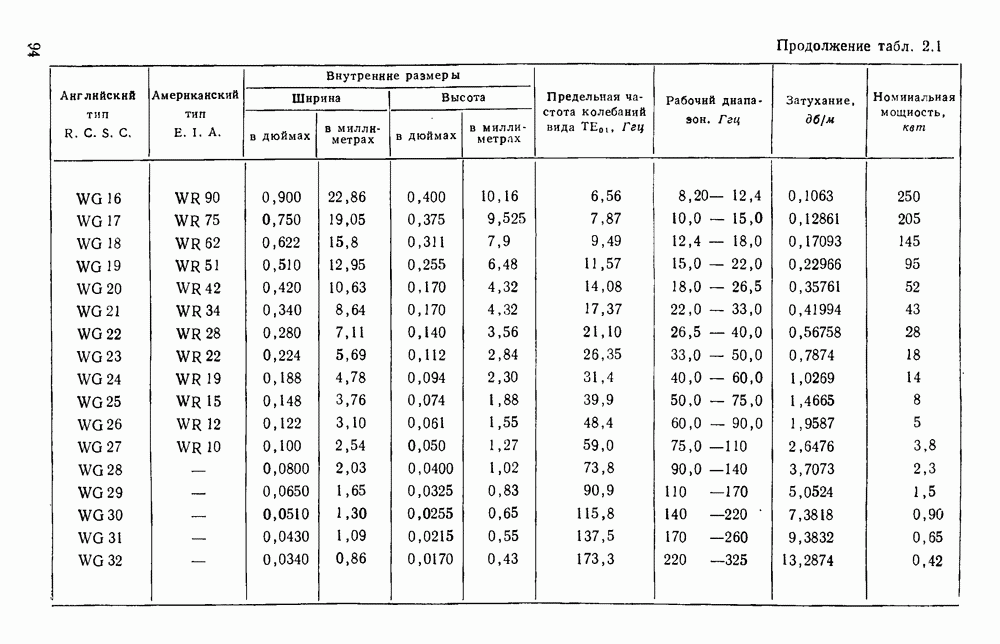
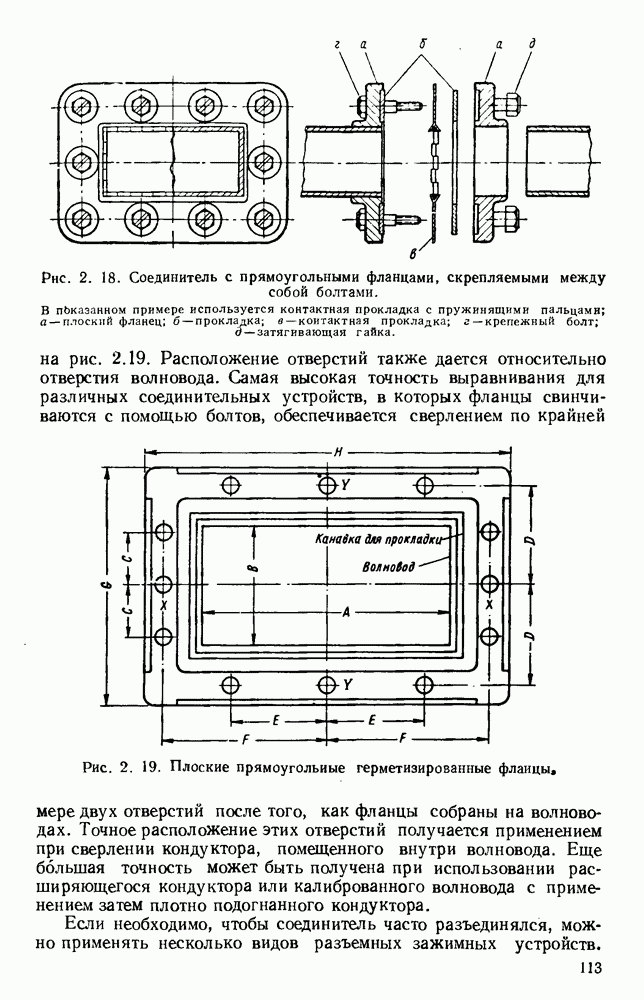
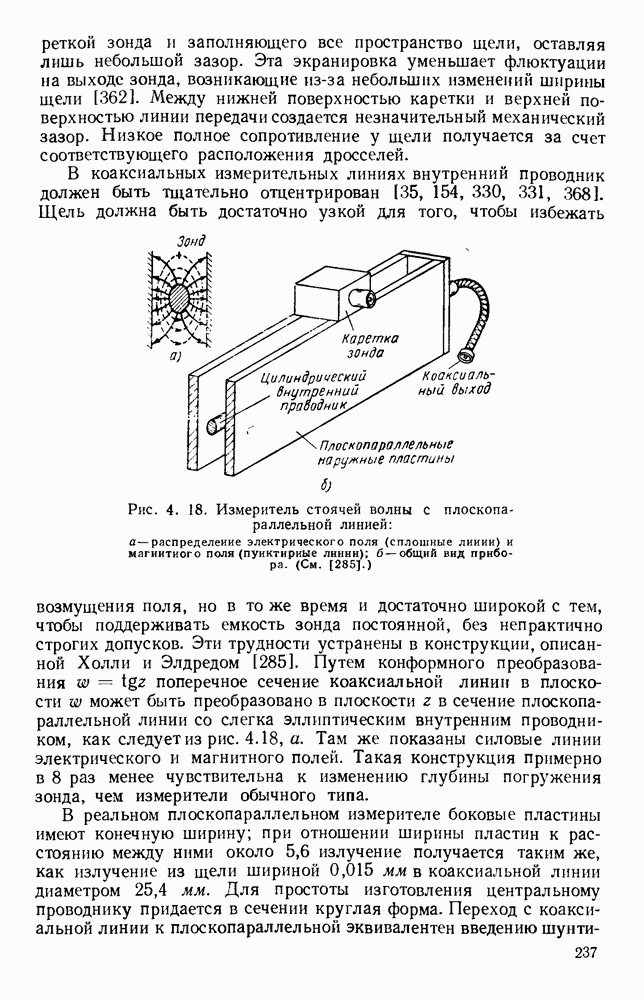
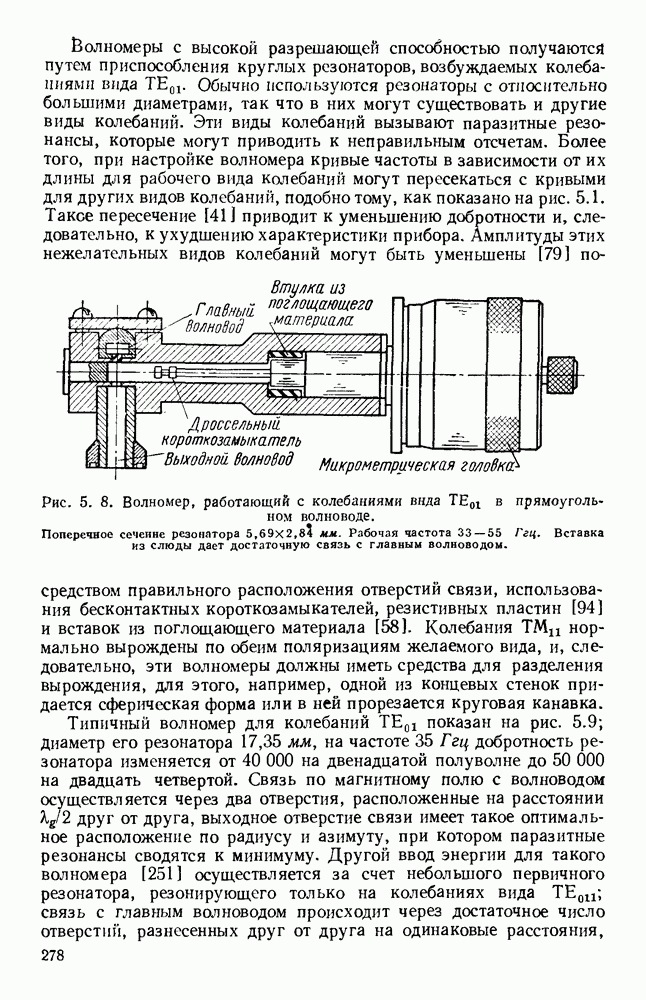
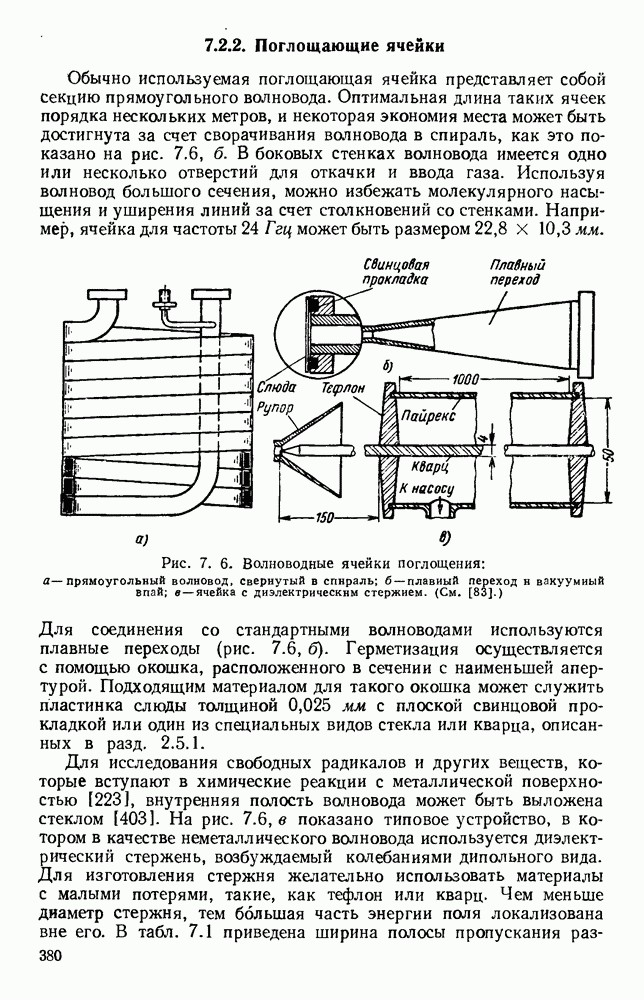
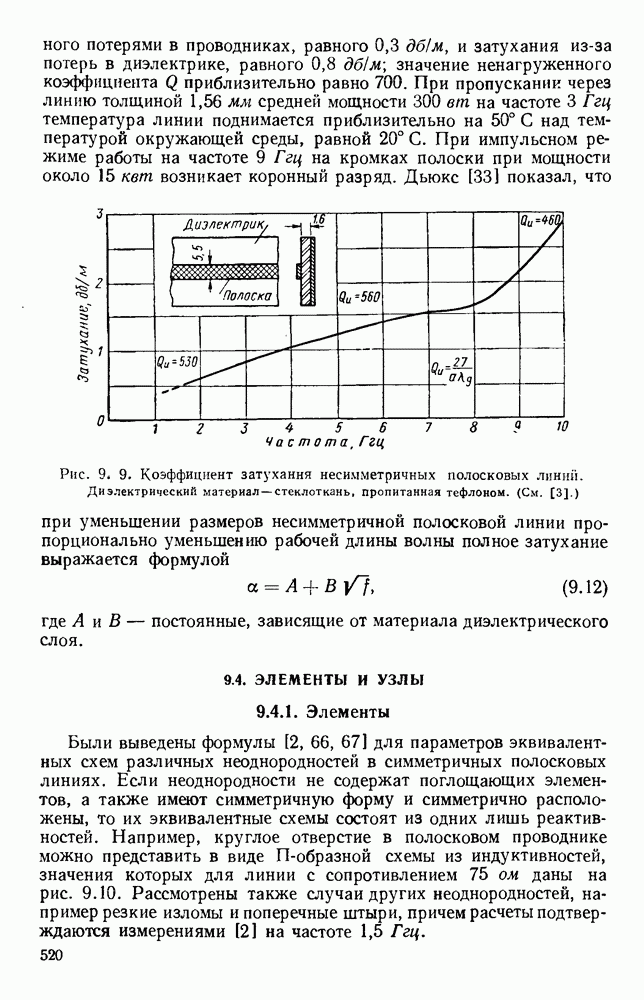
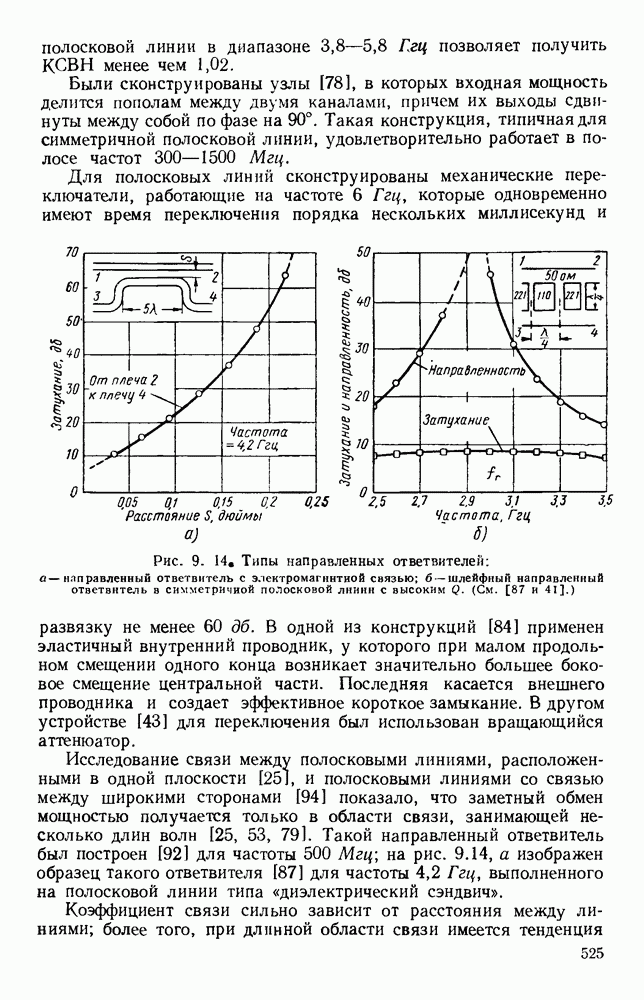
10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
10.4.1. Плоские пластины
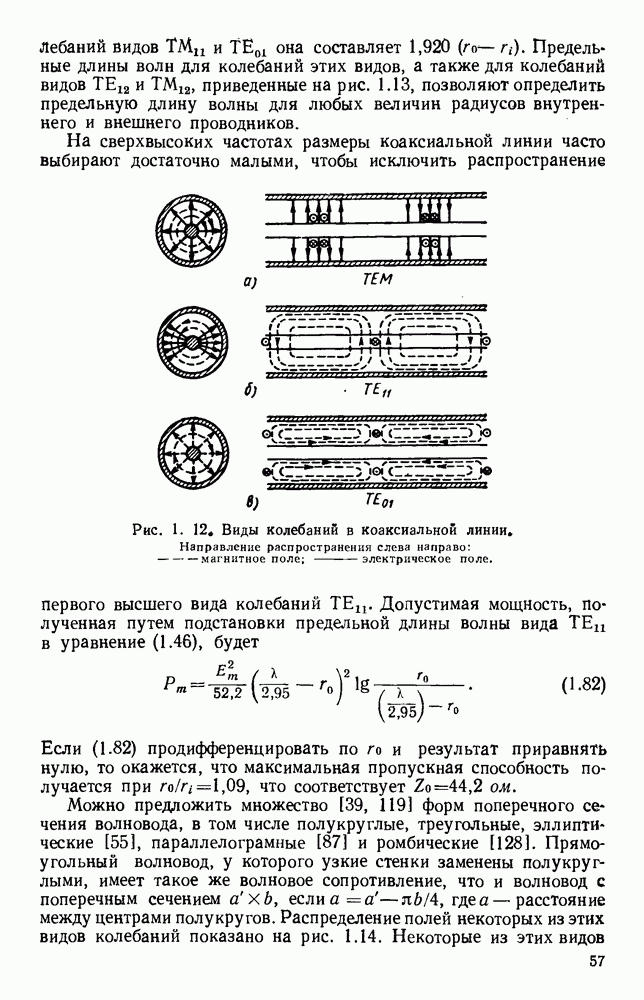
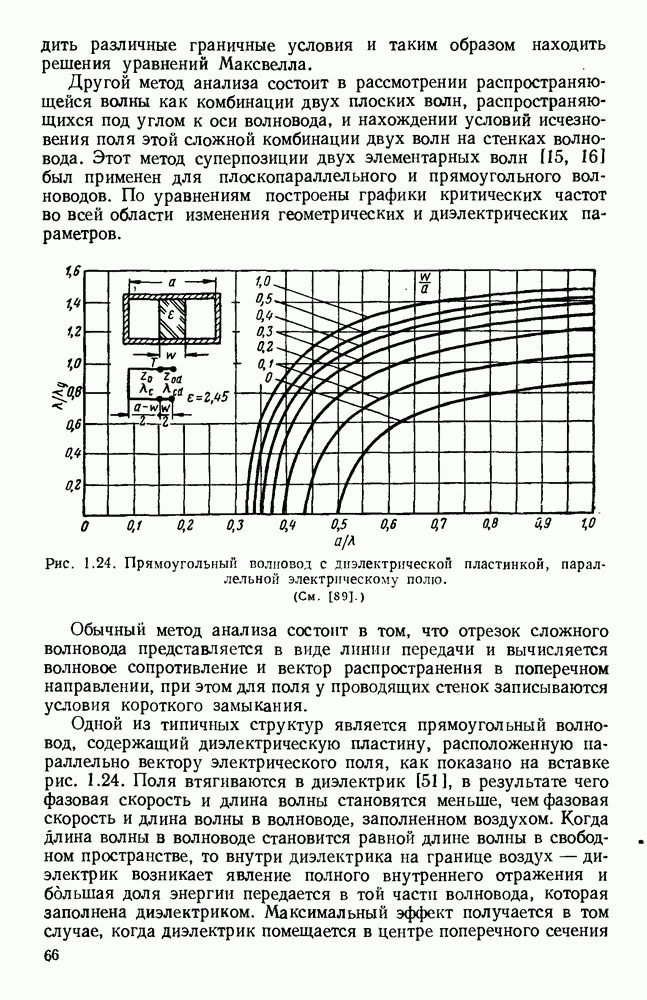
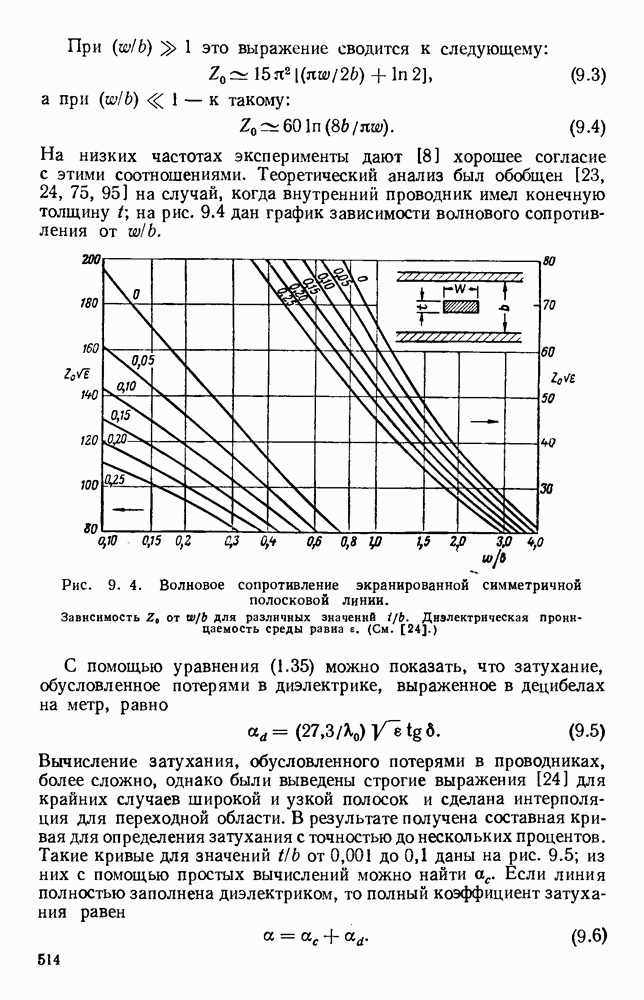
Рассматривавшиеся до сих пор волны относились к волнам типа ТМ, распространяющимся вдоль поверхности. В случае толстой диэлектрической пластины возможно, распространение волн высших видов; в зависимости от площади поперечного сечения волновода можно менять соотношение между долями энергии, текущими внутри диэлектрика и во внешней среде. Распространение электромагнитной энергии внутри диэлектрических пластин [296, 314] можно описать [261, 294, 341] с помощью уравнений Максвелла, однако критические частоты можно найти, исходя из представления волноводной волны в виде суммы двух плоских волн, симметрично распространяющихся под некоторыми углами [133].

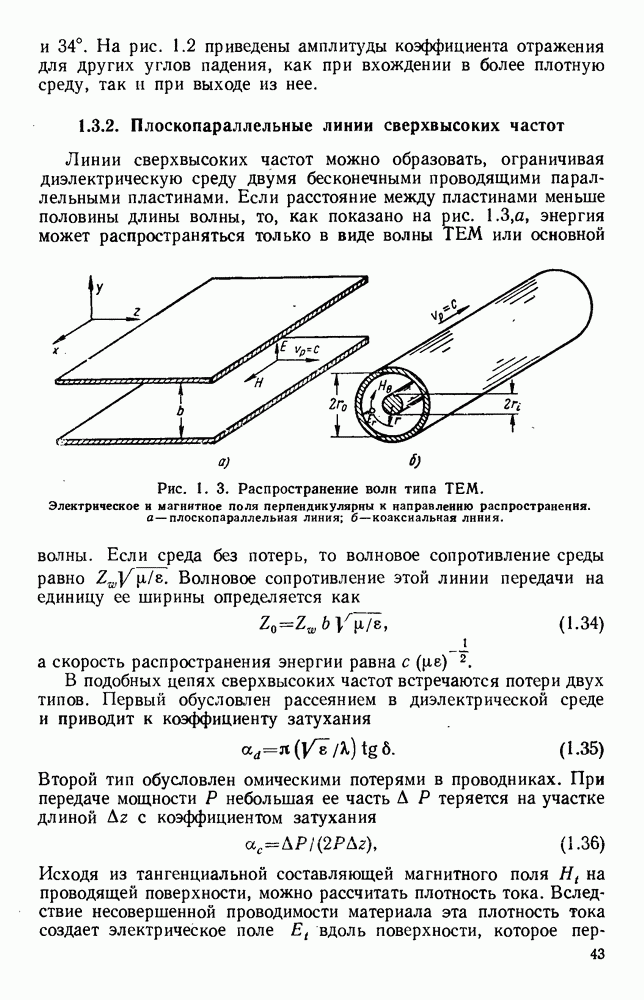
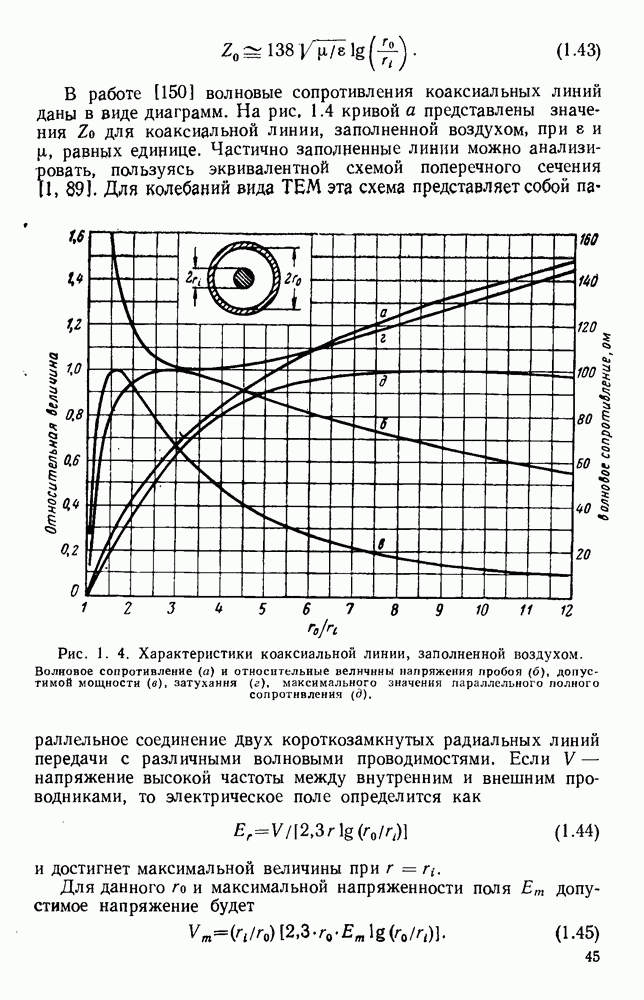
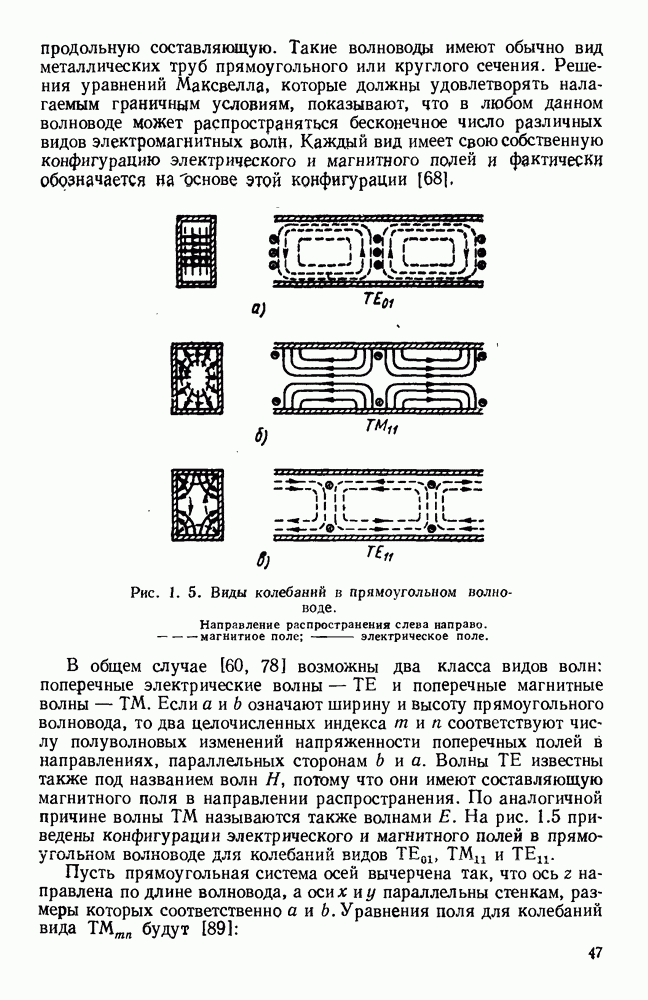
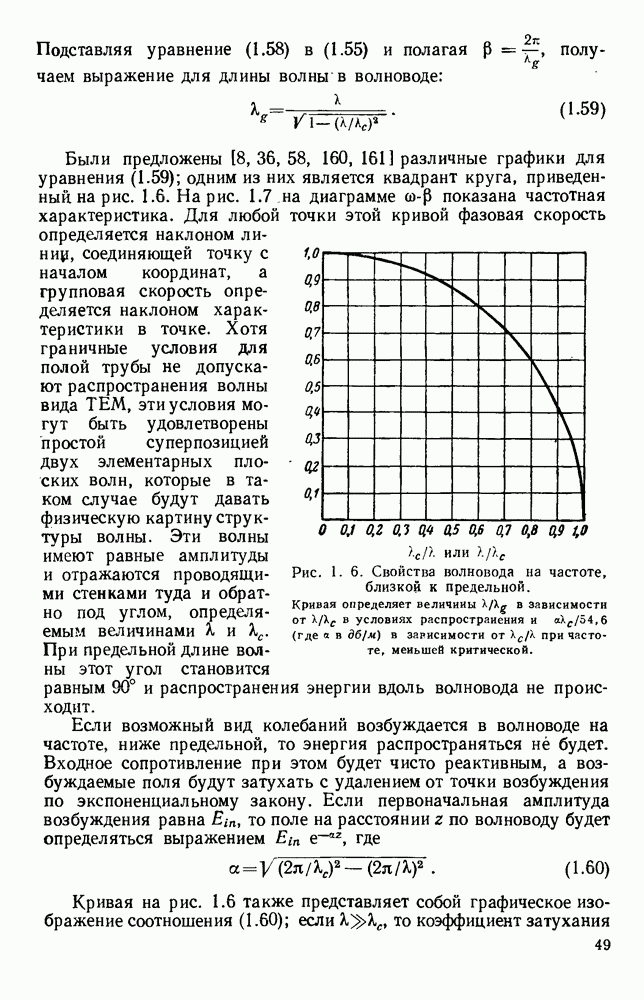
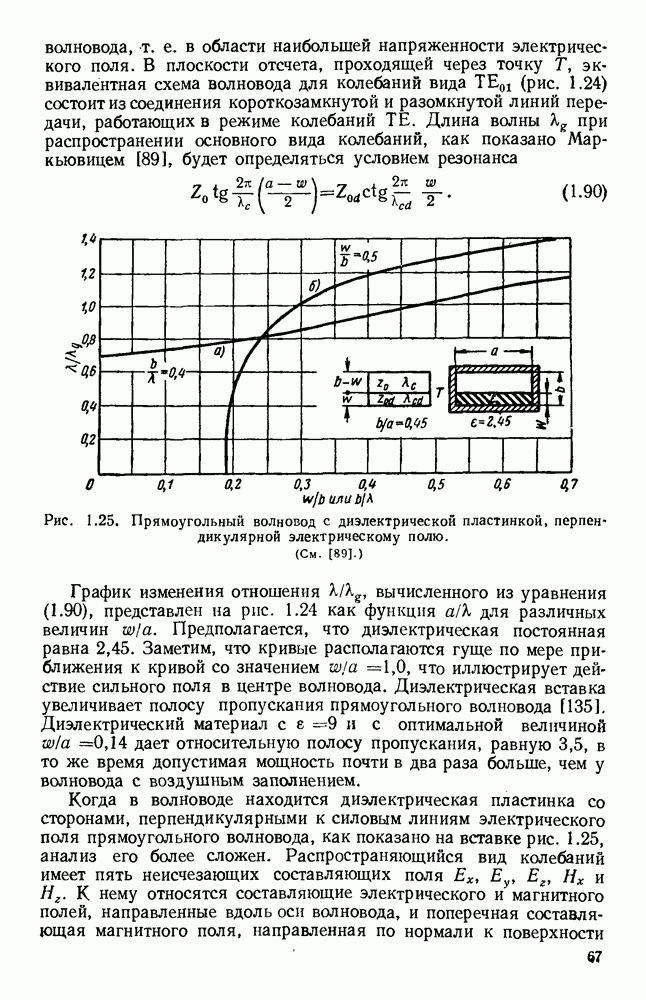
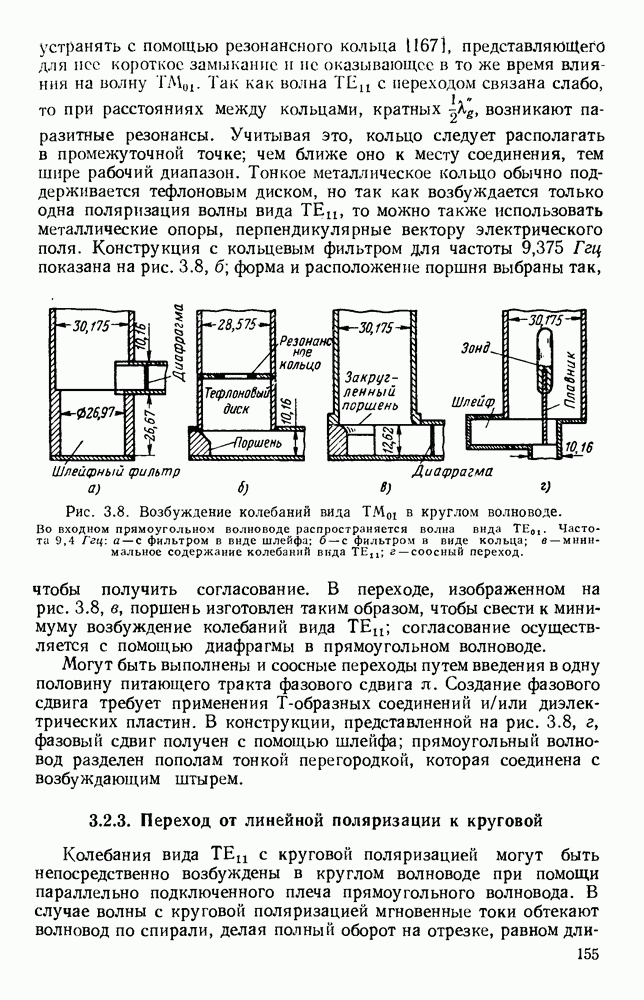
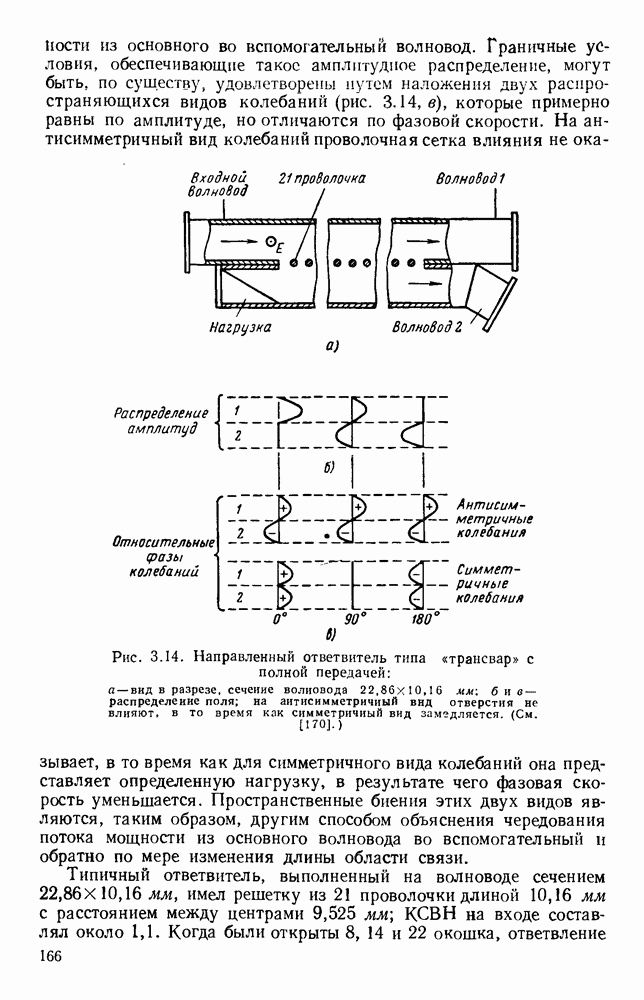
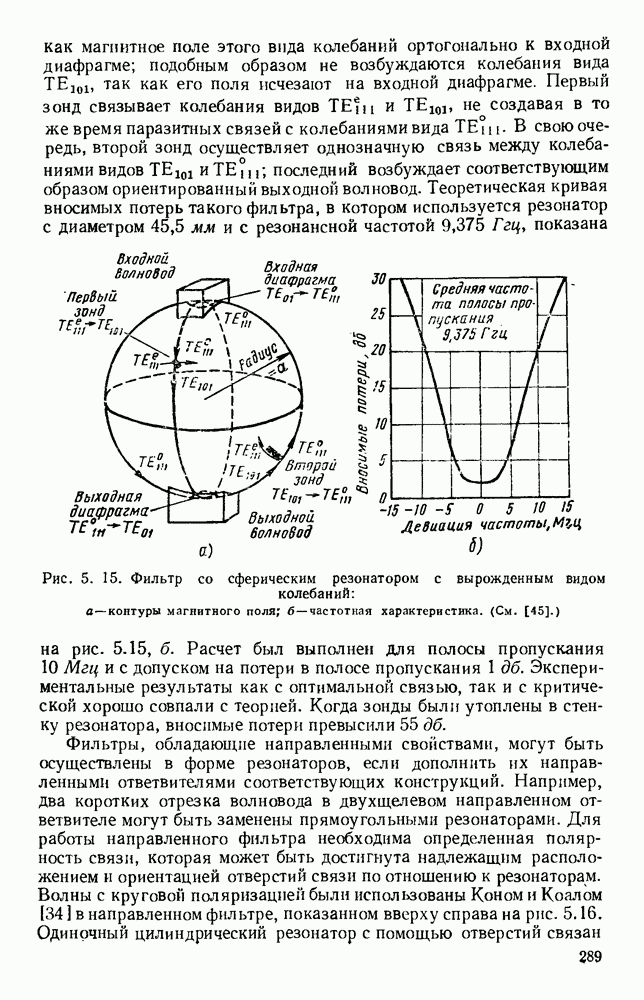
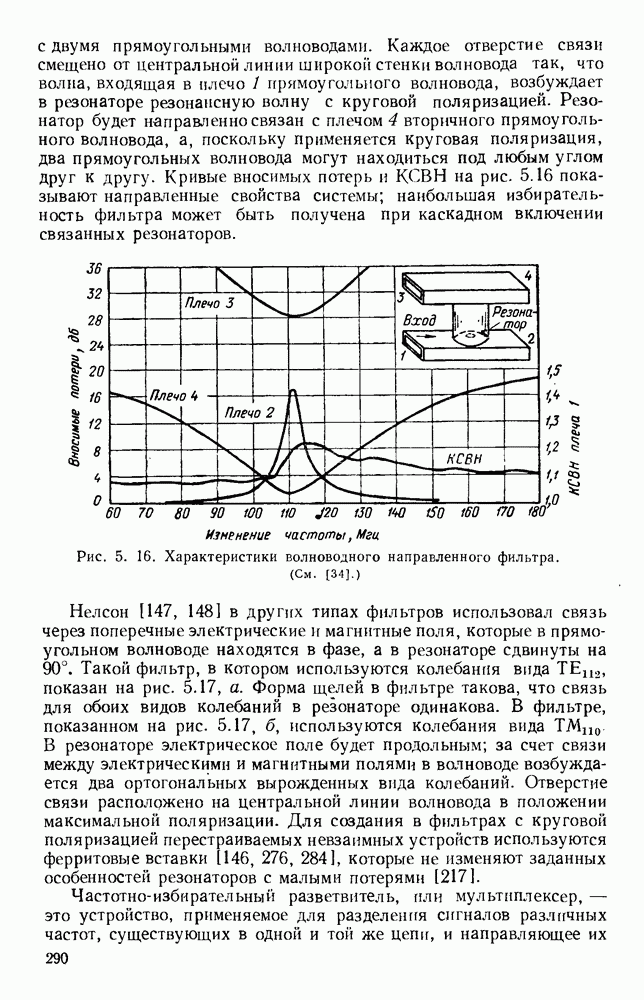
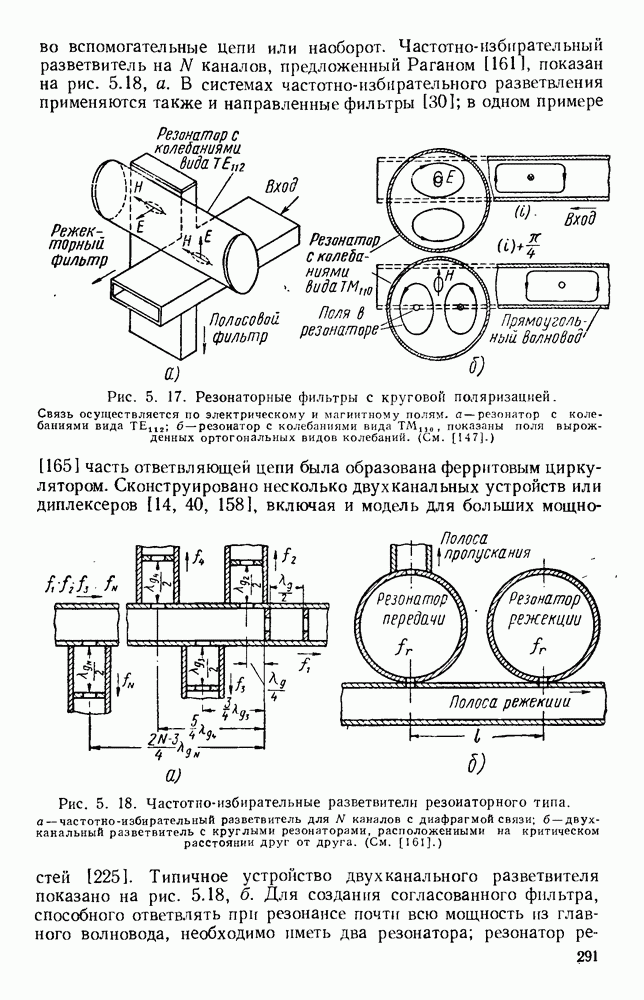
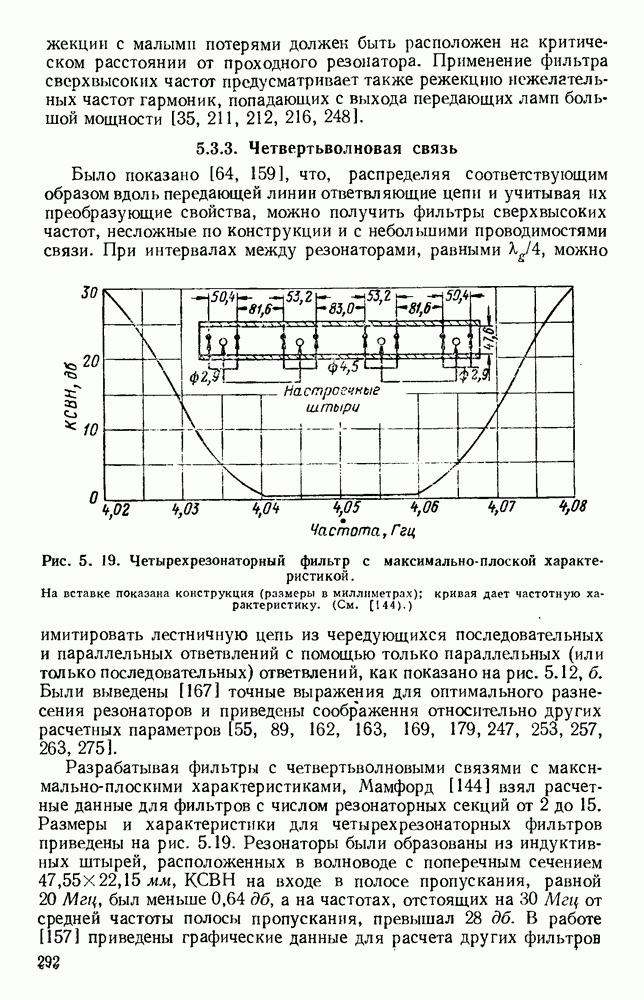
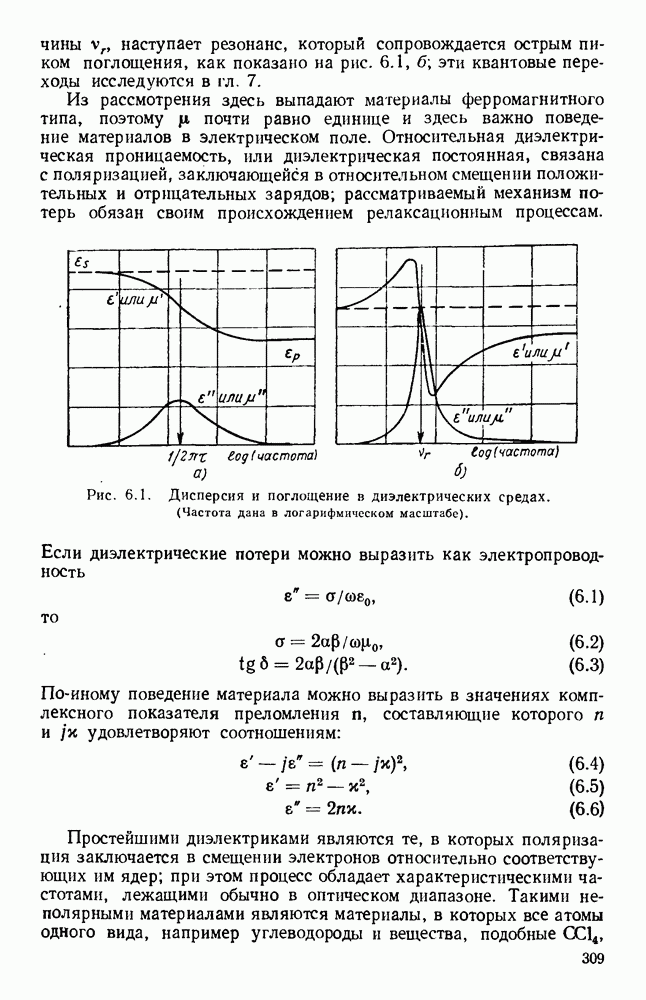
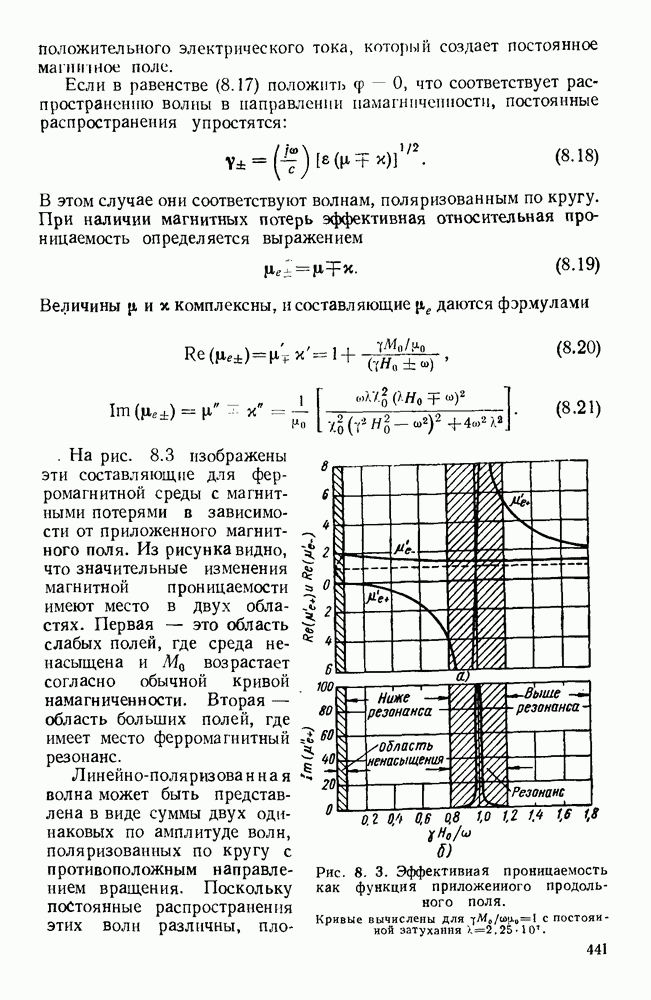
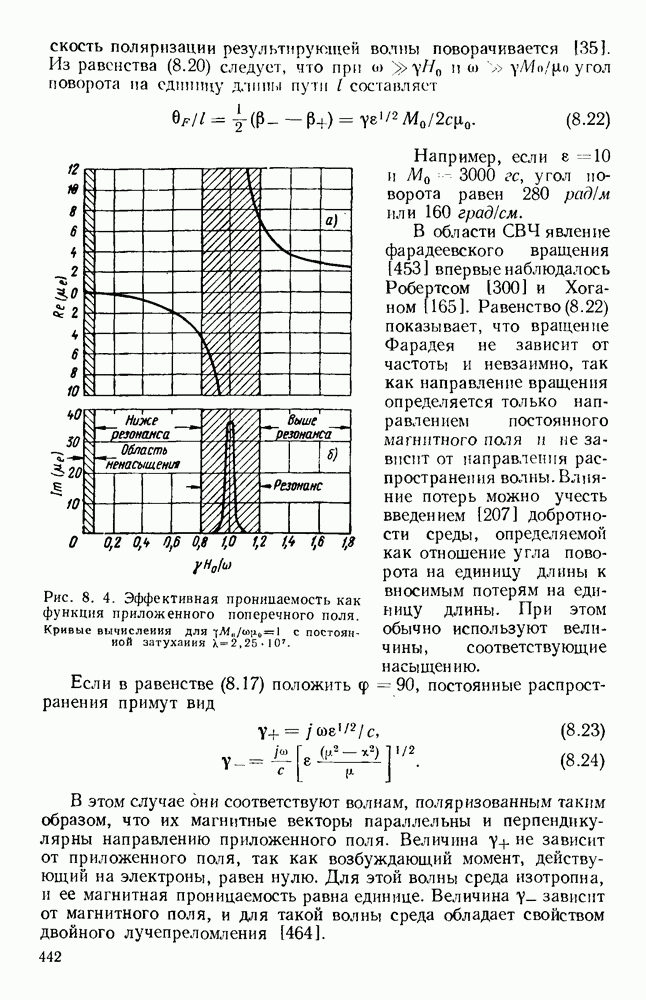
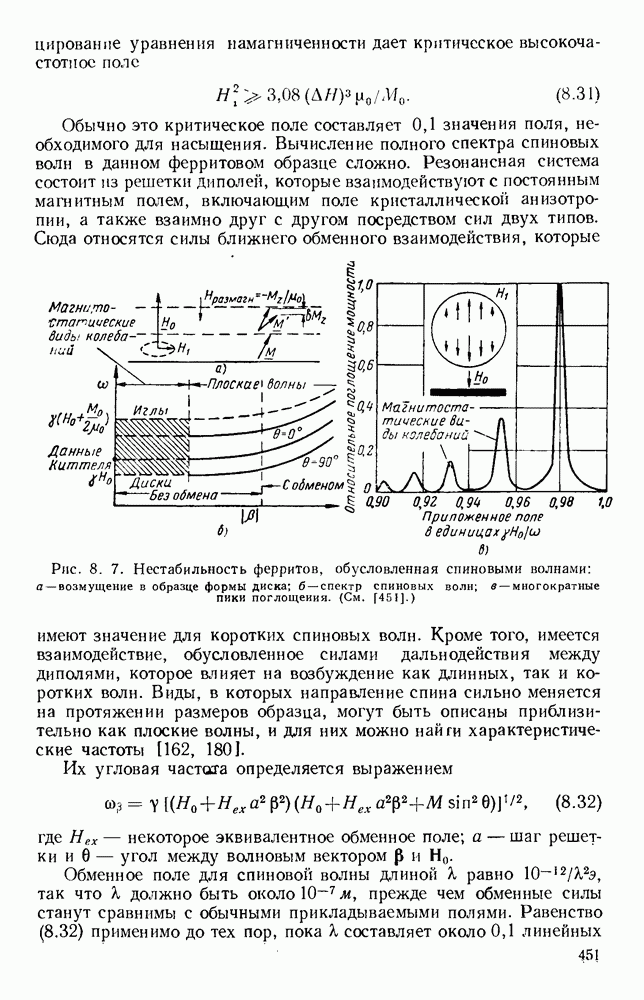
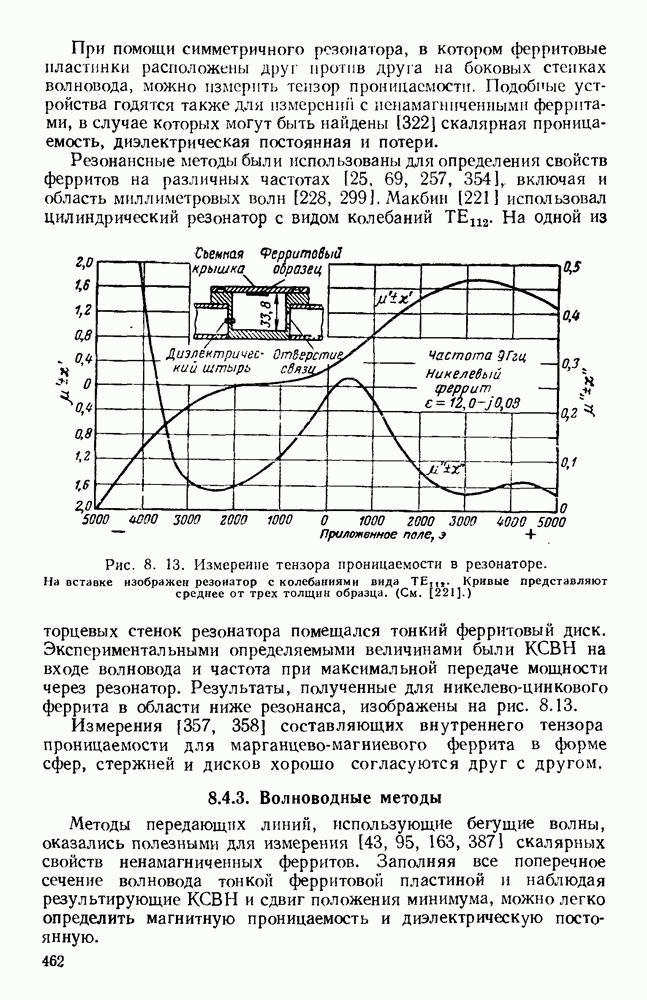
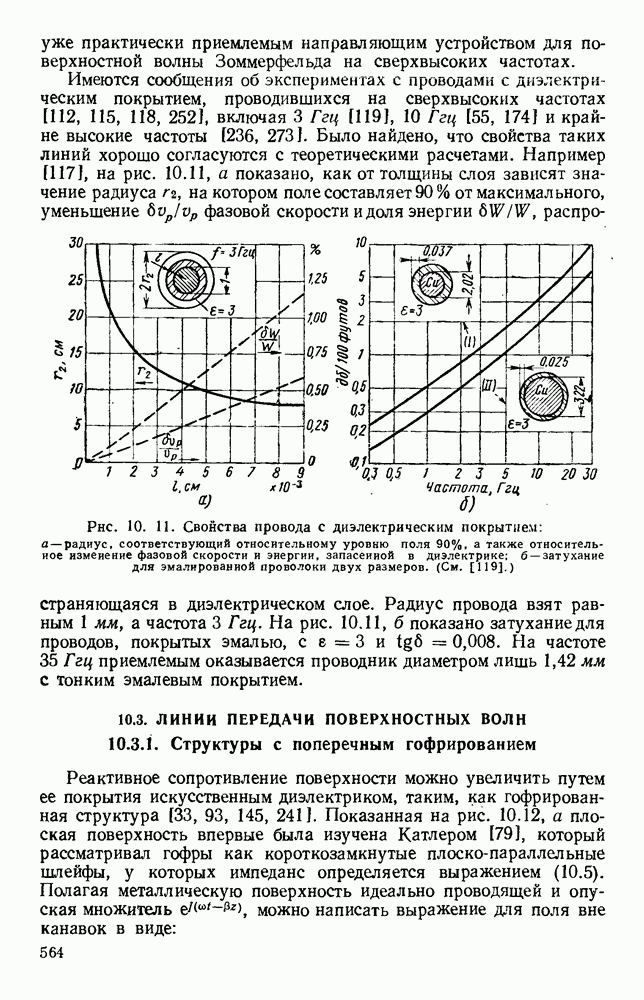
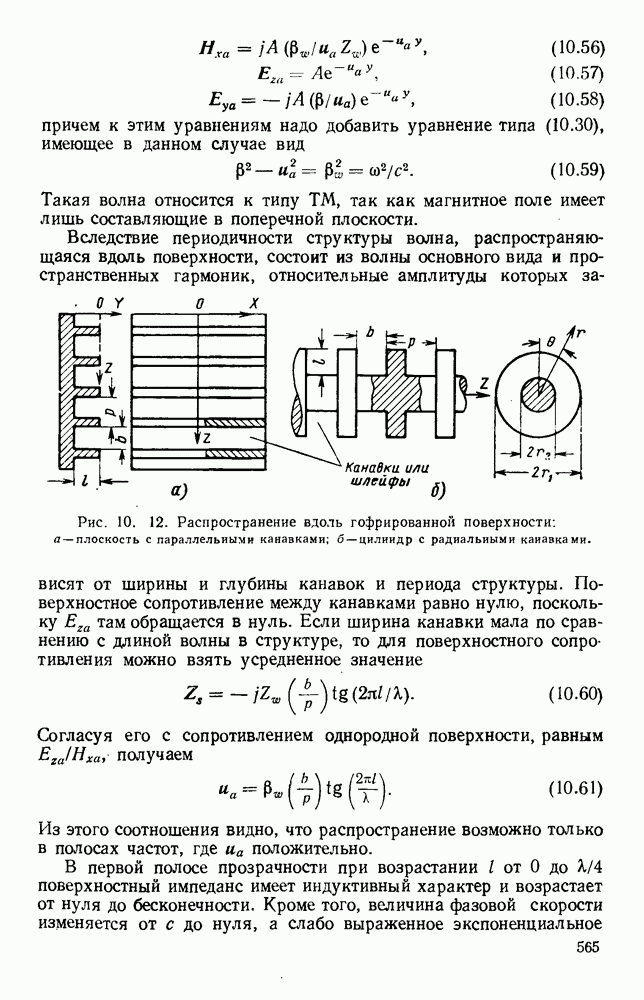
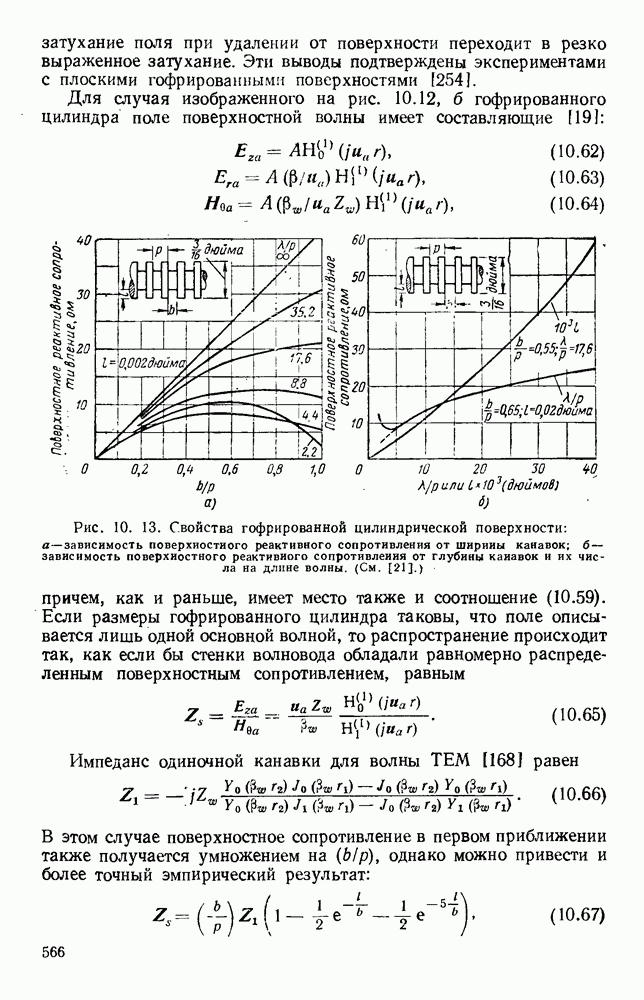
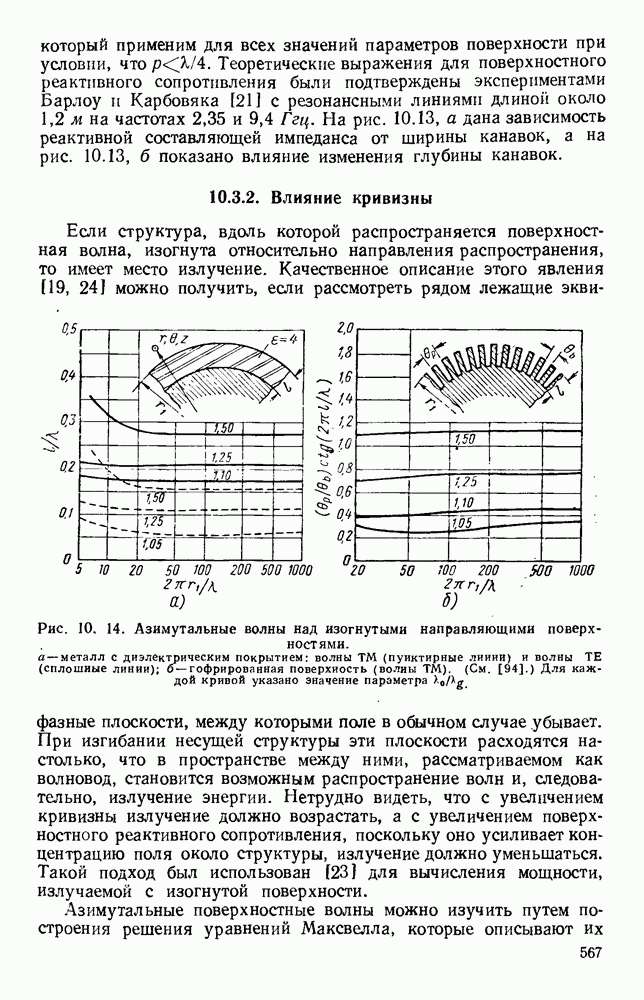
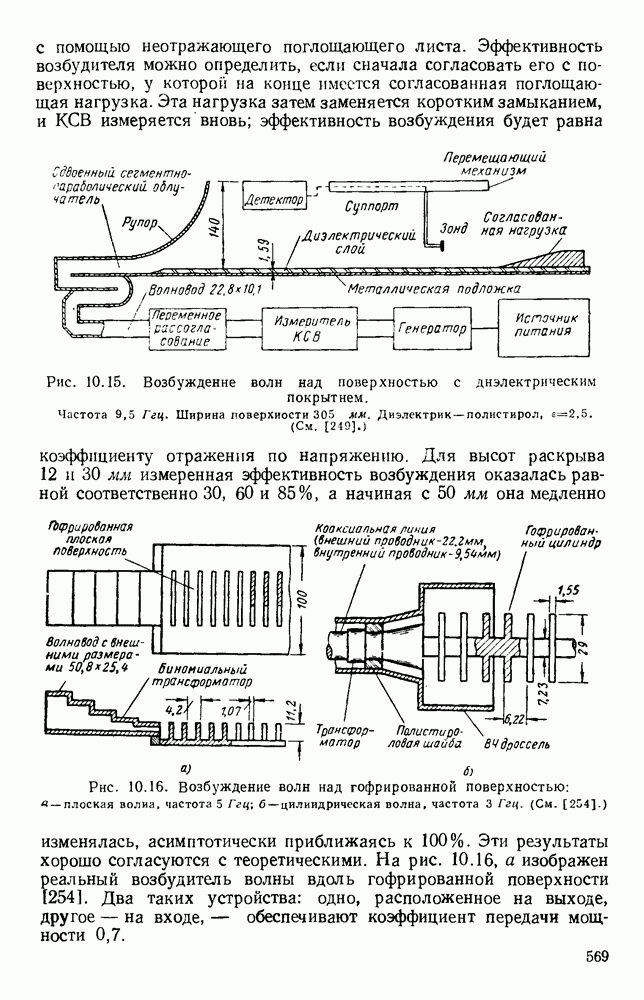
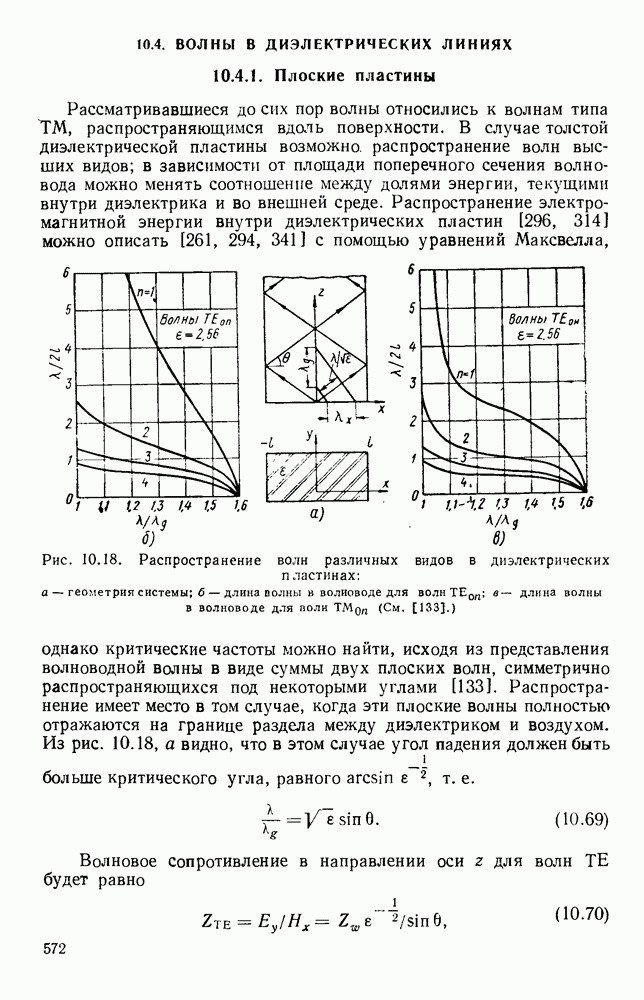
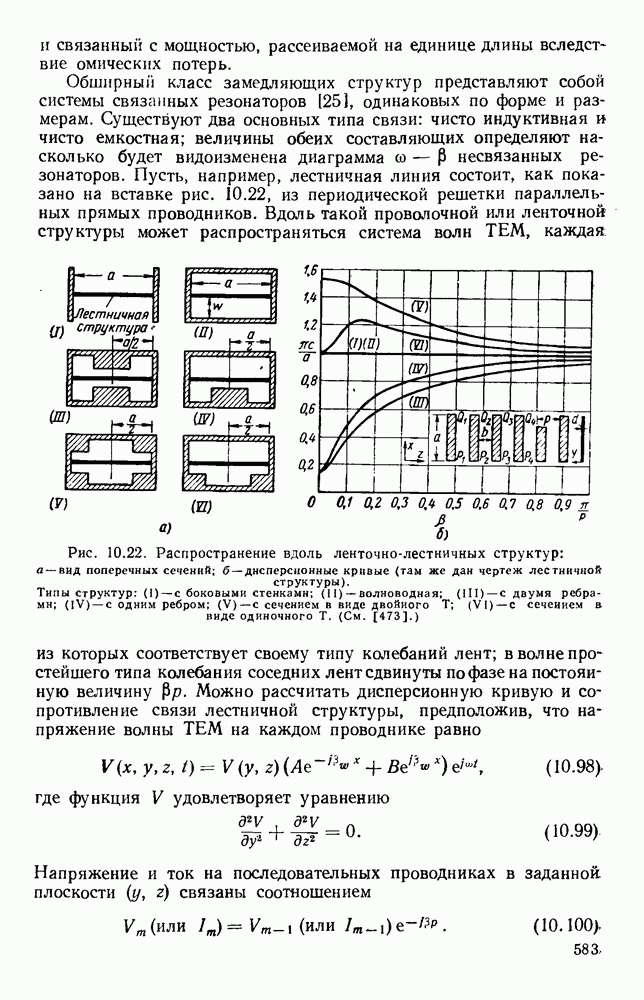
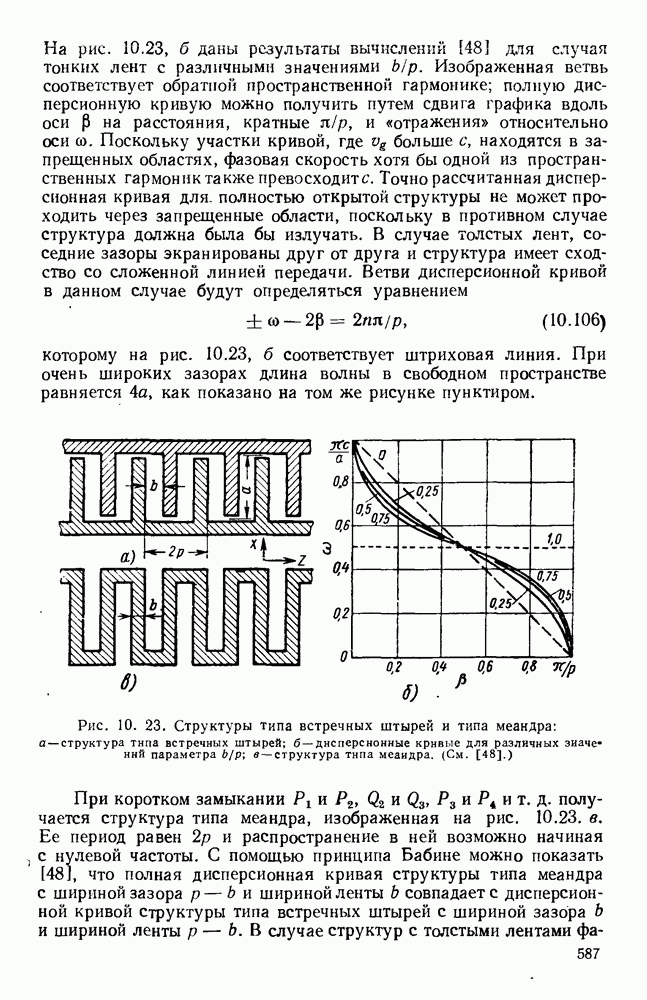
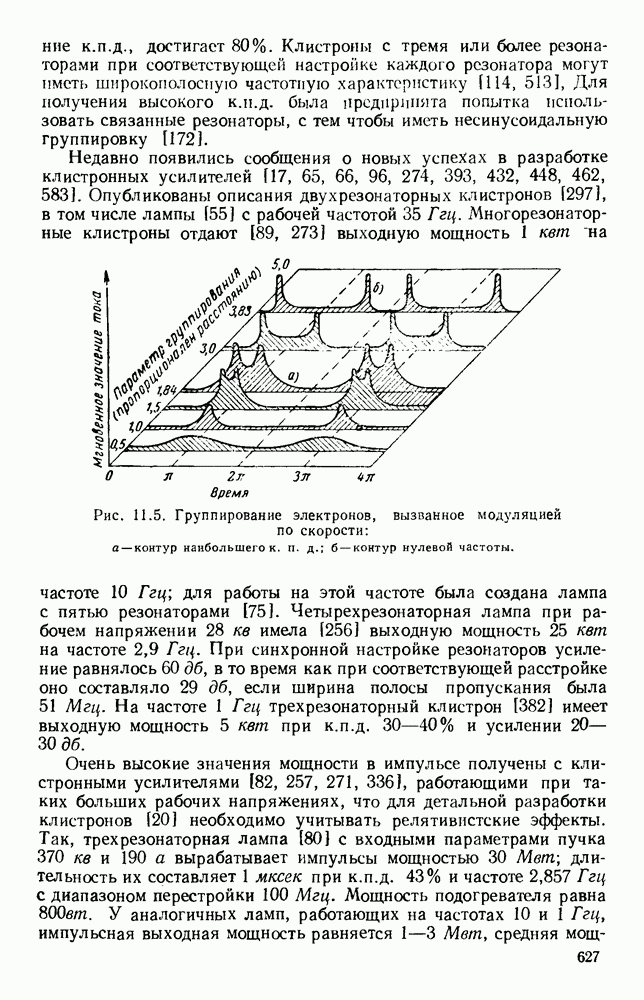
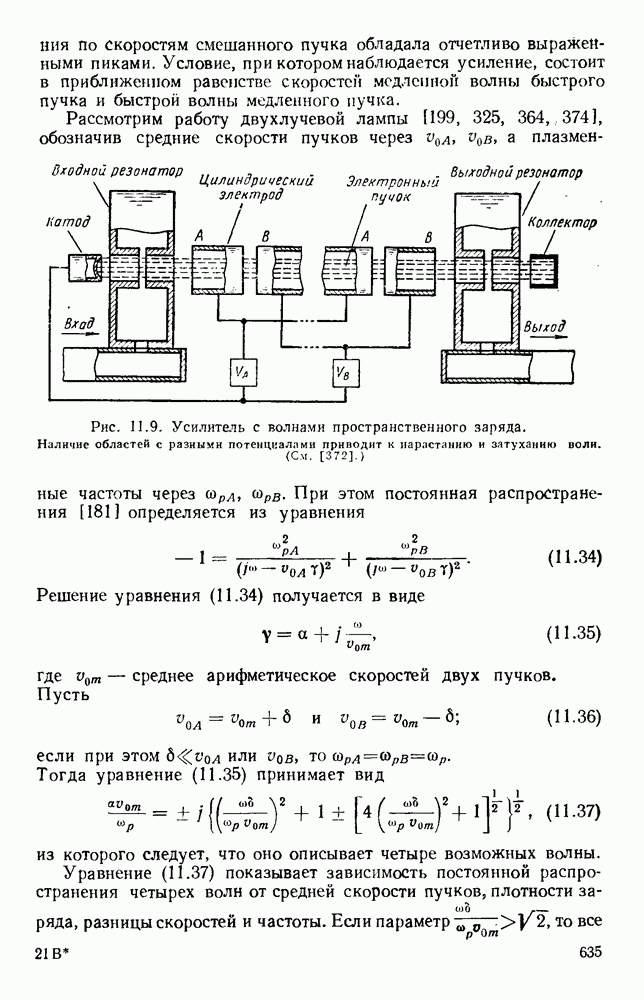
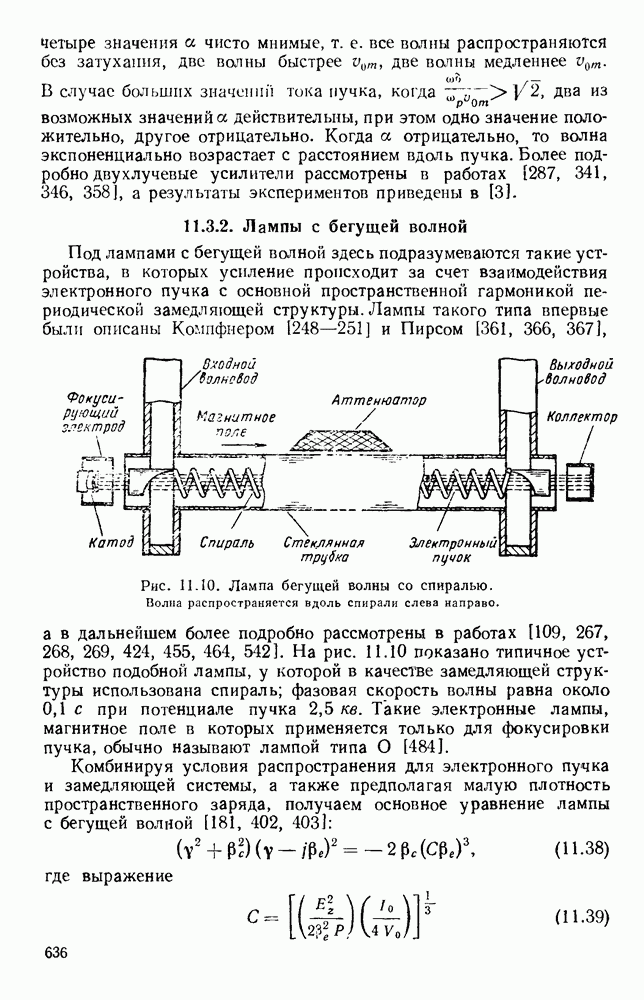
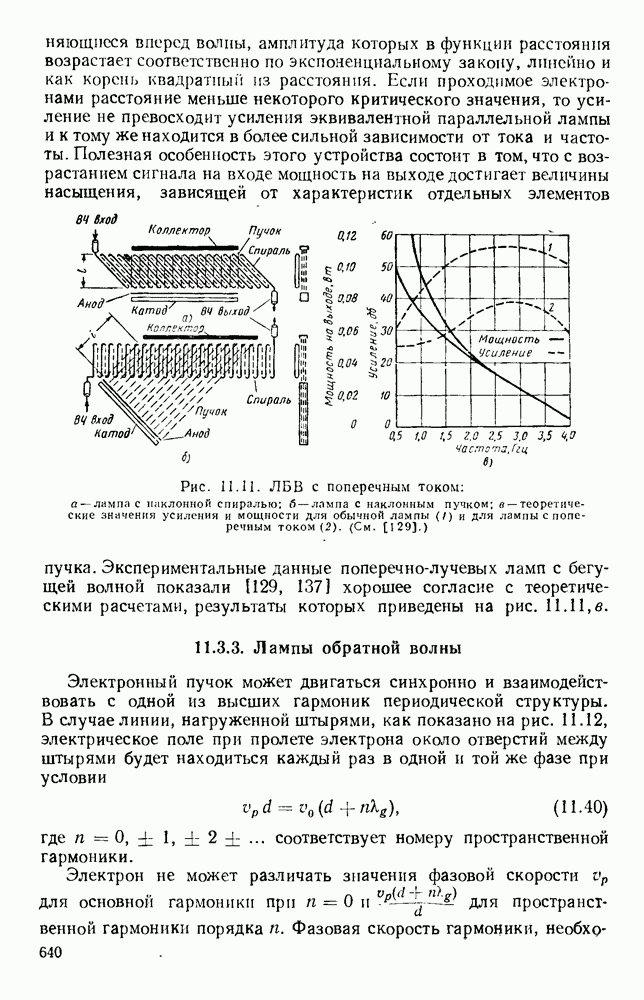
Рис. 10.18. Распространение волн различных видов в диэлектрических пластинах: а — геометрия системы; б - длина полны в волноводе для волн  ; в - длина волны в волноводе для полн
; в - длина волны в волноводе для полн  (См. [133].)
(См. [133].)
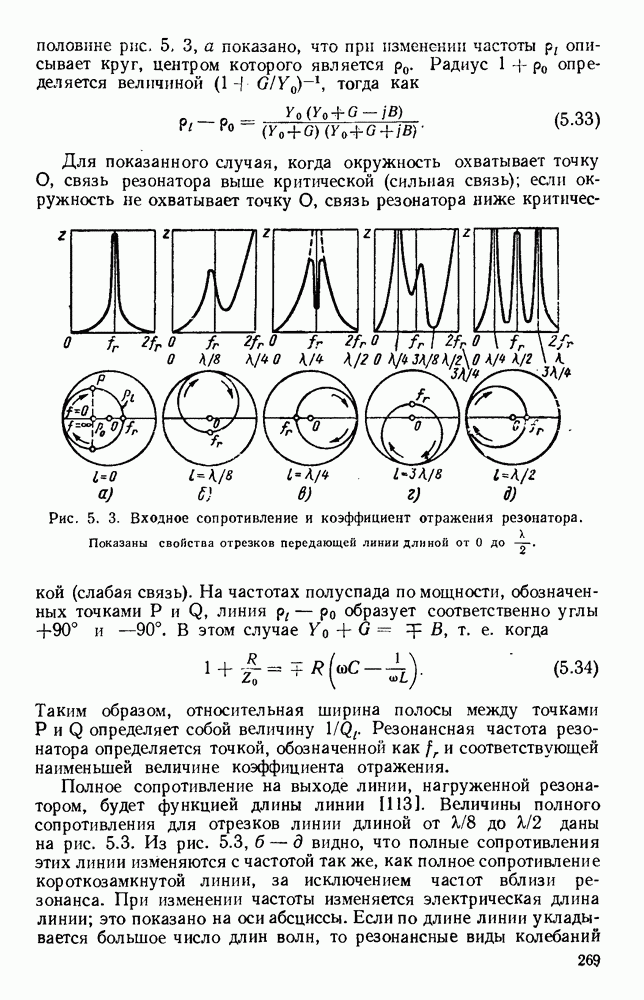
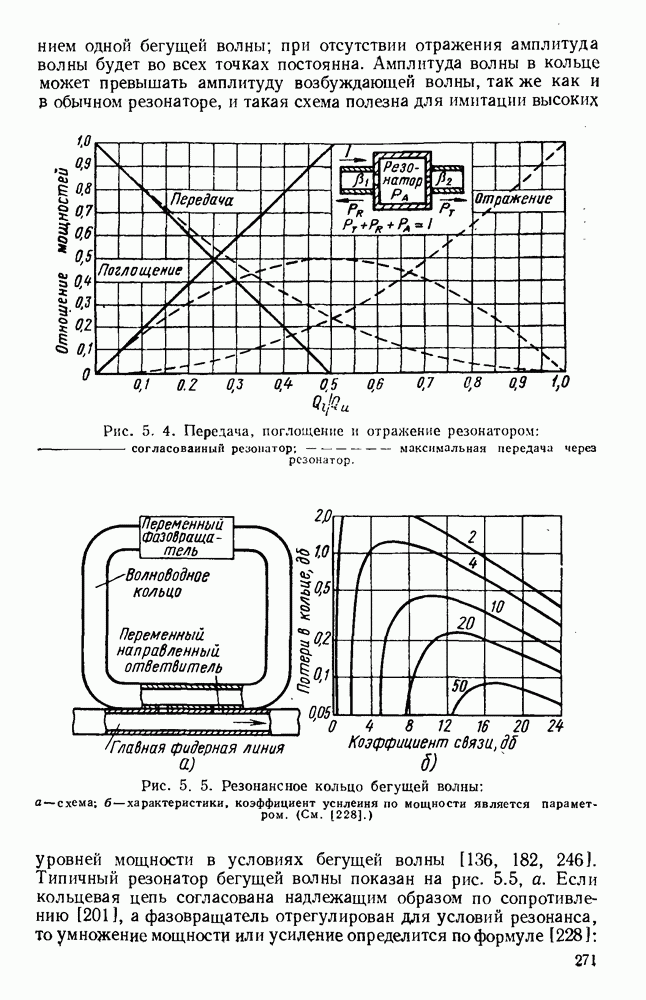
Распространение имеет место в том случае, когда эти плоские волны полностью отражаются на границе раздела между диэлектриком и воздухом.
Из рис. 10.18, а видно, что в этом случае угол падения должен быть больше критического угла, равного  т. е.
т. е.

Волновое сопротивление в направлении оси z для волн ТЕ будет равно

а для волн ТМ

Для поперечной компоненты поля, параллельной поверхности раздела, коэффициент отражения (в случае компоненты  и волн типа
и волн типа  равен
равен

 а для компоненты
а для компоненты  и волн типа ТМ он имеет вид
и волн типа ТМ он имеет вид

Мнимые члены в выражениях (10.72) и (10.73) соответствуют экспоненциальному затуханию полей вне диэлектрика. Постоянная распространения в направлении оси х вещественна и равна

Модули коэффициентов отражения всегда равны единице, что приводит к возникновению в диэлектрике поперечных стоячих волн с косинусоидальным распределением для видов с нечетными номерами и с синусоидальным распределением для видов с четными номерами. Электрическая длина  стоячей волны от средней плоскости до границы диэлектрика как в случае волн
стоячей волны от средней плоскости до границы диэлектрика как в случае волн  так и в случае волн
так и в случае волн  равна
равна

Если  длина поперечной волны, то согласно рис. 10.18, а
длина поперечной волны, то согласно рис. 10.18, а 

и, следовательно,

Из уравнений (10.76) и (10.77) получаем

Для критической частоты  откуда
откуда

Таким образом, при заданном значении  из уравнения (10.69) можно найти
из уравнения (10.69) можно найти  , а из уравнения (10.75) можно найти
, а из уравнения (10.75) можно найти  после чего из уравнения (10.78) можно определить
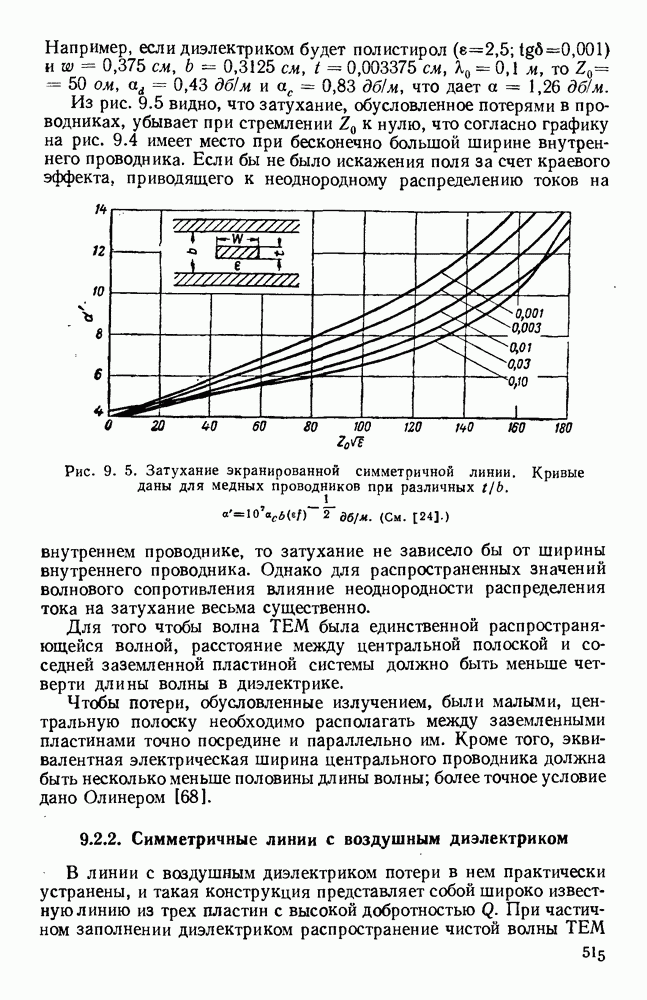
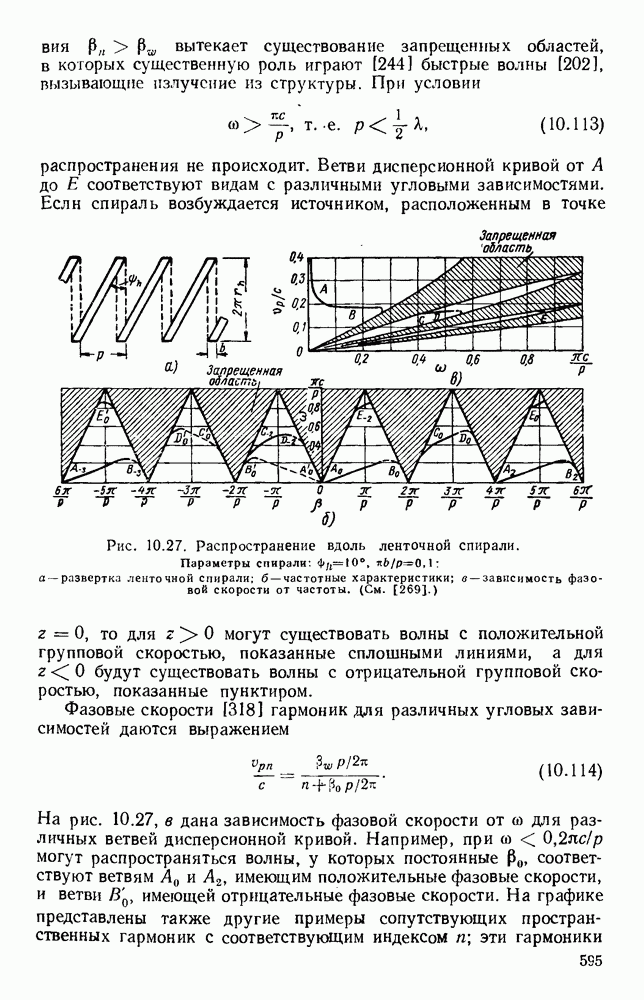
после чего из уравнения (10.78) можно определить  На рис. 10.18, б и в даны зависимости
На рис. 10.18, б и в даны зависимости  от
от  для полистирола с
для полистирола с  и различных волн типов ТЕ и ТМ. Аналогичным образом, используя вместо декартовой системы координат другие системы, можно рассмотреть случаи для проводников с диэлектрическим покрытием или для диэлектрических труб круглого и других сечений.
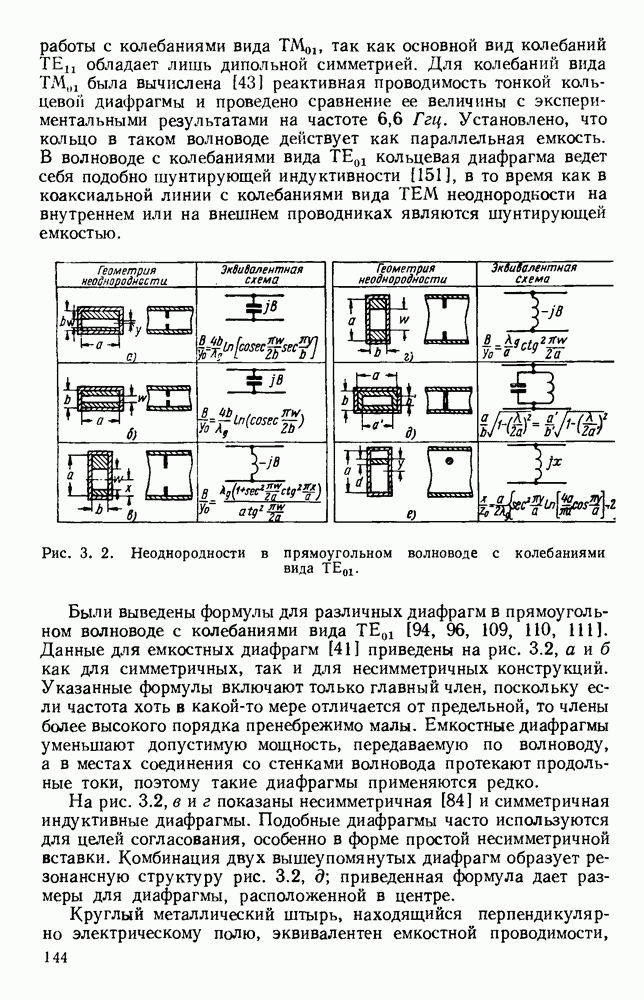
и различных волн типов ТЕ и ТМ. Аналогичным образом, используя вместо декартовой системы координат другие системы, можно рассмотреть случаи для проводников с диэлектрическим покрытием или для диэлектрических труб круглого и других сечений.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
- 1.3.3. Коаксиальные линии
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
- 1.4.2. Круглые волноводы
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
- 1.5.2. Гребневые волноводы
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
- 2.1.2. Круговая диаграмма
- 2.1.3. Широкополосное согласование
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
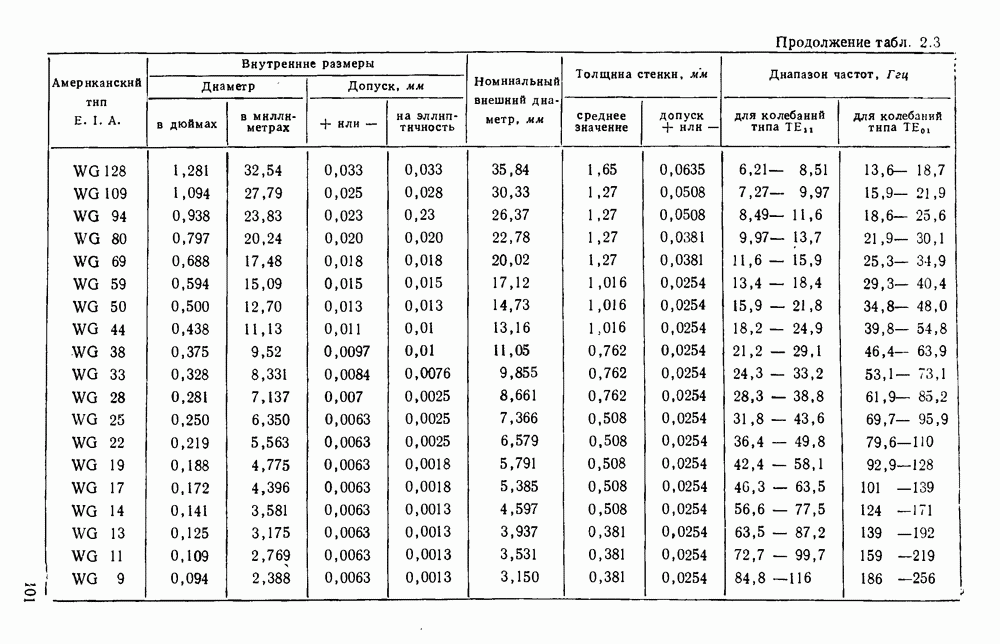
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
- 2.3.1. Прямоугольные волноводы
- 2.3.2. Круглые волноводы
- 2.3.3. Широкополосные и компактные волноводы
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
- 2.4.2. Контактные прокладки и дроссели
- 2.4.3. Крепежные и зажимные устройства
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
- 2.6.1. Изгибы, уголки и скрутки
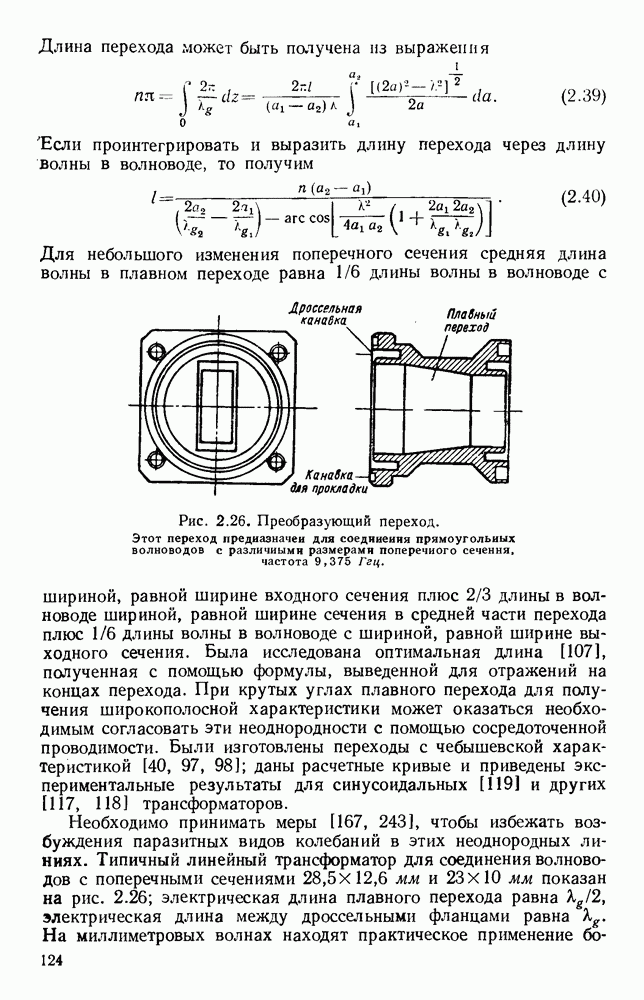
- 2.6.2. Переходы и преобразователи
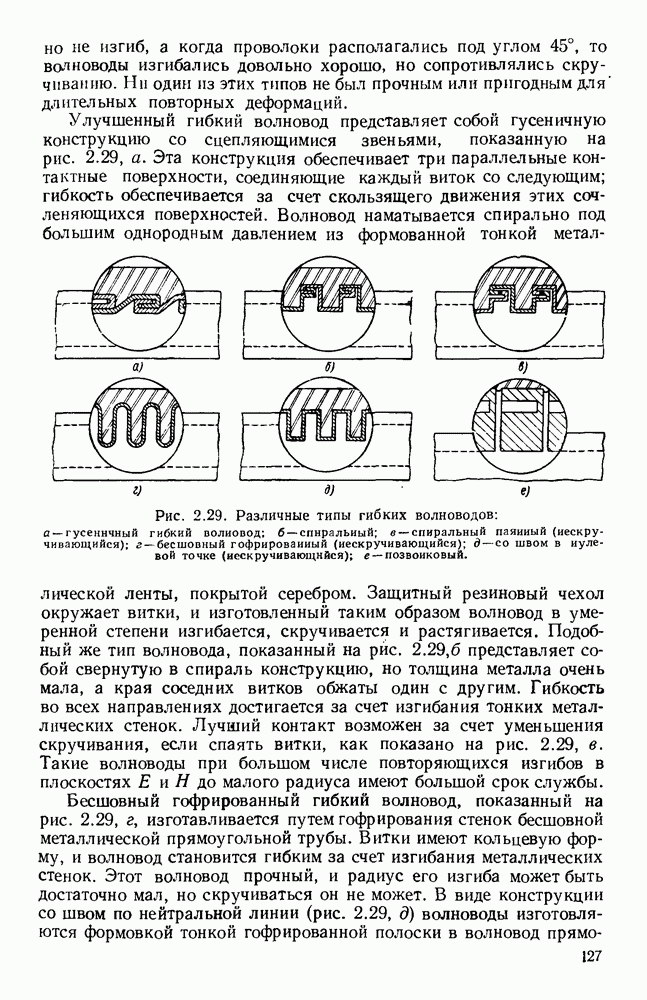
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
- 3.2.3. Переход от линейной поляризации к круговой
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
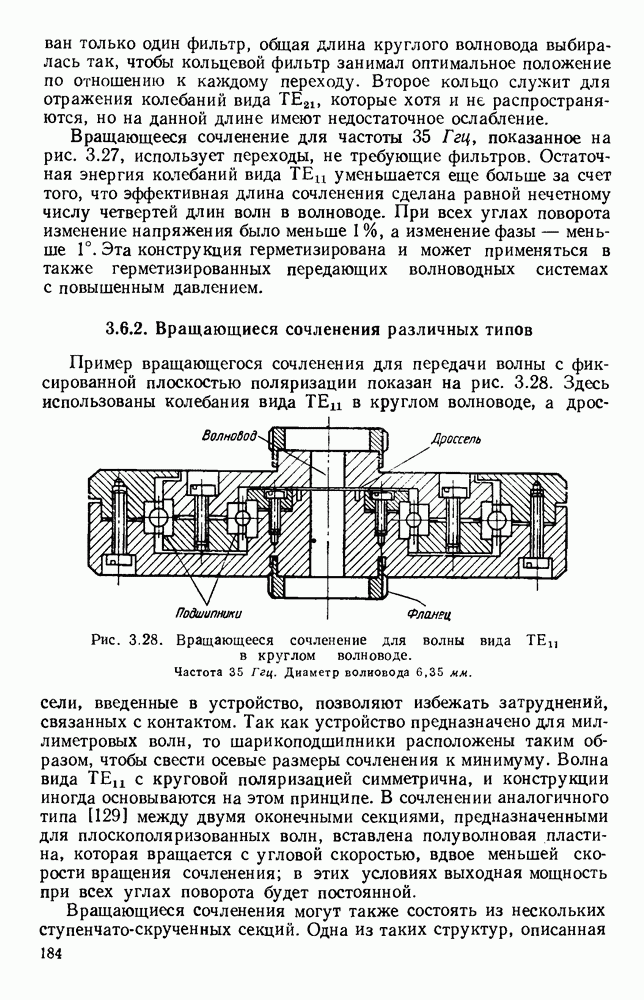
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
- 3.6.2. Вращающиеся сочленения различных типов
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
- 3.7.1. Механические переключатели с ручным управлением
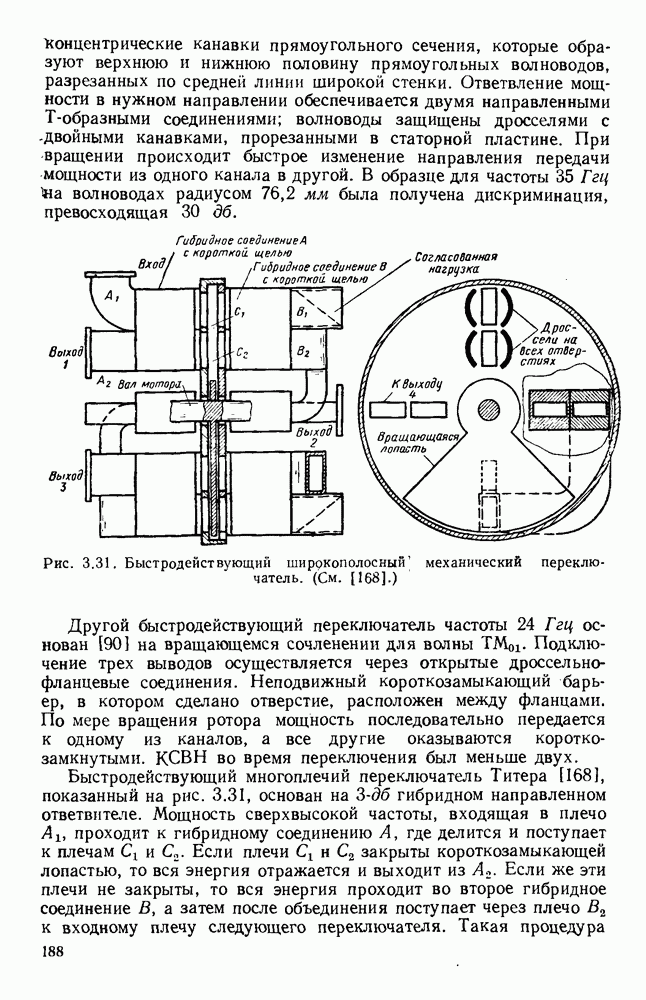
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
- 5.2.1. Волномеры с объемными резонаторами
- 5.2.2. Волноводные интерферометры
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
- 5.3.2. Связанные резонаторы
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
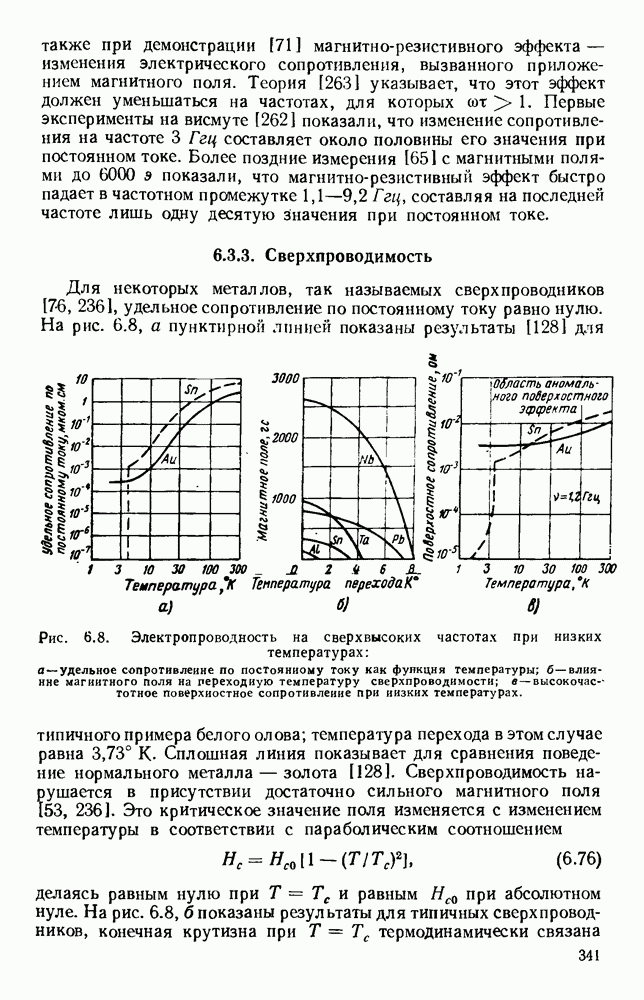
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
- 7.1.2. Форма линии и интенсивность
- 7.1.3. Сверхтонкая структура
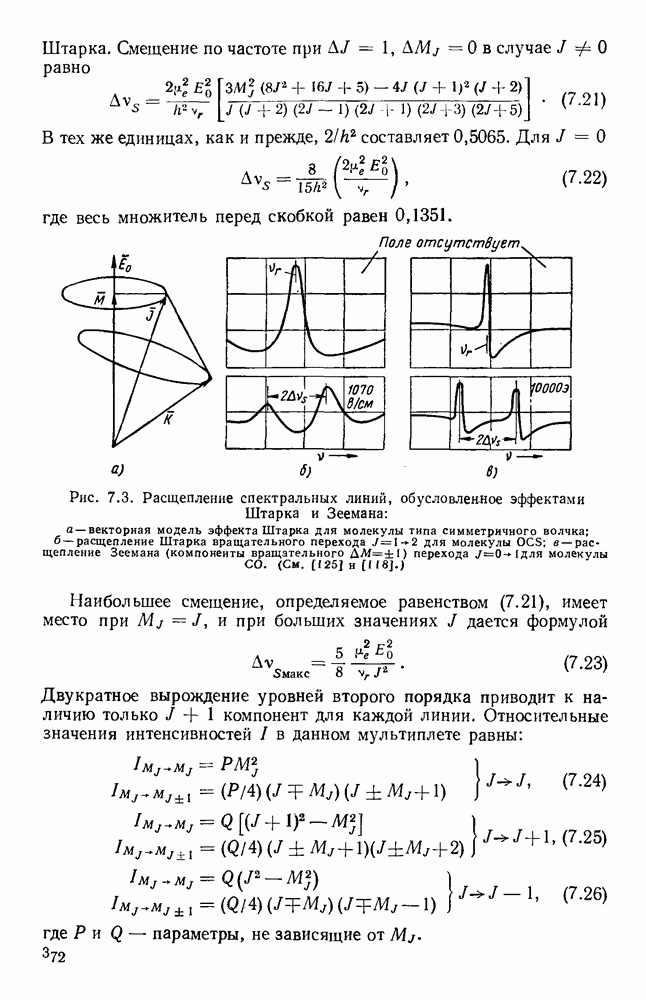
- 7.1.4. Явления Штарка и Зеемана
- 7.2. СПЕКТРОМЕТРЫ
- 7.2.2. Поглощающие ячейки
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
- 7.3.4. Времена релаксации
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
- 8.3.3. Ферритовые устройства в качестве элементов схем
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
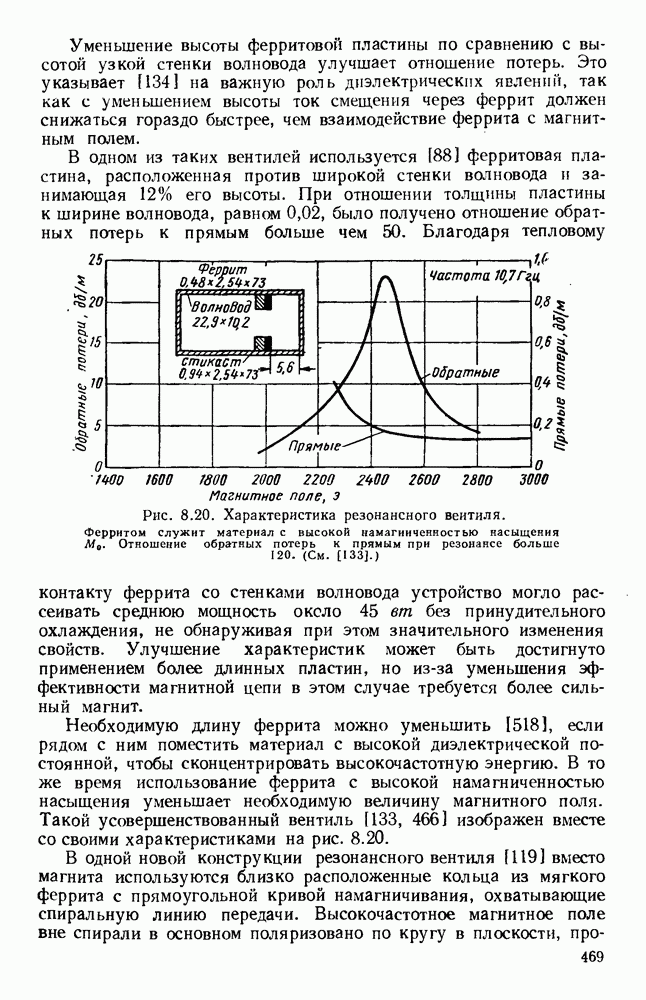
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
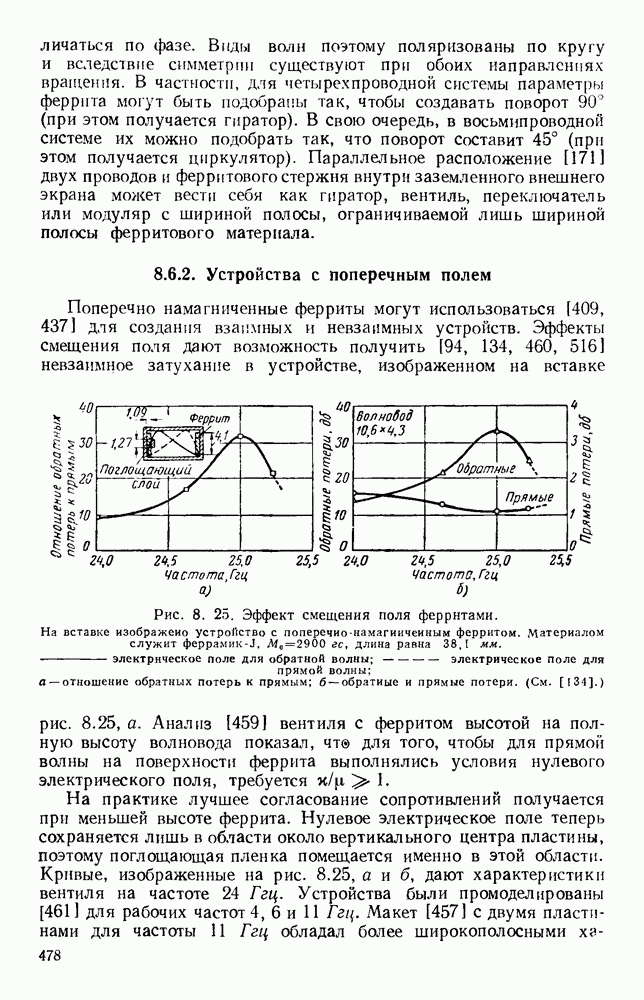
- 8.6.2. Устройства с поперечным полем
- 8.6.3. Прочие узлы
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.2.1. Линии типа «диэлектрических сэндвичей»
- 9.2.2. Симметричные линии с воздушным диэлектриком
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
- 9.4.2. Переходные устройства
- 9.4.3. Узлы полосковых систем
- 9.5. ЦЕПИ И СИСТЕМЫ
- 9.5.3. Частотные фильтры
- 9.5.4. Цепи питания антенн
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
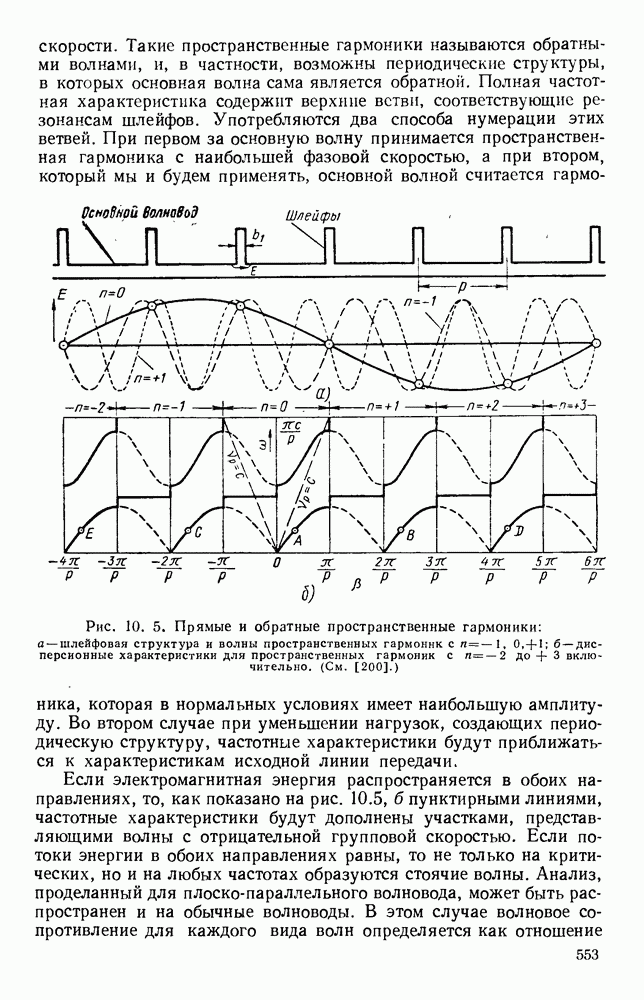
- 10.1.2. Пространственные гармоники
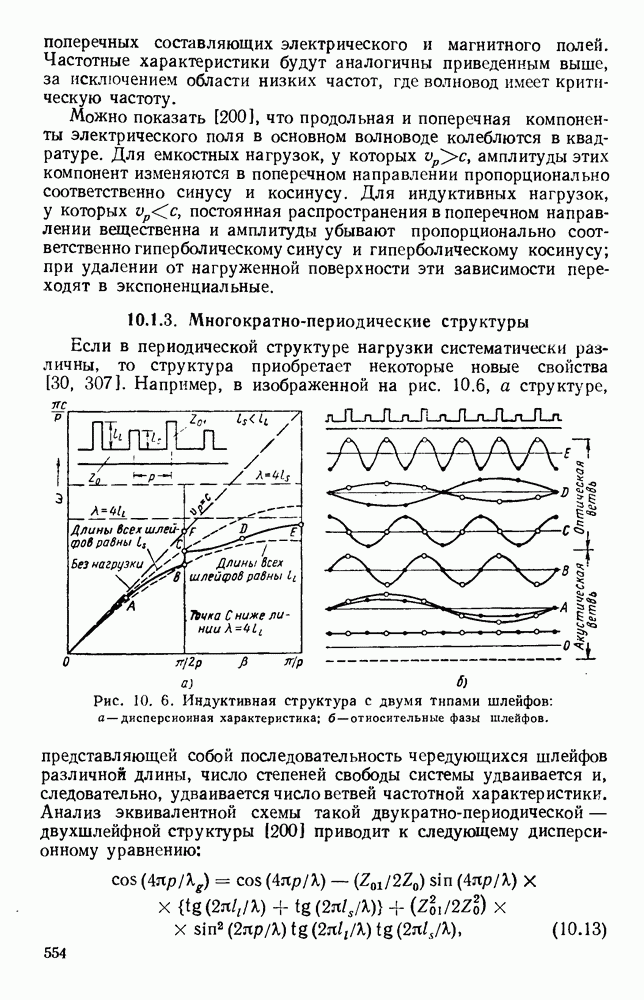
- 10.1.3. Многократно-периодические структуры
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
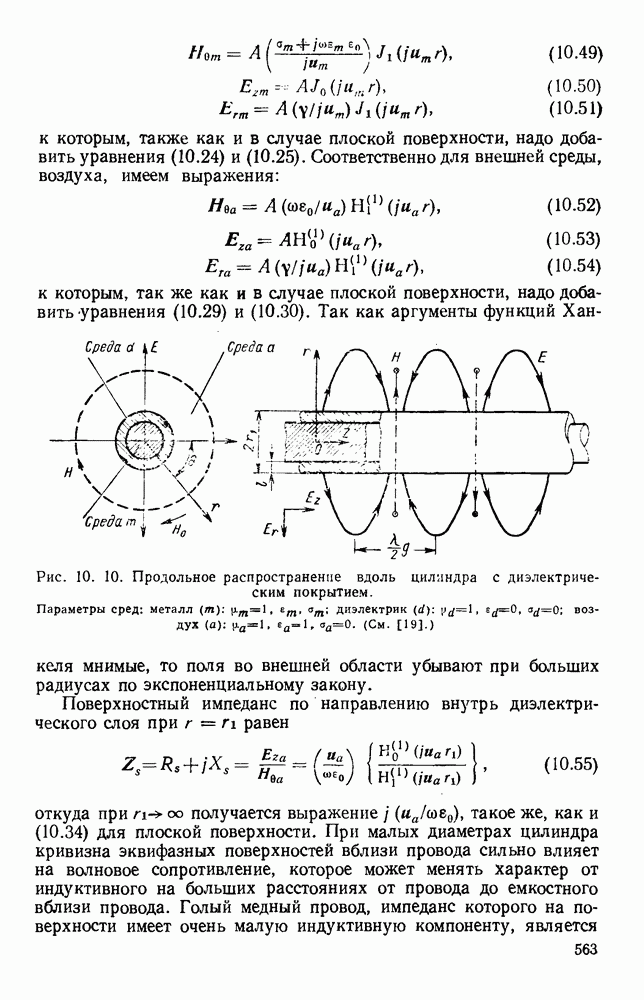
- 10.2.3. Продольные цилиндрические волны
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
- 12.2. МАГНЕТРОНЫ
- 12.2.2. Резонаторные системы
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
- 12.2.4. Рабочие характеристики
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
- 13.1.2. Типы дифракции
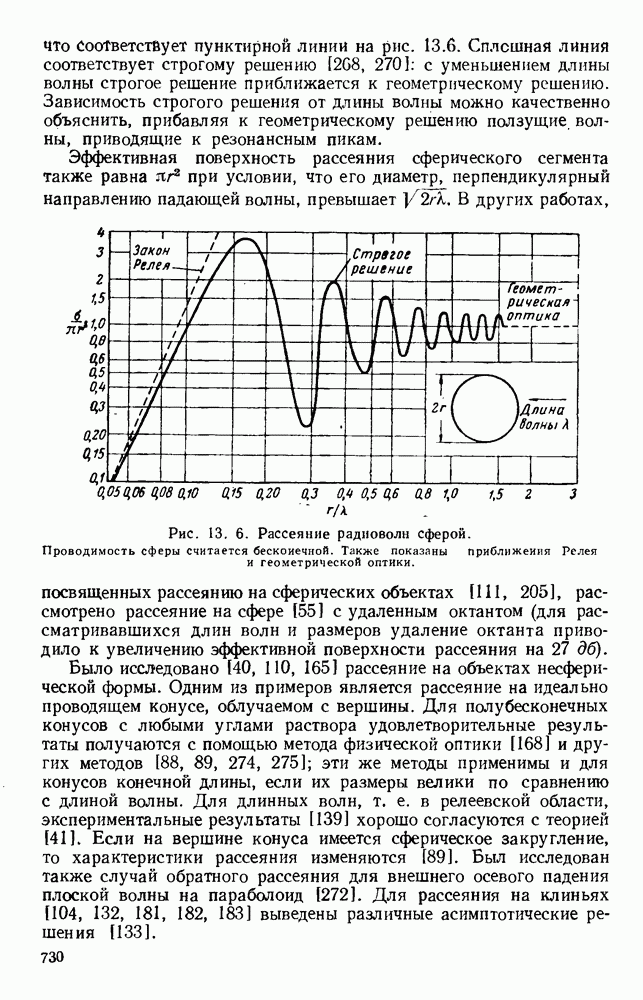
- 13.1.3. Рассеяние
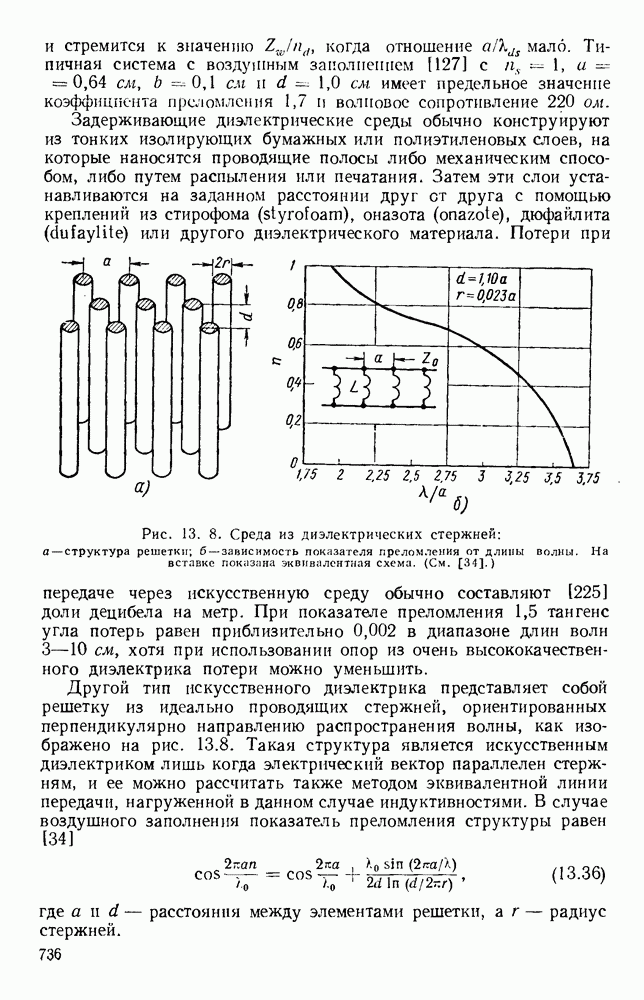
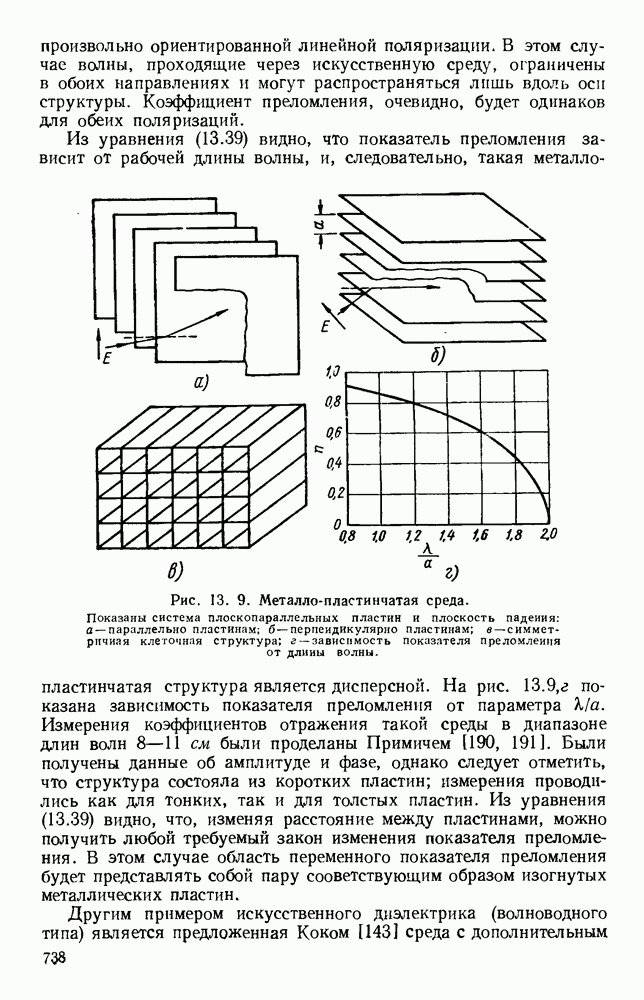
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
- 13.2.2. Структуры волноводного типа
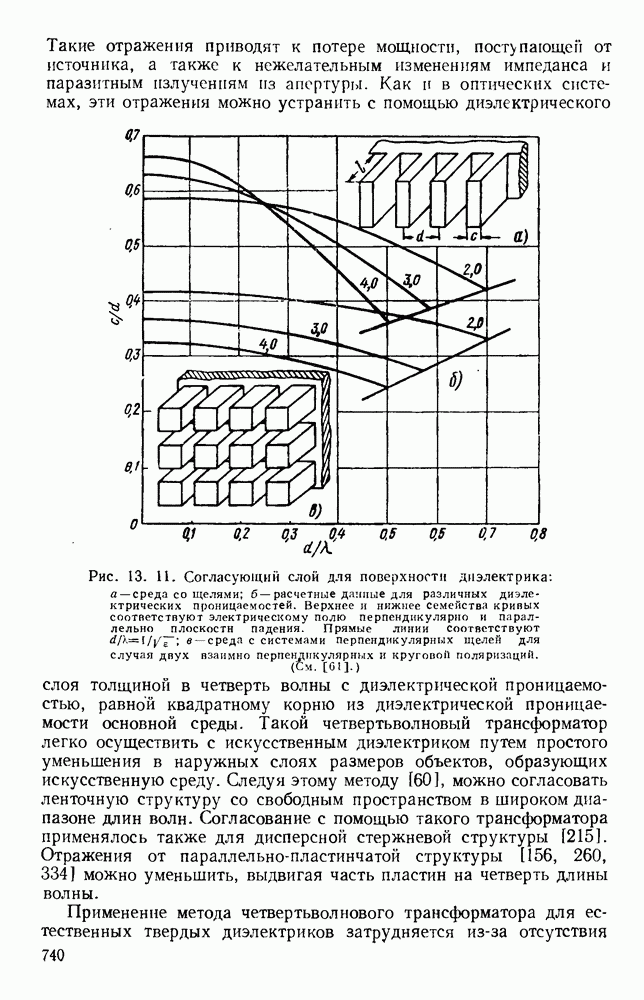
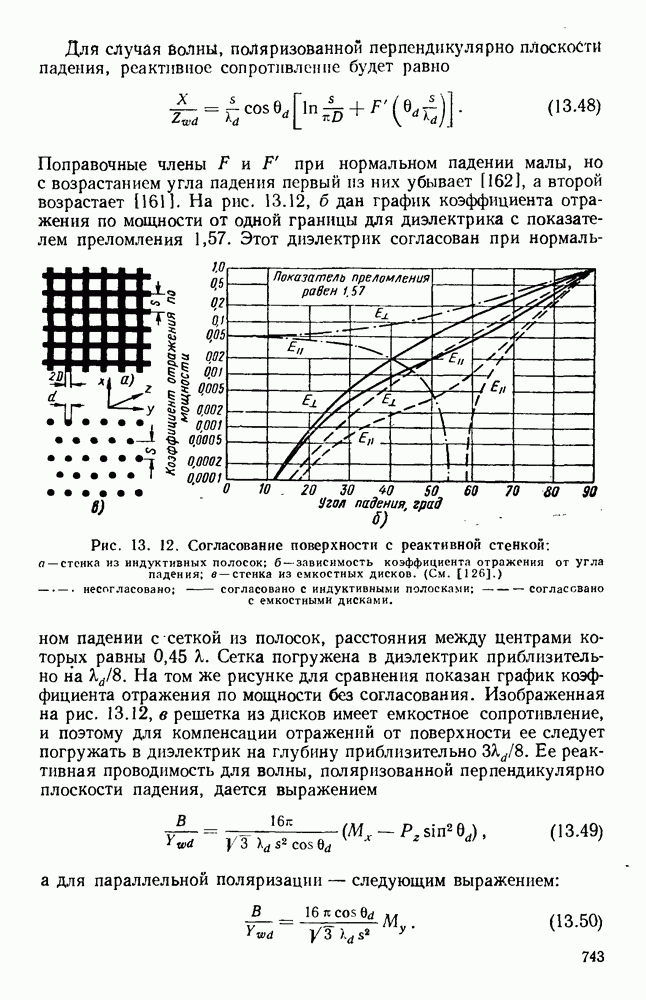
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
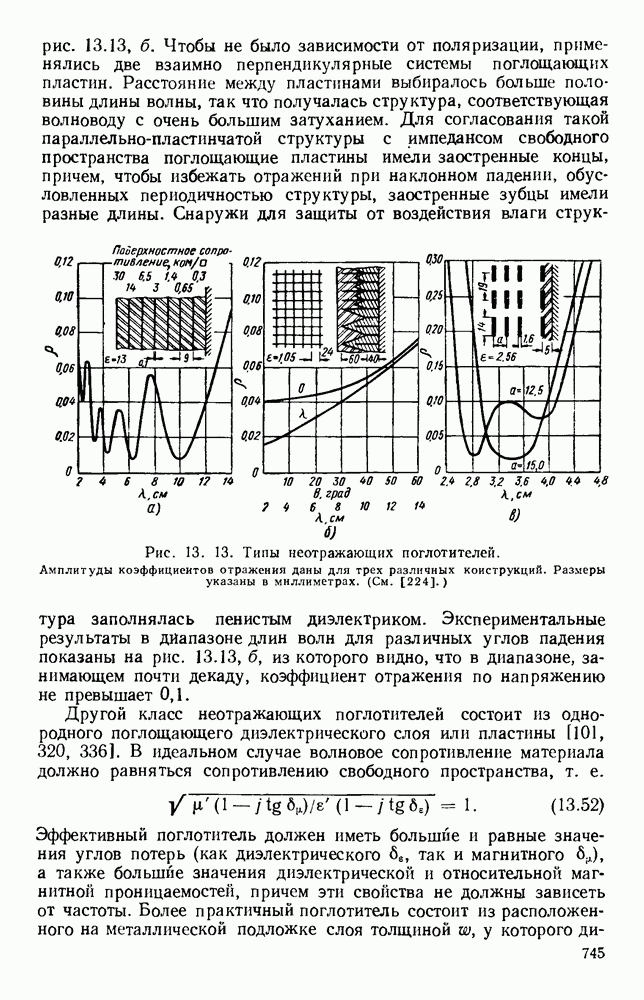
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
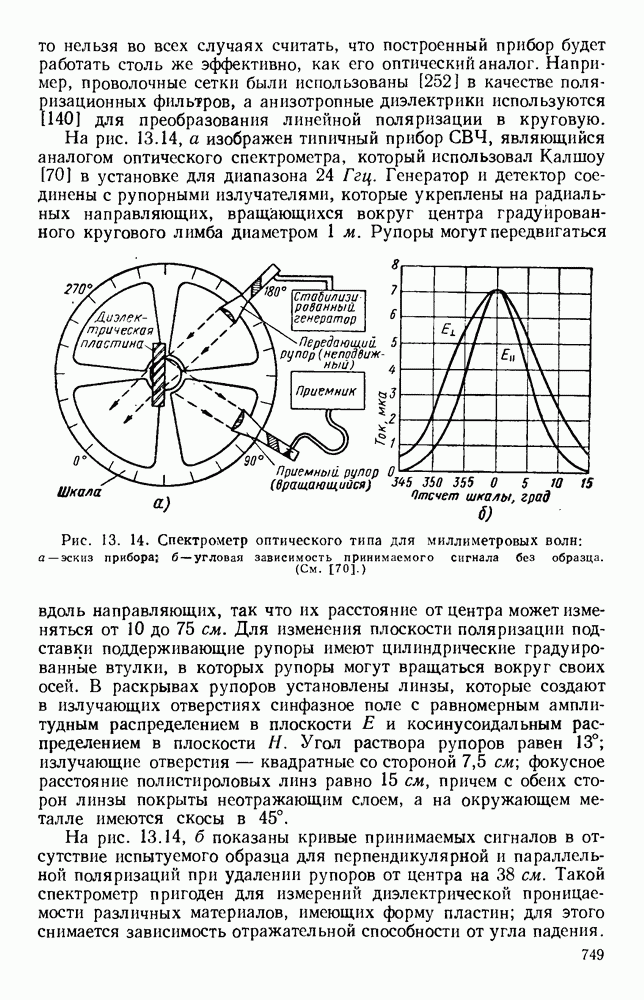
- 13.4. ПРИБОРЫ И СИСТЕМЫ
- 13.4.1. Спектрометры
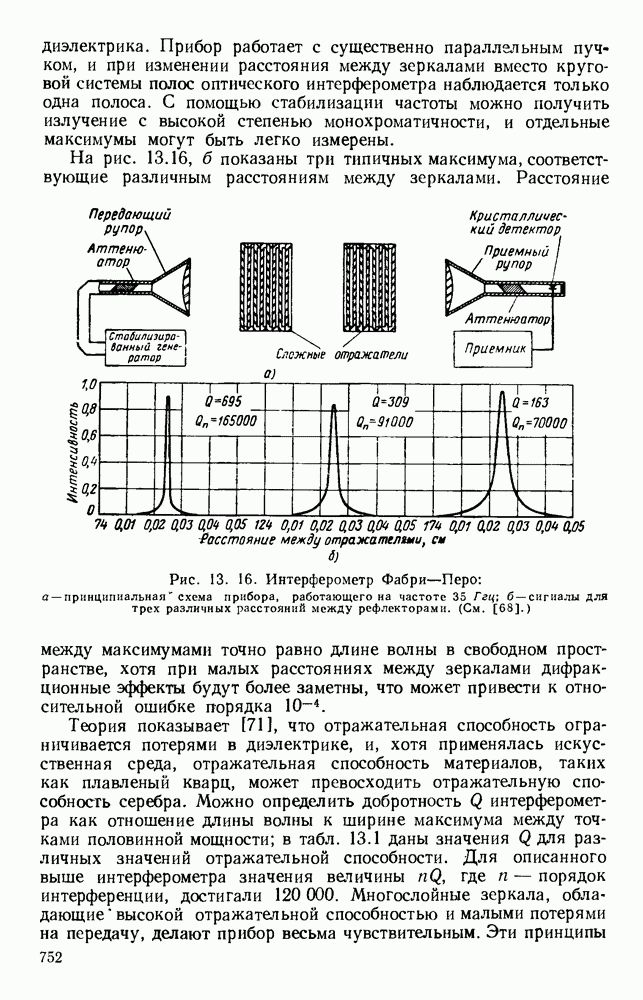
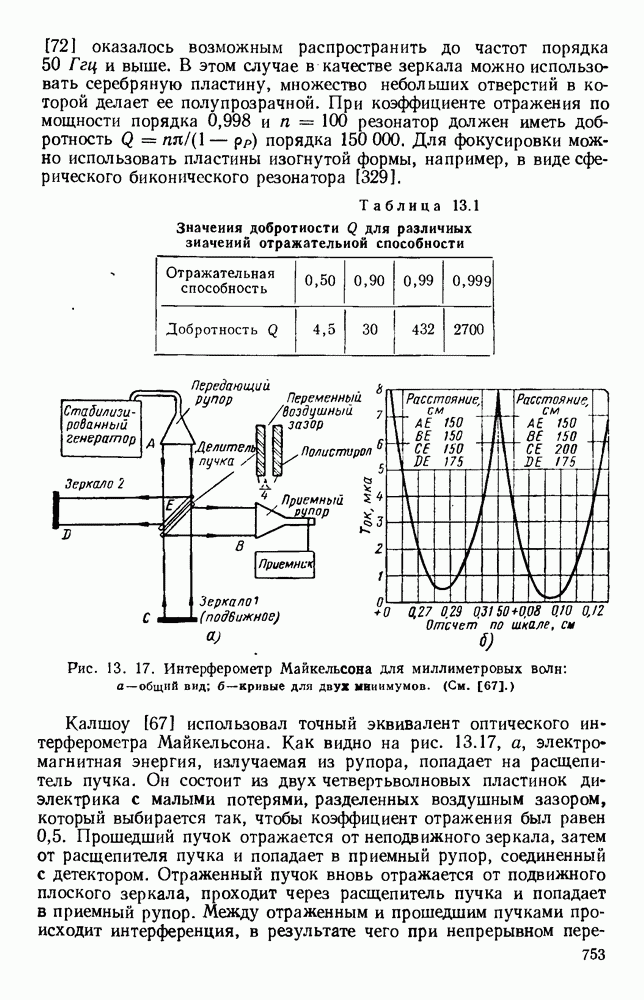
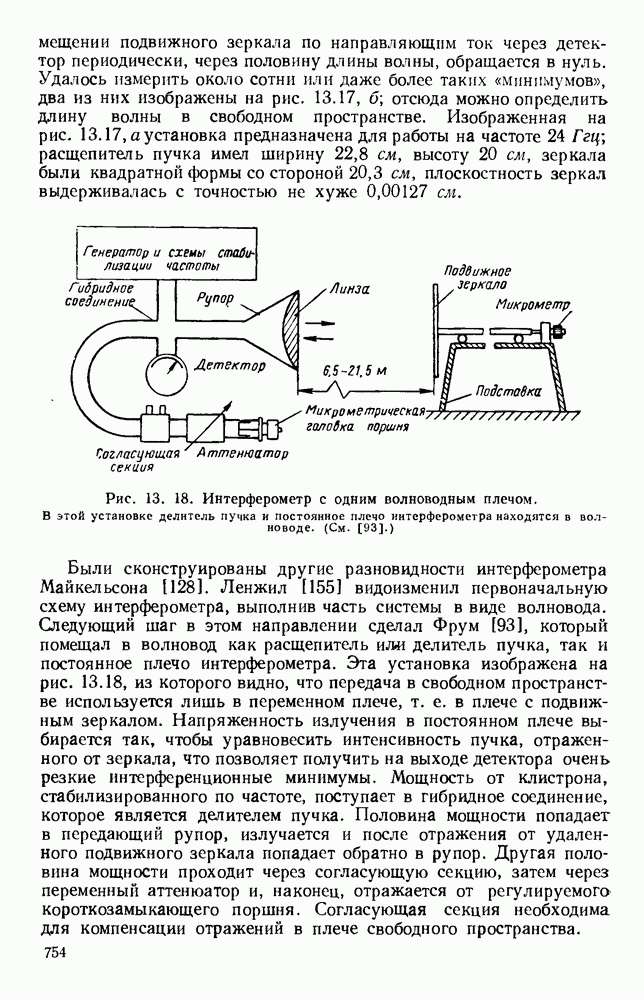
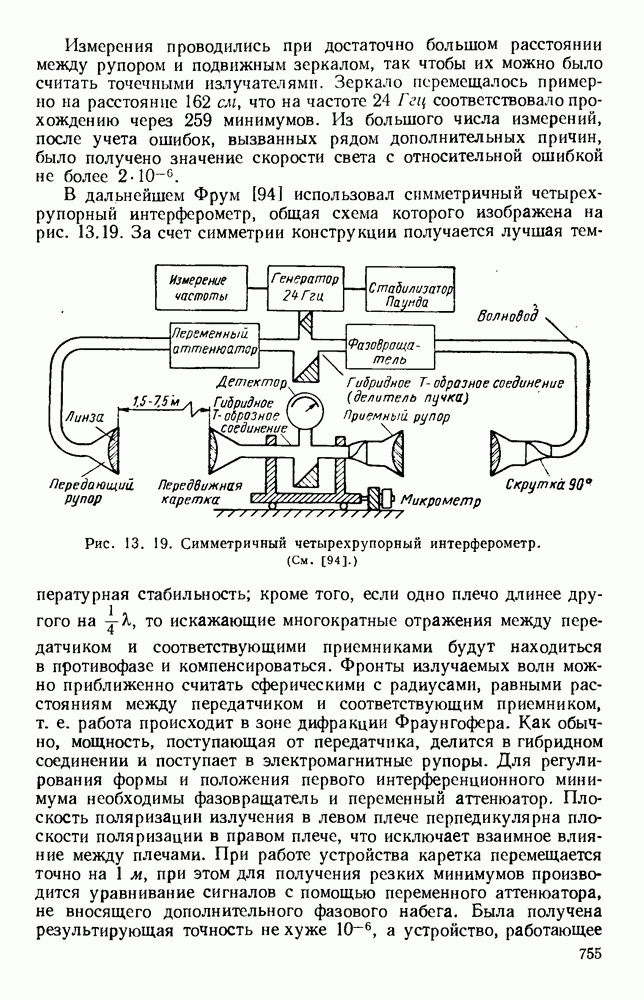
- 13.4.2. Интерферометры
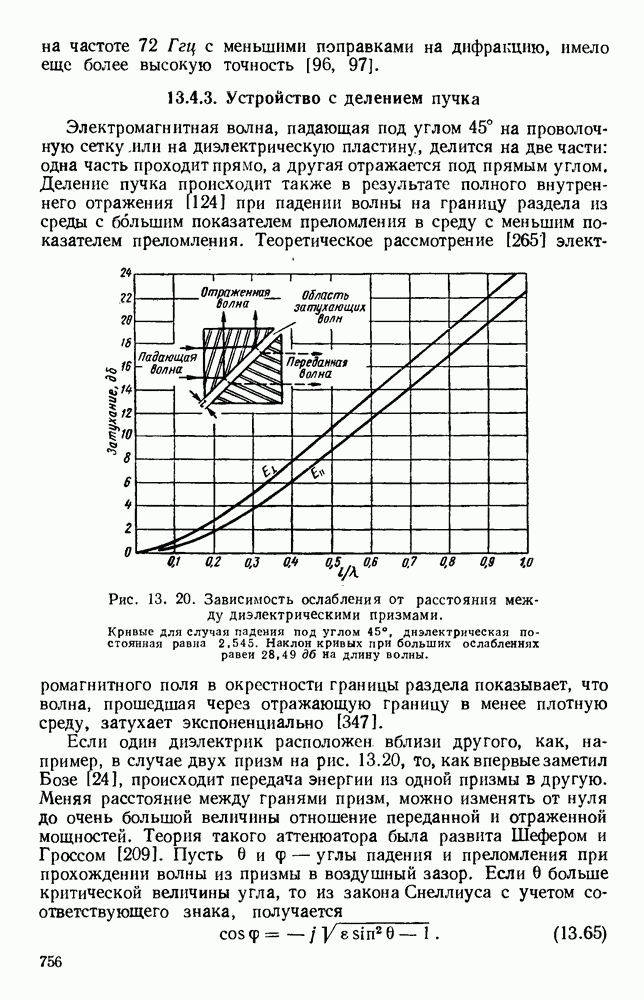
- 13.4.3. Устройство с делением пучка