| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
10.5.1. Ленточно-лестничные линии
Системы с медленными электромагнитными волнами широко применяются на практике и, хотя непрерывные диэлектрики находят ограниченное применение, обычно используются периодические структуры различных видов [32, 126, 156, 157]. Скорость распространения в таких системах должна выбираться в зависимости от конкретного применения и, например, может равняться с в линейных электронных ускорителях  в усилительных электронных лампах [243] и 0,01 с в малошумящих усилителях типа мазера [46, 83]. Хотя имеются исследования двумерных и трехмерных замедляющих структур [36, 219], мы ограничимся рассмотрением лишь структур линейного типа. Мощность Р, текущая вдоль замедляющей структуры, и энергия
в усилительных электронных лампах [243] и 0,01 с в малошумящих усилителях типа мазера [46, 83]. Хотя имеются исследования двумерных и трехмерных замедляющих структур [36, 219], мы ограничимся рассмотрением лишь структур линейного типа. Мощность Р, текущая вдоль замедляющей структуры, и энергия  запасенная на единице длины, связаны соотношением
запасенная на единице длины, связаны соотношением

Если работа прибора определяется электрическим полем в структуре, то в качестве практически важного параметра выбирается импеданс взаимодействия:

Если же для работы прибора более существенным оказывается магнитное поле, то структура характеризуется полной проводимостью связи:

Другим параметром является шунтовой импеданс, определяемый как

и связанный с мощностью, рассеиваемой на единице длины вследствие омических потерь.
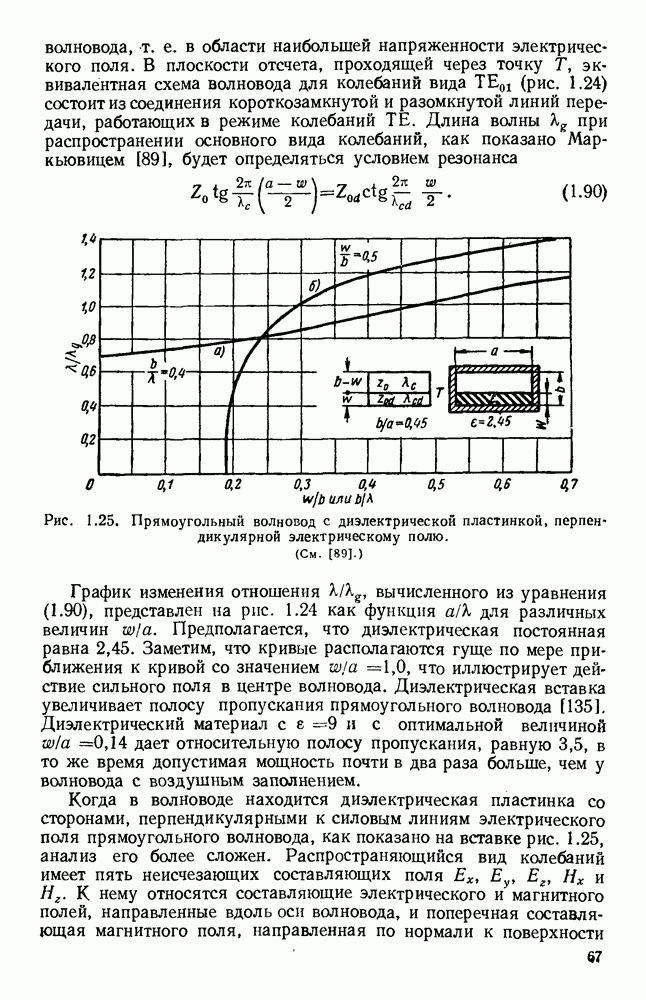
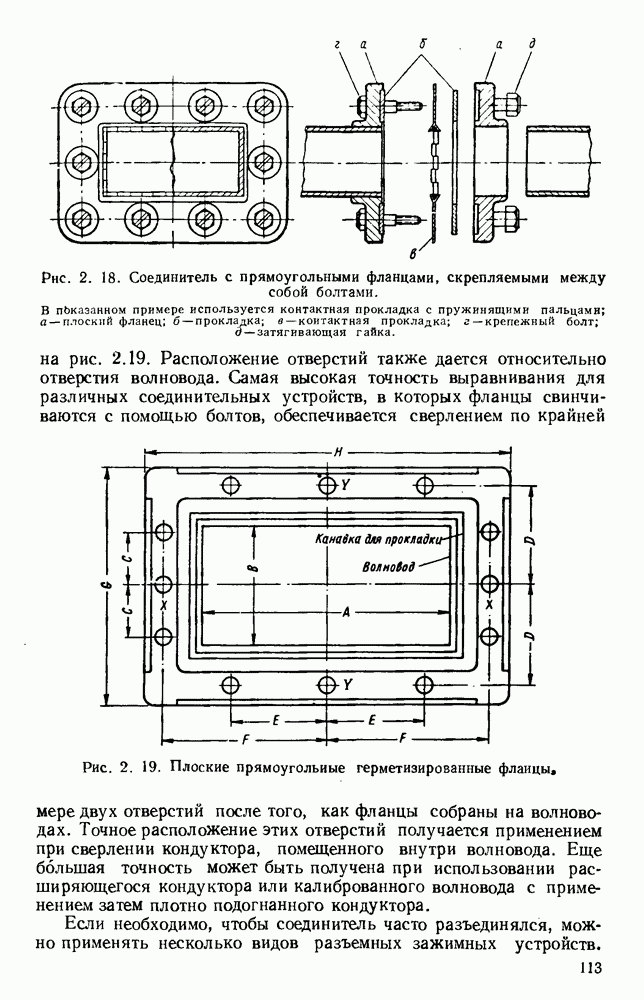
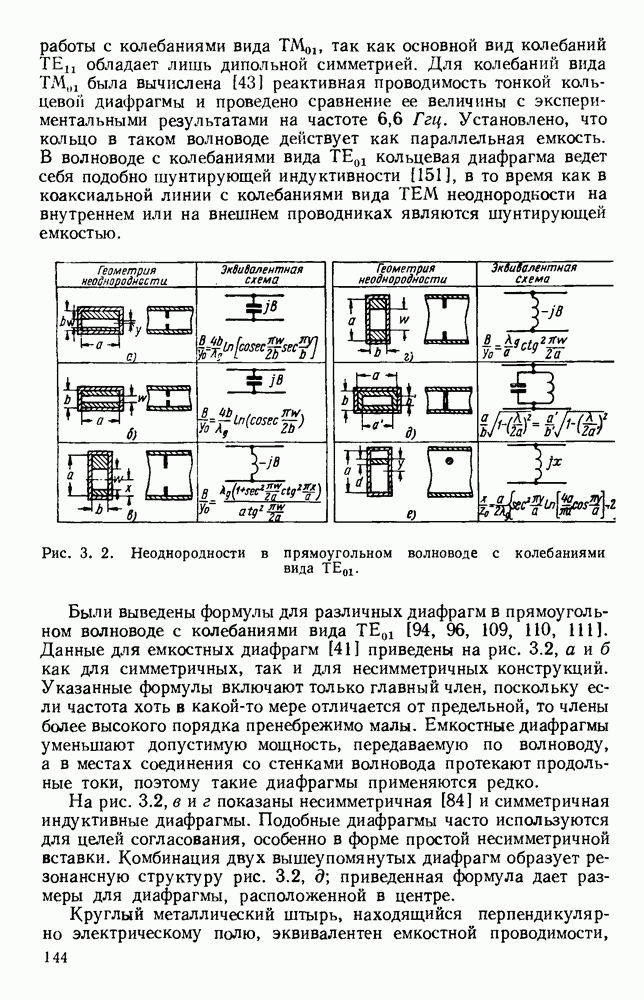
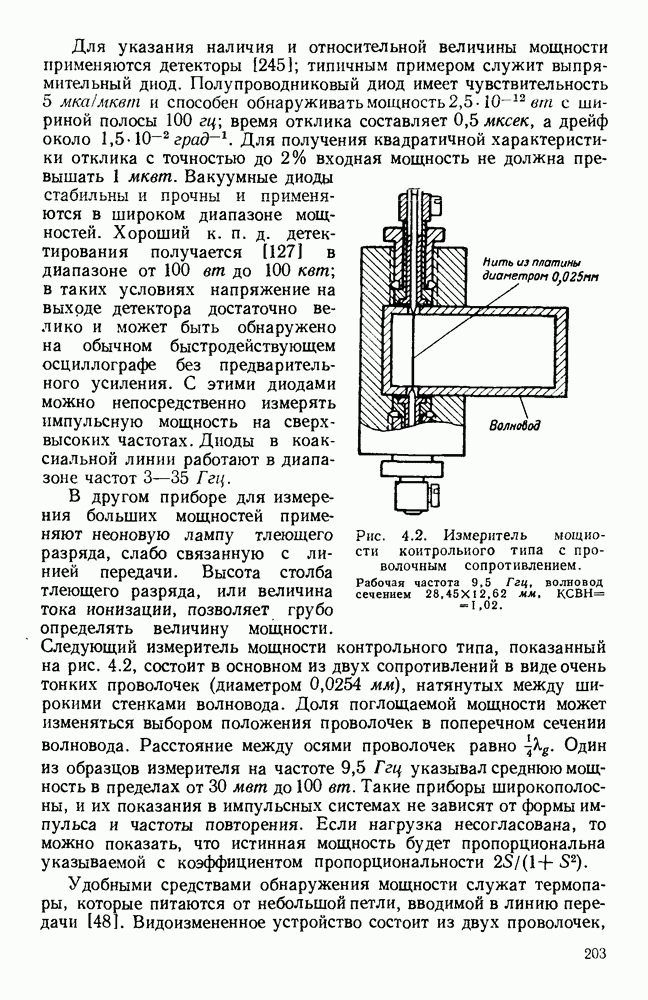
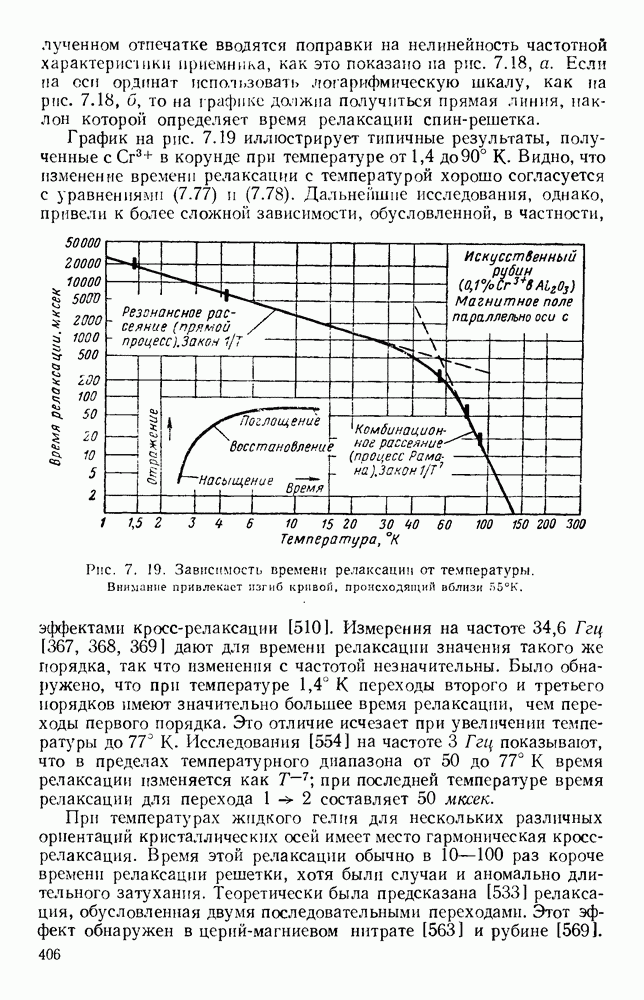
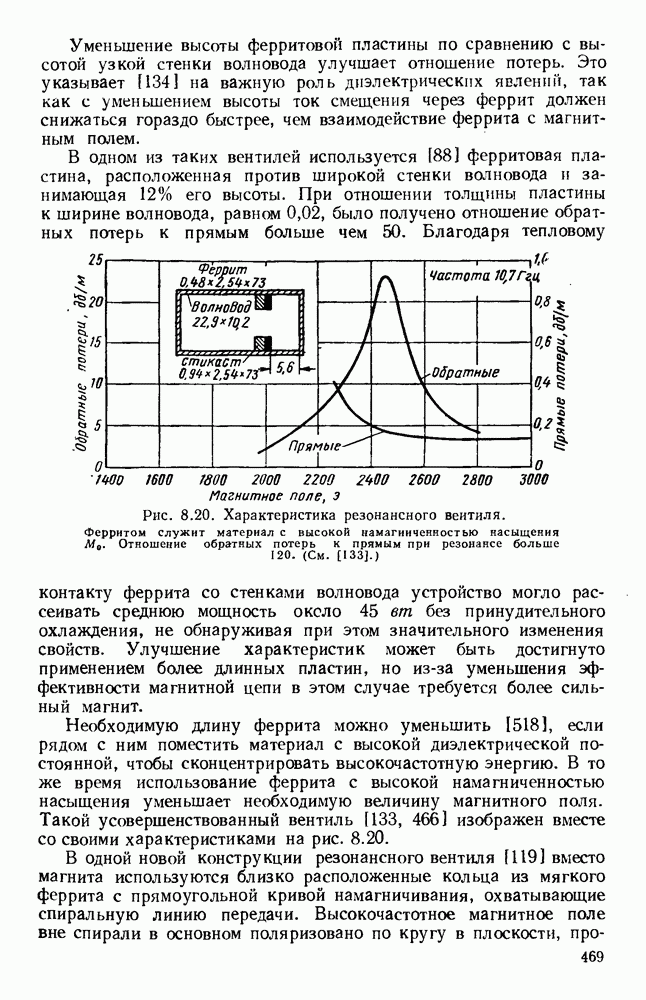
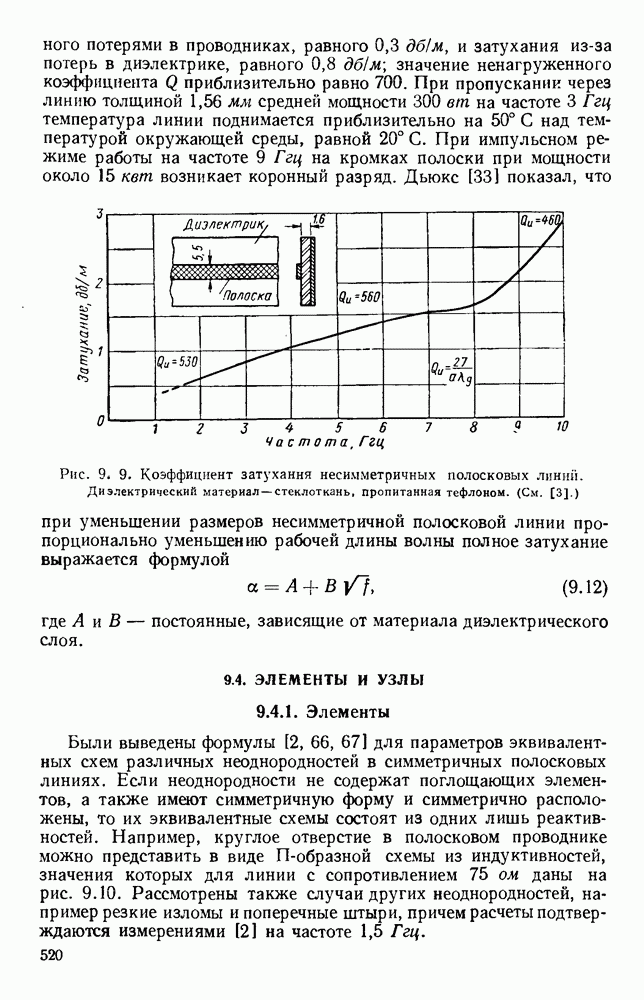
Обширный класс замедляющих структур представляют собой системы связанных резонаторов [25], одинаковых по форме и размерам. Существуют два основных типа связи: чисто индуктивная и чисто емкостная; величины обеих составляющих определяют насколько будет видоизменена диаграмма со  несвязанных резонаторов. Пусть, например, лестничная линия состоит, как показано на вставке рис. 10.22, из периодической решетки параллельных прямых проводников.
несвязанных резонаторов. Пусть, например, лестничная линия состоит, как показано на вставке рис. 10.22, из периодической решетки параллельных прямых проводников.

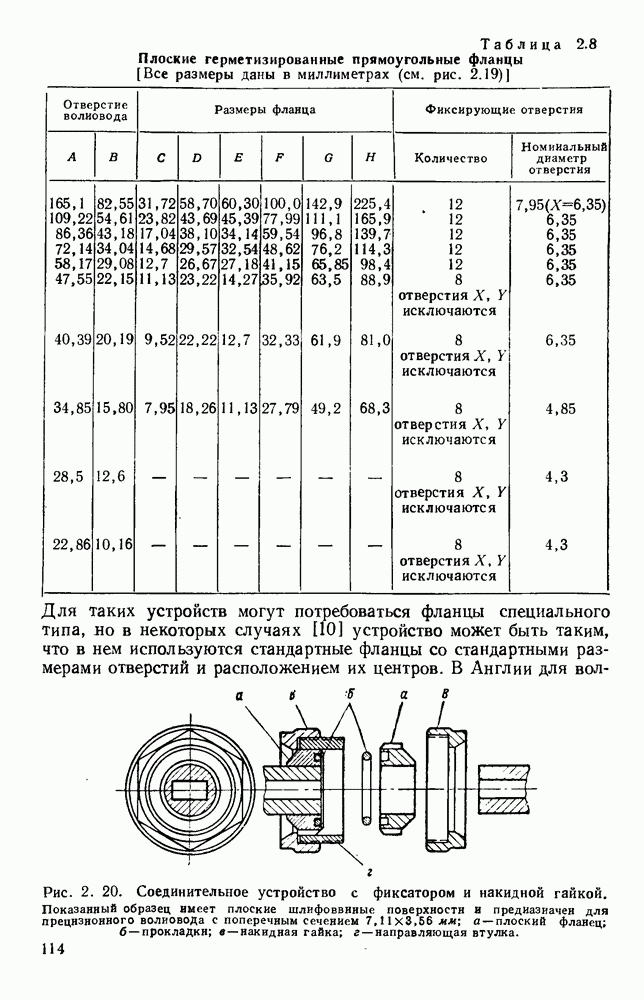
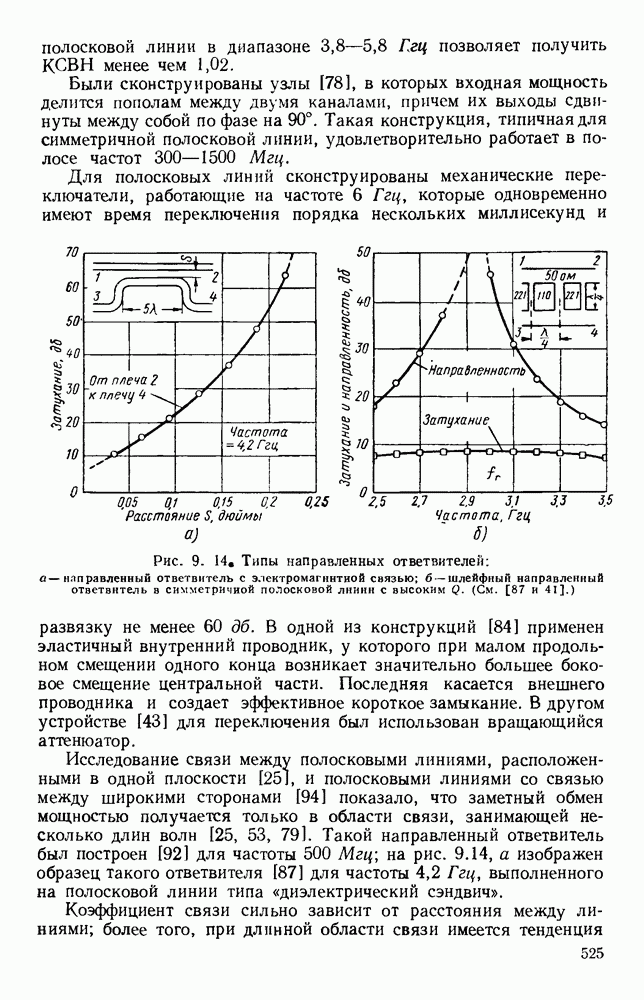
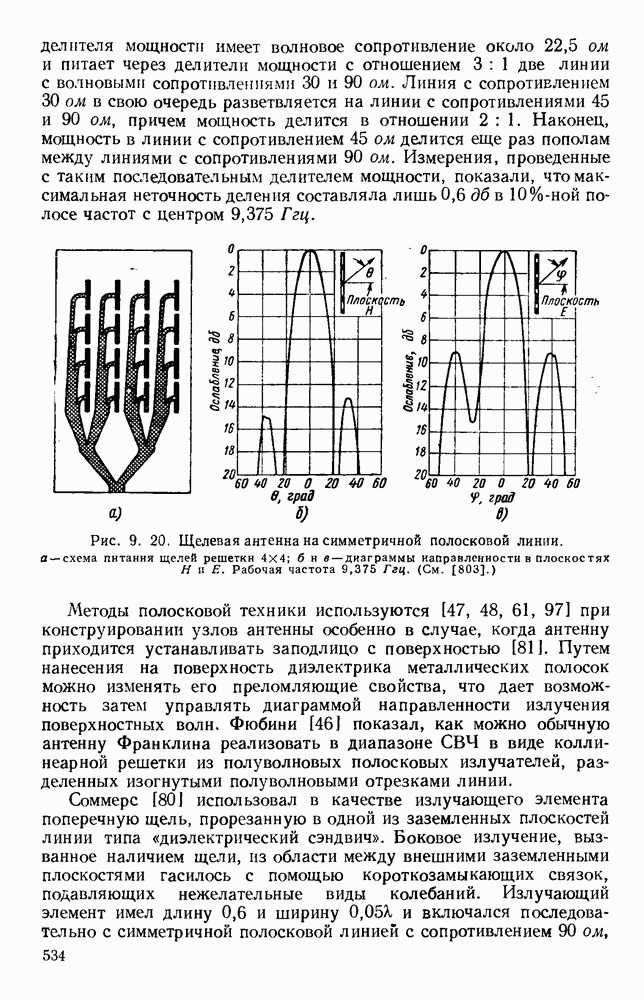
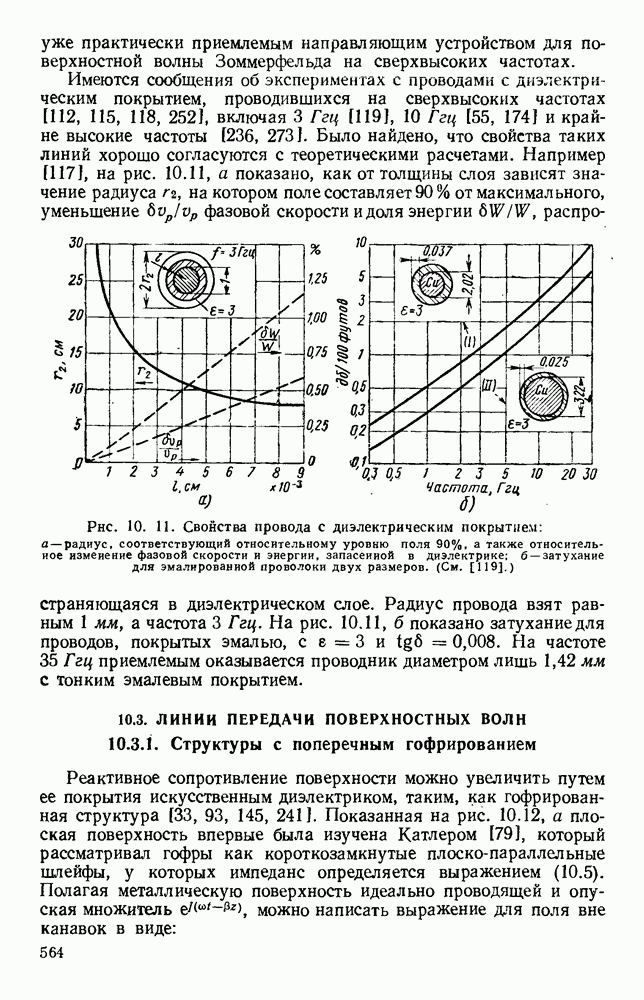
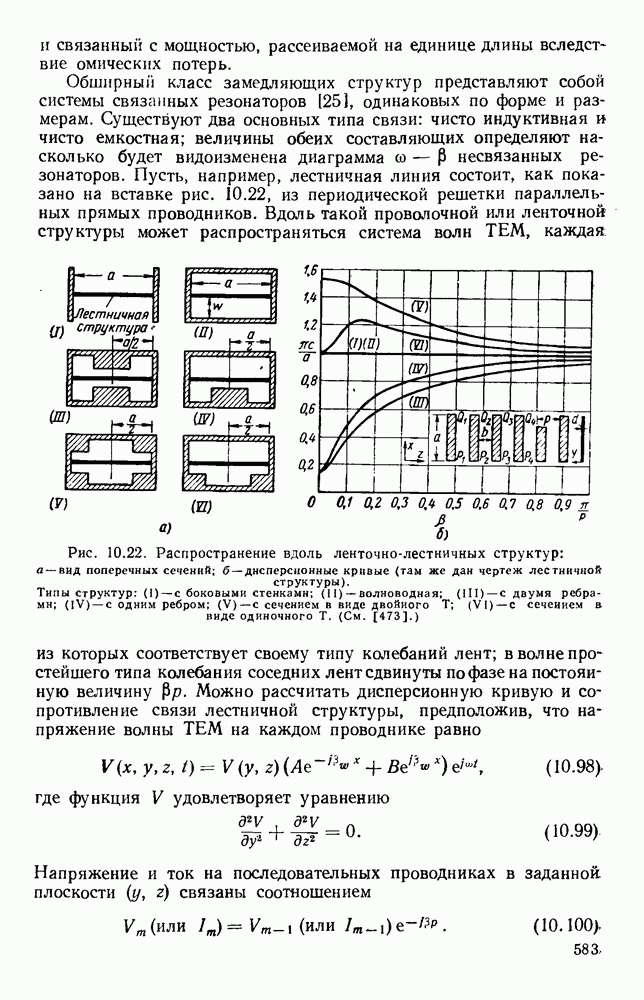
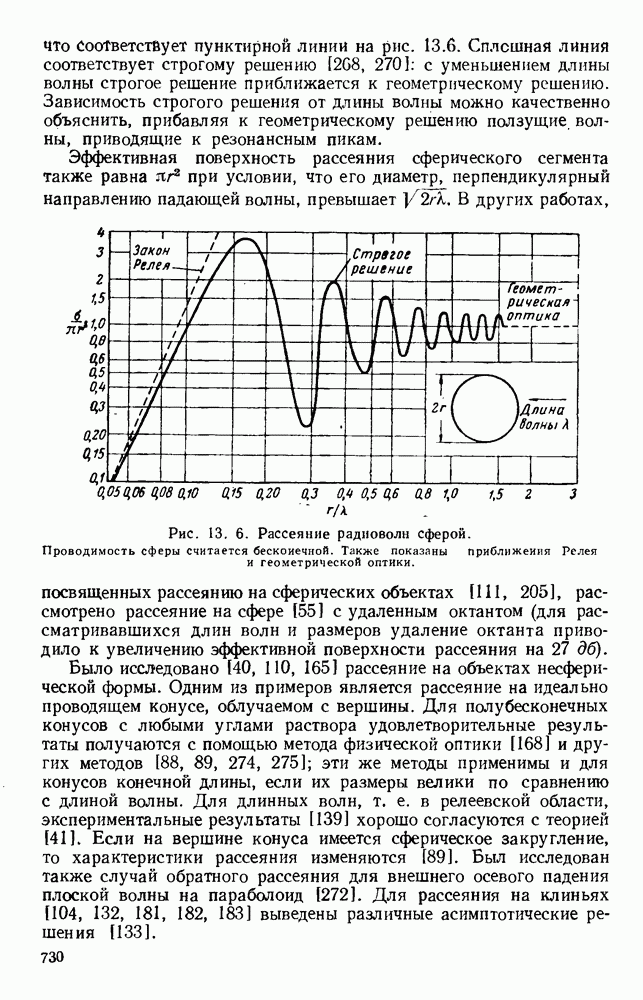
Рис. 10.22. Распространение вдоль ленточно-лестничных структур: а — вид поперечных сечений; б - дисперсионные кривые (там же дан чертеж лестничной структуры). Типы структур: (I) — с боковыми стенками; (II) - волноводная; (III) — с двумя ребрами; (IV) — с одним ребром; (V) — с сечением в виде двойного Т; (VI) - с сечеиием в виде одиночного Т. (См. [473].)
Вдоль такой проволочной или ленточной структуры может распространяться система волн ТЕМ, каждая из которых соответствует своему типу колебаний лент; в волне простейшего типа колебания соседних лент сдвинуты по фазе на постоянную величину  Можно рассчитать дисперсионную кривую и сопротивление связи лестничной структуры, предположив, что напряжение волны ТЕМ на каждом проводнике равно
Можно рассчитать дисперсионную кривую и сопротивление связи лестничной структуры, предположив, что напряжение волны ТЕМ на каждом проводнике равно

где функция V удовлетворяет уравнению

Напряжение и ток на последовательных проводниках в заданной, плоскости  связаны соотношением
связаны соотношением

Волновое сопротивление одного проводника в решетке может быть определено как

где  в силу периодичности структуры может быть любым.
в силу периодичности структуры может быть любым.
Предложенный Флетчером [102] метод определения  применим лишь к прямоугольным проводникам и основан на предположении, что составляющая
применим лишь к прямоугольным проводникам и основан на предположении, что составляющая  в области между лентами постоянна. При этом условии на общих границах различных областей производится сшивание полей. Напряжение на
в области между лентами постоянна. При этом условии на общих границах различных областей производится сшивание полей. Напряжение на  проводнике можно найти непосредственно, а ток в проводнике может быть определен интегрированием касательной компоненты магнитного поля по контуру, охватывающему проводник. Если все проводники одинаково удалены от обеих экранирующих плоскостей, то в обозначениях рис. 10.22 этот метод дает
проводнике можно найти непосредственно, а ток в проводнике может быть определен интегрированием касательной компоненты магнитного поля по контуру, охватывающему проводник. Если все проводники одинаково удалены от обеих экранирующих плоскостей, то в обозначениях рис. 10.22 этот метод дает

Численные значения суммы для практически применяемых геометрий даны Уоллингом [327]. Если  , то уравнение упрощается и имеет вид
, то уравнение упрощается и имеет вид

Леблон и Мурье [196] вычислили  используя предположение о квазиэлектростатическом распределении поля в плоскости
используя предположение о квазиэлектростатическом распределении поля в плоскости  (При таком подходе, однако, требуется измерение емкостей между различными частями структуры). Предполагалось также, что проводники имеют достаточную толщину в направлении нормали к плоскости решетки, что обеспечивает их экранировку от всех остальных проводников (за исключением соседних); для прямоугольных проводников результат сводится к формуле (10.103).
(При таком подходе, однако, требуется измерение емкостей между различными частями структуры). Предполагалось также, что проводники имеют достаточную толщину в направлении нормали к плоскости решетки, что обеспечивает их экранировку от всех остальных проводников (за исключением соседних); для прямоугольных проводников результат сводится к формуле (10.103).
С помощью метода, учитывающего взаимосвязь всех элементов, Батчер [48] точно вычислил высокочастотные поля, окружающие решетку из тонких лент. В случае, когда  а ширина лент равна ширине зазоров, этот метод дает соотношение
а ширина лент равна ширине зазоров, этот метод дает соотношение

которое следует сравнить с уравнением (10.102). Было показано, что произведение импеданса связи и групповой скорости при определенных условиях одинаково для весьма различных геометрий. Этот «множитель распределения поля» решетки в силу уравнений (10.94) и (10.95) можно записать в виде

Для пространственных гармоник, у которых  величины импеданса связи, полученные из точного решения, сильно превосходят значения, найденные приближенными методами.
величины импеданса связи, полученные из точного решения, сильно превосходят значения, найденные приближенными методами.
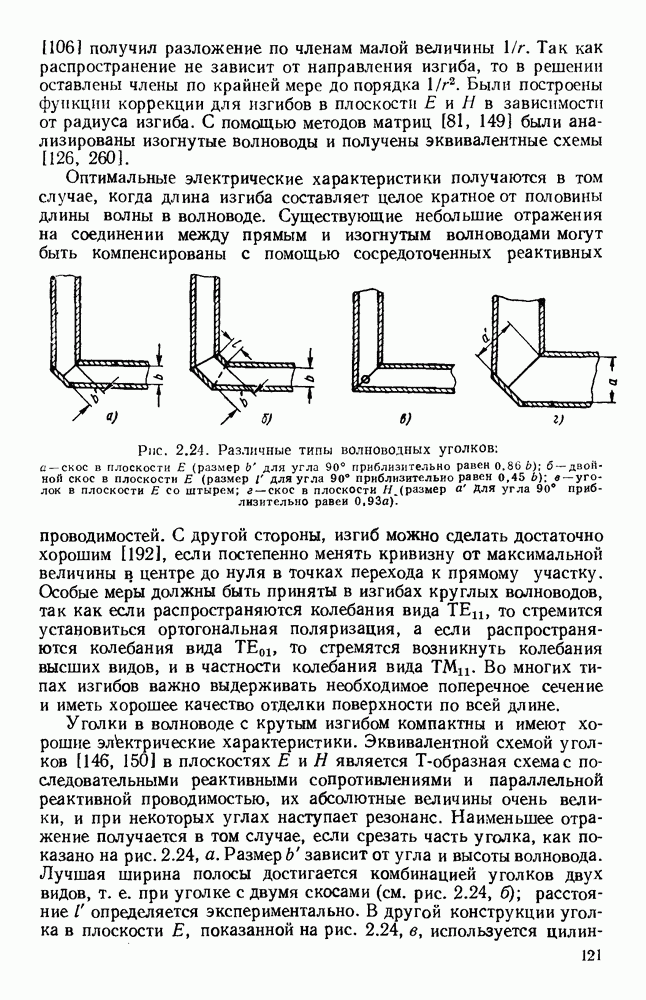
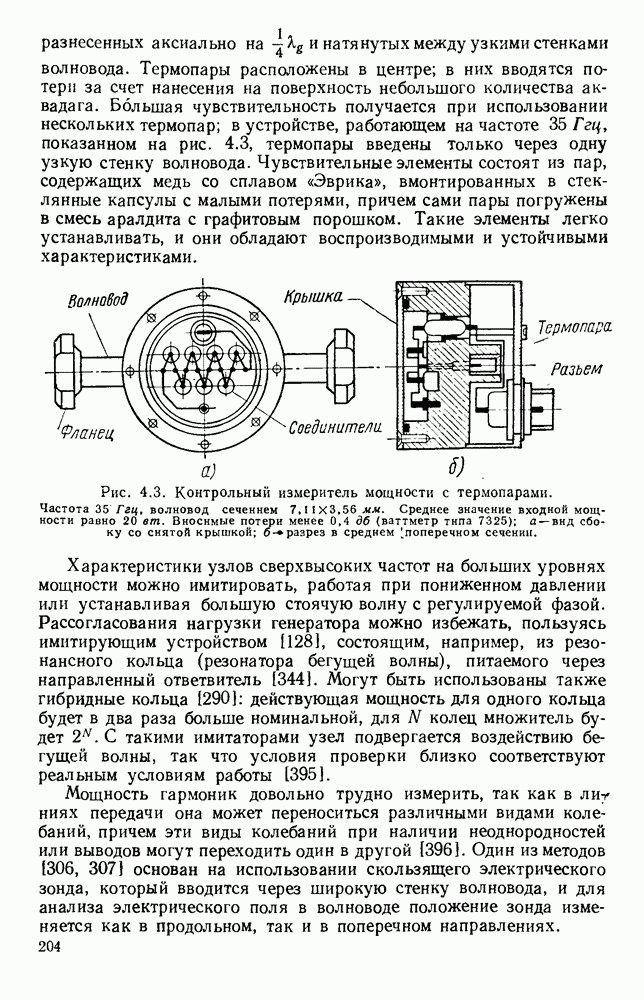
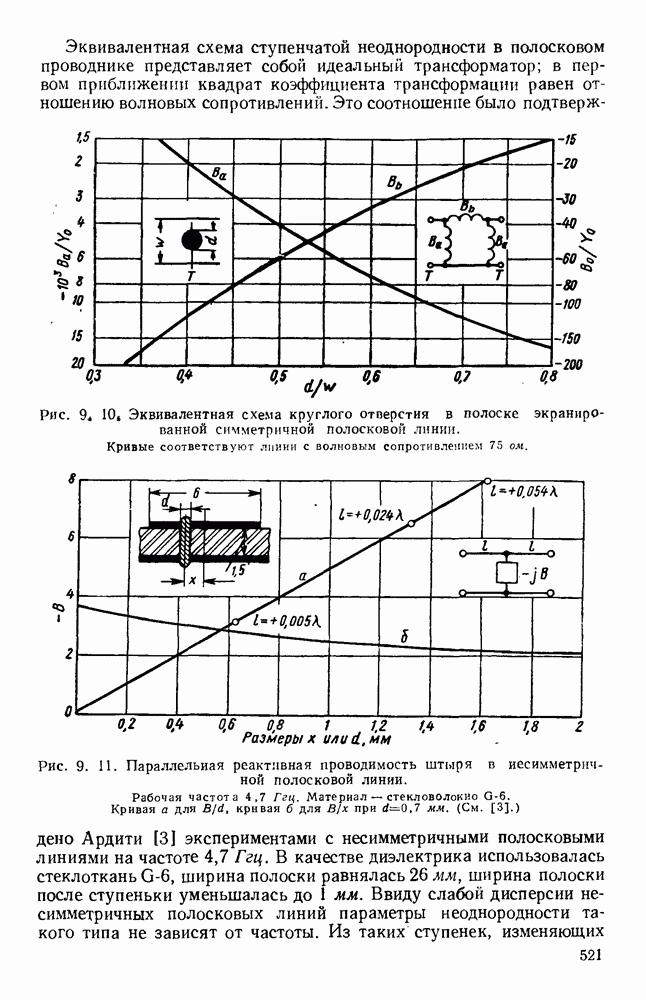
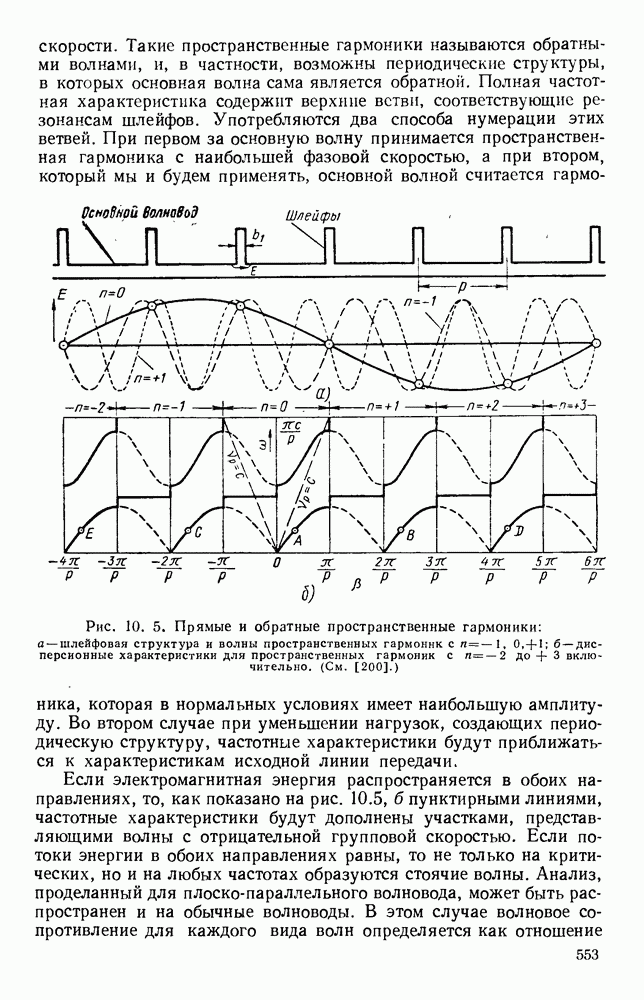
Полученные указанными методами формулы с учетом соответствующей геометрии и граничных условий были применены для расчета структур, используемых на практике. В структуре, изображенной на рис. 10.22, а, оба конца лент являются короткозамкнутыми. В случае (I) замыкание осуществляется, с помощью двух перпендикулярных боковых стенок, в случае (II) — с помощью узких боковых стенок прямоугольного волновода. Для любого значения Р на частоте, при которой к равно удвоенной длине лент, в такой решетке возможны лишь стоячие волны типа ТЕМ. Поэтому дисперсионные кривые, изображенные на рис. 10.22, б (I) и (II), представляют собой горизонтальные линии, и, поскольку групповая скорость равна нулю, в структуре распространения не происходит. В этом случае имеются как индуктивная, так и емкостная связи, которые равны по величине и взаимно компенсируются.
Если в такой цепной линии нарушить компенсацию связей [47], то можно получить полосу прозрачности конечной ширины. Для заданного значения (3 соответствующую частоту можно уменьшить, используя волновод с выступом [рис. 10.22, а (III) и (IV)], что приводит к уменьшению предельной частоты волноводов, образующихся по обе стороны цепочки. Это. приводит к искривлению дисперсионных кривых [рис. 10.22, б (III) и (IV)], и, таким образом, структура может передавать энергию. Наоборот, если использовать волновод Т-образного сечения, как показано на рис. 10.22,  и (VI), то для заданного значения
и (VI), то для заданного значения  соответствующую частоту можно увеличить.
соответствующую частоту можно увеличить.
Дисперсионная кривая для сечения волновода в виде одиночного Т имеет несколько иную форму, так как предельная частота волны  в волноводе под цепочкой оказывается выше как предельной частоты волны нулевого вида в волноводе над цепочкой, так и первой резонансной частоты лент. Можно видеть, что в обеих структурах с Т-образными волноводами у основной волны фазовая и групповая скорости направлены противоположно, т. е. эти волны являются обратными. Во всех рассмотренных лестничных линиях предельную частоту колебаний вида
в волноводе под цепочкой оказывается выше как предельной частоты волны нулевого вида в волноводе над цепочкой, так и первой резонансной частоты лент. Можно видеть, что в обеих структурах с Т-образными волноводами у основной волны фазовая и групповая скорости направлены противоположно, т. е. эти волны являются обратными. Во всех рассмотренных лестничных линиях предельную частоту колебаний вида  можно повысить, если применить более короткие ленты, которые располагаются между горизонтальными пластинами и поддерживаются боковыми стенками [223]. При этом упомянутая частота еще будет приближенно равна
можно повысить, если применить более короткие ленты, которые располагаются между горизонтальными пластинами и поддерживаются боковыми стенками [223]. При этом упомянутая частота еще будет приближенно равна
резонансной частоте короткозамкнутых лент и, следовательно, обратно пропорциональна их длине. Этот прием является важным способом расширения полосы прозрачности таких структур. Кроме того, таким путем можно осуществить передачу энергии по прямоугольному волноводу на частотах ниже предельных.
В работе [83] показано, что ленточно-лестничные линии удобно применять для получения групповых скоростей порядка  Изображенная на рис. 10.22, а (IV) структура, у которой удалена верхняя половина, весьма часто применяется в миллиметровом диапазоне для получения коэффициента замедления порядка 10. Дисперсионные характеристики и импеданс связи можно приближенно вычислить [6], рассматривая структуру как гребневой волновод, периодически нагруженный короткозамкнутыми штырями. В структурах, состоящих из двух параллельных ленточных решеток, возможны типы волн с симметричным и несимметричным распределением поля, причем практический интерес представляет лишь первый случай. Такие многорядные линии [229] имеют большой импеданс связи, широкую полосу прозрачности и малую дисперсию.
Изображенная на рис. 10.22, а (IV) структура, у которой удалена верхняя половина, весьма часто применяется в миллиметровом диапазоне для получения коэффициента замедления порядка 10. Дисперсионные характеристики и импеданс связи можно приближенно вычислить [6], рассматривая структуру как гребневой волновод, периодически нагруженный короткозамкнутыми штырями. В структурах, состоящих из двух параллельных ленточных решеток, возможны типы волн с симметричным и несимметричным распределением поля, причем практический интерес представляет лишь первый случай. Такие многорядные линии [229] имеют большой импеданс связи, широкую полосу прозрачности и малую дисперсию.  [15] показал, что распространение вдоль цепочки возможно при небольшом наклоне или изгибе лент. Поскольку в этом случае уже не требуется ни гребневого, ни Т-образного волноводов, можно весьма просто осуществить соединение нескольких цепных линий друг с другом.
[15] показал, что распространение вдоль цепочки возможно при небольшом наклоне или изгибе лент. Поскольку в этом случае уже не требуется ни гребневого, ни Т-образного волноводов, можно весьма просто осуществить соединение нескольких цепных линий друг с другом.
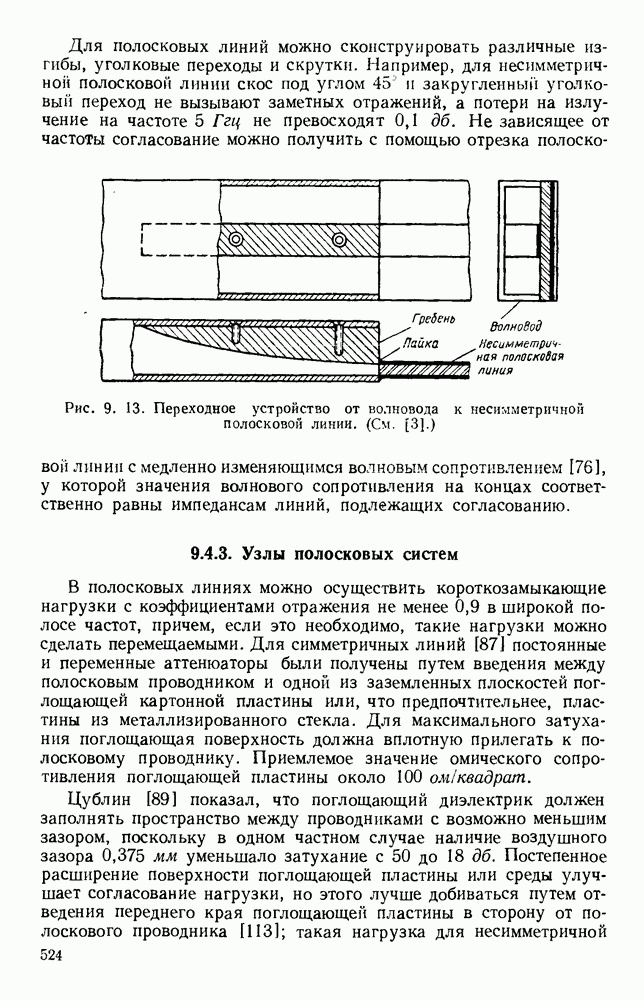
Несколько измененный вариант лестничной линии [214] состоит из решетки проводников, у которых концы отделены от стенок волновода диэлектрическими вставками. В отдельности блоки являются резонансными структурами, у которых резонансные частоты лежат ниже предельной частоты волновода. В совокупности они образуют связанную цепочку и действуют как замедляющая структура. Групповую скорость можно изменять подбором величины зазоров на концах проводников, выбором диэлектрика и подбором расстояний между блоками. Достоинством таких структур являются малые потери, простота расчета и легкость конструирования. Они особенно удобны для применения в случаях, в которых требуется сильное взаимодействие с магнитным полем.
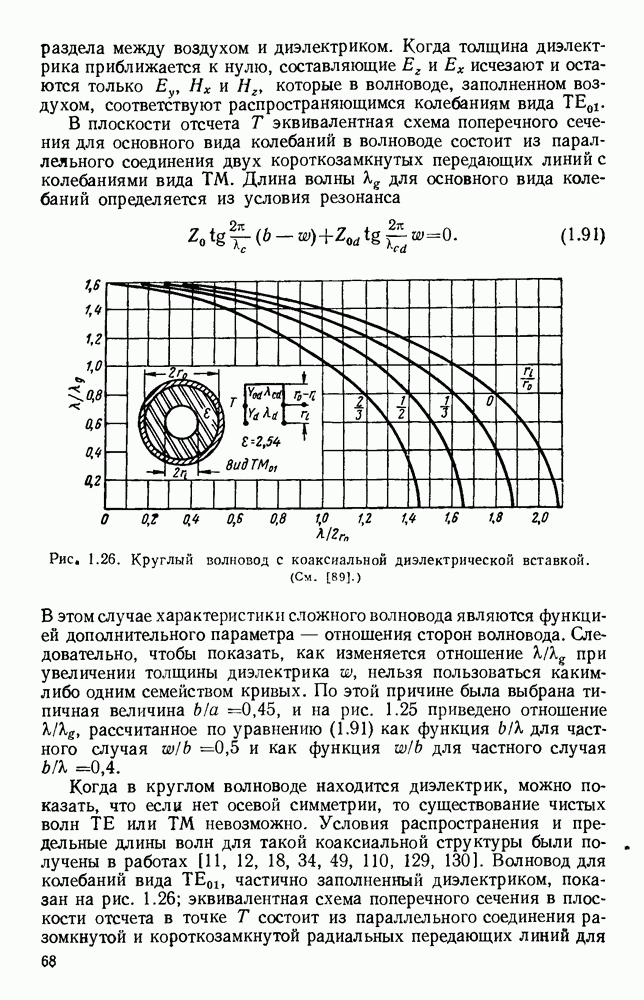
Если в изображенной на рис. 10.22 лестничной линии замкнуть накоротко концы:  а концы
а концы  оставить разомкнутыми и так до конца цепочки, то получится линия типа встречных штырей [134, 197; 231, 330], изображенная на рис. 10.23, а. Период полученной структуры равен
оставить разомкнутыми и так до конца цепочки, то получится линия типа встречных штырей [134, 197; 231, 330], изображенная на рис. 10.23, а. Период полученной структуры равен  и ее вид не изменится после сдвига вдоль оси
и ее вид не изменится после сдвига вдоль оси  на половину периода и последующего отражения в плоскости
на половину периода и последующего отражения в плоскости  Отсюда следует, что в этой структуре возможна волна, у которой электрическое поле в точке
Отсюда следует, что в этой структуре возможна волна, у которой электрическое поле в точке  отличается от поля в точке
отличается от поля в точке  лишь постоянным множителем
лишь постоянным множителем 
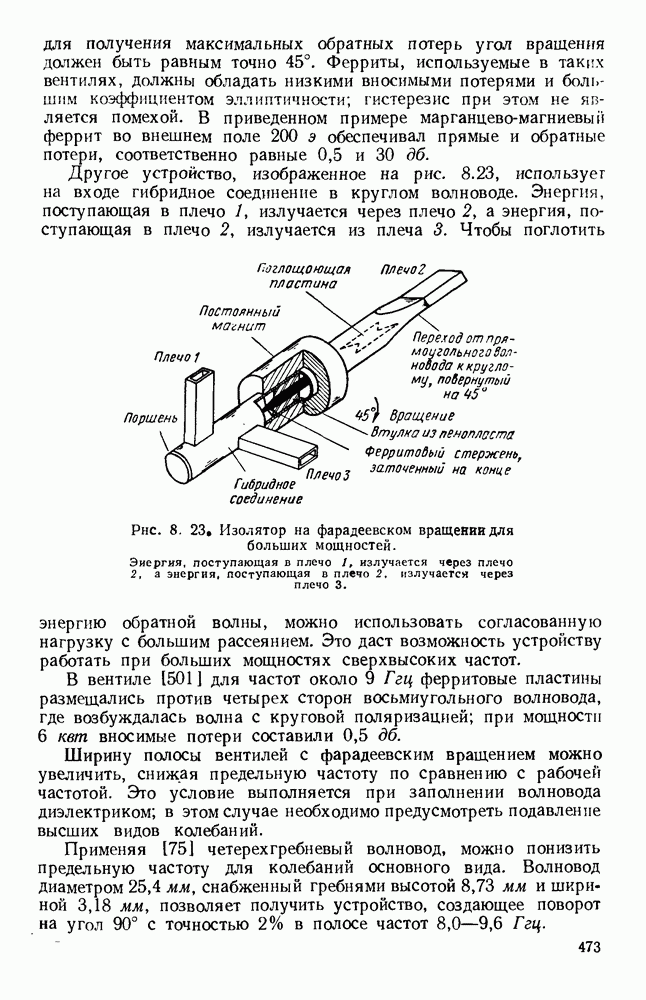
Расчет дисперсионной кривой с учетом соответствующих граничных условий проводится так же, как и для лестничной линии.
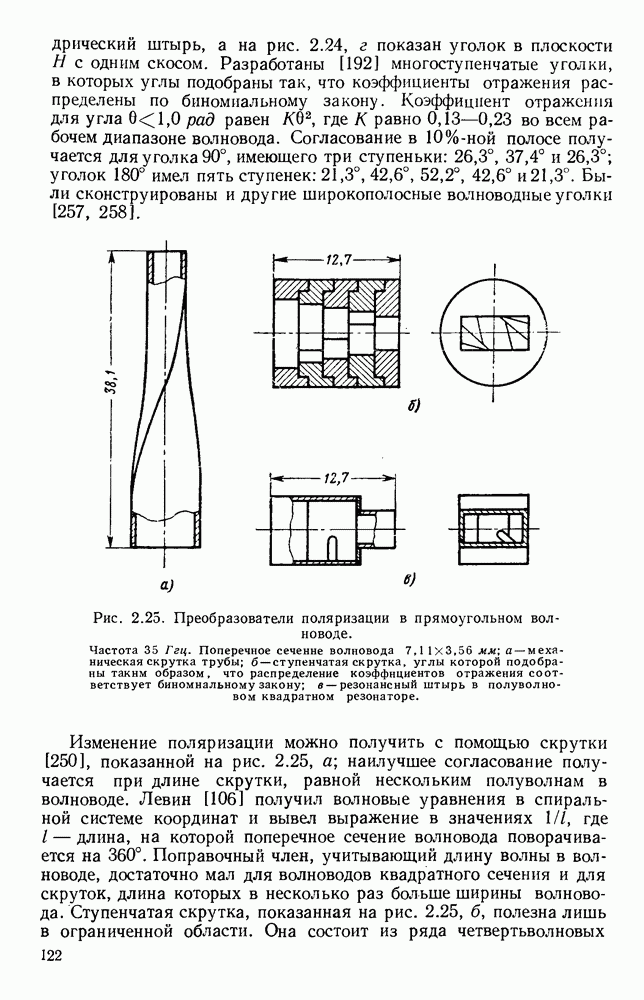
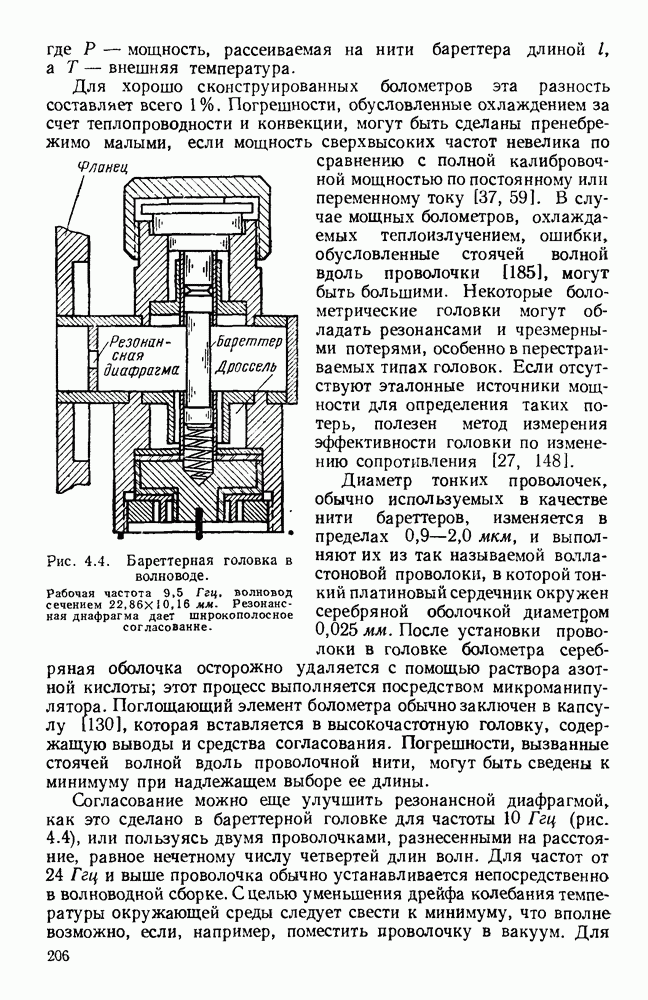
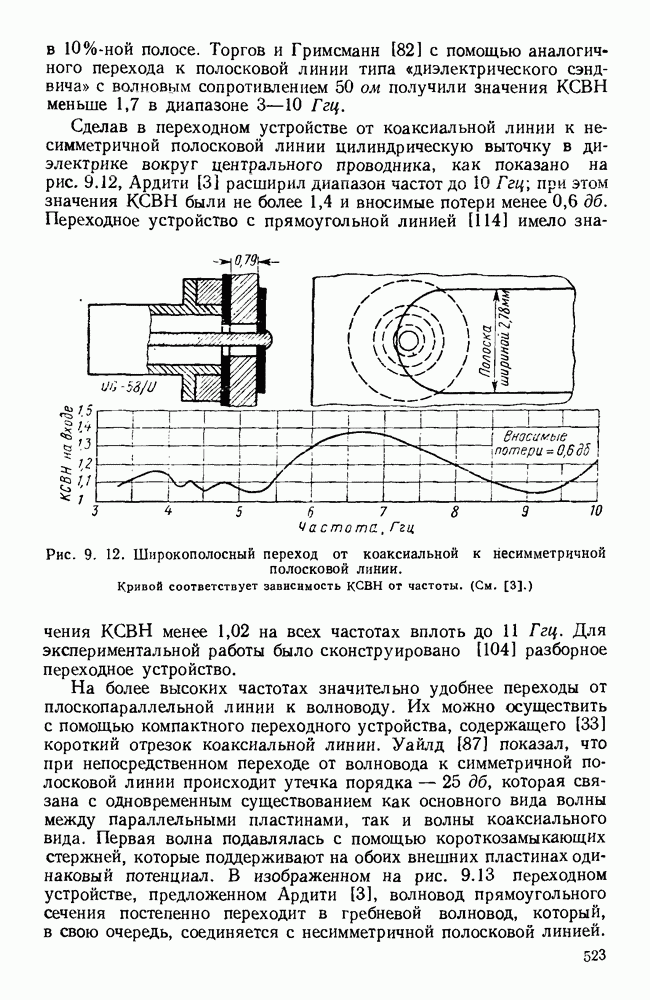
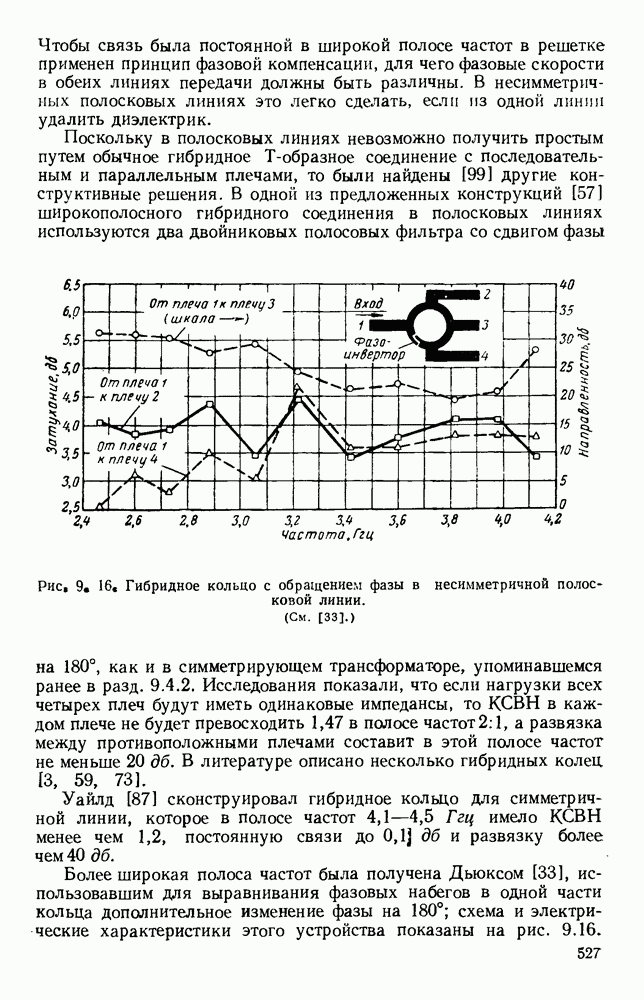
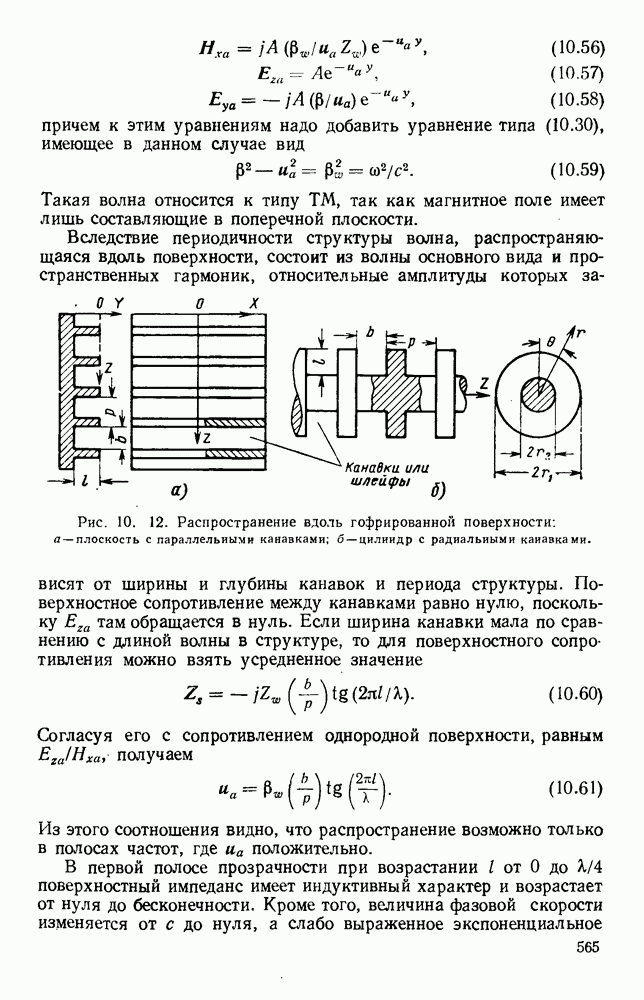
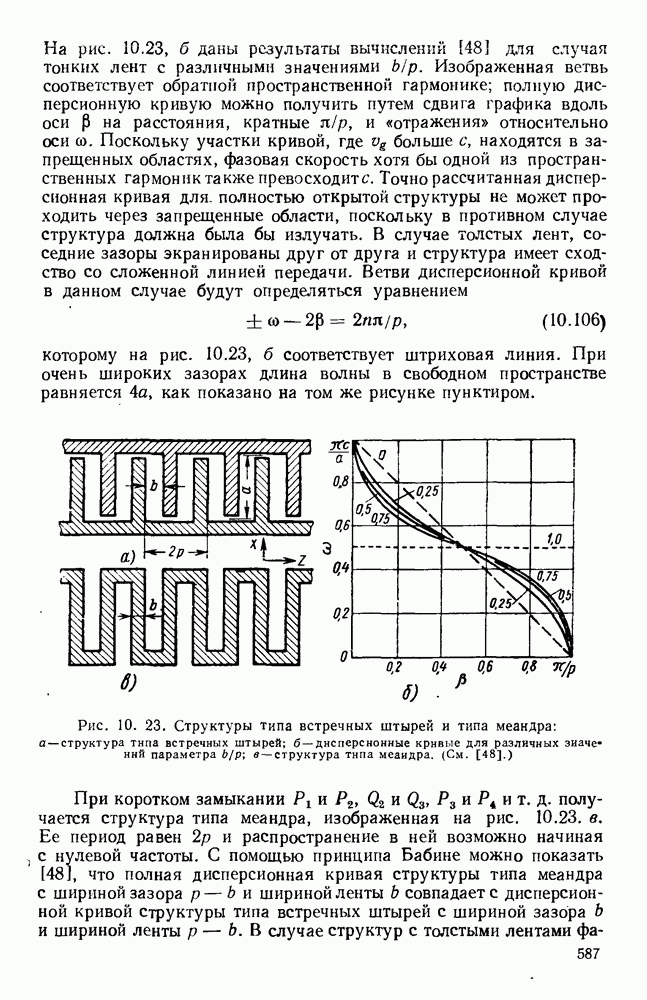
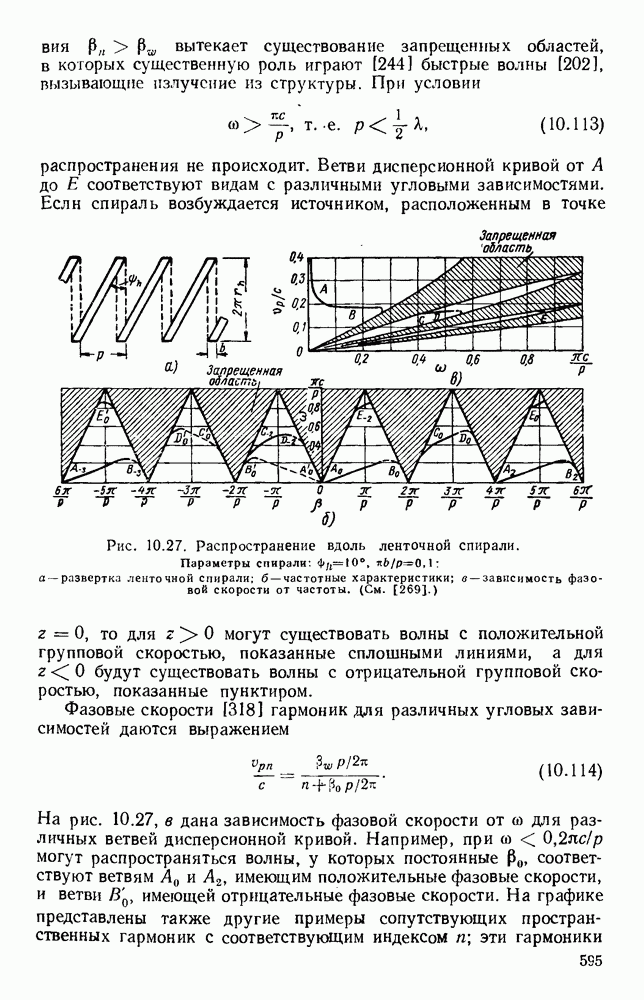
На рис. 10.23, б и даны результаты вычислении [48] для случзя тонких лент с различными значениями  Изображенная ветвь соответствует обратной пространственной гармонике; полную дисперсионную кривую можно получить путем сдвига графика вдоль оси Р на расстояния, кратные
Изображенная ветвь соответствует обратной пространственной гармонике; полную дисперсионную кривую можно получить путем сдвига графика вдоль оси Р на расстояния, кратные  и «отражения» относительно оси со. Поскольку участки кривой, где
и «отражения» относительно оси со. Поскольку участки кривой, где  больше с, находятся в запрещенных областях, фазовая скорость хотя бы одной из пространственных гармоник также превосходите. Точно рассчитанная дисперсионная кривая для, полностью открытой структуры не может проходить через запрещенные области, поскольку в противном случае структура должна была бы излучать. В случае толстых лент, соседние зазоры экранированы друг от друга и структура имеет сходство со сложенной линией передачи. Ветви дисперсионной кривой в данном случае будут определяться уравнением
больше с, находятся в запрещенных областях, фазовая скорость хотя бы одной из пространственных гармоник также превосходите. Точно рассчитанная дисперсионная кривая для, полностью открытой структуры не может проходить через запрещенные области, поскольку в противном случае структура должна была бы излучать. В случае толстых лент, соседние зазоры экранированы друг от друга и структура имеет сходство со сложенной линией передачи. Ветви дисперсионной кривой в данном случае будут определяться уравнением

которому на рис. 10.23, б соответствует штриховая линия. При очень широких зазорах длина волны в свободном пространстве равняется 4а, как показано на том же рисунке пунктиром.

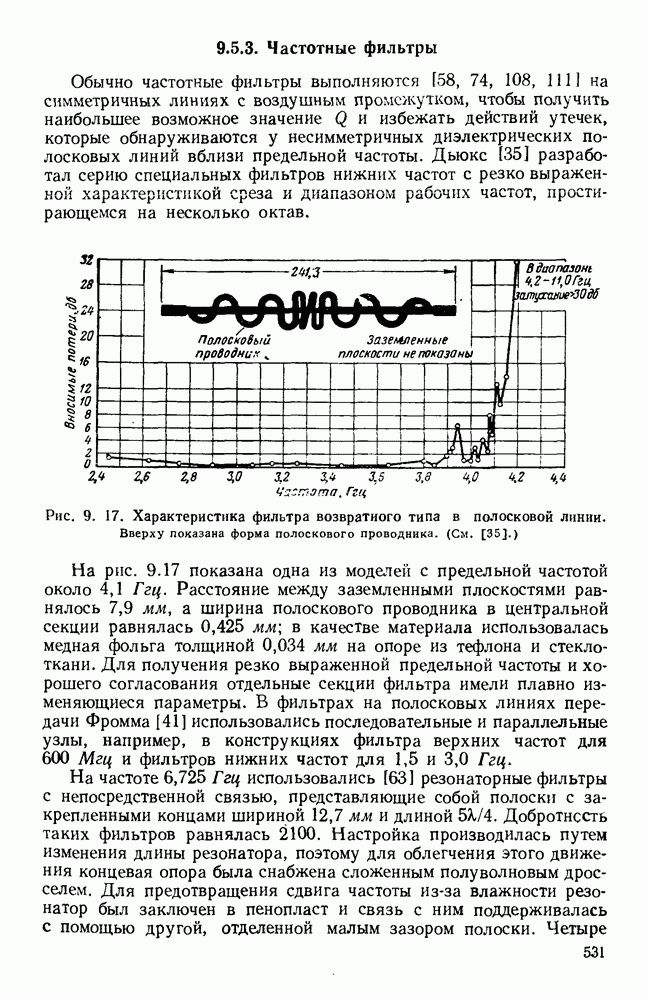
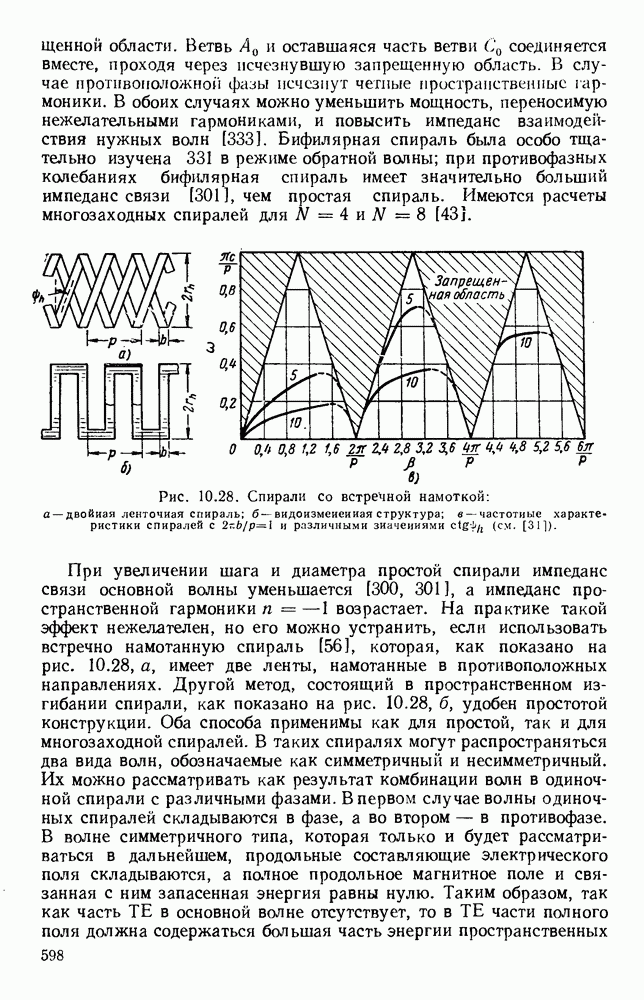
Рис. 10. 23. Структуры типа встречных штырей и типа меандра: а — структура типа встречных штырей; б - дисперсионные кривые для различных значений параметра  в — структура типа меандра. (См. [48].)
в — структура типа меандра. (См. [48].)
При коротком замыкании  и т. д. получается структура типа меандра, изображенная на рис. 10.23. в. Ее период равен
и т. д. получается структура типа меандра, изображенная на рис. 10.23. в. Ее период равен  и распространение в ней возможно начиная с нулевой частоты. С помощью принципа Бабине можно показать [48], что полная дисперсионная кривая структуры типа меандра с шириной зазора
и распространение в ней возможно начиная с нулевой частоты. С помощью принципа Бабине можно показать [48], что полная дисперсионная кривая структуры типа меандра с шириной зазора  и шириной ленты
и шириной ленты  совпадаете дисперсионной кривой структуры типа встречных штырей с шириной зазора
совпадаете дисперсионной кривой структуры типа встречных штырей с шириной зазора  и шириной ленты
и шириной ленты  В случае структур с толстыми лентами
В случае структур с толстыми лентами
фазовая и групповая скорости  пространственной гармоники определяются соответственно соотношениями
пространственной гармоники определяются соответственно соотношениями

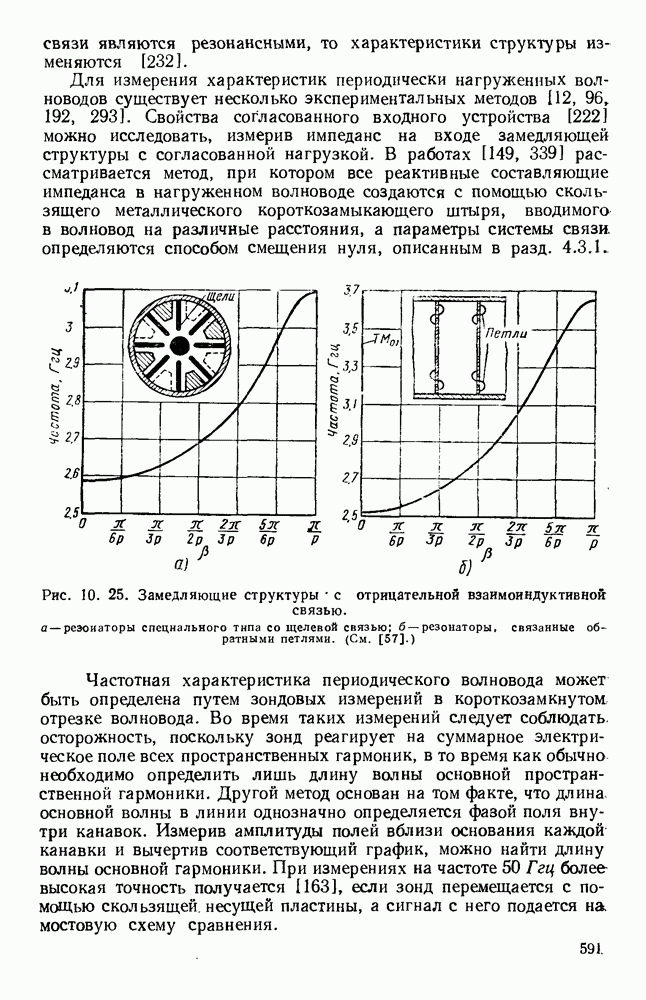
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
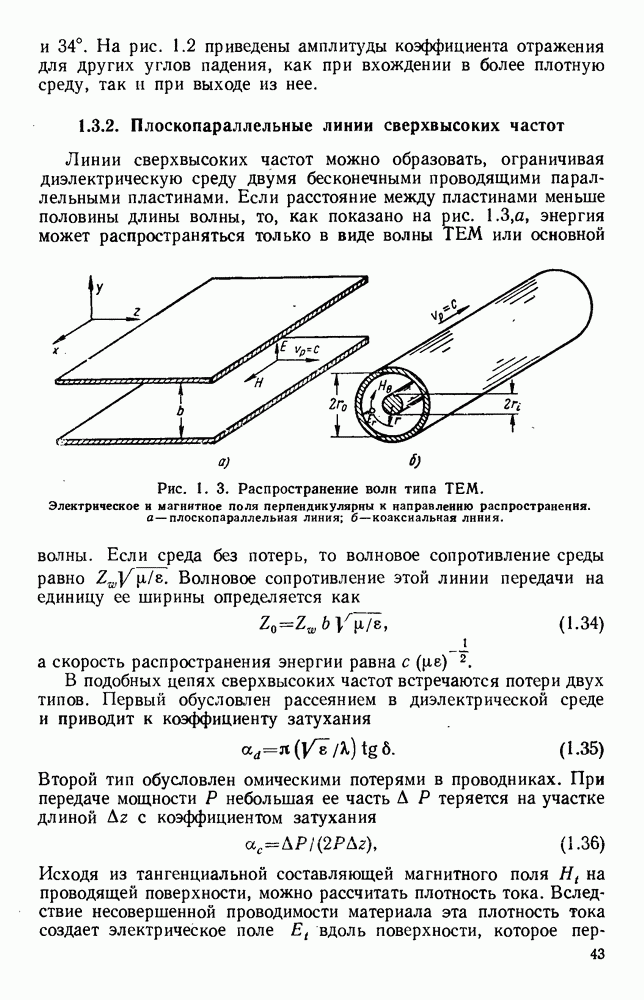
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
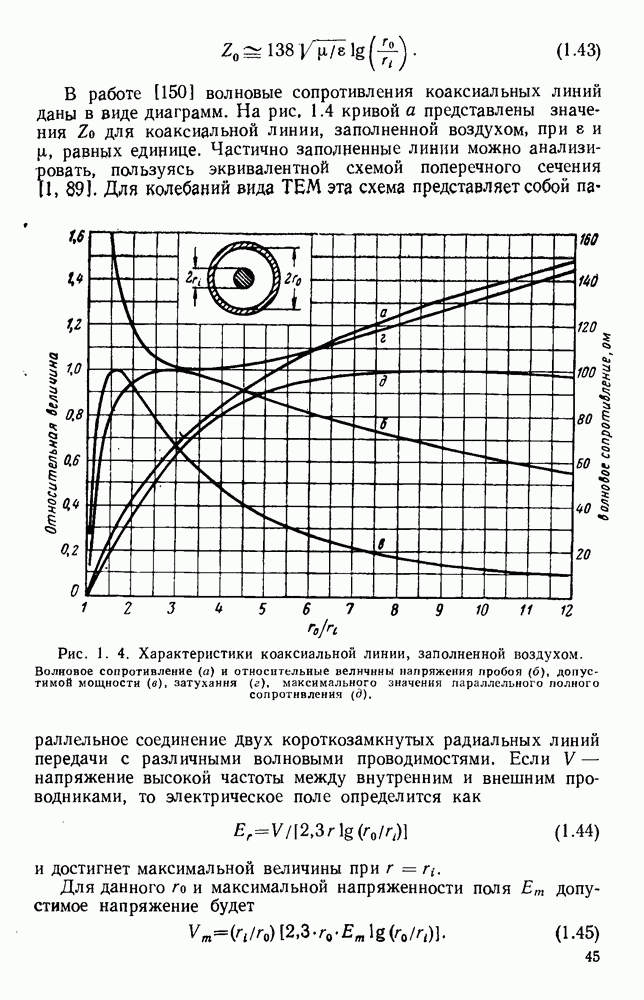
- 1.3.3. Коаксиальные линии
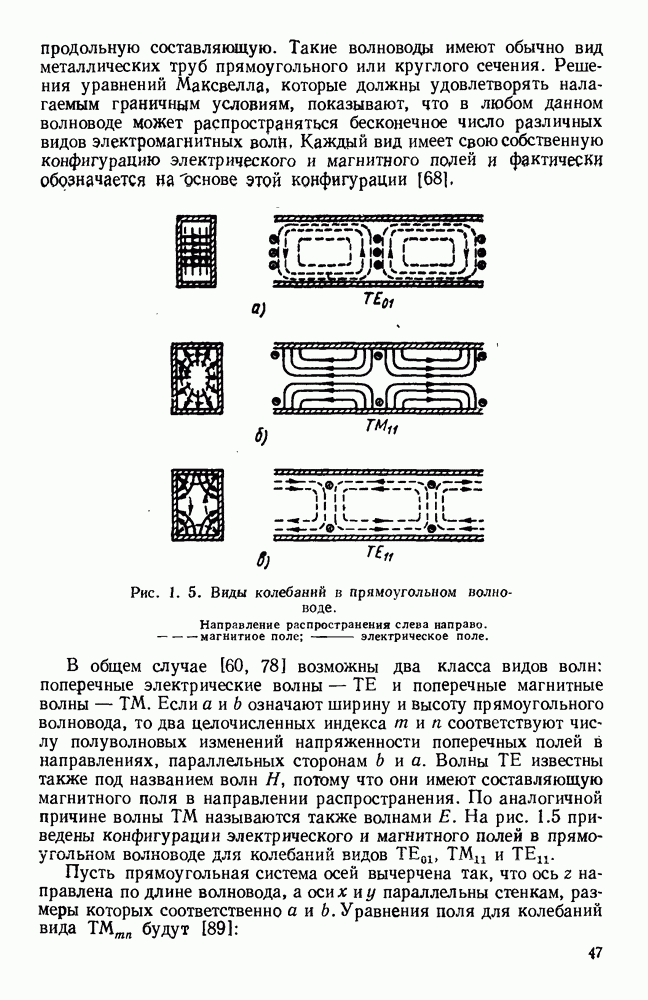
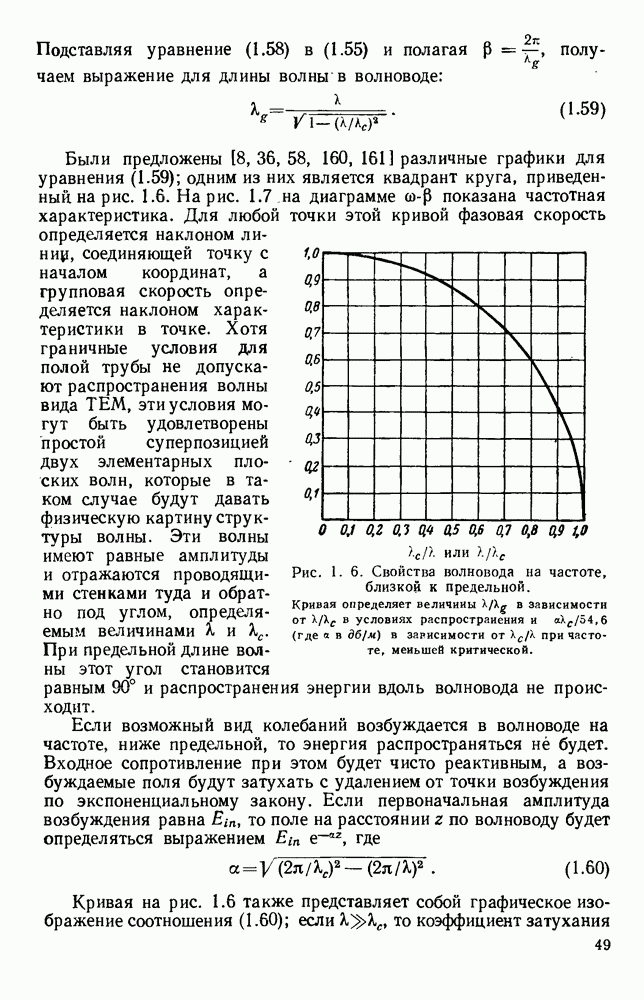
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
- 1.4.2. Круглые волноводы
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
- 1.5.2. Гребневые волноводы
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
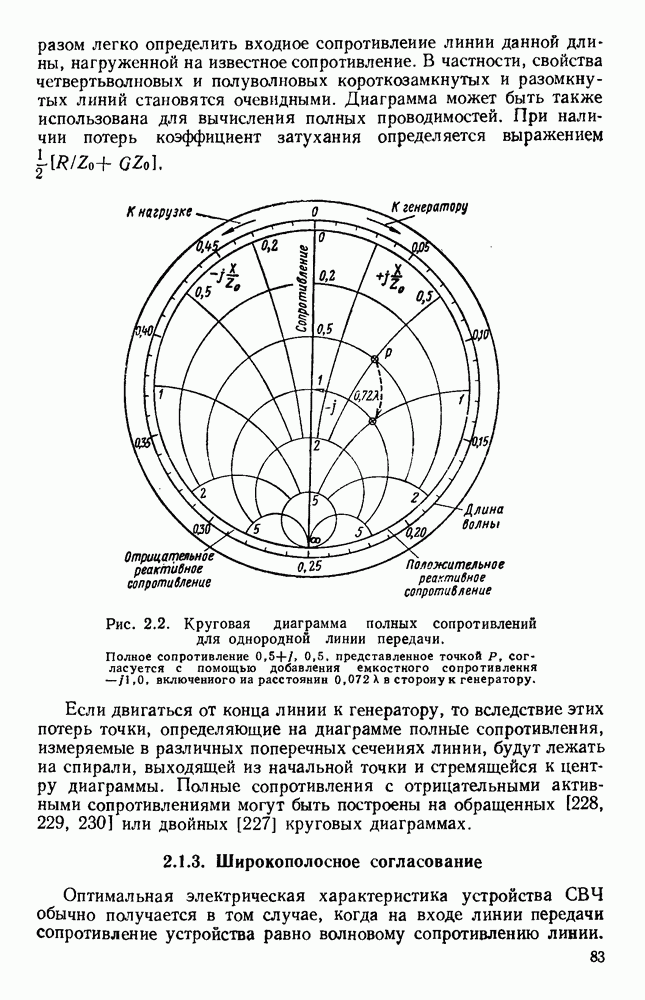
- 2.1.2. Круговая диаграмма
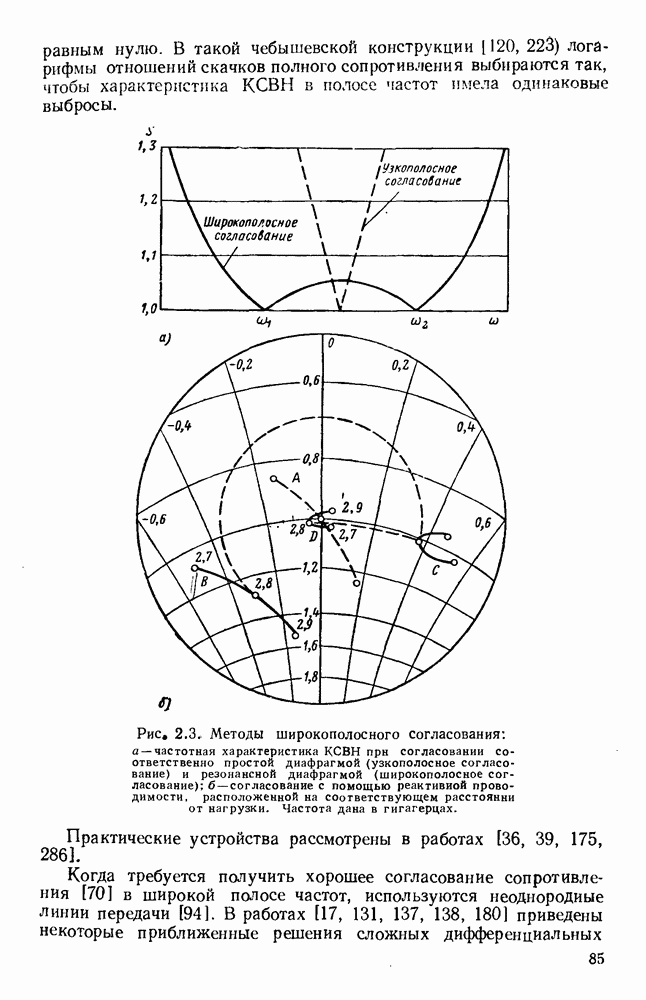
- 2.1.3. Широкополосное согласование
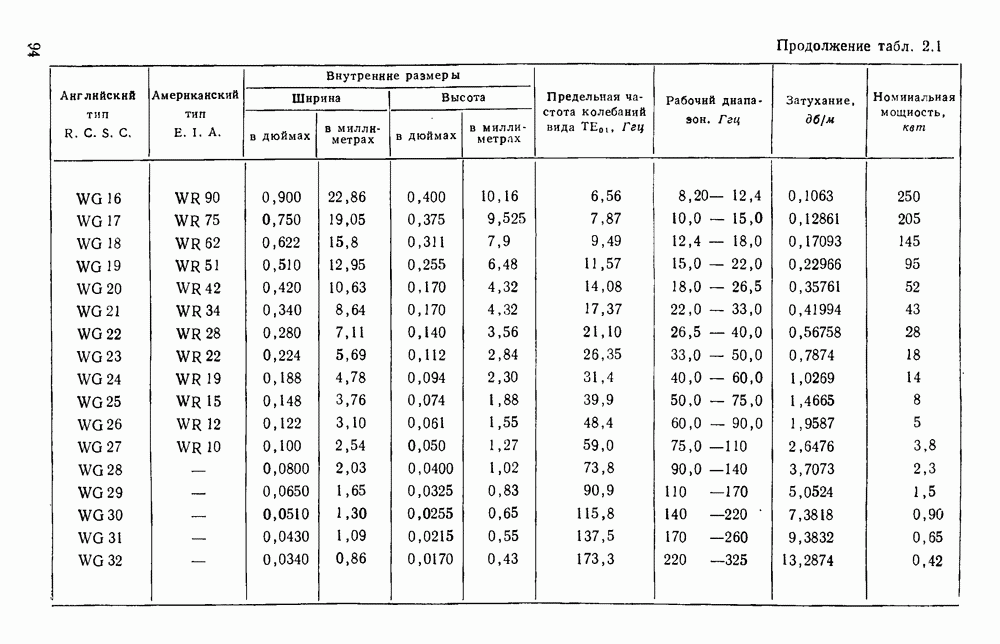
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
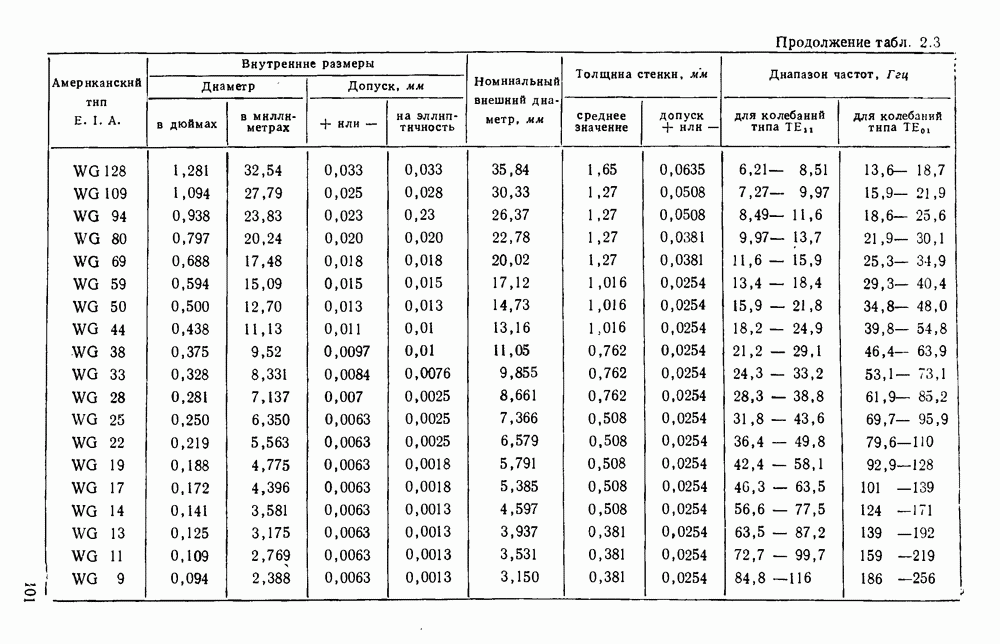
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
- 2.3.1. Прямоугольные волноводы
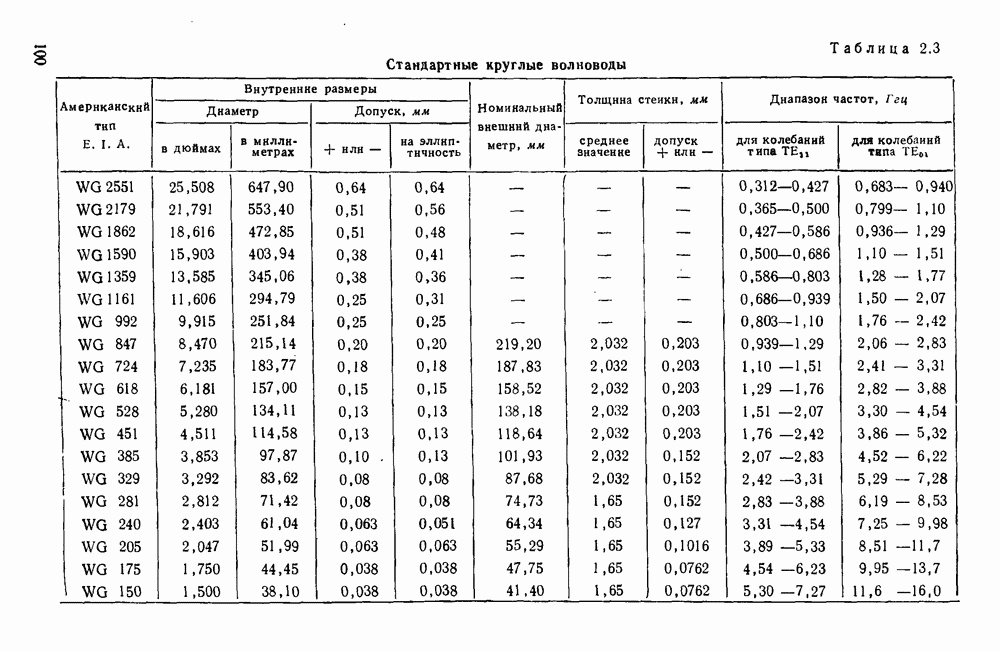
- 2.3.2. Круглые волноводы
- 2.3.3. Широкополосные и компактные волноводы
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
- 2.4.2. Контактные прокладки и дроссели
- 2.4.3. Крепежные и зажимные устройства
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
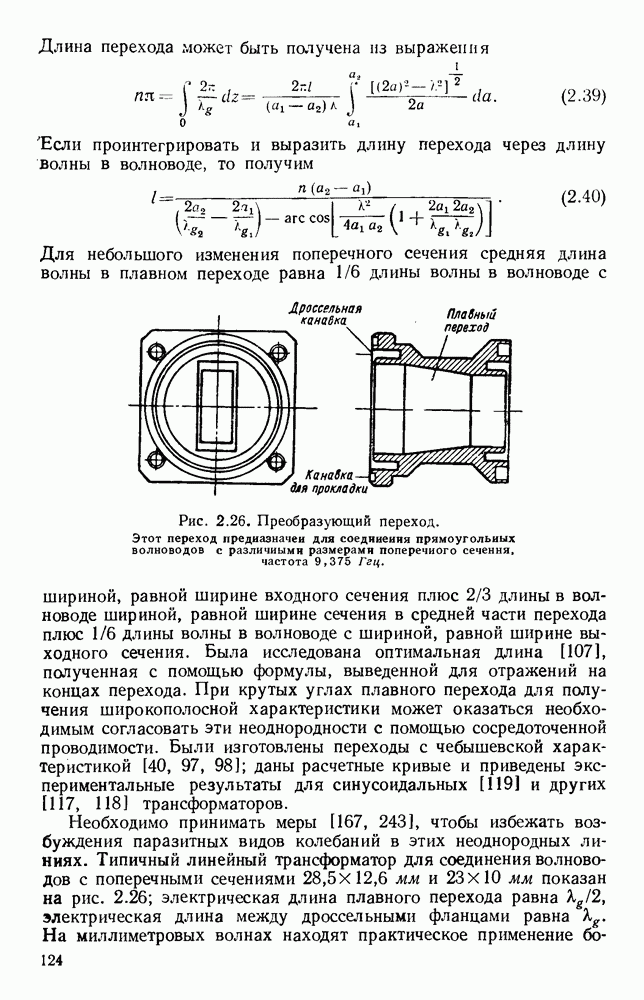
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
- 2.6.1. Изгибы, уголки и скрутки
- 2.6.2. Переходы и преобразователи
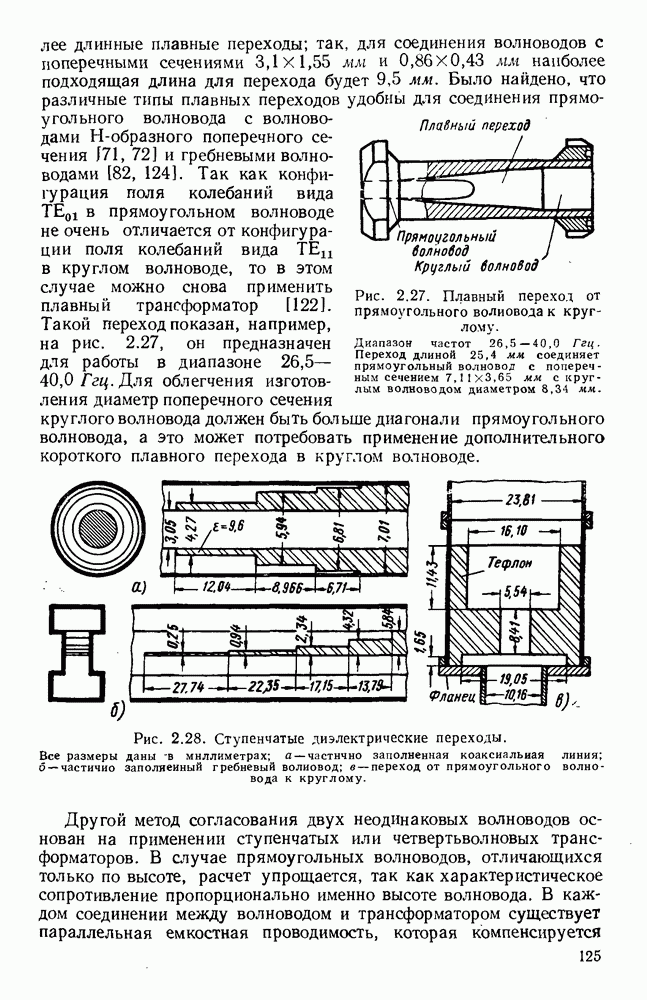
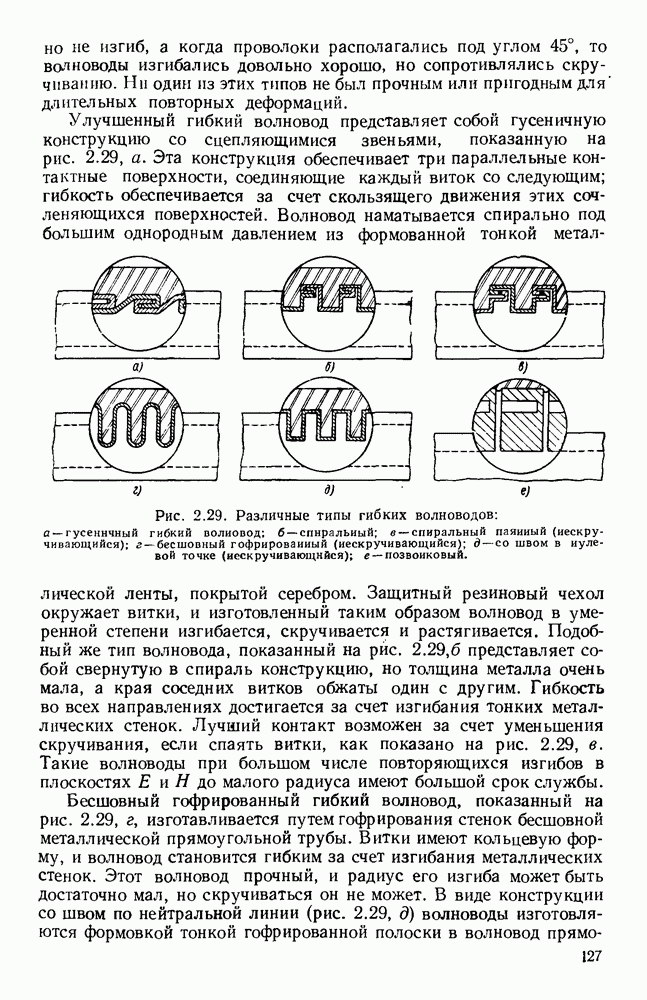
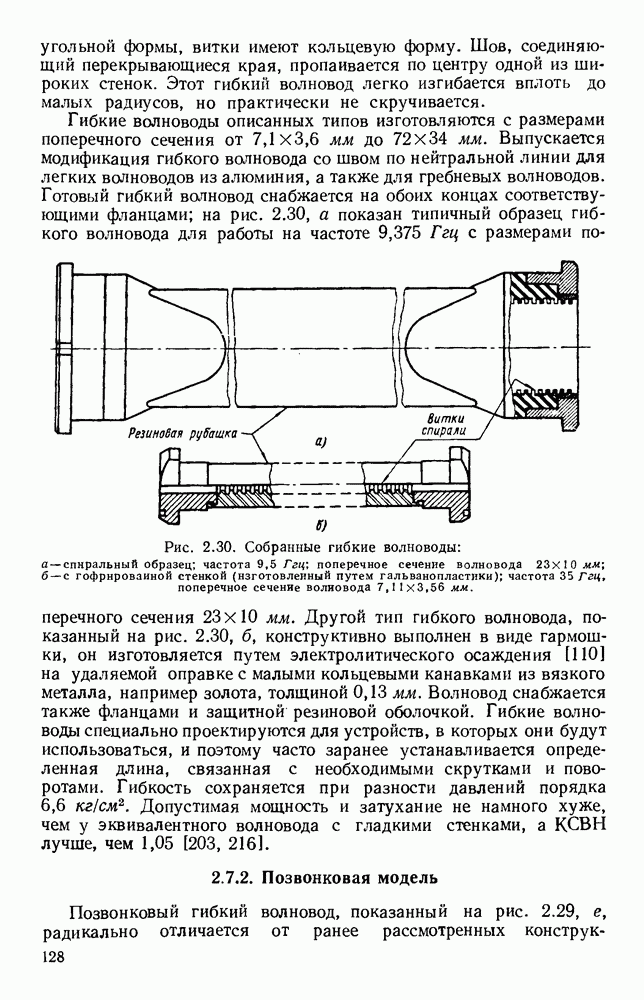
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
- 3.2.3. Переход от линейной поляризации к круговой
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
- 3.6.2. Вращающиеся сочленения различных типов
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
- 3.7.1. Механические переключатели с ручным управлением
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
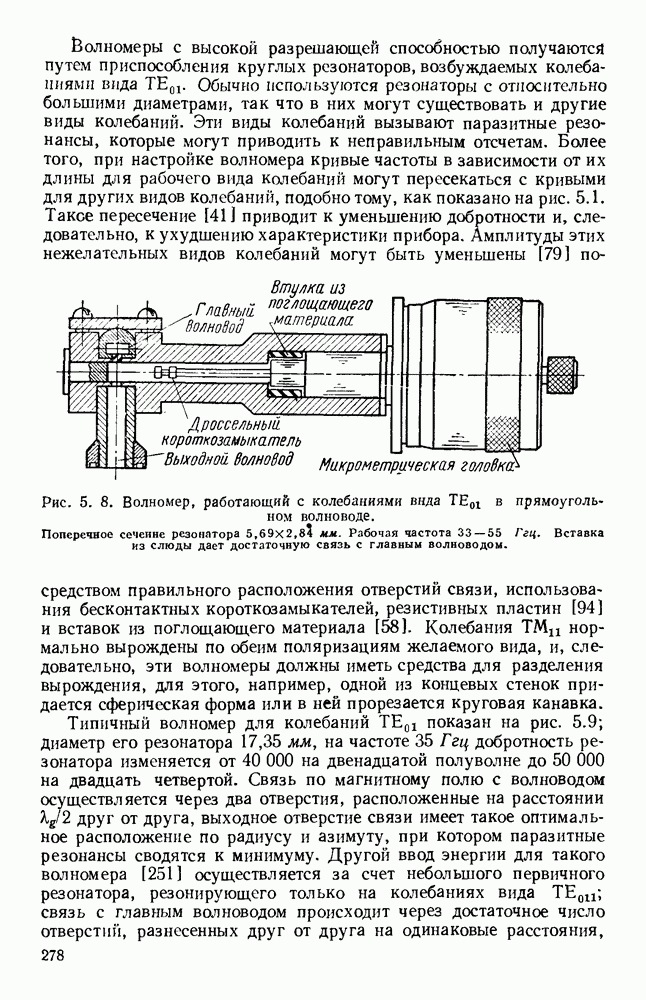
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
- 5.2.1. Волномеры с объемными резонаторами
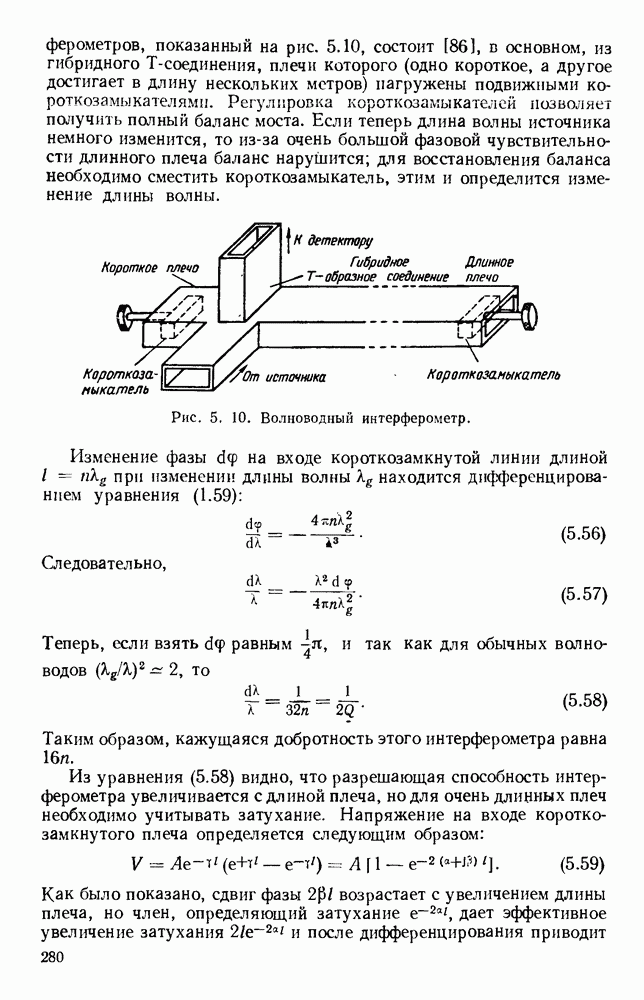
- 5.2.2. Волноводные интерферометры
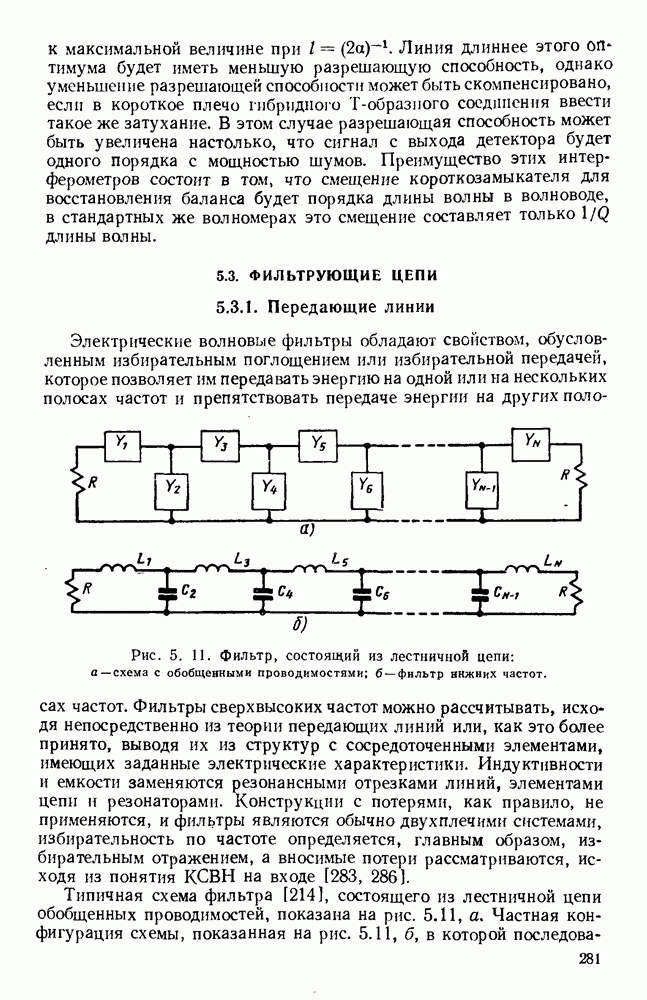
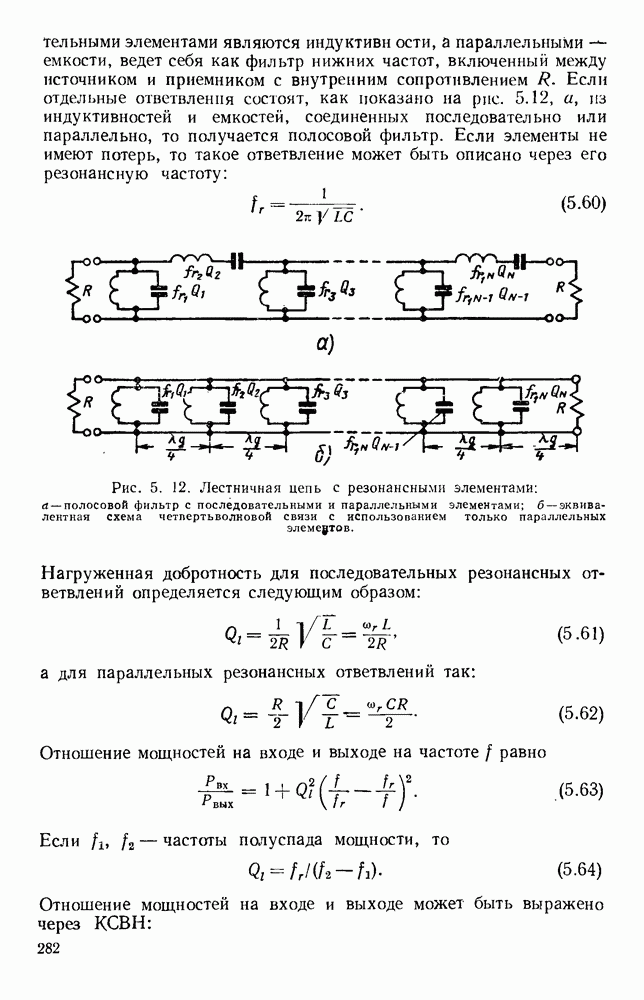
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
- 5.3.2. Связанные резонаторы
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
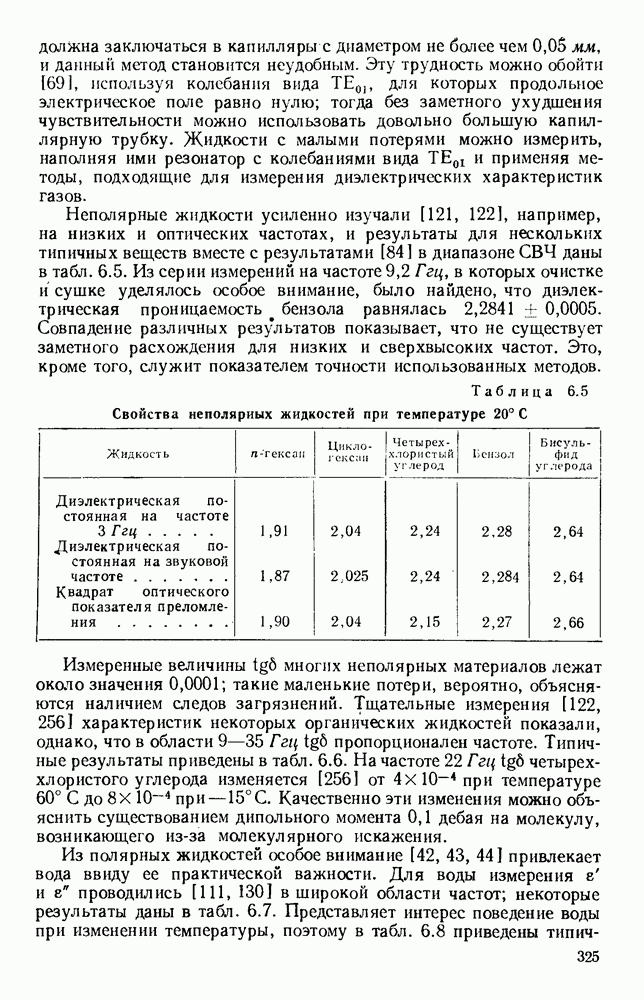
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
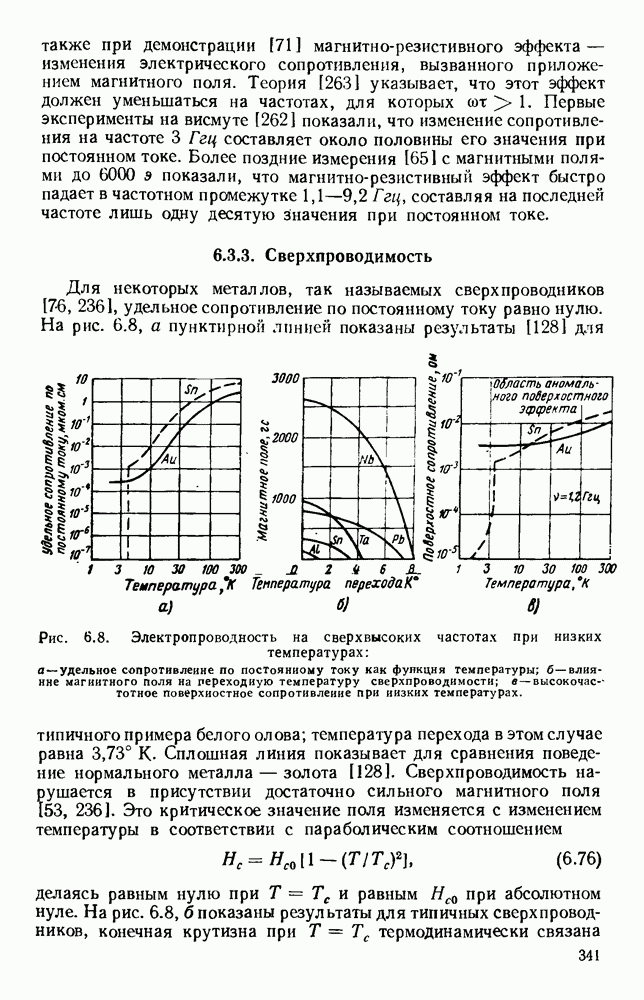
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
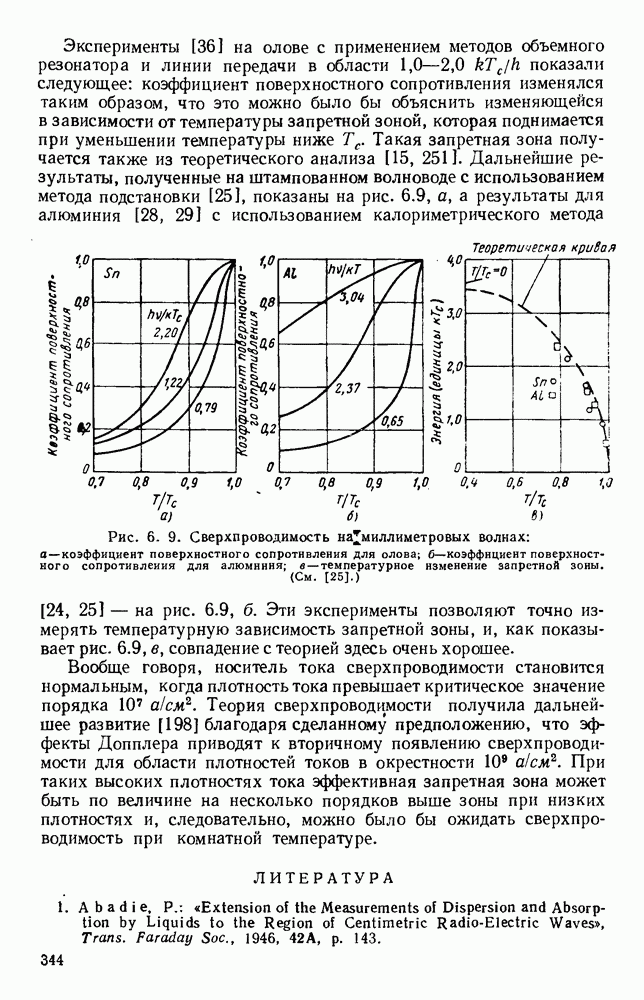
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
- 7.1.2. Форма линии и интенсивность
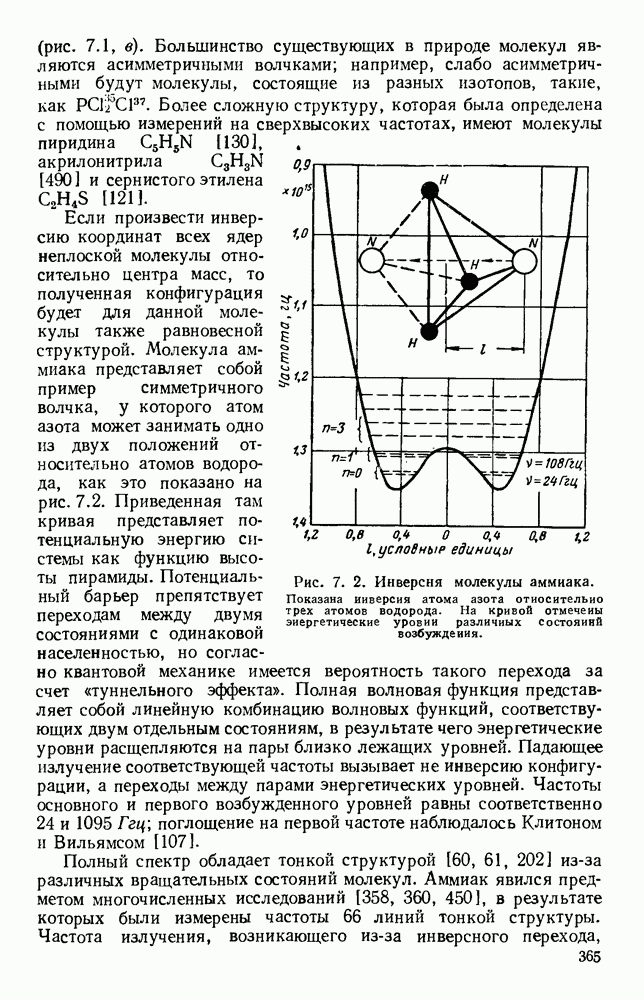
- 7.1.3. Сверхтонкая структура
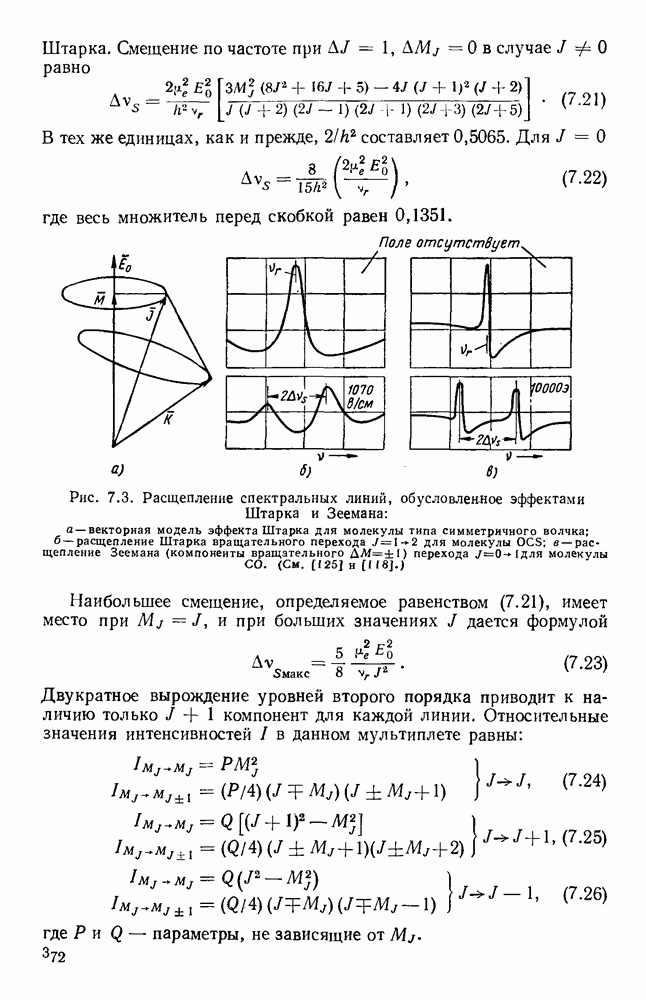
- 7.1.4. Явления Штарка и Зеемана
- 7.2. СПЕКТРОМЕТРЫ
- 7.2.2. Поглощающие ячейки
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
- 7.3.4. Времена релаксации
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
- 8.3.3. Ферритовые устройства в качестве элементов схем
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
- 8.6.2. Устройства с поперечным полем
- 8.6.3. Прочие узлы
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
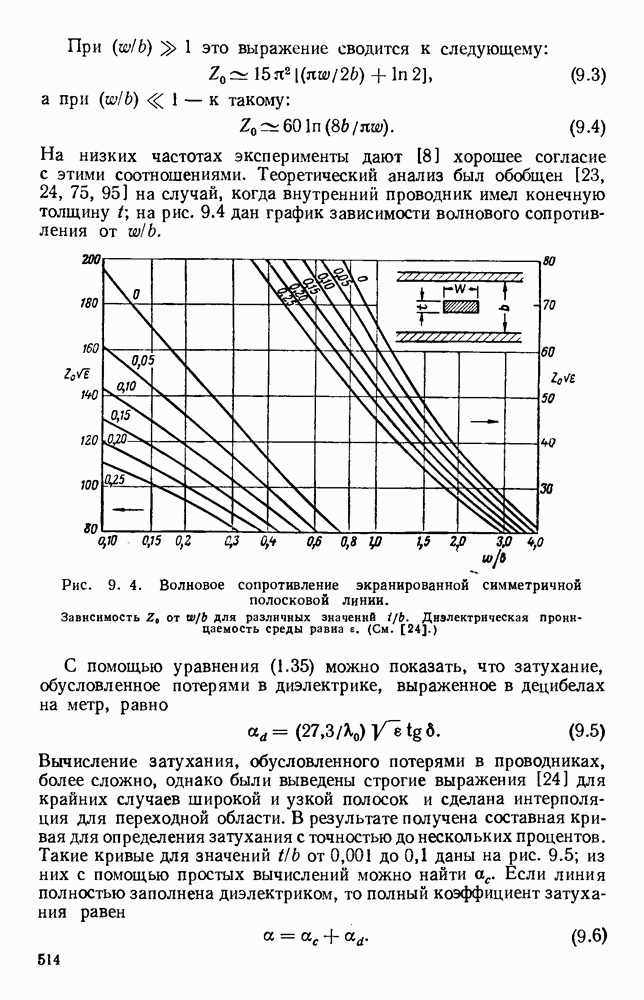
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.2.1. Линии типа «диэлектрических сэндвичей»
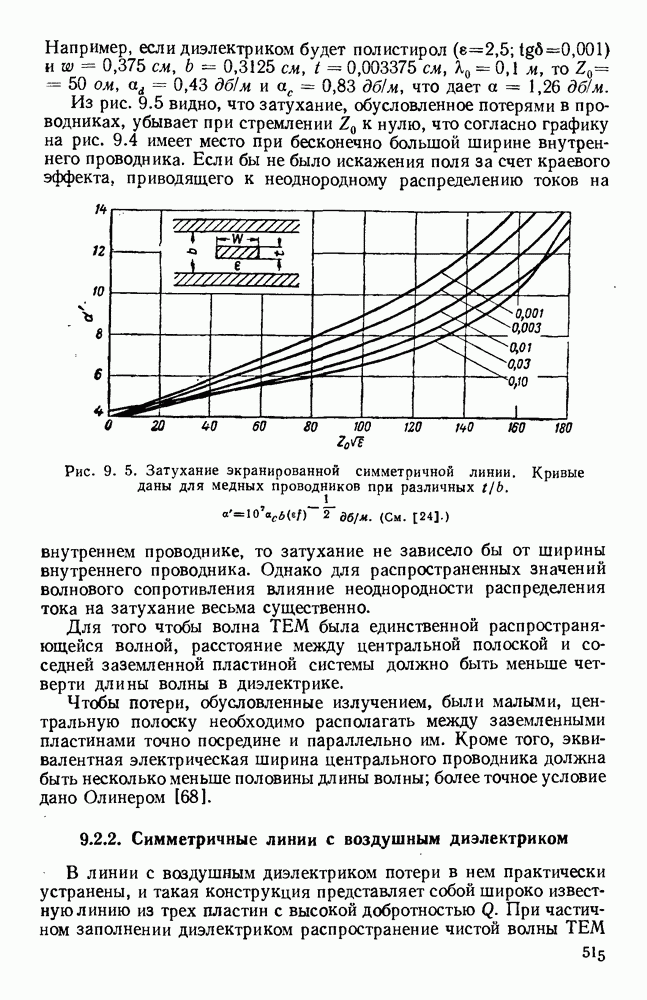
- 9.2.2. Симметричные линии с воздушным диэлектриком
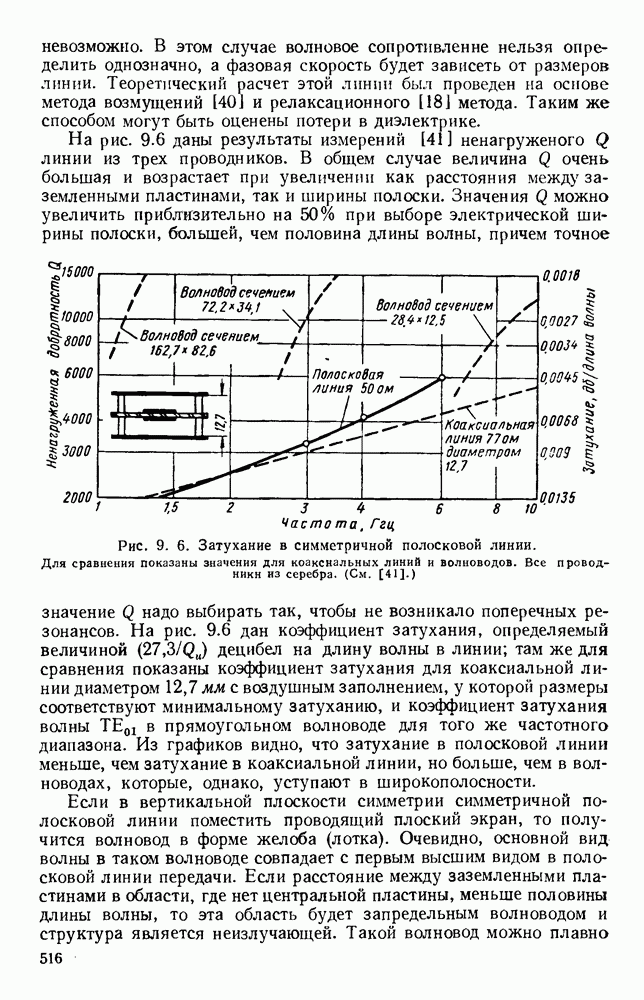
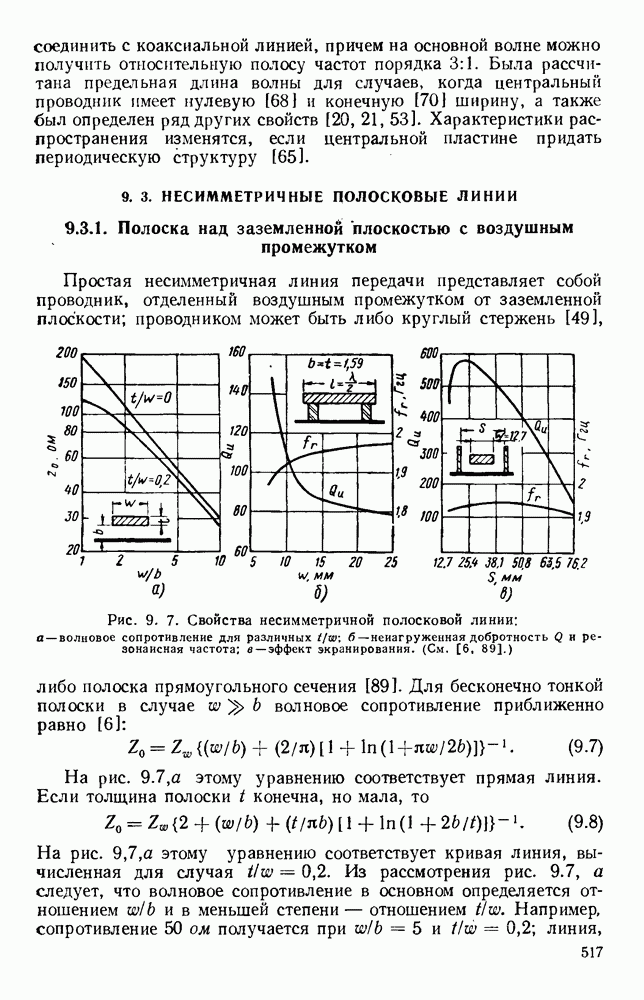
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
- 9.4.2. Переходные устройства
- 9.4.3. Узлы полосковых систем
- 9.5. ЦЕПИ И СИСТЕМЫ
- 9.5.3. Частотные фильтры
- 9.5.4. Цепи питания антенн
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
- 10.1.2. Пространственные гармоники
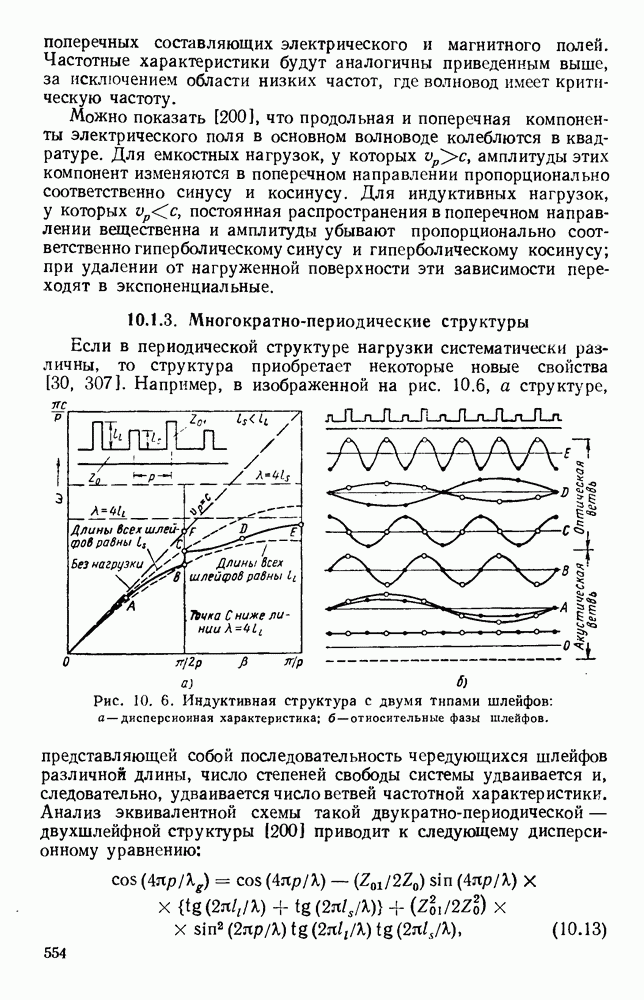
- 10.1.3. Многократно-периодические структуры
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
- 10.2.3. Продольные цилиндрические волны
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
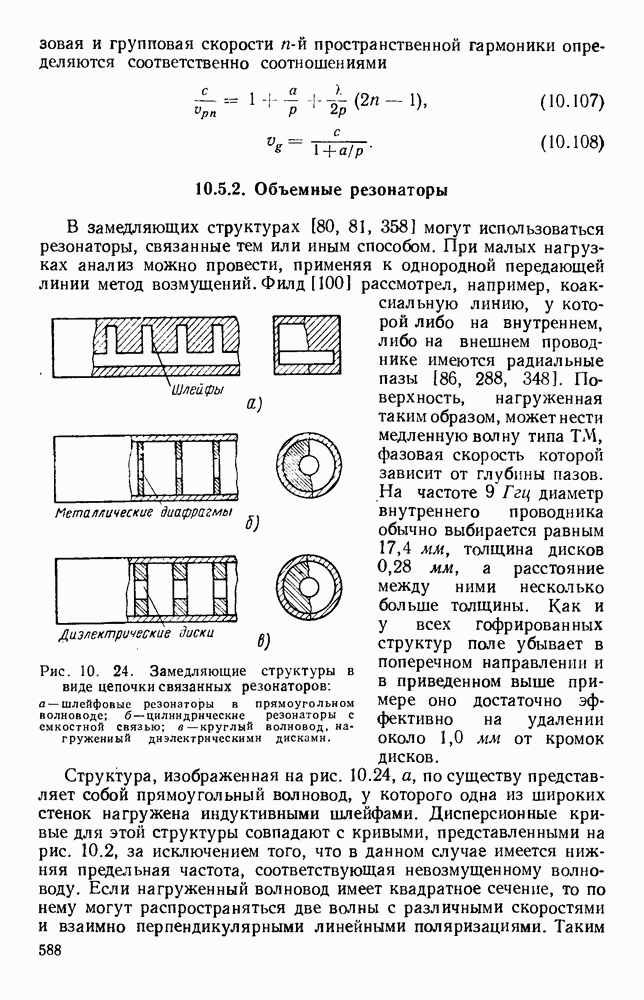
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
- 12.2. МАГНЕТРОНЫ
- 12.2.2. Резонаторные системы
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
- 12.2.4. Рабочие характеристики
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
- 13.1.2. Типы дифракции
- 13.1.3. Рассеяние
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
- 13.2.2. Структуры волноводного типа
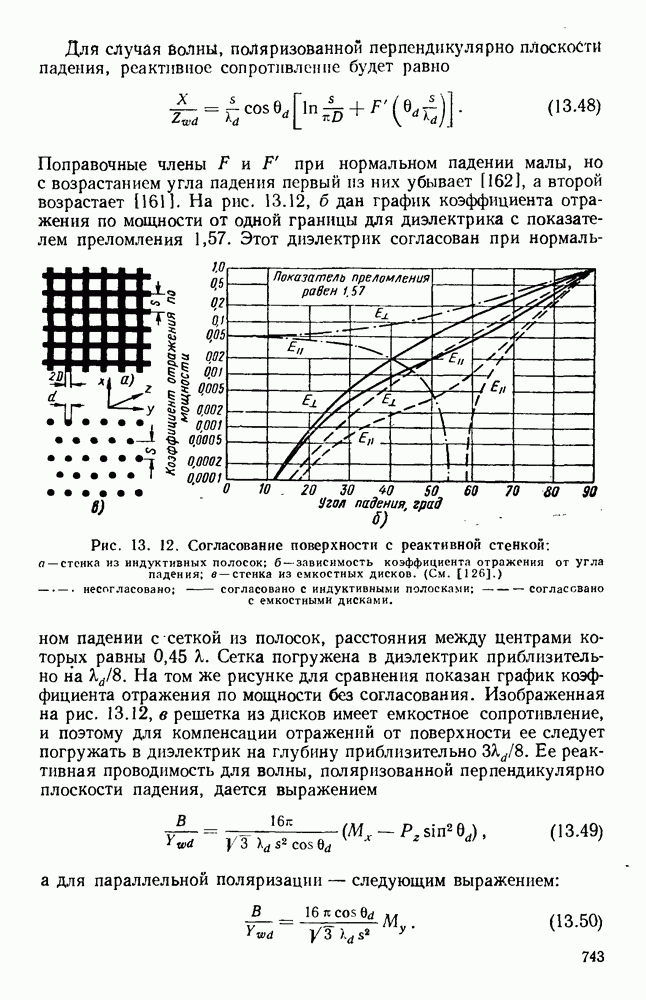
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
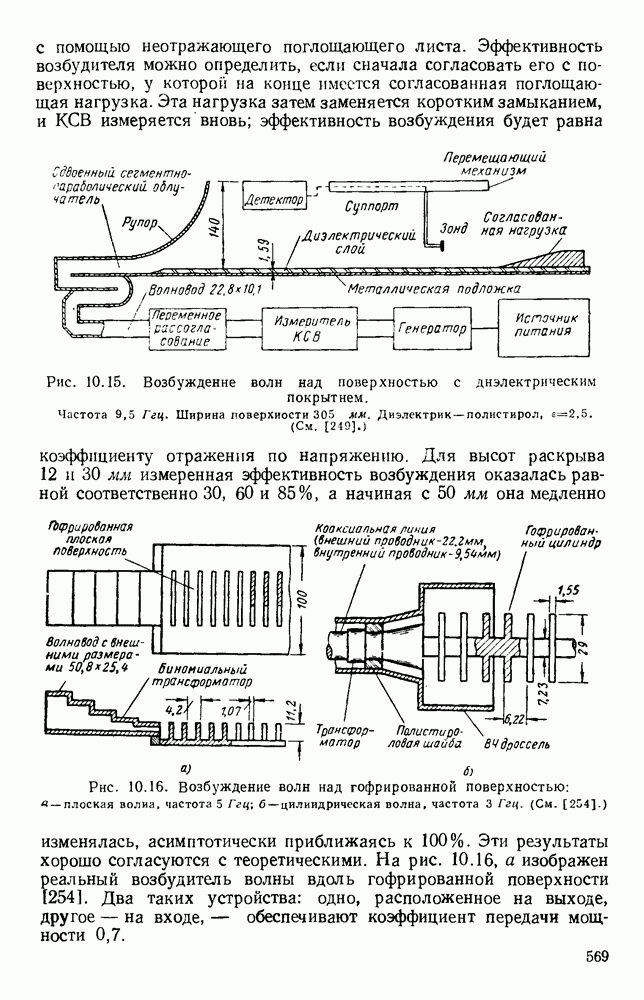
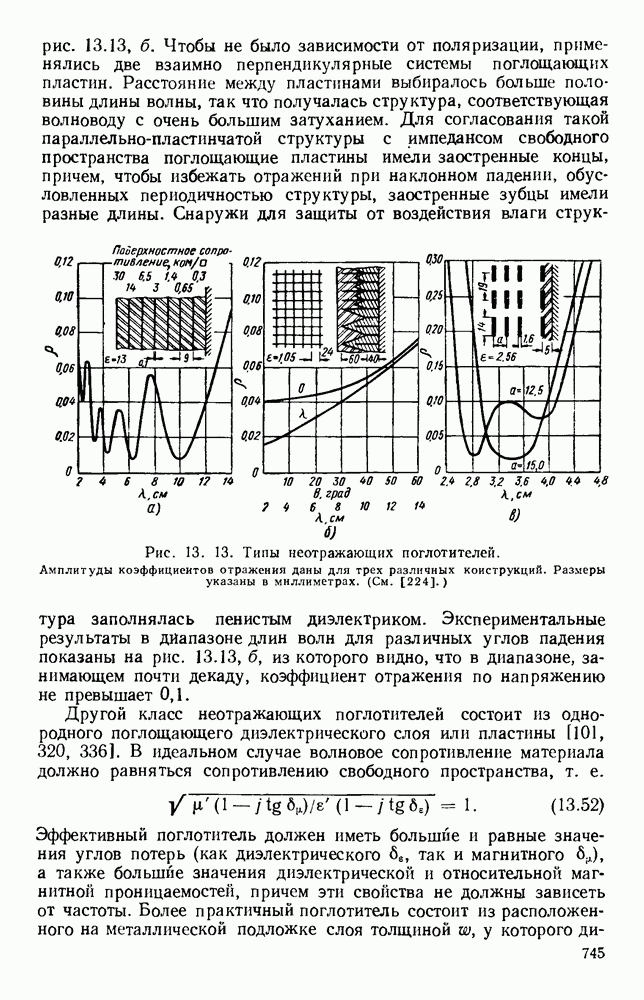
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
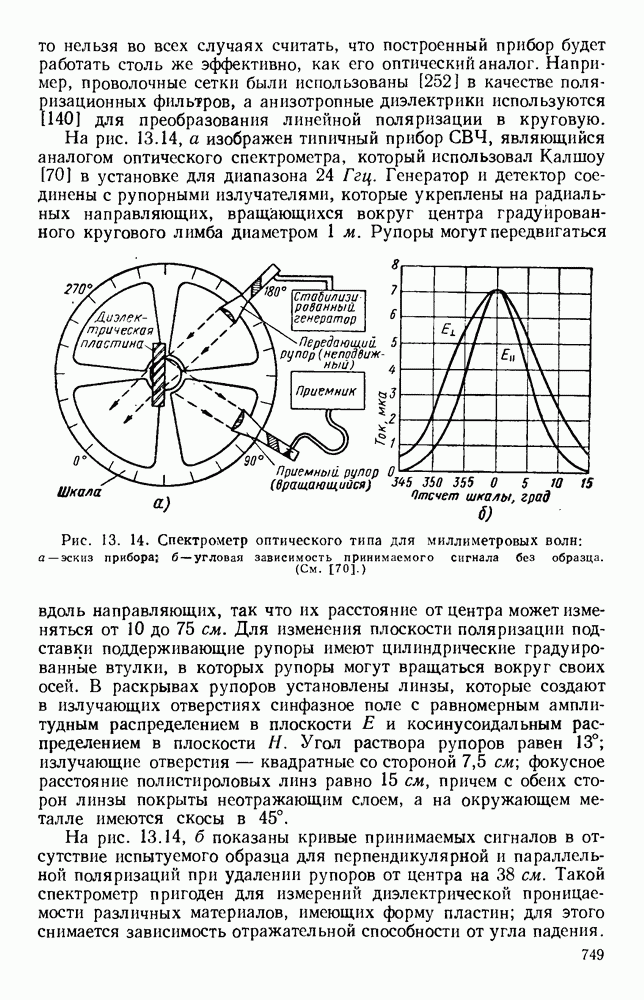
- 13.4. ПРИБОРЫ И СИСТЕМЫ
- 13.4.1. Спектрометры
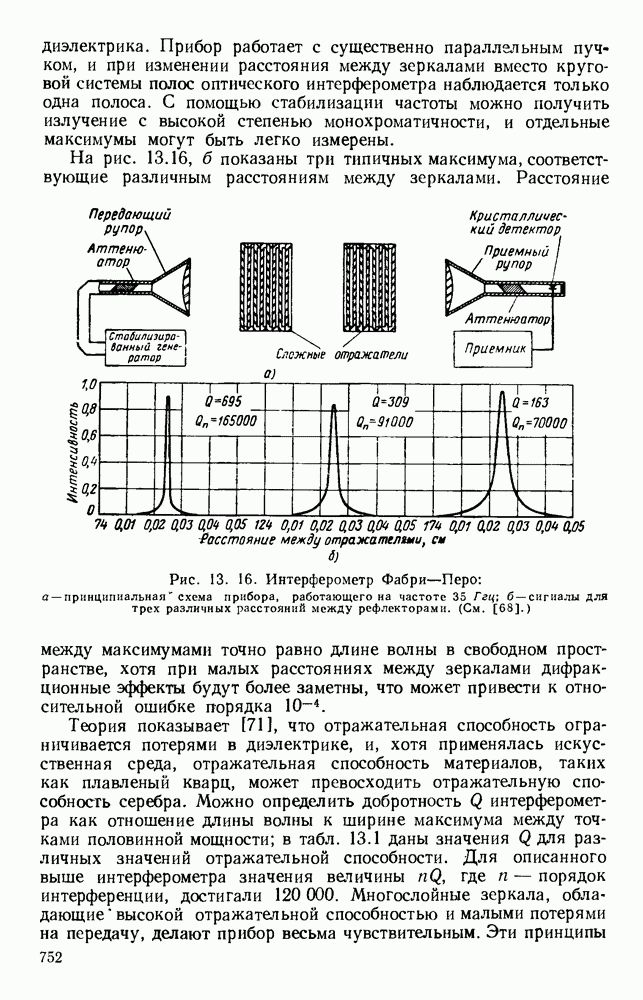
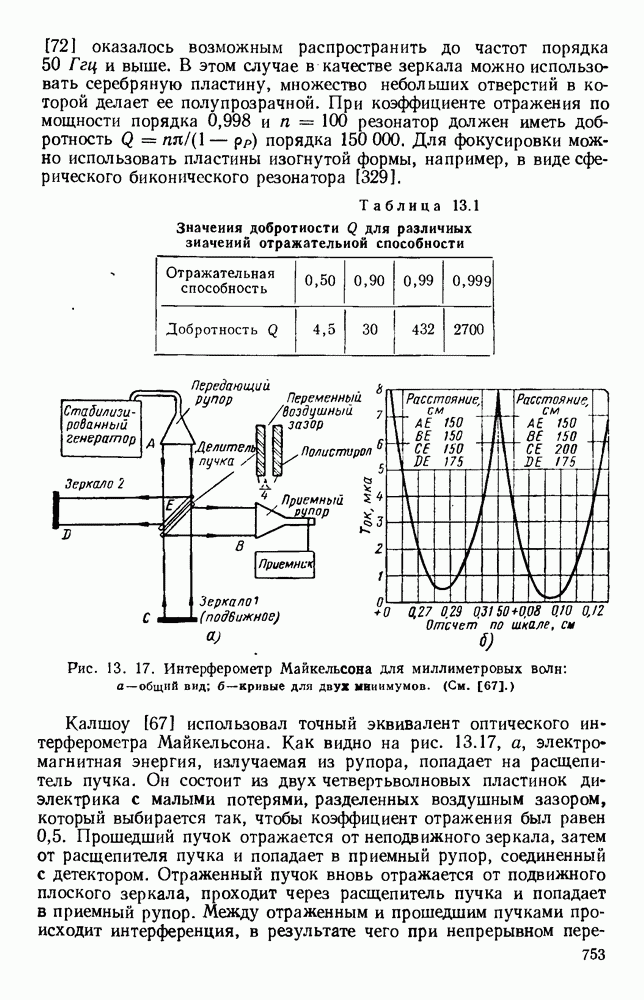
- 13.4.2. Интерферометры
- 13.4.3. Устройство с делением пучка