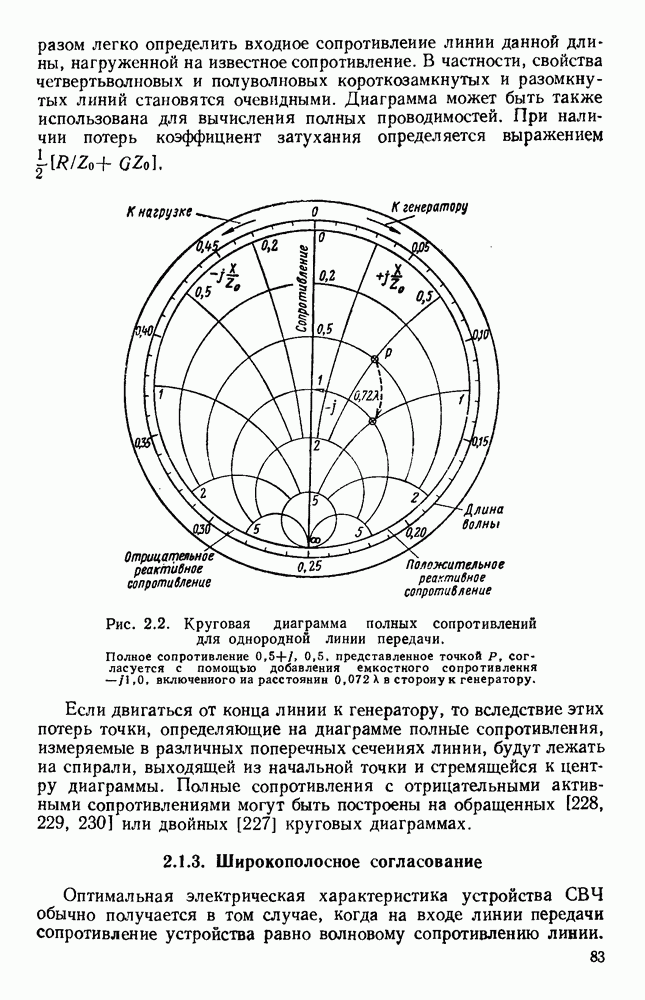
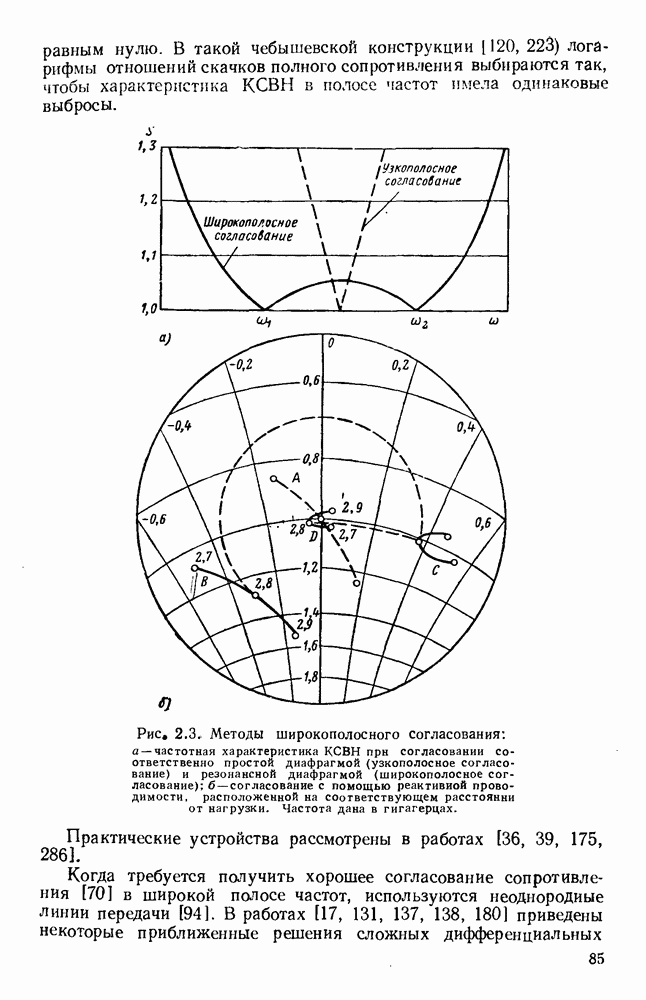
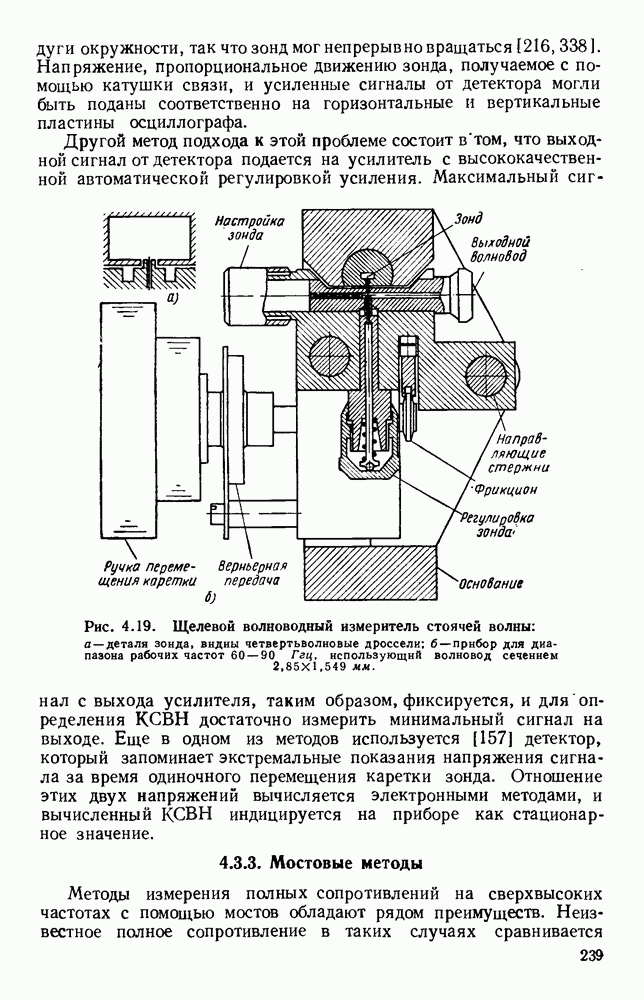
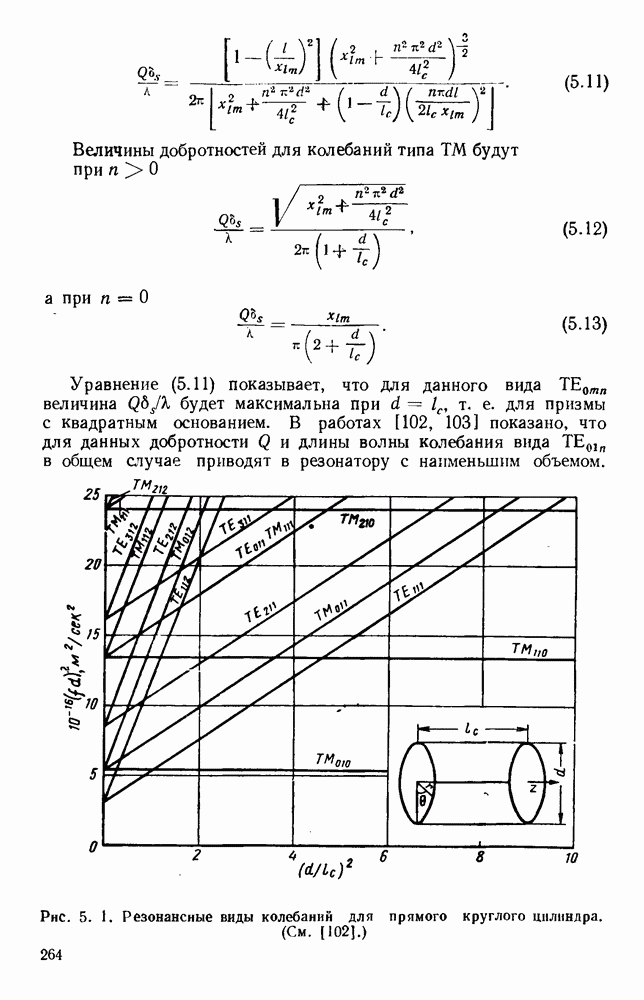
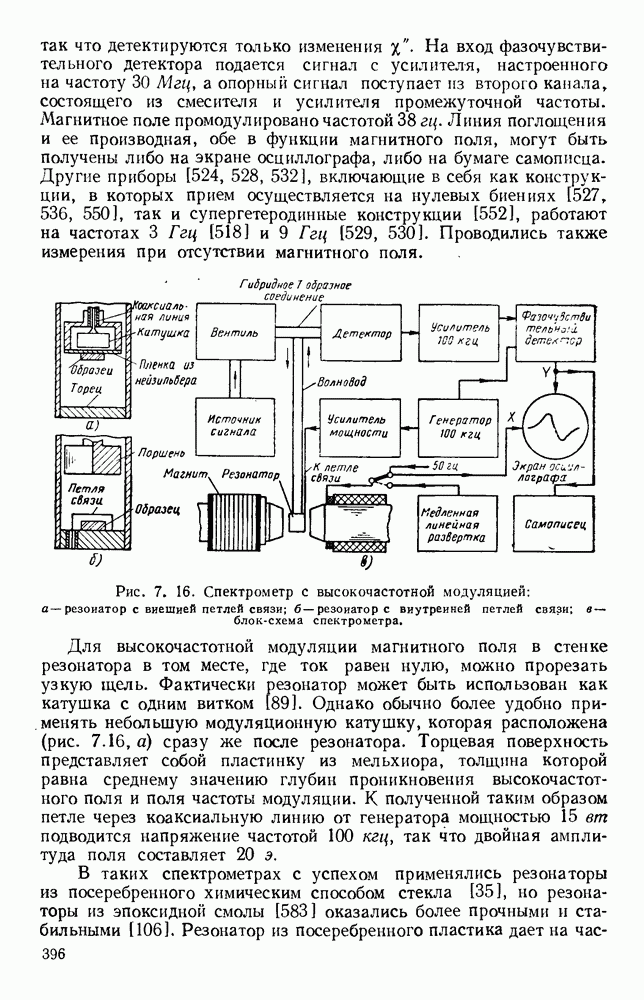
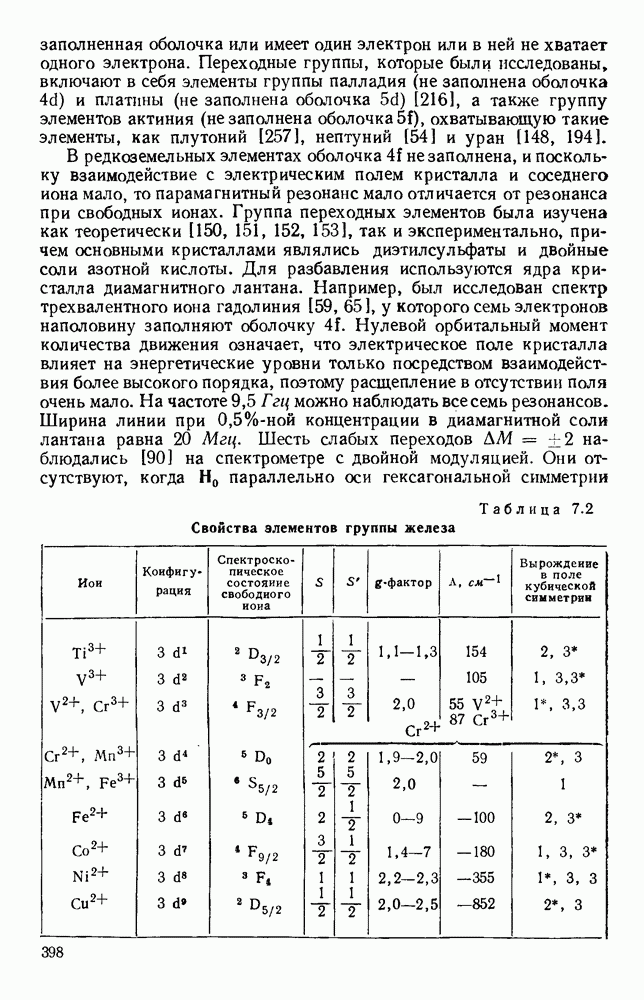
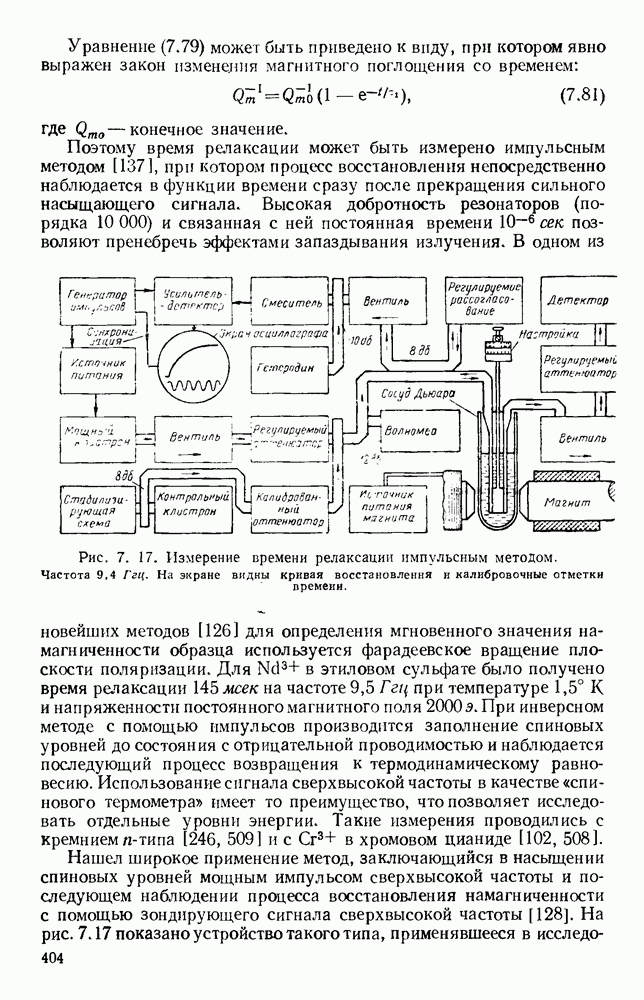
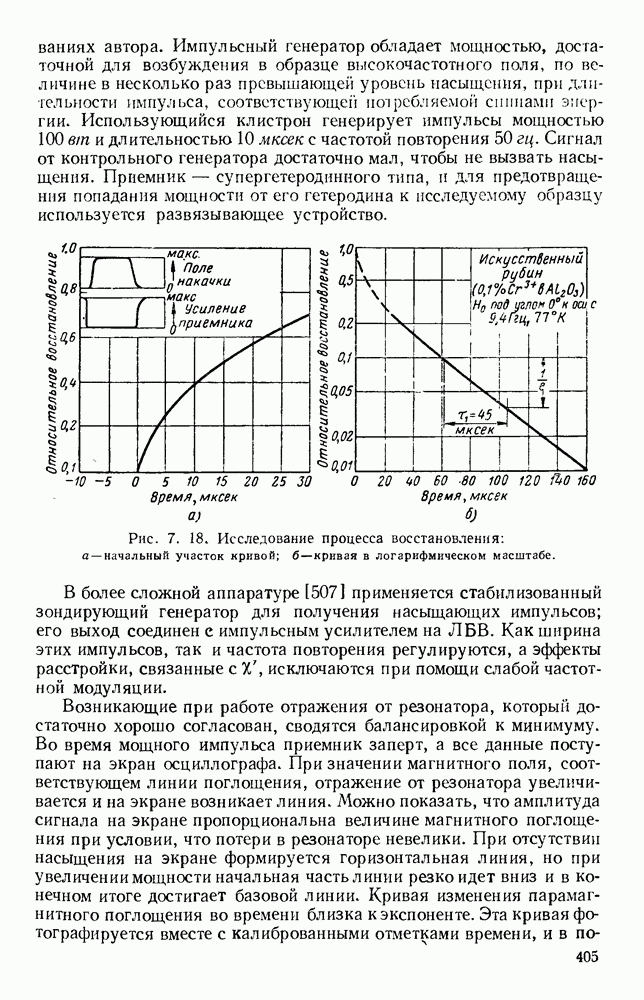
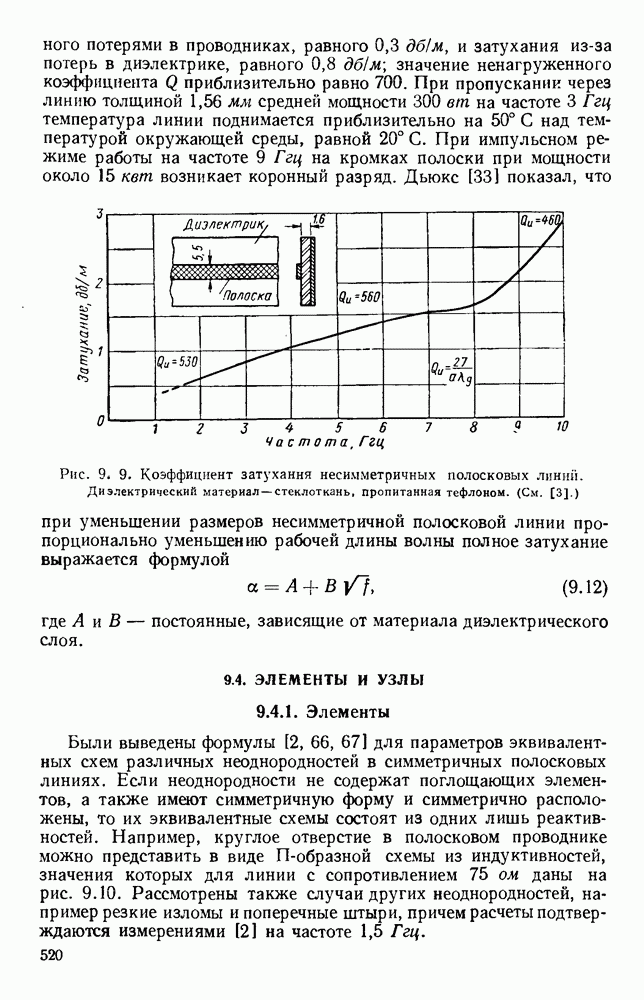
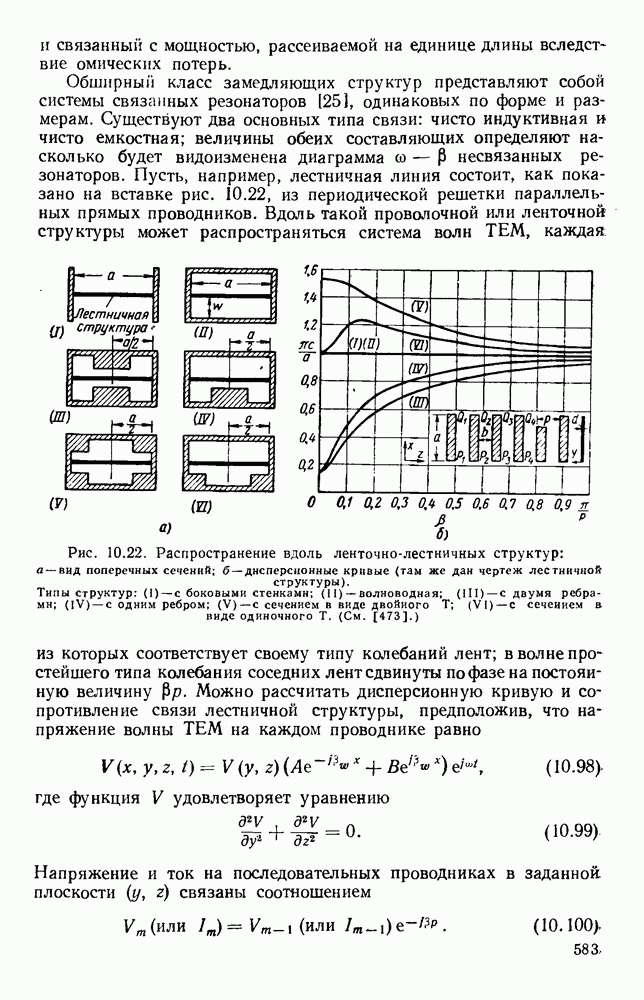
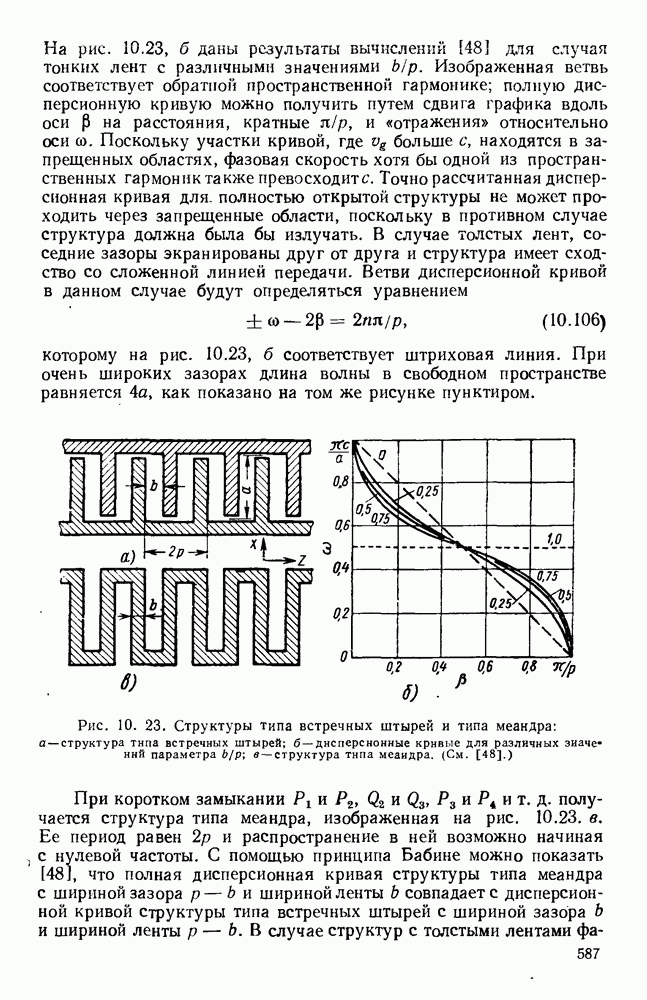
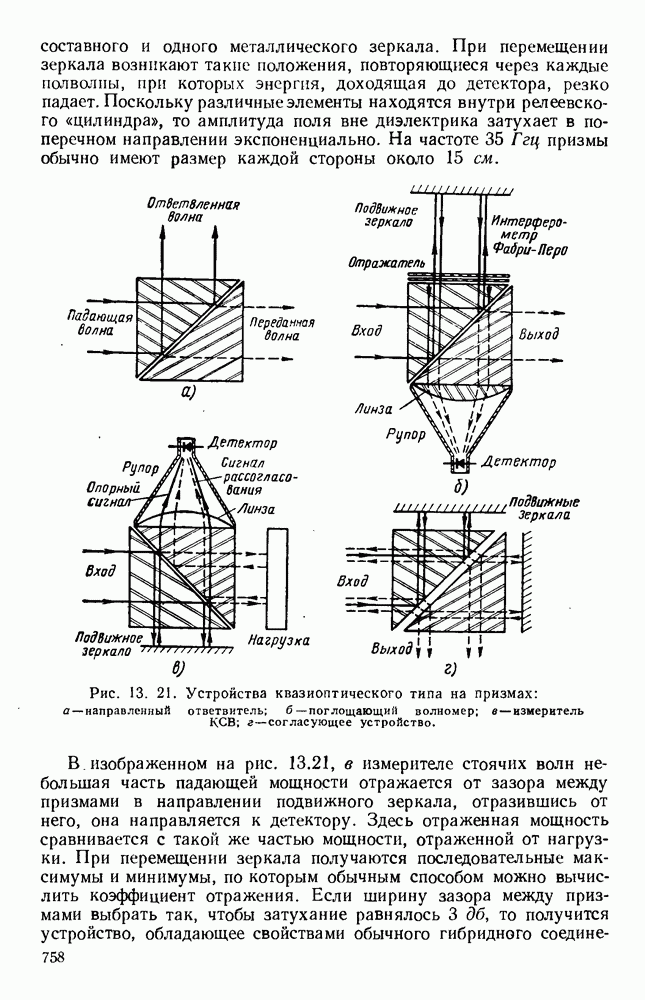
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
13.1. ИЗЛУЧЕНИЕ, ДИФРАКЦИЯ И РАССЕЯНИЕ
13.1.1. Поле излучения
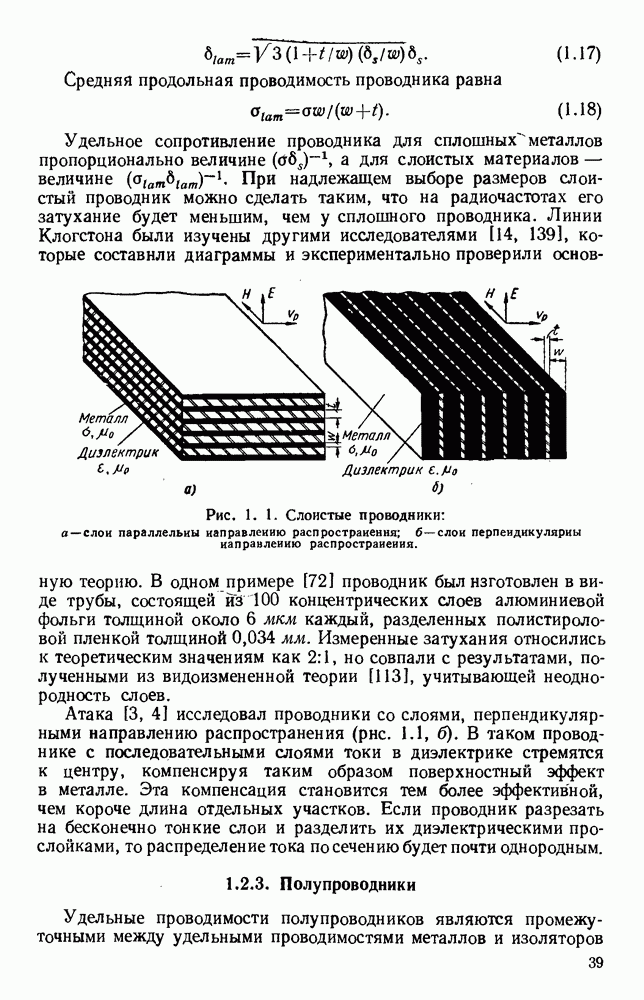
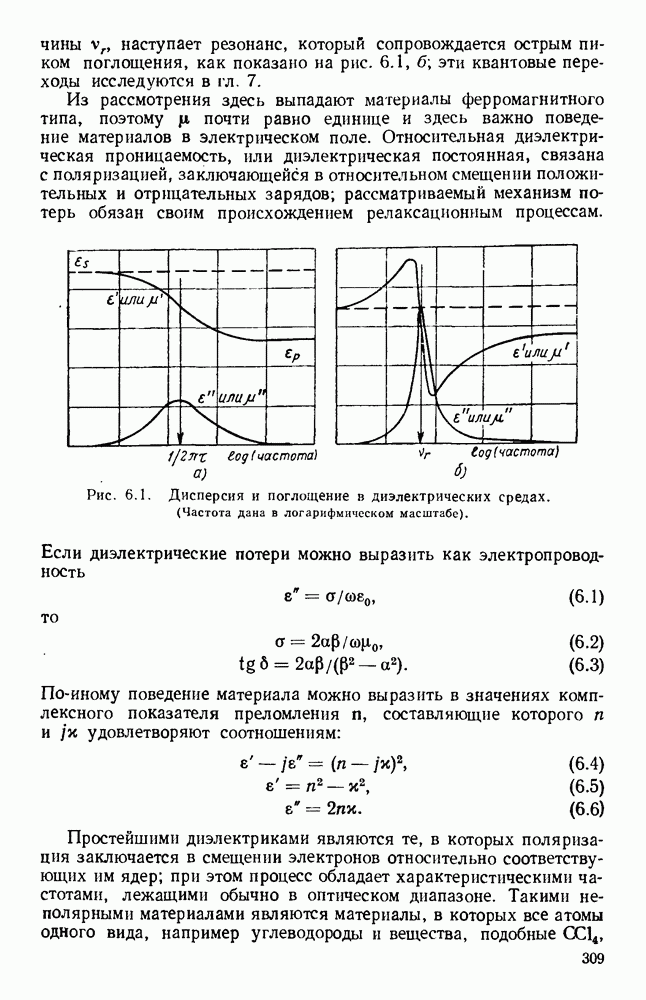
Применение оптической техники [373] на сверхвысоких частотах возможно при соответствующем учете разницы длин волн этого диапазона и оптического. Размеры излучающих поверхностей и апертур на сверхвысоких частотах обычно сравнимы с длиной волны в свободном пространстве; так, вдоль щели длиной 10 см уложится около 180 000 длин волн зеленого света  и только 10 длин волн типичного, излучения СВЧ (
и только 10 длин волн типичного, излучения СВЧ ( ). Поэтому при изучении и использовании излучения СВЧ необходимо учитывать дифракцию, т. е. учитывать влияние распределения фазы и амплитуды в излучающей апертуре.
). Поэтому при изучении и использовании излучения СВЧ необходимо учитывать дифракцию, т. е. учитывать влияние распределения фазы и амплитуды в излучающей апертуре.
Применение оптических принципов в диапазоне СВЧ имеет длинную историю [194]. Ранние работы [21, 113, 199, 248, 369] охватывали широкий круг вопросов, включая измерения с естественными [98] и искусственными [17] диэлектриками, а также применение устройств вроде вращателей поляризации [25], поляриметров [26, 27, 154], решеток [23, 364—368, 384] и интерферометров [121, 362, 363, 404]. В современных исследованиях подчеркивается аналогия [145, 146, 147, 148, 149, 173, 214] между акустическими волнами и радиволнами. Практическое применение оптической техники в диапазоне СВЧ стало возможным лишь после создания стабильных когерентных источников энергии, точных измерительных приборов, диэлектриков с улучшенными свойствами и разработки методов контроля поверхностных явлений [112, 343].
Электромагнитная энергия излучается в свободное пространство в тех случаях, когда имеется осциллирующее распределение тока вдоль проводника или поля в апертуре. Эти осцилляции создают
в области вокруг излучателя электрическое и магнитное поля, с которыми связаны запасенная и излучаемая энергии; кроме того, часть энергии рассеивается в проводящих поверхностях. Излучаемая энергия определяет активную часть входного сопротивления излучателя и связана с электрическим и магнитным полями в удаленных точках. Характеристика направленности излучения этой энергии называется диаграммой направленности: обычно диаграмма направленности в заданной плоскости определяется как графически выраженная зависимость величины напряженности электрического поля, измеряемой на заданном расстоянии от источника, от угла, измеряемого в этой же плоскости.

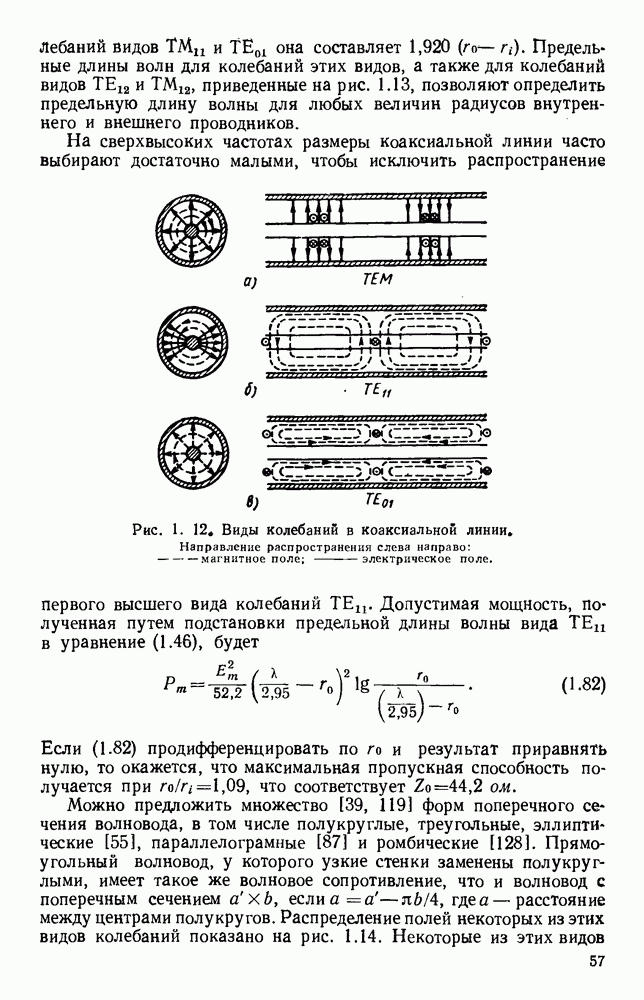
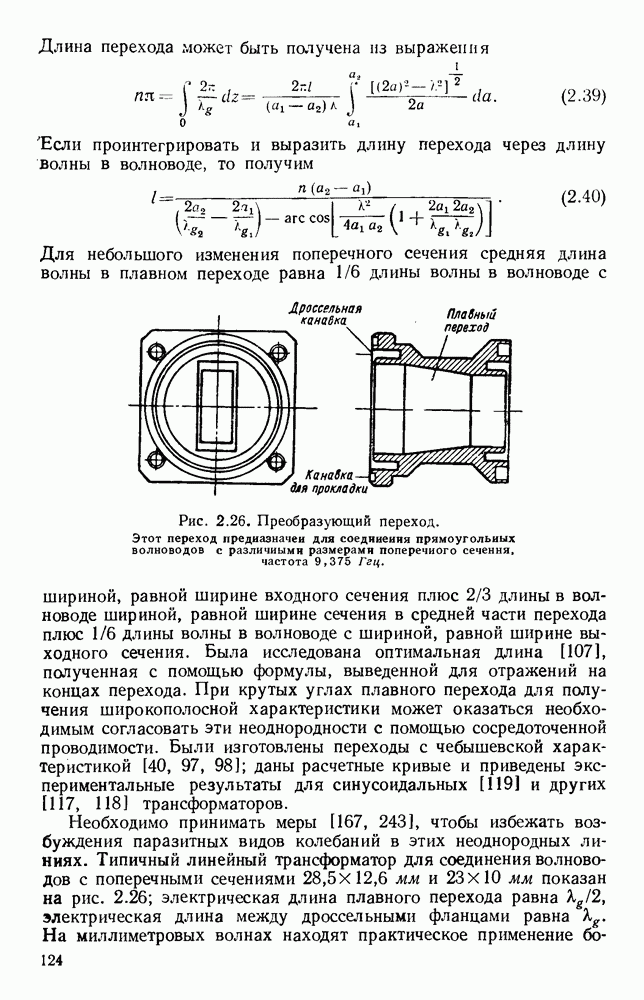
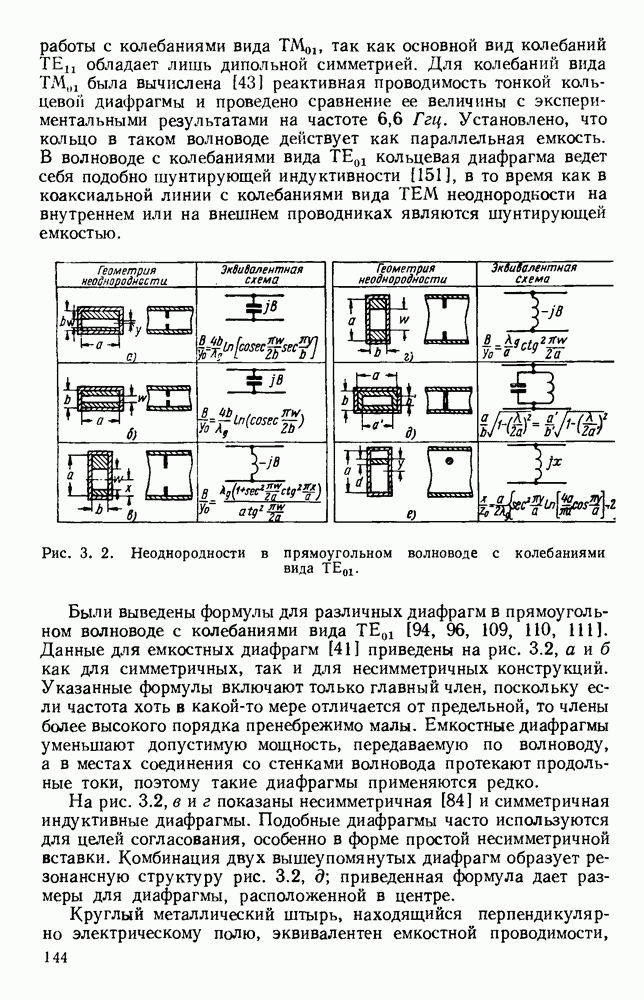
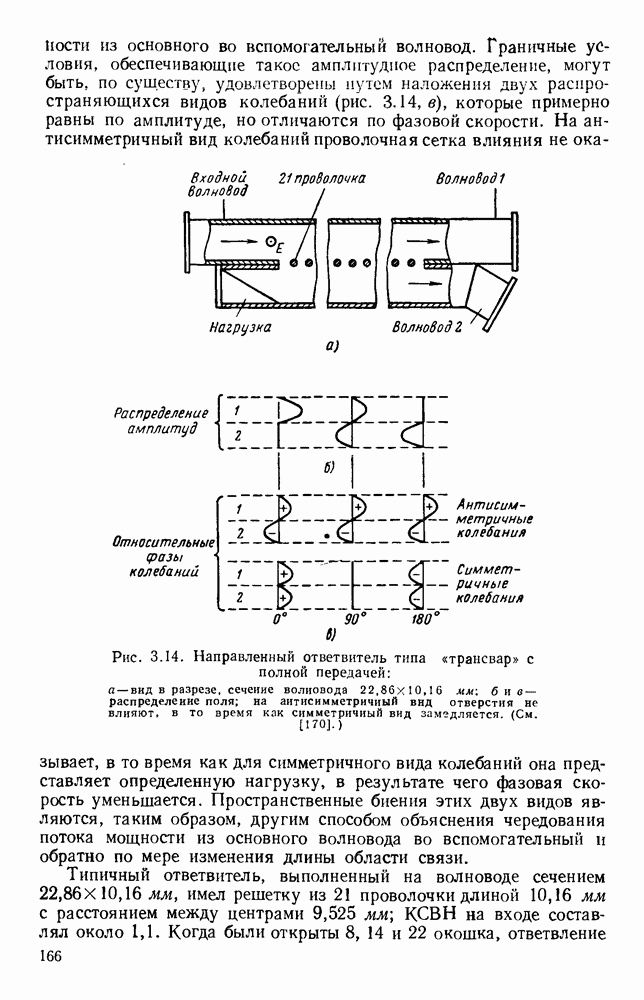
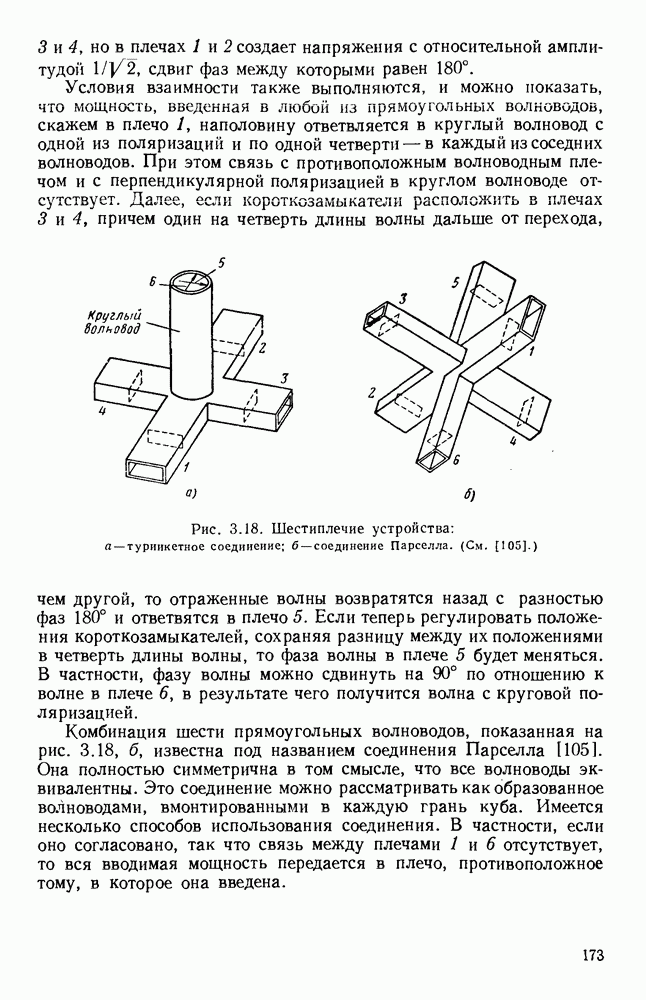
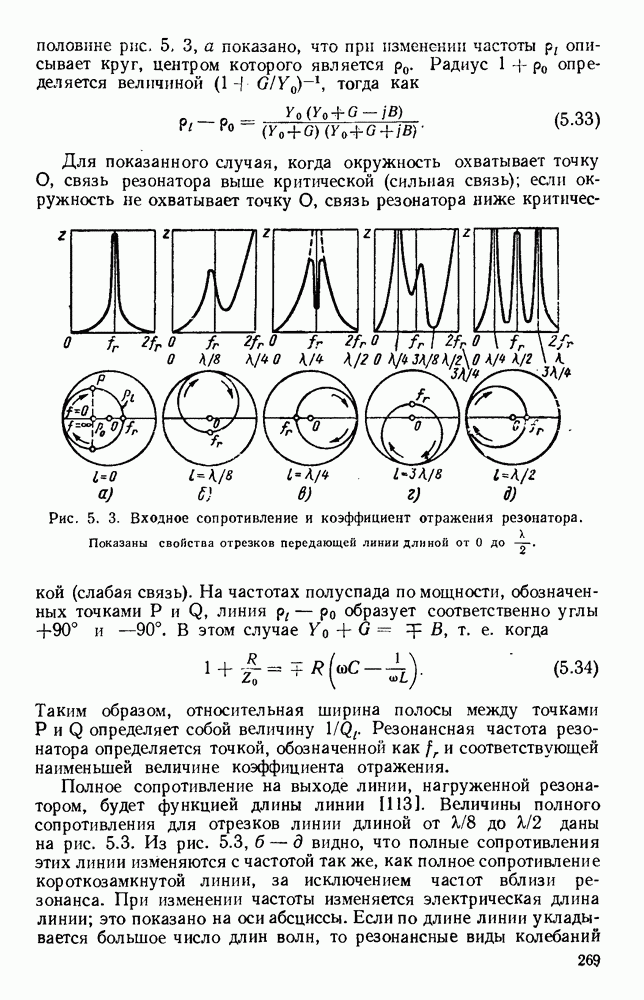
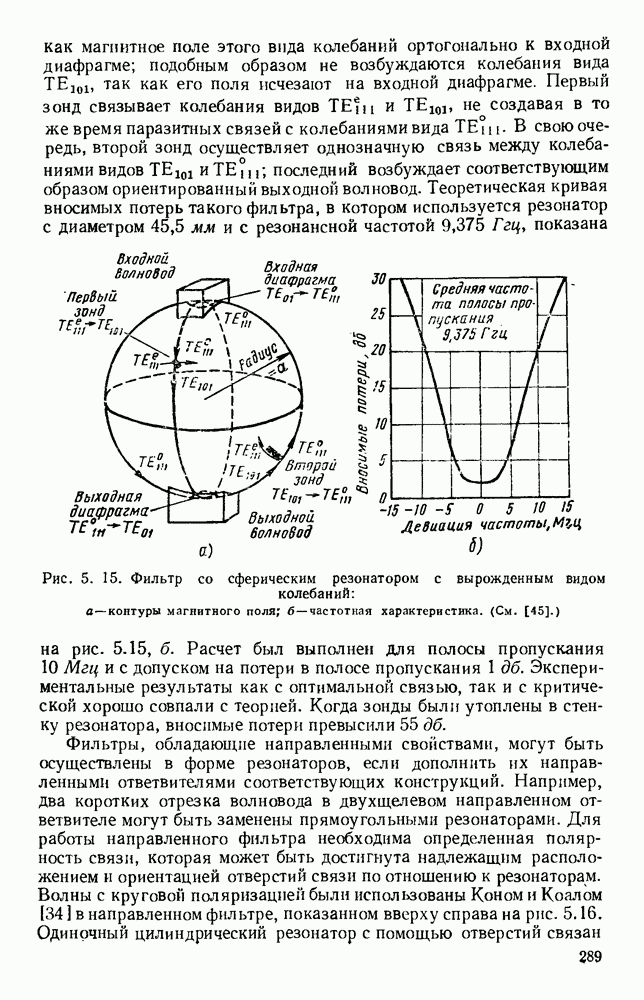
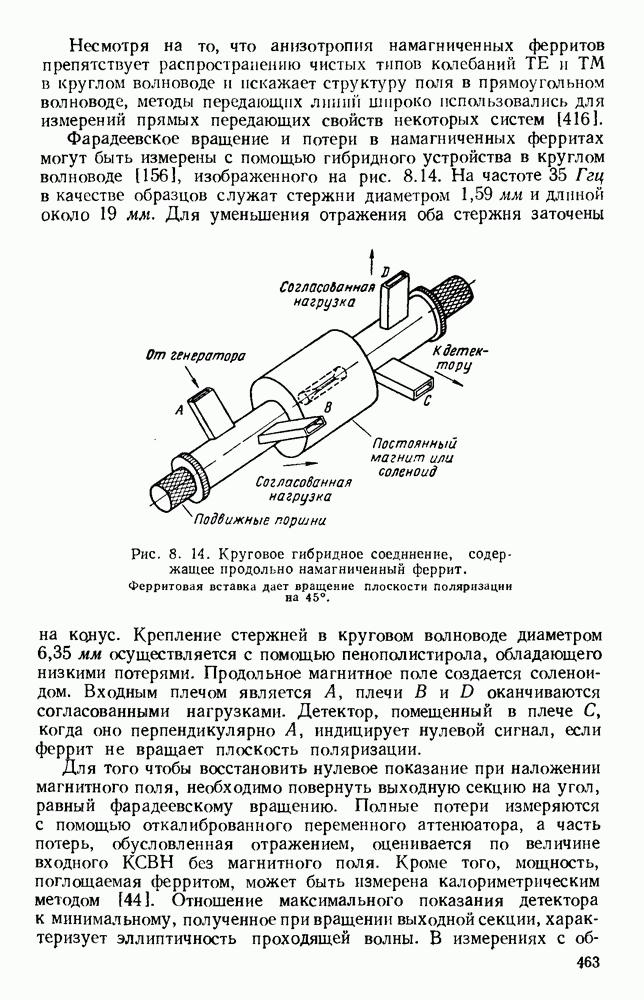
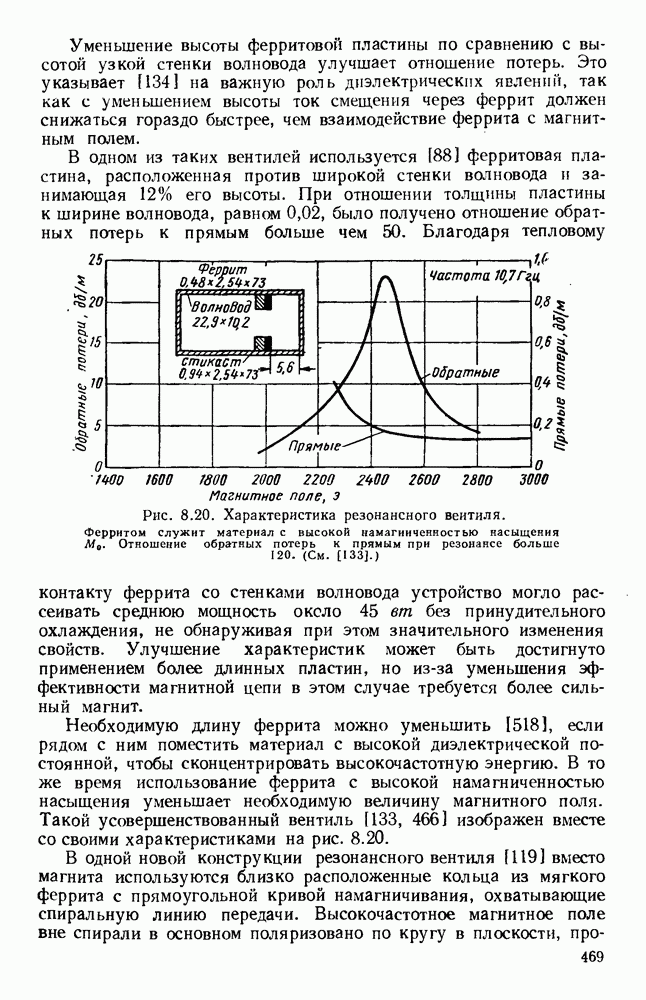
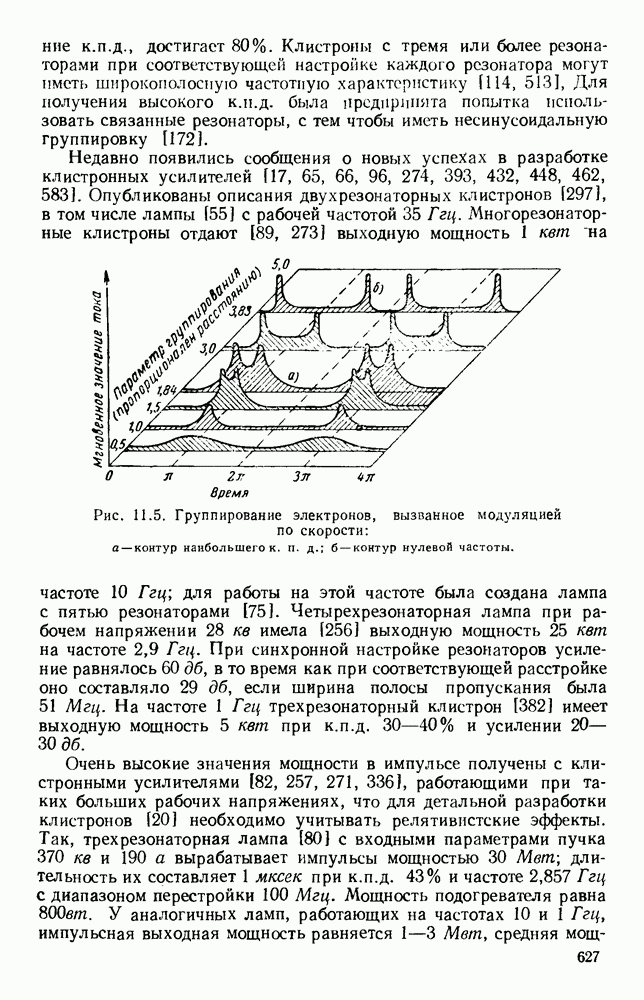
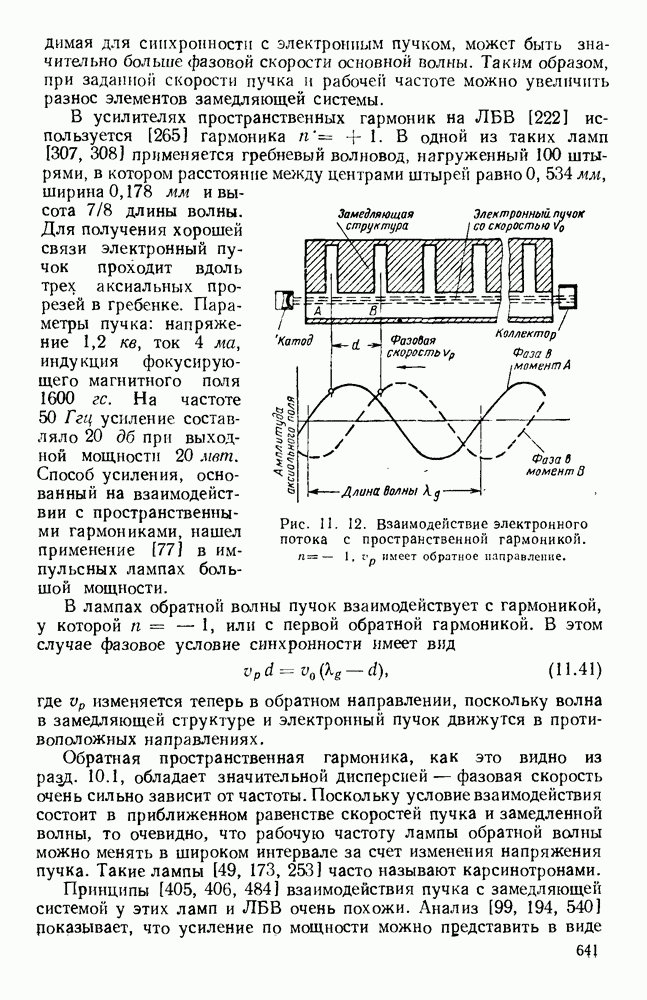
Рис. 13. 1. Поле излучения электрического диполя: а — направление электрического и магнитного поля; б - электрическое поле в электрической плоскости; в — электрическое поле в магнитной плоскости.
Коэффициент направленного действия излучателя (КНД) в заданном направлении определяется как отношение его потока мощности в единичном телесном угле к потоку мощности в единичном телесном угле изотропного излучателя с такой же полной излучаемой мощностью. Для идеализированного излучателя, который равномерно излучает в пределах телесного угла  , КНД равен
, КНД равен

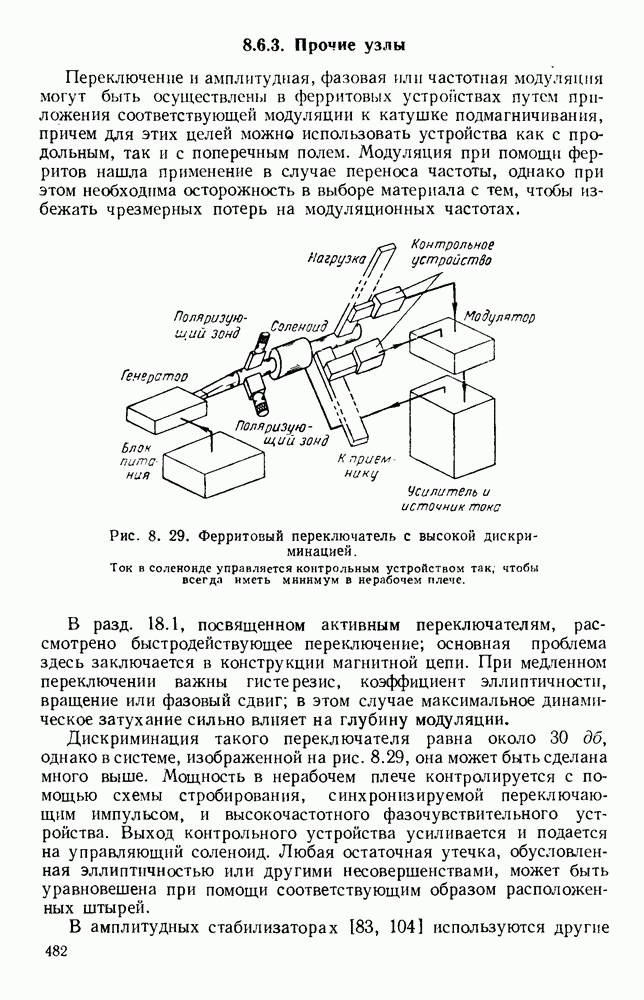
Простейшими излучателями являются электрический и магнитный диполи. Первый излучатель представляет собой небольшой прямолинейный проводник, вдоль которого течет ток высокой частоты, а второй — небольшую петлю, по которой также течет ток высокой частоты. На рис. 13.1, а показано направление векторов электромагнитного поля для электрического диполя, а на рис. 13.1, б изображена диаграмма направленности в электрической плоскости, т. е. в плоскости, содержащей электрические силовые линии.
Соответствующая диаграмма направленности в магнитной плоскости, т. е. в плоскости, содержащей магнитные силовые линии,
изображена на рис. 13.1, в. Для магнитного диполя в виде петли с током, лежащей в плоскости  этими диаграммами направленности описывается магнитное поле. Излучателем энергии СВЧ более общего вида является возбуждаемый в центре полуволновый вибратор, который можно рассматривать как резонансный отрезок линии передачи. Его диаграмма направленности в плоскости Е дается выражением [235]
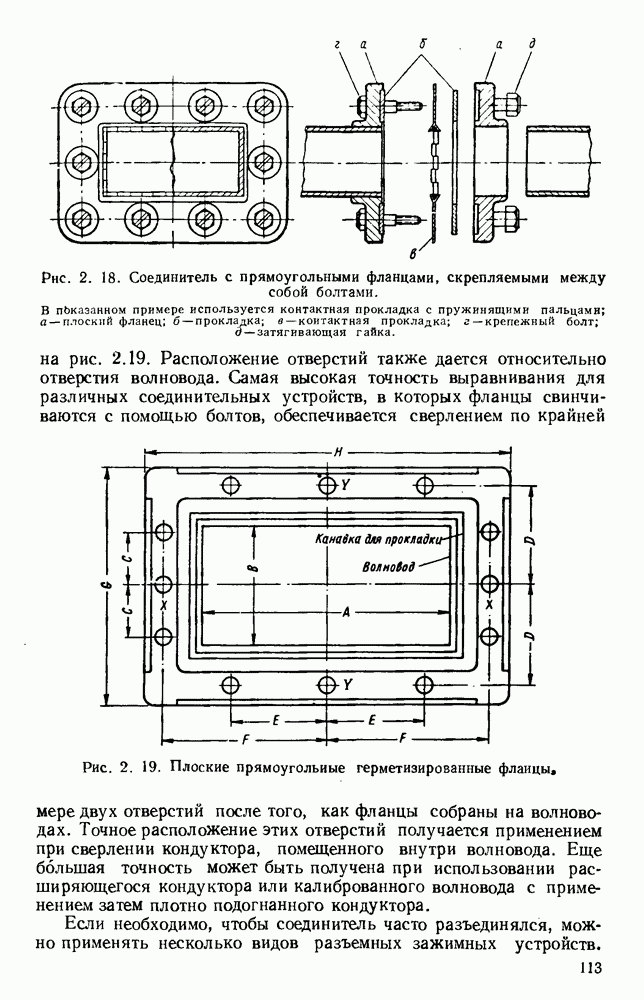
этими диаграммами направленности описывается магнитное поле. Излучателем энергии СВЧ более общего вида является возбуждаемый в центре полуволновый вибратор, который можно рассматривать как резонансный отрезок линии передачи. Его диаграмма направленности в плоскости Е дается выражением [235]

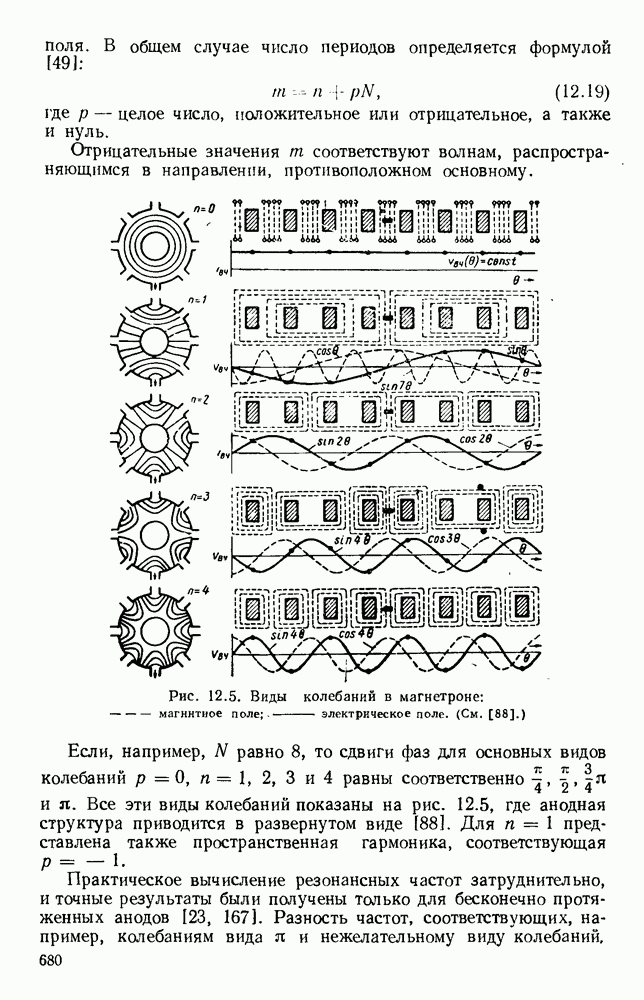
где А — постоянная; максимальное значение КНД равно 1,65.

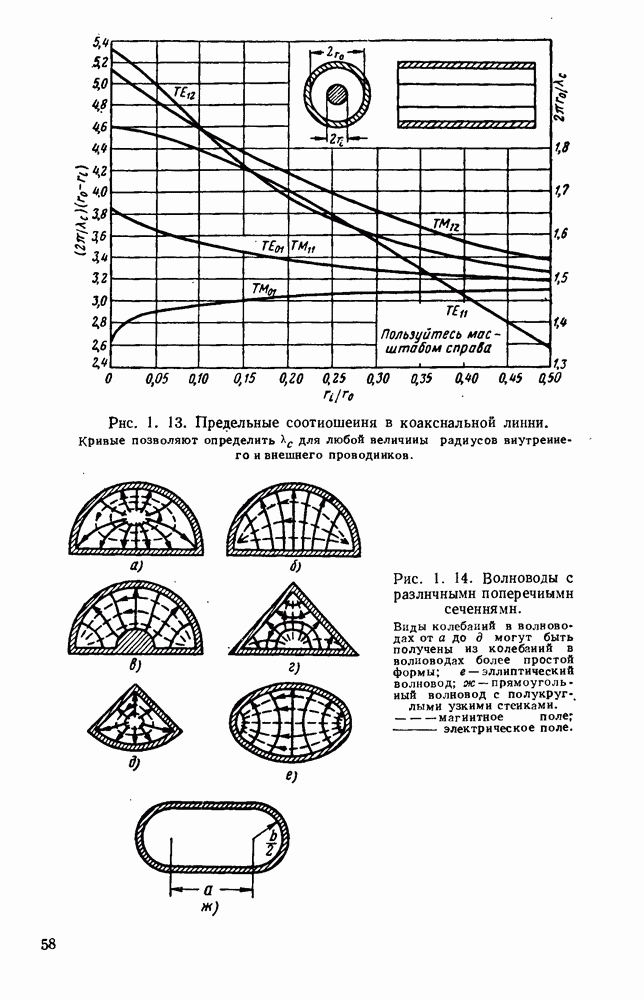
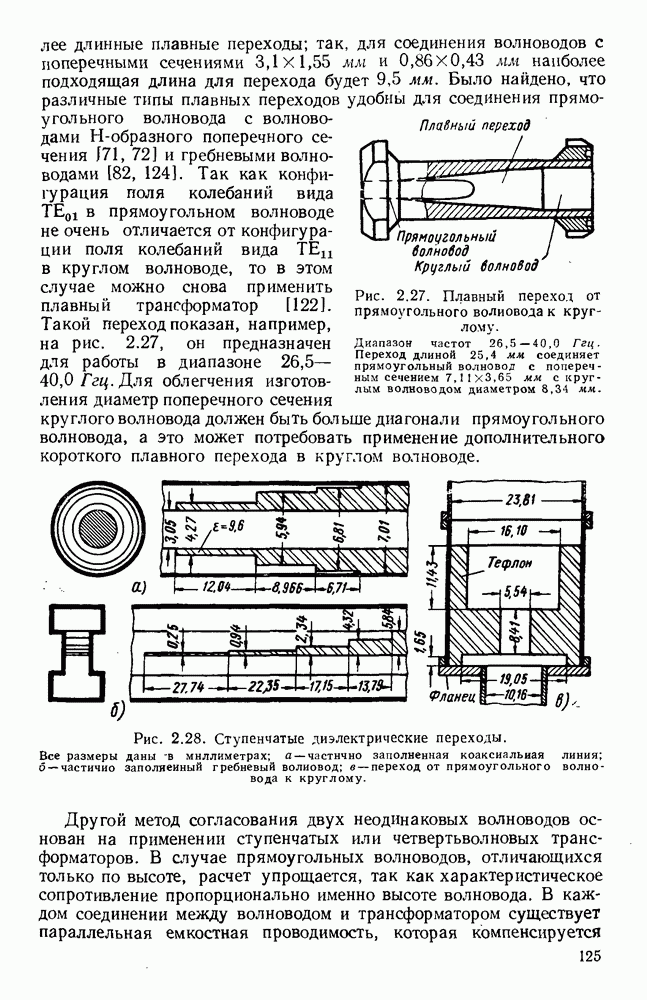
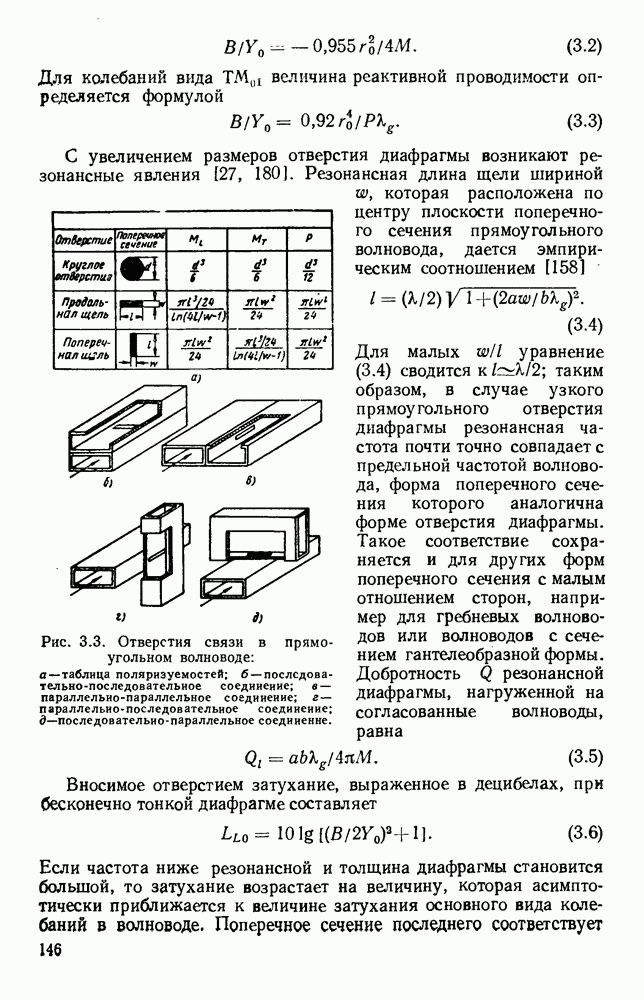
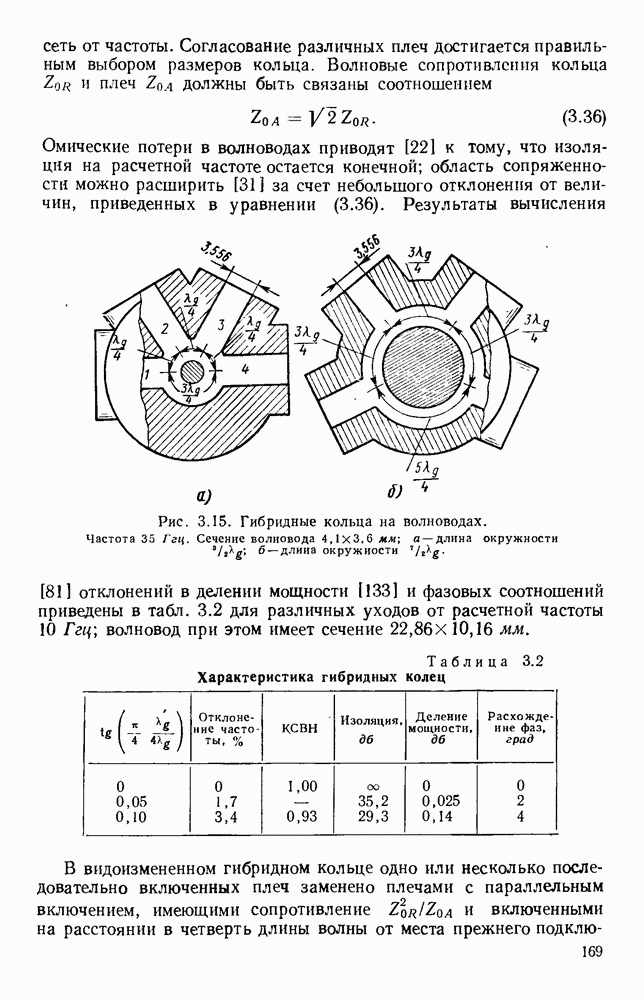
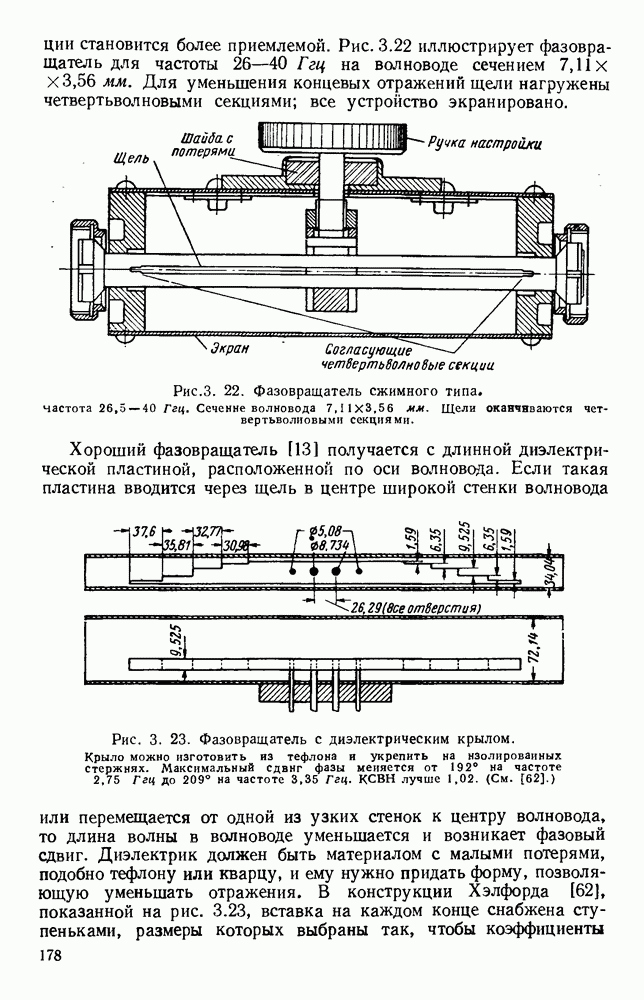
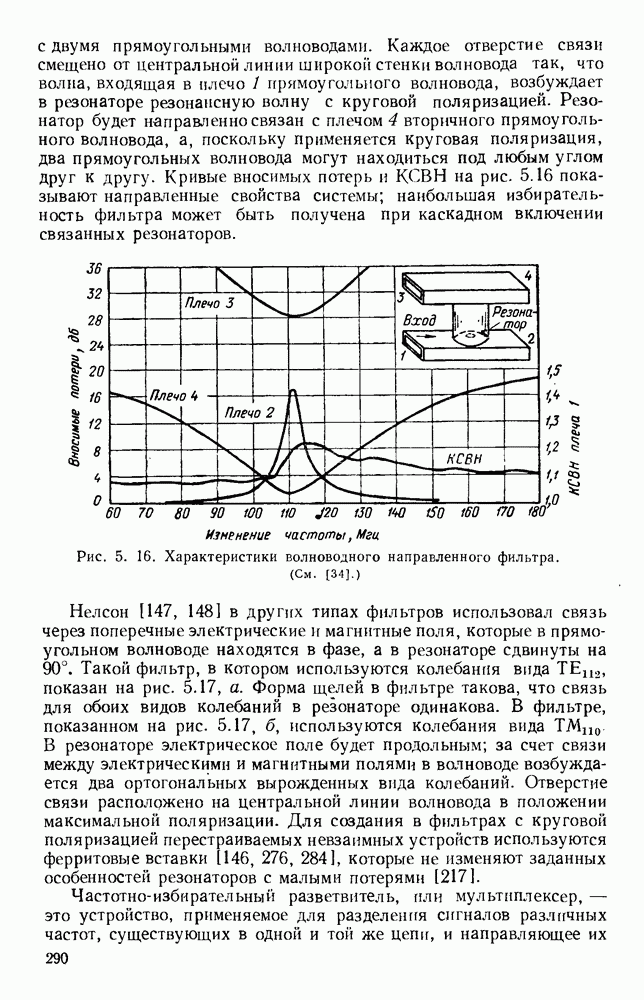
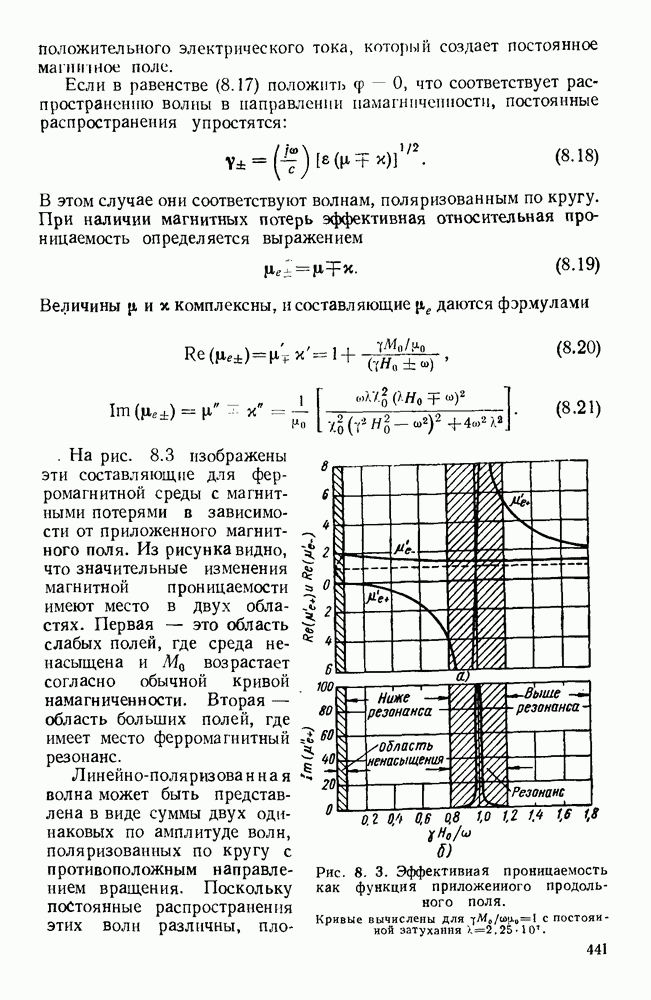
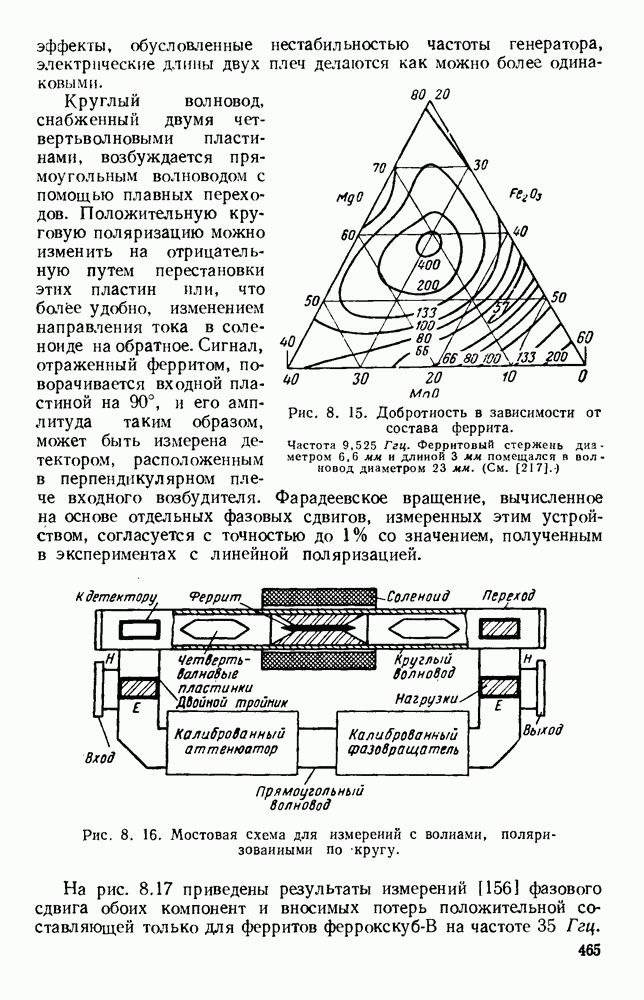
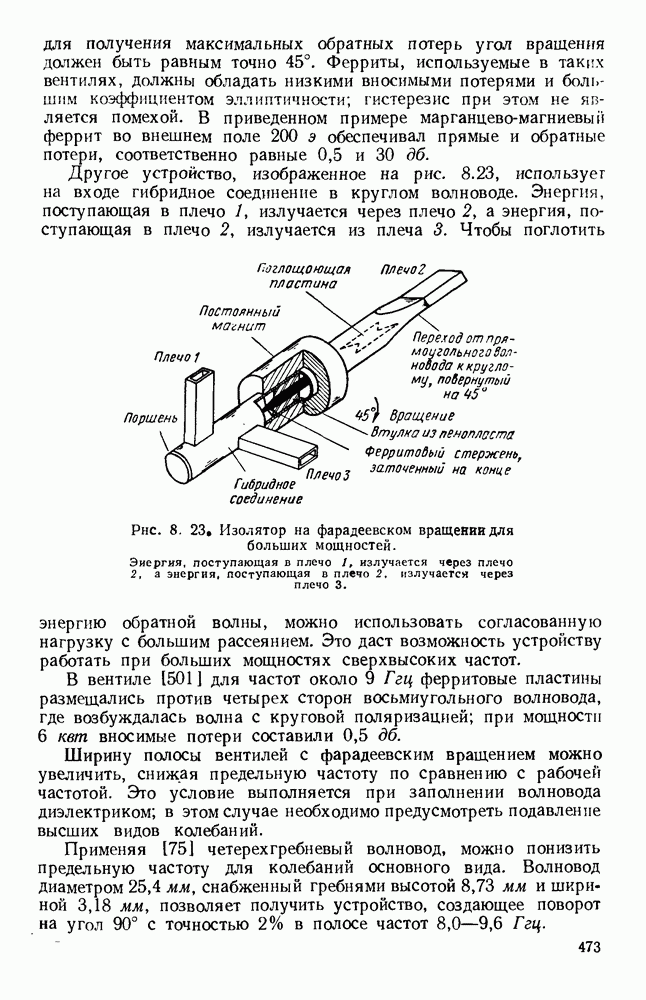
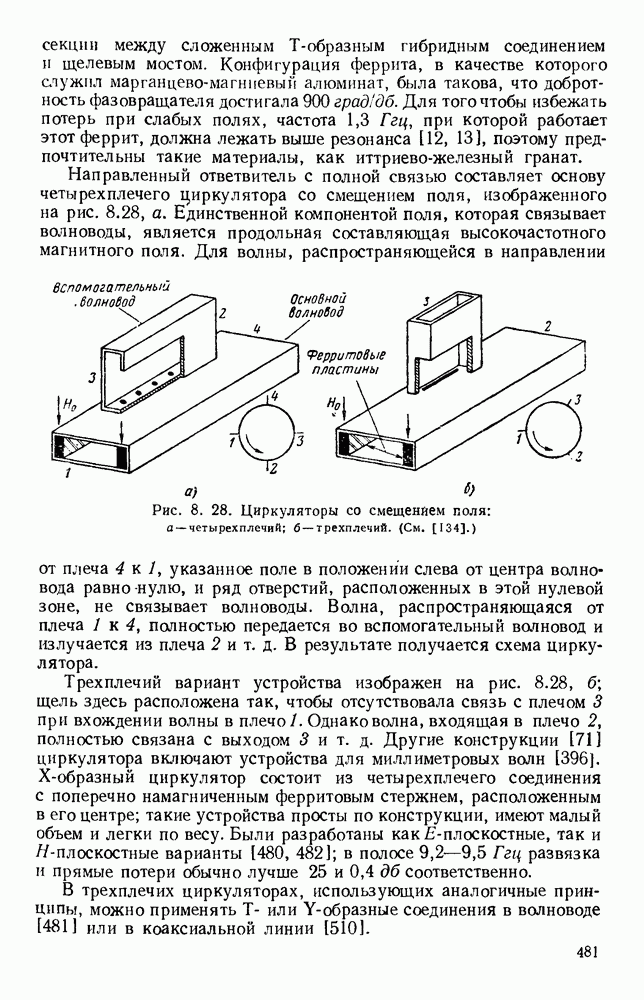
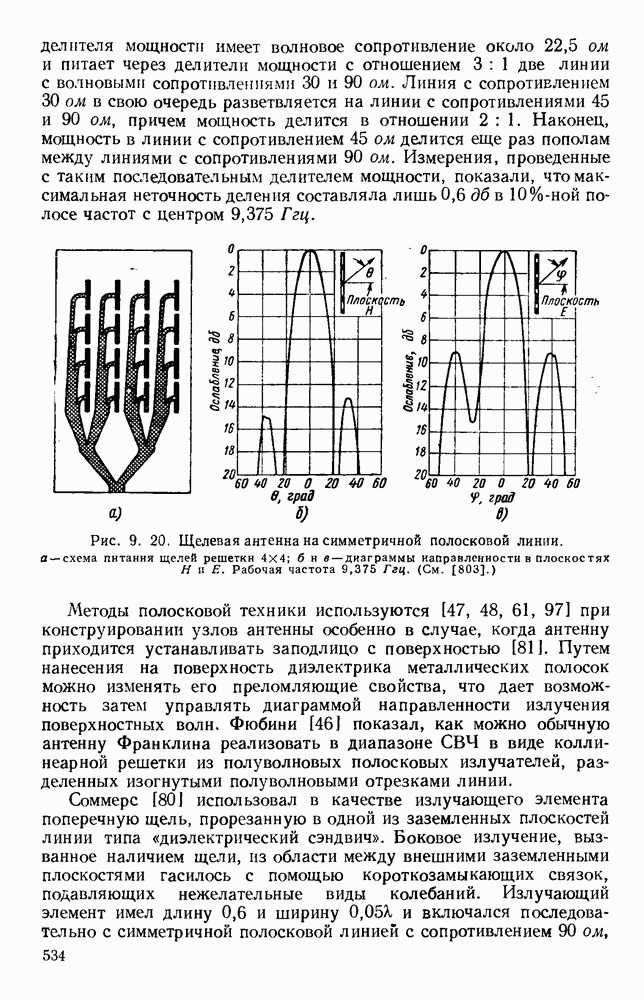
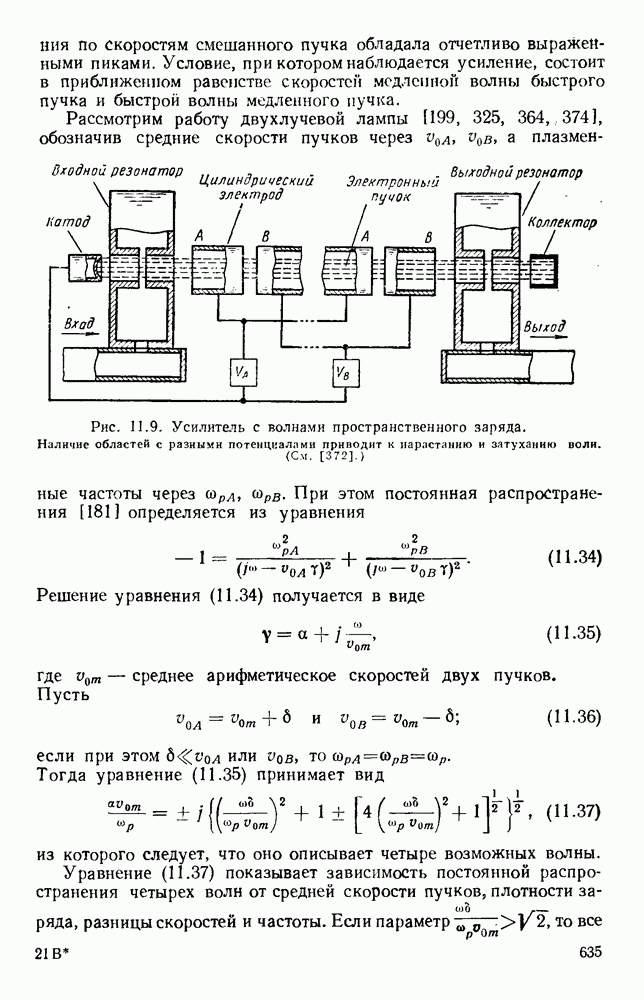
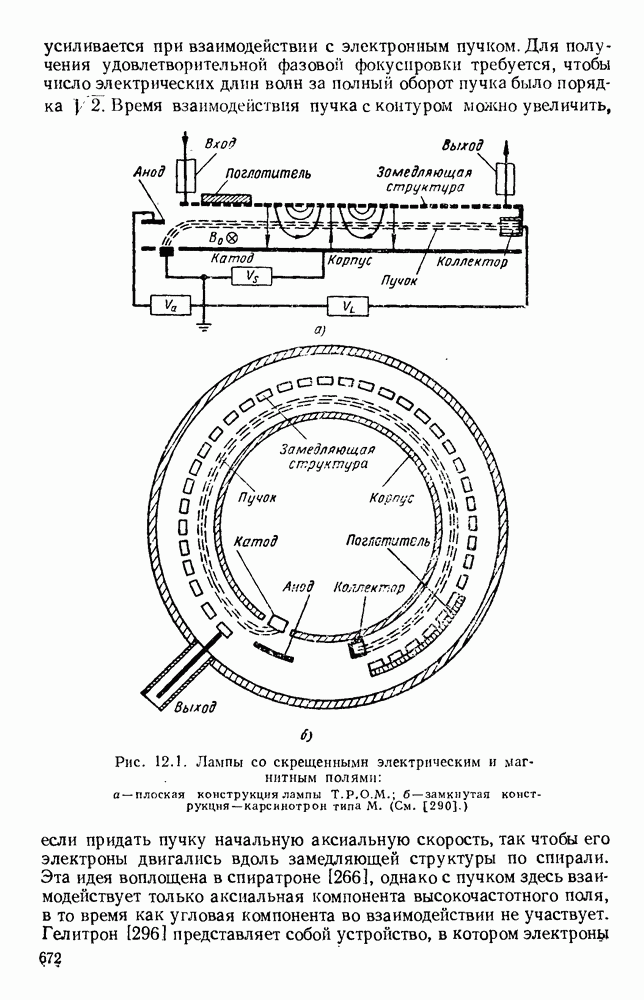
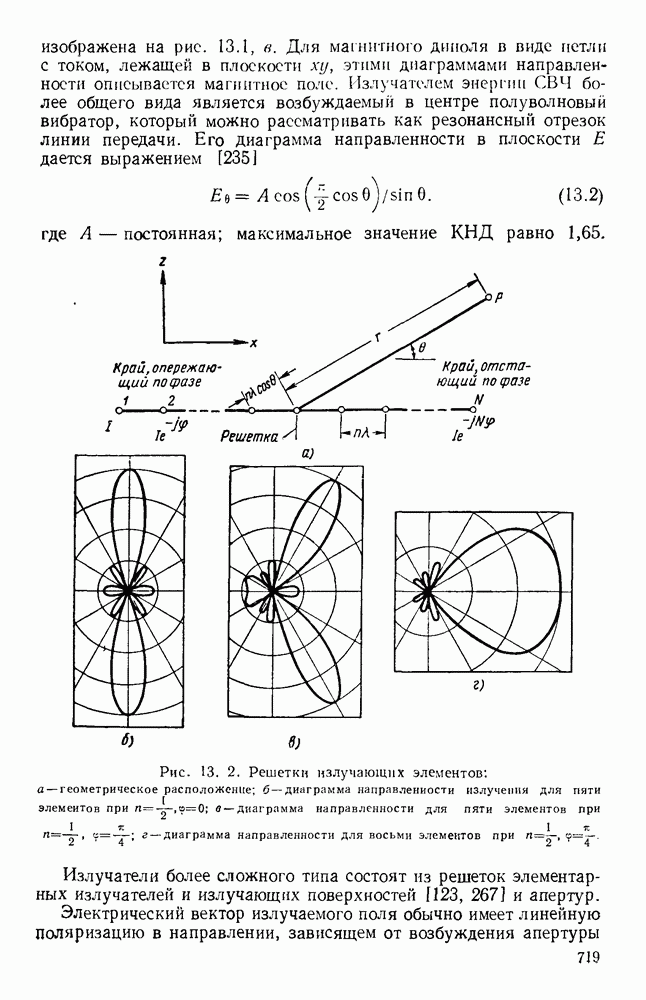
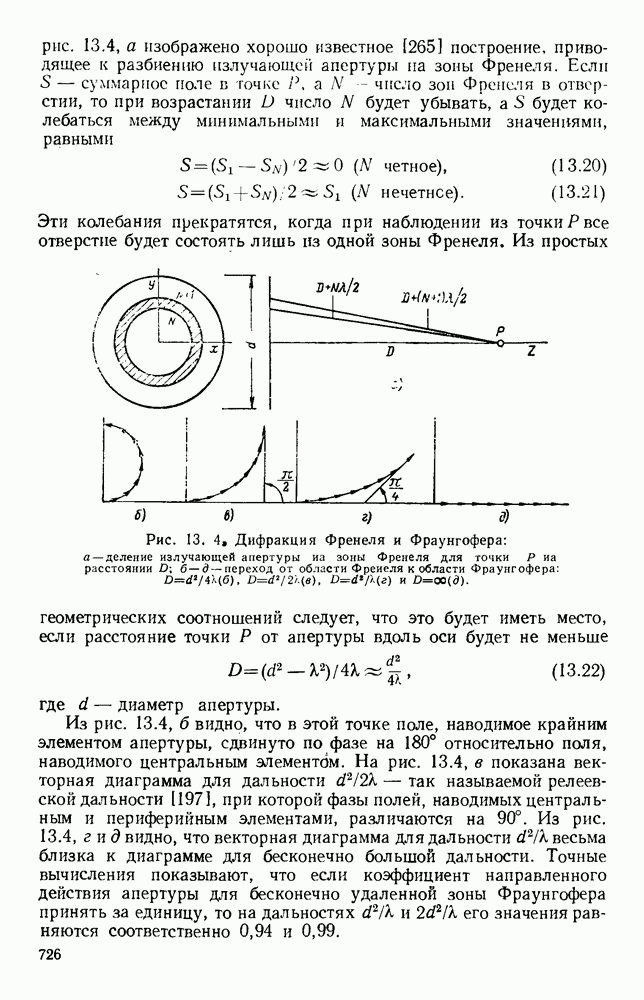
Рис. 13. 2. Решетки излучающих элементов: а — геометрическое расположение; б - диаграмма направленности излучения для пяти элементов при  в — диаграмма направленности для пяти элементов при
в — диаграмма направленности для пяти элементов при  Диаграмма направленности для восьми элементов при
Диаграмма направленности для восьми элементов при 
Излучатели более сложного типа состоят из решеток элементарных излучателей и излучающих поверхностей [123, 267] и апертур.
Электрический вектор излучаемого поля обычно имеет линейную поляризацию в направлении, зависящем от возбуждения апертуры
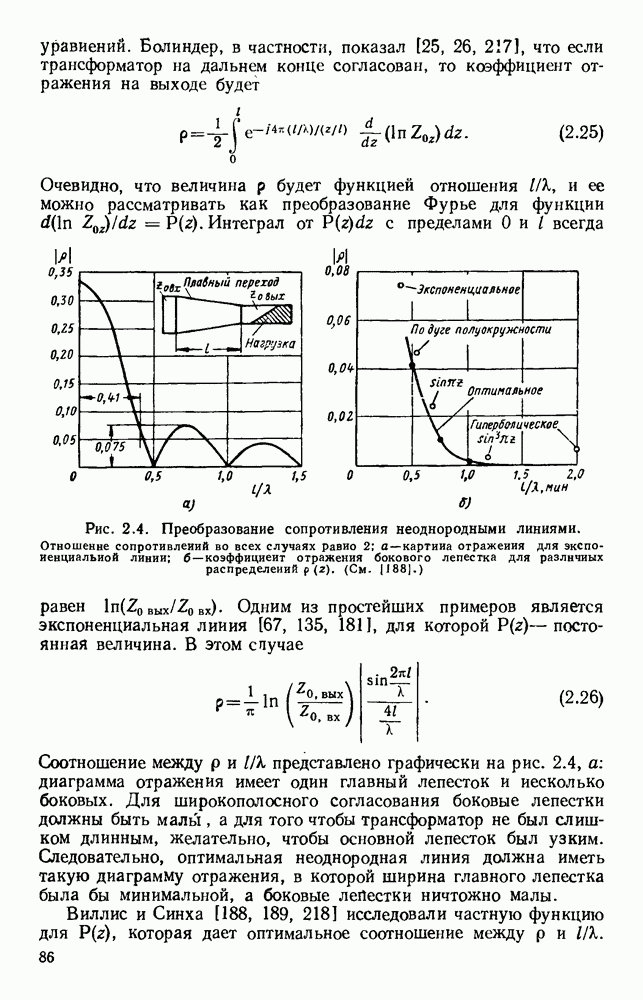
пли элементарных излучателей. С помощью соответствующих преобразователей плоскость поляризации может быть изменена. Излучение с круговой поляризацией можно получить, пропуская плоскую волну через четвертьволновую пластину. В осевом направлении излучение с круговой поляризацией можно получить также с помощью пары скрещенных полуволновых вибраторов, у которых токи равны по амплитуде и сдвинуты по фазе на 90°. В этом случае, если в каком-либо направлении получается круговая поляризация с правым вращением, то в противоположном направлении будет круговая поляризация с левым вращением. Два синфазных скрещенных вибратора, разнесенных на расстояние  дают круговую поляризацию с одинаковым вращением в обоих осевых направлениях
дают круговую поляризацию с одинаковым вращением в обоих осевых направлениях 
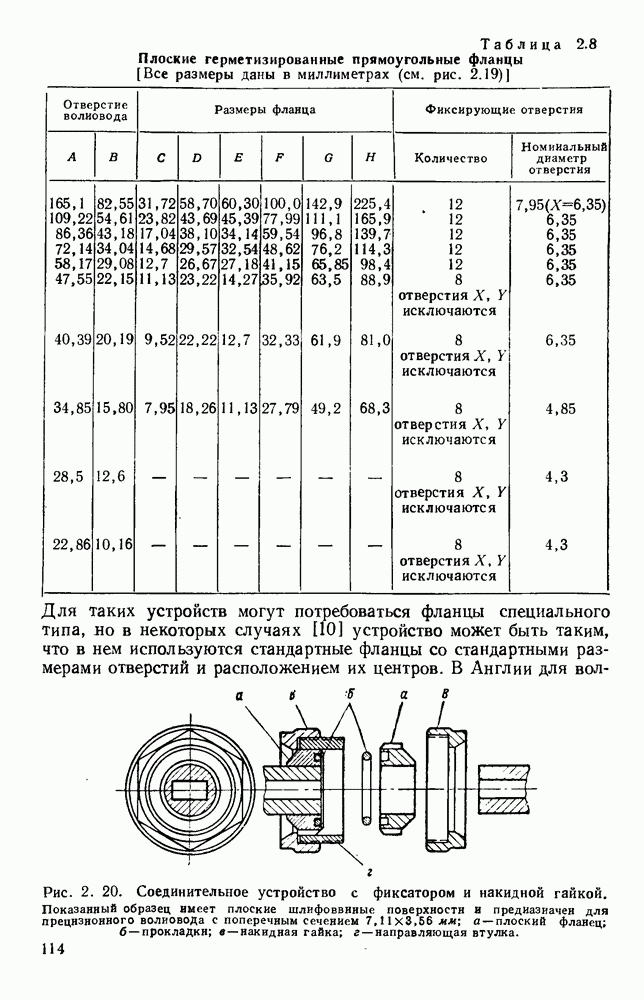
Характеристики излучения решетки из дискретных элементов обычно определяются методом суммирования. Рассмотрим линейную решетку, у которой расстояние между соседними элементами по прямой, проходящей через фазовые центры, равно  (рис. 13.2, а). Пусть амплитуды токов во всех элементах одинаковы, а фазы от элемента к элементу сдвинуты на величину
(рис. 13.2, а). Пусть амплитуды токов во всех элементах одинаковы, а фазы от элемента к элементу сдвинуты на величину  т. е. ток в элементе 2 отстает по фазе на величину
т. е. ток в элементе 2 отстает по фазе на величину  относительно тока в элементе 1 и так далее до элемента
относительно тока в элементе 1 и так далее до элемента  Диаграмму направленности такой решетки можно получить путем векторного сложения амплитуд полей каждого элемента:
Диаграмму направленности такой решетки можно получить путем векторного сложения амплитуд полей каждого элемента:

Поле  измеряется под углом
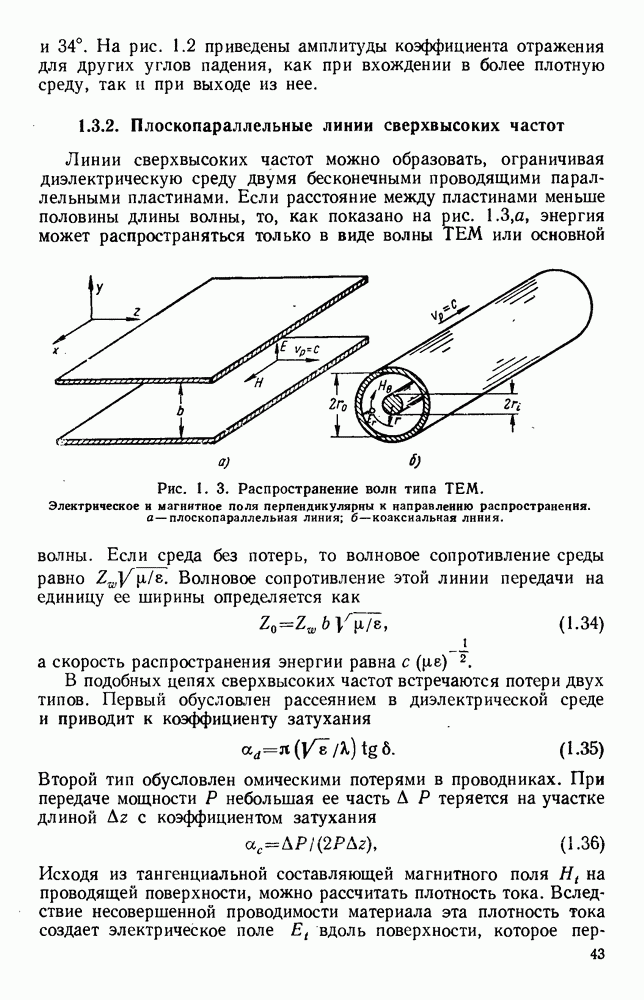
измеряется под углом  к оси решетки, А — постоянная, определяемая диаграммой направленности
к оси решетки, А — постоянная, определяемая диаграммой направленности  одного элемента. Для расчета диаграммы направленности решетки уравнение (13.3) целесообразно записать в виде
одного элемента. Для расчета диаграммы направленности решетки уравнение (13.3) целесообразно записать в виде

где множитель решетки 5 показывает, как изменяется диаграмма направленности одного элемента в присутствии остальных элементов.
Мгксимальное значение  равное
равное  достигается при
достигается при

Если  равно нулю, т. е. все элементы находятся в фазе, максимум излучения получается в направлении нормали к оси решетки, т. е. при
равно нулю, т. е. все элементы находятся в фазе, максимум излучения получается в направлении нормали к оси решетки, т. е. при  Множитель решетки 5 обращается в нуль при условии
Множитель решетки 5 обращается в нуль при условии

где k — целое число.
Вторичные максимумы находятся приблизительно посередине между нулями, т. е. при условии

где  целое число.
целое число.
Как видно из рис. 13.2, б, диаграмма направленности такой решетки, излучающей в боковом направлении, состоит из главного лепестка и ряда боковых лепестков. Уровень максимума первого бокового лепестка приблизительно на 13,5 56 ниже уровня максимума главного лепестка, а из уравнения (13.6) видно, что ширина главного лепестка, измеренная по первым нулям, равна

Из выражения (13.8) видно, что у равномерной решетки, излучающей в боковом направлении, ширина главного лепестка приблизительно равна удвоенной обратной величине от длины решетки, измеренной в длинах волн. При несинфазном возбуждении элементов получается решетка, излучающая в боковом направлении, с лучом, отклоненным от ее оси на угол  согласно уравнению (13.5). В этом случае диаграмма направленности определяется уравнением (13.4); на рис. 13.2, в изображен типичный пример такой диаграммы направленности. При
согласно уравнению (13.5). В этом случае диаграмма направленности определяется уравнением (13.4); на рис. 13.2, в изображен типичный пример такой диаграммы направленности. При  максимум диаграммы направленности находится на оси решетки. Если при этом расстояние между соседними элементами выбрано таким образом, что имеется лишь один главный лепесток, то получается решетка, излучающая в продольном направлении. В этом случае ширина главного лепестка равна
максимум диаграммы направленности находится на оси решетки. Если при этом расстояние между соседними элементами выбрано таким образом, что имеется лишь один главный лепесток, то получается решетка, излучающая в продольном направлении. В этом случае ширина главного лепестка равна

т. е. обратно пропорциональна квадратному корню из полной длины решетки, измеренной в длинах волн. Необходимую фазовую задержку можно осуществить путем возбуждения излучателей с помощью коаксиальной линии с воздушным заполнением. Типичная диаграмма направленности показана на рис. 13.2, г.
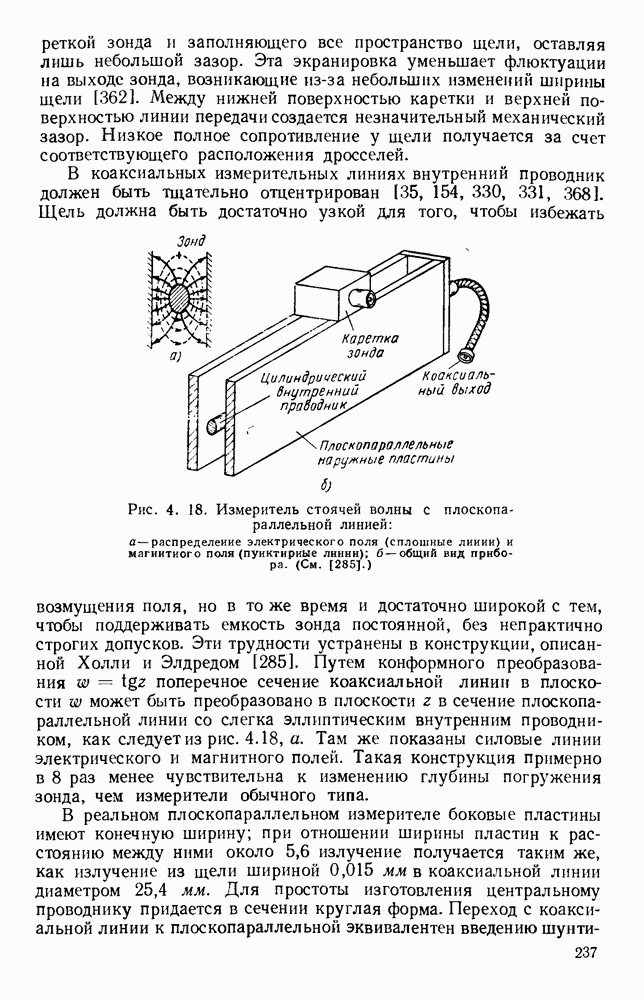
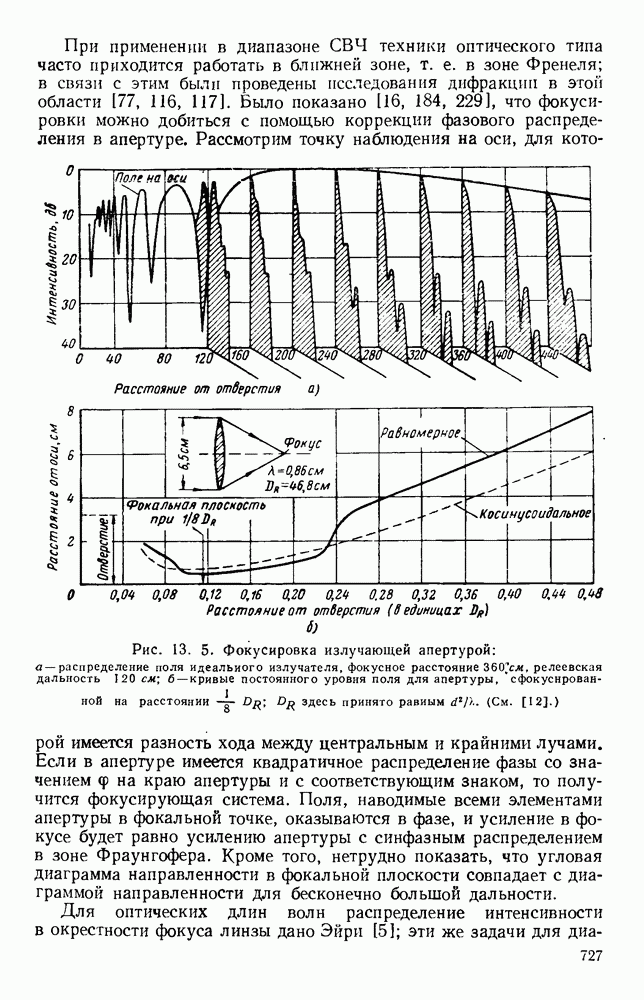
В отдельных случаях общую задачу вычисления электромагнитного поля в удаленной точке через распределение токов в апертуре можно сформулировать строго, а в большинстве случаев — с очень хорошим приближением. Применение строгих методов решения сопряжено со значительными трудностями, и, вообще говоря, приходится допускать ряд приближений. Одним из часто используемых приближений является приближение геометрической оптики, в котором принимается, что электромагнитная энергия распространяется вдоль лучей, определяемых обычными законами отражения и преломления. Траектории лучей получаются из
принципа Ферма [265] как кривые, для которых длина оптического хода стационарна относительно малых вариаций их формы. Отсюда следует, что в однородной среде лучи будут прямолинейны. Методами лучевой оптики можно также пользоваться при оценке полей излучения, которые являются непрерывными функциями угла. При этом существенно, чтобы имело место взаимно однозначное соответствие между каждой точкой апертуры и каждым направлением в диаграмме направленности. Применение оптических методов основано на предположении, что размер апертуры значительно больше длины волны, вследствии чего получаемые результаты являются лишь приближенными. Однако часто при расчете диаграмм выбирают именно эти простые методы, несмотря на грубость их приближения.
Другой приближенный метод основан на принципе Гюйгенса, согласно которому [13,309] каждая точка волнового фронта является источником вторичной сферической волны. В каждой последующий момент времени новый волновой фронт получается как огибающая этих вторичных волн. В отличие от диполя, источник Гюйгенса, рассматриваемый как элементарный излучатель, не определяет поляризации, а дает лишь скалярную величину напряженности поля и, следовательно, описывает электромагнитные волны лишь приближенно.
Скалярная форма принципа Гюйгенса была обобщена Кирхгофом. Теория Кирхгофа позволяет [318] вычислить поле с приемлемой в большинстве случаев точностью в точках, удаленных от излучающей апертуры, по распределению токов в ней. Если известны распределения амплитуды и фазы токов в апертуре, то необходимо лишь произвести векторное суммирование полей, излучаемых отдельными элементами токов. Рассмотрим излучающую поверхность, которая наводит поле в удаленной точке Р. Если Е — электрическое поле в точке элемента  излучающей поверхности
излучающей поверхности  поле, наводимое в точке Р элементом
поле, наводимое в точке Р элементом  означает производную вдоль внешней нормали, то формула Гюйгенса — Кирхгофа утверждает, что
означает производную вдоль внешней нормали, то формула Гюйгенса — Кирхгофа утверждает, что

Полное поле получается интегрированием этого выражения по излучающей апертуре. Таким образом, для равномерно освещенного прямоугольного отверстия шириной  комплексная диаграмма направленности поля излучения на больших расстояниях
комплексная диаграмма направленности поля излучения на больших расстояниях  имеет вид
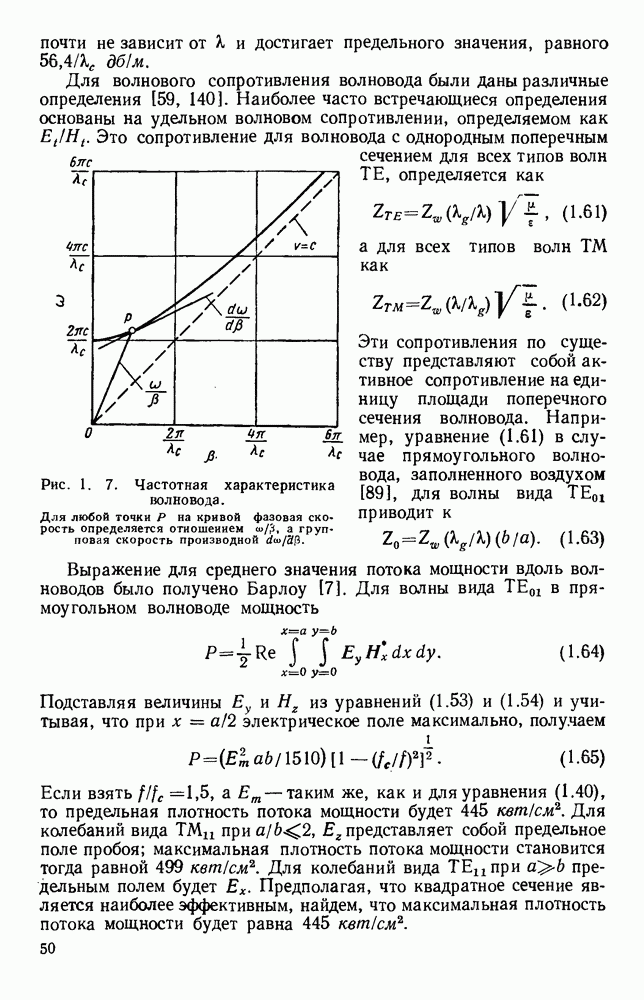
имеет вид

где у — расстояние от центра апертуры,  угол, отсчитываемый от нормали к апертуре, А — распределение токов в апертуре.
угол, отсчитываемый от нормали к апертуре, А — распределение токов в апертуре.
Это выражение справедливо для плоскости, проходящей через нормаль к прямоугольному отверстию и ось у, которая соответствует стороне, имеющей размер  угол
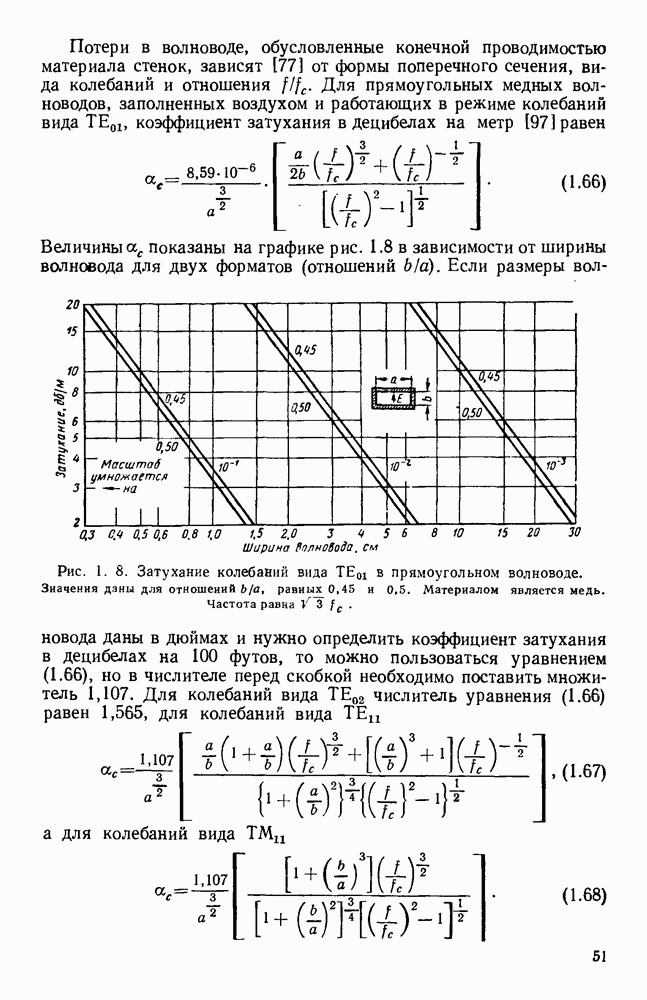
угол  отсчитывается в этой же плоскости; кроме того, предполагается, что распределение токов в апертуре допускает разделение переменных, позволяющих написать аналогичное выражение и для другой плоскости.
отсчитывается в этой же плоскости; кроме того, предполагается, что распределение токов в апертуре допускает разделение переменных, позволяющих написать аналогичное выражение и для другой плоскости.
Другой метод приближенного вычисления поля излучения основан на том, что поле в любой точке перед плоской апертурой как в дальней, так и в ближней областях можно представить в виде суммы плоских волн, распространяющихся в различных направлениях. Функция, называемая угловым спектром, которая выражает зависимость амплитуды и фазы волн, как функция направления их распространения при соответствующем выражении будет представлять преобразование Фурье для апертурного распределения. Этот факт был впервые отмечен [235] и критически изучен Букером и Клеммовым [22], давшими более полную теорию. Понятие углового спектра можно применить не только для случая апертур конечных размеров, но, и, например, при анализе дифракции на прямоугольной кромке линейки [22]. Для антенн конечных размеров угловой спектр приближенно совпадает с полярной диаграммой направленности.
Как известно [372], произвольная функция  может быть представлена в виде суммы колебании с различными частотами
может быть представлена в виде суммы колебании с различными частотами 

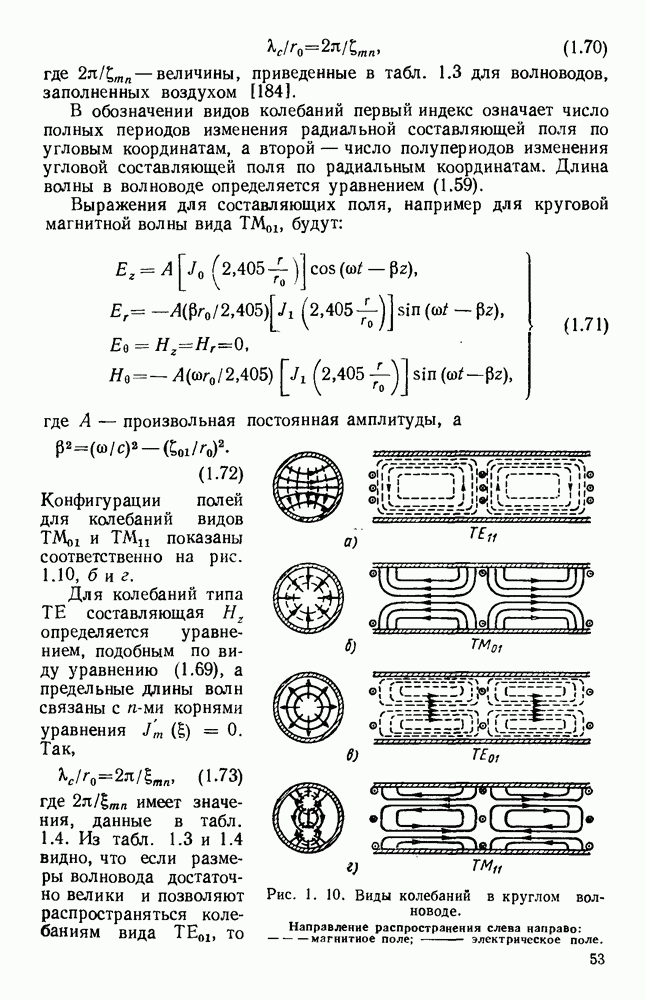
При этом частотный спектр  для функции
для функции  определяется уравнением
определяется уравнением

Функции  являются преобразованиями Фурье друг друга и, вообще говоря, комплексные. На комплексной плоскости
являются преобразованиями Фурье друг друга и, вообще говоря, комплексные. На комплексной плоскости  изображается вращающимся вектором, и уравнение (3.12) представляет собой результат сложения для многих частот. Примеры для конкретных случаев рассмотрены более подробно в § 19.3.
изображается вращающимся вектором, и уравнение (3.12) представляет собой результат сложения для многих частот. Примеры для конкретных случаев рассмотрены более подробно в § 19.3.
Рассмотрим двумерную задачу, в которой поле не зависит от координаты х и угловой спектр равен  . В этом случае электромагнитное поле в точке Р можно представить в виде [235]
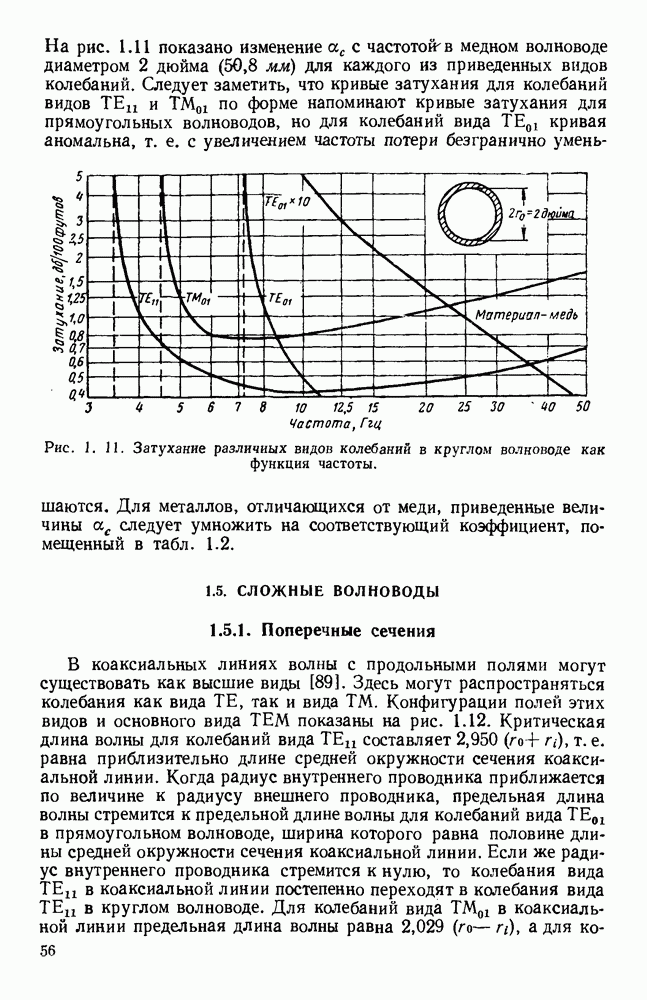
. В этом случае электромагнитное поле в точке Р можно представить в виде [235]

Это поле создается апертурным распределением

если предположить, что размер апертуры достаточно велик, чтобы можно было положить  Отсюда следует выражение для углового спектра через апертурное распределение
Отсюда следует выражение для углового спектра через апертурное распределение

На расстояниях от апертуры, значительно превышающих как ее ширину, так и длину волны, излучение становится почти радиальным, и уравнение (13.17) представляет собой обычное выражение полярной диаграммы направленности через апертурное распределение. Следует также отметить эквивалентность уравнений (13.11) и (13.17).
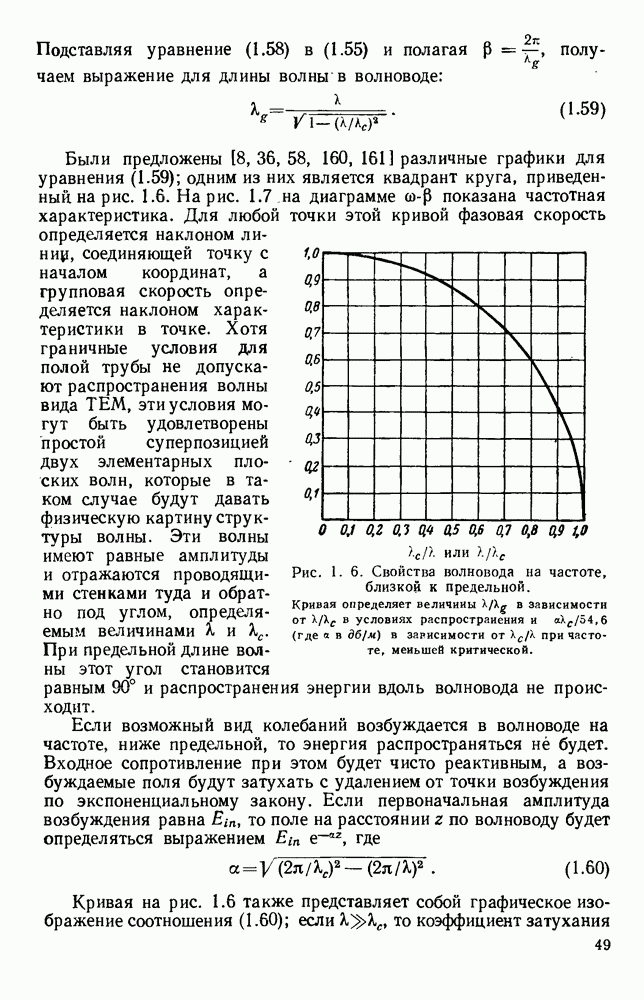
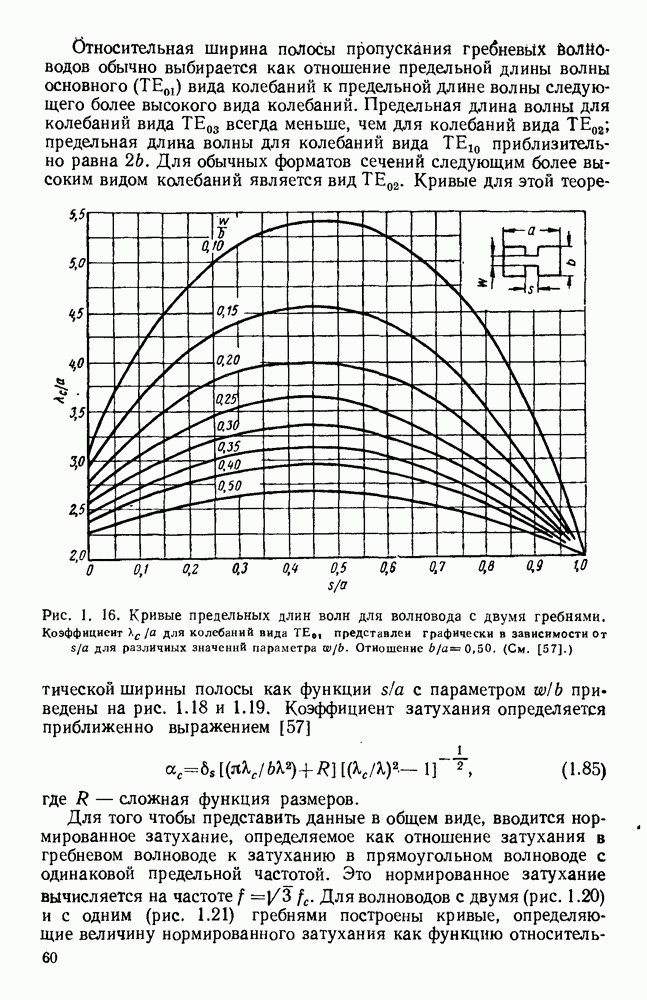
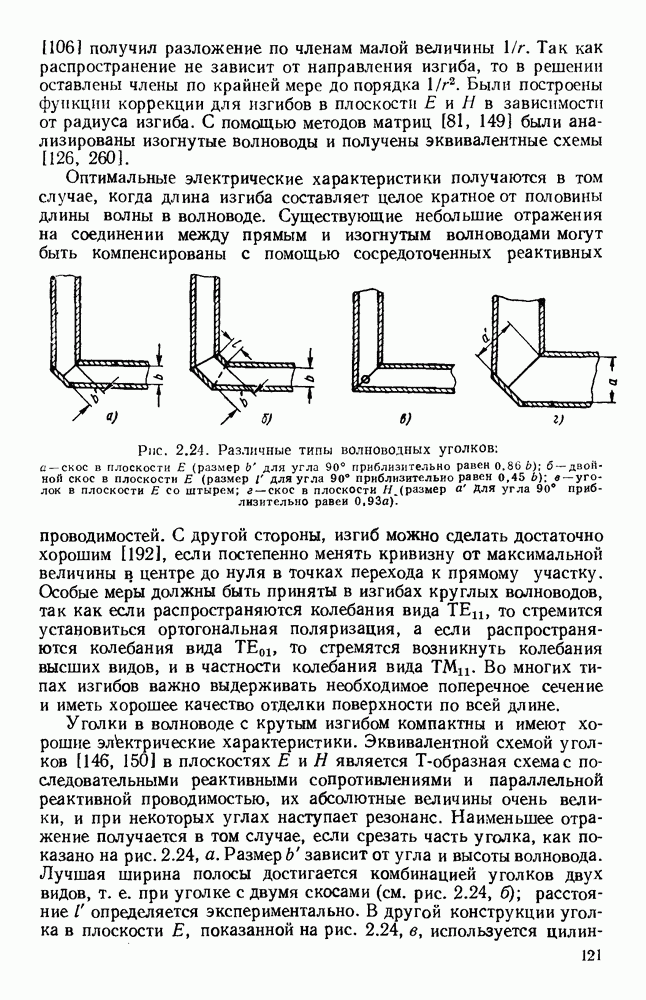
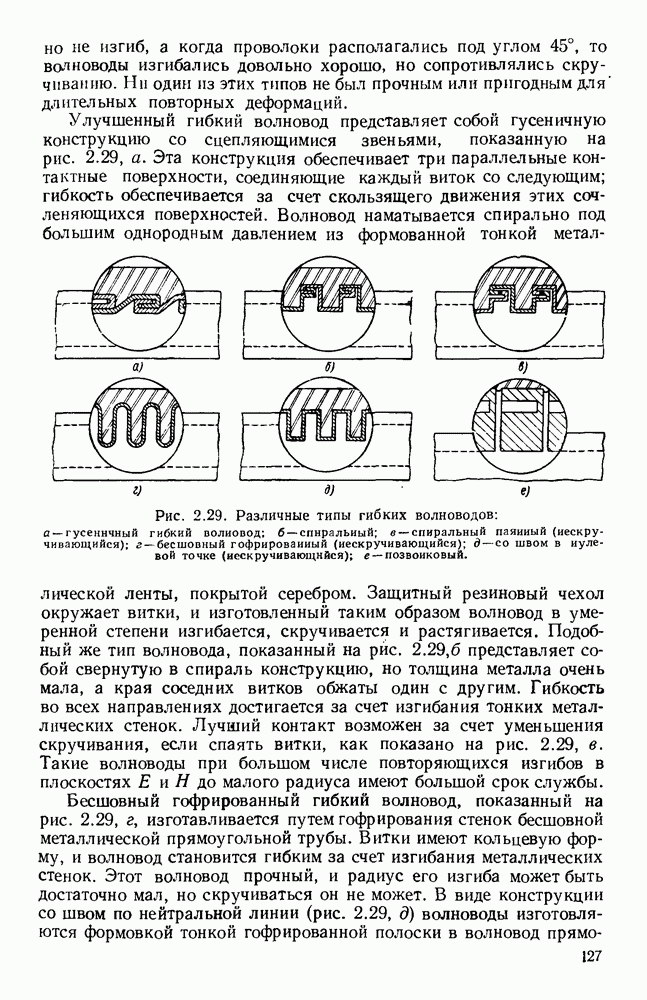
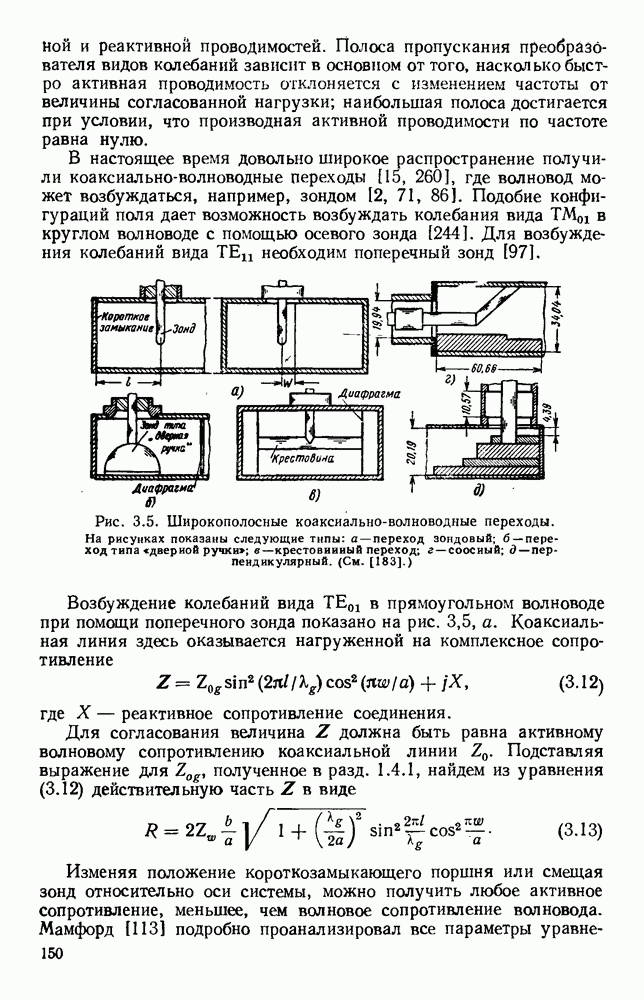
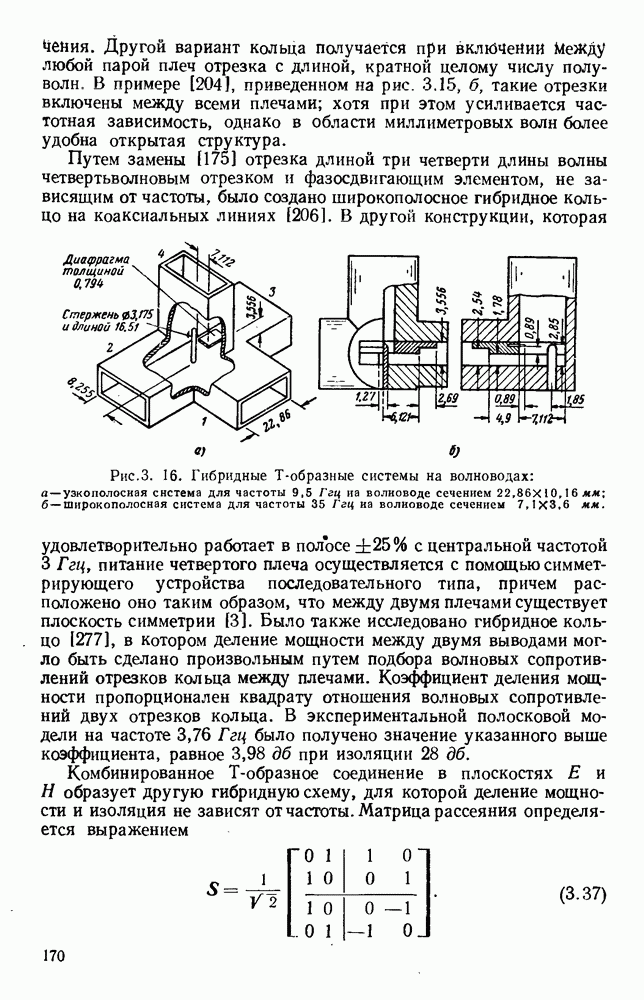
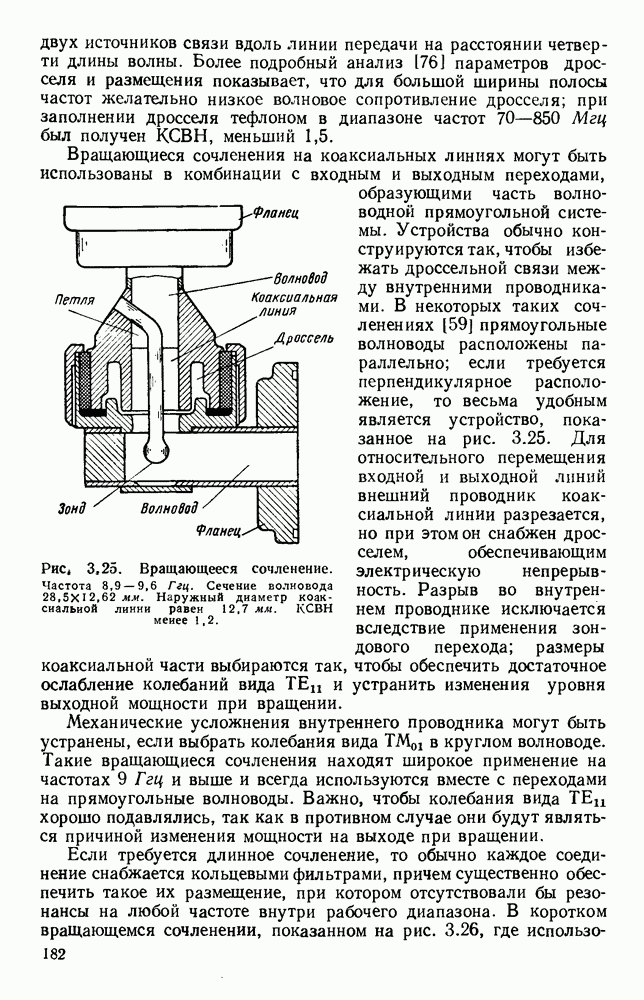
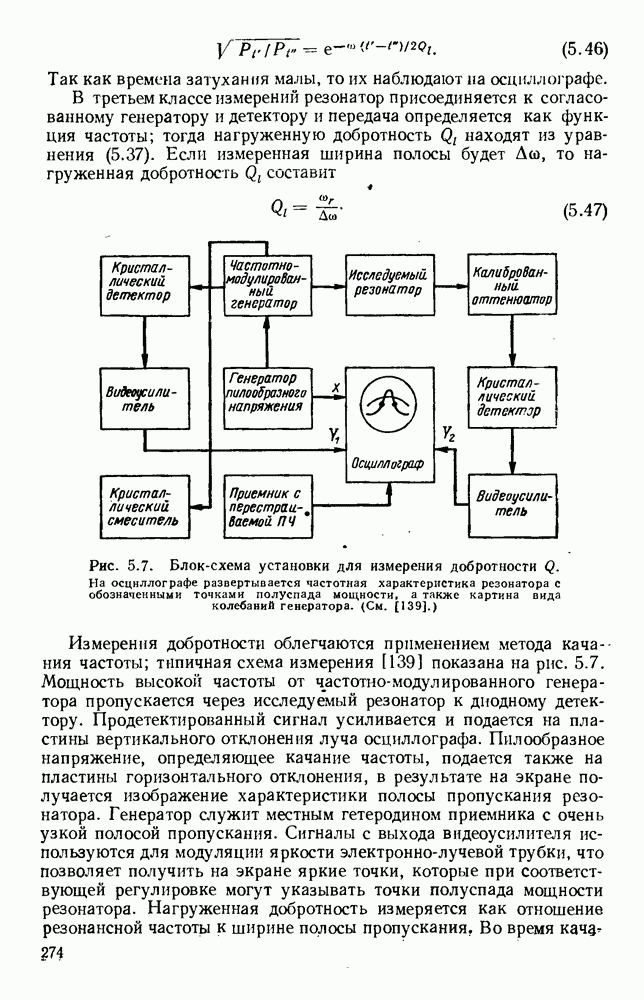
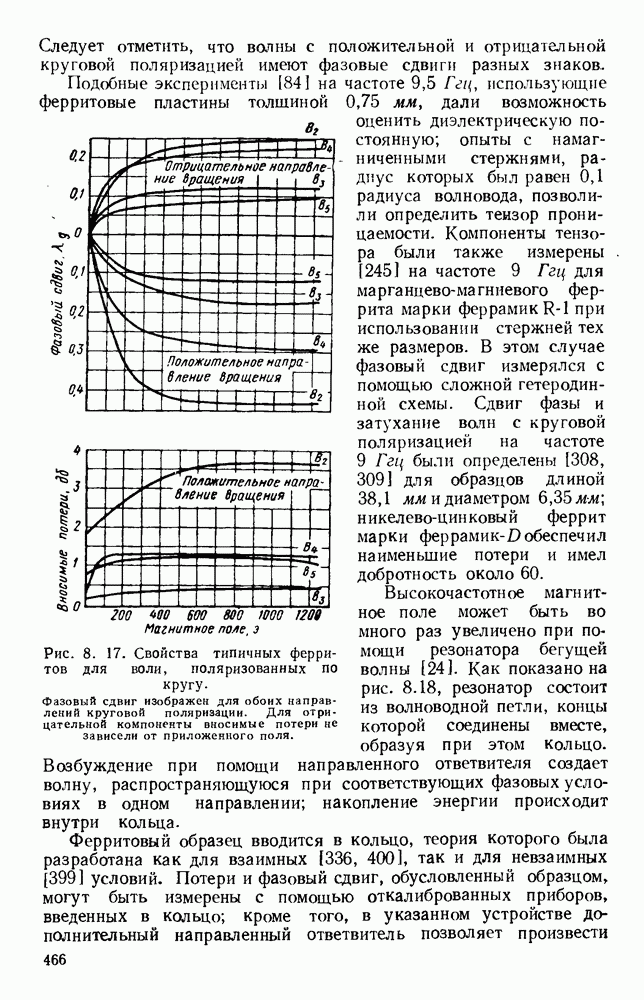
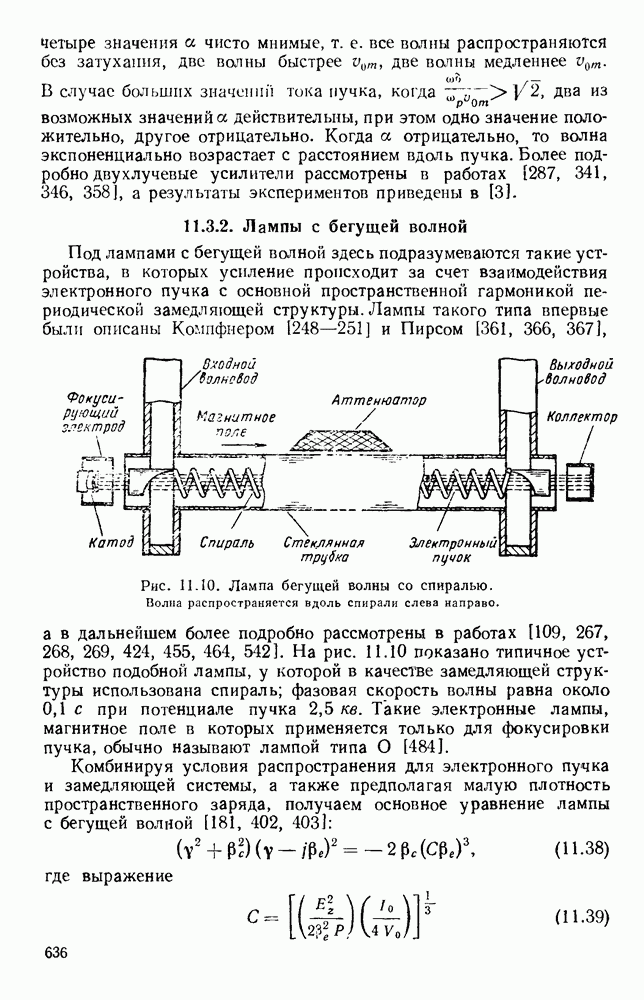
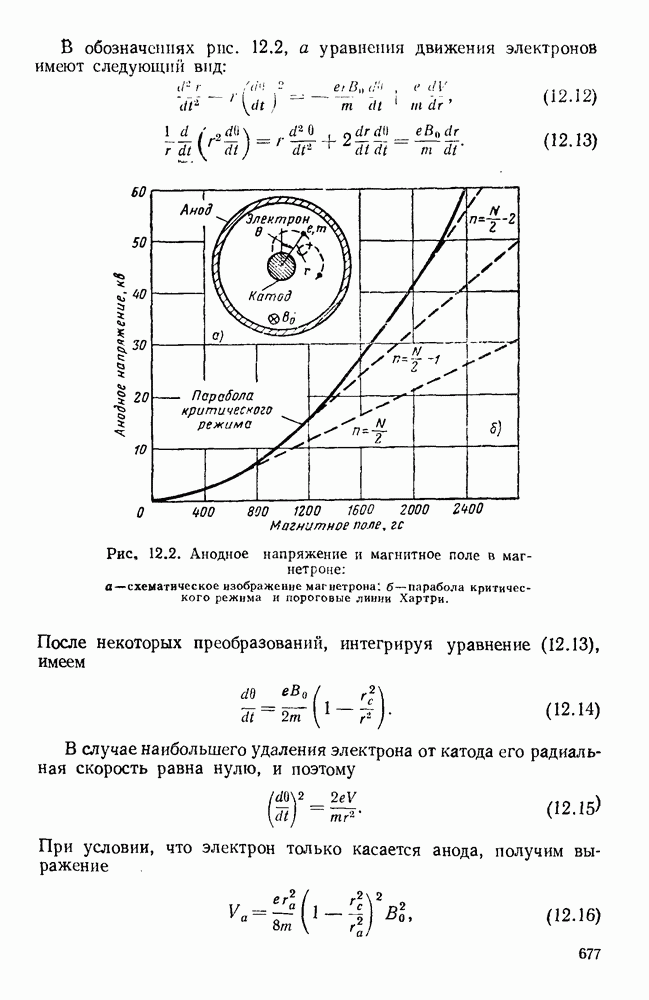
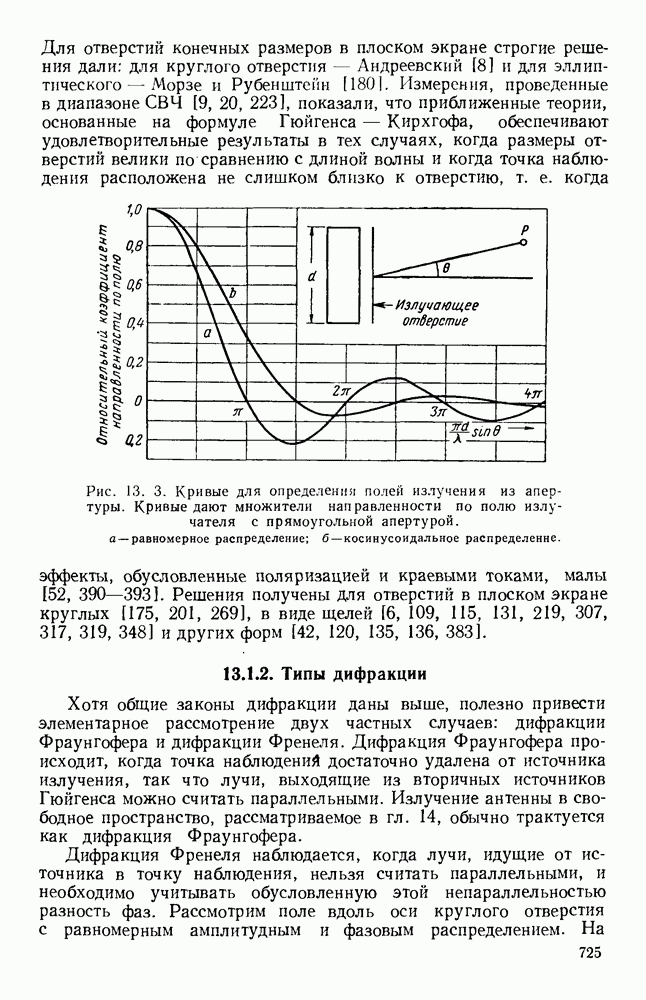
Если уравнение (13.17) применить для случая прямоугольного отверстия, освещенного линейно-поляризованным полем с равномерным распределением амплитуды и фазы, то для углового спектра получится хорошо известное выражение

где  постоянная,
постоянная, 
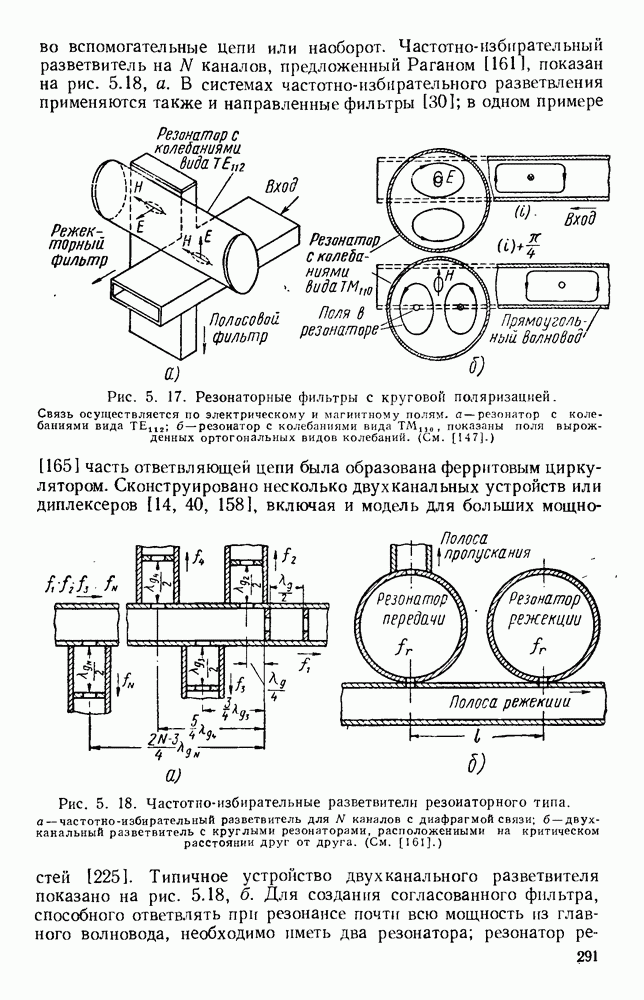
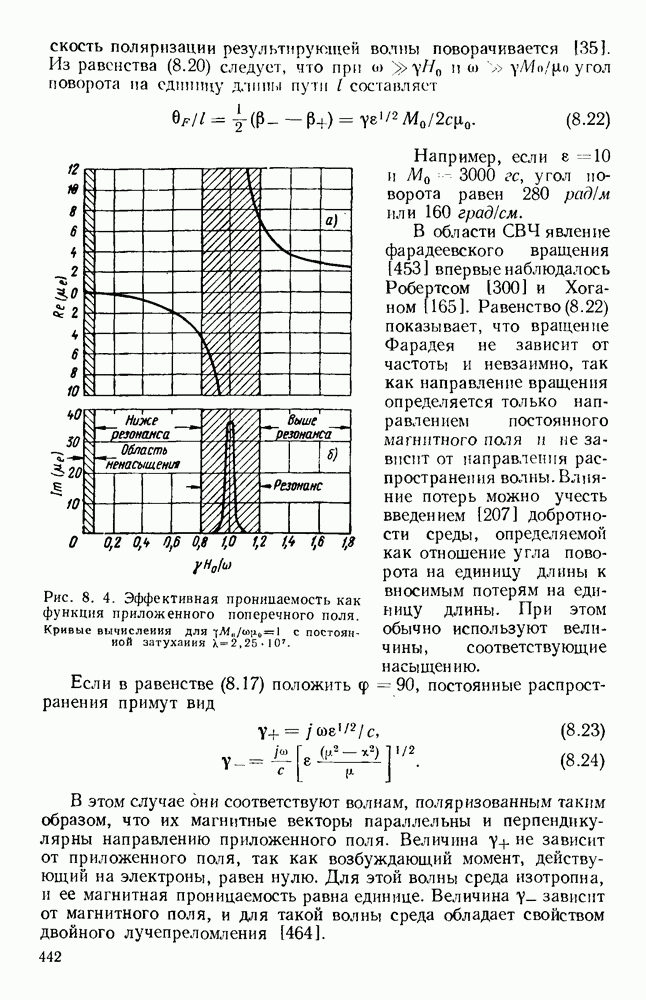
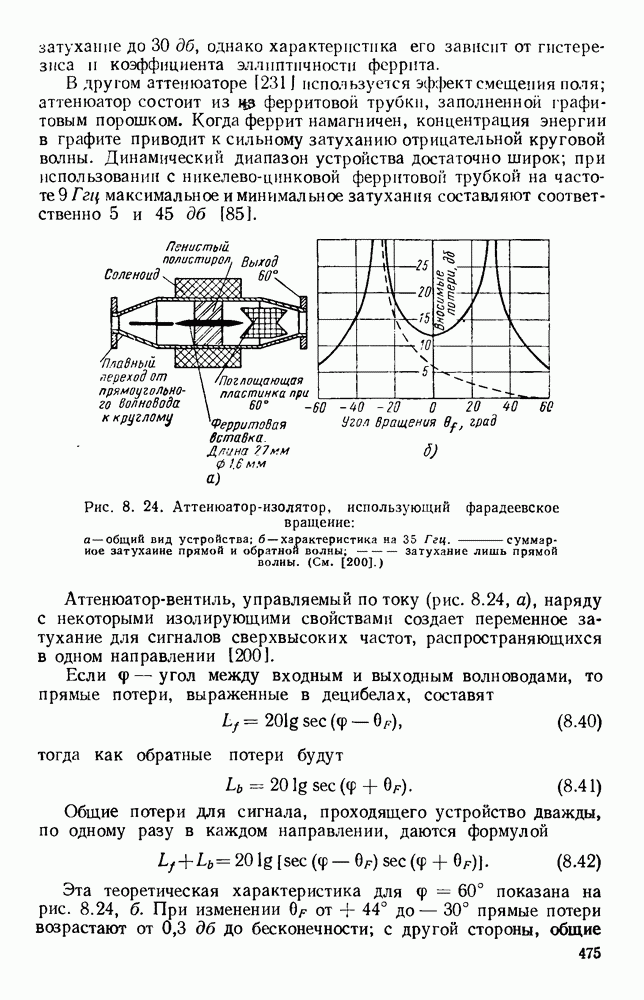
График этого углового спектра изображен на рис. 13.3 (кривая а), причем  при
при 
Аналогично для прямоугольной апертуры, освещенной линейно-поляризованным синфазным полем с амплитудным распределением, пропорциональным  угловой спектр равен
угловой спектр равен

где  постоянная.
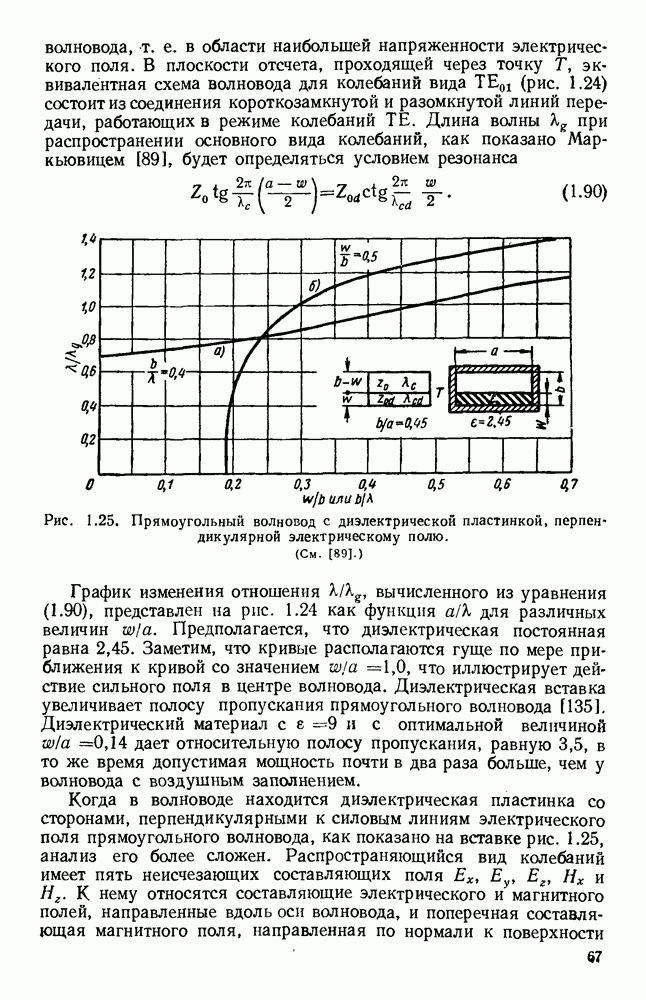
постоянная.
График этого спектра изображен на рис. 13.3 (кривая б). Следует отметить, что при таком спадающем к краям амплитудном распределении в отверстии получается заметное уменьшение уровня излучения под большими углами, т. е. уровня боковых лепестков диаграммы направленности, однако это достигается ценой расширения  главного лепестка.
главного лепестка.
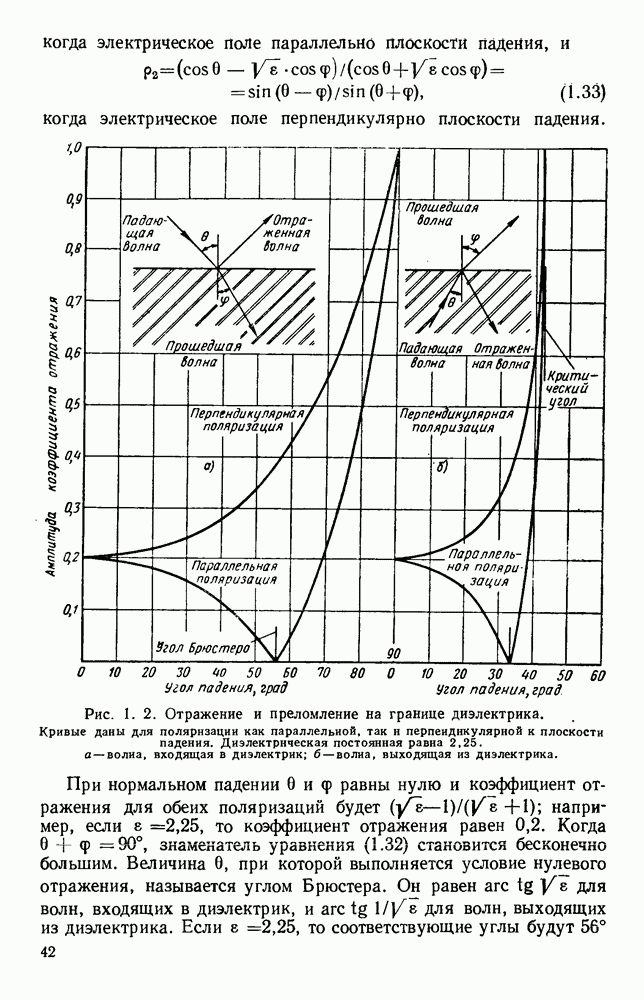
Более строгий подход к задаче дифракции был сделан Коттлером [151]: в его решении учитывается векторный характер электромагнитного поля, которое удовлетворяет уравнениям Максвелла и заданным граничным условиям. Зоммерфельд [233, 350] дал строгую теорию дифракции на отражающих экранах, в которой не используется принцип Гюйгенса, однако ввиду математической сложности эту теорию удается применить лишь для экранов простой геометрической формы, как, например, полуплоскость [187].
Для отверстий конечных размеров в плоском экране строгие решения дали: для круглого отверстия — Андреевский [8] и для эллиптического — Морзе и Рубенштейн [180]. Измерения, проведенные в диапазоне СВЧ [9, 20, 223], показали, что приближенные теории, основанные на формуле Гюйгенса — Кирхгофа, обеспечивают удовлетворительные результаты в тех случаях, когда размеры отверстий велики по сравнению с длиной волны и когда точка наблюдения расположена не слишком близко к отверстию, т. е. когда эффекты, обусловленные поляризацией и краевыми токами, малы [52, 390—393].

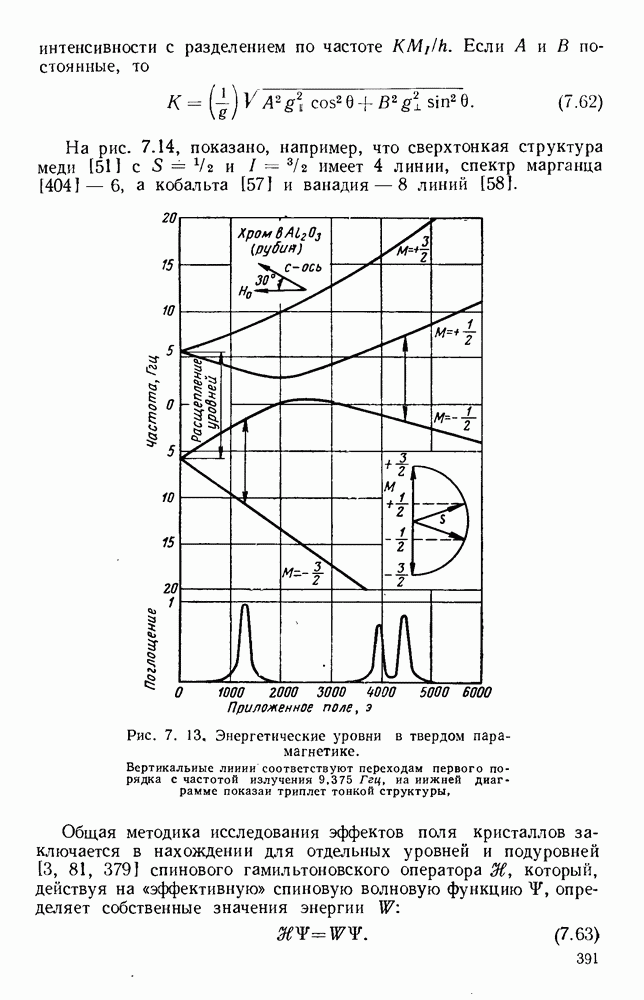
Рис. 13.3. Кривые для определения полей излучения из апертуры. Кривые дают множители направленности по полю излучателя с прямоугольной апертурой. а — равномерное распределение; б - косинусоидальное распределение.
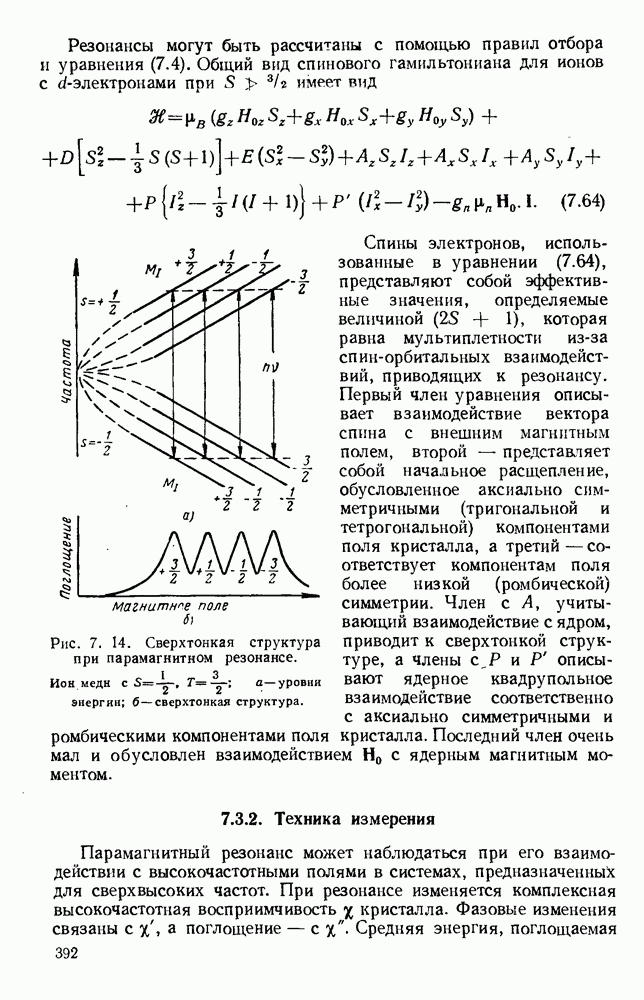
Решения получены для отверстий в плоском экране круглых [175, 201, 269], в виде щелей [6, 109, 115, 131, 219, 307, 317, 319, 348] и других форм [42, 120, 135, 136, 383].
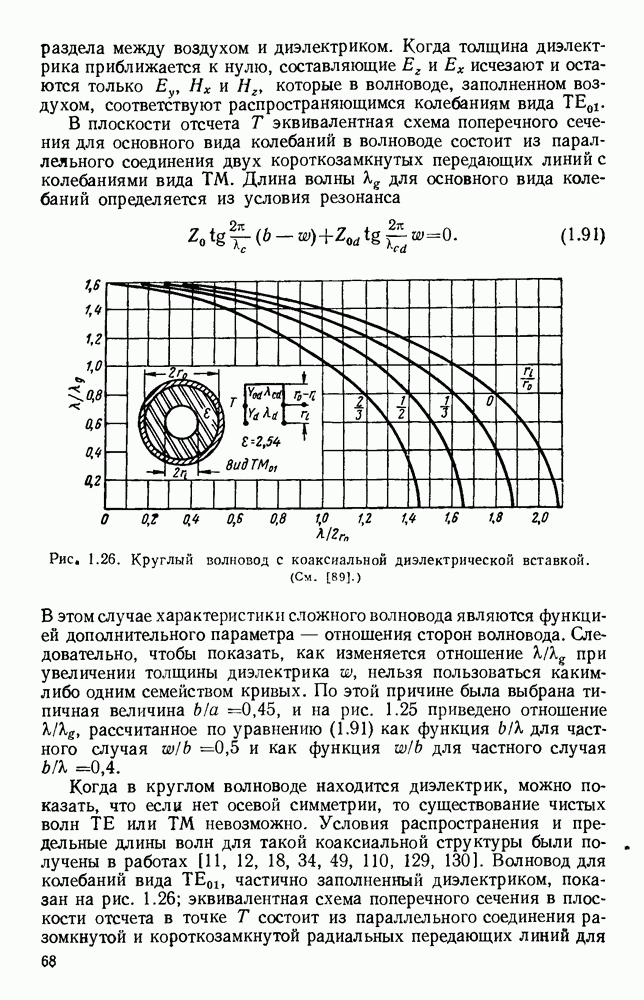
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
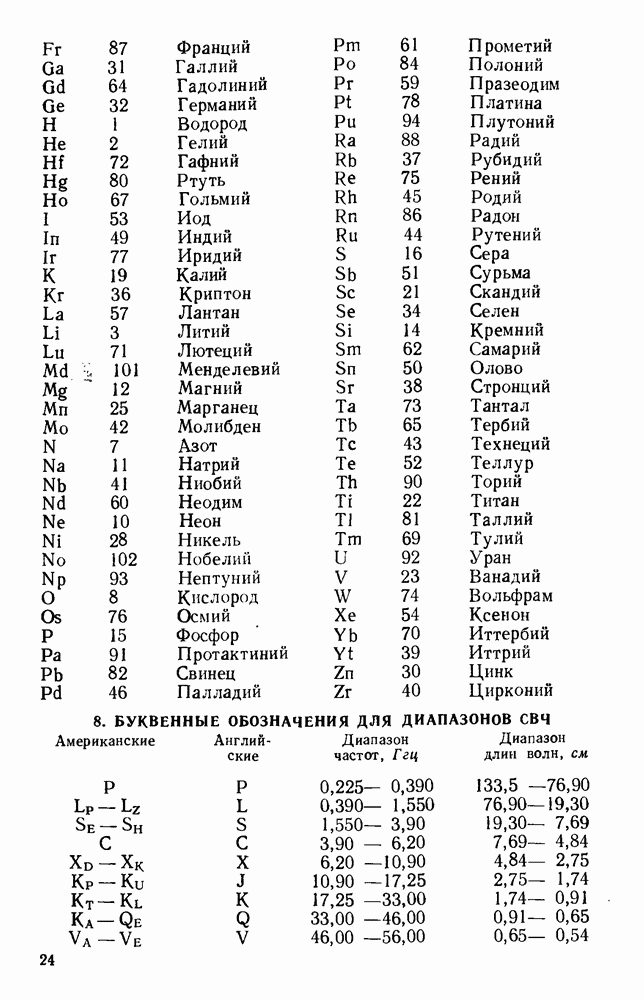
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
- 1.3.3. Коаксиальные линии
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
- 1.4.2. Круглые волноводы
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
- 1.5.2. Гребневые волноводы
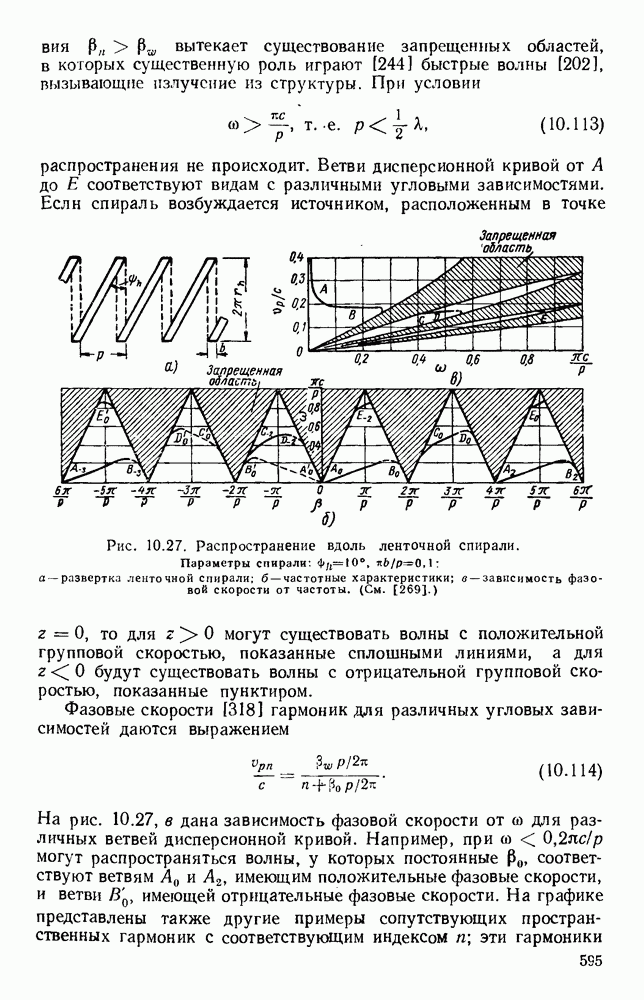
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
- 2.1.2. Круговая диаграмма
- 2.1.3. Широкополосное согласование
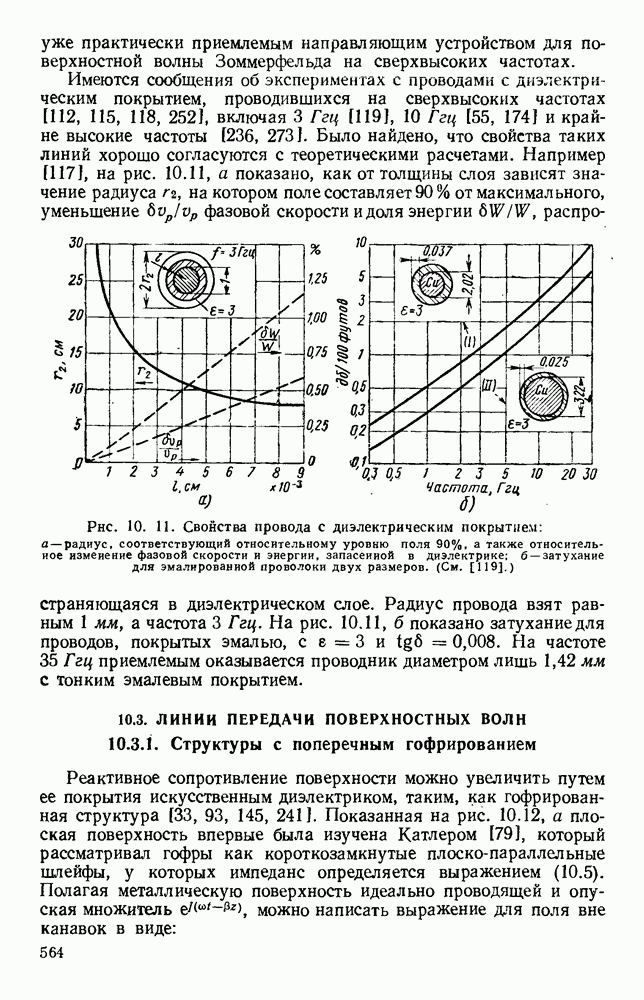
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
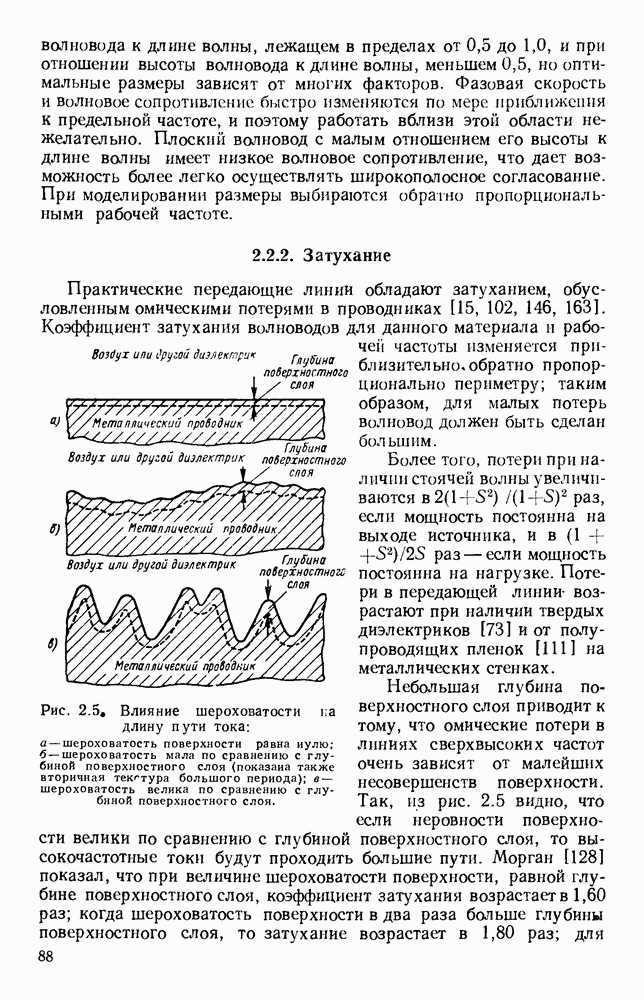
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
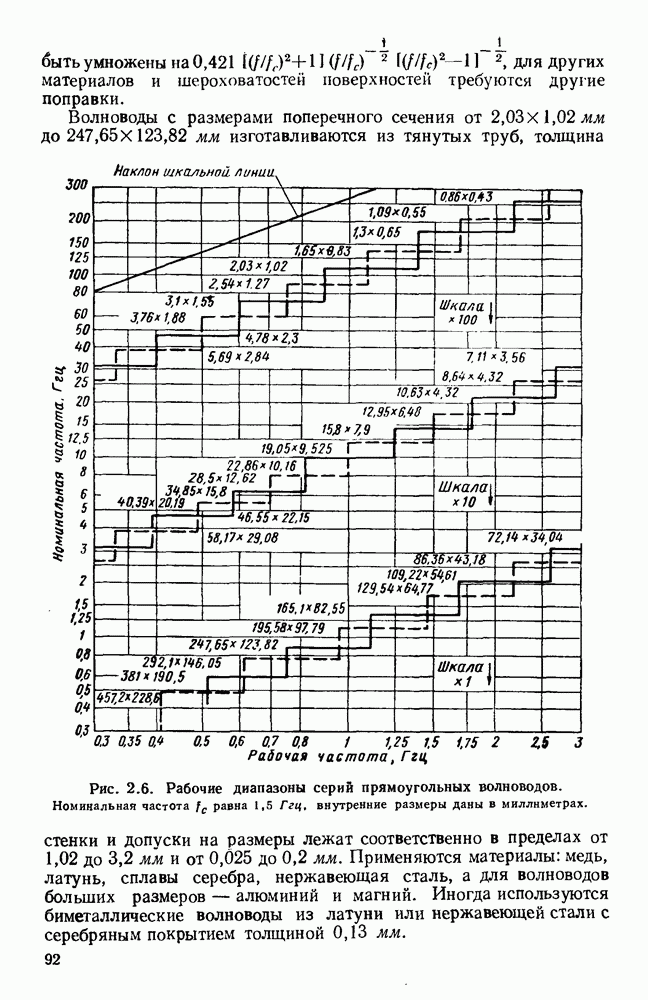
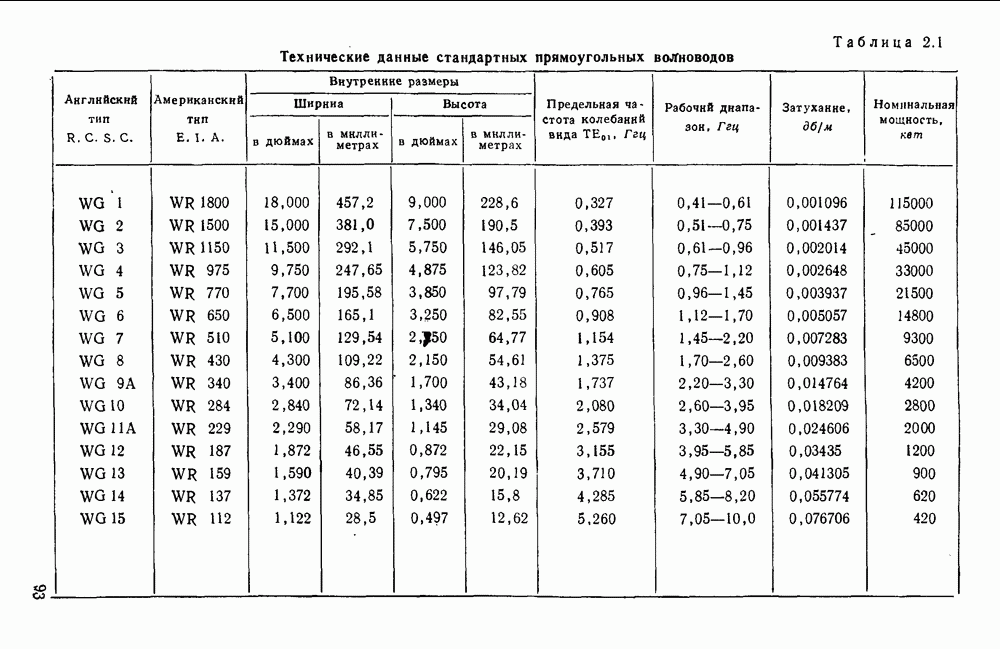
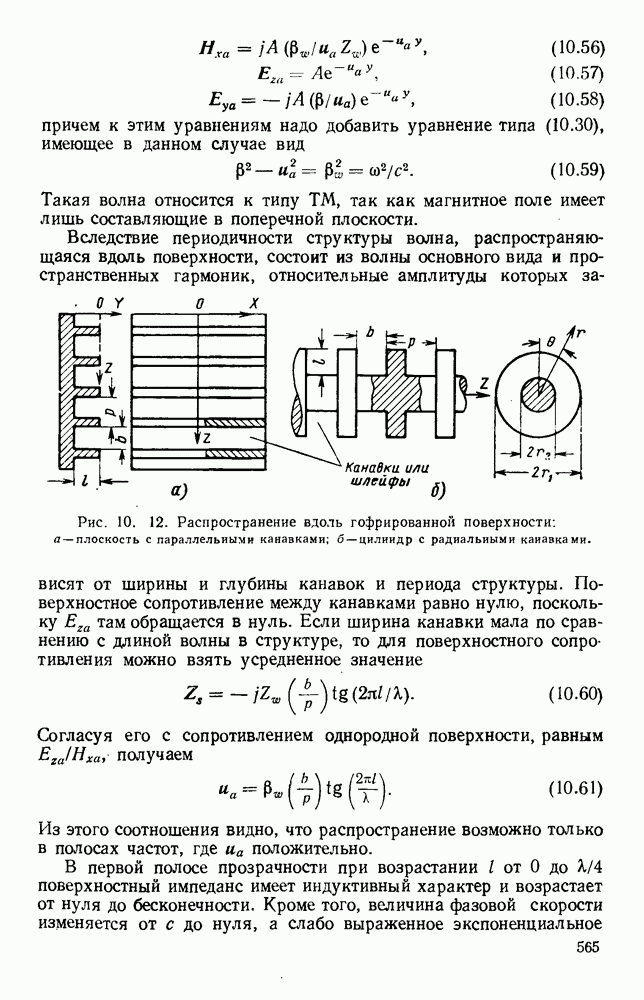
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
- 2.3.1. Прямоугольные волноводы
- 2.3.2. Круглые волноводы
- 2.3.3. Широкополосные и компактные волноводы
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
- 2.4.2. Контактные прокладки и дроссели
- 2.4.3. Крепежные и зажимные устройства
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
- 2.6.1. Изгибы, уголки и скрутки
- 2.6.2. Переходы и преобразователи
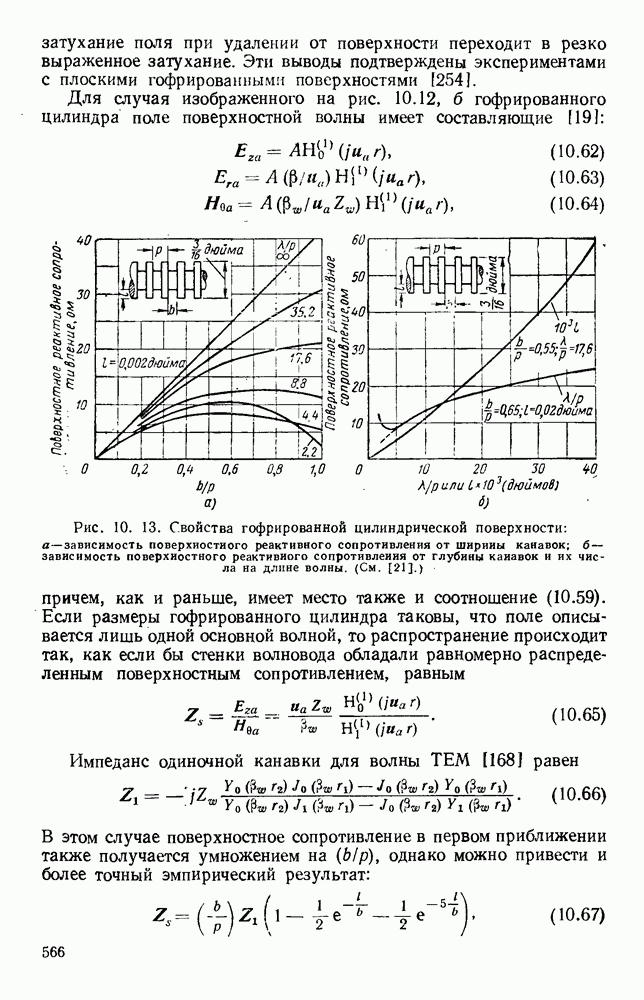
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
- 3.2.3. Переход от линейной поляризации к круговой
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
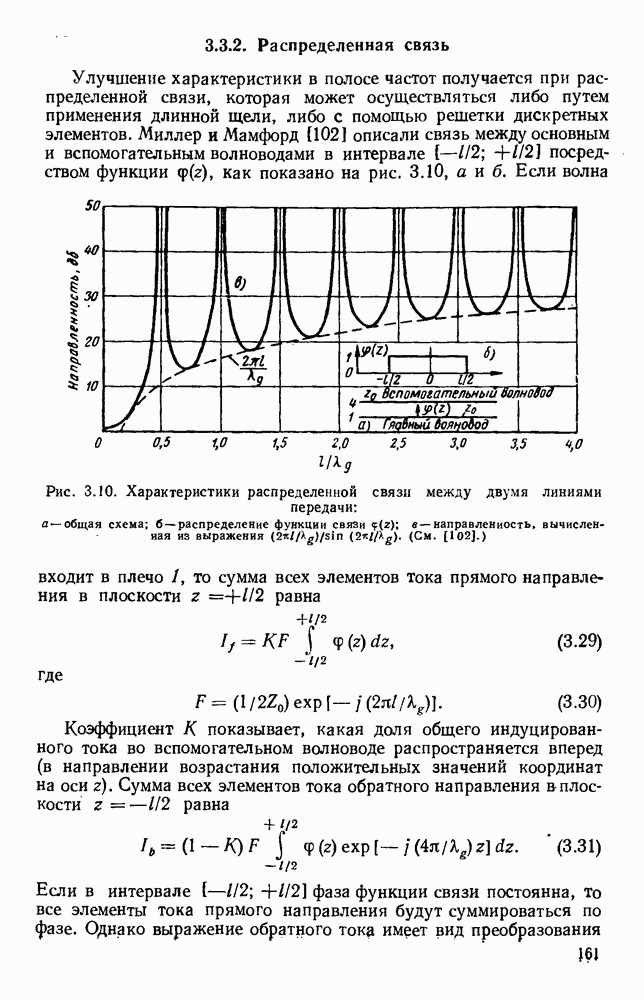
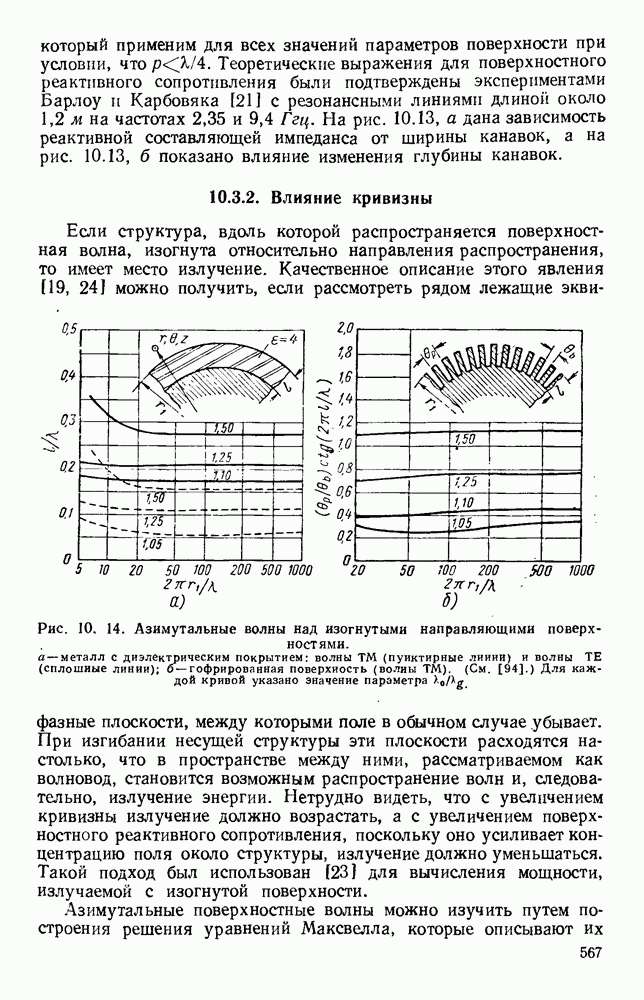
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
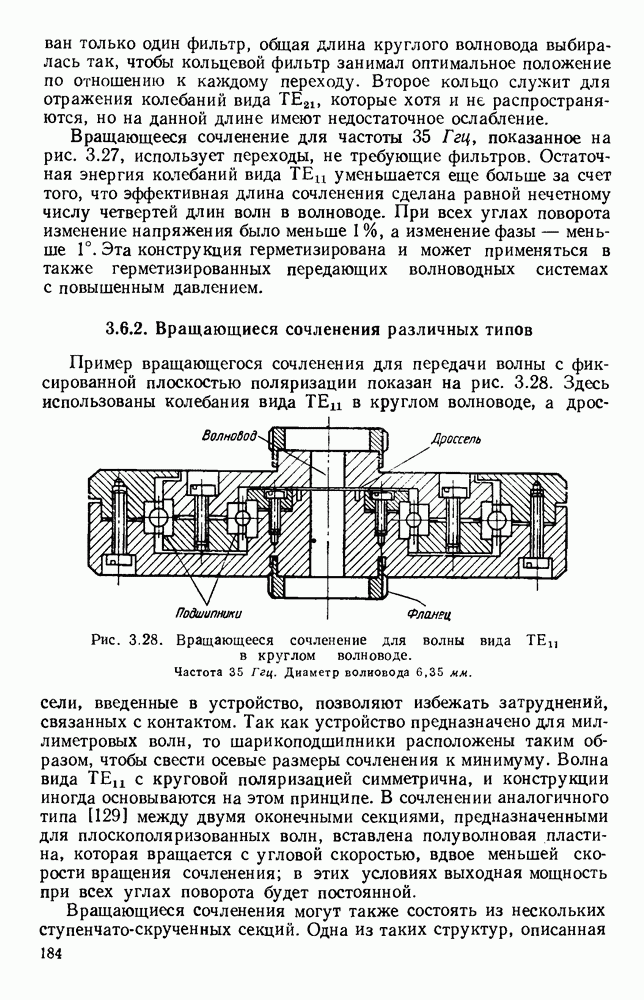
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
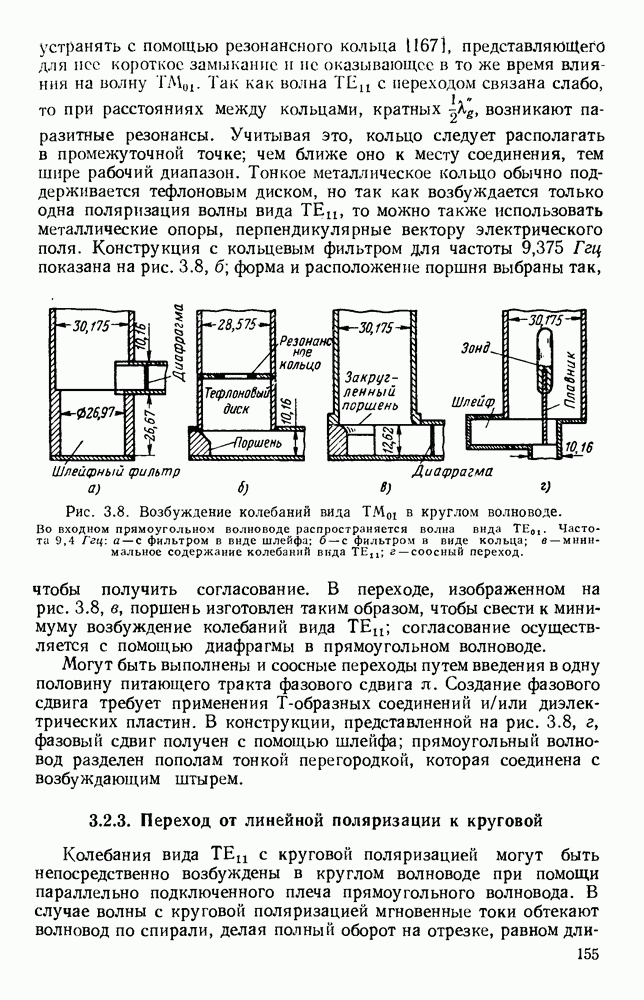
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
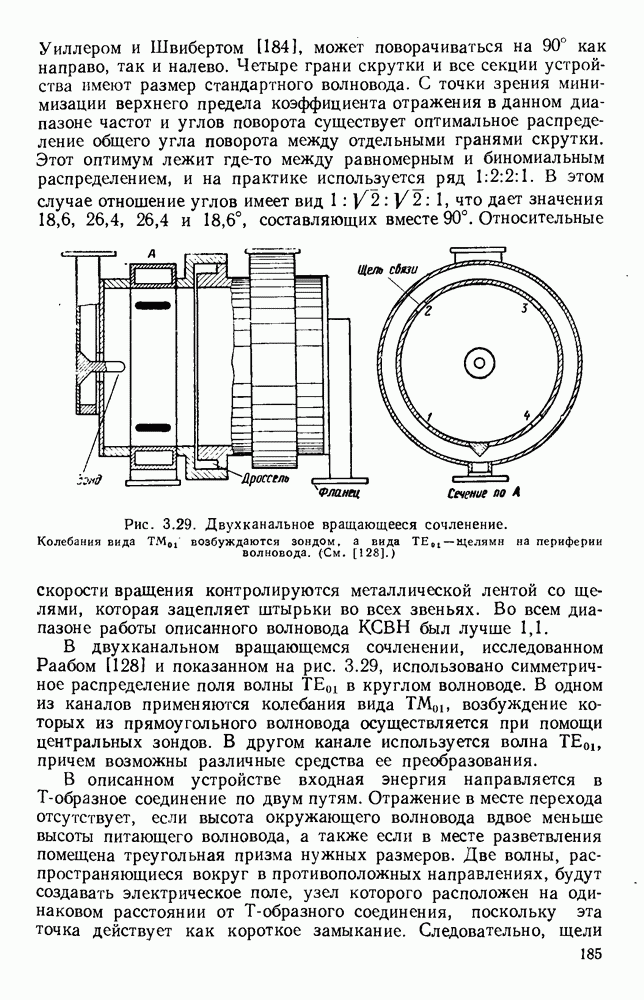
- 3.6.2. Вращающиеся сочленения различных типов
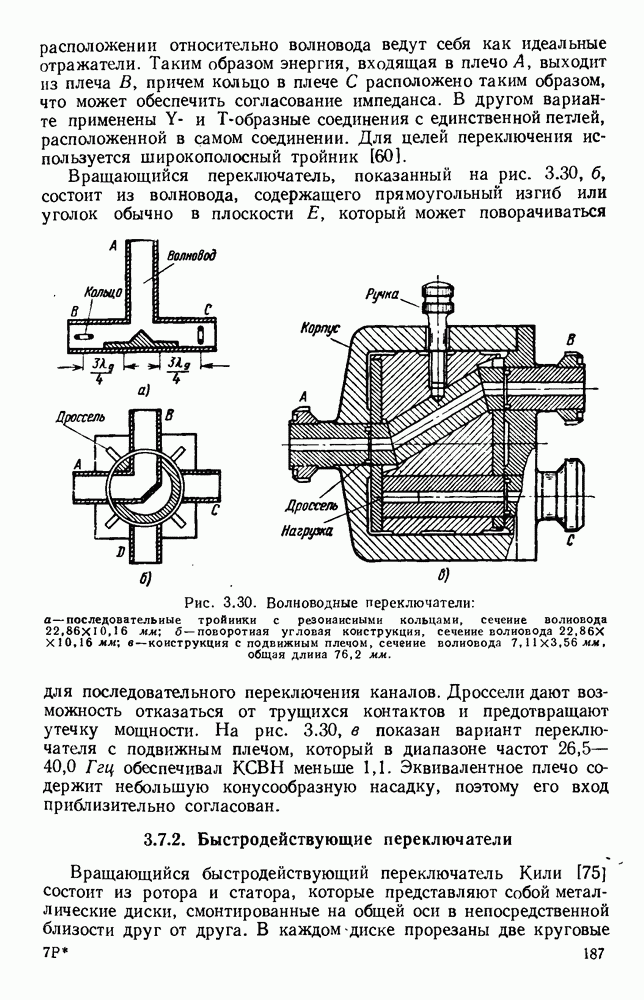
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
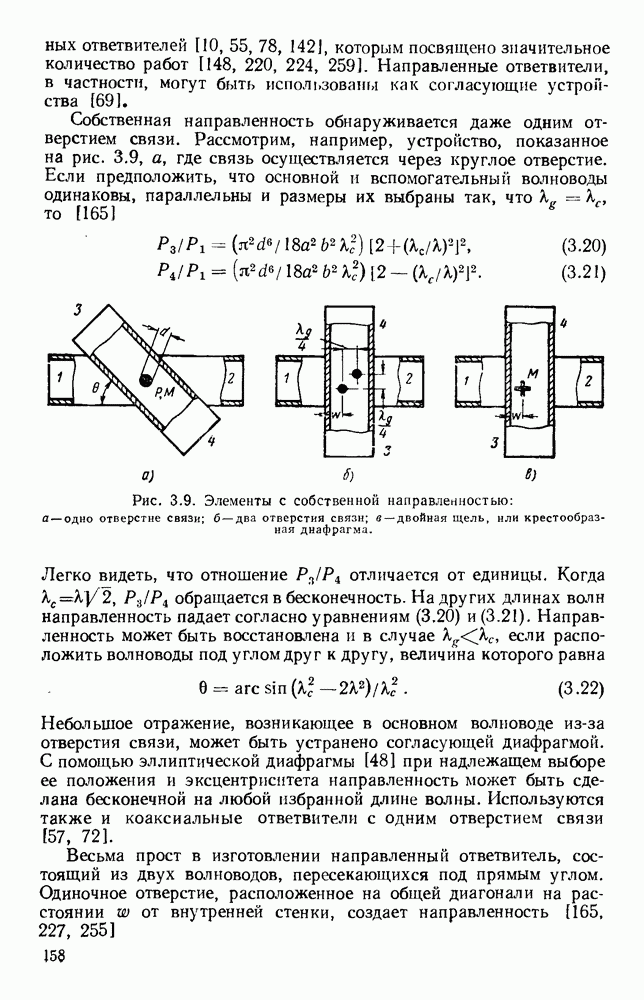
- 3.7.1. Механические переключатели с ручным управлением
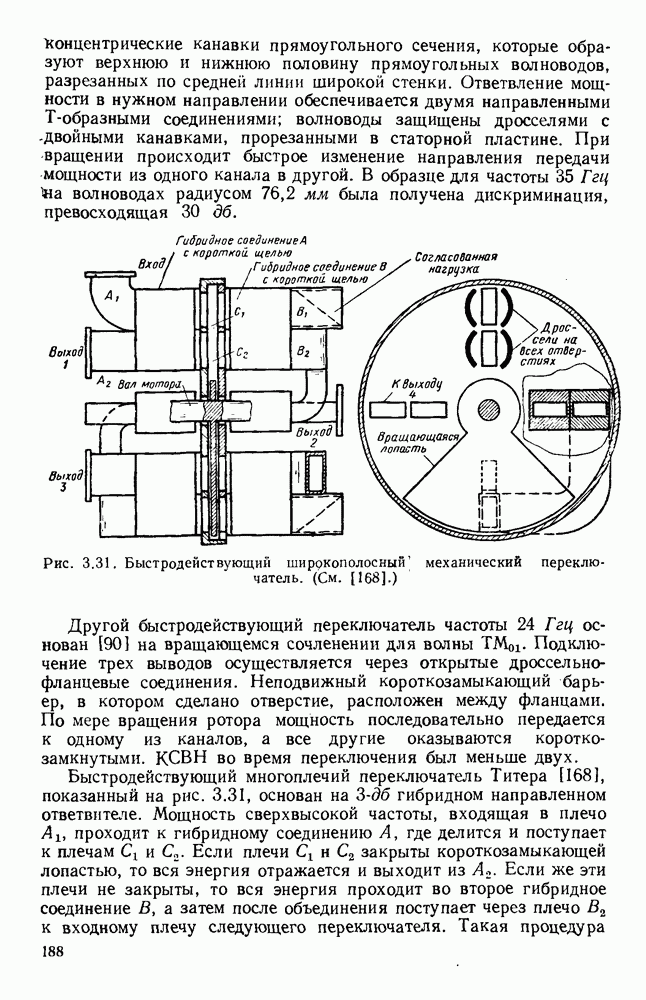
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
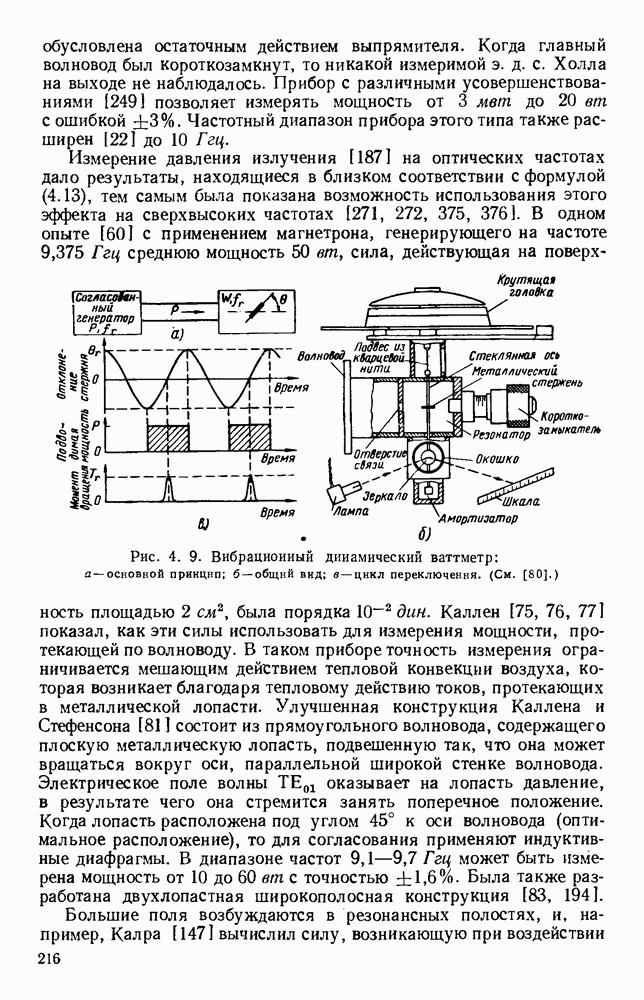
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
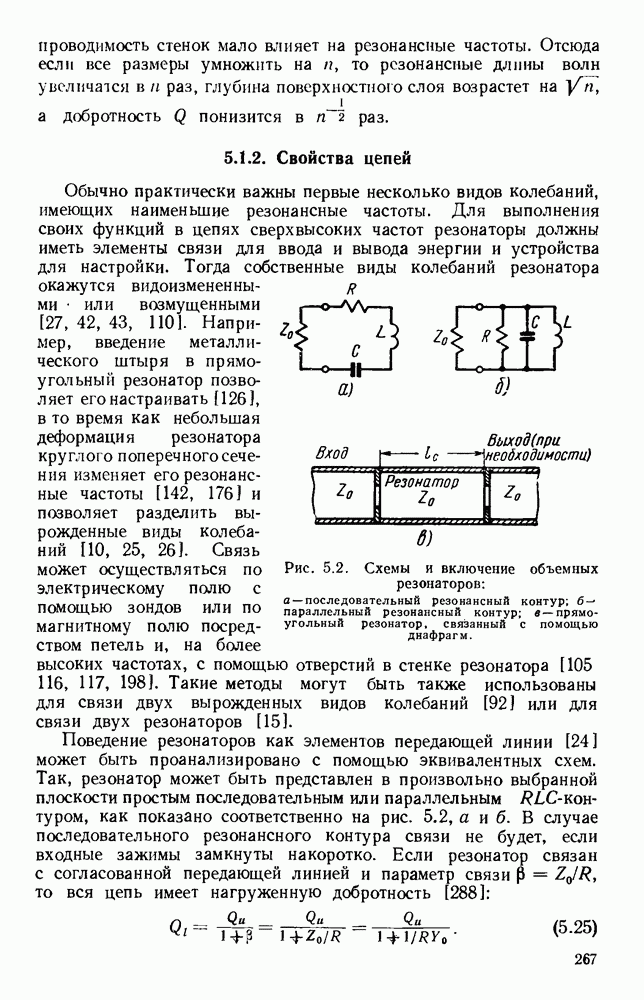
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
- 5.2.1. Волномеры с объемными резонаторами
- 5.2.2. Волноводные интерферометры
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
- 5.3.2. Связанные резонаторы
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
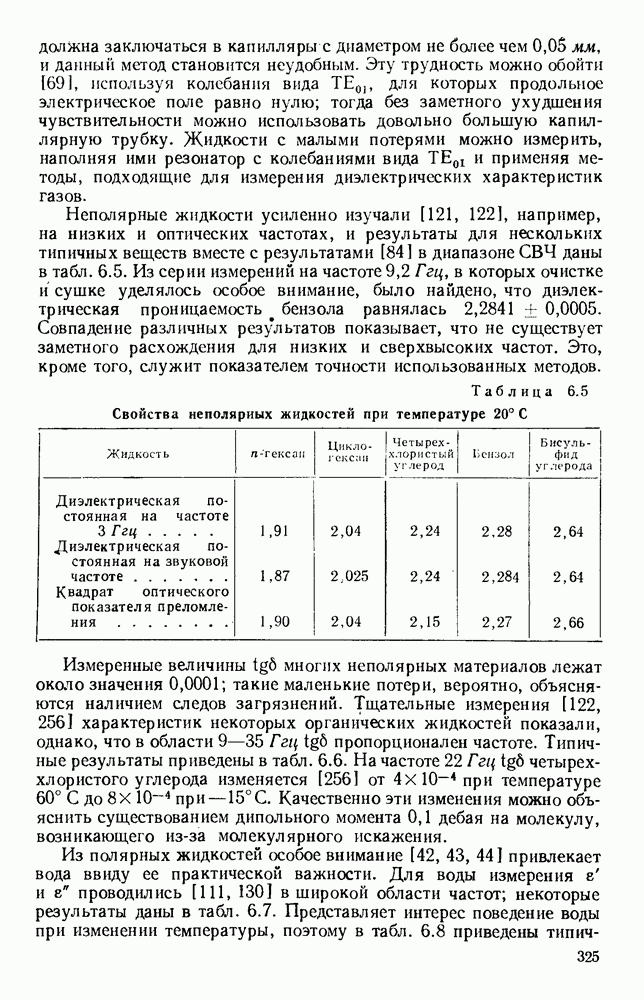
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
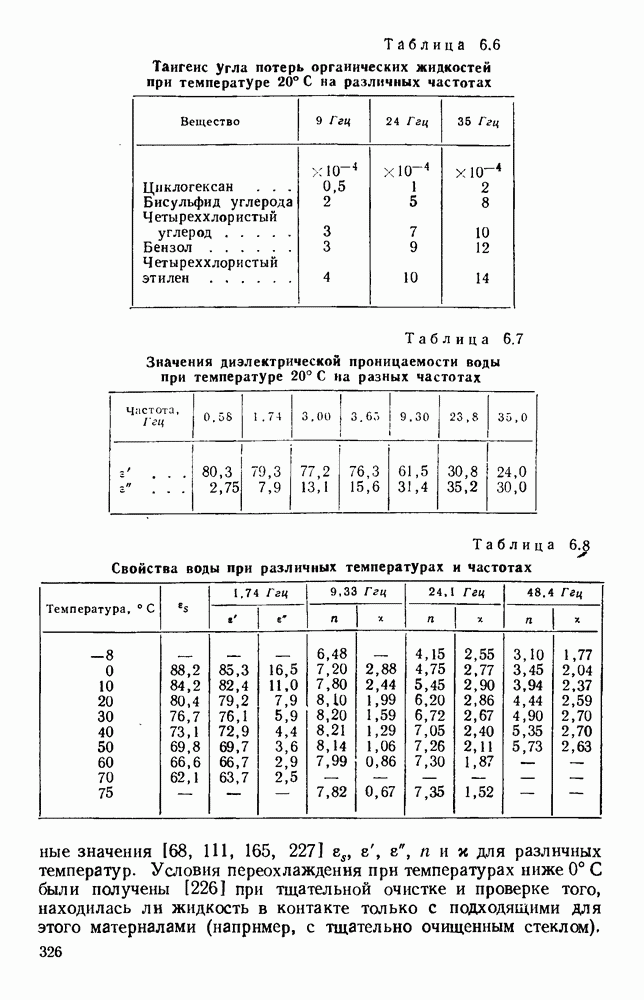
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
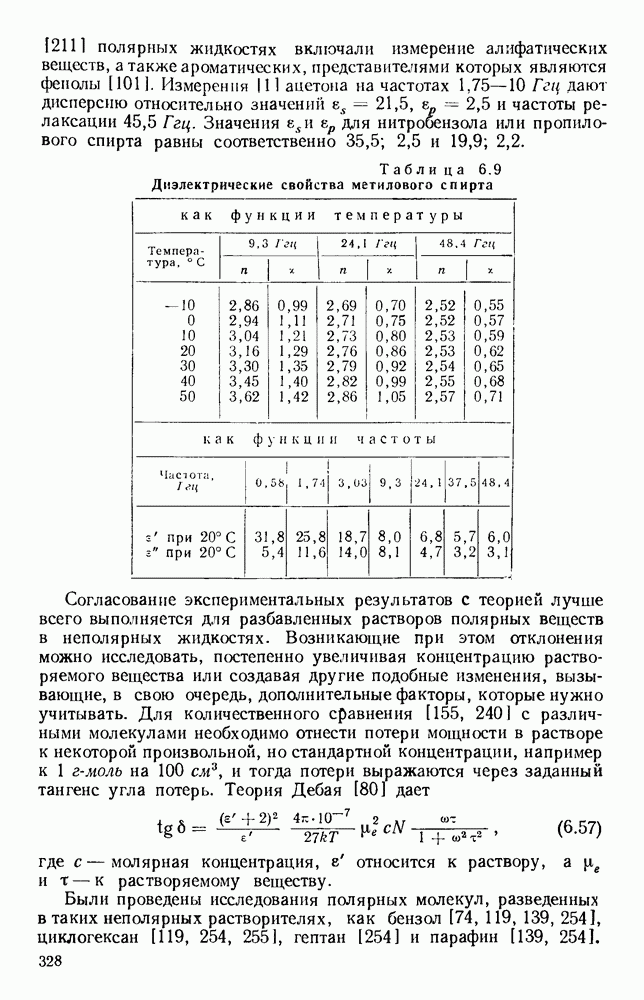
- 7.1.2. Форма линии и интенсивность
- 7.1.3. Сверхтонкая структура
- 7.1.4. Явления Штарка и Зеемана
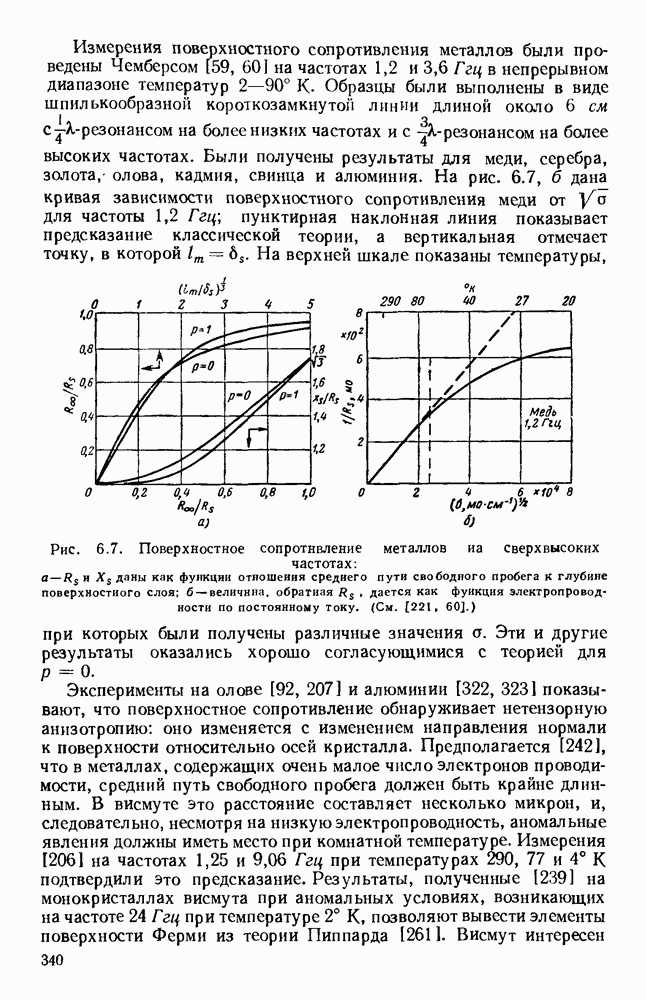
- 7.2. СПЕКТРОМЕТРЫ
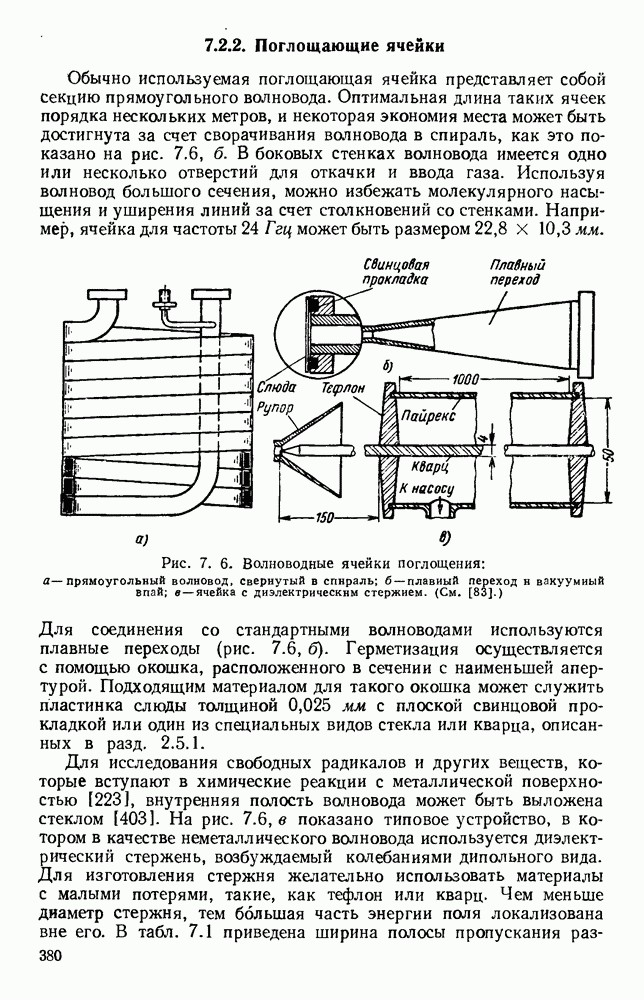
- 7.2.2. Поглощающие ячейки
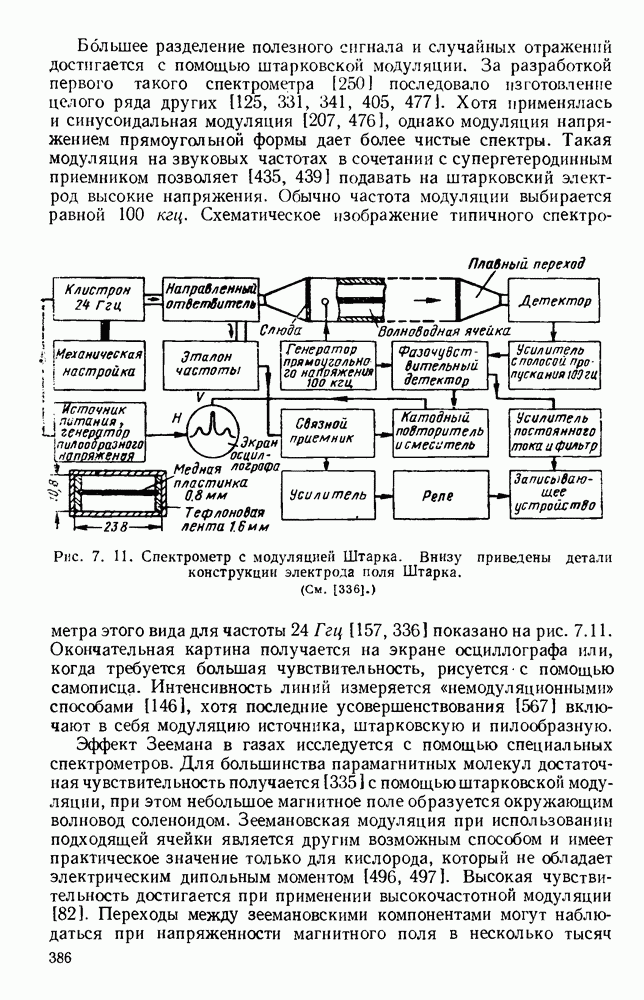
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
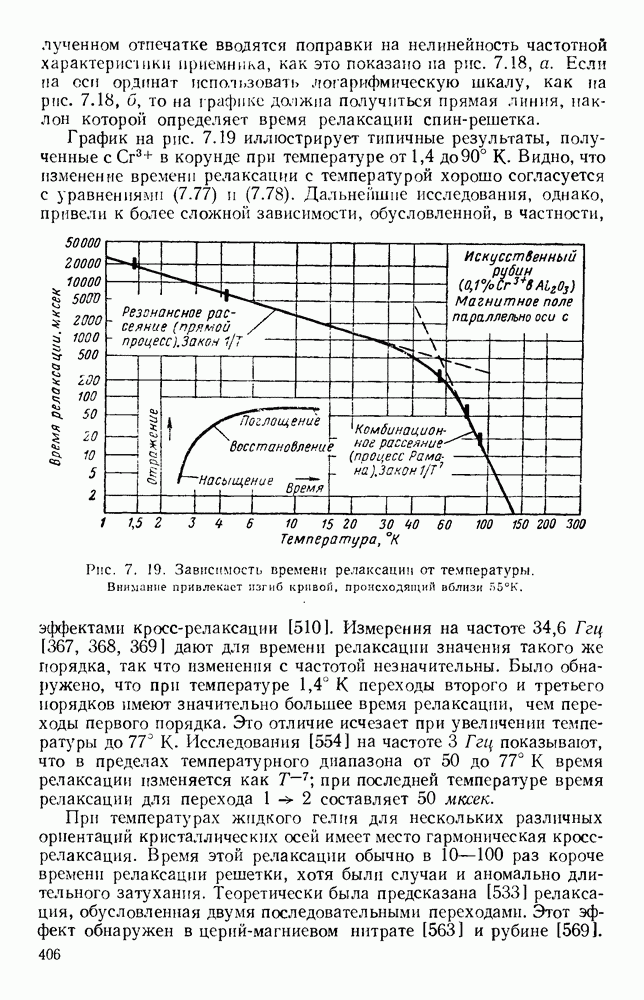
- 7.3.4. Времена релаксации
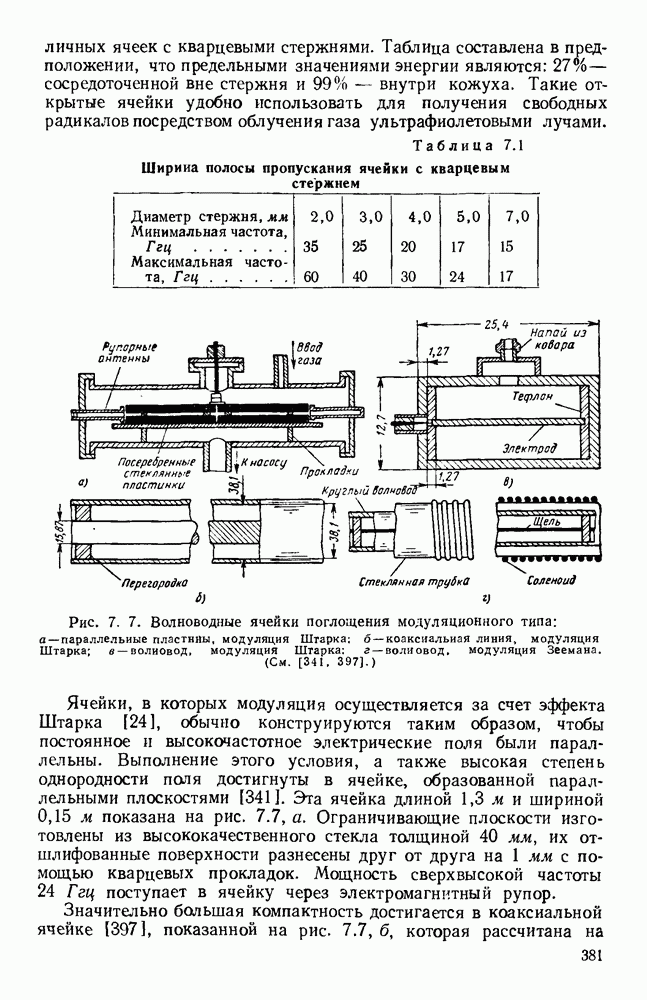
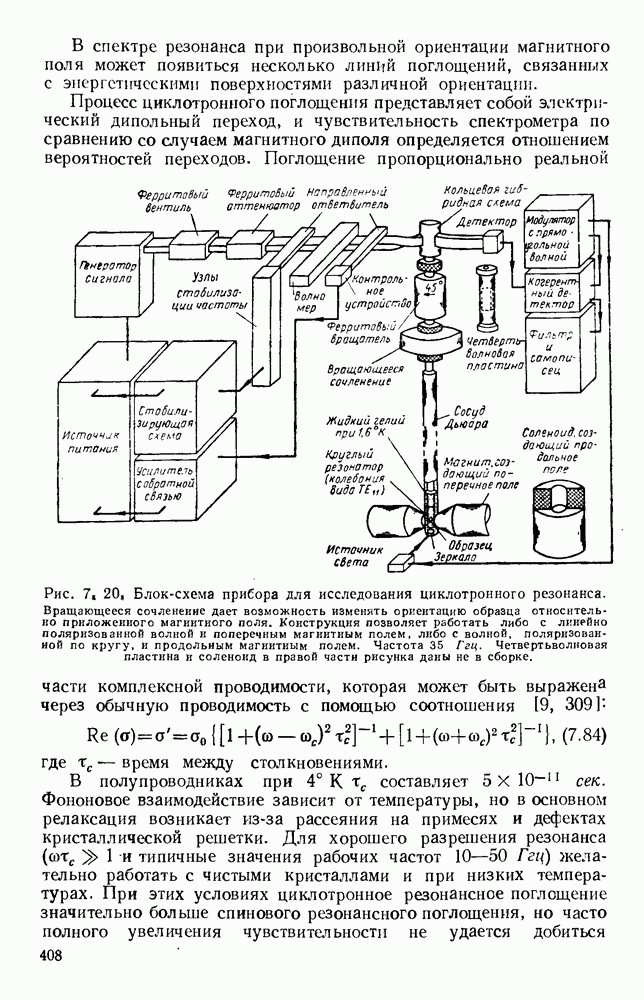
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
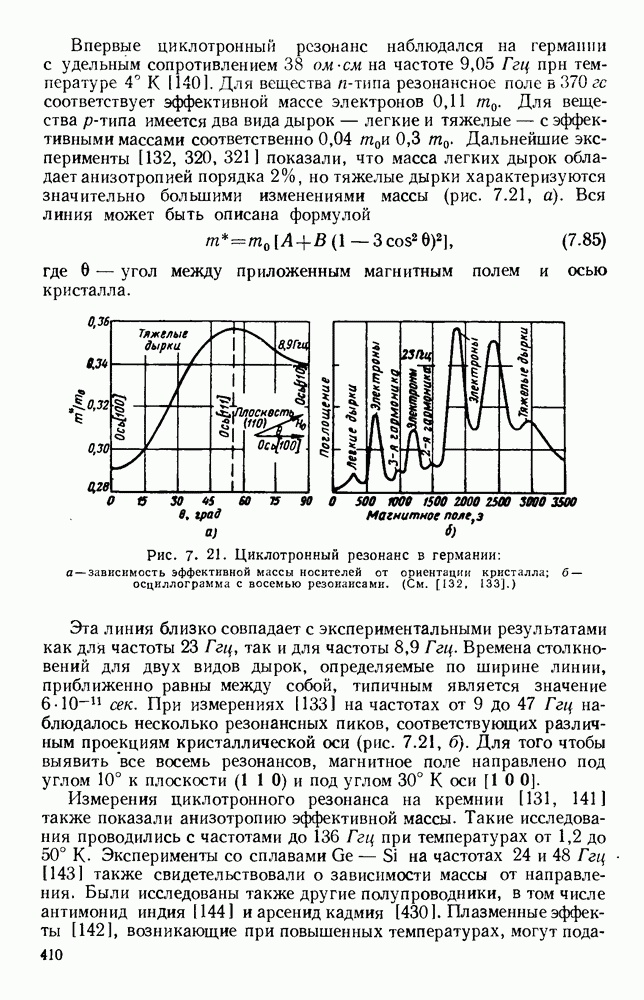
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
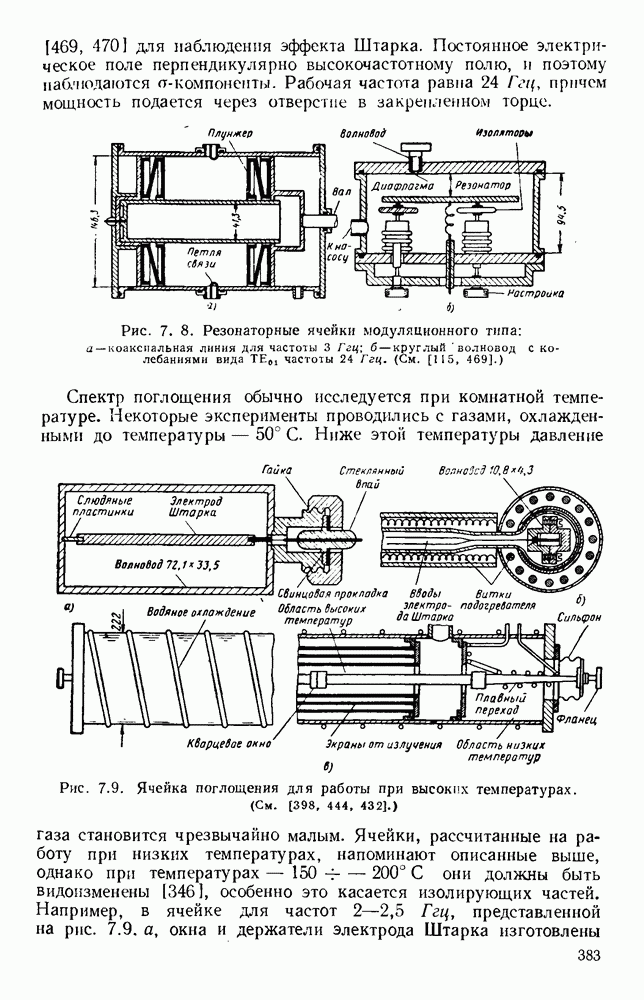
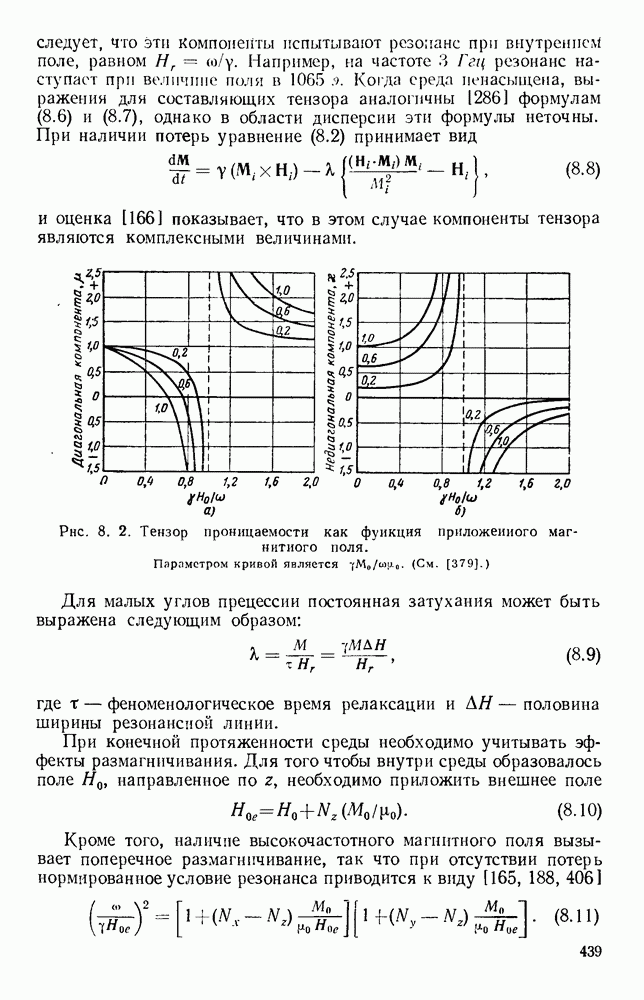
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
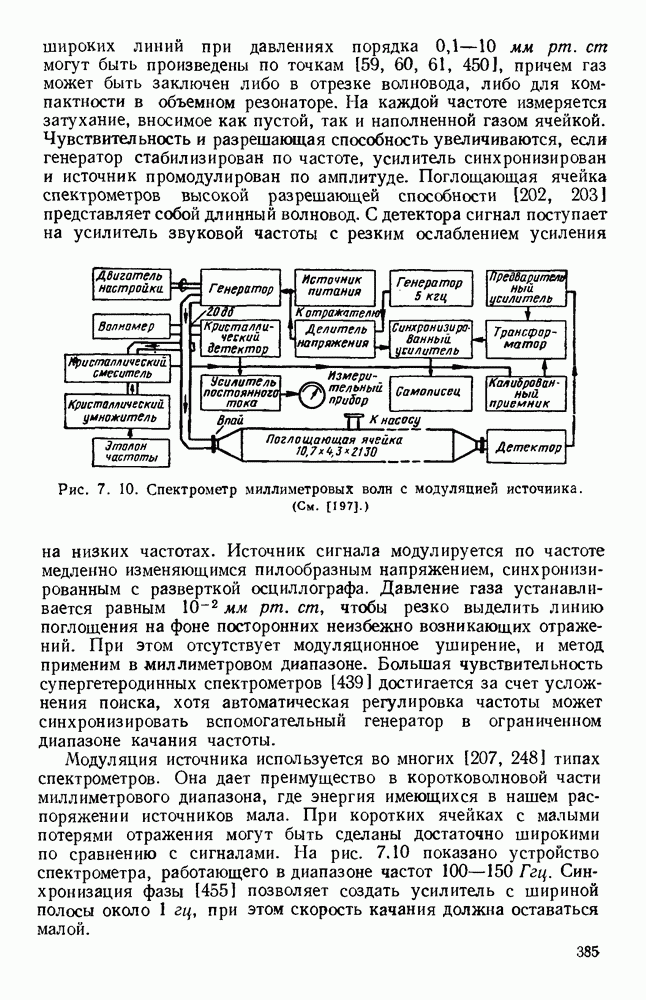
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
- 8.3.3. Ферритовые устройства в качестве элементов схем
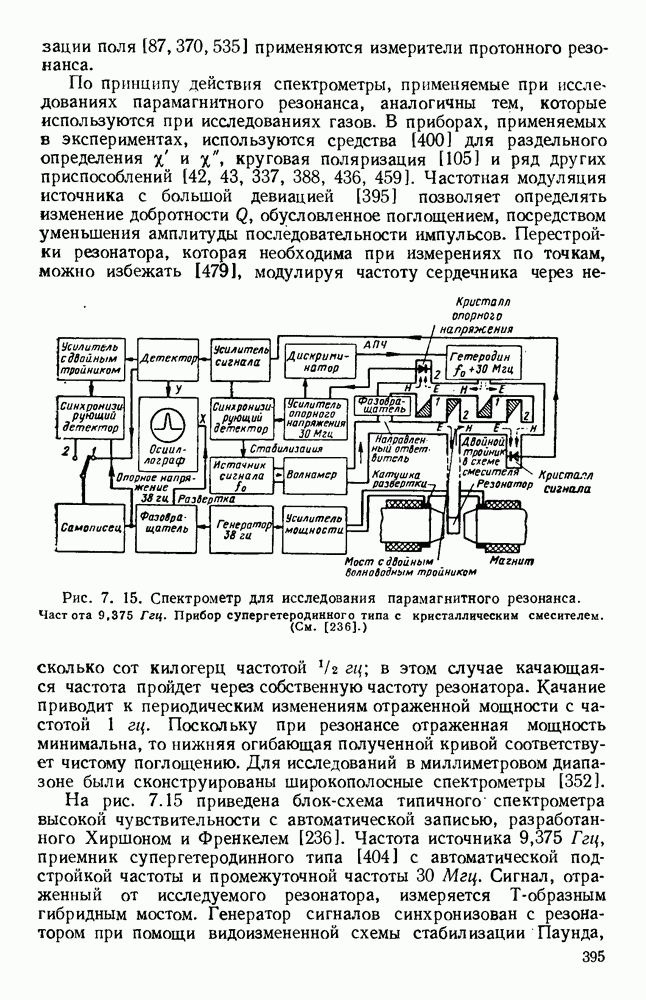
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
- 8.6.2. Устройства с поперечным полем
- 8.6.3. Прочие узлы
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.2.1. Линии типа «диэлектрических сэндвичей»
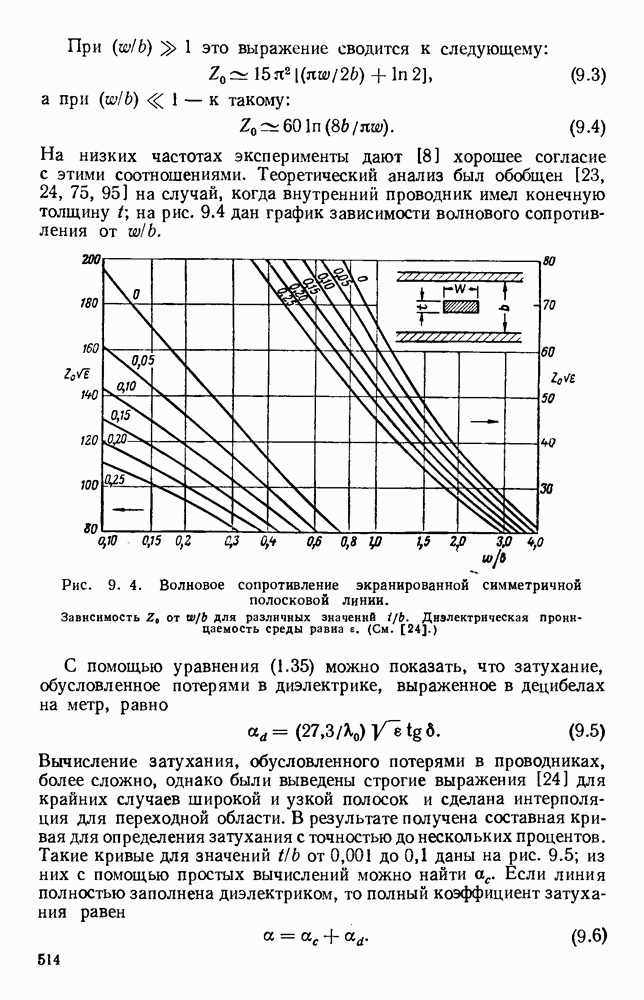
- 9.2.2. Симметричные линии с воздушным диэлектриком
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
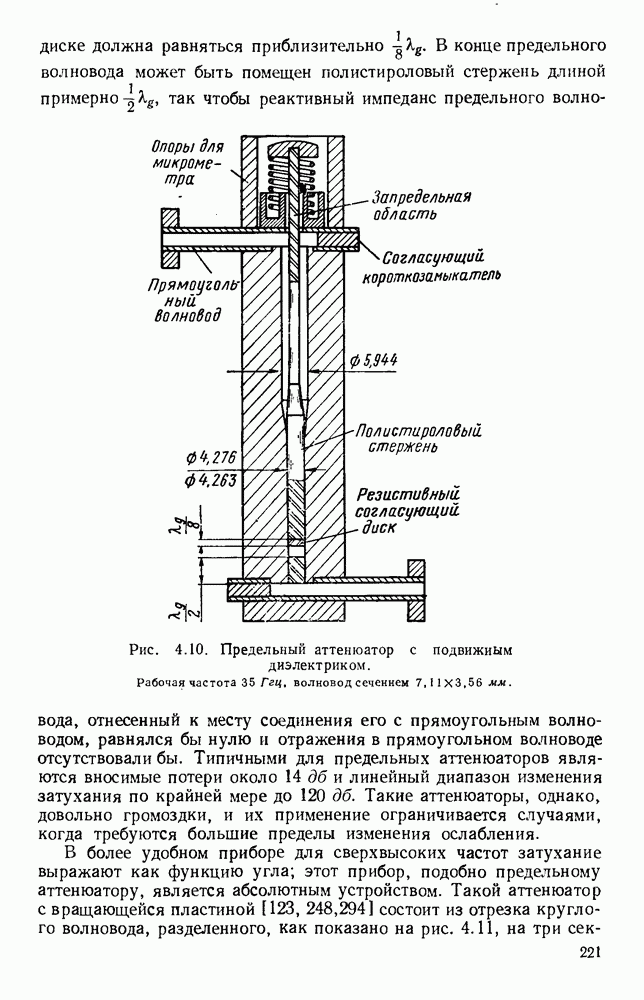
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
- 9.4.2. Переходные устройства
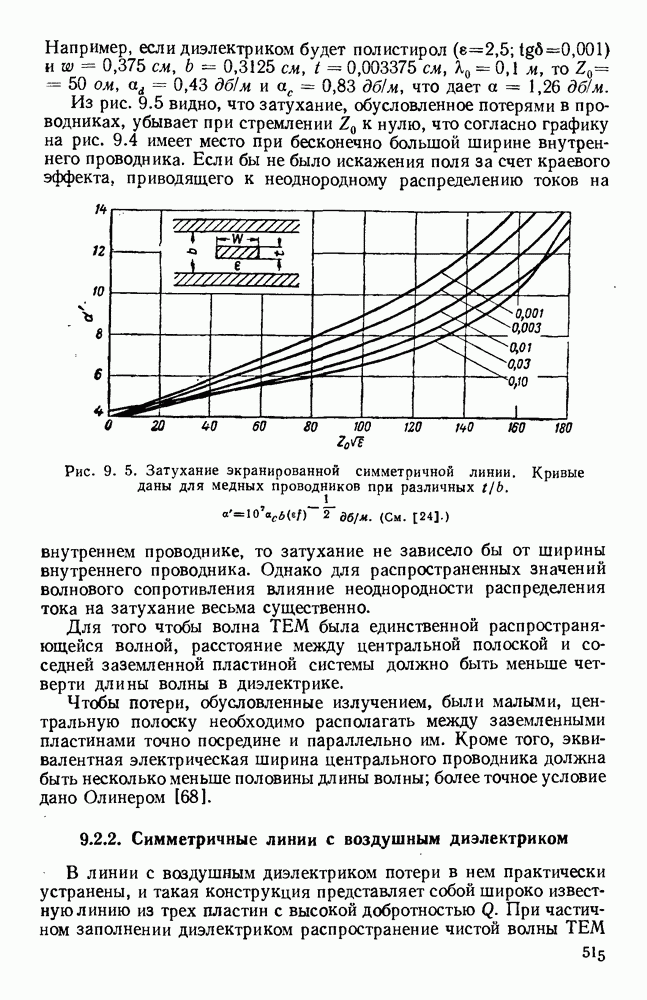
- 9.4.3. Узлы полосковых систем
- 9.5. ЦЕПИ И СИСТЕМЫ
- 9.5.3. Частотные фильтры
- 9.5.4. Цепи питания антенн
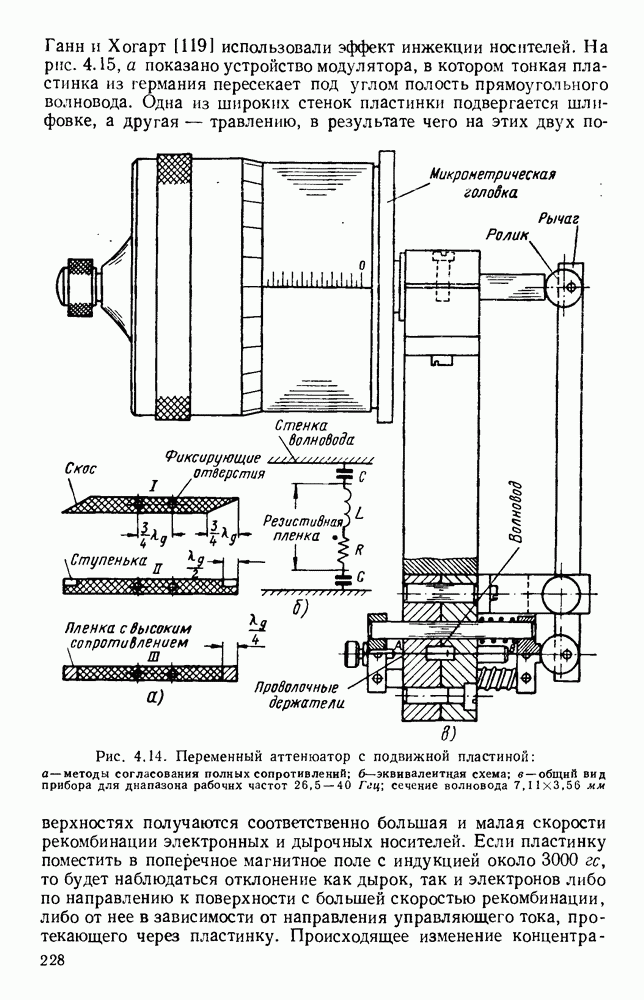
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
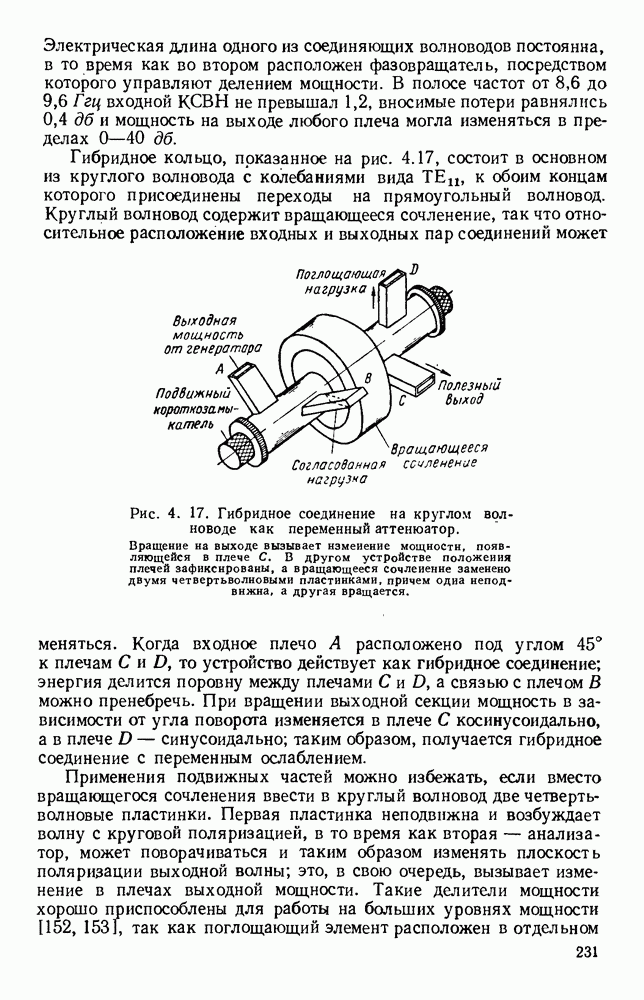
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
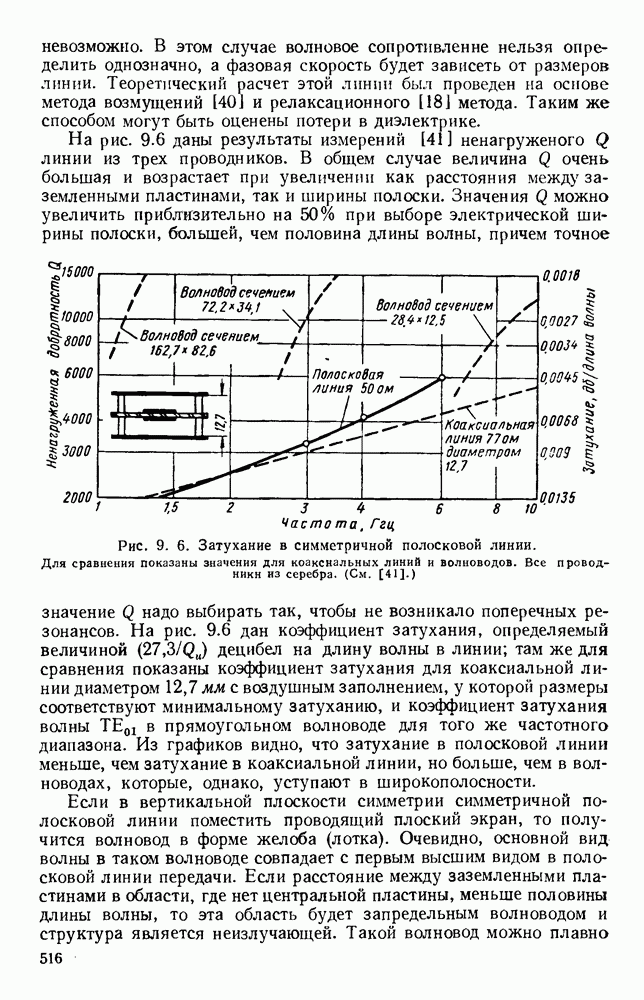
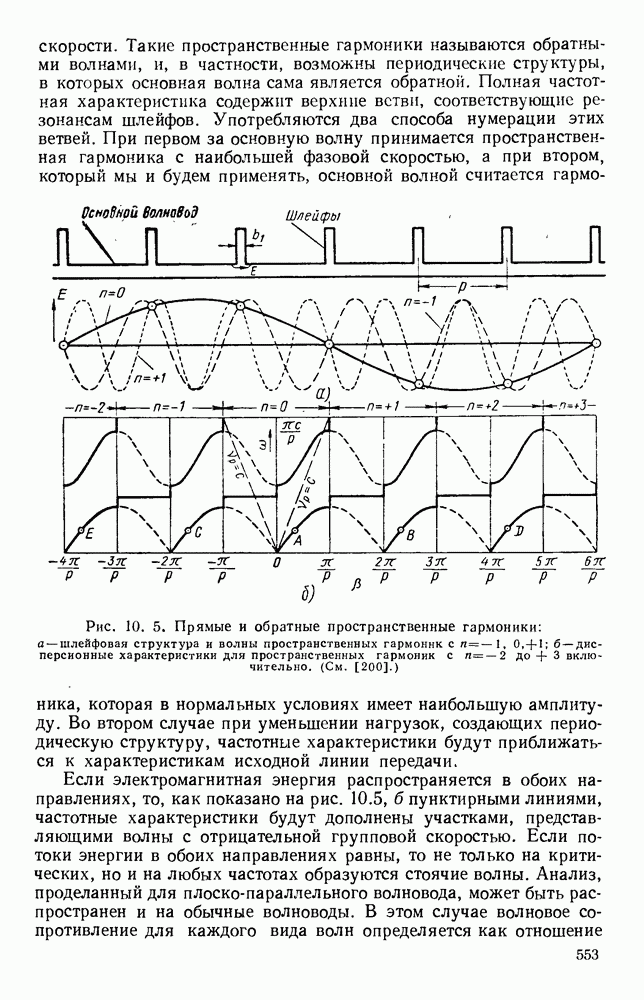
- 10.1.2. Пространственные гармоники
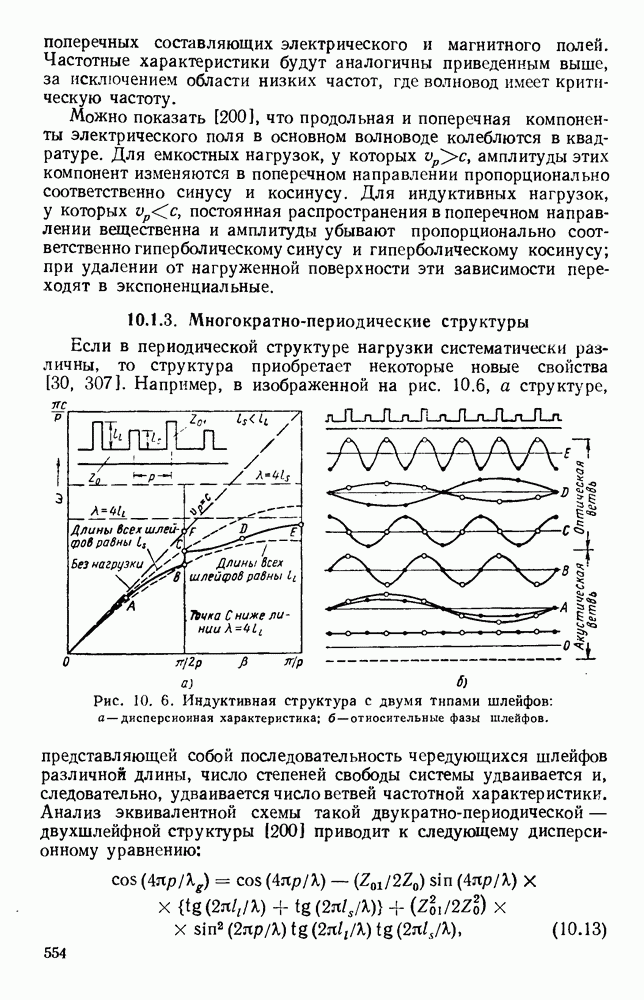
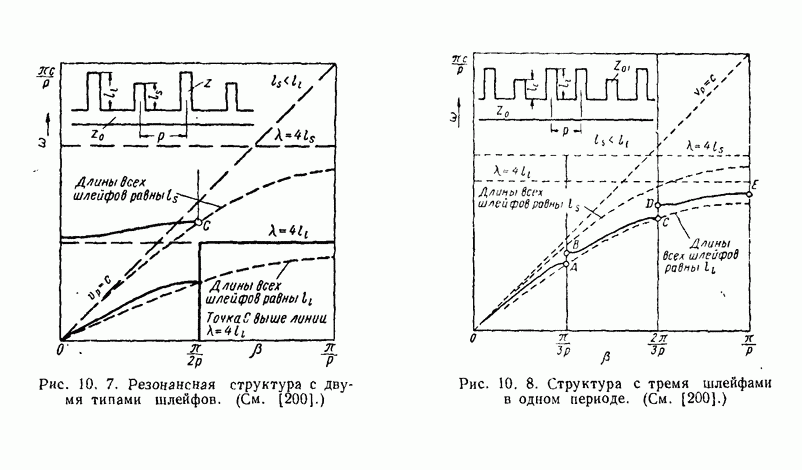
- 10.1.3. Многократно-периодические структуры
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
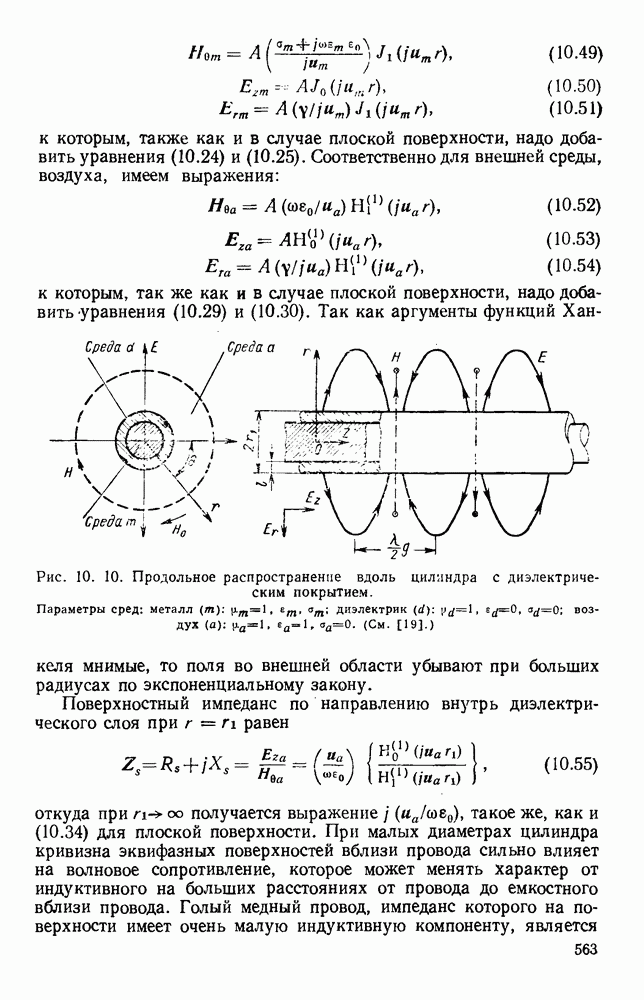
- 10.2.3. Продольные цилиндрические волны
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
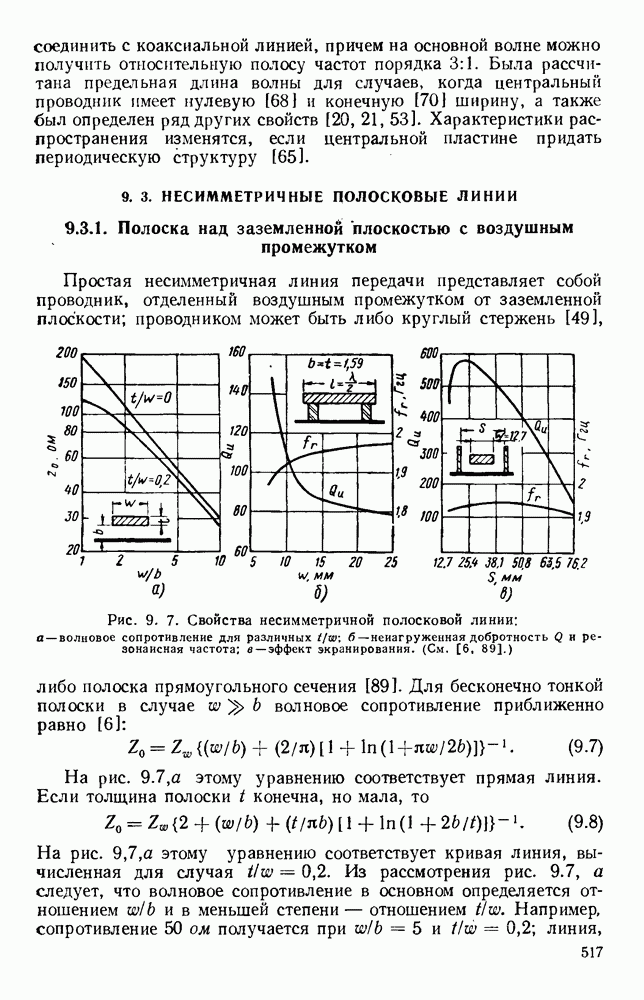
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
- 12.2. МАГНЕТРОНЫ
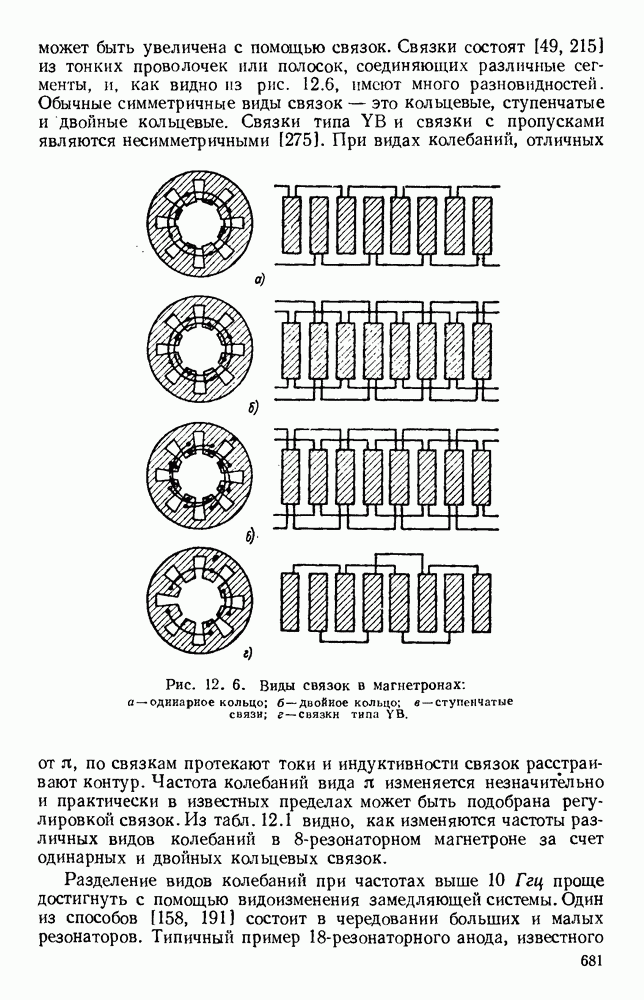
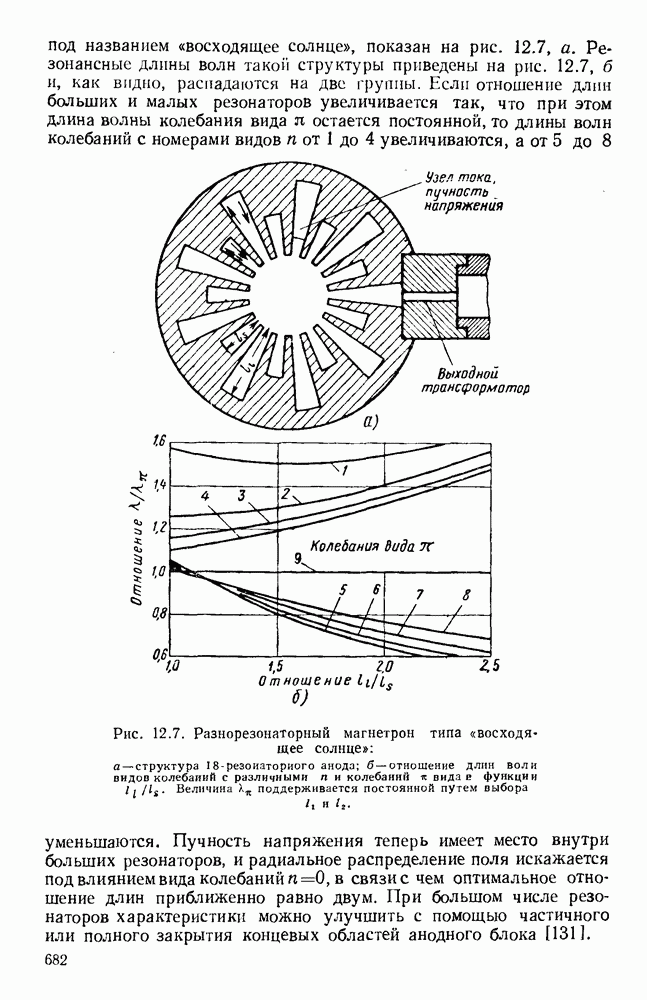
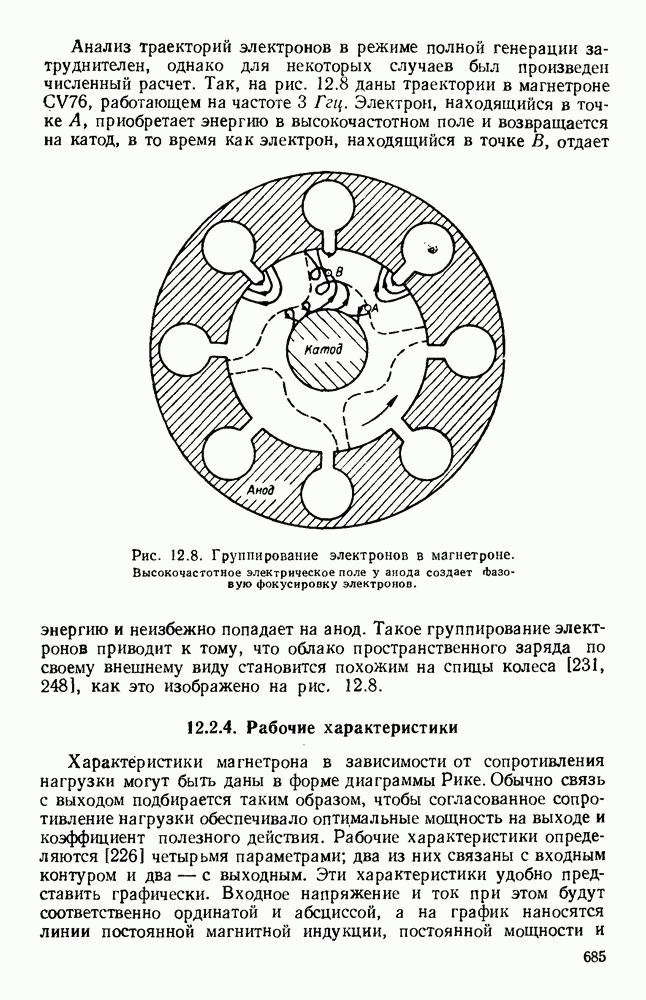
- 12.2.2. Резонаторные системы
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
- 12.2.4. Рабочие характеристики
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
- 13.1.2. Типы дифракции
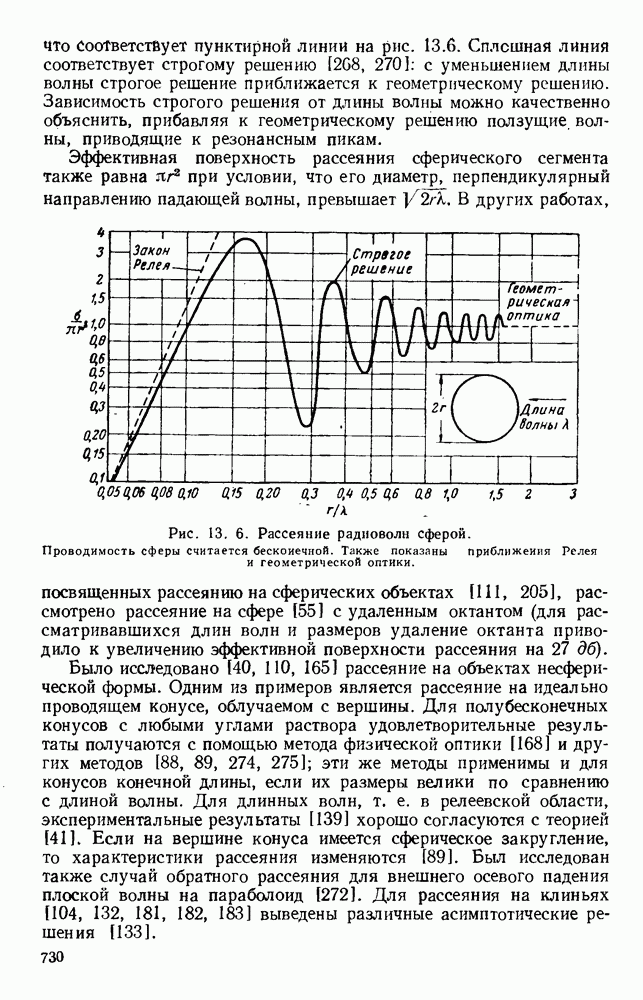
- 13.1.3. Рассеяние
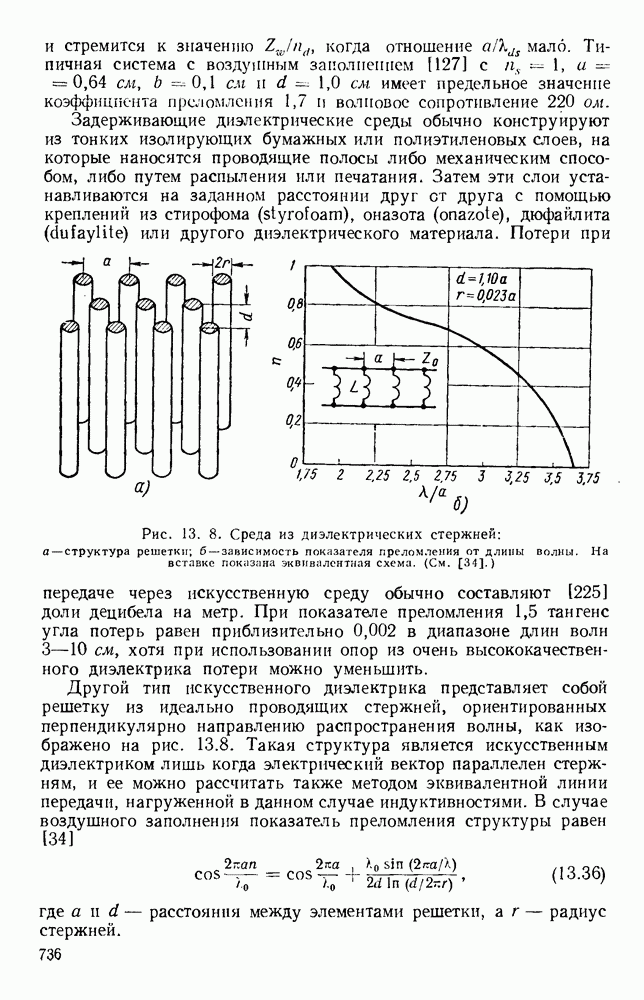
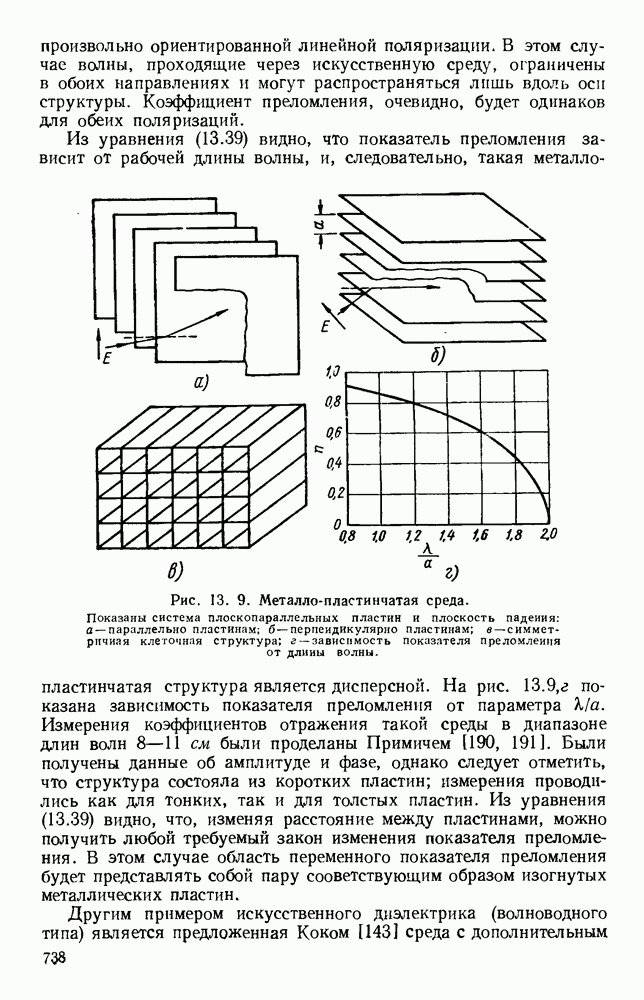
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
- 13.2.2. Структуры волноводного типа
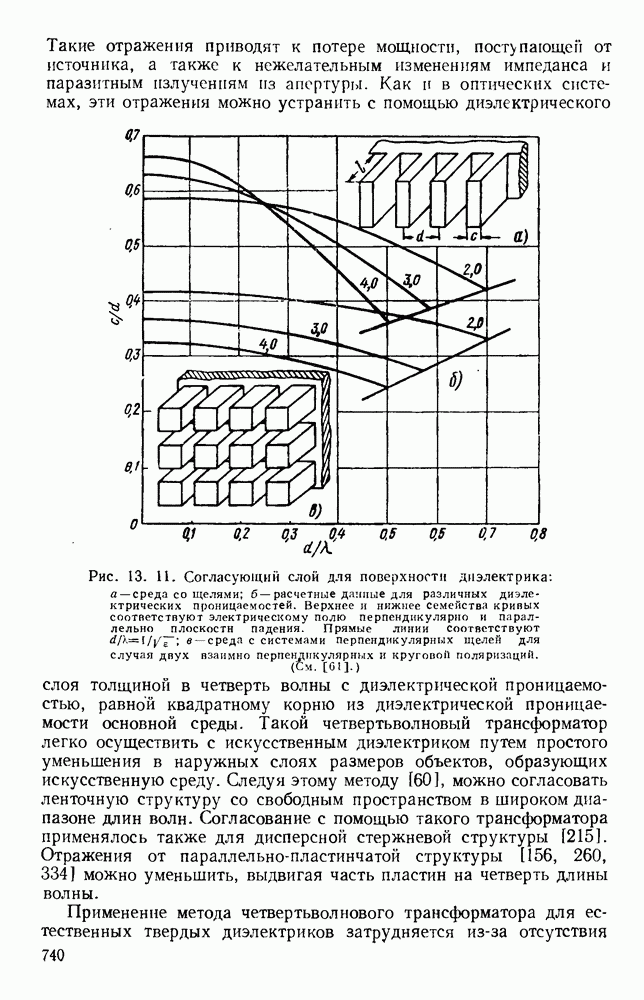
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
- 13.4. ПРИБОРЫ И СИСТЕМЫ
- 13.4.1. Спектрометры
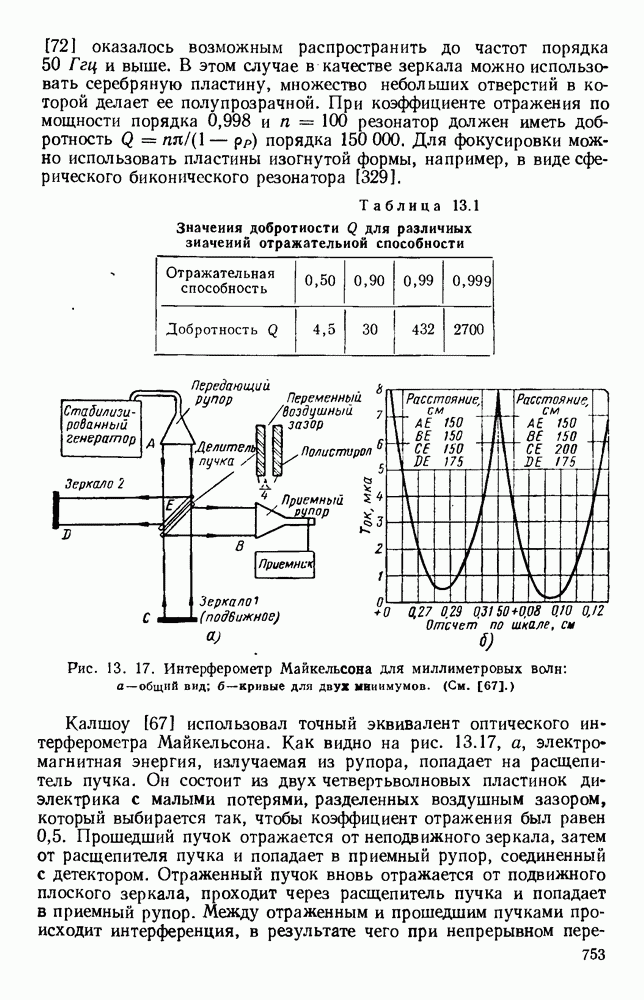
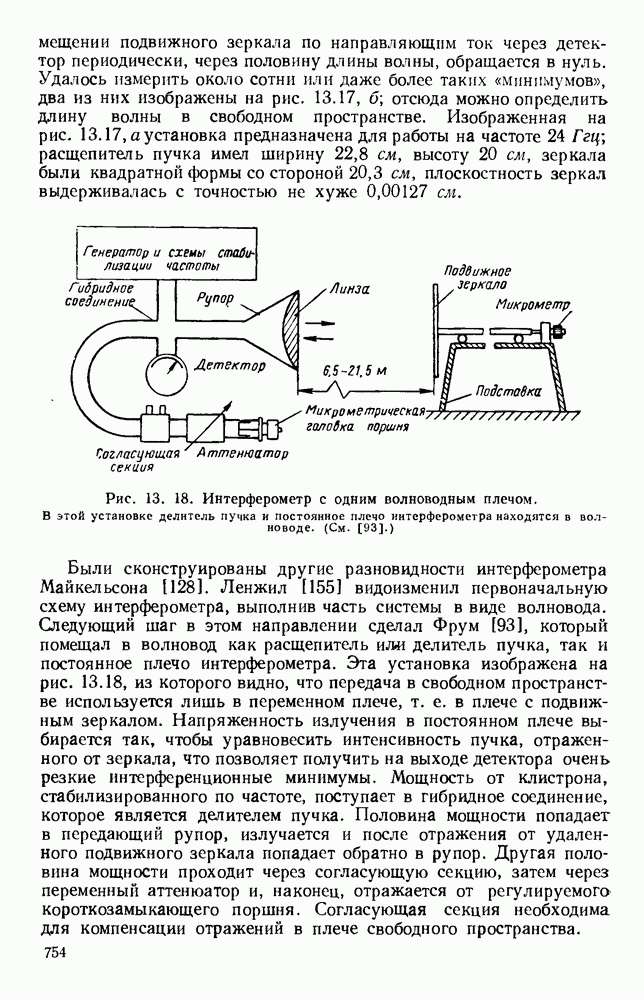
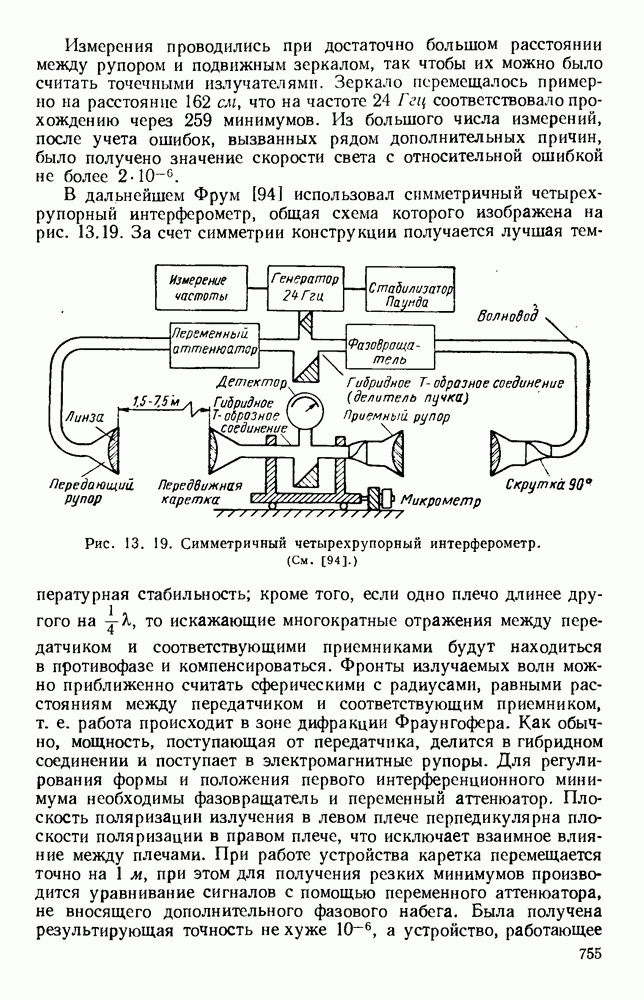
- 13.4.2. Интерферометры
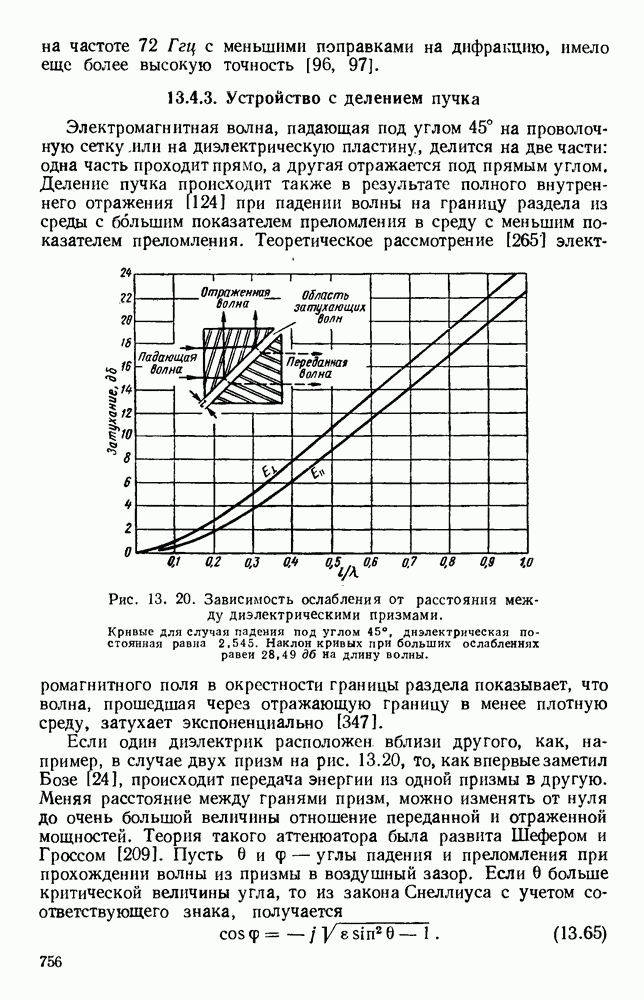
- 13.4.3. Устройство с делением пучка