| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
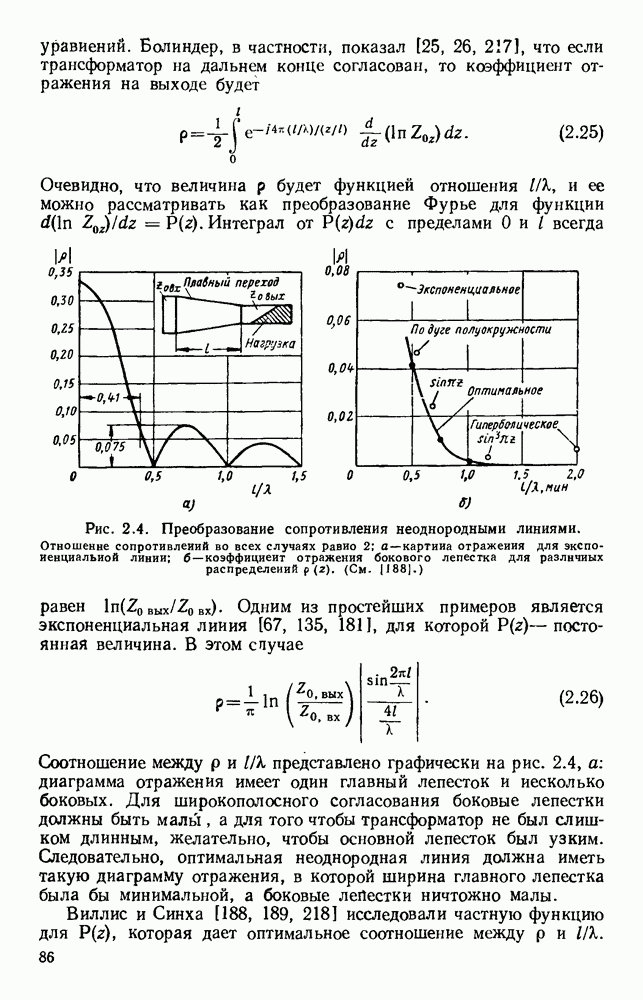
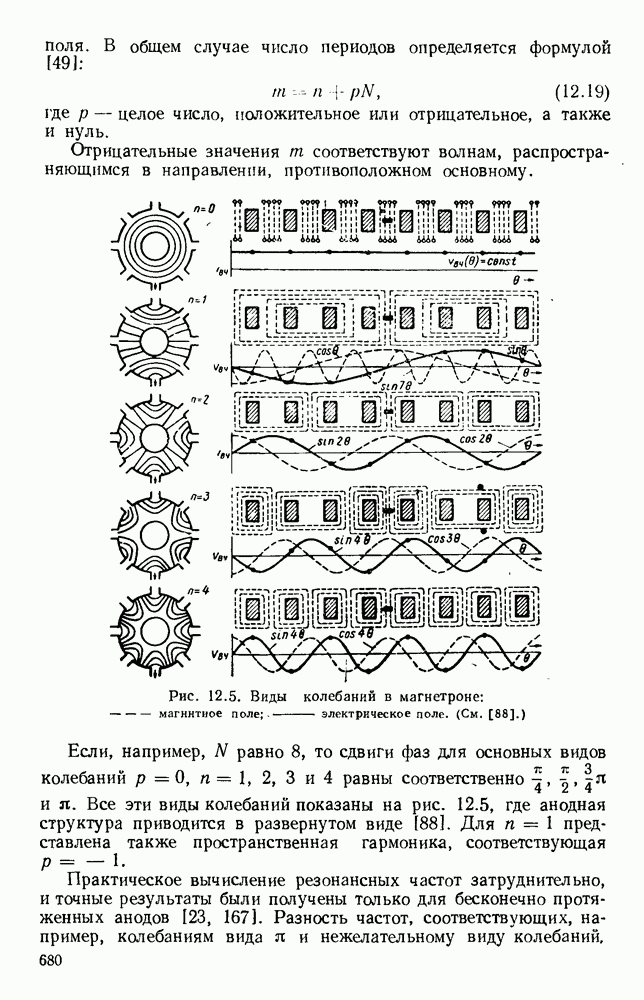
10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
10.6.1. Простая спираль
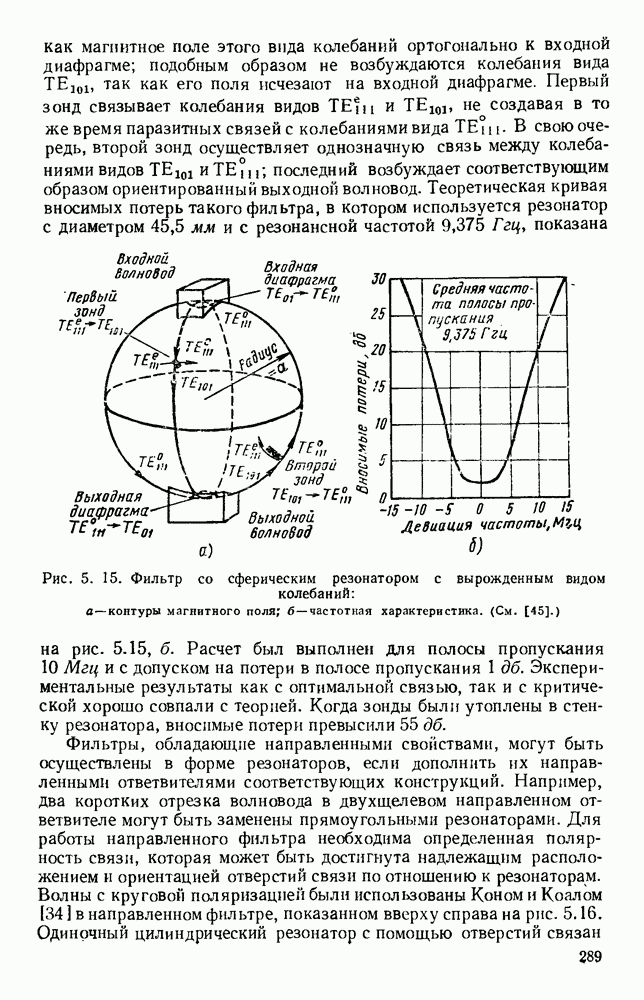
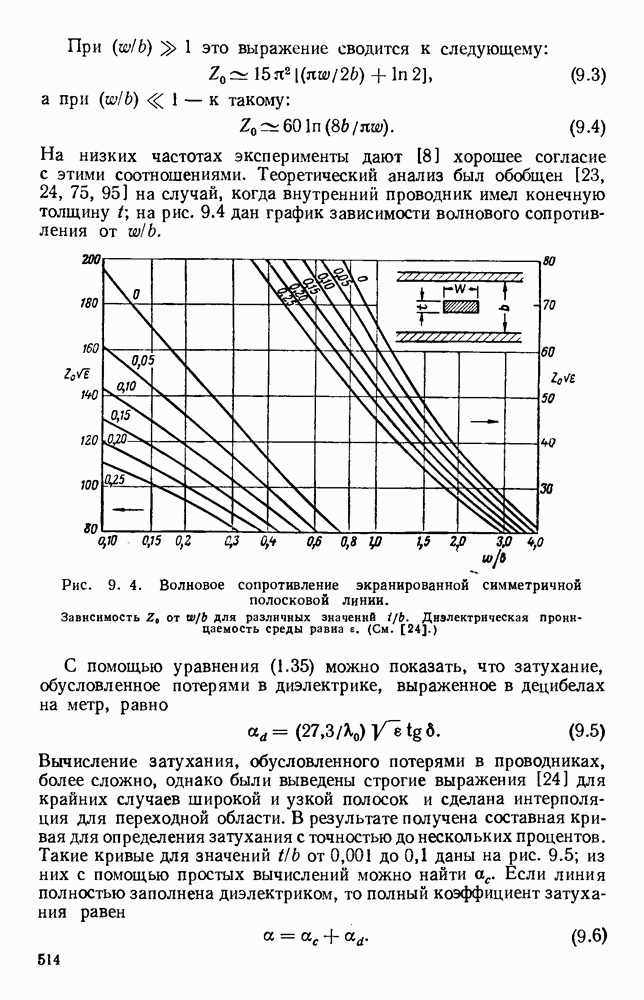
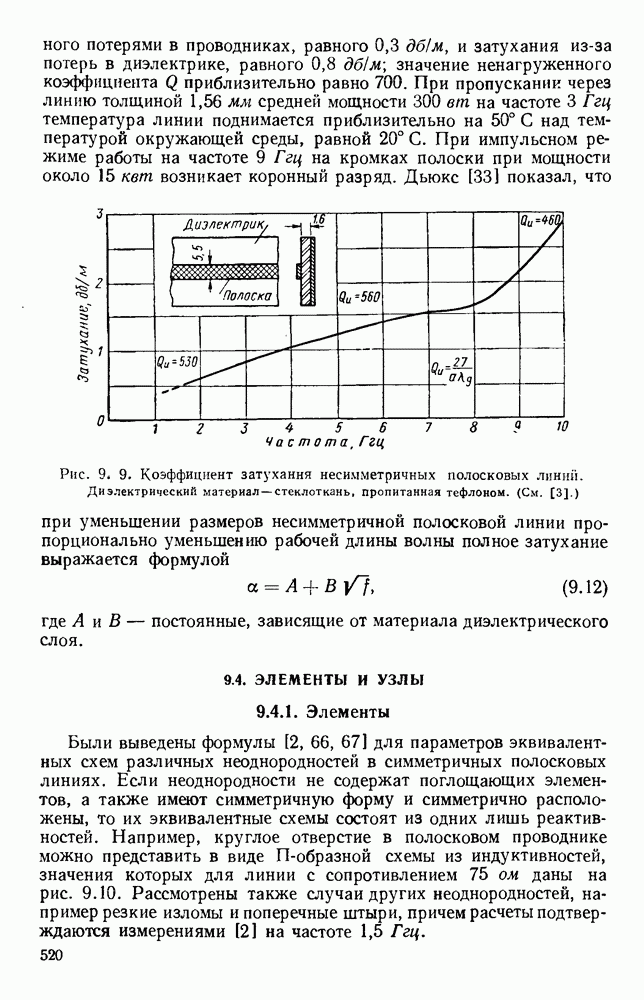
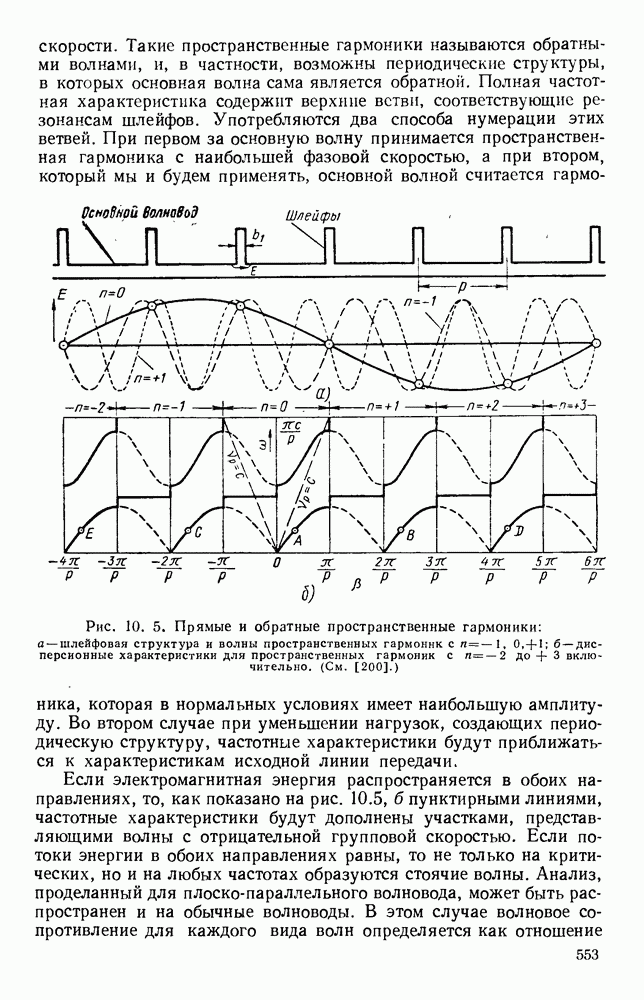
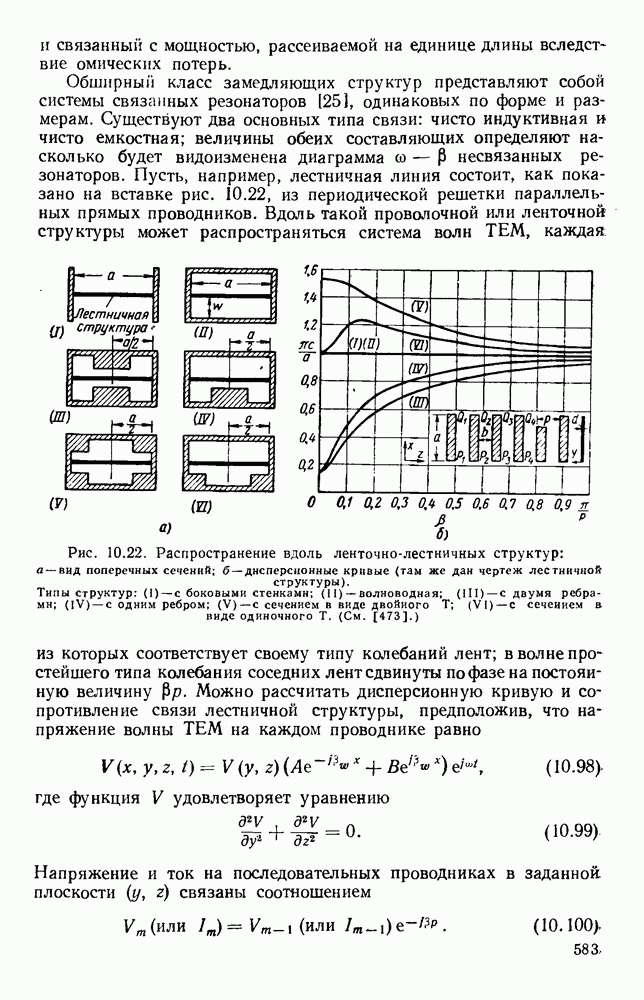
Часто применяется замедляющая структура, которая представляет собой металлический проводник, согнутый в виде круговой спирали. Распространение электромагнитных волн в такой спиральной структуре впервые было исследовано Поклингтоном [247], который полагал ее выполненой из тонкого идеально проводящего провода. Найденное решение указывало на существование бегущей волны, у которой на низких частотах осевая фазовая скорость была близка к с, а с повышением частоты уменьшалась до значения с  что эквивалентно распространению волны вдоль провода с фазовой скоростью с. Было показано [166], что в этих случаях у волны имеются продольные компоненты как электрического, так и магнитного полей, и, поскольку в плоскости волнового фронта вне спирали поля затухают, эту волну можно рассматривать как поверхностную волну типа
что эквивалентно распространению волны вдоль провода с фазовой скоростью с. Было показано [166], что в этих случаях у волны имеются продольные компоненты как электрического, так и магнитного полей, и, поскольку в плоскости волнового фронта вне спирали поля затухают, эту волну можно рассматривать как поверхностную волну типа  Чистая волна типа
Чистая волна типа  может существовать в виде одной бегущей волны лишь в простой спирали; две волны, бегущие в противоположных направлениях, образуют поверхностную волну типа
может существовать в виде одной бегущей волны лишь в простой спирали; две волны, бегущие в противоположных направлениях, образуют поверхностную волну типа  с эллиптической поляризацией, причем плоскость поляризации вращается при перемещении вдоль линии [240, 242].
с эллиптической поляризацией, причем плоскость поляризации вращается при перемещении вдоль линии [240, 242].
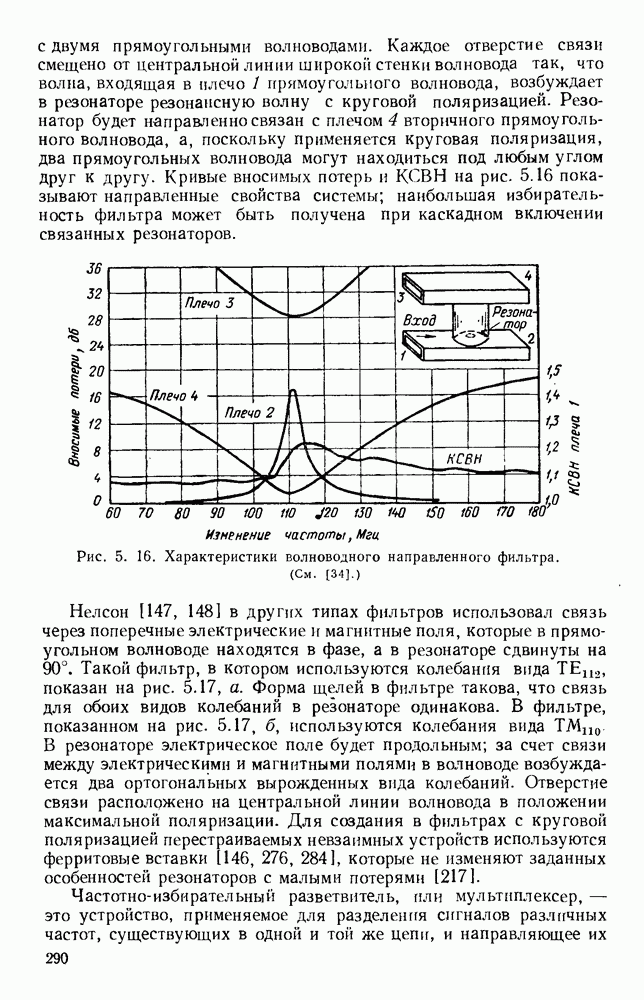
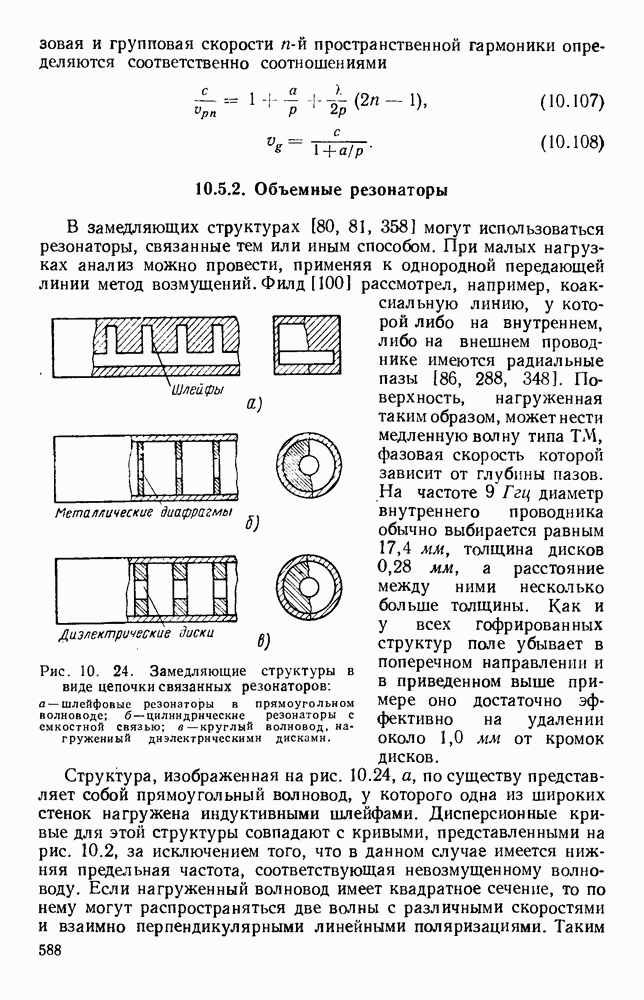
Некоторые основные свойства указанной структуры можно вывести с помощью модели, предложенной Оллендорфом [226] и другими авторами [159, 182, 183, 243], в которой спираль заменяется анизотропной цилиндрической поверхностью, проводящей лишь в направлении  В такой модели не учитывается периодичность структуры настоящей спирали и конечность размеров проводника. Сенсипер [269] показал, что решениями могут быть лишь медленные волны
В такой модели не учитывается периодичность структуры настоящей спирали и конечность размеров проводника. Сенсипер [269] показал, что решениями могут быть лишь медленные волны  которые имеют различные угловые зависимости, определяемые функциями
которые имеют различные угловые зависимости, определяемые функциями  Обычно волна с индексом
Обычно волна с индексом  на низких частотах обнаруживает сильную дисперсию, в то время как на высоких частотах ее фазовая и групповая скорости в широком интервале частот почти равны друг другу. Для волн с индексом
на низких частотах обнаруживает сильную дисперсию, в то время как на высоких частотах ее фазовая и групповая скорости в широком интервале частот почти равны друг другу. Для волн с индексом  существующих при
существующих при  картина более сложна, поскольку здесь одному значению волнового числа соответствуют несколько волн. Если обратиться к дисперсионной кривой (зависимость
картина более сложна, поскольку здесь одному значению волнового числа соответствуют несколько волн. Если обратиться к дисперсионной кривой (зависимость  от
от  то можно видеть, что для некоторых ветвей фазовая и групповая скорости имеют разные знаки, что соответствует обратным волнам. Используя для спирали модель в виде цилиндрической поверхности с анизотропной проводимостью, можно оценить величину импеданса связи, хотя экспериментальные данные [78] показывают, что получаемые при этом значения в два раза больше реальных.
то можно видеть, что для некоторых ветвей фазовая и групповая скорости имеют разные знаки, что соответствует обратным волнам. Используя для спирали модель в виде цилиндрической поверхности с анизотропной проводимостью, можно оценить величину импеданса связи, хотя экспериментальные данные [78] показывают, что получаемые при этом значения в два раза больше реальных.
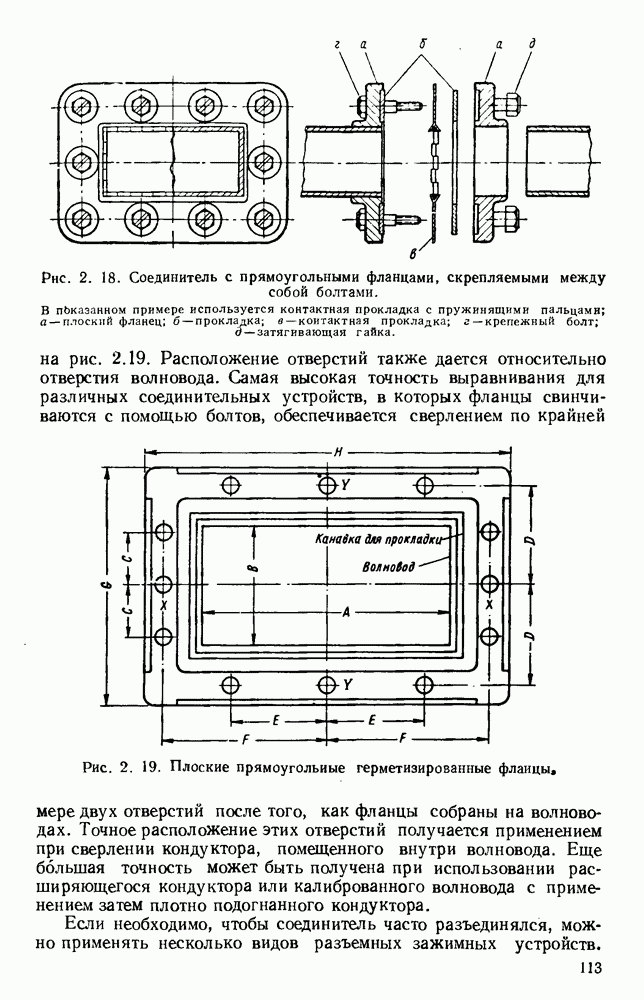
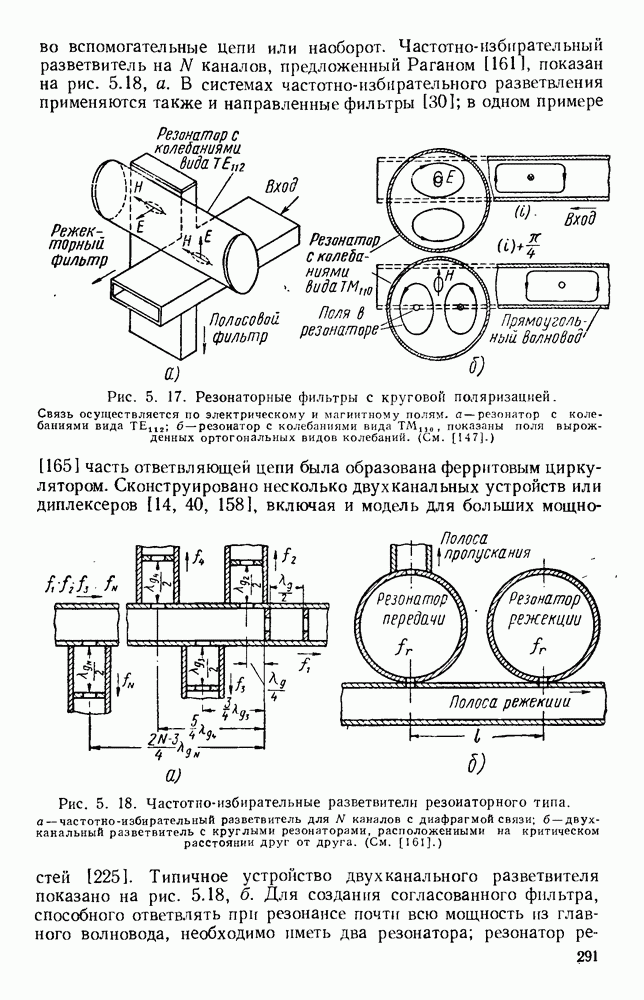
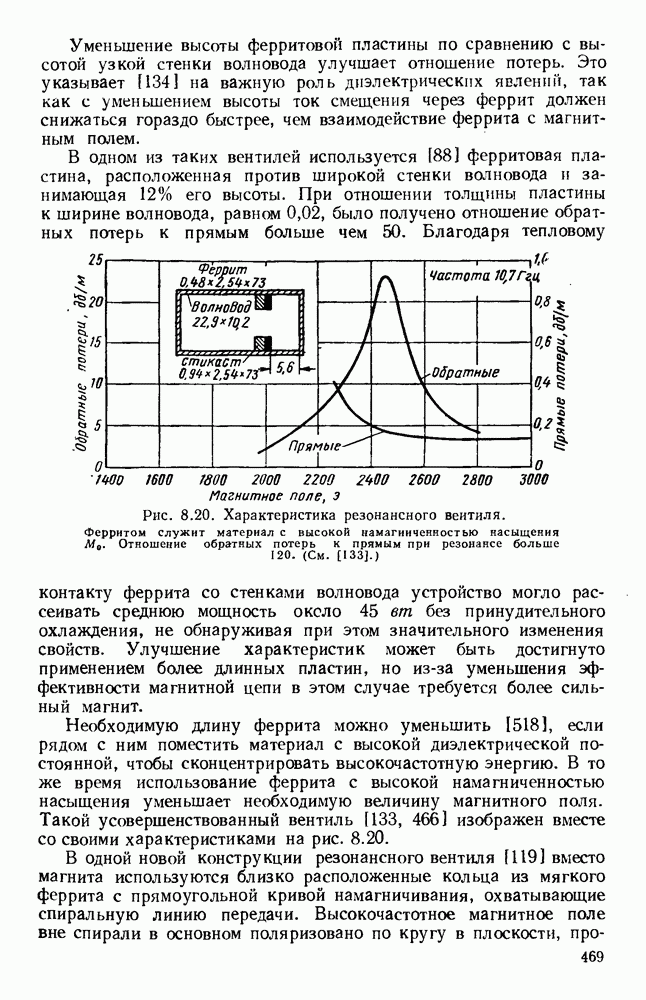
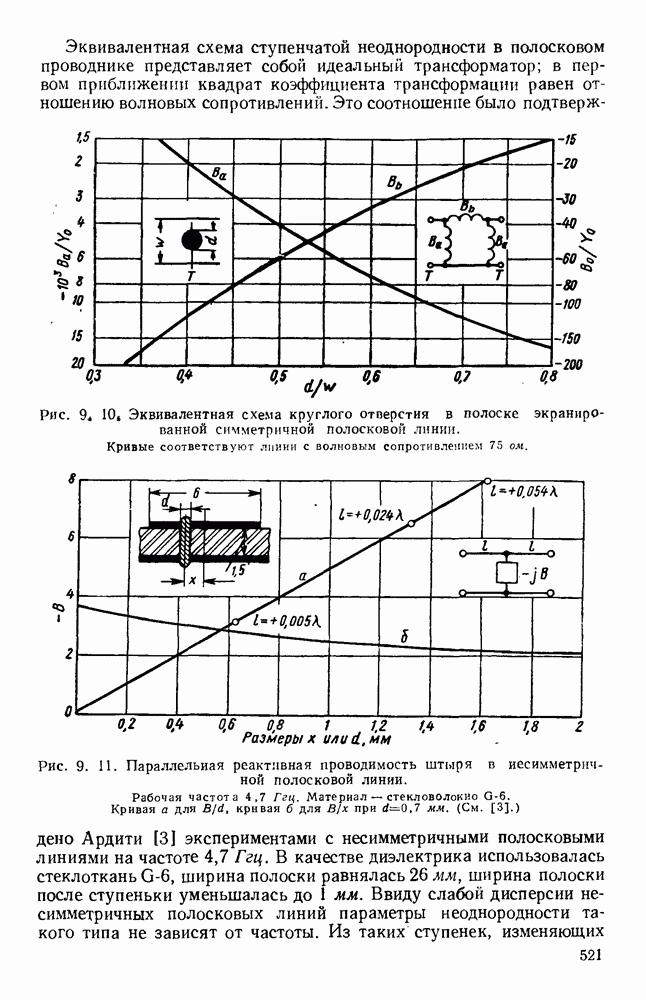
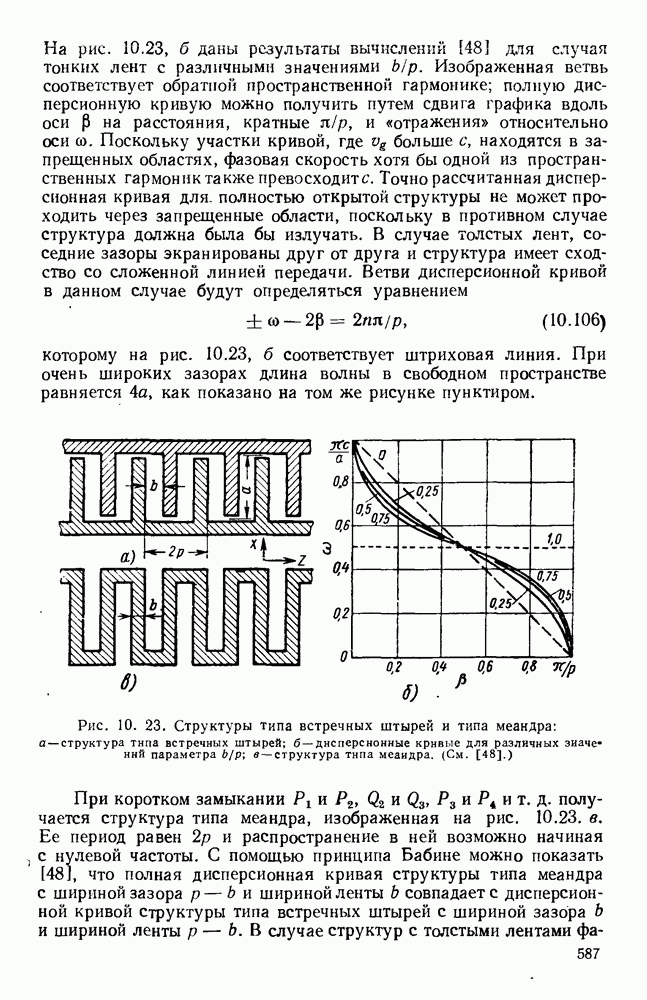
Периодичность спирали выявляется при анализе, основанном на ленточной модели, в которой считается, что проводник в радиальном направлении бесконечно тонок. Были рассмотрены структуры, состоящие из узких лент или проводов [186, 187, 188, 235, 255, 256, 286], а также аналогичные структуры с узкими щелями [317] и различными формами поперечных сечений [59]. Ленточная спираль [269] изображена на рис. 10.27, а, причем на практике ширины зазоров и проводящих лент почти равны. Очевидно, что

Из периодичности структуры следует, что при смещении на период волновая функция изменится согласно уравнению (10.1) на фазовый множитель. Каждому виду угловой зависимости соответствует полный набор пространственных гармоник [363]. Поскольку продольно смещенную спираль можно совместить с исходной путем вращения, то должно выполняться условие  Экспоненциальный множитель в выражениях для компонент поля будет иметь вид
Экспоненциальный множитель в выражениях для компонент поля будет иметь вид

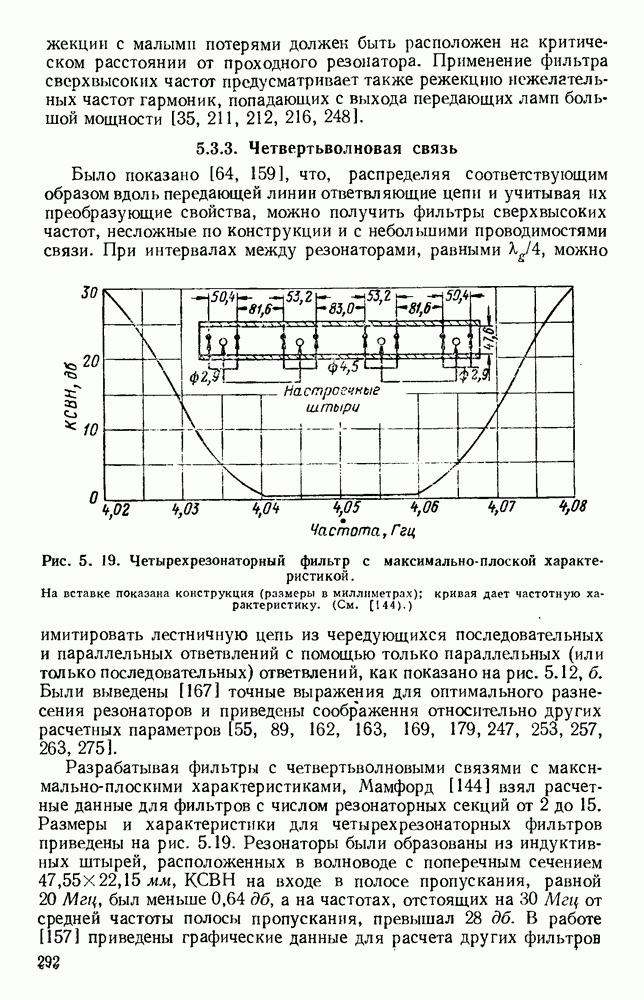
Используя граничные условия, можно получить аналитическим или графическим методом дисперсионную кривую, приведенную на рис. 10.27, б, для частного случая  Из условия
Из условия
 вытекает существование запрещенных областей, в которых существенную роль играют [244] быстрые волны [202], вызывающие излучение из структуры. При условии
вытекает существование запрещенных областей, в которых существенную роль играют [244] быстрые волны [202], вызывающие излучение из структуры. При условии

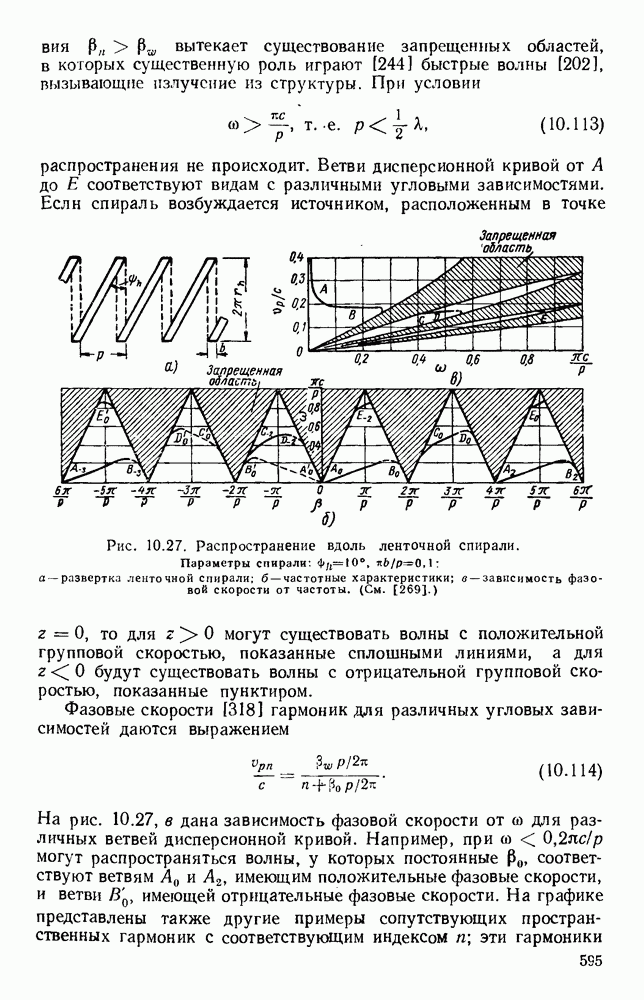
распространения не происходит. Ветви дисперсионной кривой от А до Е соответствуют видам с различными угловыми зависимостями.

Рис. 10.27. Распространение вдоль ленточной спирали. Параметры спирали:  а — развертка ленточной спирали; б - частотные характеристики; в — зависимость фазовой скорости от частоты. (См. [269].)
а — развертка ленточной спирали; б - частотные характеристики; в — зависимость фазовой скорости от частоты. (См. [269].)
Если спираль возбуждается источником, расположенным в точке  , то для
, то для  могут существовать волны с положительной групповой скоростью, показанные сплошными линиями, а для
могут существовать волны с положительной групповой скоростью, показанные сплошными линиями, а для  будут существовать волны с отрицательной групповой скоростью, показанные пунктиром.
будут существовать волны с отрицательной групповой скоростью, показанные пунктиром.
Фазовые скорости [318] гармоник для различных угловых зависимостей даются выражением

На рис. 10.27, в дана зависимость фазовой скорости от  для различных ветвей дисперсионной кривой. Например, при
для различных ветвей дисперсионной кривой. Например, при  могут распространяться волны, у которых постоянные
могут распространяться волны, у которых постоянные  соответствуют ветвям
соответствуют ветвям  имеющим положительные фазовые скорости, и ветви
имеющим положительные фазовые скорости, и ветви  имеющей отрицательные фазовые скорости. На графике представлены также другие примеры сопутствующих пространственных гармоник с соответствующим индексом
имеющей отрицательные фазовые скорости. На графике представлены также другие примеры сопутствующих пространственных гармоник с соответствующим индексом  эти гармоники
эти гармоники
наблюдались экспериментально [5, 331, 3321. Из уравнения (10.114), например, видно, что первая прямая пространственная гармоника эквивалентна по фазовой скорости основной волне в спирали радиуса  При работе на этой гармонике можно [191] использовать спираль большего размера, нежели при работе на основной гармонике
При работе на этой гармонике можно [191] использовать спираль большего размера, нежели при работе на основной гармонике
Анализ потока мощности показывает, что значительная часть мощности переносится пространственными гармониками, чем и объясняется слишком высокое значение импеданса связи, полученное с помощью приближенной модели в виде сплошной цилиндрической поверхности. Батчер [48] в своей работе рассмотрел и лестничные линии, включая расчеты дисперсионных кривых и им педанса взаимодействия ленточных спиралей. В других работах, посвященных спирали, рассмотрены максимальная передаваемая мощность [59] и затухание [141, 189, 262, 312, 367], причем с помощью поправочного множителя результаты последних работ по ленточной спирали распространены на случаи проводников других сечений.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
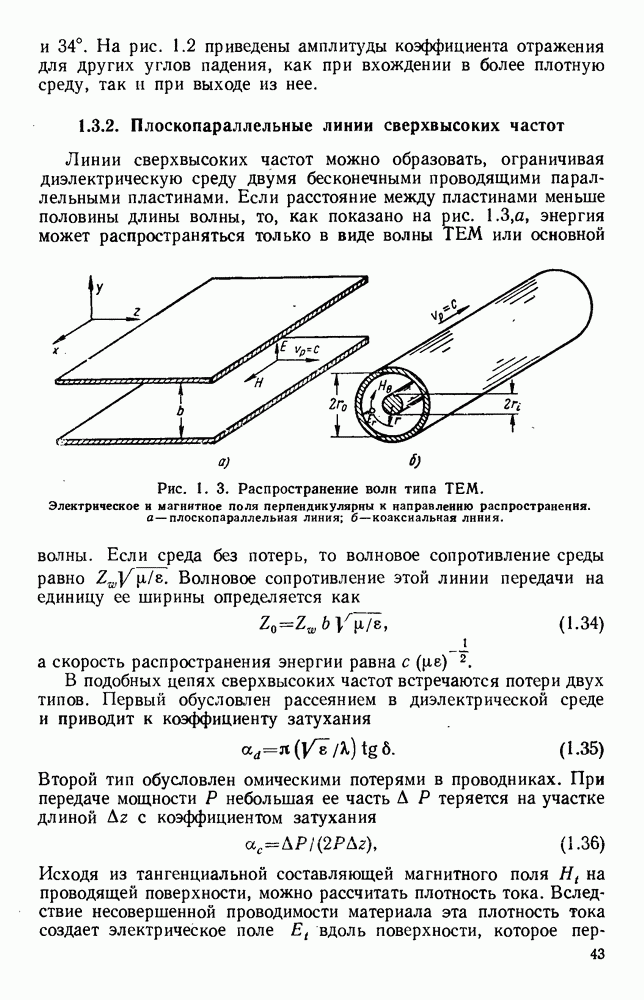
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
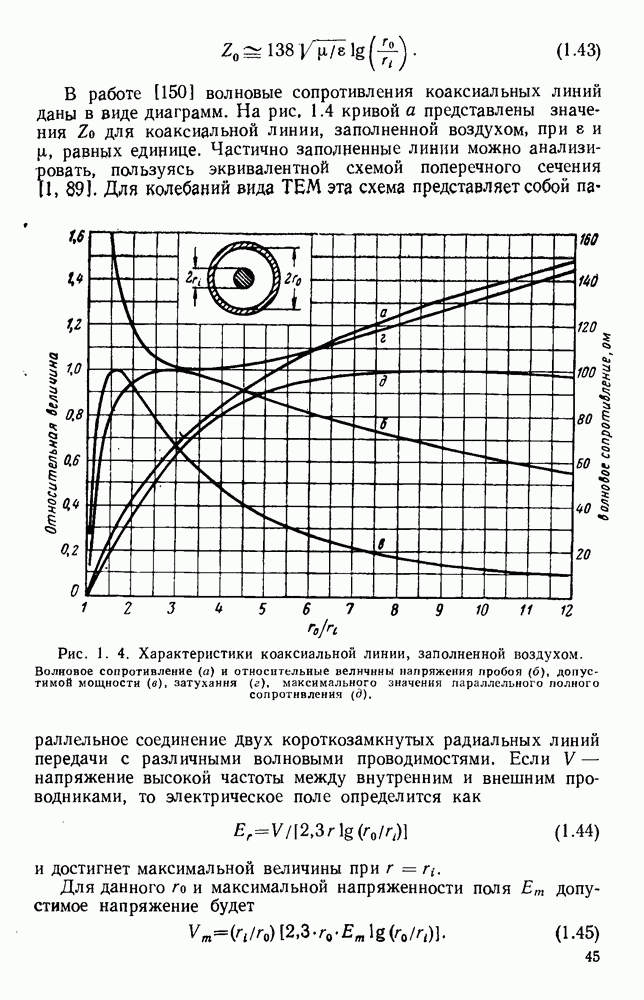
- 1.3.3. Коаксиальные линии
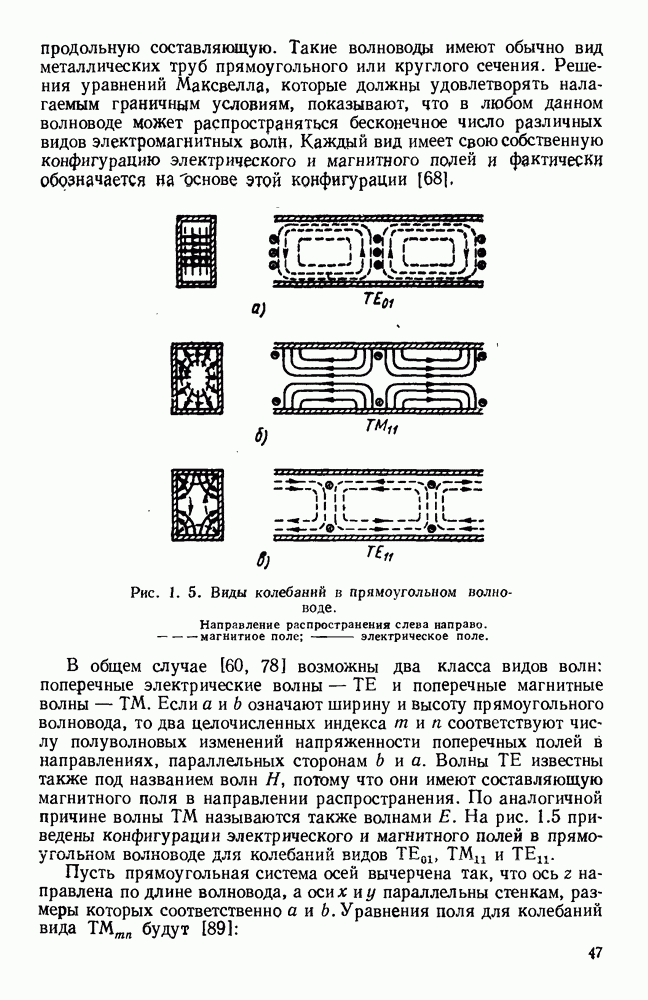
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
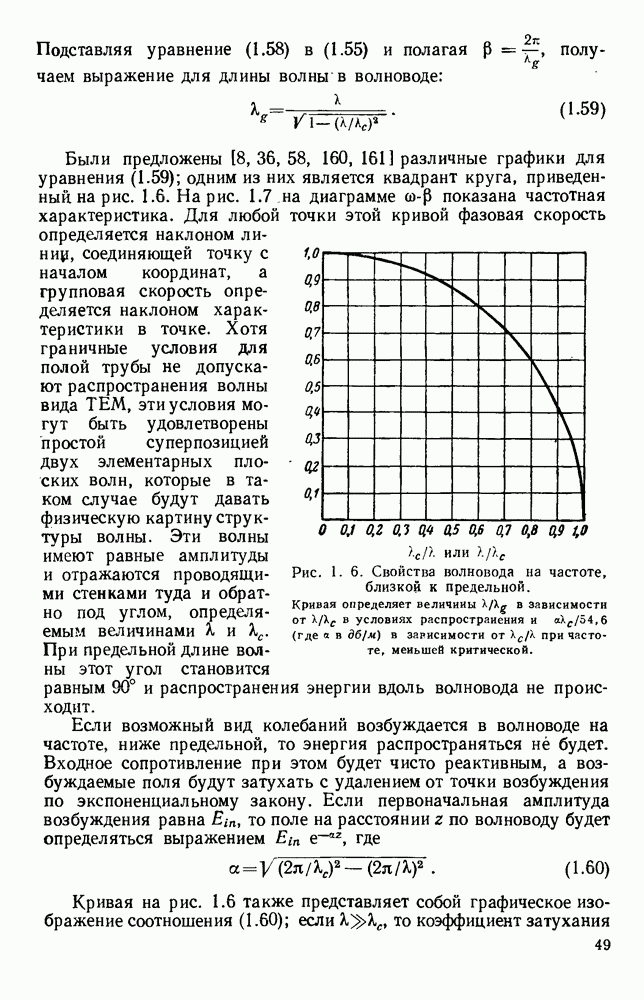
- 1.4.2. Круглые волноводы
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
- 1.5.2. Гребневые волноводы
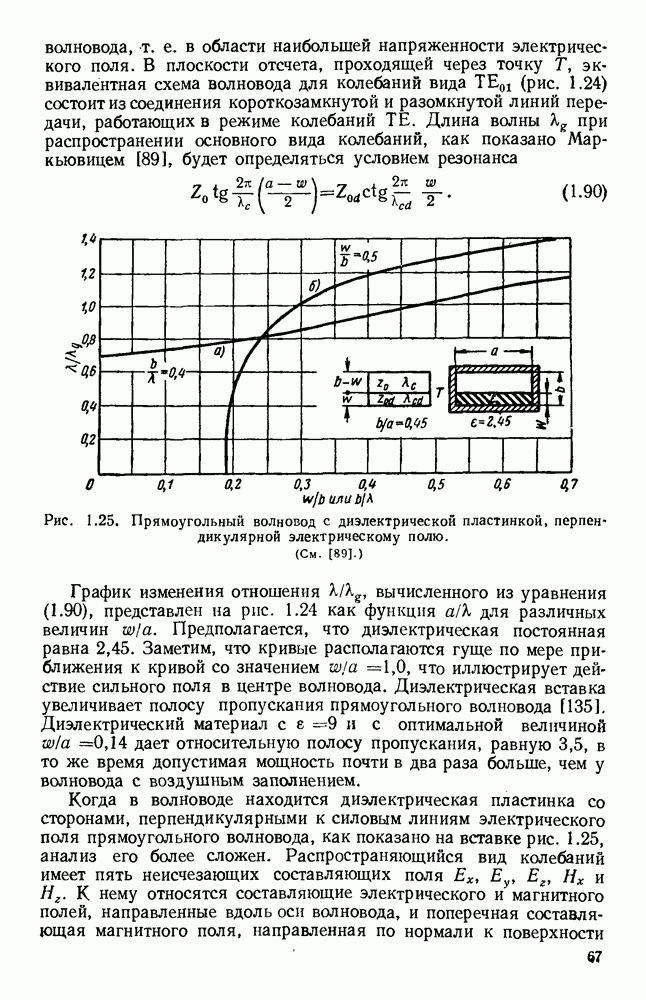
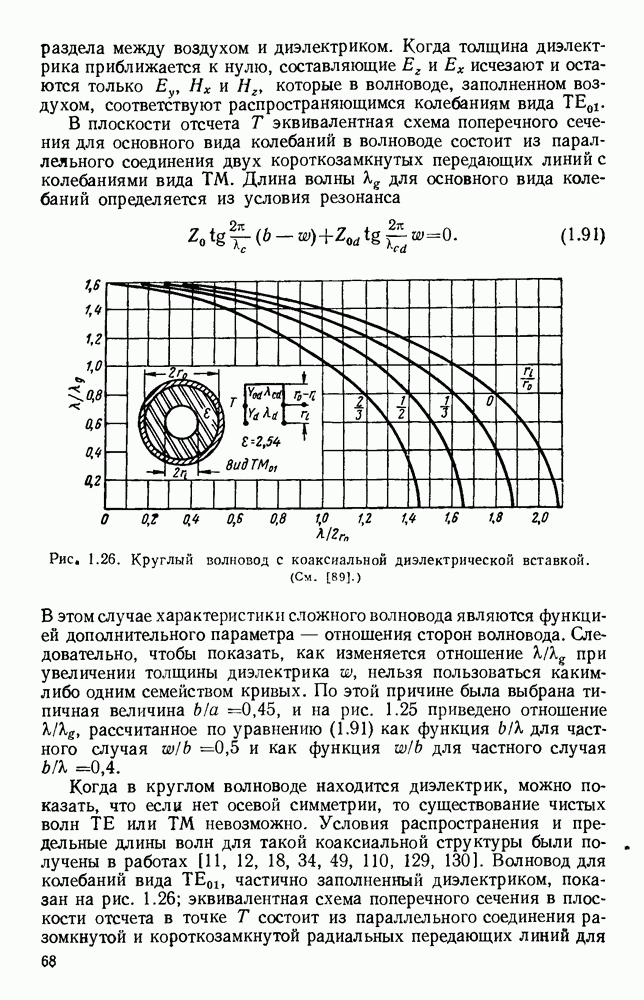
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
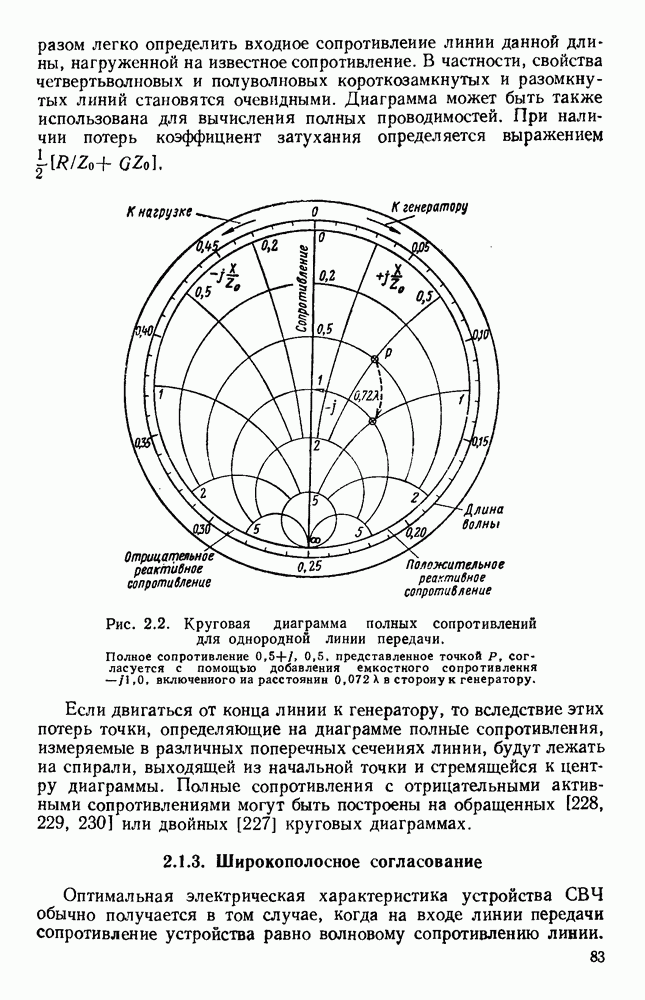
- 2.1.2. Круговая диаграмма
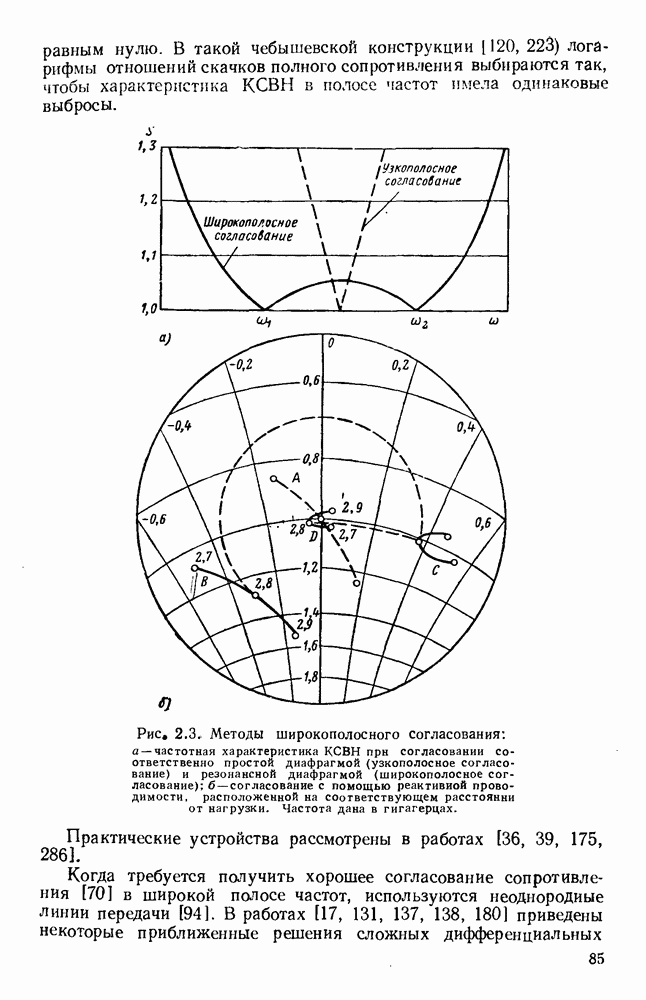
- 2.1.3. Широкополосное согласование
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
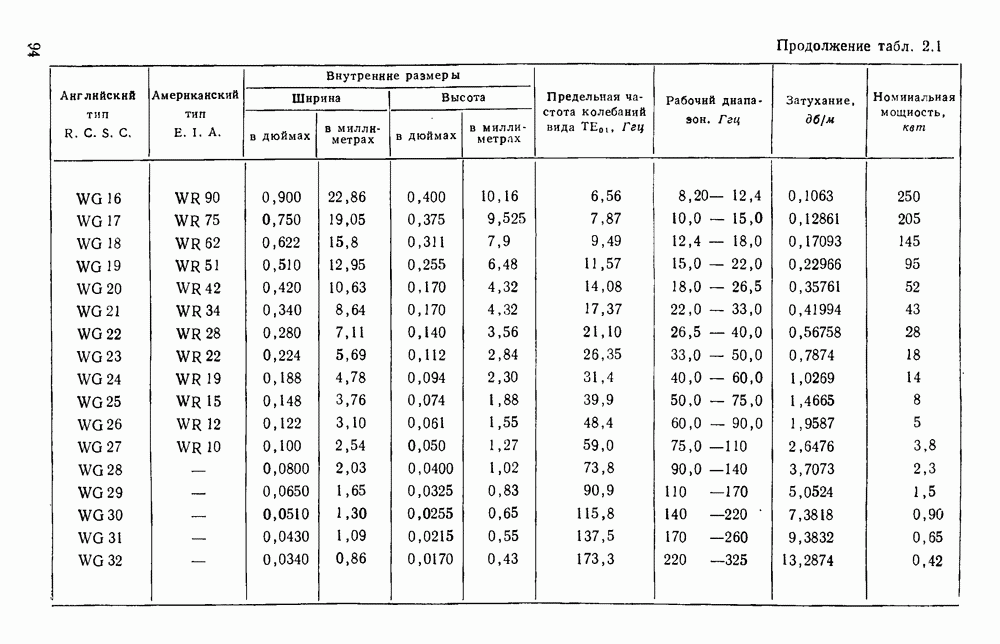
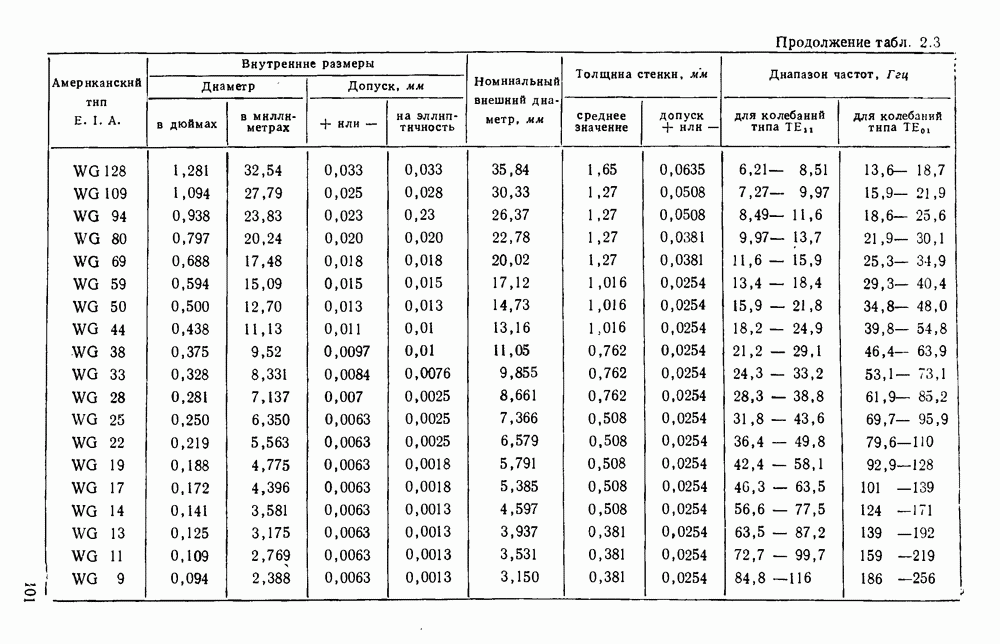
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
- 2.3.1. Прямоугольные волноводы
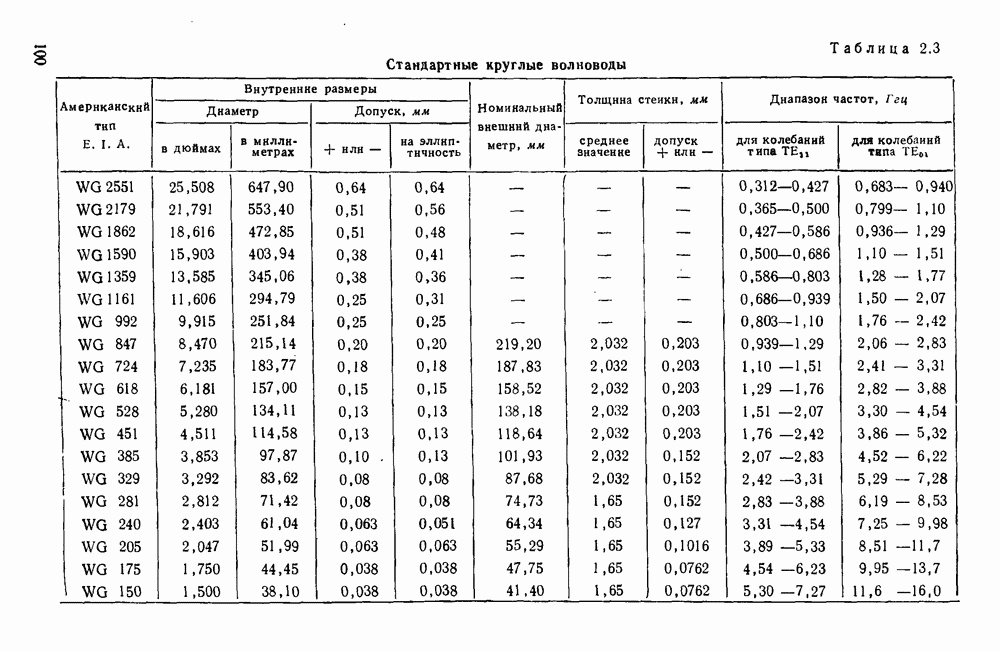
- 2.3.2. Круглые волноводы
- 2.3.3. Широкополосные и компактные волноводы
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
- 2.4.2. Контактные прокладки и дроссели
- 2.4.3. Крепежные и зажимные устройства
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
- 2.6.1. Изгибы, уголки и скрутки
- 2.6.2. Переходы и преобразователи
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
- 3.2.3. Переход от линейной поляризации к круговой
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
- 3.6.2. Вращающиеся сочленения различных типов
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
- 3.7.1. Механические переключатели с ручным управлением
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
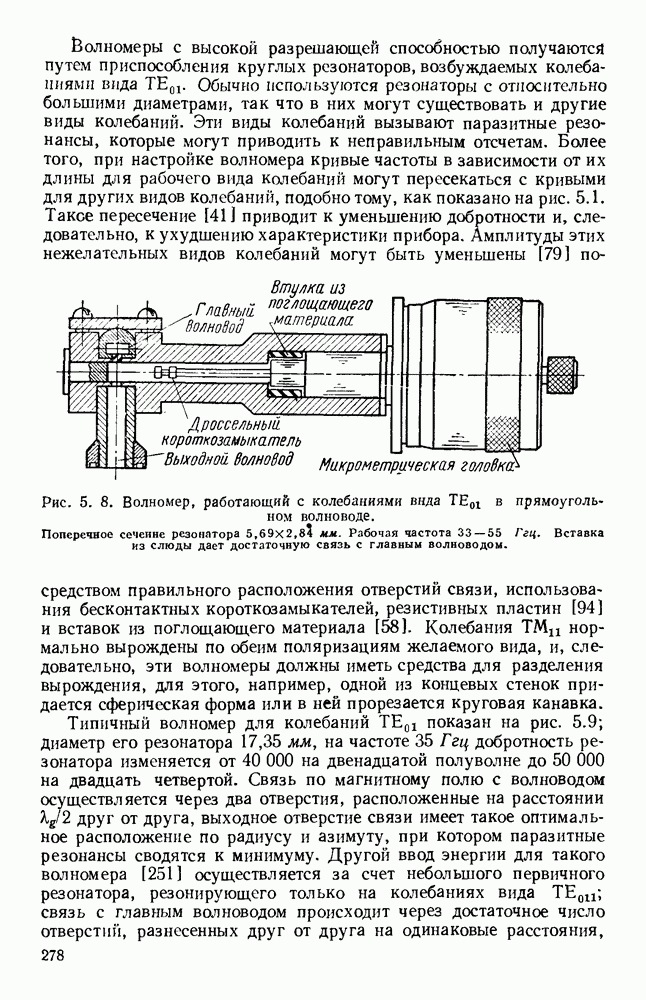
- 5.2.1. Волномеры с объемными резонаторами
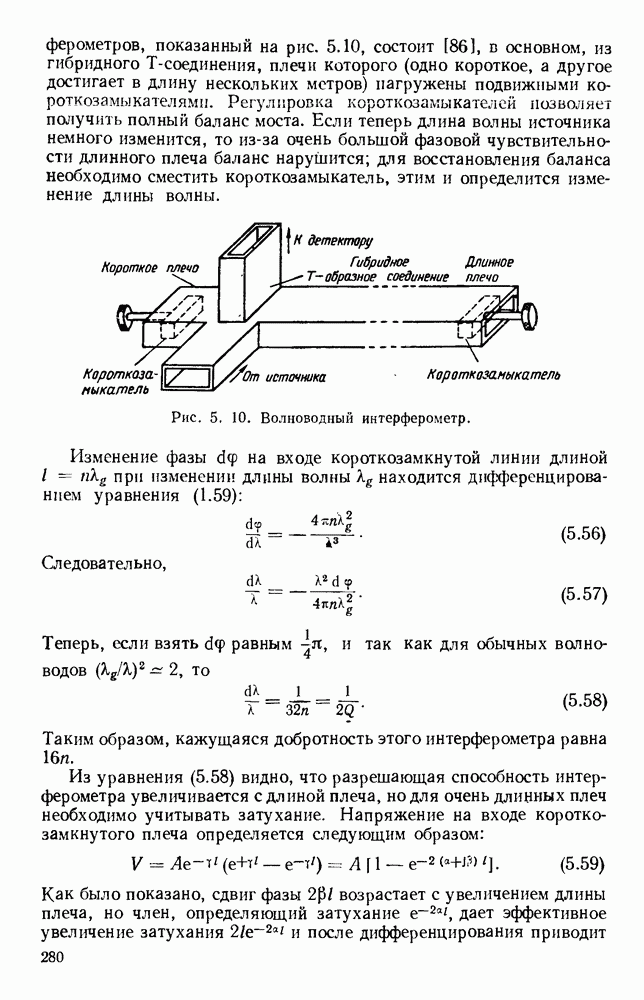
- 5.2.2. Волноводные интерферометры
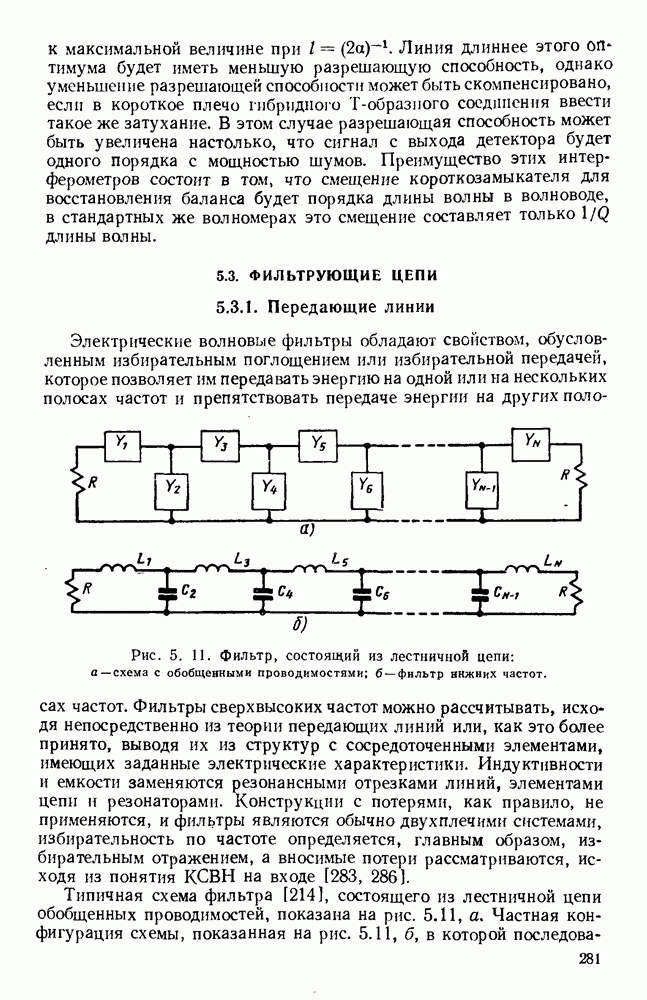
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
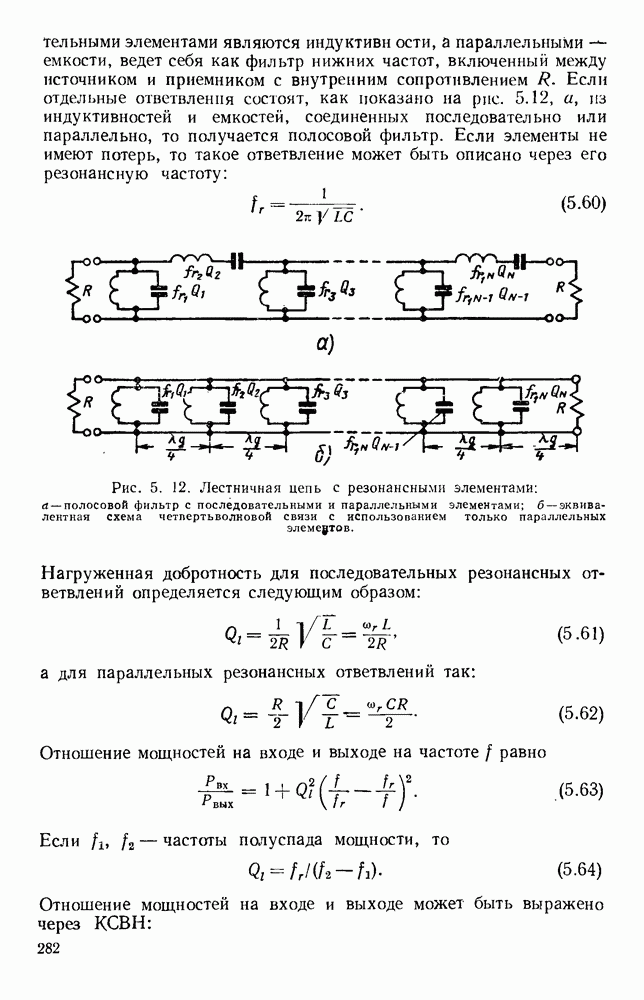
- 5.3.2. Связанные резонаторы
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
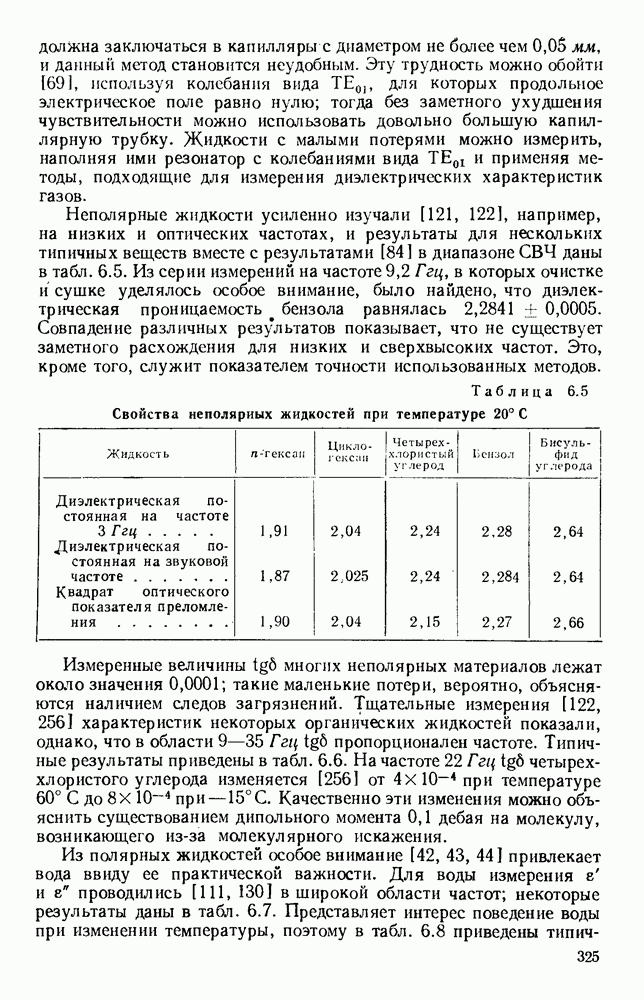
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
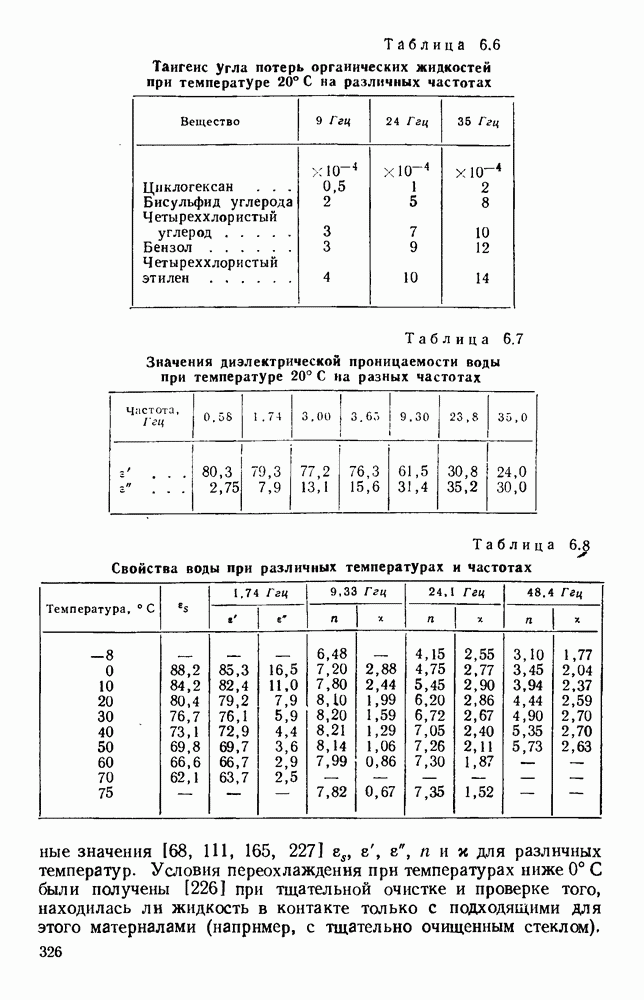
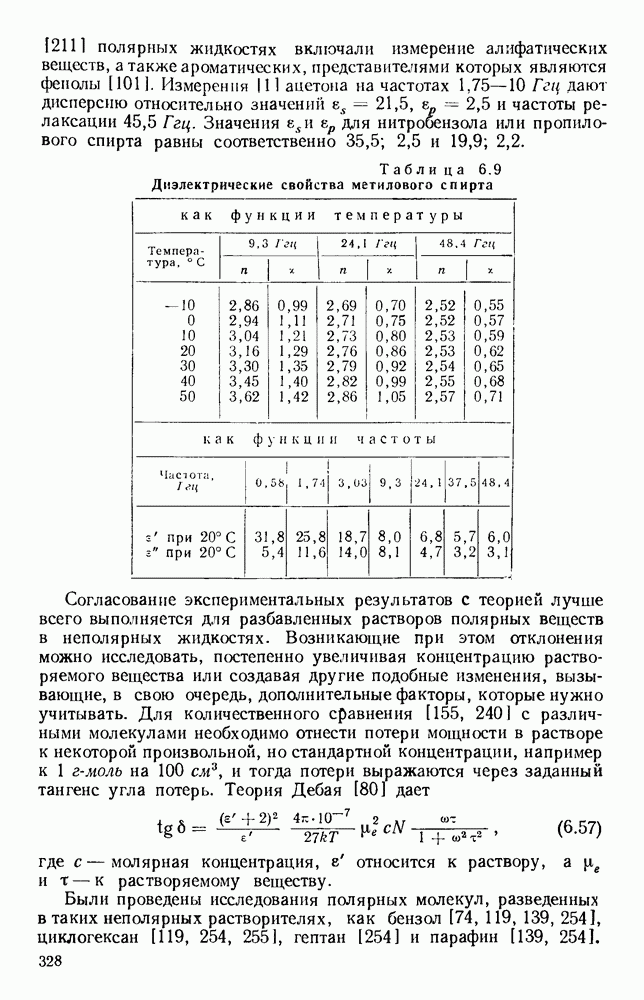
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
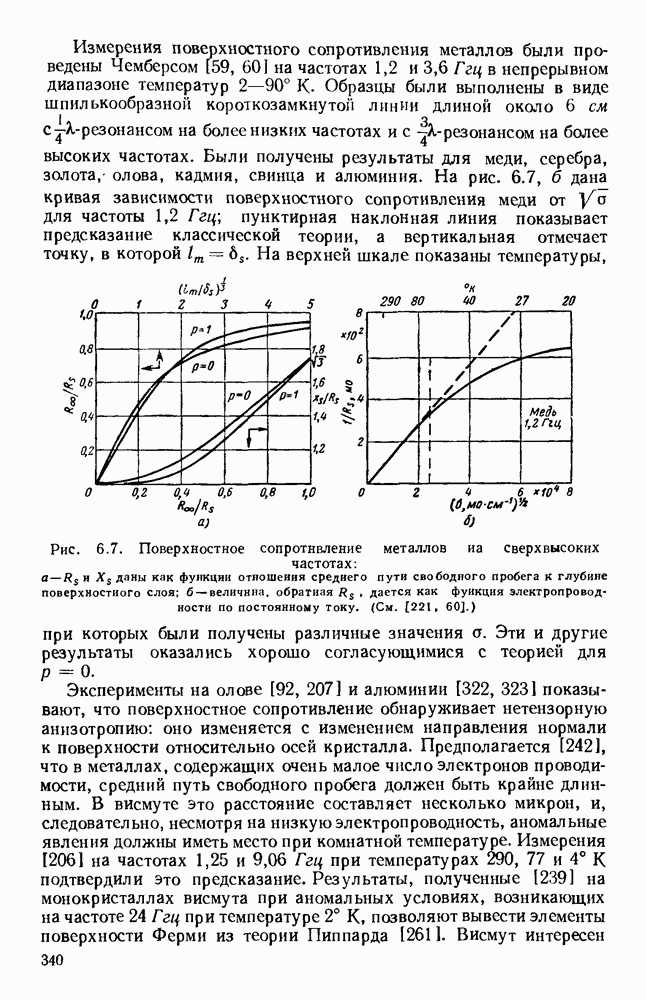
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
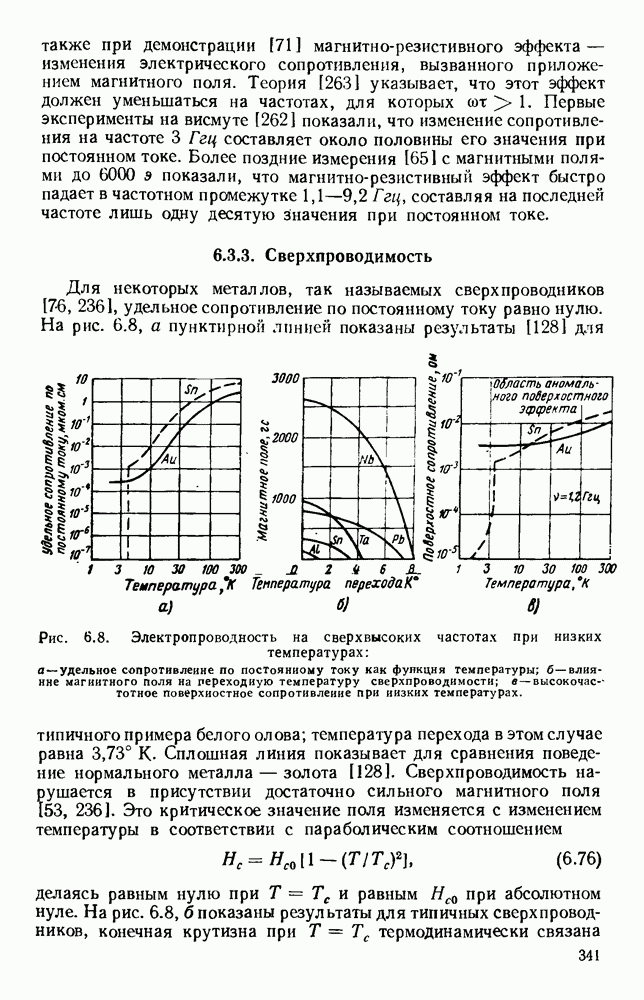
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
- 7.1.2. Форма линии и интенсивность
- 7.1.3. Сверхтонкая структура
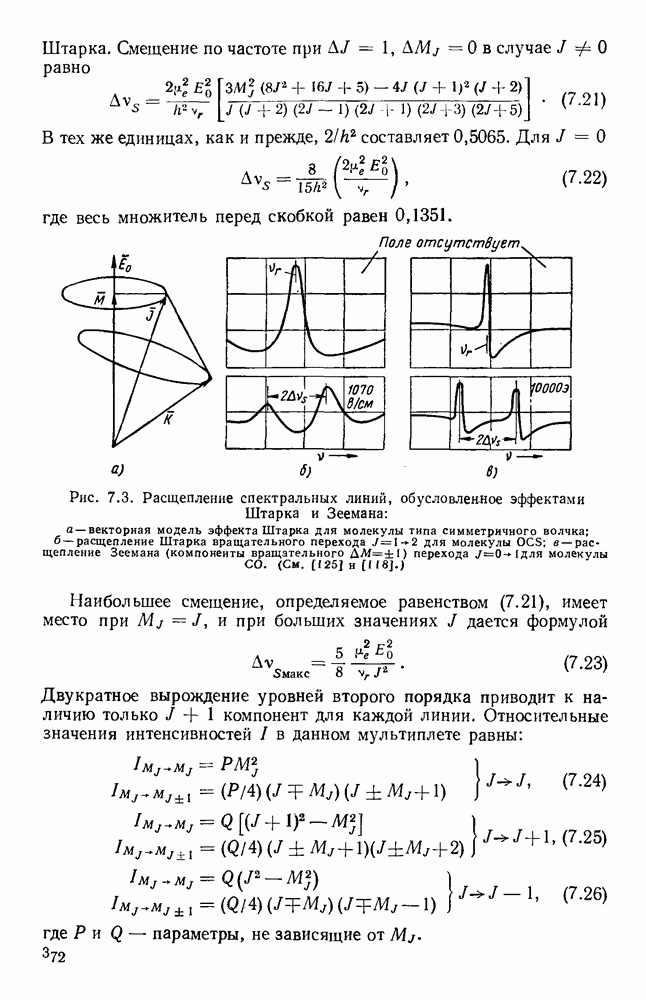
- 7.1.4. Явления Штарка и Зеемана
- 7.2. СПЕКТРОМЕТРЫ
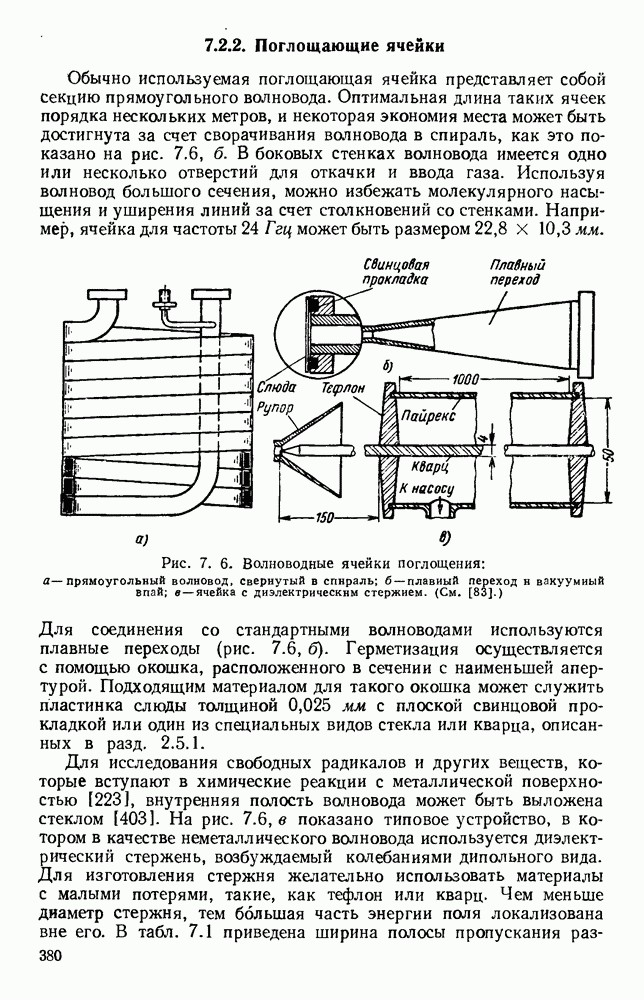
- 7.2.2. Поглощающие ячейки
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
- 7.3.4. Времена релаксации
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
- 8.3.3. Ферритовые устройства в качестве элементов схем
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
- 8.6.2. Устройства с поперечным полем
- 8.6.3. Прочие узлы
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.2.1. Линии типа «диэлектрических сэндвичей»
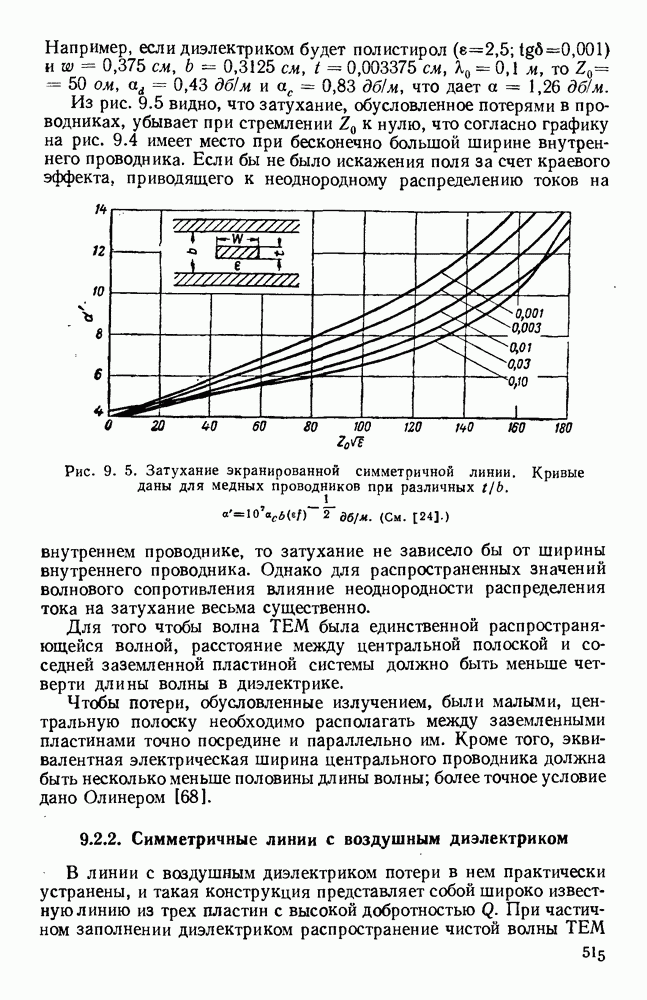
- 9.2.2. Симметричные линии с воздушным диэлектриком
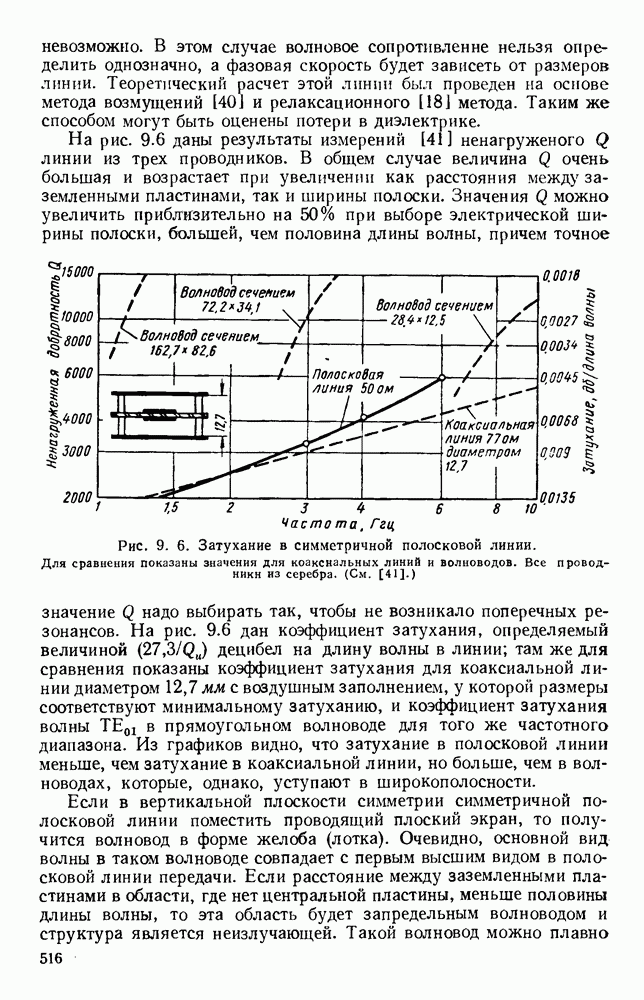
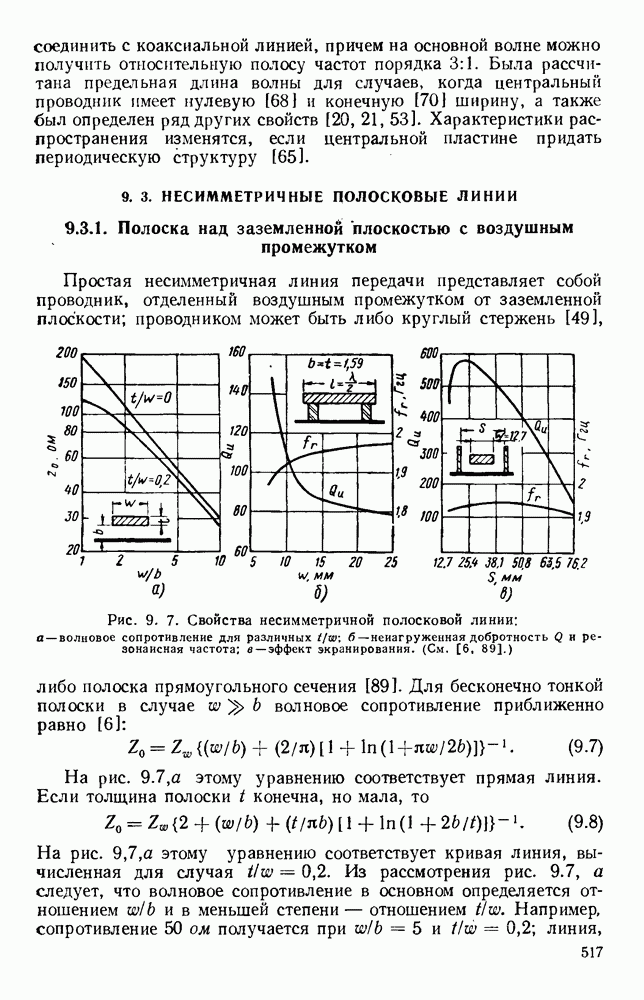
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
- 9.4.2. Переходные устройства
- 9.4.3. Узлы полосковых систем
- 9.5. ЦЕПИ И СИСТЕМЫ
- 9.5.3. Частотные фильтры
- 9.5.4. Цепи питания антенн
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
- 10.1.2. Пространственные гармоники
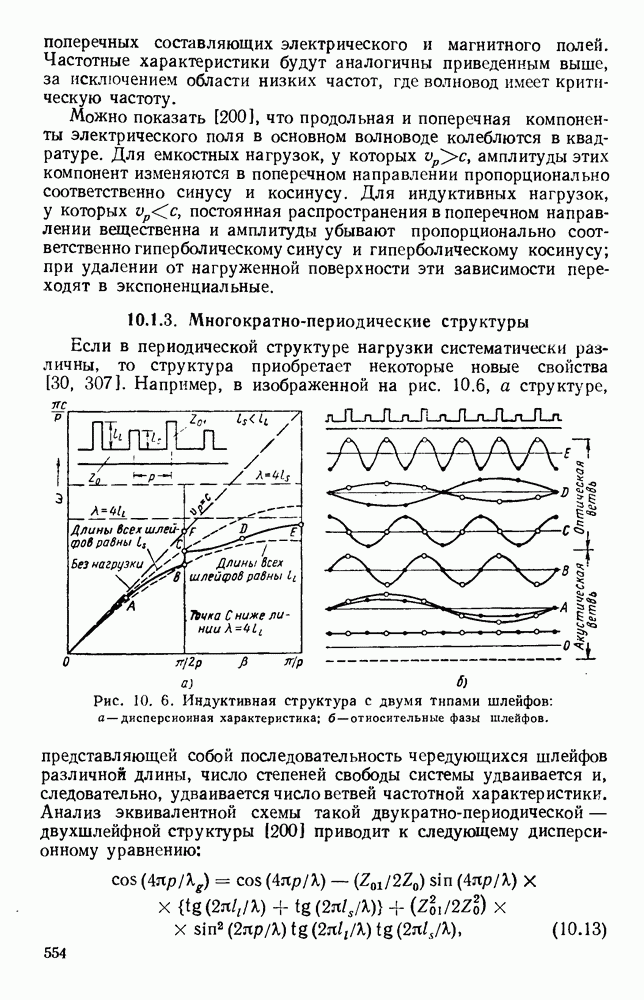
- 10.1.3. Многократно-периодические структуры
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
- 10.2.3. Продольные цилиндрические волны
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
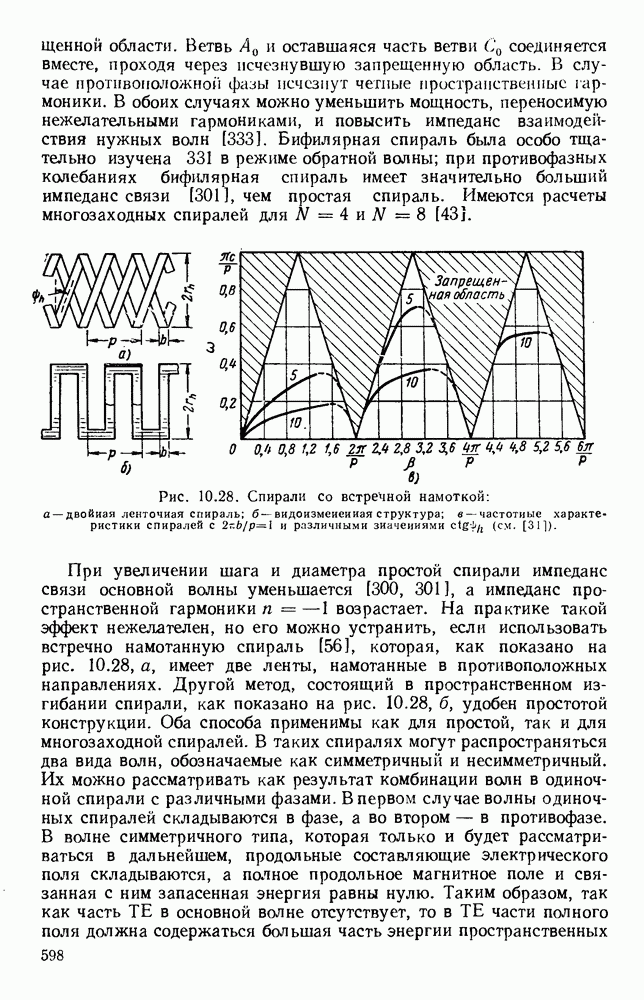
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
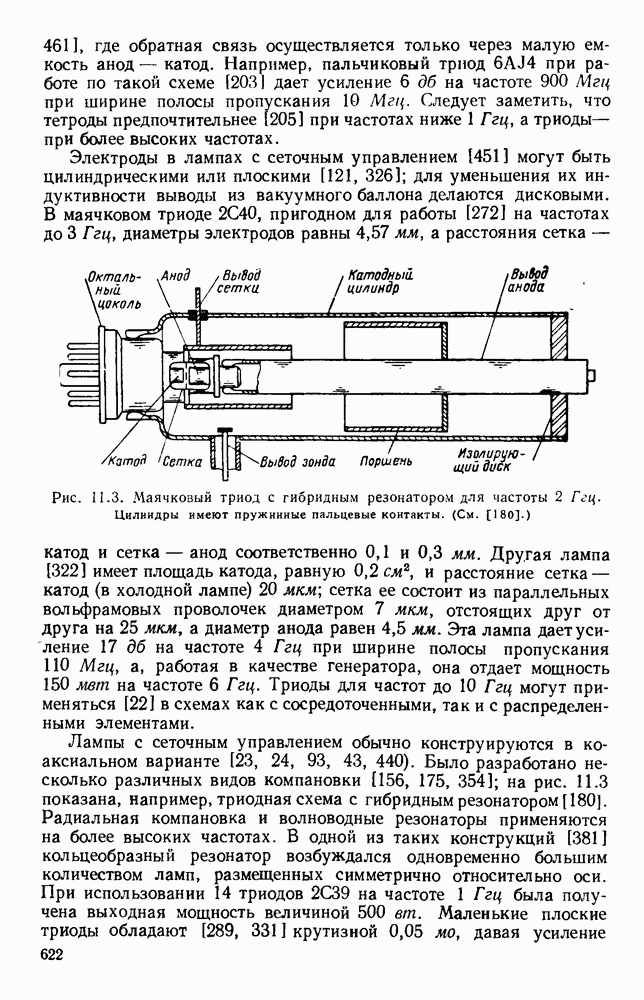
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
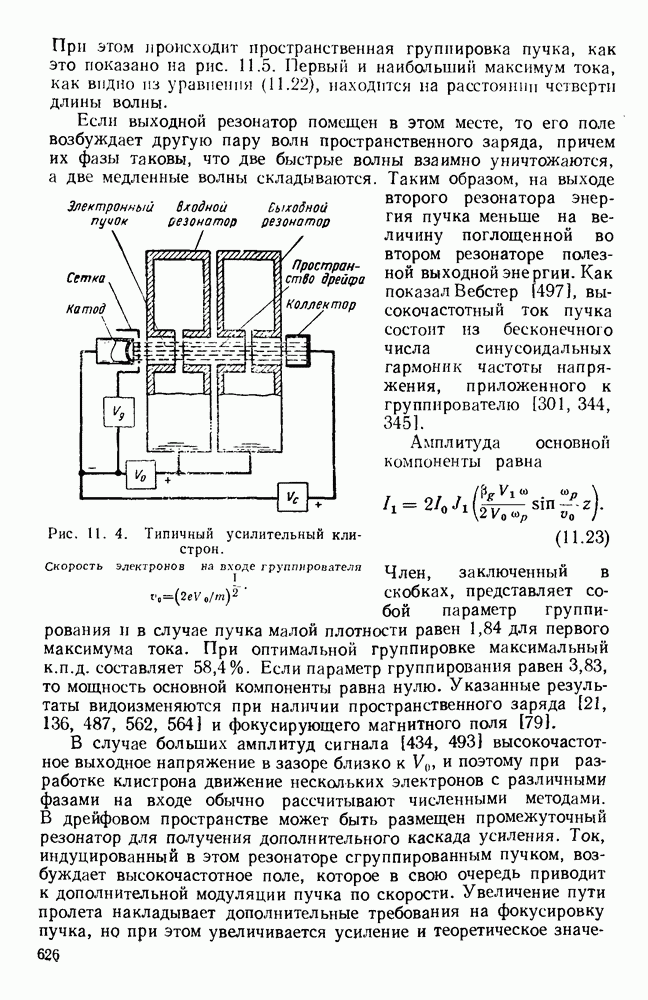
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
- 12.2. МАГНЕТРОНЫ
- 12.2.2. Резонаторные системы
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
- 12.2.4. Рабочие характеристики
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
- 13.1.2. Типы дифракции
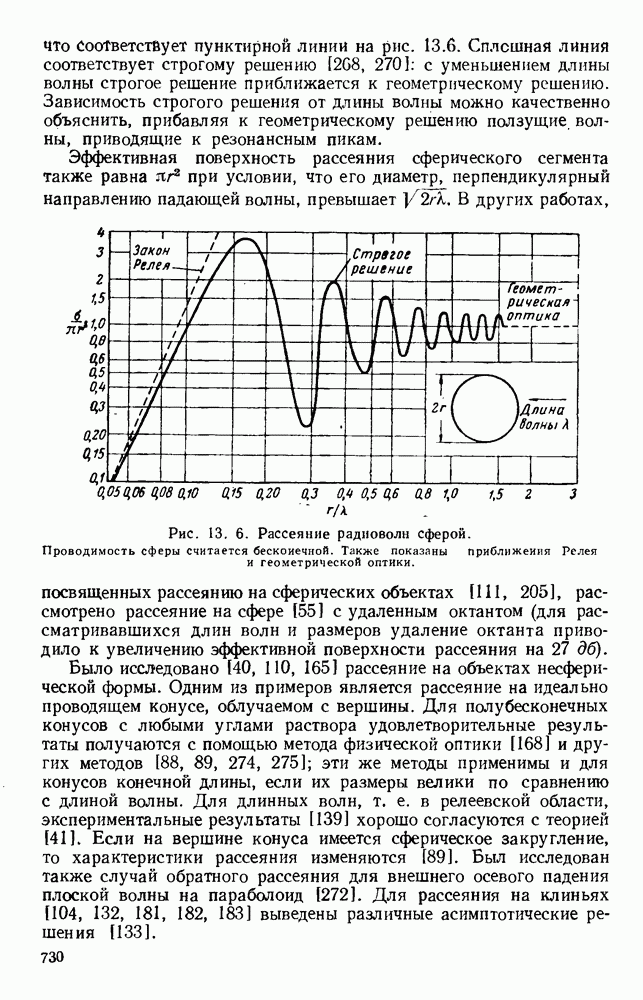
- 13.1.3. Рассеяние
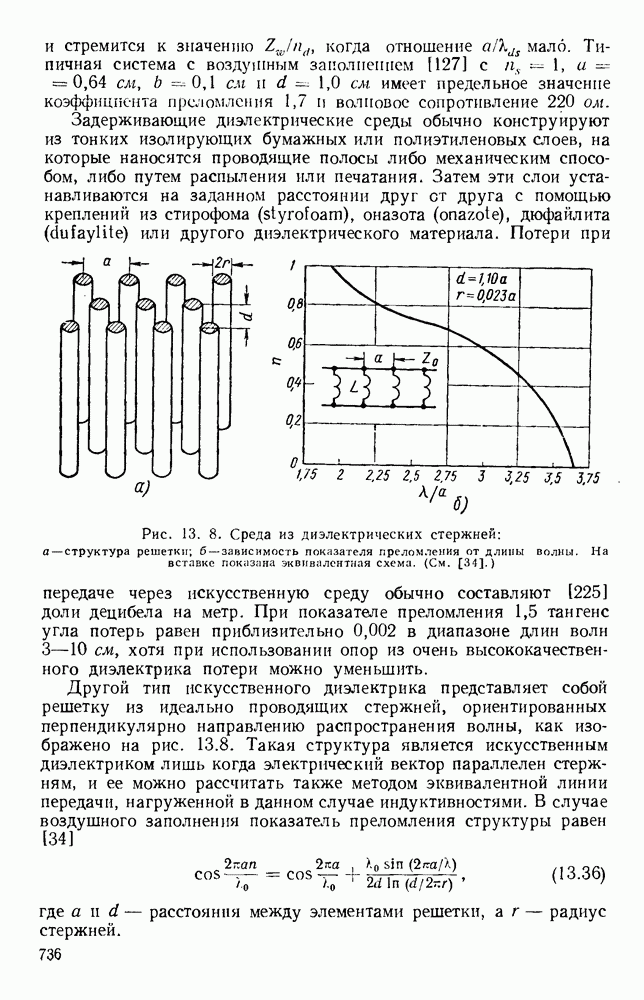
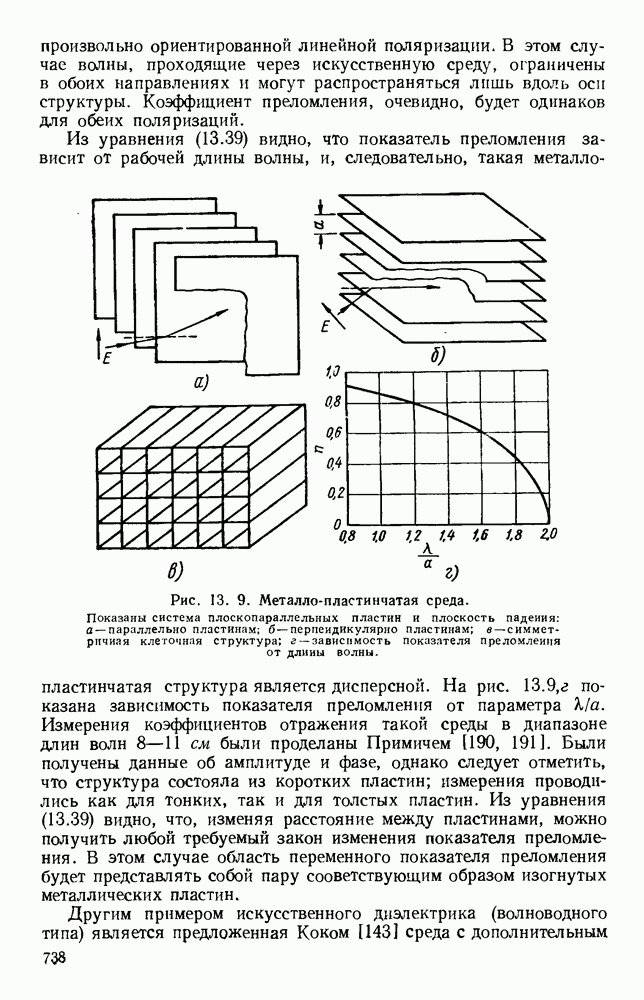
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
- 13.2.2. Структуры волноводного типа
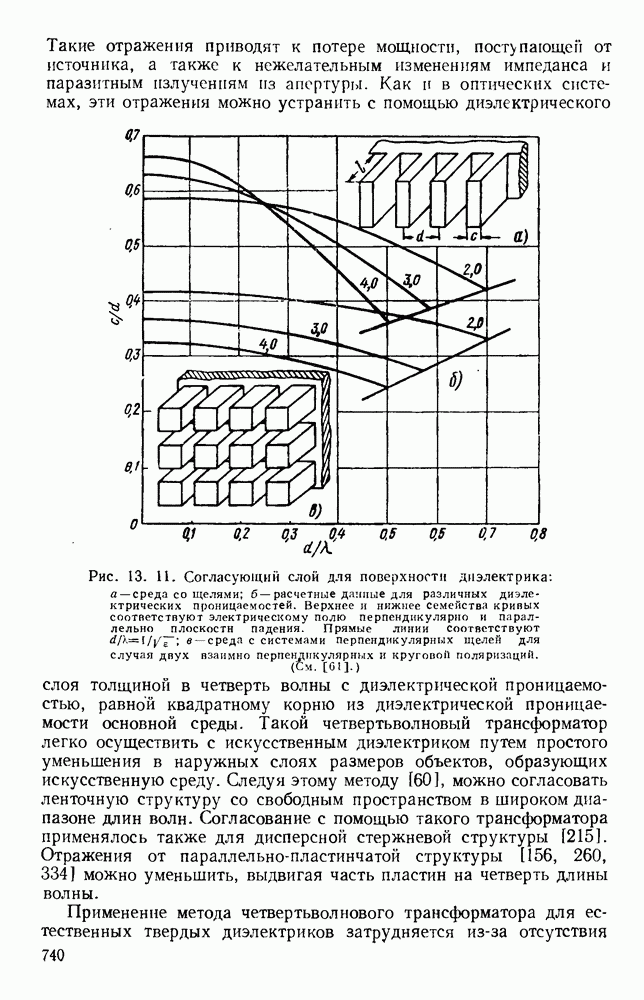
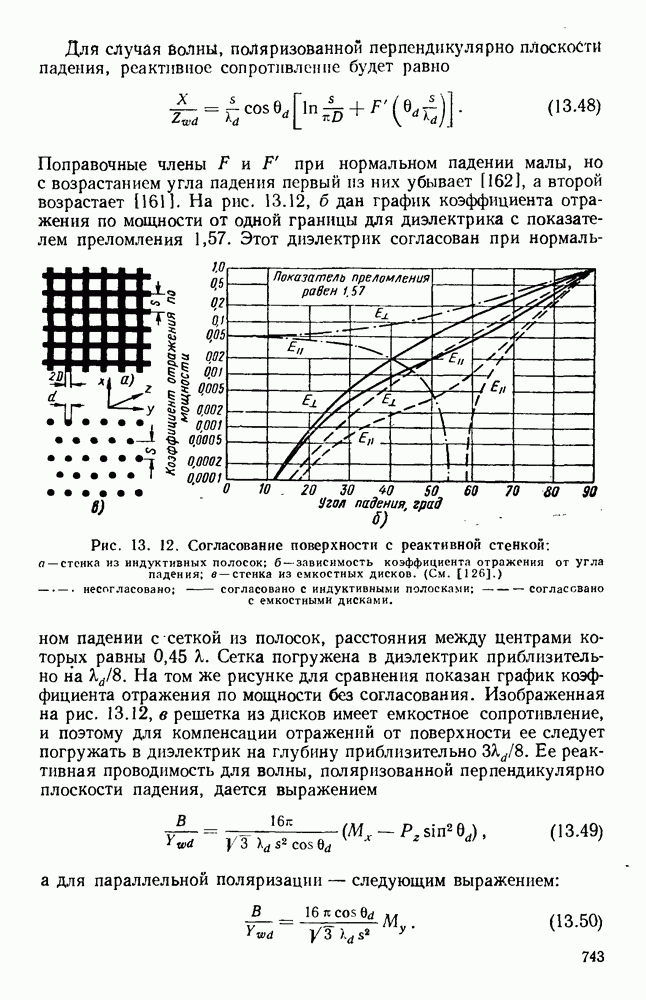
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
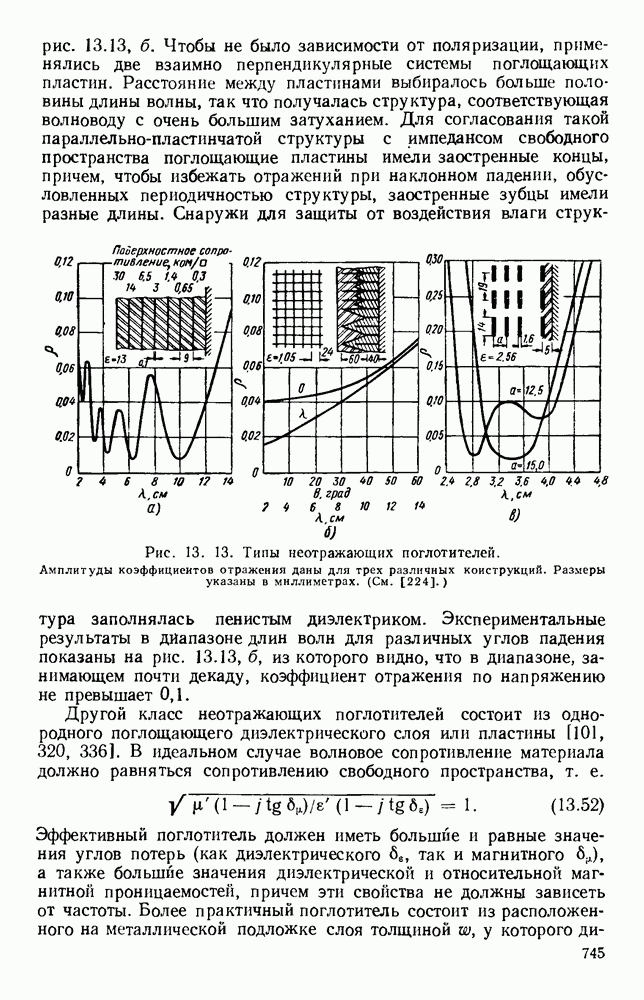
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
- 13.4. ПРИБОРЫ И СИСТЕМЫ
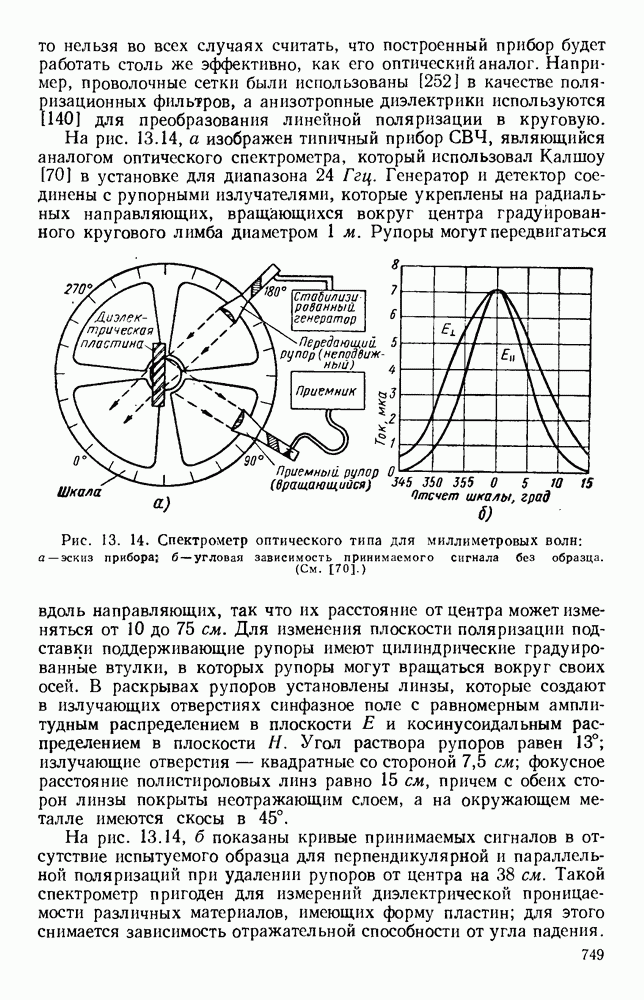
- 13.4.1. Спектрометры
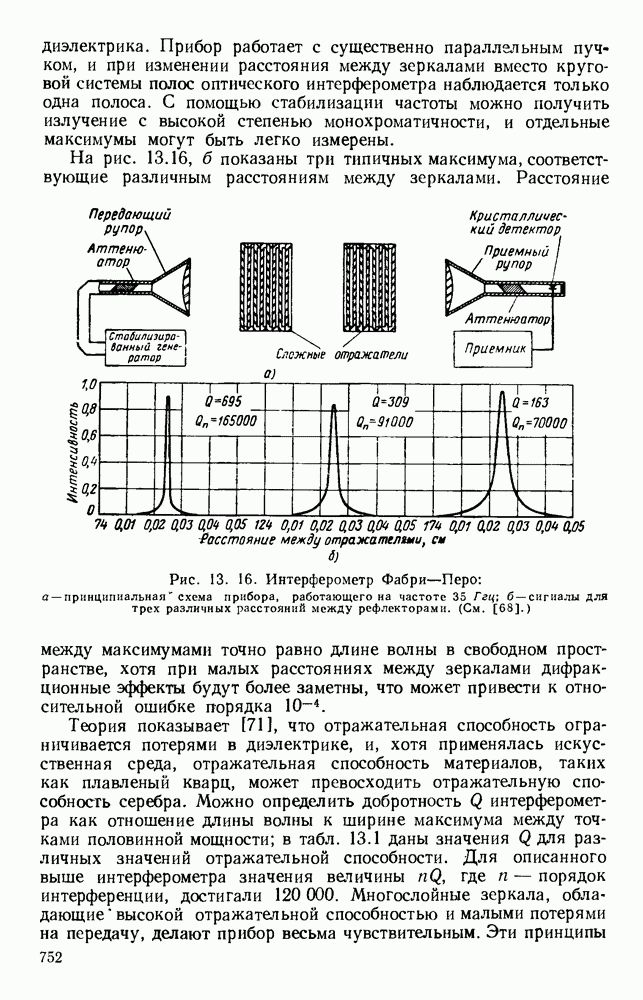
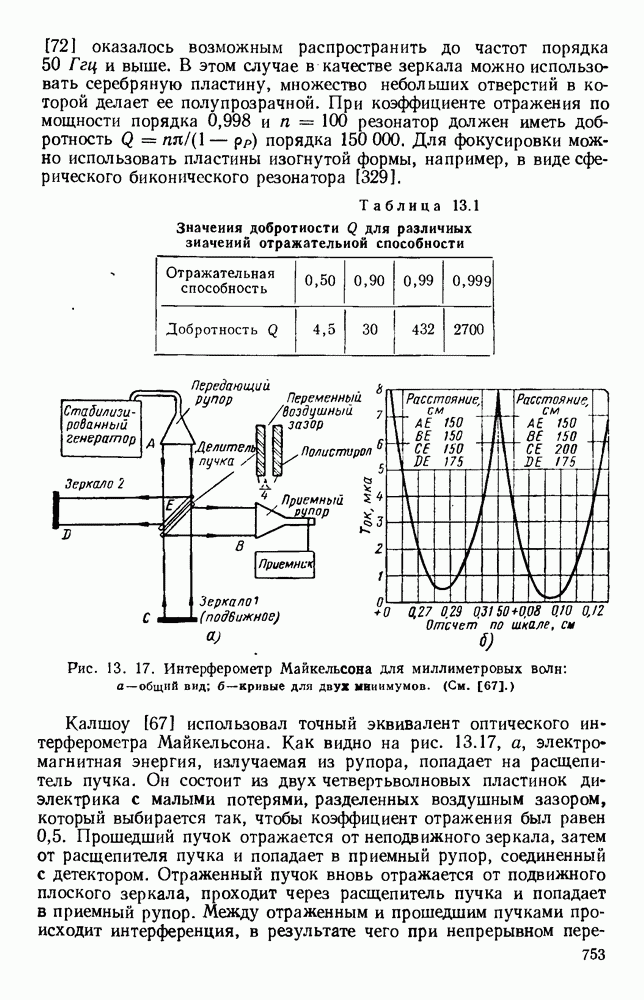
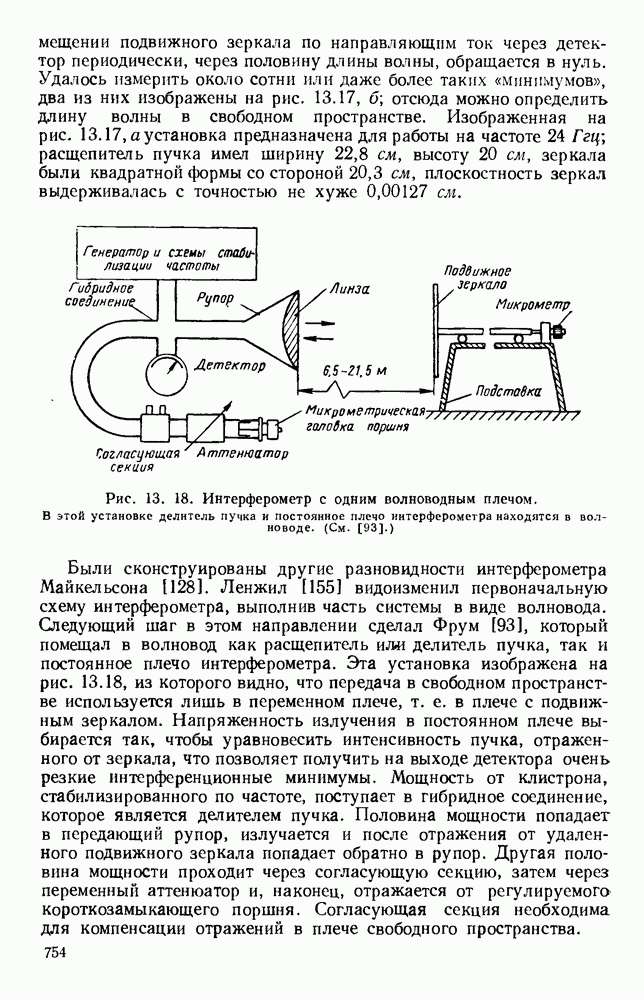
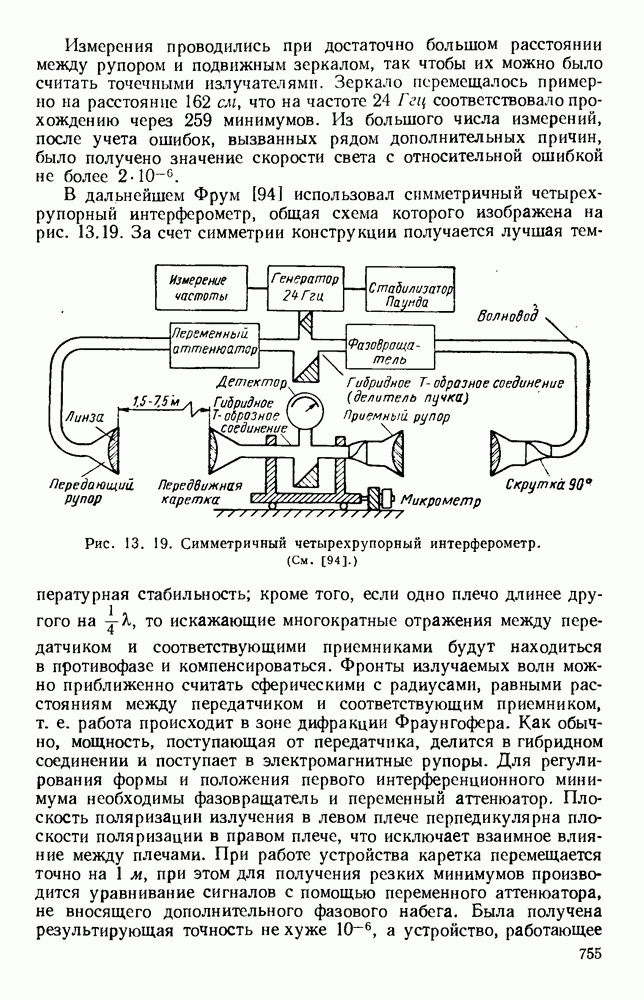
- 13.4.2. Интерферометры
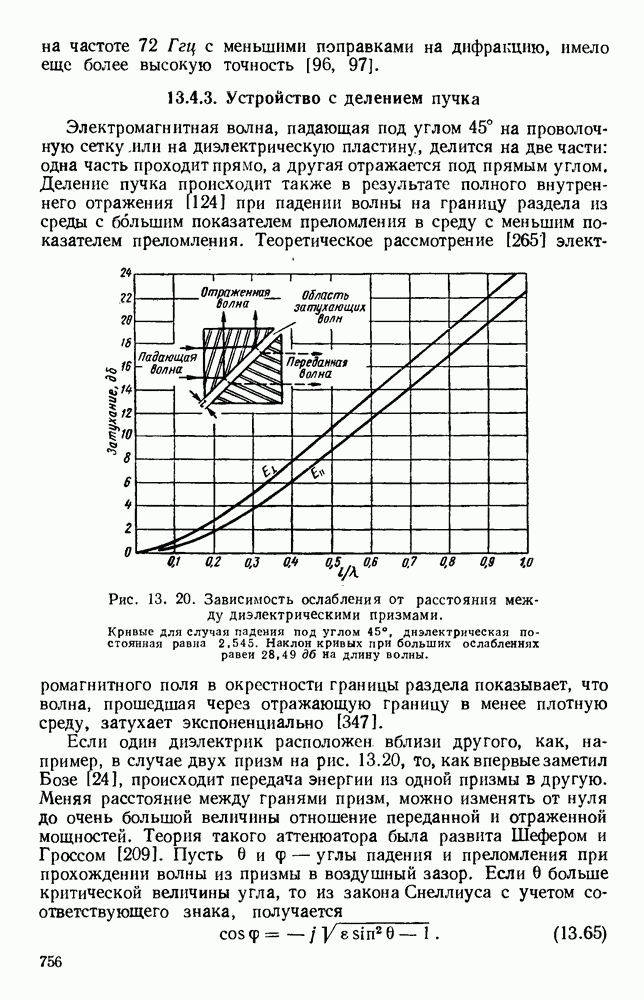
- 13.4.3. Устройство с делением пучка