| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
5.1. РЕЗОНАТОРЫ
5.1.1. Виды колебаний и добротность резонатора
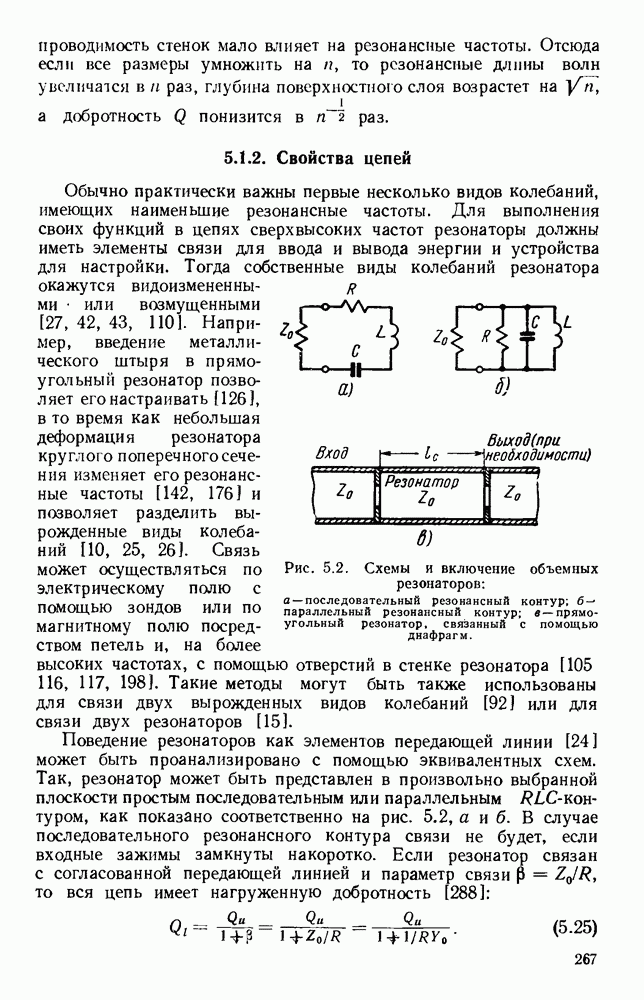
Электромагнитные резонаторы состоят в основном из диэлектрической области, ограниченной проводящими стенками.
Для некоторых частот и пространственных конфигураций существуют решения уравнений электромагнитного поля, которые удовлетворяют граничным условиям и соответствуют накоплению электромагнитной энергии в течение интервалов времени, больших по сравнению с периодами резонансных частот [178]. Эти решения называют собственными видами колебаний резонатора и их число бесконечно, а номенклатура аналогична той, что была приведена для соответствующих волноводов в разд. 4 гл. 1.
Резонансные свойства резонатора определяются его добротностью

Добротность резонатора можно вычислить, если известно магнитное поле высокой частоты и глубина поверхностного слоя материала стенок, из соотношения

где  обозначают соответственно поверхность и объем резонатора.
обозначают соответственно поверхность и объем резонатора.
Величина  является функцией только относительных размеров или формы резонатора и резонансного вида колебаний.
является функцией только относительных размеров или формы резонатора и резонансного вида колебаний.
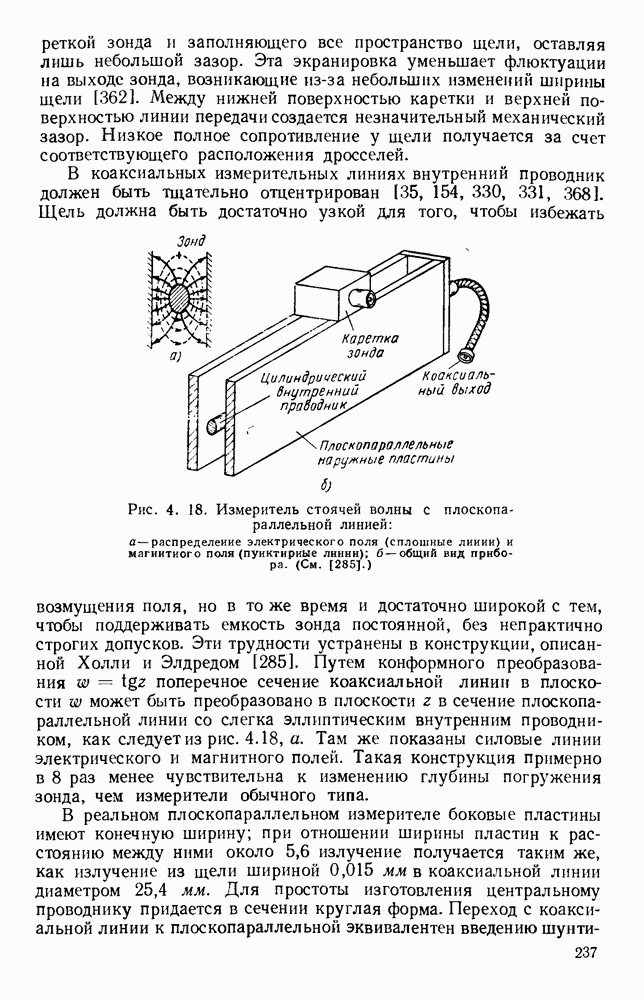
Существует большое разнообразие форм резонаторов, свойства которых послужили предметом многочисленных исследований 
Одним из простейших резонаторов является прямоугольный параллелепипед. Если длины его сторон равны  а I, тип — числа полуволн, укладывающихся соответственно вдоль этих сторон, то резонансные длины волн для колебаний видов
а I, тип — числа полуволн, укладывающихся соответственно вдоль этих сторон, то резонансные длины волн для колебаний видов  которые не имеют составляющей электрического поля Е вдоль стороны С, и колебаний видов
которые не имеют составляющей электрического поля Е вдоль стороны С, и колебаний видов  которые не имеют составляющей магнитного поля Н вдоль стороны С, определяются соотношением
которые не имеют составляющей магнитного поля Н вдоль стороны С, определяются соотношением

Добротности  для колебаний типа ТЕ при
для колебаний типа ТЕ при  определяются следующим образом [103, 139]:
определяются следующим образом [103, 139]:

Если 

Если 

Добротности  для колебаний типа ТМ при I, и и
для колебаний типа ТМ при I, и и  определяются выражением
определяются выражением

Если  то
то

Резонансные виды колебаний прямого кругового цилиндра могут быть исследованы, если обозначить через I число полных периодов, укладывающихся по периферии,  число полупериодов, укладывающихся вдоль радиуса, и
число полупериодов, укладывающихся вдоль радиуса, и  число полупериодов, укладывающихся вдоль оси. Резонансные длины волн для колебаний видов
число полупериодов, укладывающихся вдоль оси. Резонансные длины волн для колебаний видов  и
и  определяются следующим образом:
определяются следующим образом:

где  есть
есть  корень уравнения
корень уравнения  для колебаний типа ТЕ и
для колебаний типа ТЕ и  корень уравнения
корень уравнения  для колебаний типа ТМ. Величины некоторых из этих корней приведены в табл. 5.1.
для колебаний типа ТМ. Величины некоторых из этих корней приведены в табл. 5.1.
Таблица 5.1 Корни  и
и 

Уравнение (5.9) может быть переписано для резонансной частоты:

Из этого уравнения видно, что график  в функции
в функции  есть прямая линия с точкой пересечения и наклоном
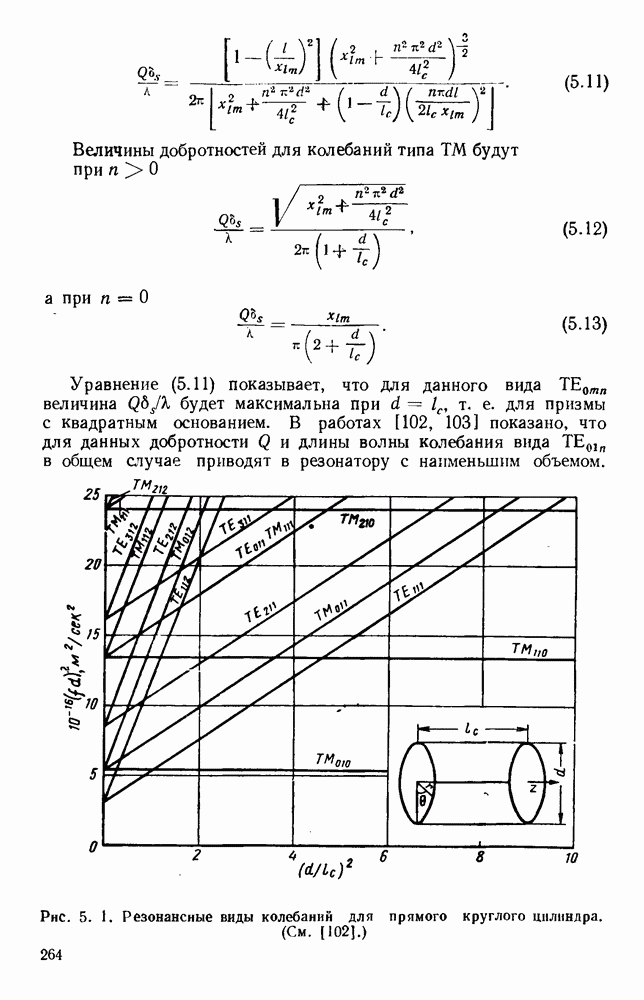
есть прямая линия с точкой пересечения и наклоном  Графики этого типа называются диаграммами видов колебаний [13, 193]. На рис. 5.1 приведен в качестве примера график для нескольких наинизших типов колебаний в прямом круглом цилиндре.
Графики этого типа называются диаграммами видов колебаний [13, 193]. На рис. 5.1 приведен в качестве примера график для нескольких наинизших типов колебаний в прямом круглом цилиндре.
Подобные диаграммы могут быть построены и для прямоугольных резонаторов с любым выбранным отношением сторон  Эти диаграммы видов колебаний очень полезны при расчете резонаторов, так как по ним видно, какие возможны виды колебаний на рабочей частоте или в диапазоне механической перестройки резонатора.
Эти диаграммы видов колебаний очень полезны при расчете резонаторов, так как по ним видно, какие возможны виды колебаний на рабочей частоте или в диапазоне механической перестройки резонатора.
Добротность  прямого круглого цилиндра для колебаний типа ТЕ определяется формулой
прямого круглого цилиндра для колебаний типа ТЕ определяется формулой

Величины добротностей для колебаний типа ТМ будут при 

а при 

Уравнение (5.11) показывает, что для данного вида  величина
величина  будет максимальна при
будет максимальна при  т. е. для призмы с квадратным основанием. В работах [102, 103] показано, что для данных добротности
т. е. для призмы с квадратным основанием. В работах [102, 103] показано, что для данных добротности  и длины волны колебания вида
и длины волны колебания вида  в общем случае приводят в резонатору с нанменьшнм объемом.
в общем случае приводят в резонатору с нанменьшнм объемом.

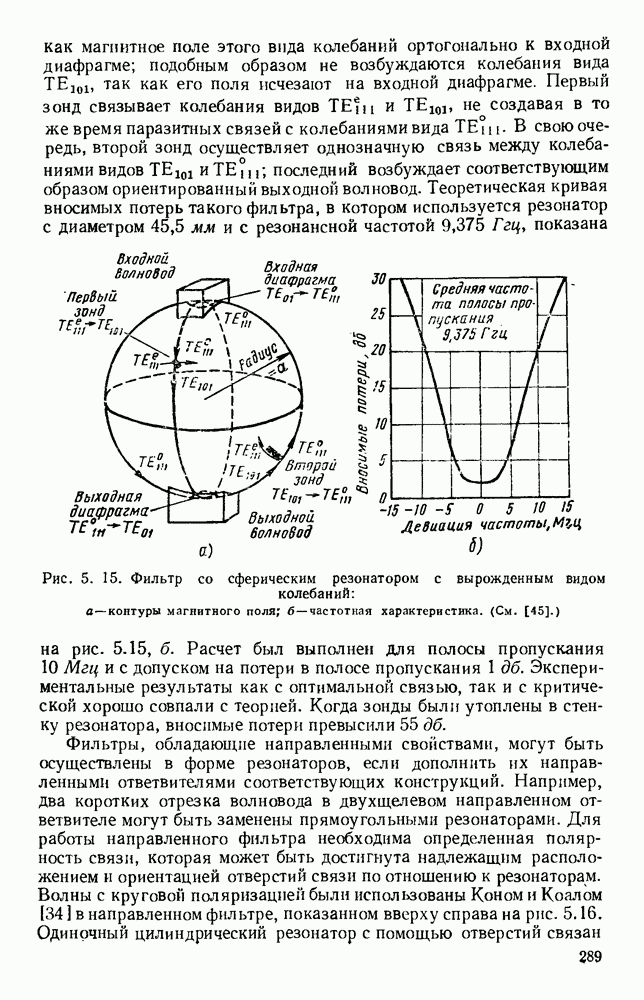
Рис. 5. 1. Резонансные виды колебаний для прямого круглого цнлиндра. (См. [102].)
Величина  равна
равна  где
где  является решением уравнения
является решением уравнения

Соответствующий диаметр и длина резонатора определяются соотношениями

Нормальные виды колебаний в полном коаксиальном резонаторе [57], образованном из круглых концентрических цилиндров, могут быть разделены на два типа ТЕ и ТМ и в дальнейшем обозначаются целыми числами  которые определяются так же, как и для круглого волноводного резонатора. Резонансные длины волн даются формулой
которые определяются так же, как и для круглого волноводного резонатора. Резонансные длины волн даются формулой

где  для колебаний типа ТМ являются корнями уравнения
для колебаний типа ТМ являются корнями уравнения

а для колебаний типа  корням» уравнения
корням» уравнения

Добротность  для основного типа колебаний ТЕМ или для колебаний вида
для основного типа колебаний ТЕМ или для колебаний вида  определяется соотношением
определяется соотношением

В частично коаксиальных или гибридных резонаторах существует центральный поршень, диаметр которого намного меньше, чем диаметр внешнего цилиндра. Внешний диаметр берется достаточно большим, чтобы в резонаторе могли существовать колебания вида  При перемещении поршня непрерывно меняется резонансная длина волны, и при полном введении поршня она становится равной резонансной длине волны колебаний
При перемещении поршня непрерывно меняется резонансная длина волны, и при полном введении поршня она становится равной резонансной длине волны колебаний  в коаксиальном резонаторе. Добротность гибридного резонатора сравнима с добротностью прямого цилиндра, но существенно изменяется в диапазоне перестройки.
в коаксиальном резонаторе. Добротность гибридного резонатора сравнима с добротностью прямого цилиндра, но существенно изменяется в диапазоне перестройки.
В случае сферических резонаторов [45, 175, 295, 298,] решение уравнений поля в сферических координатах с соответствующими граничными условиями на поверхности  определяет характеристические величины
определяет характеристические величины  для колебаний типа ТЕ следующим образом:
для колебаний типа ТЕ следующим образом:

и величины  для колебаний типа ТМ
для колебаний типа ТМ

где целочисленный индекс I обозначает  корень уравнения (5.21) или (5.22). Резонансные длины волн выражаются формулами
корень уравнения (5.21) или (5.22). Резонансные длины волн выражаются формулами

Так как корни уравнений (5.21) и (5.22) различны, то в частном случае вырожденные виды колебаний должны быть волнами одного и того же типа. С другой стороны, для  существуют четные и нечетные типы ТЕ и ТМ, имеющие одинаковую частоту. Так как
существуют четные и нечетные типы ТЕ и ТМ, имеющие одинаковую частоту. Так как  то для каждого характеристического числа существует
то для каждого характеристического числа существует  вырожденных колебаний. Подбирая соответствующее значение индекса
вырожденных колебаний. Подбирая соответствующее значение индекса  можно получить произвольное число вырождений. На сферических поверхностях, расположенных концентрически относительно начала координат, для данного значения индекса I при большем значении величины
можно получить произвольное число вырождений. На сферических поверхностях, расположенных концентрически относительно начала координат, для данного значения индекса I при большем значении величины  получается более сложное распределение поля. Подобная картина распределения поля существует в резонаторе, образованном двумя концентрическими сферами [16, 17].
получается более сложное распределение поля. Подобная картина распределения поля существует в резонаторе, образованном двумя концентрическими сферами [16, 17].
Были исследованы различные типы резонаторов, включая резонаторы эллиптического сечения [91, 291, 302], конической формы [108], тороидальные [150, 303], сигарообразные [134] и резонаторы, состоящие из конфокальных сфероидов [188] и параболоидов [7] или имеющие открытые концы [96]. Особенно широко были исследованы цилиндрические резонаторы, снабженные на торцовых стенках наконечниками, выступающими во внутрь резонансной полости, в зазоре между которыми может существовать высокочастотное электрическое поле [68, 69, 70, 132, 215, 249]. Такие резонаторы находят практическое применение в электронных лампах. Часто бывают полезны виды колебаний с круговой поляризацией, они могут существовать, например, в прямом круговом цилиндре, а возбуждаться двумя ортогональными видами колебаний  поля которых по фазе находятся в квадратуре..
поля которых по фазе находятся в квадратуре..
Приводимые до сих пор формулы для резонансной длины волны и добротности относятся к полым резонаторам. Введение диэлектрических материалов в форме колец [152] или пластин [115] изменяет оба эти параметра. Если резонатор полностью заполнен диэлектриком, то новая резонансная длина волны будет равна

Применение диэлектриков с большим  позволяет создавать на низших частотах диапазона СВЧ миниатюрные резонаторы [53, 250]. Обычно резонаторы имеют высокие добротности, и поэтому конечная
позволяет создавать на низших частотах диапазона СВЧ миниатюрные резонаторы [53, 250]. Обычно резонаторы имеют высокие добротности, и поэтому конечная
проводимость стенок мало влияет на резонансные частоты. Отсюда если все размеры умножить на  то резонансные длины волн увеличатся в
то резонансные длины волн увеличатся в  раз, глубина поверхностного слоя возрастет на
раз, глубина поверхностного слоя возрастет на  а добротность
а добротность  понизится в
понизится в  раз.
раз.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
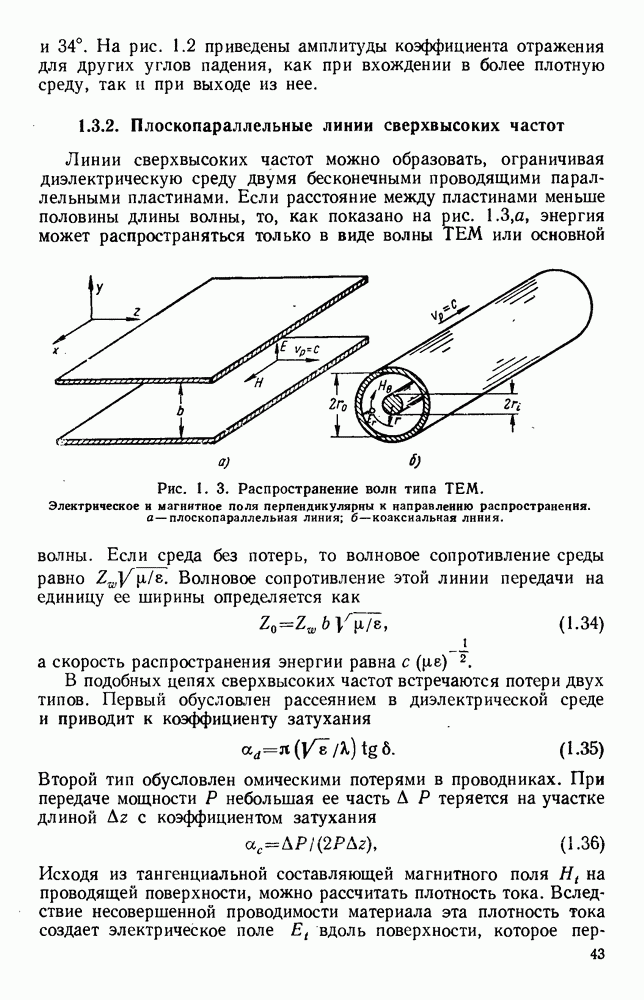
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
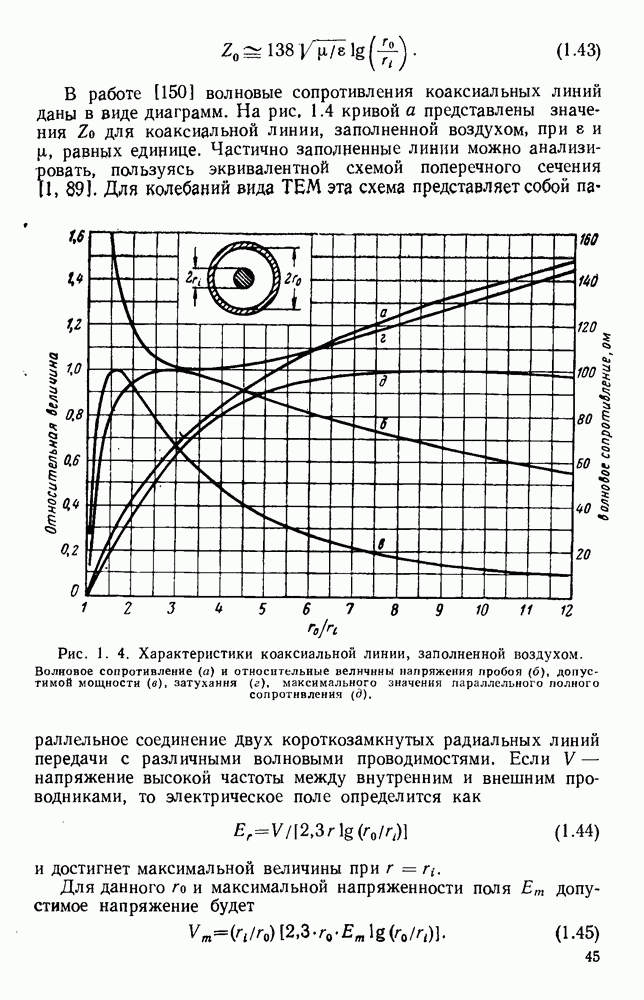
- 1.3.3. Коаксиальные линии
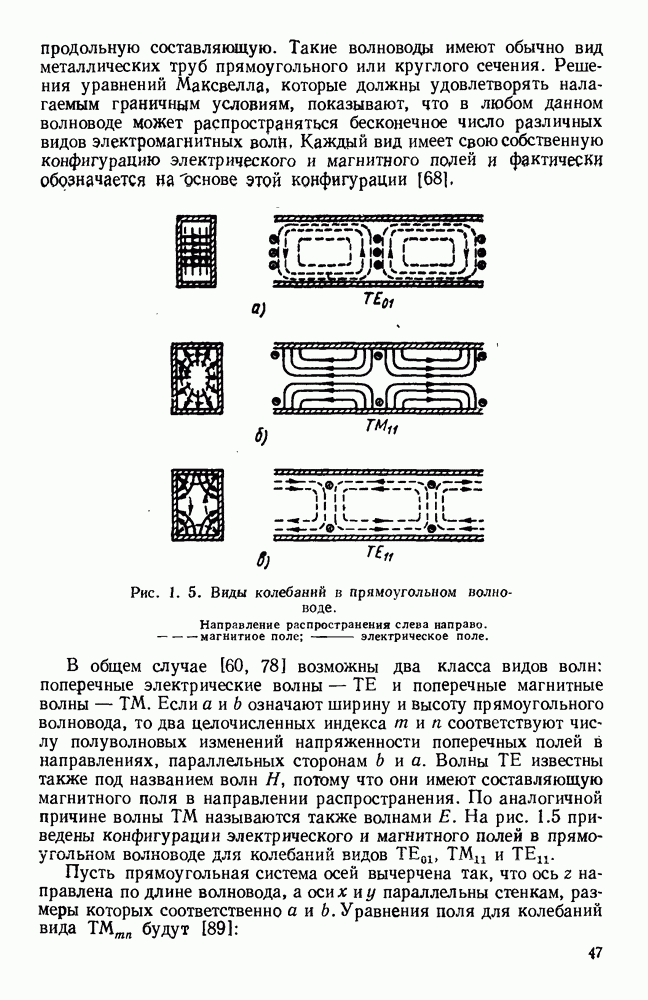
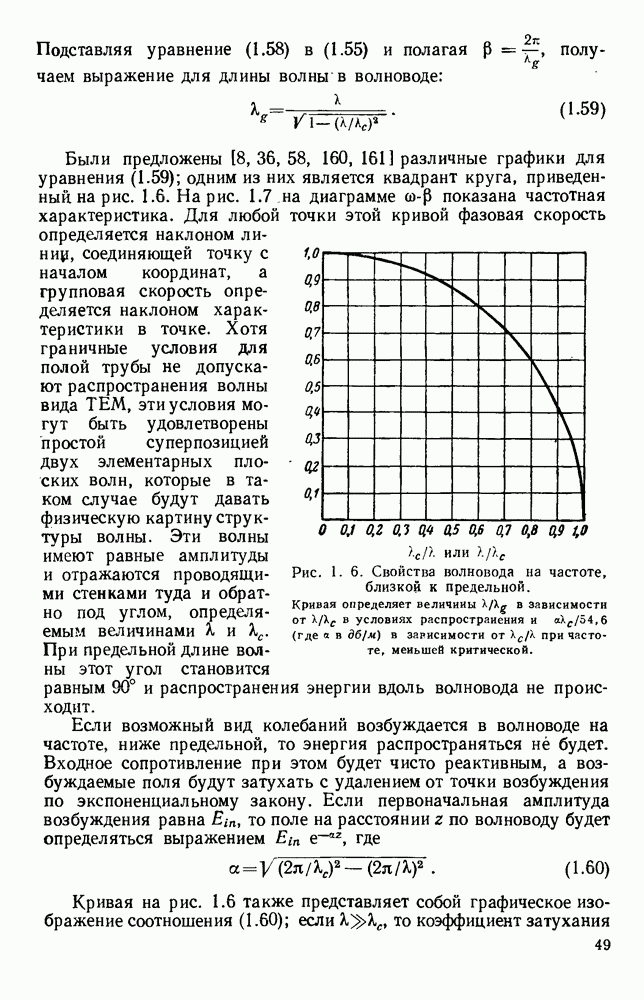
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
- 1.4.2. Круглые волноводы
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
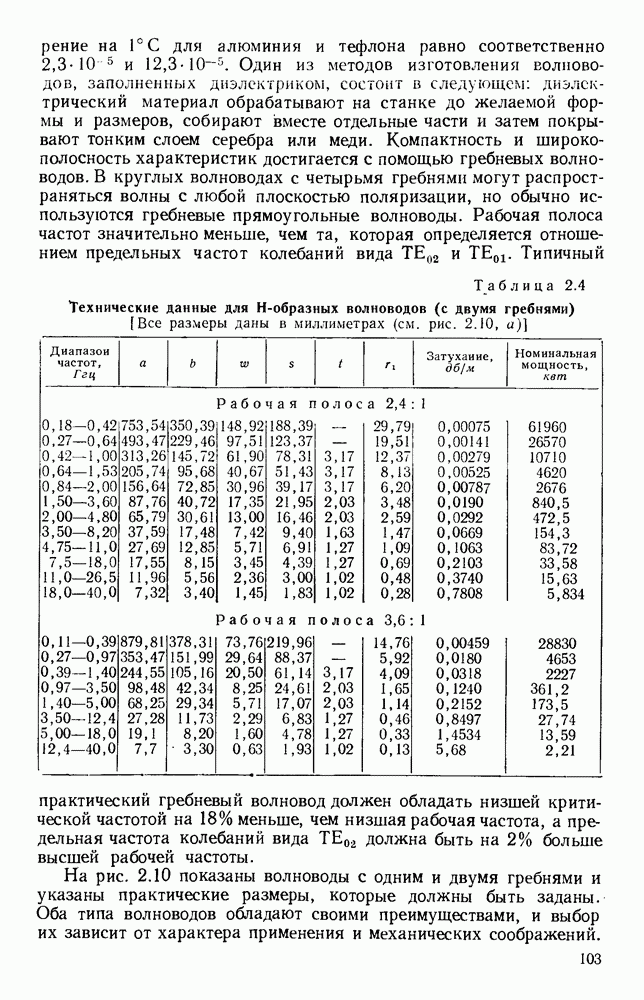
- 1.5.2. Гребневые волноводы
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
- 2.1.2. Круговая диаграмма
- 2.1.3. Широкополосное согласование
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
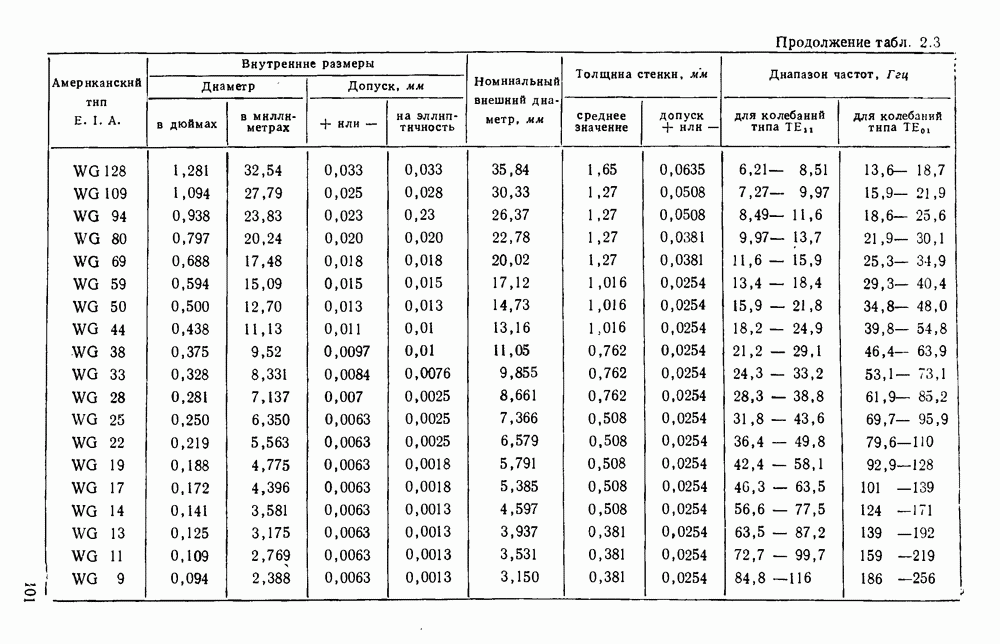
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
- 2.3.1. Прямоугольные волноводы
- 2.3.2. Круглые волноводы
- 2.3.3. Широкополосные и компактные волноводы
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
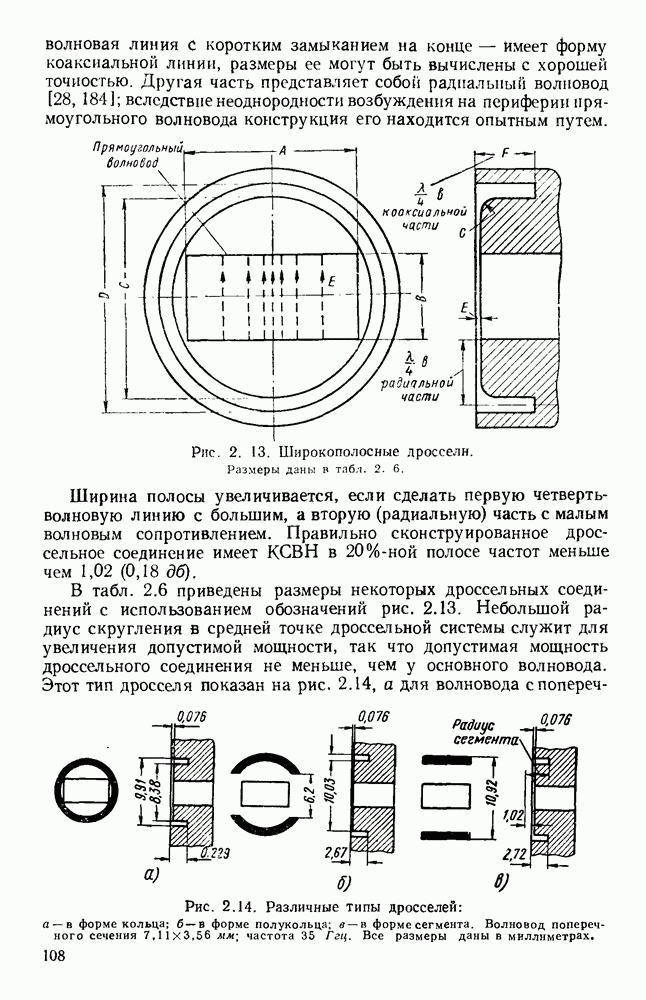
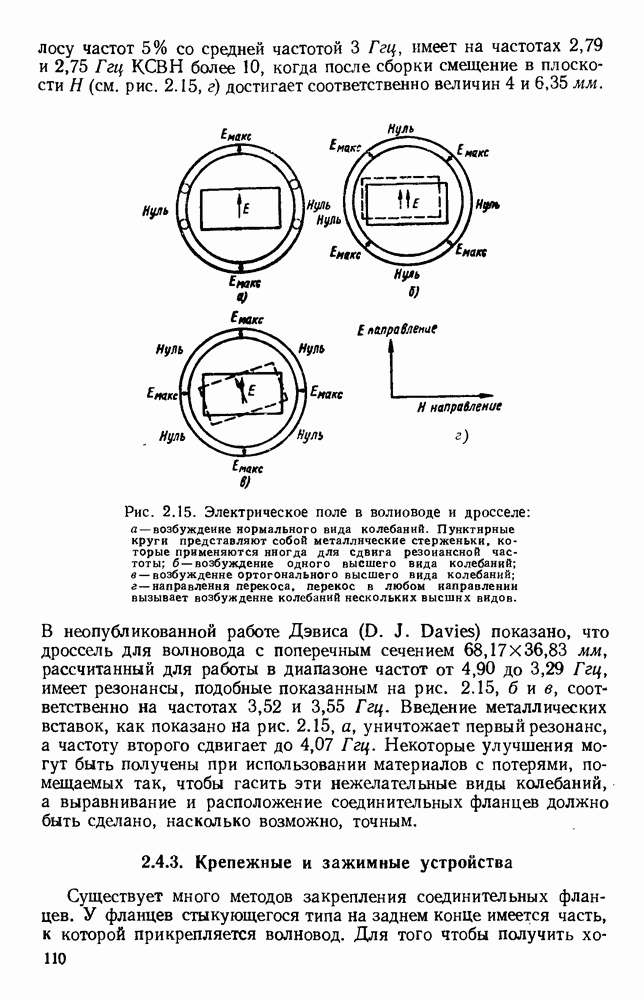
- 2.4.2. Контактные прокладки и дроссели
- 2.4.3. Крепежные и зажимные устройства
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
- 2.6.1. Изгибы, уголки и скрутки
- 2.6.2. Переходы и преобразователи
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
- 3.2.3. Переход от линейной поляризации к круговой
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
- 3.6.2. Вращающиеся сочленения различных типов
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
- 3.7.1. Механические переключатели с ручным управлением
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
- 5.2.1. Волномеры с объемными резонаторами
- 5.2.2. Волноводные интерферометры
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
- 5.3.2. Связанные резонаторы
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
- 7.1.2. Форма линии и интенсивность
- 7.1.3. Сверхтонкая структура
- 7.1.4. Явления Штарка и Зеемана
- 7.2. СПЕКТРОМЕТРЫ
- 7.2.2. Поглощающие ячейки
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
- 7.3.4. Времена релаксации
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
- 8.3.3. Ферритовые устройства в качестве элементов схем
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
- 8.6.2. Устройства с поперечным полем
- 8.6.3. Прочие узлы
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.2.1. Линии типа «диэлектрических сэндвичей»
- 9.2.2. Симметричные линии с воздушным диэлектриком
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
- 9.4.2. Переходные устройства
- 9.4.3. Узлы полосковых систем
- 9.5. ЦЕПИ И СИСТЕМЫ
- 9.5.3. Частотные фильтры
- 9.5.4. Цепи питания антенн
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
- 10.1.2. Пространственные гармоники
- 10.1.3. Многократно-периодические структуры
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
- 10.2.3. Продольные цилиндрические волны
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
- 12.2. МАГНЕТРОНЫ
- 12.2.2. Резонаторные системы
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
- 12.2.4. Рабочие характеристики
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
- 13.1.2. Типы дифракции
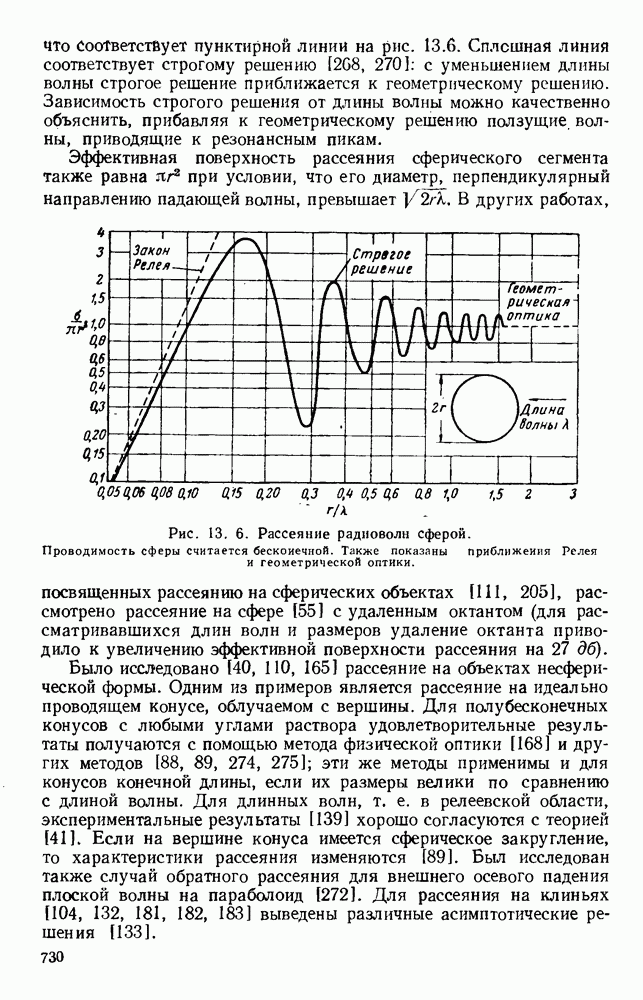
- 13.1.3. Рассеяние
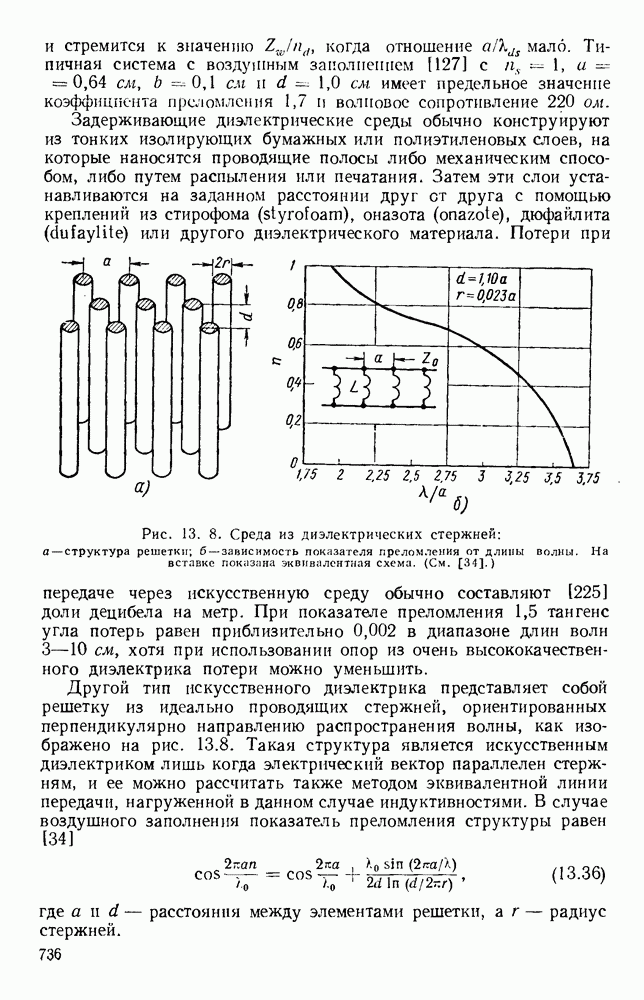
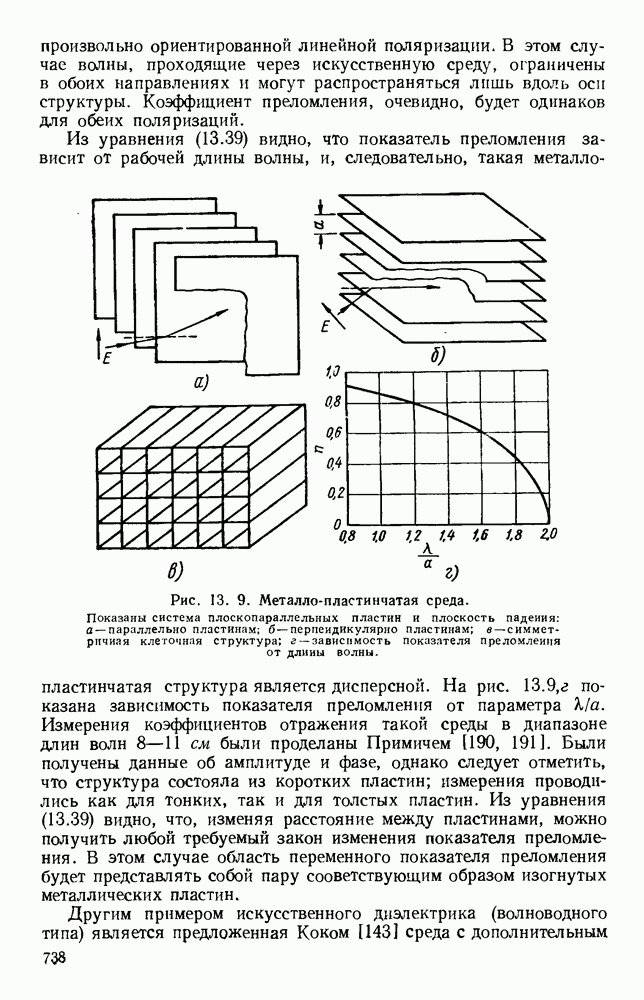
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
- 13.2.2. Структуры волноводного типа
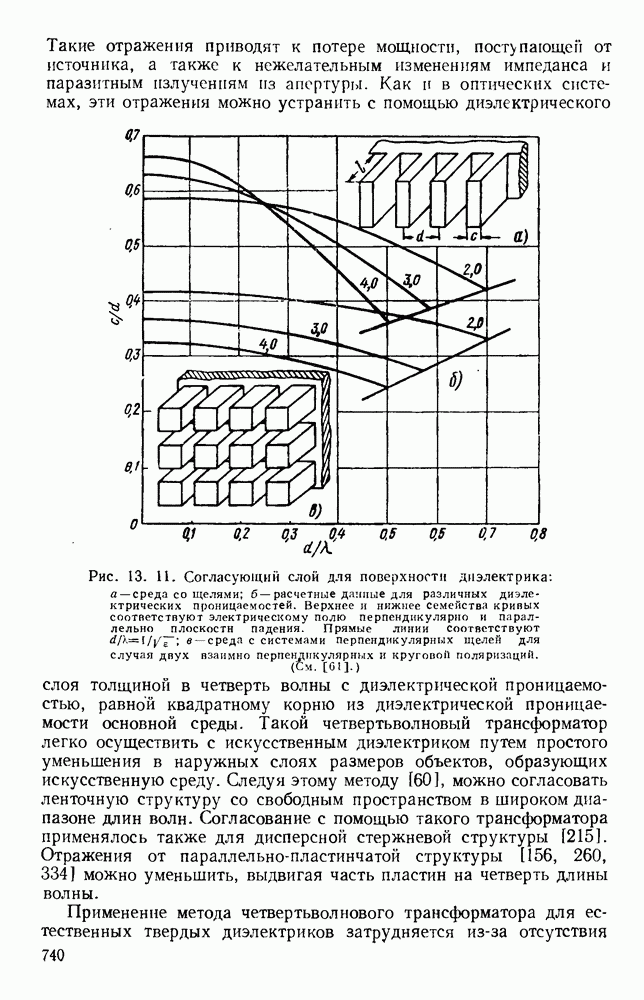
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
- 13.4. ПРИБОРЫ И СИСТЕМЫ
- 13.4.1. Спектрометры
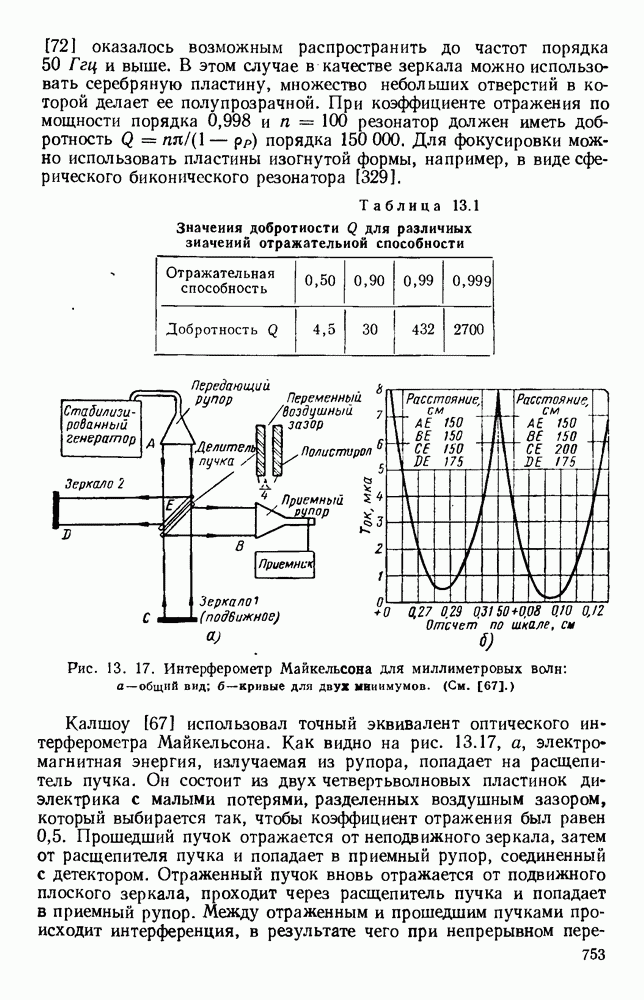
- 13.4.2. Интерферометры
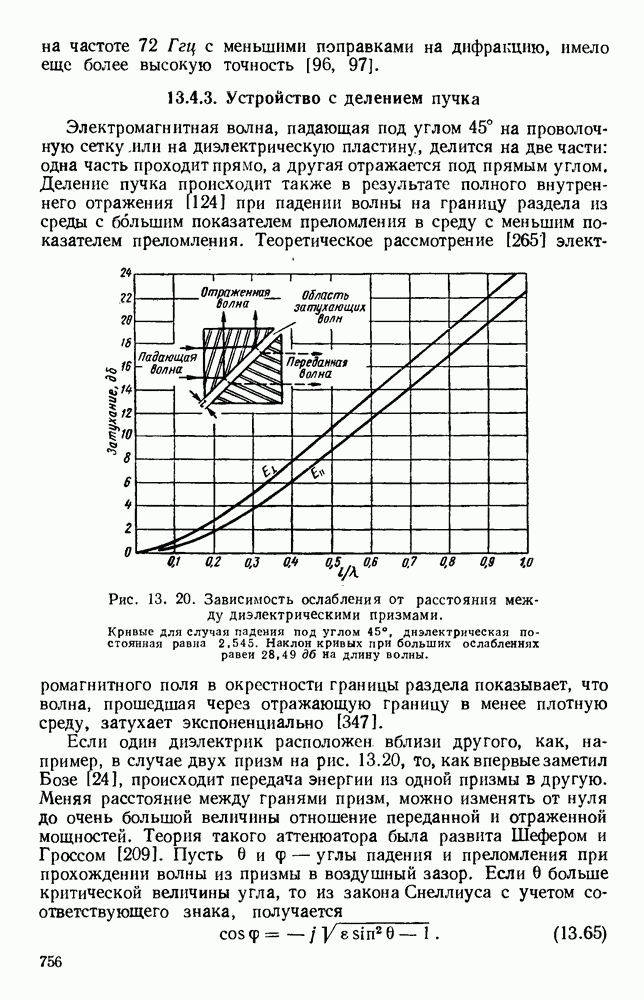
- 13.4.3. Устройство с делением пучка