| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13.1.2. Типы дифракции
Хотя общие законы дифракции даны выше, полезно привести элементарное рассмотрение двух частных случаев: дифракции Фраунгофера и дифракции Френеля. Дифракция Фраунгофера происходит, когда точка наблюдений достаточно удалена от источника излучения, так что лучи, выходящие из вторичных источников Гюйгенса можно считать параллельными. Излучение антенны в свободное пространство, рассматриваемое в гл. 14, обычно трактуется как дифракция Фраунгофера.
Дифракция Френеля наблюдается, когда лучи, идущие от источника в точку наблюдения, нельзя считать параллельными, и необходимо учитывать обусловленную этой непараллельностью разность фаз. Рассмотрим поле вдоль оси круглого отверстия с равномерным амплитудным и фазовым распределением. На
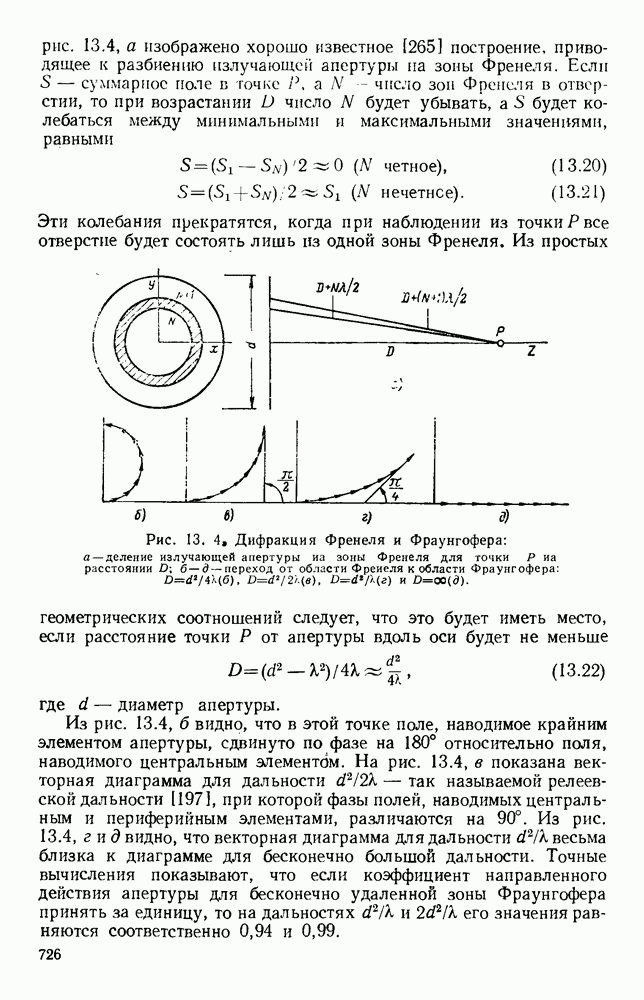
рис. 13.4, а изображено хорошо известное [265] построение, приводящее к разбиению излучающей апертуры yа зоны Френеля. Если  суммарное поле в точке
суммарное поле в точке  число зон Френеля в отверстии, то при возрастании
число зон Френеля в отверстии, то при возрастании  число N будет убывать,
число N будет убывать,  будет колебаться между минимальными и максимальными значениями, равными
будет колебаться между минимальными и максимальными значениями, равными

Эти колебания прекратятся, когда при наблюдении из точки Р все отверстие будет состоять лишь из одной зоны Френеля.

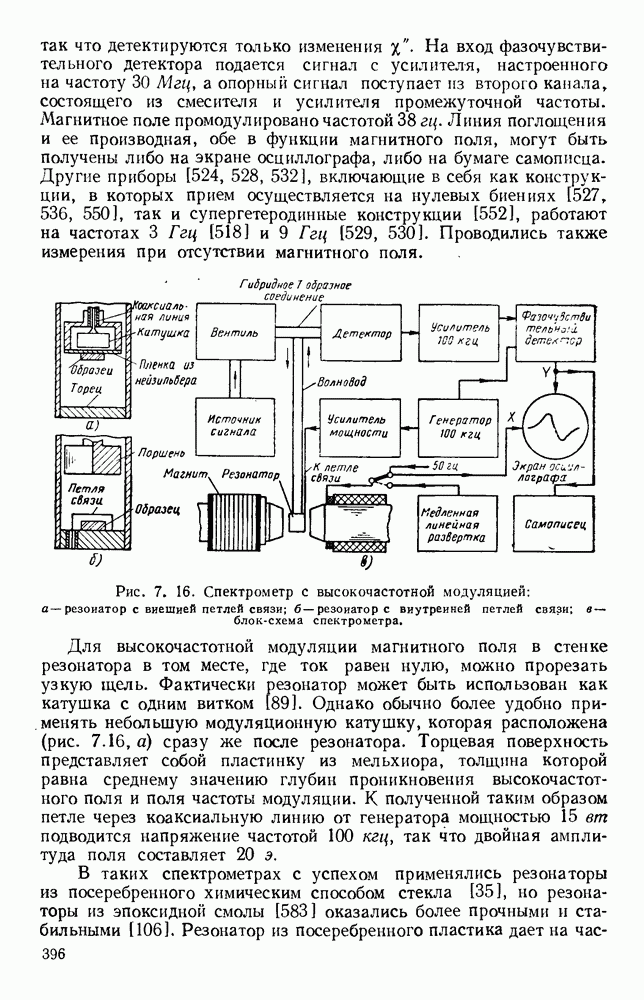
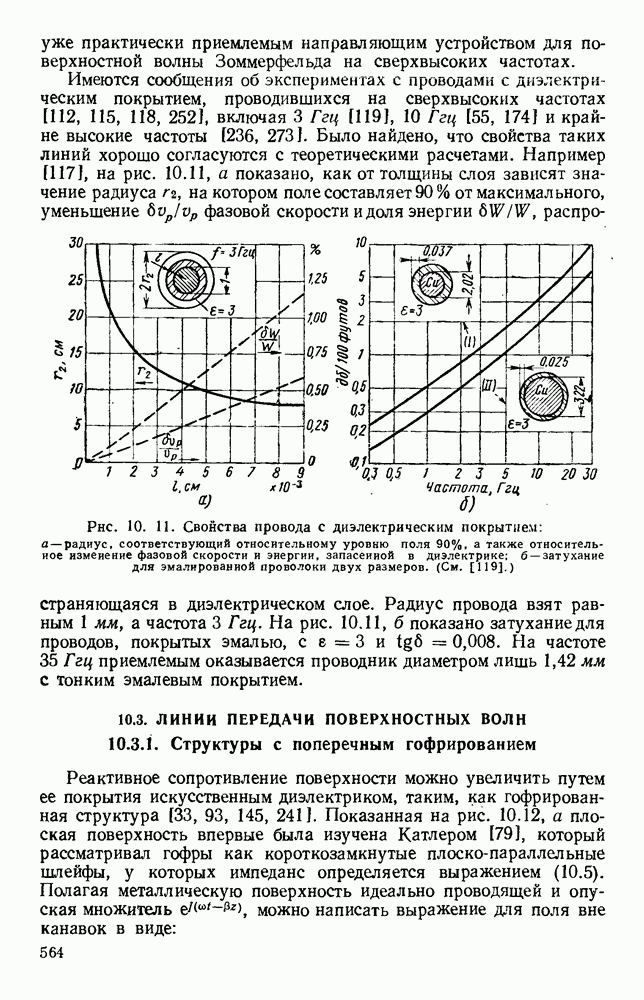
Рис. 13. 4, Дифракция Френеля и Фраунгофера: а — деление излучающей апертуры на зоны Френеля для точки Р на расстоянии D$ б-д - переход от области Фреиеля к области Фраунгофера: 
Из простых геометрических соотношений следует, что это будет иметь место, если расстояние точки Р от апертуры вдоль оси будет не меньше

где  диаметр апертуры.
диаметр апертуры.
Из рис. 13.4, б видно, что в этой точке поле, наводимое крайним элементом апертуры, сдвинуто по фазе на 180° относительно поля, наводимого центральным элементом. На рис. 13.4, в показана векторная диаграмма для дальности  так называемой релеевской дальности [197], при которой фазы полей, наводимых центральным и периферийным элементами, различаются на 90°. Из рис. 13.4, гид видно, что векторная диаграмма для дальности
так называемой релеевской дальности [197], при которой фазы полей, наводимых центральным и периферийным элементами, различаются на 90°. Из рис. 13.4, гид видно, что векторная диаграмма для дальности  весьма близка к диаграмме для бесконечно большой дальности. Точные вычисления показывают, что если коэффициент направленного действия апертуры для бесконечно удаленной зоны Фраунгофера принять за единицу, то на дальностях
весьма близка к диаграмме для бесконечно большой дальности. Точные вычисления показывают, что если коэффициент направленного действия апертуры для бесконечно удаленной зоны Фраунгофера принять за единицу, то на дальностях  его значения равняются соответственно 0,94 и 0,99.
его значения равняются соответственно 0,94 и 0,99.
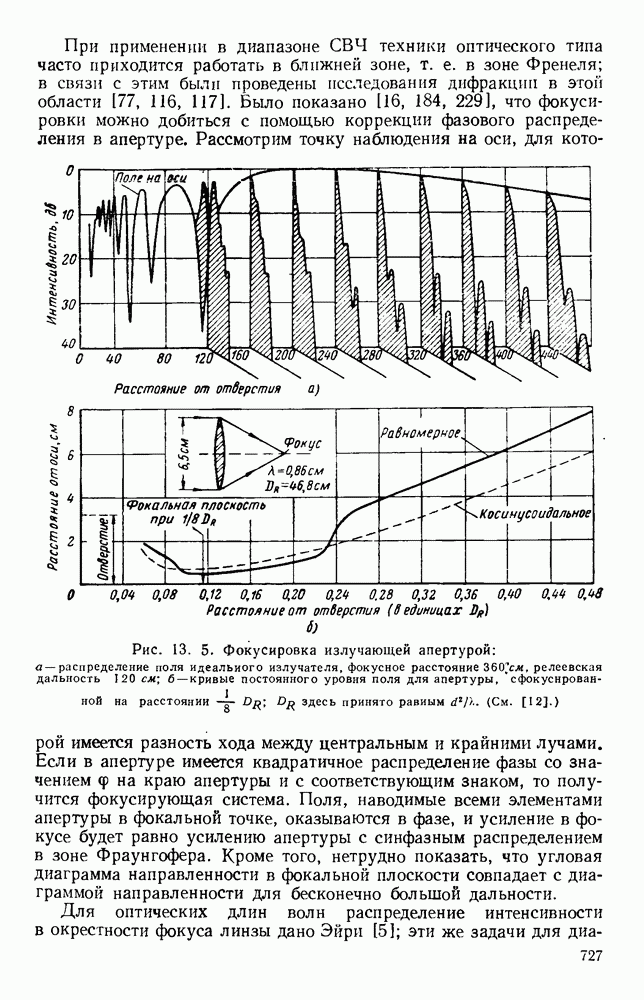
При применении в диапазоне СВЧ техники оптического типа часто приходится работать в ближней зоне, т. е. в зоне Френеля; в связи с этим были проведены исследования дифракции в этой области [77, 116, 117]. Было показано [16, 184, 229], что фокусировки можно добиться с помощью коррекции фазового распределения в апертуре.

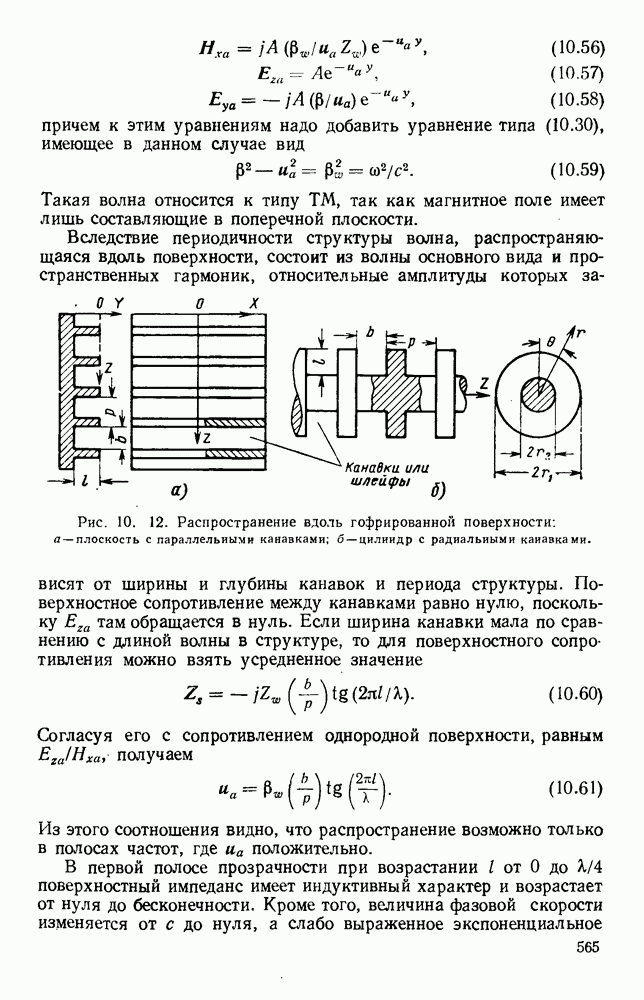
Рис. 13. 5. Фокусировка излучающей апертурой: а — распределение поля идеального излучателя, фокусное расстояние  релеевская дальность 120 см; б - кривые постоянного уровня поля для апертуры, сфокусированной на расстоянии
релеевская дальность 120 см; б - кривые постоянного уровня поля для апертуры, сфокусированной на расстоянии  здесь принято равным
здесь принято равным  (См. [12].)
(См. [12].)
Рассмотрим точку наблюдения на оси, для которой имеется разность хода между центральным и крайними лучами. Если в апертуре имеется квадратичное распределение фазы со значением  на краю апертуры и с соответствующим знаком, то получится фокусирующая система. Поля, наводимые всеми элементами апертуры в фокальной точке, оказываются в фазе, и усиление в фокусе будет равно усилению апертуры с синфазным распределением в зоне Фраунгофера. Кроме того, нетрудно показать, что угловая диаграмма направленности в фокальной плоскости совпадает с диаграммой направленности для бесконечно большой дальности.
на краю апертуры и с соответствующим знаком, то получится фокусирующая система. Поля, наводимые всеми элементами апертуры в фокальной точке, оказываются в фазе, и усиление в фокусе будет равно усилению апертуры с синфазным распределением в зоне Фраунгофера. Кроме того, нетрудно показать, что угловая диаграмма направленности в фокальной плоскости совпадает с диаграммой направленности для бесконечно большой дальности.
Для оптических длин волн распределение интенсивности в окрестности фокуса линзы дано Эйри [5]; эти же задачи для
диапазона СВЧ рассмотрены в работах [84, 85, 164, 226, 244, 330, 331]. Обычно в окрестности фокуса имеется область высокой интенсивности, близкая по форме к длинному узкому эллипсоиду и имгющая боковые лепестки с меньшей интенсивностью на различных расстояниях от оси. При прохождении волны через фокус фаза ее изменяется на 180°, причем это изменение происходит относительно медленно на протяжении многих длин волн и обусловлено возрастанием фазовой скорости в этой области [359]. Формирование фокального пятна можно проследить на рис. 13.5, а, взятом из работы Бачинского и Бекефи [12]. Следует обратить внимание на характер зависимости напряженности поля от расстояния вдоль оси в зоне Френеля. Аналогичные диаграммы направленности изучались [80] на сверхвысокочастотной модели человеческого глаза.
Фокусирование излучения, приводящее к образованию фокального пятна в зоне Френеля, изучалось как средство улучшения поперечного линейного разрешения в неопубликованной работе Мередита (R. Meredith). Допустим, что для фокусирования излучения в некоторую точку, лежащую на оси, требуется квадратичное распределение фазы  Если в действительности в отверстии существует распределение фазы
Если в действительности в отверстии существует распределение фазы  то из рассматриваемой точки будет наблюдаться квадратичное распределение фазы
то из рассматриваемой точки будет наблюдаться квадратичное распределение фазы  Угловая диаграмма направленности в этой точке будет совпадать с диаграммой направленности в дальней зоне для отверстия с квадратичным распределением фазы
Угловая диаграмма направленности в этой точке будет совпадать с диаграммой направленности в дальней зоне для отверстия с квадратичным распределением фазы  Отсюда можно вычислить поперечные линейные размеры главного лепестка диаграммы направленности.
Отсюда можно вычислить поперечные линейные размеры главного лепестка диаграммы направленности.
На рис. 13.5, б дан пример, когда фокус находится на расстоянии, равном одной восьмой релеевской дальности. При фокусировании на таком близком расстоянии продольный размер фокального пятна мал и ширина луча в дальней зоне оказывается большой, причем луч при равномерном распределении амплитуд в отверстии оказывается шире, нежели при спадающем к краям распределении. Наименьший поперечный размер, или круг наименьшего рассеяния, будет немного смещен из фокальной плоскости ближе к отверстию. Графики соответствуют случаю квадратной апертуры со стороной
6,5 см при частоте  Для более широкой апертуры этот эффект выражен слабее, т. е. минимальный разрешаемый круг будет находиться ближе к фокальной плоскости. Показано [354], что минимальный диаметр фокального «пятна» имеет порядок длины волны.
Для более широкой апертуры этот эффект выражен слабее, т. е. минимальный разрешаемый круг будет находиться ближе к фокальной плоскости. Показано [354], что минимальный диаметр фокального «пятна» имеет порядок длины волны.
Можно сформировать такие пучки электромагнитных волн, у которых на некоторой дальности в зоне Френеля поперечное амплитудное распределение будет повторяться [344]. С помощью соответствующих фазовращателей можно восстановить и первоначальное распределение фазы, в результате чего получится новая зона Френеля с той же самой конфигурацией поля. Последовательное повторение таких шагов путем пропускания пучка через систему равноразнесенных фазирующих устройств позволит
направлять луч без уменьшения плотностп энергии. В системе [345], работающей на частоте  луч фокусировался с помощью 10 диэлектрических линзовых преобразователей, отстоящих друг от друга на расстоянии
луч фокусировался с помощью 10 диэлектрических линзовых преобразователей, отстоящих друг от друга на расстоянии  при этом полные потери составляли 1,9 дб [377].
при этом полные потери составляли 1,9 дб [377].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
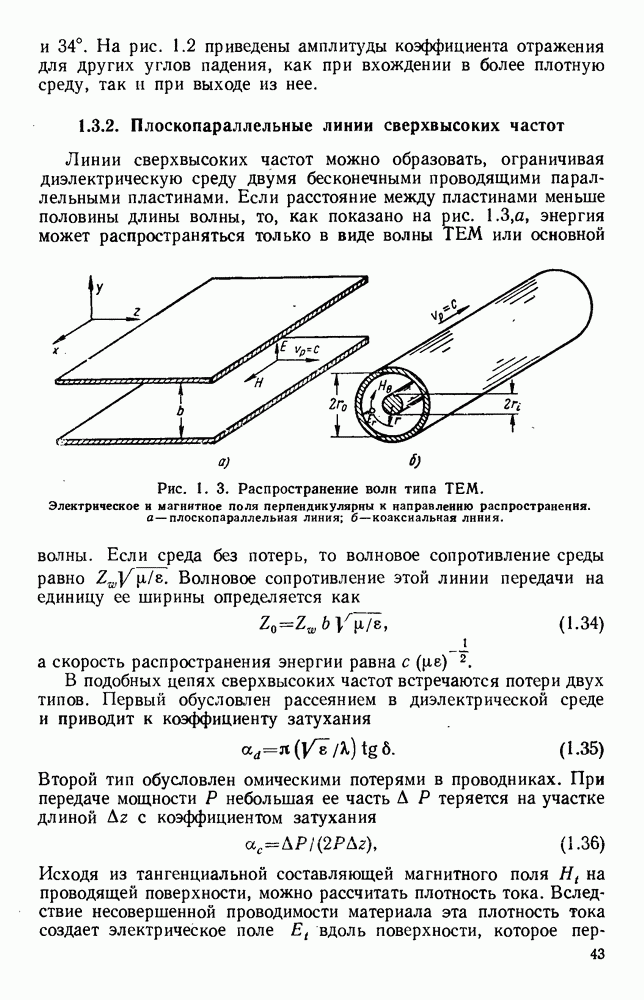
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
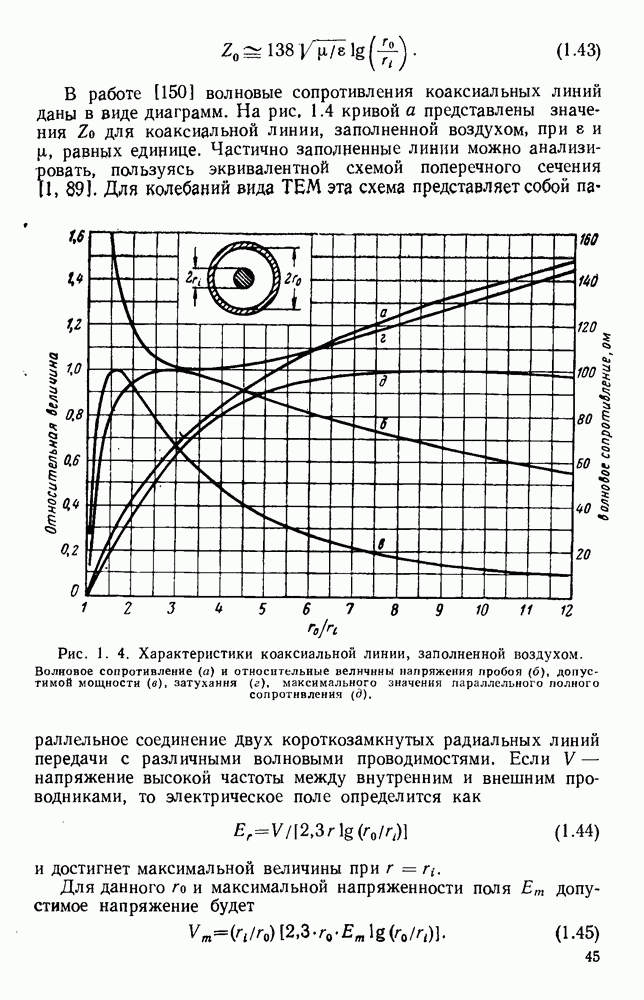
- 1.3.3. Коаксиальные линии
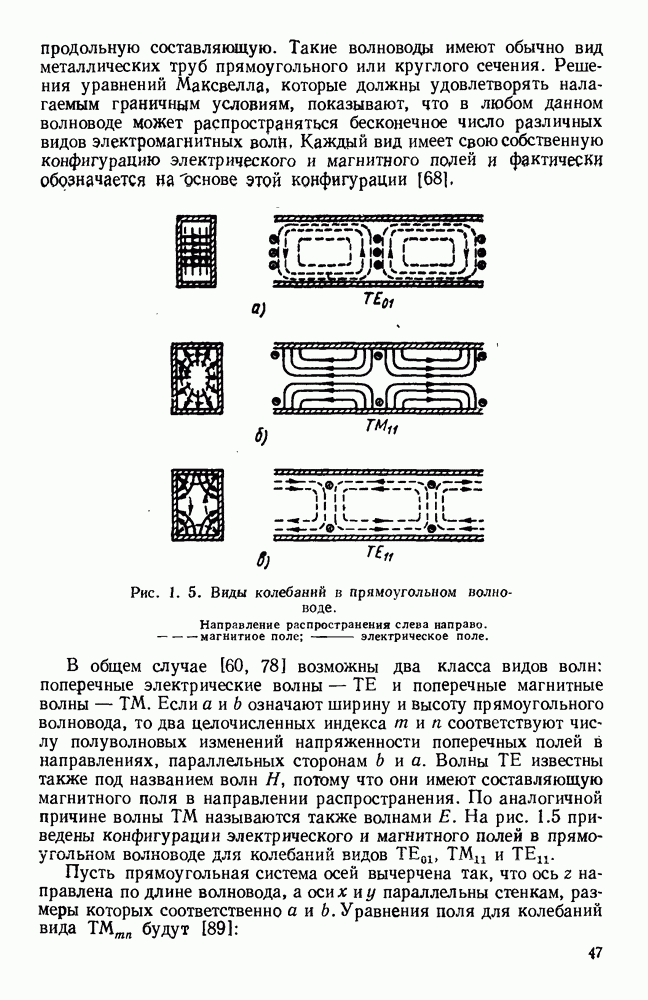
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
- 1.4.2. Круглые волноводы
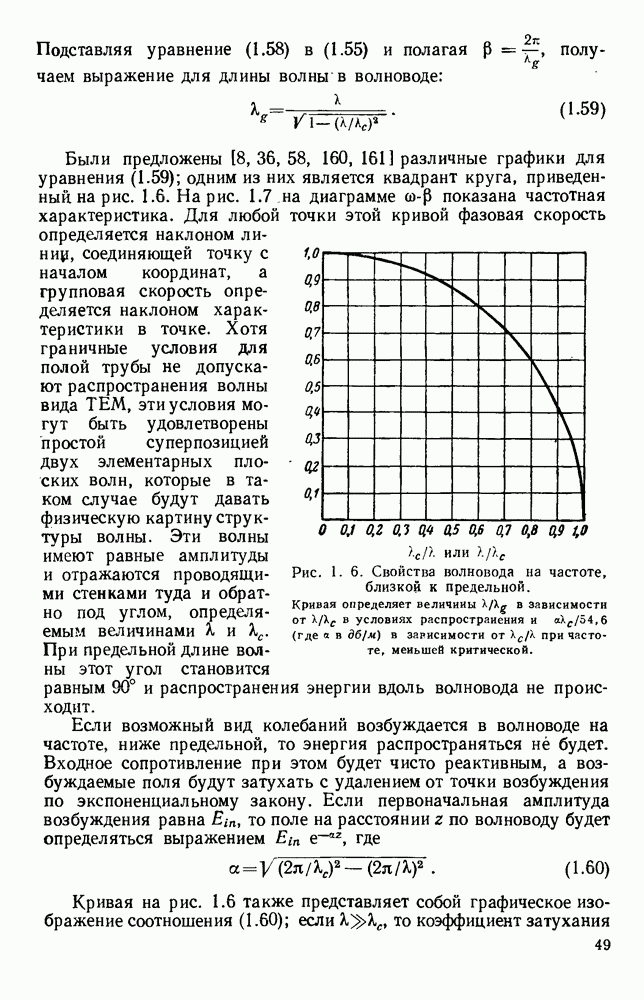
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
- 1.5.2. Гребневые волноводы
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
- 2.1.2. Круговая диаграмма
- 2.1.3. Широкополосное согласование
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
- 2.3.1. Прямоугольные волноводы
- 2.3.2. Круглые волноводы
- 2.3.3. Широкополосные и компактные волноводы
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
- 2.4.2. Контактные прокладки и дроссели
- 2.4.3. Крепежные и зажимные устройства
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
- 2.6.1. Изгибы, уголки и скрутки
- 2.6.2. Переходы и преобразователи
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
- 3.2.3. Переход от линейной поляризации к круговой
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
- 3.6.2. Вращающиеся сочленения различных типов
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
- 3.7.1. Механические переключатели с ручным управлением
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
- 5.2.1. Волномеры с объемными резонаторами
- 5.2.2. Волноводные интерферометры
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
- 5.3.2. Связанные резонаторы
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
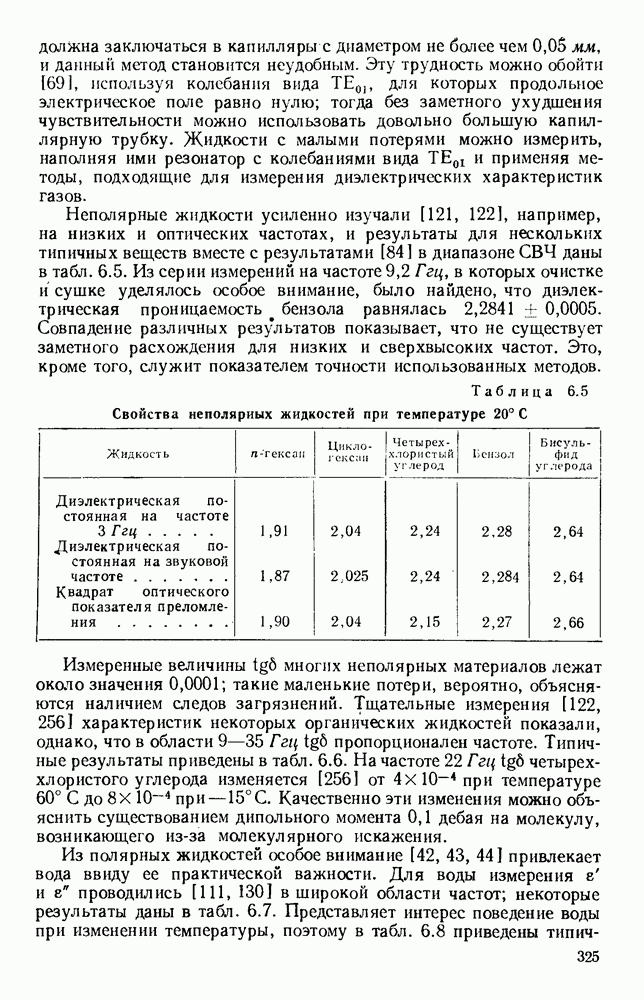
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
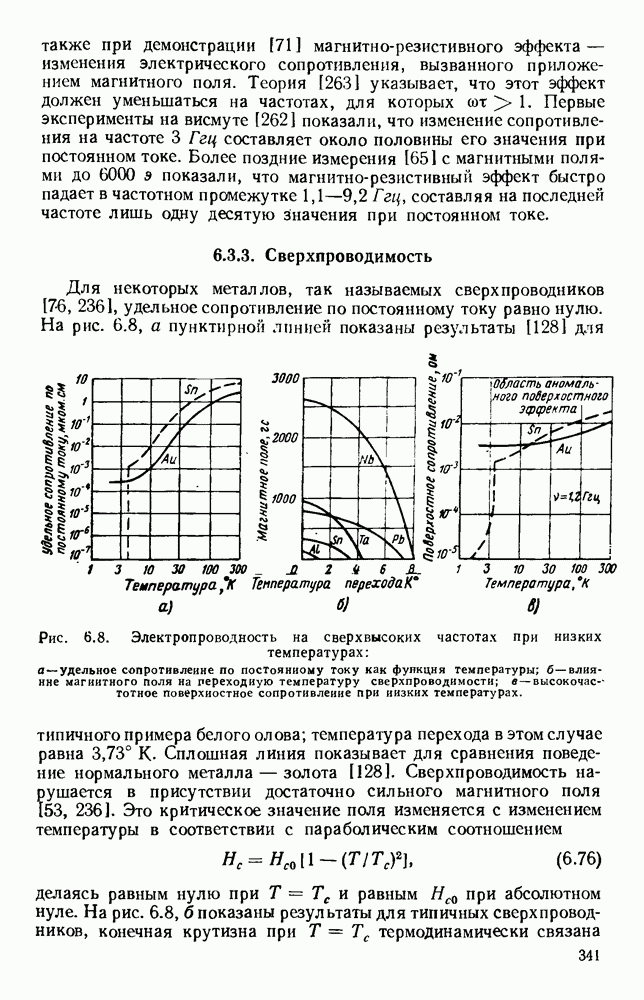
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
- 7.1.2. Форма линии и интенсивность
- 7.1.3. Сверхтонкая структура
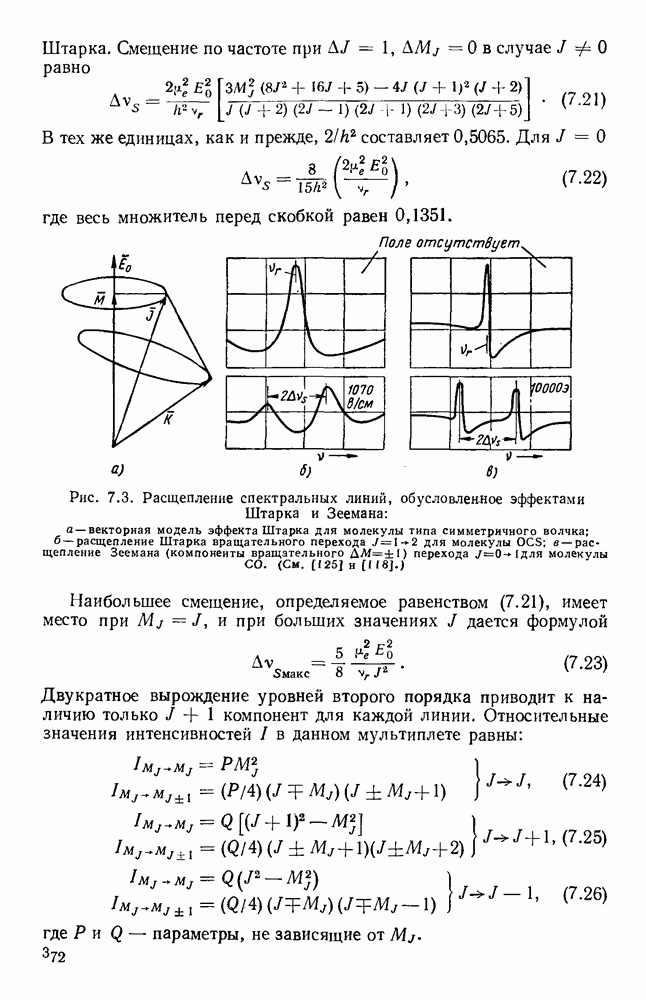
- 7.1.4. Явления Штарка и Зеемана
- 7.2. СПЕКТРОМЕТРЫ
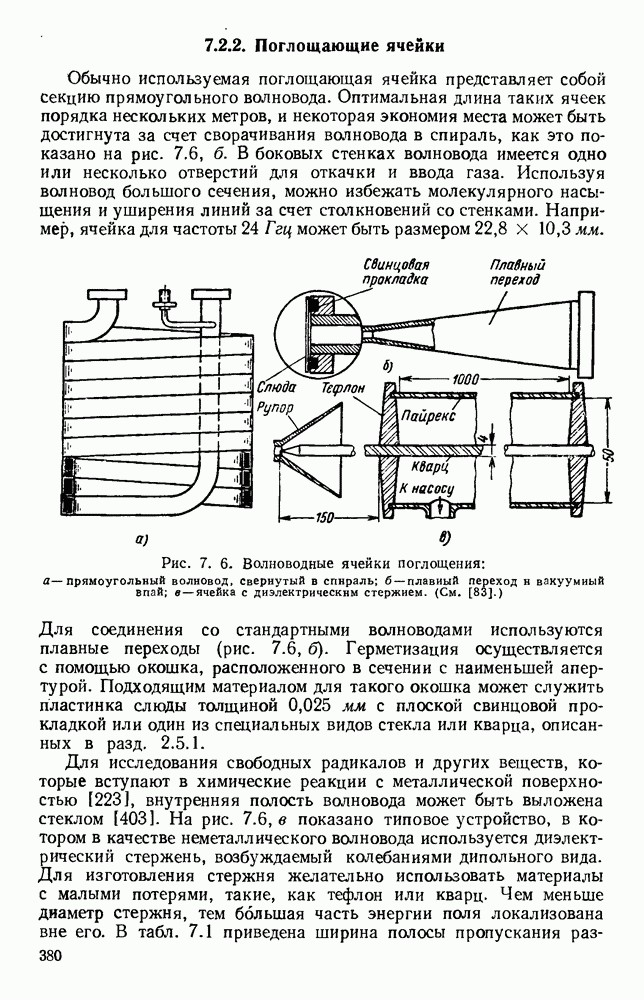
- 7.2.2. Поглощающие ячейки
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
- 7.3.4. Времена релаксации
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
- 8.3.3. Ферритовые устройства в качестве элементов схем
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
- 8.6.2. Устройства с поперечным полем
- 8.6.3. Прочие узлы
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.2.1. Линии типа «диэлектрических сэндвичей»
- 9.2.2. Симметричные линии с воздушным диэлектриком
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
- 9.4.2. Переходные устройства
- 9.4.3. Узлы полосковых систем
- 9.5. ЦЕПИ И СИСТЕМЫ
- 9.5.3. Частотные фильтры
- 9.5.4. Цепи питания антенн
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
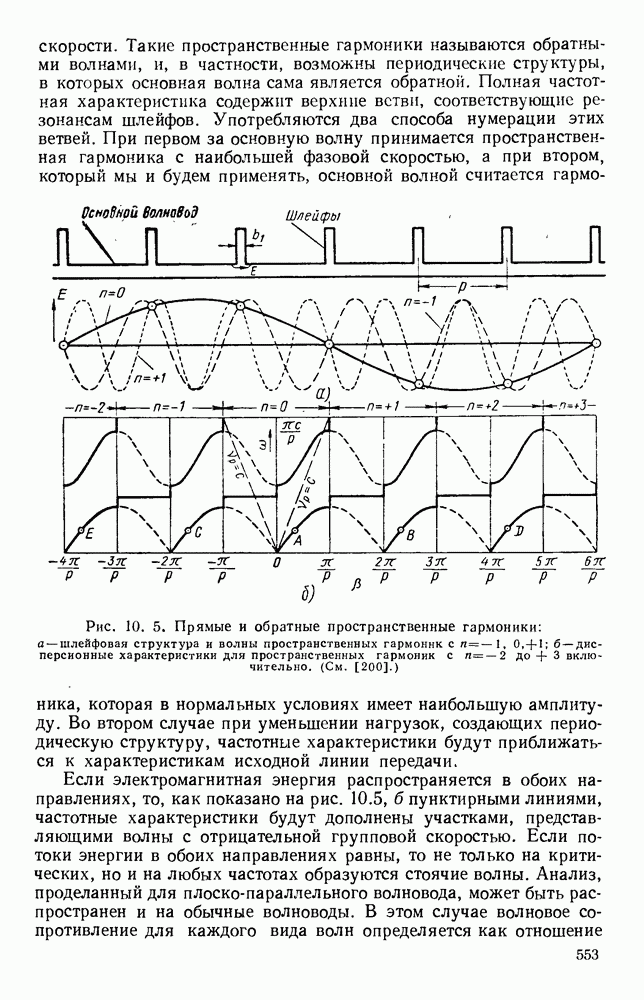
- 10.1.2. Пространственные гармоники
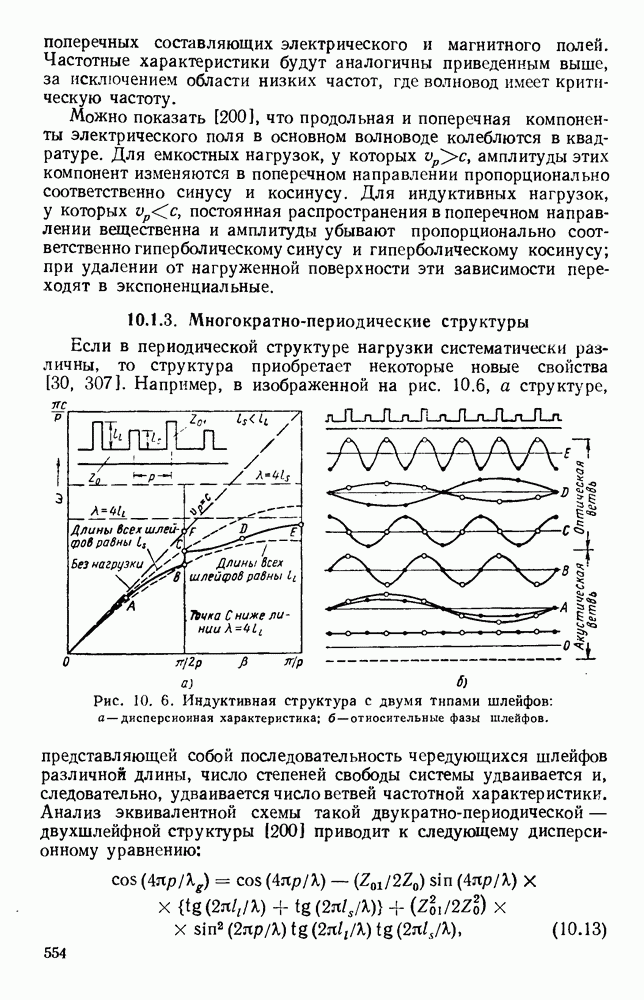
- 10.1.3. Многократно-периодические структуры
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
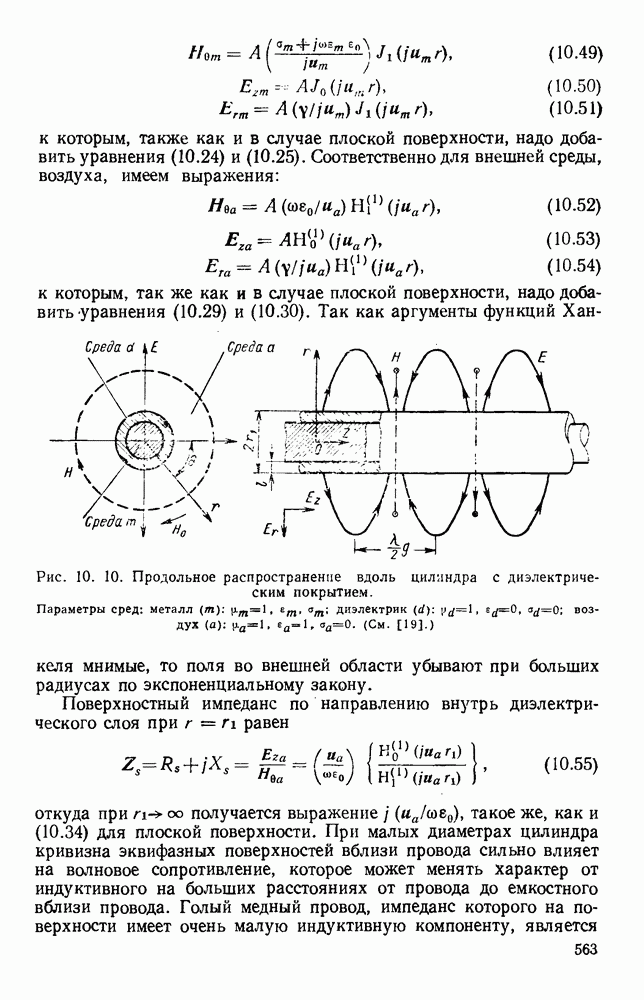
- 10.2.3. Продольные цилиндрические волны
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
- 12.2. МАГНЕТРОНЫ
- 12.2.2. Резонаторные системы
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
- 12.2.4. Рабочие характеристики
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
- 13.1.2. Типы дифракции
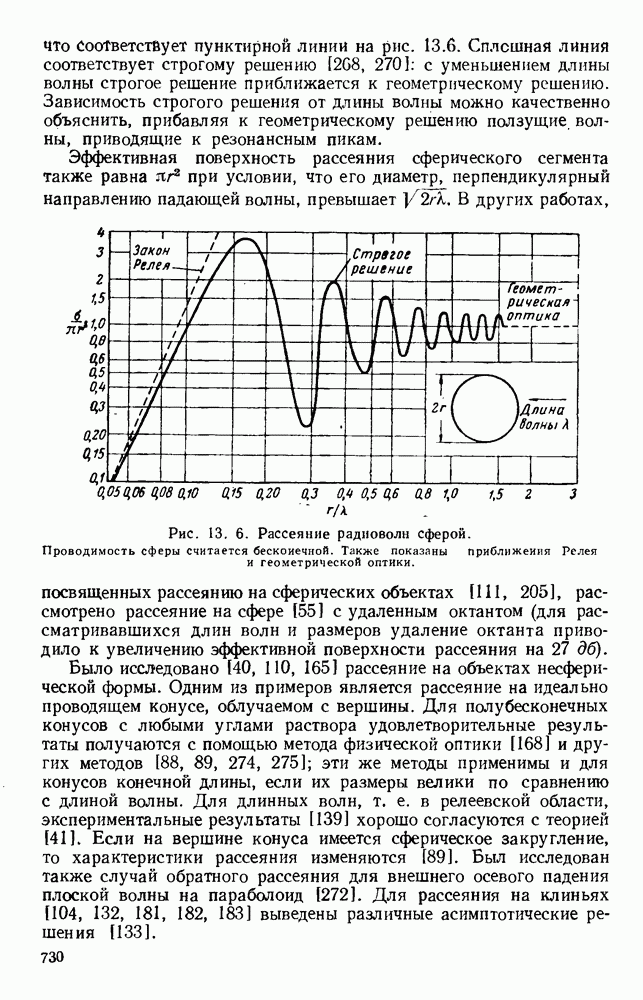
- 13.1.3. Рассеяние
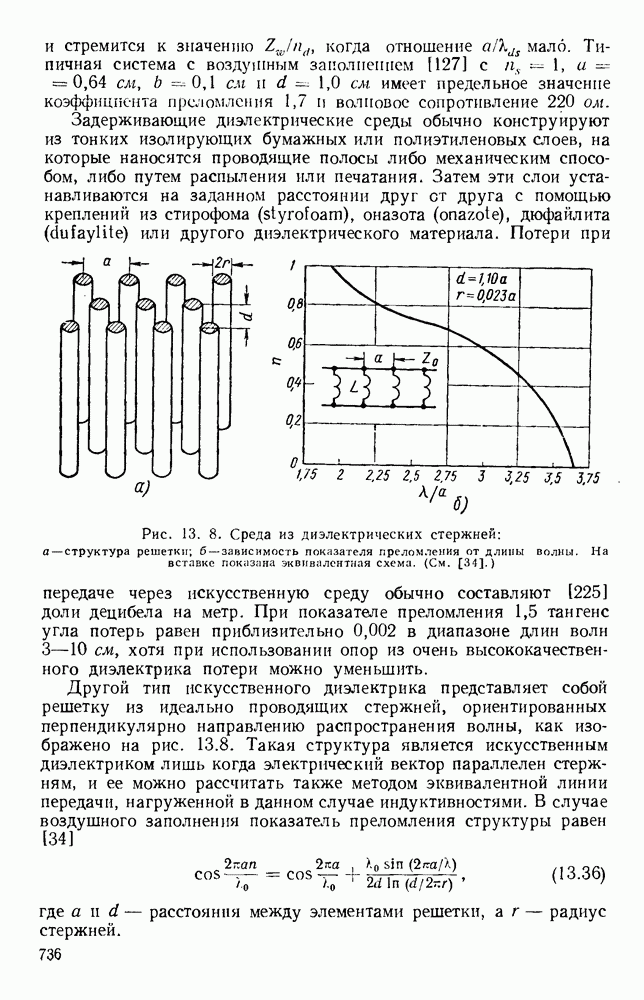
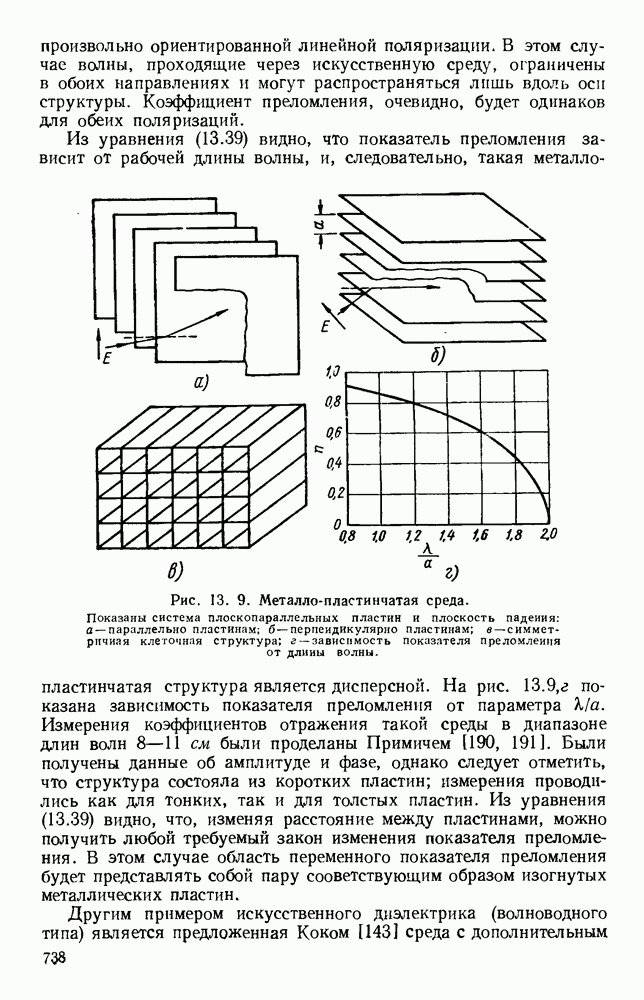
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
- 13.2.2. Структуры волноводного типа
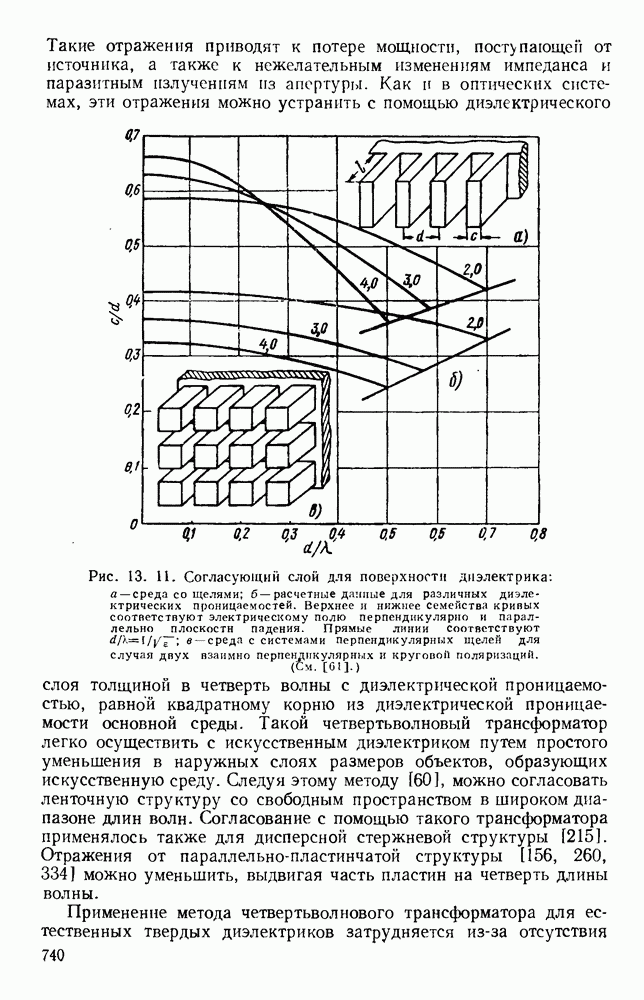
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
- 13.4. ПРИБОРЫ И СИСТЕМЫ
- 13.4.1. Спектрометры
- 13.4.2. Интерферометры
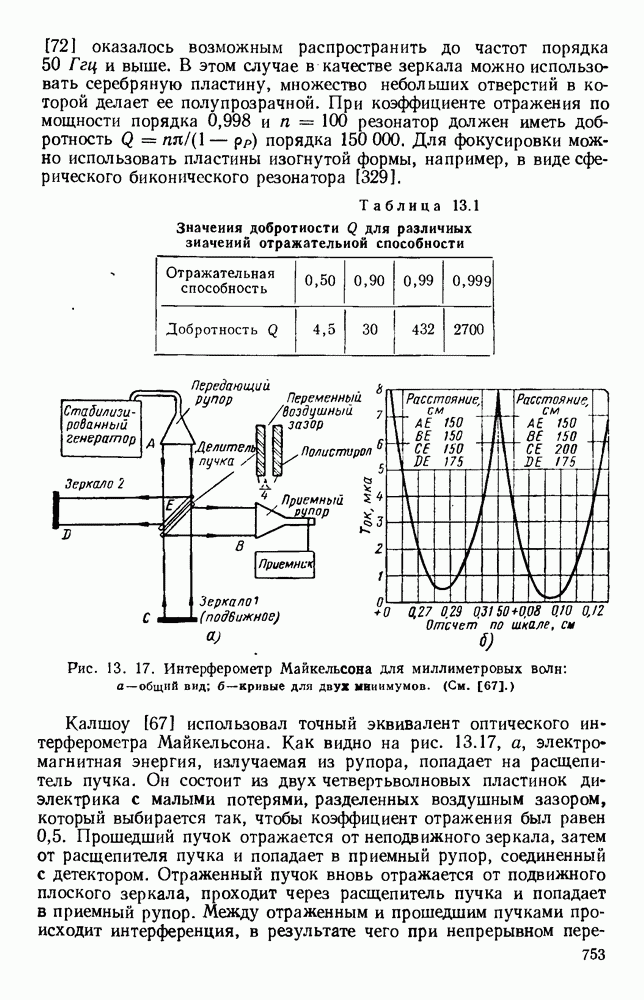
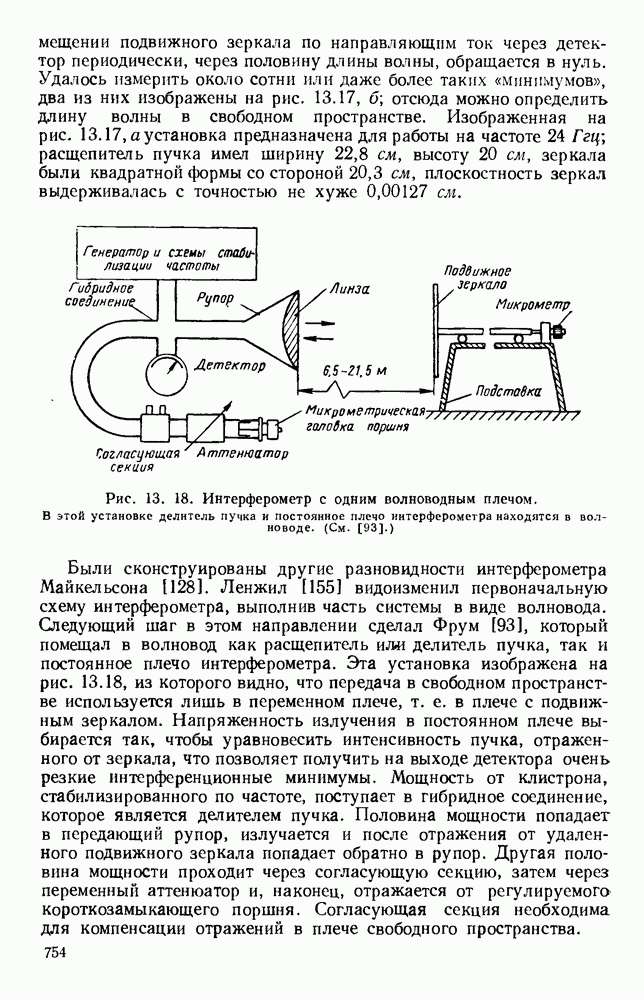
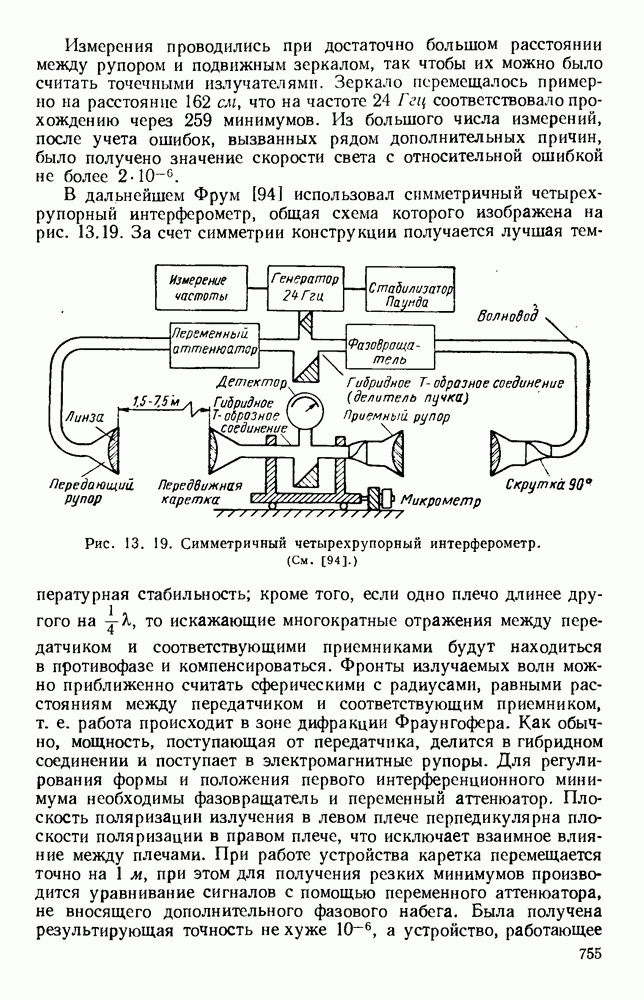
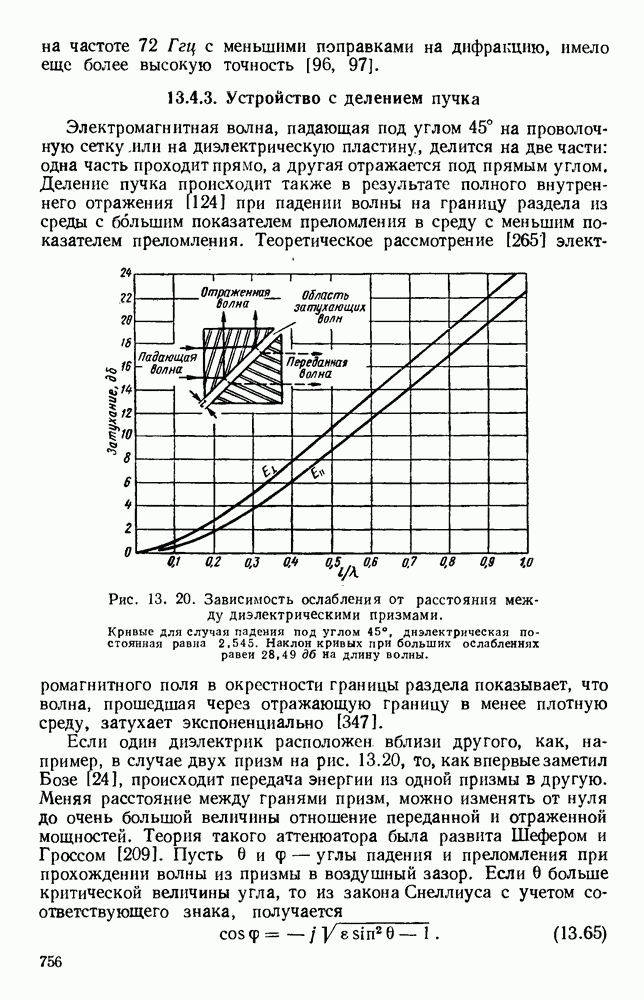
- 13.4.3. Устройство с делением пучка