| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.1.2. Форма линии и интенсивность
Естественная ширина и форма линий поглощения на сверхвысоких частотах подвержены влиянию многочисленных факторов, таких, как эффект Допплера, уширение за счет давления и столкновений и насыщение [285]. Естественная ширина линий с точки зрения классической теории определяется радиационным торможением [447], а с точки зрения квантовой механики — возмущением молекулы колебаниями электромагнитного поля свободного пространства. При обычных температурах основную роль играет поле теплового излучения. Естественная ширина линий в этом случае равна

где  квантовомеханический матричный элемент дипольного момента.
квантовомеханический матричный элемент дипольного момента.
При частоте излучаемых волн  из уравнения (7.6) имеем
из уравнения (7.6) имеем  гц. Если заключить газ в объемный резонатор, обладающий определенными собственными частотами, то многие переходы становятся запрещенными.
гц. Если заключить газ в объемный резонатор, обладающий определенными собственными частотами, то многие переходы становятся запрещенными.
Пусть молекула движется со скоростью  параллельно направлению распространения поглощаемого излучения. Тогда из-за эффекта Допплера происходит сдвиг частоты
параллельно направлению распространения поглощаемого излучения. Тогда из-за эффекта Допплера происходит сдвиг частоты  При максвелловском распределении по скоростям для молекул с молекулярным весом М форма линии определяется функцией
При максвелловском распределении по скоростям для молекул с молекулярным весом М форма линии определяется функцией

так что

Для  при частоте 24 Ггц и температуре 300° К ширина линии, определяемая эффектом Допплера, равна
при частоте 24 Ггц и температуре 300° К ширина линии, определяемая эффектом Допплера, равна  Допплеровское уширение уменьшается при увеличении веса молекул, при понижении температуры и в том случае, когда молекулярное движение ограничено направлениями, перпендикулярными волновому вектору излучения сверхвысоких частот.
Допплеровское уширение уменьшается при увеличении веса молекул, при понижении температуры и в том случае, когда молекулярное движение ограничено направлениями, перпендикулярными волновому вектору излучения сверхвысоких частот.
В области давлений, представляющих практический интерес, уширение линий связано главным образом с взаимодействием поглощающих частиц со своими ближайшими соседями. Детали процесса столкновения не имеют значения, поскольку время столкновения  мало по сравнению с периодом колебаний и средним временем между столкновениями.
мало по сравнению с периодом колебаний и средним временем между столкновениями.
Делалось много различных предположений [129, 328] относительно фазы и амплитуды колебаний частицы сразу после столкновения, но как классическое [181, 467, 468] решение, так и квантовое [293], в предположении распределения Больцмана, хорошо согласуются с опытом. Результирующее выражение для формы линии имеет вид

где  Для относительно узких линий, какие обычно наблюдаются в сантиметровом диапазоне,
Для относительно узких линий, какие обычно наблюдаются в сантиметровом диапазоне,  и уравнение (7.8) переходит в функцию Лоренца:
и уравнение (7.8) переходит в функцию Лоренца:

которая имеет максимальное значенне  Величина
Величина  представляет собой общую ширину линии между точками с половинной мощностью.
представляет собой общую ширину линии между точками с половинной мощностью.
Интенсивность спектральной линии является функцией коэффициента поглощения, значение которого  для любой частоты определяется как
для любой частоты определяется как

Максимальный коэффициент поглощения на метр определяется выражением

где  соответствует температуре 300° К и давлению
соответствует температуре 300° К и давлению 
Доля молекул  находящихся в данном состоянии, определяется формулой Больцмана:
находящихся в данном состоянии, определяется формулой Больцмана:

Суммарная интенсивность линии равна

Эксперименты показали, что для кислорода формула (7.8) справедлива в области давлений от долей миллиметра ртутного столба [15, 198] вплоть до одной атмосферы [37, 317, 434]. Однако из результатов опытов с  следует, что «хвосты» линии 24 Ггц обладают значительно большей интенсивностью, чем определяемая по формуле (7.8). Для объяснения формы линии аммиака [44, 450] требуется, чтобы
следует, что «хвосты» линии 24 Ггц обладают значительно большей интенсивностью, чем определяемая по формуле (7.8). Для объяснения формы линии аммиака [44, 450] требуется, чтобы  оставалось приблизительно постоянным при давлениях свыше 30 см
оставалось приблизительно постоянным при давлениях свыше 30 см  и уменьшалось при давлениях свыше одной атмосферы [55, 420], что необходимо для выполнения равенства (7.8). Эти и подобные результаты 137] для
и уменьшалось при давлениях свыше одной атмосферы [55, 420], что необходимо для выполнения равенства (7.8). Эти и подобные результаты 137] для  объясняются взаимодействием [11, 270, 338] и многократными столкновениями [56, 59,313,314].
объясняются взаимодействием [11, 270, 338] и многократными столкновениями [56, 59,313,314].
Увеличение ширины линии может быть вызвано собственным уширением [284], посторонними молекулами [423] и уменьшением температуры [163]. При высоком давлении поглощение [46] имеет место в газах с неполярными молекулами. Столкновения молекул газа со стенками сосуда прерывают процесс поглощения, что приводит к уширению линий. Расчет [127] дает следующее значение ширины линии при 300° К:

где  соответственно полные поверхность и объем сосуда.
соответственно полные поверхность и объем сосуда.
Если поместить, например, аммиак между двумя параллельными плоскостями, разнесенными на  то
то  составит
составит  Уширения линий, вызванные разными процессами, складываются друг с другом так, что суммарная ширина линий, определяемая столкновениями и эффектом Допплера [136], будет задана следующим выражением:
Уширения линий, вызванные разными процессами, складываются друг с другом так, что суммарная ширина линий, определяемая столкновениями и эффектом Допплера [136], будет задана следующим выражением:

Поглощение монохроматического излучения газом представляет собой процесс, стремящийся нарушить тепловое равновесие между различными энергетическими состояниями. В сантиметровом диапазоне скорость обмена энергией между различными состояниями сравнима со скоростью ее поглощения. При низких давлениях и высоких плотностях энергии отклонение от теплового равновесия становится настолько заметным, что скорость поглощения оказывается независимой от плотности падающей энергии. При этих условиях насыщения верхние и нижние энергетические состояния заполнены одинаково и

где  плотность потока энергии.
плотность потока энергии.
Таким образом, максимальная поглощаемая мощность составляет один квант на молекулу за одно соударение, умноженный на вероятность нахождения молекулы после столкновения в низшем
энергетическом состоянии после столкновения. Уменьшение плотности потока энергии на сантиметр длины составляет

где  измеряется в
измеряется в  в дебаях и
в дебаях и  в мегагерцах.
в мегагерцах.
При неполном насыщении форма линии определяется выражением [293, 425]

которое при малых  переходит в (7.9). Эффект насыщения впервые наблюдался и был наиболее полно исследован на аммиаке [59,450]. Эксперименты с этим газом подтвердили справедливость уравнения (7.18), соответственно модифицированного при наличии объемного резонатора [59] и волновода [99]. Хорошее согласие теории [291, 292] и эксперимента [376] получено также при очень низких давлениях, когда существенно уширение линий из-за эффекта Допплера.
переходит в (7.9). Эффект насыщения впервые наблюдался и был наиболее полно исследован на аммиаке [59,450]. Эксперименты с этим газом подтвердили справедливость уравнения (7.18), соответственно модифицированного при наличии объемного резонатора [59] и волновода [99]. Хорошее согласие теории [291, 292] и эксперимента [376] получено также при очень низких давлениях, когда существенно уширение линий из-за эффекта Допплера.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
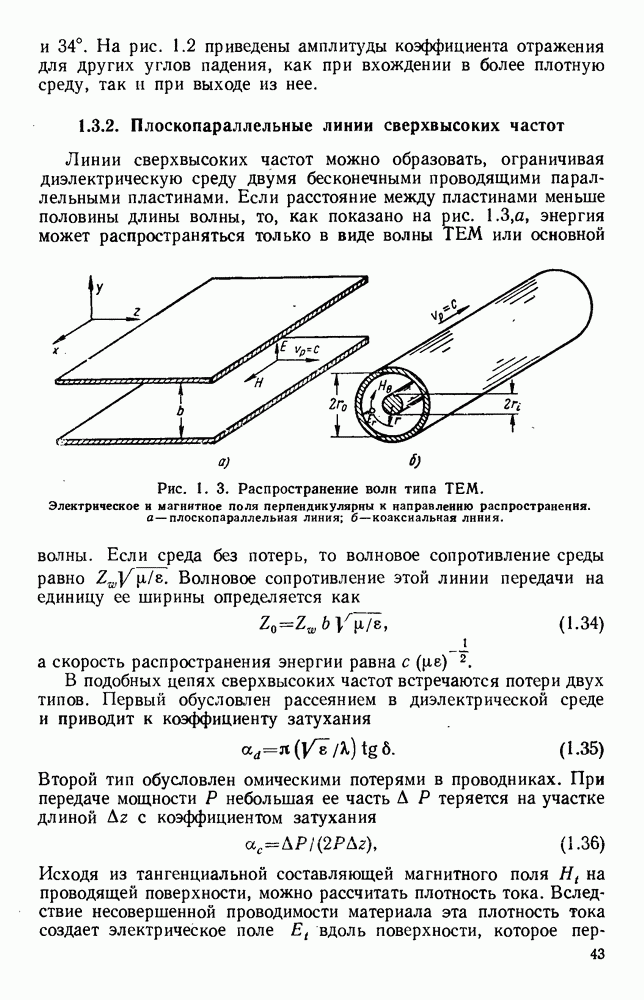
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
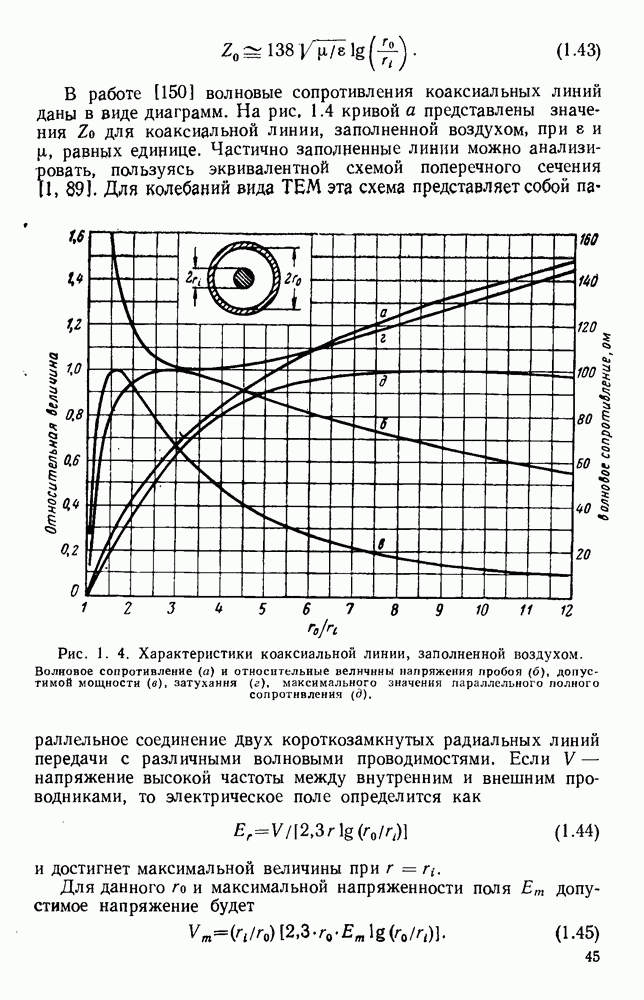
- 1.3.3. Коаксиальные линии
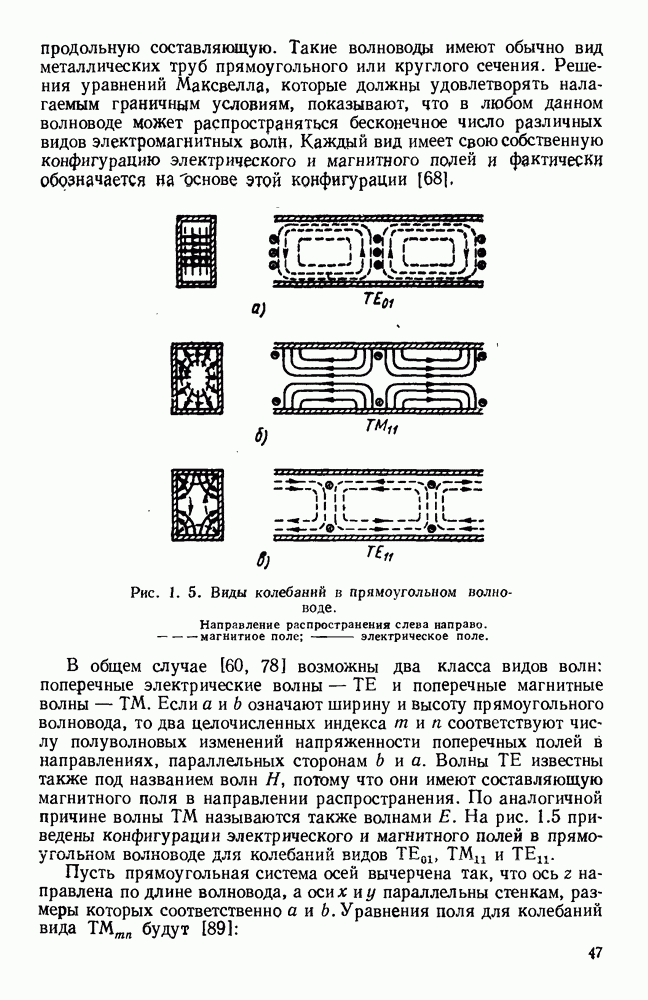
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
- 1.4.2. Круглые волноводы
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
- 1.5.2. Гребневые волноводы
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
- 2.1.2. Круговая диаграмма
- 2.1.3. Широкополосное согласование
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
- 2.3.1. Прямоугольные волноводы
- 2.3.2. Круглые волноводы
- 2.3.3. Широкополосные и компактные волноводы
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
- 2.4.2. Контактные прокладки и дроссели
- 2.4.3. Крепежные и зажимные устройства
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
- 2.6.1. Изгибы, уголки и скрутки
- 2.6.2. Переходы и преобразователи
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
- 3.2.3. Переход от линейной поляризации к круговой
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
- 3.6.2. Вращающиеся сочленения различных типов
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
- 3.7.1. Механические переключатели с ручным управлением
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
- 5.2.1. Волномеры с объемными резонаторами
- 5.2.2. Волноводные интерферометры
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
- 5.3.2. Связанные резонаторы
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
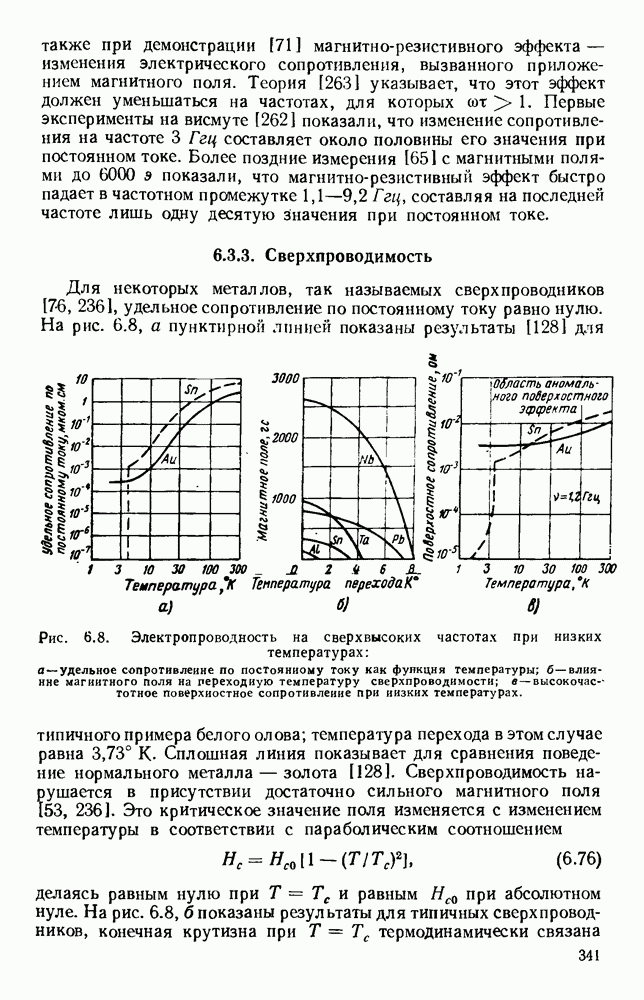
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
- 7.1.2. Форма линии и интенсивность
- 7.1.3. Сверхтонкая структура
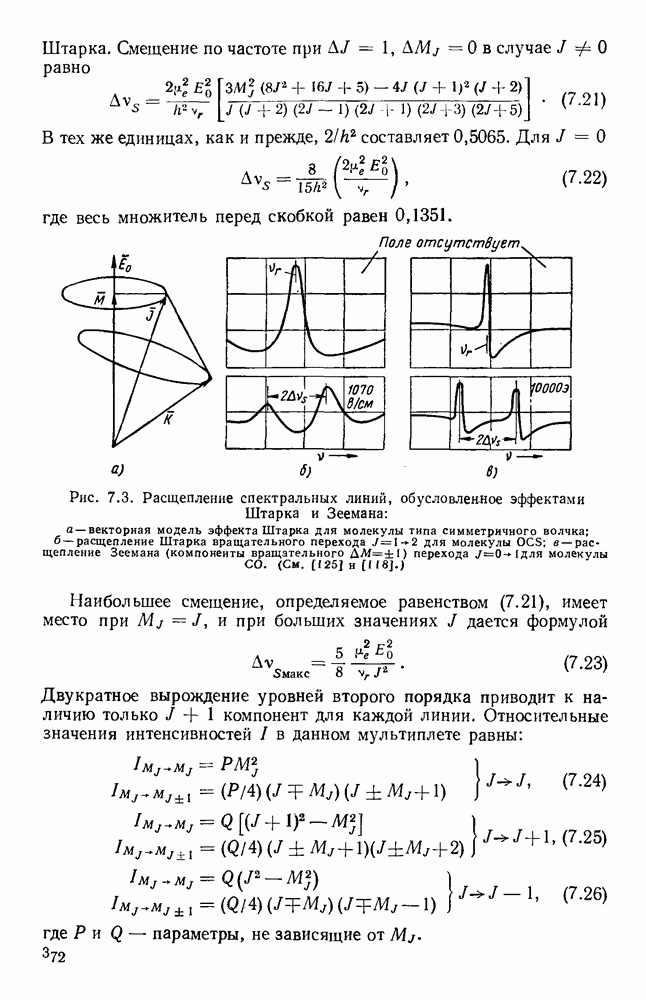
- 7.1.4. Явления Штарка и Зеемана
- 7.2. СПЕКТРОМЕТРЫ
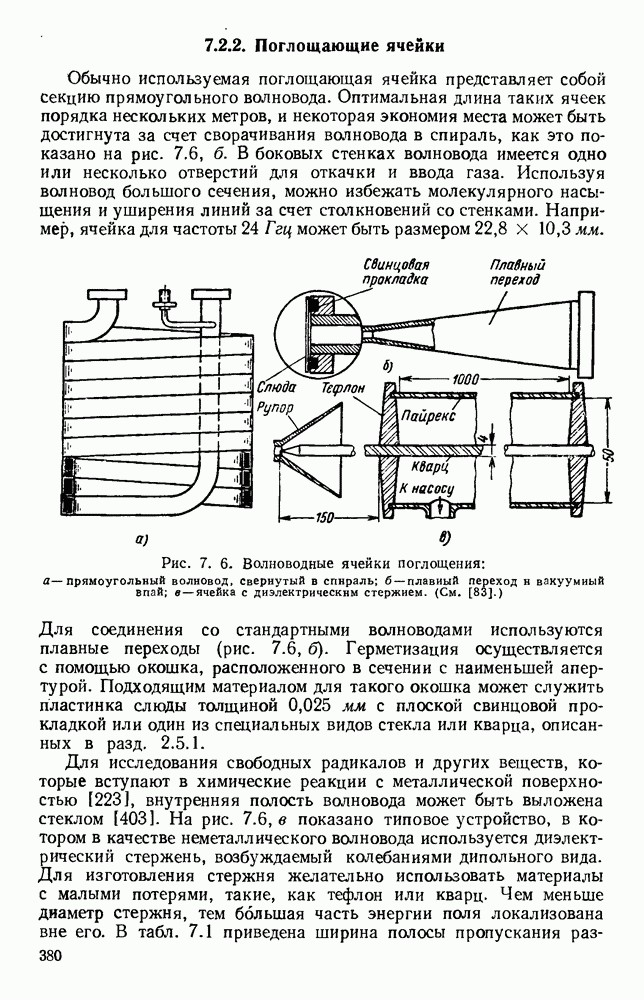
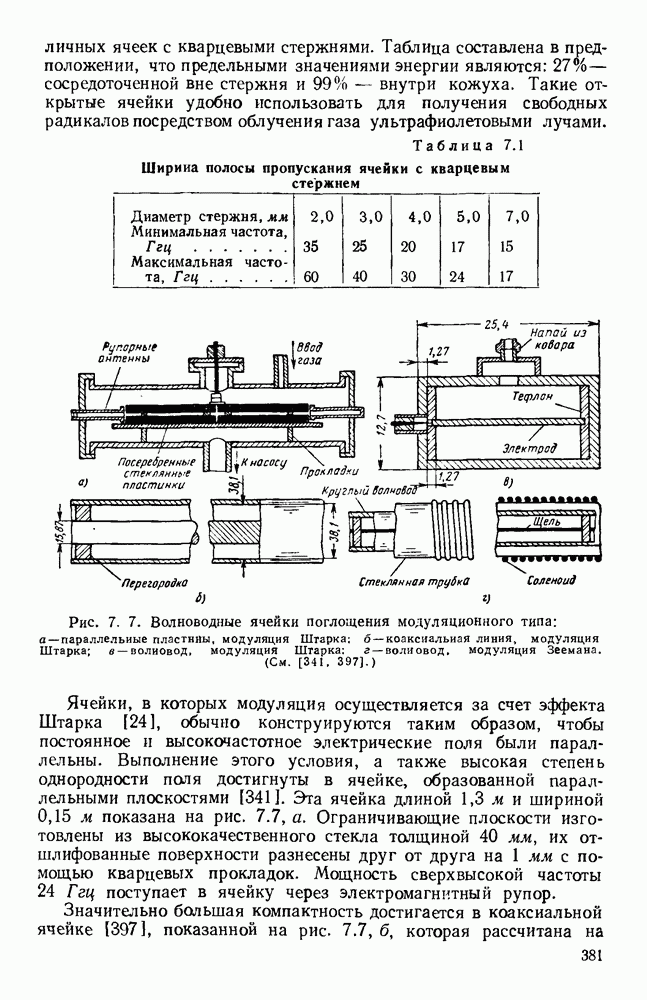
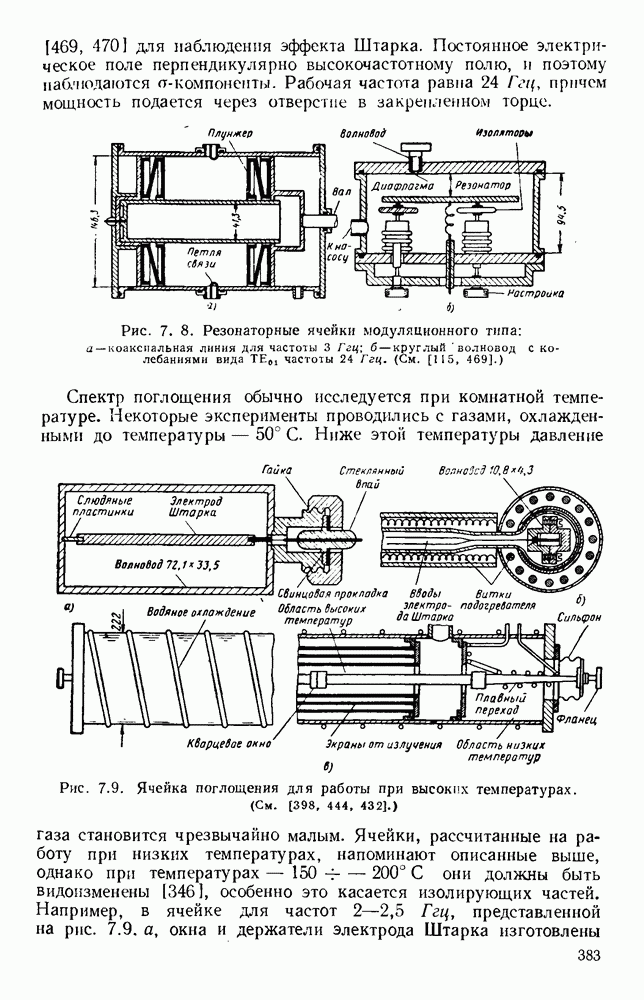
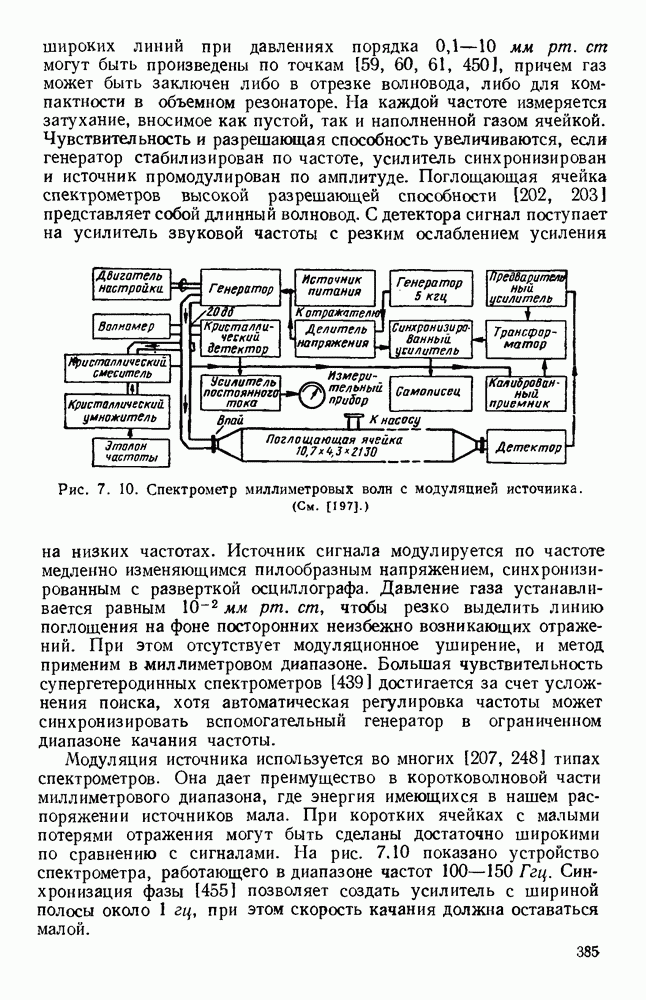
- 7.2.2. Поглощающие ячейки
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
- 7.3.4. Времена релаксации
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
- 8.3.3. Ферритовые устройства в качестве элементов схем
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
- 8.6.2. Устройства с поперечным полем
- 8.6.3. Прочие узлы
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.2.1. Линии типа «диэлектрических сэндвичей»
- 9.2.2. Симметричные линии с воздушным диэлектриком
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
- 9.4.2. Переходные устройства
- 9.4.3. Узлы полосковых систем
- 9.5. ЦЕПИ И СИСТЕМЫ
- 9.5.3. Частотные фильтры
- 9.5.4. Цепи питания антенн
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
- 10.1.2. Пространственные гармоники
- 10.1.3. Многократно-периодические структуры
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
- 10.2.3. Продольные цилиндрические волны
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
- 12.2. МАГНЕТРОНЫ
- 12.2.2. Резонаторные системы
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
- 12.2.4. Рабочие характеристики
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
- 13.1.2. Типы дифракции
- 13.1.3. Рассеяние
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
- 13.2.2. Структуры волноводного типа
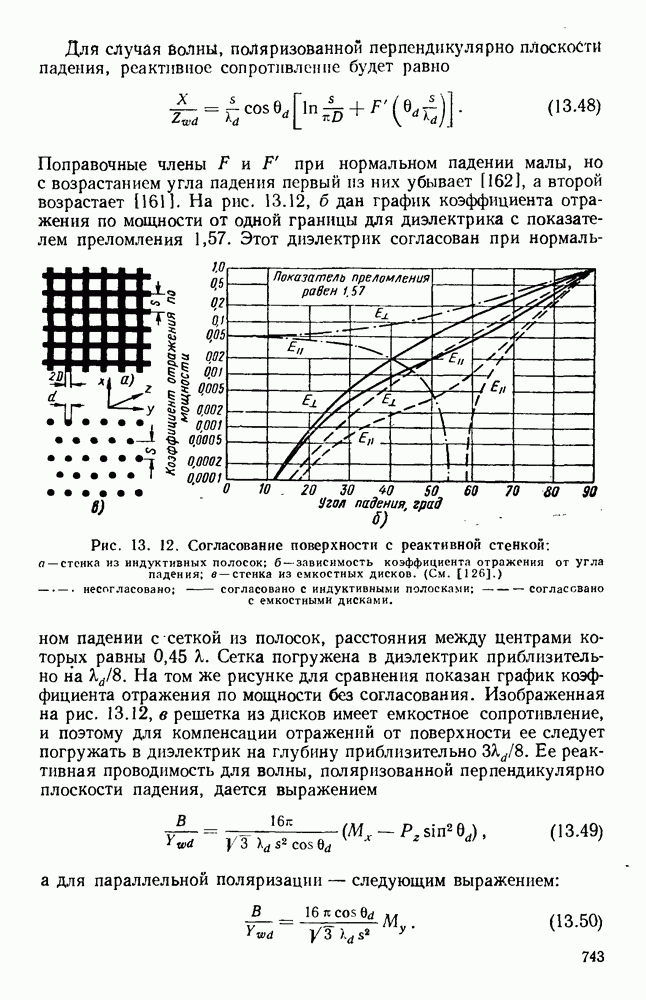
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
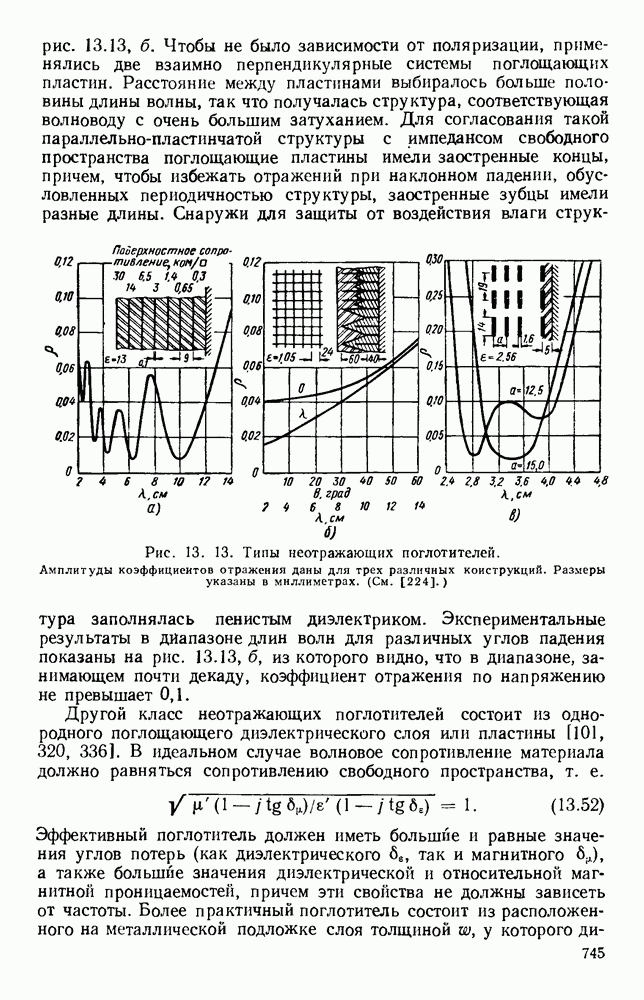
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
- 13.4. ПРИБОРЫ И СИСТЕМЫ
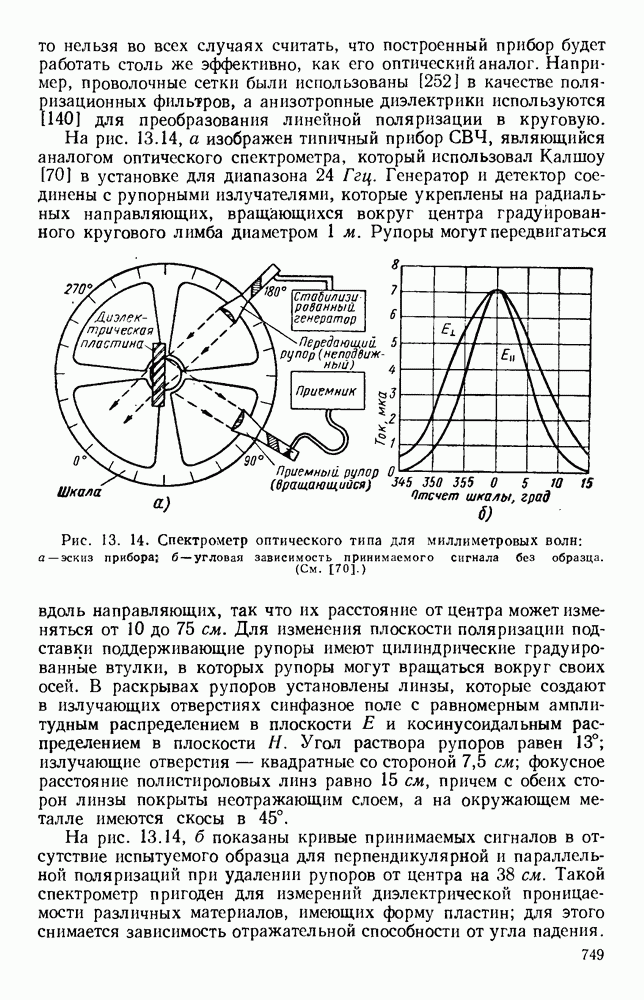
- 13.4.1. Спектрометры
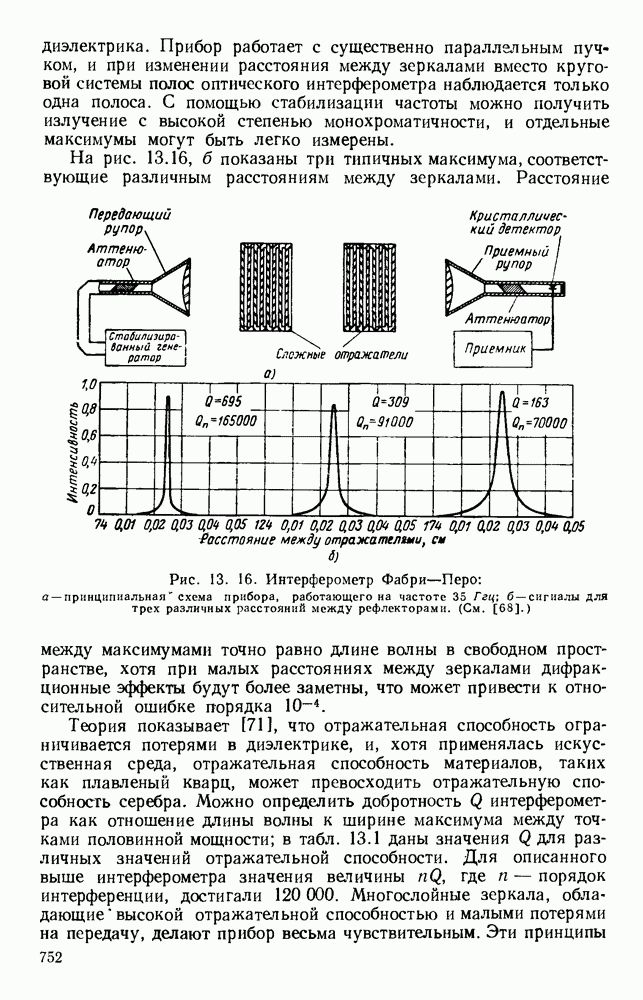
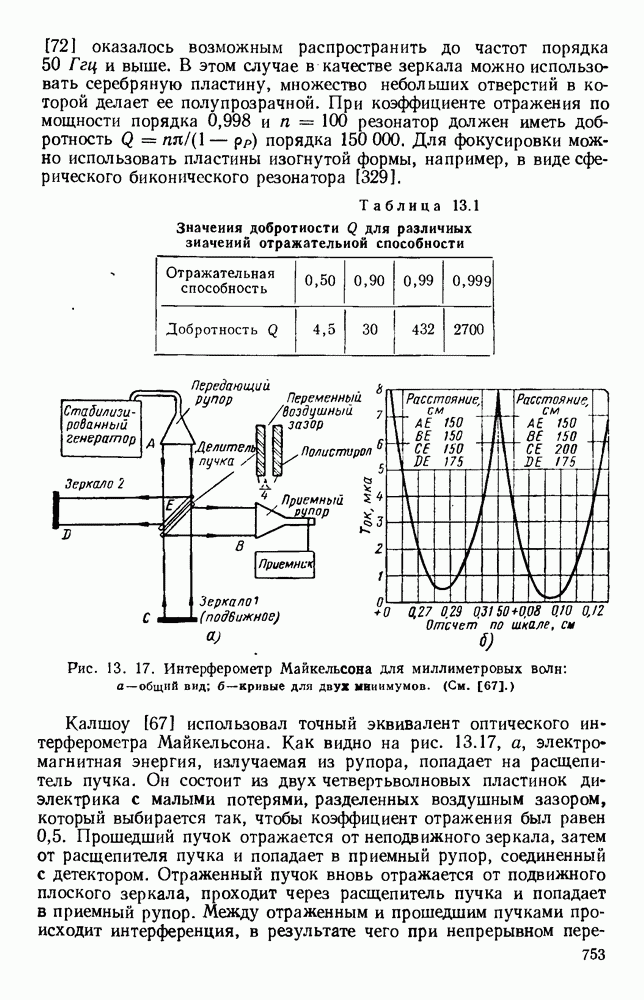
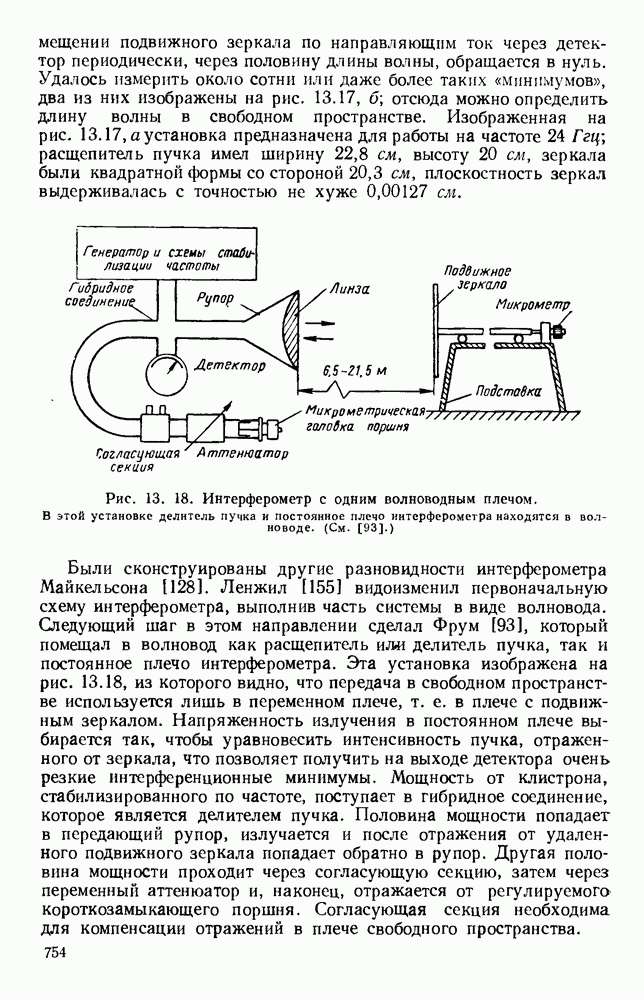
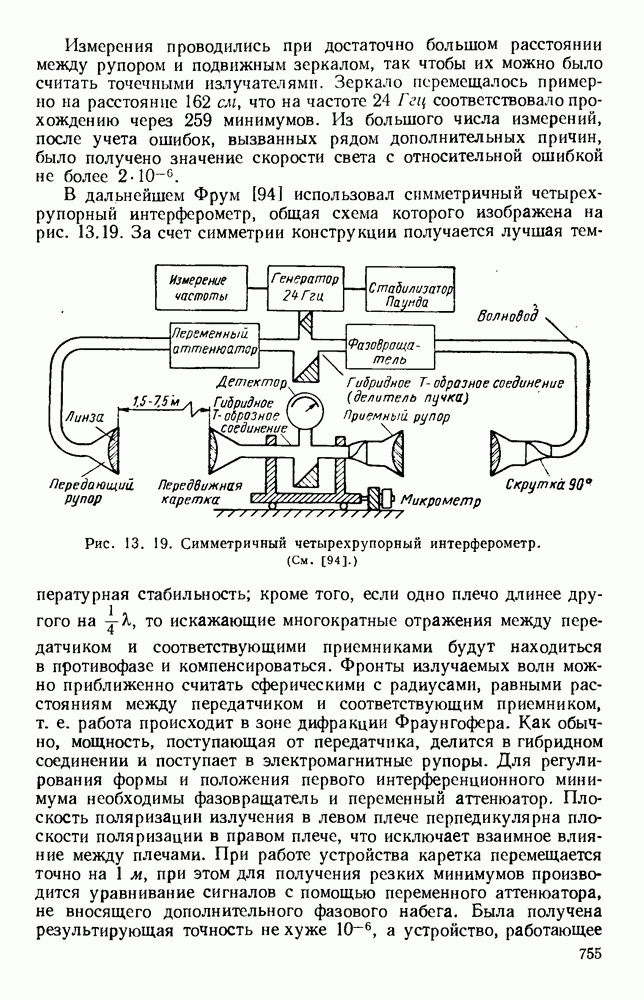
- 13.4.2. Интерферометры
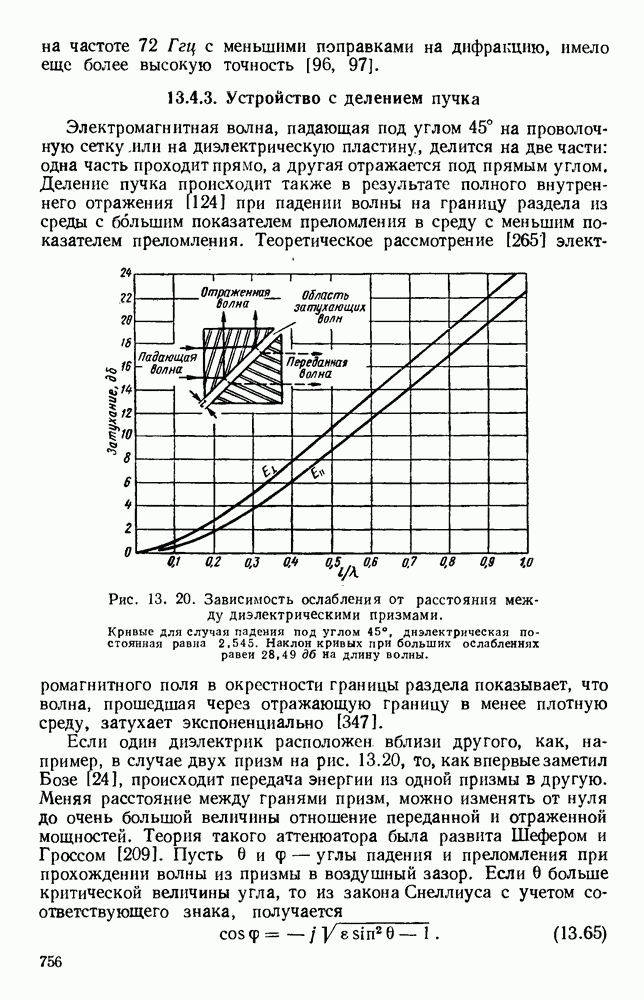
- 13.4.3. Устройство с делением пучка