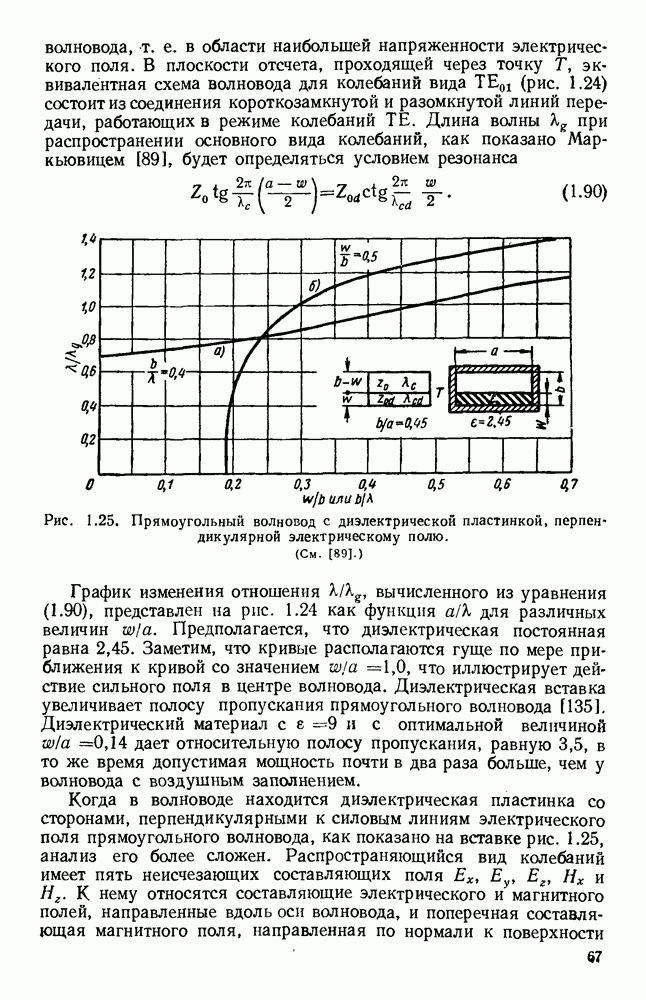
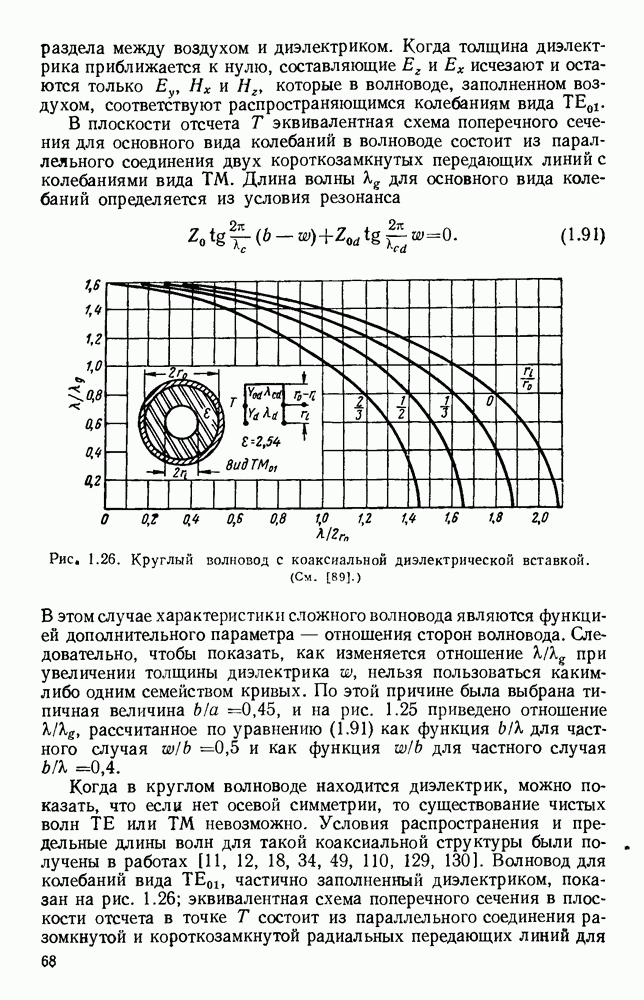
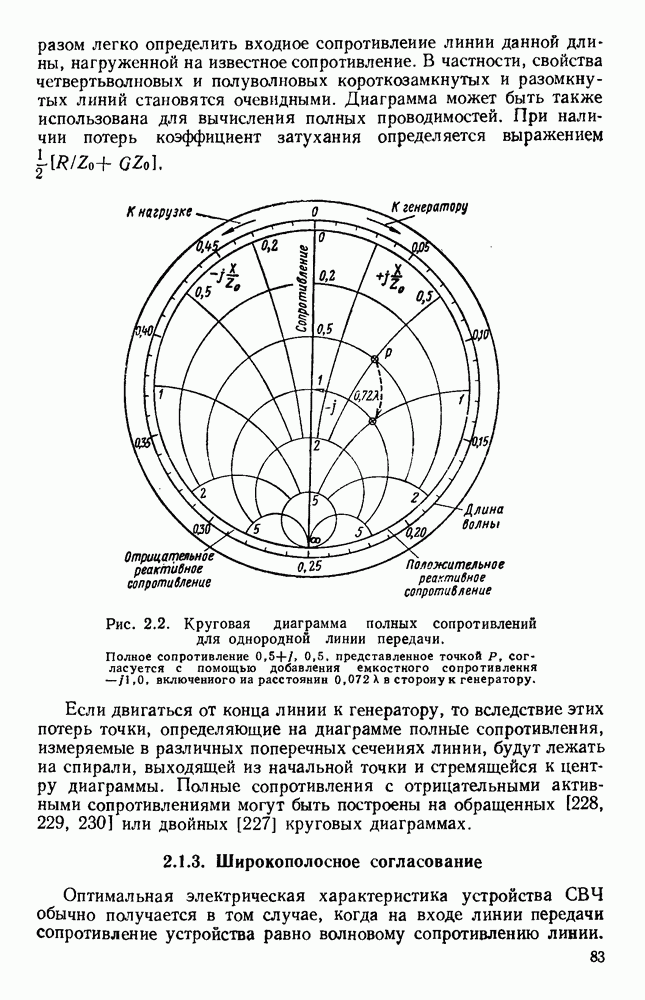
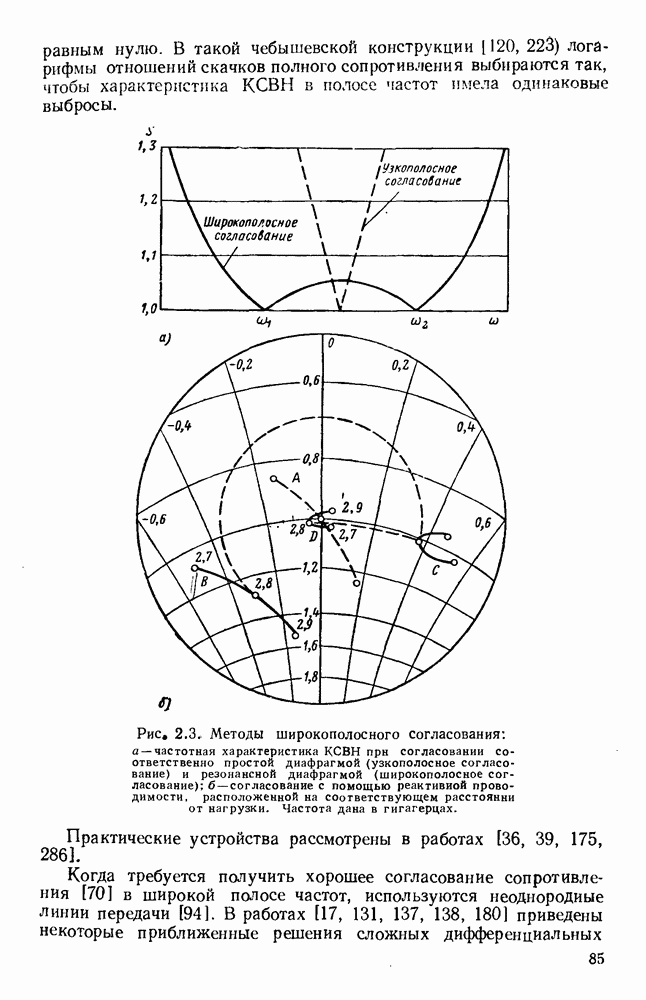
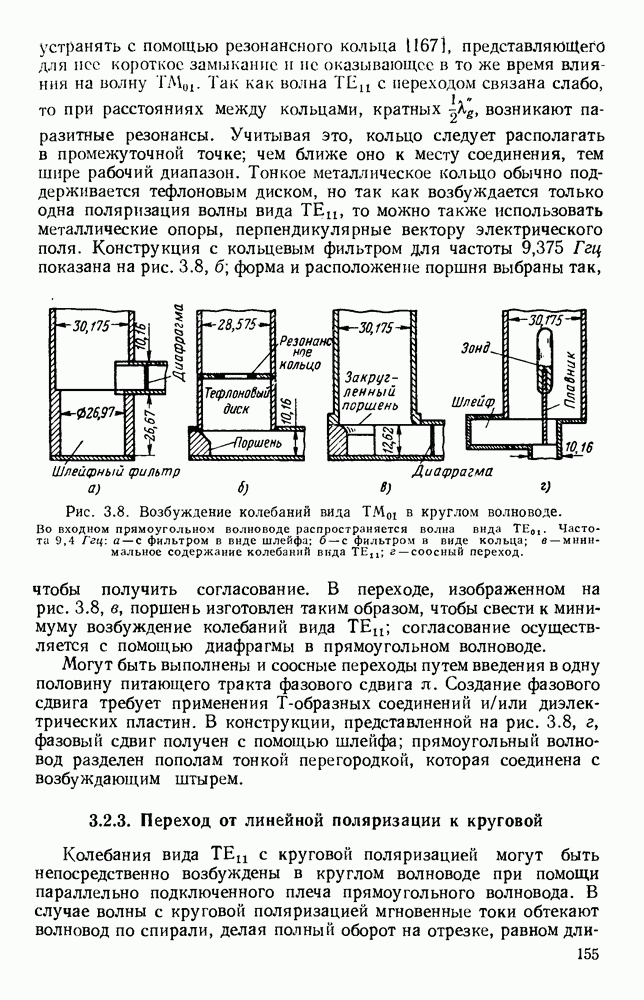
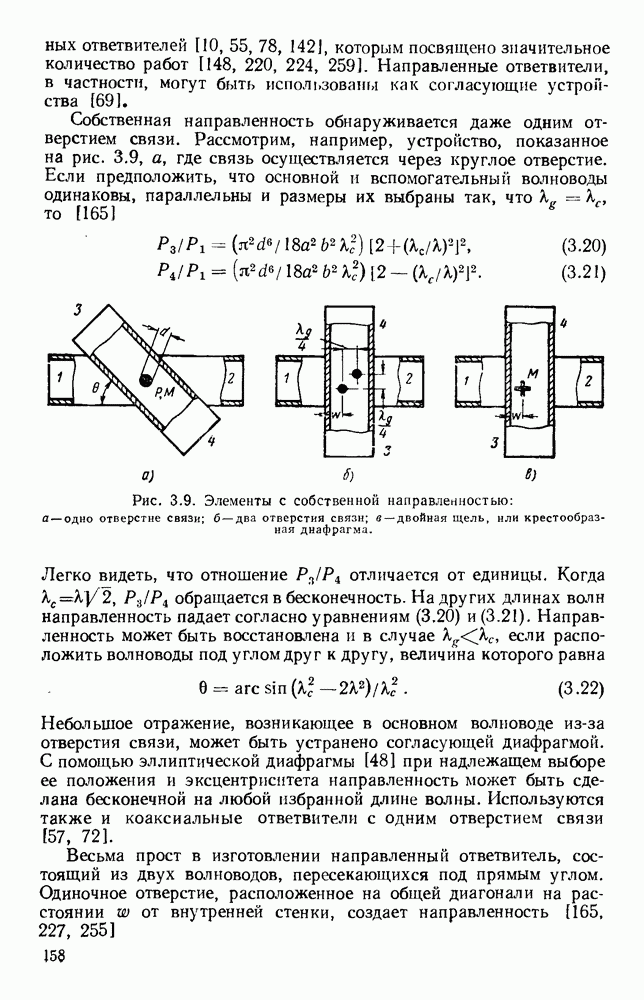
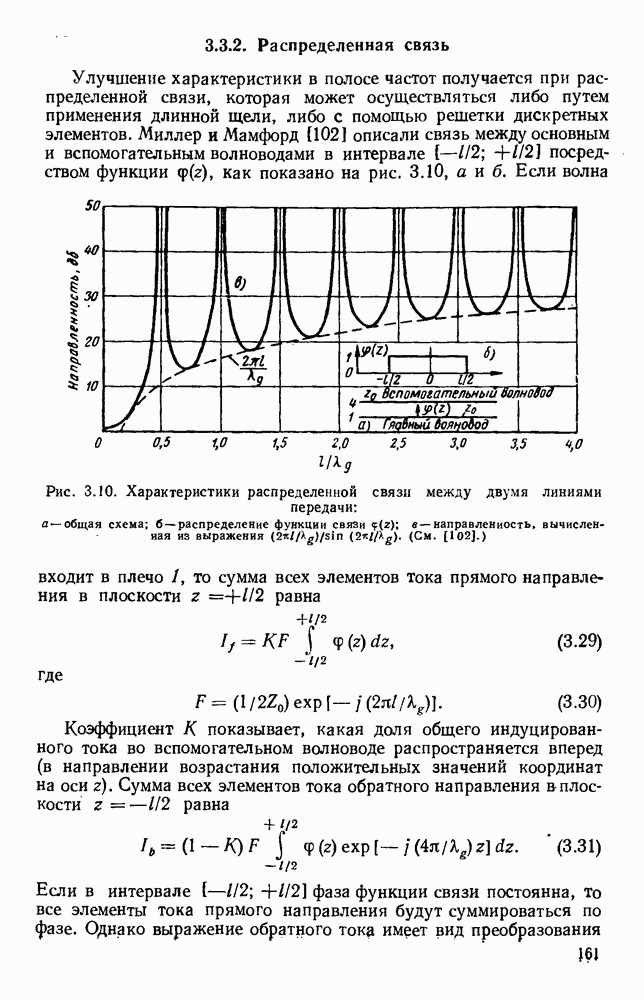
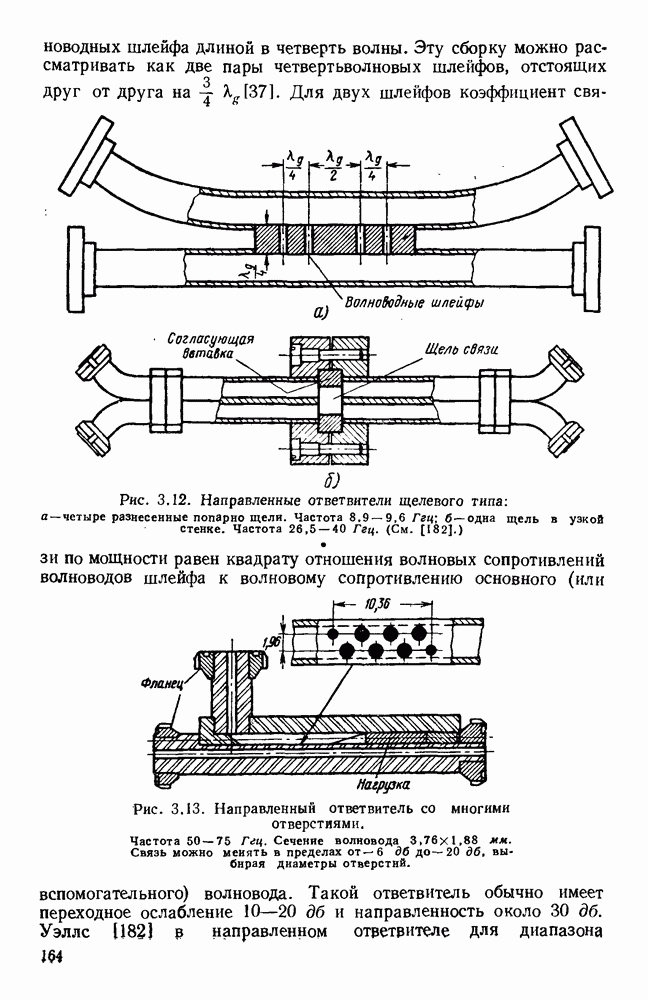
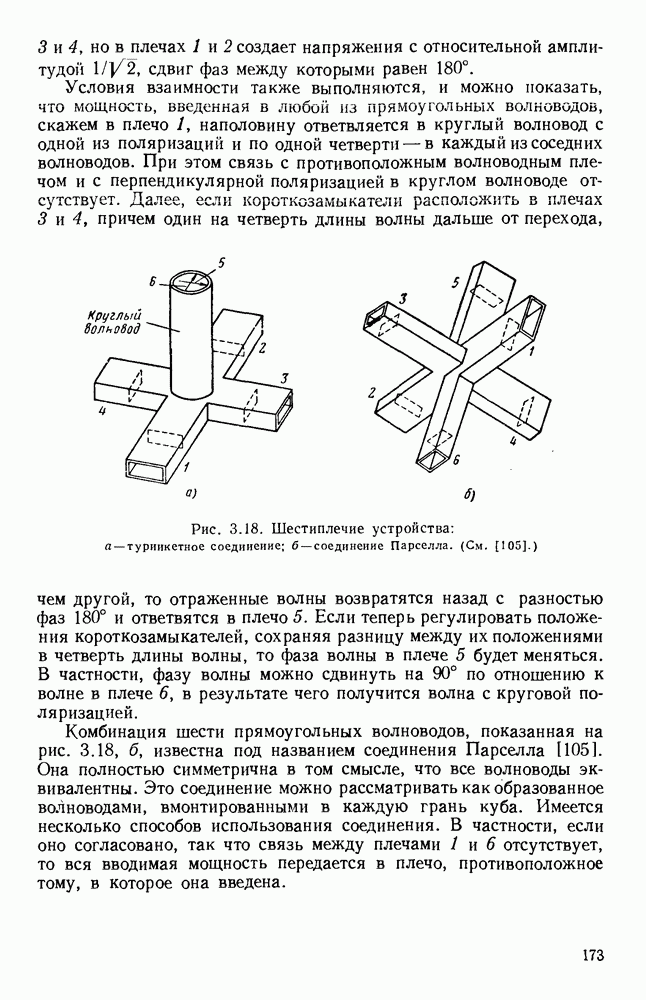
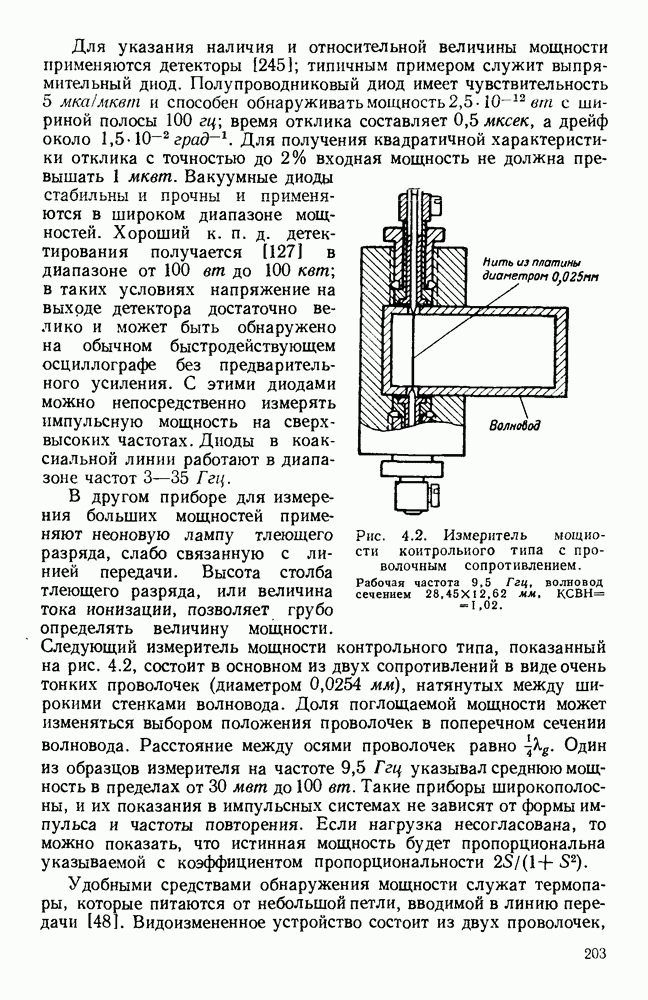
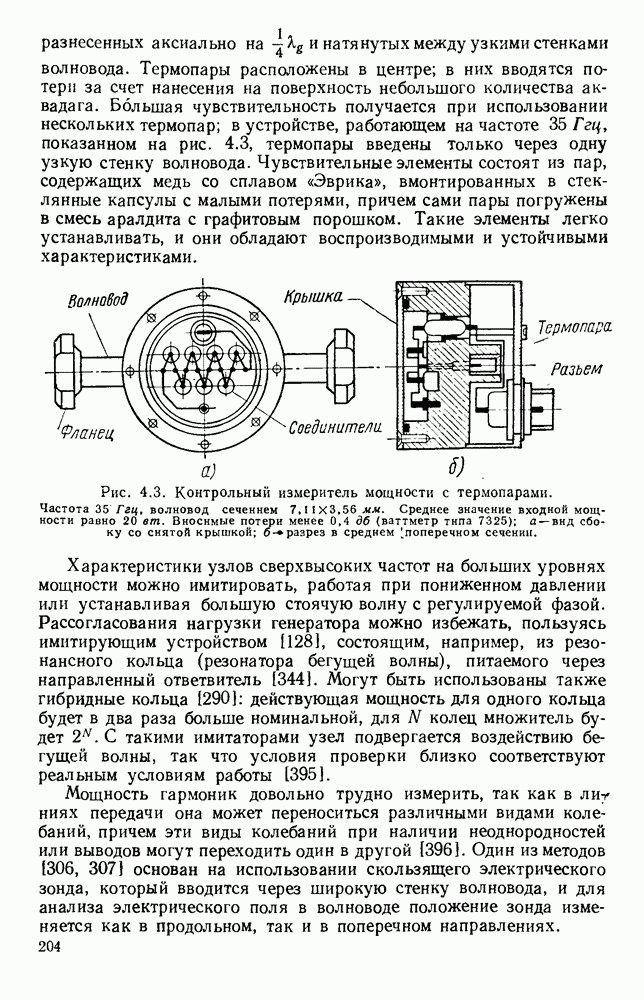
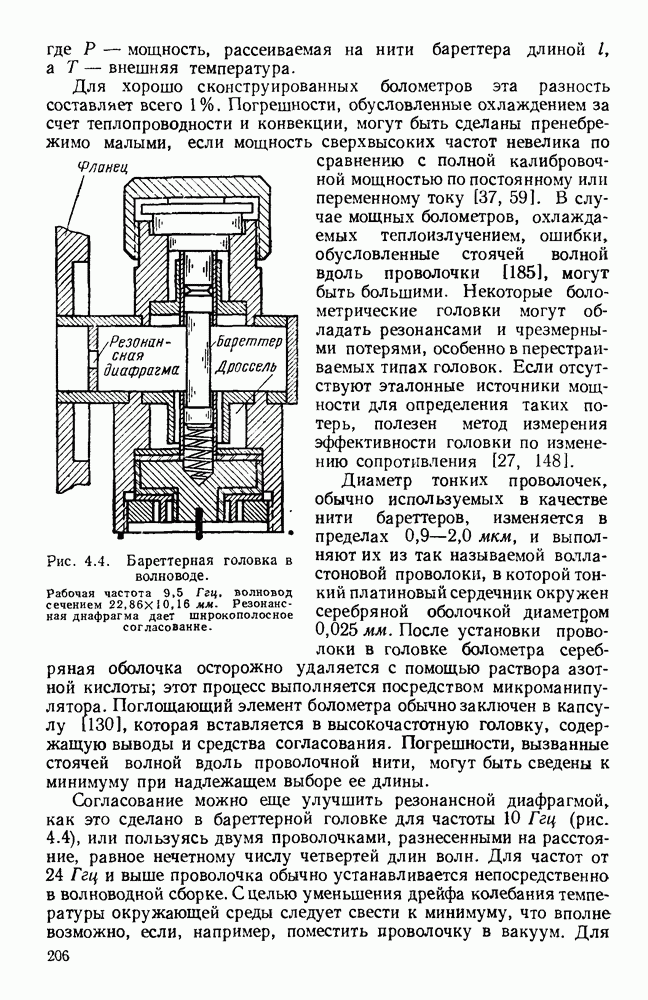
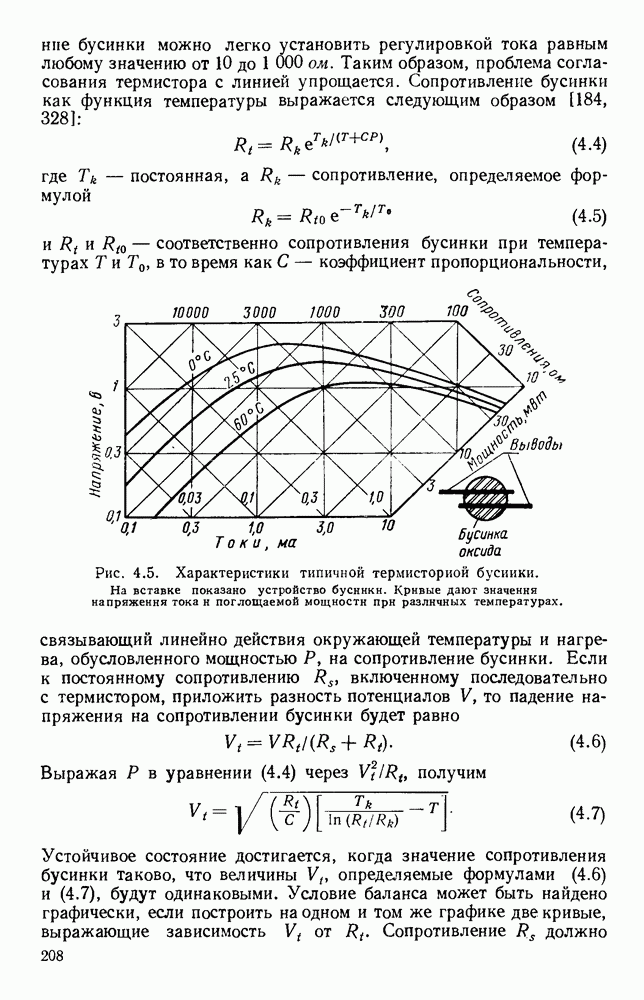
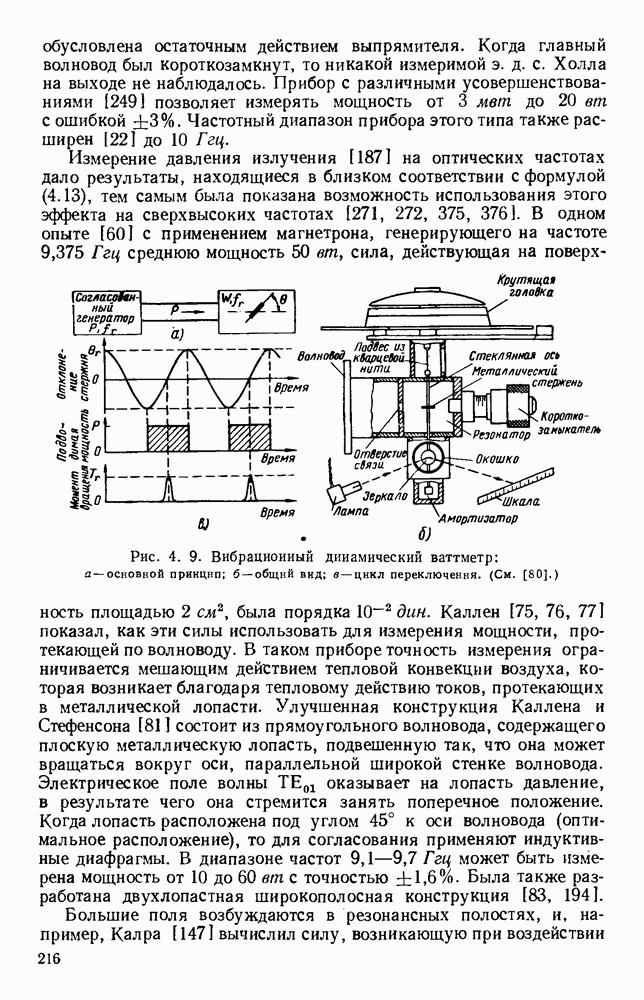
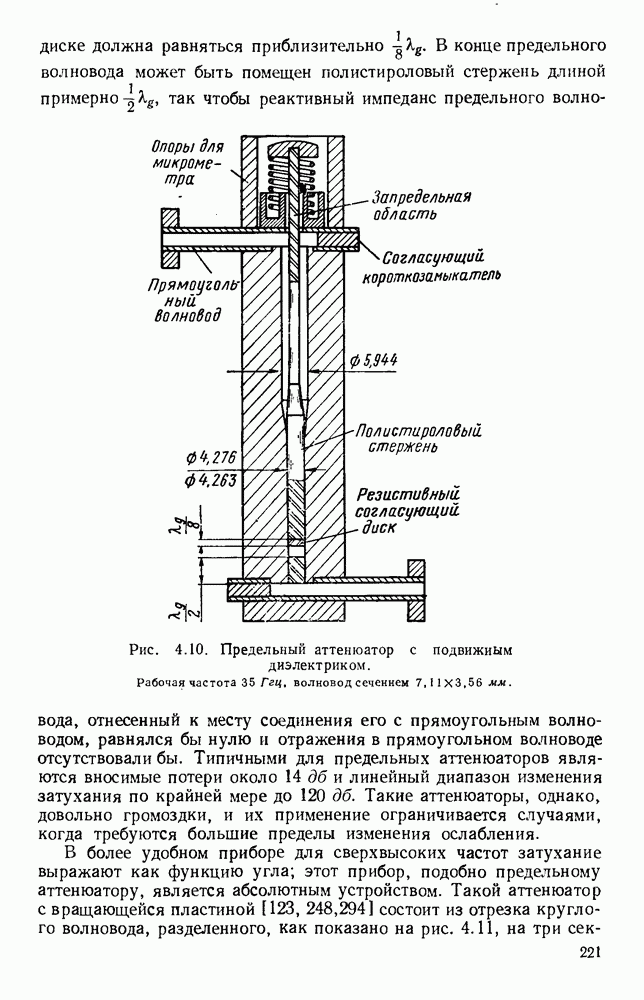
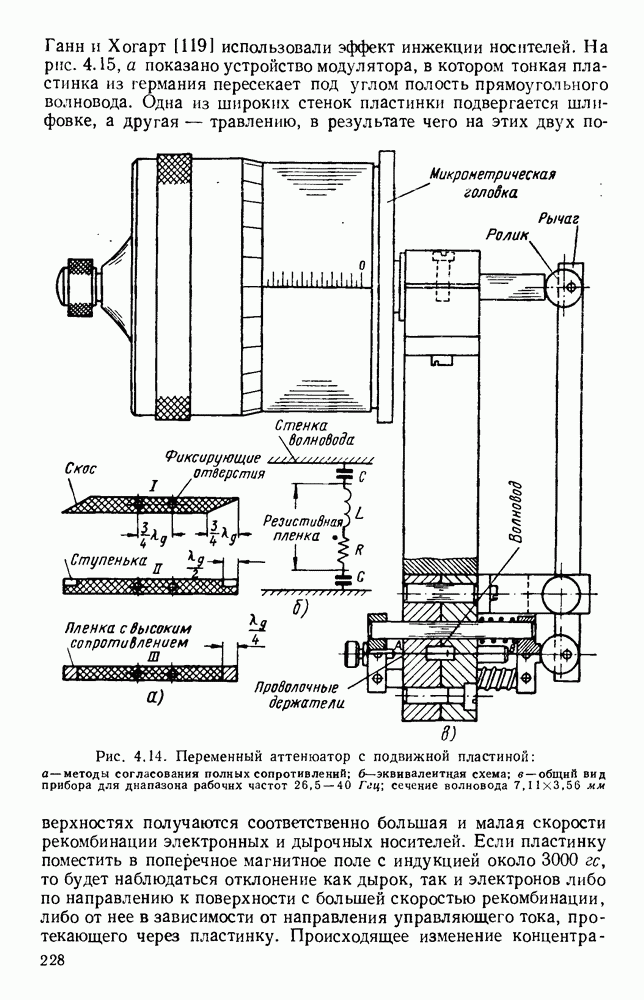
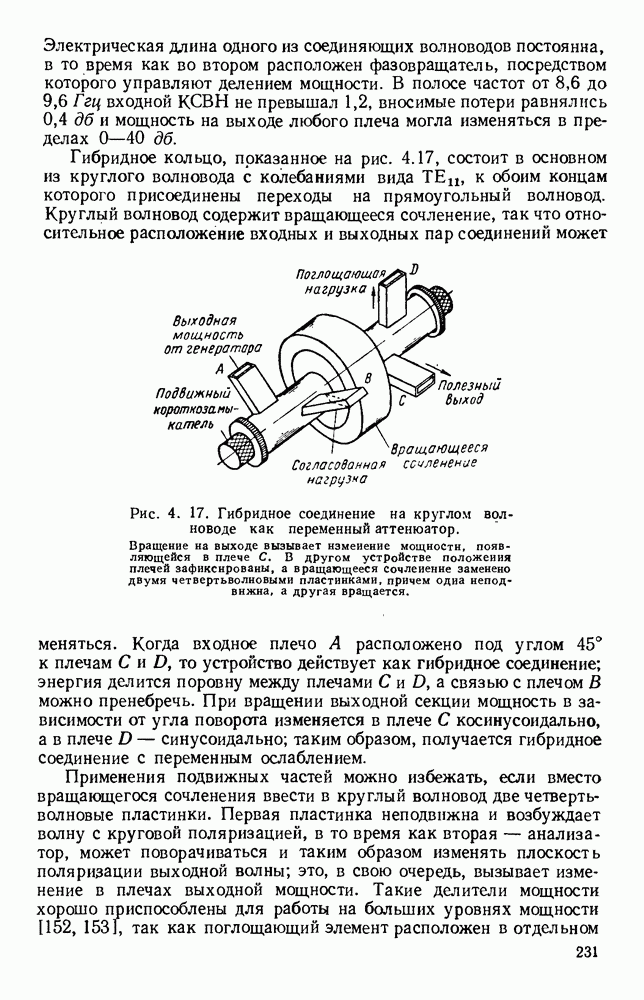
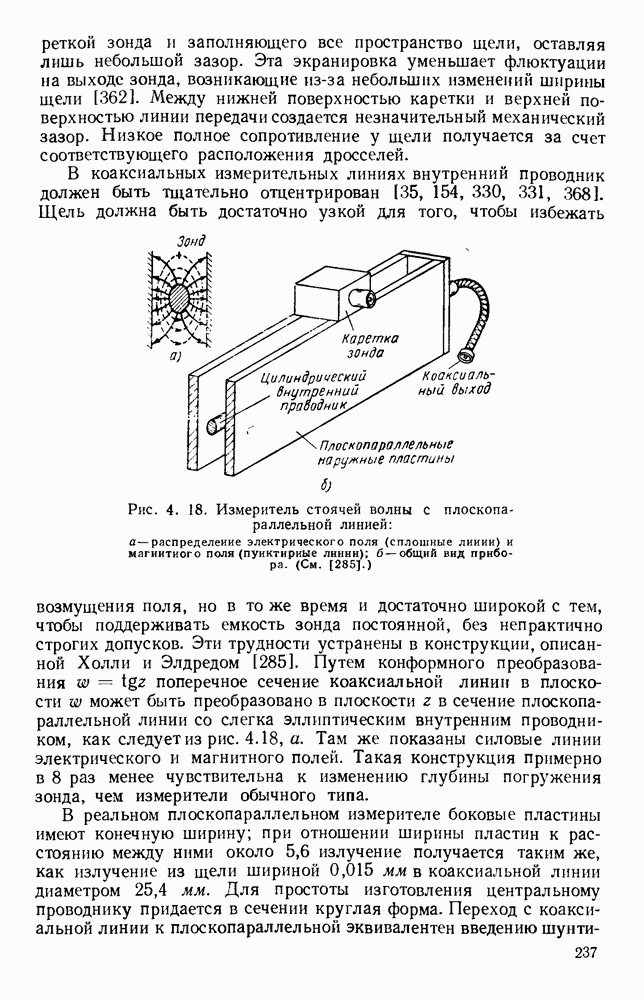
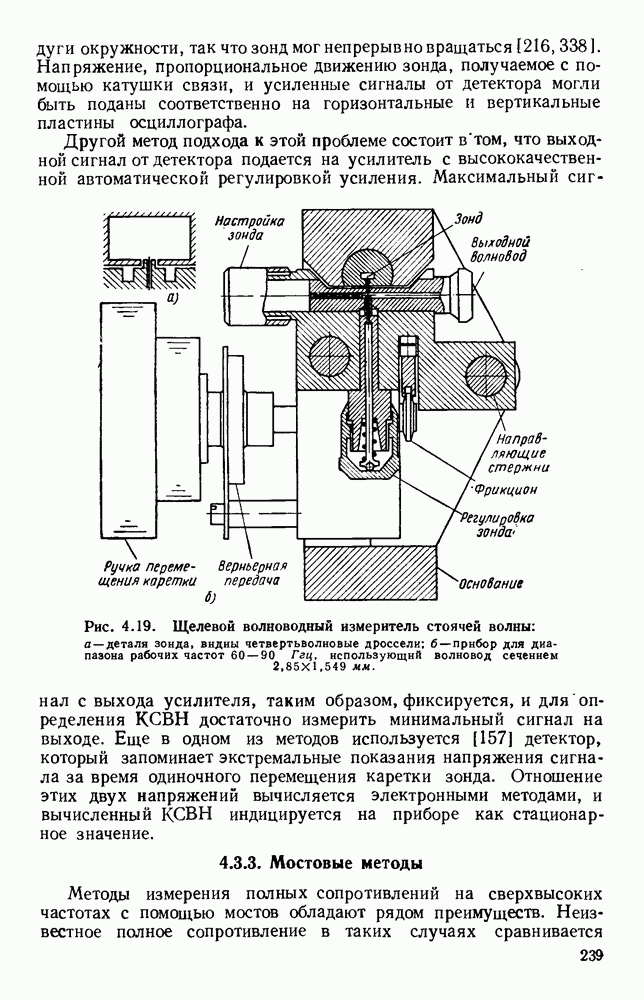
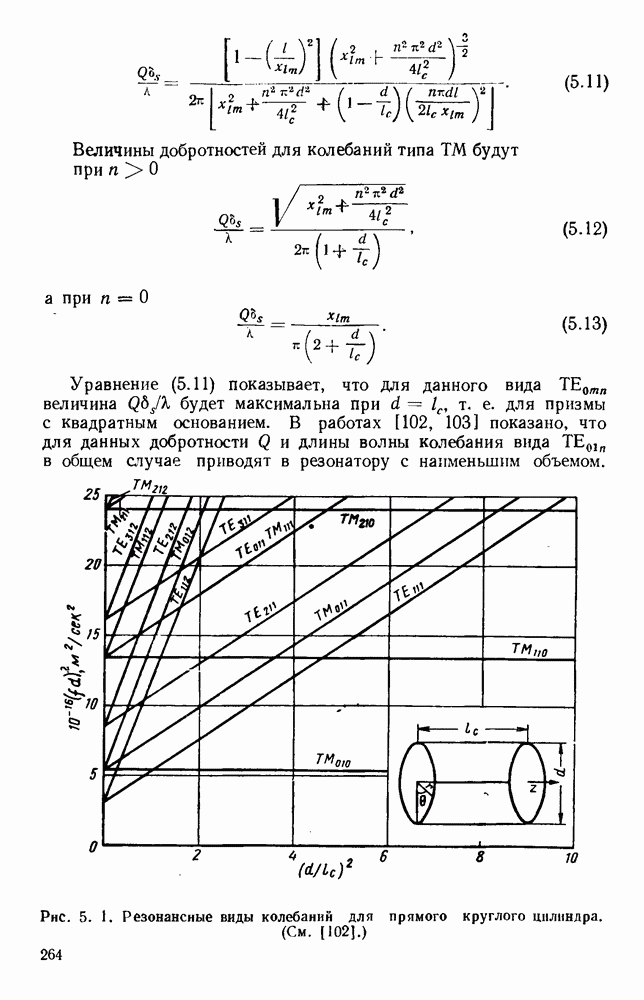
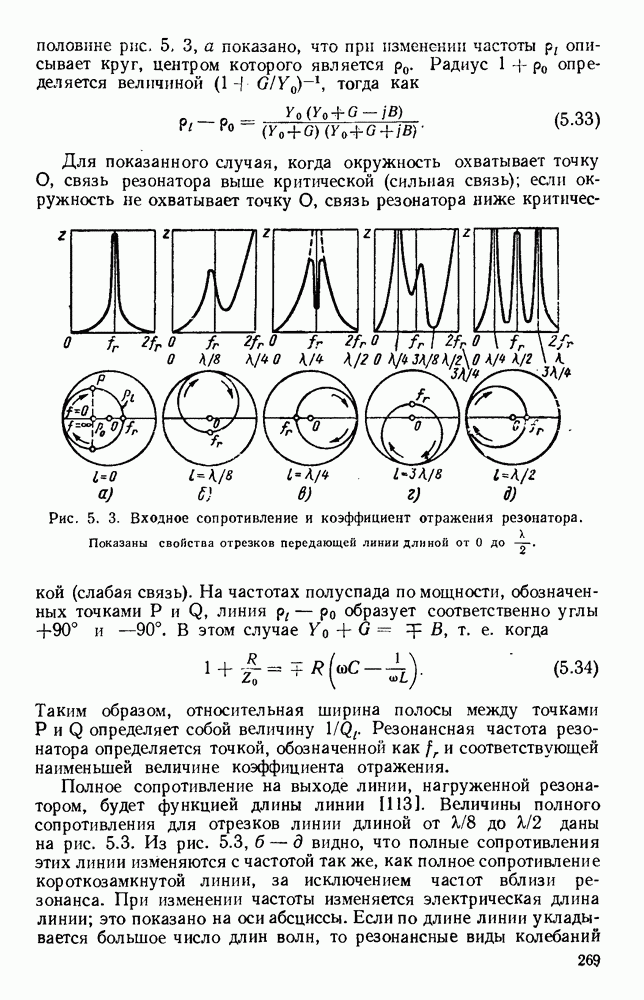
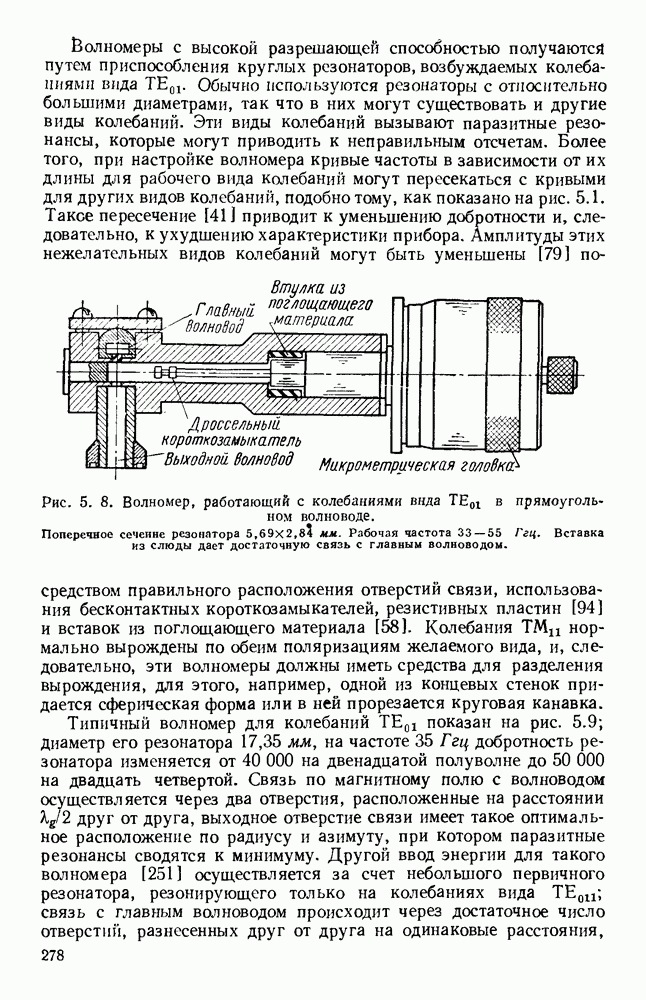
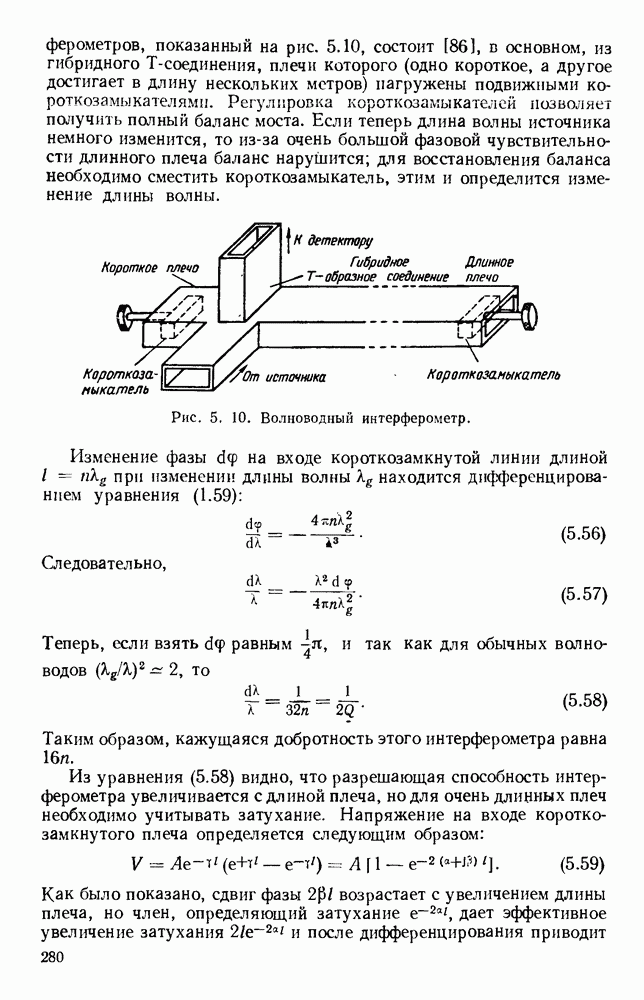
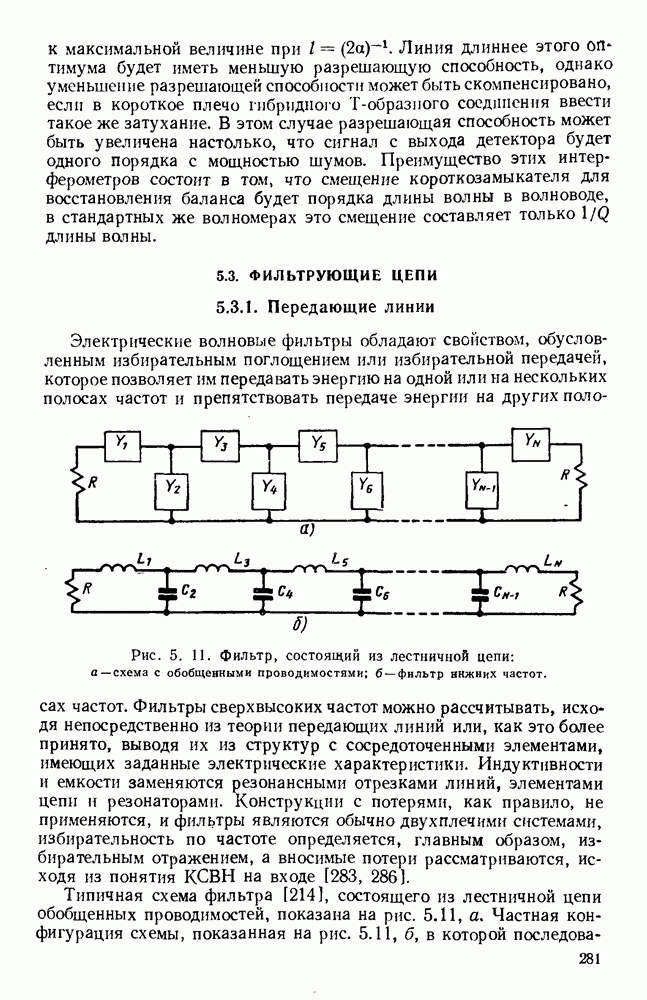
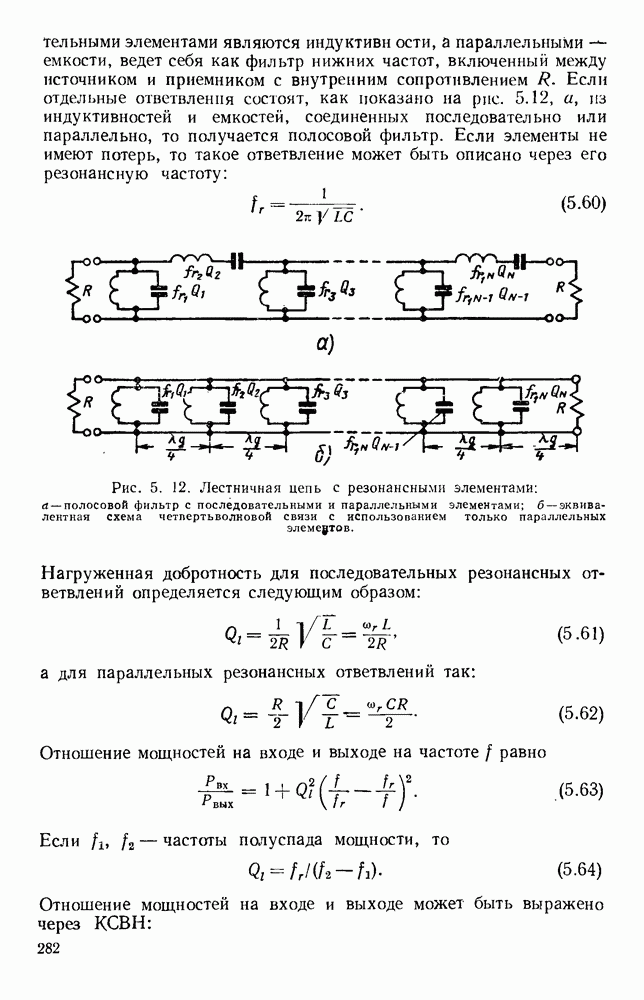
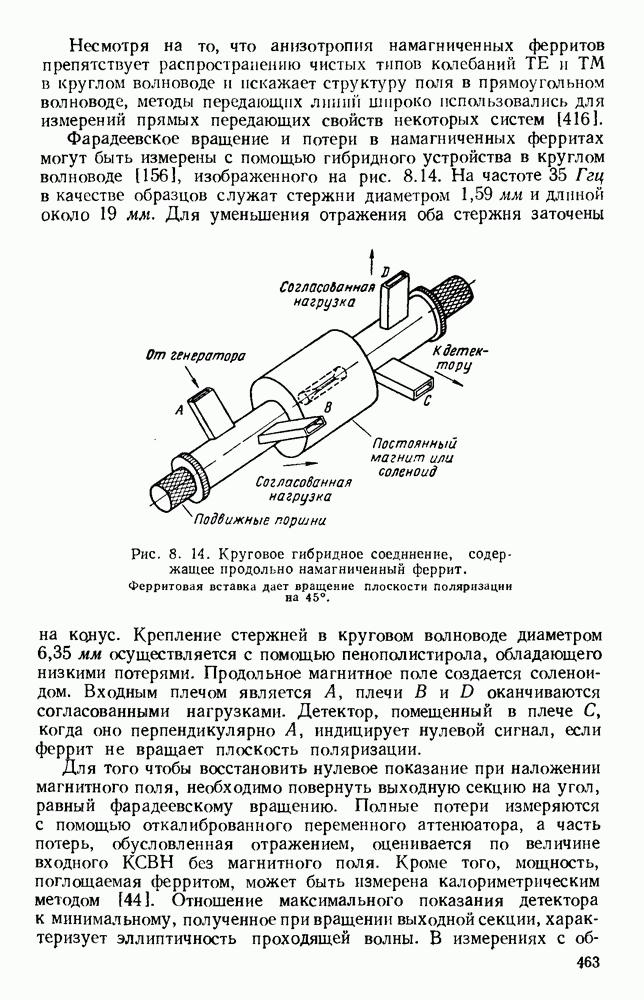
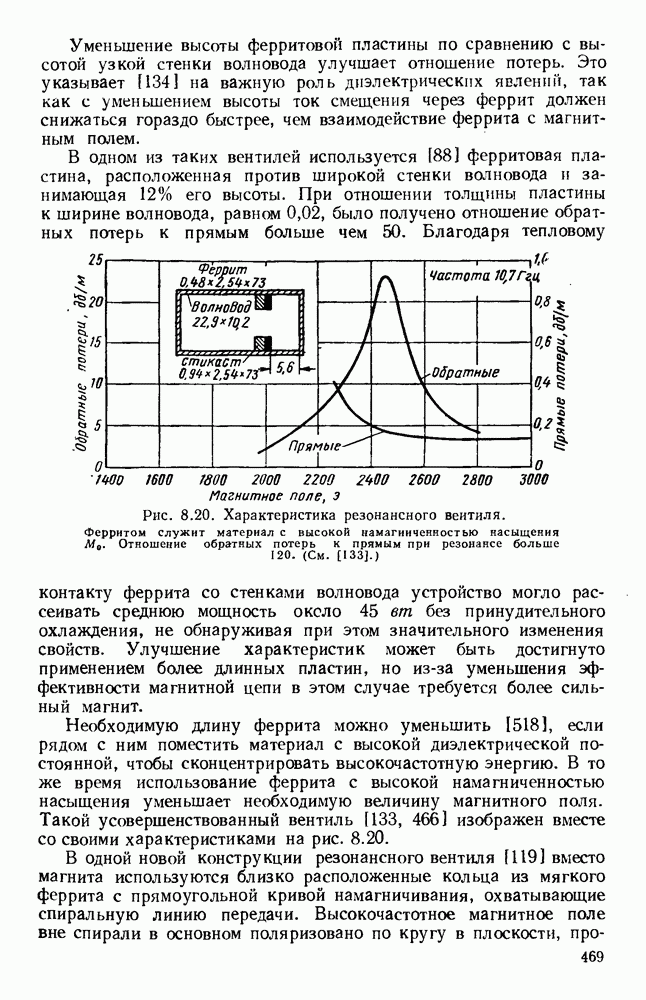
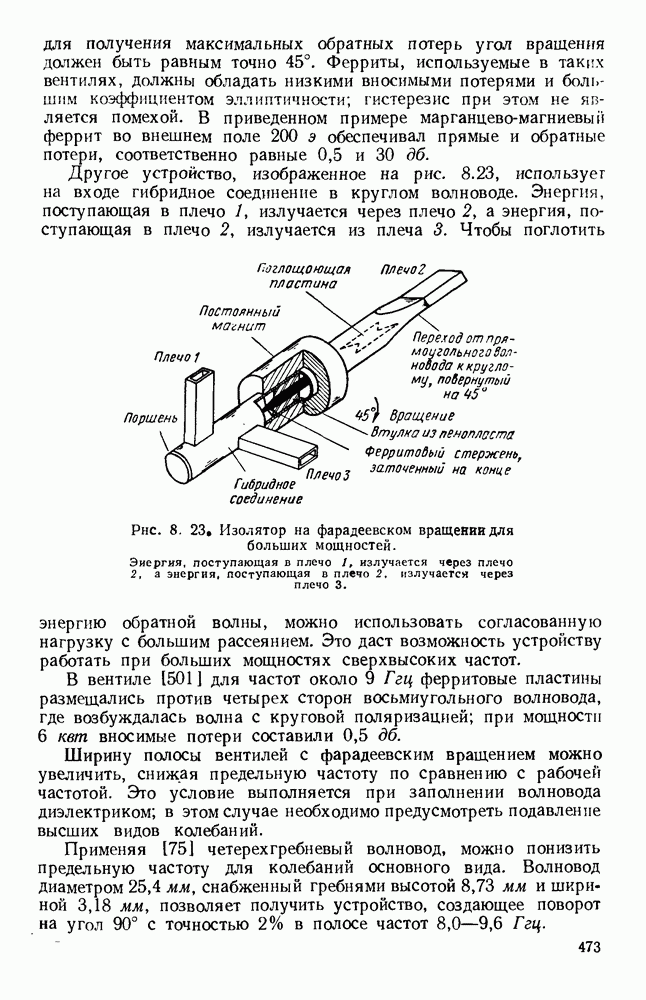
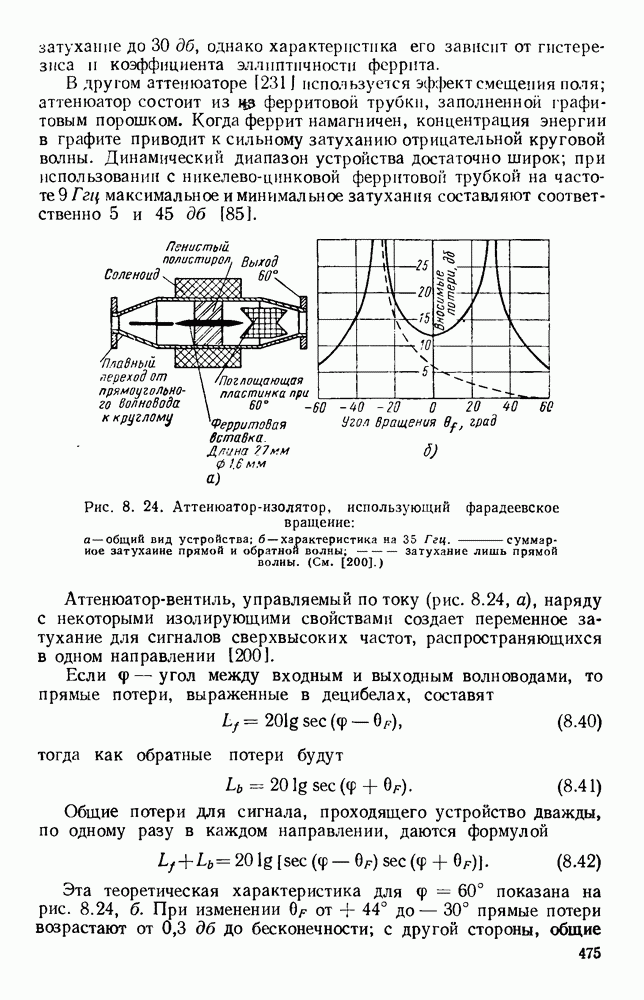
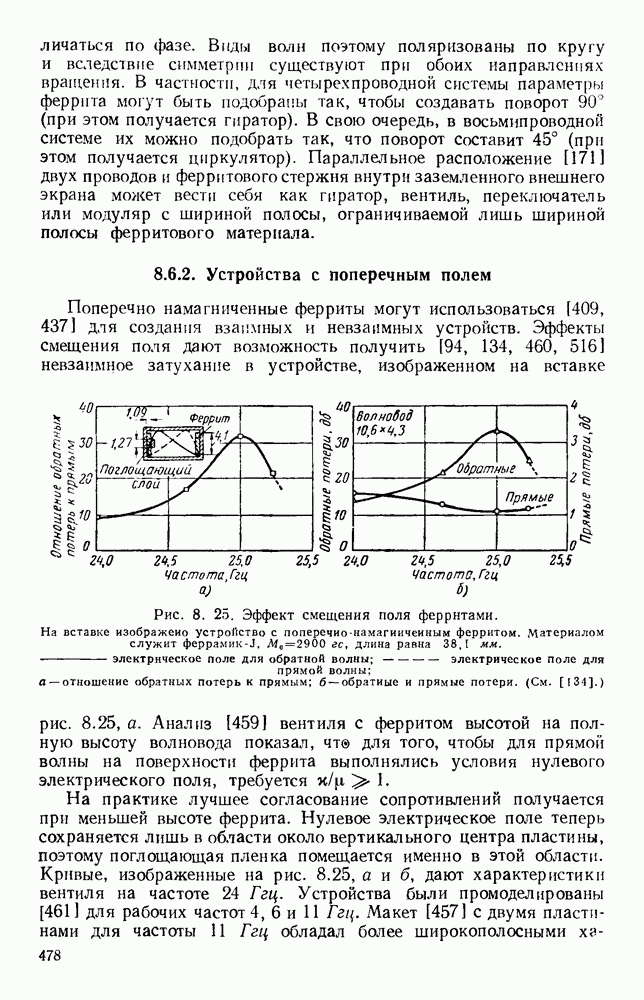
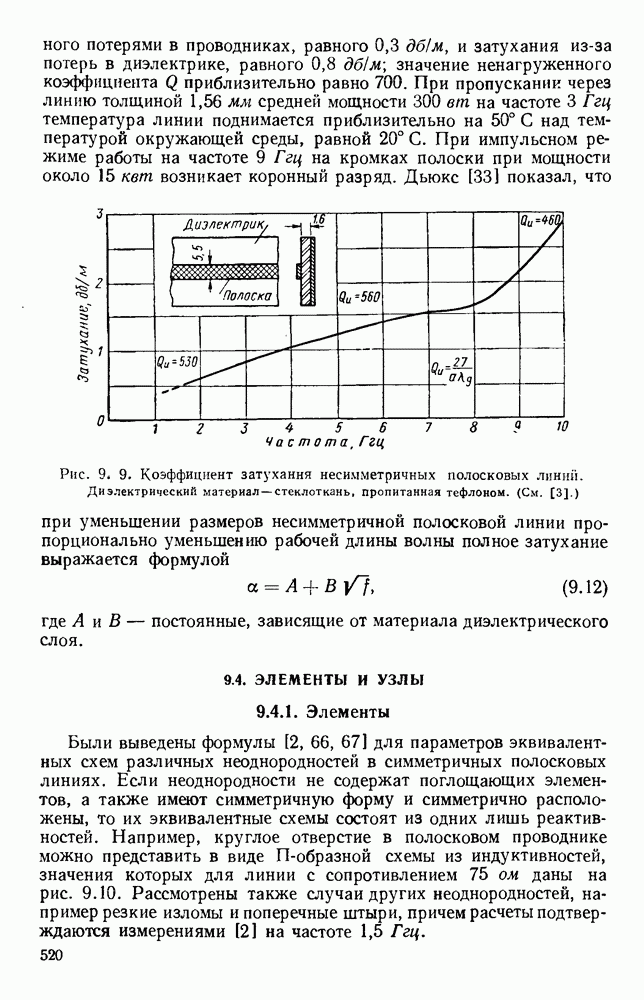
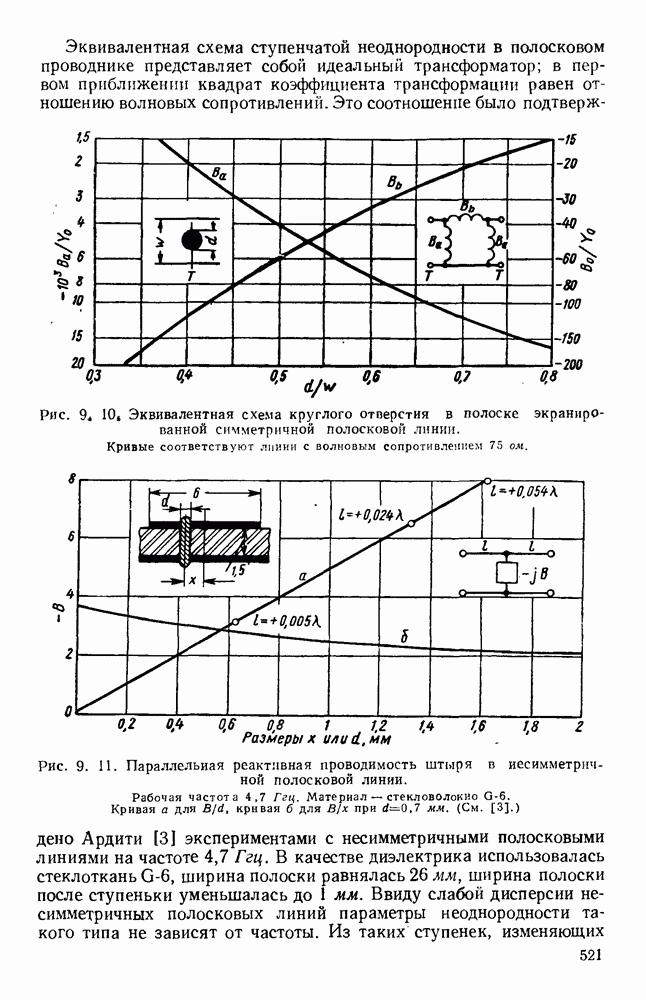
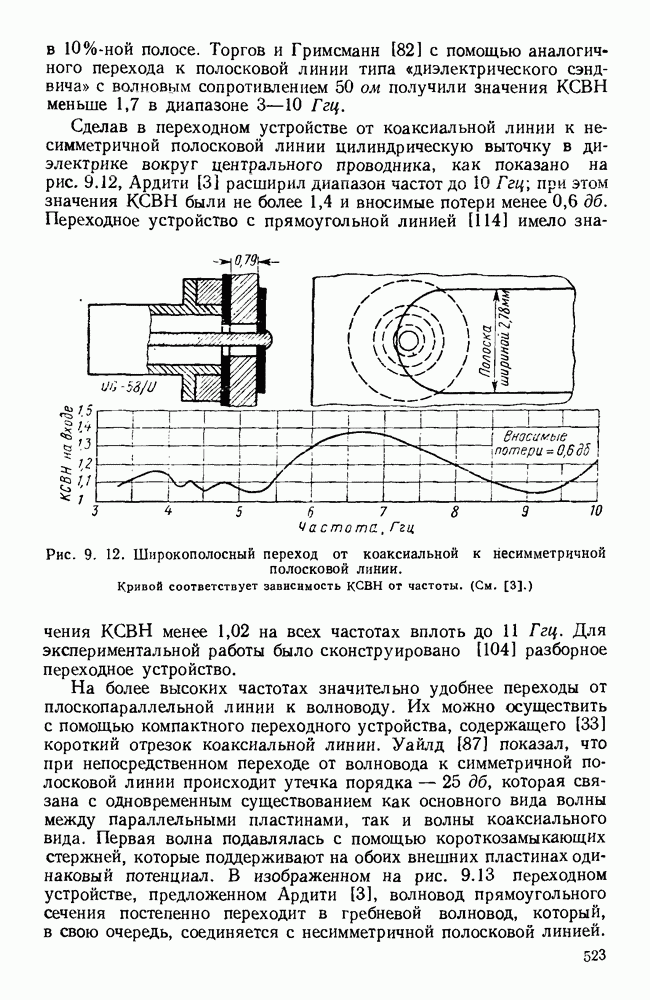
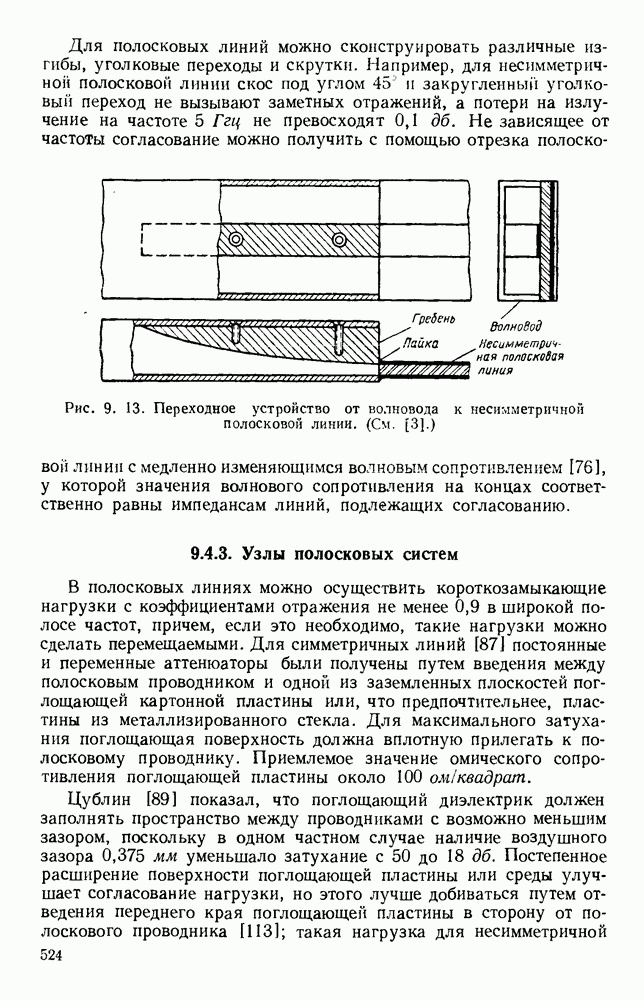
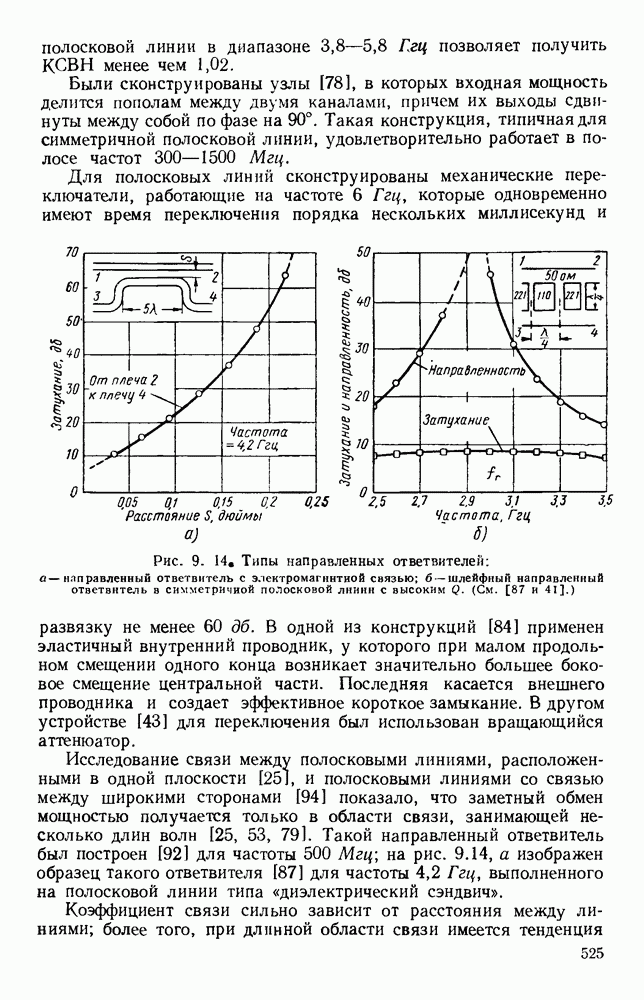
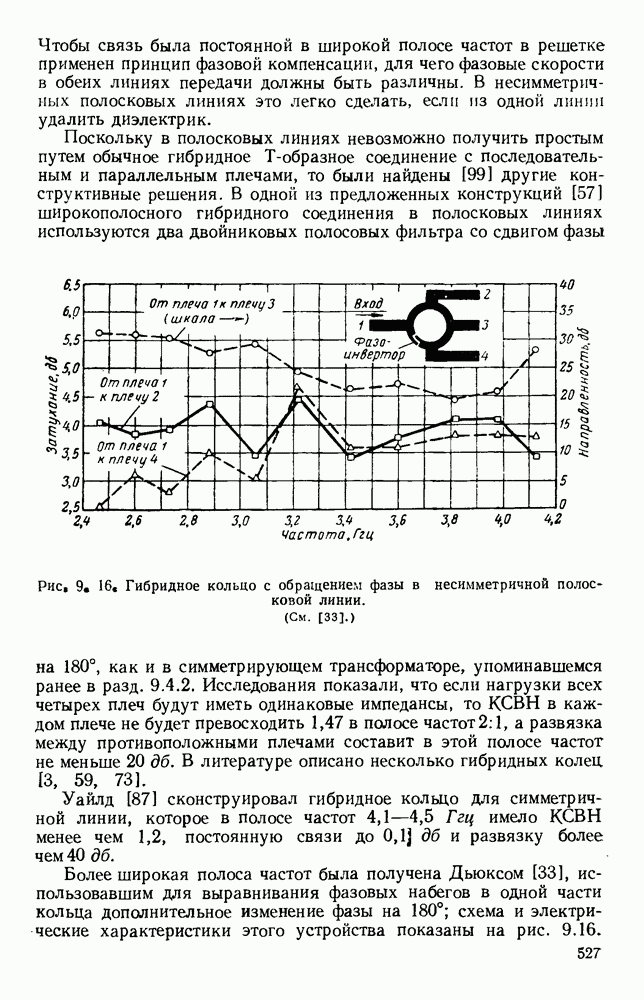
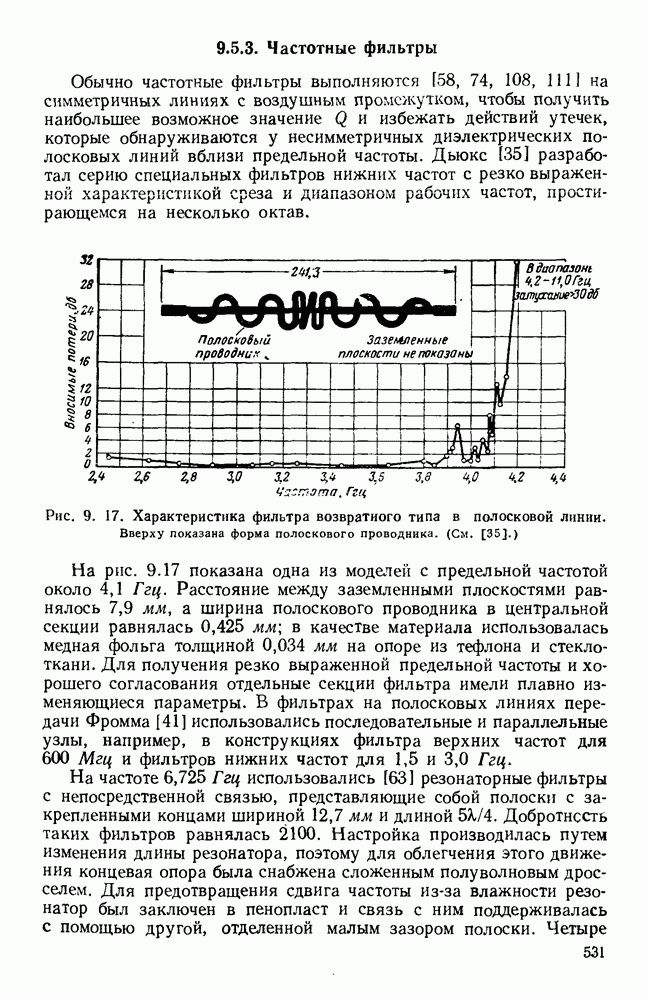
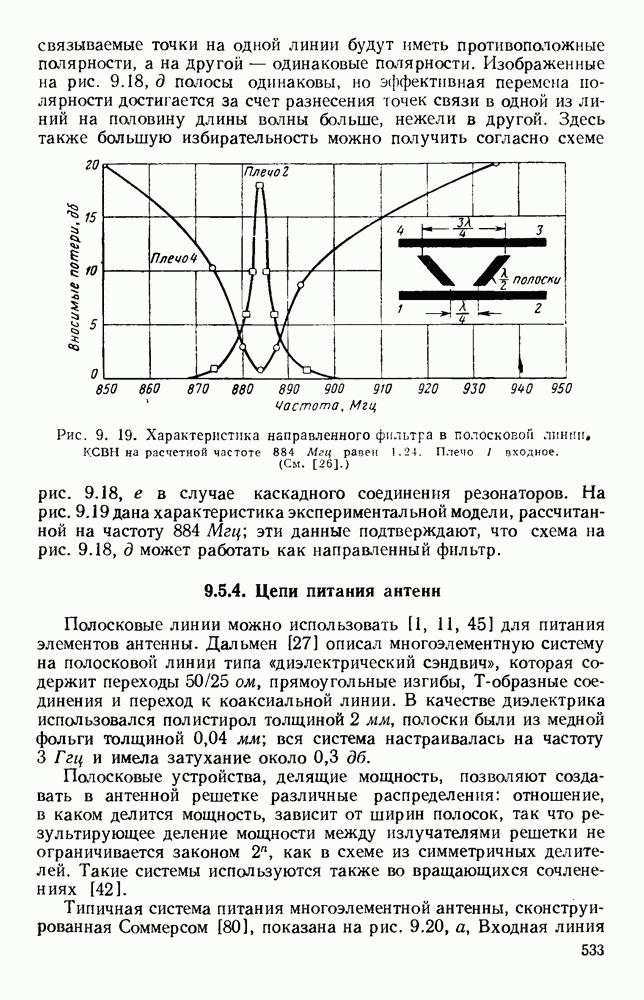
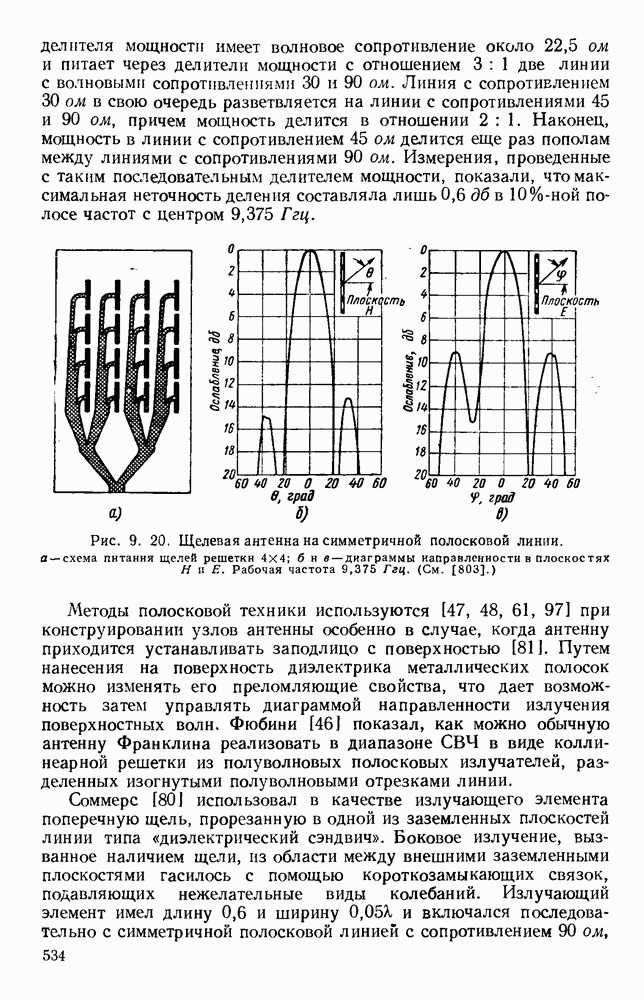
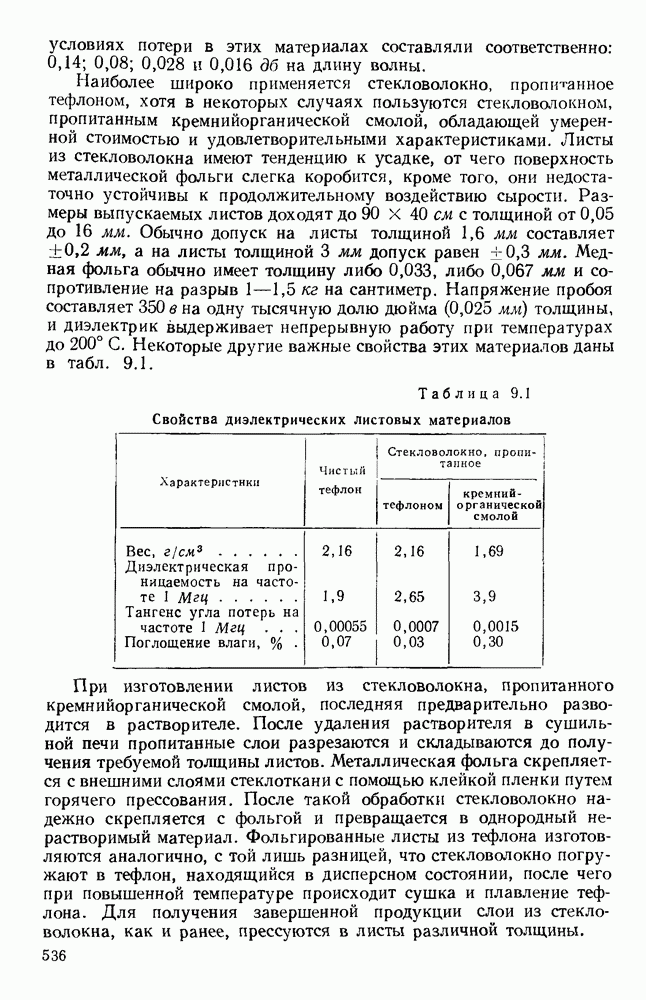
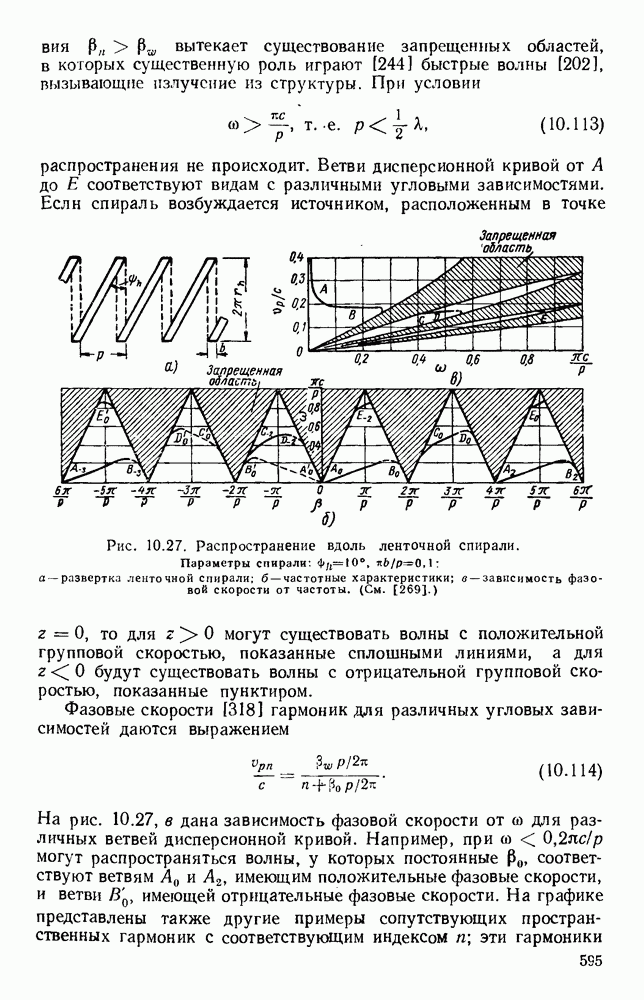
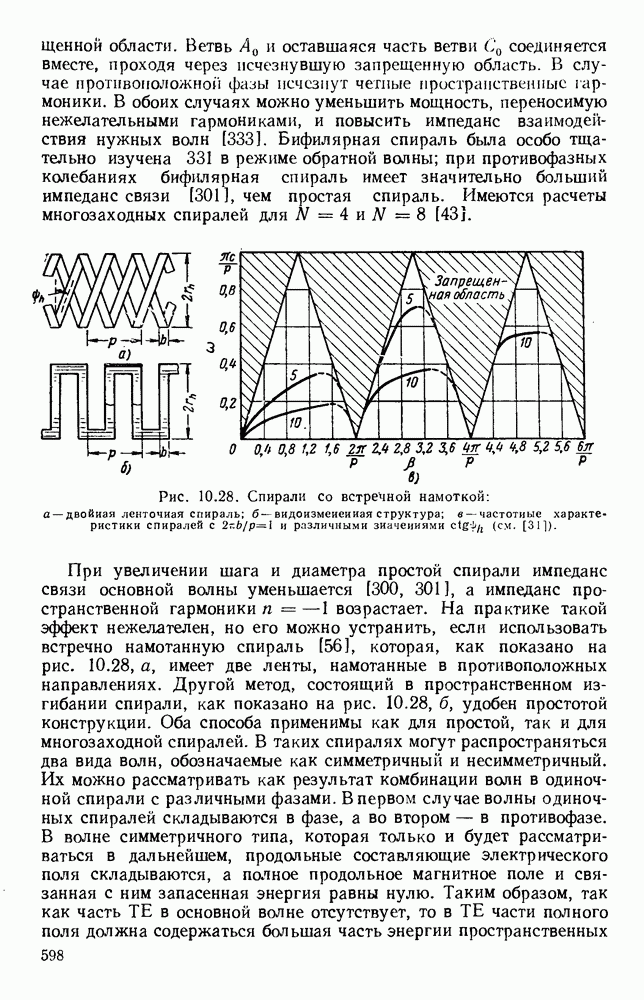
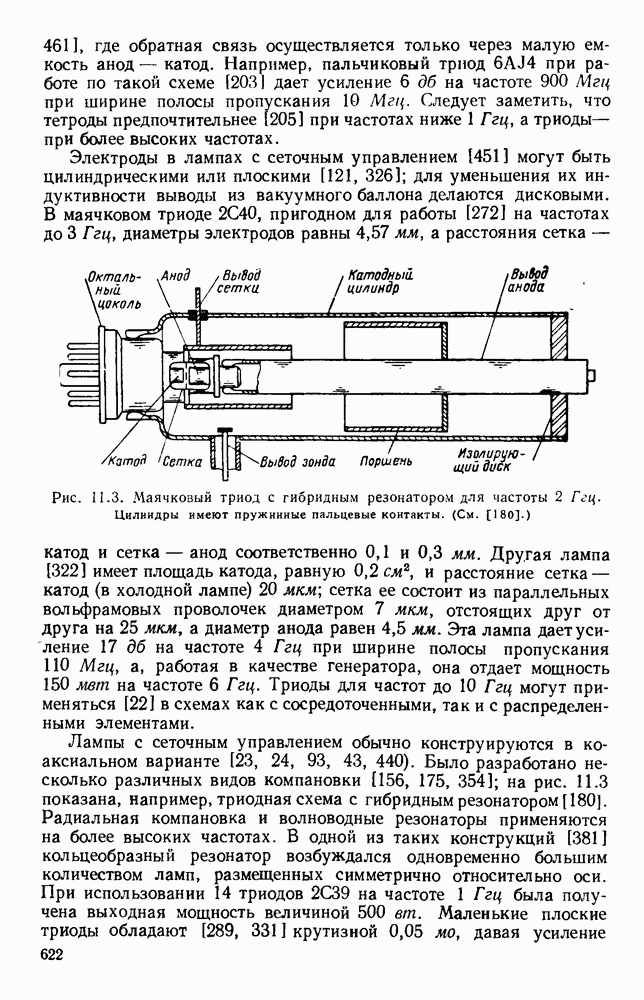
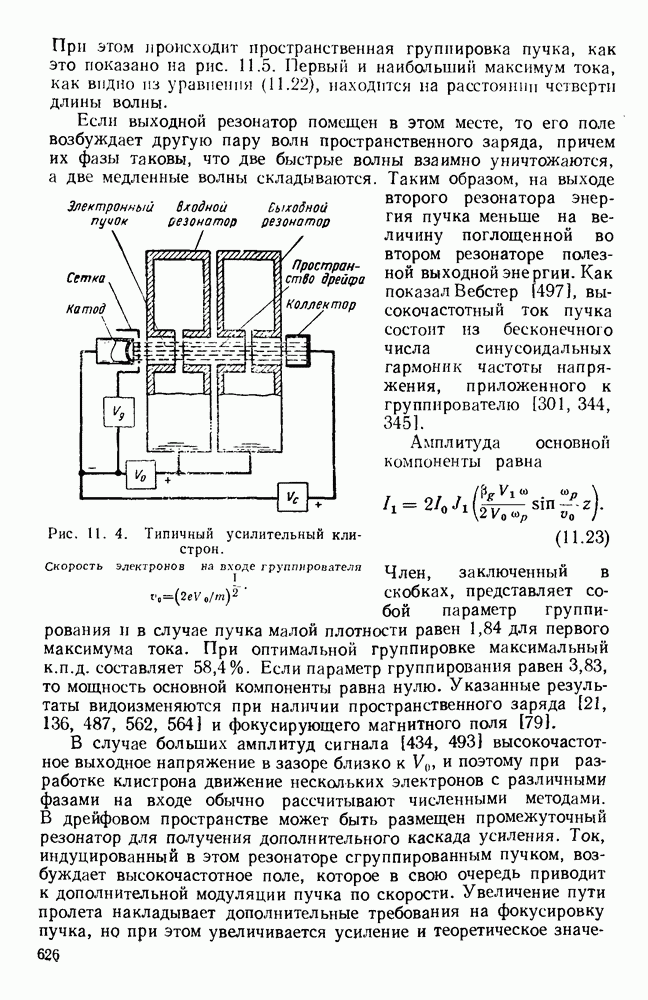
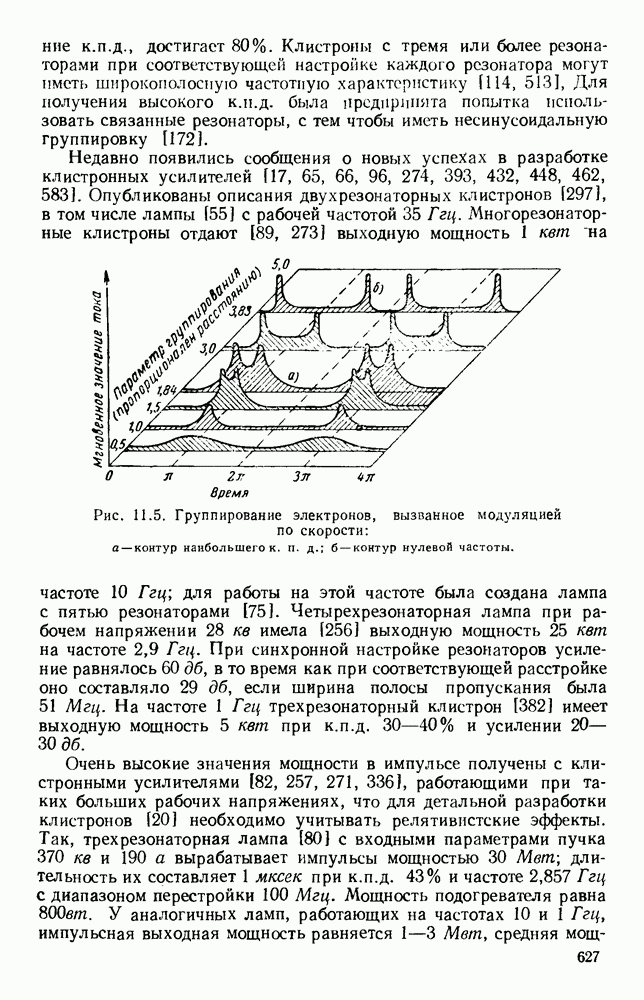
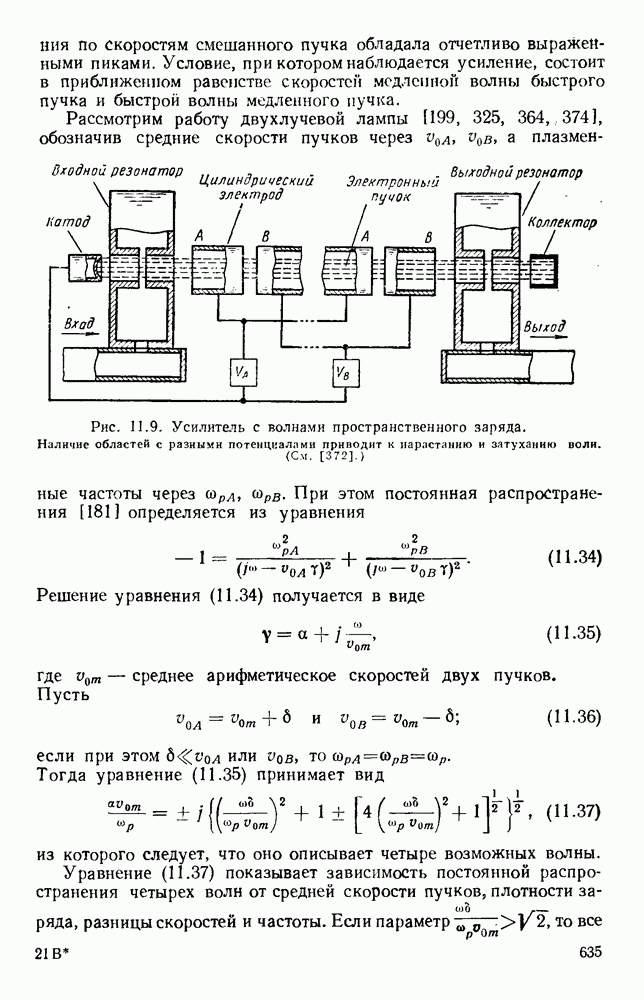
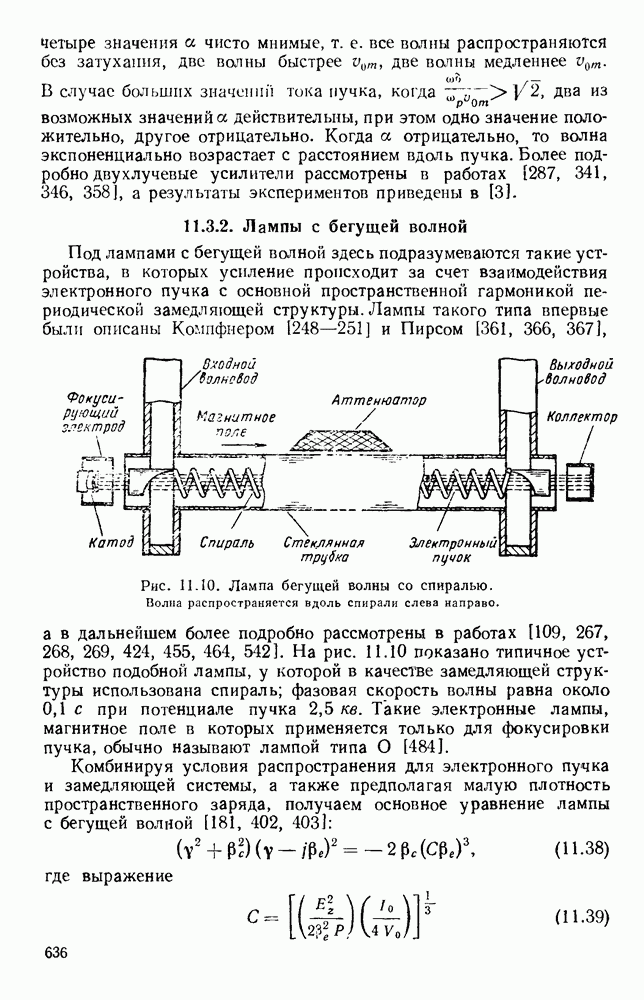
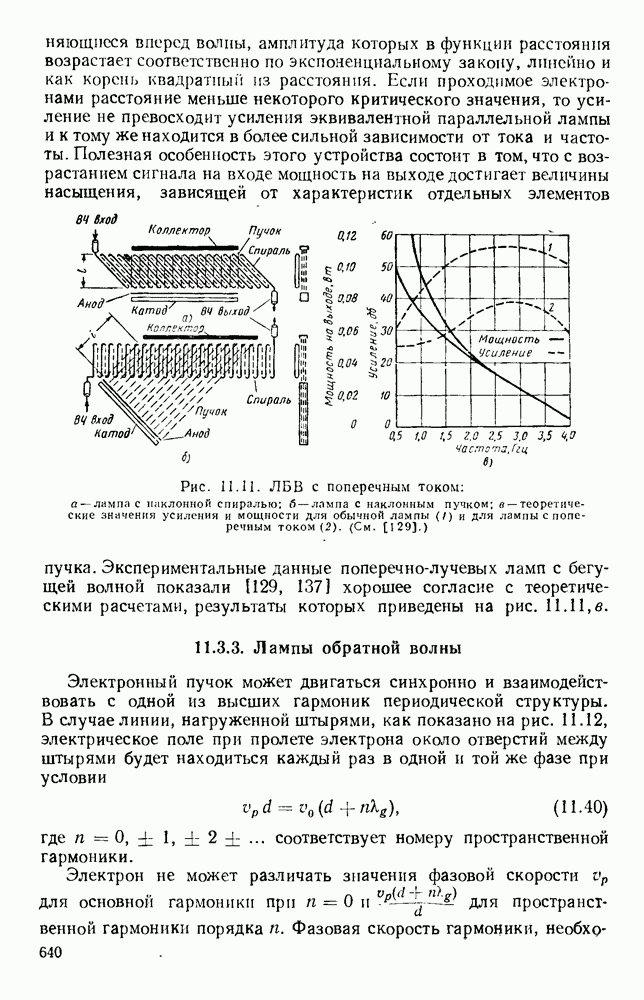
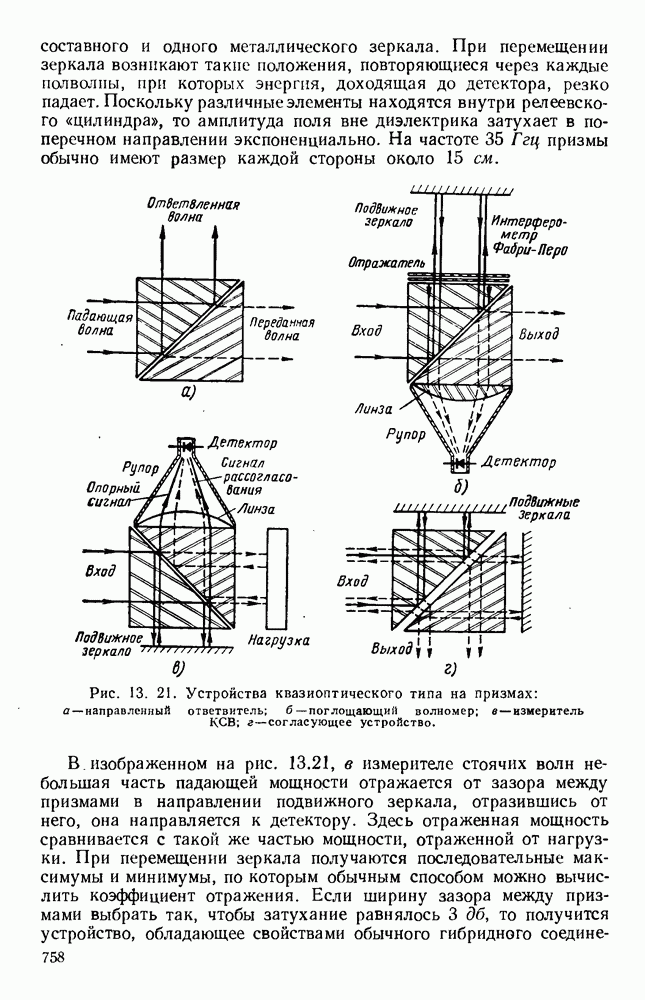
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
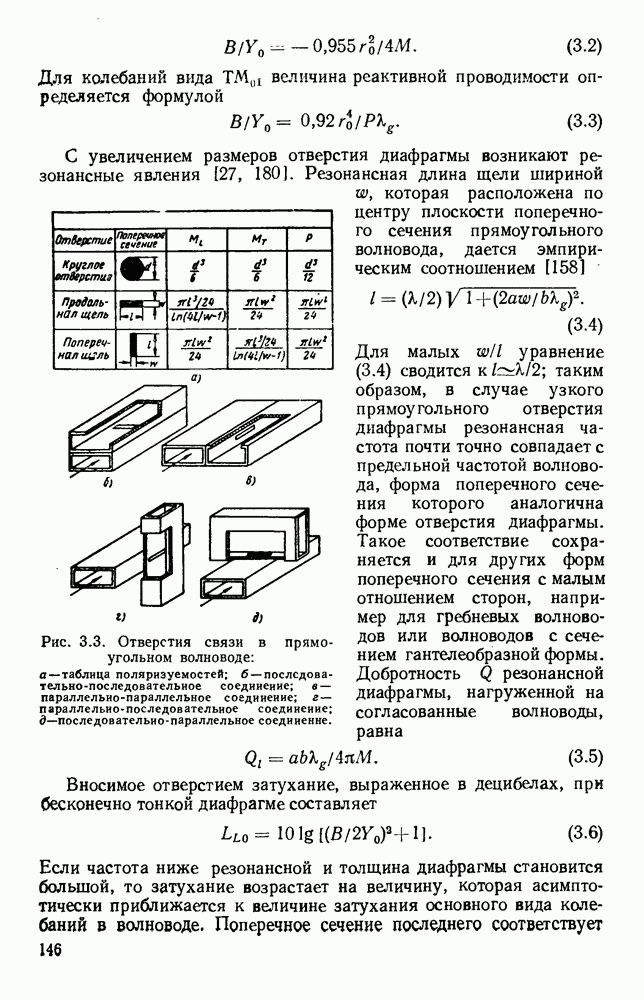
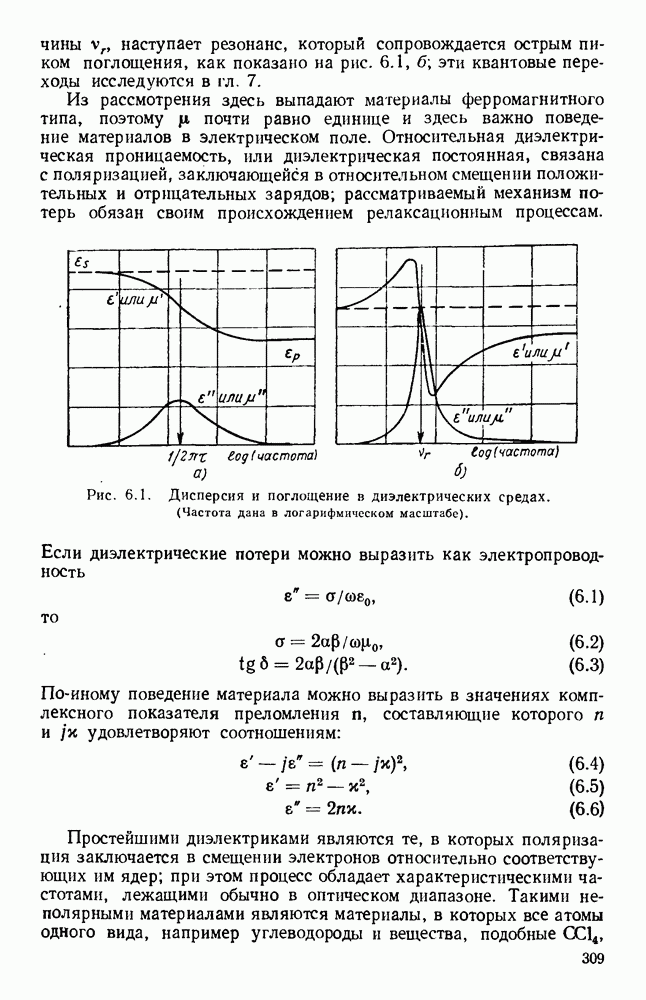
6.3.2. Аномальное поведение
При температуре, близкой к комнатной, рассеяние носителей зарядов в металле, обусловленное температурными колебаниями решетки, вызывает линейную зависимость удельного сопротивления по постоянному току от температуры. В этой области, выше температуры Дебая,  больше энергии фонона, соответствующей максимальной частоте колебаний решетки. Ниже температуры Дебая рассеяние решетки быстро ослабевает и удельное сопротивление уменьшается пропорционально пятой степени значения температуры. В совершенных кристаллах вблизи нулевой температуры сопротивление должно было бы исчезнуть, но большинство обычных металлов проявляет остаточное удельное сопротивление, составляющее
больше энергии фонона, соответствующей максимальной частоте колебаний решетки. Ниже температуры Дебая рассеяние решетки быстро ослабевает и удельное сопротивление уменьшается пропорционально пятой степени значения температуры. В совершенных кристаллах вблизи нулевой температуры сопротивление должно было бы исчезнуть, но большинство обычных металлов проявляет остаточное удельное сопротивление, составляющее  от его значения при комнатной температуре в зависимости от несовершенств решетки. Проводящими материалами, используемыми в качестве элементов цепей, обычно являются медь, серебро, золото и алюминий; их удельные проводимости при комнатной температуре совершенно подобны друг другу.
от его значения при комнатной температуре в зависимости от несовершенств решетки. Проводящими материалами, используемыми в качестве элементов цепей, обычно являются медь, серебро, золото и алюминий; их удельные проводимости при комнатной температуре совершенно подобны друг другу.
За исключением ферромагнитных материалов [116], магнитная проницаемость металлов обычно равняется примерно единице, и уравнение (6.71) можно переписать так:

Эксперименты при очень низких температурах показывают, однако, что  не уменьшается непрерывно с увеличением
не уменьшается непрерывно с увеличением  для всех обычных металлов
для всех обычных металлов  обнаруживает более высокие значения, чем те, которые указываются уравнением (6.74). Такое аномальное поведение [203] хороших проводников при низких температурах и высоких частотах получается потому, что средняя длина свободного пробега электронов проводимости становится большой по сравнению с глубиной поверхностного слоя.
обнаруживает более высокие значения, чем те, которые указываются уравнением (6.74). Такое аномальное поведение [203] хороших проводников при низких температурах и высоких частотах получается потому, что средняя длина свободного пробега электронов проводимости становится большой по сравнению с глубиной поверхностного слоя.
Этот эффект был исследован теоретически [10, 81, 106, 145, 204, 207, 209, 221]. Если рассматривать упрощенную модель газа свободных электронов для одновалентного металла, такого как медь, то эта теория дает

Поскольку о при комнатной температуре равняется  то
то  составляет около
составляет около  На частоте
На частоте  уравнение (6.72) дает
уравнение (6.72) дает  так что
так что  По мере того как температура уменьшается,
По мере того как температура уменьшается,  увеличивается и, в конце концов,
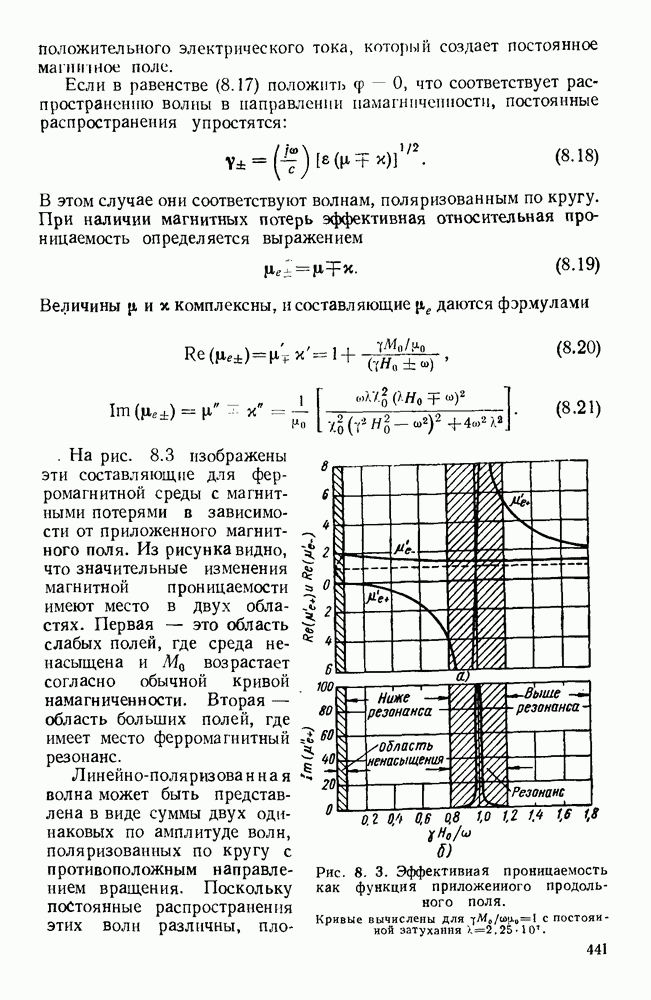
увеличивается и, в конце концов,  проходит через значение единица и достигает значения, близкого к 40. Для металлов, у которых остаточное сопротивление может быть сделано меньше сопротивления меди, отношение
проходит через значение единица и достигает значения, близкого к 40. Для металлов, у которых остаточное сопротивление может быть сделано меньше сопротивления меди, отношение  становится очень большим, и при таком условии поверхностное сопротивление почти не зависит от удельной проводимости по постоянному току и пропорционально
становится очень большим, и при таком условии поверхностное сопротивление почти не зависит от удельной проводимости по постоянному току и пропорционально 
Теория аномального поверхностного эффекта выражалась количественно [221] через параметр  для двух граничных случаев. В одном из них
для двух граничных случаев. В одном из них  предполагалось, что электроны при столкновении с поверхностью металла испытывают зеркальное отражение, не теряя своих скоростей дрейфа; в другом случае
предполагалось, что электроны при столкновении с поверхностью металла испытывают зеркальное отражение, не теряя своих скоростей дрейфа; в другом случае  предполагалось, что они претерпевают диффузное рассеяние, теряя свои скорости дрейфа. В аномальной области поле быстро падает с расстоянием z от поверхности, так что большая часть его заключена в слое, толщина которого намного меньше, чем
предполагалось, что они претерпевают диффузное рассеяние, теряя свои скорости дрейфа. В аномальной области поле быстро падает с расстоянием z от поверхности, так что большая часть его заключена в слое, толщина которого намного меньше, чем  Это быстрое уменьшение, однако, не сохраняется, и, в конце концов, на большом расстоянии от поверхности поле изменяется приближенно по закону
Это быстрое уменьшение, однако, не сохраняется, и, в конце концов, на большом расстоянии от поверхности поле изменяется приближенно по закону  так что существует длинный хвост малой амплитуды, проникающий в металл на расстояние порядка среднего пути свободного пробега. Фаза поля в металле изменяется с расстоянием и в хвосте, грубо говоря, находится в противофазе с полем вблизи поверхности. Активная и реактивная составляющие поверхностного сопротивления показаны на рис. 6.7, а. Для коротких путей свободного пробега и фиксированного значения
так что существует длинный хвост малой амплитуды, проникающий в металл на расстояние порядка среднего пути свободного пробега. Фаза поля в металле изменяется с расстоянием и в хвосте, грубо говоря, находится в противофазе с полем вблизи поверхности. Активная и реактивная составляющие поверхностного сопротивления показаны на рис. 6.7, а. Для коротких путей свободного пробега и фиксированного значения  пропорционально
пропорционально  равно
равно  При увеличении
При увеличении  стремится к постоянному значению
стремится к постоянному значению  в крайней аномальной области,
в крайней аномальной области,  стремится к
стремится к  В дальнейшем отметим, что два крайних случая поверхностных условий дают очень похожие результаты.
В дальнейшем отметим, что два крайних случая поверхностных условий дают очень похожие результаты.
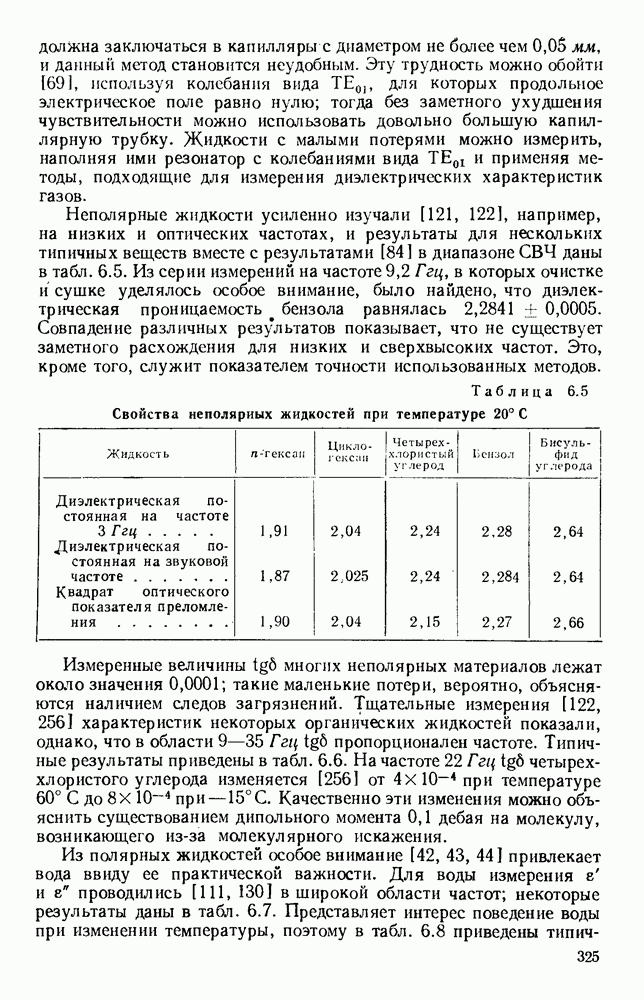
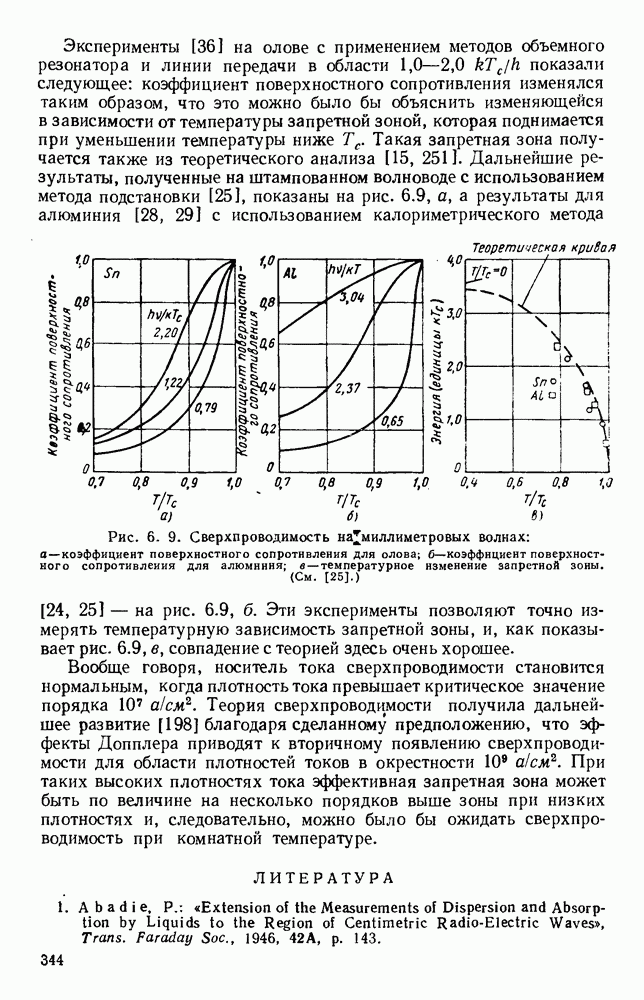
Измерения поверхностного сопротивления металлов были проведены Чемберсом [59, 60] на частотах  в непрерывном диапазоне температур 2—90° К- Образцы были выполнены в виде шпилькообразной короткозамкнутой линии длиной около 6 см с--резонансом на более низких частотах и с
в непрерывном диапазоне температур 2—90° К- Образцы были выполнены в виде шпилькообразной короткозамкнутой линии длиной около 6 см с--резонансом на более низких частотах и с  -резонансом на более высоких частотах. Были получены результаты для меди, серебра, золота, - олова, кадмия, свинца и алюминия. На рис. 6.7, б дана кривая зависимости поверхностного сопротивления меди от У о для частоты
-резонансом на более высоких частотах. Были получены результаты для меди, серебра, золота, - олова, кадмия, свинца и алюминия. На рис. 6.7, б дана кривая зависимости поверхностного сопротивления меди от У о для частоты  пунктирная наклонная линия показывает предсказание классической теории, а вертикальная отмечает точку, в которой
пунктирная наклонная линия показывает предсказание классической теории, а вертикальная отмечает точку, в которой  На верхней шкале показаны температуры, ри которых были получены различные значения
На верхней шкале показаны температуры, ри которых были получены различные значения 

Рис. 6.7. Поверхностное сопротивление металлов на сверхвысоких частотах: а —  даны как функции отношения среднего пути свободного пробега к глубине поверхностного слоя; б - величина, обратная
даны как функции отношения среднего пути свободного пробега к глубине поверхностного слоя; б - величина, обратная  дается как функция электропроводности по постоянному току. (См. [221, 60].)
дается как функция электропроводности по постоянному току. (См. [221, 60].)
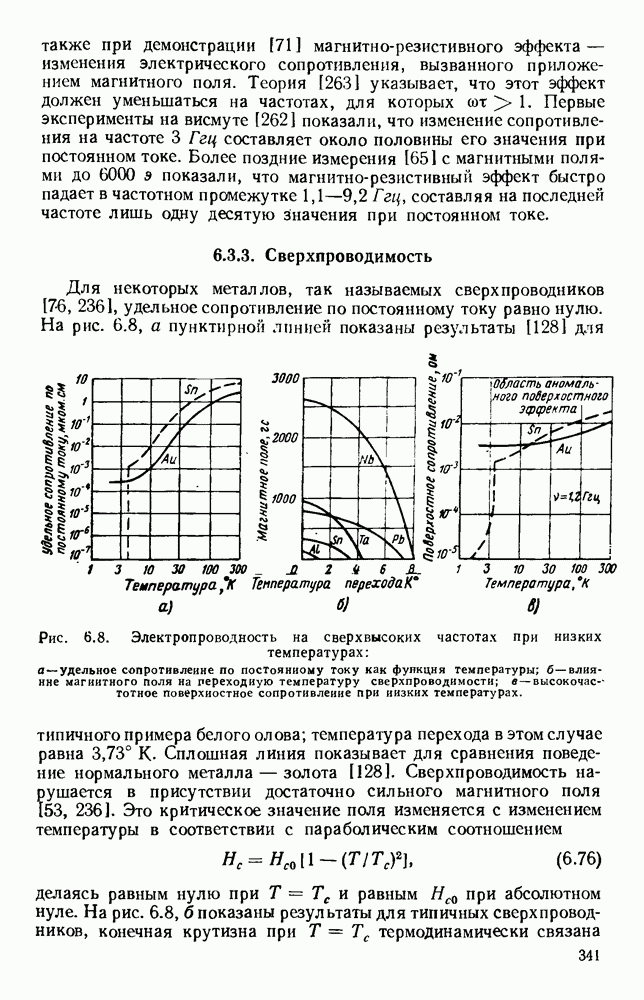
Эти и другие результаты оказались хорошо согласующимися с теорией для 
Эксперименты на олове [92, 207] и алюминии [322, 323] показывают, что поверхностное сопротивление обнаруживает нетензорную анизотропию: оно изменяется с изменением направления нормали к поверхности относительно осей кристалла. Предполагается [242], что в металлах, содержащих очень малое число электронов проводимости, средний путь свободного пробега должен быть крайне длинным. В висмуте это расстояние составляет несколько микрон, и, следовательно, несмотря на низкую электропроводность, аномальные явления должны иметь место при комнатной температуре. Измерения [206] на частотах 1,25 и  при температурах 290, 77 и 4° К подтвердили это предсказание. Результаты, полученные [239] на монокристаллах висмута при аномальных условиях, возникающих на частоте 24 Ггц при температуре 2° К, позволяют вывести элементы поверхности Ферми из теории Пиппарда [261]. Висмут интересен
при температурах 290, 77 и 4° К подтвердили это предсказание. Результаты, полученные [239] на монокристаллах висмута при аномальных условиях, возникающих на частоте 24 Ггц при температуре 2° К, позволяют вывести элементы поверхности Ферми из теории Пиппарда [261]. Висмут интересен
также при демонстрации [71] магнитно-резистивного эффекта — изменения электрического сопротивления, вызванного приложением магнитного поля. Теория [263] указывает, что этот эффект должен уменьшаться на частотах, для которых сот  Первые эксперименты на висмуте [262] показали, что изменение сопротивления на частоте
Первые эксперименты на висмуте [262] показали, что изменение сопротивления на частоте  составляет около половины его значения при постоянном токе. Более поздние измерения [65] с магнитными полями до 6000 9 показали, что магнитно-резистивный эффект быстро падает в частотном промежутке
составляет около половины его значения при постоянном токе. Более поздние измерения [65] с магнитными полями до 6000 9 показали, что магнитно-резистивный эффект быстро падает в частотном промежутке  составляя на последней частоте лишь одну десятую значения при постоянном токе.
составляя на последней частоте лишь одну десятую значения при постоянном токе.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
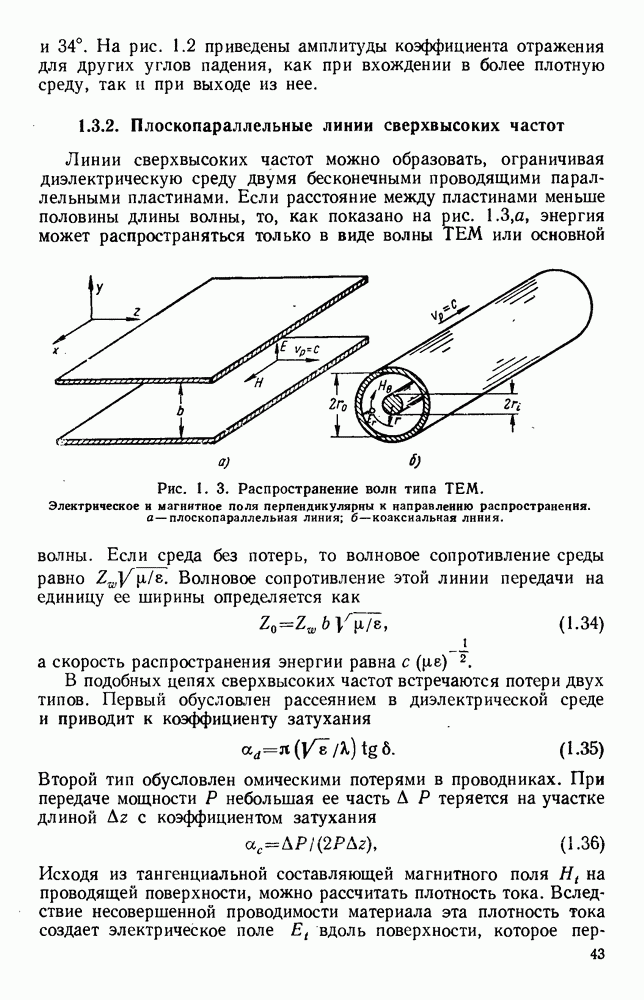
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
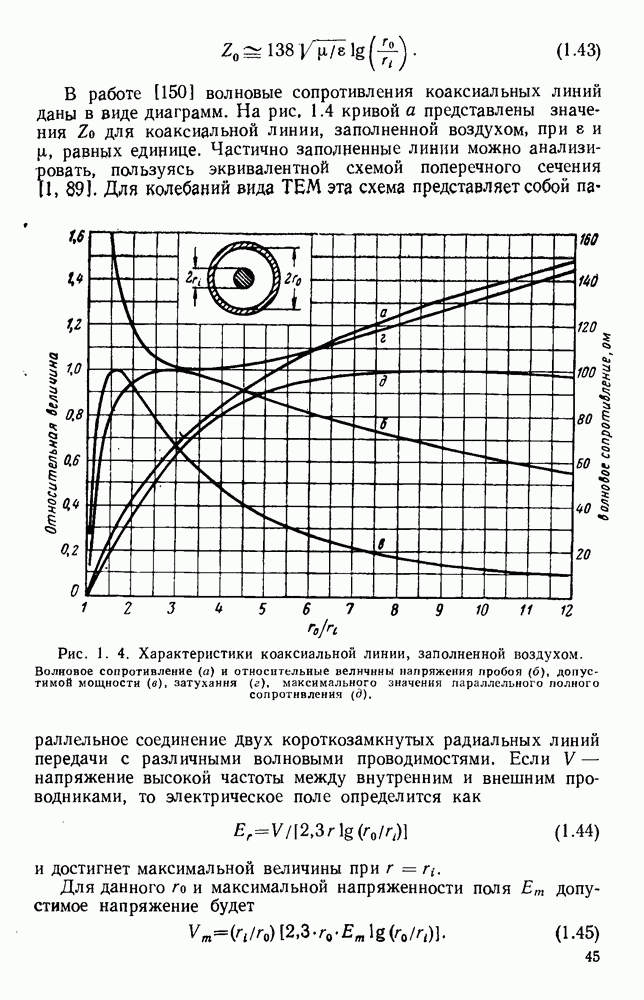
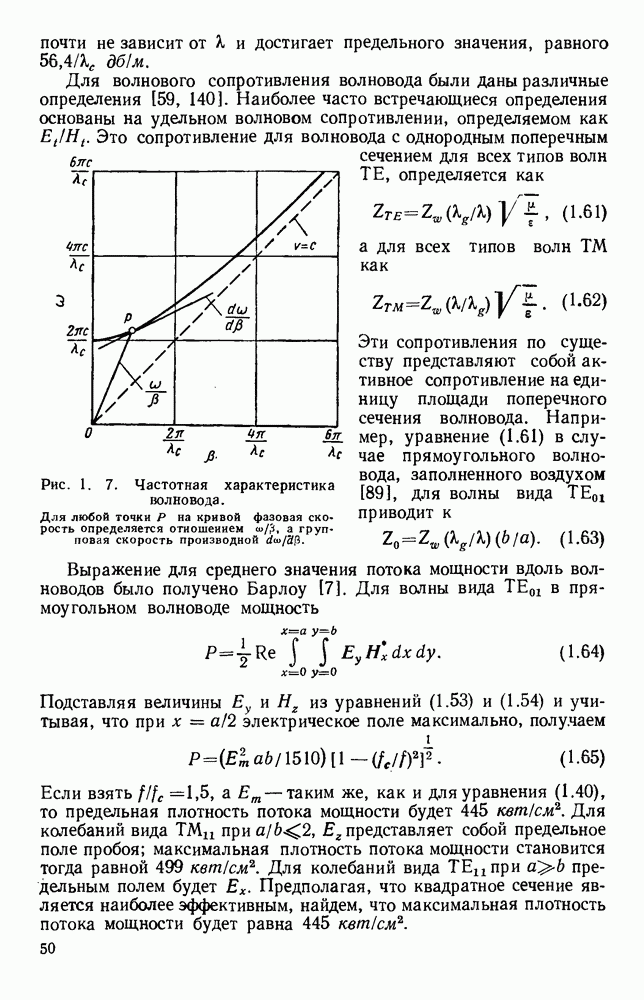
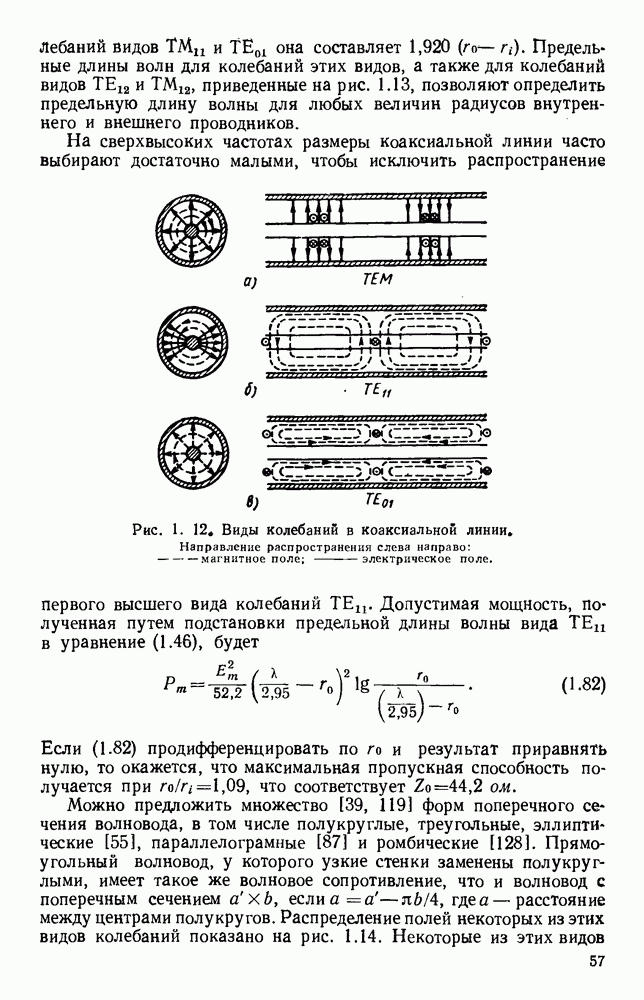
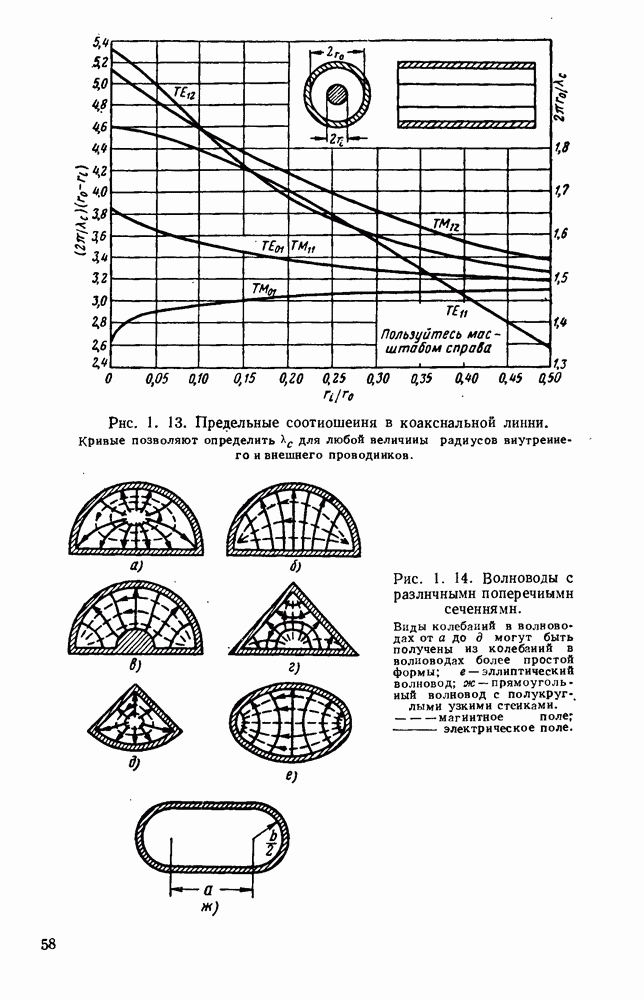
- 1.3.3. Коаксиальные линии
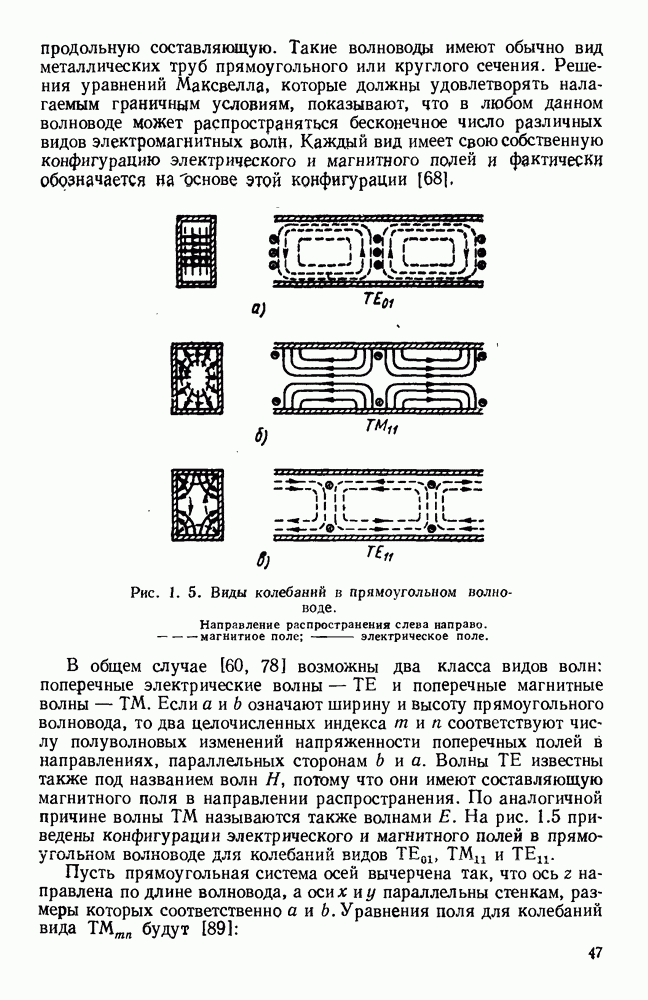
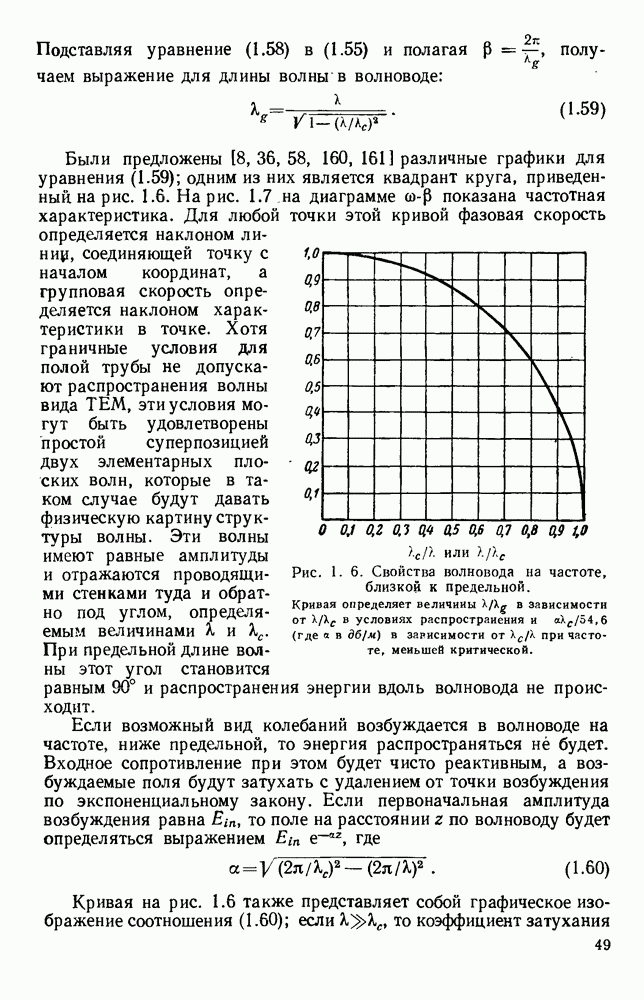
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
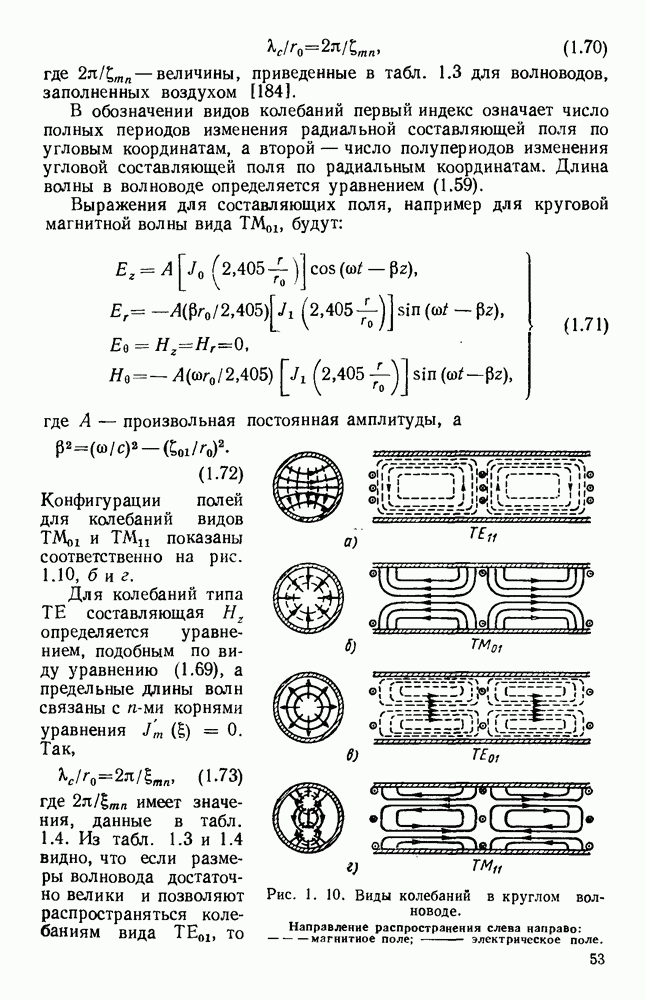
- 1.4.2. Круглые волноводы
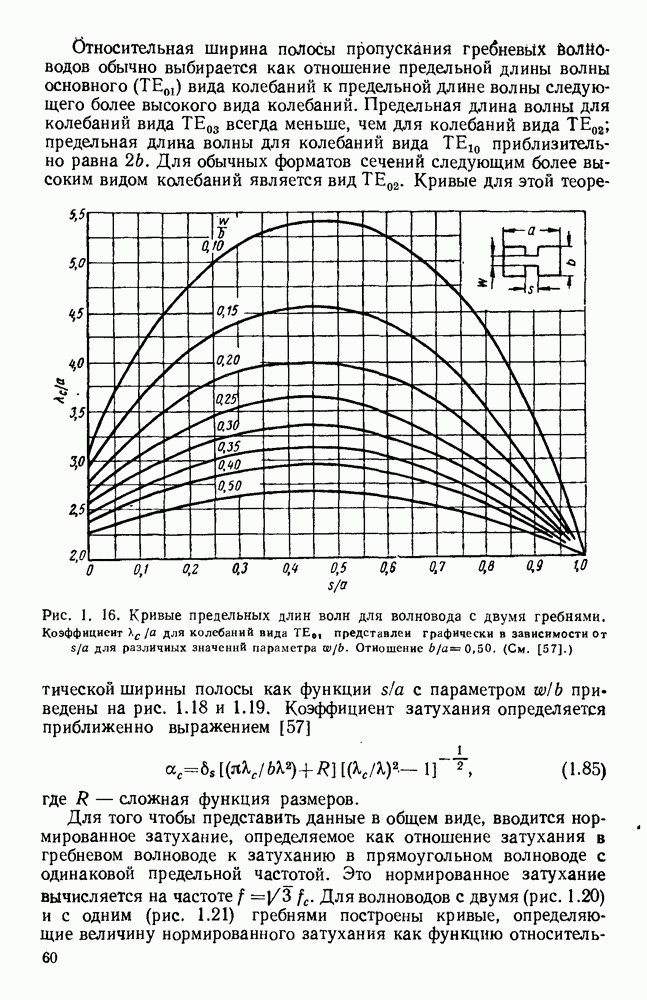
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
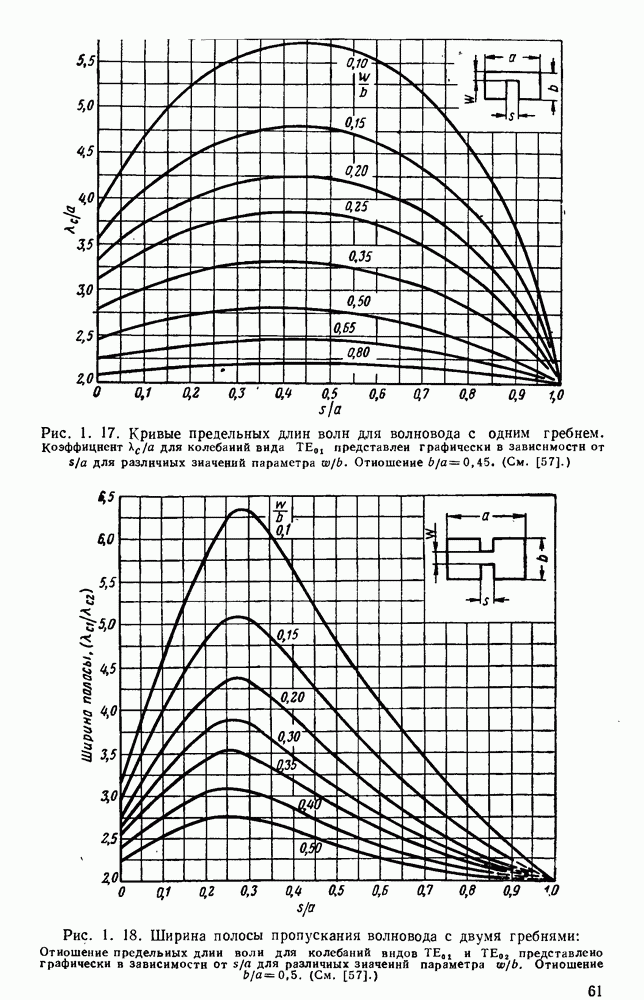
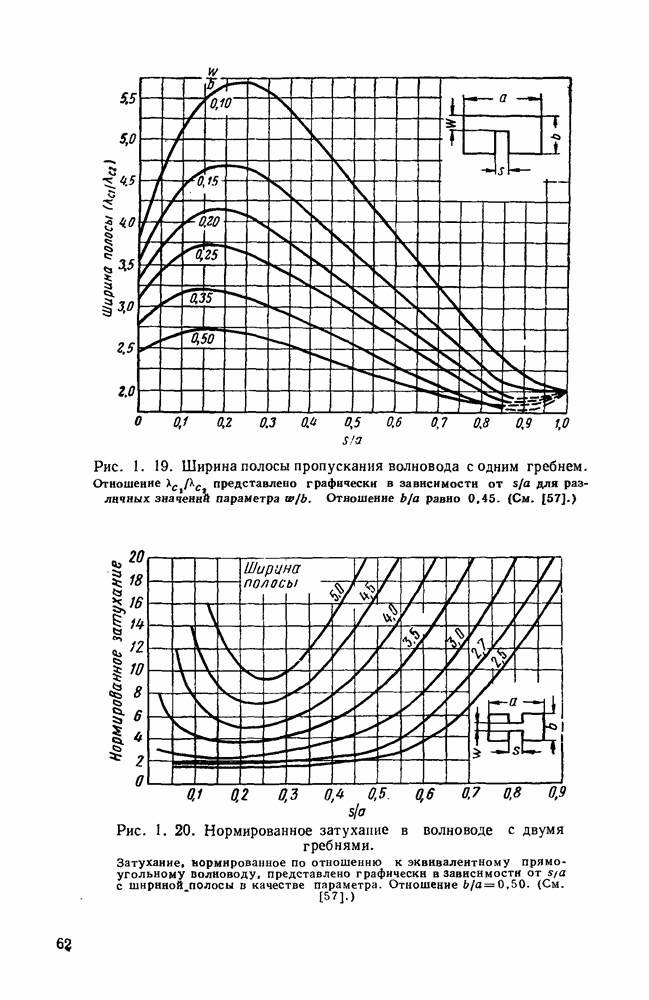
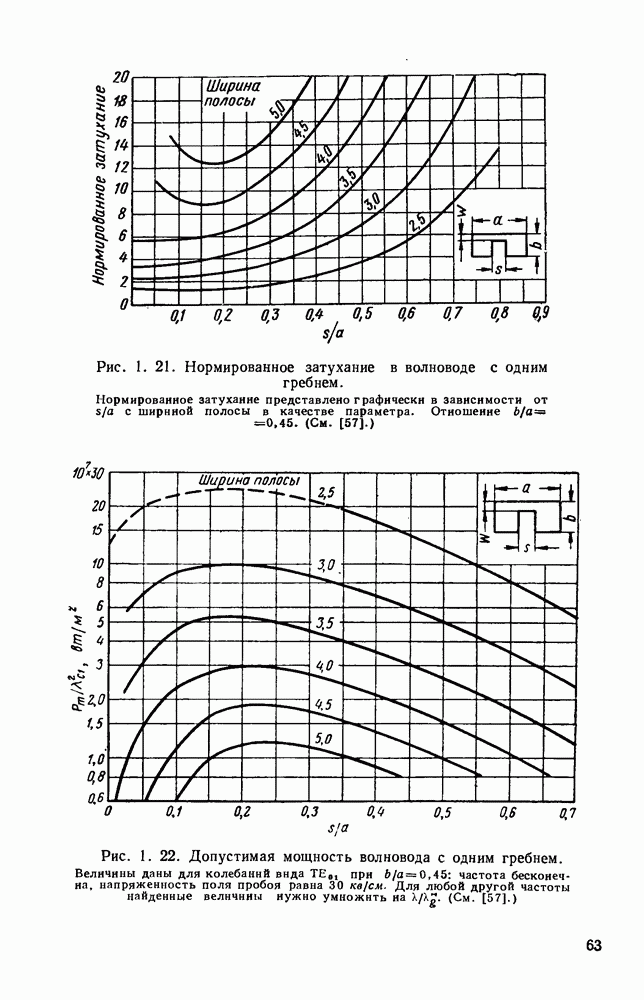
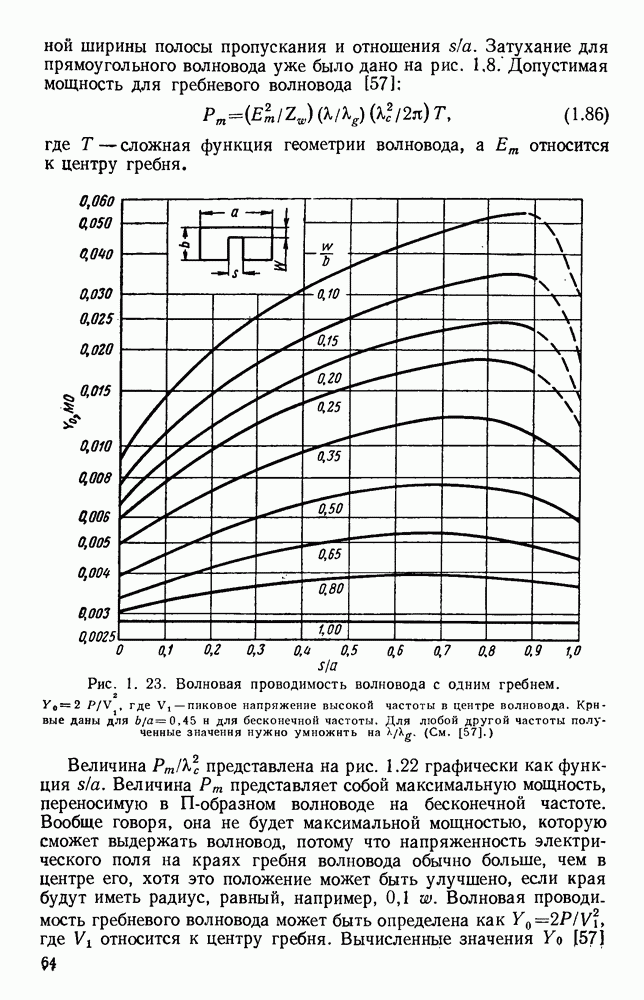
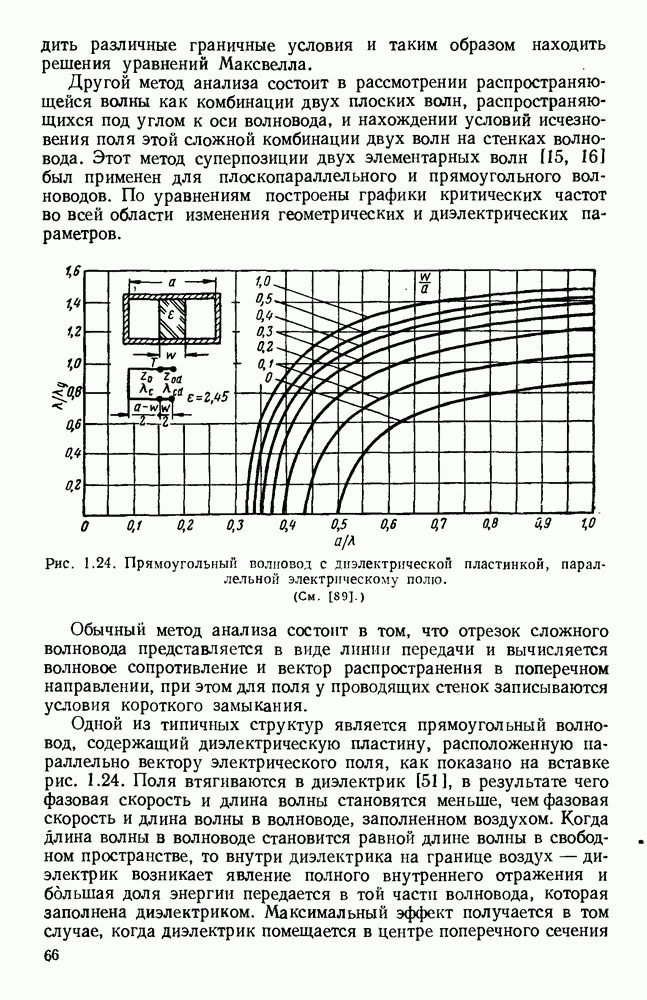
- 1.5.2. Гребневые волноводы
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
- 2.1.2. Круговая диаграмма
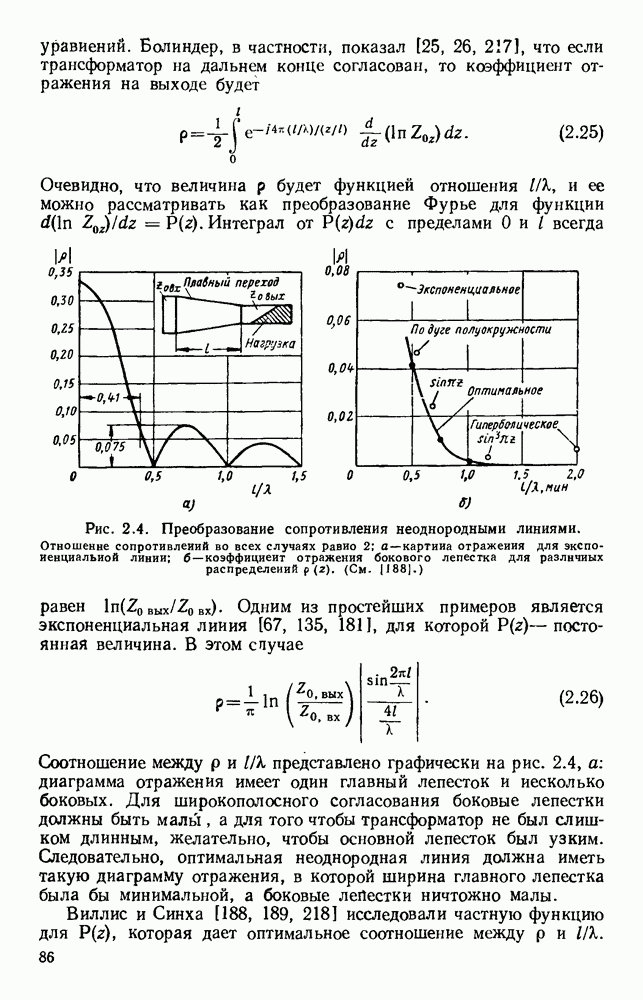
- 2.1.3. Широкополосное согласование
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
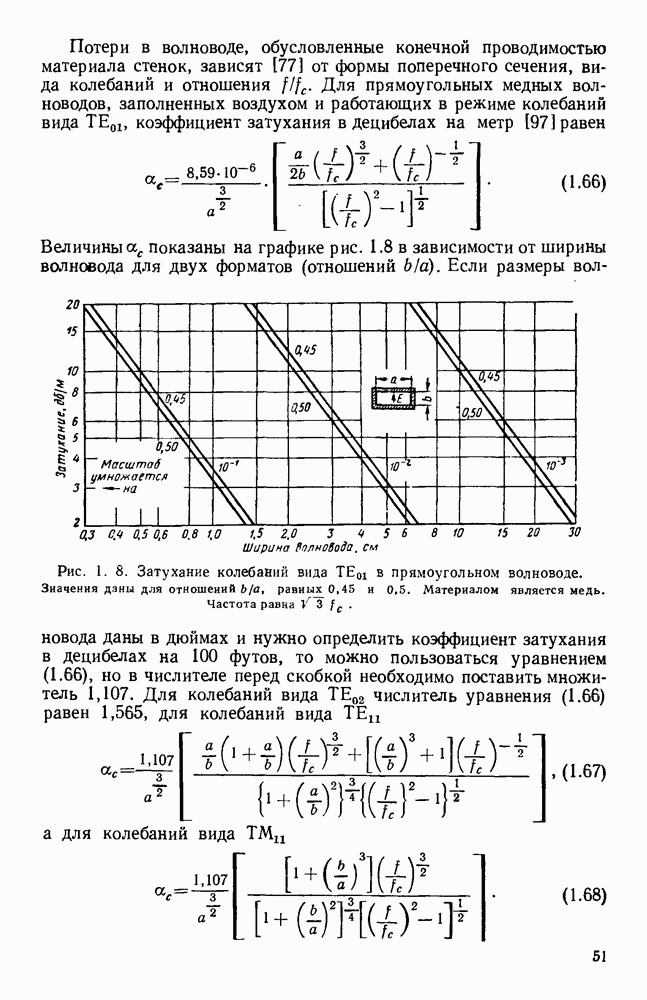
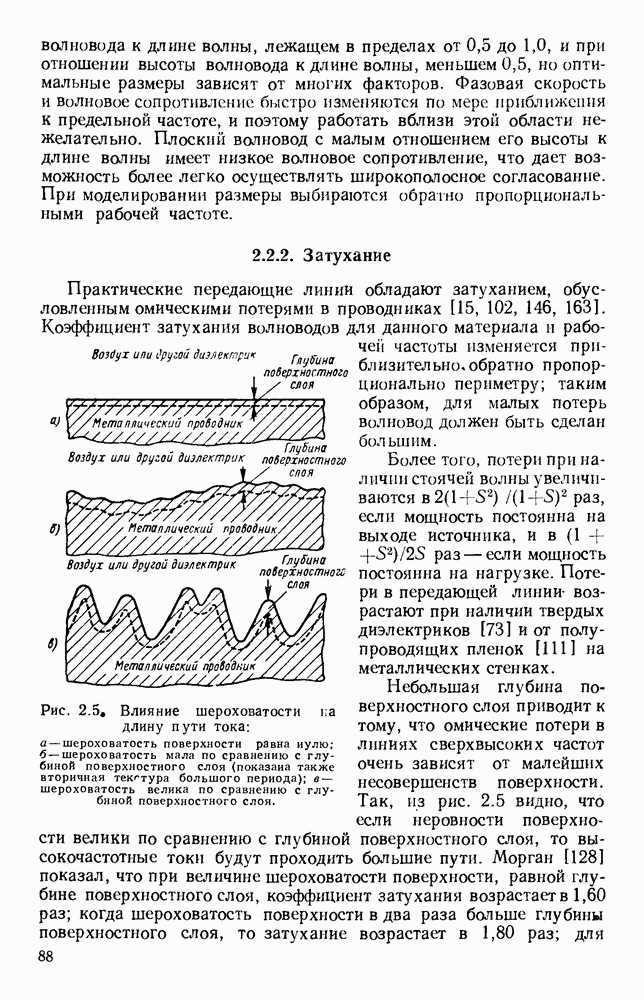
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
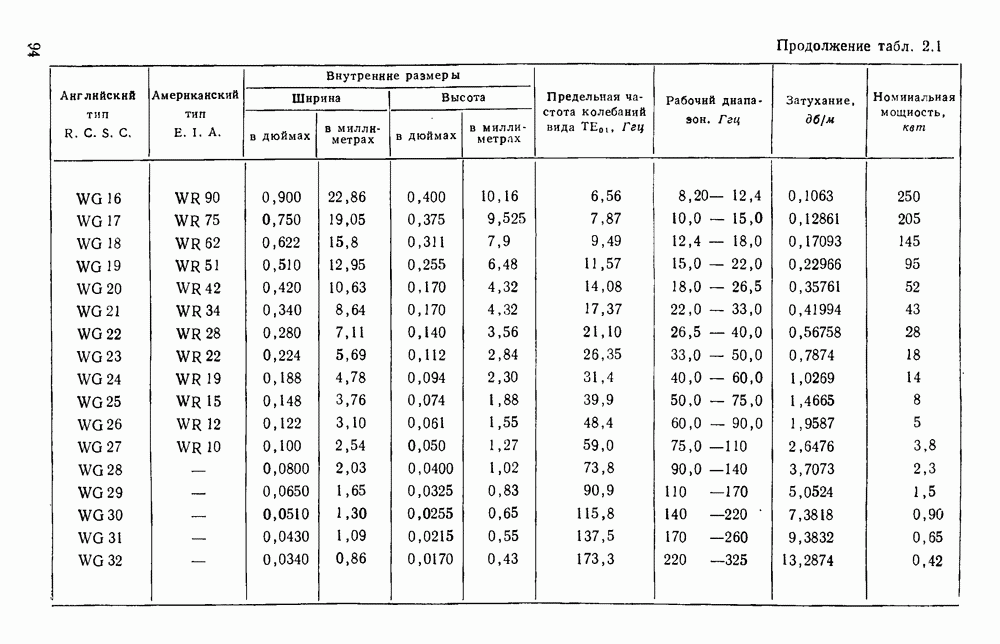
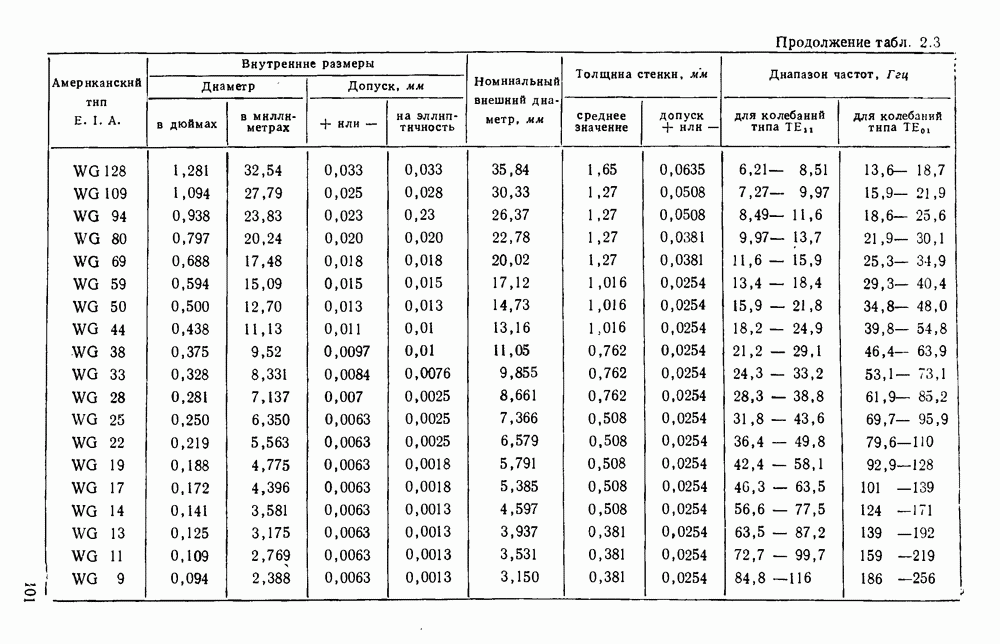
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
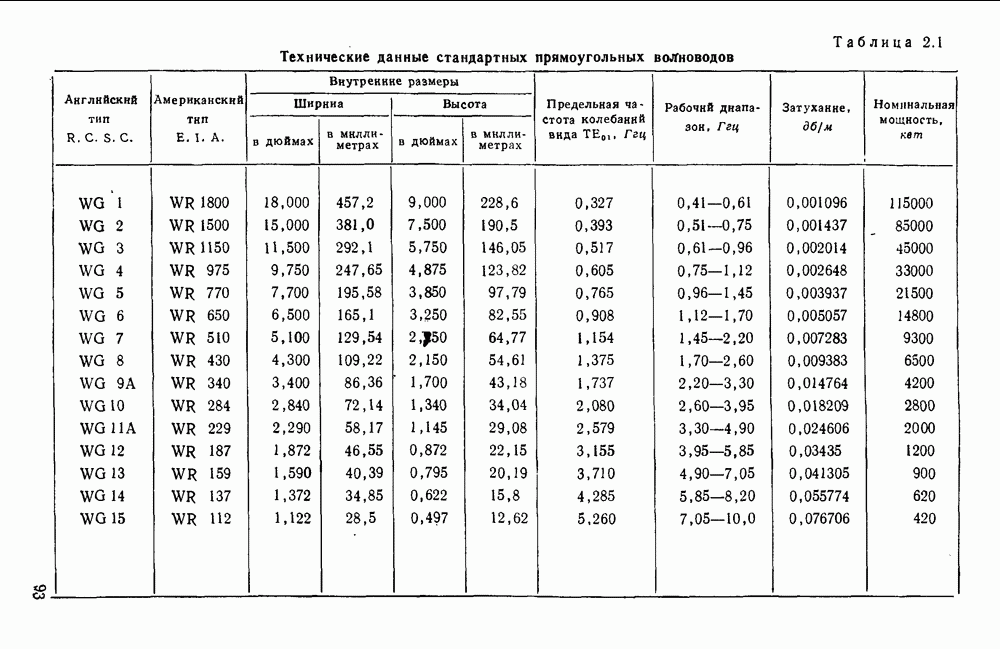
- 2.3.1. Прямоугольные волноводы
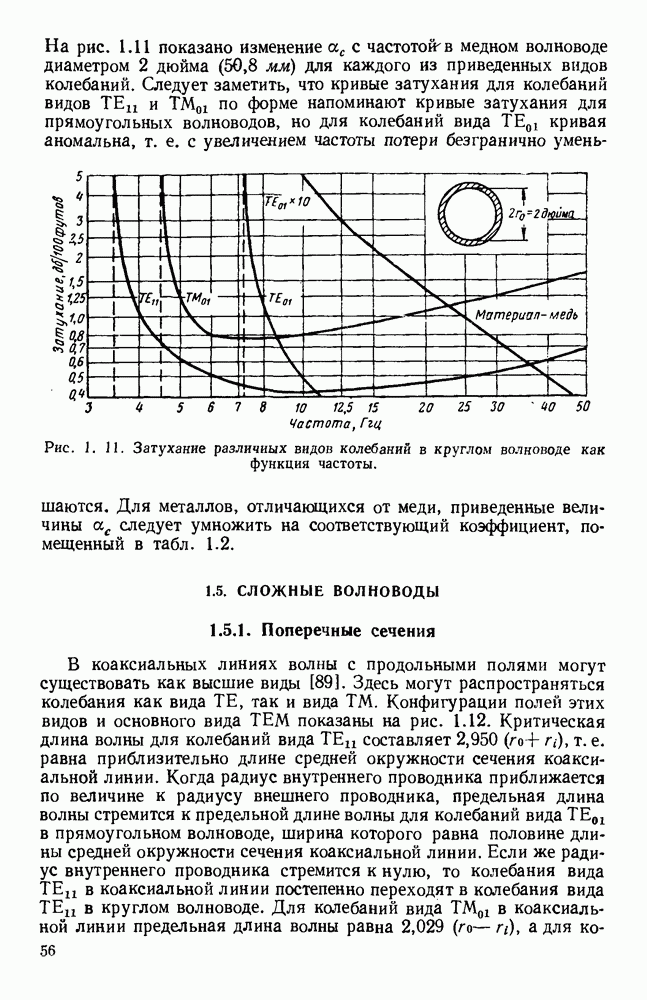
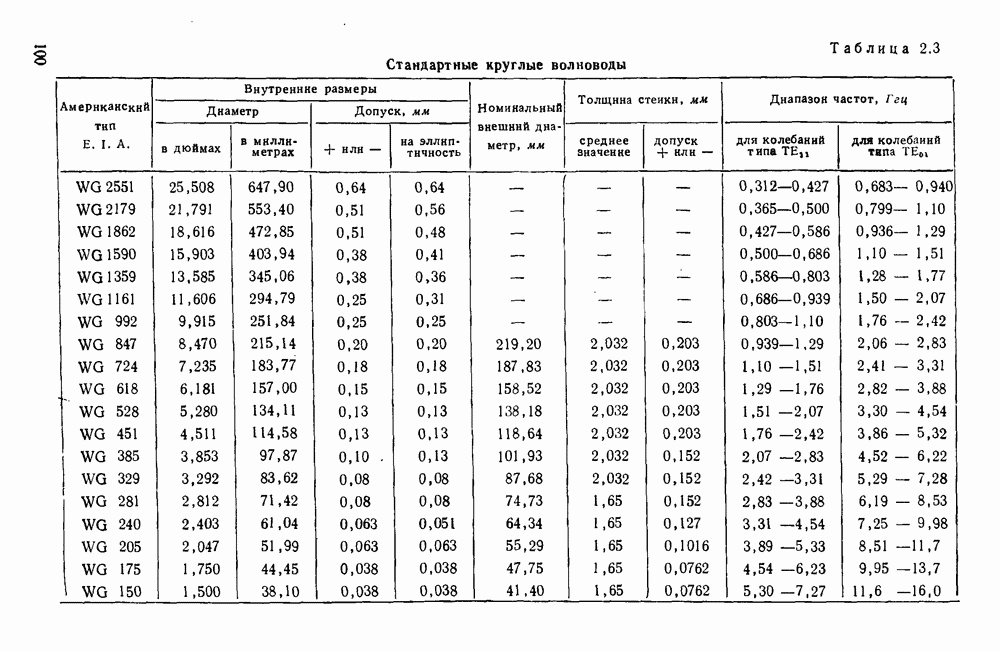
- 2.3.2. Круглые волноводы
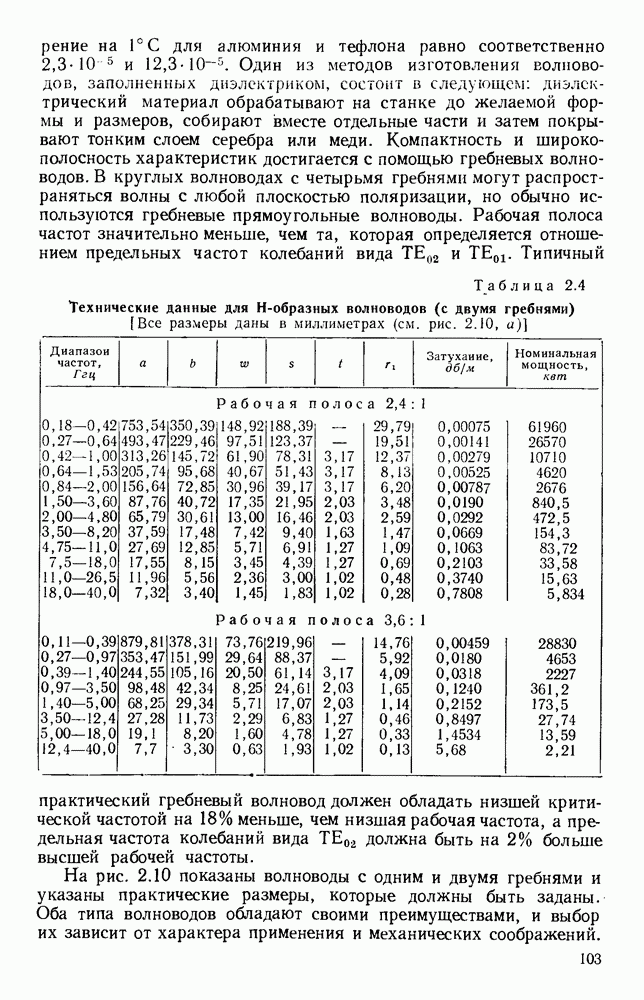
- 2.3.3. Широкополосные и компактные волноводы
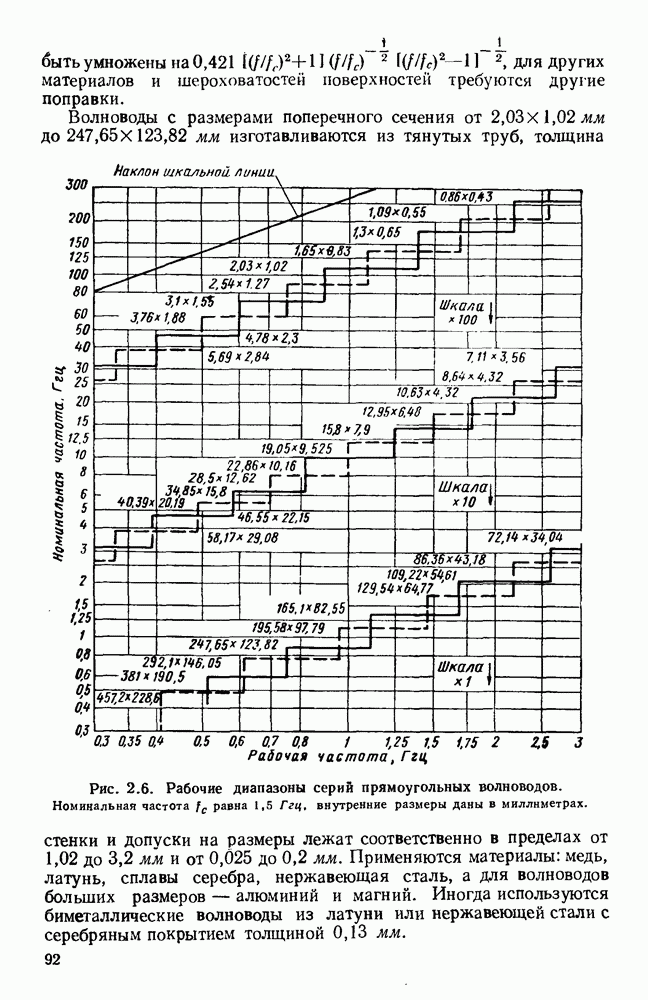
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
- 2.4.2. Контактные прокладки и дроссели
- 2.4.3. Крепежные и зажимные устройства
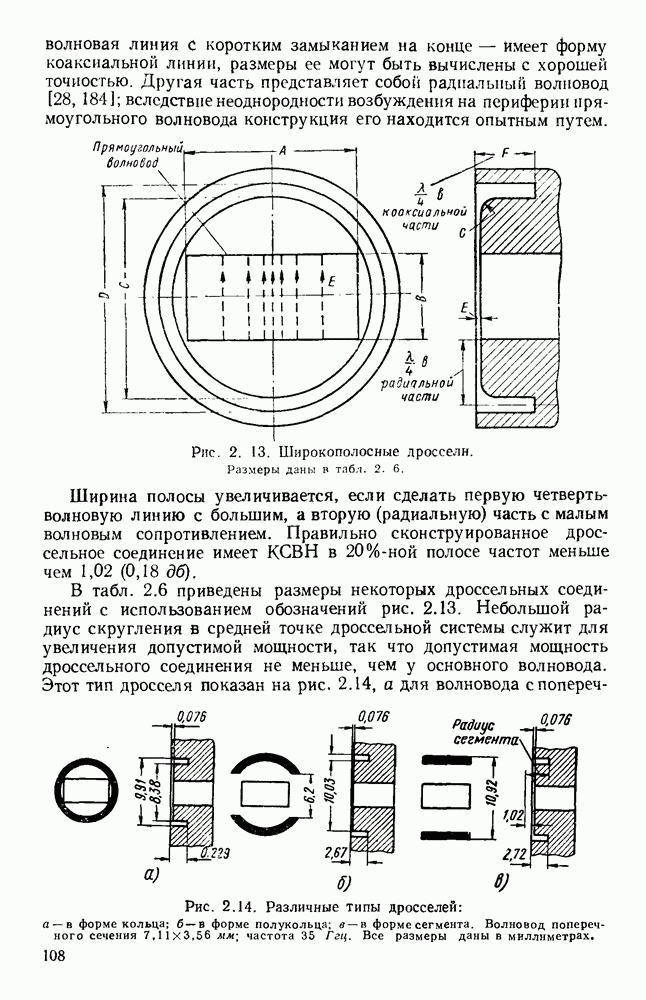
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
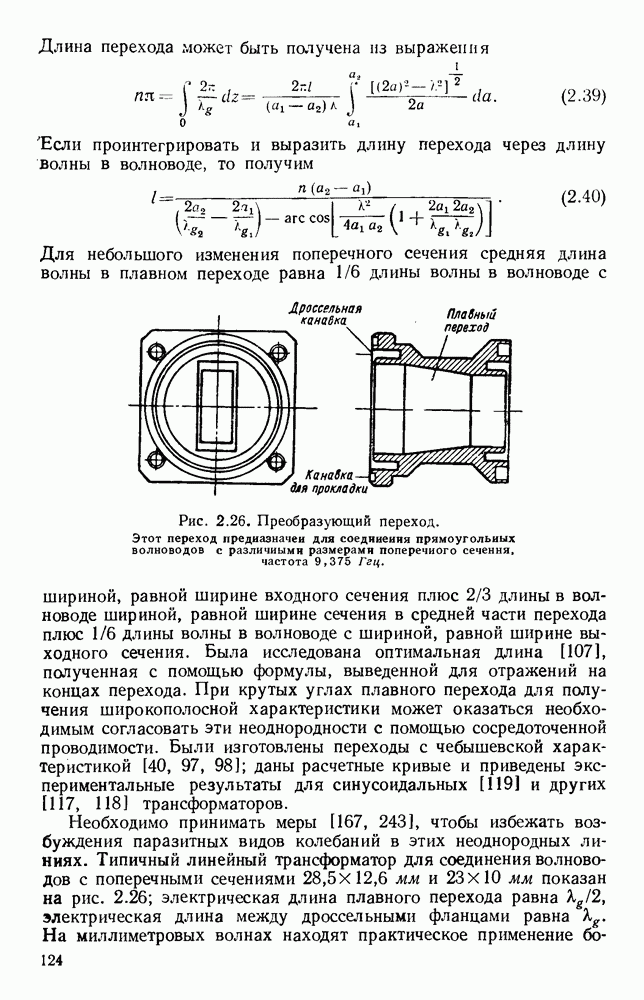
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
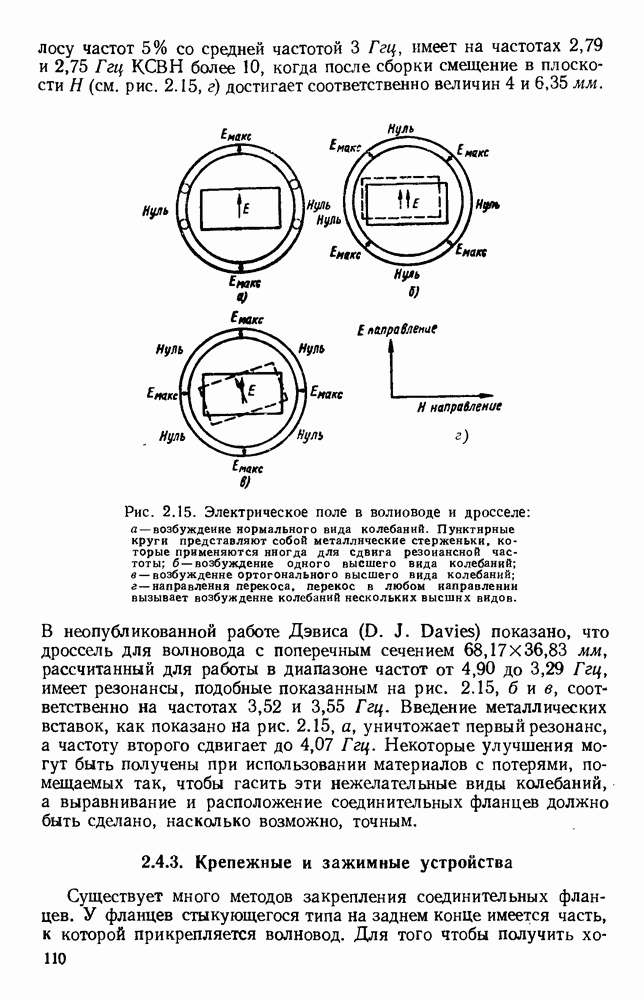
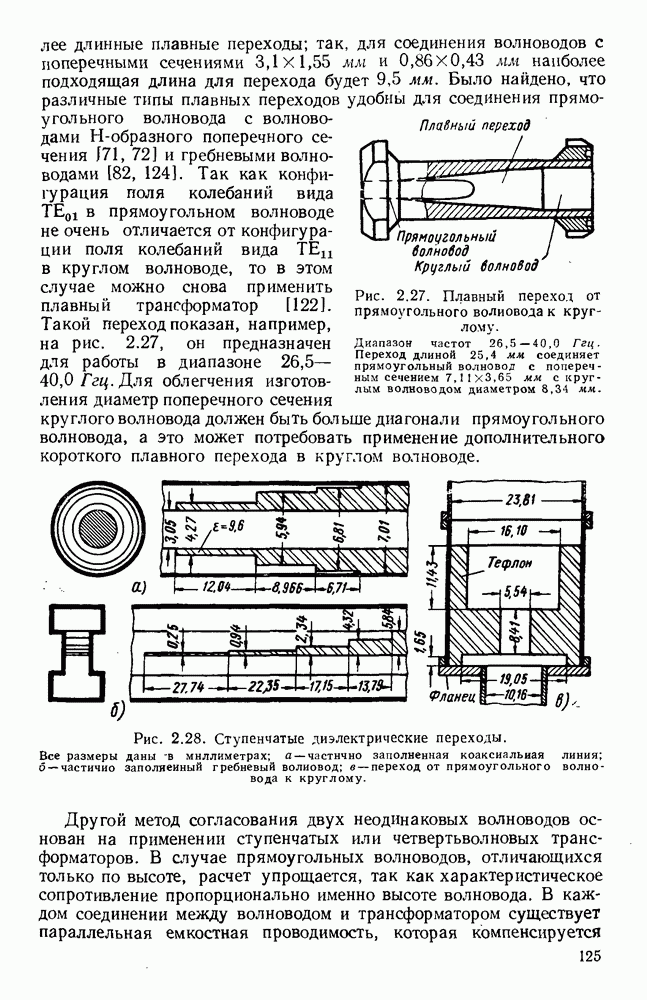
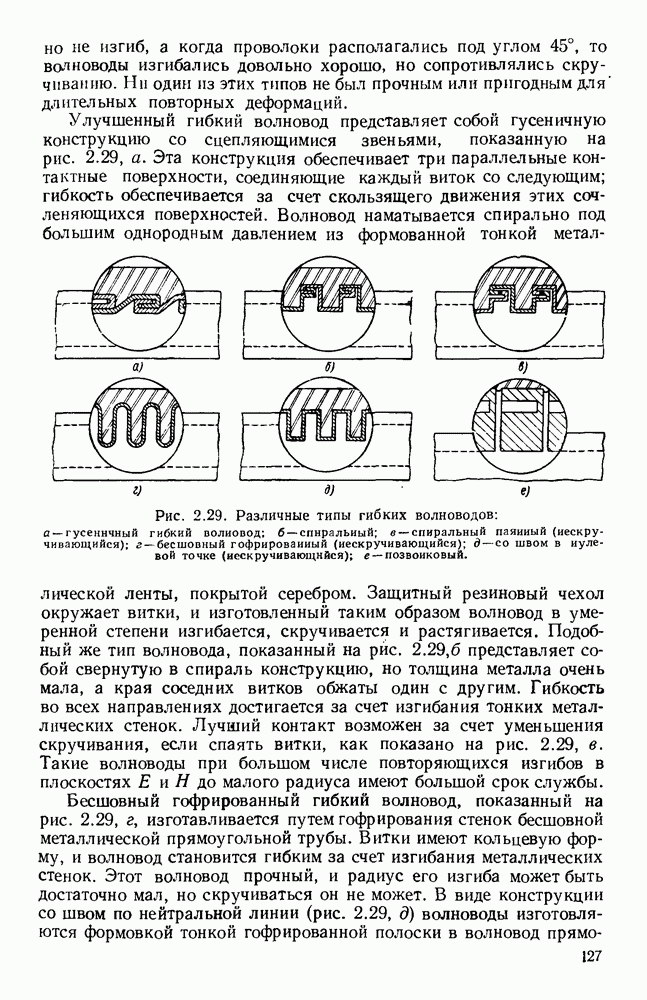
- 2.6.1. Изгибы, уголки и скрутки
- 2.6.2. Переходы и преобразователи
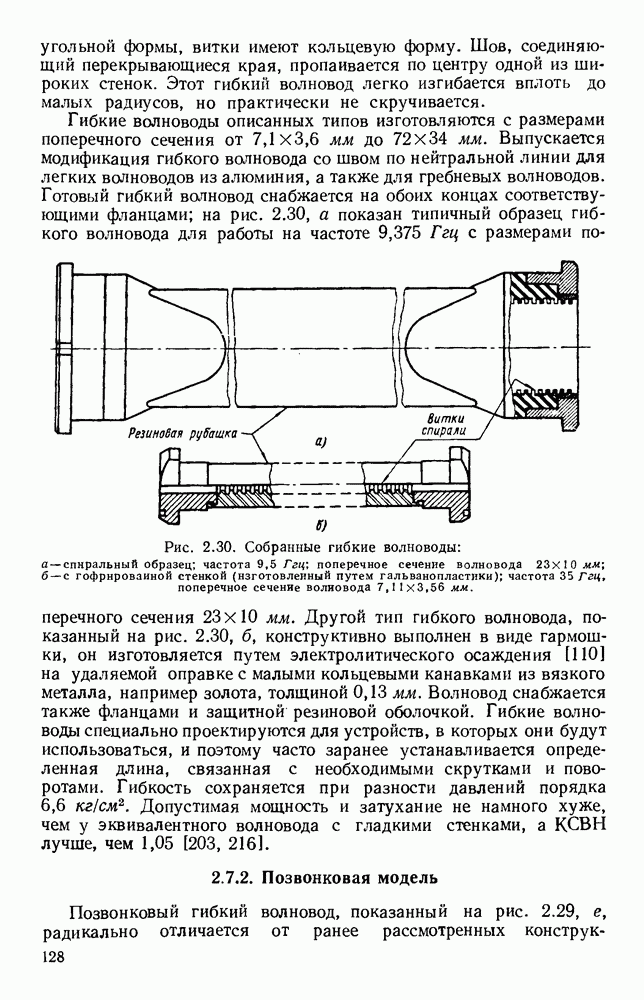
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
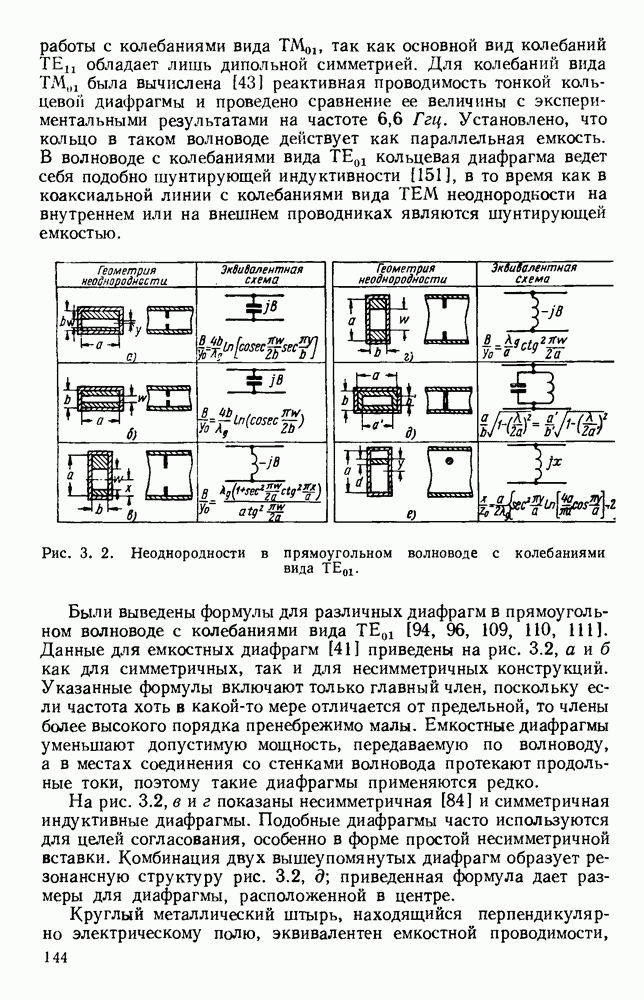
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
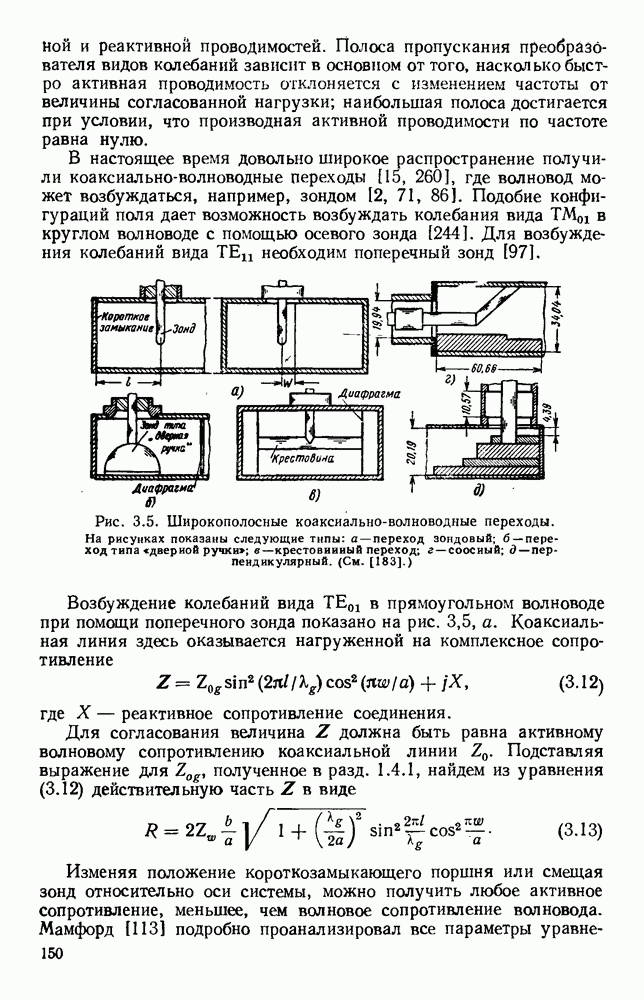
- 3.2.3. Переход от линейной поляризации к круговой
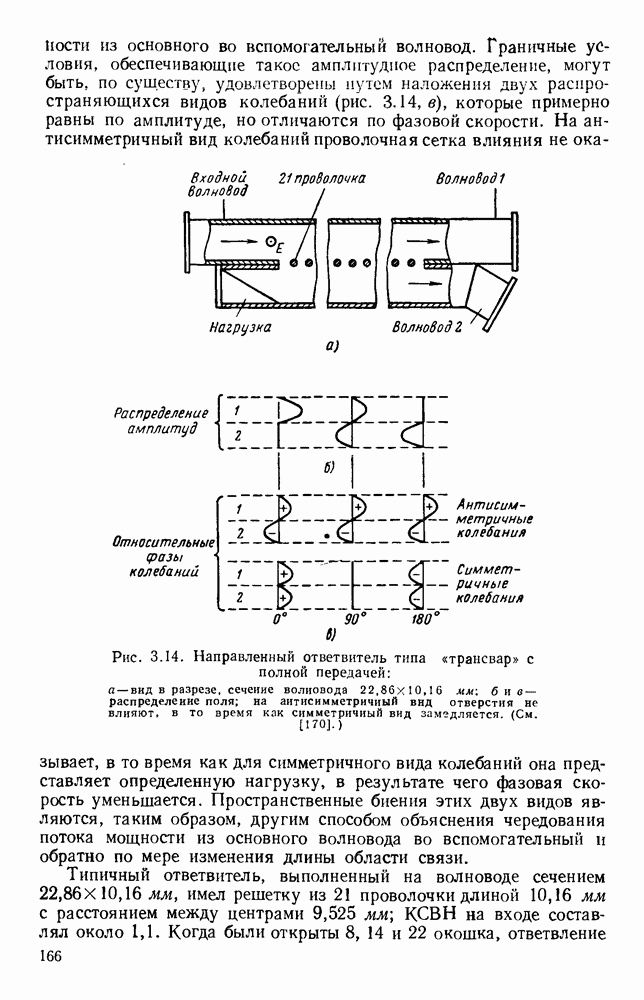
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
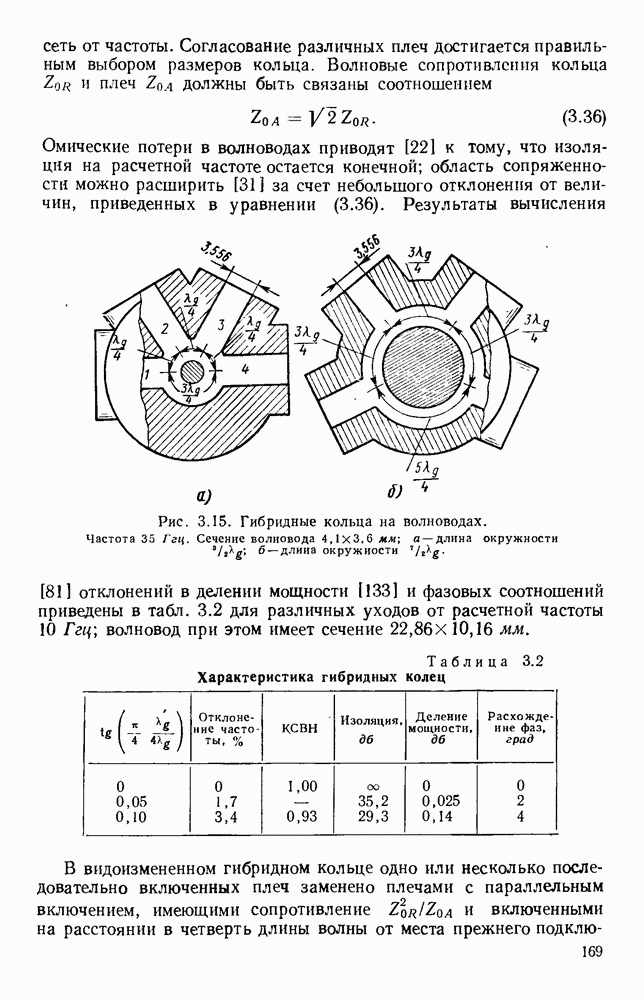
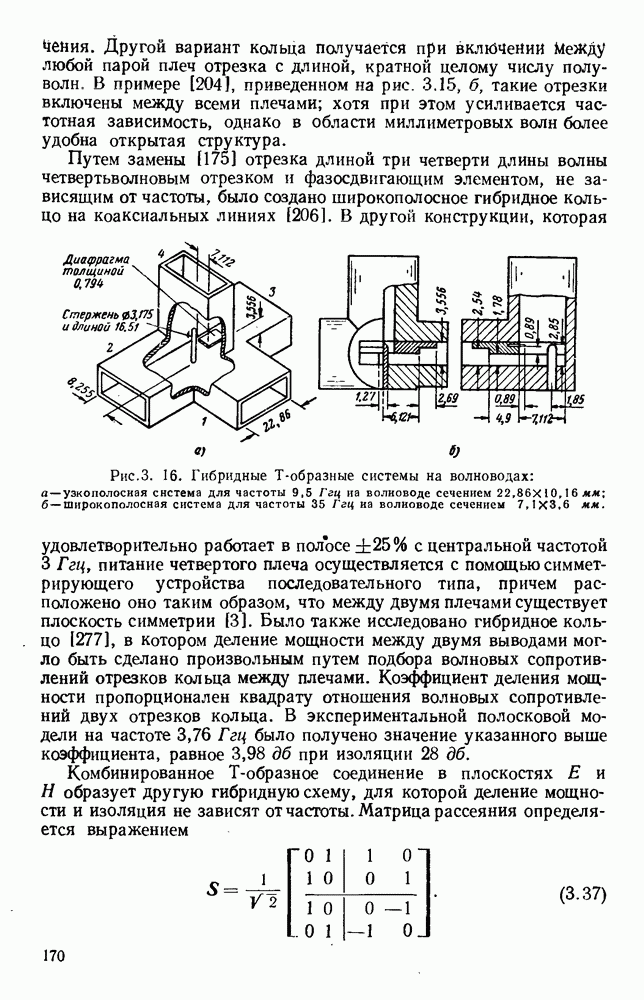
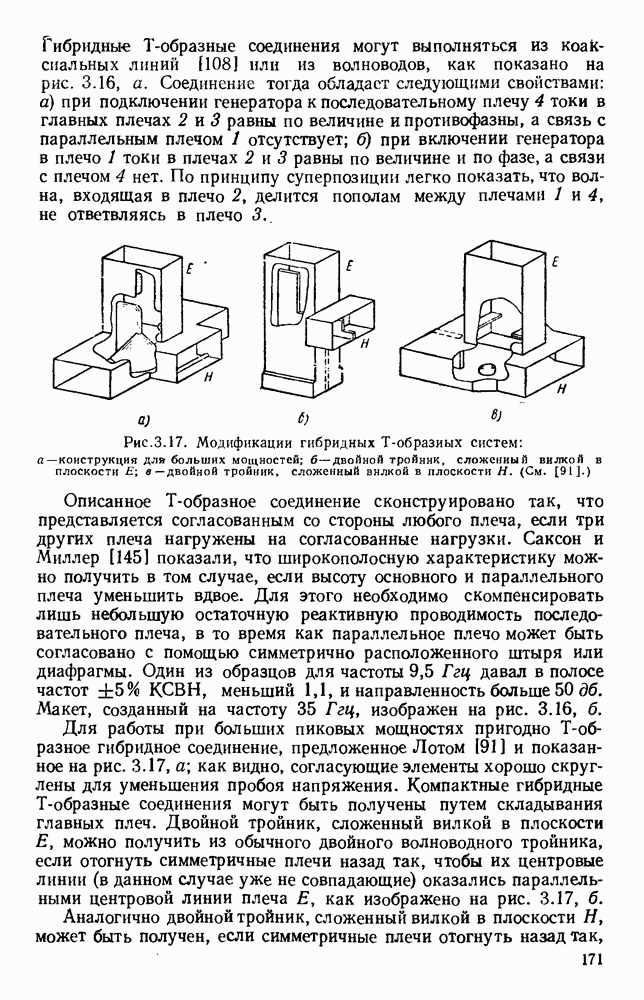
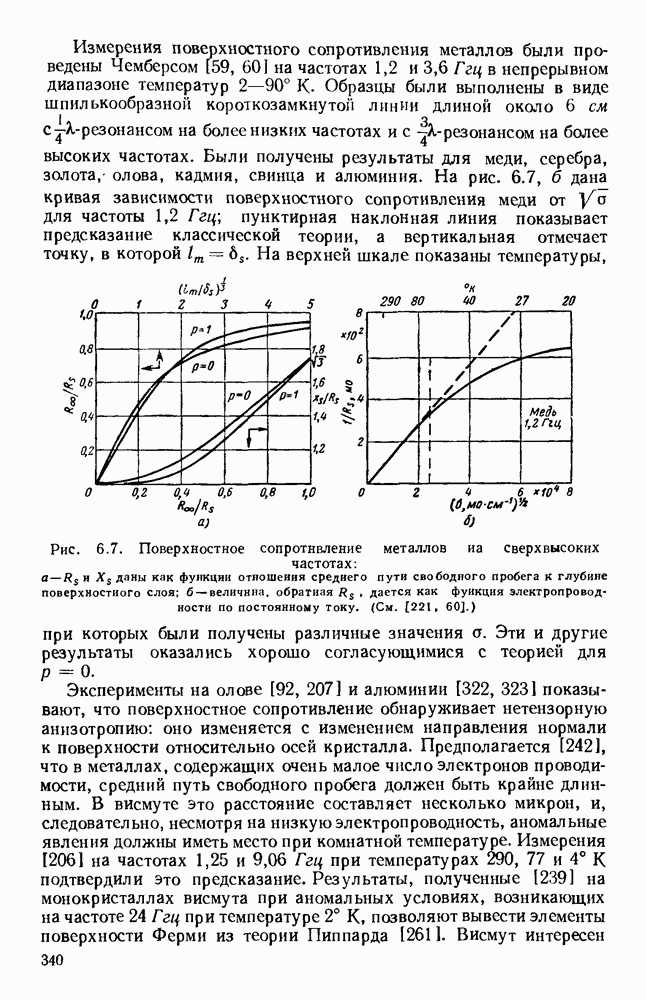
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
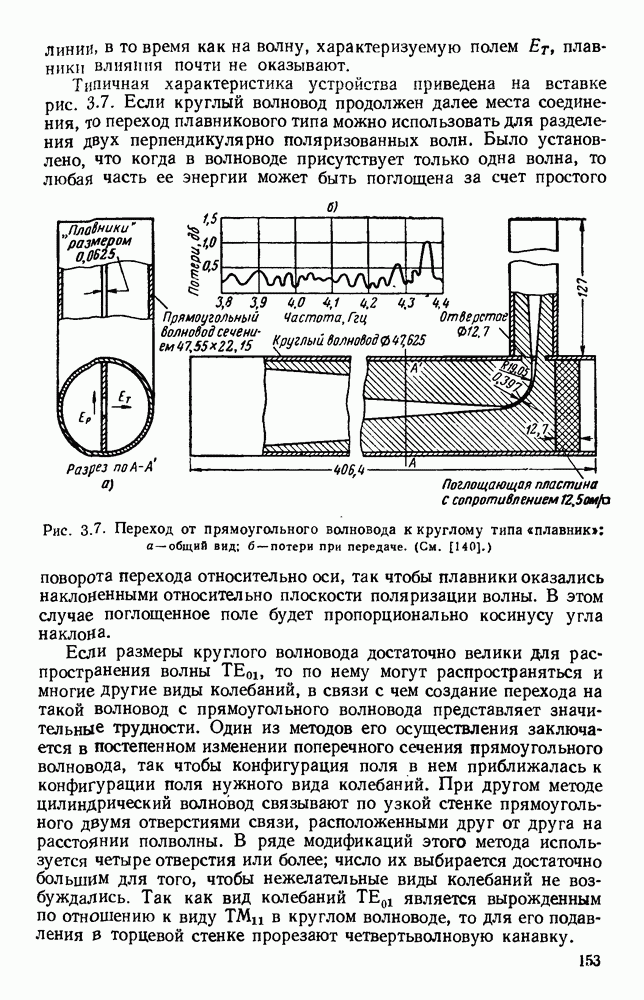
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
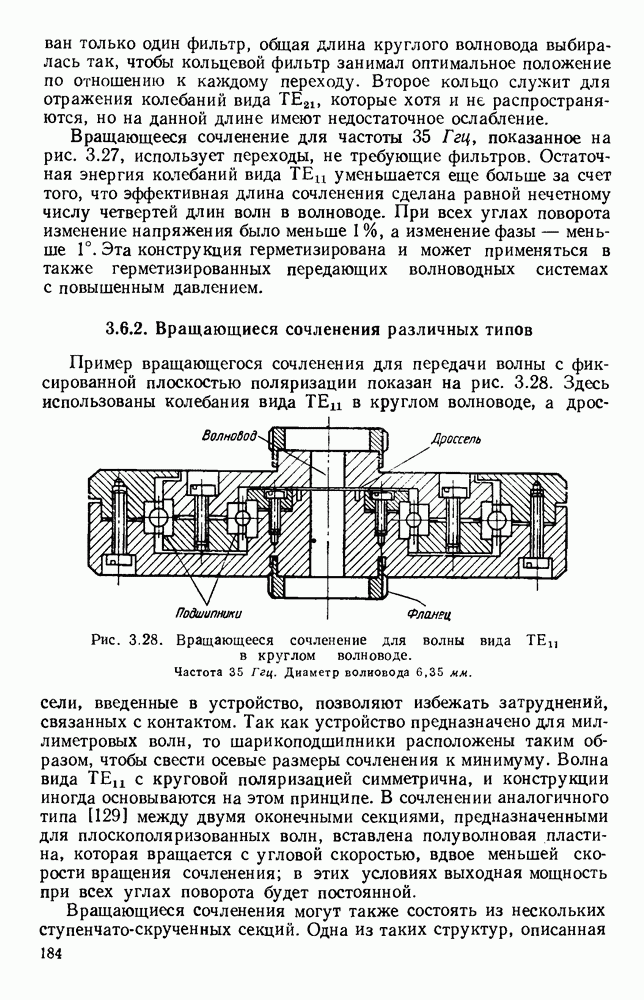
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
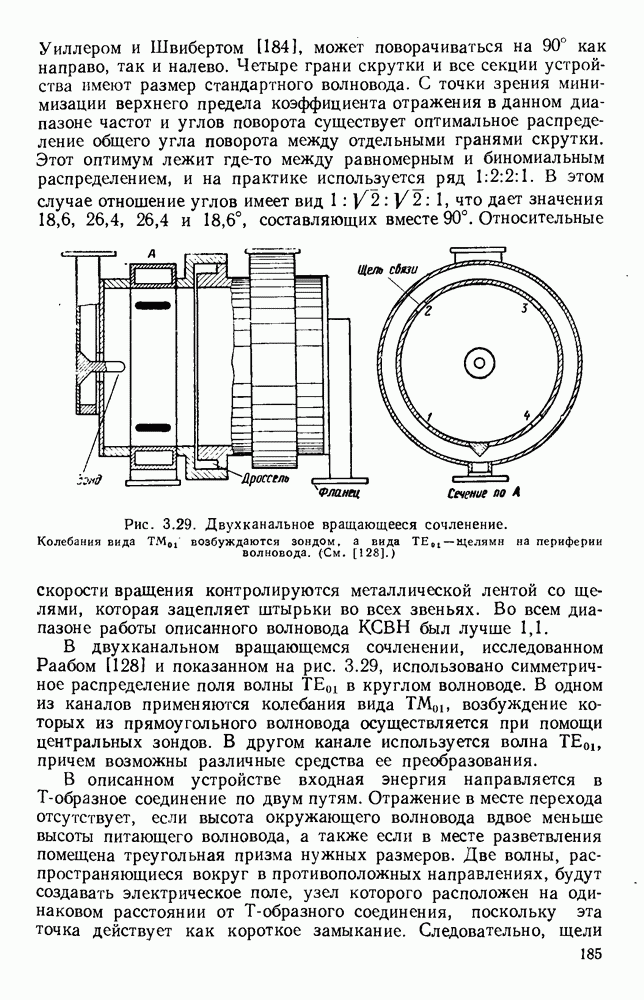
- 3.6.2. Вращающиеся сочленения различных типов
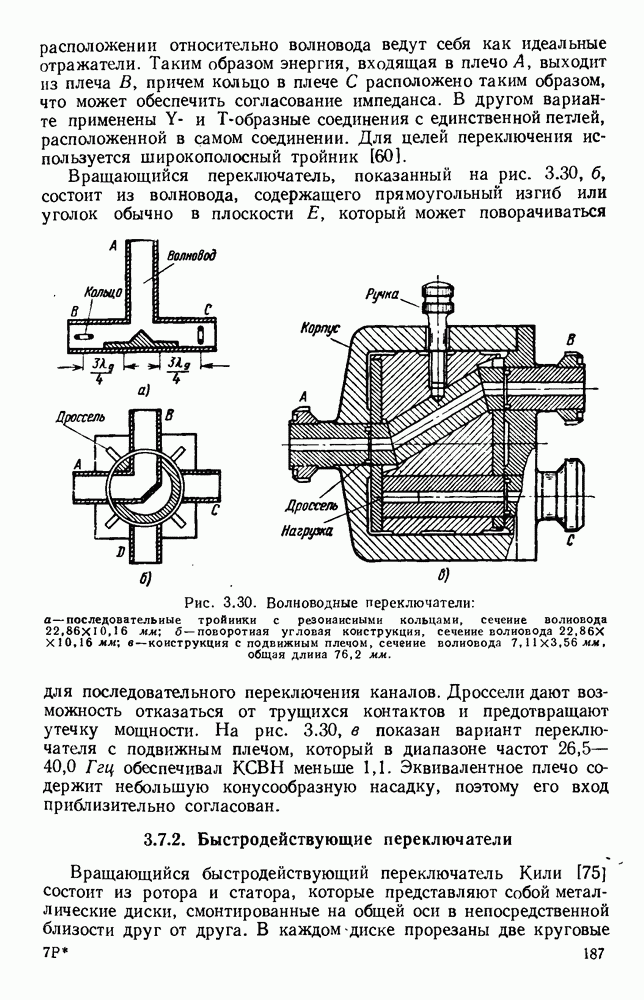
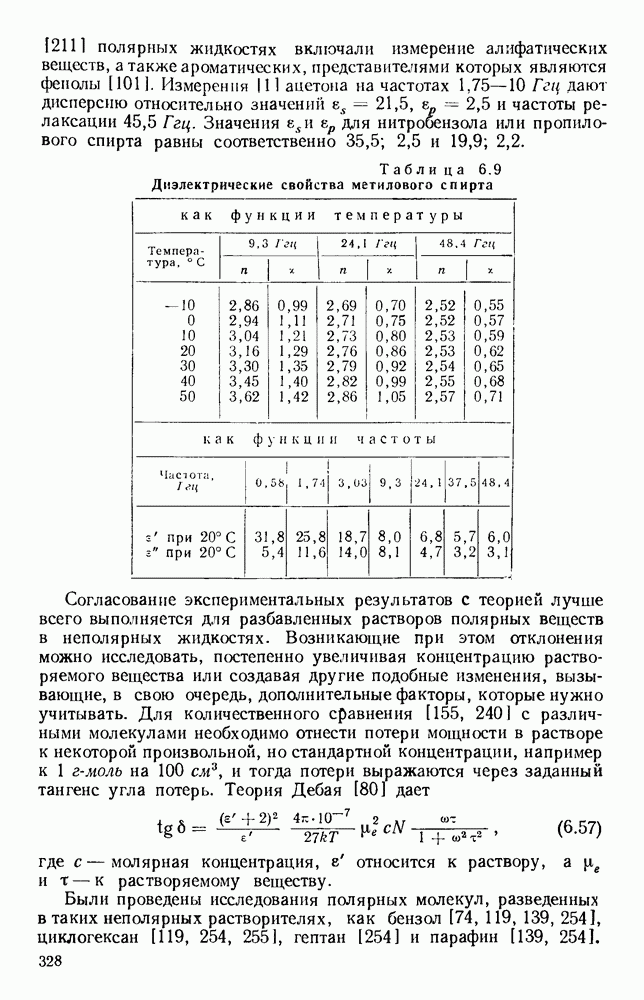
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
- 3.7.1. Механические переключатели с ручным управлением
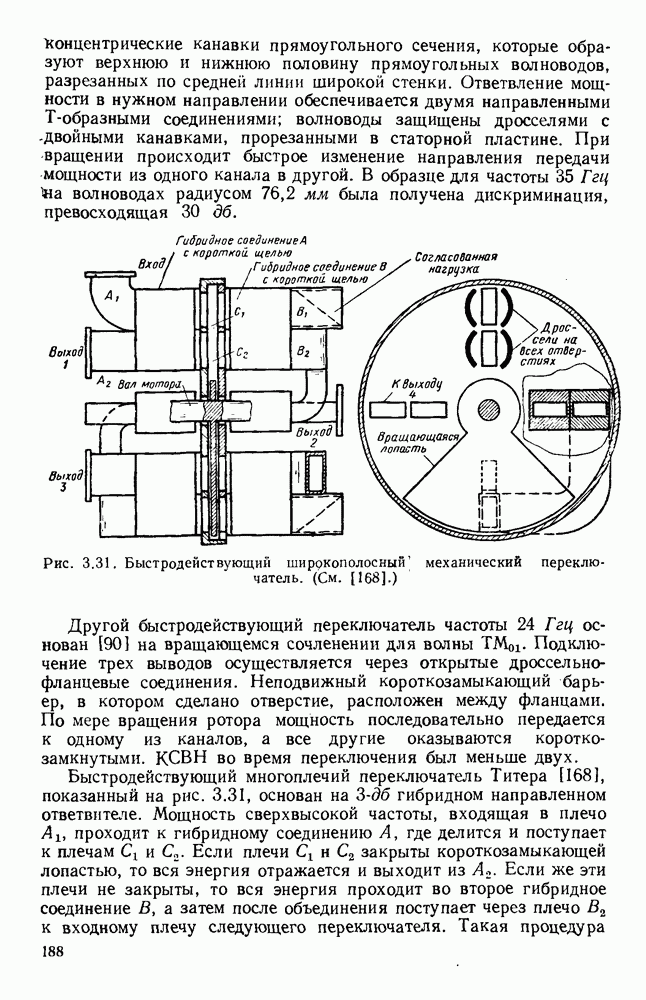
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
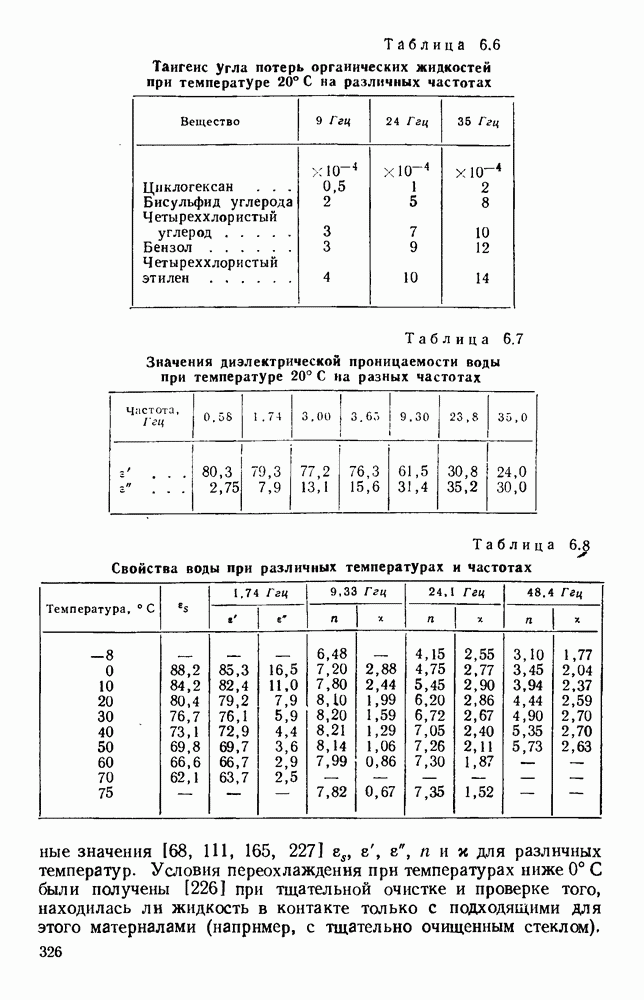
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
- 5.2.1. Волномеры с объемными резонаторами
- 5.2.2. Волноводные интерферометры
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
- 5.3.2. Связанные резонаторы
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
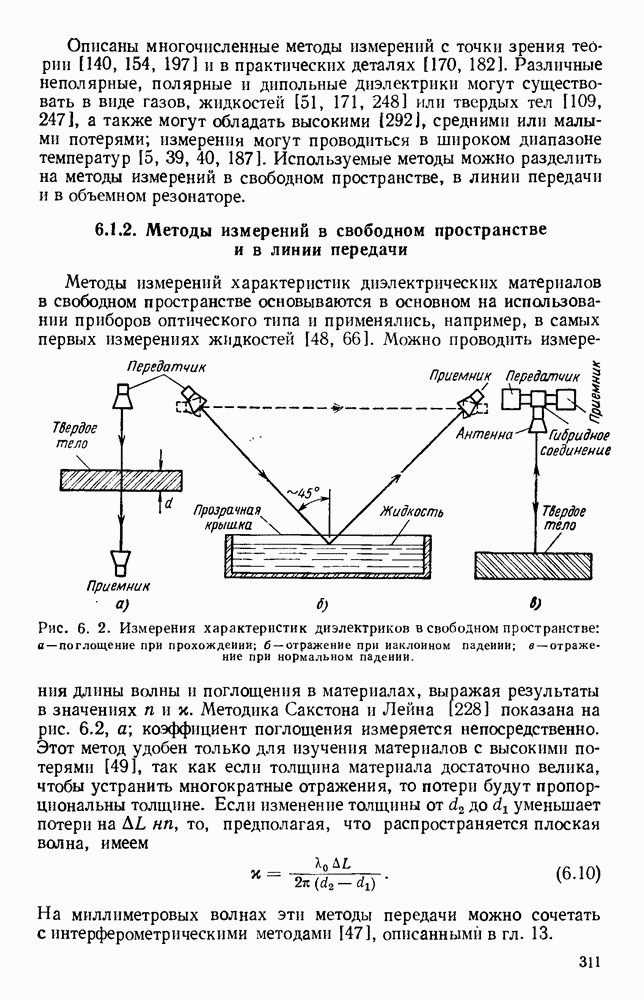
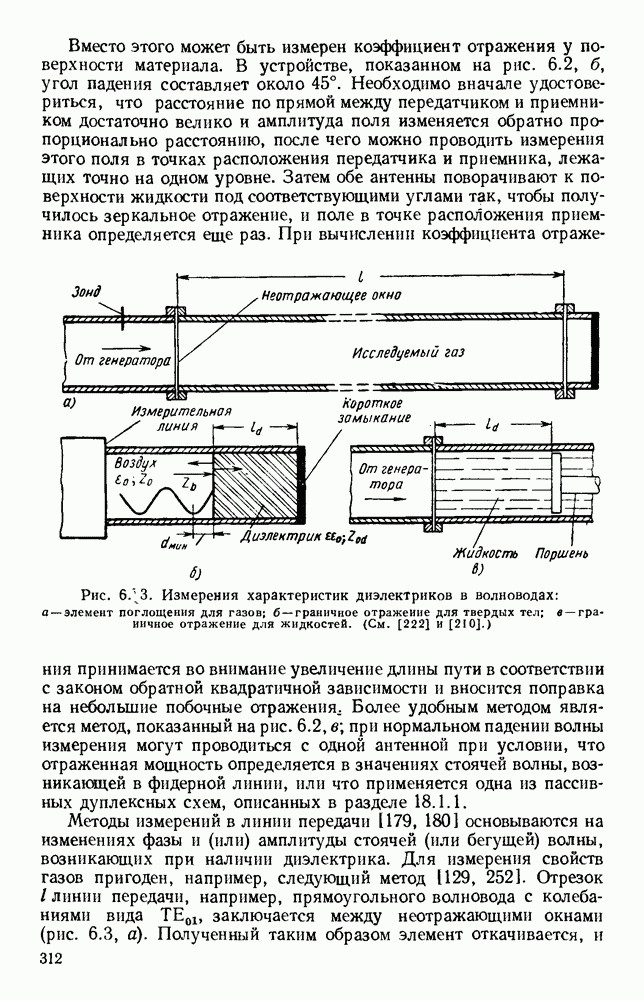
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
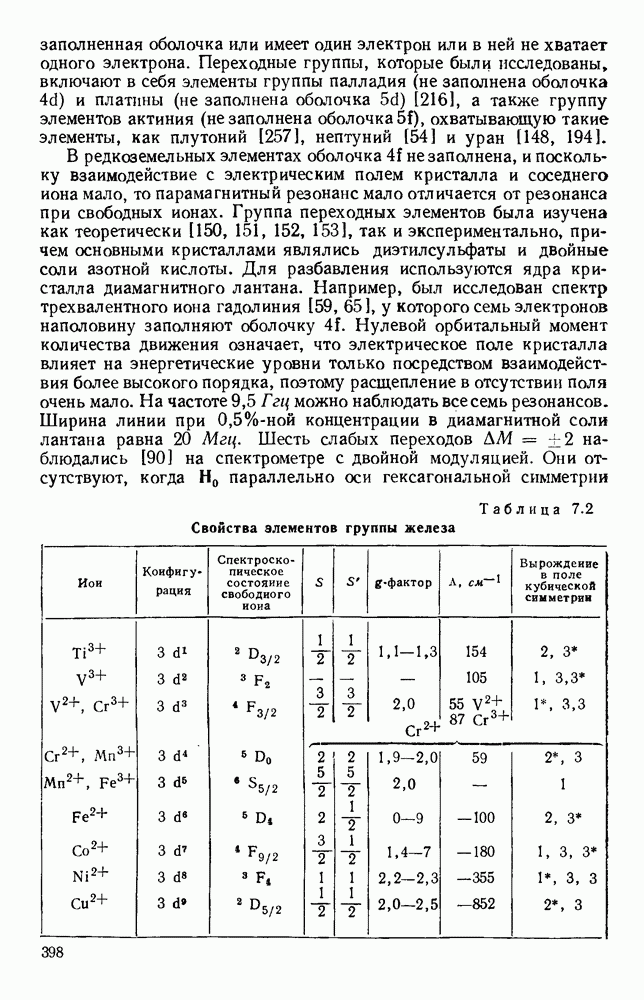
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
- 7.1.2. Форма линии и интенсивность
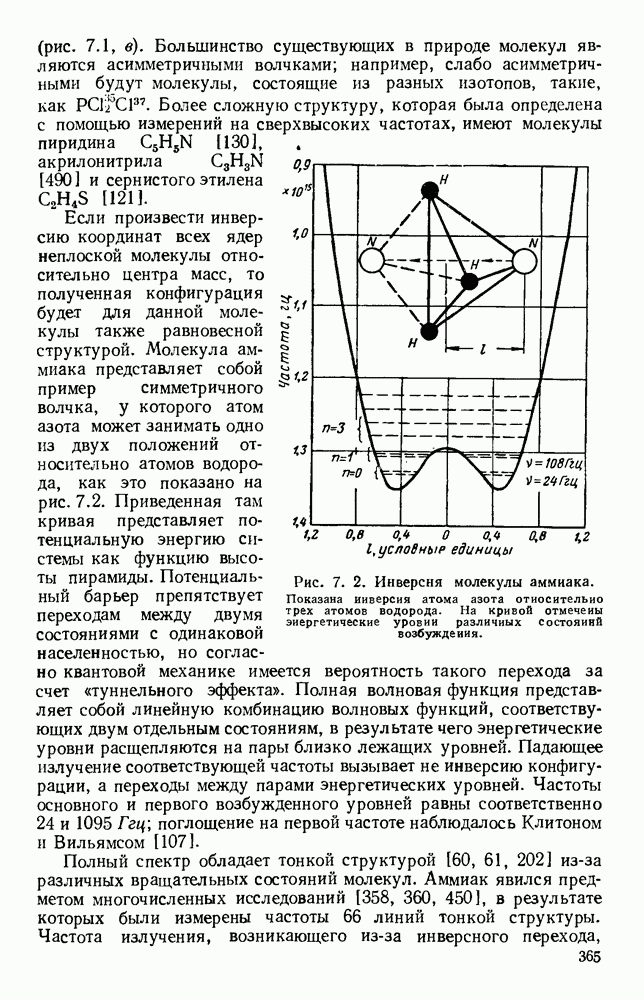
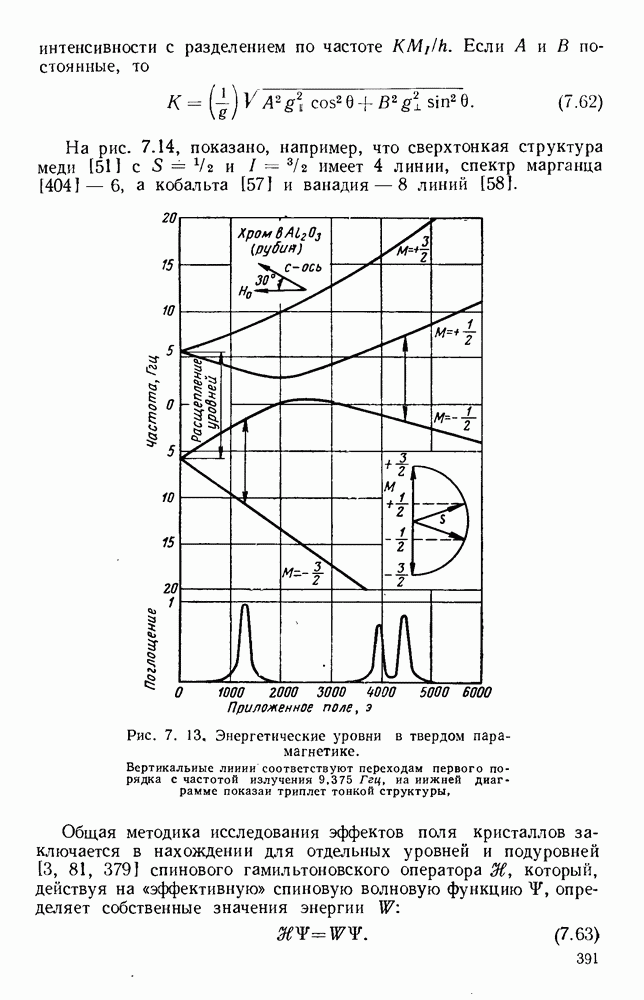
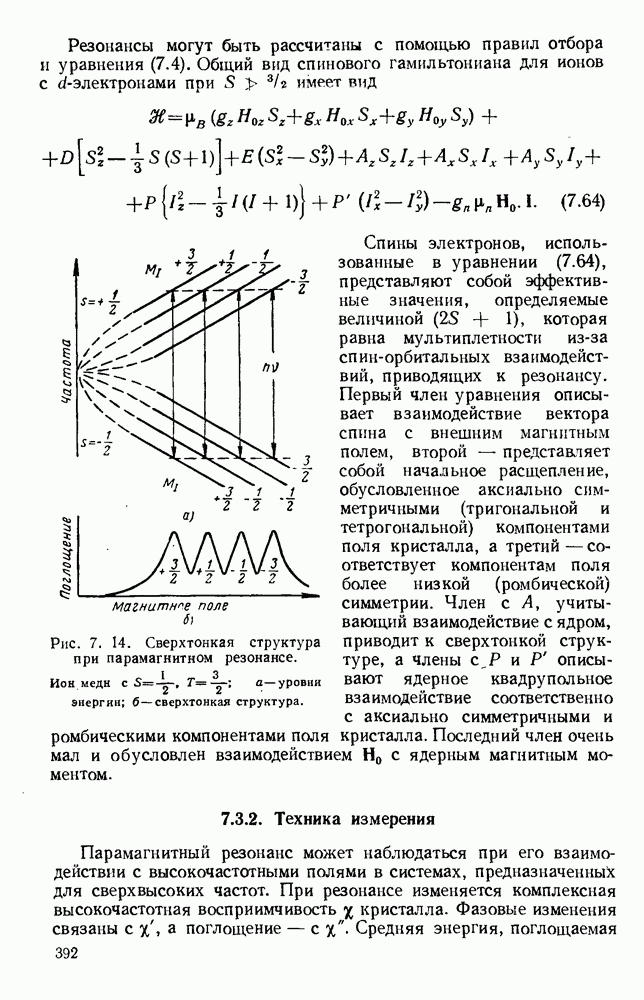
- 7.1.3. Сверхтонкая структура
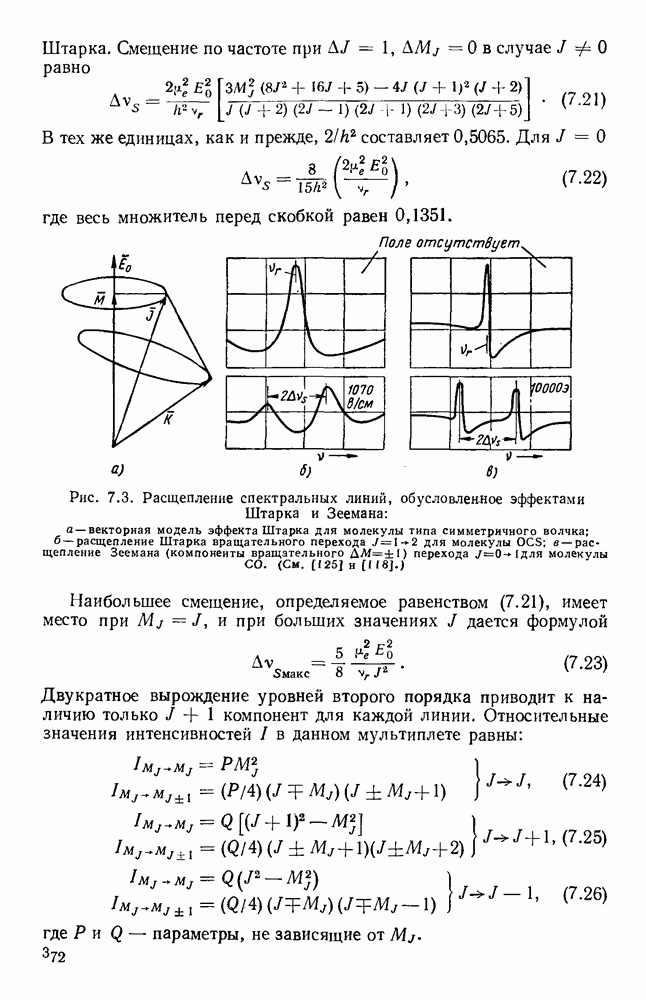
- 7.1.4. Явления Штарка и Зеемана
- 7.2. СПЕКТРОМЕТРЫ
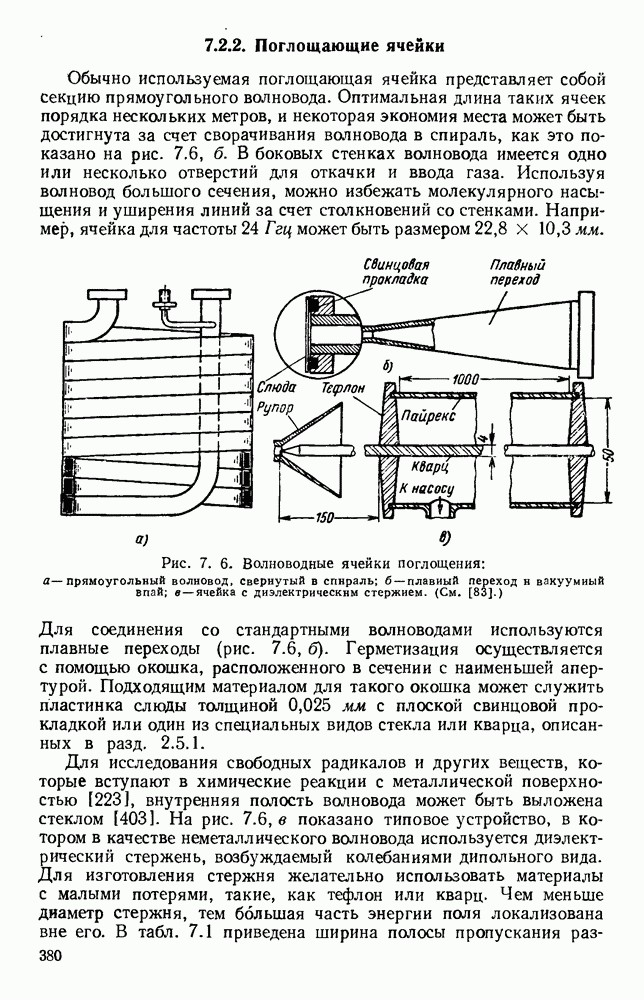
- 7.2.2. Поглощающие ячейки
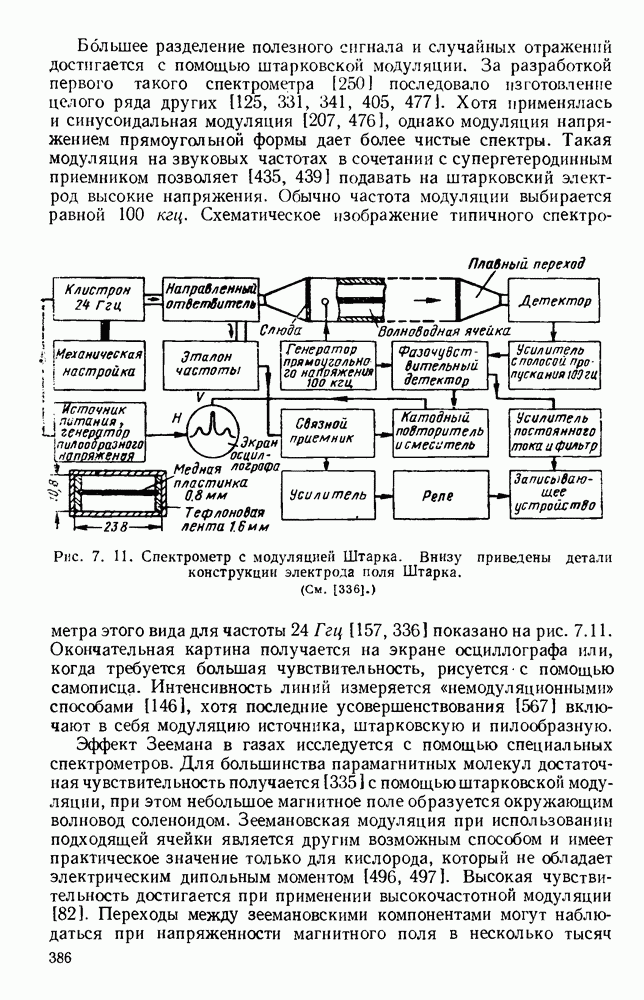
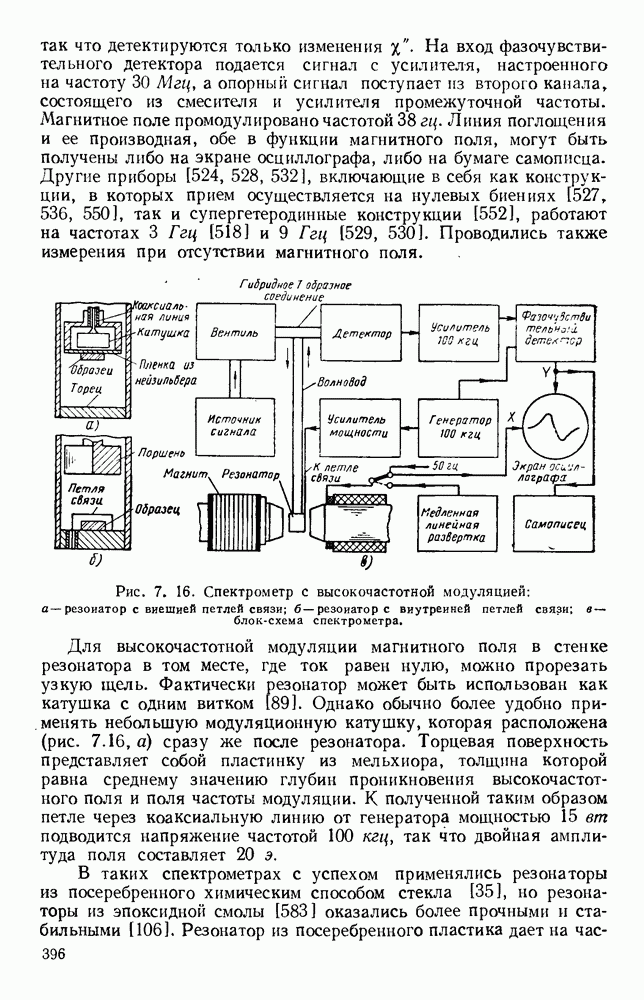
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
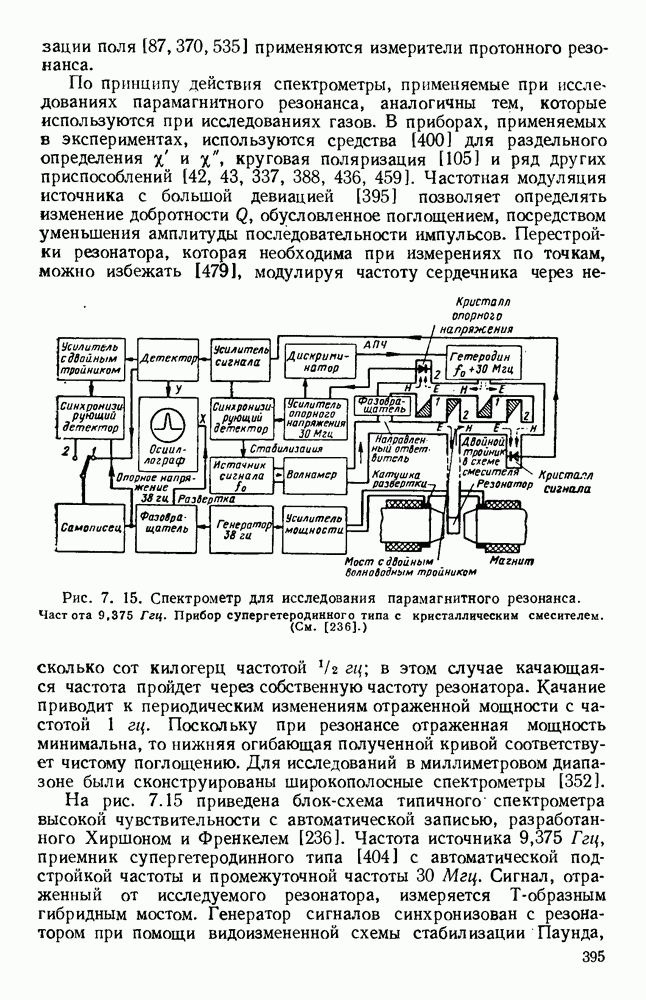
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
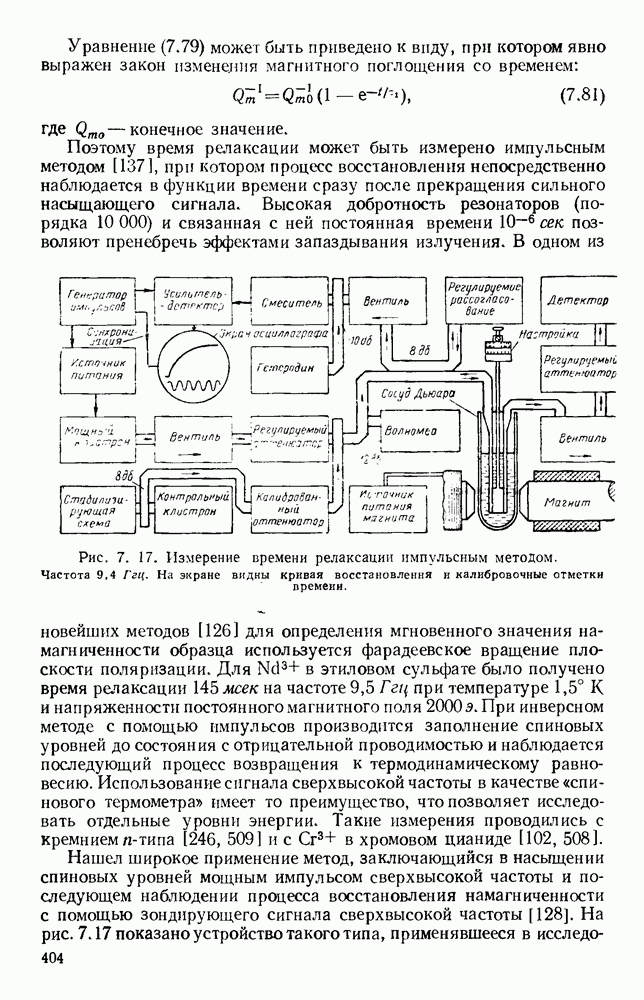
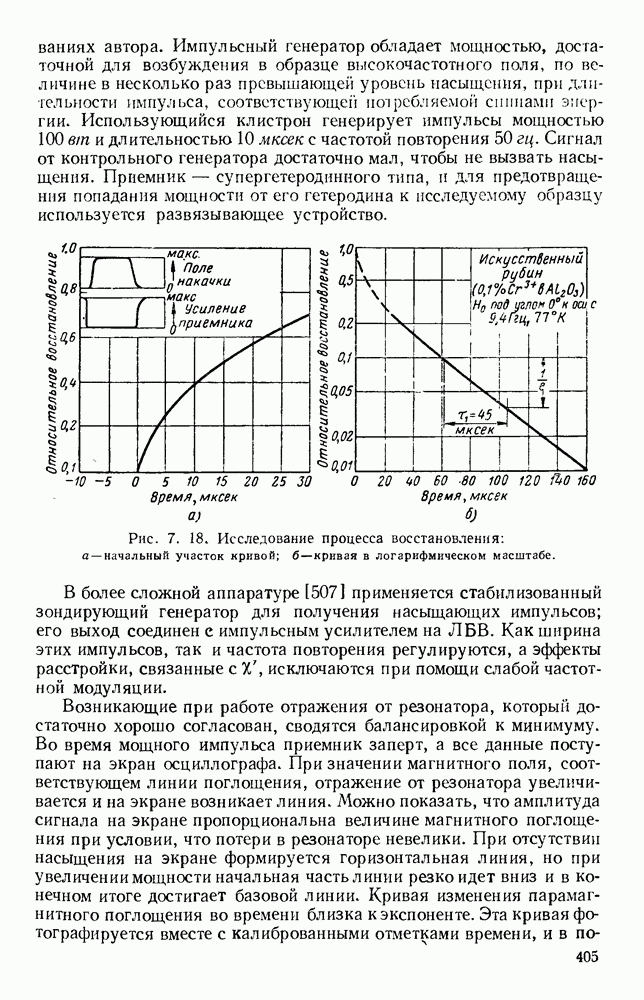
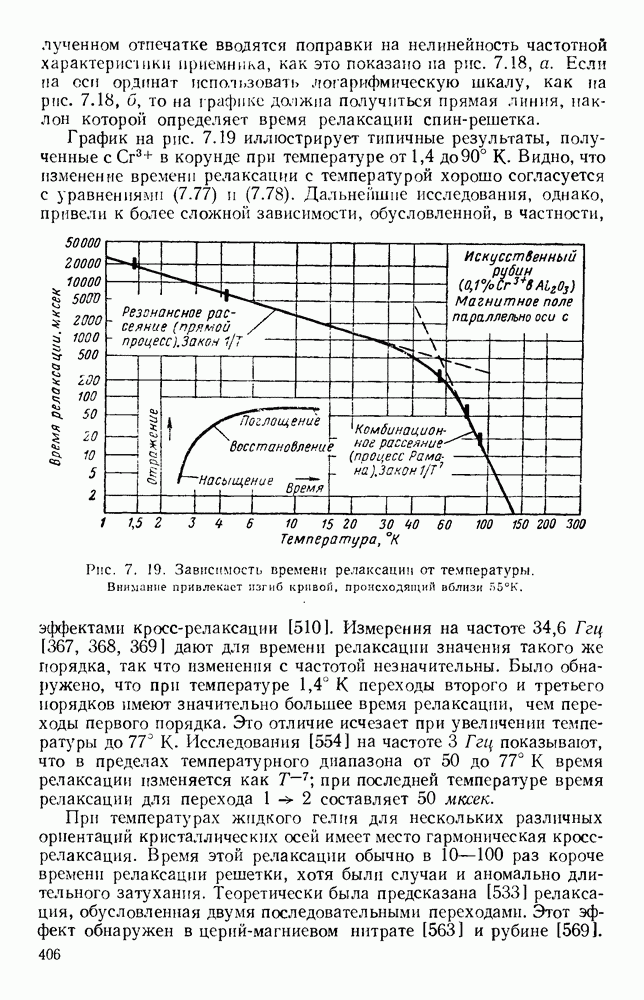
- 7.3.4. Времена релаксации
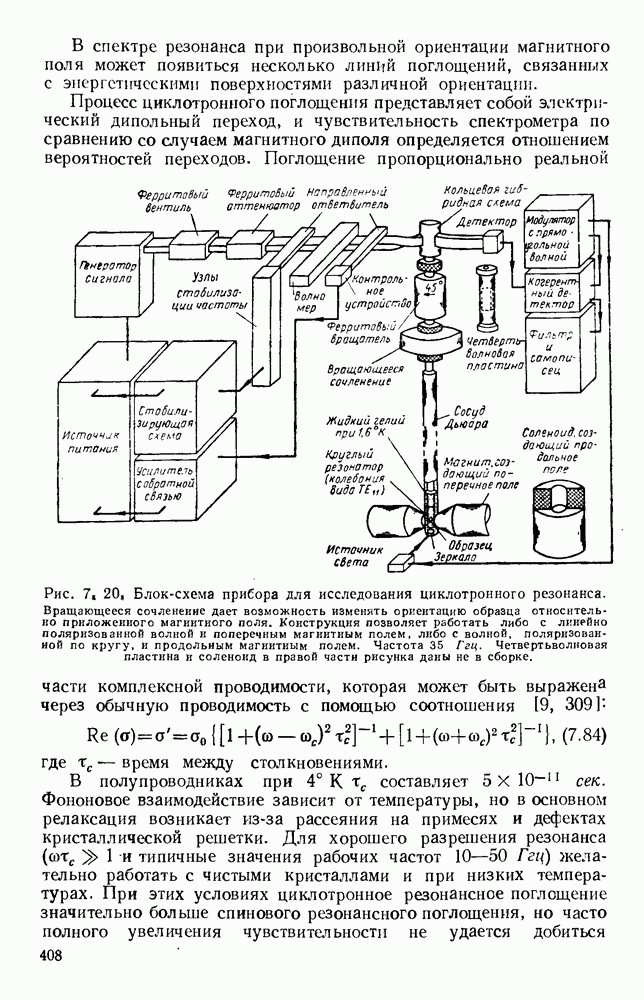
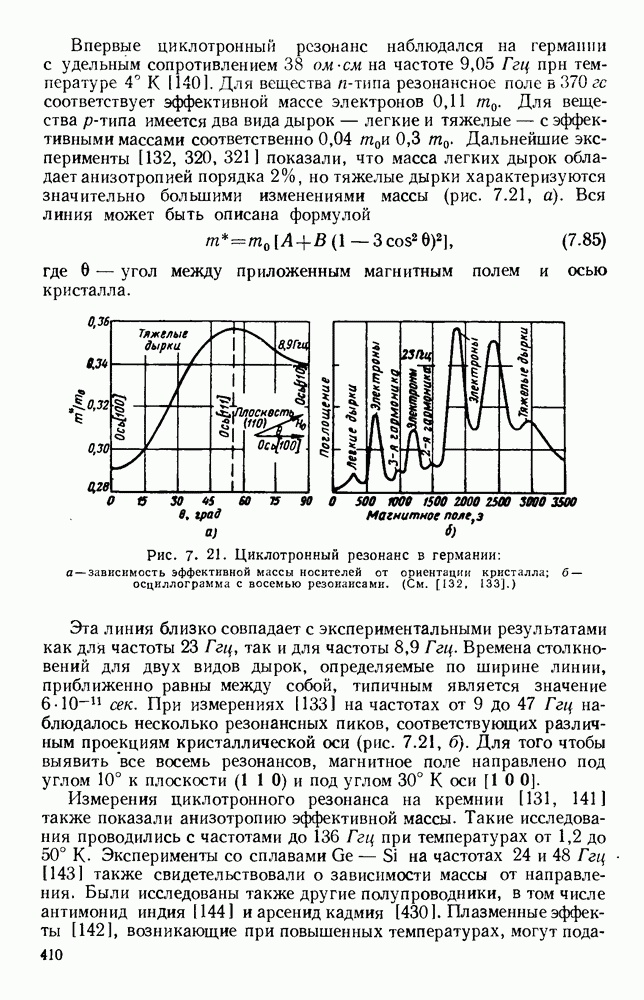
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
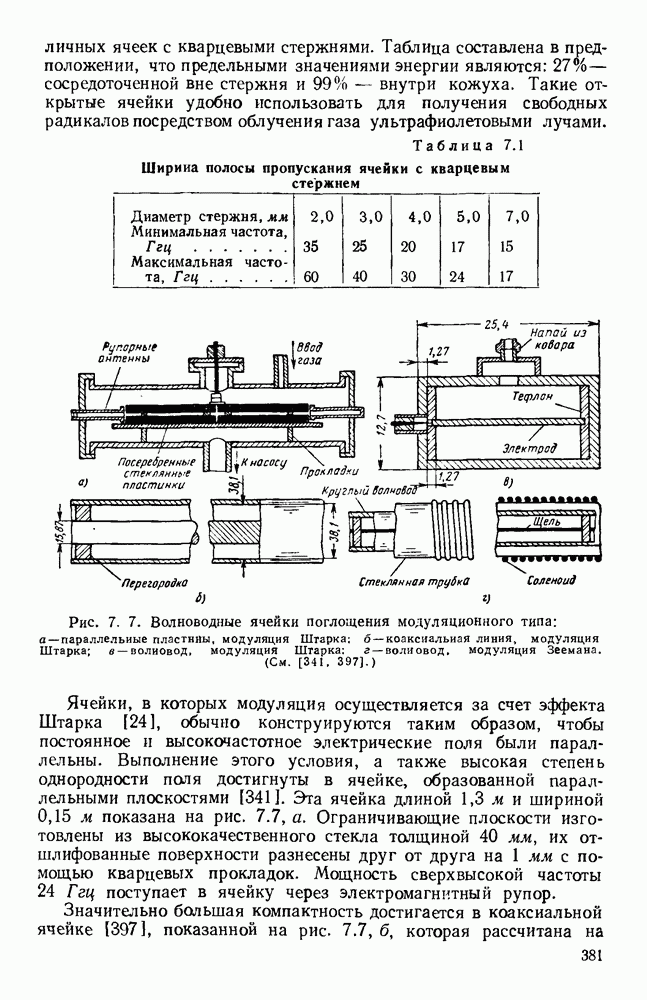
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
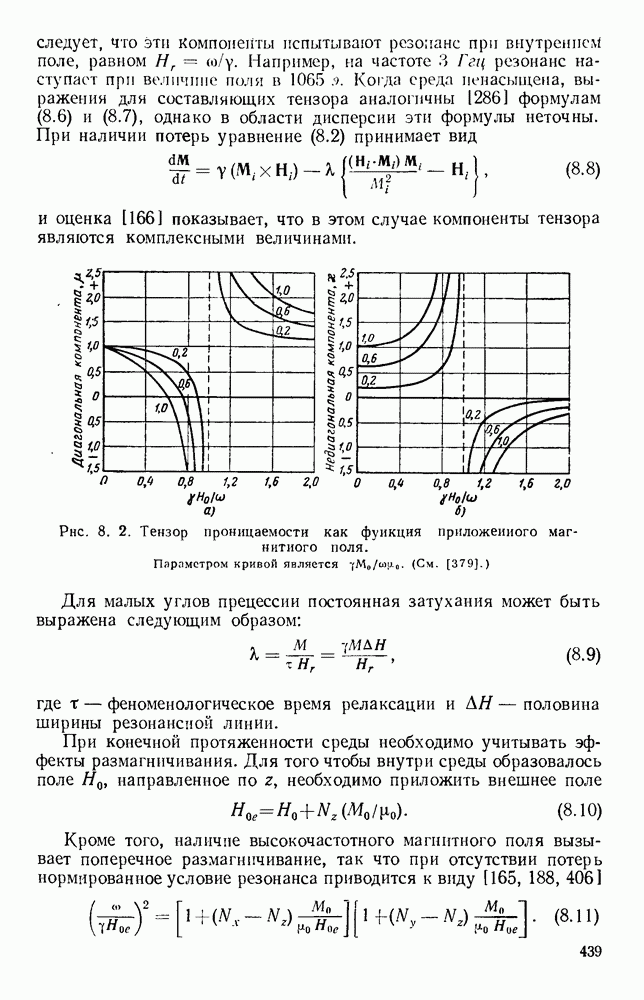
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
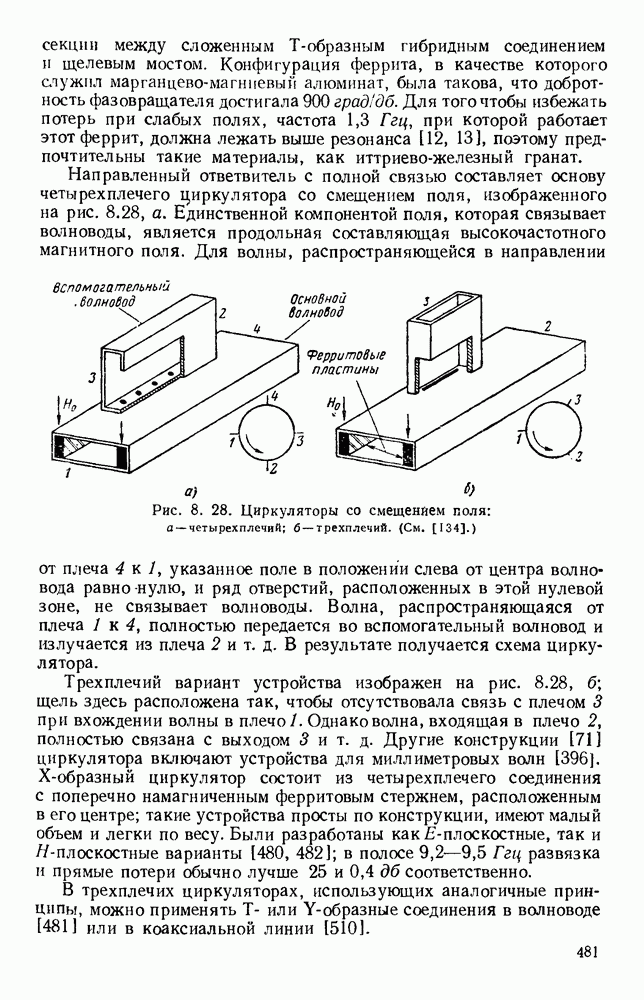
- 8.3.3. Ферритовые устройства в качестве элементов схем
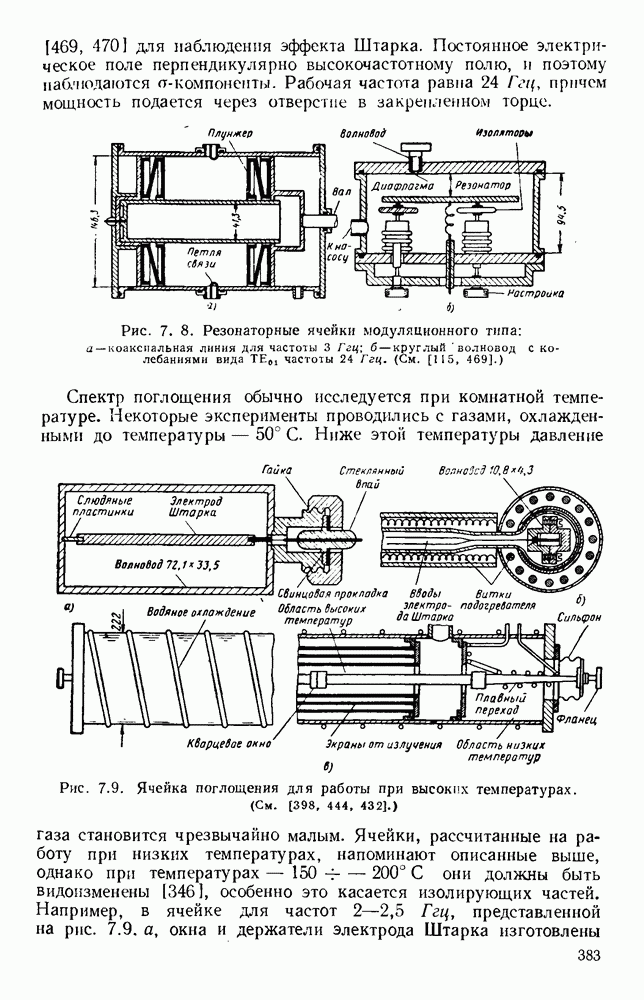
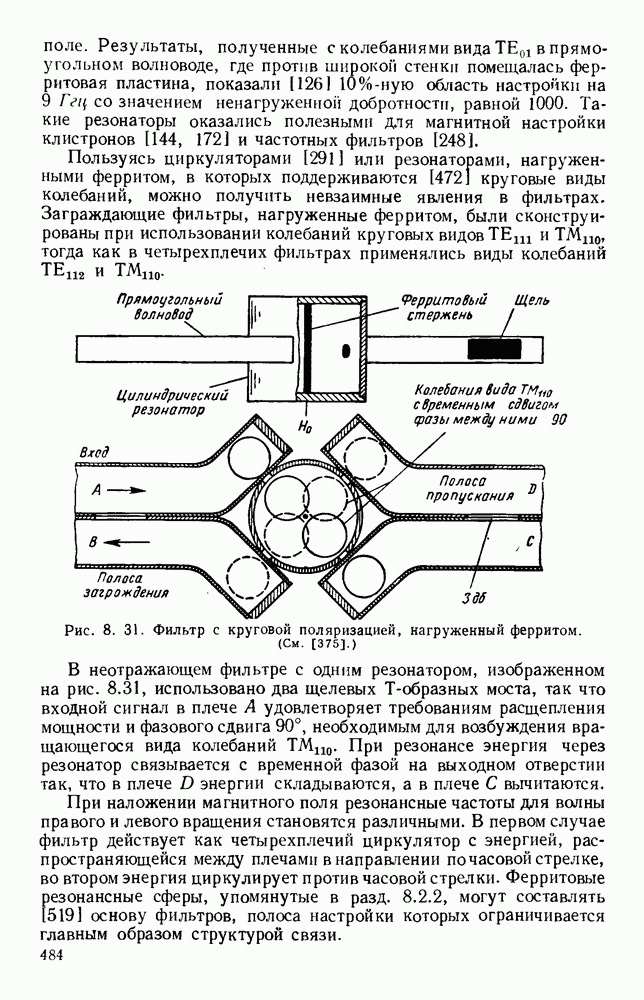
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
- 8.6.2. Устройства с поперечным полем
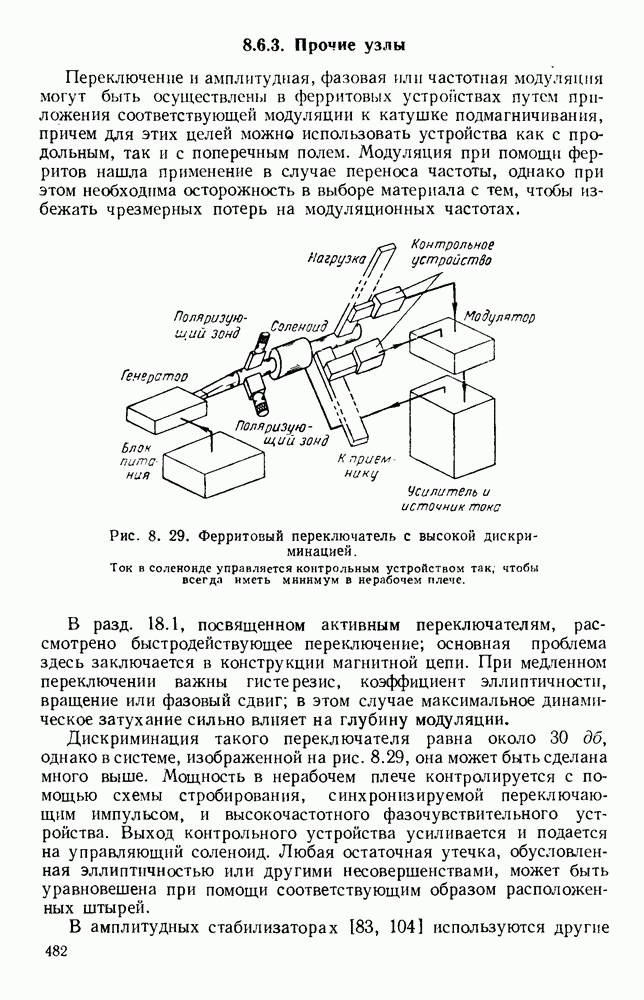
- 8.6.3. Прочие узлы
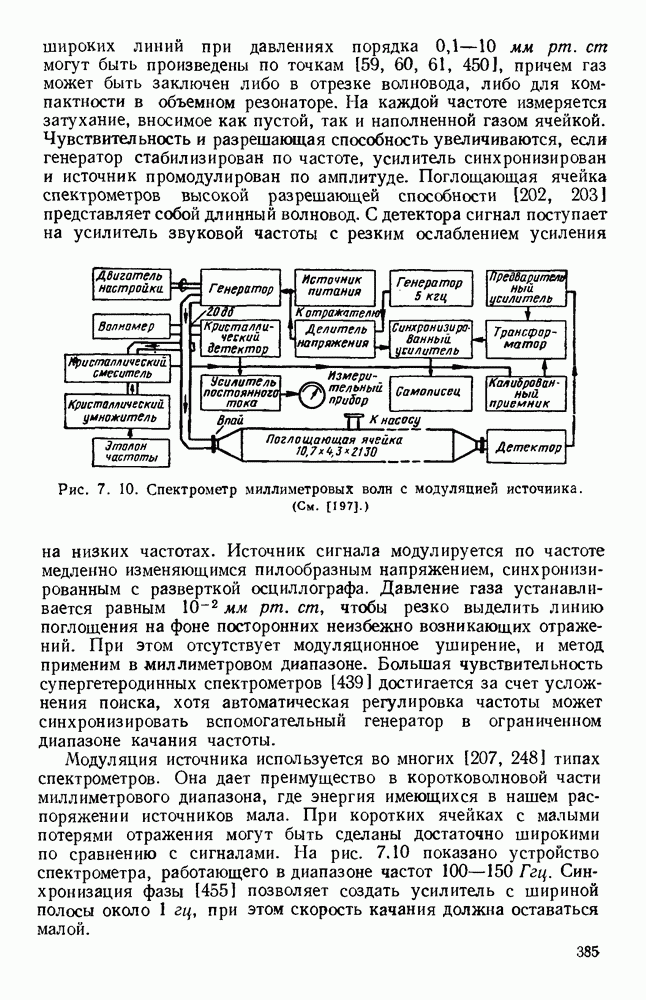
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
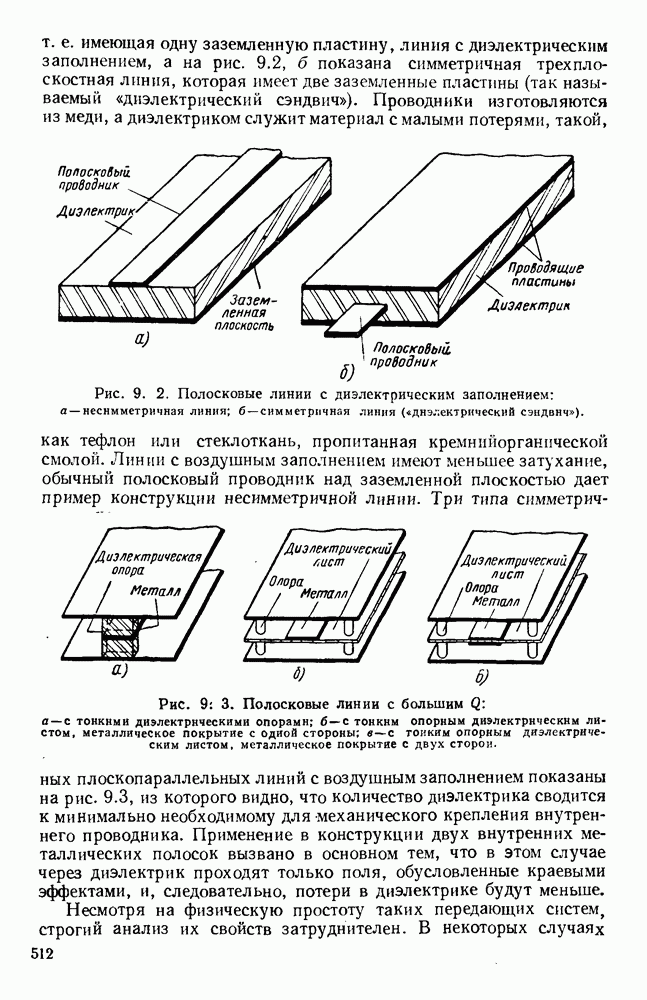
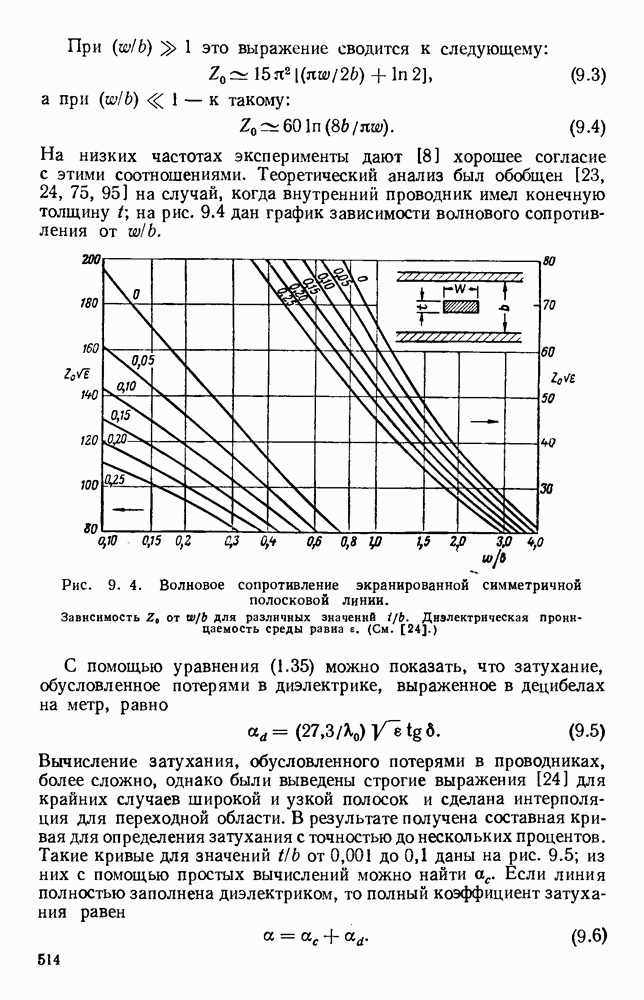
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.2.1. Линии типа «диэлектрических сэндвичей»
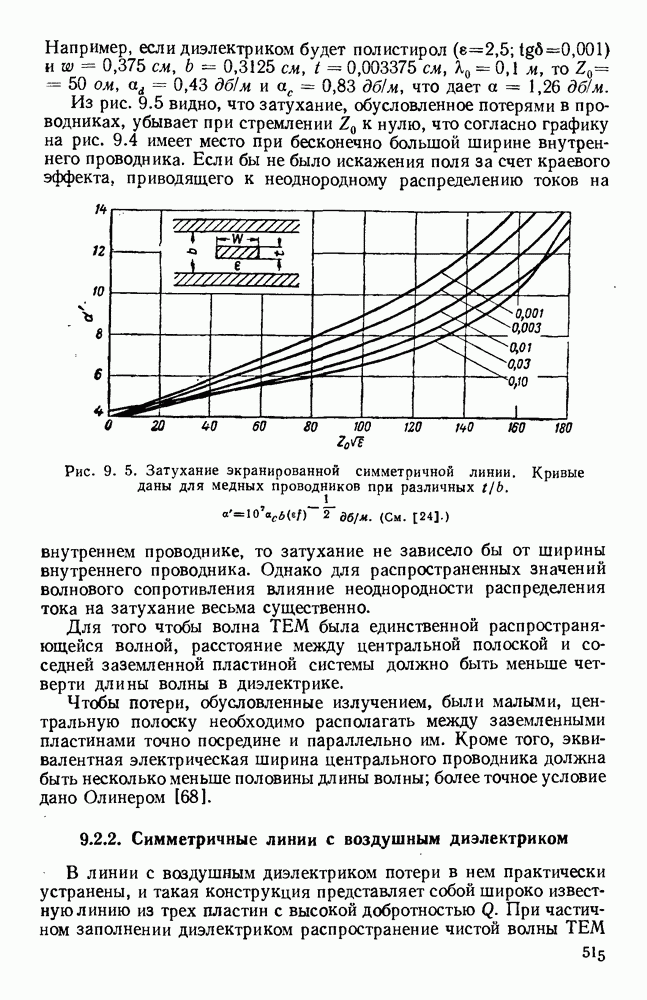
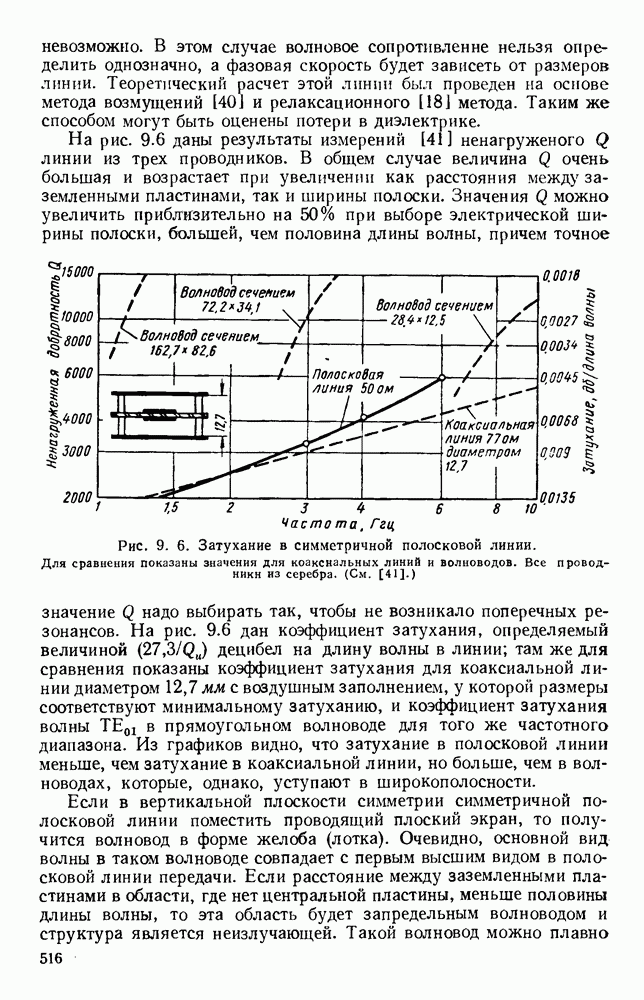
- 9.2.2. Симметричные линии с воздушным диэлектриком
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
- 9.4.2. Переходные устройства
- 9.4.3. Узлы полосковых систем
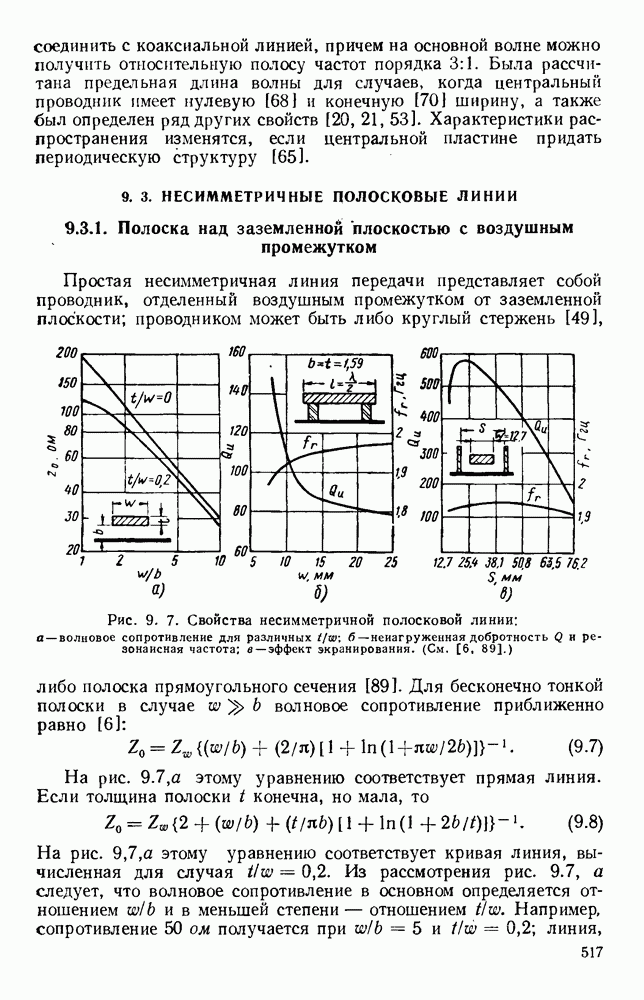
- 9.5. ЦЕПИ И СИСТЕМЫ
- 9.5.3. Частотные фильтры
- 9.5.4. Цепи питания антенн
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
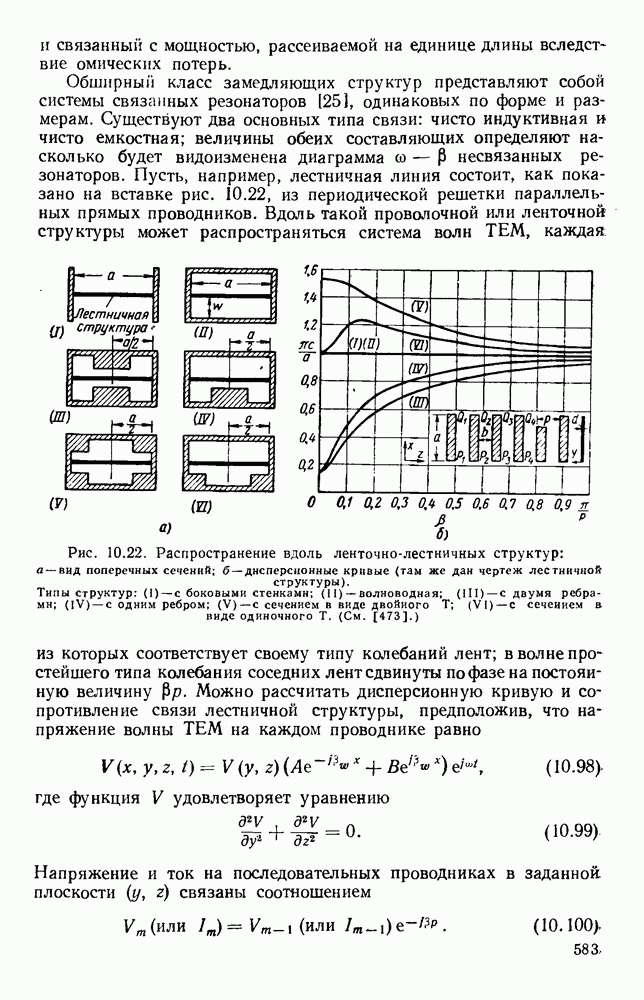
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
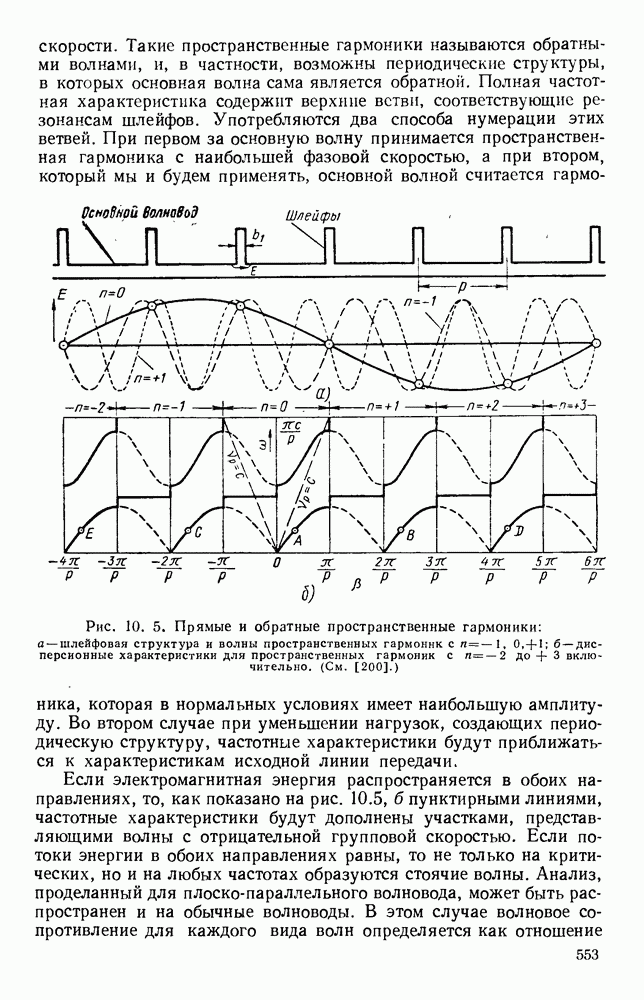
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
- 10.1.2. Пространственные гармоники
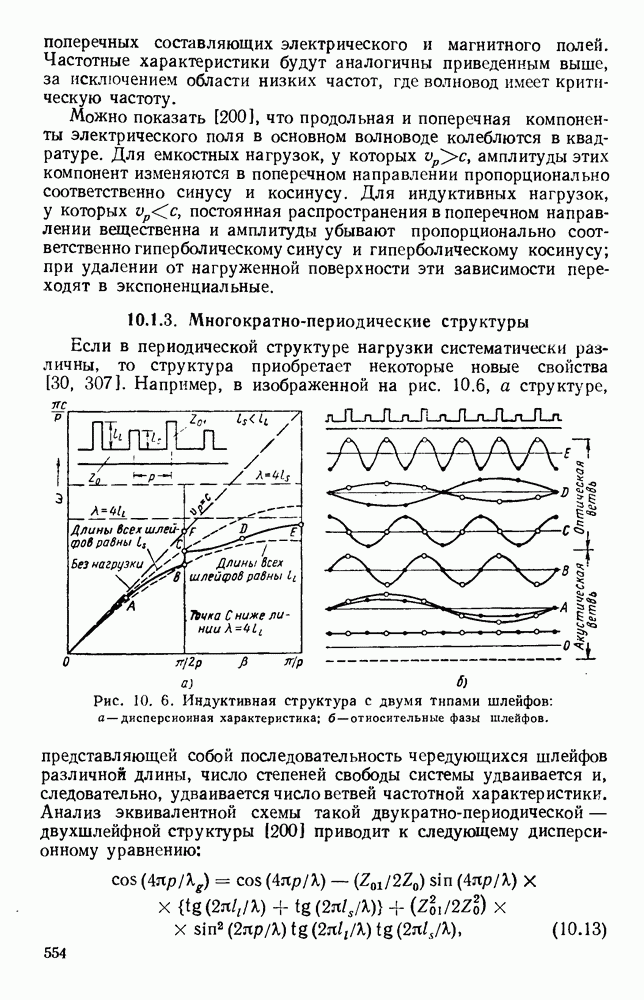
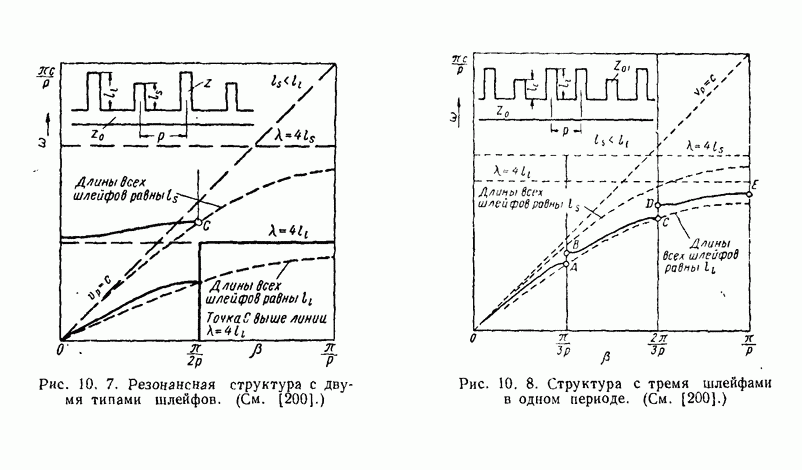
- 10.1.3. Многократно-периодические структуры
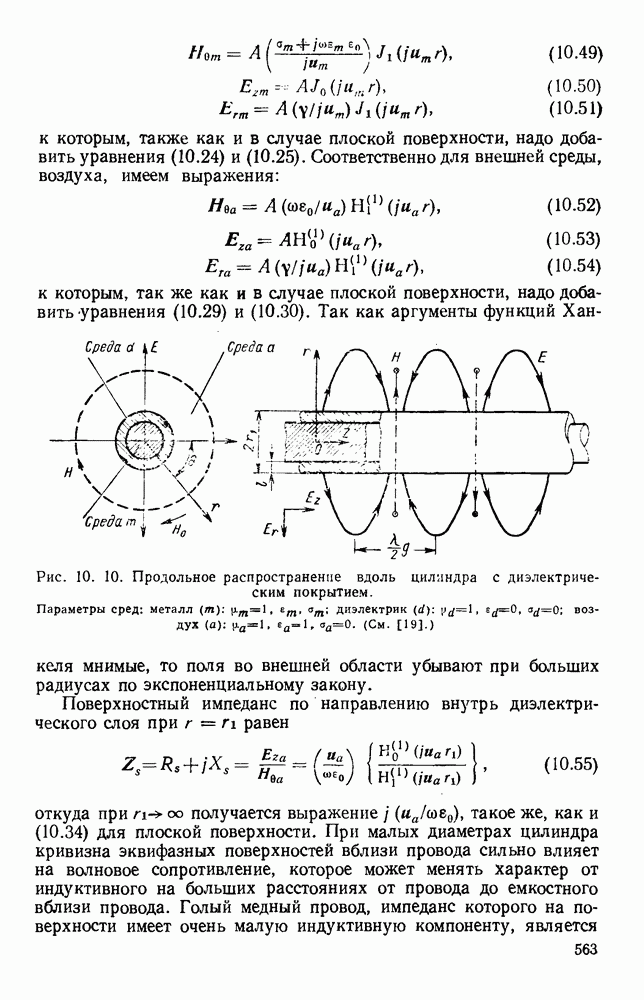
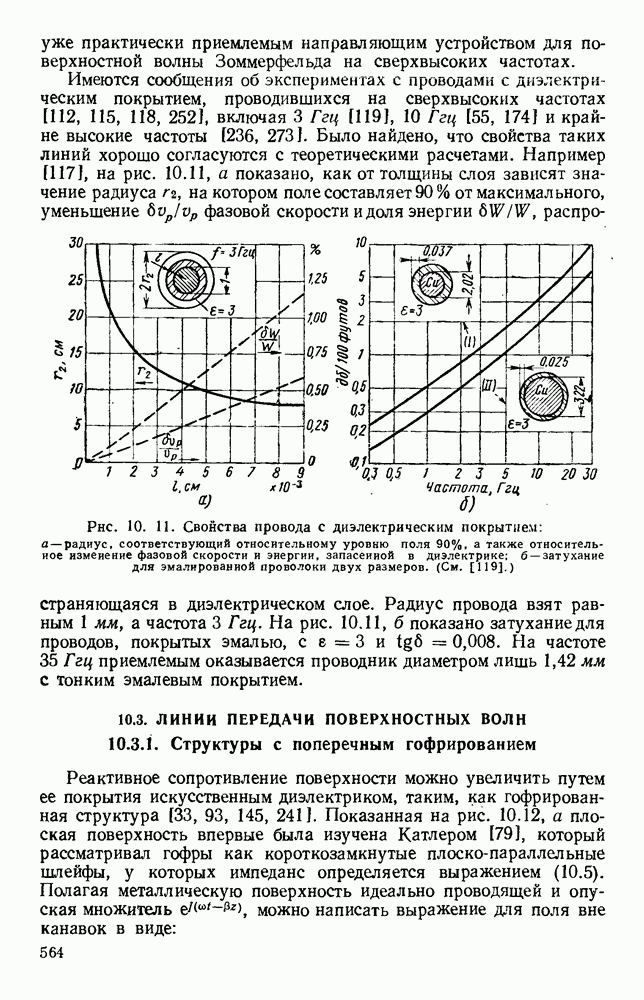
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
- 10.2.3. Продольные цилиндрические волны
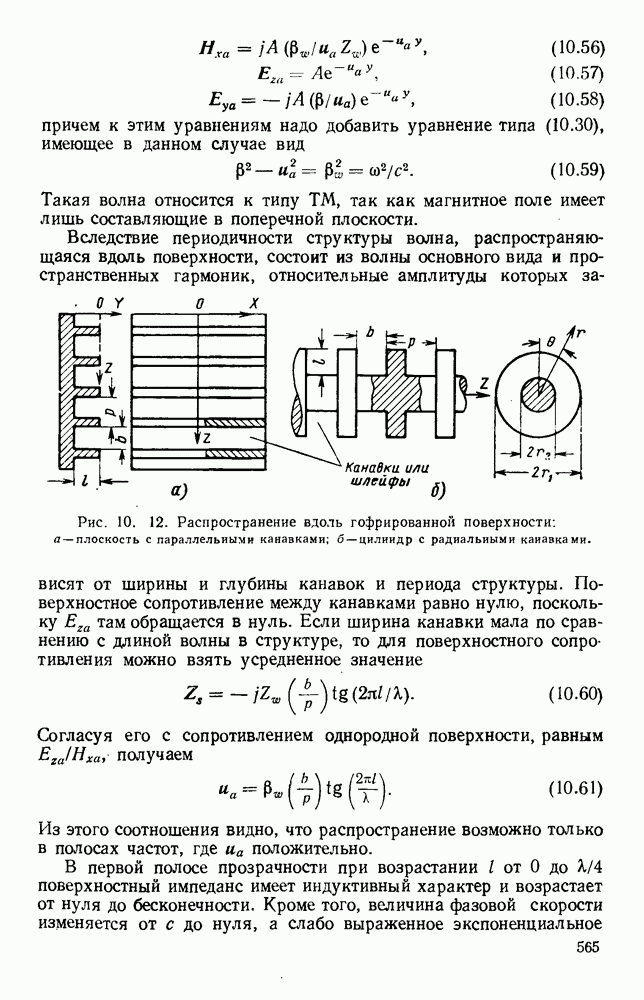
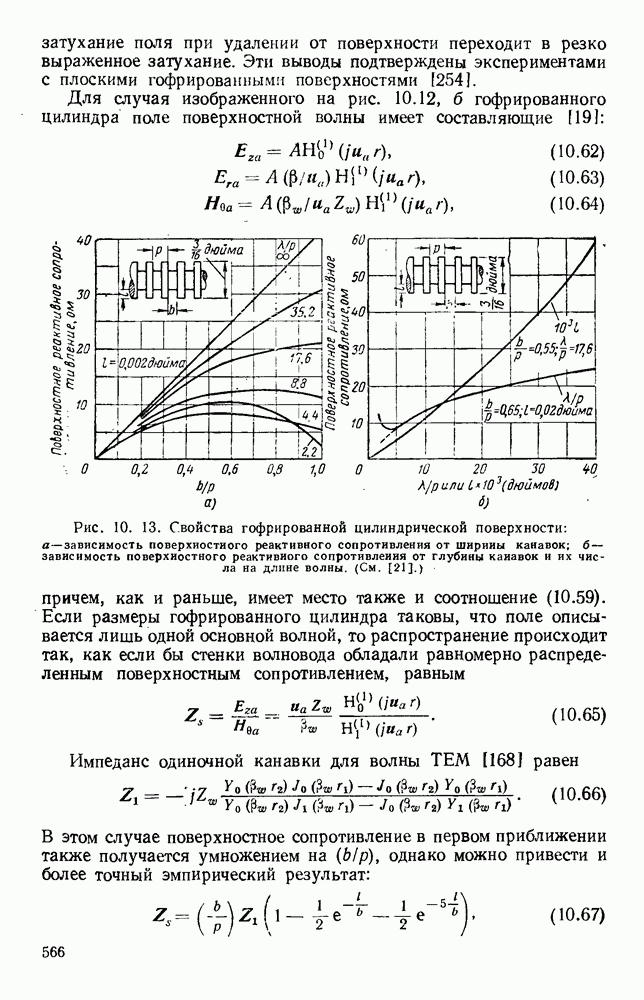
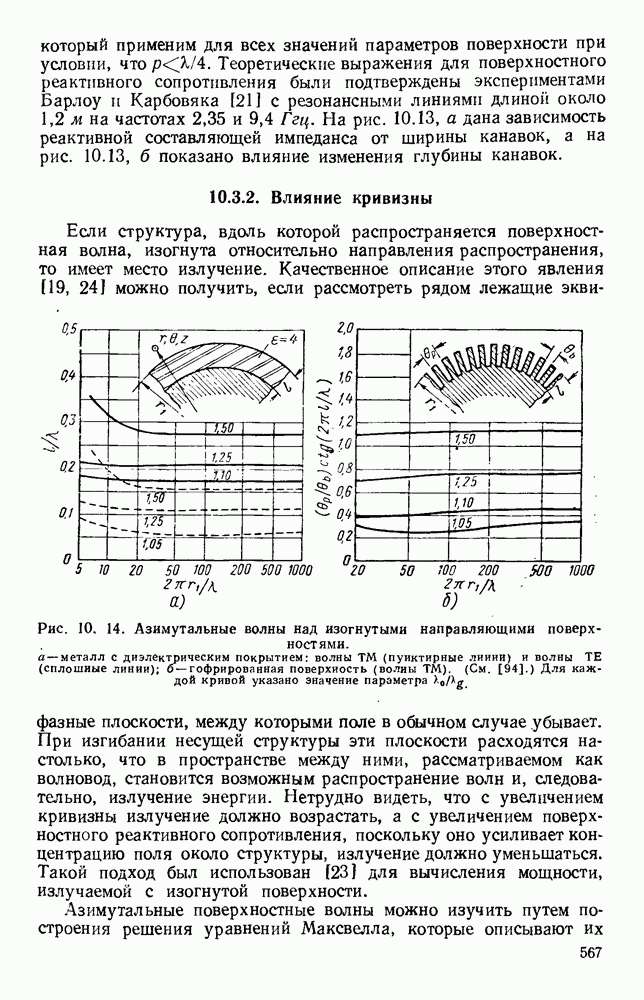
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
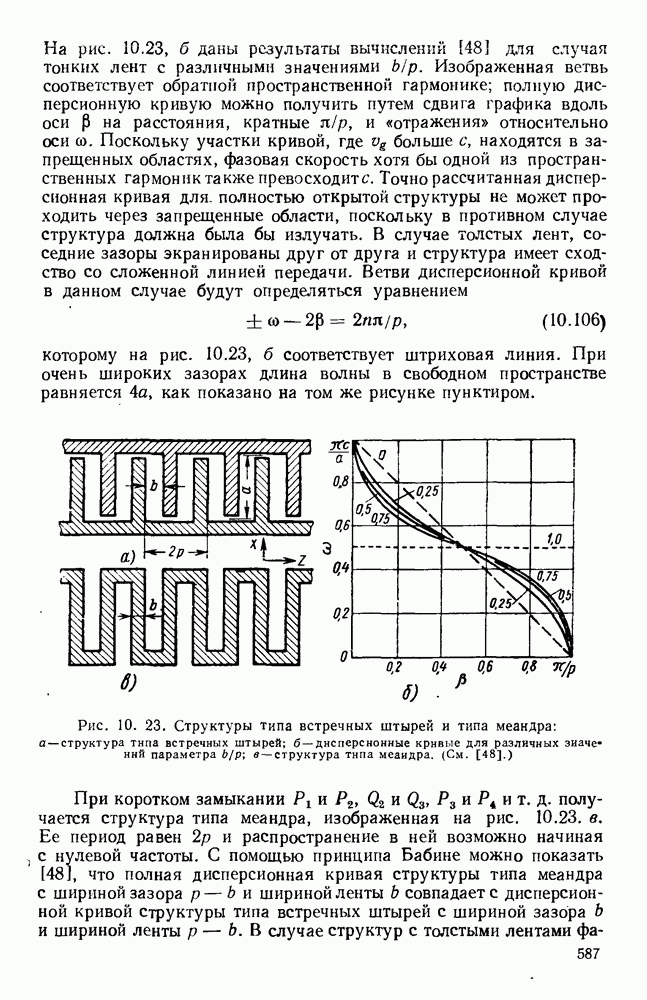
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
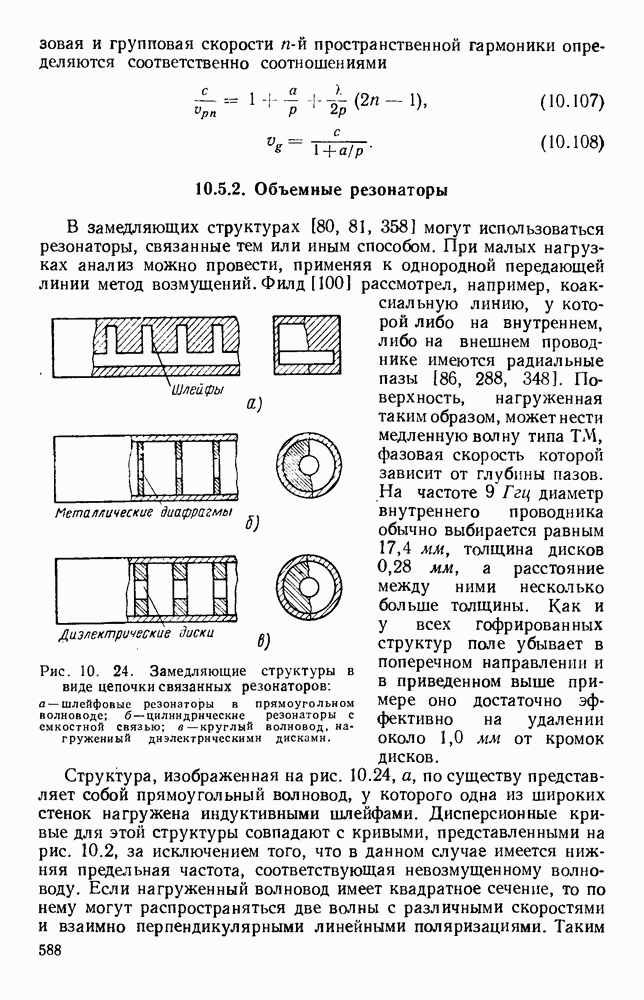
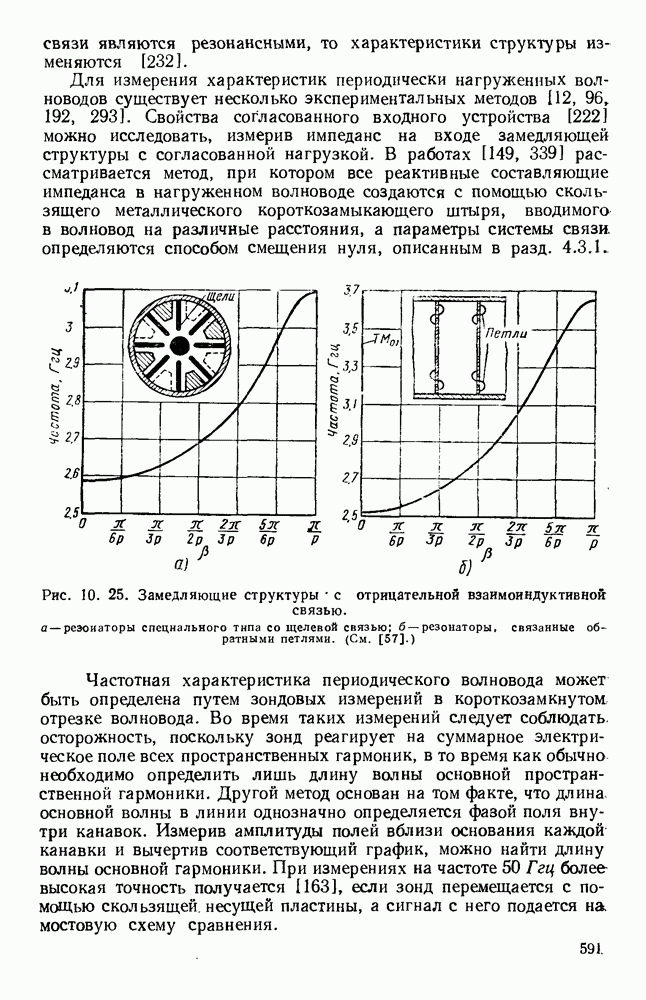
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
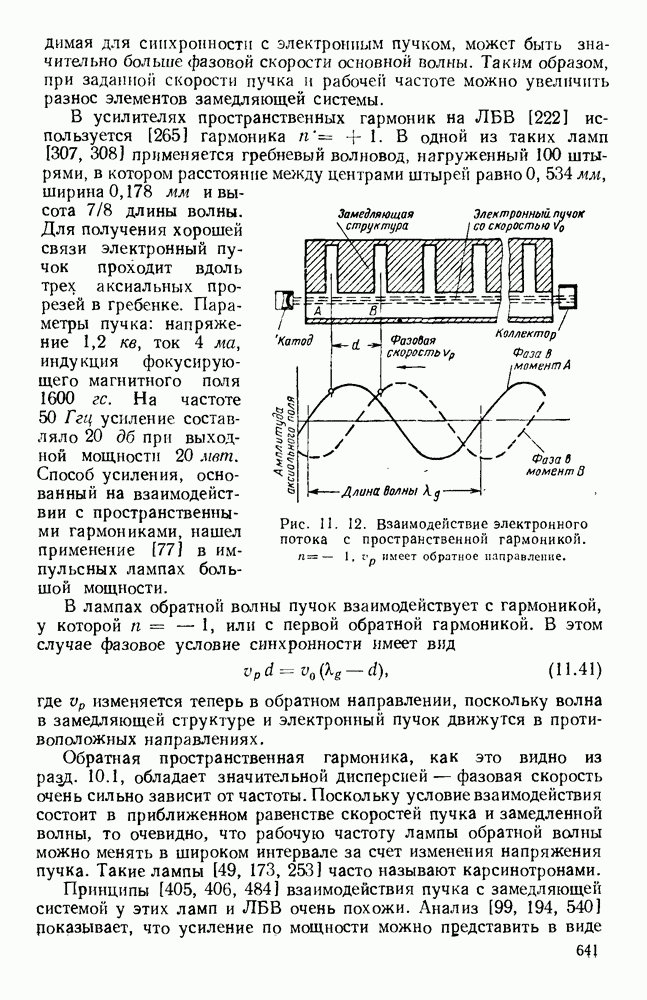
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
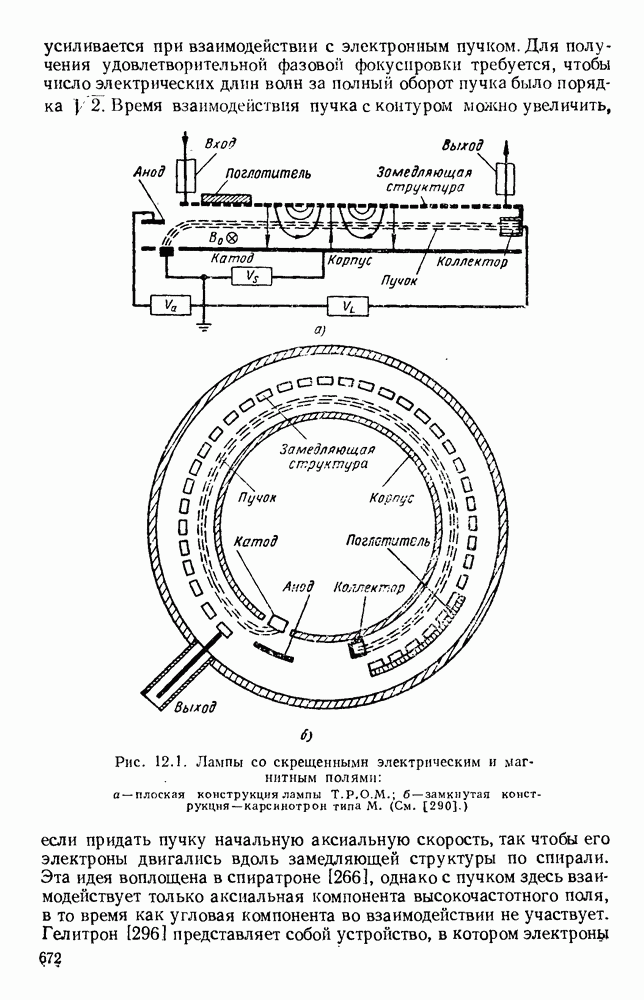
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
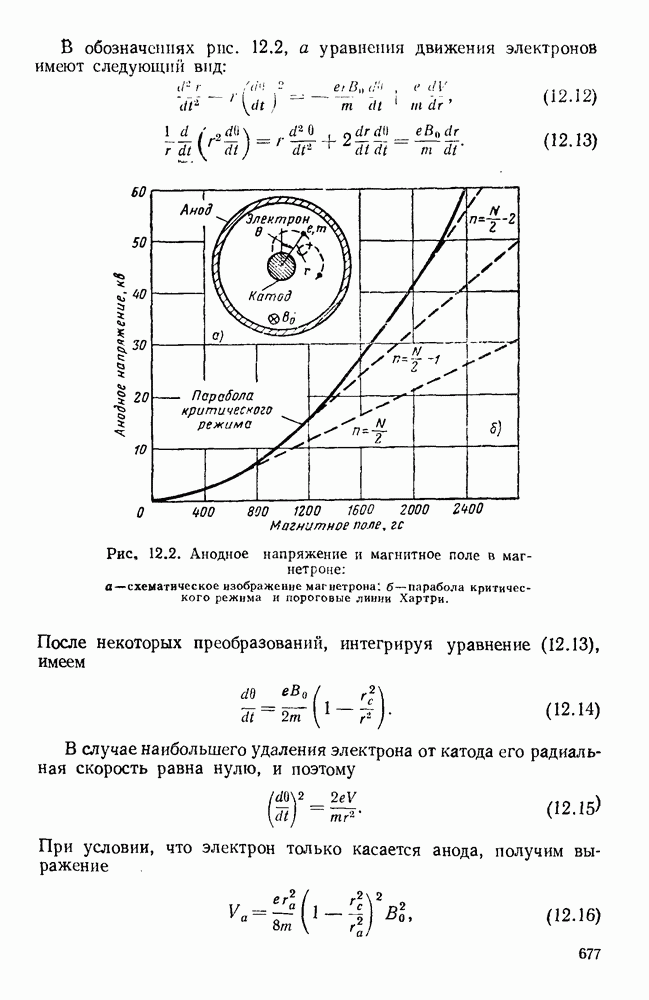
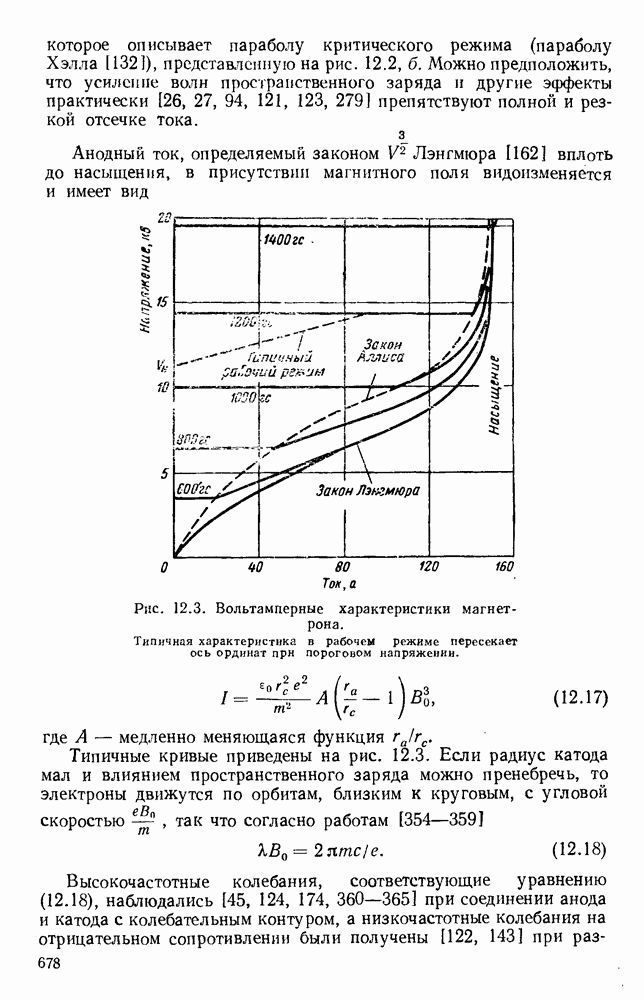
- 12.2. МАГНЕТРОНЫ
- 12.2.2. Резонаторные системы
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
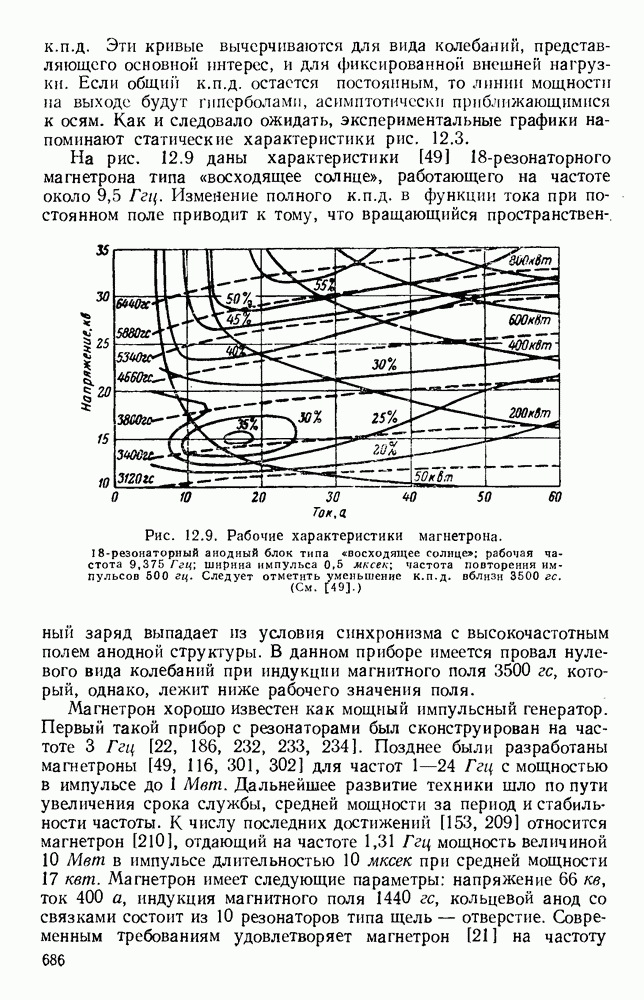
- 12.2.4. Рабочие характеристики
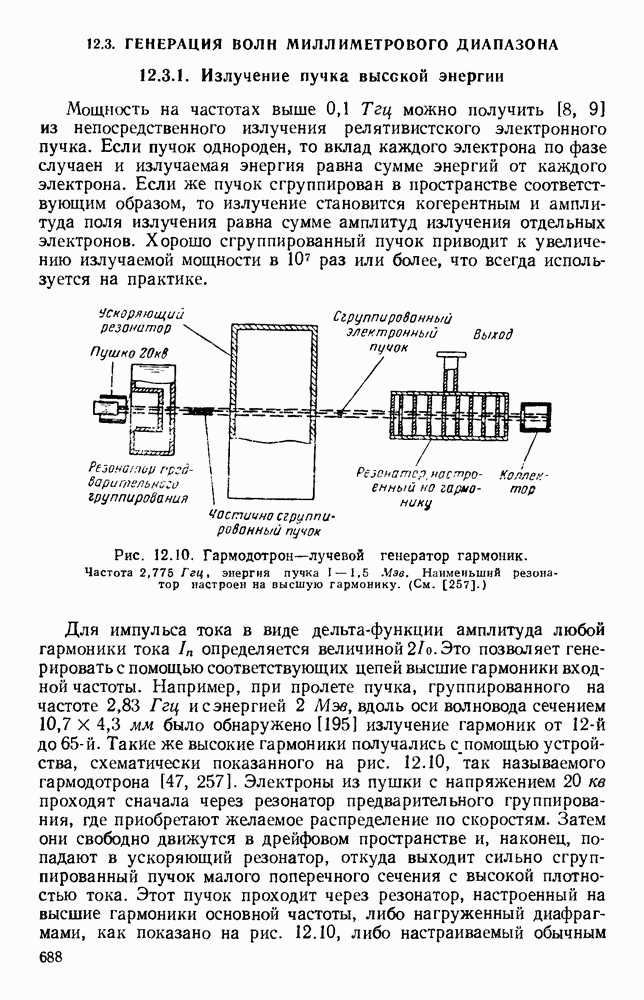
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
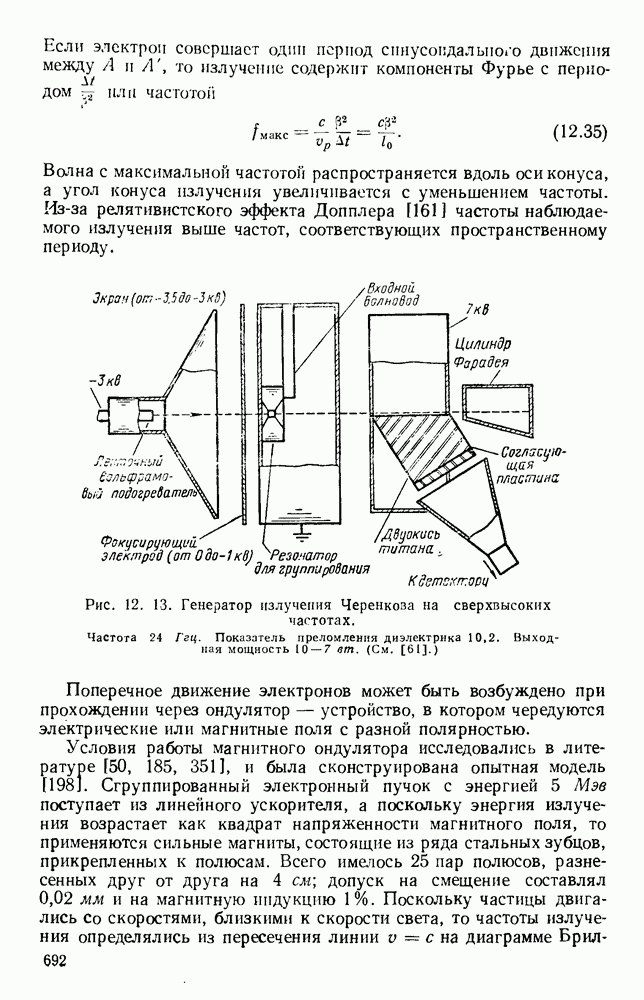
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
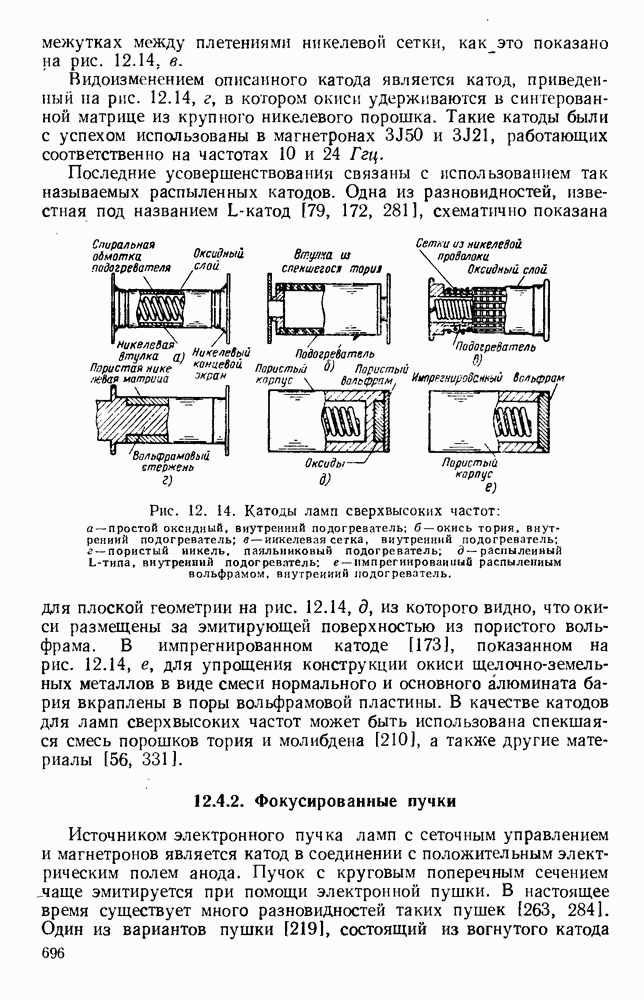
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
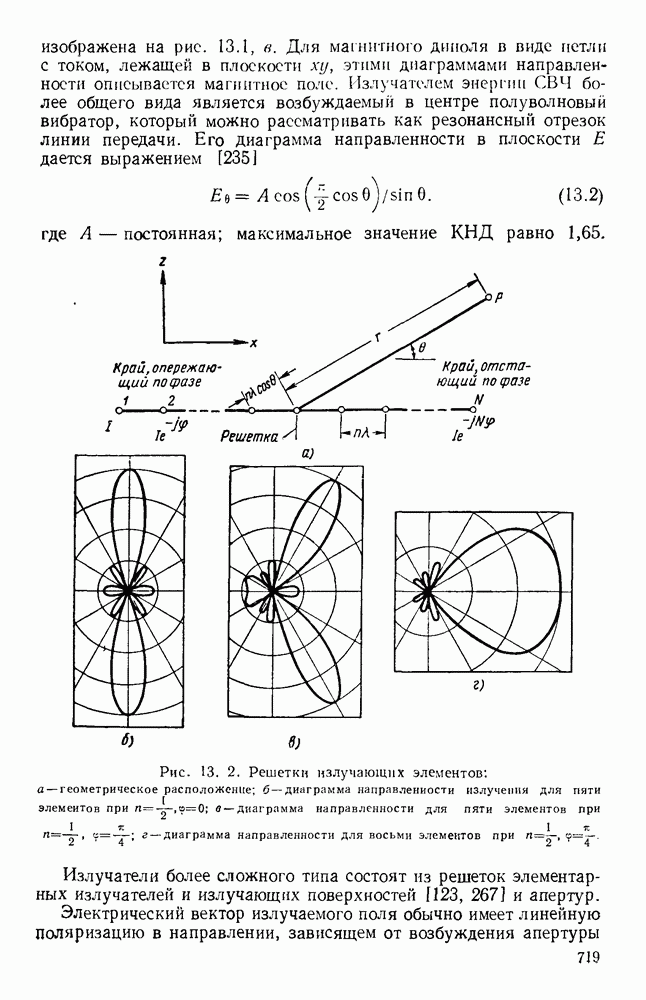
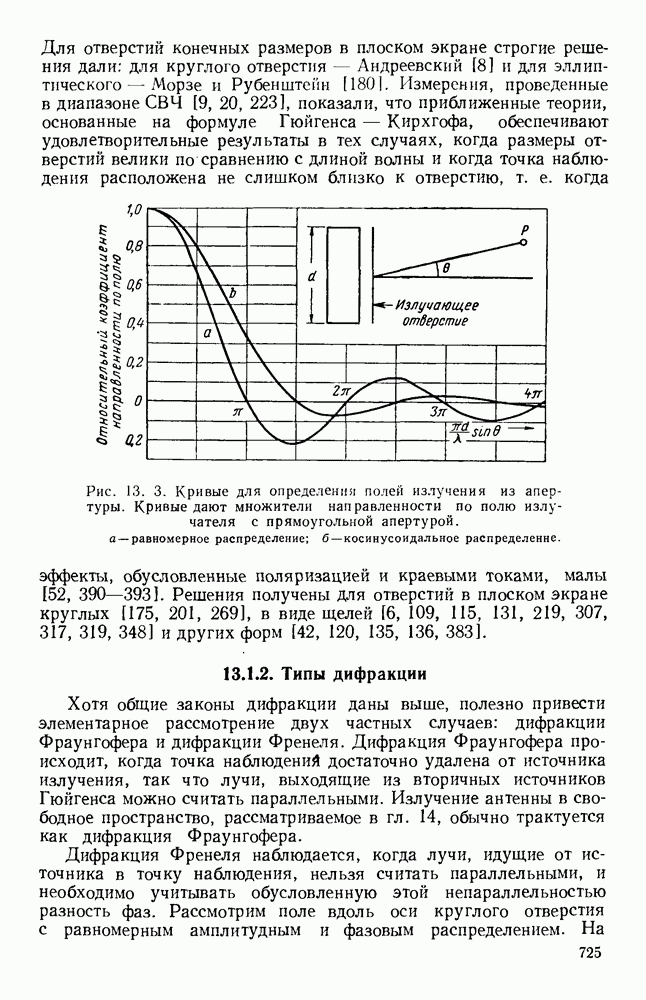
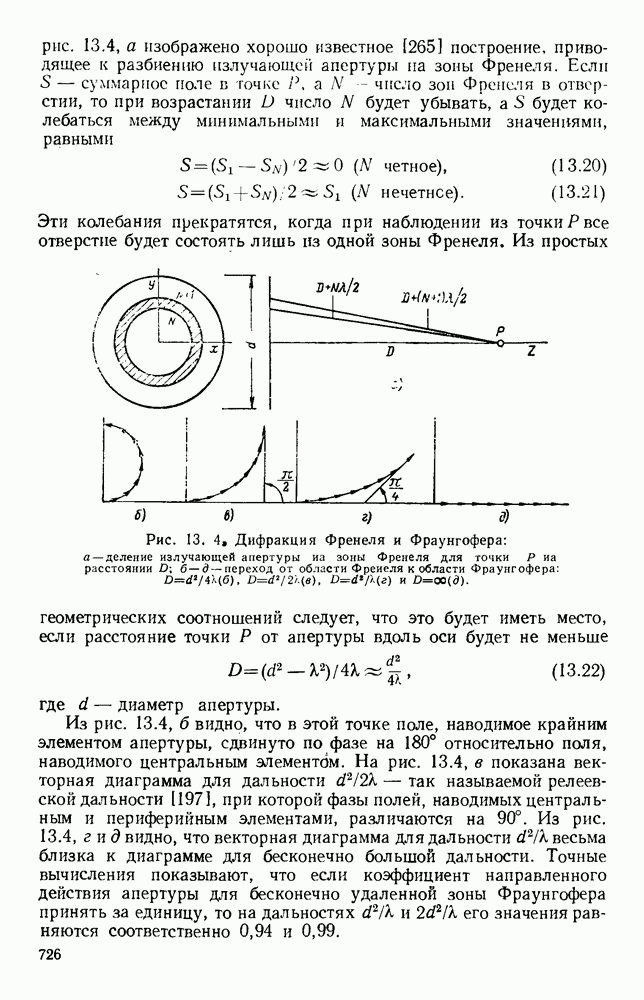
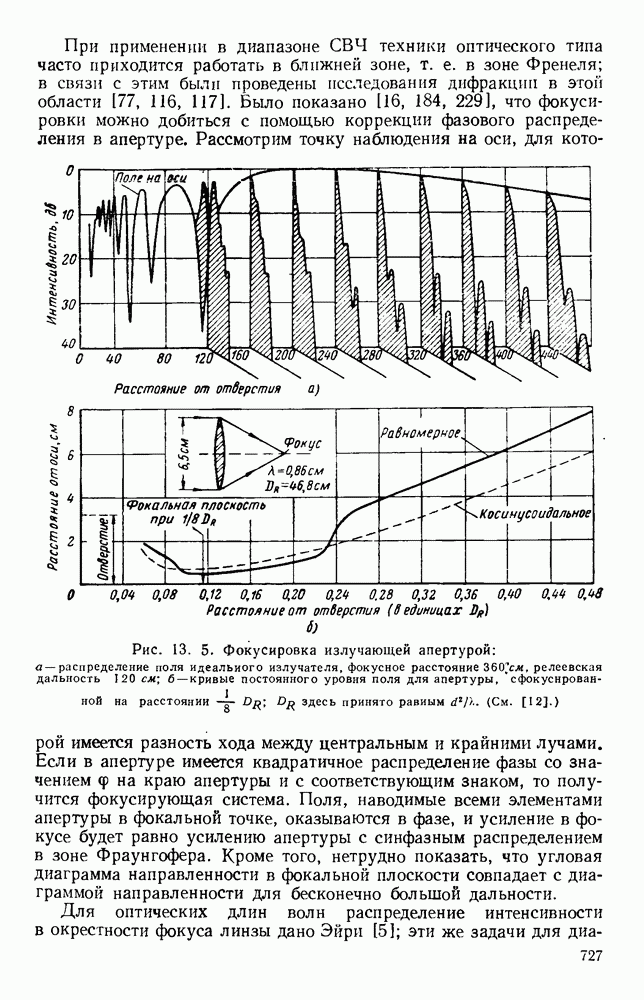
- 13.1.2. Типы дифракции
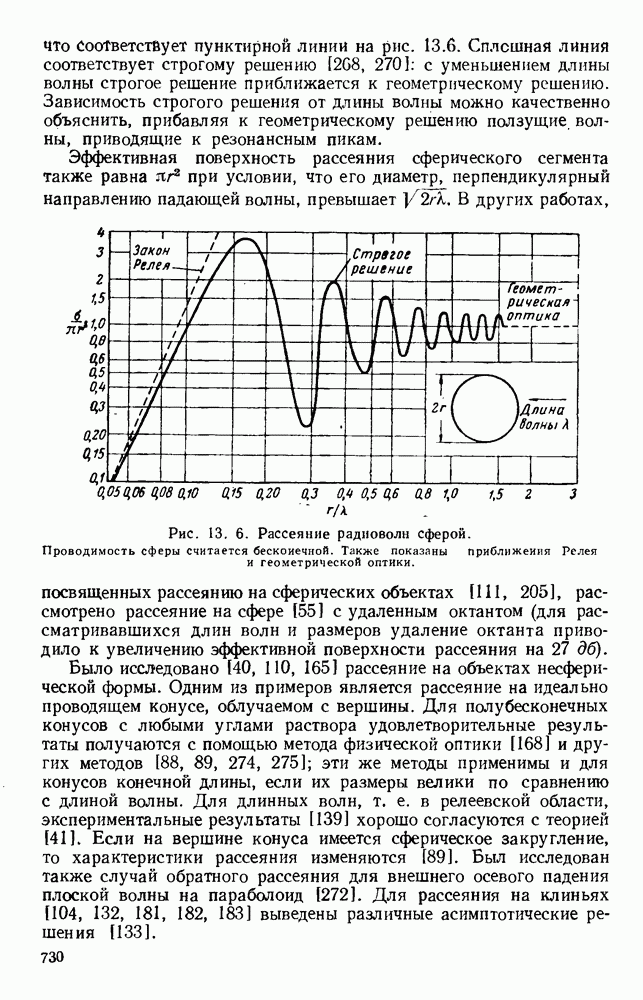
- 13.1.3. Рассеяние
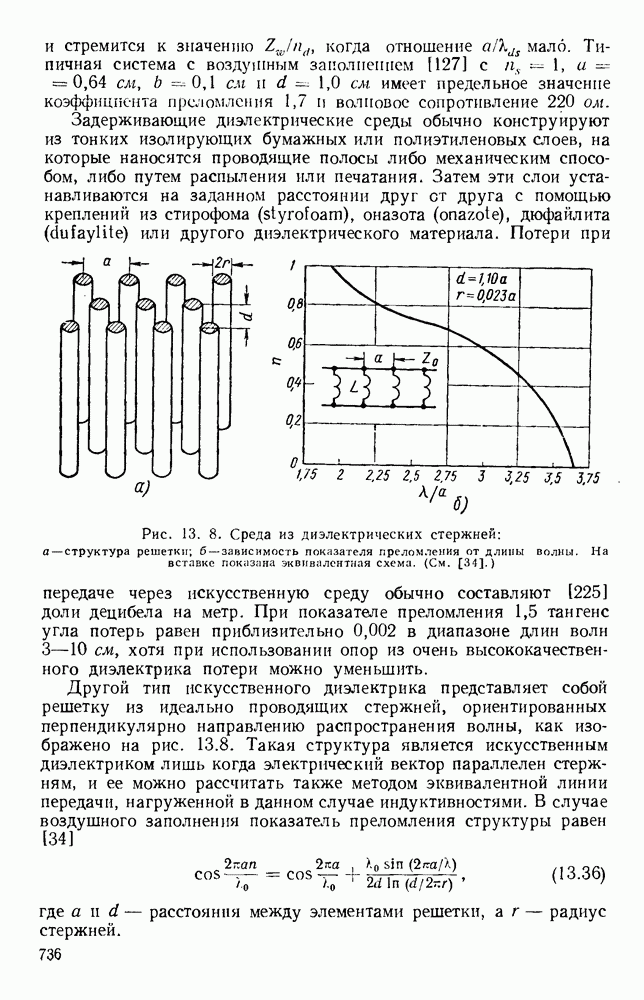
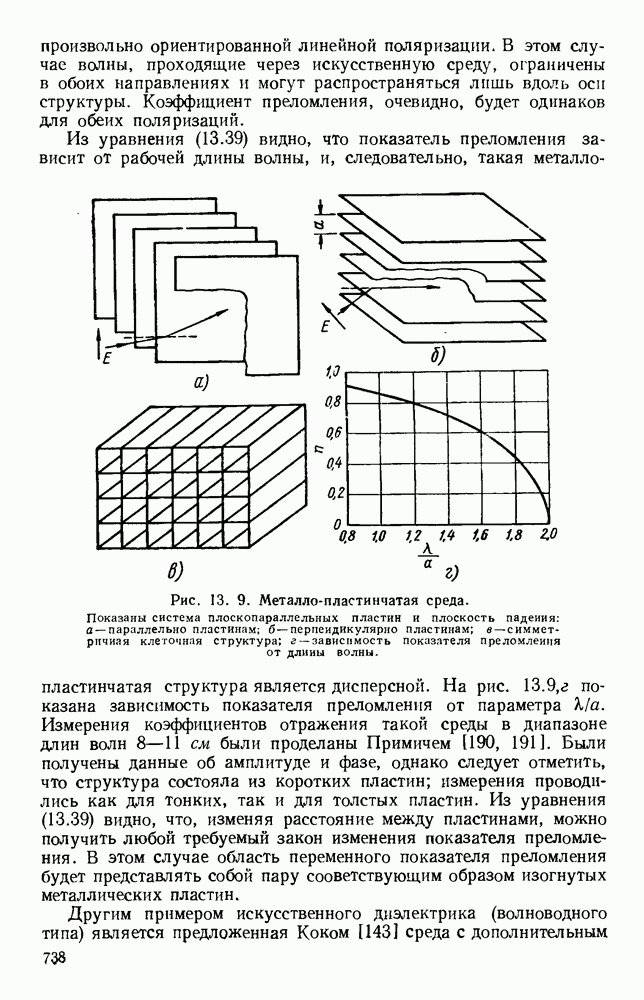
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
- 13.2.2. Структуры волноводного типа
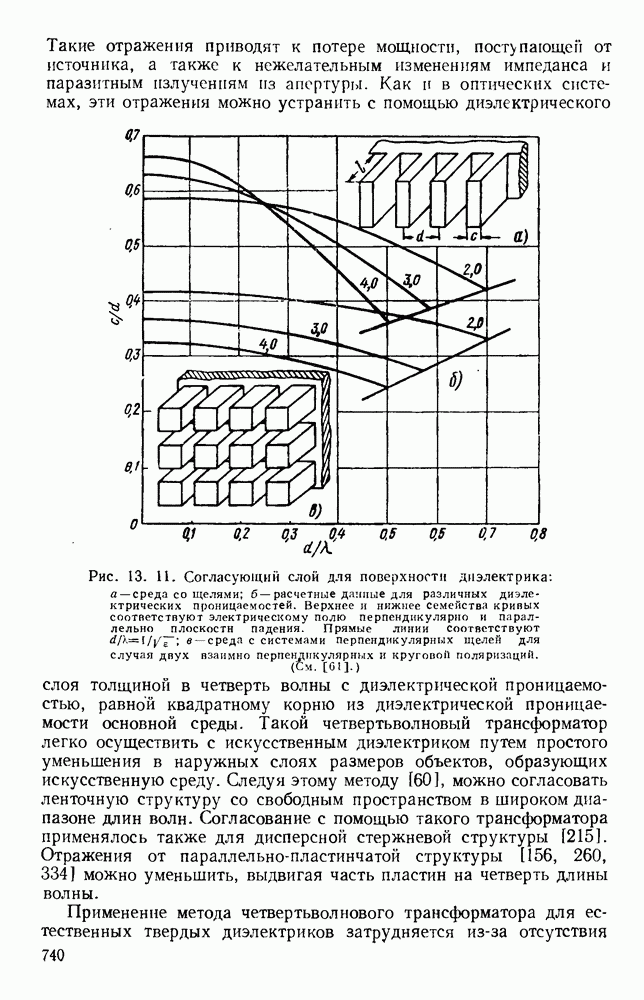
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
- 13.4. ПРИБОРЫ И СИСТЕМЫ
- 13.4.1. Спектрометры
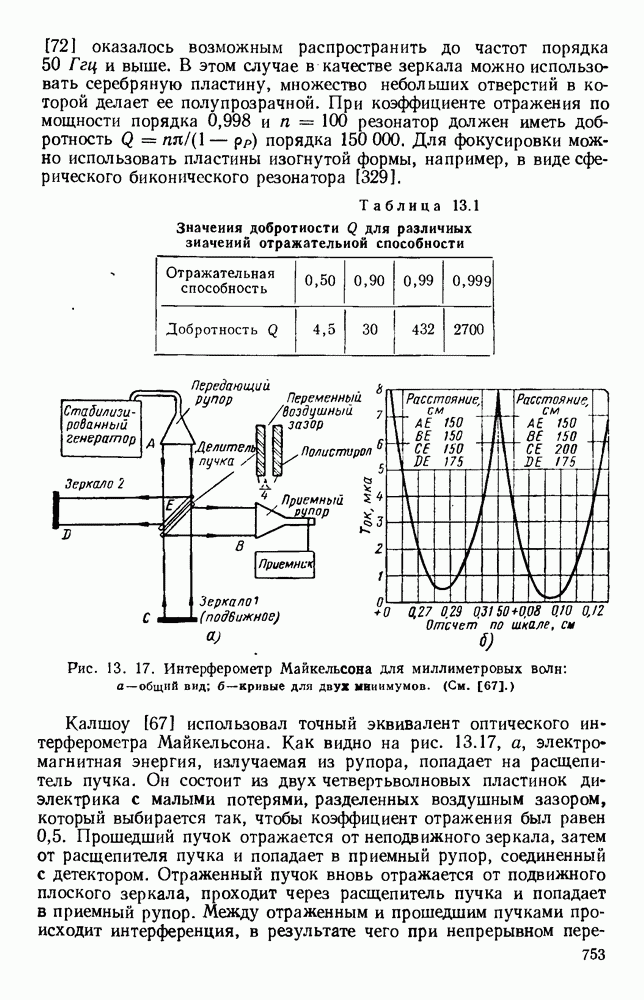
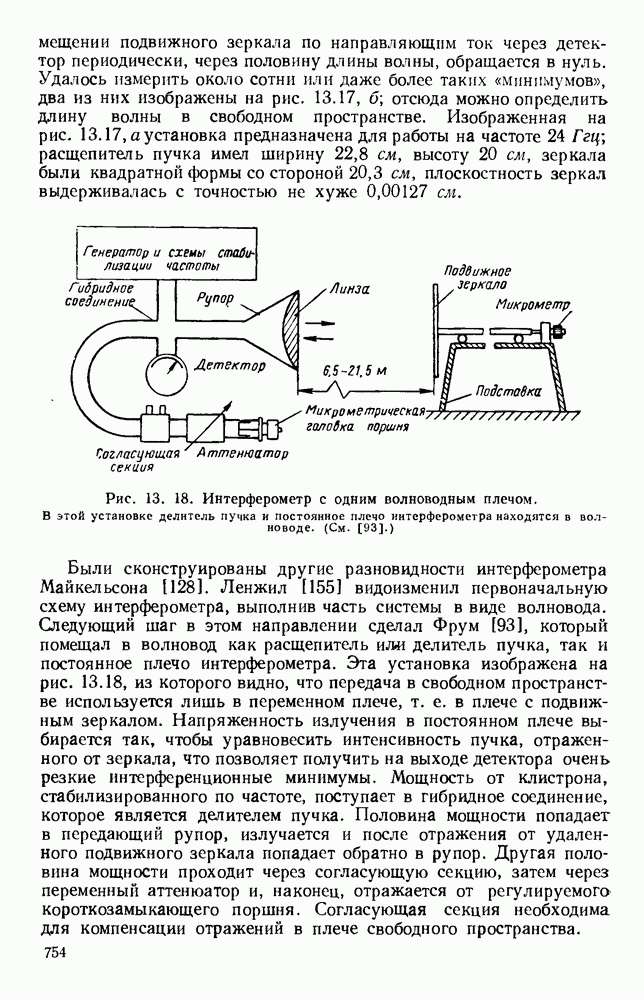
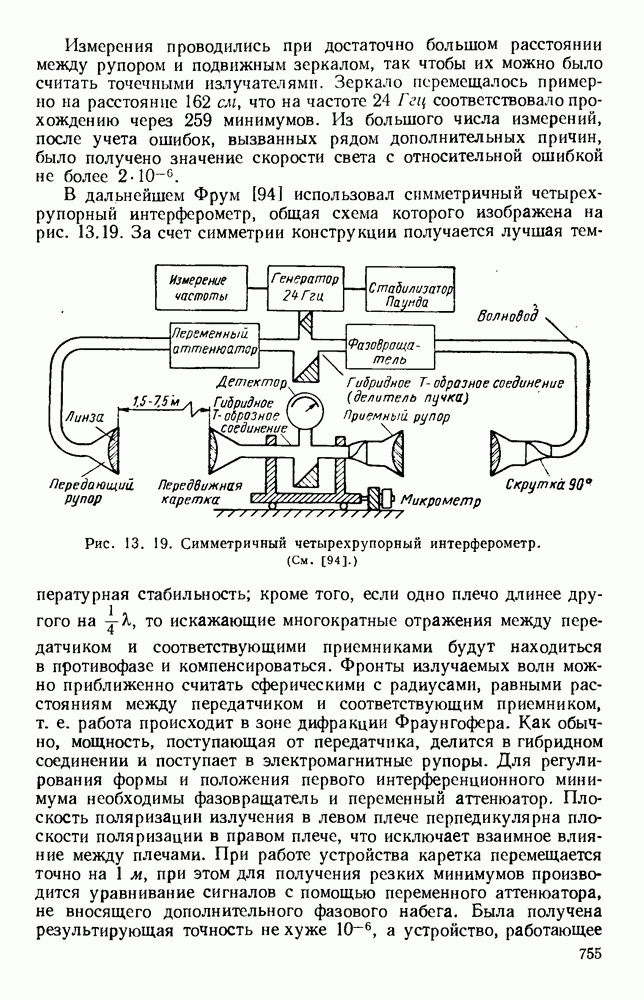
- 13.4.2. Интерферометры
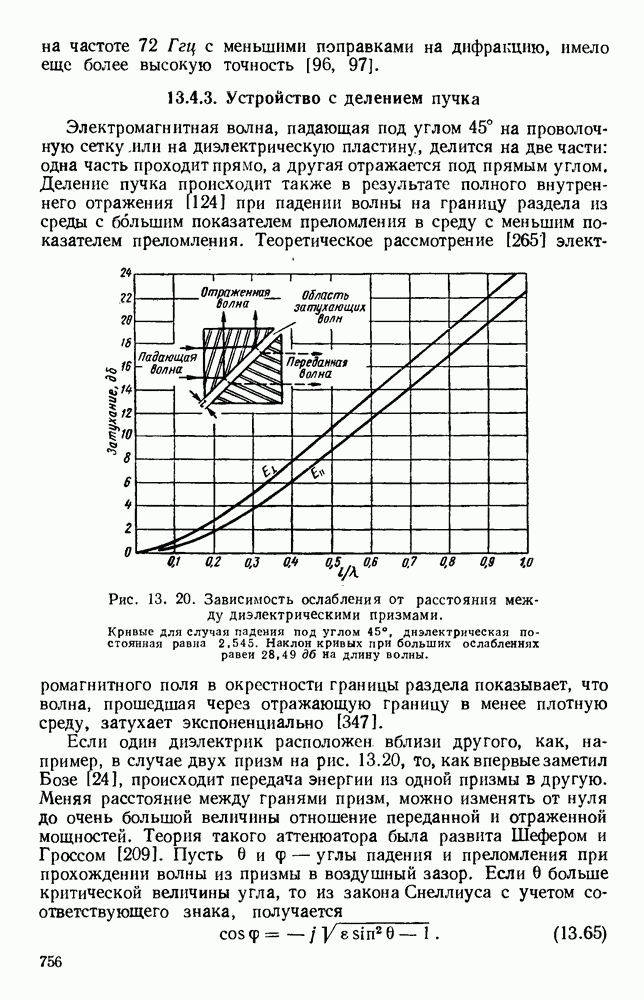
- 13.4.3. Устройство с делением пучка