| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
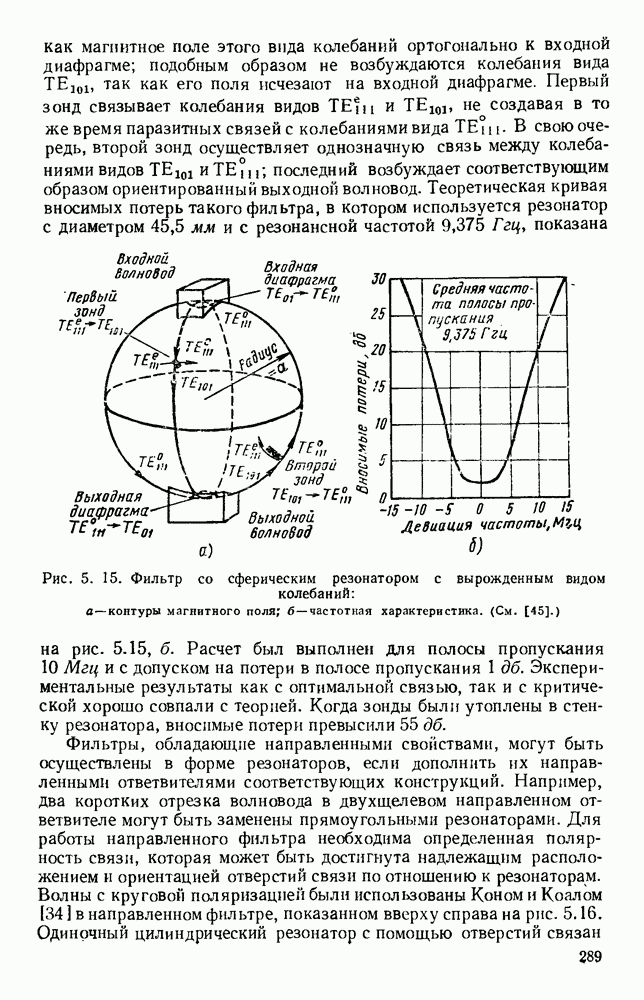
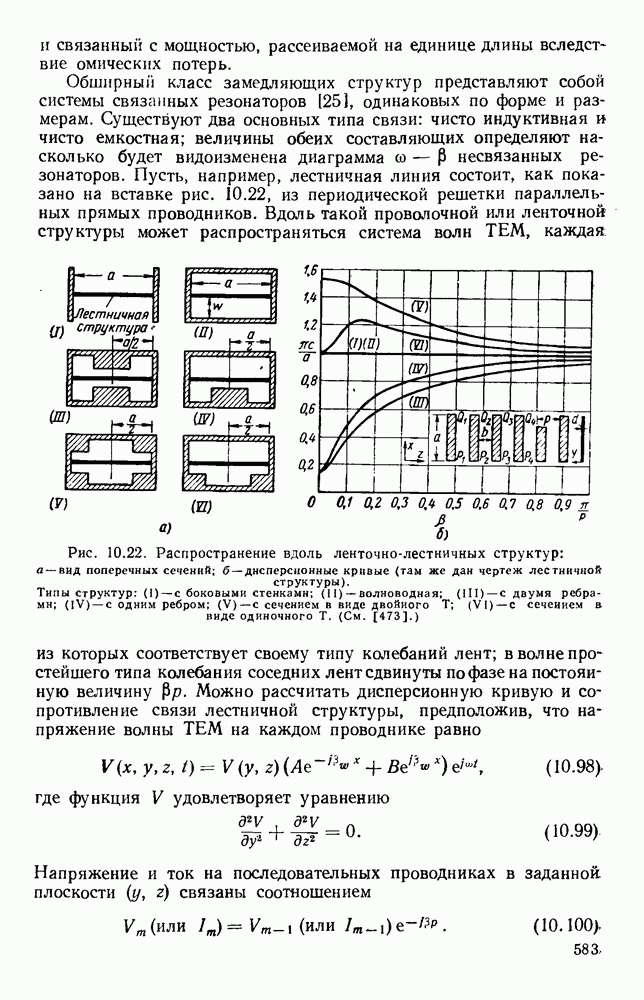
1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
1.3.1. Отражение и преломление на границе
Электромагнитные волны могут направляться проводящими или изолирующими поверхностями, которые в этом случае образуют цепи. Рассмотрим сначала случай, когда электромагнитная волна падает под прямым углом на бесконечный плоский проводящий лист. Если распространение происходит по оси  а
а  направлены соответственно по осям у и х, то волну можно описать уравнениями
направлены соответственно по осям у и х, то волну можно описать уравнениями

где

Чтобы сделать тангенциальную составляющую электрического поля на внешней поверхности проводника равной нулю, следует предположить, что существует поле, равное по величине и противоположное по знаку полю, определяемому уравнениями (1.24) и (1.25). Это вторичное поле характеризуется отраженной волной, определяемой уравнениями

и

Падающая и отраженная волны создают стоячие волны, которые для электрического поля определяются суммой уравнений (1.24) и

Для магнитного поля они определяются суммой уравнений (1.25) и (1.27):

Если положить на проводнике  то составляющая
то составляющая  будет равна нулю в точках
будет равна нулю в точках  определяемых соотношением
определяемых соотношением  где
где  Электромагнитная волна, падающая на отражающую поверхность, оказывает давление с силой, равной
Электромагнитная волна, падающая на отражающую поверхность, оказывает давление с силой, равной  для свободного пространства. Коэффициент 2 обусловлен тем, что направление распространения, а следовательно, и вектор Пойнтинга изменяют знак. На поверхности раздела между свободным пространством и диэлектриком имеет место как отражение, так и преломление. Если, как показано на вставке рис. 1.2,
для свободного пространства. Коэффициент 2 обусловлен тем, что направление распространения, а следовательно, и вектор Пойнтинга изменяют знак. На поверхности раздела между свободным пространством и диэлектриком имеет место как отражение, так и преломление. Если, как показано на вставке рис. 1.2,  будут соответственно углами падения и преломления, то закон Снелля, для волны, входящей в диэлектрик, дает
будут соответственно углами падения и преломления, то закон Снелля, для волны, входящей в диэлектрик, дает

а для волны, выходящей из диэлектрика:

В последнем случае для углов падения, больших, чем  возникает явление полного внутреннего отражения. Отра женная волна распространяется всегда под углом
возникает явление полного внутреннего отражения. Отра женная волна распространяется всегда под углом  . Ее амплитуда для случая преломления в более плотной среде определяется коэффициентами Френеля:
. Ее амплитуда для случая преломления в более плотной среде определяется коэффициентами Френеля:

когда электрическое поле параллельно плоскости падения, и

когда электрическое поле перпендикулярно плоскости падения.

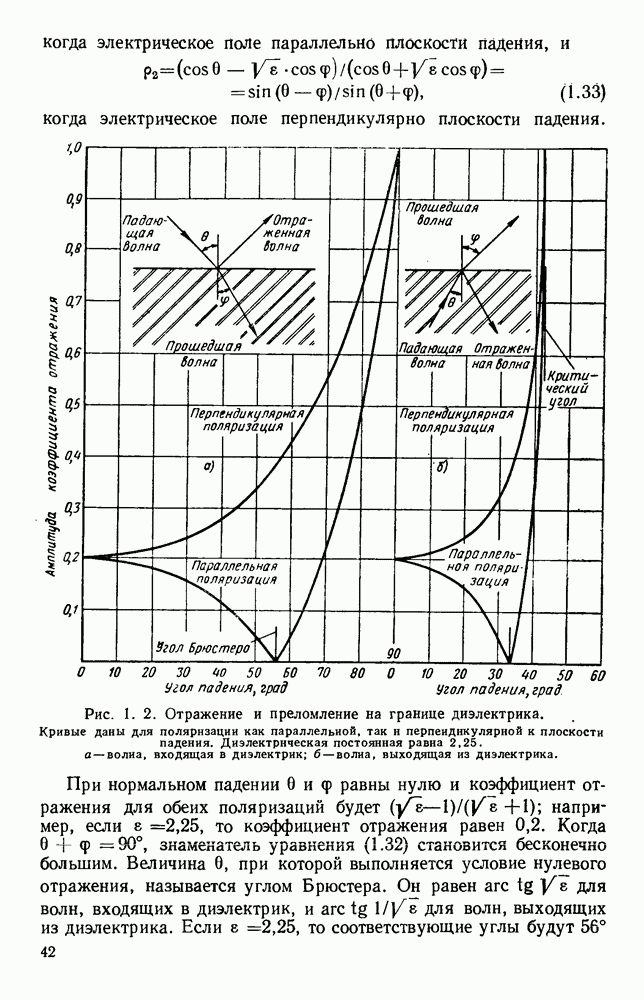
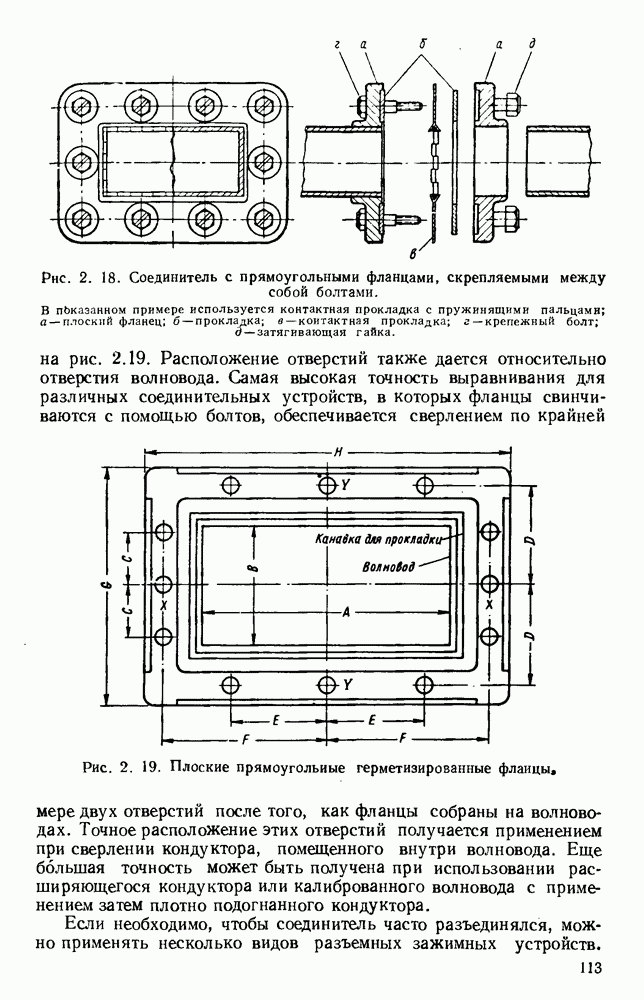
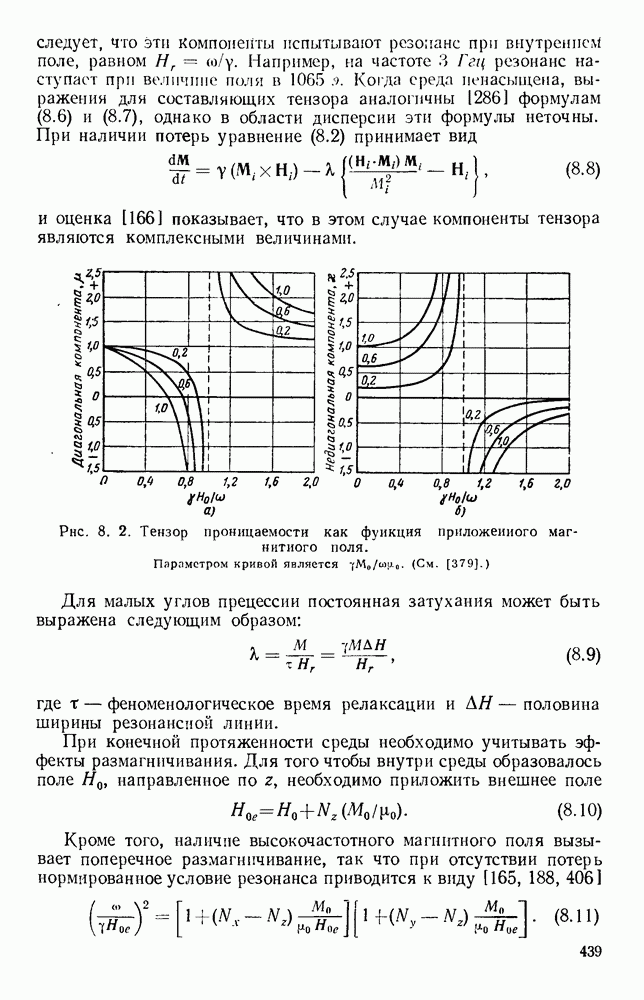
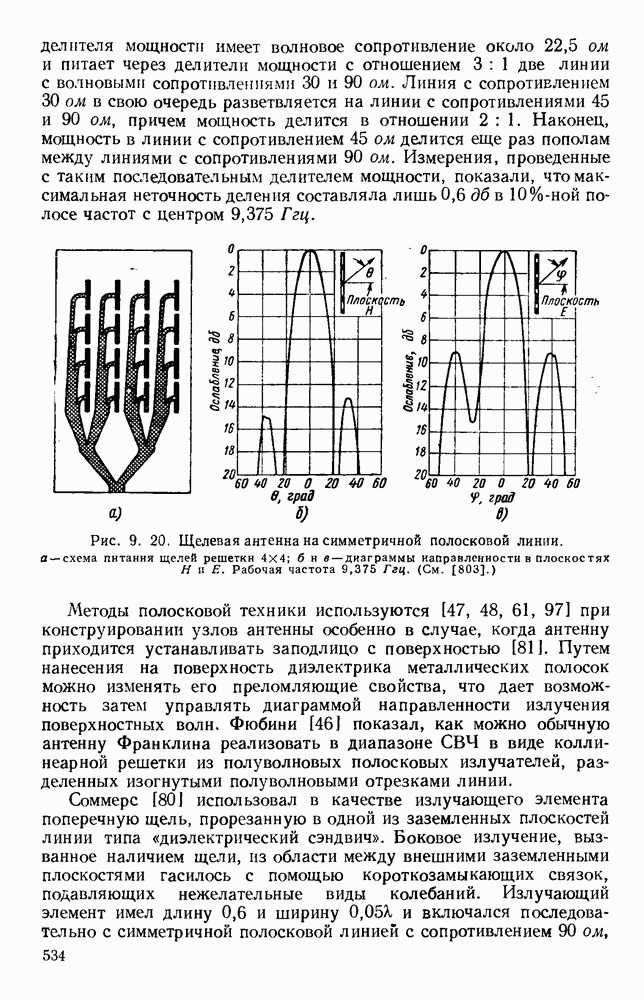
Рис. 1. 2. Отражение и преломление на границе диэлектрика.
Кривые даны для поляризации как параллельной, так и перпендикулярной к плоскости падения. Диэлектрическая постоянная равна 2,25. а — волна, входящая в диэлектрик; б - волна, выходящая из диэлектрика.
При нормальном падении  равны нулю и коэффициент отражения для обеих поляризаций будет
равны нулю и коэффициент отражения для обеих поляризаций будет  например, если
например, если  то коэффициент отражения равен 0,2. Когда
то коэффициент отражения равен 0,2. Когда  знаменатель уравнения (1.32) становится бесконечно большим. Величина 0, при которой выполняется условие нулевого отражения, называется углом Брюстера. Он равен
знаменатель уравнения (1.32) становится бесконечно большим. Величина 0, при которой выполняется условие нулевого отражения, называется углом Брюстера. Он равен  для волн, входящих в диэлектрик, и
для волн, входящих в диэлектрик, и  для волн, выходящих из диэлектрика. Если
для волн, выходящих из диэлектрика. Если  то соответствующие углы будут 56°
то соответствующие углы будут 56°
и 34°. На рис. 1.2 приведены амплитуды коэффициента отражения для других углов падения, как при вхождении в более плотную среду, так и при выходе из нее.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
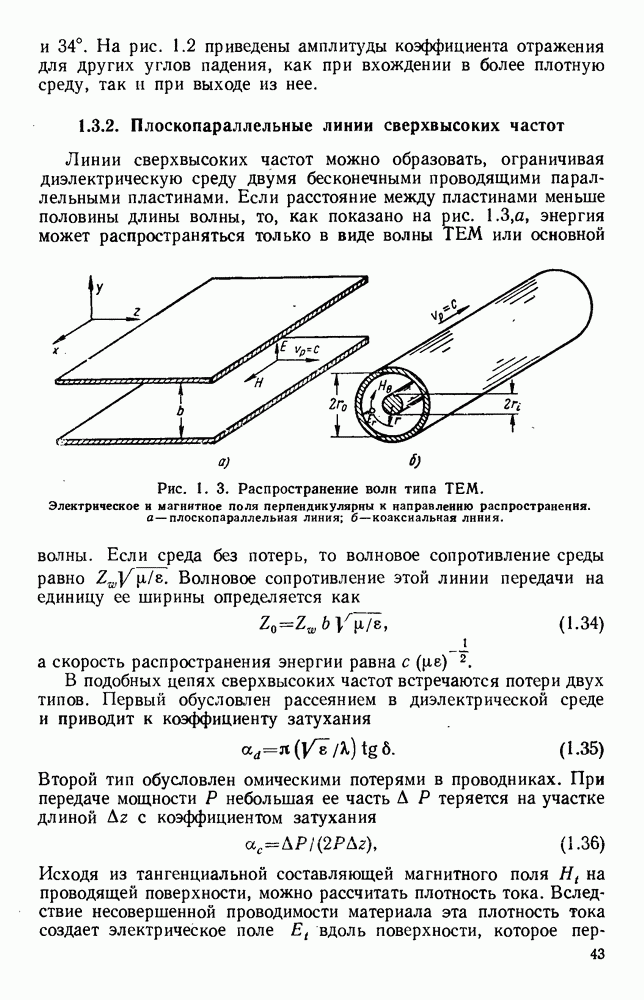
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
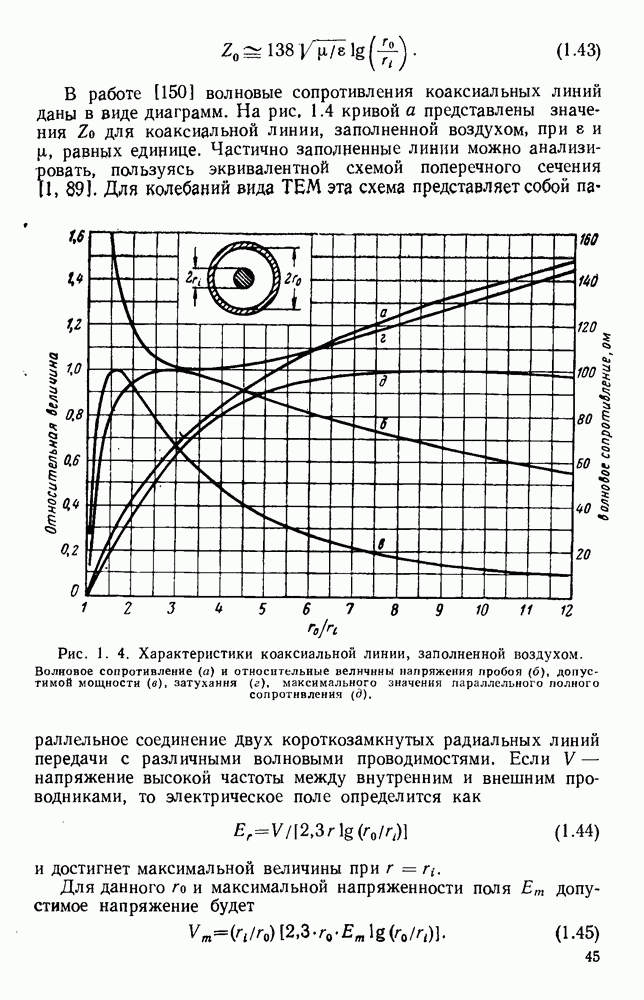
- 1.3.3. Коаксиальные линии
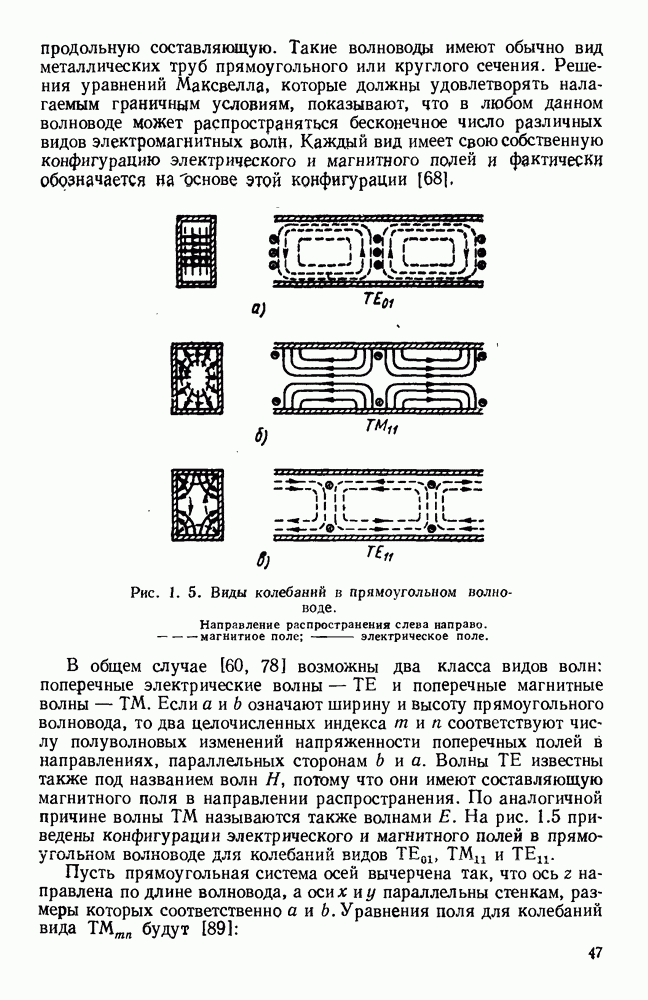
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
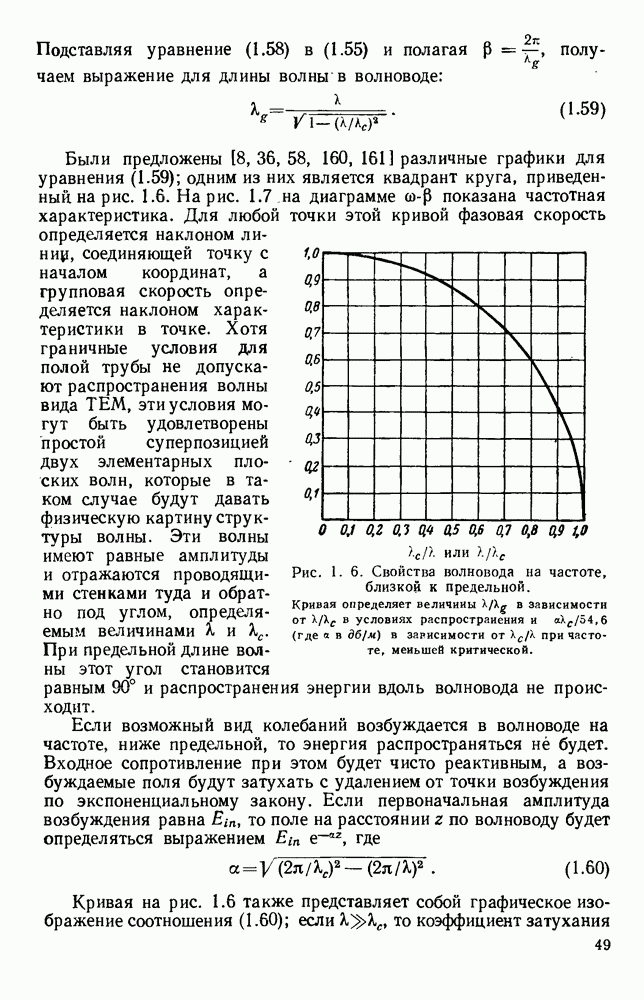
- 1.4.2. Круглые волноводы
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
- 1.5.2. Гребневые волноводы
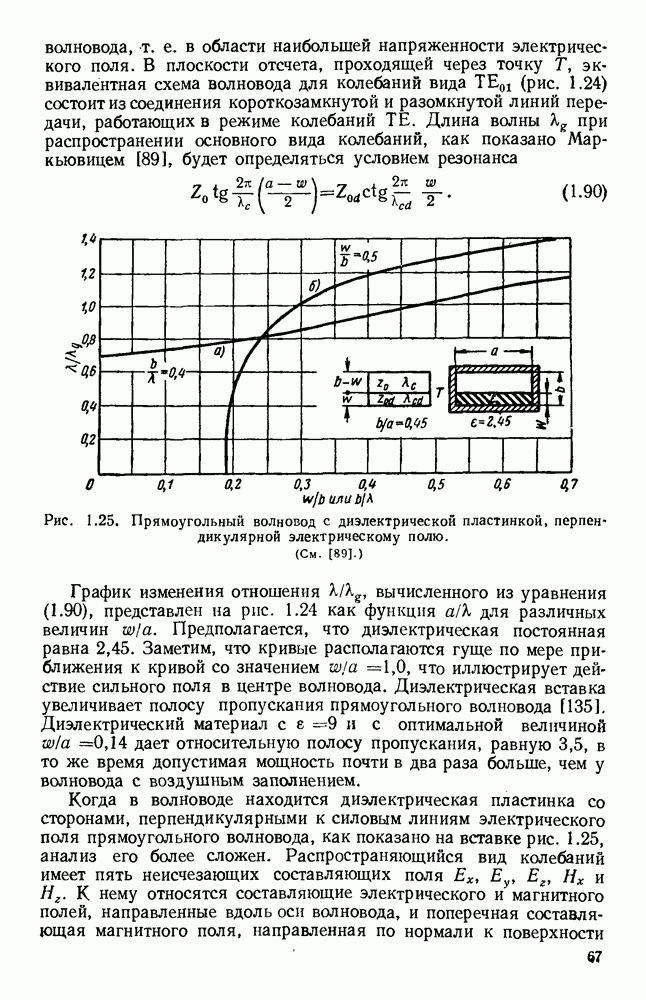
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
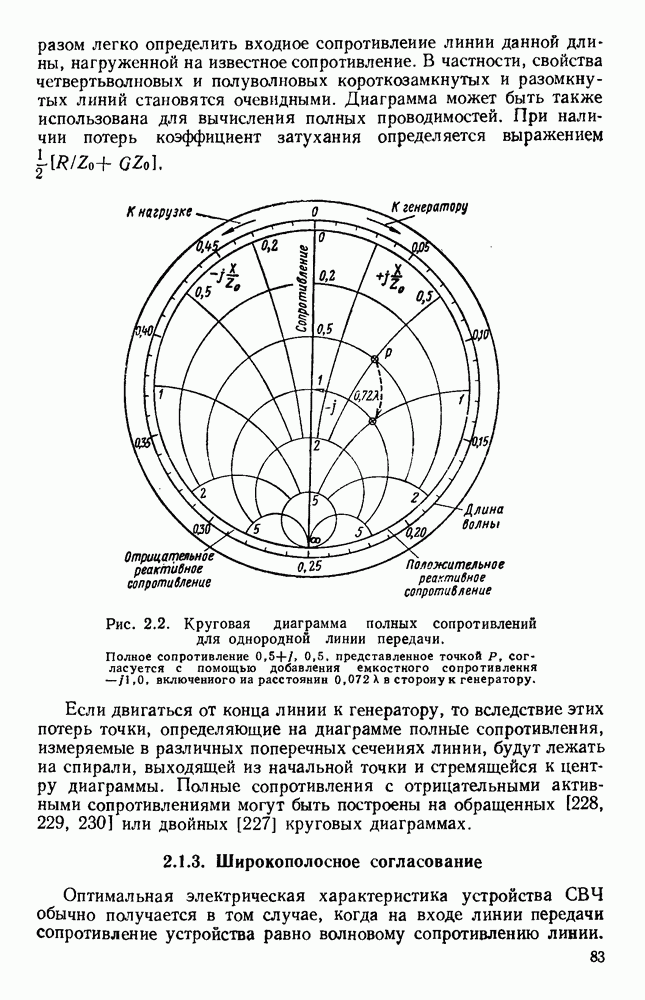
- 2.1.2. Круговая диаграмма
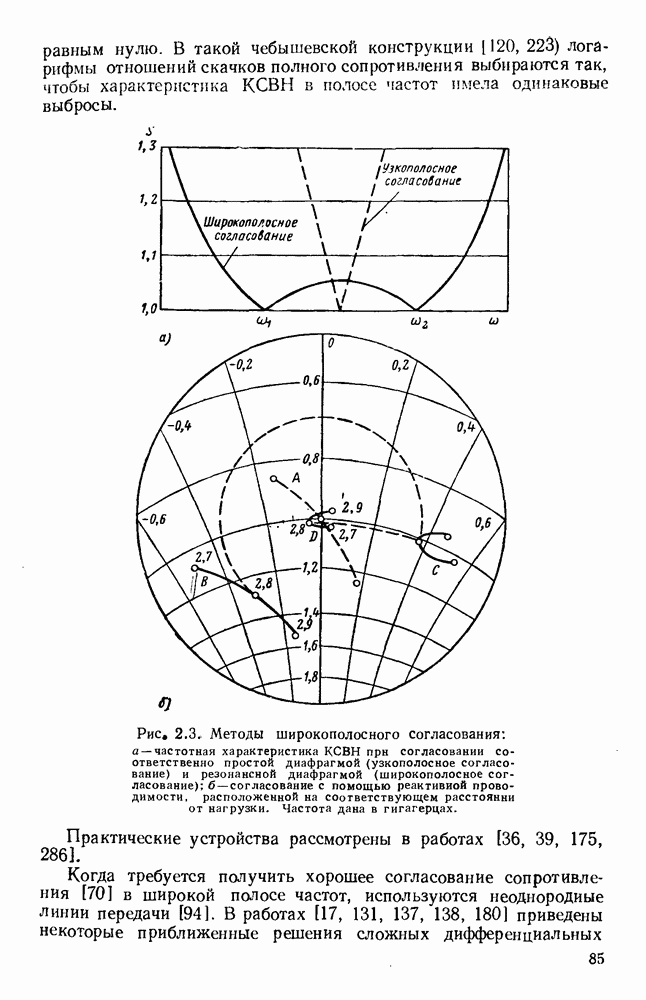
- 2.1.3. Широкополосное согласование
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
- 2.3.1. Прямоугольные волноводы
- 2.3.2. Круглые волноводы
- 2.3.3. Широкополосные и компактные волноводы
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
- 2.4.2. Контактные прокладки и дроссели
- 2.4.3. Крепежные и зажимные устройства
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
- 2.6.1. Изгибы, уголки и скрутки
- 2.6.2. Переходы и преобразователи
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
- 3.2.3. Переход от линейной поляризации к круговой
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
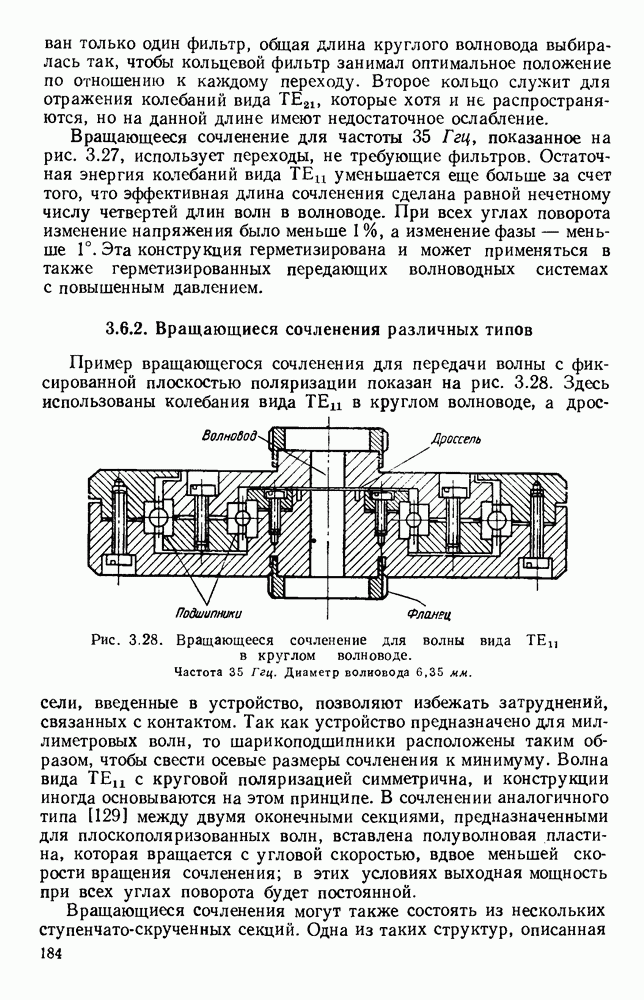
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
- 3.6.2. Вращающиеся сочленения различных типов
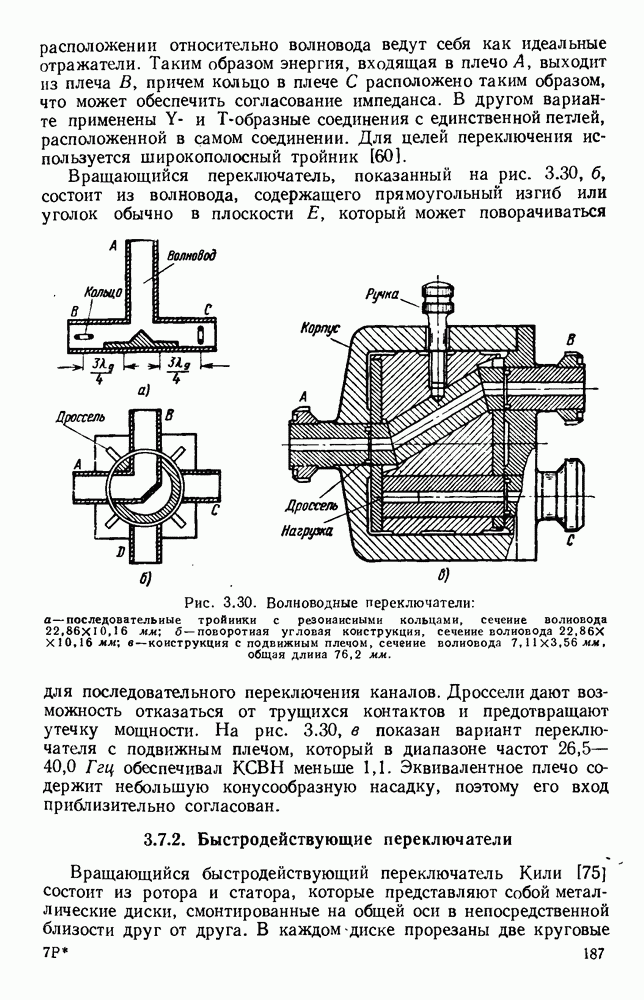
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
- 3.7.1. Механические переключатели с ручным управлением
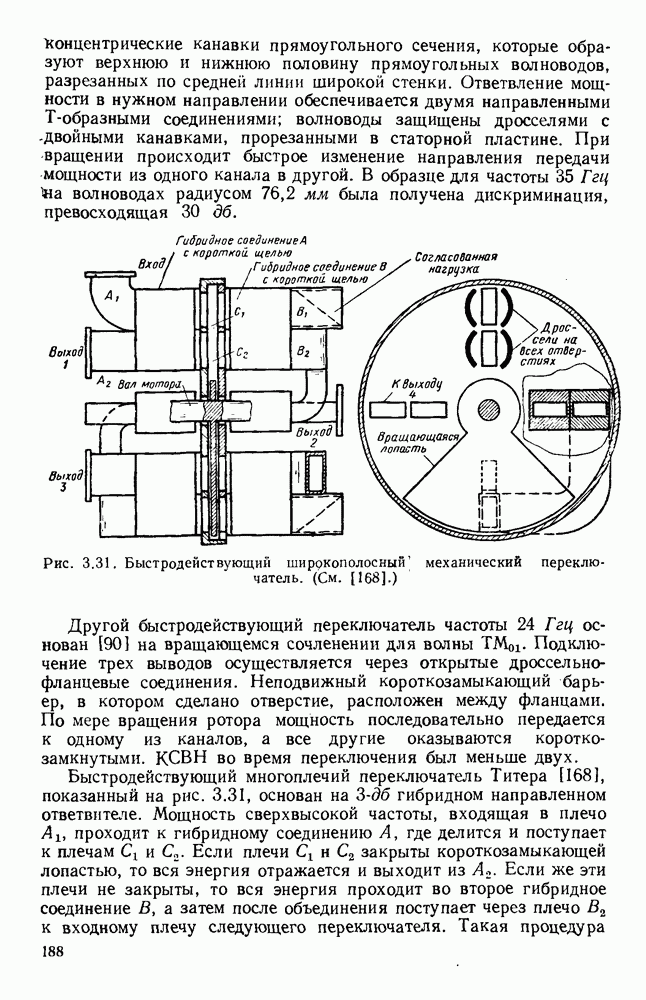
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
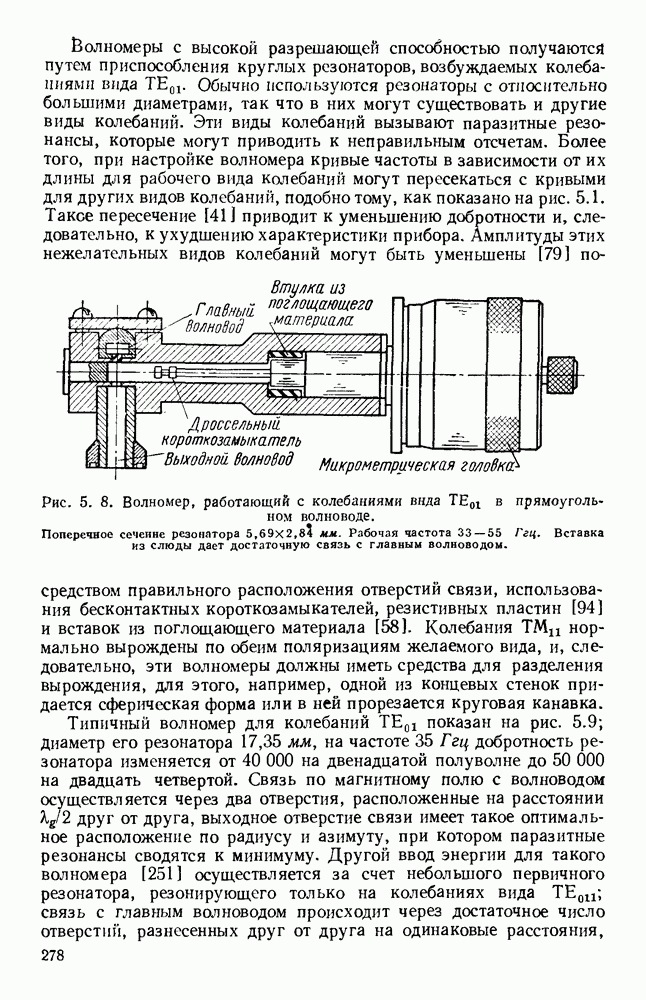
- 5.2.1. Волномеры с объемными резонаторами
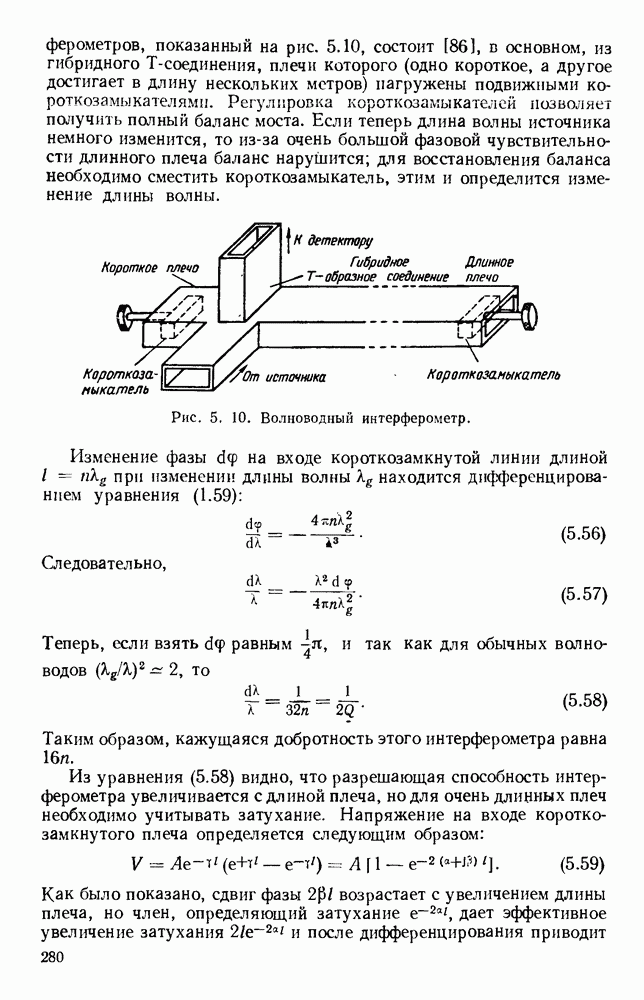
- 5.2.2. Волноводные интерферометры
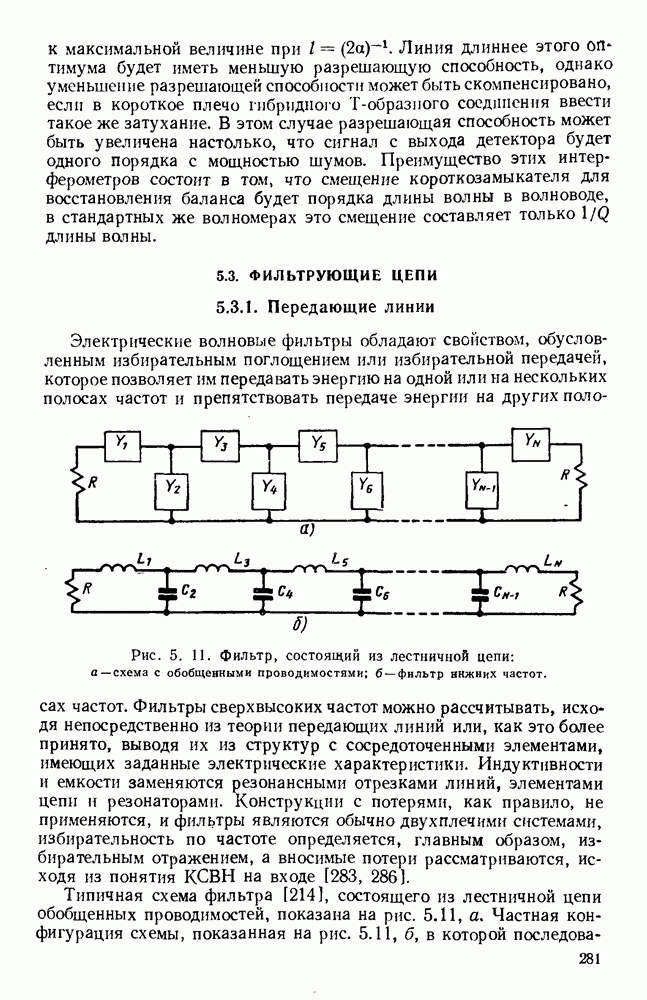
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
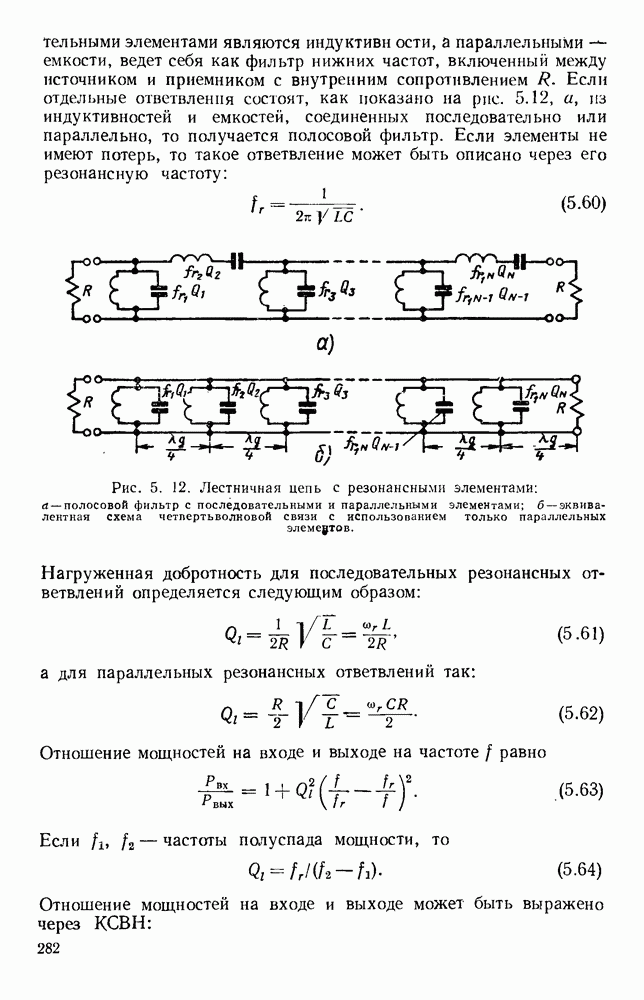
- 5.3.2. Связанные резонаторы
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
- 7.1.2. Форма линии и интенсивность
- 7.1.3. Сверхтонкая структура
- 7.1.4. Явления Штарка и Зеемана
- 7.2. СПЕКТРОМЕТРЫ
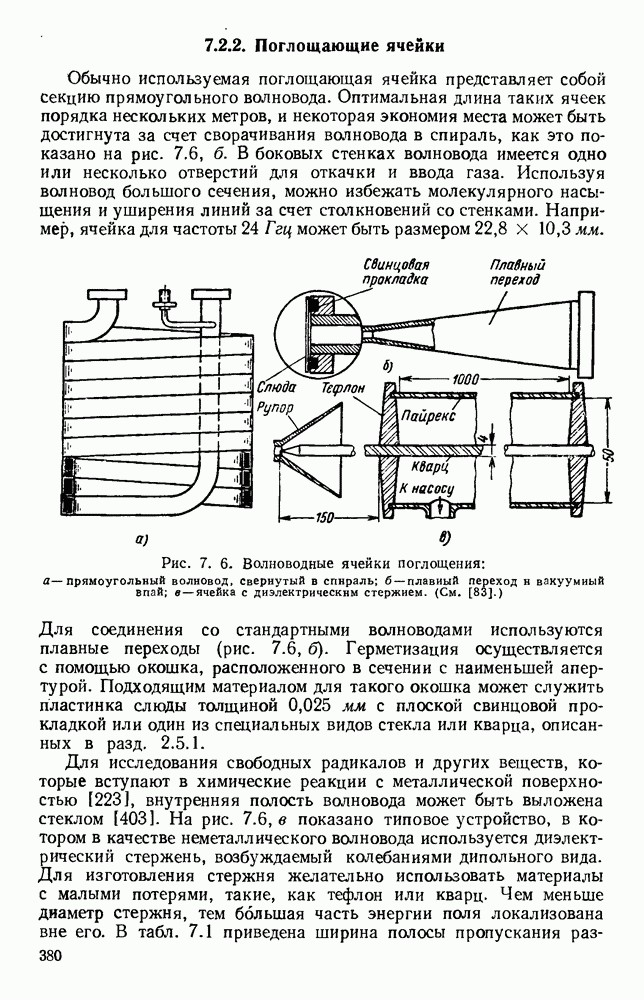
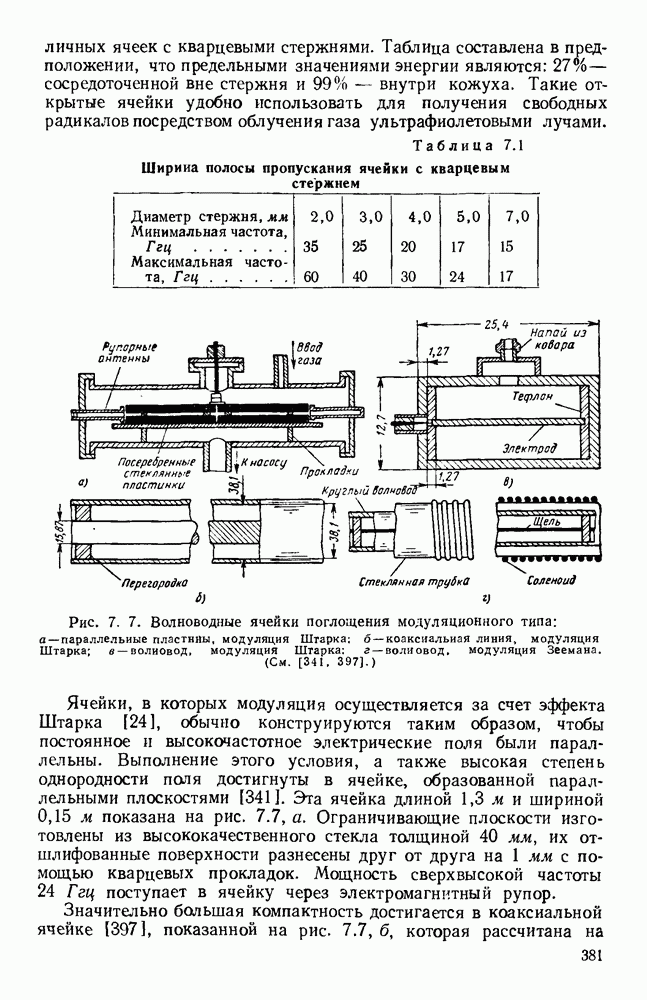
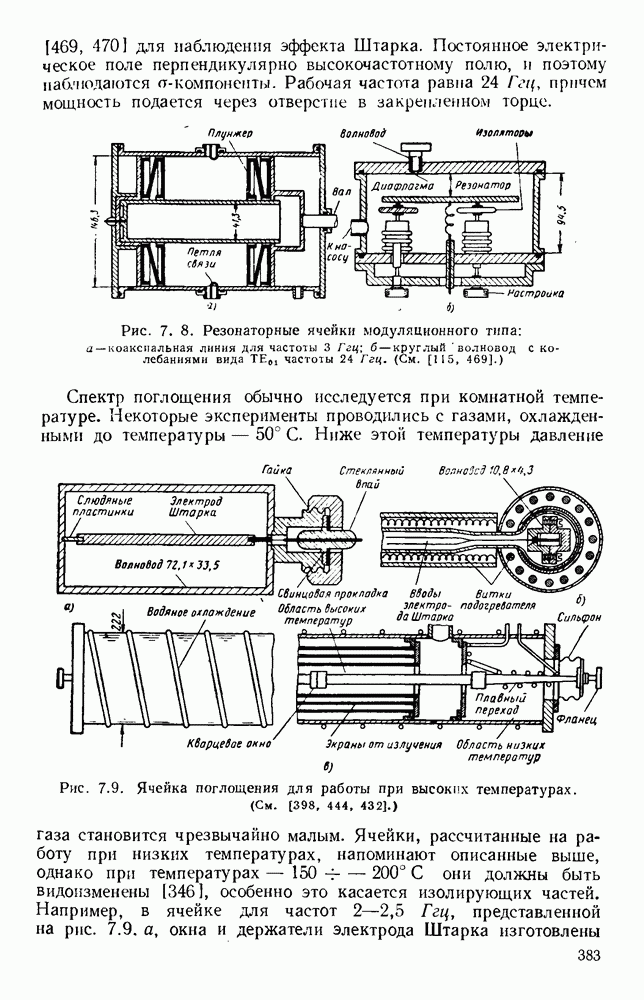
- 7.2.2. Поглощающие ячейки
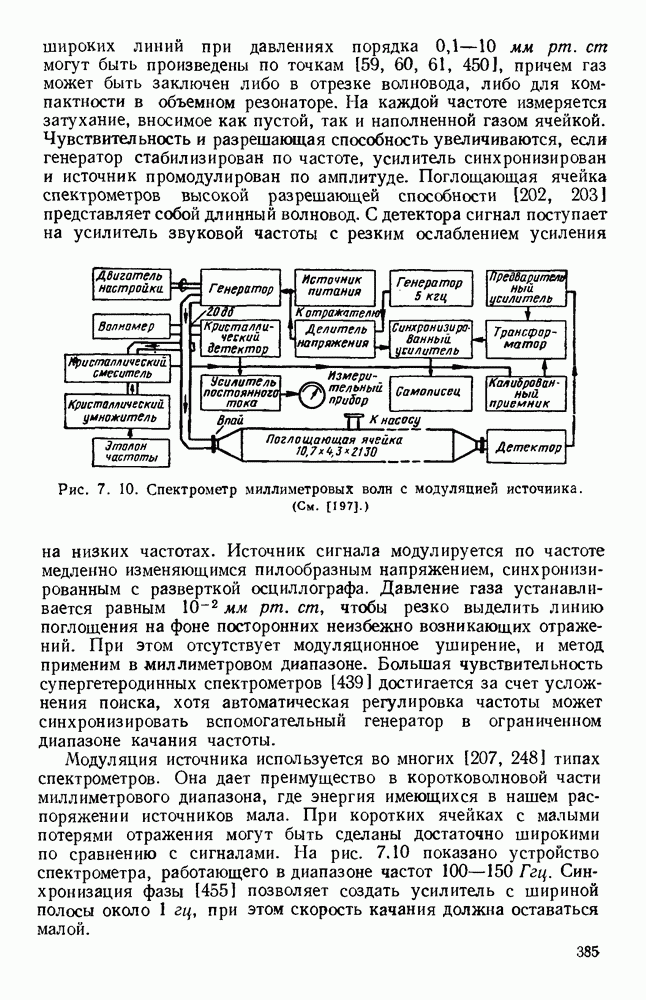
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
- 7.3.4. Времена релаксации
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
- 8.3.3. Ферритовые устройства в качестве элементов схем
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
- 8.6.2. Устройства с поперечным полем
- 8.6.3. Прочие узлы
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
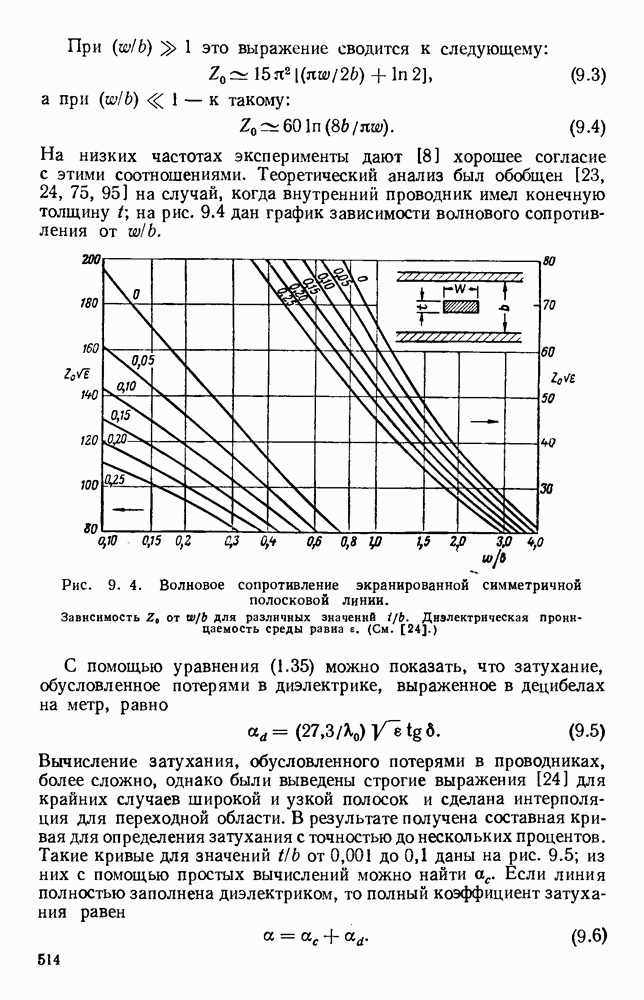
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.2.1. Линии типа «диэлектрических сэндвичей»
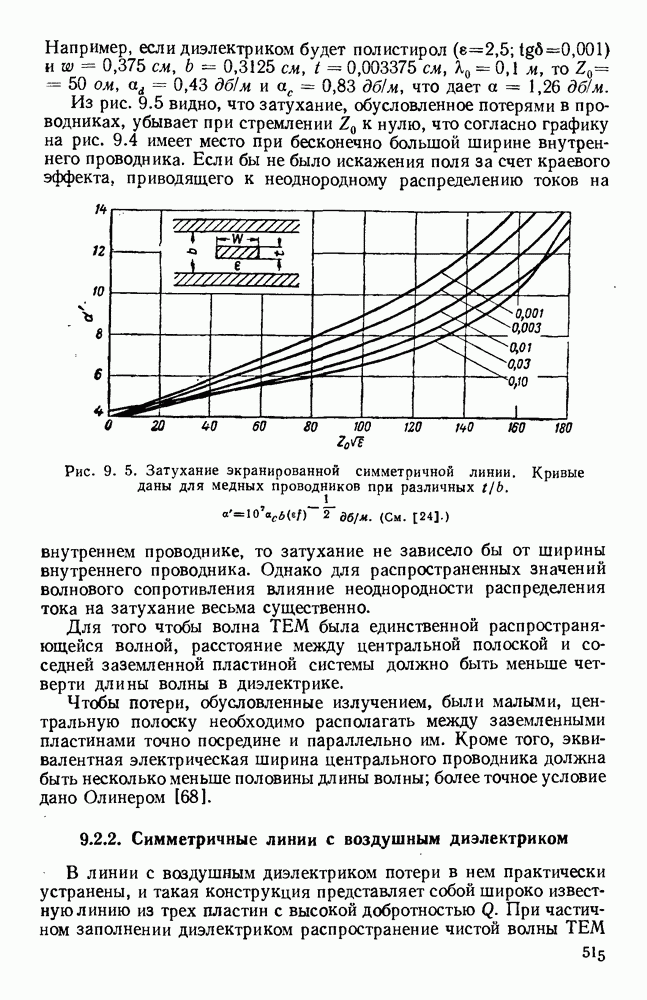
- 9.2.2. Симметричные линии с воздушным диэлектриком
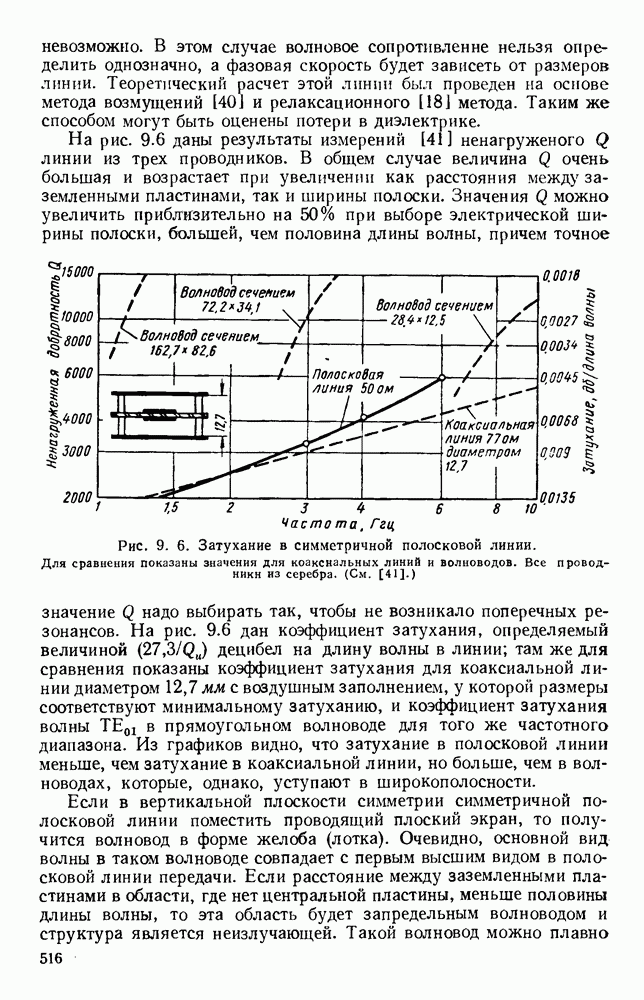
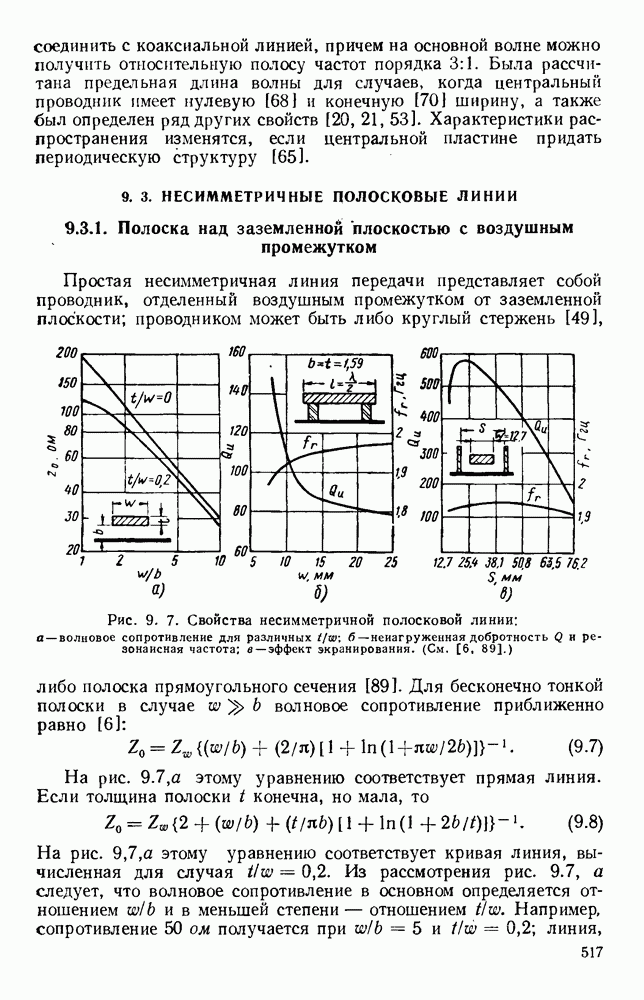
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
- 9.4.2. Переходные устройства
- 9.4.3. Узлы полосковых систем
- 9.5. ЦЕПИ И СИСТЕМЫ
- 9.5.3. Частотные фильтры
- 9.5.4. Цепи питания антенн
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
- 10.1.2. Пространственные гармоники
- 10.1.3. Многократно-периодические структуры
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
- 10.2.3. Продольные цилиндрические волны
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
- 12.2. МАГНЕТРОНЫ
- 12.2.2. Резонаторные системы
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
- 12.2.4. Рабочие характеристики
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
- 13.1.2. Типы дифракции
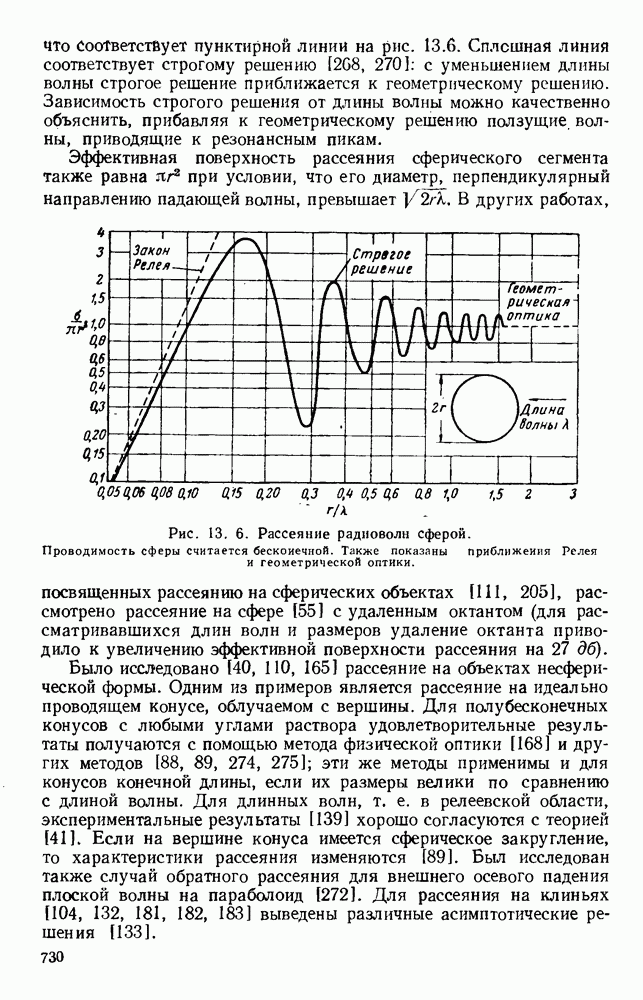
- 13.1.3. Рассеяние
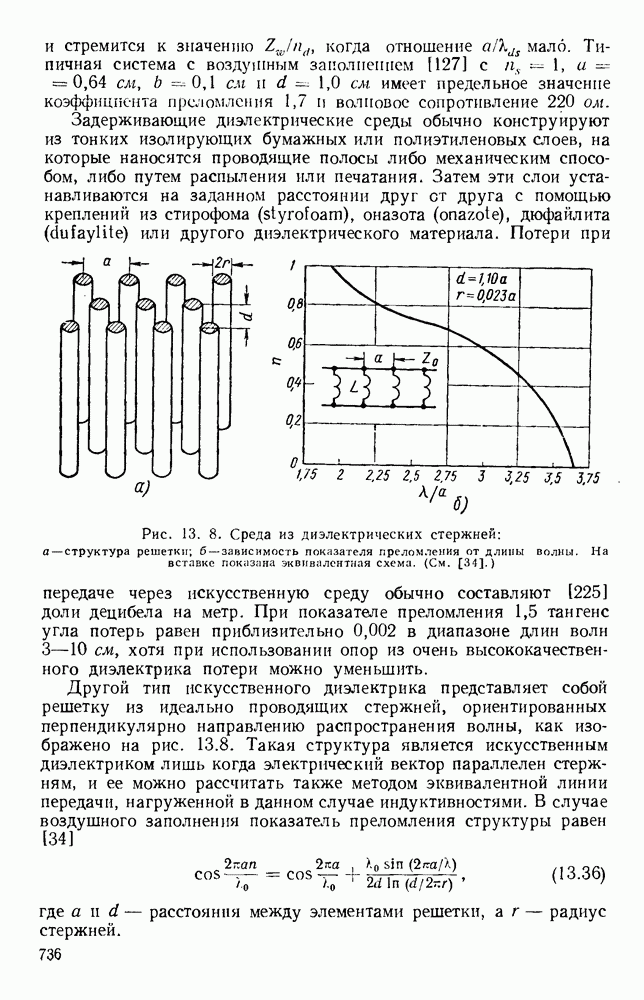
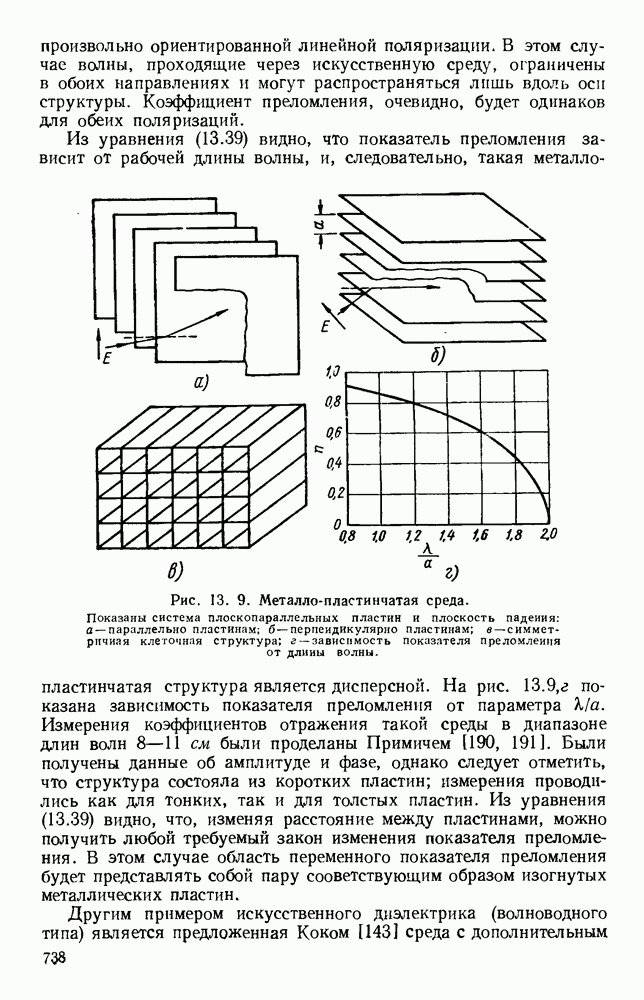
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
- 13.2.2. Структуры волноводного типа
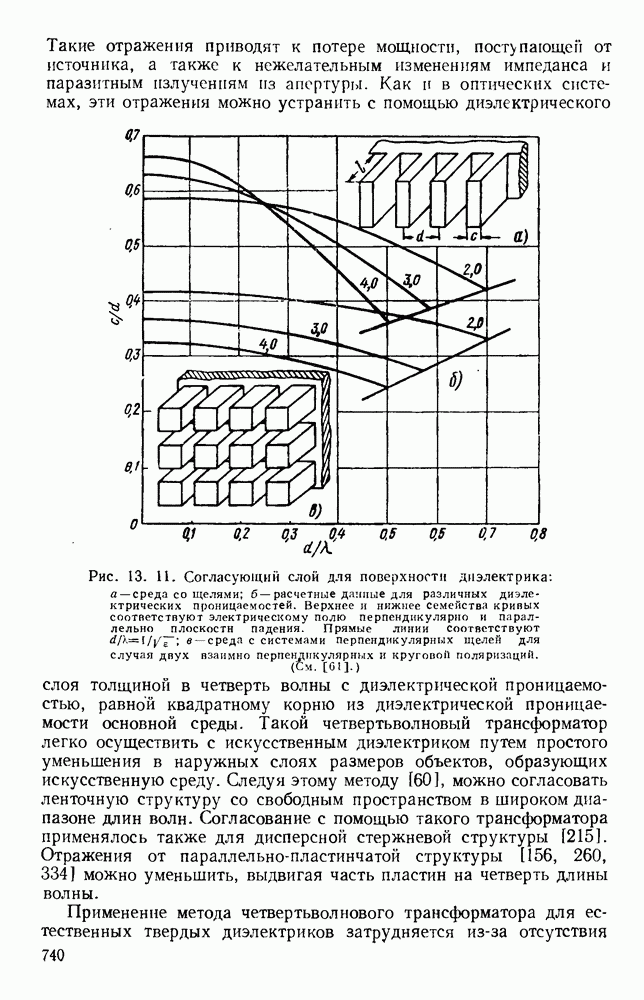
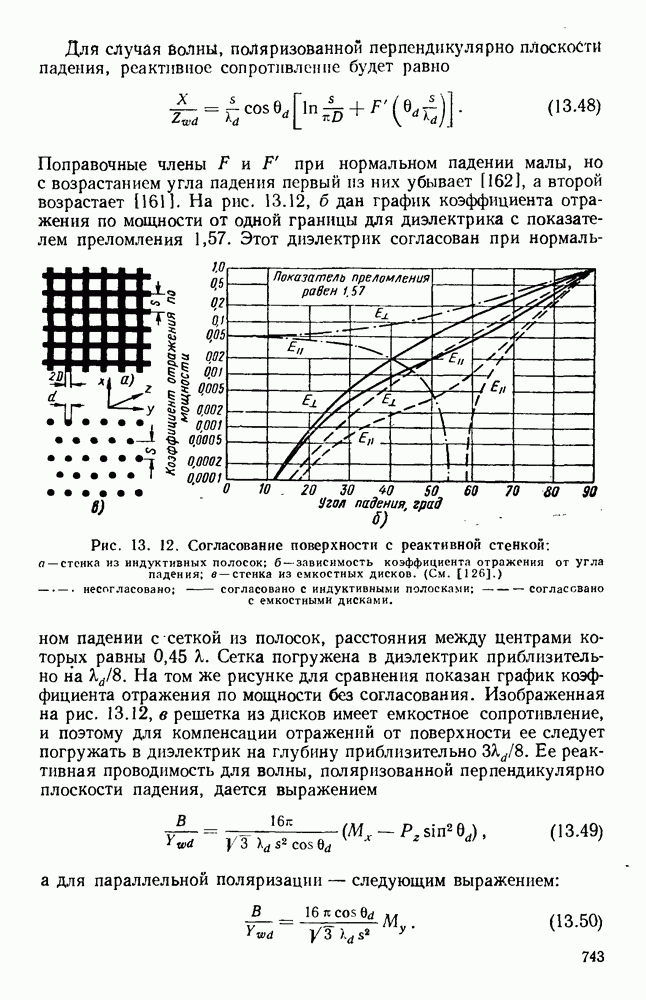
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
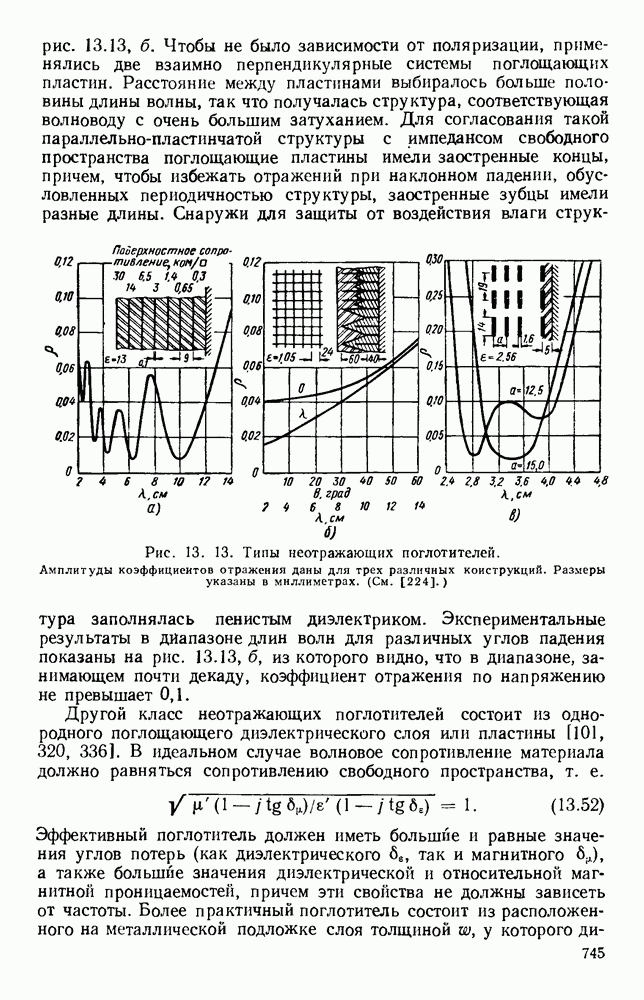
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
- 13.4. ПРИБОРЫ И СИСТЕМЫ
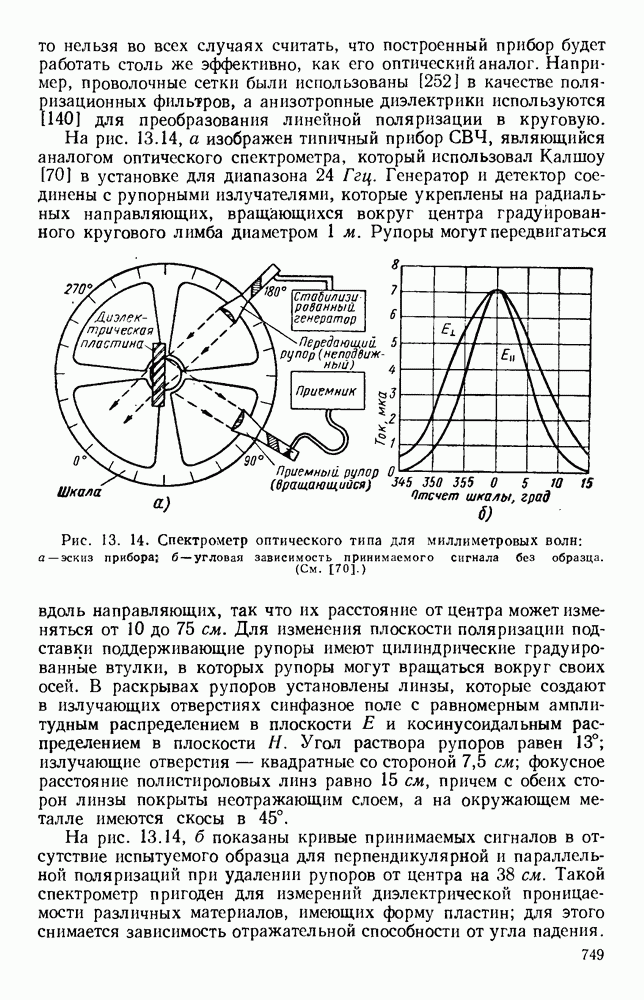
- 13.4.1. Спектрометры
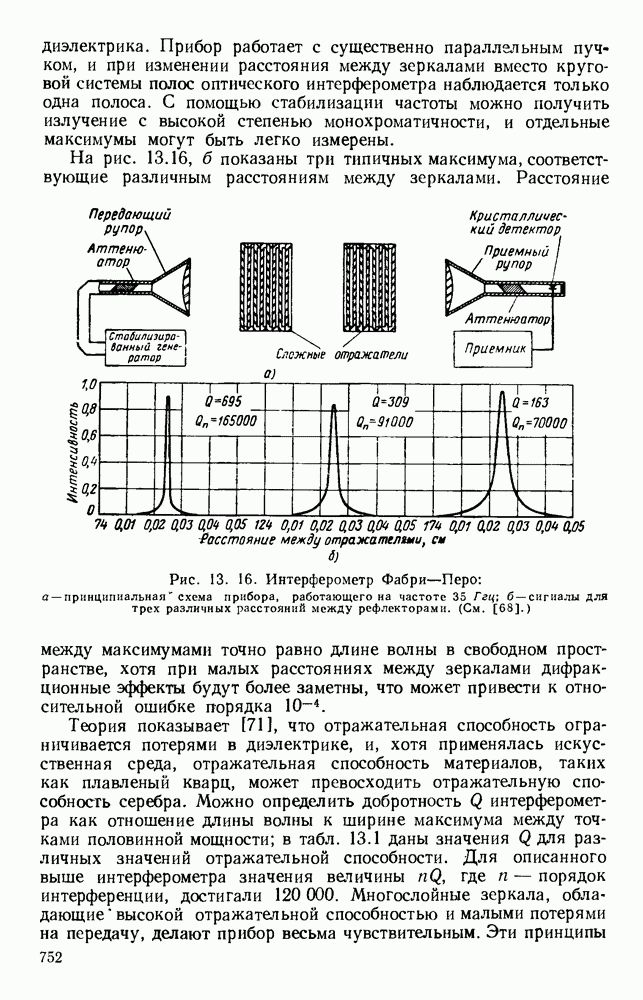
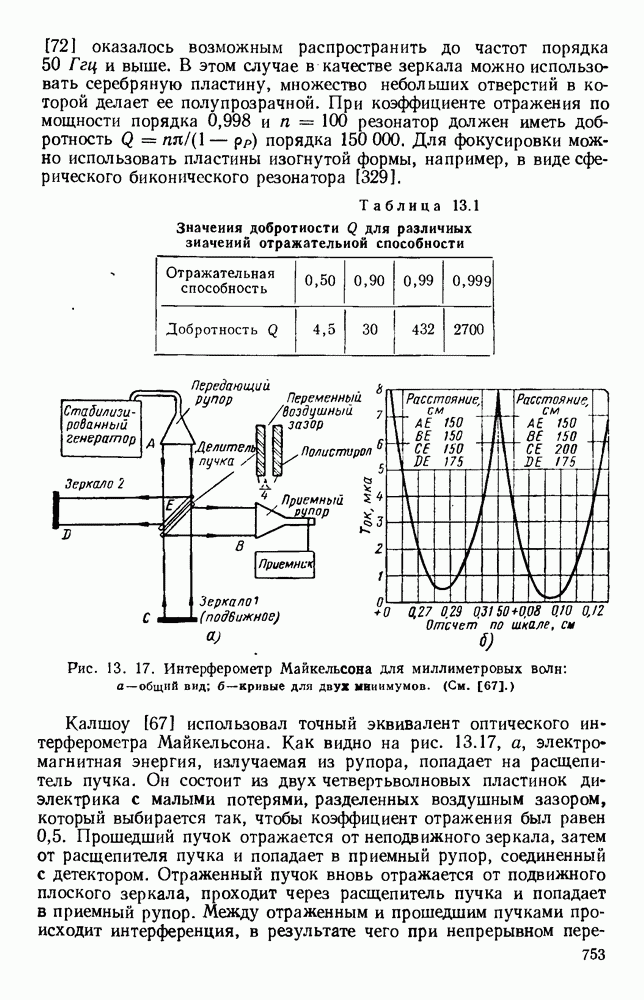
- 13.4.2. Интерферометры
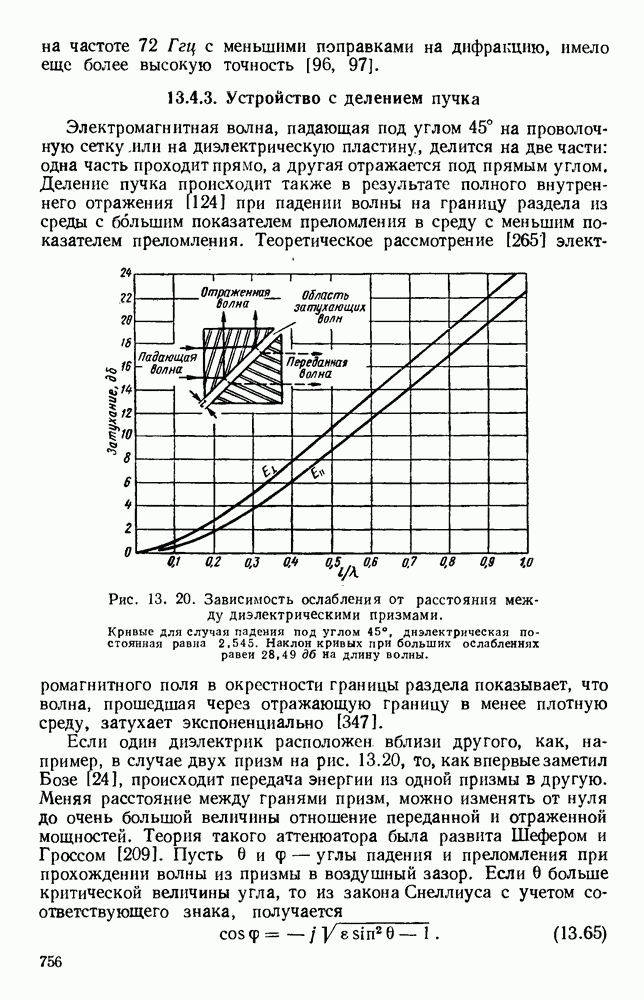
- 13.4.3. Устройство с делением пучка