| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.1.4. Явления Штарка и Зеемана
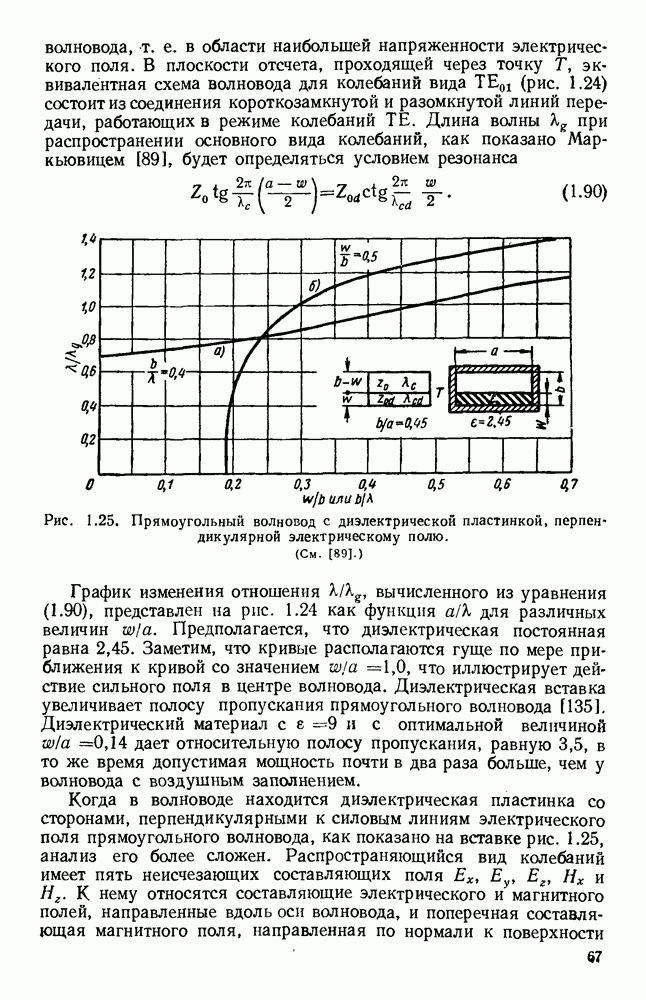
Вращательный спектр молекулы, имеющей электрический момент, подвергается изменениям в присутствии постоянного электрического поля. Явление Штарка, обусловленное воздействием электрического поля на дипольный момент молекулы, изменяет вращательное движение последней. Аналогично изменяется движение молекулы, обладающей магнитным моментом, в постоянном магнитном поле из-за явления Зеемана. Главное свойство этих явлений состоит в снятии пространственного  вырождения уровней энергии. Если внешнее поле направлено вдоль оси
вырождения уровней энергии. Если внешнее поле направлено вдоль оси  то угловой момент
то угловой момент  может иметь
может иметь  значений проекции на эту ось, что соответствует целым значениям
значений проекции на эту ось, что соответствует целым значениям  до
до  Когда постоянный электрический или магнитный момент молекулы
Когда постоянный электрический или магнитный момент молекулы  имеет проекцию на вектор
имеет проекцию на вектор  то
то  проекций будут иметь значения
проекций будут иметь значения  или
или  что приводит к возникновению линейного эффекта Штарка или Зеемана. Если существует только индуцированный электрический момент, пропорциональный полю, то имеет место квадратичный эффект с
что приводит к возникновению линейного эффекта Штарка или Зеемана. Если существует только индуцированный электрический момент, пропорциональный полю, то имеет место квадратичный эффект с  значениями уровней энергии. Сходство явлений Штарка и Зеемана позволяет развить теорию сразу для обоих эффектов [108]. При напряженности электрического поля в несколько тысяч вольт
значениями уровней энергии. Сходство явлений Штарка и Зеемана позволяет развить теорию сразу для обоих эффектов [108]. При напряженности электрического поля в несколько тысяч вольт
на сантиметр или напряженности магнитного поля в несколько тысяч эрстед энергии взаимодействия в явлениях Штарка и Зеемана малы по сравнению с энергией вращения, что позволяет использовать квантовомеханическую теорию возмущеиий.
Эффект Штарка может быть исследован при вращении линейной молекулы, момент количества движения которой направлен перпендикулярно электрическому полю. Поле стремится повернуть диполь и ускорить его вращение, если он направлен по полю, или замедлить вращение диполя, если он направлен против поля. Поэтому диполи чаще ориентируются в сторону от направления поля, чем по нему, и в среднем направлены навстречу полю. Можно показать, что изменение энергии, обусловленное полем, равно

Очевидно, что изменяется также средняя скорость вращения молекул.
Если при вращении линейной молекулы ее момент направлен параллельно или антипараллельно электрическому полю, то изменение энергии опять определяется уравнением (7.19), но теперь оно отрицательно. Таким образом, при произвольной ориентации вращающихся молекул среднее изменение энергии равно нулю.
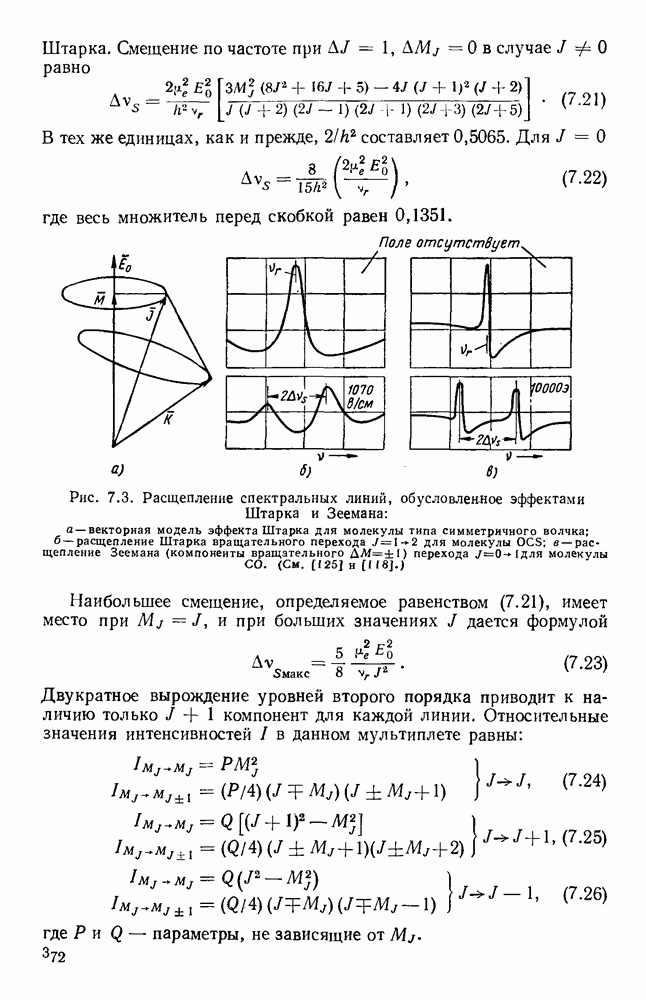
У молекул типа симметричного волчка наблюдается линейный эффект Штарка, что следует, например, из рис. 7.3, а, на котором  направлено вдоль оси симметрии и, значит, вдоль вектора К. Вектор
направлено вдоль оси симметрии и, значит, вдоль вектора К. Вектор  быстро прецессирует вокруг
быстро прецессирует вокруг  в то время как К прецессирует вокруг
в то время как К прецессирует вокруг  значительно медленнее. Для переходов
значительно медленнее. Для переходов  при векторе ВЧ электрического поля, параллельном
при векторе ВЧ электрического поля, параллельном  что обычно выполняется в экспериментах, имеем следующие правила отбора:
что обычно выполняется в экспериментах, имеем следующие правила отбора:  При этих условиях происходит смещение по частоте невозмущенной линии вращательного спектра на
При этих условиях происходит смещение по частоте невозмущенной линии вращательного спектра на

Если  выражено в мегагерцах,
выражено в мегагерцах,  в дебаях,
в дебаях,  в вольтах на сантиметр, то множитель
в вольтах на сантиметр, то множитель  равен 1,0064. Максимальное расщепление, которое происходит при
равен 1,0064. Максимальное расщепление, которое происходит при  приблизительно обратно пропорционально
приблизительно обратно пропорционально  при
при  оно равно
оно равно  Переходы
Переходы  дают
дают  -компоненты; существует набор этих компонент для всех значений К, исключая нуль. Поскольку
-компоненты; существует набор этих компонент для всех значений К, исключая нуль. Поскольку  -компоненты линий нулевого поля расположены очень близко, то их расщепление из-за линейного эффекта Штарка трудно разрешить. Переходы
-компоненты линий нулевого поля расположены очень близко, то их расщепление из-за линейного эффекта Штарка трудно разрешить. Переходы  или
или  -компоненты, обладают круговой поляризацией и наблюдаются при дипольном электрическом поглощении только в том случае, когда
-компоненты, обладают круговой поляризацией и наблюдаются при дипольном электрическом поглощении только в том случае, когда  перпендикулярно вектору ВЧ электрического поля.
перпендикулярно вектору ВЧ электрического поля.
Для линейных молекул и для уровней  у молекул типа симметричного волчка имеет место только квадратичный эффект
у молекул типа симметричного волчка имеет место только квадратичный эффект
Штарка. Смещение по частоте при  в случае
в случае  О равно
О равно

В тех же единицах, как и прежде,  составляет 0,5065. Для
составляет 0,5065. Для 

где весь множитель перед скобкой равен 0,1351.

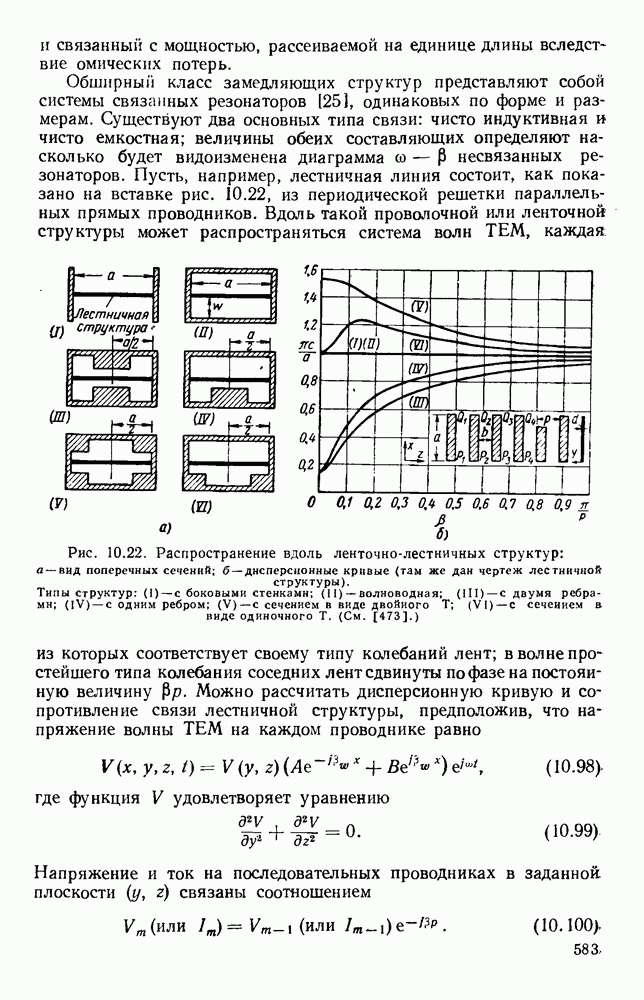
Рис. 7.3. Расщепление спектральных линий, обусловленное эффектами Штарка и Зеемана: а — векторная модель эффекта Штарка для молекулы типа симметричного волчка; б - расщепление Штарка вращательного перехода  для молекулы
для молекулы  в — расщепление Зеемана (компоненты вращательного
в — расщепление Зеемана (компоненты вращательного  перехода
перехода  для молекулы
для молекулы  (См. [125] и [118].)
(См. [125] и [118].)
Наибольшее смещение, определяемое равенством (7.21), имеет место при  и при больших значениях
и при больших значениях  дается формулой
дается формулой

Двукратное вырождение уровней второго порядка приводит к наличию только  компонент для каждой линии. Относительные значения интенсивностей I в данном мультиплете равны:
компонент для каждой линии. Относительные значения интенсивностей I в данном мультиплете равны:

где  параметры, не зависящие от
параметры, не зависящие от 
Молекулы типа асимметричного волчка сложнее для анализа, но все же расщепления уровней энергии из-за эффекта Штарка были выражены через коэффициенты интенсивности линий [119, 199].
Квадратичный эффект Штарка часто наблюдается в радиоспектроскопии, и на рис. 7.3, б показаны результаты для  [125]. Определение дипольного момента с помощью эффекта Штарка дает значение равное 0,72 дебая. Другой типичной молекулой, изучаемой теми же методами в диапазоне
[125]. Определение дипольного момента с помощью эффекта Штарка дает значение равное 0,72 дебая. Другой типичной молекулой, изучаемой теми же методами в диапазоне  является молекула окиси азота [96]. Быстрое уменьшение штарковского расщепления с ростом
является молекула окиси азота [96]. Быстрое уменьшение штарковского расщепления с ростом  как это видно из формулы (7.23), ограничивает точность измерений для сравнительно легких молекул, особенно при малом дипольном моменте. Например, на переходе
как это видно из формулы (7.23), ограничивает точность измерений для сравнительно легких молекул, особенно при малом дипольном моменте. Например, на переходе  были сделаны точные измерения для молекулы
были сделаны точные измерения для молекулы  [413], дипольный момент которой оказался равным 0,166 дебая.
[413], дипольный момент которой оказался равным 0,166 дебая.
Дипольный момент аммиака вследствие инверсного расщепления не строго постоянен. Следовательно, расщепление его уровней происходит только из-за квадратичного эффекта Штарка и в тех же единицах [122, 350] равно

Найденное при исследовании квадрупольного расщепления [275] значение составляет 1,468 дебая [113]. Вероятности переходов или интенсивности линий будут подчиняться [12] тому же закону, что и уравнение (7.27) для расщепленных частот, т. е.

При наличии сверхтонкой структуры эффект Штарка видоизменяется [161, 330]. Величина расщепления зависит от соотношения энергий сверхтонкой структуры и штарковского расщепления; в промежуточном случае, например, результаты измерений хорошо согласуются с теорией [413]. Большие электрические поля, порядка  в/см, могут в некоторых случаях нарушить распределение электронов в молекуле или относительное расположение атомов, что приводит к поляризации молекулы и изменению ее энергии [199]. Этот эффект очень мал, но такие индуцированные дипольные моменты могут вызвать вращательные переходы в неполярных молекулах. Если штарковское поле само изменяется, то возникают новые явления [290, 453], когда частота изменения становится сравнимой с шириной линии поглощения. Когда частота модуляции делается равной частоте спектральной линии, имеет место резонанс [18], эффект Штарка становится очень большим и за точкой резонанса меняет знак.
в/см, могут в некоторых случаях нарушить распределение электронов в молекуле или относительное расположение атомов, что приводит к поляризации молекулы и изменению ее энергии [199]. Этот эффект очень мал, но такие индуцированные дипольные моменты могут вызвать вращательные переходы в неполярных молекулах. Если штарковское поле само изменяется, то возникают новые явления [290, 453], когда частота изменения становится сравнимой с шириной линии поглощения. Когда частота модуляции делается равной частоте спектральной линии, имеет место резонанс [18], эффект Штарка становится очень большим и за точкой резонанса меняет знак.
Магнитный момент, обусловленный вращением самой молекулы или электронов, приводит к увеличению зеемановского расщепления
[381]. Для таких молекул зеемановское изменение магнитной энергии в присутствии внешнего магнитного поля  может быть представлено [160, 277, 279, 280] в виде
может быть представлено [160, 277, 279, 280] в виде

а для молекул со значительно меньшим магнитным моментом ядер — формулой

В дополнение к линейному эффекту Зеемана имеет место более слабый квадратичный эффект, пропорциональный 
Если ВЧ электрическое поле параллельно  то
то  и
и  -компоненты перехода
-компоненты перехода  определяются уравнением
определяются уравнением

Когда же  то
то  -компоненты определяются уравнением
-компоненты определяются уравнением

где  относятся к более низкому энергетическому состоянию Если
относятся к более низкому энергетическому состоянию Если  -фактор остается постоянным, то из (7.31) видно, что
-фактор остается постоянным, то из (7.31) видно, что  -компоненты не подвержены эффекту Зеемана, в то время как <т-компоненты, согласно (7.32), распадаются на две линии, имеющие частоты
-компоненты не подвержены эффекту Зеемана, в то время как <т-компоненты, согласно (7.32), распадаются на две линии, имеющие частоты

ВЧ поле с круговой поляризацией в зависимости от направления вращения возбуждает ту или другую  -компоненту. Относительные интенсивности различных линий даются теми же формулами
-компоненту. Относительные интенсивности различных линий даются теми же формулами  Эффект Зеемана видоизменяется в молекулах, имеющих сверхтонкую структуру, например, таких, как молекула [449] аммиака. Типичное зеемановское расщепление для
Эффект Зеемана видоизменяется в молекулах, имеющих сверхтонкую структуру, например, таких, как молекула [449] аммиака. Типичное зеемановское расщепление для  показано на рис. 7.3, в [118] для
показано на рис. 7.3, в [118] для  -компонент перехода
-компонент перехода 
Если молекулы находятся в параллельных магнитном и электрическом полях, то эффекты Штарка и Зеемана для слабых полей складываются; для случая же перпендикулярных друг другу полей расщепление более сложно [108]. Возникают переходы между зеемановскими составляющими уровня энергии, соответствующими  Частоты излучения этих переходов возрастают с увеличением
Частоты излучения этих переходов возрастают с увеличением  более или менее линейно. Если магнитный момент молекулы имеет порядок магнетона Бора, то эти частоты попадают в сантиметровый диапазон. В работах [39 и 231] даны экспериментальные результаты для нескольких парамагнитных газов.
более или менее линейно. Если магнитный момент молекулы имеет порядок магнетона Бора, то эти частоты попадают в сантиметровый диапазон. В работах [39 и 231] даны экспериментальные результаты для нескольких парамагнитных газов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
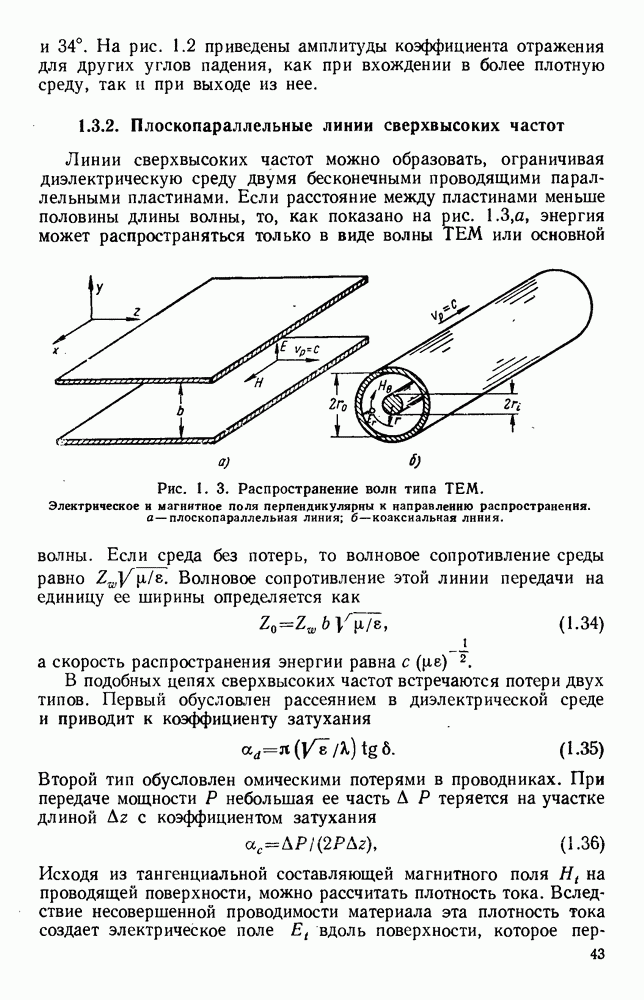
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
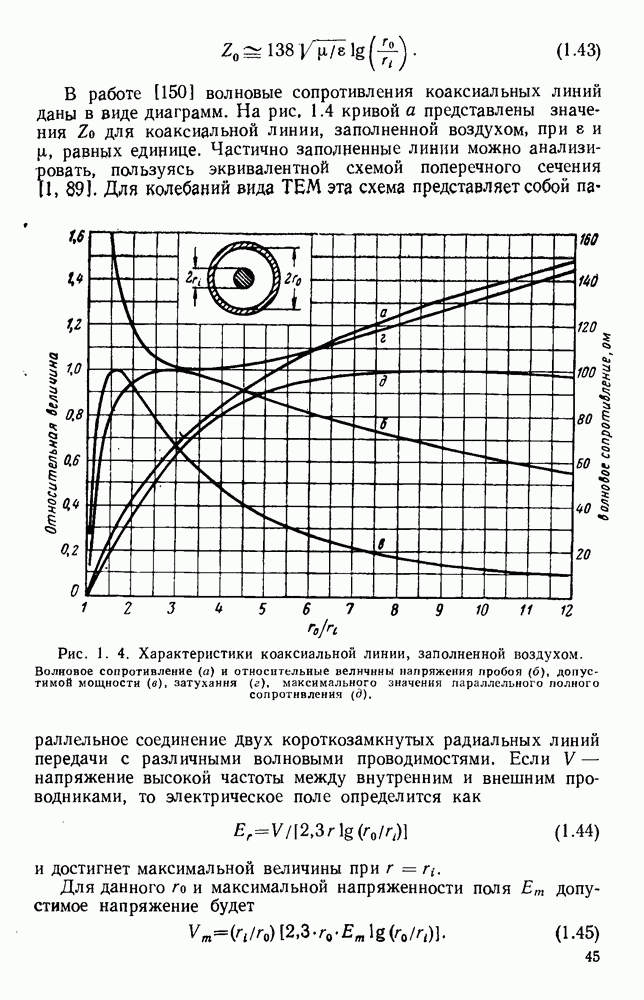
- 1.3.3. Коаксиальные линии
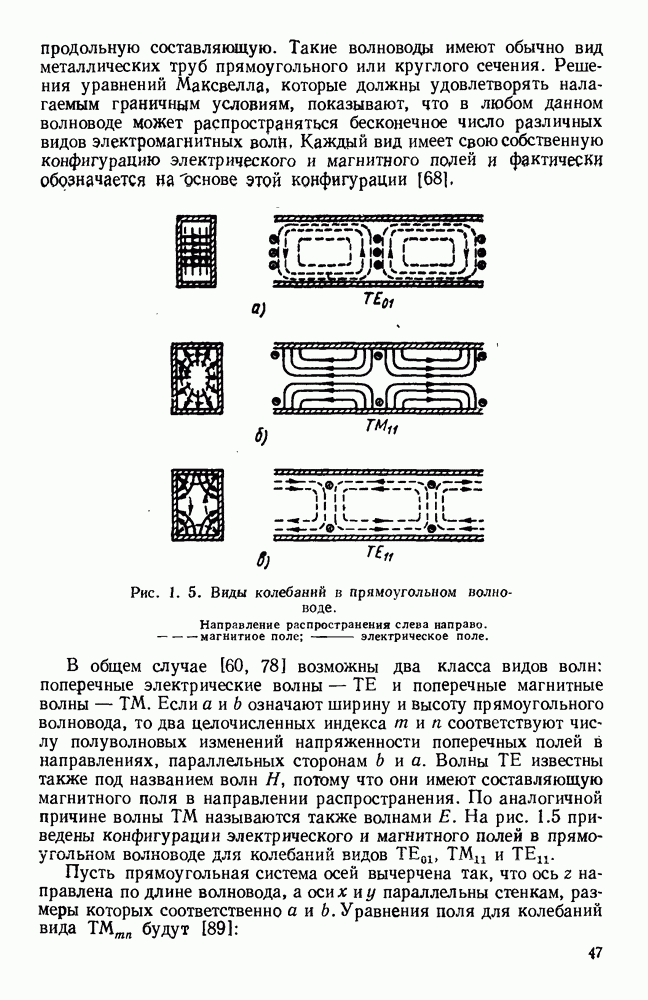
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
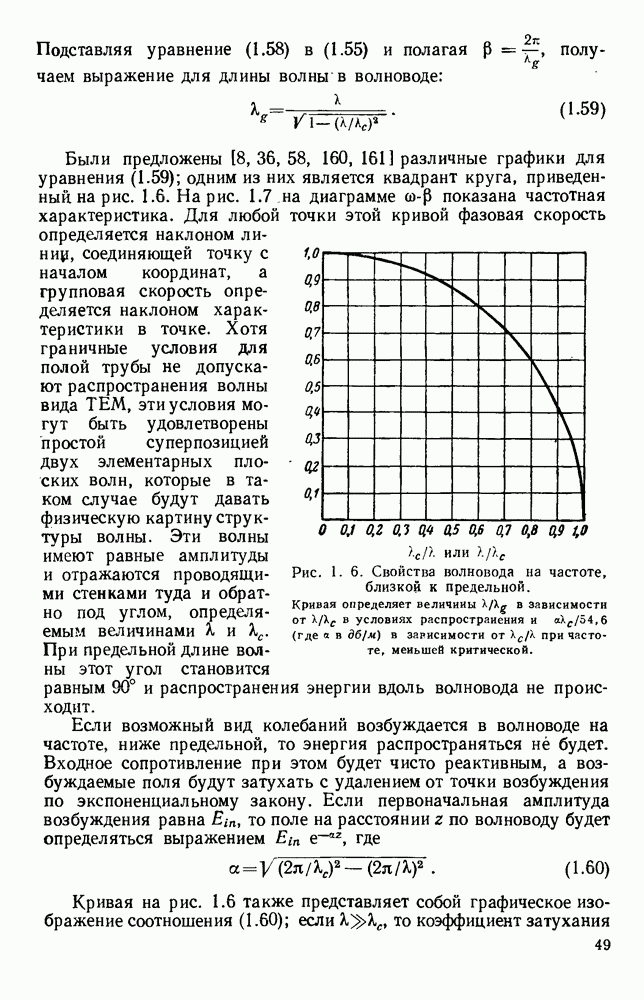
- 1.4.2. Круглые волноводы
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
- 1.5.2. Гребневые волноводы
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
- 2.1.2. Круговая диаграмма
- 2.1.3. Широкополосное согласование
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
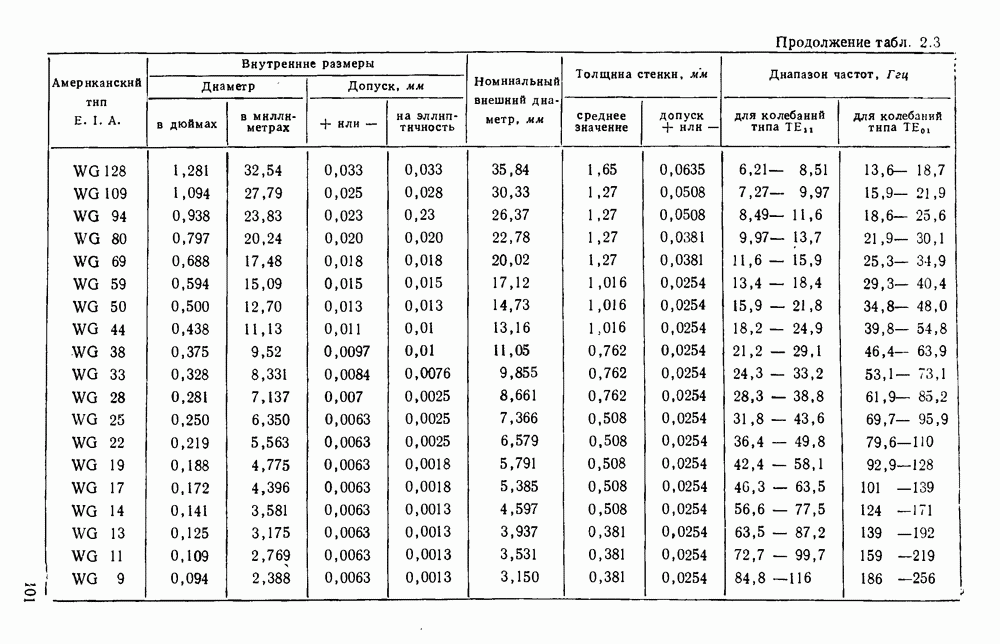
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
- 2.3.1. Прямоугольные волноводы
- 2.3.2. Круглые волноводы
- 2.3.3. Широкополосные и компактные волноводы
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
- 2.4.2. Контактные прокладки и дроссели
- 2.4.3. Крепежные и зажимные устройства
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
- 2.6.1. Изгибы, уголки и скрутки
- 2.6.2. Переходы и преобразователи
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
- 3.2.3. Переход от линейной поляризации к круговой
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
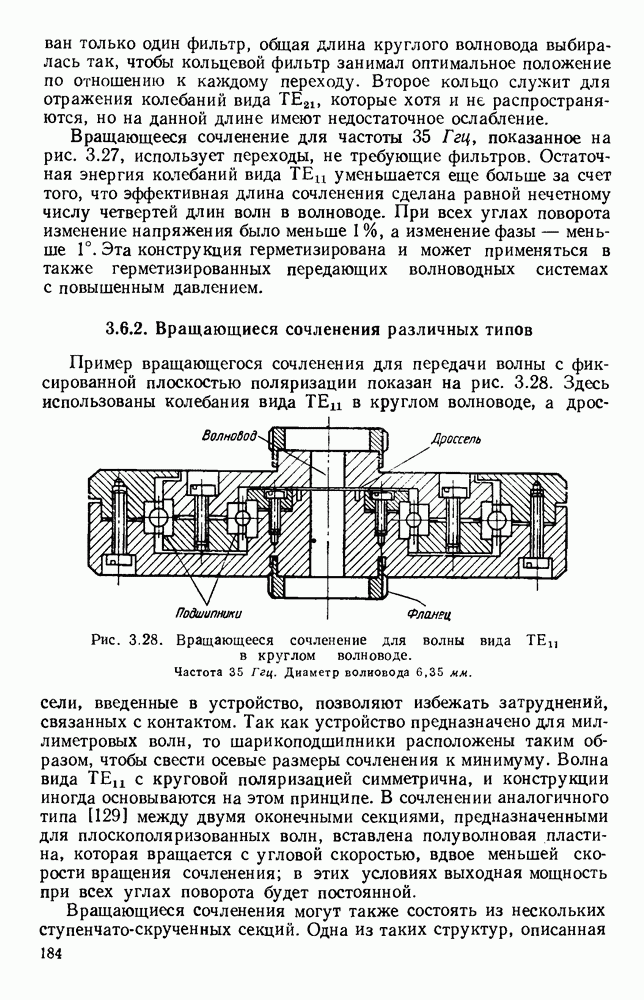
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
- 3.6.2. Вращающиеся сочленения различных типов
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
- 3.7.1. Механические переключатели с ручным управлением
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
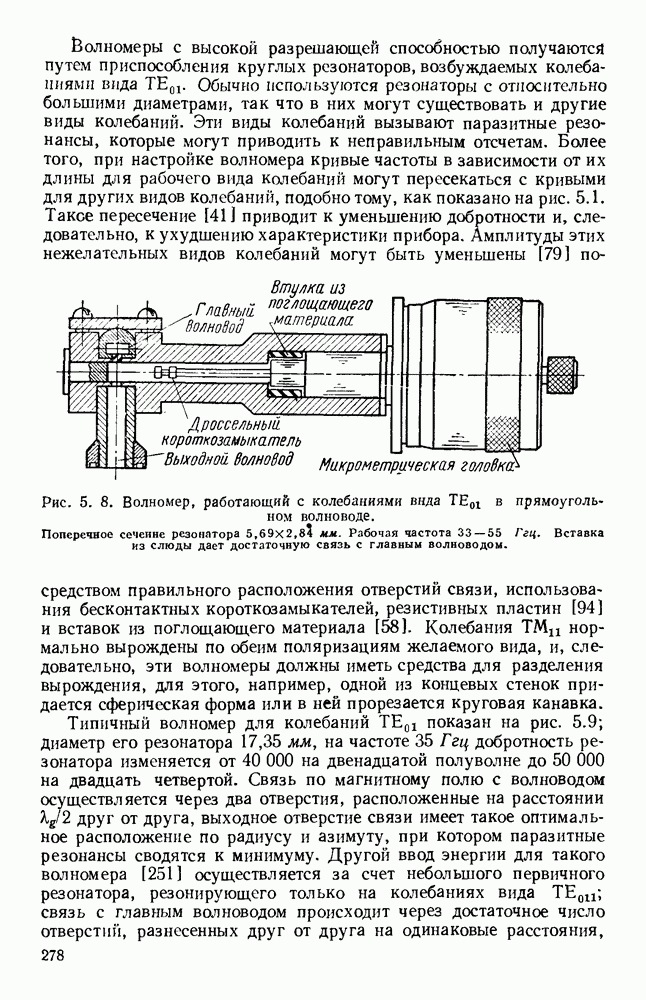
- 5.2.1. Волномеры с объемными резонаторами
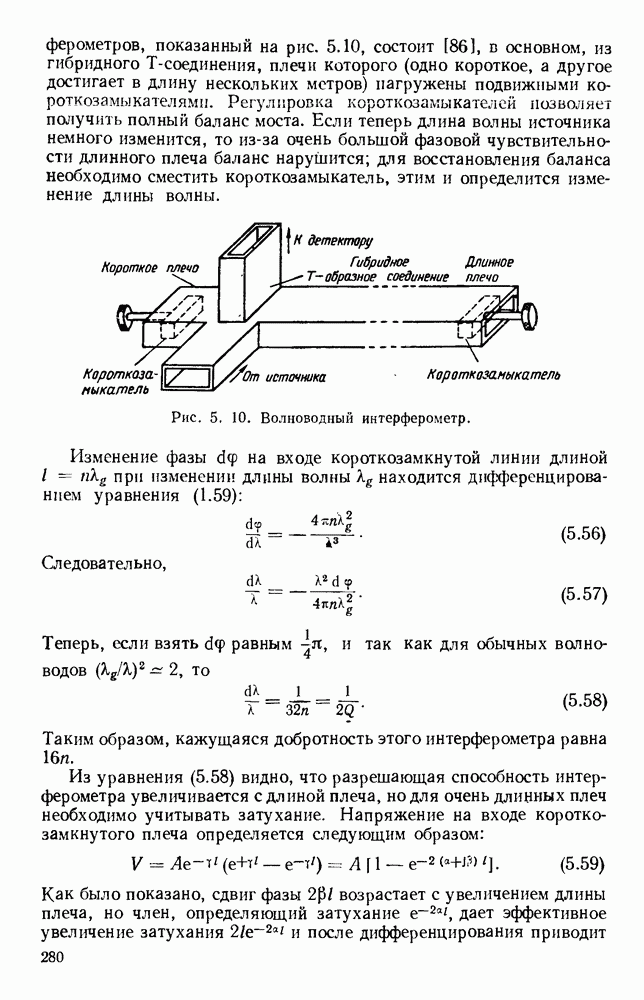
- 5.2.2. Волноводные интерферометры
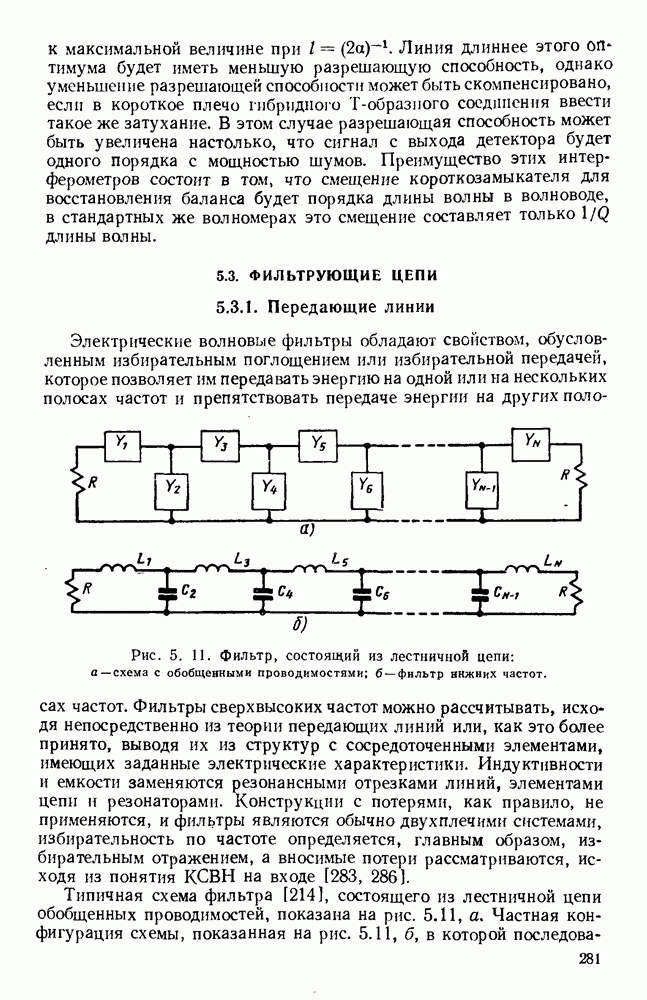
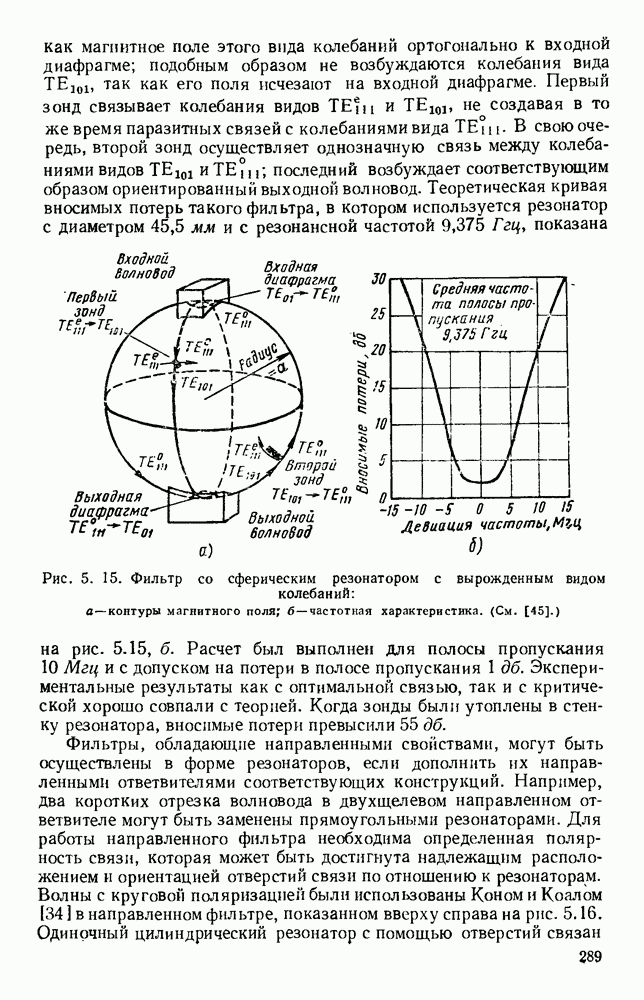
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
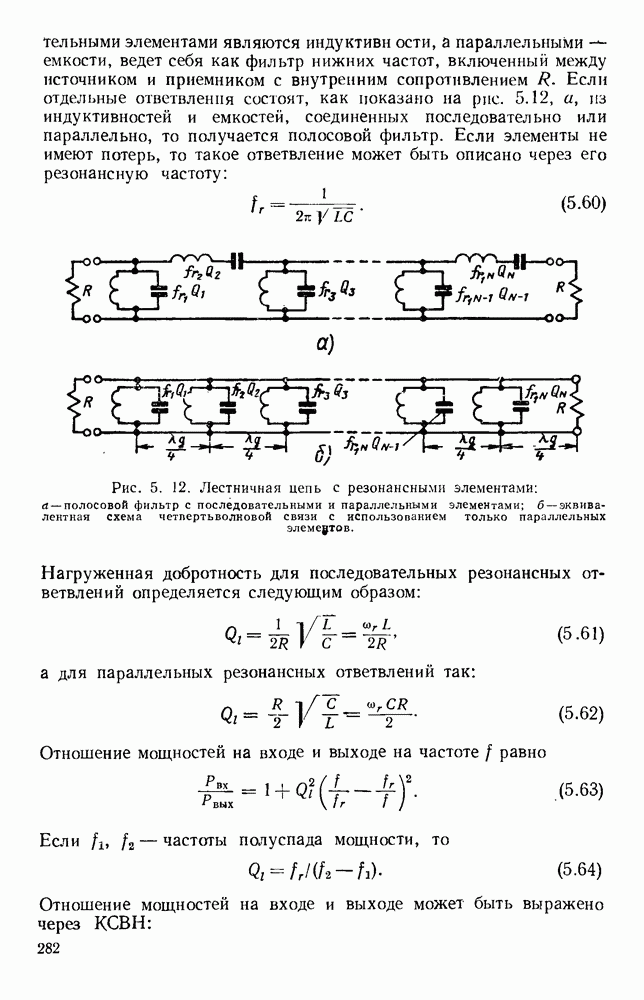
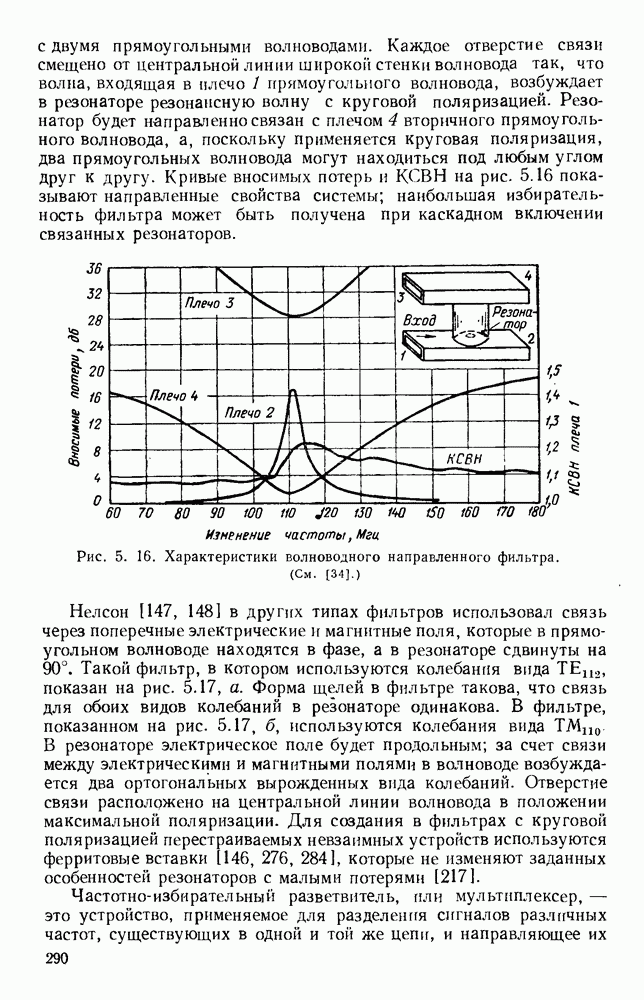
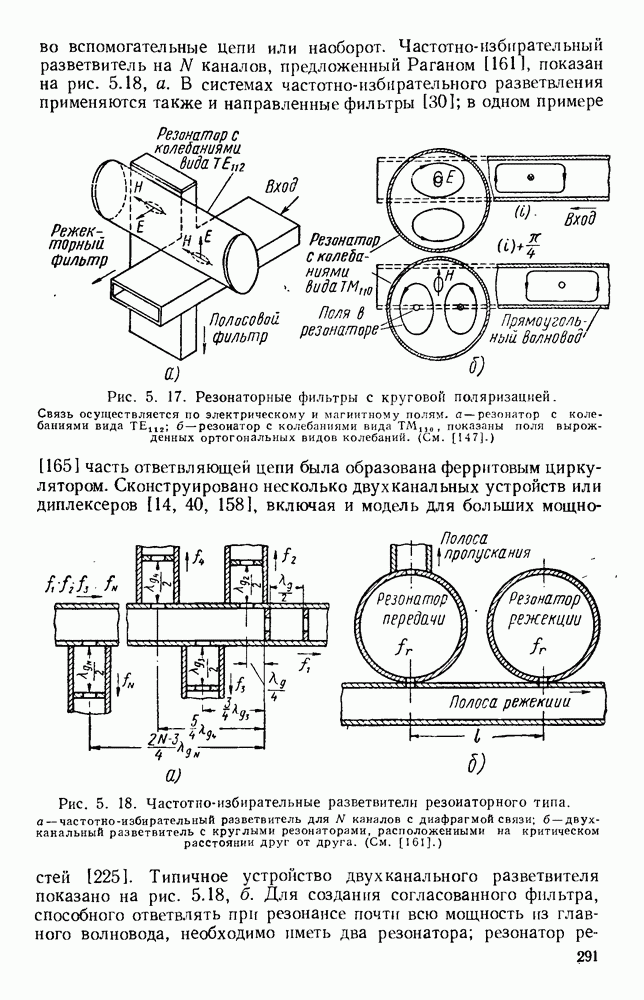
- 5.3.2. Связанные резонаторы
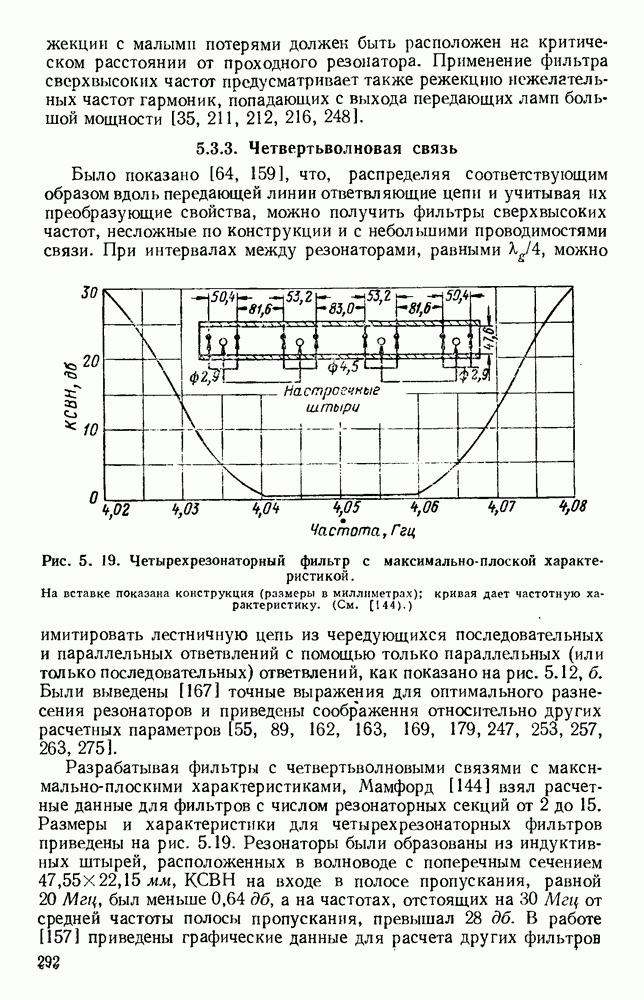
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
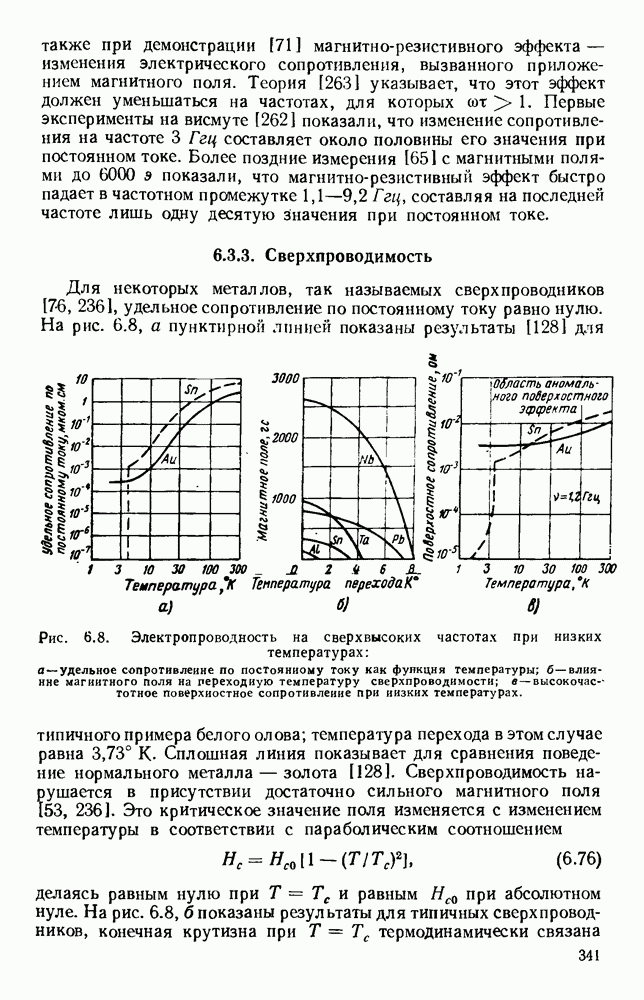
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
- 7.1.2. Форма линии и интенсивность
- 7.1.3. Сверхтонкая структура
- 7.1.4. Явления Штарка и Зеемана
- 7.2. СПЕКТРОМЕТРЫ
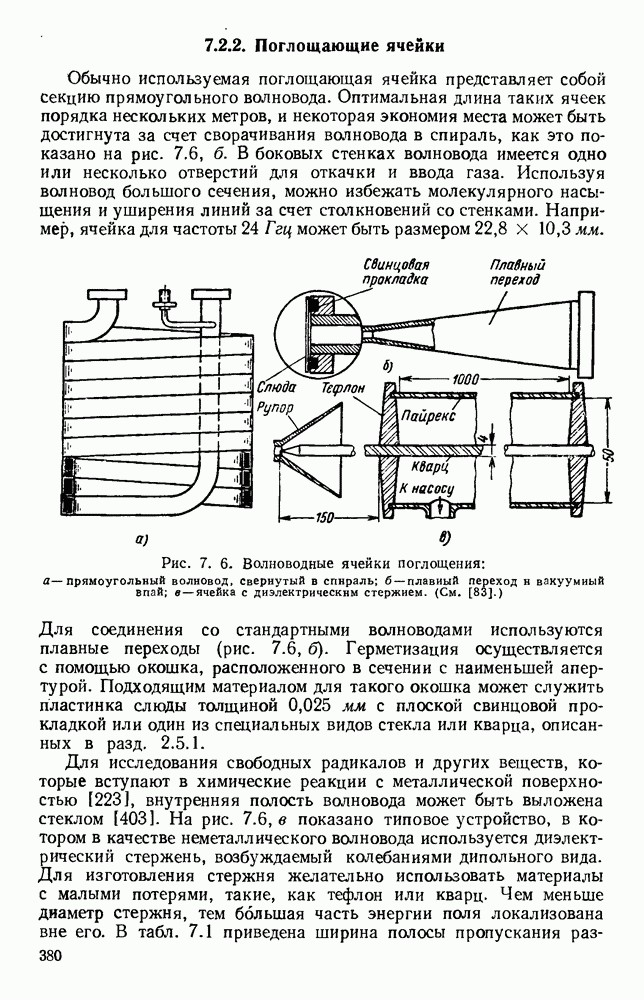
- 7.2.2. Поглощающие ячейки
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
- 7.3.4. Времена релаксации
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
- 8.3.3. Ферритовые устройства в качестве элементов схем
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
- 8.6.2. Устройства с поперечным полем
- 8.6.3. Прочие узлы
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.2.1. Линии типа «диэлектрических сэндвичей»
- 9.2.2. Симметричные линии с воздушным диэлектриком
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
- 9.4.2. Переходные устройства
- 9.4.3. Узлы полосковых систем
- 9.5. ЦЕПИ И СИСТЕМЫ
- 9.5.3. Частотные фильтры
- 9.5.4. Цепи питания антенн
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
- 10.1.2. Пространственные гармоники
- 10.1.3. Многократно-периодические структуры
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
- 10.2.3. Продольные цилиндрические волны
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
- 12.2. МАГНЕТРОНЫ
- 12.2.2. Резонаторные системы
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
- 12.2.4. Рабочие характеристики
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
- 13.1.2. Типы дифракции
- 13.1.3. Рассеяние
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
- 13.2.2. Структуры волноводного типа
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
- 13.4. ПРИБОРЫ И СИСТЕМЫ
- 13.4.1. Спектрометры
- 13.4.2. Интерферометры
- 13.4.3. Устройство с делением пучка