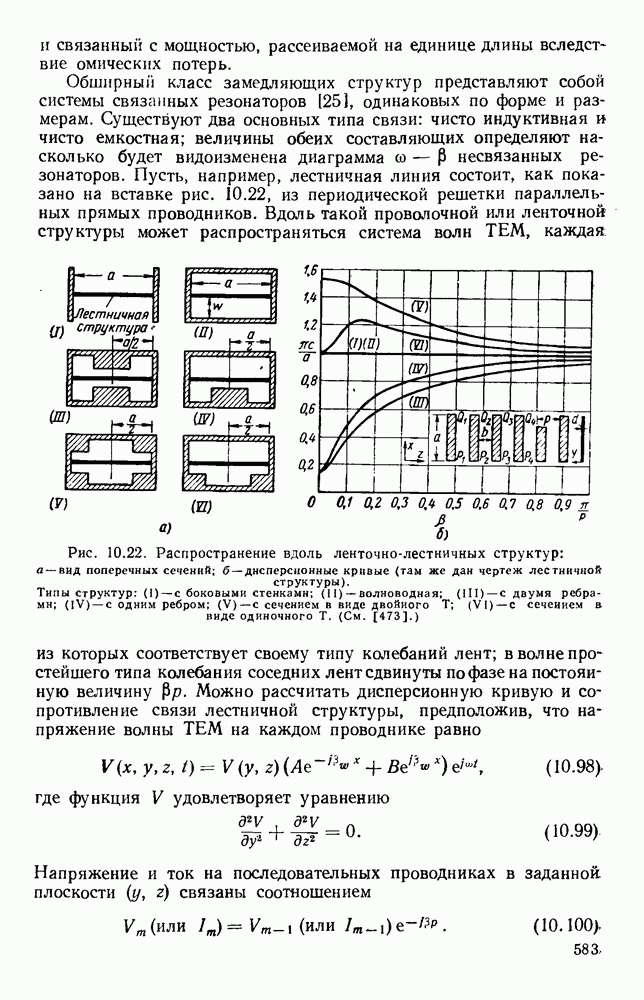
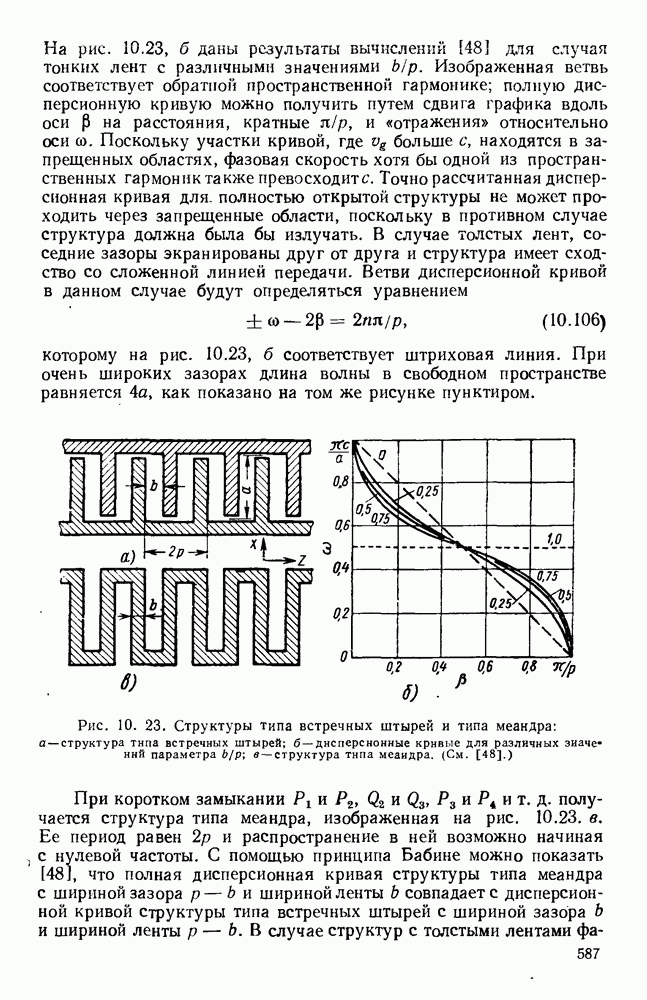
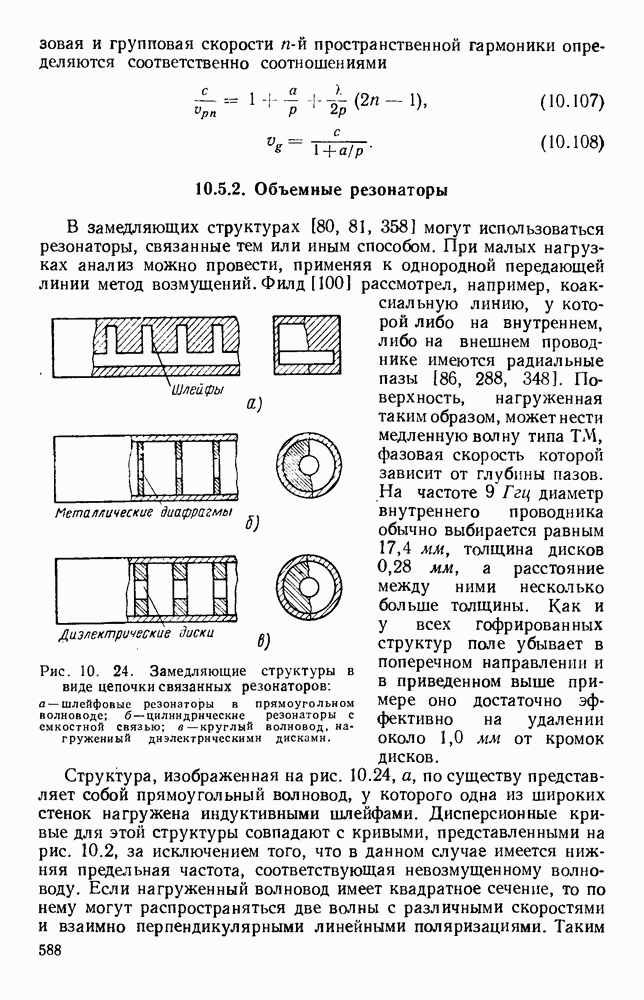
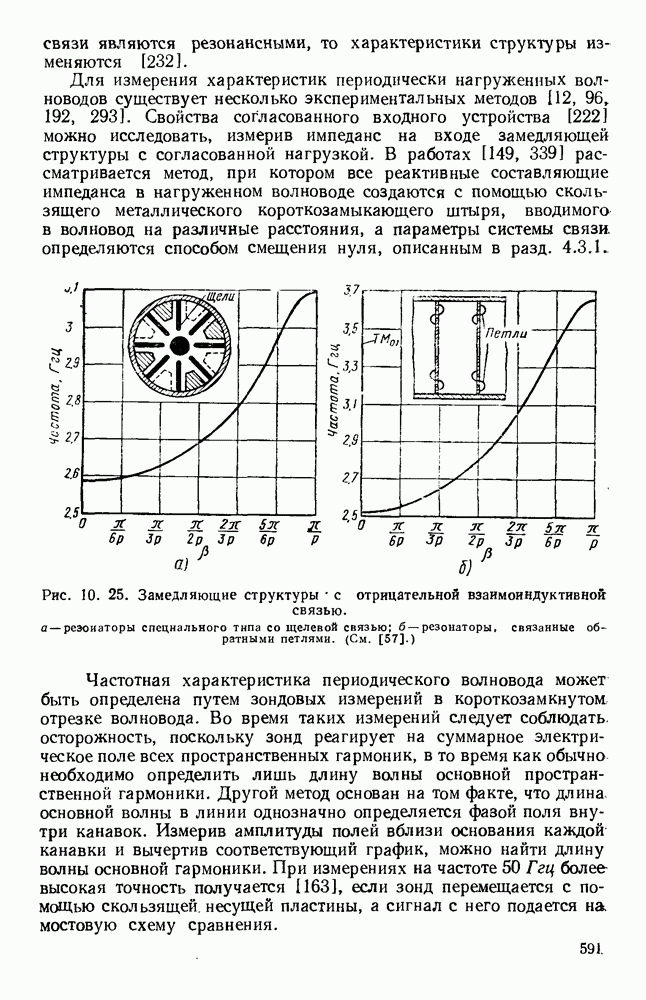
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
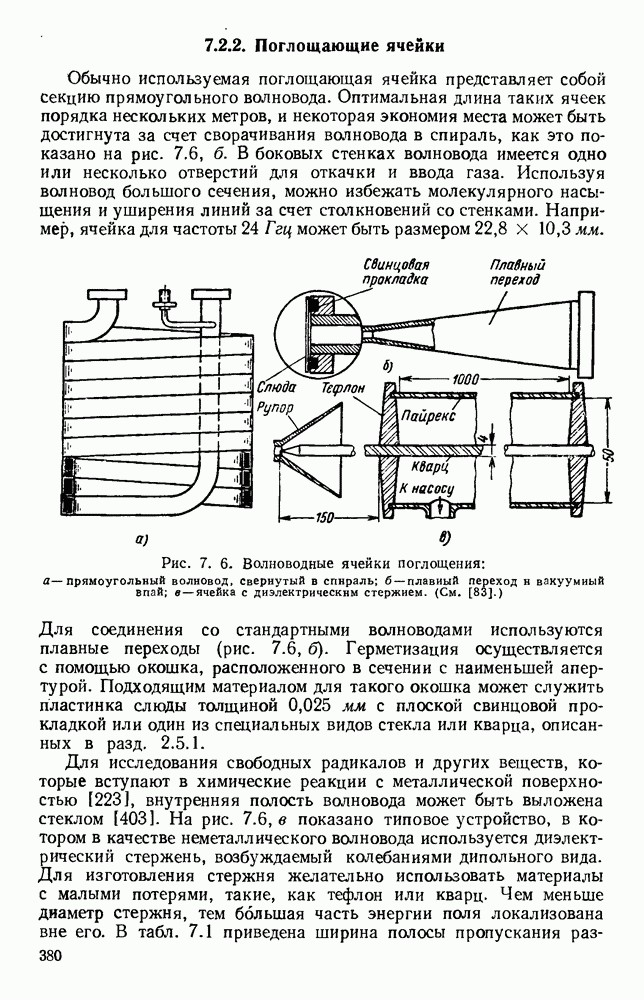
10.4.2. Цилиндрические стержни
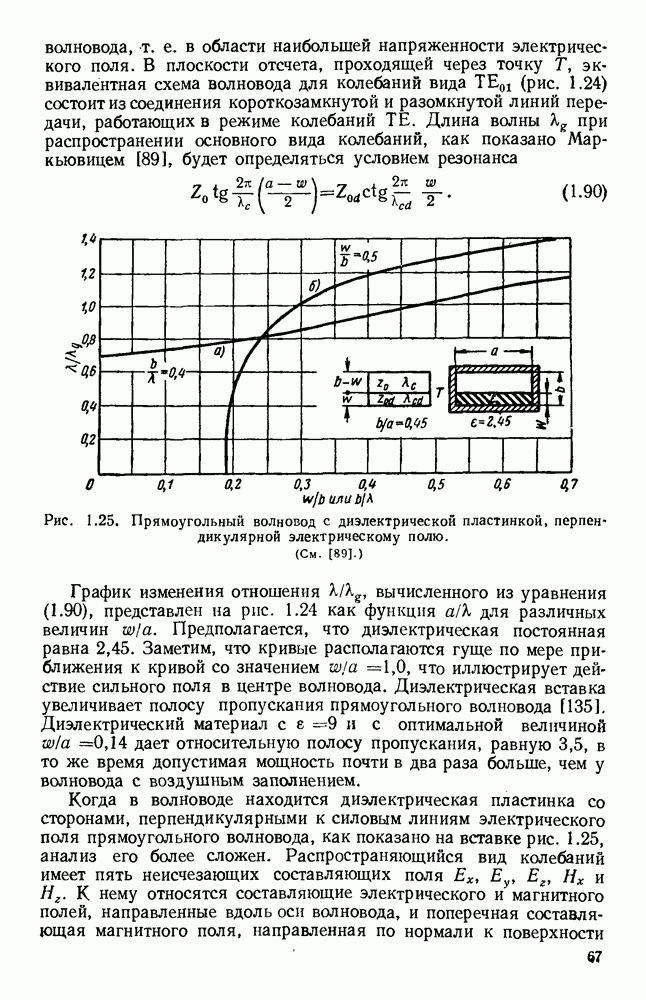
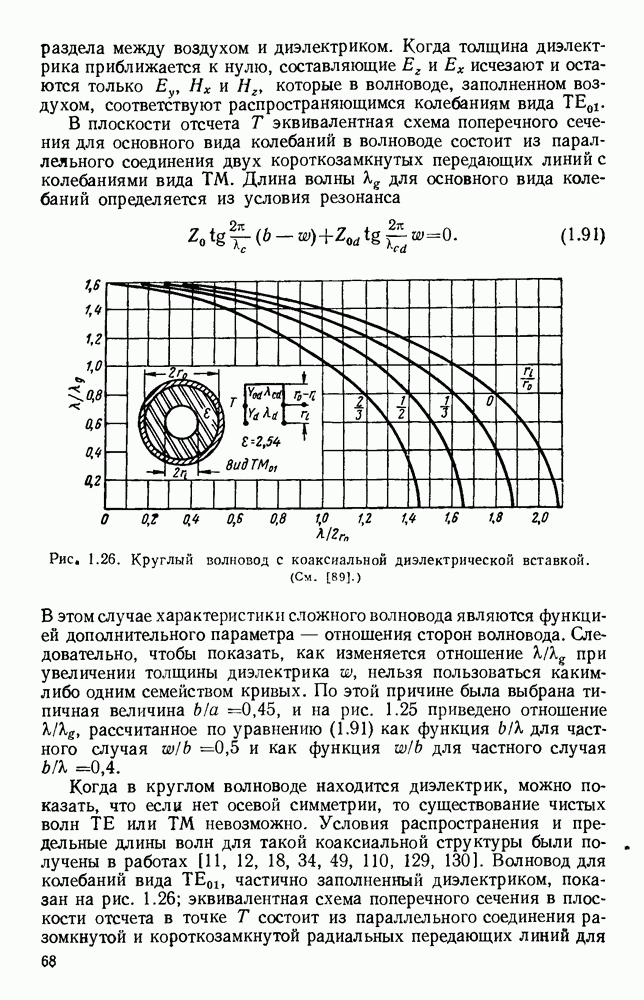
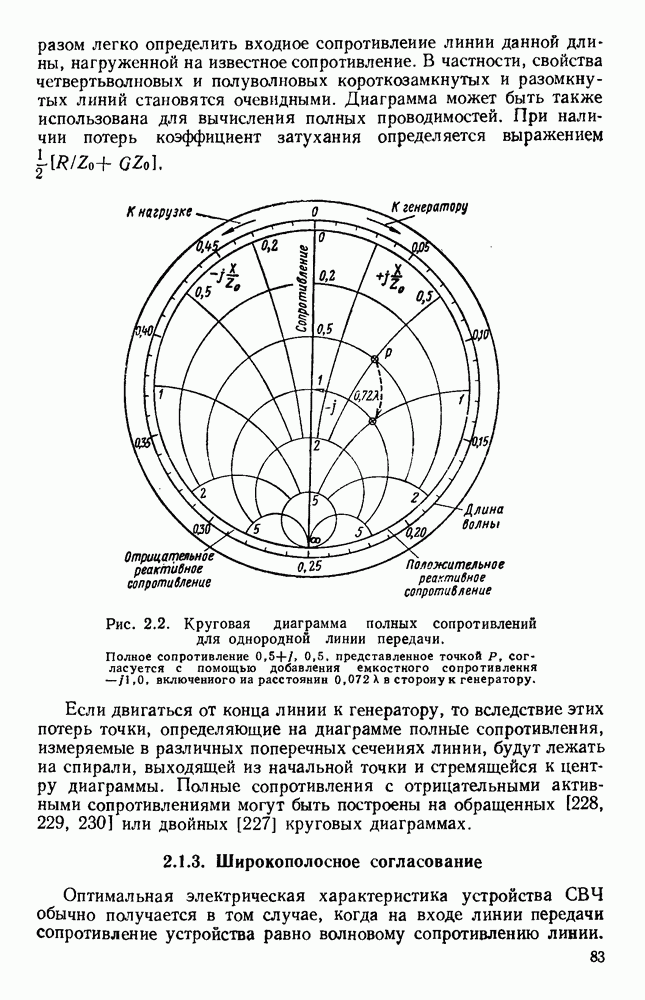
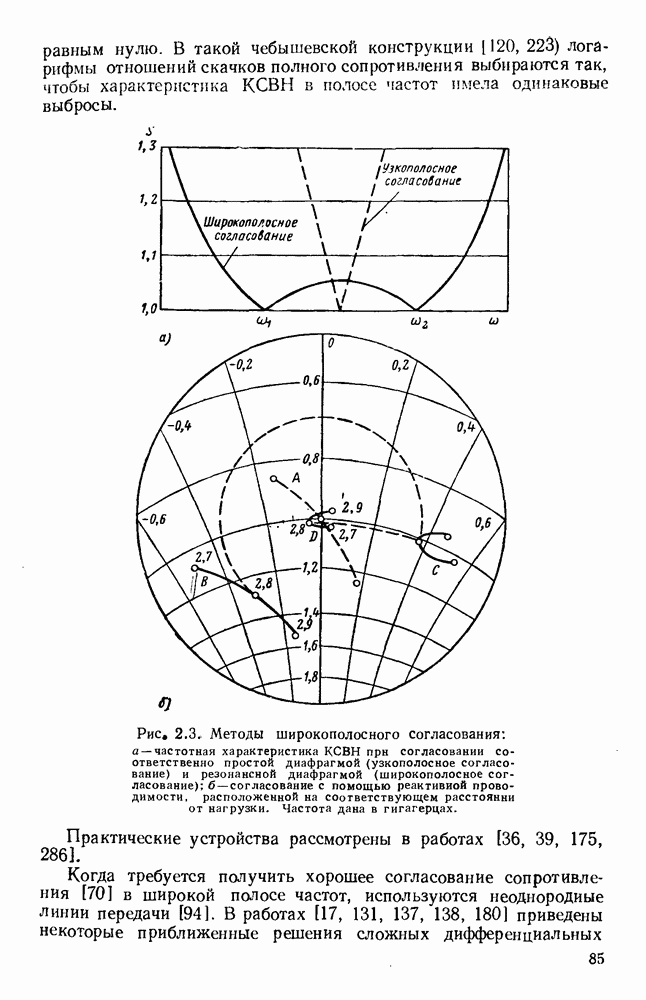
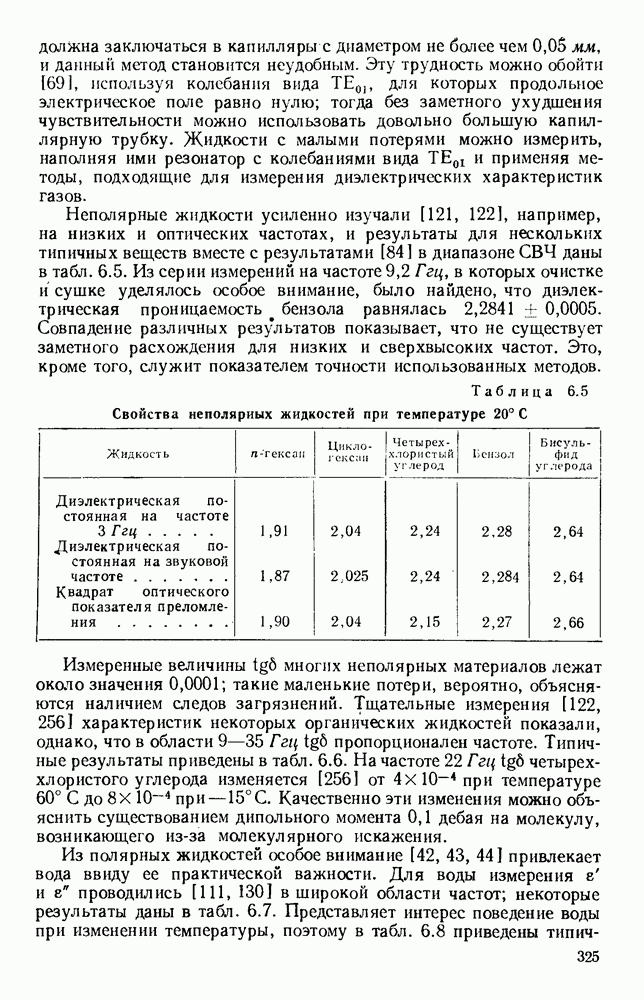
Теория волн, распространяющихся без излучения вдоль диэлектрического стержня, дана Хондросом и Дебаем [138] и проверена экспериментально Цаном [344] и Шривером [266]. Эти волны изучались в прошлом [64, 185, 250, 258, 259, 282), в настоящее время они также являются предметом широкого исследования [1, 148, 154, 295, 338, 373].
Обычно при анализе [50, 95] используется цилиндрическая система координат  , у которой ось
, у которой ось  направлена вдоль оси стержня радиуса
направлена вдоль оси стержня радиуса  Если опустить множитель
Если опустить множитель  то продольные компоненты векторов поля внутри стержня запишутся в виде
то продольные компоненты векторов поля внутри стержня запишутся в виде

Для области вне стержня  будем иметь следующие выражения:
будем иметь следующие выражения: 

к которым, как и раньше, надо присоединить уравнение (10.30). Аналогичные выражения имеют место и для остальных компонент поля. Из уравнения (10.30) и (10.82) получим

Из граничных условий получается другое соотношение между на и на и таким образом при заданных значениях  эти величины могут быть определены.
эти величины могут быть определены.
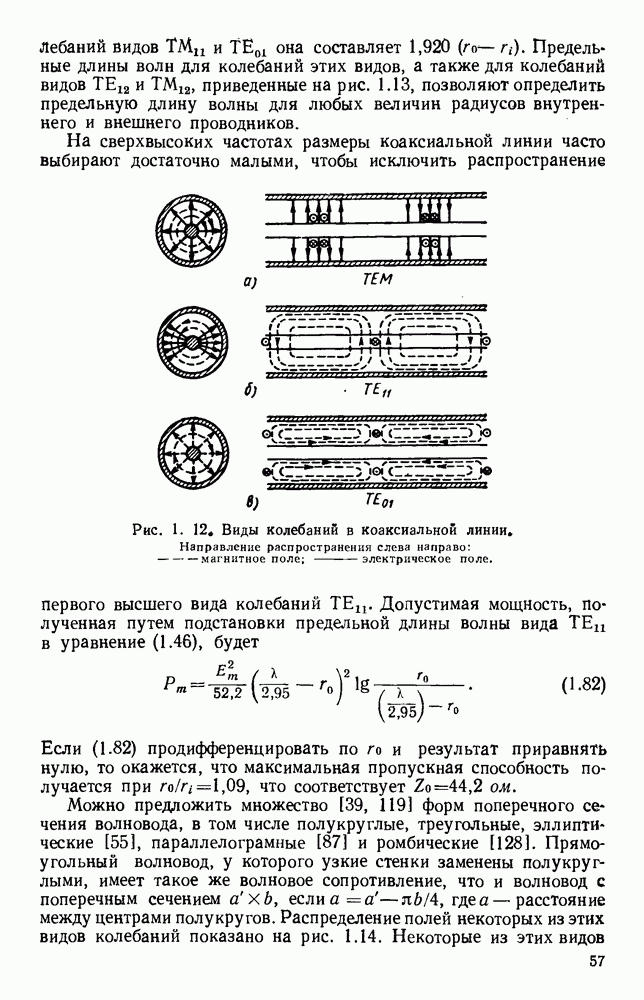
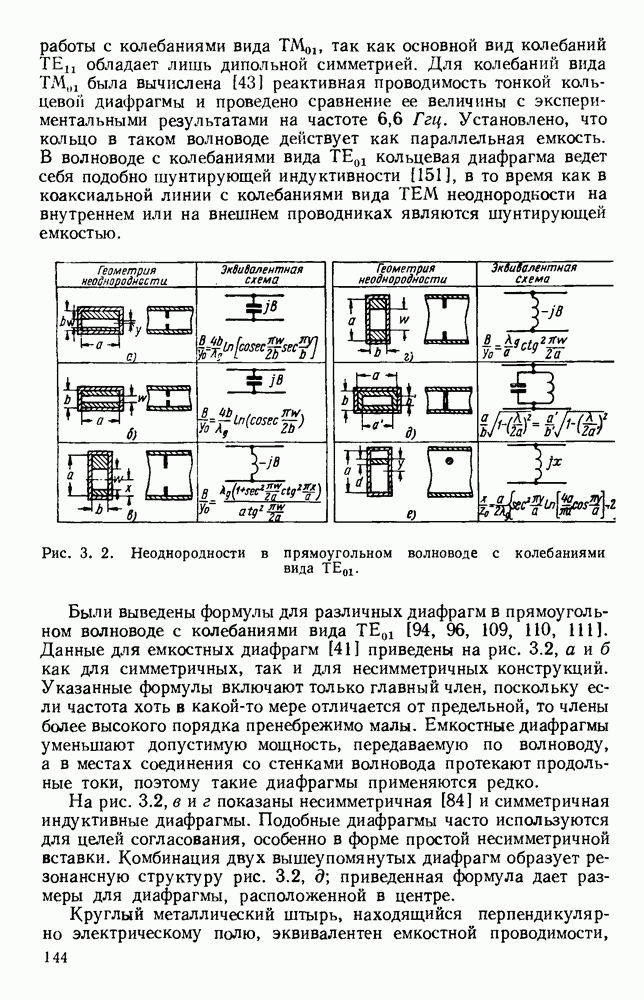
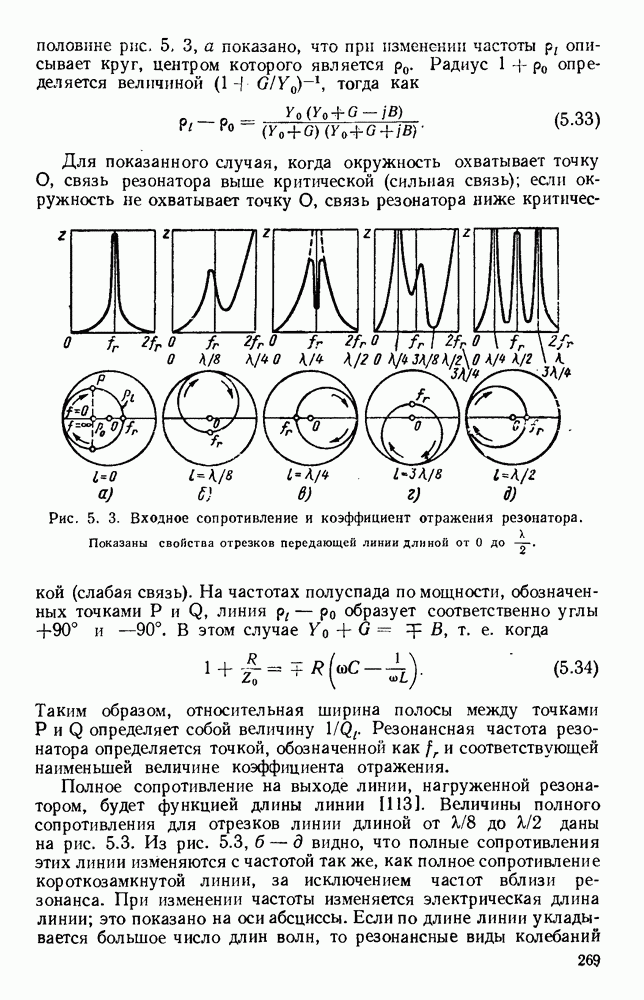
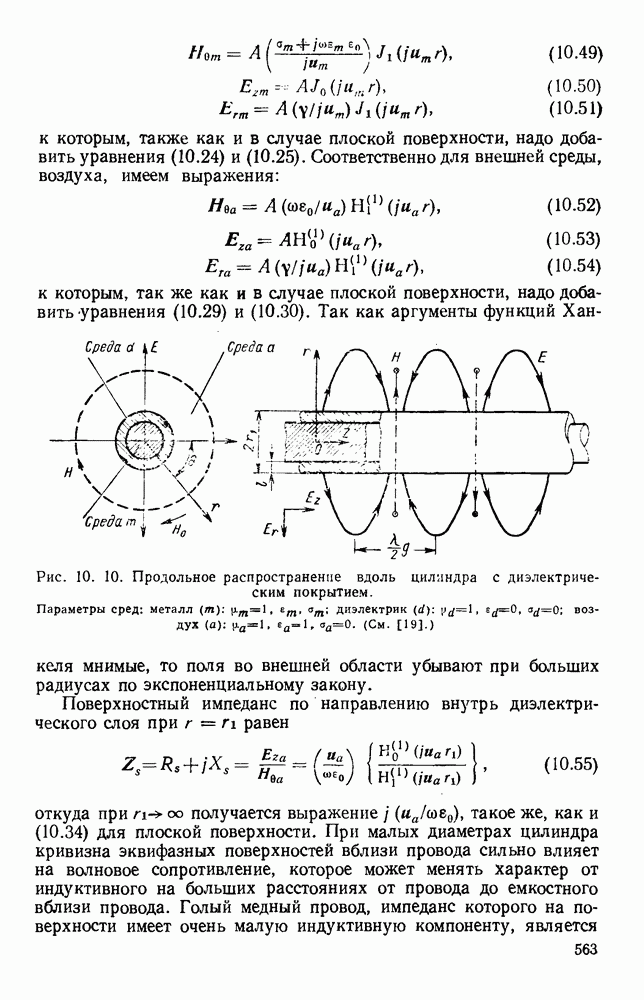
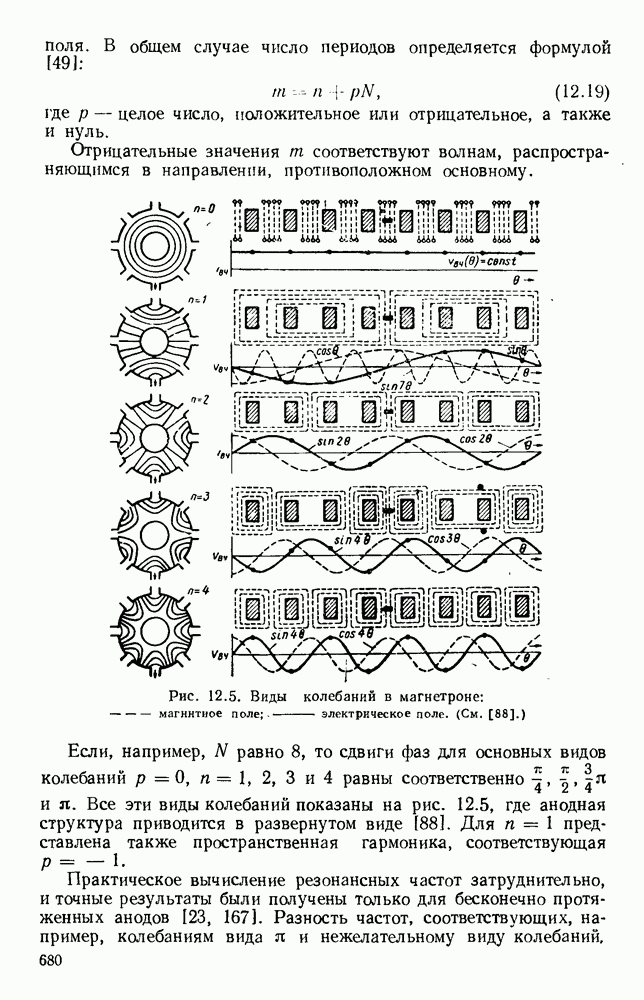
Как показано на рис. 10.19, а, при  поля обладают симметрией вращения и в этом случае возможны два решения. Одно соответствует волне типа ТМ, у которой магнитные силовые линии являются окружностями с центрами на оси стержня. Электрические
поля обладают симметрией вращения и в этом случае возможны два решения. Одно соответствует волне типа ТМ, у которой магнитные силовые линии являются окружностями с центрами на оси стержня. Электрические
силовые линии расположены в меридиональных плоскостях, проходящих через ось стержня; они уходят в бесконечность, асимптотически приближаясь к плоскостям, перпендикулярным стержню и отстоящим друг от друга на Я 
Другое решение соответствует волне типа ТЕ, у которой векторы электрического и магнитного полей меняются местами. При  появляется несимметричная, или «дипольная», волна, которую, грубо говоря, можно представить как поле от синусоидально распределенной и перпендикулярной оси стержня поляризации диэлектрика и которая распространяется вдоль диэлектрика. У этой волны нет критической частоты и она, таким образом, может существовать в случае тонких стержней или низких частот. Дипольную волну можно рассматривать как волну смешанного типа
появляется несимметричная, или «дипольная», волна, которую, грубо говоря, можно представить как поле от синусоидально распределенной и перпендикулярной оси стержня поляризации диэлектрика и которая распространяется вдоль диэлектрика. У этой волны нет критической частоты и она, таким образом, может существовать в случае тонких стержней или низких частот. Дипольную волну можно рассматривать как волну смешанного типа  представляющую собой суперпозицию волн ТМ и ТЕ, у которых фазы и амплитуды подобраны так, чтобы удовлетворялись граничные условия.
представляющую собой суперпозицию волн ТМ и ТЕ, у которых фазы и амплитуды подобраны так, чтобы удовлетворялись граничные условия.

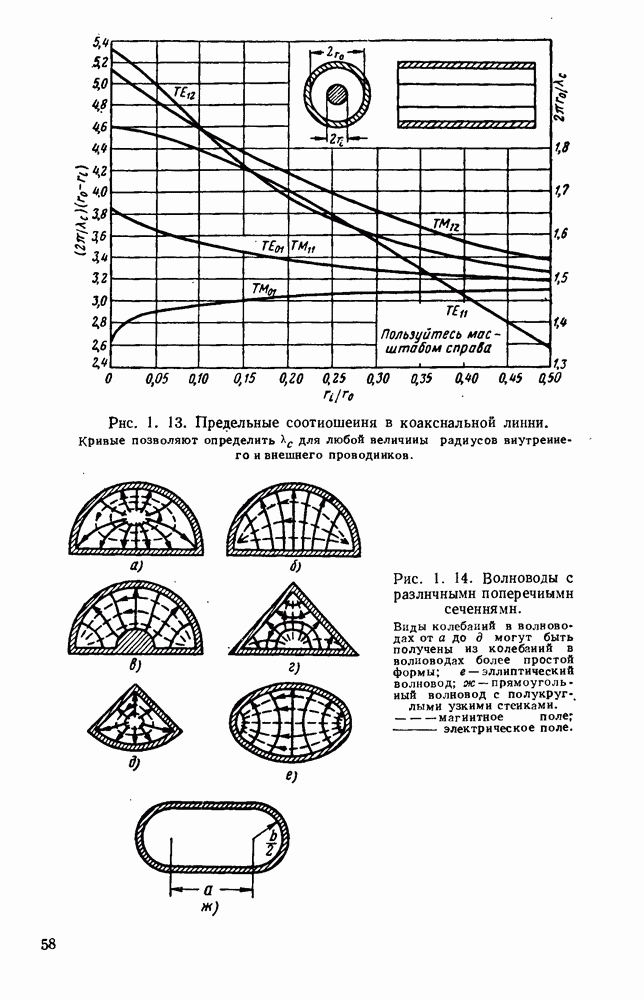
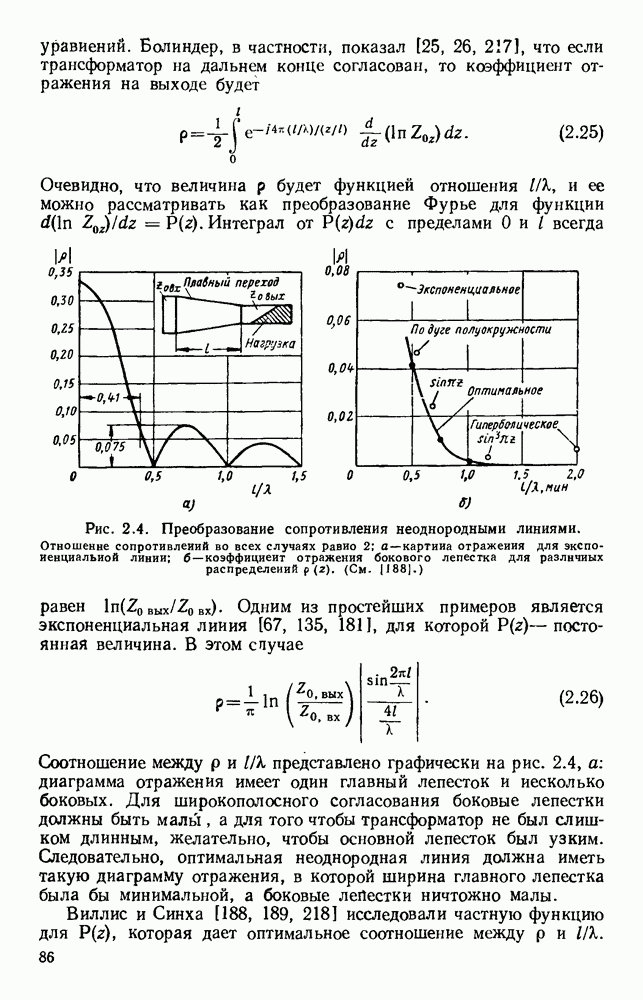
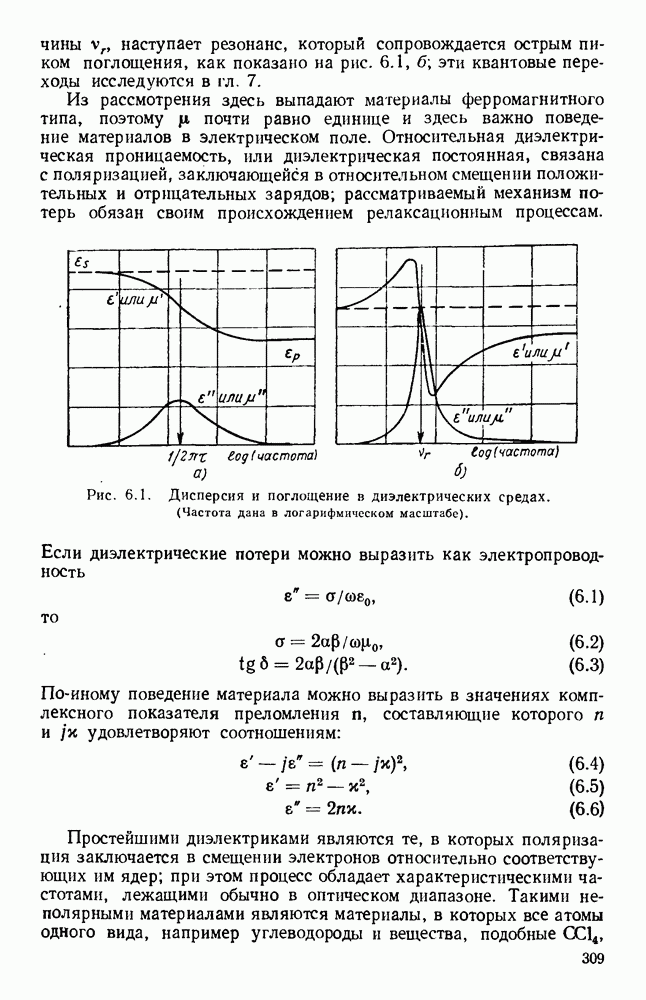
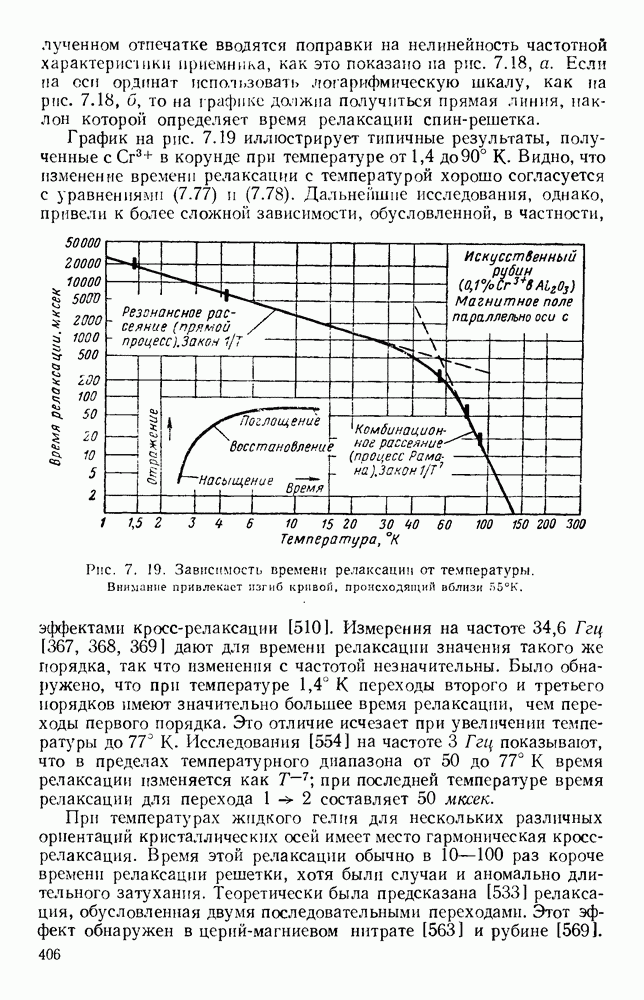
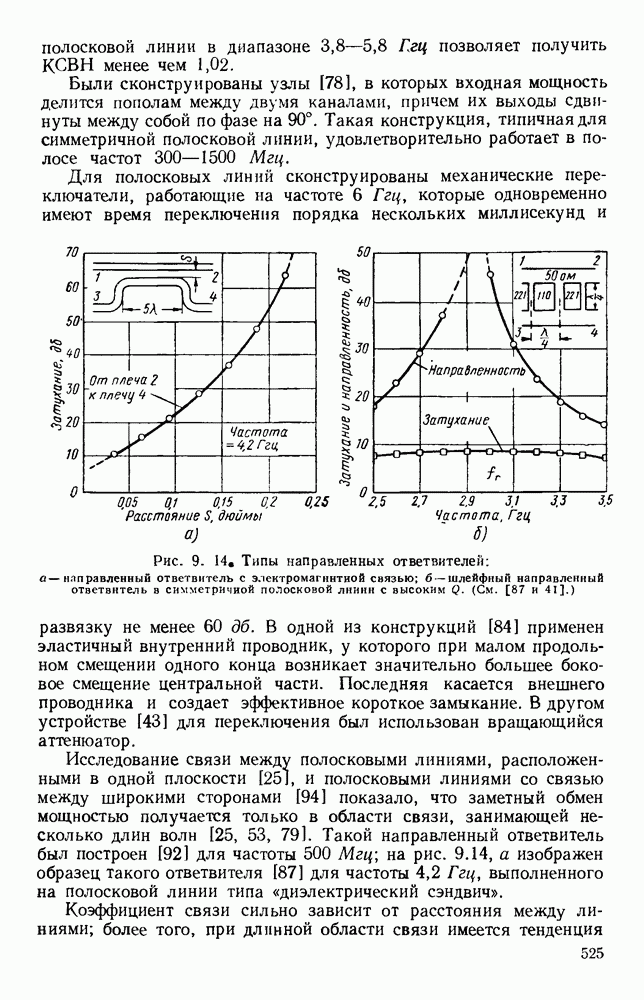
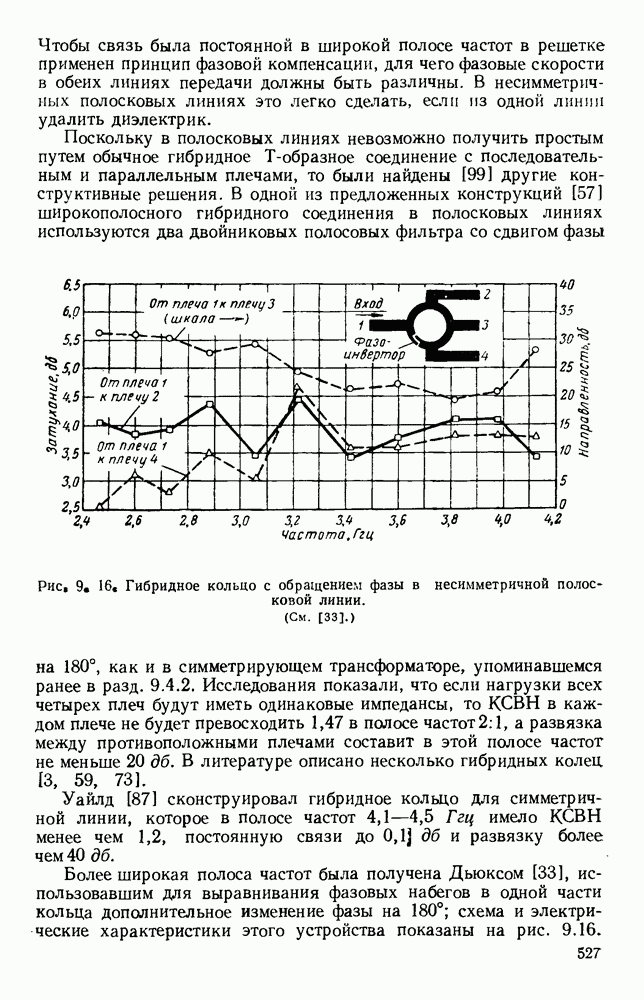
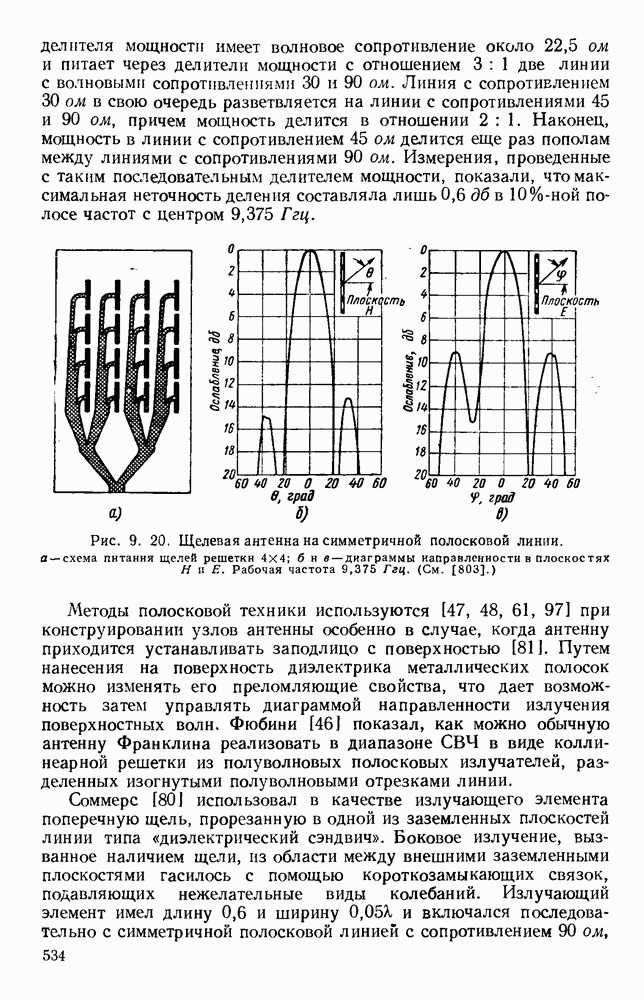
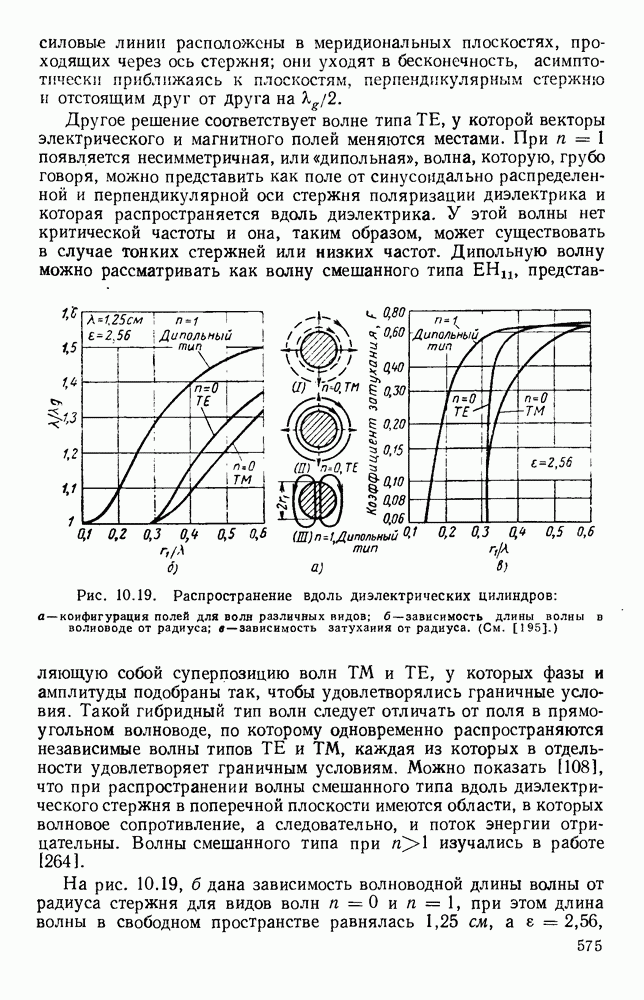
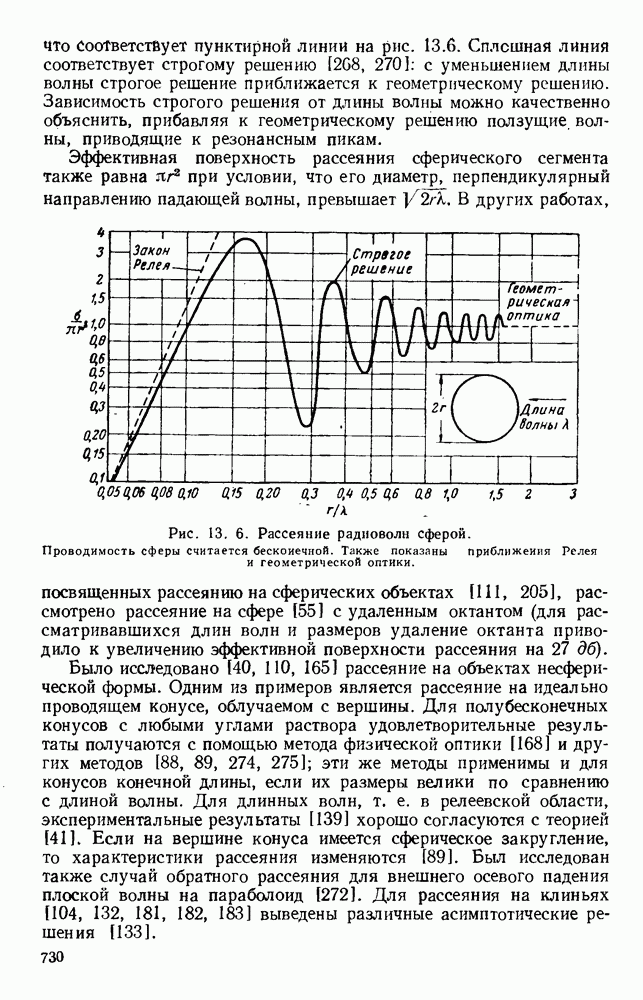
Рис. 10.19. Распространение вдоль диэлектрических цилиндров: а — конфигурация полей для волн различных видов; б - зависимость длины волны в волноводе от радиуса; в - зависимость затухания от радиуса. (См. [195].)
Такой гибридный тип волн следует отличать от поля в прямоугольном волноводе, по которому одновременно распространяются независимые волны типов ТЕ и ТМ, каждая из которых в отдельности удовлетворяет граничным условиям. Можно показать [108], что при распространении волны смешанного типа вдоль диэлектрического стержня в поперечной плоскости имеются области, в которых волновое сопротивление, а следовательно, и поток энергии отрицательны. Волны смешанного типа при  изучались в работе [264].
изучались в работе [264].
На рис. 10.19, б дана зависимость волноводной длины волны от радиуса стержня для видов волн  при этом длина волны в свободном пространстве равнялась 1,25 см, а
при этом длина волны в свободном пространстве равнялась 1,25 см, а 
что соответствует полистиролу. Коэффициент затухания в децибелах на метр определяется формулой

где  безразмерная величина, график которой дан на рис. 10.19, в.
безразмерная величина, график которой дан на рис. 10.19, в.
При больших радиусах стержня величина  приближается к значению
приближается к значению  соответствующему плоской волне, а при малых радиусах она уменьшается, так как возрастает доля энергии, распространяющаяся вне стержня. Аналогичные неизлучающие виды волн могут также существовать в диэлектрических трубах [315].
соответствующему плоской волне, а при малых радиусах она уменьшается, так как возрастает доля энергии, распространяющаяся вне стержня. Аналогичные неизлучающие виды волн могут также существовать в диэлектрических трубах [315].
В случае  волну типа ТМ в диэлектрическом стержне можно возбудить [89, 147] либо из открытого конца коаксиальной линии с волной типа ТЕМ, либо из открытого конца круглого волновода с волной
волну типа ТМ в диэлектрическом стержне можно возбудить [89, 147] либо из открытого конца коаксиальной линии с волной типа ТЕМ, либо из открытого конца круглого волновода с волной  [10]. В случае
[10]. В случае  волну типа ТЕ можно возбудить с помощью металлического экрана со щелями, которые имеют соответствующую ориентацию и возбуждаются необходимым образом. Распределение поля у волны, соответствующей
волну типа ТЕ можно возбудить с помощью металлического экрана со щелями, которые имеют соответствующую ориентацию и возбуждаются необходимым образом. Распределение поля у волны, соответствующей  приблизительно совпадает с распределением поля у волны
приблизительно совпадает с распределением поля у волны  в круглом волноводе, поэтому подходящий переход получается, если в открытый конец волновода вставить диэлектрический стержень, диаметр которого постепенно уменьшается для минимизации отражений. У части стержня, находящейся вне волновода, диаметр может постепенно изменяться до желаемых размеров.
в круглом волноводе, поэтому подходящий переход получается, если в открытый конец волновода вставить диэлектрический стержень, диаметр которого постепенно уменьшается для минимизации отражений. У части стержня, находящейся вне волновода, диаметр может постепенно изменяться до желаемых размеров.
Проведенное на частоте 24 Ггц экспериментальное исследование такой волны [51] показало, что направляющий эффект сохранялся даже в том случае, когда диаметр стержня составлял долю длины волны. Для полистироловых стержней коэффициент затухания был порядка  что хорошо согласуется с уравнением (10.86). У резонатора, образованного отрезком диэлектрического стержня, находящимся между плоскими зеркалами с площадью
что хорошо согласуется с уравнением (10.86). У резонатора, образованного отрезком диэлектрического стержня, находящимся между плоскими зеркалами с площадью  максимальное значение
максимальное значение  достигало 53 000. Если диэлектрический стержень поместить внутрь металлической трубы [310], то характеристики распространения в диэлектрическом стержне, очевидно, изменятся. В случае волн типа ТМ, распространяющихся вдоль диэлектрического стержня с потерями, можно показать [22], что если радиус стержня превышает некоторое предельное значение, то поверхностный импеданс имеет индуктивный характер, и, наоборот, при меньших радиусах поверхностный импеданс имеет емкостный характер. Для стержня из перспекса
достигало 53 000. Если диэлектрический стержень поместить внутрь металлической трубы [310], то характеристики распространения в диэлектрическом стержне, очевидно, изменятся. В случае волн типа ТМ, распространяющихся вдоль диэлектрического стержня с потерями, можно показать [22], что если радиус стержня превышает некоторое предельное значение, то поверхностный импеданс имеет индуктивный характер, и, наоборот, при меньших радиусах поверхностный импеданс имеет емкостный характер. Для стержня из перспекса  и радиусом 0,987 см на частотах ниже
и радиусом 0,987 см на частотах ниже  фазовая скорость превосходит скорость света.
фазовая скорость превосходит скорость света.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
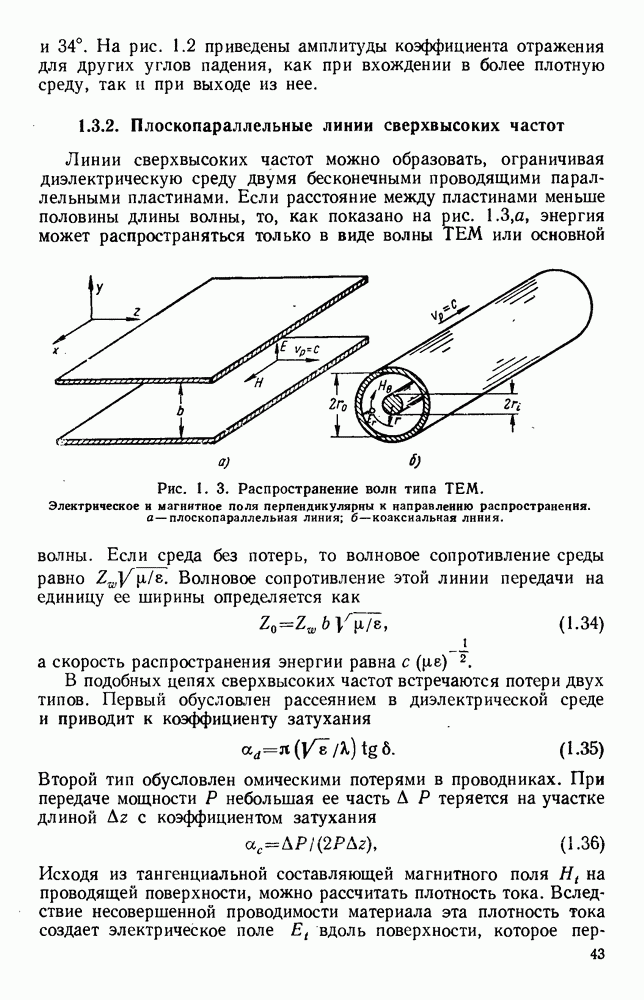
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
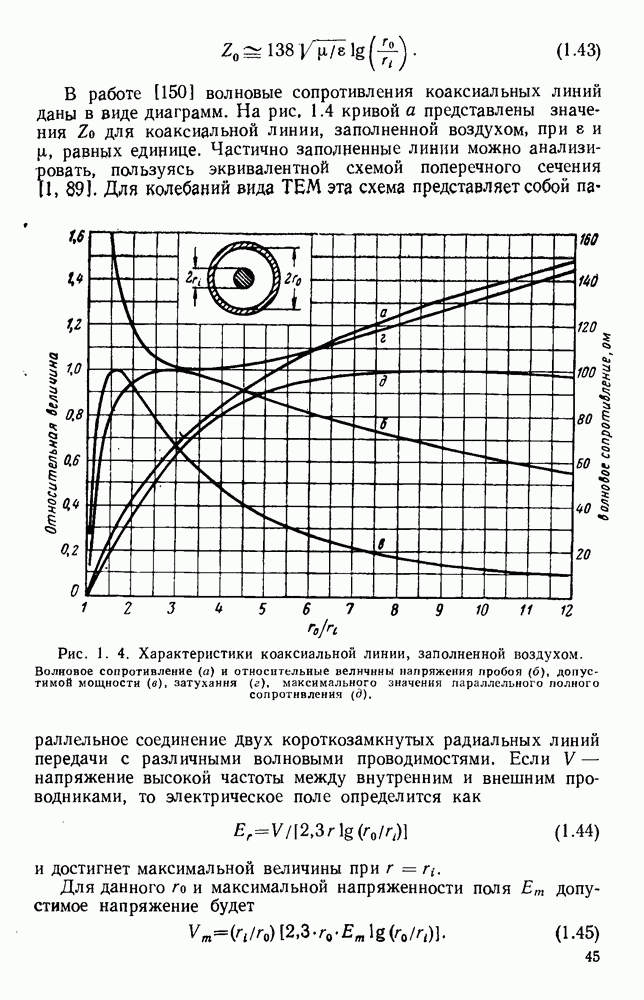
- 1.3.3. Коаксиальные линии
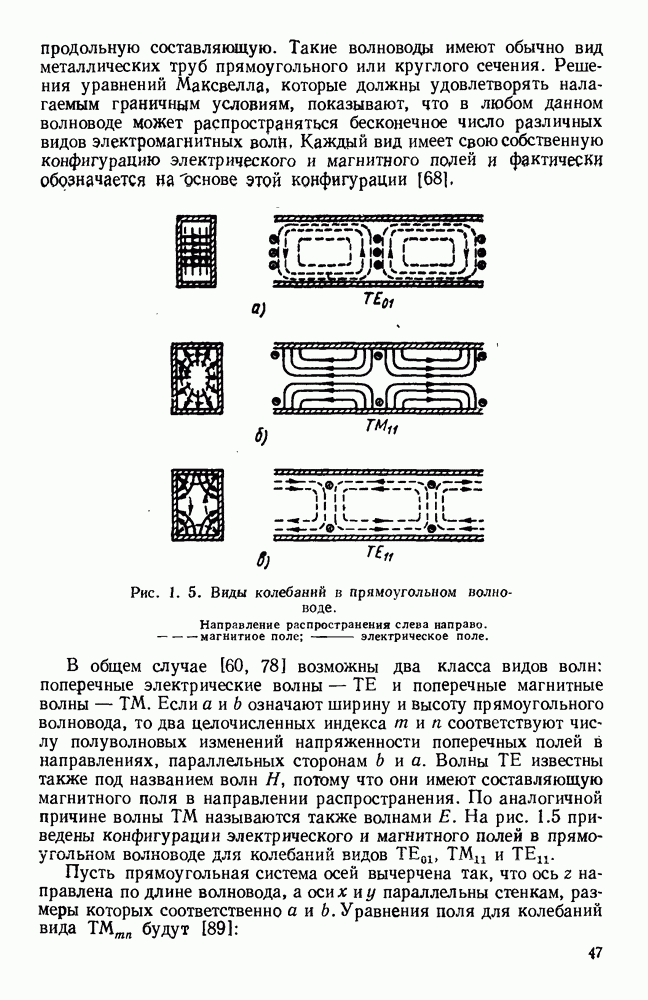
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
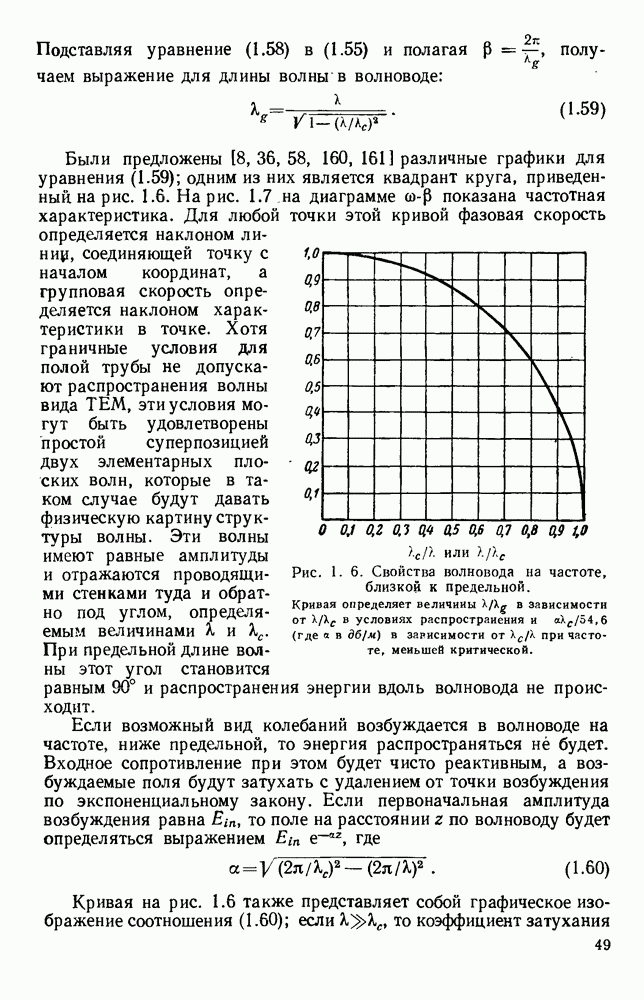
- 1.4.2. Круглые волноводы
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
- 1.5.2. Гребневые волноводы
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
- 2.1.2. Круговая диаграмма
- 2.1.3. Широкополосное согласование
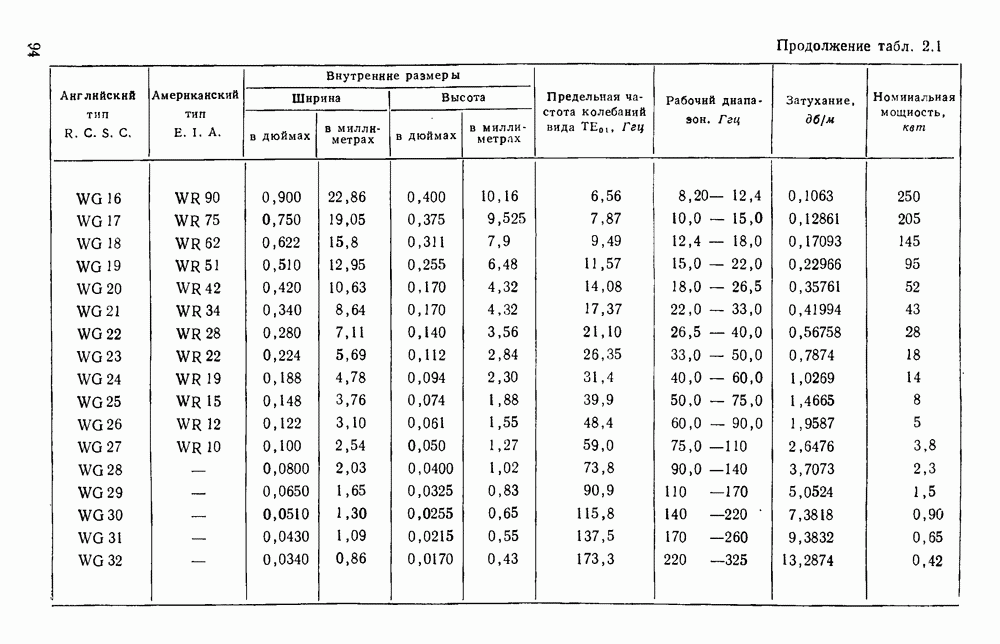
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
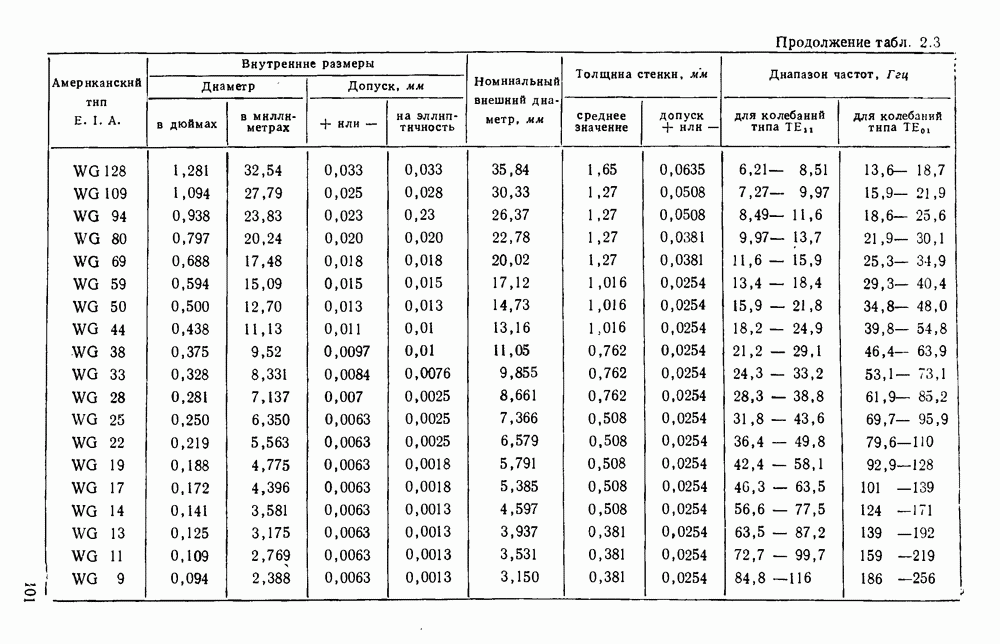
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
- 2.3.1. Прямоугольные волноводы
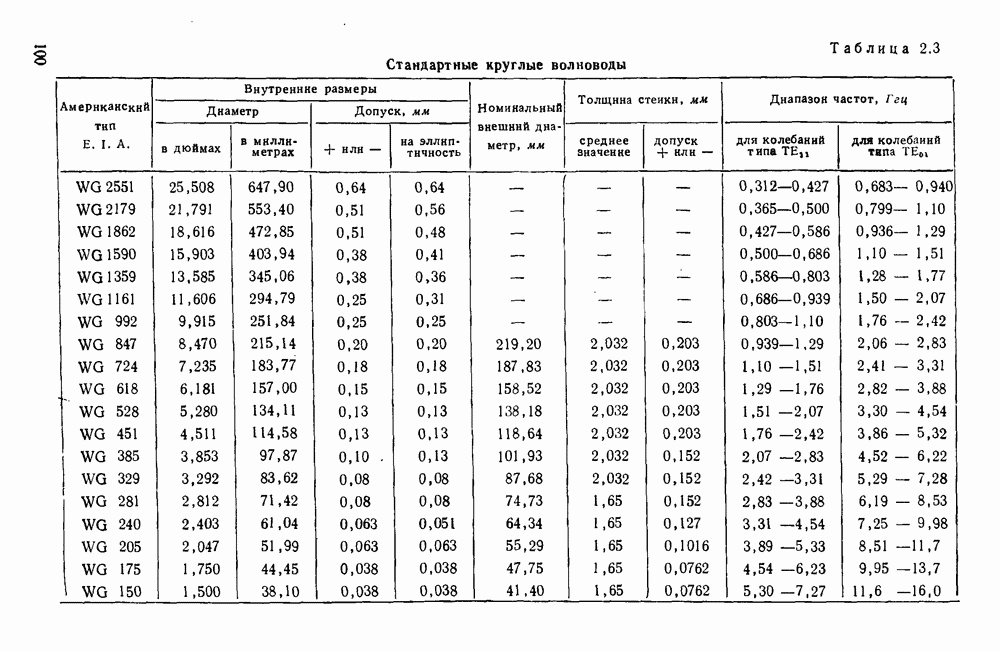
- 2.3.2. Круглые волноводы
- 2.3.3. Широкополосные и компактные волноводы
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
- 2.4.2. Контактные прокладки и дроссели
- 2.4.3. Крепежные и зажимные устройства
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
- 2.6.1. Изгибы, уголки и скрутки
- 2.6.2. Переходы и преобразователи
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
- 3.2.3. Переход от линейной поляризации к круговой
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
- 3.6.2. Вращающиеся сочленения различных типов
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
- 3.7.1. Механические переключатели с ручным управлением
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
- 5.2.1. Волномеры с объемными резонаторами
- 5.2.2. Волноводные интерферометры
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
- 5.3.2. Связанные резонаторы
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
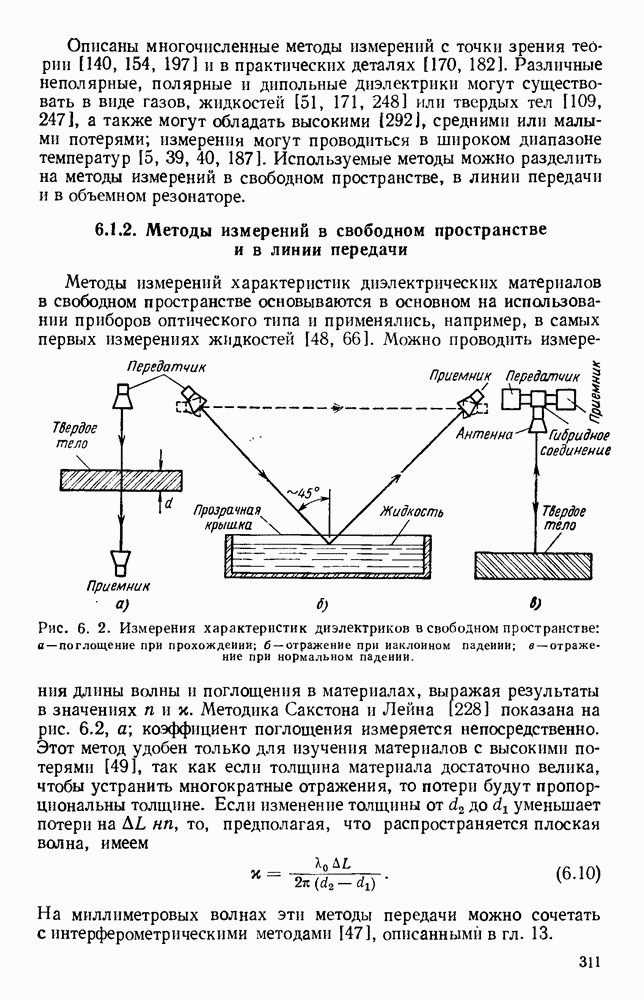
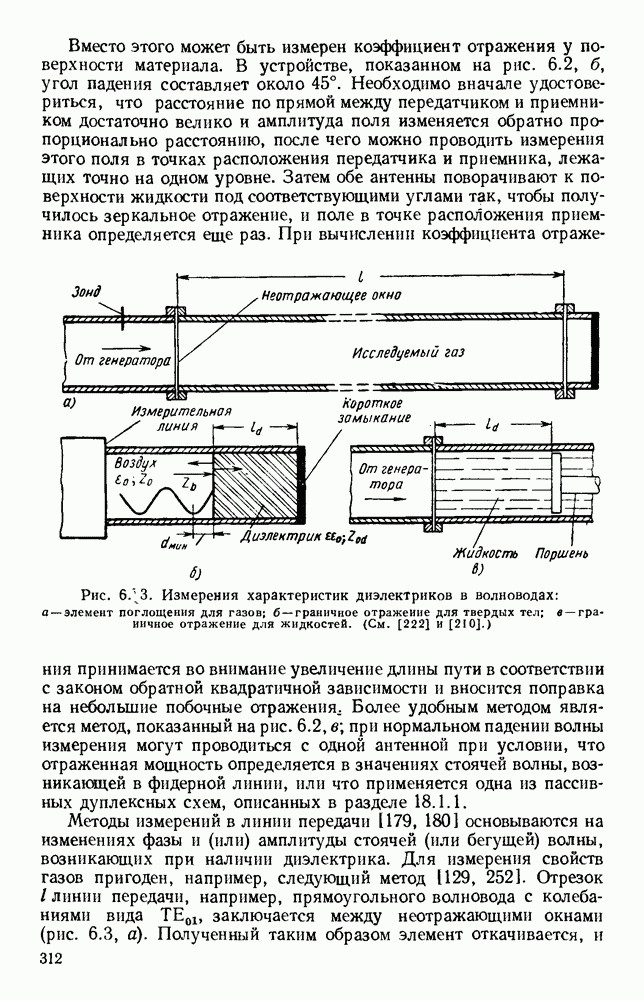
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
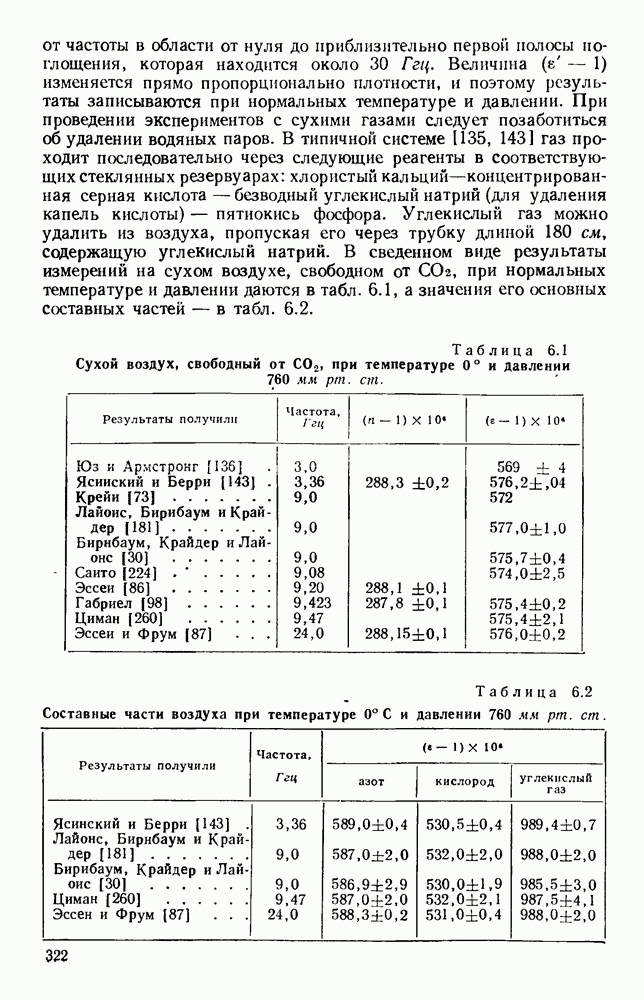
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
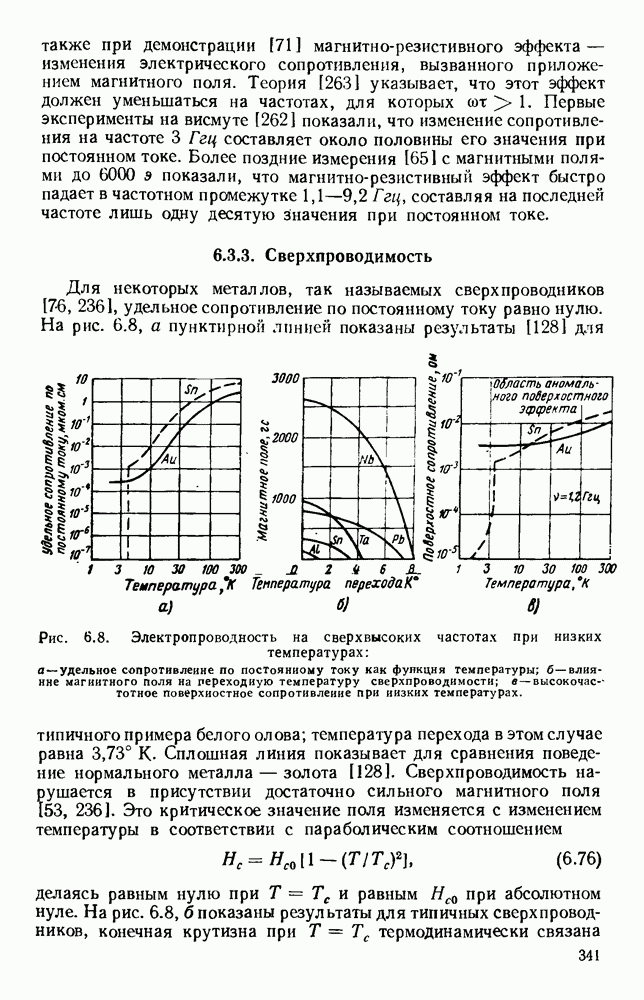
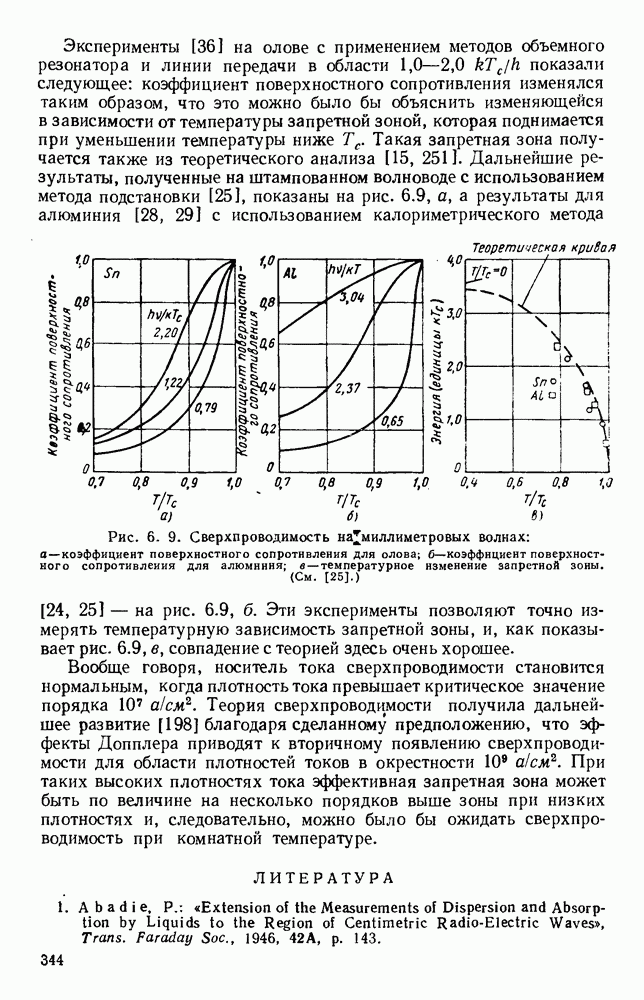
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
- 7.1.2. Форма линии и интенсивность
- 7.1.3. Сверхтонкая структура
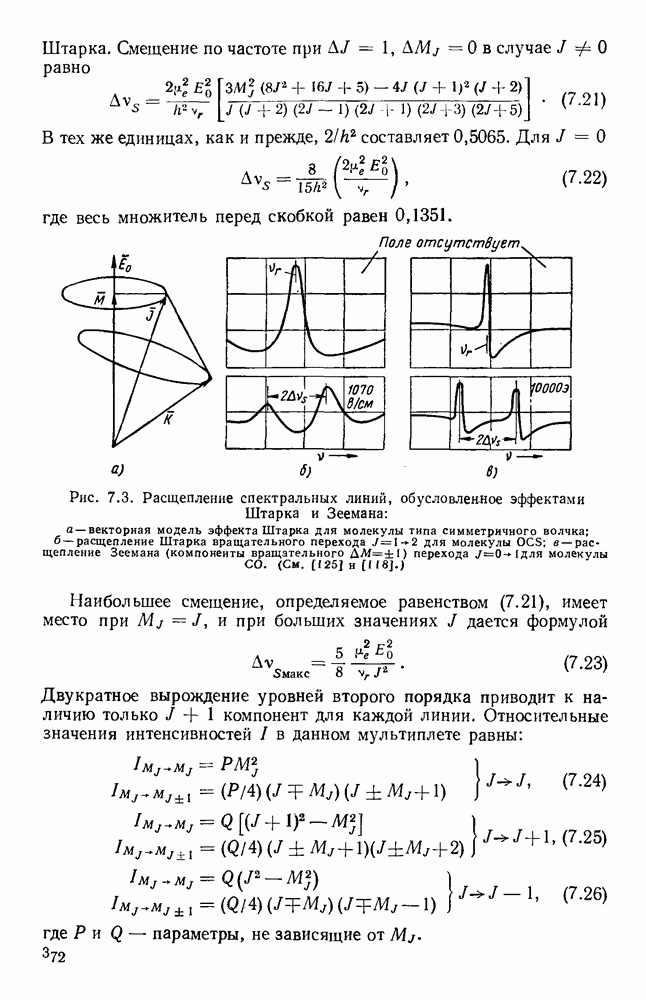
- 7.1.4. Явления Штарка и Зеемана
- 7.2. СПЕКТРОМЕТРЫ
- 7.2.2. Поглощающие ячейки
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
- 7.3.4. Времена релаксации
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
- 8.3.3. Ферритовые устройства в качестве элементов схем
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
- 8.6.2. Устройства с поперечным полем
- 8.6.3. Прочие узлы
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
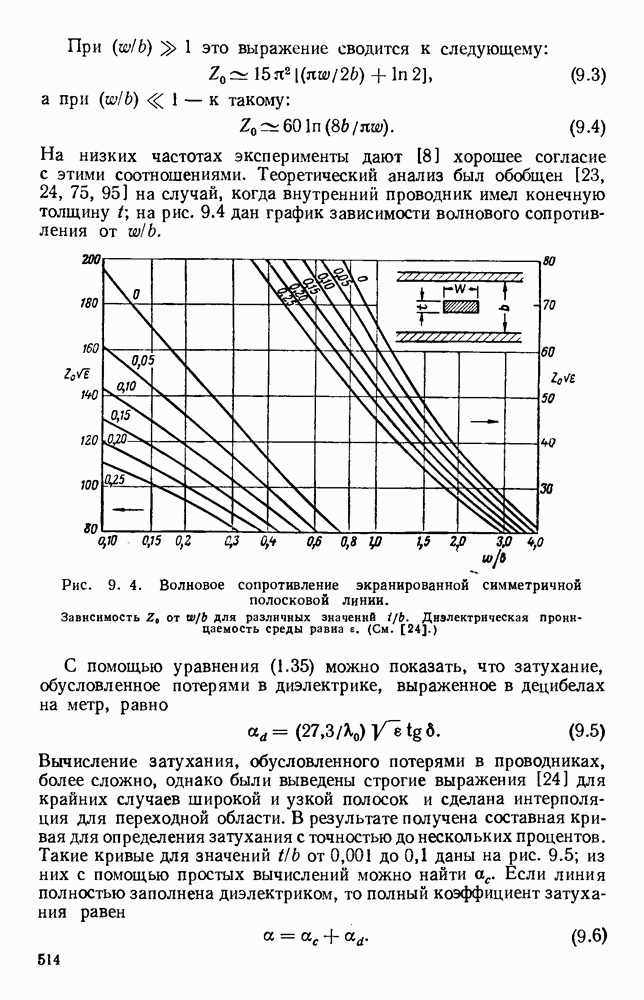
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.2.1. Линии типа «диэлектрических сэндвичей»
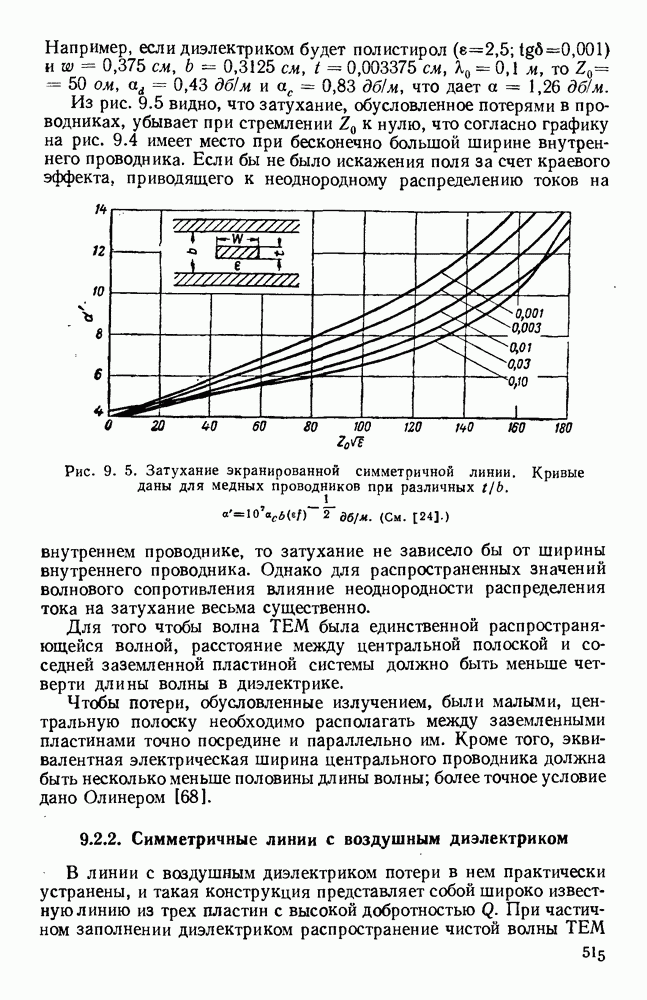
- 9.2.2. Симметричные линии с воздушным диэлектриком
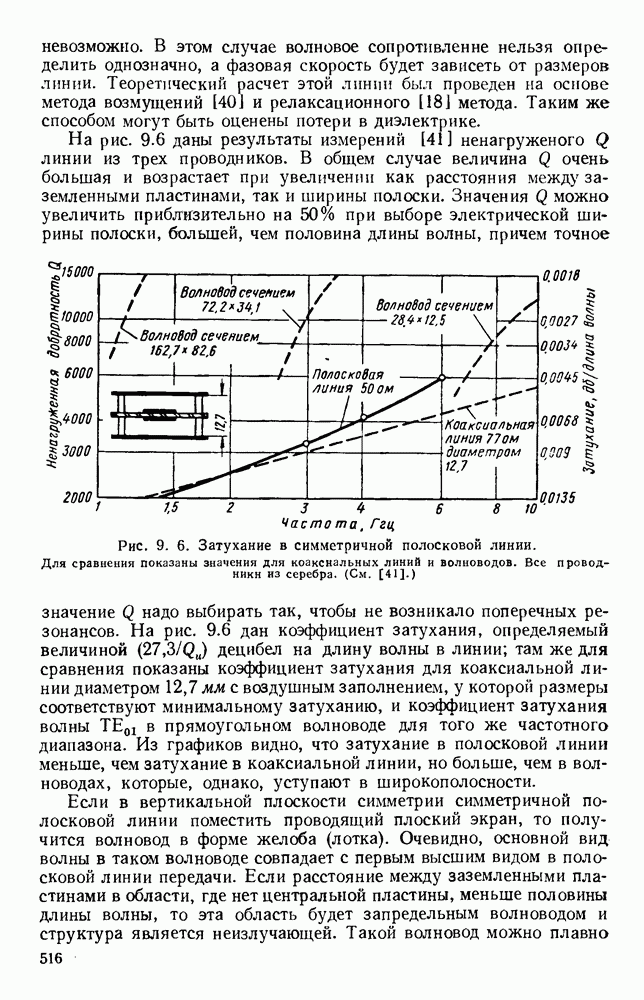
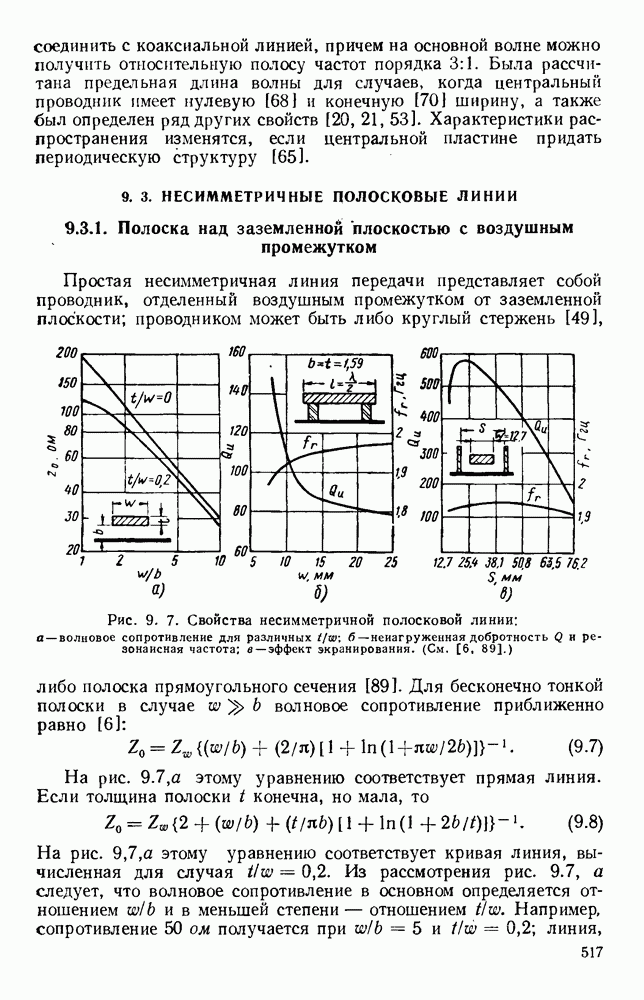
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
- 9.4.2. Переходные устройства
- 9.4.3. Узлы полосковых систем
- 9.5. ЦЕПИ И СИСТЕМЫ
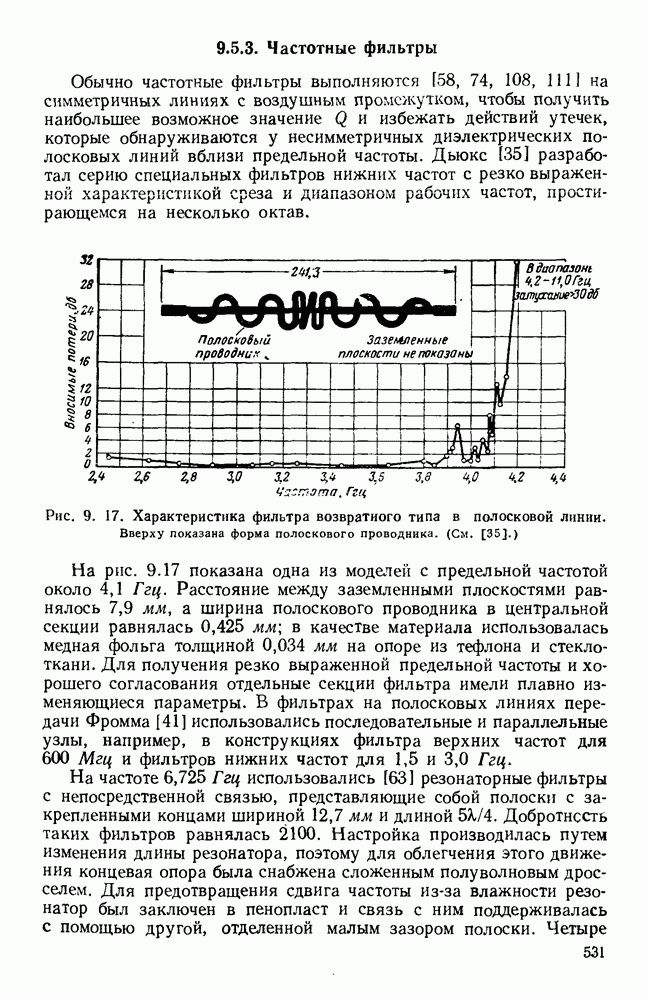
- 9.5.3. Частотные фильтры
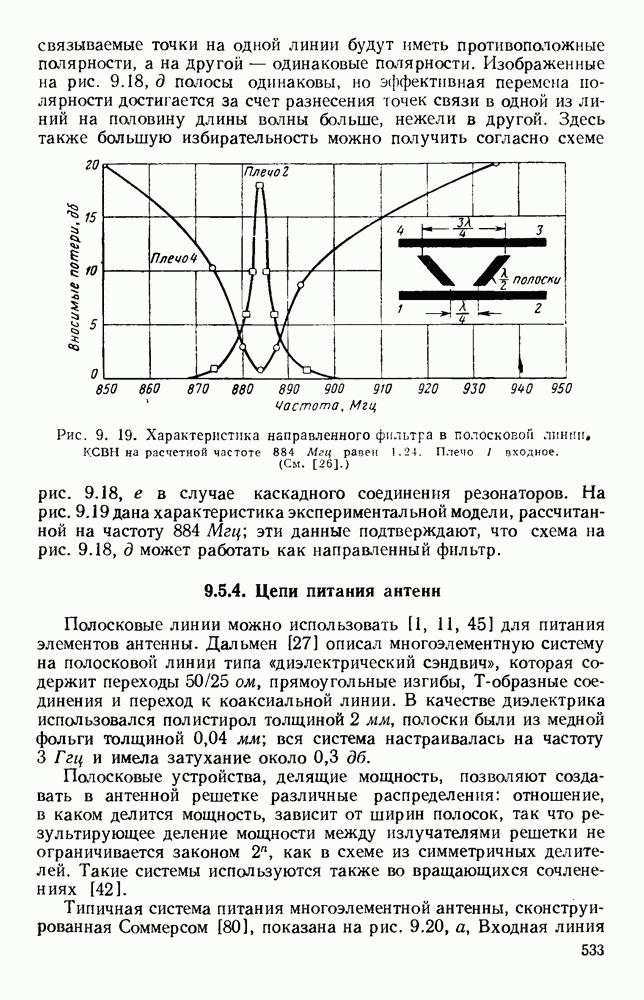
- 9.5.4. Цепи питания антенн
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
- 10.1.2. Пространственные гармоники
- 10.1.3. Многократно-периодические структуры
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
- 10.2.3. Продольные цилиндрические волны
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
- 12.2. МАГНЕТРОНЫ
- 12.2.2. Резонаторные системы
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
- 12.2.4. Рабочие характеристики
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
- 13.1.2. Типы дифракции
- 13.1.3. Рассеяние
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
- 13.2.2. Структуры волноводного типа
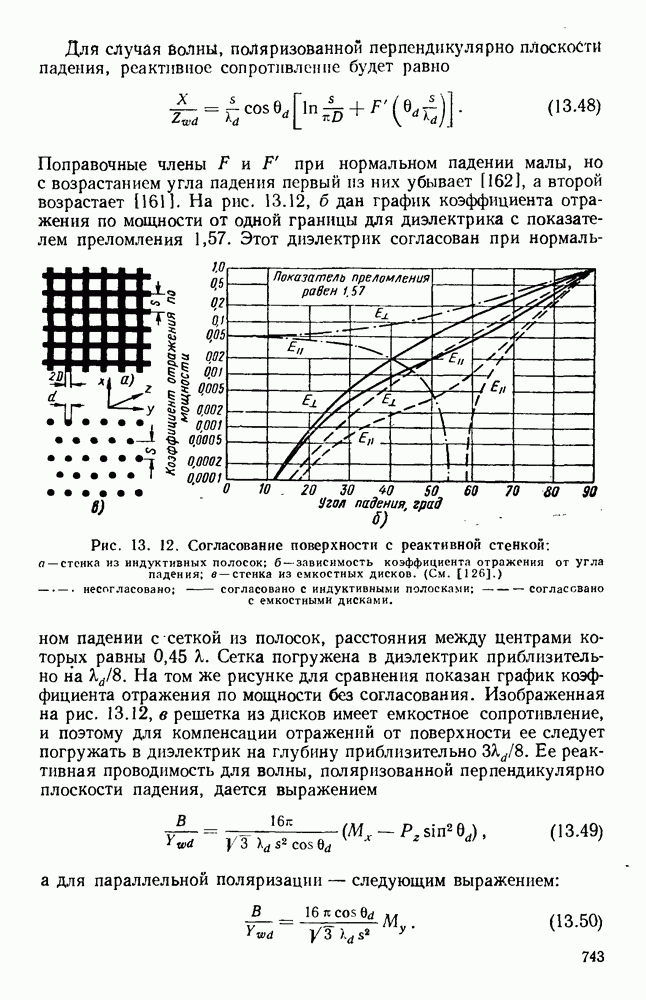
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
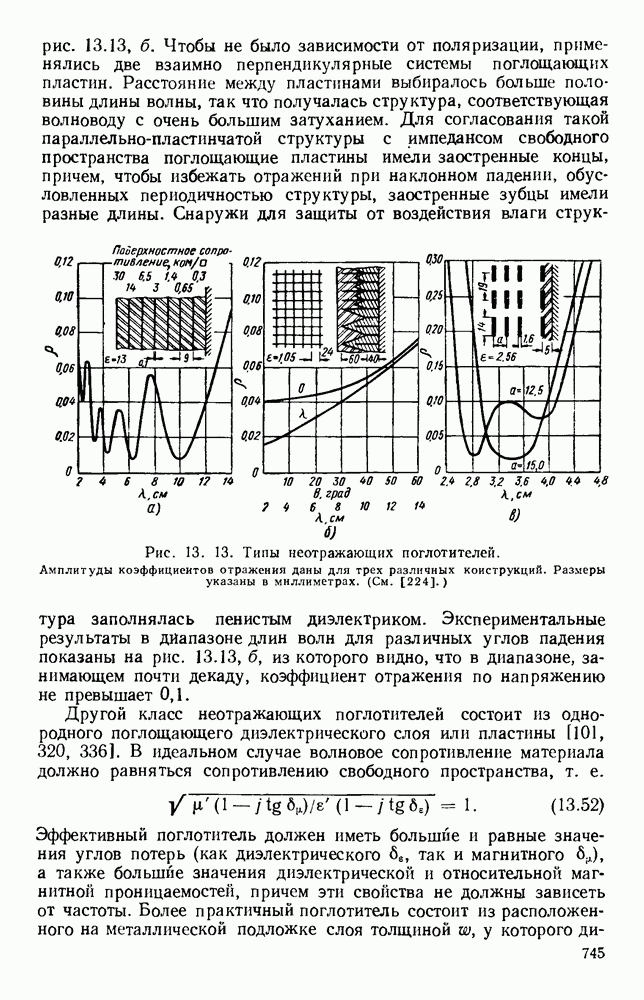
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
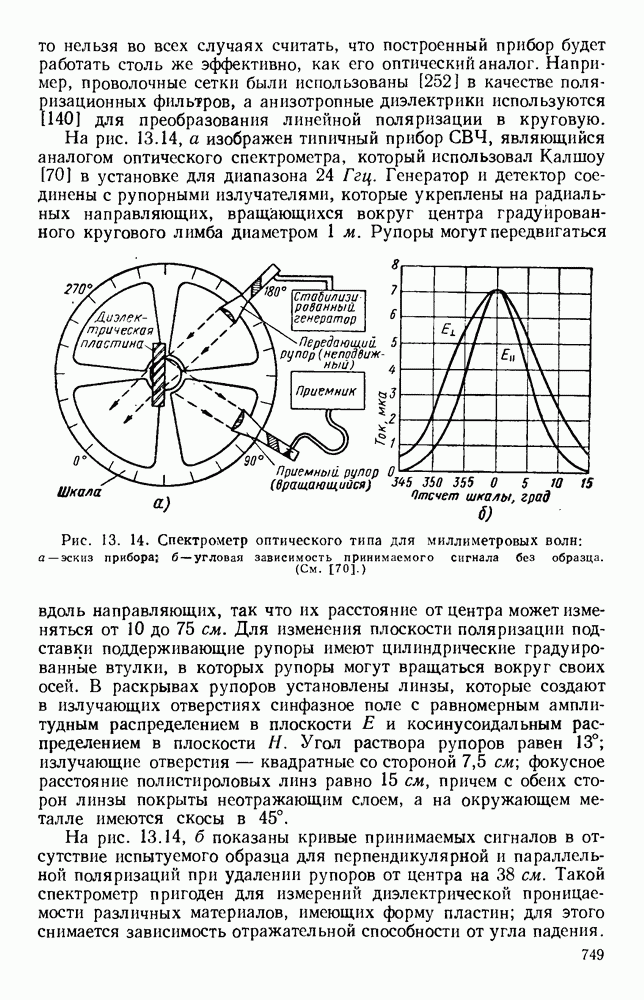
- 13.4. ПРИБОРЫ И СИСТЕМЫ
- 13.4.1. Спектрометры
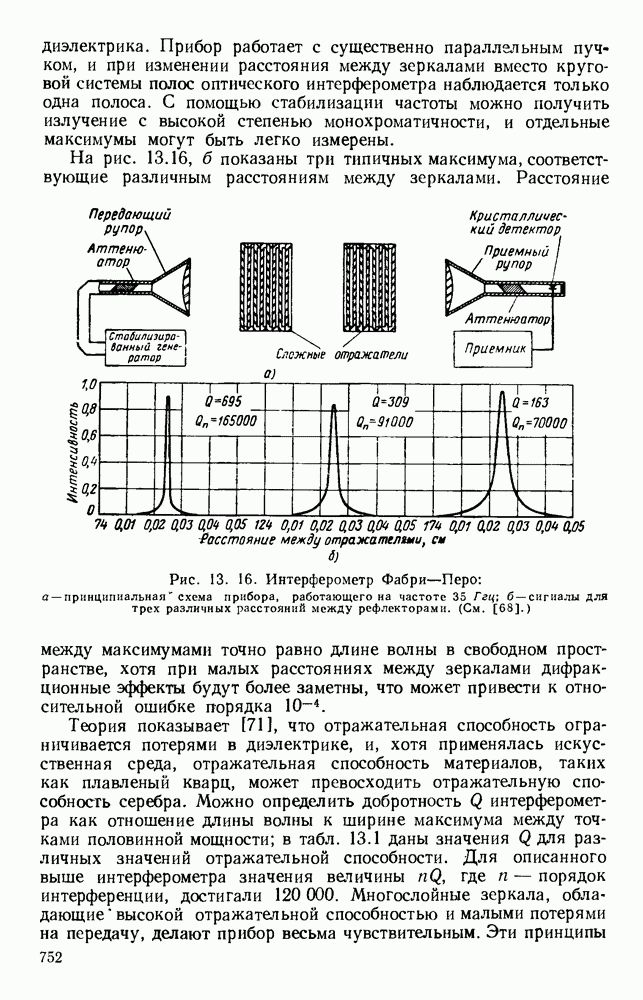
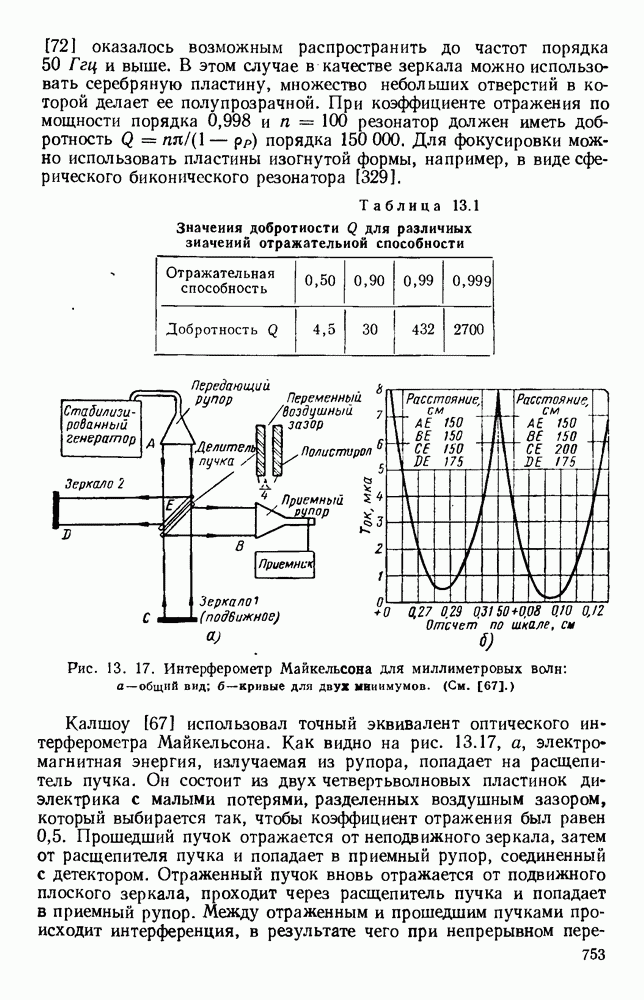
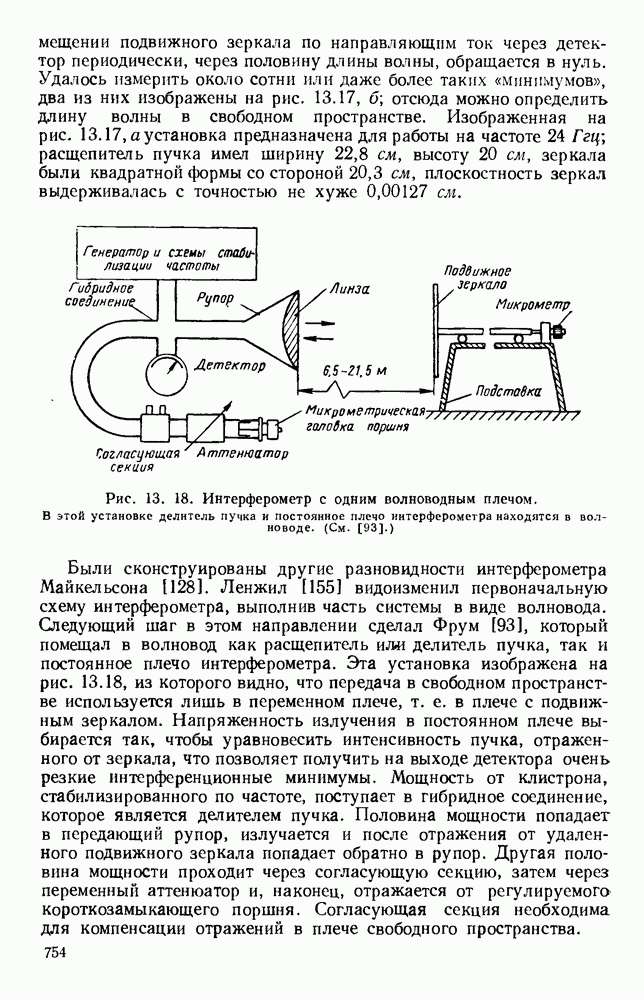
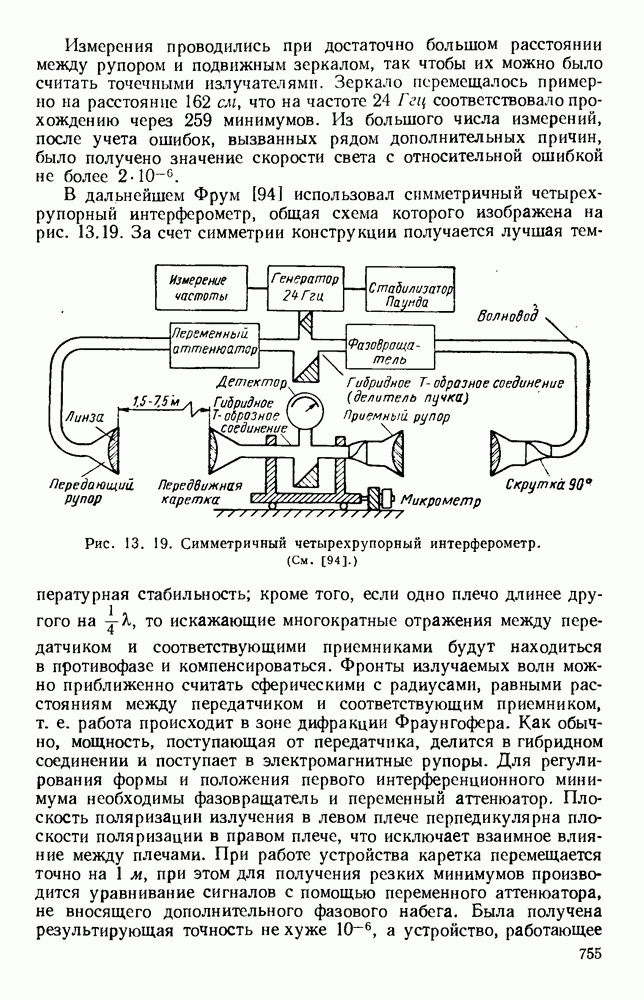
- 13.4.2. Интерферометры
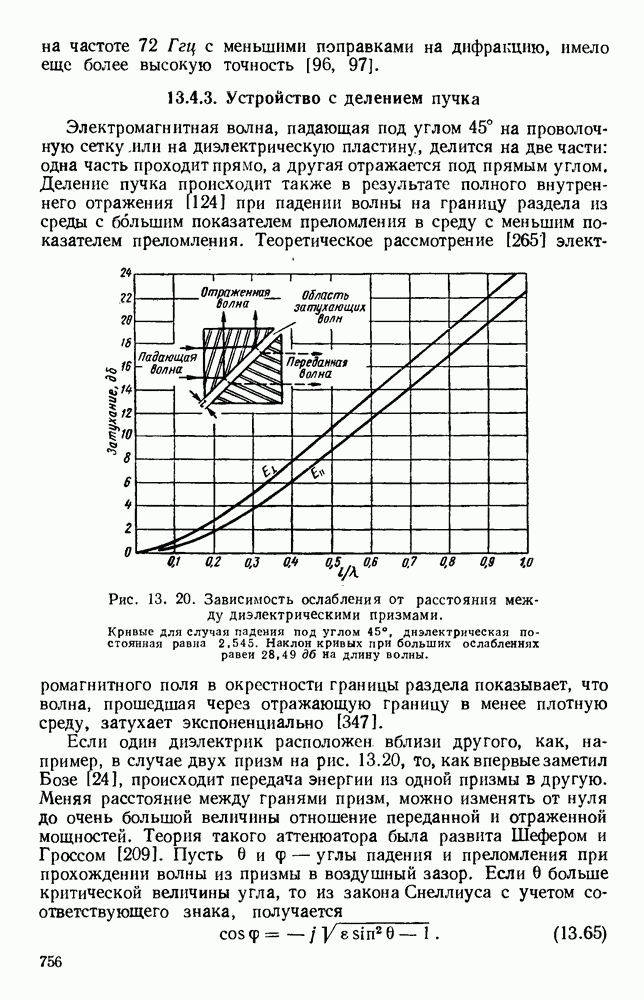
- 13.4.3. Устройство с делением пучка