| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
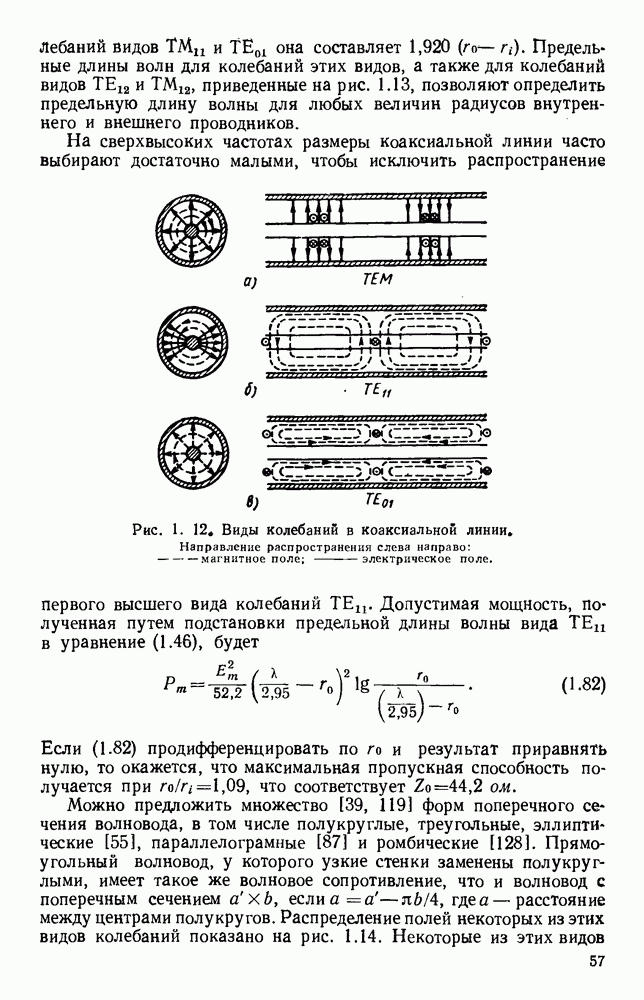
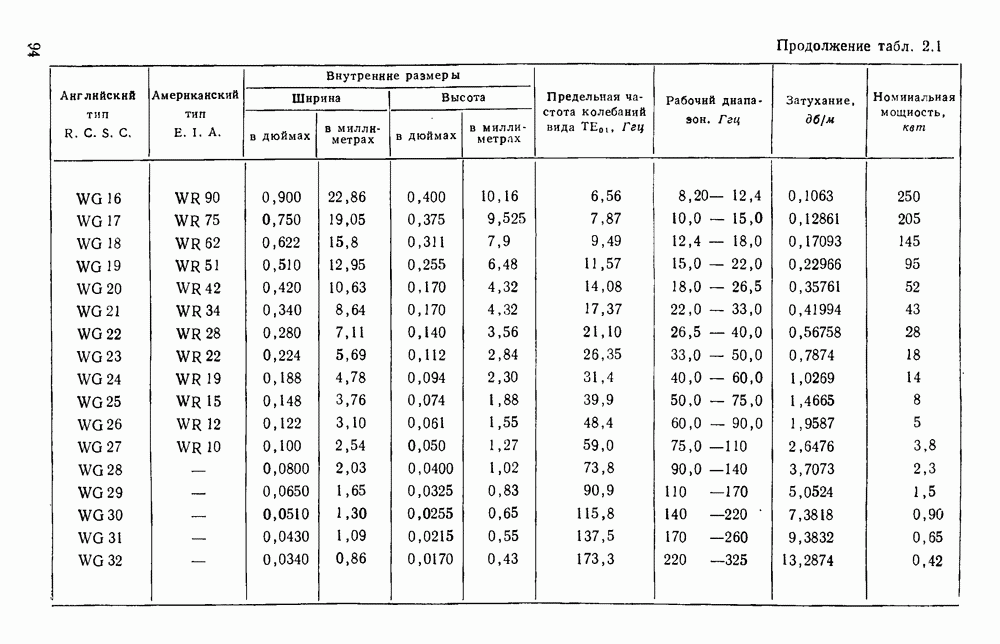
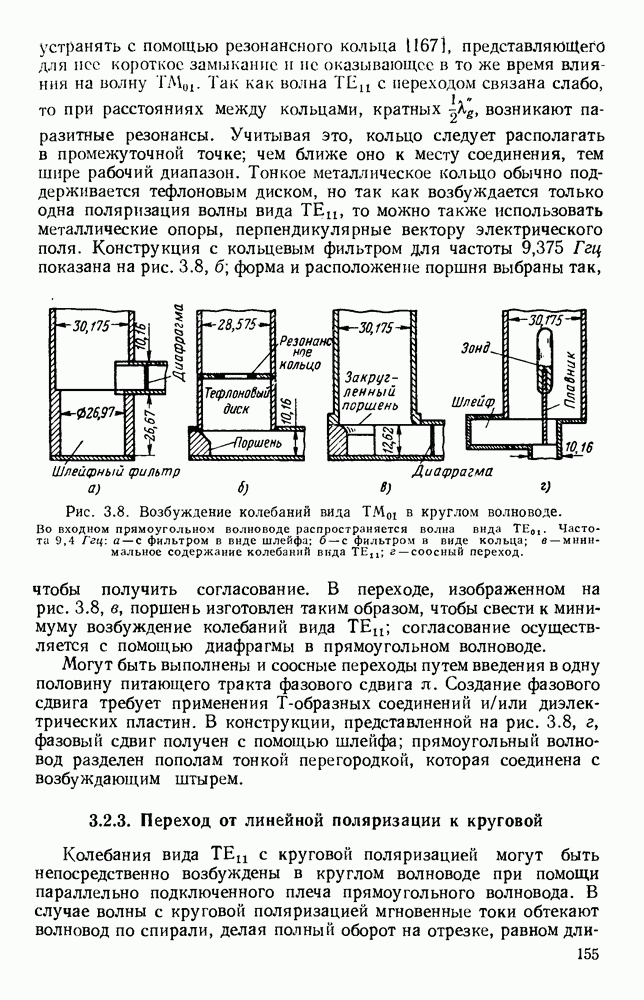
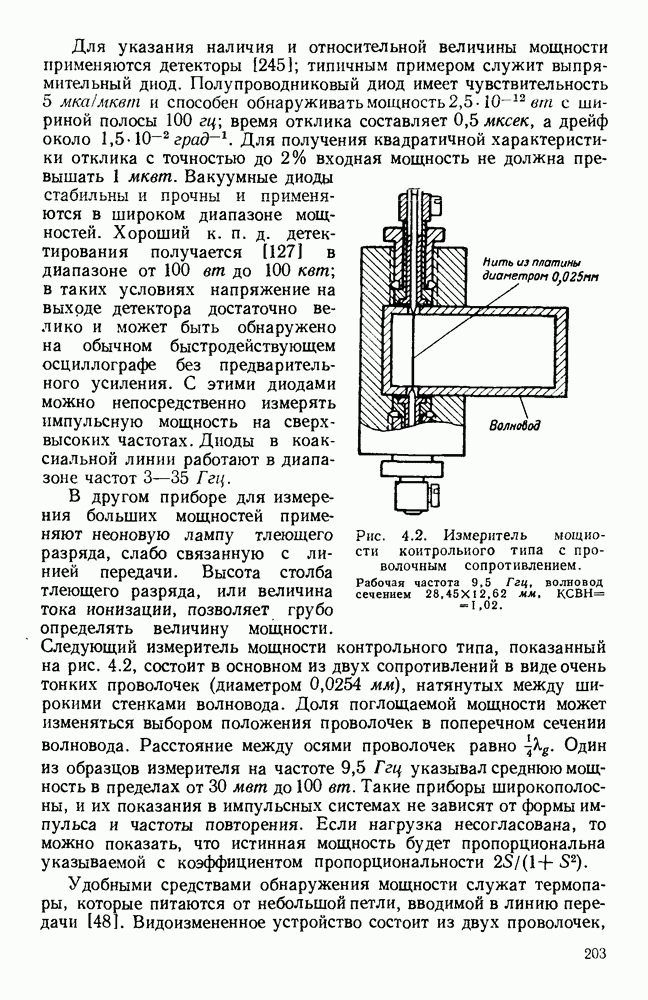
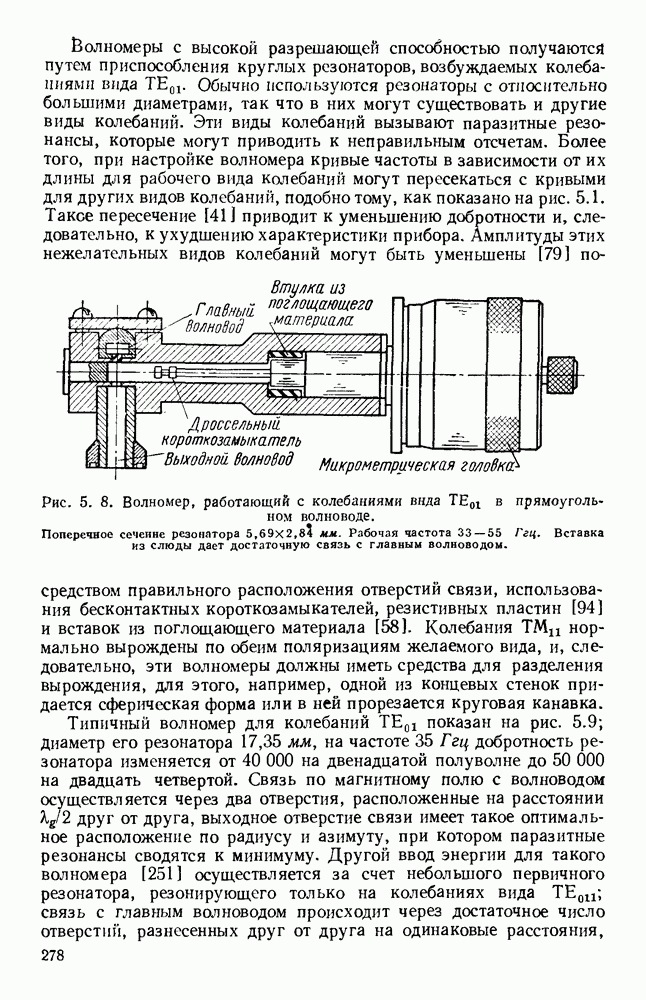
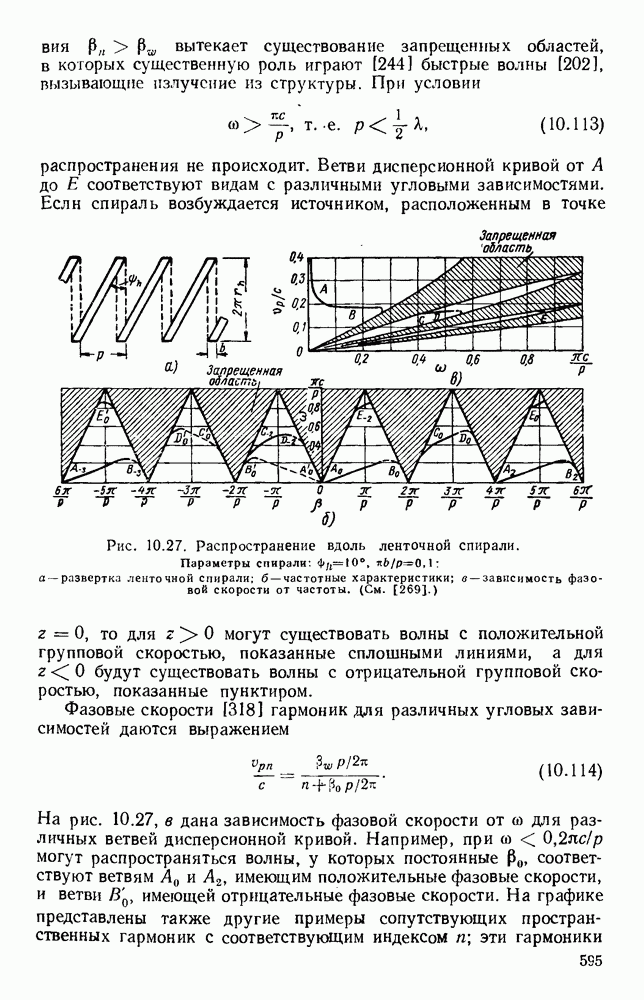
1.5.2. Гребневые волноводы
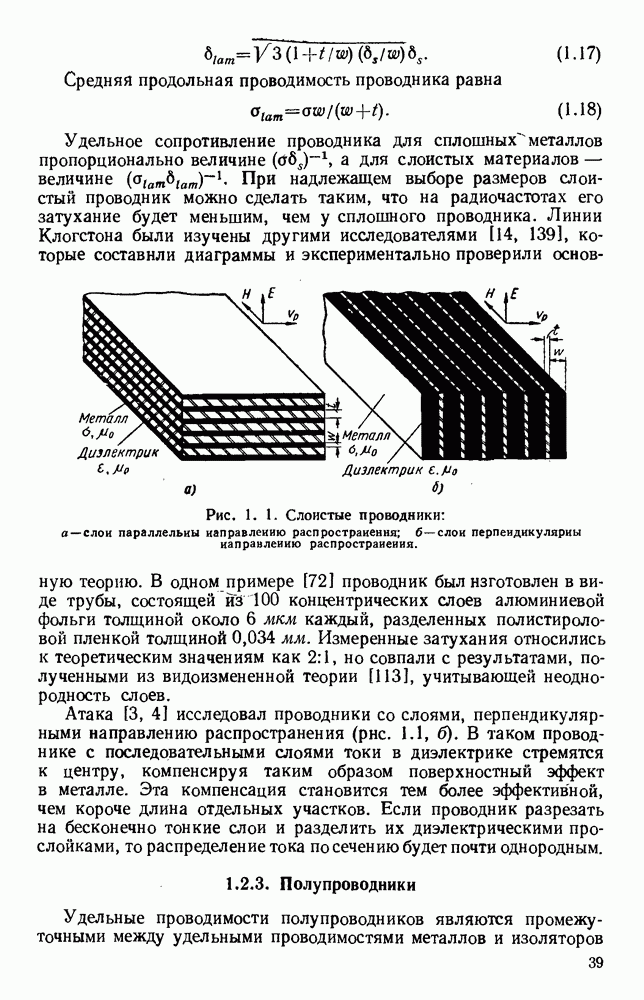
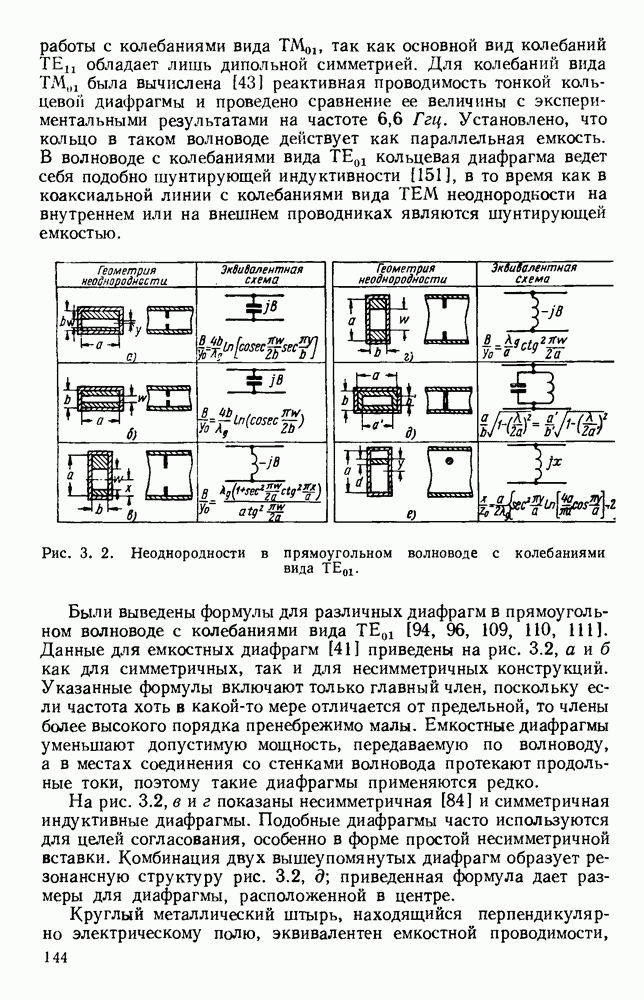
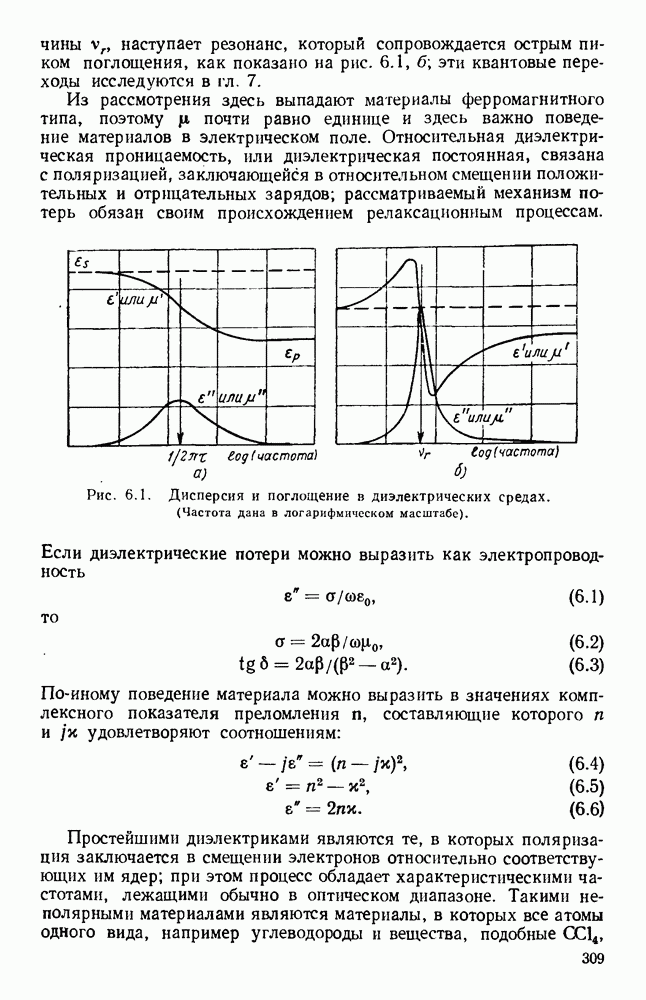
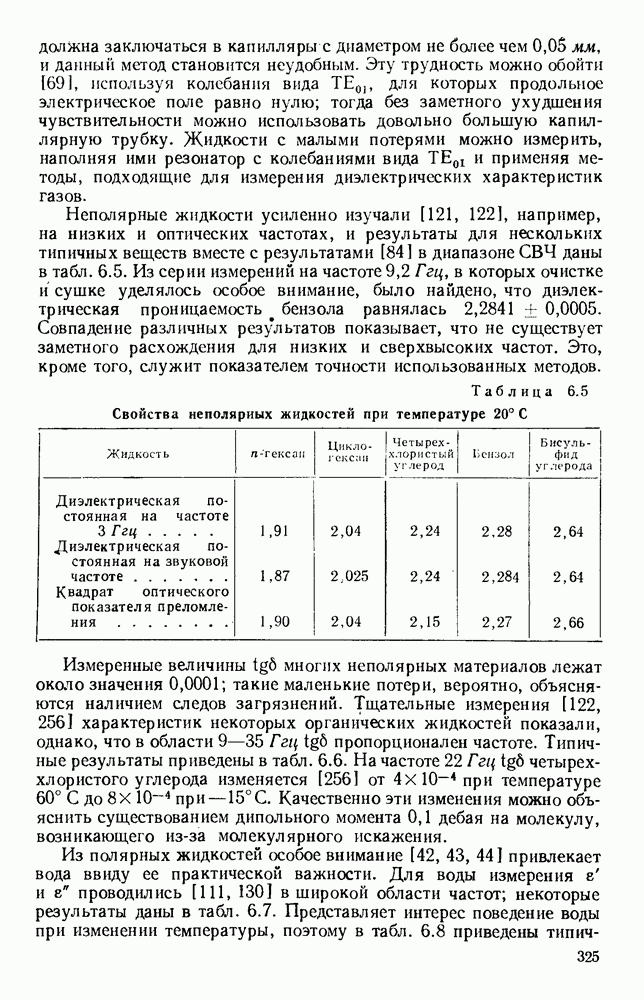
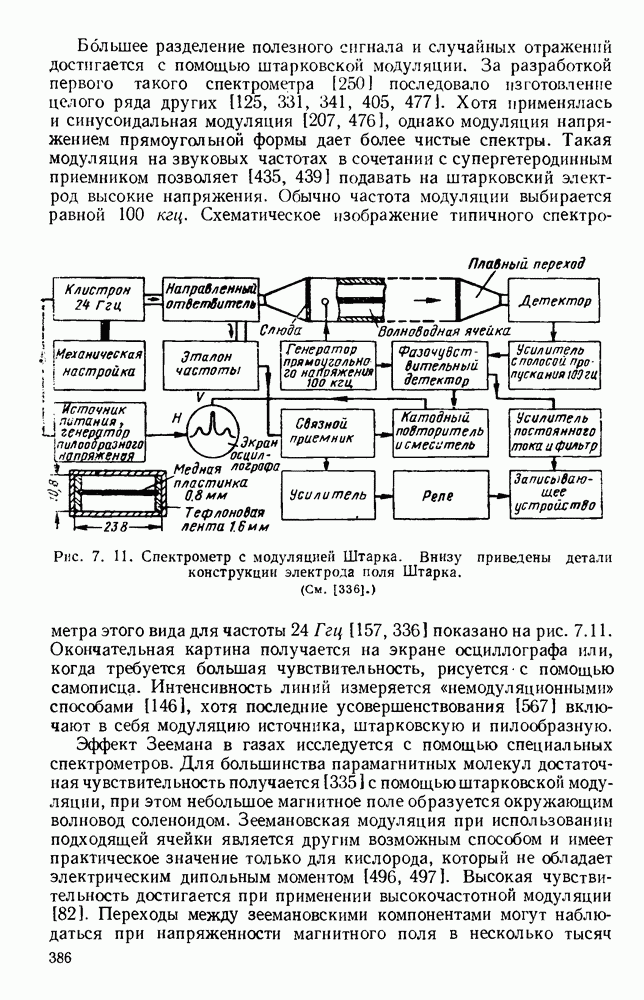
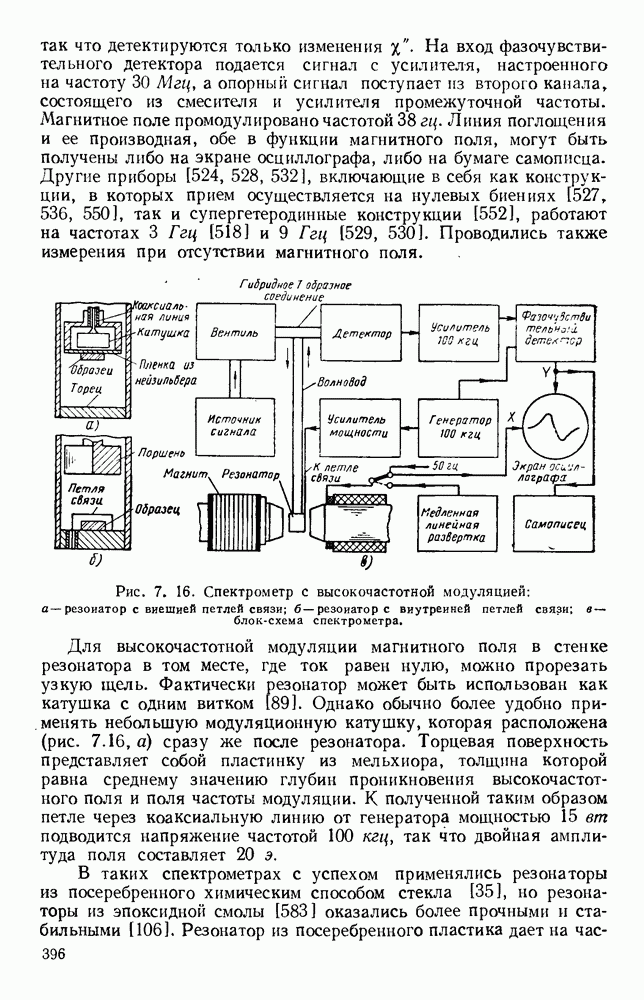
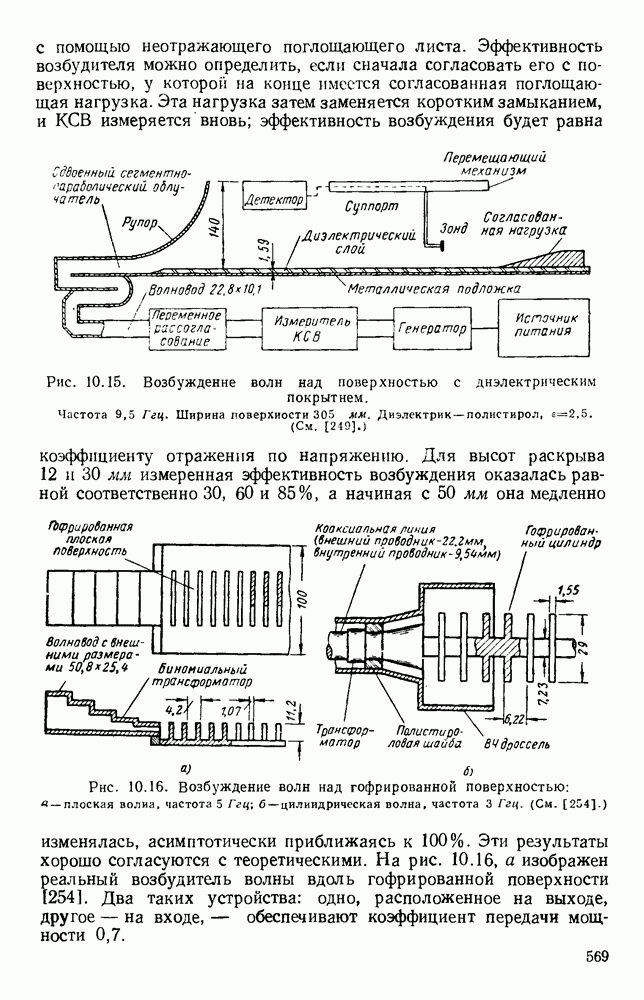
Гребневые волноводы показаны на рис. 1.15, а и  Свойства таких волноводов хорошо изучены [19, 41, 45, 89, 93, 94, 132]; Хопфер [57] на основе эквивалентной схемы, показанной на рис. 1.15, в, рассчитал их точные данные.
Свойства таких волноводов хорошо изучены [19, 41, 45, 89, 93, 94, 132]; Хопфер [57] на основе эквивалентной схемы, показанной на рис. 1.15, в, рассчитал их точные данные.

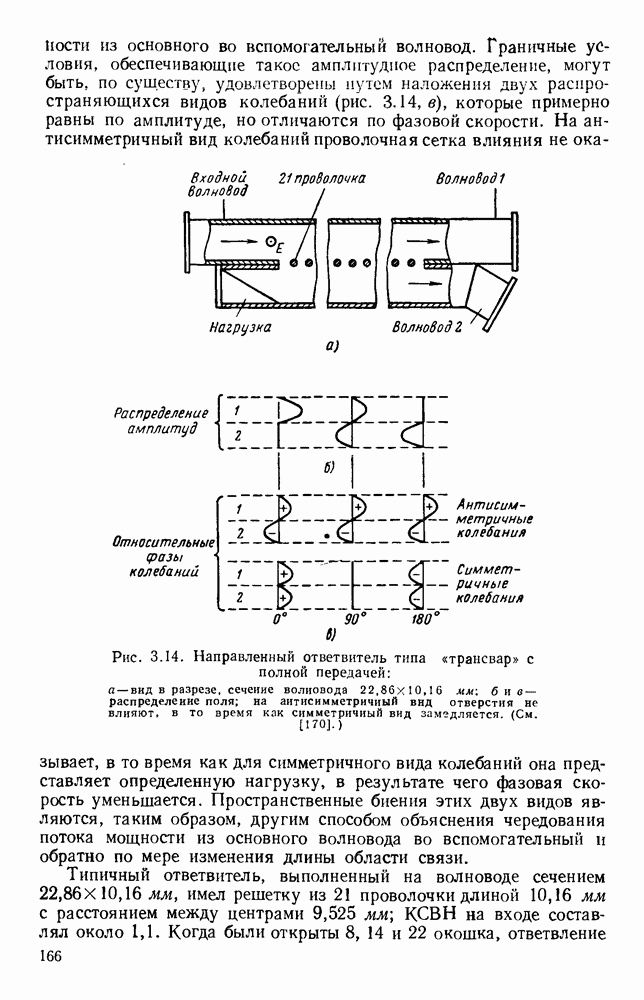
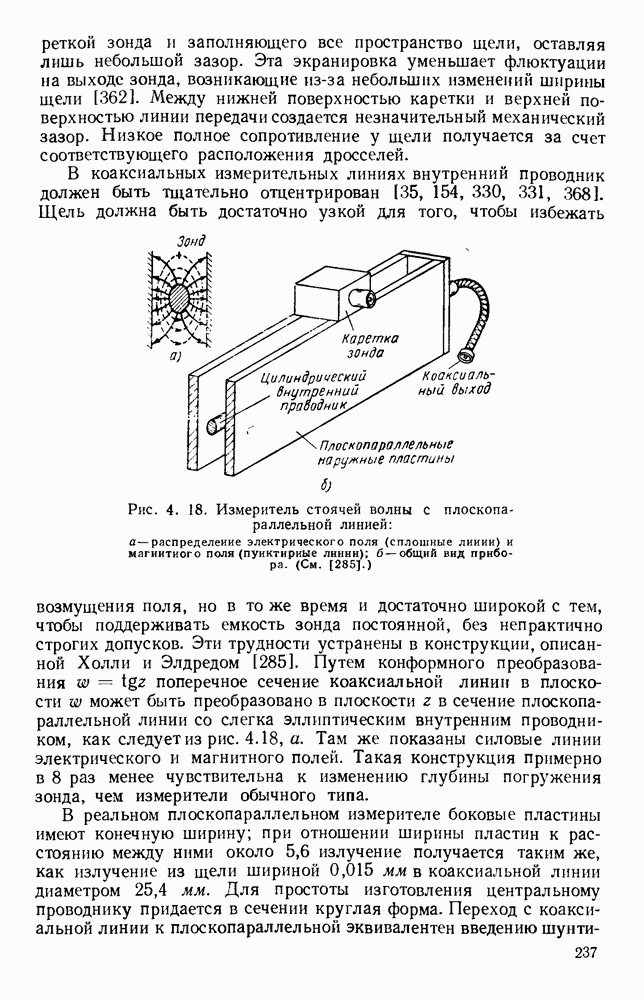
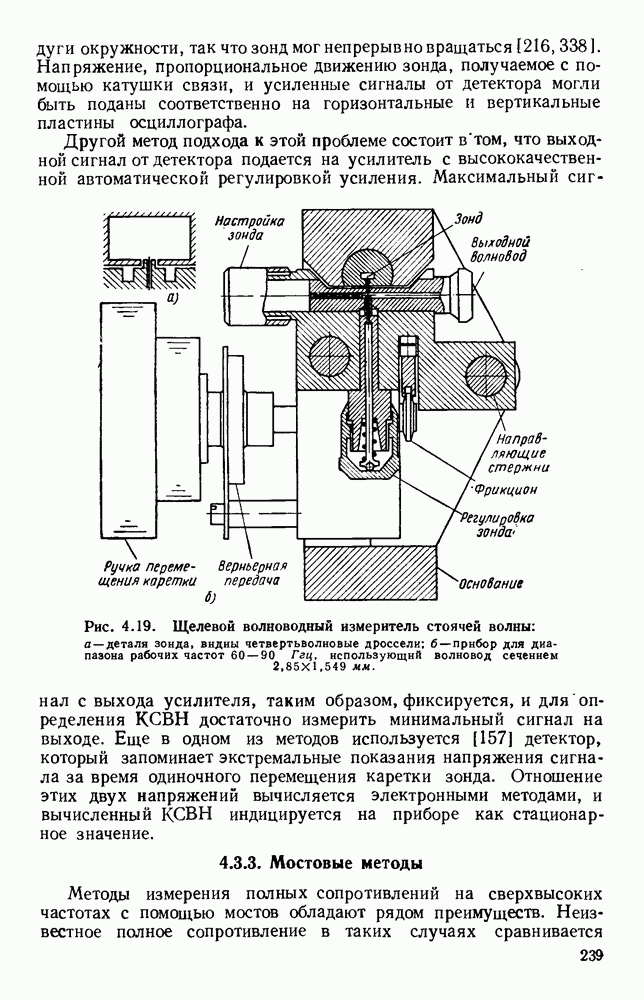
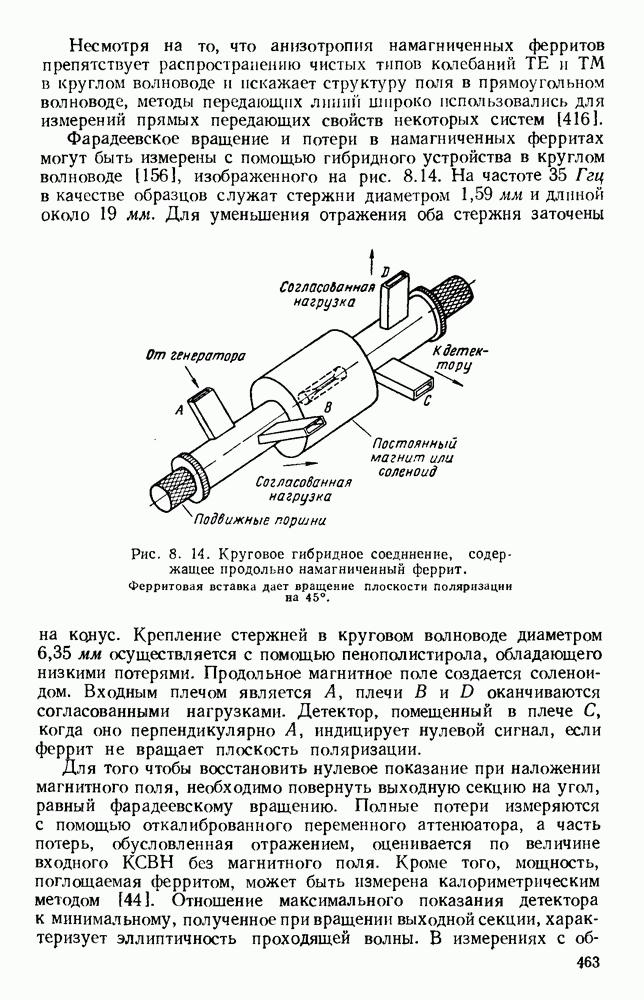
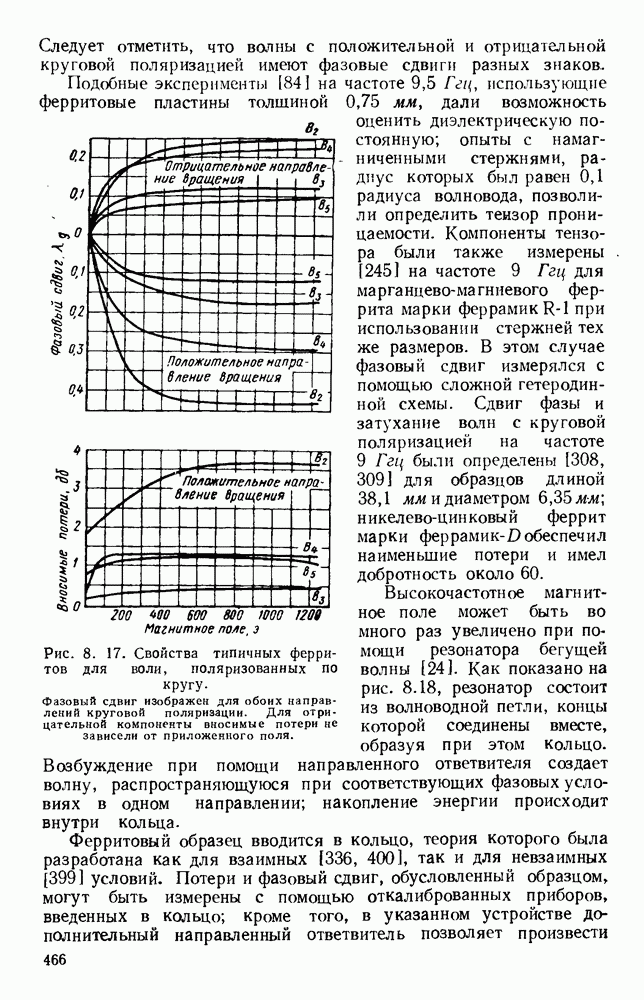
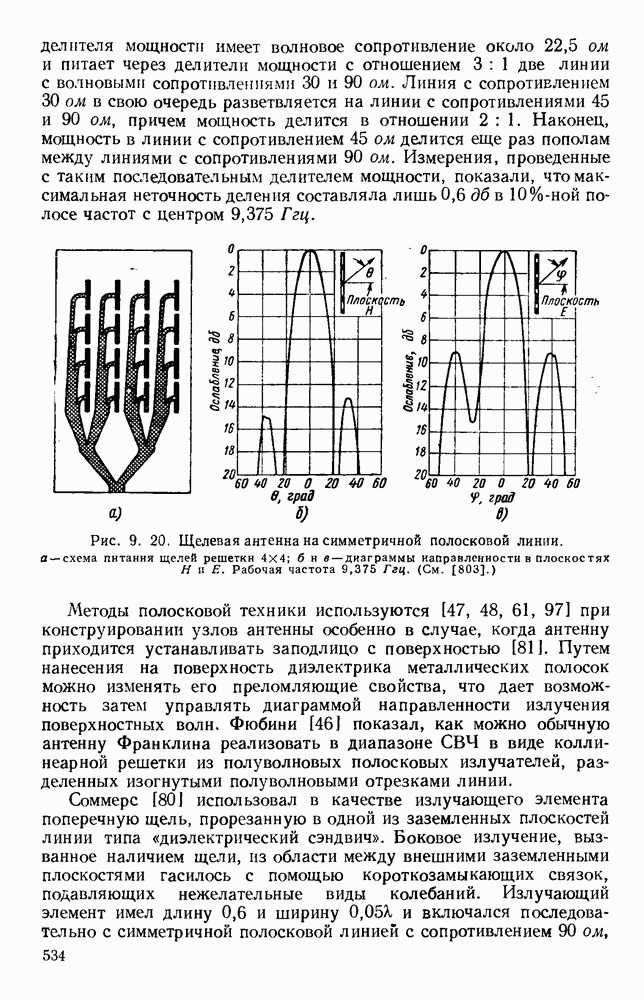
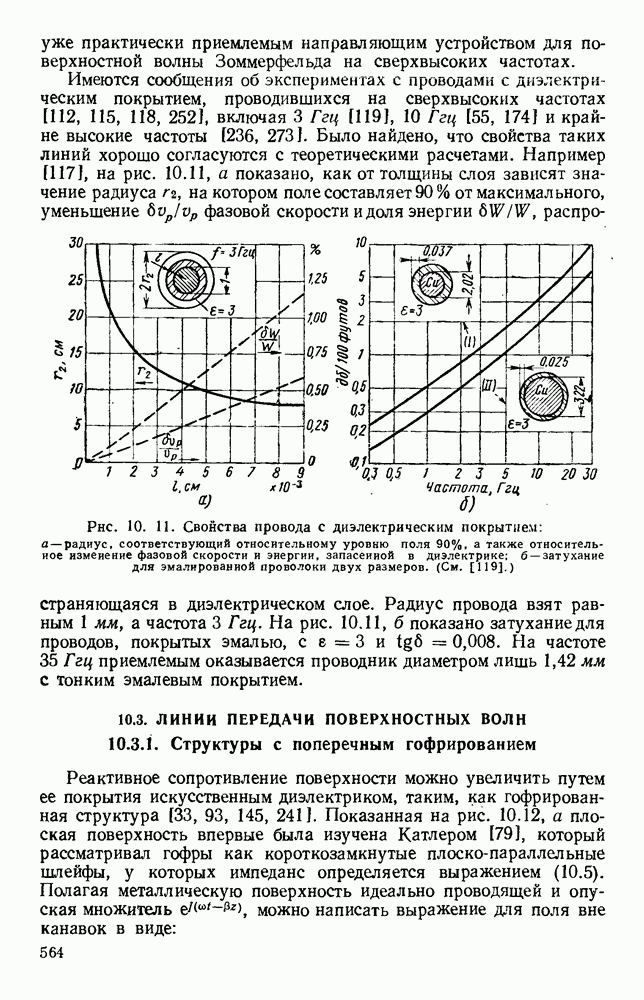
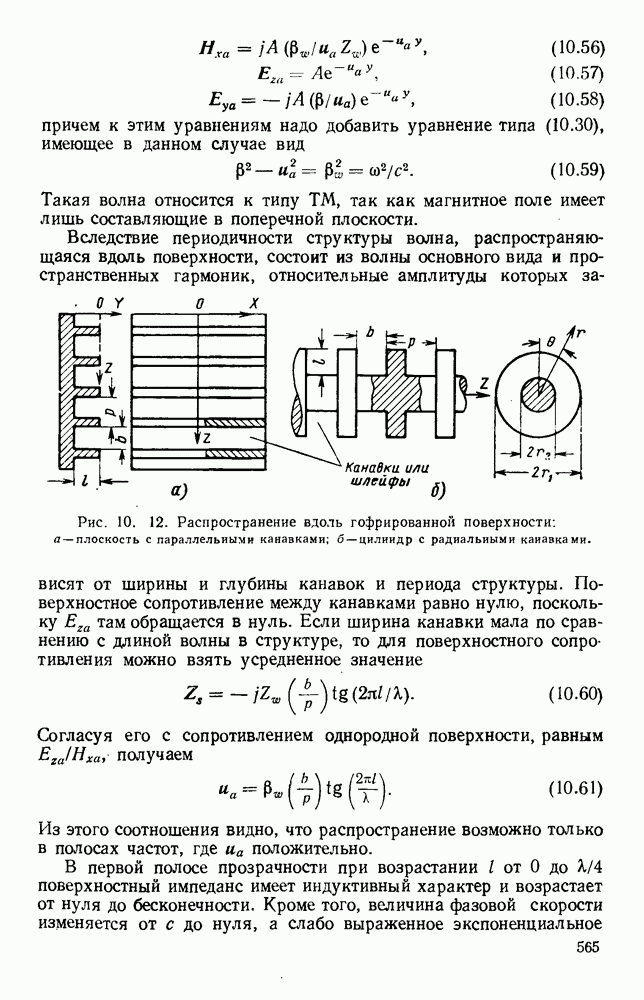
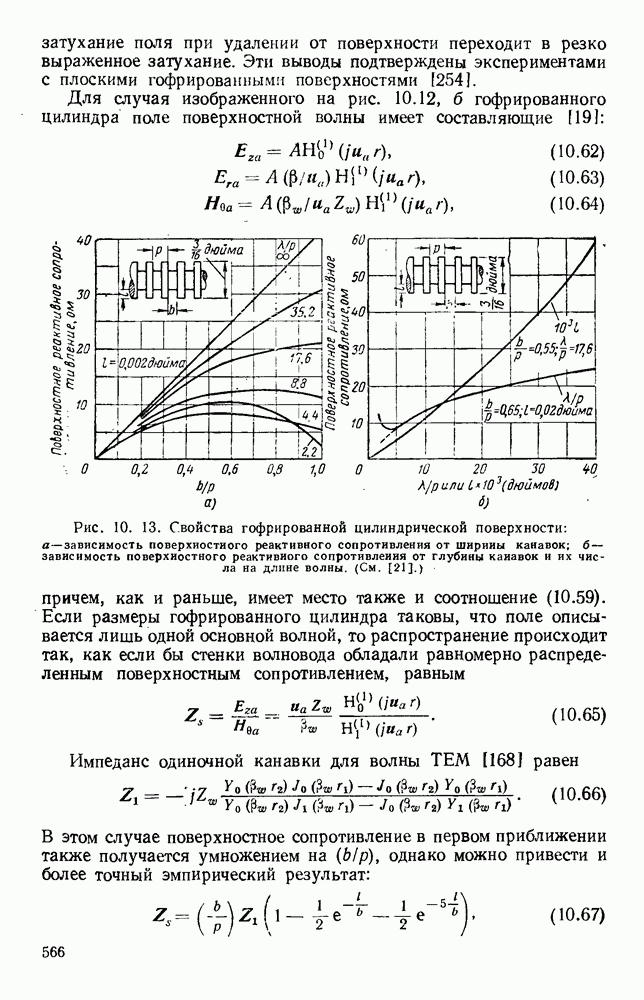
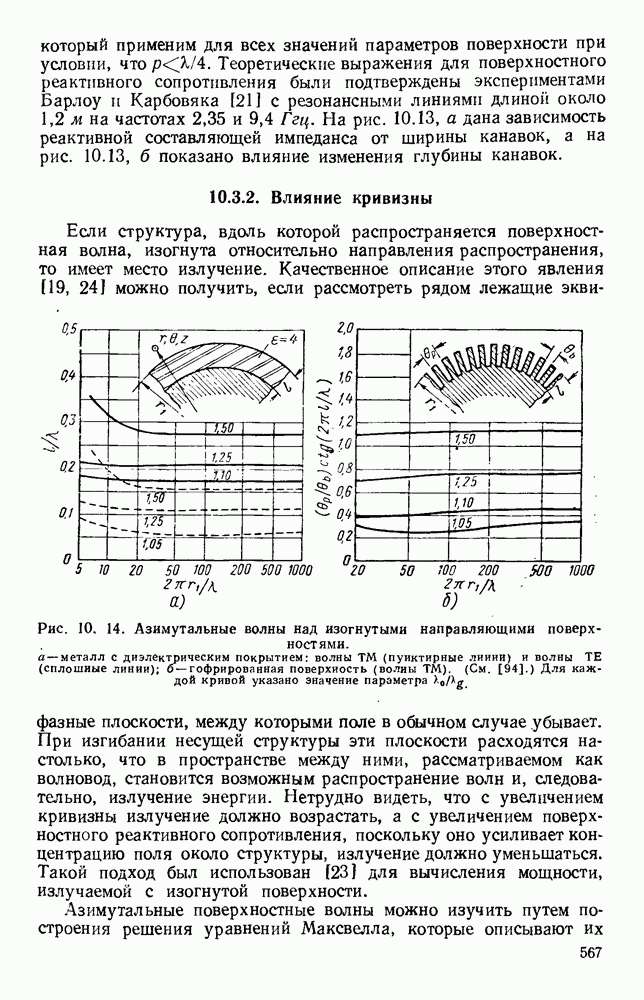
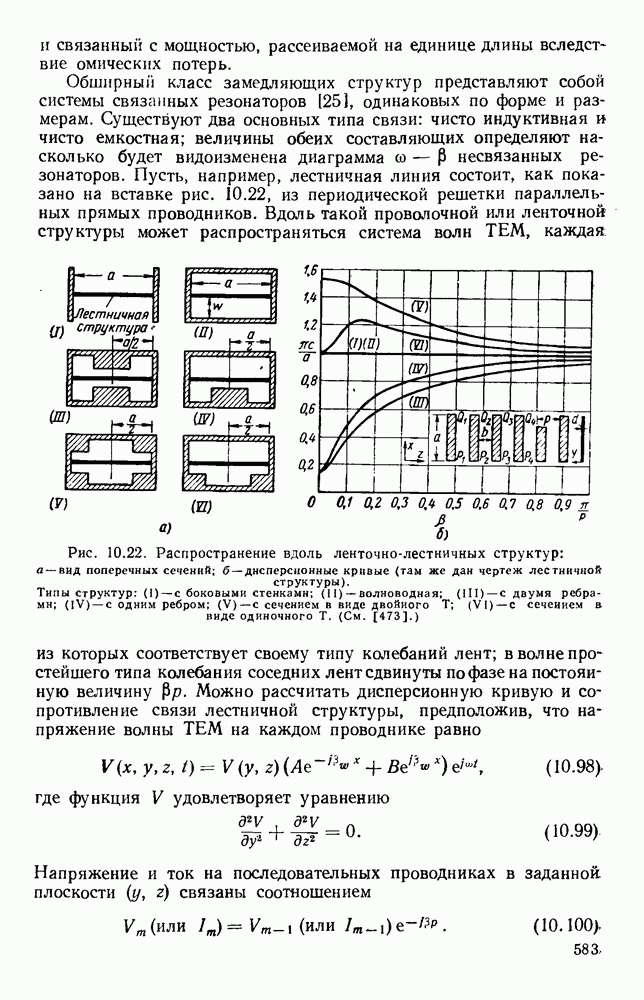
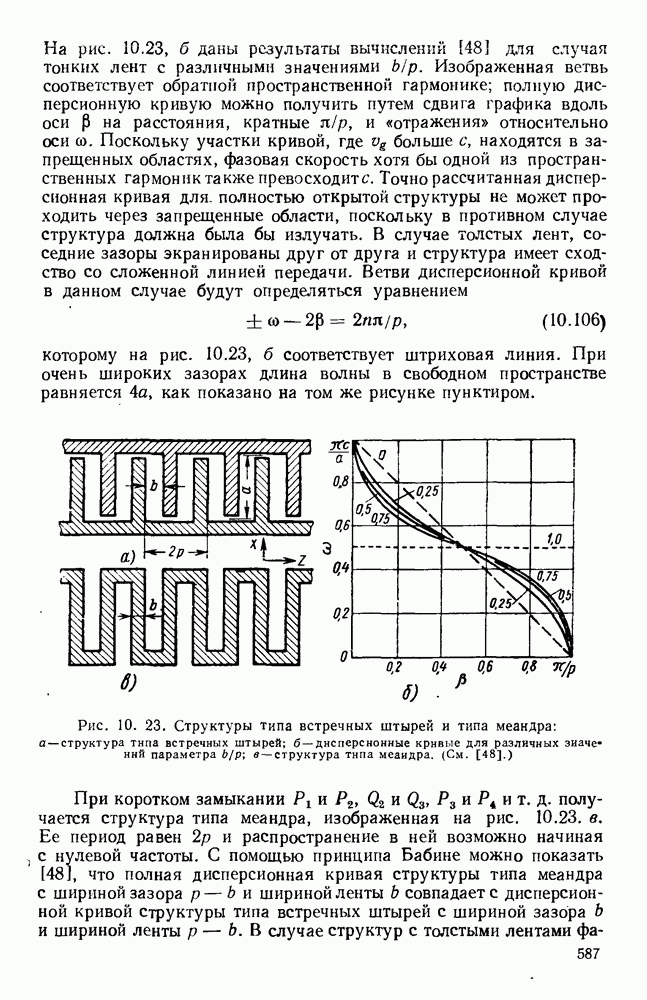
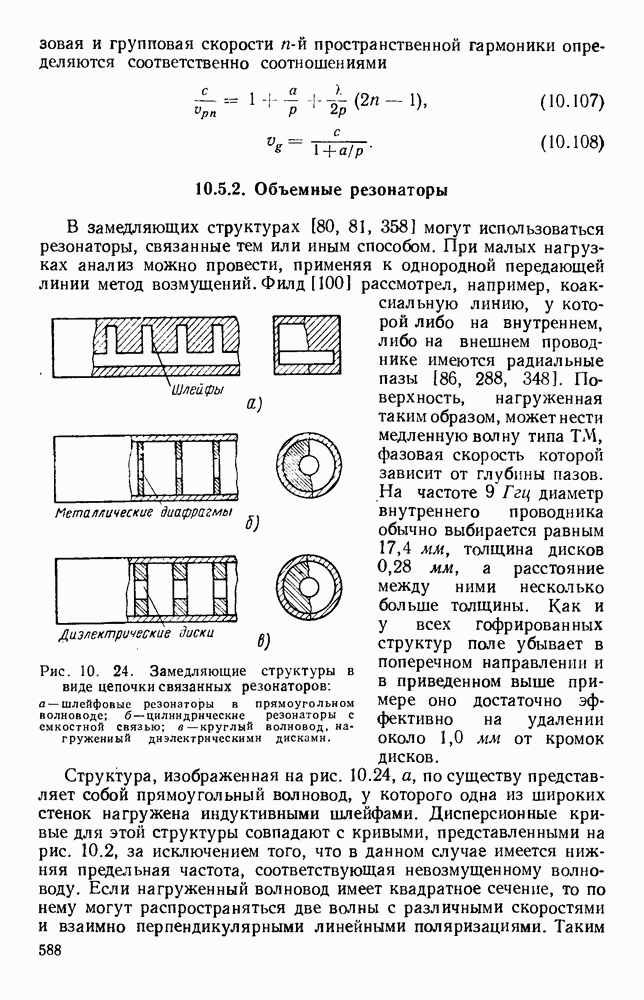
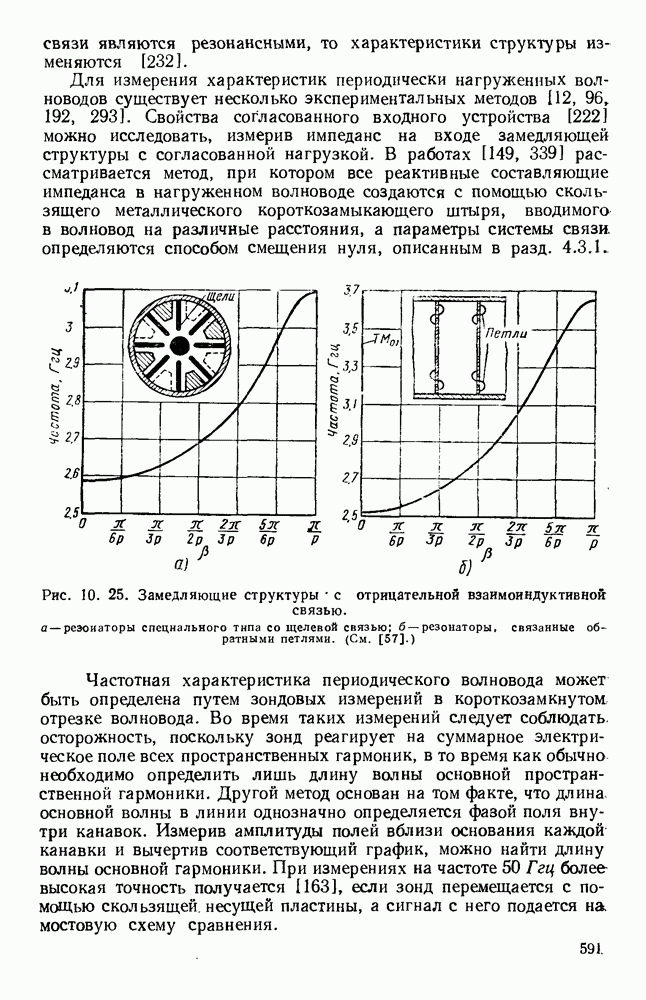
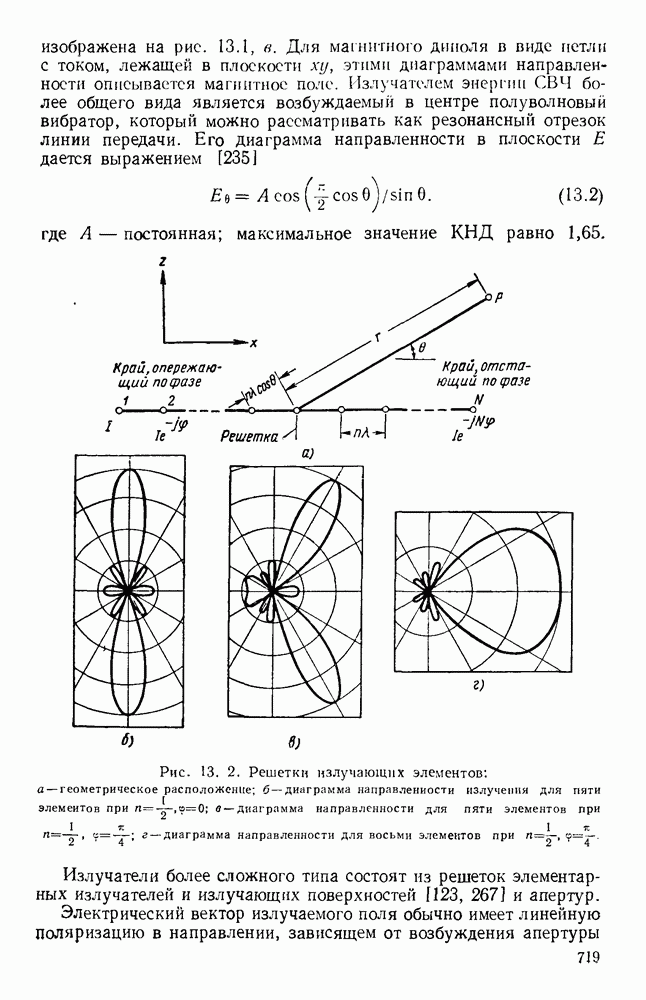
Рис. 1. 15. Геометрия н схемное представление гребневых волноводов. а — волновод с одним гребнем; б - волновод с двумя гребнями; в — эквивалентная схема.
Соотношения, управляющие условиями прекращения распространения колебаний в гребневых волноводах для колебаний вида  выглядят следующим образом:
выглядят следующим образом:
для нечетных 

для четных 

где 
Характеристические проводимости определяются как

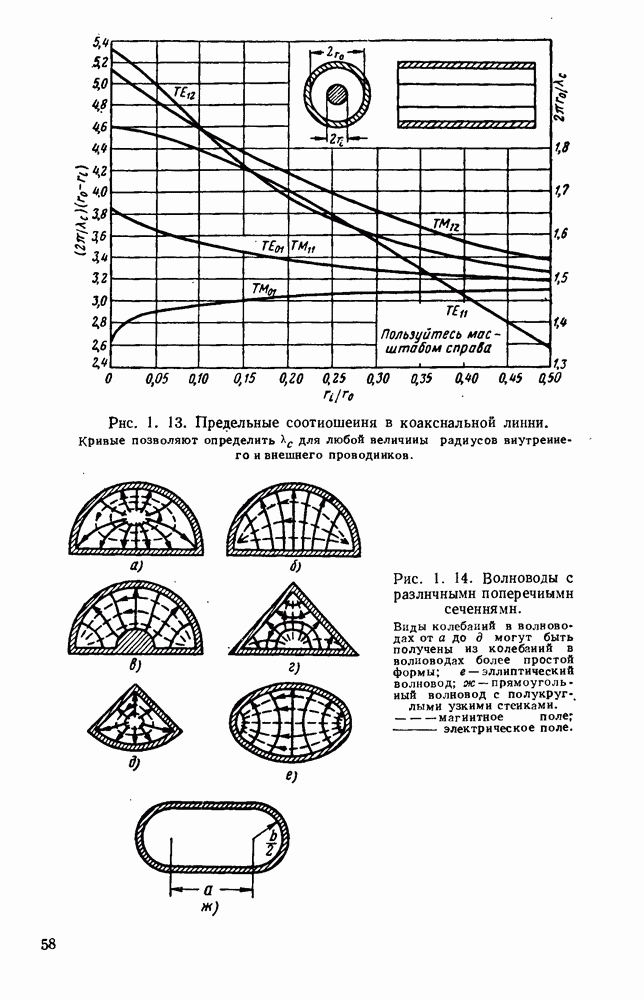
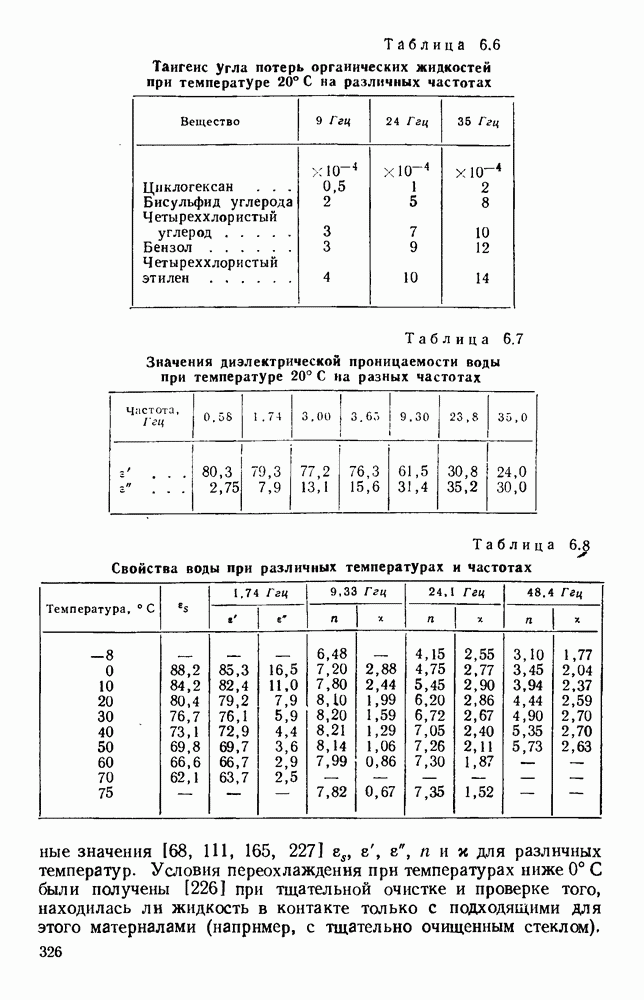
Полученная величина [89] нормированной проводимости, представляющая собой действие ступенчатой неоднородности, позволяет вычислить критические длины волн. Величины  для колебаний вида
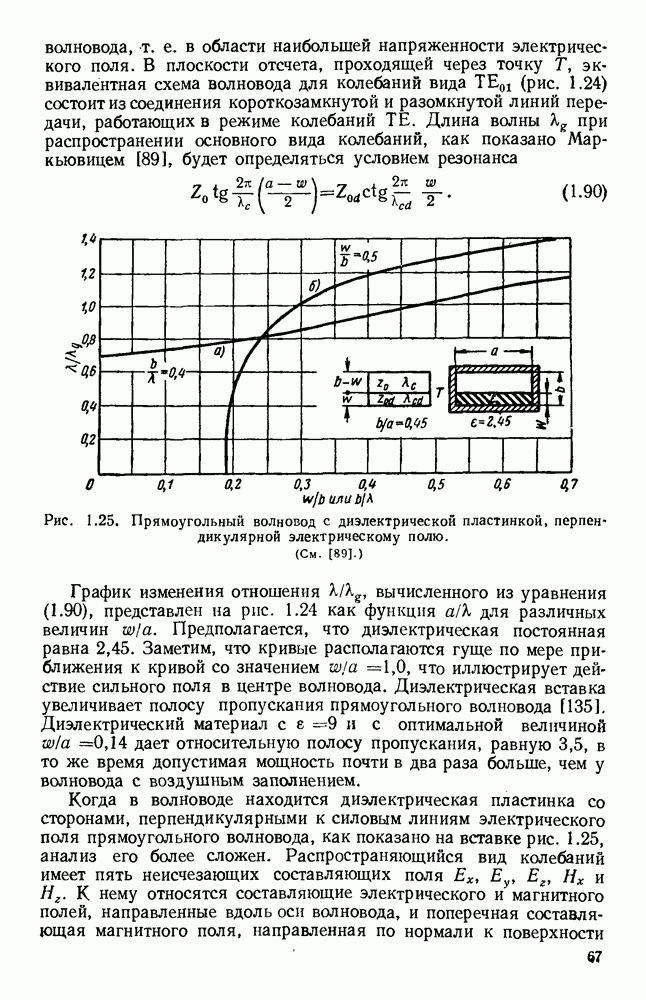
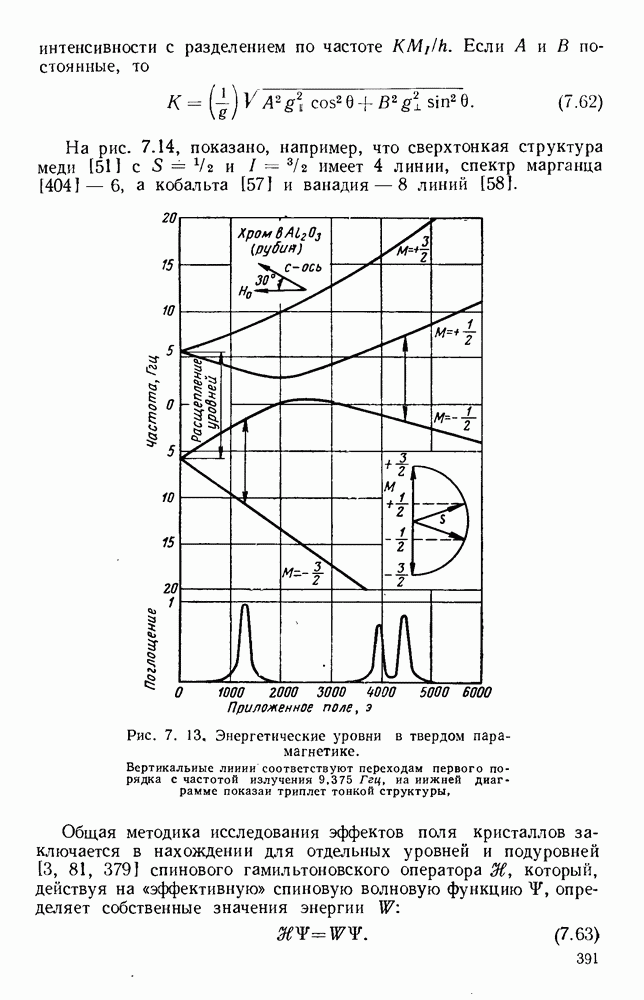
для колебаний вида  графически представлены на рис. 1.16; кривые построены для Н-образного волновода с отношением
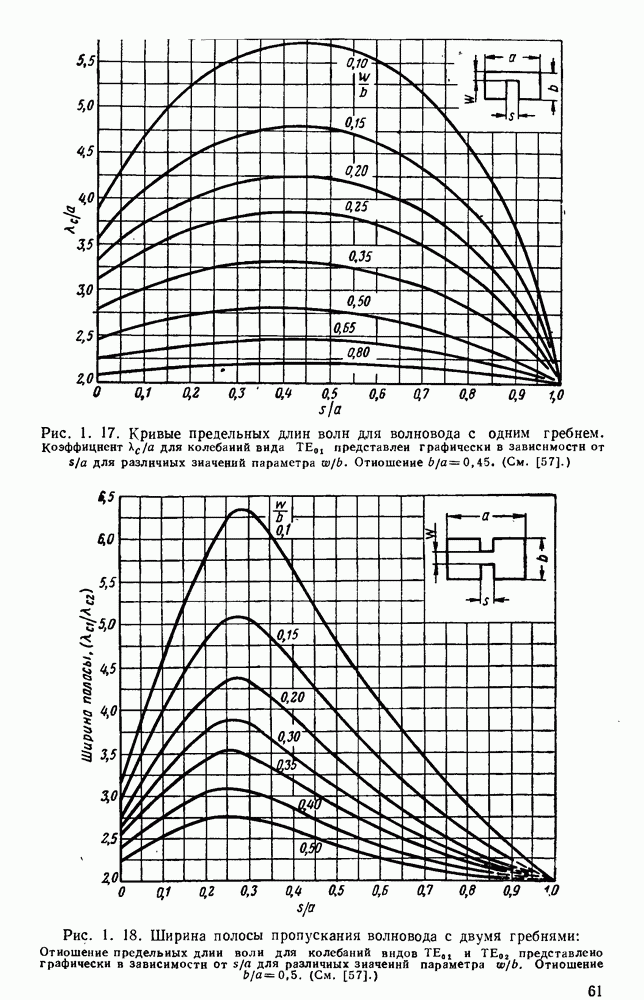
графически представлены на рис. 1.16; кривые построены для Н-образного волновода с отношением  равным 0,5. Графики для П-образного волновода, но с отношением
равным 0,5. Графики для П-образного волновода, но с отношением  равным 0,45, приведены на рис. 1.17.
равным 0,45, приведены на рис. 1.17.
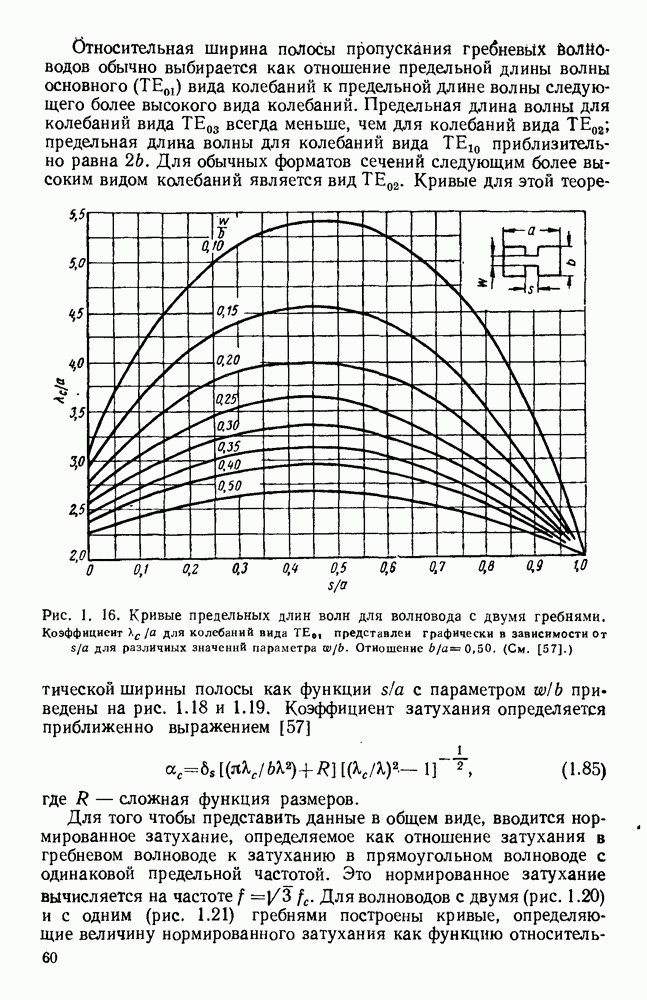
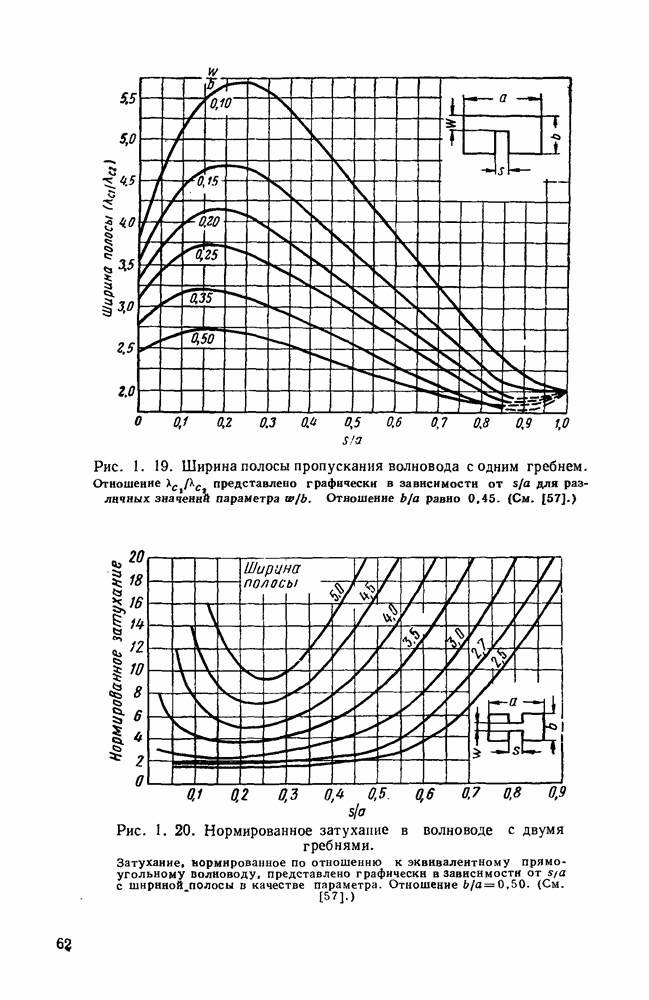
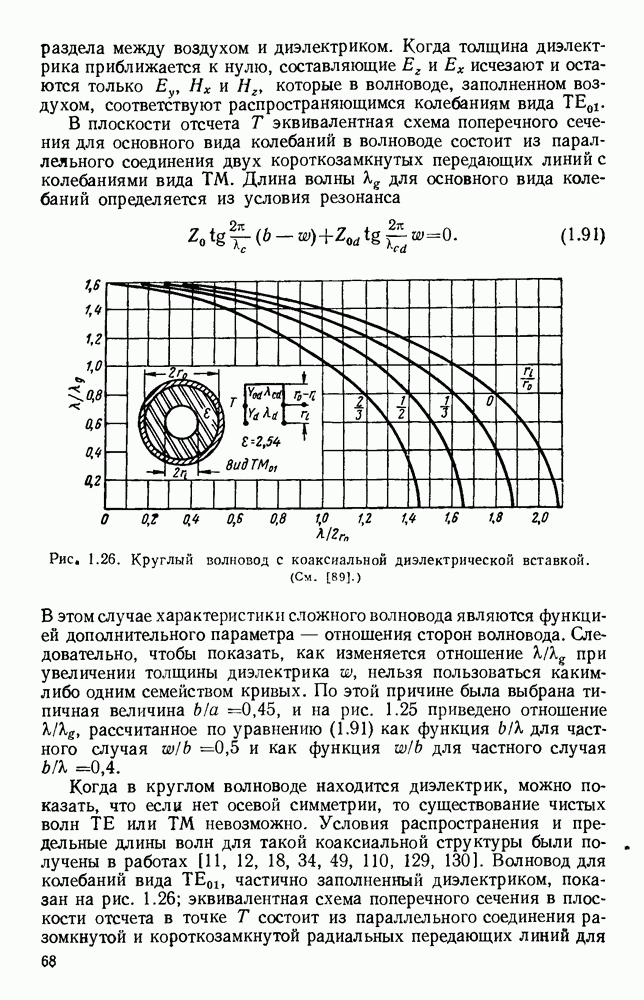
Относительная ширина полосы пропускания гребневых волноводов обычно выбирается как отношение предельной длины волны основного  вида колебаний к предельной длине волны следующего более высокого вида колебаний. Предельная длина волны для колебаний вида
вида колебаний к предельной длине волны следующего более высокого вида колебаний. Предельная длина волны для колебаний вида  всегда меньше, чем для колебаний вида
всегда меньше, чем для колебаний вида  предельная длина волны для колебаний вида
предельная длина волны для колебаний вида  приблизительно равна
приблизительно равна  Для обычных форматов сечений следующим более высоким видом колебаний является вид
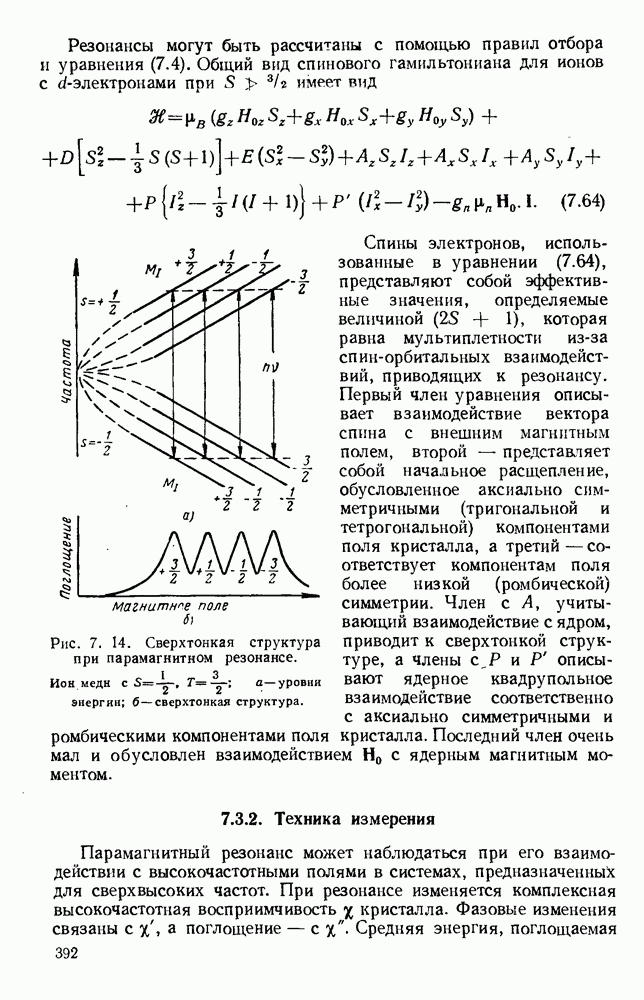
Для обычных форматов сечений следующим более высоким видом колебаний является вид  Кривые для этой теоретической ширины полосы как функции
Кривые для этой теоретической ширины полосы как функции  с параметром
с параметром  при ведены на рис. 1.18 и 1.19.
при ведены на рис. 1.18 и 1.19.

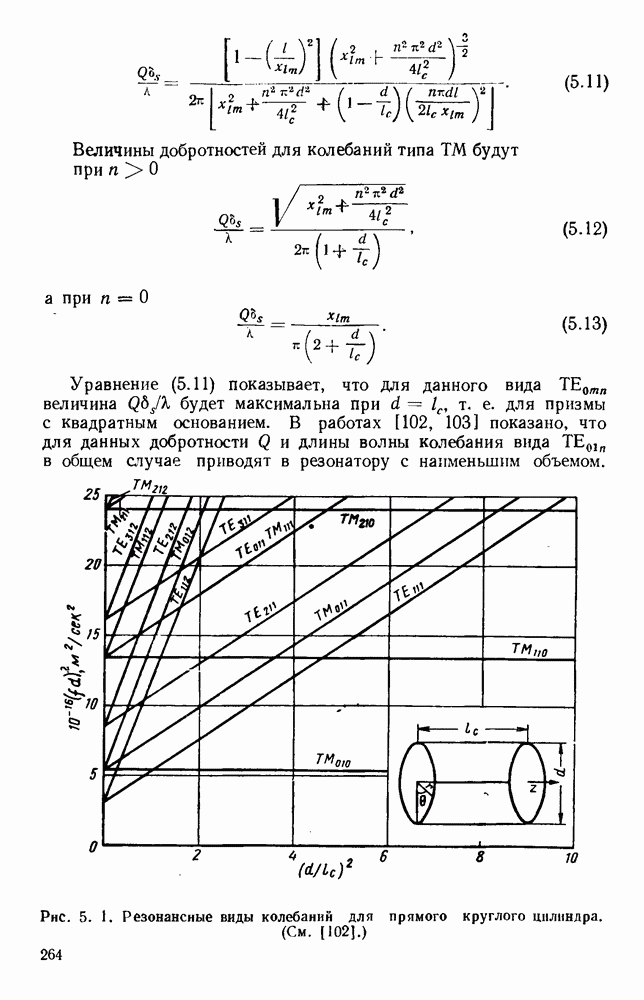
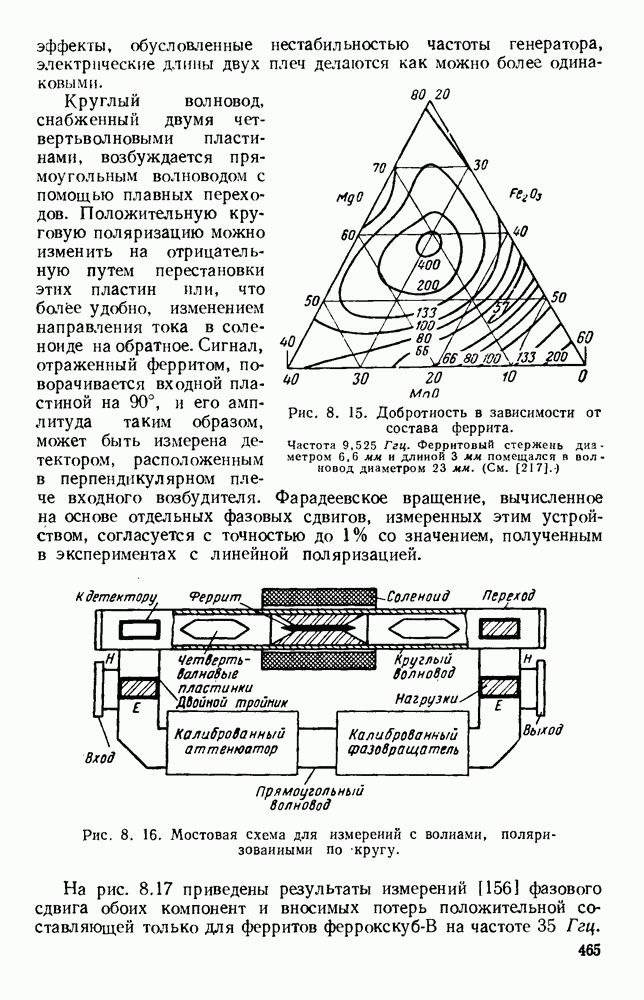
Рис. 1. 16. Кривые предельных длин волн для волновода с двумя гребнями. Коэффициент  для колебаний вида
для колебаний вида  представлен графически в зависимости от
представлен графически в зависимости от  для различных значений параметра
для различных значений параметра  Отношение
Отношение  (См. [57].)
(См. [57].)
Коэффициент затухания определяется приближенно выражением [57]

где  сложная функция размеров.
сложная функция размеров.
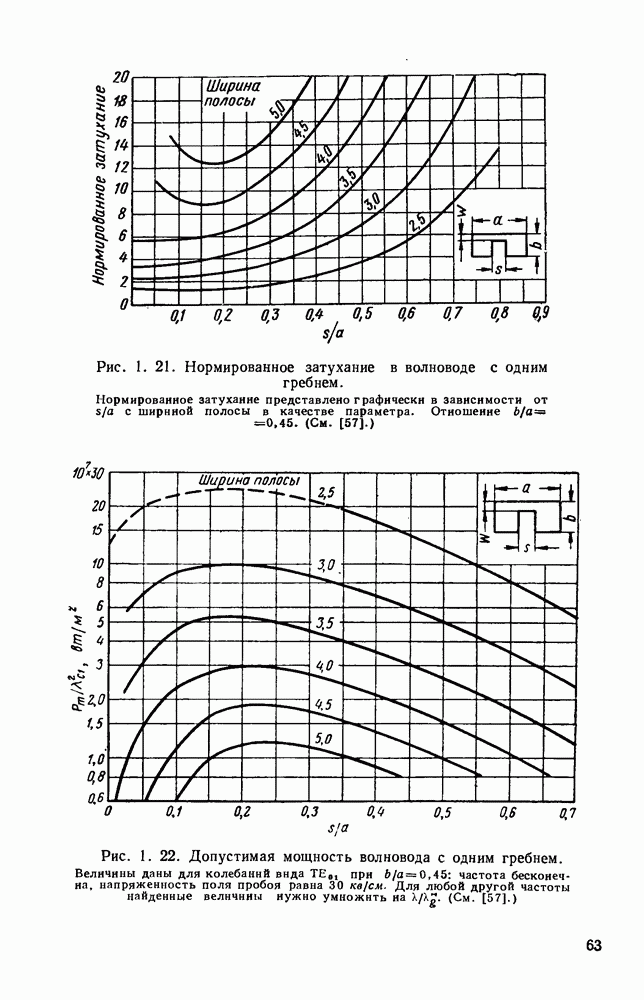
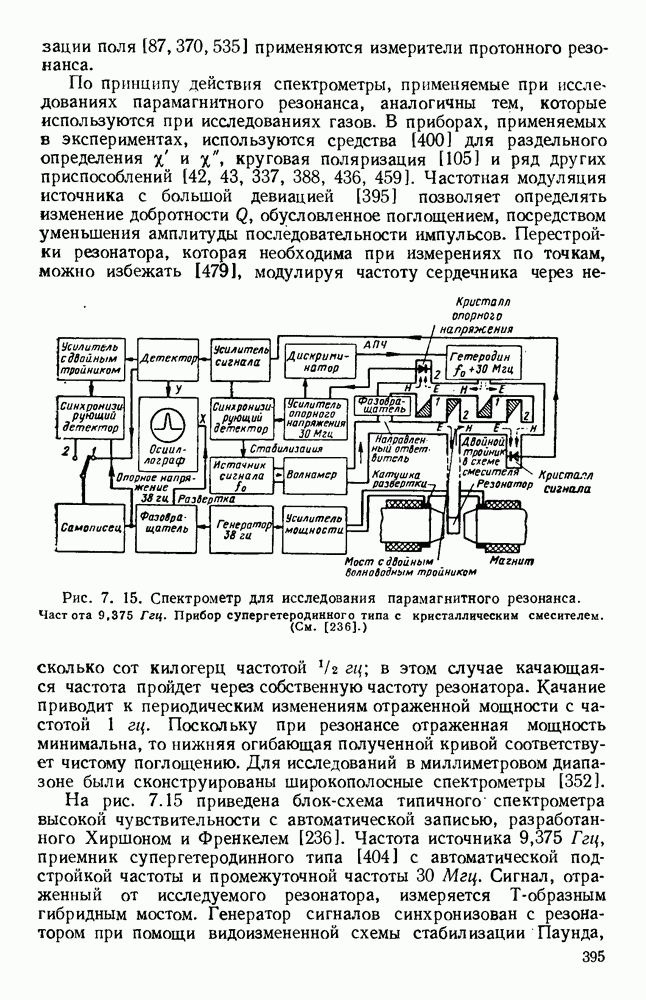
Для того чтобы представить данные в общем виде, вводится нормированное затухание, определяемое как отношение затухания в гребневом волноводе к затуханию в прямоугольном волноводе с одинаковой предельной частотой. Это нормированное затухание вычисляется на частоте  Для волноводов с двумя (рис. 1.20) и с одним (рис. 1.21) гребнями построены кривые, определяющие величину нормированного затухания как функцию
Для волноводов с двумя (рис. 1.20) и с одним (рис. 1.21) гребнями построены кривые, определяющие величину нормированного затухания как функцию

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)
относительной ширины полосы пропускания и отношения  Затухание для прямоугольного волновода уже было дано на рис. 1,8. Допустимая мощность для гребневого волновода [571;
Затухание для прямоугольного волновода уже было дано на рис. 1,8. Допустимая мощность для гребневого волновода [571;

где Т — сложная функция геометрии волновода, а  относится к центру гребня.
относится к центру гребня.

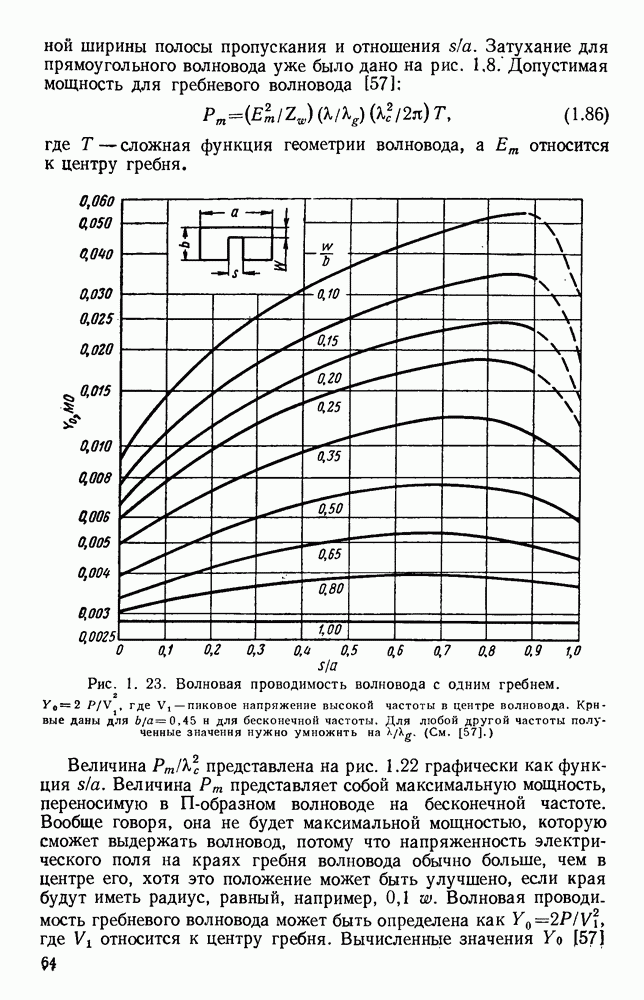
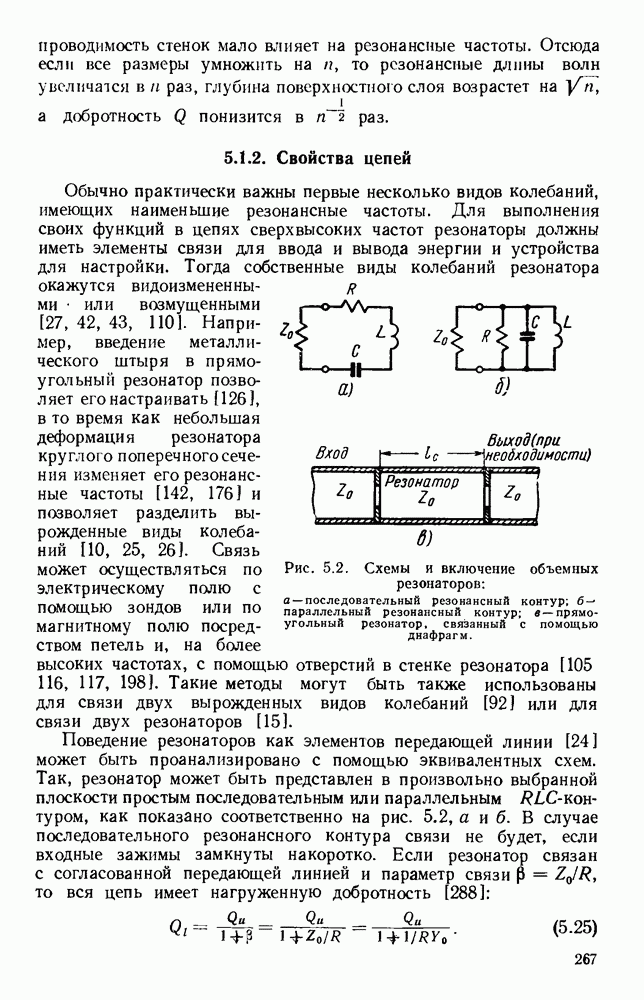
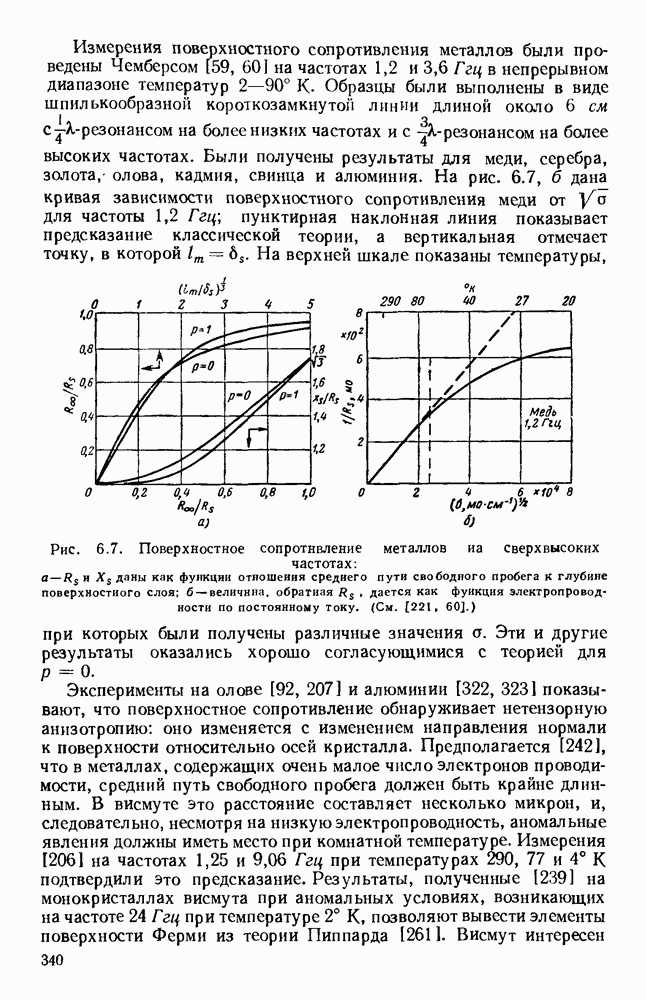
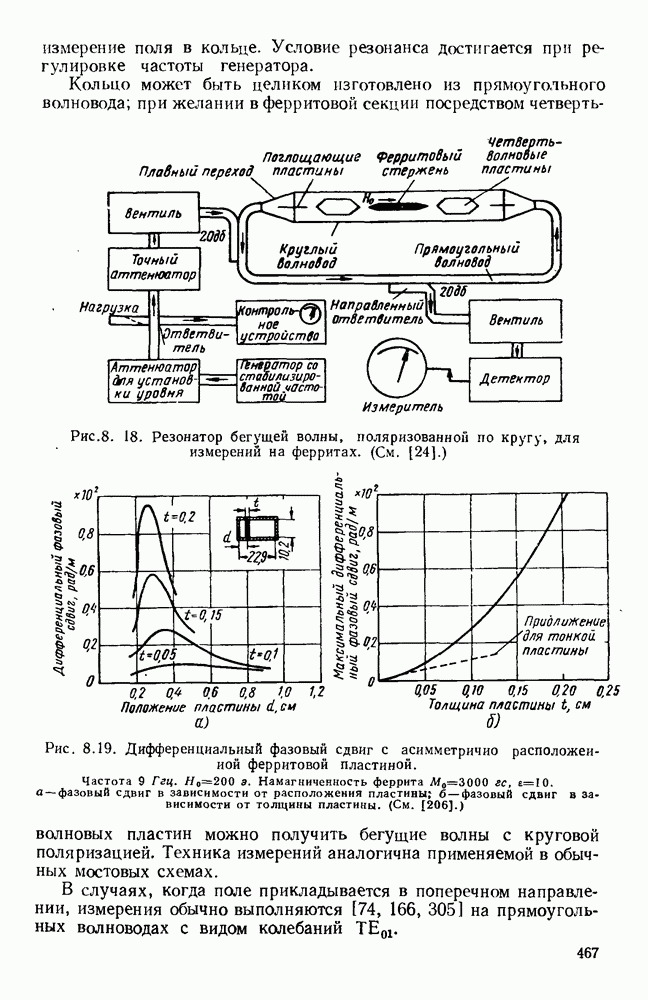
Рис. 1. 23. Волновая проводимость волновода с одним гребнем.  где
где  пиковое напряжение высокой частоты в центре волновода. Кривые даны для
пиковое напряжение высокой частоты в центре волновода. Кривые даны для  и для бесконечной частоты. Для любой другой частоты полученные значения нужно умножить на
и для бесконечной частоты. Для любой другой частоты полученные значения нужно умножить на  (См, [57].)
(См, [57].)
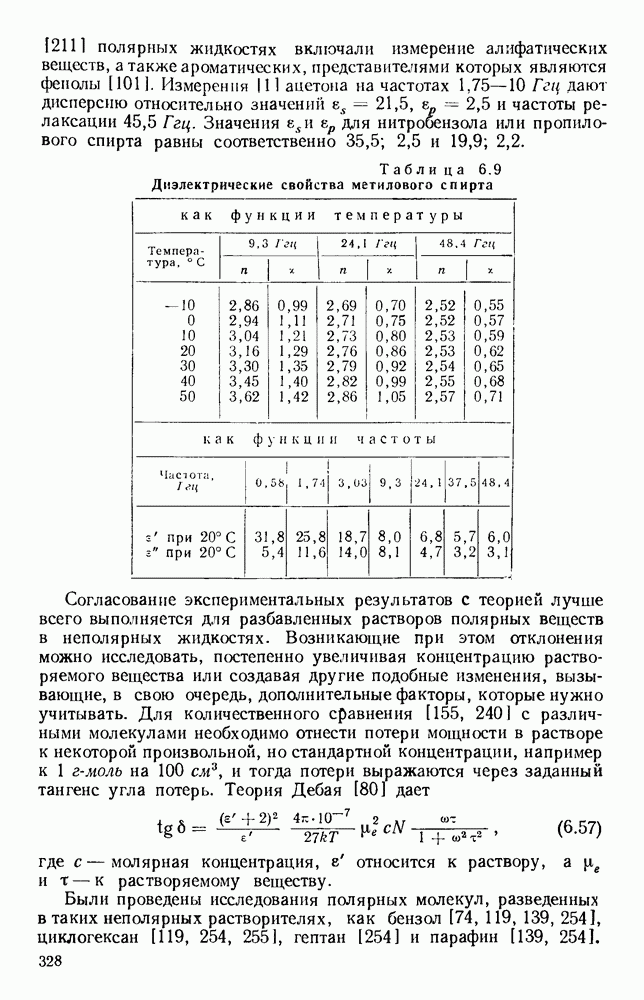
Величина  представлена на рис. 1.22 графически как функция
представлена на рис. 1.22 графически как функция  Величина
Величина  представляет собой максимальную мощность, переносимую в П-образном волноводе на бесконечной частоте. Вообще говоря, она не будет максимальной мощностью, которую сможет выдержать волновод, потому что напряженность электрического поля на краях гребня волновода обычно больше, чем в центре его, хотя это положение может быть улучшено, если края будут иметь радиус, равный, например,
представляет собой максимальную мощность, переносимую в П-образном волноводе на бесконечной частоте. Вообще говоря, она не будет максимальной мощностью, которую сможет выдержать волновод, потому что напряженность электрического поля на краях гребня волновода обычно больше, чем в центре его, хотя это положение может быть улучшено, если края будут иметь радиус, равный, например,  Волновая проводи, мость гребневого волновода может быть определена как
Волновая проводи, мость гребневого волновода может быть определена как  где
где  относится к центру гребня. Вычисленные значения
относится к центру гребня. Вычисленные значения  [57]
[57]
представлены графически на рис. 1.23. Значения проводимостей соответствуют бесконечной частоте и, для того, чтобы получить правильную величину, их необходимо умножить на коэффициент 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
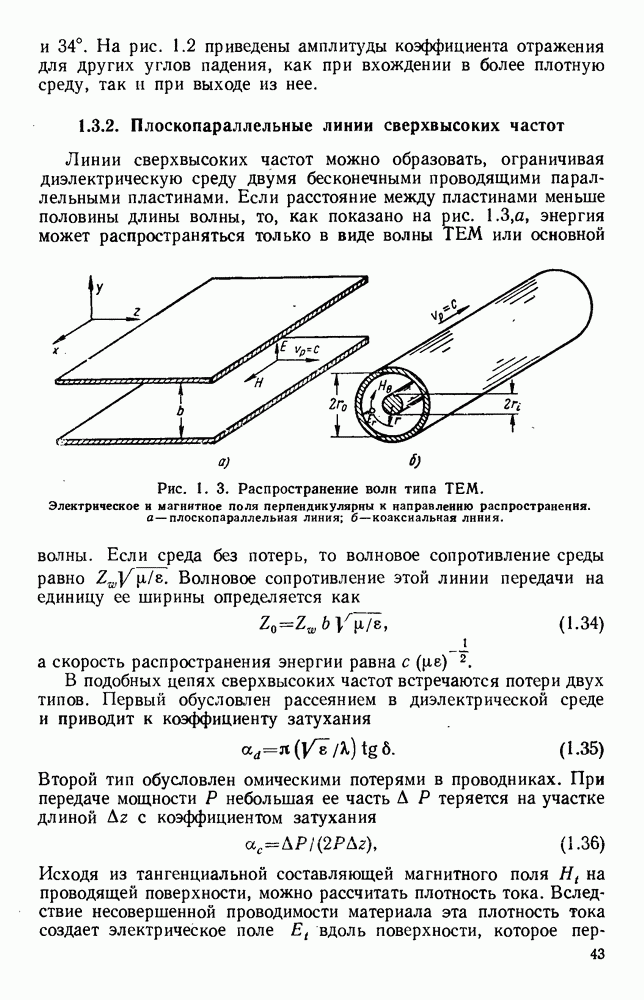
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
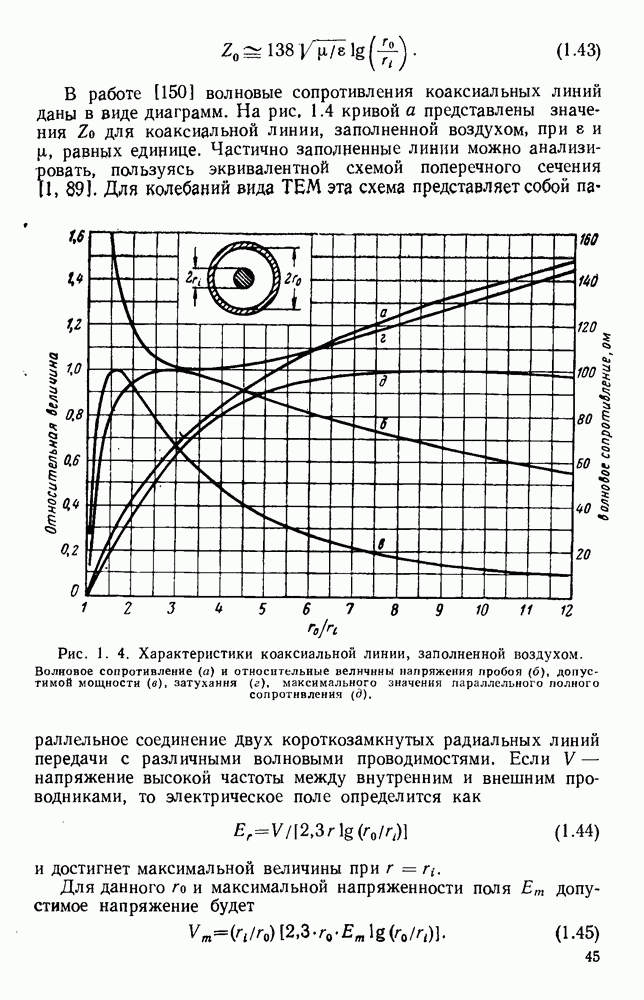
- 1.3.3. Коаксиальные линии
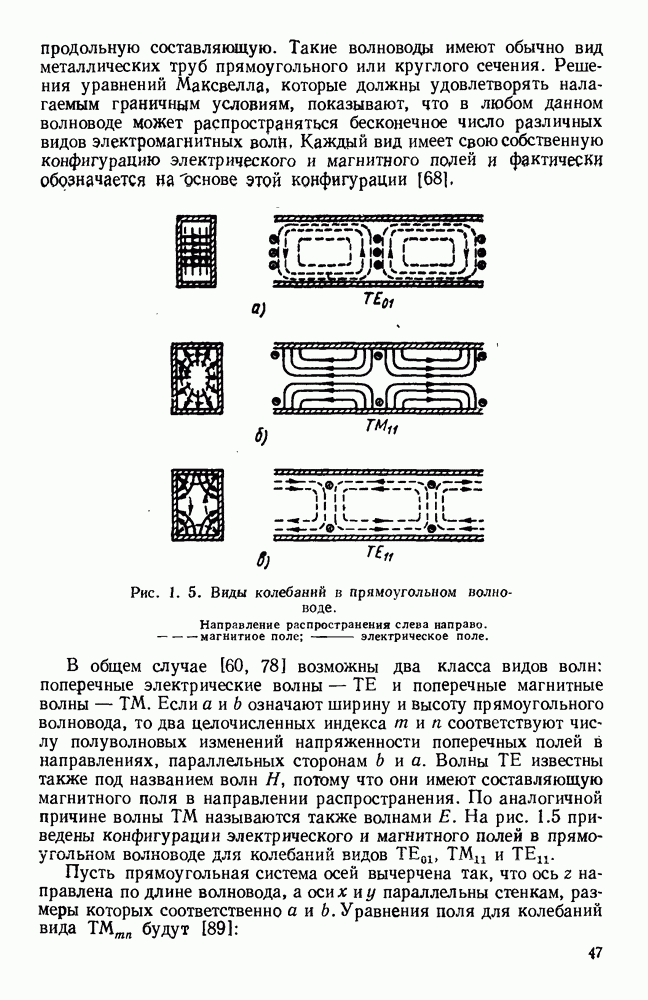
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
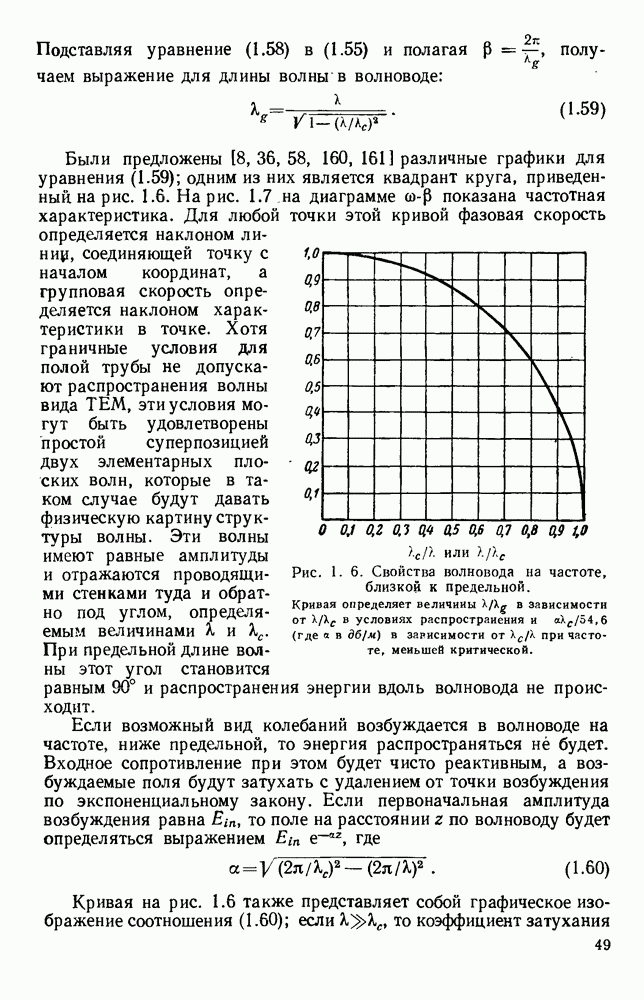
- 1.4.2. Круглые волноводы
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
- 1.5.2. Гребневые волноводы
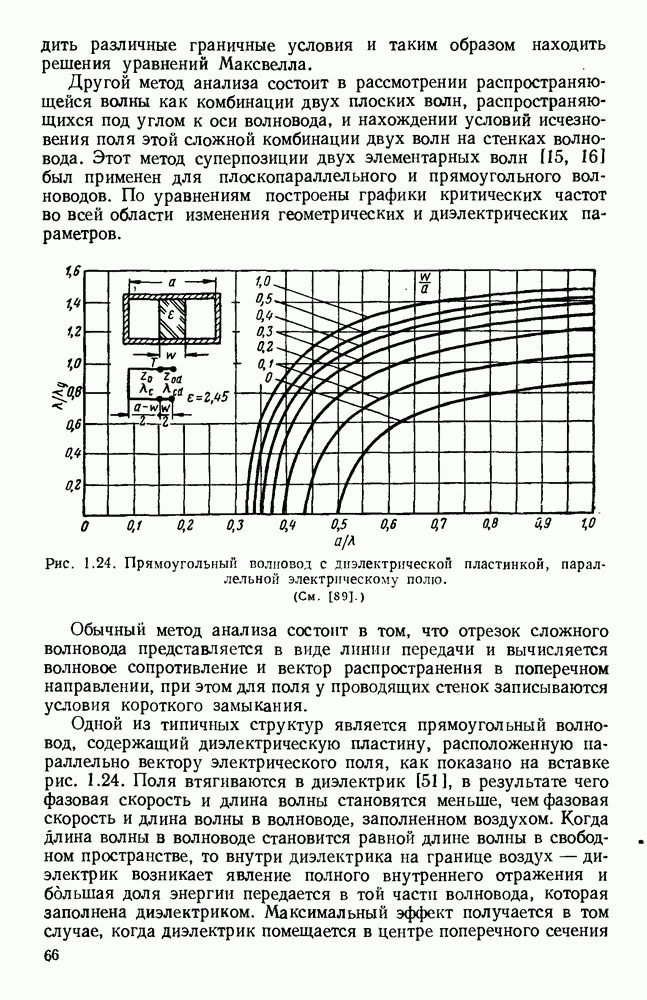
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
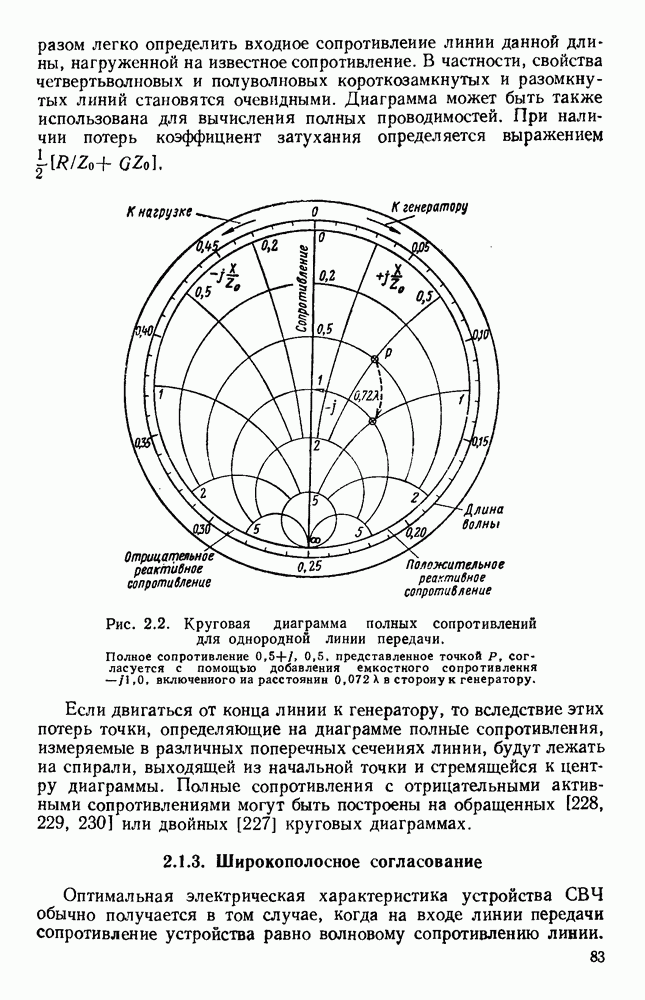
- 2.1.2. Круговая диаграмма
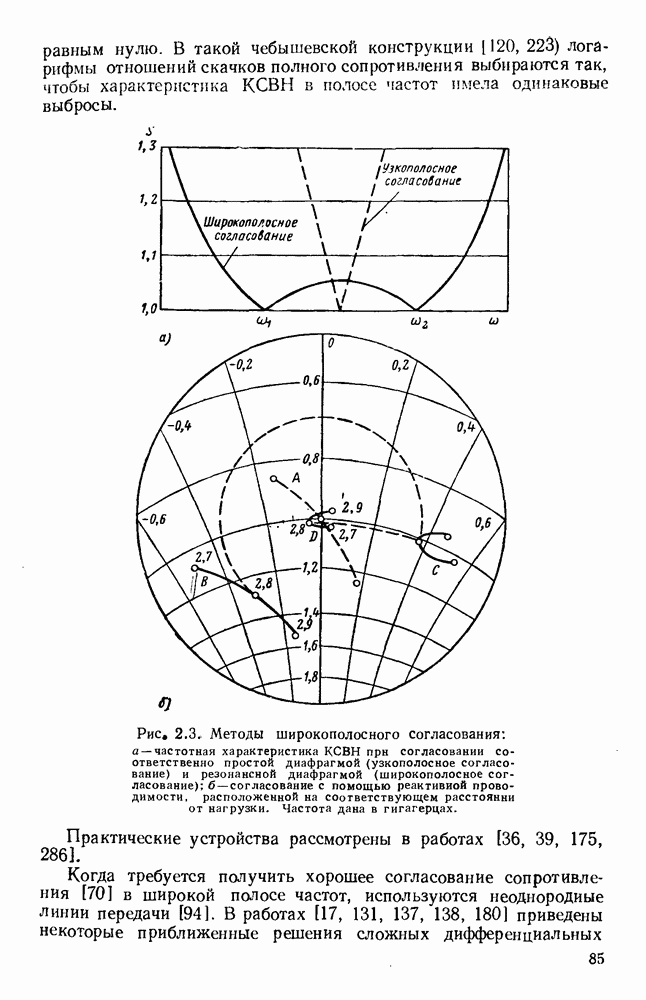
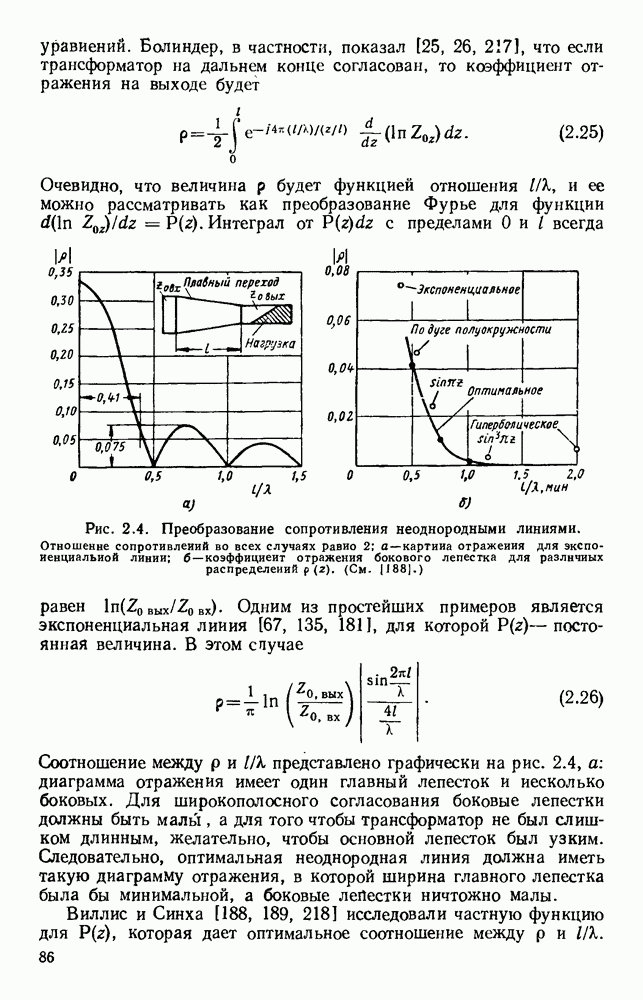
- 2.1.3. Широкополосное согласование
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
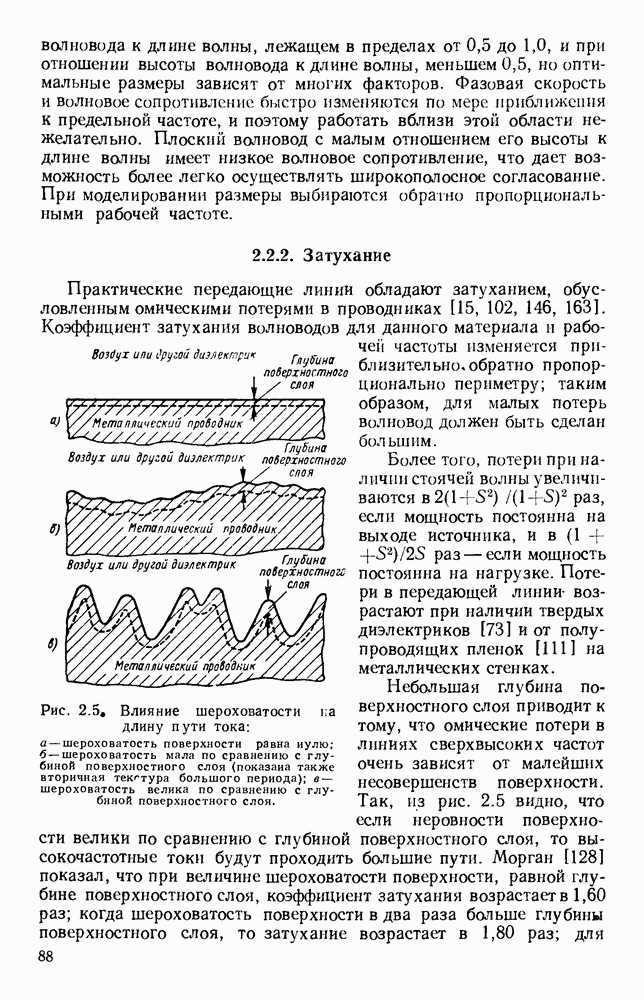
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
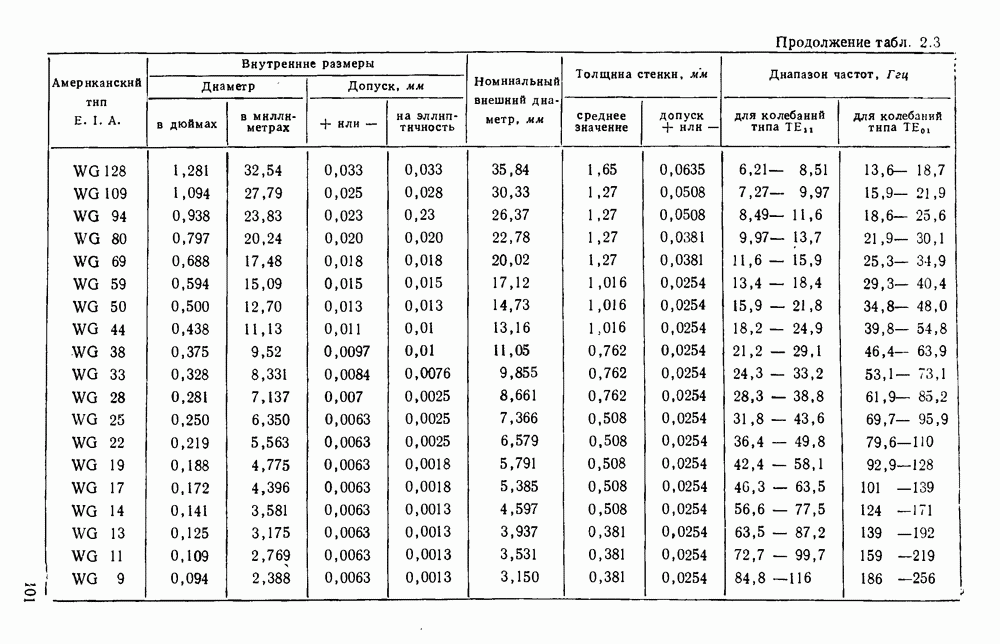
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
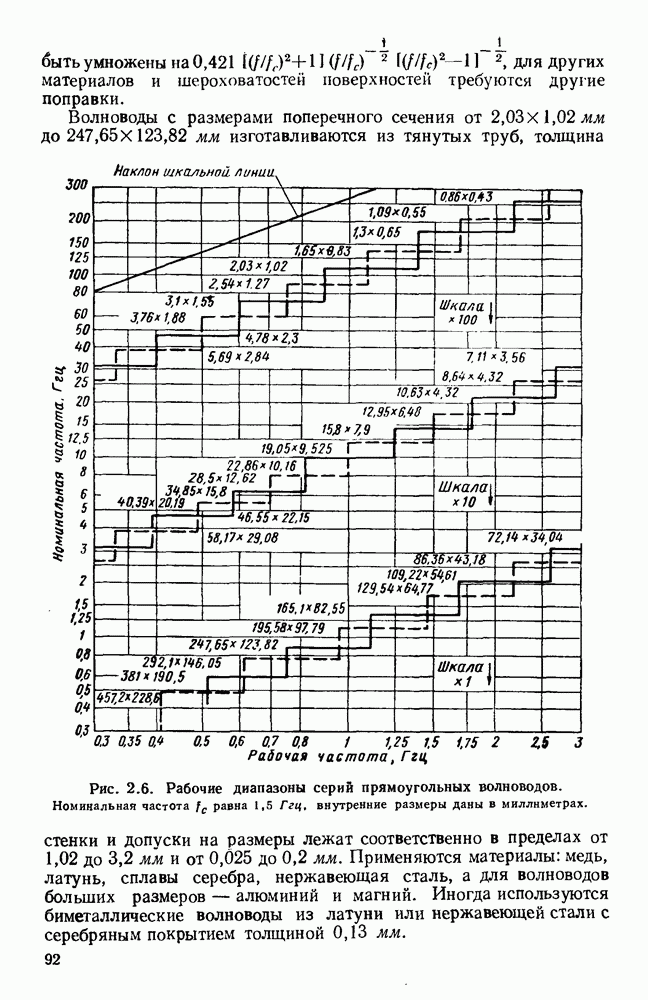
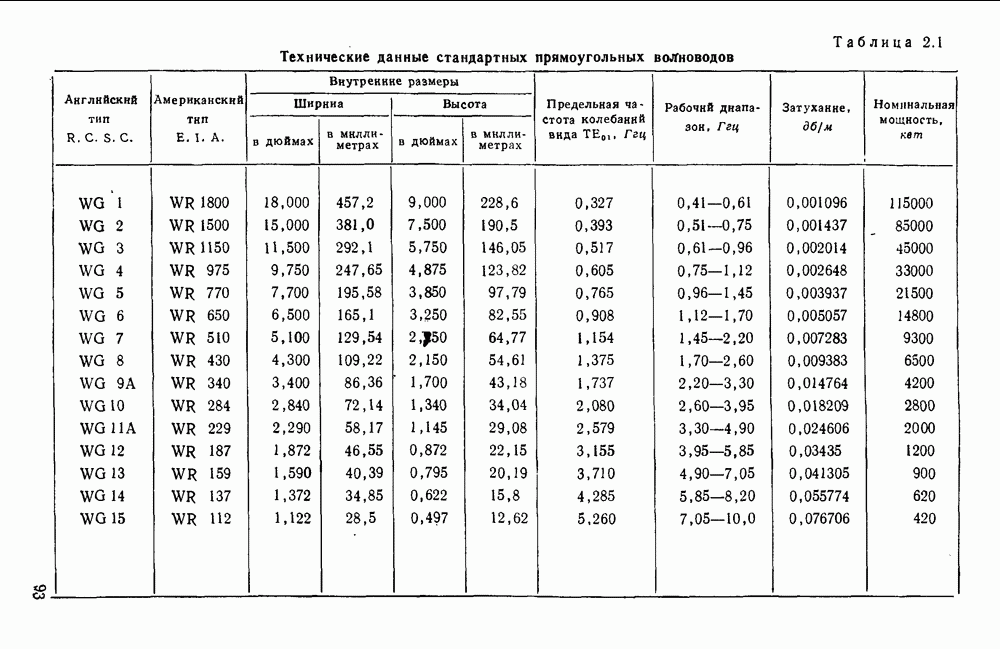
- 2.3.1. Прямоугольные волноводы
- 2.3.2. Круглые волноводы
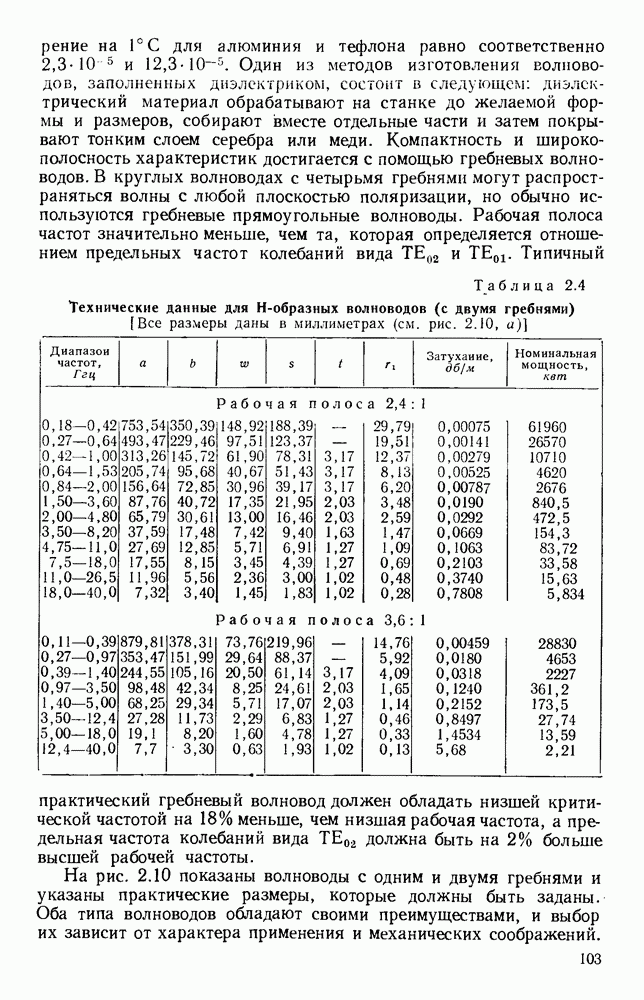
- 2.3.3. Широкополосные и компактные волноводы
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
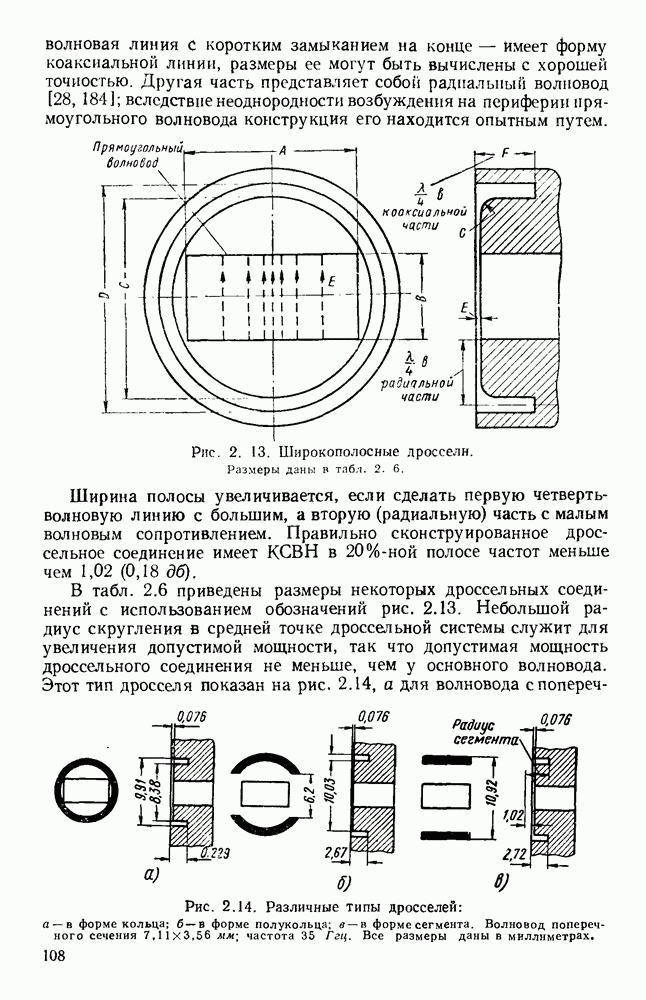
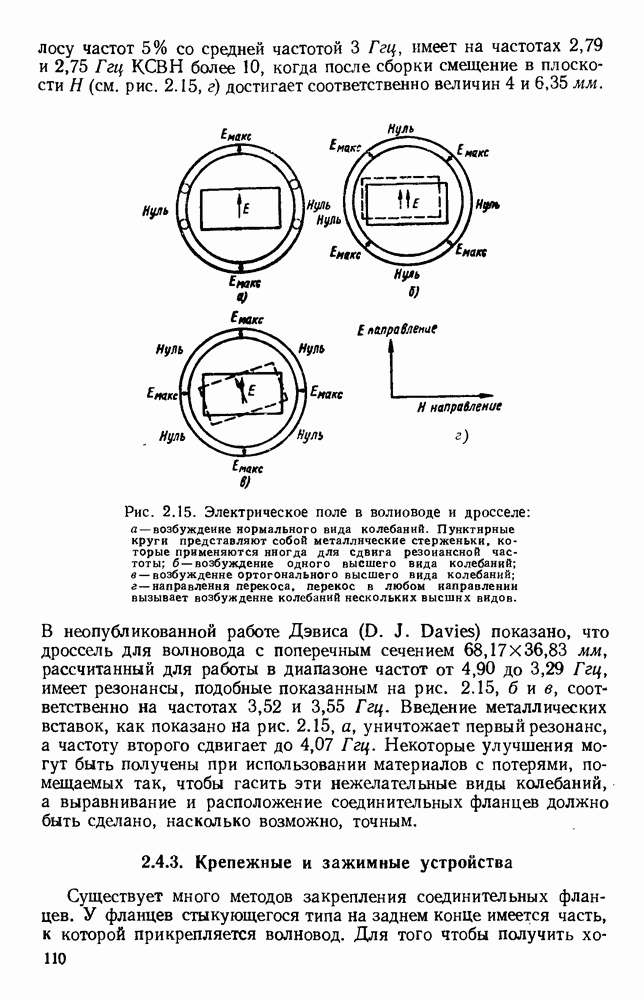
- 2.4.2. Контактные прокладки и дроссели
- 2.4.3. Крепежные и зажимные устройства
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
- 2.6.1. Изгибы, уголки и скрутки
- 2.6.2. Переходы и преобразователи
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
- 3.2.3. Переход от линейной поляризации к круговой
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
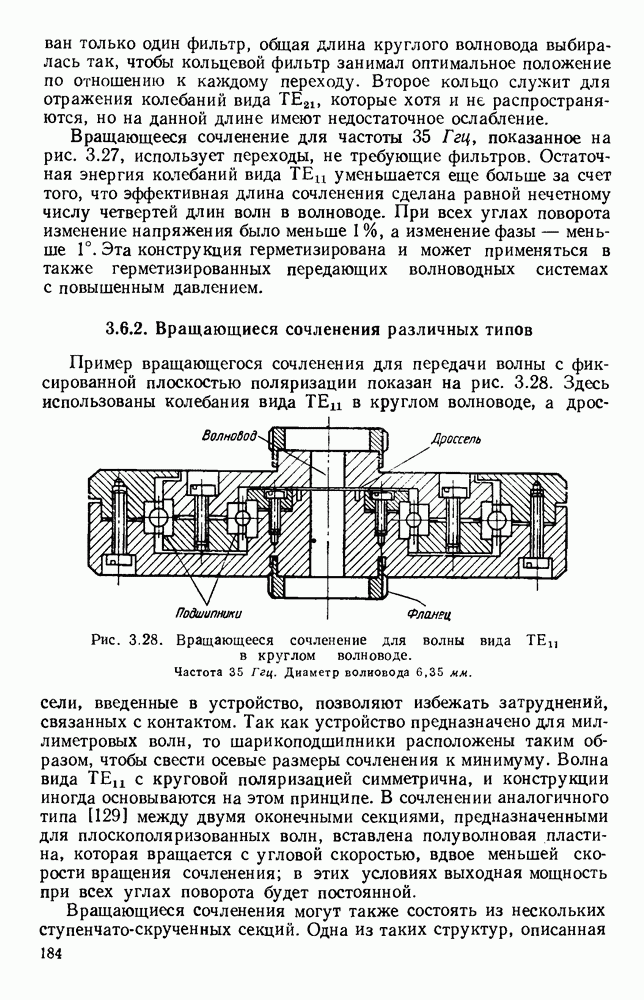
- 3.6.2. Вращающиеся сочленения различных типов
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
- 3.7.1. Механические переключатели с ручным управлением
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
- 5.2.1. Волномеры с объемными резонаторами
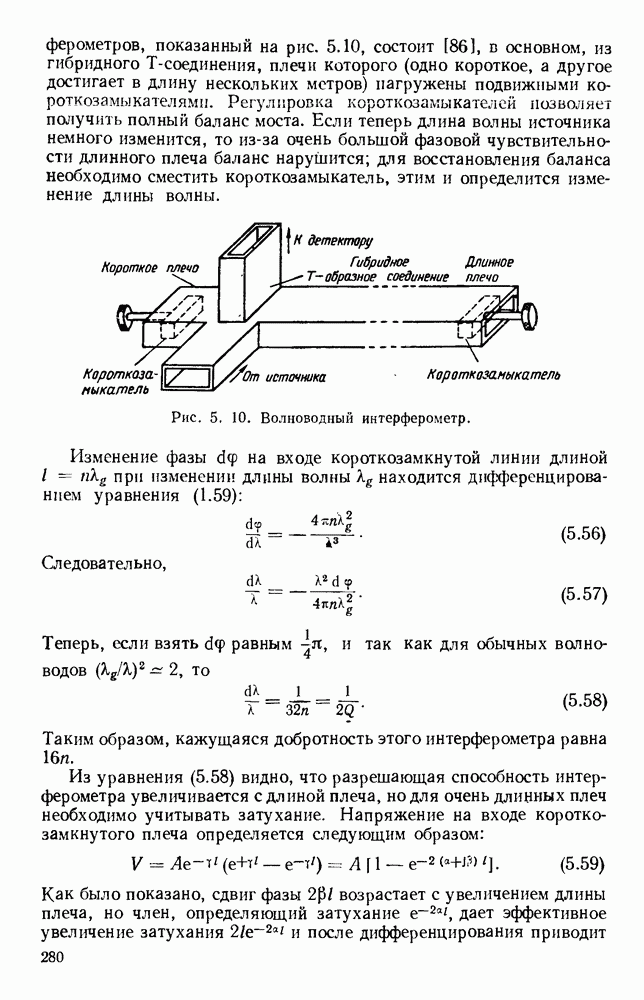
- 5.2.2. Волноводные интерферометры
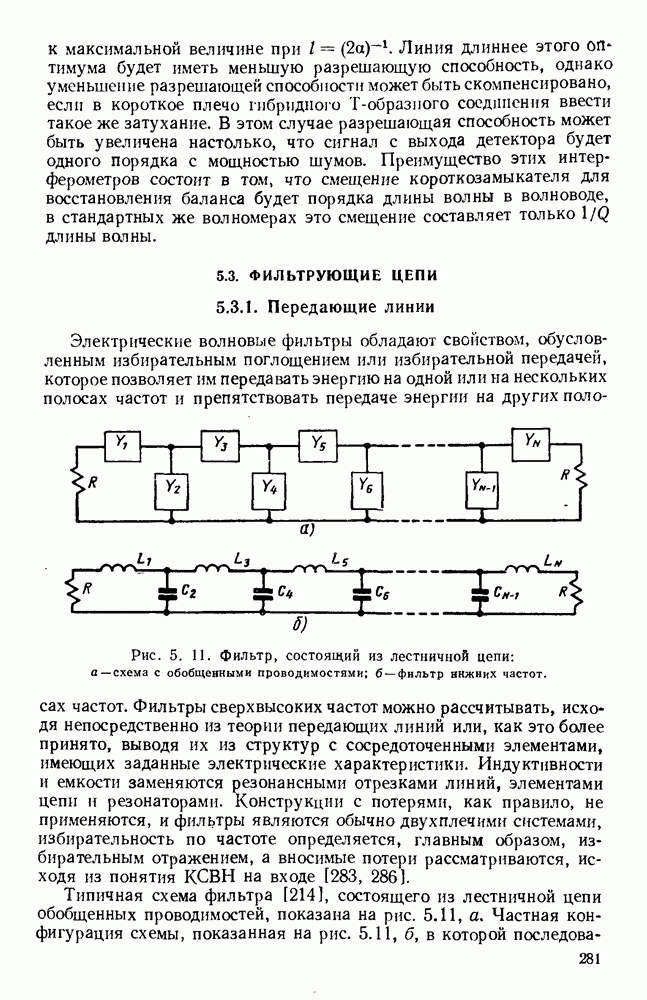
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
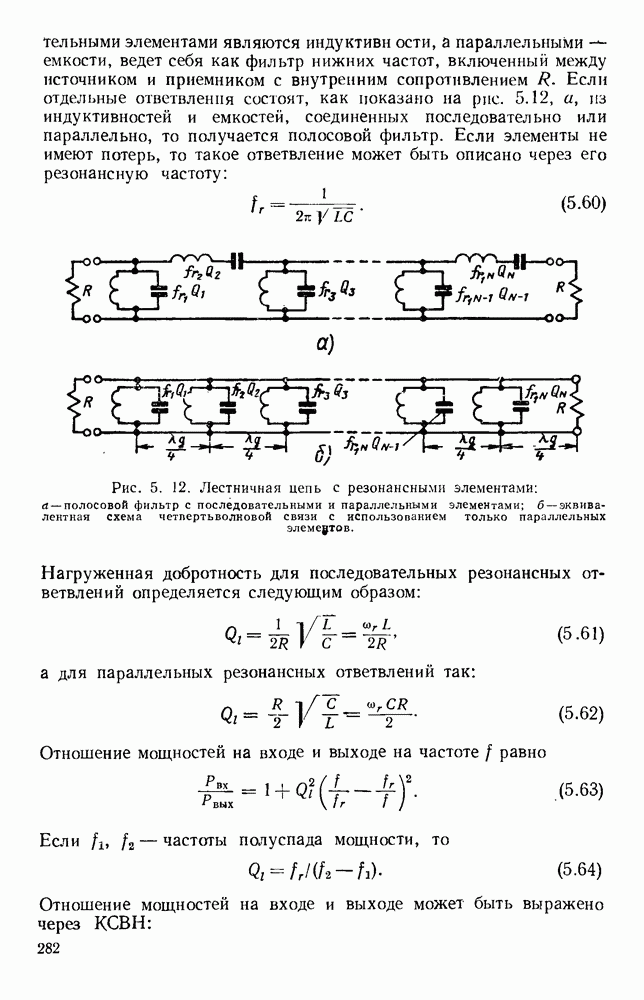
- 5.3.2. Связанные резонаторы
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
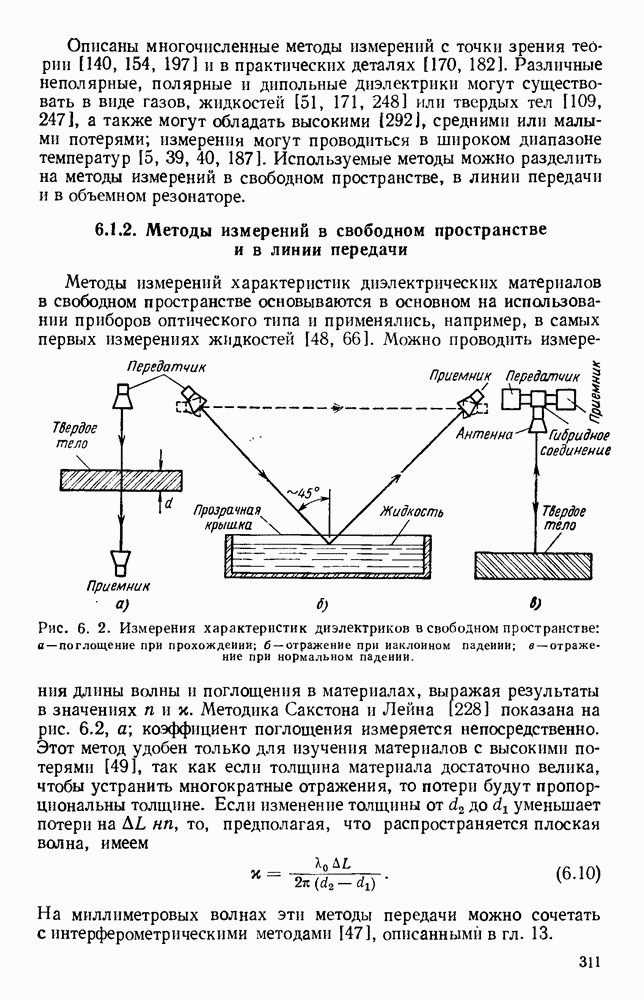
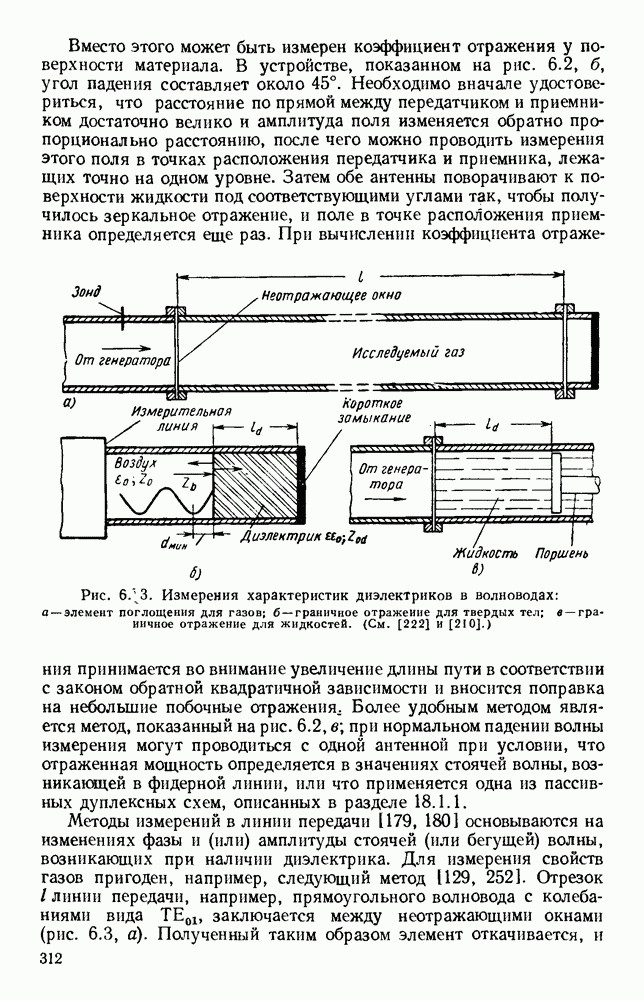
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
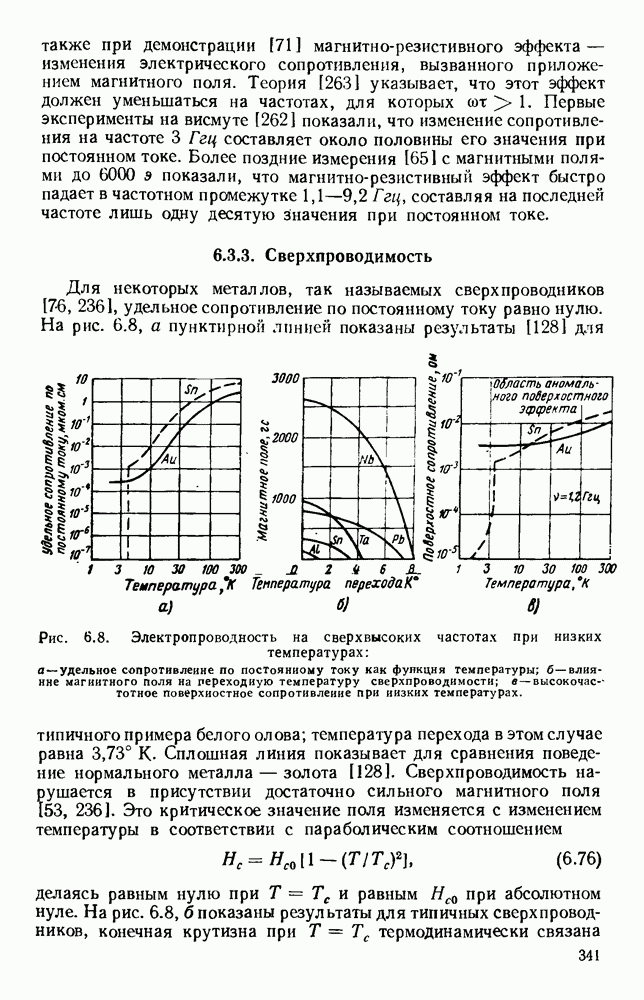
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
- 7.1.2. Форма линии и интенсивность
- 7.1.3. Сверхтонкая структура
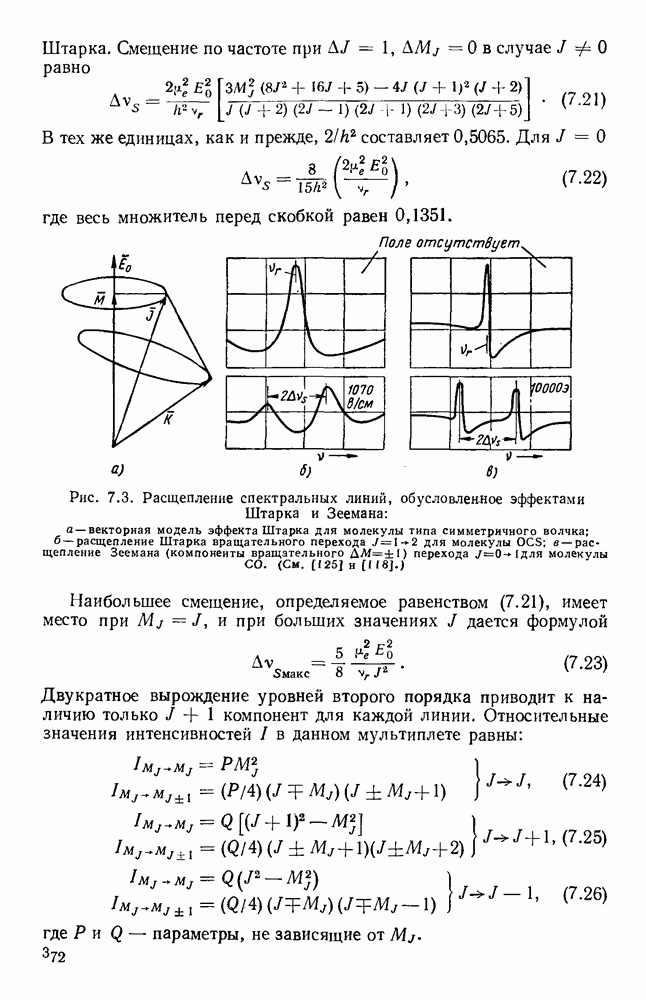
- 7.1.4. Явления Штарка и Зеемана
- 7.2. СПЕКТРОМЕТРЫ
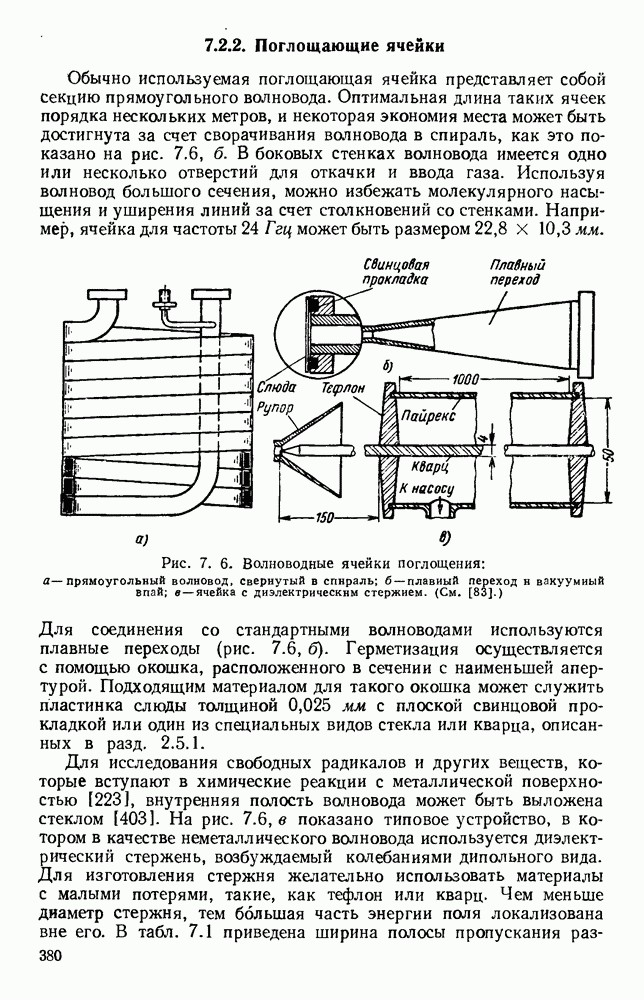
- 7.2.2. Поглощающие ячейки
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
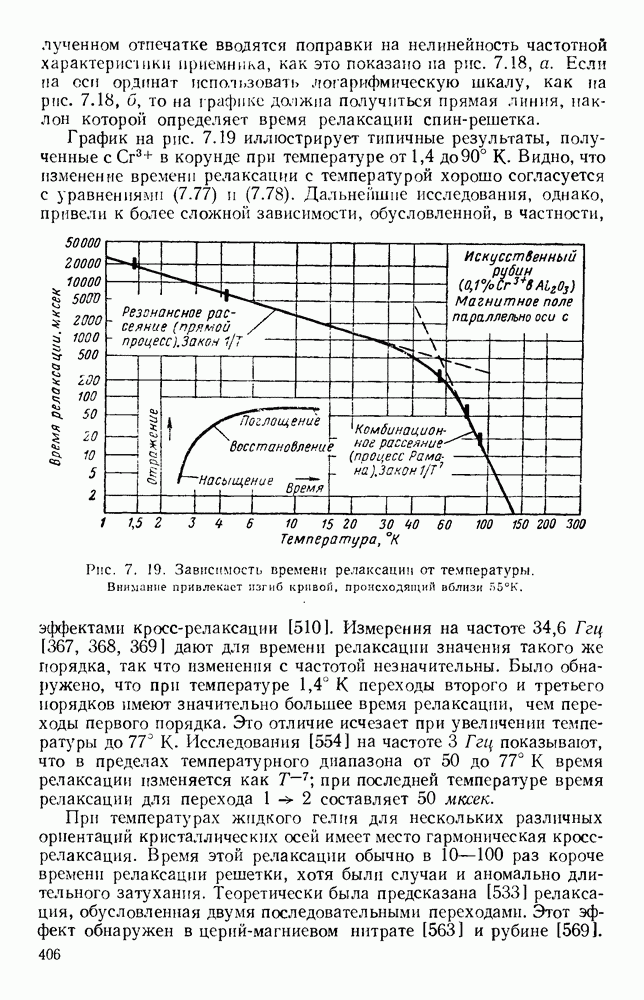
- 7.3.4. Времена релаксации
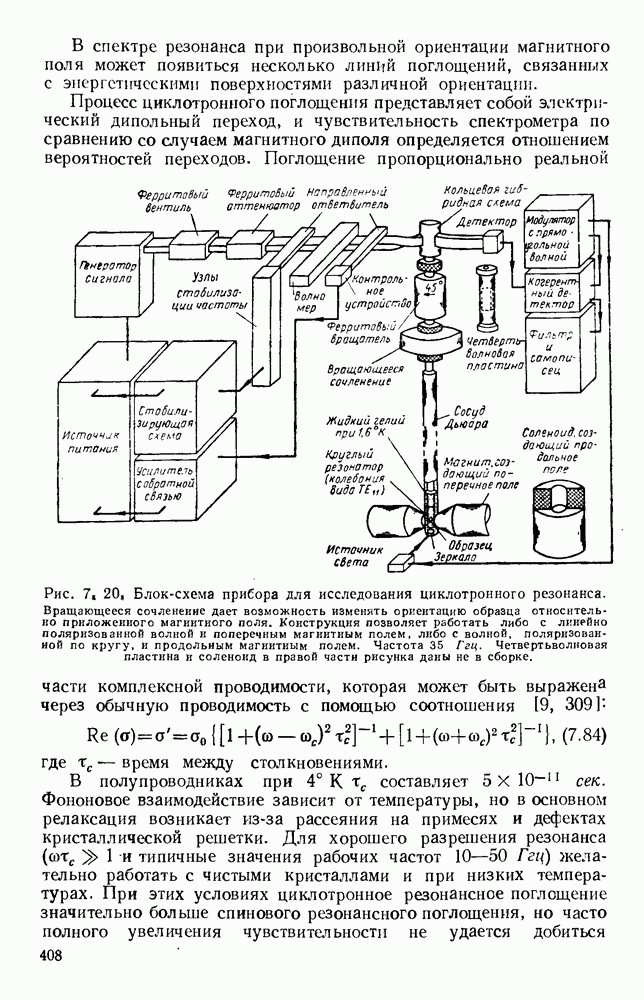
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
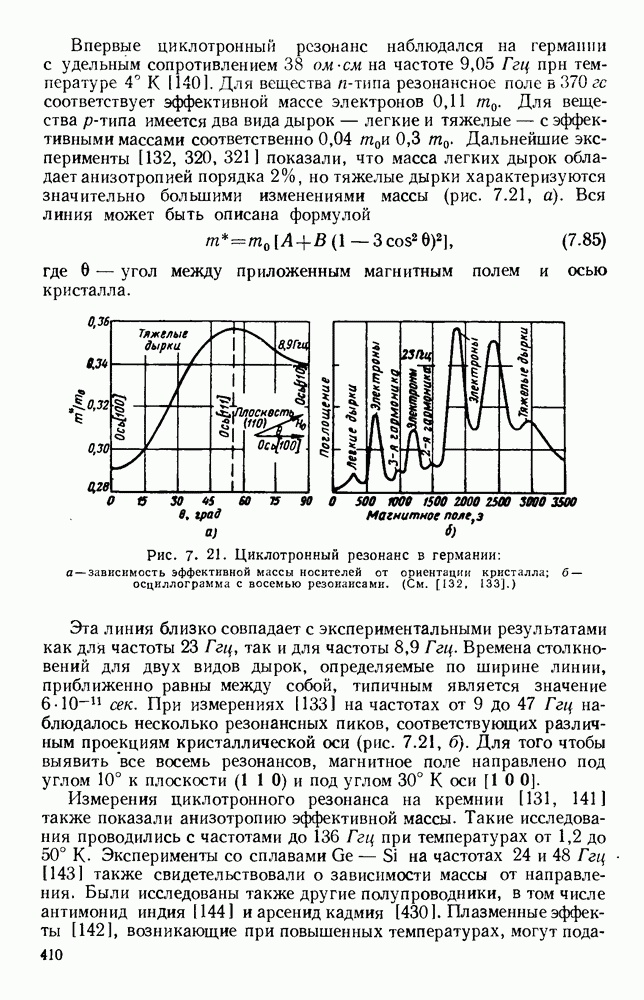
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
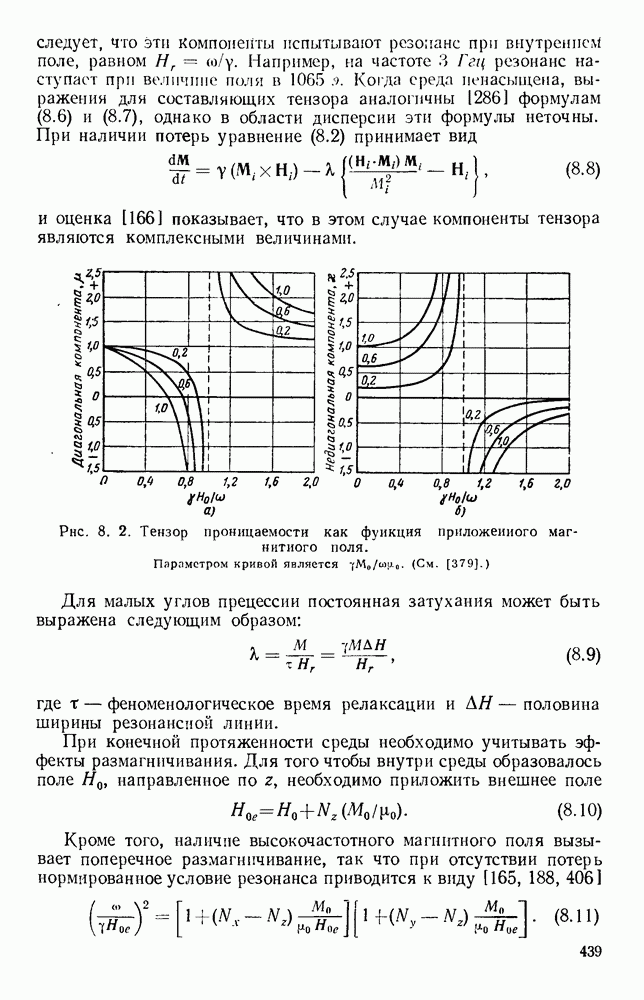
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
- 8.3.3. Ферритовые устройства в качестве элементов схем
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
- 8.6.2. Устройства с поперечным полем
- 8.6.3. Прочие узлы
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
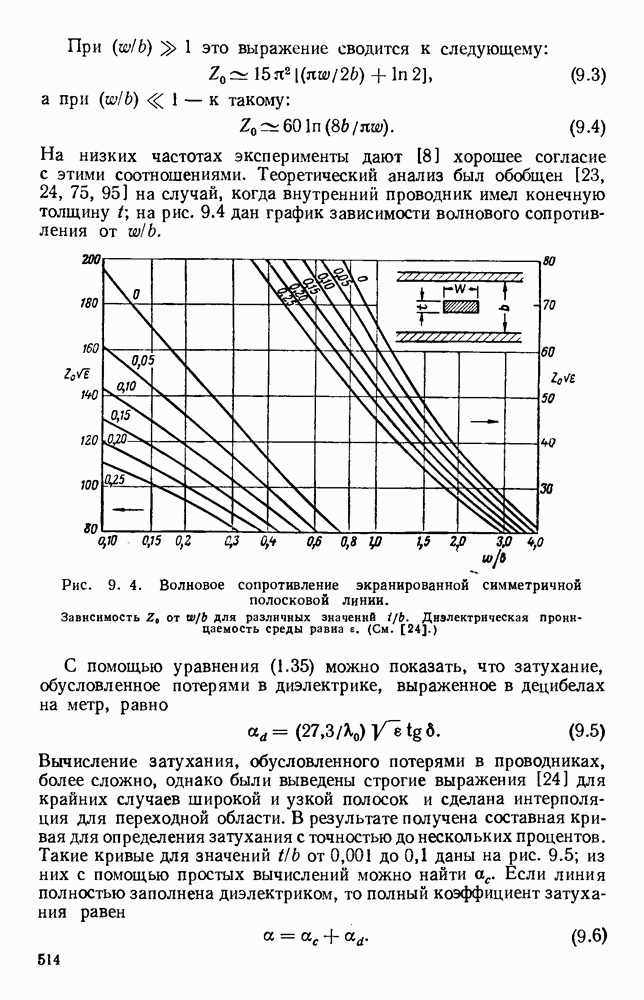
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.2.1. Линии типа «диэлектрических сэндвичей»
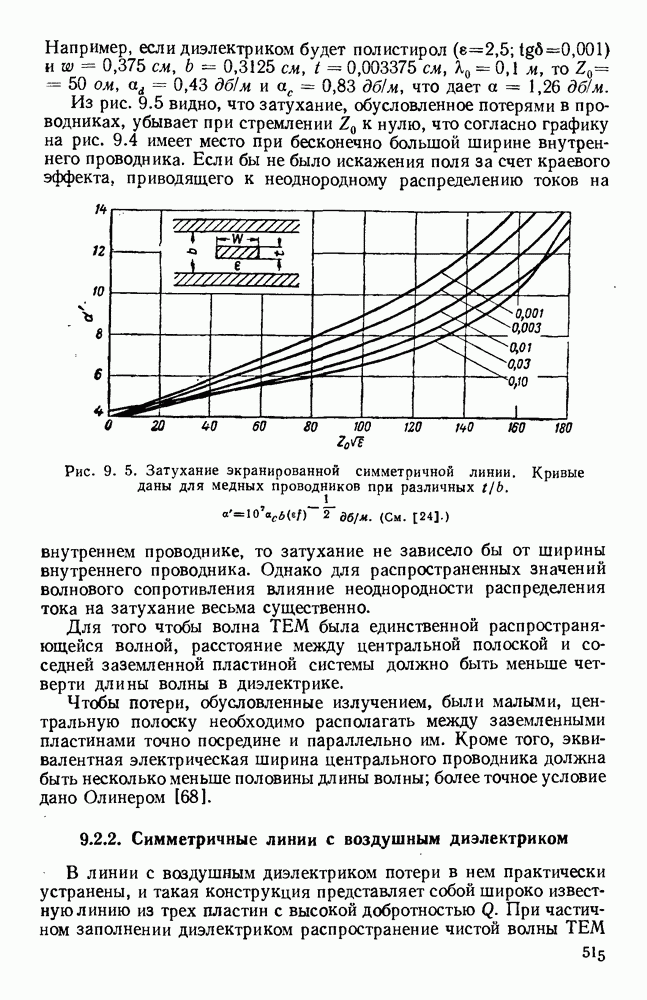
- 9.2.2. Симметричные линии с воздушным диэлектриком
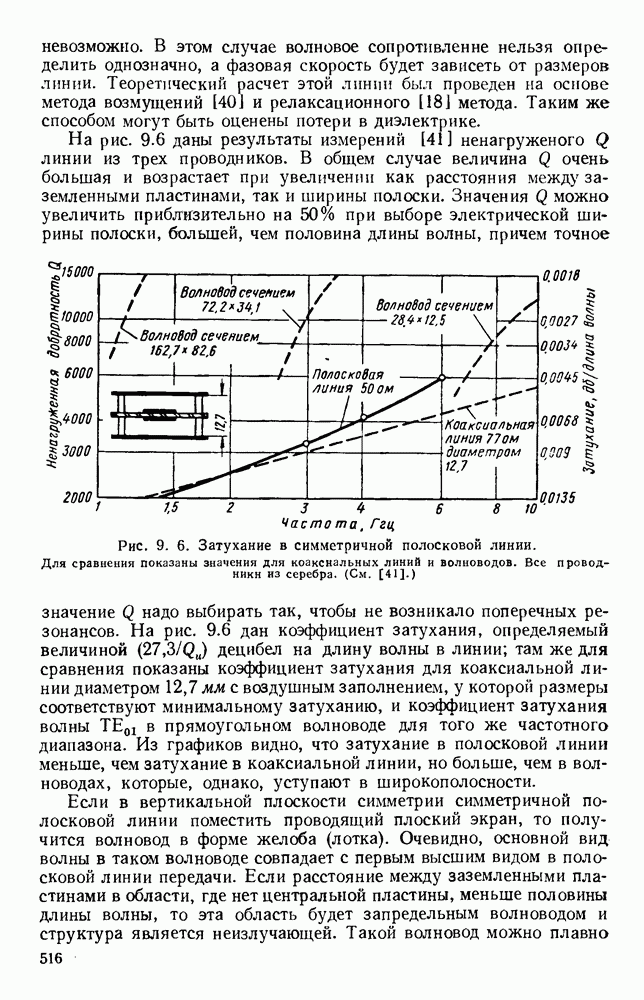
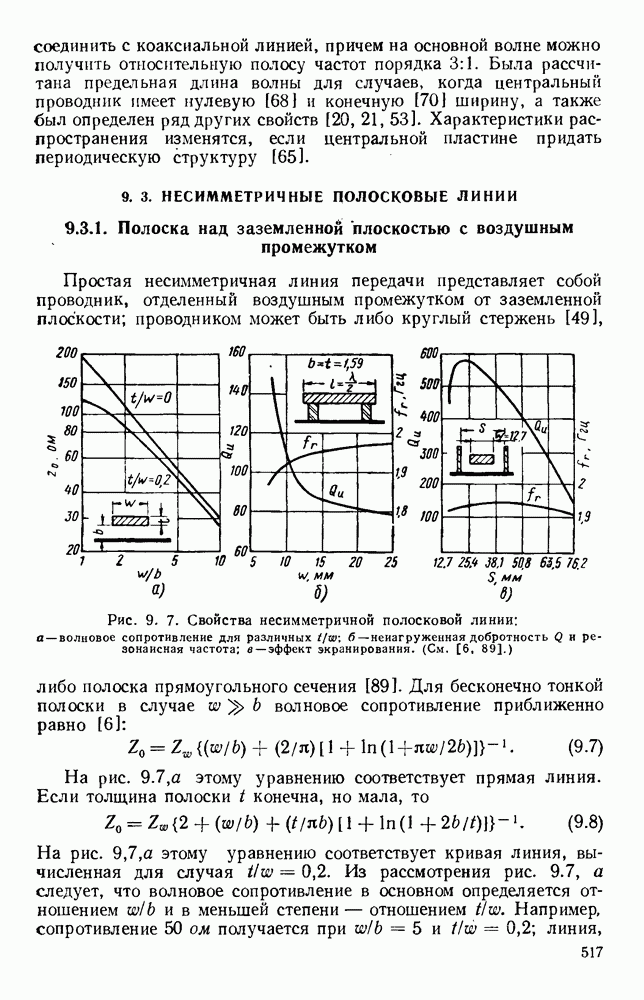
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
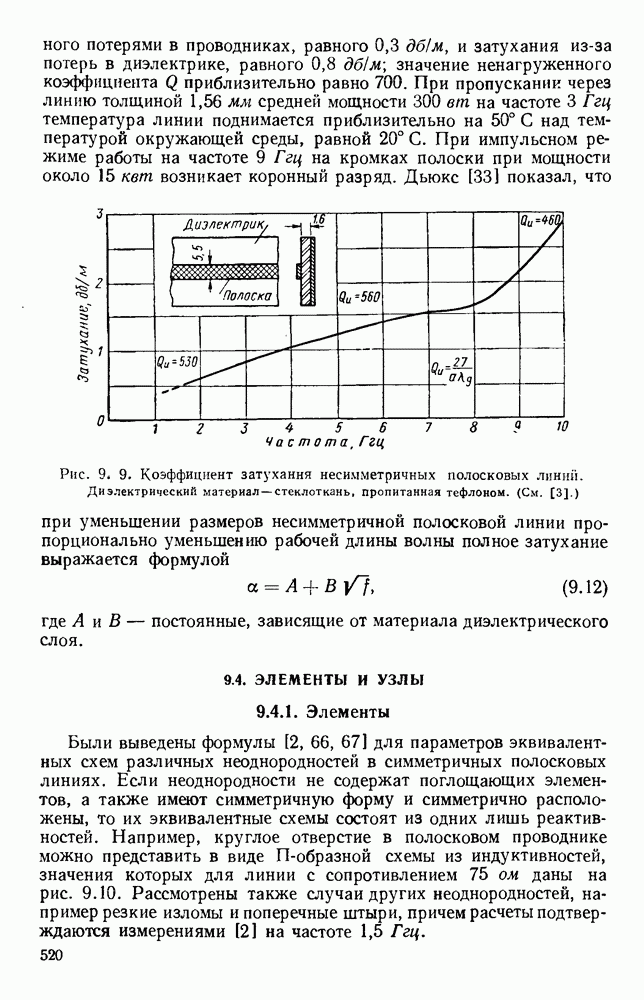
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
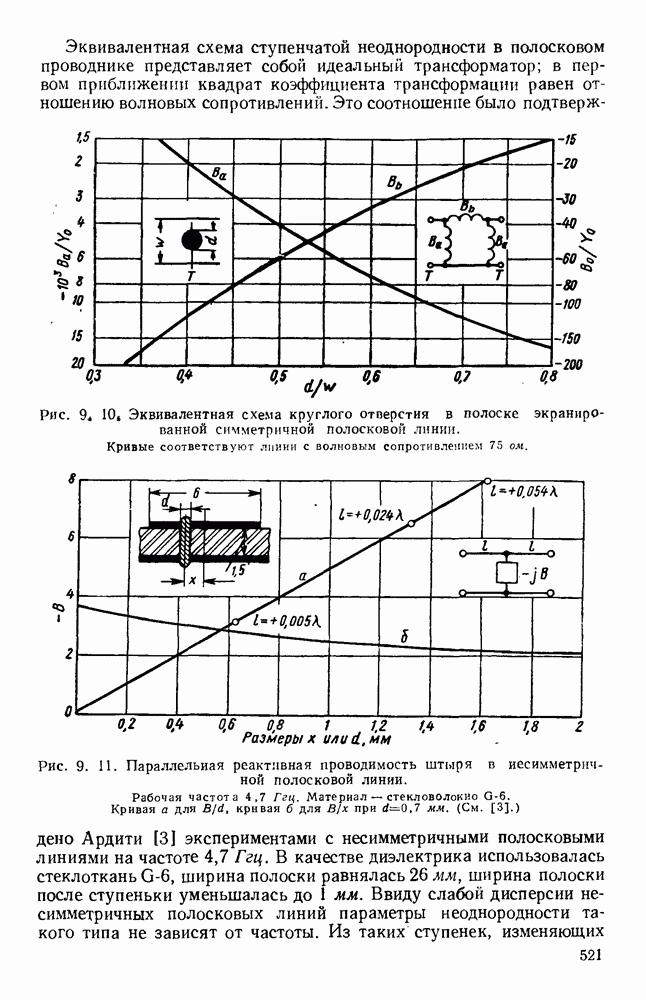
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
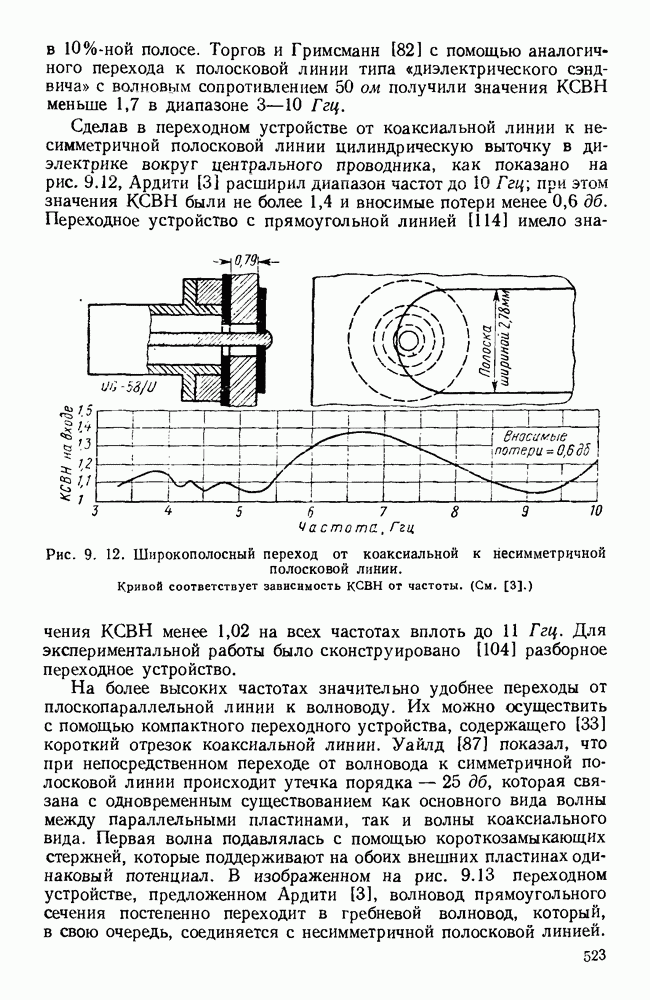
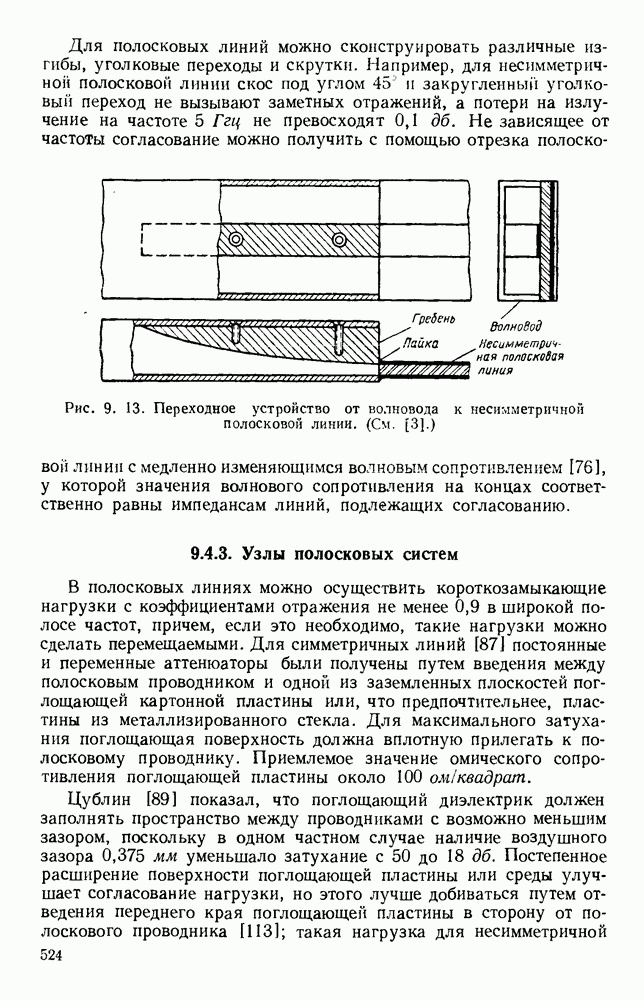
- 9.4.2. Переходные устройства
- 9.4.3. Узлы полосковых систем
- 9.5. ЦЕПИ И СИСТЕМЫ
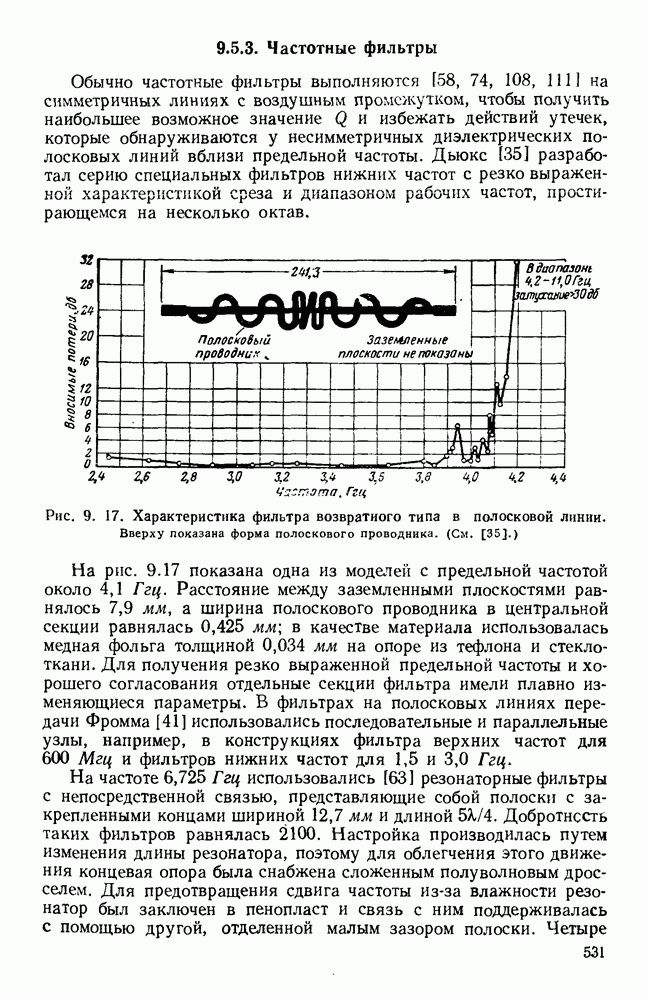
- 9.5.3. Частотные фильтры
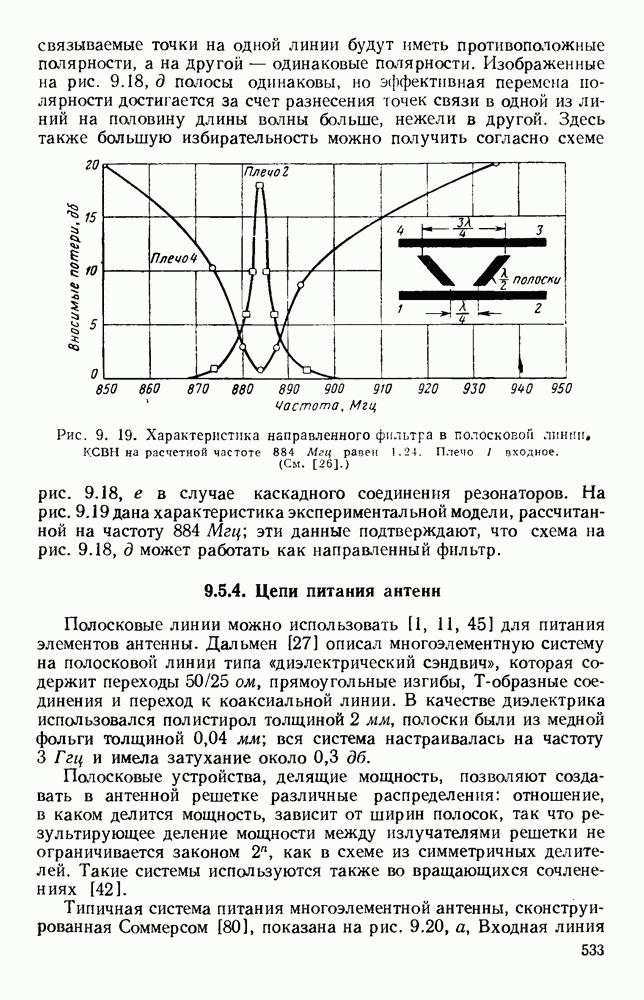
- 9.5.4. Цепи питания антенн
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
- 10.1.2. Пространственные гармоники
- 10.1.3. Многократно-периодические структуры
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
- 10.2.3. Продольные цилиндрические волны
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
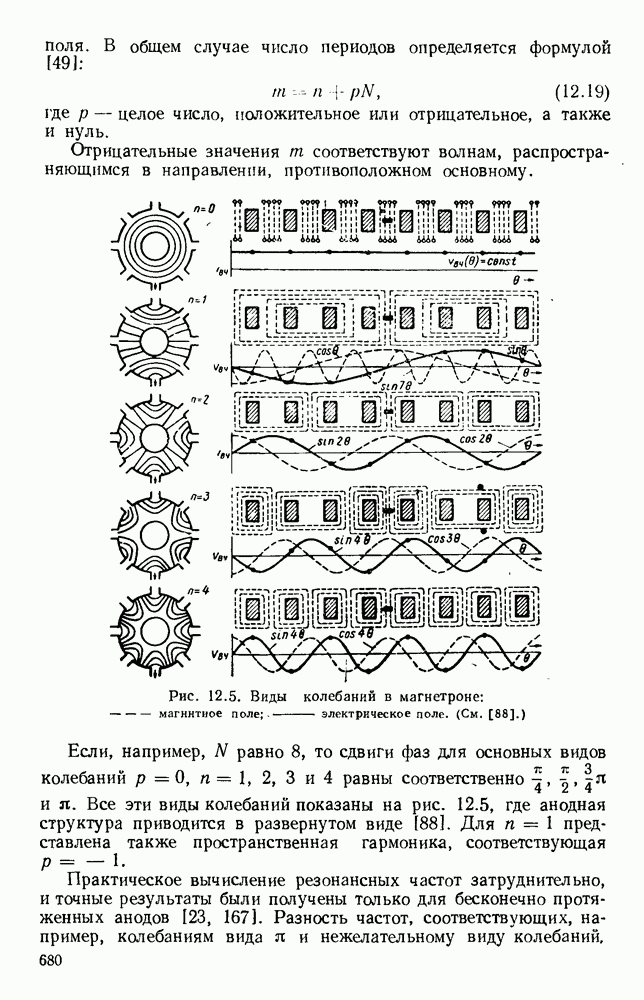
- 12.2. МАГНЕТРОНЫ
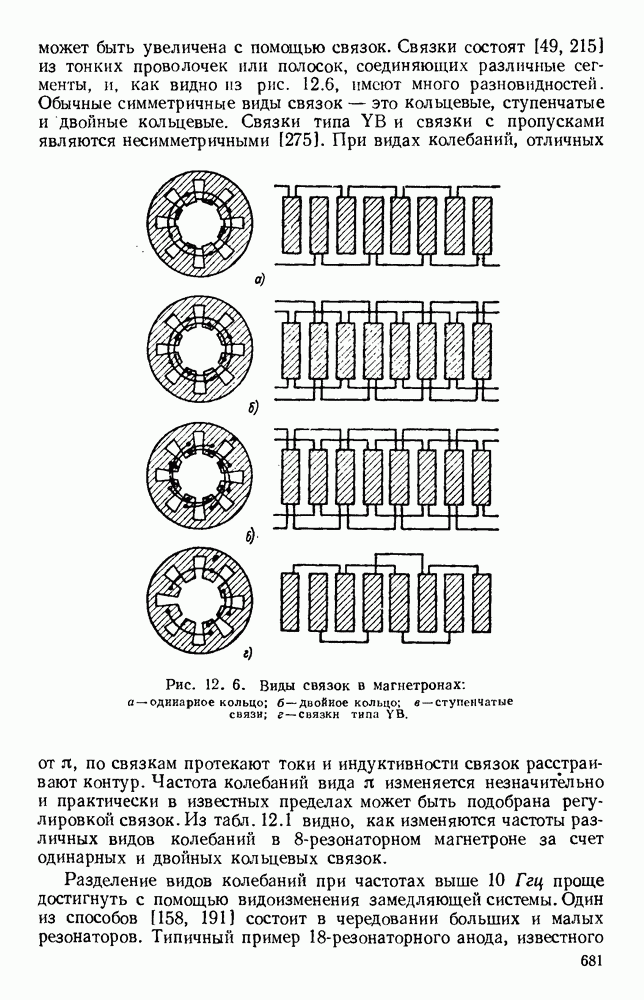
- 12.2.2. Резонаторные системы
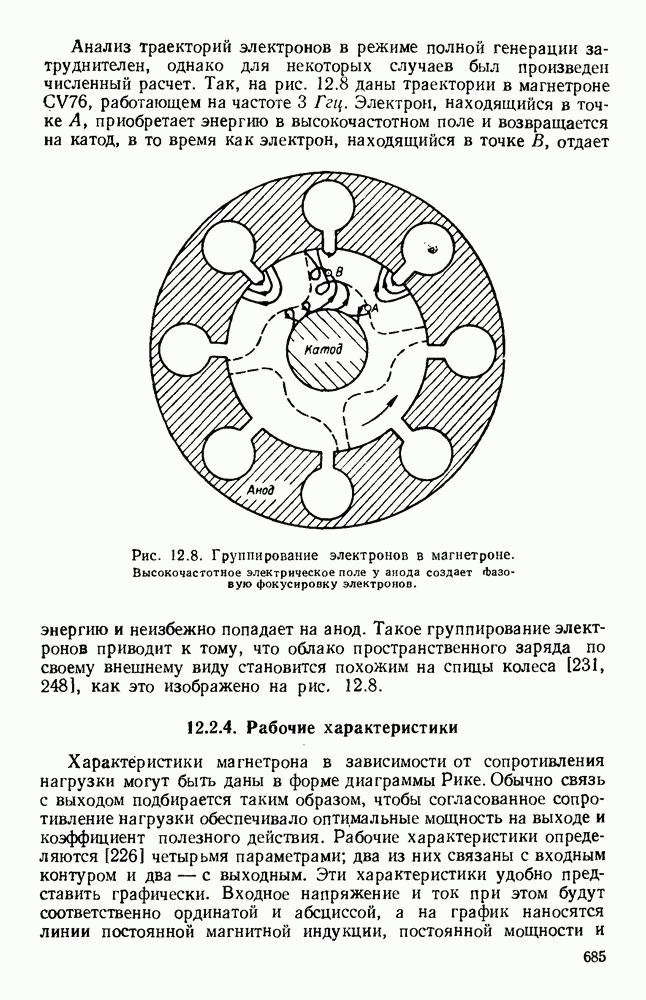
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
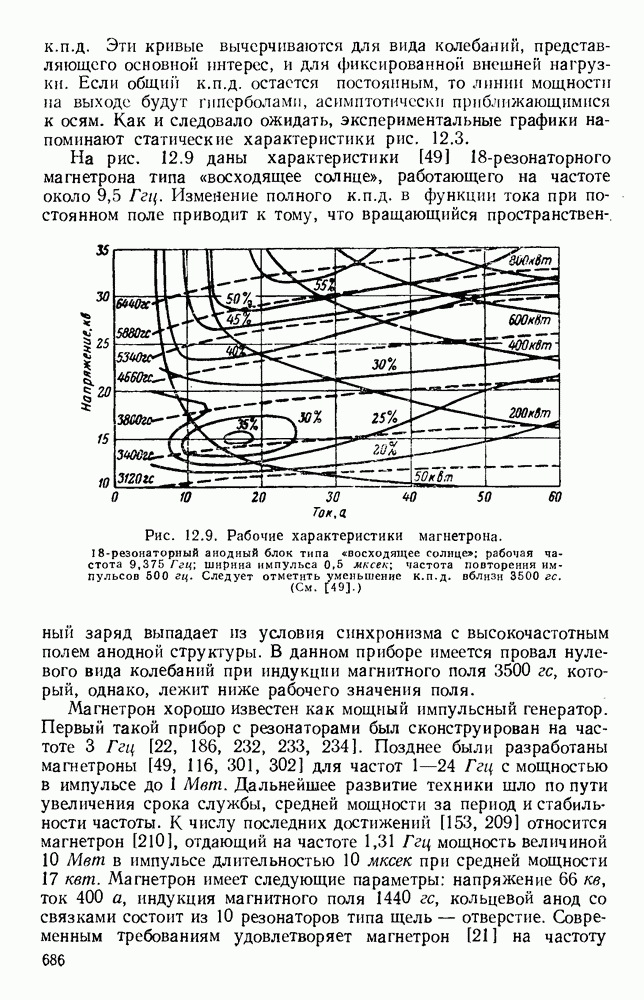
- 12.2.4. Рабочие характеристики
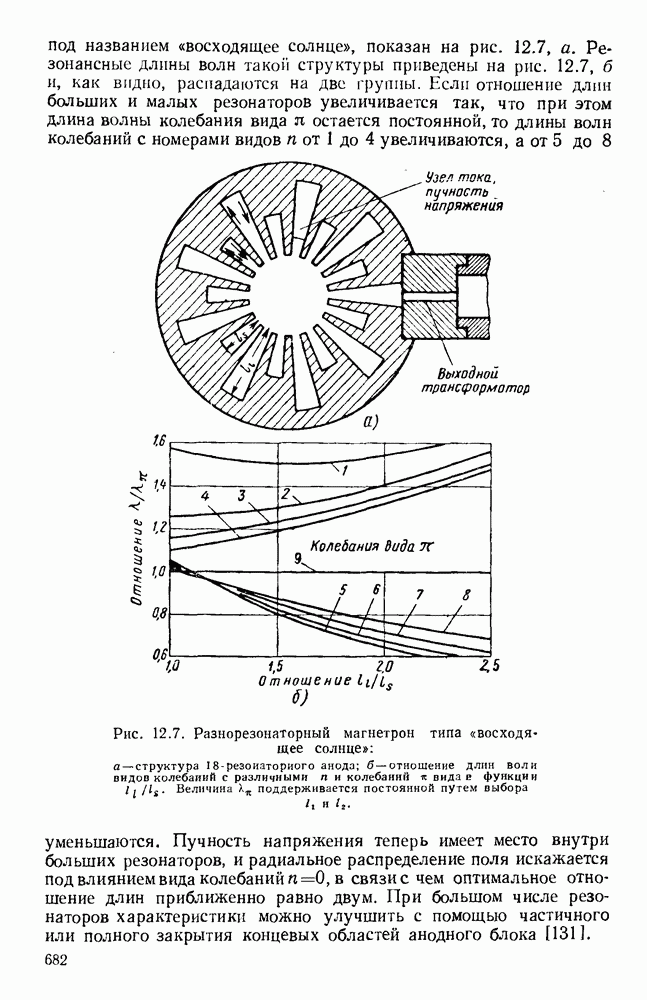
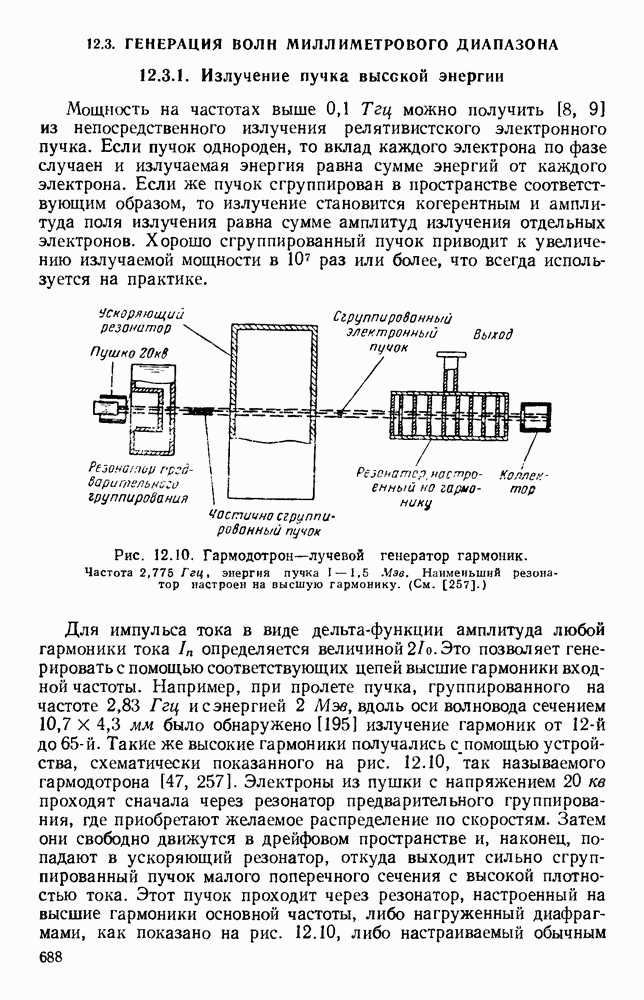
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
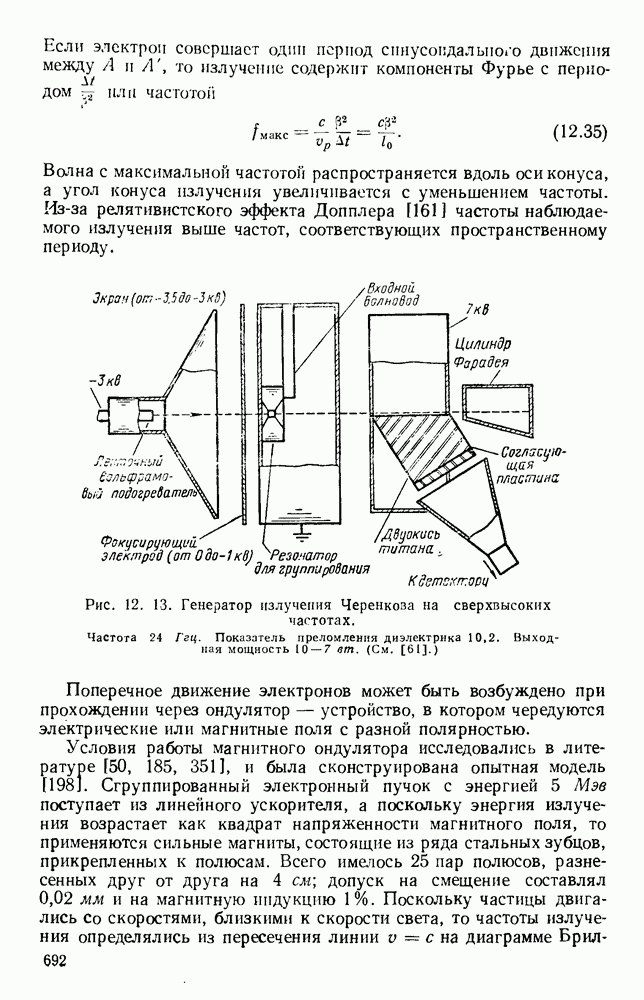
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
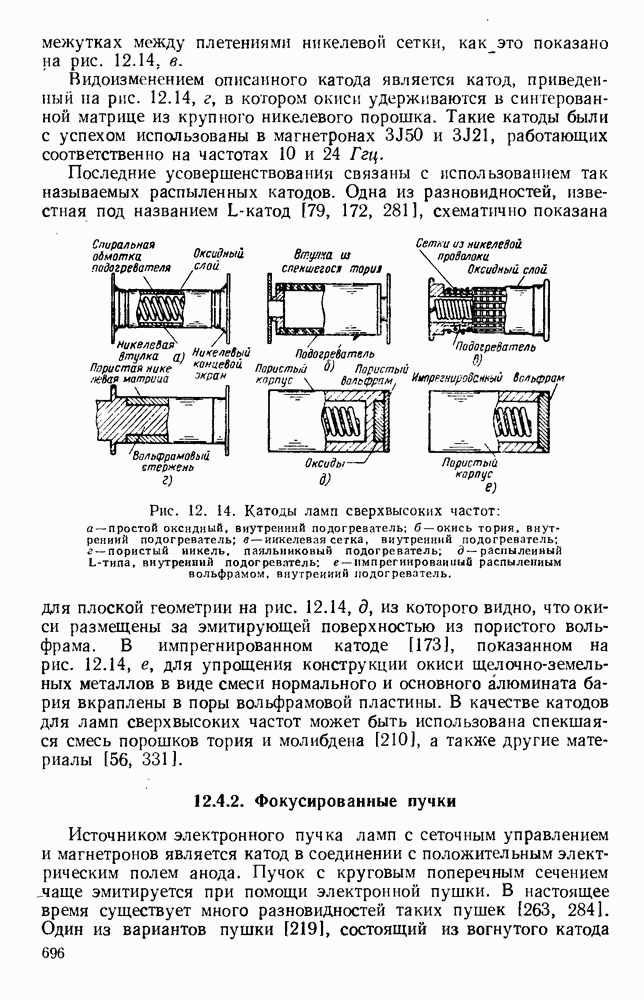
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
- 13.1.2. Типы дифракции
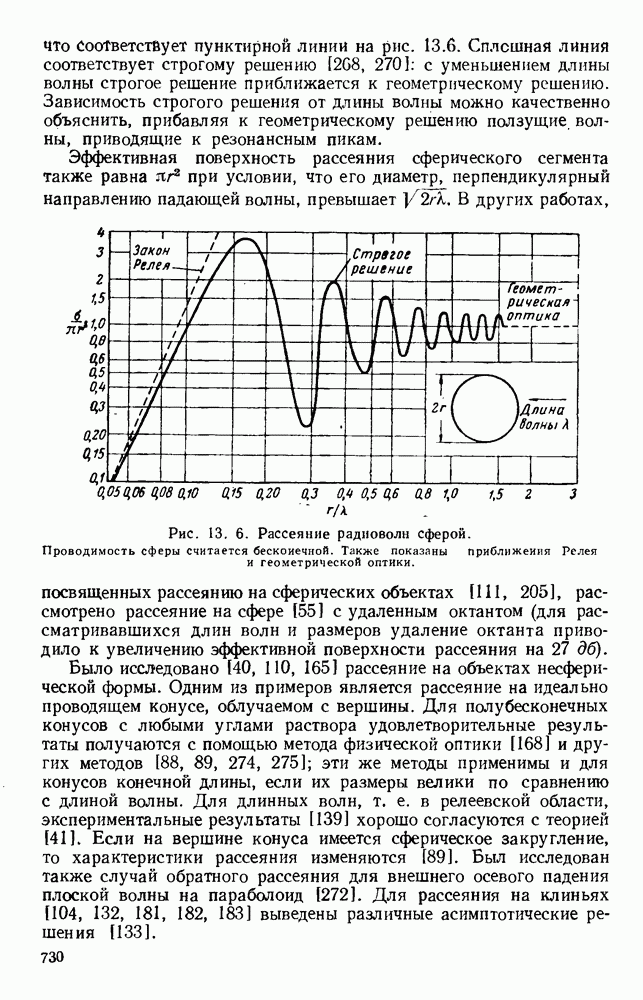
- 13.1.3. Рассеяние
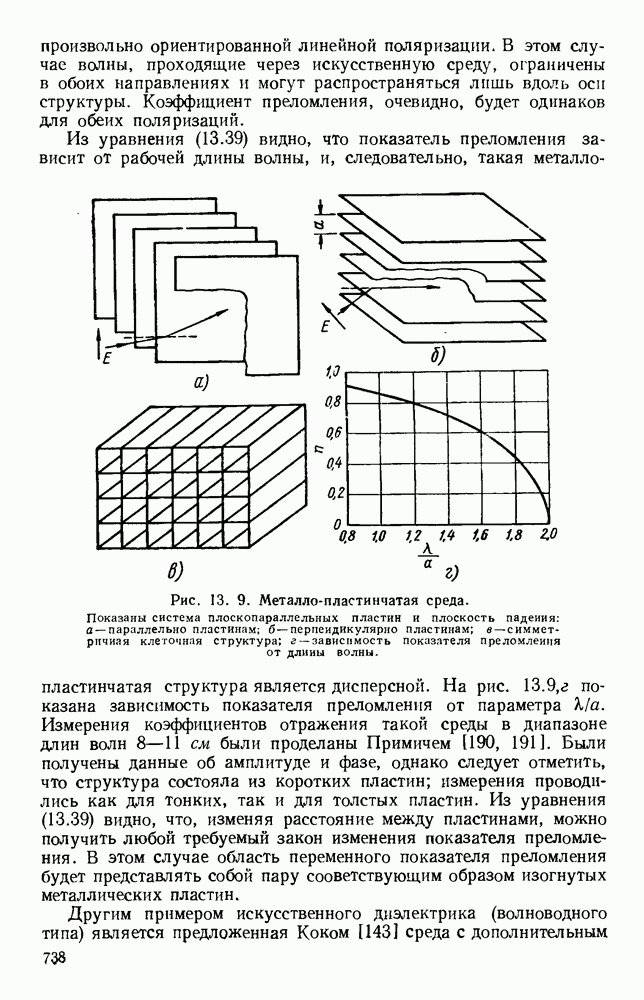
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
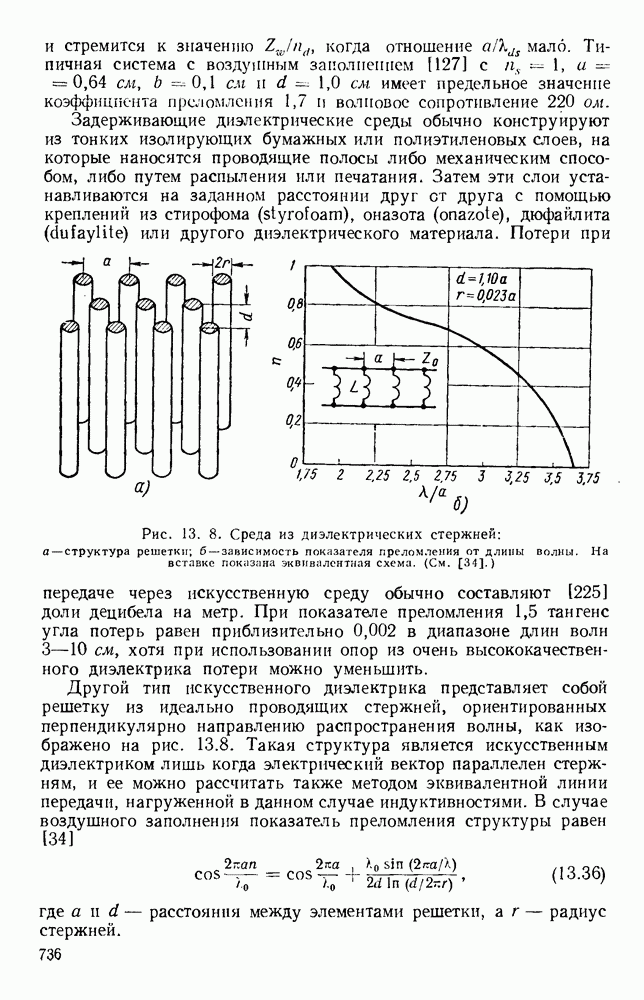
- 13.2.2. Структуры волноводного типа
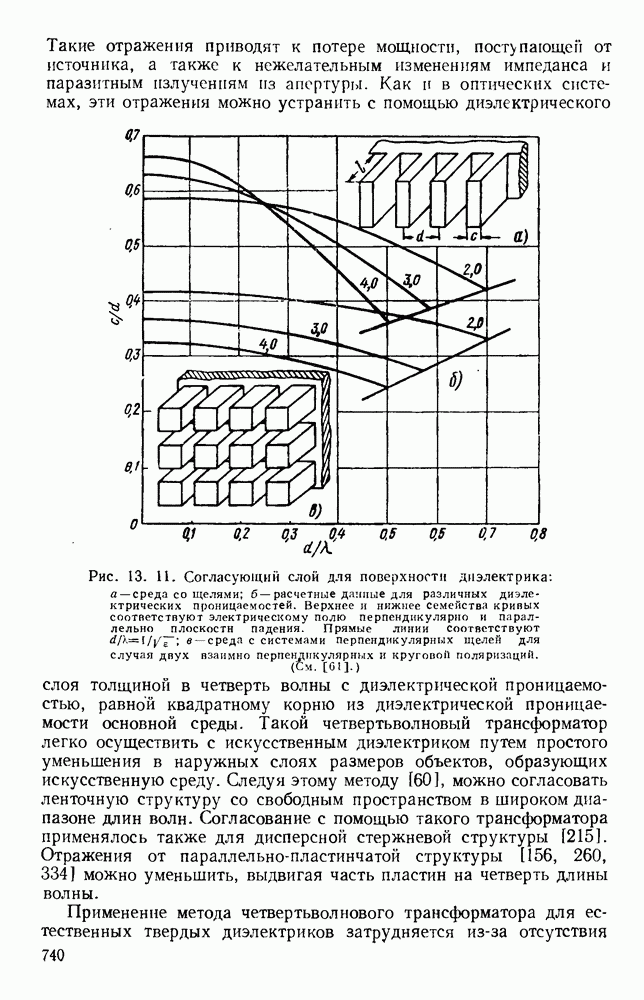
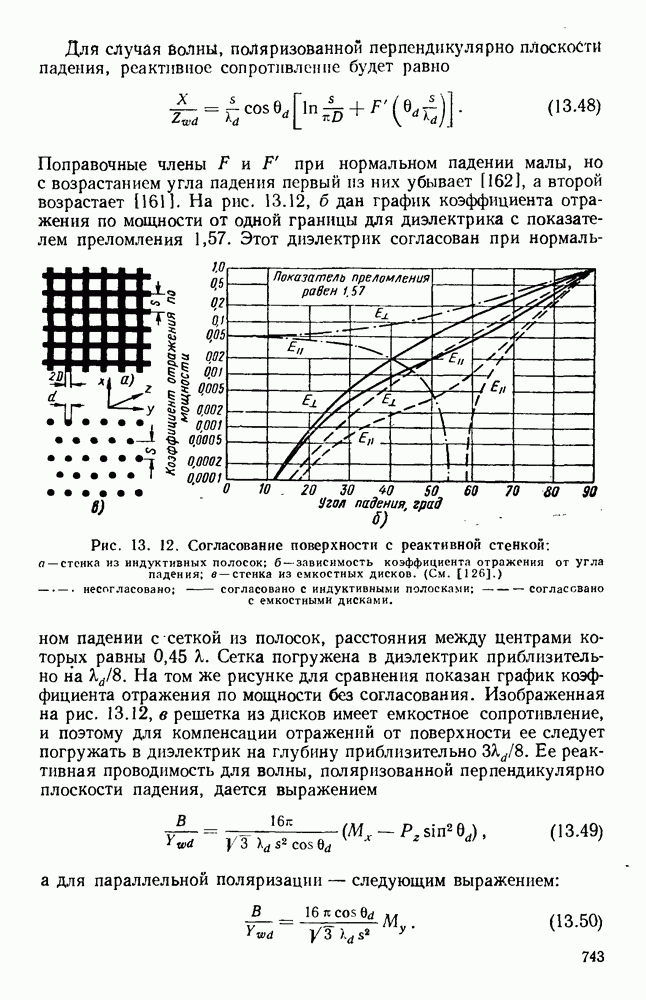
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
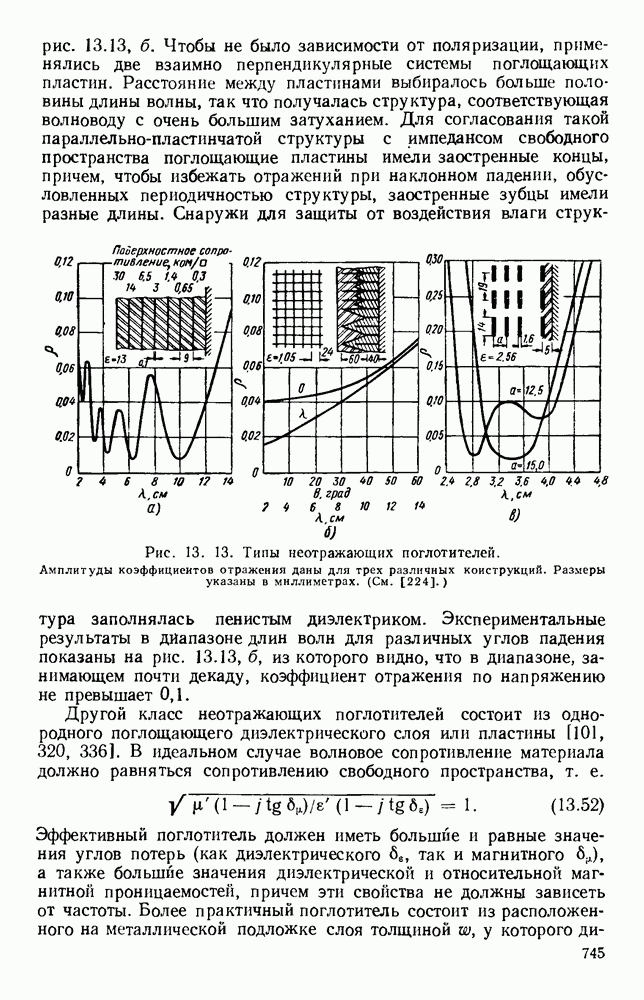
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
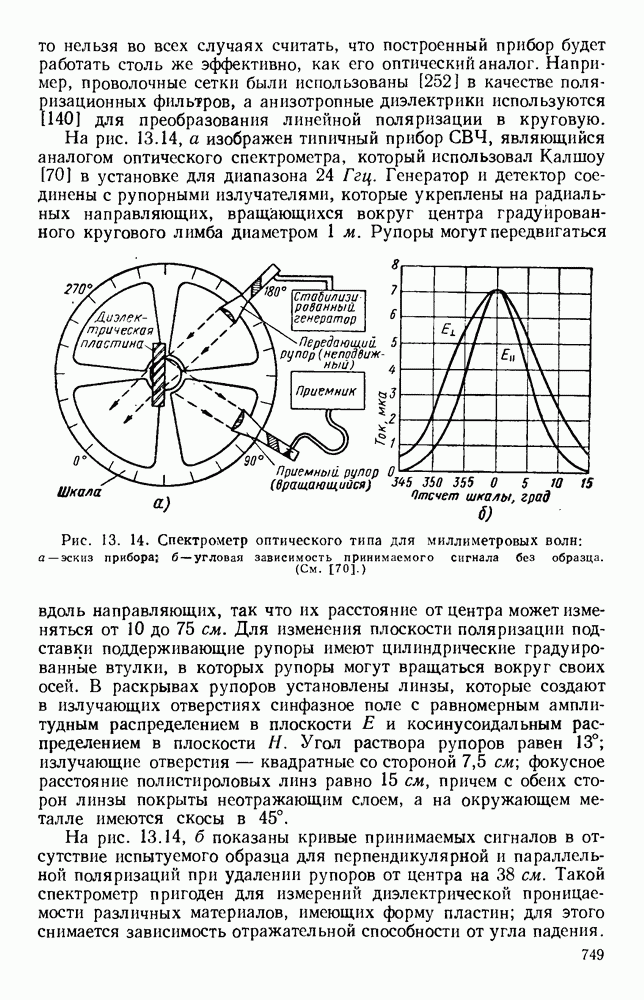
- 13.4. ПРИБОРЫ И СИСТЕМЫ
- 13.4.1. Спектрометры
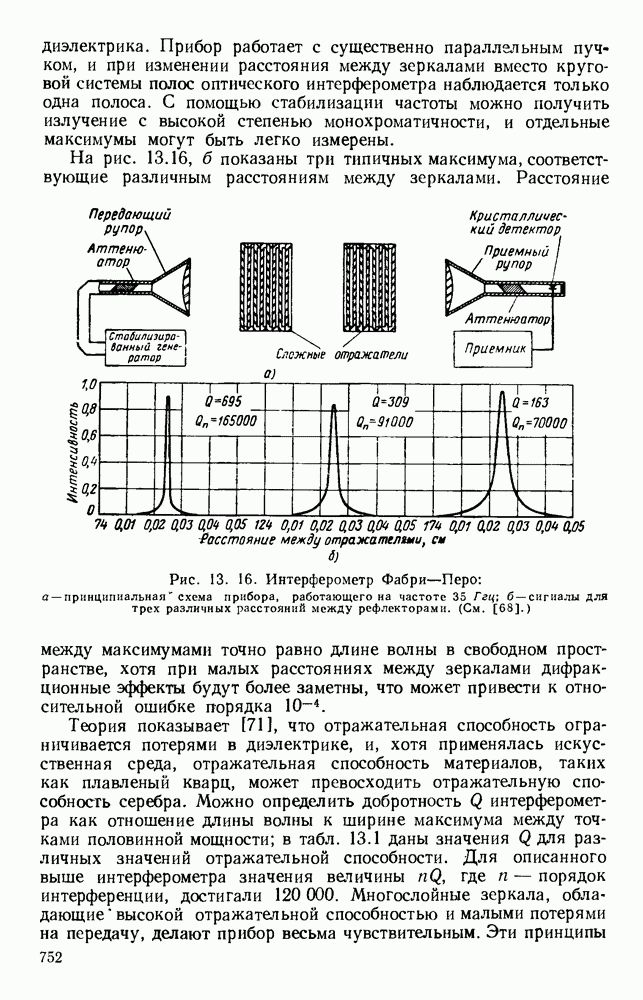
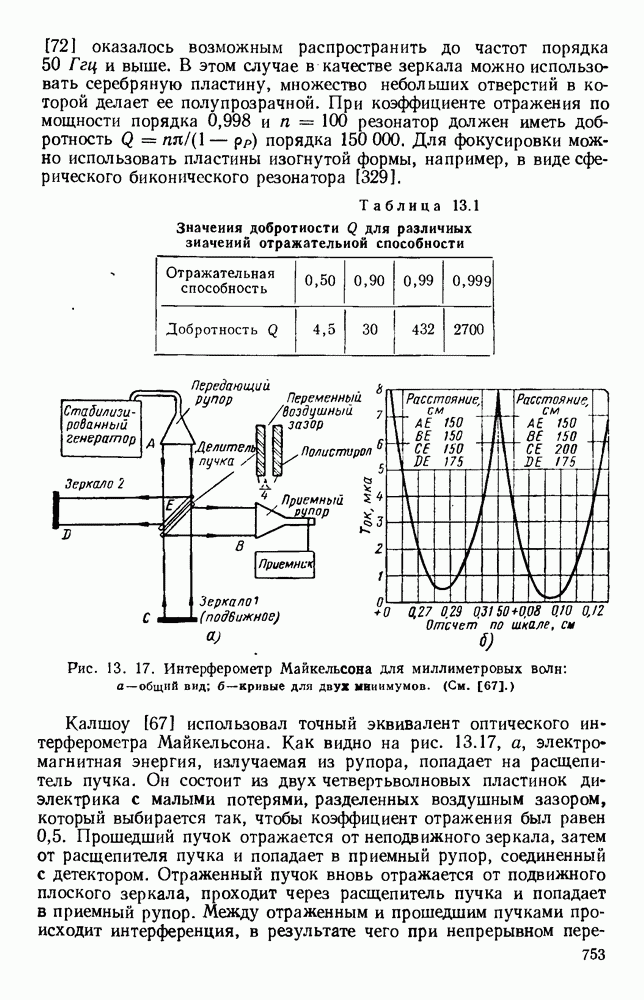
- 13.4.2. Интерферометры
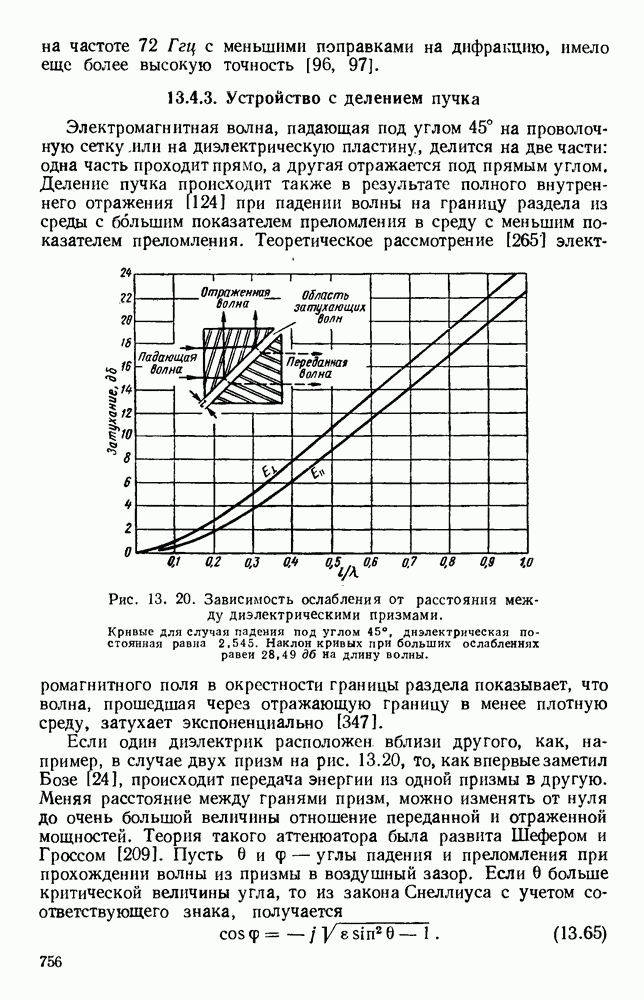
- 13.4.3. Устройство с делением пучка