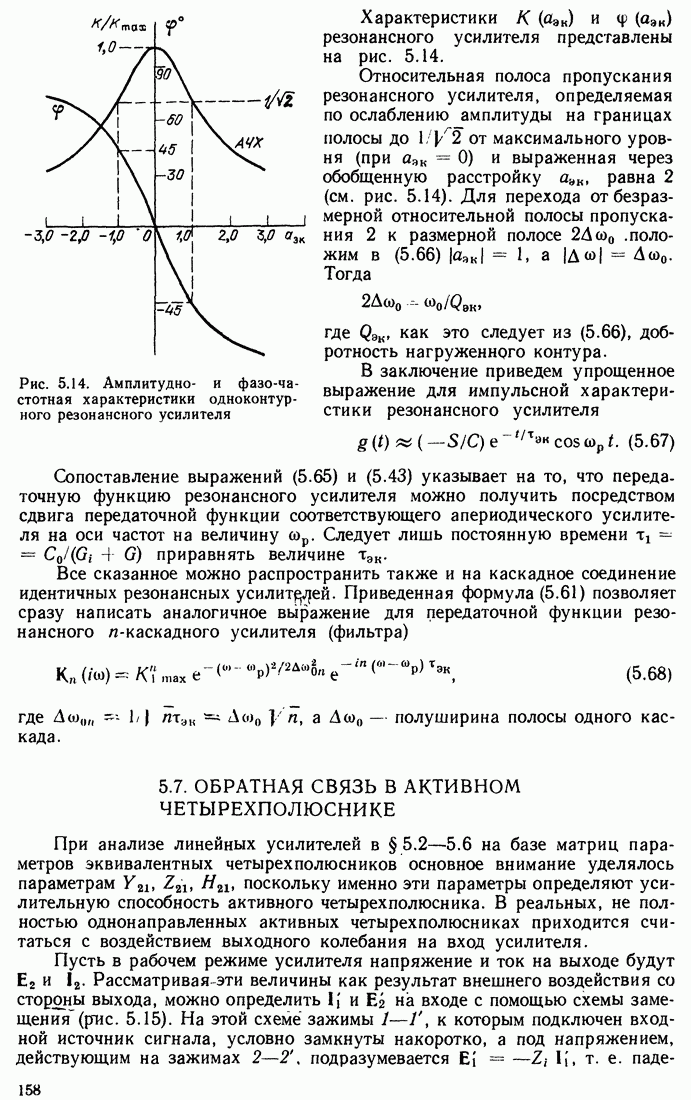
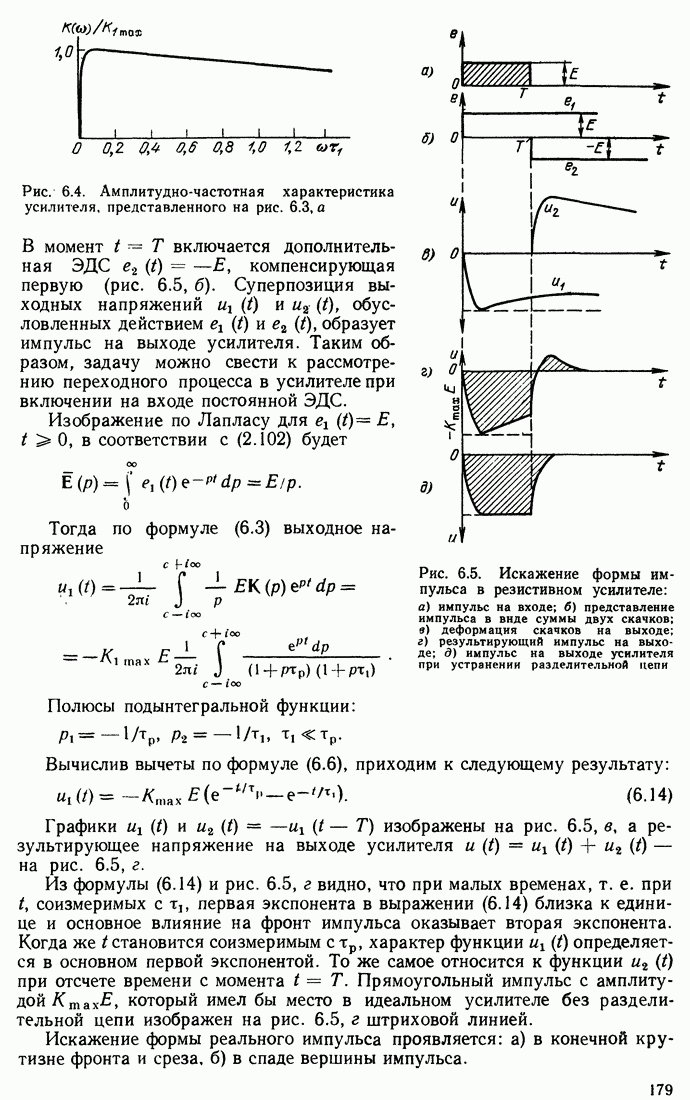
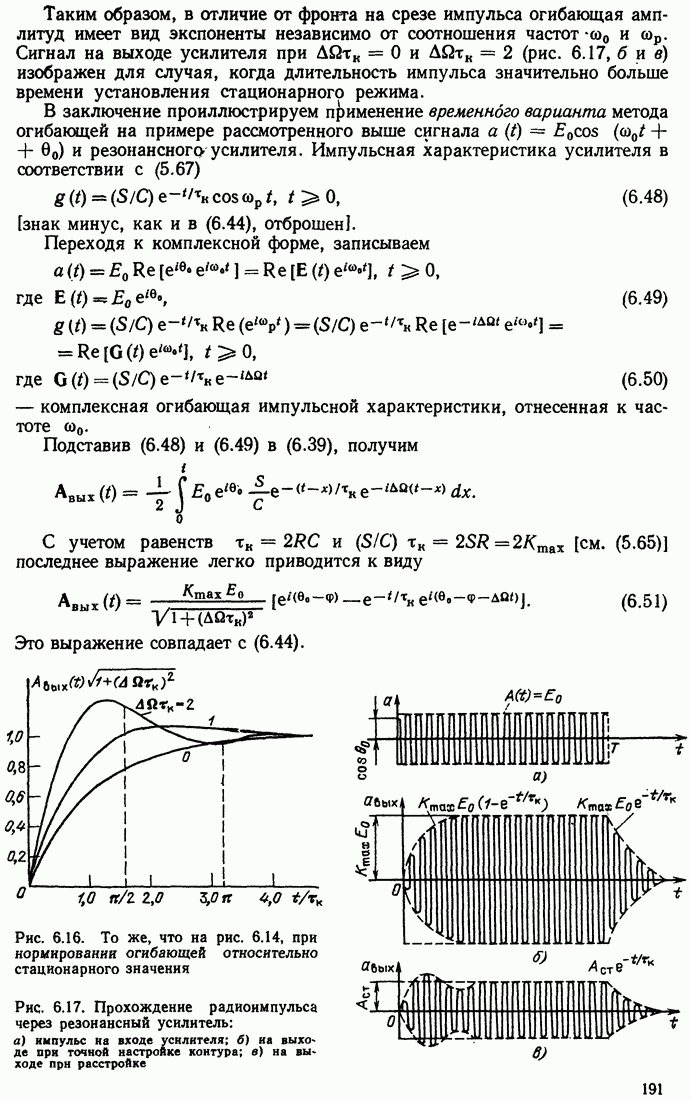
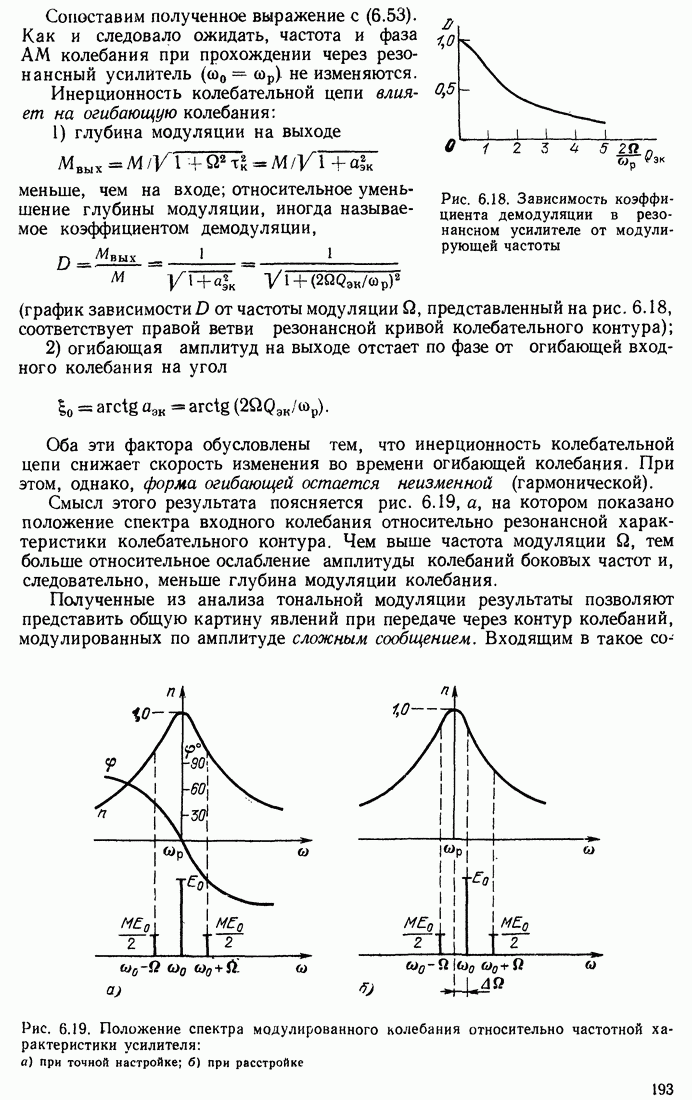
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
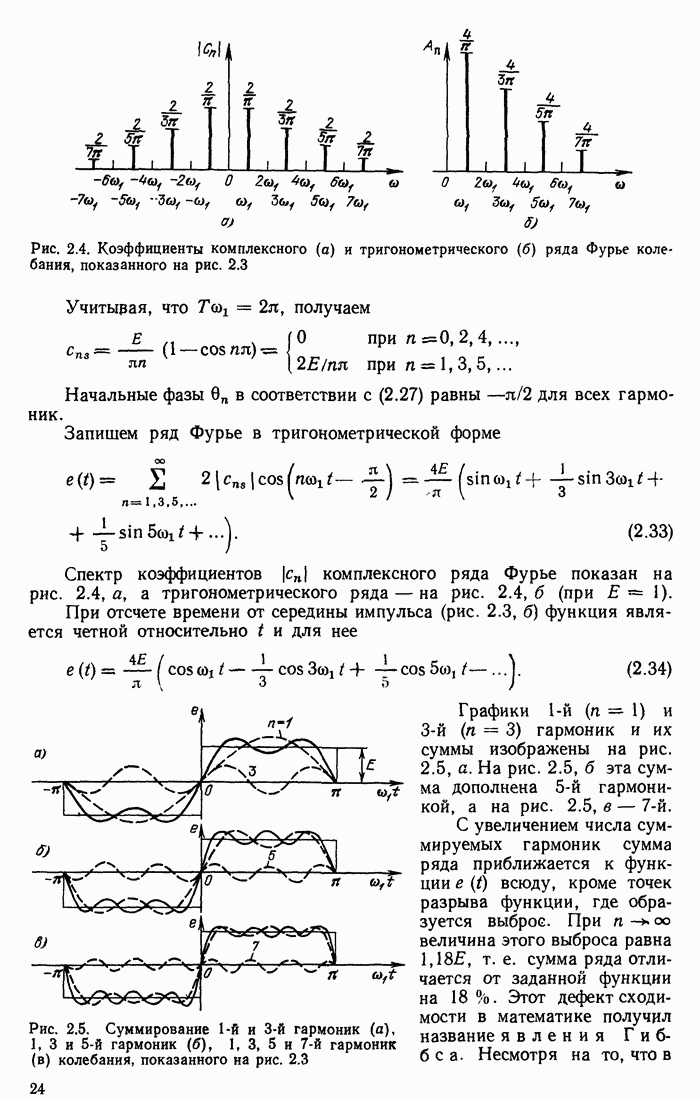
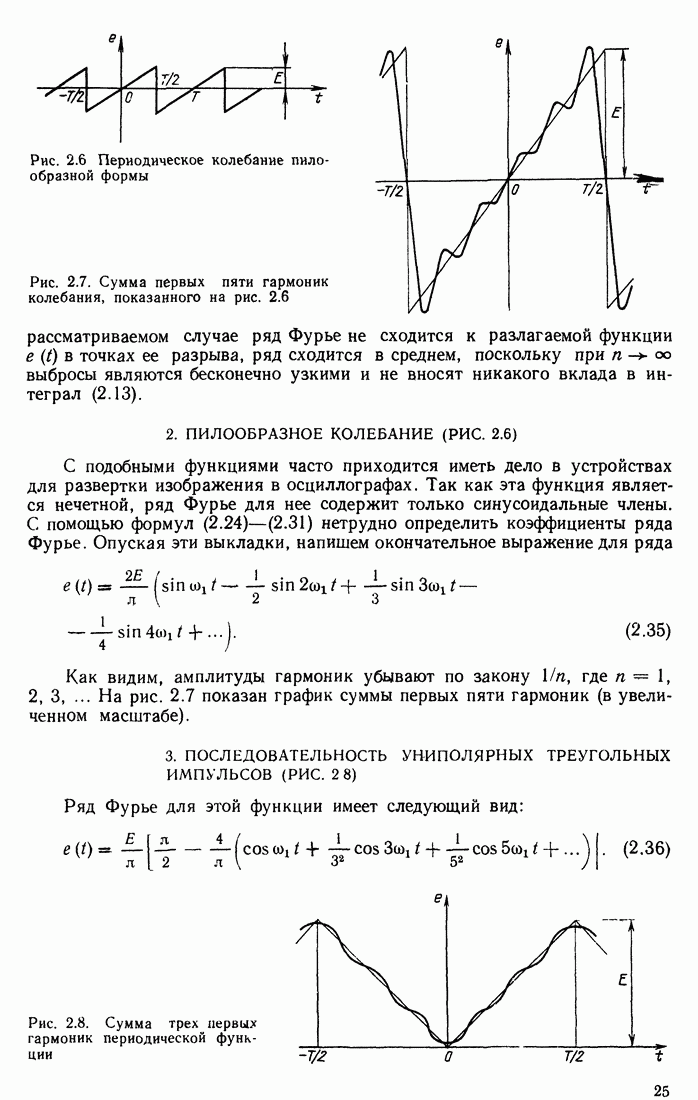
13.4. СИГНАЛ И ПОМЕХА НА ВЫХОДЕ СОГЛАСОВАННОГО ФИЛЬТРА
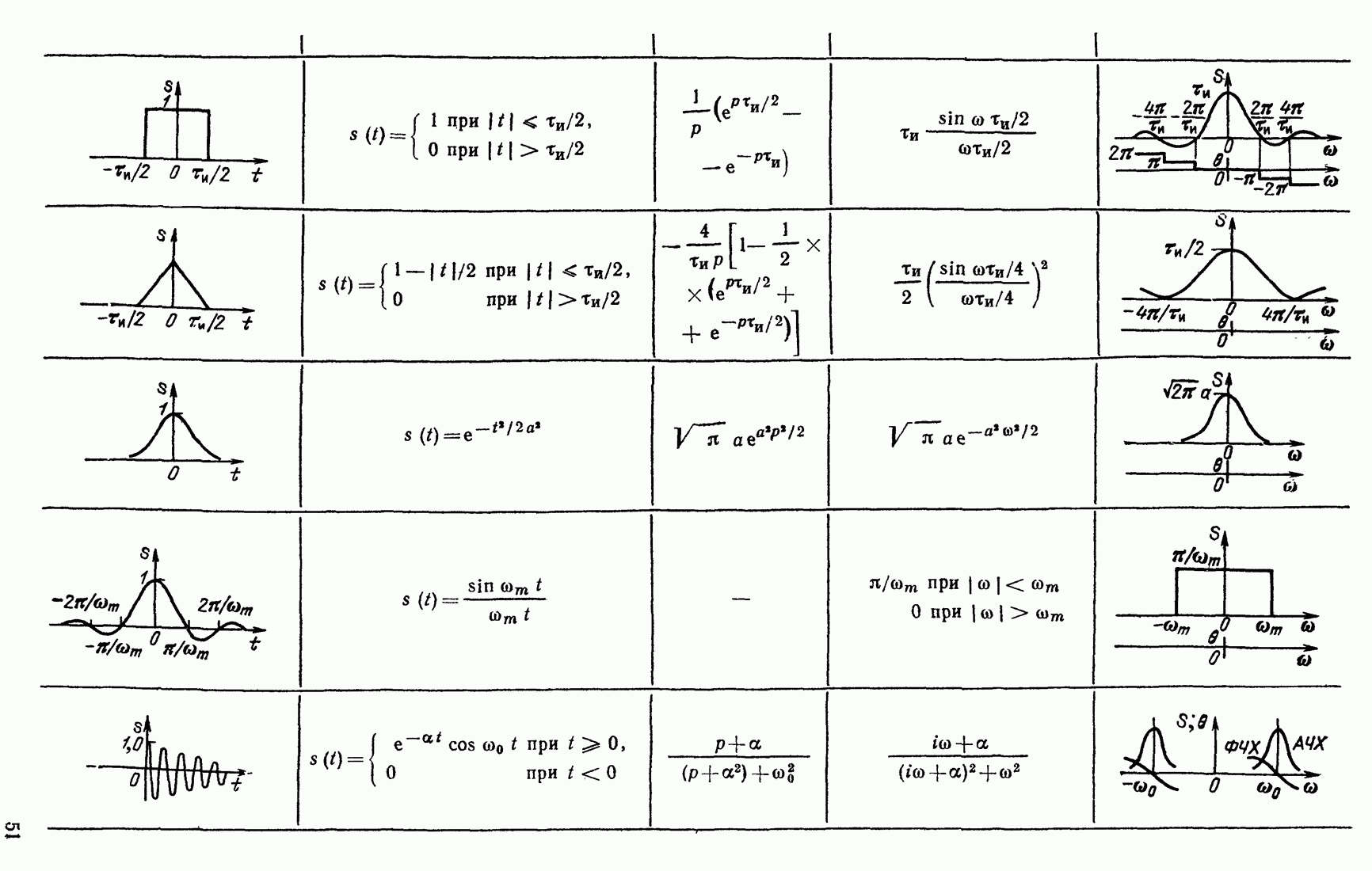
Для определения формы сигнала на выходе используем общее выражение

Подставив в него соотношение (13.8), получим
 (13.17)
(13.17)
Сопоставим это выражение с (2.136). Нетрудно видеть, что интеграл в правой части выражения (13.17) есть не что иное, как корреляционная функция входного сигнала  , в которой аргумент
, в которой аргумент  заменен на
заменен на  . Таким образом, приходим к важному выводу, что
. Таким образом, приходим к важному выводу, что
 (13.18)
(13.18)
и соответственно

Итак, сигнал на выходе согласованного фильтра с точностью до постоянного коэффициента А совпадает с корреляционной функцией входного сигнала.
Для построения графика функции  по заданной функции
по заданной функции  достаточно в последней заменить на
достаточно в последней заменить на  (и учесть коэффициент А). При
(и учесть коэффициент А). При  , т. е. при
, т. е. при  величина
величина  равна энергии сигнала. Следовательно, пиковое значение сигнала
равна энергии сигнала. Следовательно, пиковое значение сигнала
 (13.20)
(13.20)
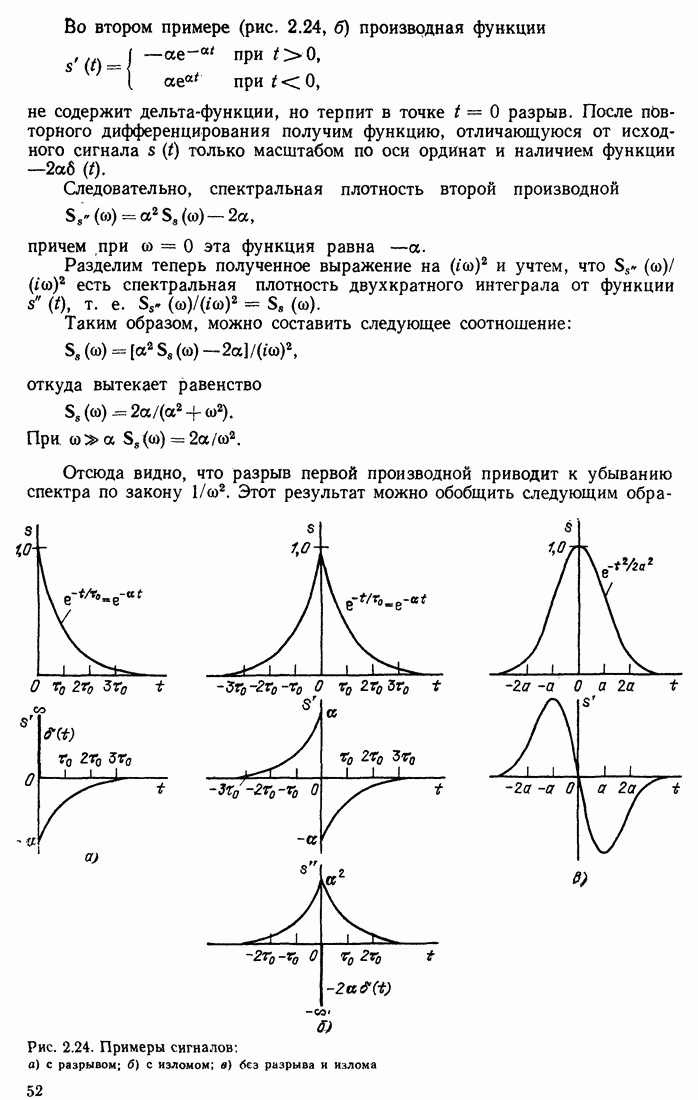
Рассмотрим теперь параметры и статистические характеристики шума на выходе согласованного фильтра. При действии белого шума с нормальным законом распределения (именно такой шум и представляет основной интерес для практики) распределение шума на выходе линейного фильтра остается нормальным. Спектр шума на выходе, как это ясно из (7.2) и рис. 13.3,  . Следовательно, корреляционная функция шума на выходе согласованного фильтра
. Следовательно, корреляционная функция шума на выходе согласованного фильтра
 (13.21)
(13.21)
Подставляя  и учитывая выражение (2.136), получаем
и учитывая выражение (2.136), получаем
 (13.22)
(13.22)
Отсюда следует, что корреляционная функция шума на выходе согласованного фильтра по форме совпадает с корреляционной функцией входного сигнала (и, следовательно, с самим выходным сигналом).
Приравнивая  , находим дисперсию (среднюю мощность) шума на выходе
, находим дисперсию (среднюю мощность) шума на выходе
 (13.23)
(13.23)
Составим отношение пикового значения сигнала  к среднеквадратическому значению шума авых. В соответствии с формулами (13.19) и (13.23) приходим к результату (13.9):
к среднеквадратическому значению шума авых. В соответствии с формулами (13.19) и (13.23) приходим к результату (13.9):  .
.
Итак, при белом шуме отношение сигнал-шум не выхода фильтра, согласованного с сигналом, зависит только от энергии сигнала и энергетического спектра шума 
Из этого заключения следует, что при заданных энергии и ширине спектра сигналу можно придавать различную форму, выгодную для решения конкретной задачи.
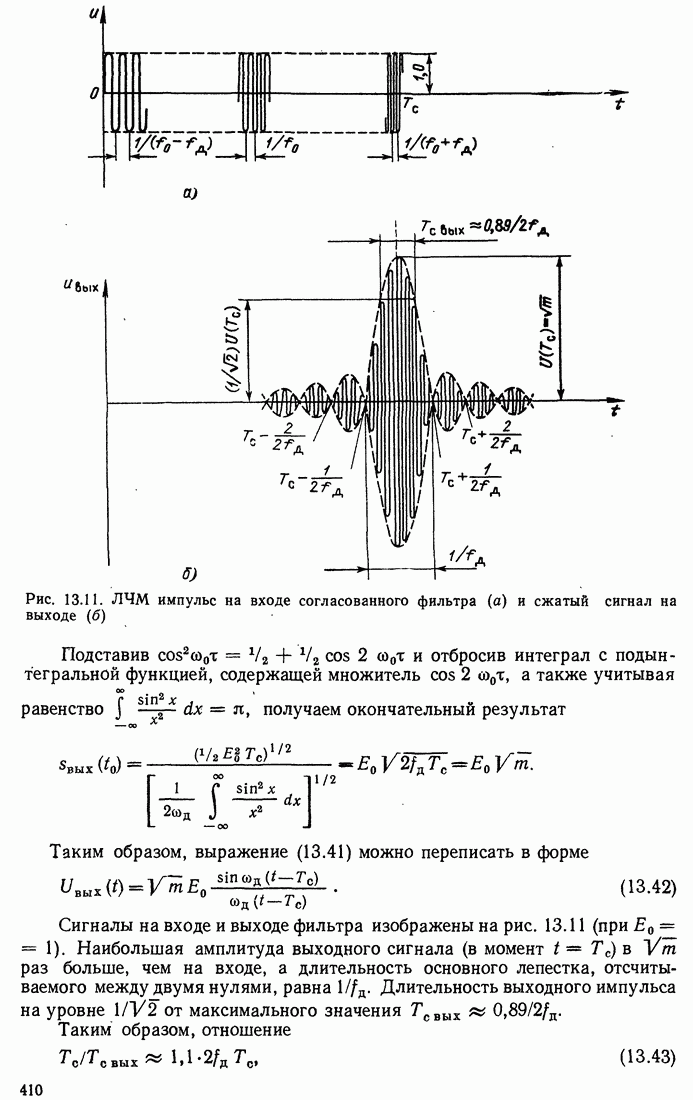
Так, для повышения скрытности передачи целесообразно удлинять сигнал при соответствующем уменьшении амплитуды  . Это приводит к уменьшению отношения сигнал-помеха на входах любых радиоприемных устройств, что затрудняет извлечение информации из смеси сигнал + шум. Лишь в приемнике с фильтром, согласованным с данным сигналом, восстанавливается наибольшее возможное при заданной энергии отношение сигнал-помеха. Следует, конечно, обеспечить неизменную ширину спектра при удлинении сигнала. Это можно осуществить, введя внутриимпульсную модуляцию, например частотную. Пример подобного сигнала — импульса с линейной ЧМ (ЛЧM импульс) был рассмотрен в § 3.7, п. 3.
. Это приводит к уменьшению отношения сигнал-помеха на входах любых радиоприемных устройств, что затрудняет извлечение информации из смеси сигнал + шум. Лишь в приемнике с фильтром, согласованным с данным сигналом, восстанавливается наибольшее возможное при заданной энергии отношение сигнал-помеха. Следует, конечно, обеспечить неизменную ширину спектра при удлинении сигнала. Это можно осуществить, введя внутриимпульсную модуляцию, например частотную. Пример подобного сигнала — импульса с линейной ЧМ (ЛЧM импульс) был рассмотрен в § 3.7, п. 3.
Удлинение радиоимпульса, дополняемое внутри импульсной модуляцией, позволяет также снизить пиковую мощность генератора в передатчике при заданной энергии сигнала и при сохранении разрешающей способности сигнала (после сжатия в согласованном фильтре). Это преимущество более подробно рассматривается в § 13.5, п. 2.
Уточним смысл коэффициента А, фигурирующего во многих предыдущих выражениях. При определении отношения сигнал-помеха [см. (13.9)] в уточнении нет необходимости, однако при рассмотрении сигнала и помехи порознь, как, например, в выражениях (13.20) и (13.22), необходимо учитывать, что А — размерный коэффициент. Удобно нормировать А так, чтобы энергии входного и выходного сигналов были одинаковы, тем самым исключая из анализа усиление сигнала по энергии.
Энергия входного сигнала  , а выходного
, а выходного
 (13.24)
(13.24)
Приравнивая  величине Э, получаем условие нормирования коэффициента А
величине Э, получаем условие нормирования коэффициента А
 (13.25)
(13.25)
Подставив этот результат в (13.20), находим пик сжатого сигнала

Таким образом, пик сжатого сигнала (в отсутствие усиления) выражен через корреляционную функцию исходного сигнала  . Применение выражения (13.26) иллюстрируется примерами, приведенными в следующем параграфе.
. Применение выражения (13.26) иллюстрируется примерами, приведенными в следующем параграфе.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- Глава 1. ОБЩАЯ ХАРАКТЕРИСТИКА РАДИОТЕХНИЧЕСКИХ ПРОЦЕССОВ, СИГНАЛОВ И ЦЕПЕЙ
- 1.1. ПЕРЕДАЧА СИГНАЛОВ НА РАССТОЯНИЕ И ИСПОЛЬЗУЕМЫЕ В РАДИОТЕХНИКЕ ЧАСТОТЫ
- 1.2. ПРЕОБРАЗОВАНИЕ СИГНАЛОВ В РАДИОТЕХНИЧЕСКИХ СИСТЕМАХ
- 1.3. КЛАССИФИКАЦИЯ СИГНАЛОВ, ИСПОЛЬЗУЕМЫХ В РАДИОТЕХНИКЕ
- 1.4. РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И МЕТОДЫ ИХ АНАЛИЗА
- 1.5. ПРОБЛЕМА ПОМЕХОУСТОЙЧИВОСТИ И ЭЛЕКТРОМАГНИТНОЙ СОВМЕСТИМОСТИ РАДИОТЕХНИЧЕСКИХ СИСТЕМ
- Глава 2. ХАРАКТЕРИСТИКИ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
- 2.2. ПРЕДСТАВЛЕНИЕ ПРОИЗВОЛЬНОГО СИГНАЛА В ВИДЕ СУММЫ ЭЛЕМЕНТАРНЫХ КОЛЕБАНИИ
- 2.3. ГАРМОНИЧЕСКИЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ
- 2.4. СПЕКТРЫ ПРОСТЕЙШИХ ПЕРИОДИЧЕСКИХ СИГНАЛОВ
- 2.5. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ В СПЕКТРЕ ПЕРИОДИЧЕСКОГО СИГНАЛА
- 2.6. ГАРМОНИЧЕСКИЙ АНАЛИЗ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
- 2.7. СООТНОШЕНИЕ МЕЖДУ СПЕКТРАМИ ОДИНОЧНОГО ИМПУЛЬСА И ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ИМПУЛЬСОВ
- 2.8. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 2.9. РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ В СПЕКТРЕ НЕПЕРИОДИЧЕСКОГО СИГНАЛА
- 2.10. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ СПЕКТРОВ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
- 2.11. БЕСКОНЕЧНО КОРОТКИЙ ИМПУЛЬС С ЕДИНИЧНОЙ ПЛОЩАДЬЮ (ДЕЛЬТА-ФУНКЦИЯ)
- 2.12. СООТНОШЕНИЕ МЕЖДУ ДЛИТЕЛЬНОСТЬЮ СИГНАЛА И ШИРИНОЙ ЕГО СПЕКТРА. СКОРОСТЬ УБЫВАНИЯ СПЕКТРА
- 2.13. СПЕКТРЫ НЕКОТОРЫХ НЕИНТЕГРИРУЕМЫХ ФУНКЦИЙ
- 2.14. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ НА ПЛОСКОСТИ КОМПЛЕКСНОЙ ЧАСТОТЫ
- 2.15. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ С ОГРАНИЧЕННОЙ ПОЛОСОЙ ЧАСТОТ В ВИДЕ РЯДА КОТЕЛЬНИКОВА
- 2.16. ТЕОРЕМА ОТСЧЕТОВ В ЧАСТОТНОЙ ОБЛАСТИ
- 2.17. ДИСКРЕТИЗОВАННЫЕ СИГНАЛЫ
- 2.18. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
- 2.19. СООТНОШЕНИЕ МЕЖДУ КОРРЕЛЯЦИОННОЙ ФУНКЦИЕЙ И СПЕКТРАЛЬНОЙ ХАРАКТЕРИСТИКОЙ СИГНАЛА
- Глава 3. МОДУЛИРОВАННЫЕ КОЛЕБАНИЯ
- 3.2. РАДИОСИГНАЛЫ С АМПЛИТУДНОЙ МОДУЛЯЦИЕЙ
- 3.3. СПЕКТР АМПЛИТУДНО-МОДУЛИРОВАННОГО КОЛЕБАНИЯ
- 3.4. УГЛОВАЯ МОДУЛЯЦИЯ. ФАЗА И МГНОВЕННАЯ ЧАСТОТА КОЛЕБАНИЯ
- 3.5. СПЕКТР КОЛЕБАНИЯ ПРИ УГЛОВОЙ МОДУЛЯЦИИ. ОБЩИЕ СООТНОШЕНИЯ
- 3.6. СПЕКТР КОЛЕБАНИЯ ПРИ ГАРМОНИЧЕСКОЙ УГЛОВОЙ МОДУЛЯЦИИ
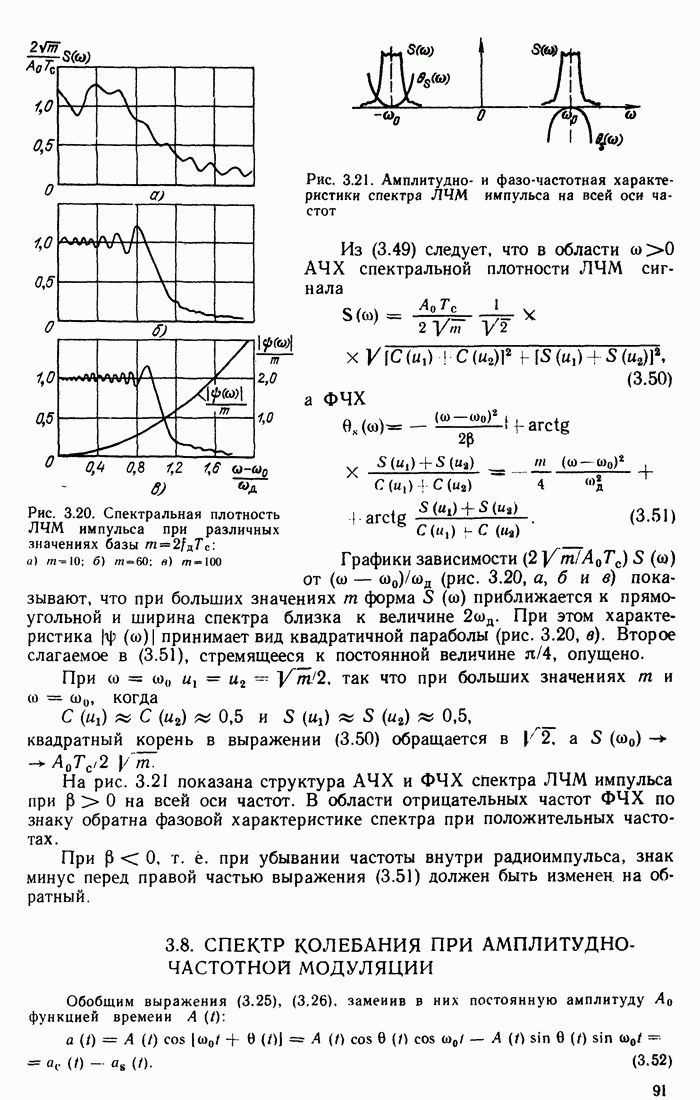
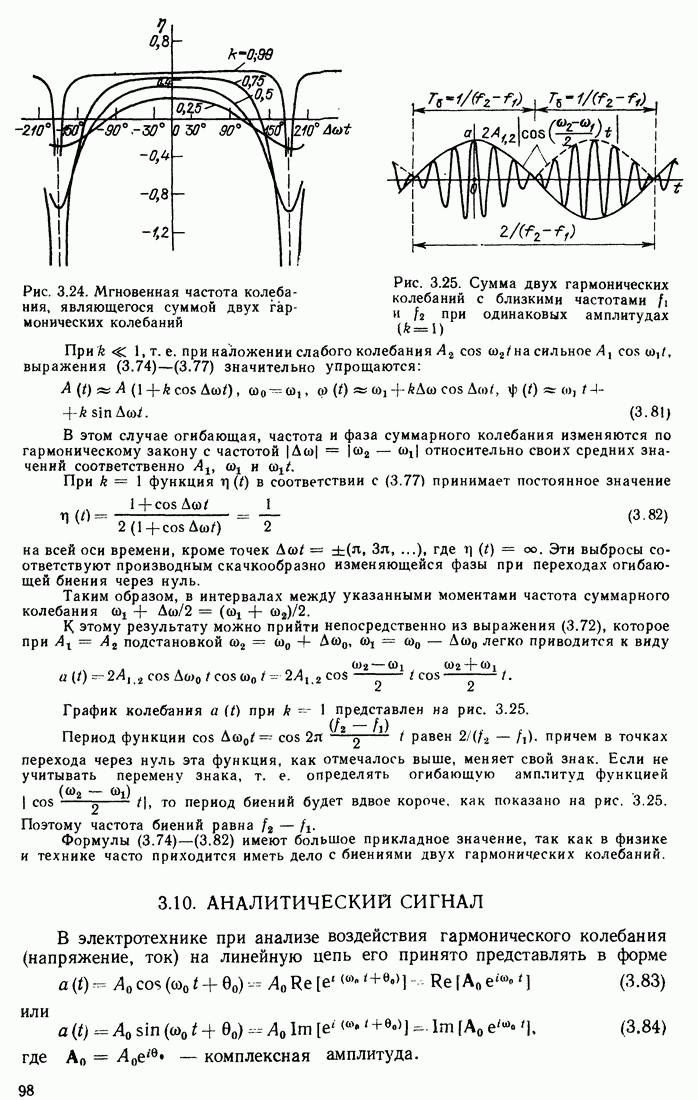
- 3.7. СПЕКТР РАДИОИМПУЛЬСА С ЧАСТОТНО-МОДУЛИРОВАННЫМ ЗАПОЛНЕНИЕМ
- 3.8. СПЕКТР КОЛЕБАНИЯ ПРИ АМПЛИТУДНО-ЧАСТОТНОЙ МОДУЛЯЦИИ
- 3.9. ОГИБАЮЩАЯ, ФАЗА И ЧАСТОТА УЗКОПОЛОСНОГО СИГНАЛА
- 3.10. АНАЛИТИЧЕСКИЙ СИГНАЛ
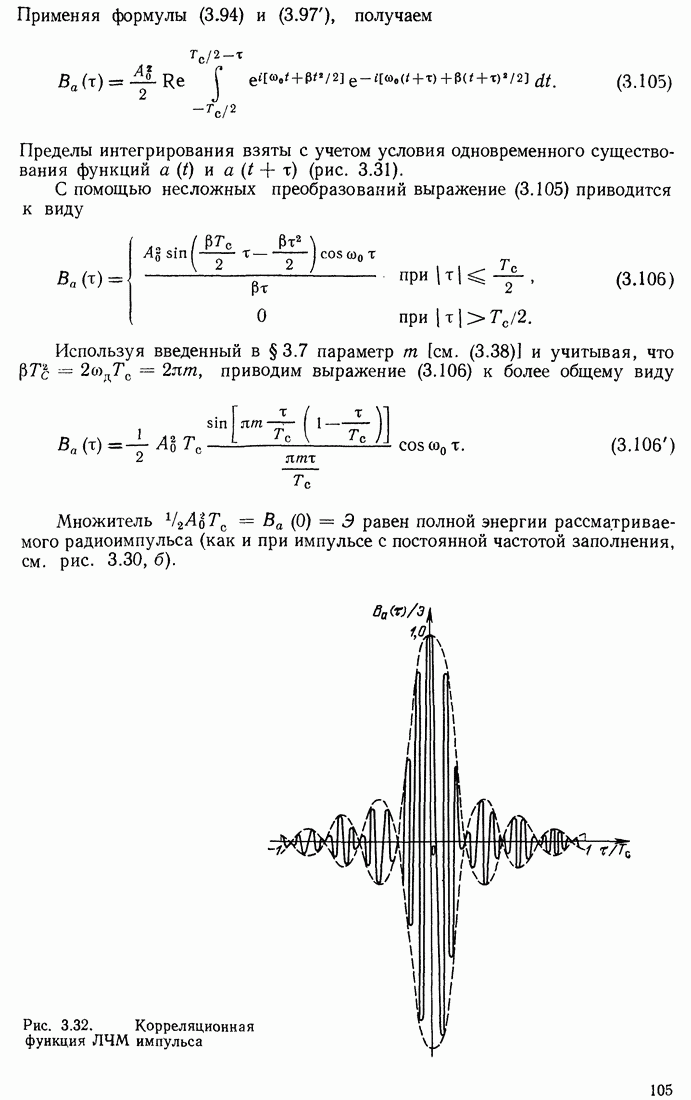
- 3.11. КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ МОДУЛИРОВАННОГО КОЛЕБАНИЯ
- 3.12. ДИСКРЕТИЗАЦИЯ УЗКОПОЛОСНОГО СИГНАЛА
- Глава 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ СИГНАЛОВ
- 4.2. ВИДЫ СЛУЧАЙНЫХ ПРОЦЕССОВ. ПРИМЕРЫ
- 4.3. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ МОЩНОСТИ СЛУЧАЙНОГО ПРОЦЕССА
- 4.4. СООТНОШЕНИЕ МЕЖДУ СПЕКТРАЛЬНОЙ ПЛОТНОСТЬЮ И КОВАРИАЦИОННОЙ ФУНКЦИЕЙ СЛУЧАЙНОГО ПРОЦЕССА
- 4.5. ВЗАИМНАЯ КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ И ВЗАИМНАЯ СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ДВУХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 4.6. УЗКОПОЛОСНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- 4.7. КОМПЛЕКСНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- 4.8. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ. ПРОСТРАНСТВО СИГНАЛОВ
- 4.9. ПРОСТРАНСТВО СЛУЧАЙНЫХ СИГНАЛОВ
- Глава 5. ЛИНЕЙНЫЕ РАДИОТЕХНИЧЕСКИЕ ЦЕПИ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
- 5.1. ОПРЕДЕЛЕНИЯ И СВОЙСТВА АКТИВНЫХ ЦЕПЕЙ
- 5.2. АКТИВНЫЙ ЧЕТЫРЕХПОЛЮСНИК КАК ЛИНЕЙНЫЙ УСИЛИТЕЛЬ
- 5.3. ЧАСТОТНЫЕ И ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ РАДИОЭЛЕКТРОННЫХ ЦЕПЕЙ
- 5.4. АПЕРИОДИЧЕСКИЙ УСИЛИТЕЛЬ
- 5.5. КАСКАДНОЕ СОЕДИНЕНИЕ ИДЕНТИЧНЫХ АПЕРИОДИЧЕСКИХ УСИЛИТЕЛЕЙ
- 5.6. РЕЗОНАНСНЫЙ УСИЛИТЕЛЬ
- 5.7. ОБРАТНАЯ СВЯЗЬ В АКТИВНОМ ЧЕТЫРЕХПОЛЮСНИКЕ
- 5.8. ПРИМЕНЕНИЕ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗИ ДЛЯ УЛУЧШЕНИЯ ХАРАКТЕРИСТИК УСИЛИТЕЛЯ
- 5.9. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АКТИВНЫХ ЦЕПЕЙ С ОБРАТНОЙ СВЯЗЬЮ. АЛГЕБРАИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
- 5.10. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
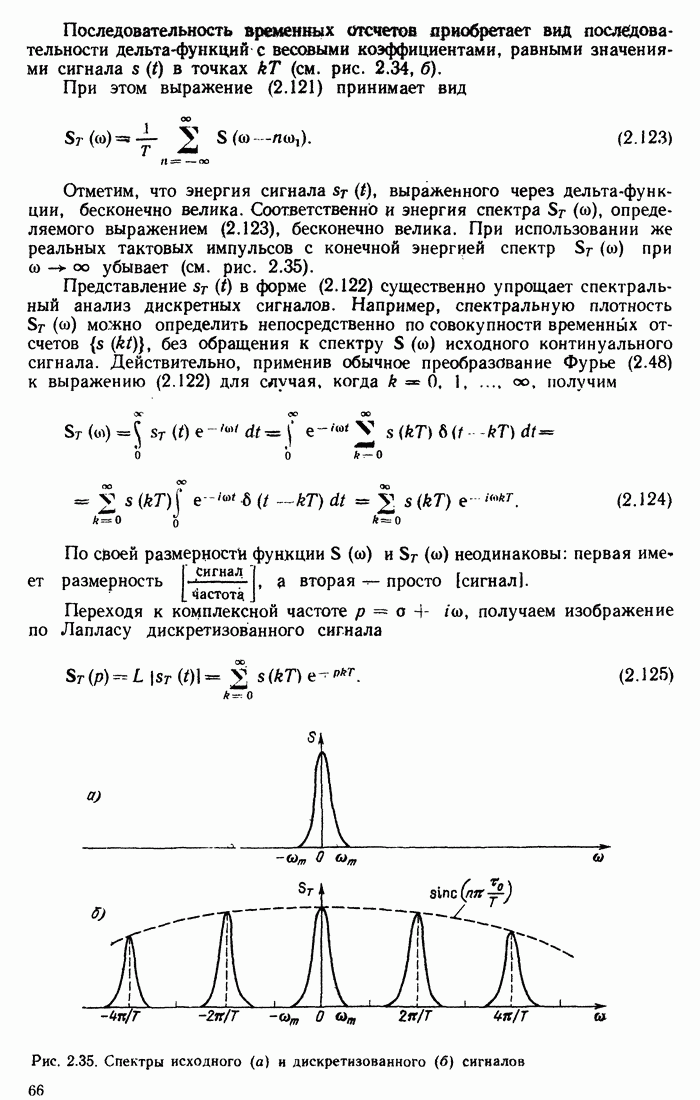
- Глава 6. ПРОХОЖДЕНИЕ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
- 6.2. СПЕКТРАЛЬНЫЙ МЕТОД
- 6.3. МЕТОД ИНТЕГРАЛА НАЛОЖЕНИЯ
- 6.4. ПРОХОЖДЕНИЕ ДИСКРЕТНЫХ СИГНАЛОВ ЧЕРЕЗ АПЕРИОДИЧЕСКИЙ УСИЛИТЕЛЬ
- 6.5. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ СИГНАЛОВ
- 6.6. АНАЛИЗ РАДИОСИГНАЛОВ В ИЗБИРАТЕЛЬНЫХ ЦЕПЯХ. МЕТОД ОГИБАЮЩЕЙ
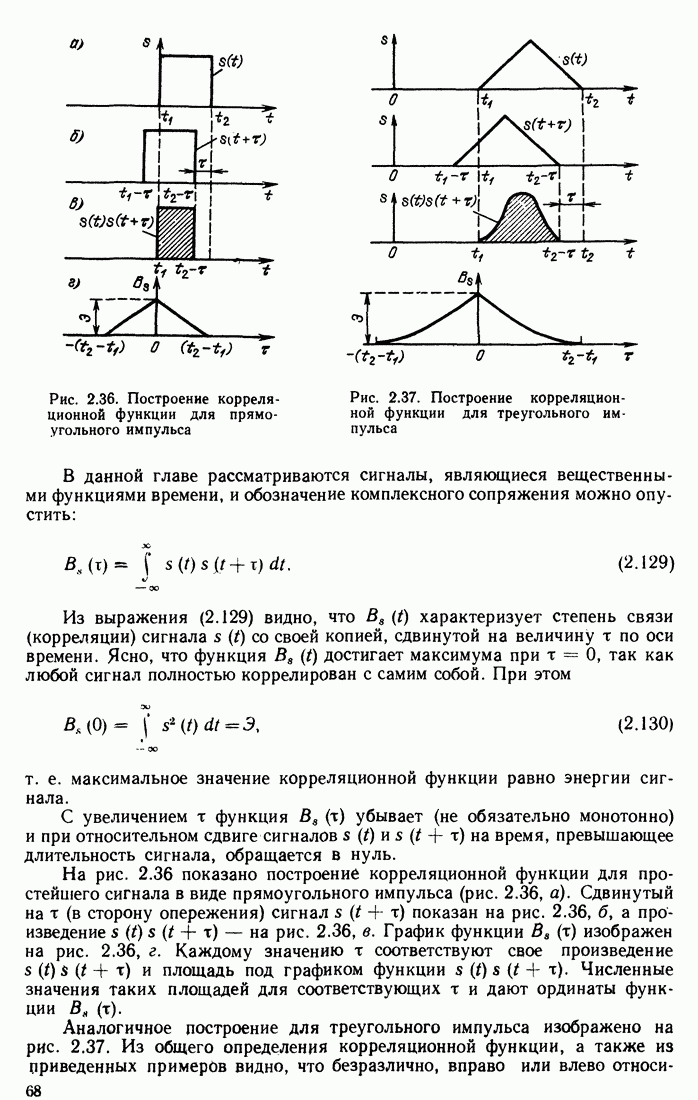
- 6.7. ПРОХОЖДЕНИЕ РАДИОИМПУЛЬСА ЧЕРЕЗ РЕЗОНАНСНЫЙ УСИЛИТЕЛЬ
- 6.8. ЛИНЕЙНЫЕ ИСКАЖЕНИЯ АМПЛИТУДНО-МОДУЛИРОВАННОГО КОЛЕБАНИЯ В РЕЗОНАНСНОМ УСИЛИТЕЛЕ
- 6.9. ПРОХОЖДЕНИЕ ФАЗОМАНИПУЛИРОВАННОГО КОЛЕБАНИЯ ЧЕРЕЗ РЕЗОНАНСНУЮ ЦЕПЬ
- 6.10. ПРОХОЖДЕНИЕ ЧАСТОТНО-МАНИПУЛИРОВАННОГО КОЛЕБАНИЯ ЧЕРЕЗ ИЗБИРАТЕЛЬНУЮ ЦЕПЬ
- 6.11. ПРОХОЖДЕНИЕ ЧАСТОТНО-МОДУЛИРОВАННОГО КОЛЕБАНИЯ ЧЕРЕЗ ИЗБИРАТЕЛЬНЫЕ ЦЕПИ
- Глава 7. ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
- 7.1. ПРЕОБРАЗОВАНИЕ ХАРАКТЕРИСТИК СЛУЧАЙНОГО ПРОЦЕССА В ЛИНЕЙНЫХ ЦЕПЯХ
- 7.2. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ МОЩНОСТИ И КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ СЛУЧАЙНОГО ПРОЦЕССА НА ВЫХОДЕ ЦЕПИ
- 7.3. ХАРАКТЕРИСТИКИ СОБСТВЕННЫХ ШУМОВ В РАДИОЭЛЕКТРОННЫХ ЦЕПЯХ
- 7.4. ДИФФЕРЕНЦИРОВАНИЕ СЛУЧАЙНОЙ ФУНКЦИИ
- 7.5. ИНТЕГРИРОВАНИЕ СЛУЧАЙНОЙ ФУНКЦИИ
- 7.6. ПАРАМЕТРЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОГО ПРОЦЕССА НА ВЫХОДЕ ЛИНЕЙНОЙ ЦЕПИ. ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ
- 7.7. НОРМАЛИЗАЦИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ В УЗКОПОЛОСНЫХ ЛИНЕЙНЫХ ЦЕПЯХ
- Глава 8. НЕЛИНЕЙНЫЕ ЦЕПИ И МЕТОДЫ ИХ АНАЛИЗА
- 8.2. АППРОКСИМАЦИЯ НЕЛИНЕЙНЫХ ХАРАКТЕРИСТИК
- 8.3. ВОЗДЕЙСТВИЕ УЗКОПОЛОСНОГО РАДИОСИГНАЛА НА БЕЗЫНЕРЦИОННЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ
- 8.4. ВОЗДЕЙСТВИЕ БИГАРМОНИЧЕСКОГО КОЛЕБАНИЯ НА НЕЛИНЕЙНЫЙ РЕЗИСТИВНЫЙ ЭЛЕМЕНТ
- 8.5. НЕЛИНЕЙНОЕ РЕЗОНАНСНОЕ УСИЛЕНИЕ
- 8.6. УМНОЖЕНИЕ ЧАСТОТЫ
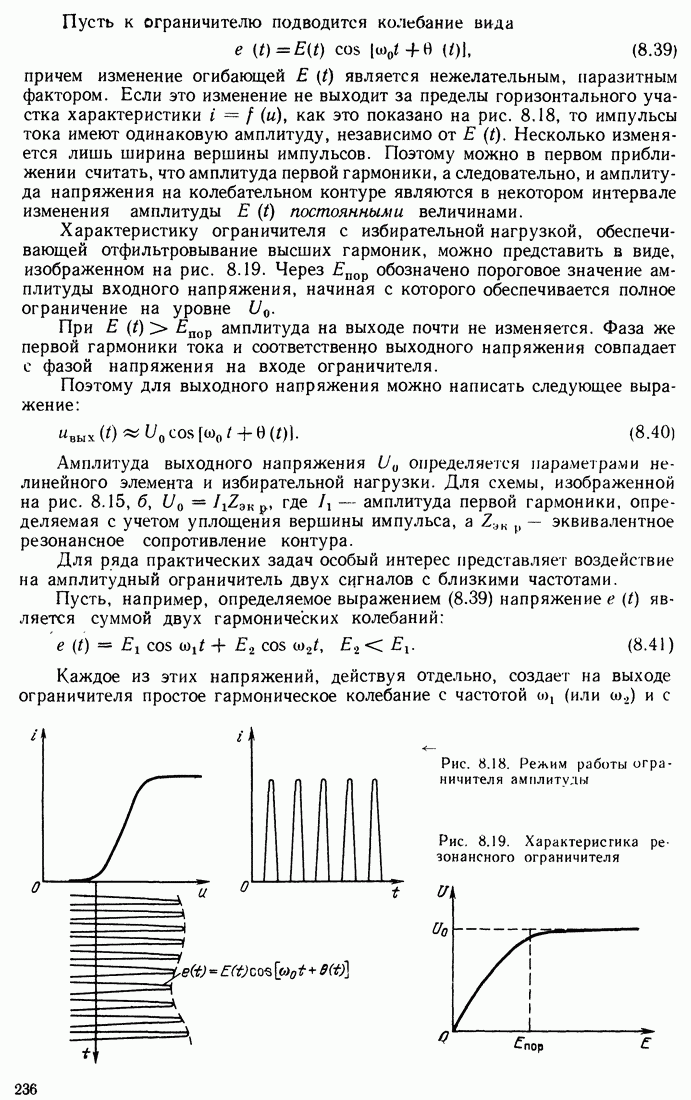
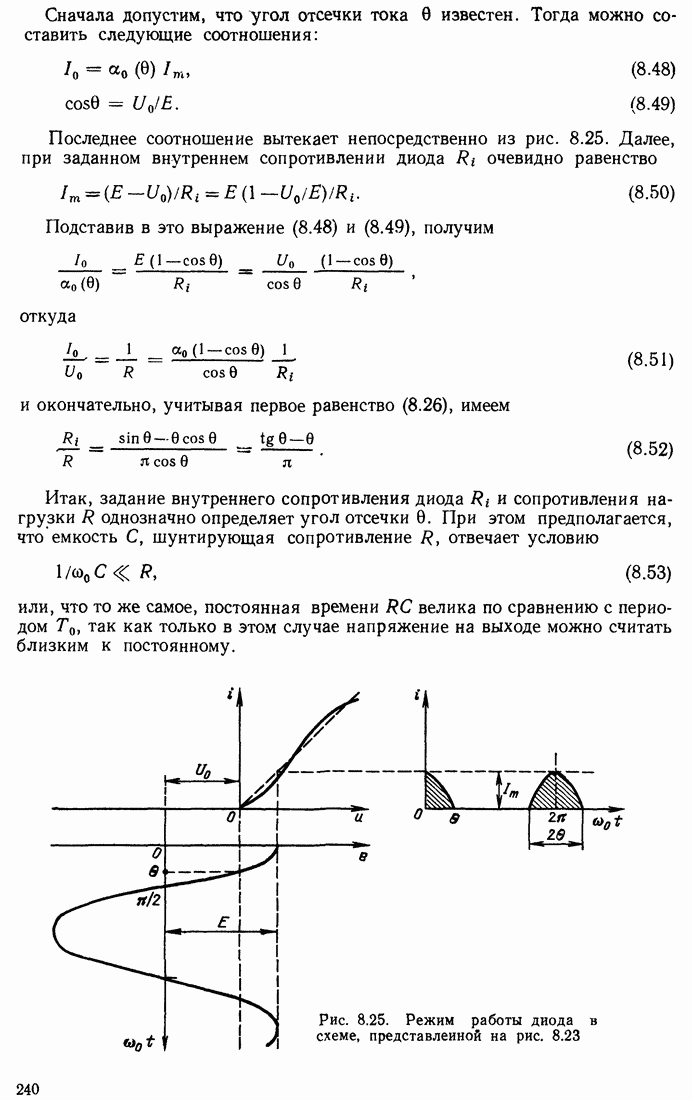
- 8.7. АМПЛИТУДНОЕ ОГРАНИЧЕНИЕ
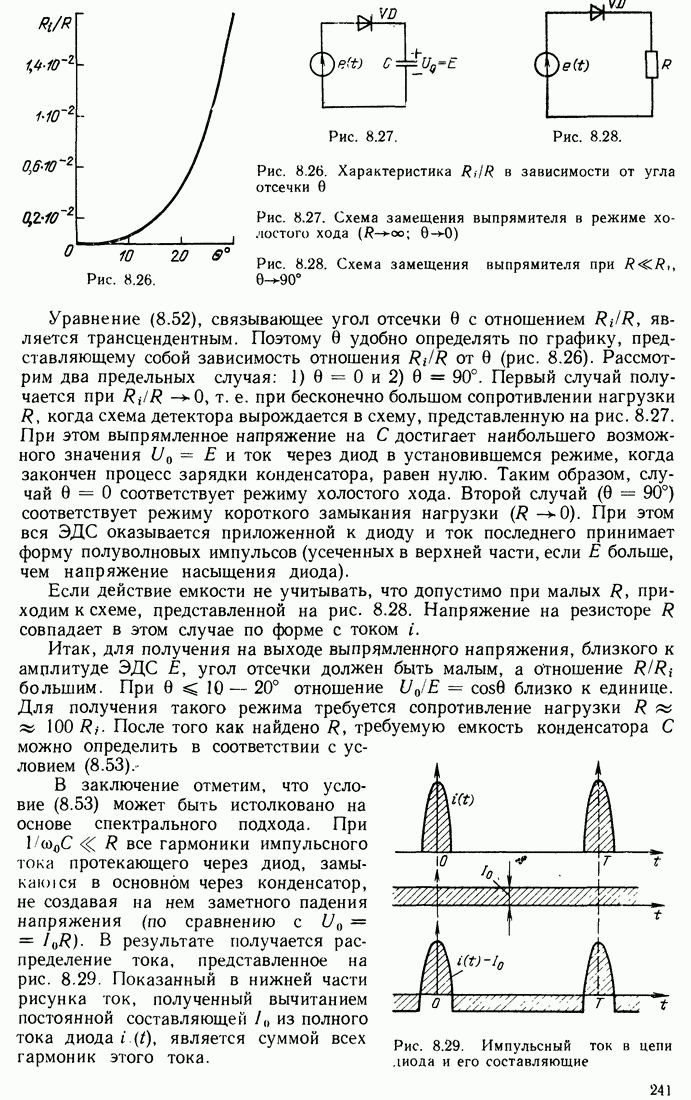
- 8.8. НЕЛИНЕЙНАЯ ЦЕПЬ С ФИЛЬТРАЦИЕЙ ПОСТОЯННОГО ТОКА (ВЫПРЯМЛЕНИЕ)
- 8.9. АМПЛИТУДНОЕ ДЕТЕКТИРОВАНИЕ
- 8.10. ЧАСТОТНОЕ И ФАЗОВОЕ ДЕТЕКТИРОВАНИЕ
- 8.11. ПРЕОБРАЗОВАНИЕ ЧАСТОТЫ СИГНАЛА
- 8.12. СИНХРОННОЕ ДЕТЕКТИРОВАНИЕ
- 8.13. ПОЛУЧЕНИЕ АМПЛИТУДНО-МОДУЛИРОВАННЫХ КОЛЕБАНИИ
- 8.14. РЕЗОНАНС В КОЛЕБАТЕЛЬНОМ КОНТУРЕ С НЕЛИНЕЙНОЙ ЕМКОСТЬЮ
- 8.15. ВОЗДЕЙСТВИЕ ГАРМОНИЧЕСКОГО СИГНАЛА НА НЕЛИНЕЙНУЮ ЕМКОСТЬ. УМНОЖИТЕЛЬ ЧАСТОТЫ НА ВАРАКТОРЕ
- 8.16. ВОЗДЕЙСТВИЕ ДВУХ ГАРМОНИЧЕСКИХ КОЛЕБАНИИ НА ЦЕПЬ С НЕЛИНЕЙНЫМ ЭНЕРГОЕМКИМ ЭЛЕМЕНТОМ
- 8.17. ТЕОРЕМА МЭНЛИ—РОУ
- 8.18. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ ЦЕПЯХ ПО ЗАДАННОМУ ДИФФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ
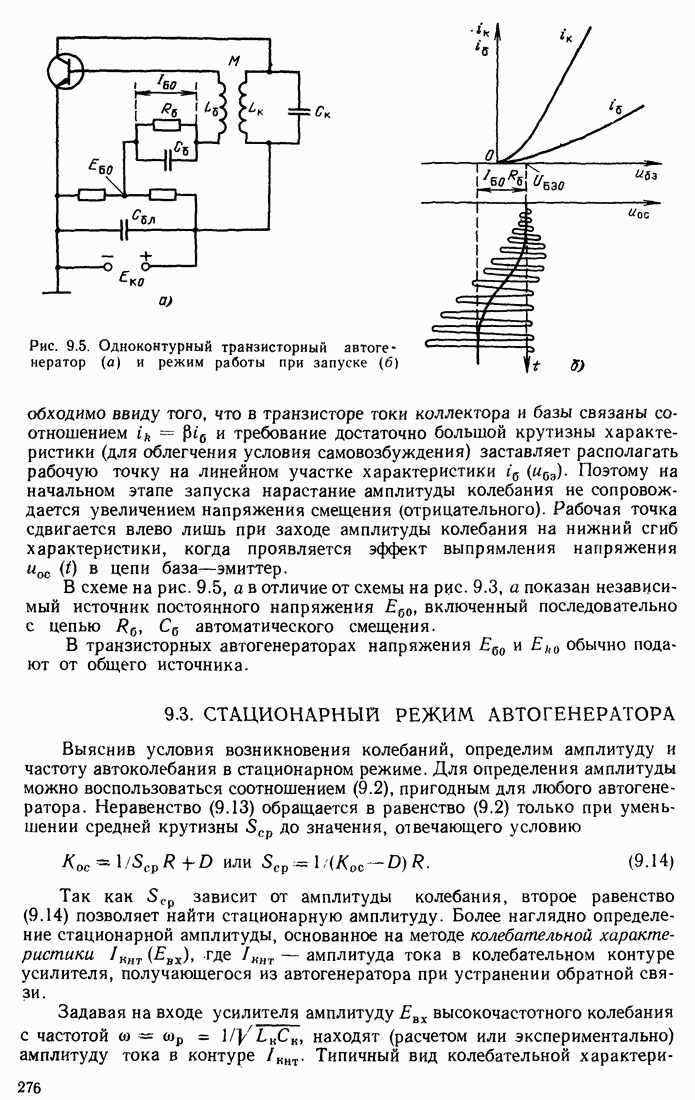
- Глава 9. ГЕНЕРИРОВАНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 9.1. АВТОКОЛЕБАТЕЛЬНАЯ СИСТЕМА
- 9.2. ВОЗНИКНОВЕНИЕ КОЛЕБАНИЯ В АВТОГЕНЕРАТОРЕ
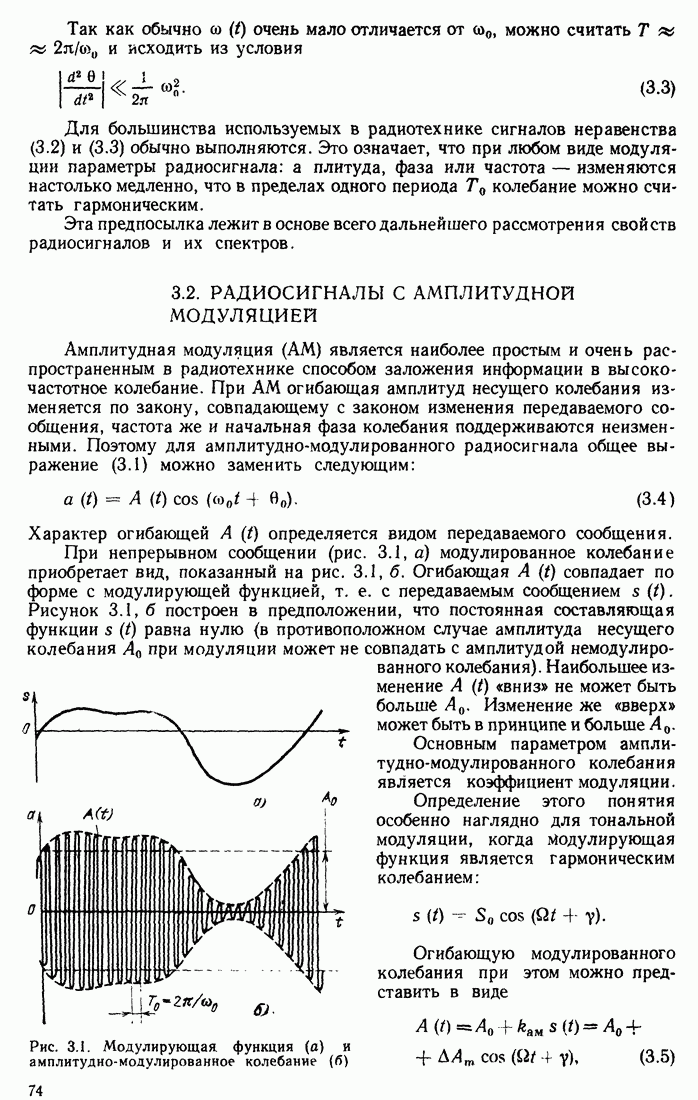
- 9.3. СТАЦИОНАРНЫЙ РЕЖИМ АВТОГЕНЕРАТОРА
- 9.4. МЯГКИЙ И ЖЕСТКИЙ РЕЖИМЫ САМОВОЗБУЖДЕНИЯ
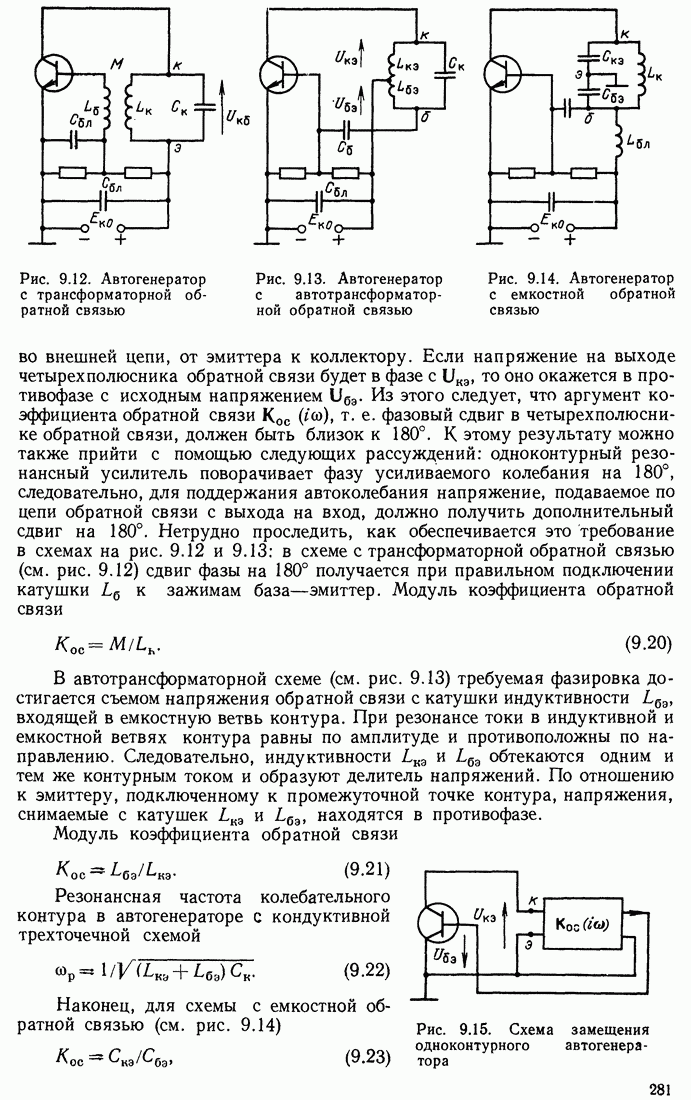
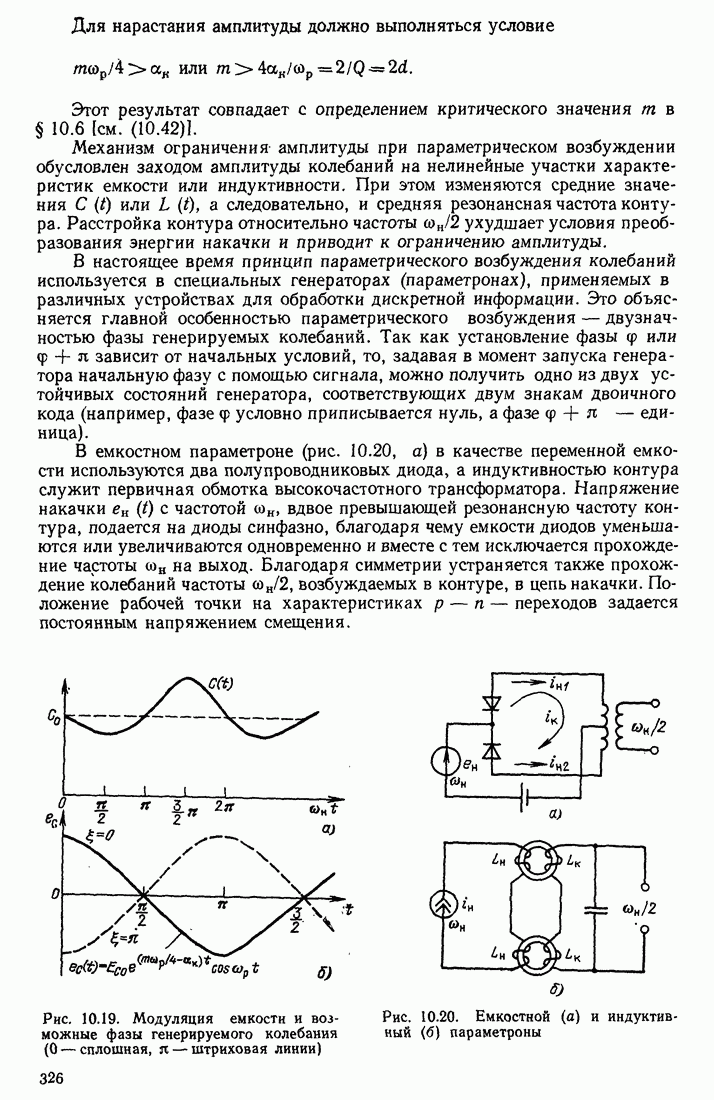
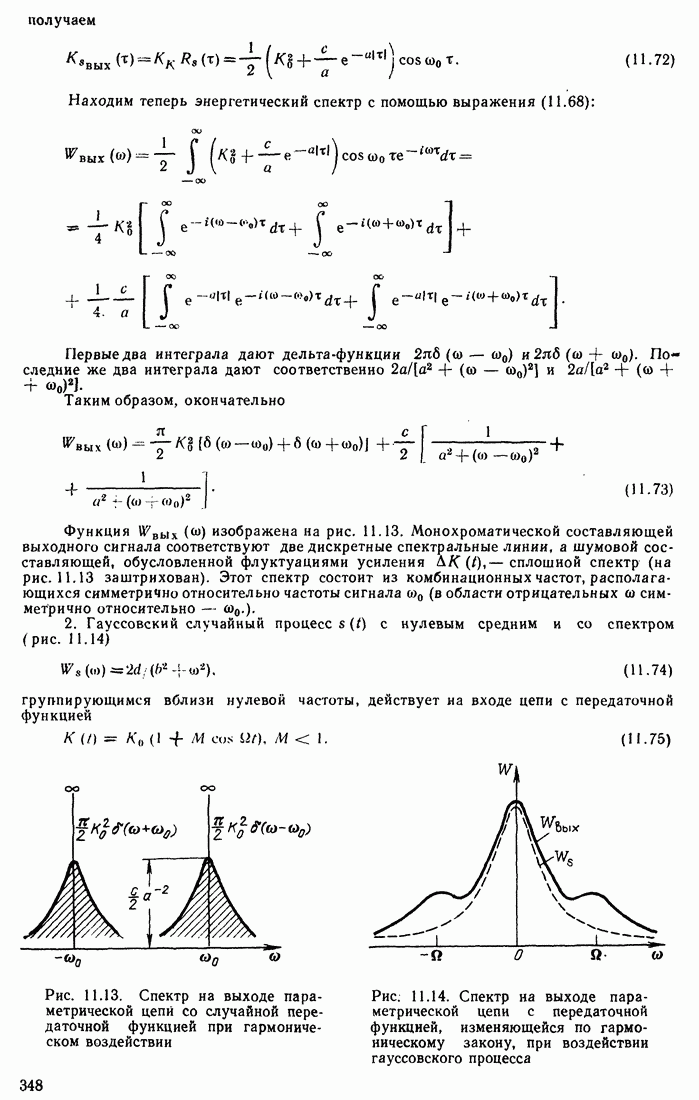
- 9.5. ПРИМЕРЫ СХЕМ АВТОГЕНЕРАТОРОВ
- 9.6. НЕЛИНЕЙНОЕ УРАВНЕНИЕ АВТОГЕНЕРАТОРА
- 9.7. МЕТОД ФАЗОВОЙ ПЛОСКОСТИ
- 9.8. ФАЗОВЫЕ ПОРТРЕТЫ АВТОГЕНЕРАТОРА
- 9.9. АВТОГЕНЕРАТОРЫ С ВНУТРЕННЕЙ ОБРАТНОЙ СВЯЗЬЮ
- 9.10. АВТОГЕНЕРАТОР С ЛИНИЕЙ ЗАДЕРЖКИ В ЦЕПИ ОБРАТНОЙ СВЯЗИ
- 9.11. RC-ГЕНЕРАТОРЫ
- 9.12. ДЕЙСТВИЕ ГАРМОНИЧЕСКОЙ ЭДС НА ЦЕПИ С ПОЛОЖИТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ. РЕГЕНЕРАЦИЯ
- 9.13. ДЕЙСТВИЕ ГАРМОНИЧЕСКОЙ ЭДС НА АВТОГЕНЕРАТОР. ЗАХВАТЫВАНИЕ ЧАСТОТЫ
- 9.14. УГЛОВАЯ МОДУЛЯЦИЯ В АВТОГЕНЕРАТОРЕ
- Глава 10. ЦЕПИ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10.1. ОБЩИЕ ХАРАКТЕРИСТИКИ ЦЕПЕЙ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10.2. ПРОХОЖДЕНИЕ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10.3. ПРИМЕР ОПРЕДЕЛЕНИЯ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ ПАРАМЕТРИЧЕСКОЙ ЦЕПИ
- 10.4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЦЕПИ С ПЕРИОДИЧЕСКИ ИЗМЕНЯЮЩИМСЯ ПАРАМЕТРОМ
- 10.5. ПРИНЦИП ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ СИГНАЛОВ
- 10.6. ОДНОКОНТУРНЫЙ ПАРАМЕТРИЧЕСКИЙ УСИЛИТЕЛЬ
- 10.7. ДВУХКОНТУРНЫЙ ПАРАМЕТРИЧЕСКИЙ УСИЛИТЕЛЬ
- 10.8. ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИИ
- 10.9. СОПОСТАВЛЕНИЕ ПАРАМЕТРИЧЕСКИХ И НЕЛИНЕЙНЫХ ПРЕОБРАЗОВАНИИ СИГНАЛОВ
- Глава 11. ВОЗДЕЙСТВИЕ СЛУЧАЙНЫХ КОЛЕБАНИЙ НА НЕЛИНЕЙНЫЕ И ПАРАМЕТРИЧЕСКИЕ ЦЕПИ
- 11.2. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА В БЕЗЫНЕРЦИОННЫХ НЕЛИНЕЙНЫХ ЦЕПЯХ
- 11.3. ПРЕОБРАЗОВАНИЕ СПЕКТРА СЛУЧАЙНОГО ПРОЦЕССА В БЕЗЫНЕРЦИОННОМ НЕЛИНЕЙНОМ ЭЛЕМЕНТЕ
- 11.4. ВОЗДЕЙСТВИЕ УЗКОПОЛОСНОГО ШУМА НА АМПЛИТУДНЫЙ ДЕТЕКТОР
- 11.6. СОВМЕСТНОЕ ВОЗДЕЙСТВИЕ ГАРМОНИЧЕСКОГО СИГНАЛА И ГАУССОВСКОГО ШУМА НА АМПЛИТУДНЫЙ ДЕТЕКТОР
- 11.6. СОВМЕСТНОЕ ВОЗДЕЙСТВИЕ ГАРМОНИЧЕСКОГО СИГНАЛА И ГАУССОВСКОГО ШУМА НА ЧАСТОТНЫЙ ДЕТЕКТОР
- 11.7. ВЗАИМОДЕЙСТВИЕ ГАРМОНИЧЕСКОГО СИГНАЛА И ГАУССОВСКОГО ШУМА В АМПЛИТУДНОМ ОГРАНИЧИТЕЛЕ С РЕЗОНАНСНОЙ НАГРУЗКОЙ
- 11.8. КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ И СПЕКТР СЛУЧАЙНОГО ПРОЦЕССА В ЛИНЕЙНОЙ ПАРАМЕТРИЧЕСКОЙ ЦЕПИ
- 11.9. ВЛИЯНИЕ МУЛЬТИПЛИКАТИВНОЙ ПОМЕХИ НА ЗАКОН РАСПРЕДЕЛЕНИЯ СИГНАЛА
- Глава 12. ДИСКРЕТНАЯ ОБРАБОТКА СИГНАЛОВ. ЦИФРОВЫЕ ФИЛЬТРЫ
- 12.2. ПРИНЦИП ДИСКРЕТНОЙ ФИЛЬТРАЦИИ
- 12.3. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЦИФРОВОГО ФИЛЬТРА
- 12.4. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СИГНАЛОВ
- 12.5. ПРИМЕНЕНИЕ МЕТОДА Z-ПРЕОБРАЗОВАНИЯ ДЛЯ АНАЛИЗА ДИСКРЕТНЫХ СИГНАЛОВ И ЦЕПЕЙ
- 12.6. Z-ПРЕОБРАЗОВАНИЕ BPEMEHHЫХ ФУНКЦИЙ
- 12.7. z-ПРЕОБРАЗОВАНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ДИСКРЕТНЫХ ЦЕПЕЙ
- 12.8. ПРИМЕРЫ АНАЛИЗА ЦИФРОВЫХ ФИЛЬТРОВ
- 12.9. ЦИФРОВЫЕ ФИЛЬТРЫ С КОМПЛЕКСНЫМИ ВЕСОВЫМИ КОЭФФИЦИЕНТАМИ
- 12.10. ПРЕОБРАЗОВАНИЕ АНАЛОГ—ЦИФРА. ШУМЫ КВАНТОВАНИЯ
- 12.11. ПРЕОБРАЗОВАНИЕ ЦИФРА—АНАЛОГ И ВОССТАНОВЛЕНИЕ КОНТИНУАЛЬНОГО СИГНАЛА
- 12.12. БЫСТРОДЕЙСТВИЕ АРИФМЕТИЧЕСКОГО УСТРОЙСТВА ЦИФРОВОГО ФИЛЬТРА
- 12.13. АЛГОРИТМ ЦИФРОВОЙ ФИЛЬТРАЦИИ ВО ВРЕМЕННОЙ И ЧАСТОТНОЙ ОБЛАСТЯХ
- 12.14. БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 12.15. СПЕКТРАЛЬНЫЙ АНАЛИЗ НА БАЗЕ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 12.16. ПРИМЕНЕНИЕ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ В УСТРОЙСТВАХ ОБРАБОТКИ СИГНАЛОВ
- Глава 13. ПРИНЦИПЫ ОПТИМАЛЬНОЙ ЛИНЕЙНОИ ФИЛЬТРАЦИИ СИГНАЛА НА ФОНЕ ПОМЕХ
- 13.2. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ОПТИМАЛЬНОГО ФИЛЬТРА
- 13.3. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА СОГЛАСОВАННОГО ФИЛЬТРА. ФИЗИЧЕСКАЯ ОСУЩЕСТВИМОСТЬ
- 13.4. СИГНАЛ И ПОМЕХА НА ВЫХОДЕ СОГЛАСОВАННОГО ФИЛЬТРА
- 13.5. ПРИМЕРЫ ПОСТРОЕНИЯ СОГЛАСОВАННЫХ ФИЛЬТРОВ
- 13.6. ФОРМИРОВАНИЕ СИГНАЛА, СОПРЯЖЕННОГО С ЗАДАННЫМ ФИЛЬТРОМ
- 13.7. ФИЛЬТРАЦИЯ ЗАДАННОГО СИГНАЛА ПРИ НЕБЕЛОМ ШУМЕ
- 13.8. ФИЛЬТРАЦИЯ СИГНАЛА С НЕИЗВЕСТНОЙ НАЧАЛЬНОЙ ФАЗОЙ
- 13.9. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ КОМПЛЕКСНОГО СИГНАЛА. КВАДРАТУРНАЯ ОБРАБОТКА
- 13.10. ЦИФРОВОЙ СОГЛАСОВАННЫЙ ФИЛЬТР
- Глава 14. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ НЕКОТОРЫМИ СПЕЦИАЛЬНЫМИ ФУНКЦИЯМИ
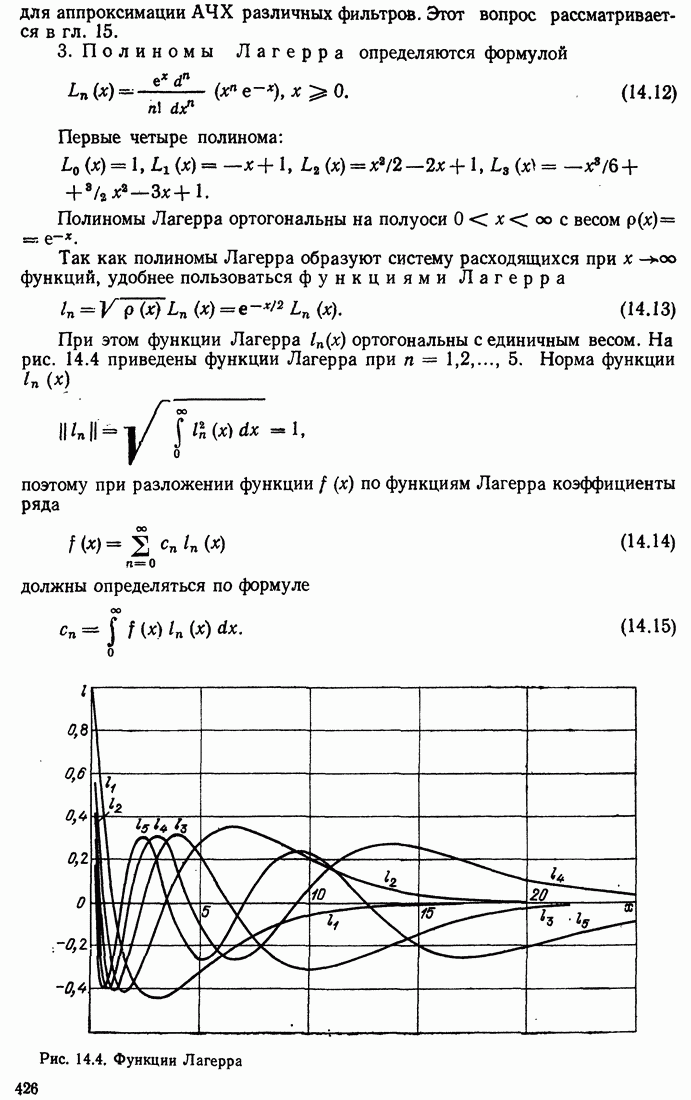
- 14.2. ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ И ФУНКЦИИ НЕПРЕРЫВНОГО ТИПА
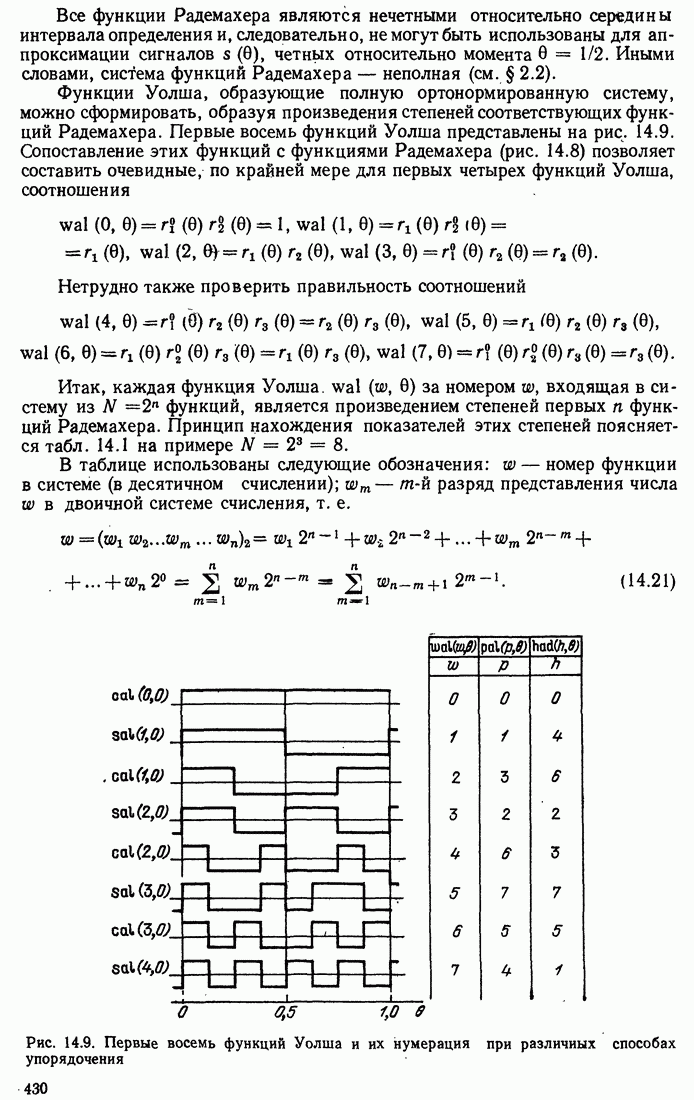
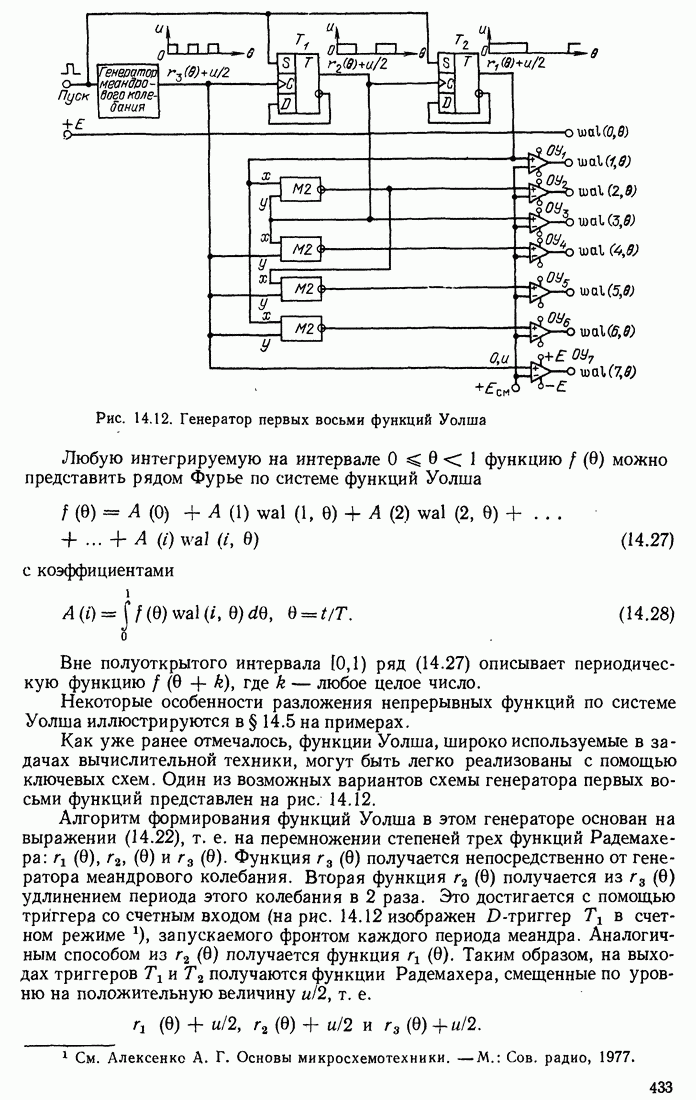
- 14.3. ФУНКЦИИ УОЛША
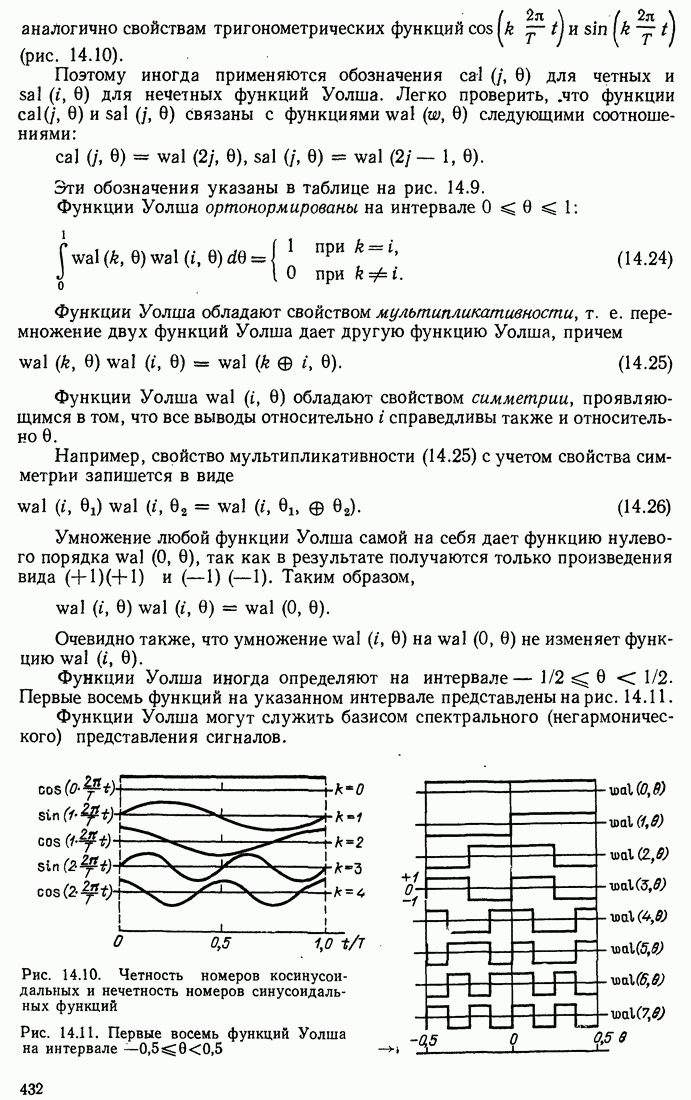
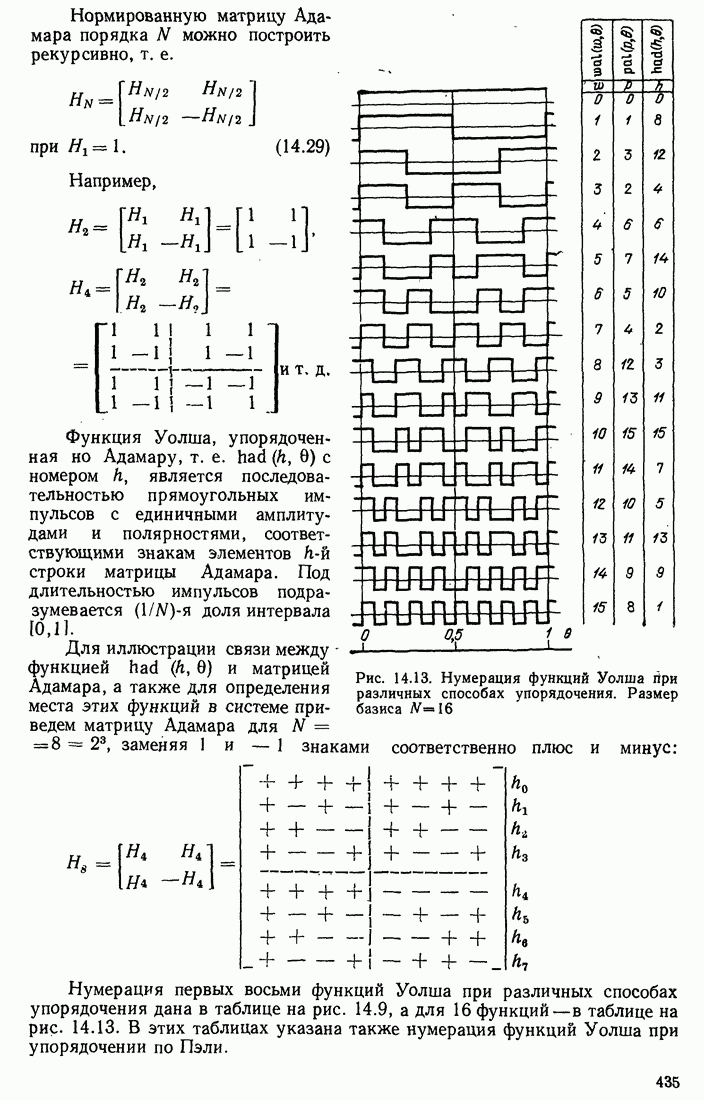
- 14.4. РАЗЛИЧНЫЕ СПОСОБЫ НУМЕРАЦИИ ФУНКЦИЙ УОЛША
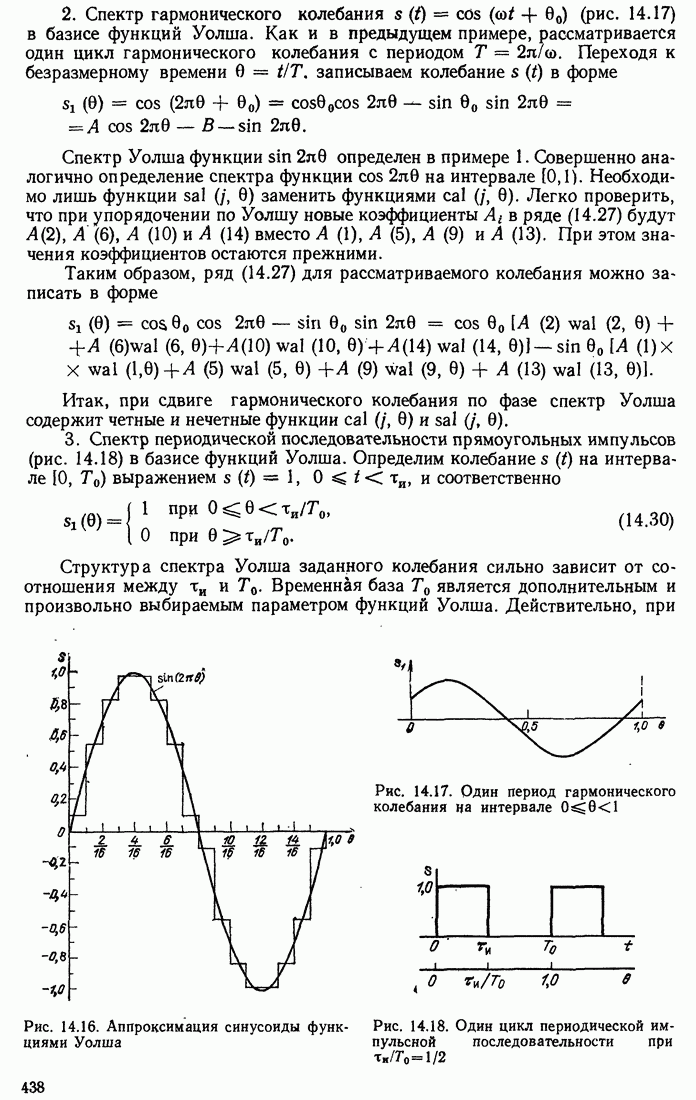
- 14.5. ПРИМЕРЫ ПРИМЕНЕНИЯ ФУНКЦИЙ УОЛША
- 14.6. ДИСКРЕТНЫЕ ФУНКЦИИ УОЛША
- Глава 15. ЭЛЕМЕНТЫ СИНТЕЗА ЛИНЕЙНЫХ РАДИОЦЕПЕЙ
- 15.2. ПРЕДСТАВЛЕНИЕ АНАЛОГОВОГО ЧЕТЫРЕХПОЛЮСНИКА КАСКАДНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТАРНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ
- 15.3. РЕАЛИЗАЦИЯ БЕЗЫНДУКТИВНОСТНОИ ЦЕПИ ВТОРОГО ПОРЯДКА
- 15.4. ОСОБЕННОСТИ СИНТЕЗА ЧЕТЫРЕХПОЛЮСНИКА ПО ЗАДАННОЙ АМПЛИТУДНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ
- 15.5. СИНТЕЗ ФИЛЬТРА НИЖНИХ ЧАСТОТ. ФИЛЬТР БАТТЕРВОРТА
- 15.6. ПРИМЕР СИНТЕЗА ФИЛЬТРА БАТТЕРВОРТА ВТОРОГО ПОРЯДКА
- 15.7. ФИЛЬТР ЧЕБЫШЕВА (НИЖНИХ ЧАСТОТ)
- 15.8. СИНТЕЗ РАЗЛИЧНЫХ ФИЛЬТРОВ НА ОСНОВЕ ФИЛЬТРА НИЖНИХ ЧАСТОТ
- 15.9. СВЯЗЬ МЕЖДУ АМПЛИТУДНО- И ФАЗОЧАСТОТНОЙ ХАРАКТЕРИСТИКАМИ В ЦИФРОВЫХ ЦЕПЯХ
- 15.10. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ФЧХ ЦИФРОВОГО ФИЛЬТРА ПО ЗАДАННОЙ АЧХ
- 15.11. СИНТЕЗ ЦИФРОВЫХ ФИЛЬТРОВ. ОБЩИЕ ЗАМЕЧАНИЯ
- 15.12. СИНТЕЗ ЦИФРОВЫХ ФИЛЬТРОВ ПО АНАЛОГОВОМУ ПРОТОТИПУ
- 15.13. МЕТОД ИНВАРИАНТНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- Глава 16. ОБОБЩЕННАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ СИГНАЛОВ. КЕПСТРАЛЬНЫЙ АНАЛИЗ
- 16.1. ОБОБЩЕННЫЙ ПРИНЦИП СУПЕРПОЗИЦИИ
- 16.2. ОБОБЩЕННАЯ СХЕМА ГОМОМОРФНОЙ ОБРАБОТКИ СИГНАЛОВ
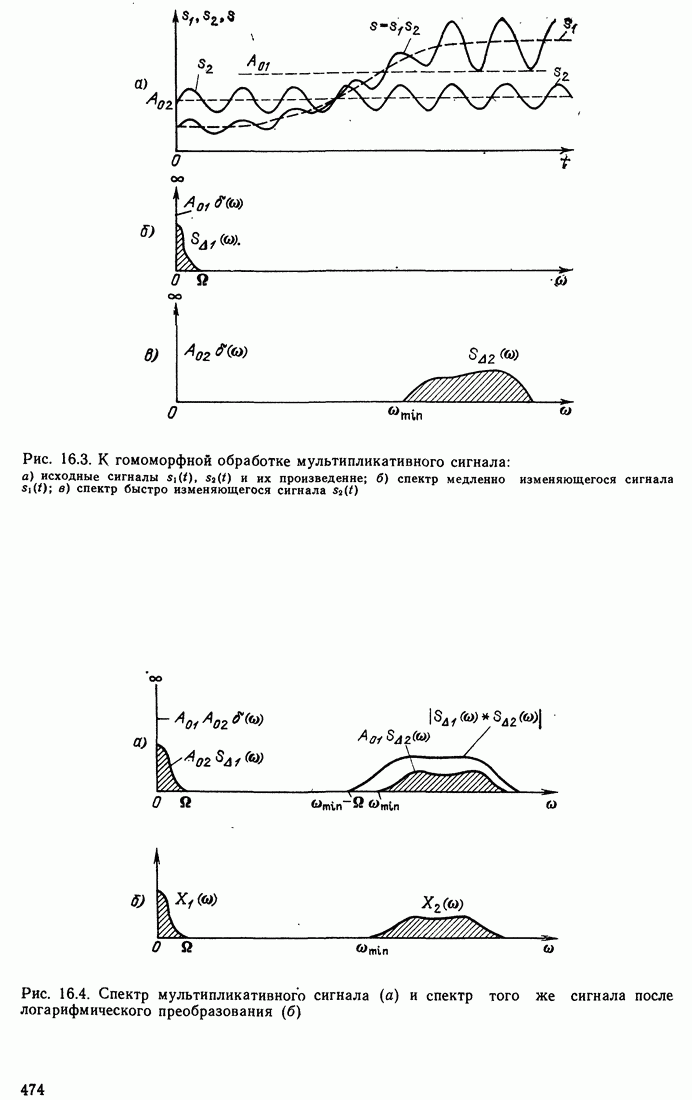
- 16.3. ГОМОМОРФНАЯ ОБРАБОТКА МУЛЬТИПЛИКАТИВНОГО СИГНАЛА
- 16.4. ГОМОМОРФНАЯ ОБРАБОТКА СВЕРНУТОГО СИГНАЛА
- 16.5. КЕПСТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ. КЕПСТР МОЩНОСТИ
- 16.6. ОПРЕДЕЛЕНИЕ ЗАДЕРЖКИ СИГНАЛА
- 16.7. ПРИМЕР ОПРЕДЕЛЕНИЯ ЗАДЕРЖКИ СИГНАЛА
- 16.8. ВЛИЯНИЕ ПОМЕХ
- 16.9. КОМПЛЕКСНЫЙ КЕПСТР
- 16.10. СВОЙСТВА КОМПЛЕКСНОГО КЕПСТРА
- 16.11. НЕКОТОРЫЕ СВОЙСТВА КЕПСТРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ
- Приложение 1. ПРАВИЛА ПЕРЕХОДА ОТ ИЗОБРАЖЕНИЯ ПО ЛАПЛАСУ Ls(p) К СПЕКТРАЛЬНОЙ ПЛОТНОСТИ S(w)
- Приложение 2. ПРАВИЛО ПРЕОБРАЗОВАНИЯ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ ПРИ ИНТЕГРИРОВАНИИ СИГНАЛА
- Приложение 3. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ УЗКОПОЛОСНОГО СИГНАЛА С НЕИЗВЕСТНОЙ НАЧАЛЬНОЙ ФАЗОЙ
- Приложение 4. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ КОМПЛЕКСНОГО СИГНАЛА
- Приложение 5. О НЕОДНОЗНАЧНОСТИ ОПРЕДЕЛЕНИЯ ФАЗОЧАСТОТНОЙ ХАРАКТЕРИСТИКИ СПЕКТРА СИГНАЛА
- СПИСОК ЛИТЕРАТУРЫ