| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.12. СООТНОШЕНИЕ МЕЖДУ ДЛИТЕЛЬНОСТЬЮ СИГНАЛА И ШИРИНОЙ ЕГО СПЕКТРА. СКОРОСТЬ УБЫВАНИЯ СПЕКТРА
Из предыдущих параграфов уже ясно, что чем меньше длительность сигнала, тем шире его спектр. Для установления количественных соотношений между указанными параметрами сигнала необходимо условиться об определении понятий длительность сигнала и ширина его спектра. В практике применяются различные определения, выбор которых зависит от назначения сигнала, его формы, а также от структуры спектра. В некоторых случаях выбор является произвольным. Так, ширину спектра прямоугольного импульса определяют либо как основание главного лепестка (например, в п. 1 § 2.10), либо на уровне  от максимального значения спектральной плотности. Длительность колоколообразного импульса (см. § 2.10, п. 3) и ширину его спектра иногда определяют на уровне 0,606 от максимального значения соответственно
от максимального значения спектральной плотности. Длительность колоколообразного импульса (см. § 2.10, п. 3) и ширину его спектра иногда определяют на уровне 0,606 от максимального значения соответственно  или
или  . Часто пользуются энергетическим критерием, понимая под шириной спектра полосу частот, содержащую заданную долю полной энергии сигнала.
. Часто пользуются энергетическим критерием, понимая под шириной спектра полосу частот, содержащую заданную долю полной энергии сигнала.
Для практики важное значение имеет также оценка протяженности «хвостов» спектра вне полосы частот, содержащей основную часть энергии сигнала.
1. ОПРЕДЕЛЕНИЕ ПРОИЗВЕДЕНИЯ ПОЛОСА Х ДЛИТЕЛЬНОСТЬ
Для выявления предельных соотношений, связывающих длительность сигнала и ширину спектра, в современной теории сигналов большое распространение получил метод моментов.
По аналогии с понятием момента инерции в механике эффективную длительность сигнала  можно определить выражением
можно определить выражением

где середина импульса  определяется из условия
определяется из условия

Имеется в виду, что функция  интегрируема с квадратом (сигнал с конечной энергией).
интегрируема с квадратом (сигнал с конечной энергией).
Аналогично эффективная ширина спектра  определяется выражением
определяется выражением

Так как модуль спектра  не зависит от смещения
не зависит от смещения  во времени, можно положить
во времени, можно положить  Наконец, сигнал
Наконец, сигнал  можно нормировать таким образом, чтобы его энергия Э равнялась единице и, следовательно,
можно нормировать таким образом, чтобы его энергия Э равнялась единице и, следовательно,

При этих условиях выражения для  и принимают вид
и принимают вид

и, следовательно, произведение длительность x полоса

Нужно иметь в виду, что  являются среднеквадратическими отклонениями соответственно от
являются среднеквадратическими отклонениями соответственно от  и
и  . Поэтому полную длительность сигнала следует приравнять
. Поэтому полную длительность сигнала следует приравнять  а полную ширину спектра (включая и область отрицательных частот) — величине
а полную ширину спектра (включая и область отрицательных частот) — величине  .
.
Произведение зависит от формы сигнала, однако оно не может быть меньше 1/2. Оказывается, что наименьшее возможное значение  соответствует колоколообразному импульсу.
соответствует колоколообразному импульсу.
Метод моментов применим не к любым сигналам. Из выражений для  видно, что функция
видно, что функция  с увеличением t должна убывать быстрее, чем
с увеличением t должна убывать быстрее, чем  , а функция
, а функция  — быстрее, чем
— быстрее, чем  так как в противном случае соответствующие интегралы стремятся к бесконечности (расходятся).
так как в противном случае соответствующие интегралы стремятся к бесконечности (расходятся).
В частности, это относится к спёктру строго прямоугольного импульса, когда

В этом случае выражение для не имеет смысла и оценку эффективной ширины спектра прямоугольного импульса приходится основывать на иных критериях.
Рассмотрим некоторые простые сигналы типа видеоимпульсов, т. е. сигналов, спектр которых сосредоточен в области низких частот, и определим с помощью равенства Парсеваля энергию, содержащуюся в полосе  от
от  до некоторой граничной частоты
до некоторой граничной частоты  :
:

Относя затем  к полной энергии импульса Э, определяем коэффициент
к полной энергии импульса Э, определяем коэффициент

характеризующий концентрацию энергии в заданной полосе.
В качестве исходного сигнала примем прямоугольный импульс, затем рассмотрим треугольный и колоколообразный (гауссовский). Последний особенно показателен, так как для него обеспечивается максимально возможная концентрация энергии спектра в заданной полосе  .
.
Для прямоугольного импульса в соответствии с (2.68)

Вычислив интеграл, получим

где  - интегральный синус.
- интегральный синус.
Переходя к аргументу  , записываем
, записываем

Для треугольного импульса, спектральная плотность которого определяется формулой (2.73), а полная энергия 

Рис. 2.23. Доля энергии сигнала в полосе  (а) и деформация импульса при усечении спектра (б)
(а) и деформация импульса при усечении спектра (б)

где 
Для гауссовского импульса в соответствии с (2.77) получаем

где  — полная энергия гауссовского импульса, а функция
— полная энергия гауссовского импульса, а функция

Учитывая, что длительность гауссовского импульса определена в п. 3 § 2.10 и равна  , аргумент функции
, аргумент функции  можно записать в форме
можно записать в форме  Функции
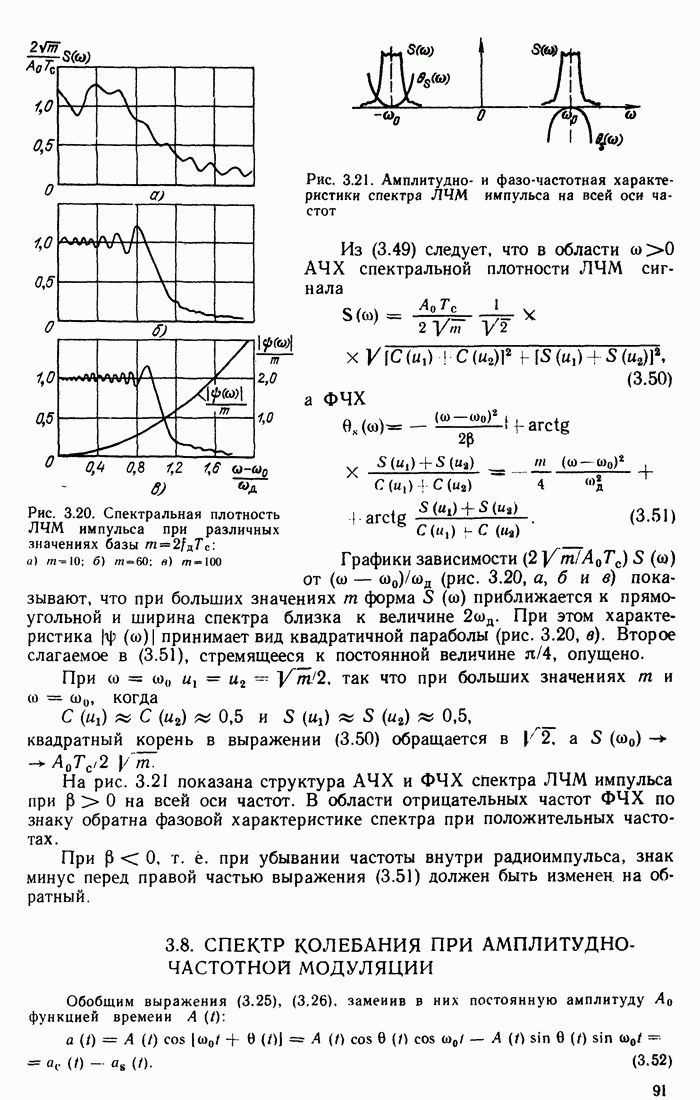
Функции  для трех импульсов представлены на рис. 2.23, а.
для трех импульсов представлены на рис. 2.23, а.
Итак, значение произведения  требующееся для заданного
требующееся для заданного  максимально для прямоугольного импульса (при
максимально для прямоугольного импульса (при  ) и минимально для гауссовского. В частности, уровню
) и минимально для гауссовского. В частности, уровню  соответствуют значения
соответствуют значения  , равные 1,8; 0,94 и 0,48.
, равные 1,8; 0,94 и 0,48.
Выбор границы спектра по энергетическому критерию в некоторых практических задачах не всегда приемлем. Так, если при обработке импульса требуется сохранить его форму достаточно близкой к прямоугольной, то  должно быть гораздо больше единицы. Для иллюстрации этого важного положения на рис. 2.23, б показаны исходный импульс (штриховая линия) и его деформация при усечении спектра на уровнях
должно быть гораздо больше единицы. Для иллюстрации этого важного положения на рис. 2.23, б показаны исходный импульс (штриховая линия) и его деформация при усечении спектра на уровнях  .
.
В любом случае при заданной форме сигнала сжатие его во времени с целью, например, повышения точности определения момента его появления неизбежно сопровождается расширением спектра, что заставляет расширять полосу пропускания измерительного устройства.
Аналогично сжатие спектра импульса с целью повышения точности, измерения частоты неизбежно сопровождается растяжением сигнала во времени, что требует удлинения времени наблюдения (измерения). Невозможность одновременно сконцентрировать сигнал в узкой полосе частот и в коротком интервале времени представляет собой одно из проявлений известного в физике принципа неопределенности.
Вопрос о величине произведения длительность X полоса актуален в связи с проблемой электромагнитной совместимости, возникающей при взаимных помехах радиостанций. С этой точки зрения наиболее желательна форма импульсов, близкая к колоколообразной.
2. СКОРОСТЬ УБЫВАНИЯ СПЕКТРА ВНЕ ОСНОВНОЙ ПОЛОСЫ
Для выявления связи между поведением  в области относительно высоких частот и структурой сигнала s(t) воспользуемся свойствами таких испытательных сигналов, как единичный импульс и единичный скачок.
в области относительно высоких частот и структурой сигнала s(t) воспользуемся свойствами таких испытательных сигналов, как единичный импульс и единичный скачок.
Единичный импульс  является единственной функцией, имеющей неубывающую спектральную плотность на всей оси частот —
является единственной функцией, имеющей неубывающую спектральную плотность на всей оси частот — 
Поэтому можно утверждать, что сигнал  , спектр которого вне основной полосы не убывает с ростом
, спектр которого вне основной полосы не убывает с ростом  , содержит в своем составе дельтафункцию (в реальных условиях достаточно мощный короткий импульс).
, содержит в своем составе дельтафункцию (в реальных условиях достаточно мощный короткий импульс).
Далее, единственной функцией времени, имеющей спектральную плотность вида  является единичный скачок и
является единичный скачок и  . Следовательно, убывание хвоста спектра сигнала
. Следовательно, убывание хвоста спектра сигнала  по закону
по закону  свидетельствует о наличии в функции
свидетельствует о наличии в функции  скачков, т. е. разрывов непрерывности. Но в точках разрыва производная функции обращается в дельта-функцию (с постоянным коэффициентом, равным величине скачка). Поэтому убывание спектра пропорционально
скачков, т. е. разрывов непрерывности. Но в точках разрыва производная функции обращается в дельта-функцию (с постоянным коэффициентом, равным величине скачка). Поэтому убывание спектра пропорционально  указывает на наличие дельта-функции в составе производной
указывает на наличие дельта-функции в составе производной  Это рассуждение можно продолжить и для производных сигнала
Это рассуждение можно продолжить и для производных сигнала  более высоких порядков.
более высоких порядков.
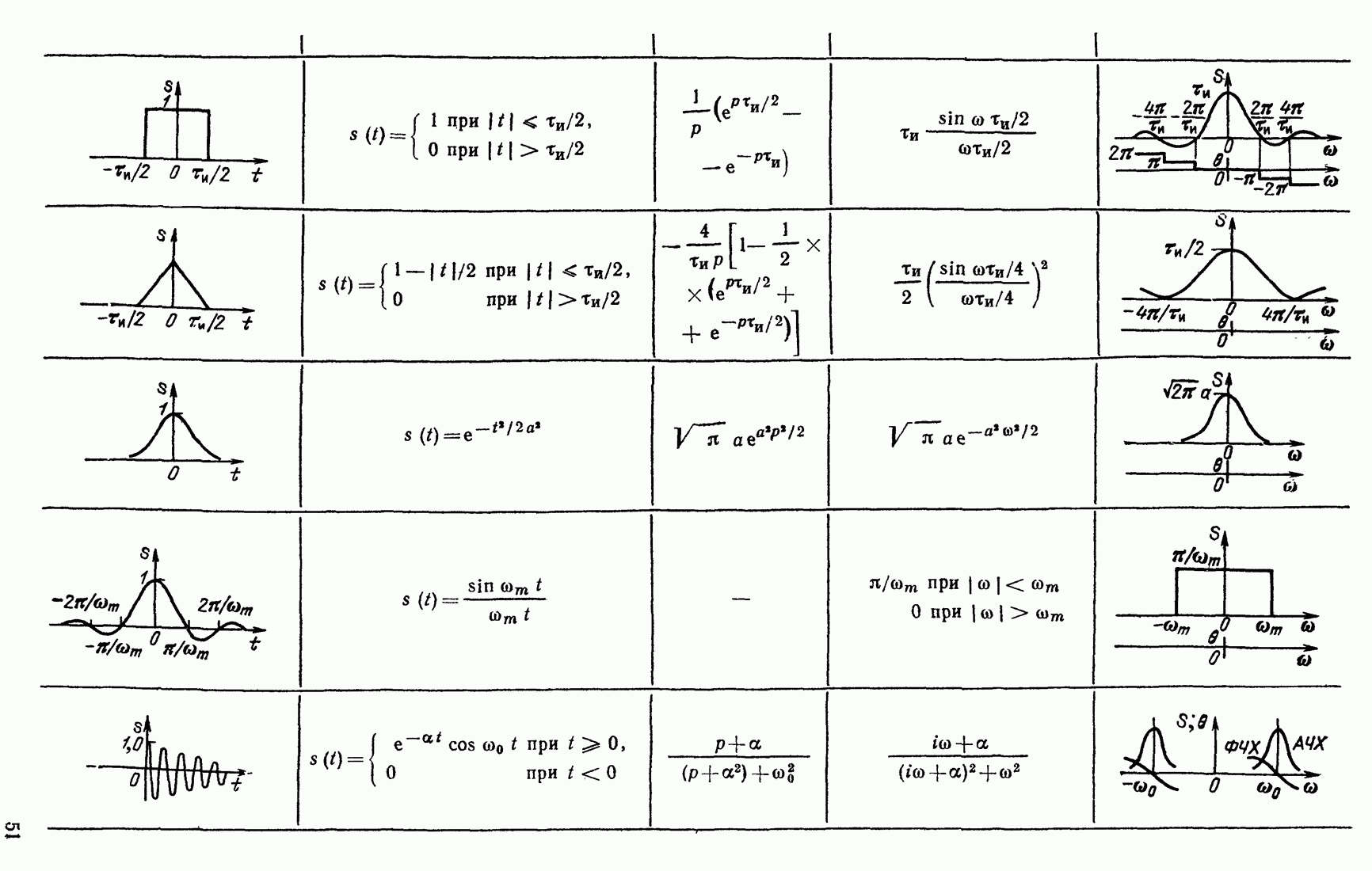
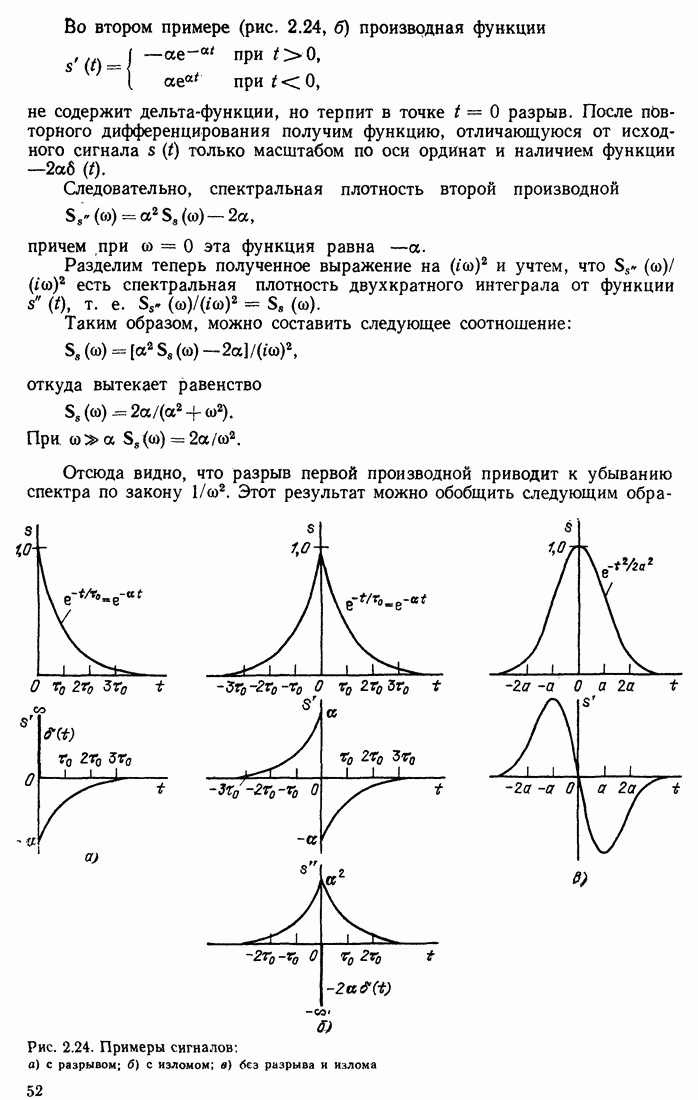
Проиллюстрируем сказанное примерами трех сигналов, представленных на рис. 2.24: с разрывом, с изломом и «гладкого» сигнала (без разрывов и изломов).
В первом примере (рис. 2.24, а) производная  определяется выражением
определяется выражением

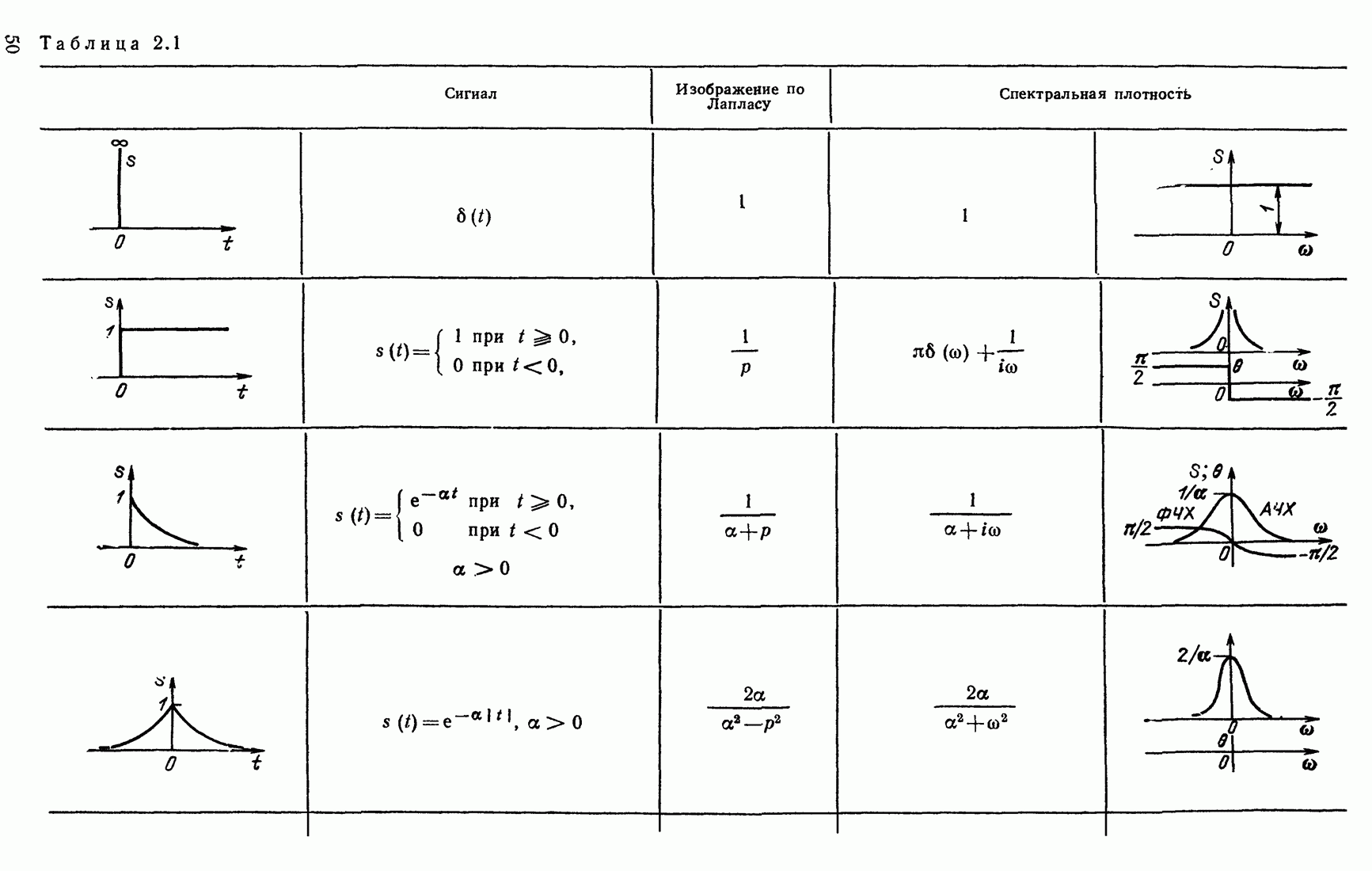
и спектральная плотность функции  в соответствии с табл. 2.1
в соответствии с табл. 2.1

Для определения спектральной плотности сигнала  , являющегося интегралом от
, являющегося интегралом от  , можно исходить из выражения
, можно исходить из выражения

В данном случае операция  законна, поскольку
законна, поскольку  [см. (2.60)].
[см. (2.60)].
При  спектральная плотность
спектральная плотность  . Как видно из рис. 2.24, а, это объясняется наличием функции
. Как видно из рис. 2.24, а, это объясняется наличием функции  в первой производной сигнала s(t).
в первой производной сигнала s(t).
Таблица 2.1
(см. скан)
Таблица 2.1 (продолжение)
(см. скан)
Во втором примере (рис. 2.24, б) производная функции

не содержит дельта-функции, но терпит в точке  разрыв. После повторного дифференцирования получим функцию, отличающуюся от исходного сигнала
разрыв. После повторного дифференцирования получим функцию, отличающуюся от исходного сигнала  только масштабом по оси ординат и наличием функции
только масштабом по оси ординат и наличием функции  .
.
Следовательно, спектральная плотность второй производной

причем при  эта функция равна
эта функция равна  .
.
Разделим теперь полученное выражение на  и учтем, что
и учтем, что  есть спектральная плотность двухкратного интеграла от функции
есть спектральная плотность двухкратного интеграла от функции  , т. е.
, т. е.  .
.
Таким образом, можно составить следующее соотношение:

откуда вытекает равенство

При 
Отсюда видно, что разрыв первой производной приводит к убыванию спектра по закону  . Этот результат можно обобщить следующим образом: вне основной полосы частотный спектр убывает по закону
. Этот результат можно обобщить следующим образом: вне основной полосы частотный спектр убывает по закону  где
где  — порядок производной, при котором возникает первый разрыв.
— порядок производной, при котором возникает первый разрыв.

Рис. 2.24. Примеры сигналов: а) с разрывом; б) с изломом; в) без разрыва и излома
С этой точки зрения сигнал, показанный на рис. 2.24, в, производные которого непрерывны при всех значениях  , вплоть до
, вплоть до  должен обладать спектром, скорость убывания которого является максимально возможной. Этот вывод согласуется с тем, что произведение длительность
должен обладать спектром, скорость убывания которого является максимально возможной. Этот вывод согласуется с тем, что произведение длительность  полоса минимальна для колоколообразного импульса (см. п. 1 данного параграфа).
полоса минимальна для колоколообразного импульса (см. п. 1 данного параграфа).
Основываясь на приведенных рассуждениях нетрудно также объяснить происхождение пульсации спектра вне основной полосы частот. Периодическая пульсация с неубывающими максимумами может возникать только в результате интерференции спектров двух дельта-функций, разнесенных во времени. Спектр прямоугольного импульса, пульсирующий с максимумами, убывающими по закону  является наглядным примером интерференции спектров двух единичных скачков.
является наглядным примером интерференции спектров двух единичных скачков.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- Глава 1. ОБЩАЯ ХАРАКТЕРИСТИКА РАДИОТЕХНИЧЕСКИХ ПРОЦЕССОВ, СИГНАЛОВ И ЦЕПЕЙ
- 1.1. ПЕРЕДАЧА СИГНАЛОВ НА РАССТОЯНИЕ И ИСПОЛЬЗУЕМЫЕ В РАДИОТЕХНИКЕ ЧАСТОТЫ
- 1.2. ПРЕОБРАЗОВАНИЕ СИГНАЛОВ В РАДИОТЕХНИЧЕСКИХ СИСТЕМАХ
- 1.3. КЛАССИФИКАЦИЯ СИГНАЛОВ, ИСПОЛЬЗУЕМЫХ В РАДИОТЕХНИКЕ
- 1.4. РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И МЕТОДЫ ИХ АНАЛИЗА
- 1.5. ПРОБЛЕМА ПОМЕХОУСТОЙЧИВОСТИ И ЭЛЕКТРОМАГНИТНОЙ СОВМЕСТИМОСТИ РАДИОТЕХНИЧЕСКИХ СИСТЕМ
- Глава 2. ХАРАКТЕРИСТИКИ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
- 2.2. ПРЕДСТАВЛЕНИЕ ПРОИЗВОЛЬНОГО СИГНАЛА В ВИДЕ СУММЫ ЭЛЕМЕНТАРНЫХ КОЛЕБАНИИ
- 2.3. ГАРМОНИЧЕСКИЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ
- 2.4. СПЕКТРЫ ПРОСТЕЙШИХ ПЕРИОДИЧЕСКИХ СИГНАЛОВ
- 2.5. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ В СПЕКТРЕ ПЕРИОДИЧЕСКОГО СИГНАЛА
- 2.6. ГАРМОНИЧЕСКИЙ АНАЛИЗ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
- 2.7. СООТНОШЕНИЕ МЕЖДУ СПЕКТРАМИ ОДИНОЧНОГО ИМПУЛЬСА И ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ИМПУЛЬСОВ
- 2.8. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 2.9. РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ В СПЕКТРЕ НЕПЕРИОДИЧЕСКОГО СИГНАЛА
- 2.10. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ СПЕКТРОВ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
- 2.11. БЕСКОНЕЧНО КОРОТКИЙ ИМПУЛЬС С ЕДИНИЧНОЙ ПЛОЩАДЬЮ (ДЕЛЬТА-ФУНКЦИЯ)
- 2.12. СООТНОШЕНИЕ МЕЖДУ ДЛИТЕЛЬНОСТЬЮ СИГНАЛА И ШИРИНОЙ ЕГО СПЕКТРА. СКОРОСТЬ УБЫВАНИЯ СПЕКТРА
- 2.13. СПЕКТРЫ НЕКОТОРЫХ НЕИНТЕГРИРУЕМЫХ ФУНКЦИЙ
- 2.14. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ НА ПЛОСКОСТИ КОМПЛЕКСНОЙ ЧАСТОТЫ
- 2.15. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ С ОГРАНИЧЕННОЙ ПОЛОСОЙ ЧАСТОТ В ВИДЕ РЯДА КОТЕЛЬНИКОВА
- 2.16. ТЕОРЕМА ОТСЧЕТОВ В ЧАСТОТНОЙ ОБЛАСТИ
- 2.17. ДИСКРЕТИЗОВАННЫЕ СИГНАЛЫ
- 2.18. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
- 2.19. СООТНОШЕНИЕ МЕЖДУ КОРРЕЛЯЦИОННОЙ ФУНКЦИЕЙ И СПЕКТРАЛЬНОЙ ХАРАКТЕРИСТИКОЙ СИГНАЛА
- Глава 3. МОДУЛИРОВАННЫЕ КОЛЕБАНИЯ
- 3.2. РАДИОСИГНАЛЫ С АМПЛИТУДНОЙ МОДУЛЯЦИЕЙ
- 3.3. СПЕКТР АМПЛИТУДНО-МОДУЛИРОВАННОГО КОЛЕБАНИЯ
- 3.4. УГЛОВАЯ МОДУЛЯЦИЯ. ФАЗА И МГНОВЕННАЯ ЧАСТОТА КОЛЕБАНИЯ
- 3.5. СПЕКТР КОЛЕБАНИЯ ПРИ УГЛОВОЙ МОДУЛЯЦИИ. ОБЩИЕ СООТНОШЕНИЯ
- 3.6. СПЕКТР КОЛЕБАНИЯ ПРИ ГАРМОНИЧЕСКОЙ УГЛОВОЙ МОДУЛЯЦИИ
- 3.7. СПЕКТР РАДИОИМПУЛЬСА С ЧАСТОТНО-МОДУЛИРОВАННЫМ ЗАПОЛНЕНИЕМ
- 3.8. СПЕКТР КОЛЕБАНИЯ ПРИ АМПЛИТУДНО-ЧАСТОТНОЙ МОДУЛЯЦИИ
- 3.9. ОГИБАЮЩАЯ, ФАЗА И ЧАСТОТА УЗКОПОЛОСНОГО СИГНАЛА
- 3.10. АНАЛИТИЧЕСКИЙ СИГНАЛ
- 3.11. КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ МОДУЛИРОВАННОГО КОЛЕБАНИЯ
- 3.12. ДИСКРЕТИЗАЦИЯ УЗКОПОЛОСНОГО СИГНАЛА
- Глава 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ СИГНАЛОВ
- 4.2. ВИДЫ СЛУЧАЙНЫХ ПРОЦЕССОВ. ПРИМЕРЫ
- 4.3. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ МОЩНОСТИ СЛУЧАЙНОГО ПРОЦЕССА
- 4.4. СООТНОШЕНИЕ МЕЖДУ СПЕКТРАЛЬНОЙ ПЛОТНОСТЬЮ И КОВАРИАЦИОННОЙ ФУНКЦИЕЙ СЛУЧАЙНОГО ПРОЦЕССА
- 4.5. ВЗАИМНАЯ КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ И ВЗАИМНАЯ СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ДВУХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 4.6. УЗКОПОЛОСНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- 4.7. КОМПЛЕКСНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- 4.8. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ. ПРОСТРАНСТВО СИГНАЛОВ
- 4.9. ПРОСТРАНСТВО СЛУЧАЙНЫХ СИГНАЛОВ
- Глава 5. ЛИНЕЙНЫЕ РАДИОТЕХНИЧЕСКИЕ ЦЕПИ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
- 5.1. ОПРЕДЕЛЕНИЯ И СВОЙСТВА АКТИВНЫХ ЦЕПЕЙ
- 5.2. АКТИВНЫЙ ЧЕТЫРЕХПОЛЮСНИК КАК ЛИНЕЙНЫЙ УСИЛИТЕЛЬ
- 5.3. ЧАСТОТНЫЕ И ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ РАДИОЭЛЕКТРОННЫХ ЦЕПЕЙ
- 5.4. АПЕРИОДИЧЕСКИЙ УСИЛИТЕЛЬ
- 5.5. КАСКАДНОЕ СОЕДИНЕНИЕ ИДЕНТИЧНЫХ АПЕРИОДИЧЕСКИХ УСИЛИТЕЛЕЙ
- 5.6. РЕЗОНАНСНЫЙ УСИЛИТЕЛЬ
- 5.7. ОБРАТНАЯ СВЯЗЬ В АКТИВНОМ ЧЕТЫРЕХПОЛЮСНИКЕ
- 5.8. ПРИМЕНЕНИЕ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗИ ДЛЯ УЛУЧШЕНИЯ ХАРАКТЕРИСТИК УСИЛИТЕЛЯ
- 5.9. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АКТИВНЫХ ЦЕПЕЙ С ОБРАТНОЙ СВЯЗЬЮ. АЛГЕБРАИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
- 5.10. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- Глава 6. ПРОХОЖДЕНИЕ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
- 6.2. СПЕКТРАЛЬНЫЙ МЕТОД
- 6.3. МЕТОД ИНТЕГРАЛА НАЛОЖЕНИЯ
- 6.4. ПРОХОЖДЕНИЕ ДИСКРЕТНЫХ СИГНАЛОВ ЧЕРЕЗ АПЕРИОДИЧЕСКИЙ УСИЛИТЕЛЬ
- 6.5. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ СИГНАЛОВ
- 6.6. АНАЛИЗ РАДИОСИГНАЛОВ В ИЗБИРАТЕЛЬНЫХ ЦЕПЯХ. МЕТОД ОГИБАЮЩЕЙ
- 6.7. ПРОХОЖДЕНИЕ РАДИОИМПУЛЬСА ЧЕРЕЗ РЕЗОНАНСНЫЙ УСИЛИТЕЛЬ
- 6.8. ЛИНЕЙНЫЕ ИСКАЖЕНИЯ АМПЛИТУДНО-МОДУЛИРОВАННОГО КОЛЕБАНИЯ В РЕЗОНАНСНОМ УСИЛИТЕЛЕ
- 6.9. ПРОХОЖДЕНИЕ ФАЗОМАНИПУЛИРОВАННОГО КОЛЕБАНИЯ ЧЕРЕЗ РЕЗОНАНСНУЮ ЦЕПЬ
- 6.10. ПРОХОЖДЕНИЕ ЧАСТОТНО-МАНИПУЛИРОВАННОГО КОЛЕБАНИЯ ЧЕРЕЗ ИЗБИРАТЕЛЬНУЮ ЦЕПЬ
- 6.11. ПРОХОЖДЕНИЕ ЧАСТОТНО-МОДУЛИРОВАННОГО КОЛЕБАНИЯ ЧЕРЕЗ ИЗБИРАТЕЛЬНЫЕ ЦЕПИ
- Глава 7. ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
- 7.1. ПРЕОБРАЗОВАНИЕ ХАРАКТЕРИСТИК СЛУЧАЙНОГО ПРОЦЕССА В ЛИНЕЙНЫХ ЦЕПЯХ
- 7.2. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ МОЩНОСТИ И КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ СЛУЧАЙНОГО ПРОЦЕССА НА ВЫХОДЕ ЦЕПИ
- 7.3. ХАРАКТЕРИСТИКИ СОБСТВЕННЫХ ШУМОВ В РАДИОЭЛЕКТРОННЫХ ЦЕПЯХ
- 7.4. ДИФФЕРЕНЦИРОВАНИЕ СЛУЧАЙНОЙ ФУНКЦИИ
- 7.5. ИНТЕГРИРОВАНИЕ СЛУЧАЙНОЙ ФУНКЦИИ
- 7.6. ПАРАМЕТРЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОГО ПРОЦЕССА НА ВЫХОДЕ ЛИНЕЙНОЙ ЦЕПИ. ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ
- 7.7. НОРМАЛИЗАЦИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ В УЗКОПОЛОСНЫХ ЛИНЕЙНЫХ ЦЕПЯХ
- Глава 8. НЕЛИНЕЙНЫЕ ЦЕПИ И МЕТОДЫ ИХ АНАЛИЗА
- 8.2. АППРОКСИМАЦИЯ НЕЛИНЕЙНЫХ ХАРАКТЕРИСТИК
- 8.3. ВОЗДЕЙСТВИЕ УЗКОПОЛОСНОГО РАДИОСИГНАЛА НА БЕЗЫНЕРЦИОННЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ
- 8.4. ВОЗДЕЙСТВИЕ БИГАРМОНИЧЕСКОГО КОЛЕБАНИЯ НА НЕЛИНЕЙНЫЙ РЕЗИСТИВНЫЙ ЭЛЕМЕНТ
- 8.5. НЕЛИНЕЙНОЕ РЕЗОНАНСНОЕ УСИЛЕНИЕ
- 8.6. УМНОЖЕНИЕ ЧАСТОТЫ
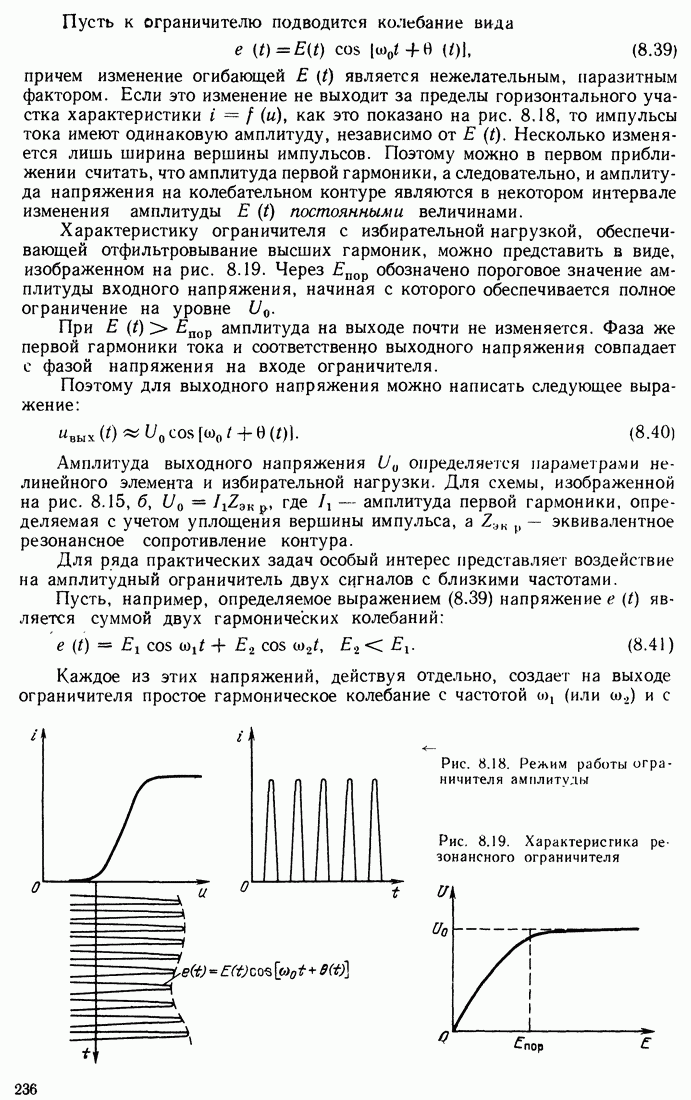
- 8.7. АМПЛИТУДНОЕ ОГРАНИЧЕНИЕ
- 8.8. НЕЛИНЕЙНАЯ ЦЕПЬ С ФИЛЬТРАЦИЕЙ ПОСТОЯННОГО ТОКА (ВЫПРЯМЛЕНИЕ)
- 8.9. АМПЛИТУДНОЕ ДЕТЕКТИРОВАНИЕ
- 8.10. ЧАСТОТНОЕ И ФАЗОВОЕ ДЕТЕКТИРОВАНИЕ
- 8.11. ПРЕОБРАЗОВАНИЕ ЧАСТОТЫ СИГНАЛА
- 8.12. СИНХРОННОЕ ДЕТЕКТИРОВАНИЕ
- 8.13. ПОЛУЧЕНИЕ АМПЛИТУДНО-МОДУЛИРОВАННЫХ КОЛЕБАНИИ
- 8.14. РЕЗОНАНС В КОЛЕБАТЕЛЬНОМ КОНТУРЕ С НЕЛИНЕЙНОЙ ЕМКОСТЬЮ
- 8.15. ВОЗДЕЙСТВИЕ ГАРМОНИЧЕСКОГО СИГНАЛА НА НЕЛИНЕЙНУЮ ЕМКОСТЬ. УМНОЖИТЕЛЬ ЧАСТОТЫ НА ВАРАКТОРЕ
- 8.16. ВОЗДЕЙСТВИЕ ДВУХ ГАРМОНИЧЕСКИХ КОЛЕБАНИИ НА ЦЕПЬ С НЕЛИНЕЙНЫМ ЭНЕРГОЕМКИМ ЭЛЕМЕНТОМ
- 8.17. ТЕОРЕМА МЭНЛИ—РОУ
- 8.18. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ ЦЕПЯХ ПО ЗАДАННОМУ ДИФФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ
- Глава 9. ГЕНЕРИРОВАНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 9.1. АВТОКОЛЕБАТЕЛЬНАЯ СИСТЕМА
- 9.2. ВОЗНИКНОВЕНИЕ КОЛЕБАНИЯ В АВТОГЕНЕРАТОРЕ
- 9.3. СТАЦИОНАРНЫЙ РЕЖИМ АВТОГЕНЕРАТОРА
- 9.4. МЯГКИЙ И ЖЕСТКИЙ РЕЖИМЫ САМОВОЗБУЖДЕНИЯ
- 9.5. ПРИМЕРЫ СХЕМ АВТОГЕНЕРАТОРОВ
- 9.6. НЕЛИНЕЙНОЕ УРАВНЕНИЕ АВТОГЕНЕРАТОРА
- 9.7. МЕТОД ФАЗОВОЙ ПЛОСКОСТИ
- 9.8. ФАЗОВЫЕ ПОРТРЕТЫ АВТОГЕНЕРАТОРА
- 9.9. АВТОГЕНЕРАТОРЫ С ВНУТРЕННЕЙ ОБРАТНОЙ СВЯЗЬЮ
- 9.10. АВТОГЕНЕРАТОР С ЛИНИЕЙ ЗАДЕРЖКИ В ЦЕПИ ОБРАТНОЙ СВЯЗИ
- 9.11. RC-ГЕНЕРАТОРЫ
- 9.12. ДЕЙСТВИЕ ГАРМОНИЧЕСКОЙ ЭДС НА ЦЕПИ С ПОЛОЖИТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ. РЕГЕНЕРАЦИЯ
- 9.13. ДЕЙСТВИЕ ГАРМОНИЧЕСКОЙ ЭДС НА АВТОГЕНЕРАТОР. ЗАХВАТЫВАНИЕ ЧАСТОТЫ
- 9.14. УГЛОВАЯ МОДУЛЯЦИЯ В АВТОГЕНЕРАТОРЕ
- Глава 10. ЦЕПИ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10.1. ОБЩИЕ ХАРАКТЕРИСТИКИ ЦЕПЕЙ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10.2. ПРОХОЖДЕНИЕ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10.3. ПРИМЕР ОПРЕДЕЛЕНИЯ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ ПАРАМЕТРИЧЕСКОЙ ЦЕПИ
- 10.4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЦЕПИ С ПЕРИОДИЧЕСКИ ИЗМЕНЯЮЩИМСЯ ПАРАМЕТРОМ
- 10.5. ПРИНЦИП ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ СИГНАЛОВ
- 10.6. ОДНОКОНТУРНЫЙ ПАРАМЕТРИЧЕСКИЙ УСИЛИТЕЛЬ
- 10.7. ДВУХКОНТУРНЫЙ ПАРАМЕТРИЧЕСКИЙ УСИЛИТЕЛЬ
- 10.8. ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИИ
- 10.9. СОПОСТАВЛЕНИЕ ПАРАМЕТРИЧЕСКИХ И НЕЛИНЕЙНЫХ ПРЕОБРАЗОВАНИИ СИГНАЛОВ
- Глава 11. ВОЗДЕЙСТВИЕ СЛУЧАЙНЫХ КОЛЕБАНИЙ НА НЕЛИНЕЙНЫЕ И ПАРАМЕТРИЧЕСКИЕ ЦЕПИ
- 11.2. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА В БЕЗЫНЕРЦИОННЫХ НЕЛИНЕЙНЫХ ЦЕПЯХ
- 11.3. ПРЕОБРАЗОВАНИЕ СПЕКТРА СЛУЧАЙНОГО ПРОЦЕССА В БЕЗЫНЕРЦИОННОМ НЕЛИНЕЙНОМ ЭЛЕМЕНТЕ
- 11.4. ВОЗДЕЙСТВИЕ УЗКОПОЛОСНОГО ШУМА НА АМПЛИТУДНЫЙ ДЕТЕКТОР
- 11.6. СОВМЕСТНОЕ ВОЗДЕЙСТВИЕ ГАРМОНИЧЕСКОГО СИГНАЛА И ГАУССОВСКОГО ШУМА НА АМПЛИТУДНЫЙ ДЕТЕКТОР
- 11.6. СОВМЕСТНОЕ ВОЗДЕЙСТВИЕ ГАРМОНИЧЕСКОГО СИГНАЛА И ГАУССОВСКОГО ШУМА НА ЧАСТОТНЫЙ ДЕТЕКТОР
- 11.7. ВЗАИМОДЕЙСТВИЕ ГАРМОНИЧЕСКОГО СИГНАЛА И ГАУССОВСКОГО ШУМА В АМПЛИТУДНОМ ОГРАНИЧИТЕЛЕ С РЕЗОНАНСНОЙ НАГРУЗКОЙ
- 11.8. КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ И СПЕКТР СЛУЧАЙНОГО ПРОЦЕССА В ЛИНЕЙНОЙ ПАРАМЕТРИЧЕСКОЙ ЦЕПИ
- 11.9. ВЛИЯНИЕ МУЛЬТИПЛИКАТИВНОЙ ПОМЕХИ НА ЗАКОН РАСПРЕДЕЛЕНИЯ СИГНАЛА
- Глава 12. ДИСКРЕТНАЯ ОБРАБОТКА СИГНАЛОВ. ЦИФРОВЫЕ ФИЛЬТРЫ
- 12.2. ПРИНЦИП ДИСКРЕТНОЙ ФИЛЬТРАЦИИ
- 12.3. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЦИФРОВОГО ФИЛЬТРА
- 12.4. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СИГНАЛОВ
- 12.5. ПРИМЕНЕНИЕ МЕТОДА Z-ПРЕОБРАЗОВАНИЯ ДЛЯ АНАЛИЗА ДИСКРЕТНЫХ СИГНАЛОВ И ЦЕПЕЙ
- 12.6. Z-ПРЕОБРАЗОВАНИЕ BPEMEHHЫХ ФУНКЦИЙ
- 12.7. z-ПРЕОБРАЗОВАНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ДИСКРЕТНЫХ ЦЕПЕЙ
- 12.8. ПРИМЕРЫ АНАЛИЗА ЦИФРОВЫХ ФИЛЬТРОВ
- 12.9. ЦИФРОВЫЕ ФИЛЬТРЫ С КОМПЛЕКСНЫМИ ВЕСОВЫМИ КОЭФФИЦИЕНТАМИ
- 12.10. ПРЕОБРАЗОВАНИЕ АНАЛОГ—ЦИФРА. ШУМЫ КВАНТОВАНИЯ
- 12.11. ПРЕОБРАЗОВАНИЕ ЦИФРА—АНАЛОГ И ВОССТАНОВЛЕНИЕ КОНТИНУАЛЬНОГО СИГНАЛА
- 12.12. БЫСТРОДЕЙСТВИЕ АРИФМЕТИЧЕСКОГО УСТРОЙСТВА ЦИФРОВОГО ФИЛЬТРА
- 12.13. АЛГОРИТМ ЦИФРОВОЙ ФИЛЬТРАЦИИ ВО ВРЕМЕННОЙ И ЧАСТОТНОЙ ОБЛАСТЯХ
- 12.14. БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 12.15. СПЕКТРАЛЬНЫЙ АНАЛИЗ НА БАЗЕ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 12.16. ПРИМЕНЕНИЕ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ В УСТРОЙСТВАХ ОБРАБОТКИ СИГНАЛОВ
- Глава 13. ПРИНЦИПЫ ОПТИМАЛЬНОЙ ЛИНЕЙНОИ ФИЛЬТРАЦИИ СИГНАЛА НА ФОНЕ ПОМЕХ
- 13.2. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ОПТИМАЛЬНОГО ФИЛЬТРА
- 13.3. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА СОГЛАСОВАННОГО ФИЛЬТРА. ФИЗИЧЕСКАЯ ОСУЩЕСТВИМОСТЬ
- 13.4. СИГНАЛ И ПОМЕХА НА ВЫХОДЕ СОГЛАСОВАННОГО ФИЛЬТРА
- 13.5. ПРИМЕРЫ ПОСТРОЕНИЯ СОГЛАСОВАННЫХ ФИЛЬТРОВ
- 13.6. ФОРМИРОВАНИЕ СИГНАЛА, СОПРЯЖЕННОГО С ЗАДАННЫМ ФИЛЬТРОМ
- 13.7. ФИЛЬТРАЦИЯ ЗАДАННОГО СИГНАЛА ПРИ НЕБЕЛОМ ШУМЕ
- 13.8. ФИЛЬТРАЦИЯ СИГНАЛА С НЕИЗВЕСТНОЙ НАЧАЛЬНОЙ ФАЗОЙ
- 13.9. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ КОМПЛЕКСНОГО СИГНАЛА. КВАДРАТУРНАЯ ОБРАБОТКА
- 13.10. ЦИФРОВОЙ СОГЛАСОВАННЫЙ ФИЛЬТР
- Глава 14. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ НЕКОТОРЫМИ СПЕЦИАЛЬНЫМИ ФУНКЦИЯМИ
- 14.2. ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ И ФУНКЦИИ НЕПРЕРЫВНОГО ТИПА
- 14.3. ФУНКЦИИ УОЛША
- 14.4. РАЗЛИЧНЫЕ СПОСОБЫ НУМЕРАЦИИ ФУНКЦИЙ УОЛША
- 14.5. ПРИМЕРЫ ПРИМЕНЕНИЯ ФУНКЦИЙ УОЛША
- 14.6. ДИСКРЕТНЫЕ ФУНКЦИИ УОЛША
- Глава 15. ЭЛЕМЕНТЫ СИНТЕЗА ЛИНЕЙНЫХ РАДИОЦЕПЕЙ
- 15.2. ПРЕДСТАВЛЕНИЕ АНАЛОГОВОГО ЧЕТЫРЕХПОЛЮСНИКА КАСКАДНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТАРНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ
- 15.3. РЕАЛИЗАЦИЯ БЕЗЫНДУКТИВНОСТНОИ ЦЕПИ ВТОРОГО ПОРЯДКА
- 15.4. ОСОБЕННОСТИ СИНТЕЗА ЧЕТЫРЕХПОЛЮСНИКА ПО ЗАДАННОЙ АМПЛИТУДНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ
- 15.5. СИНТЕЗ ФИЛЬТРА НИЖНИХ ЧАСТОТ. ФИЛЬТР БАТТЕРВОРТА
- 15.6. ПРИМЕР СИНТЕЗА ФИЛЬТРА БАТТЕРВОРТА ВТОРОГО ПОРЯДКА
- 15.7. ФИЛЬТР ЧЕБЫШЕВА (НИЖНИХ ЧАСТОТ)
- 15.8. СИНТЕЗ РАЗЛИЧНЫХ ФИЛЬТРОВ НА ОСНОВЕ ФИЛЬТРА НИЖНИХ ЧАСТОТ
- 15.9. СВЯЗЬ МЕЖДУ АМПЛИТУДНО- И ФАЗОЧАСТОТНОЙ ХАРАКТЕРИСТИКАМИ В ЦИФРОВЫХ ЦЕПЯХ
- 15.10. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ФЧХ ЦИФРОВОГО ФИЛЬТРА ПО ЗАДАННОЙ АЧХ
- 15.11. СИНТЕЗ ЦИФРОВЫХ ФИЛЬТРОВ. ОБЩИЕ ЗАМЕЧАНИЯ
- 15.12. СИНТЕЗ ЦИФРОВЫХ ФИЛЬТРОВ ПО АНАЛОГОВОМУ ПРОТОТИПУ
- 15.13. МЕТОД ИНВАРИАНТНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- Глава 16. ОБОБЩЕННАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ СИГНАЛОВ. КЕПСТРАЛЬНЫЙ АНАЛИЗ
- 16.1. ОБОБЩЕННЫЙ ПРИНЦИП СУПЕРПОЗИЦИИ
- 16.2. ОБОБЩЕННАЯ СХЕМА ГОМОМОРФНОЙ ОБРАБОТКИ СИГНАЛОВ
- 16.3. ГОМОМОРФНАЯ ОБРАБОТКА МУЛЬТИПЛИКАТИВНОГО СИГНАЛА
- 16.4. ГОМОМОРФНАЯ ОБРАБОТКА СВЕРНУТОГО СИГНАЛА
- 16.5. КЕПСТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ. КЕПСТР МОЩНОСТИ
- 16.6. ОПРЕДЕЛЕНИЕ ЗАДЕРЖКИ СИГНАЛА
- 16.7. ПРИМЕР ОПРЕДЕЛЕНИЯ ЗАДЕРЖКИ СИГНАЛА
- 16.8. ВЛИЯНИЕ ПОМЕХ
- 16.9. КОМПЛЕКСНЫЙ КЕПСТР
- 16.10. СВОЙСТВА КОМПЛЕКСНОГО КЕПСТРА
- 16.11. НЕКОТОРЫЕ СВОЙСТВА КЕПСТРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ
- Приложение 1. ПРАВИЛА ПЕРЕХОДА ОТ ИЗОБРАЖЕНИЯ ПО ЛАПЛАСУ Ls(p) К СПЕКТРАЛЬНОЙ ПЛОТНОСТИ S(w)
- Приложение 2. ПРАВИЛО ПРЕОБРАЗОВАНИЯ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ ПРИ ИНТЕГРИРОВАНИИ СИГНАЛА
- Приложение 3. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ УЗКОПОЛОСНОГО СИГНАЛА С НЕИЗВЕСТНОЙ НАЧАЛЬНОЙ ФАЗОЙ
- Приложение 4. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ КОМПЛЕКСНОГО СИГНАЛА
- Приложение 5. О НЕОДНОЗНАЧНОСТИ ОПРЕДЕЛЕНИЯ ФАЗОЧАСТОТНОЙ ХАРАКТЕРИСТИКИ СПЕКТРА СИГНАЛА
- СПИСОК ЛИТЕРАТУРЫ