| << Предыдущий параграф | Следующий параграф >> |
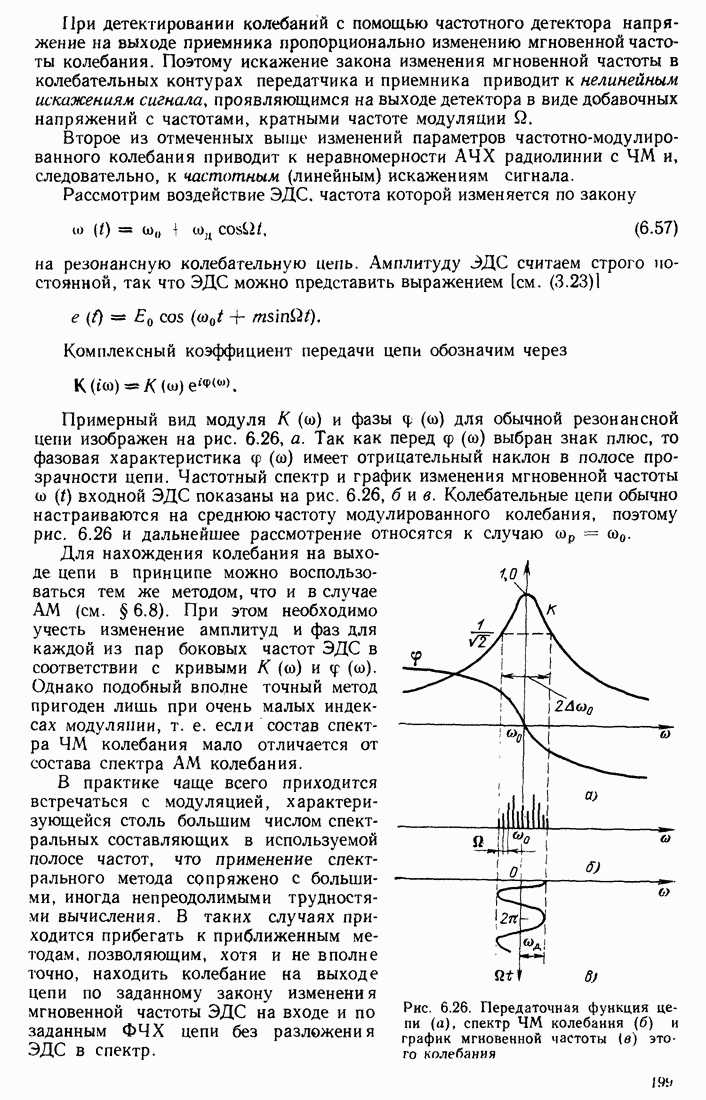
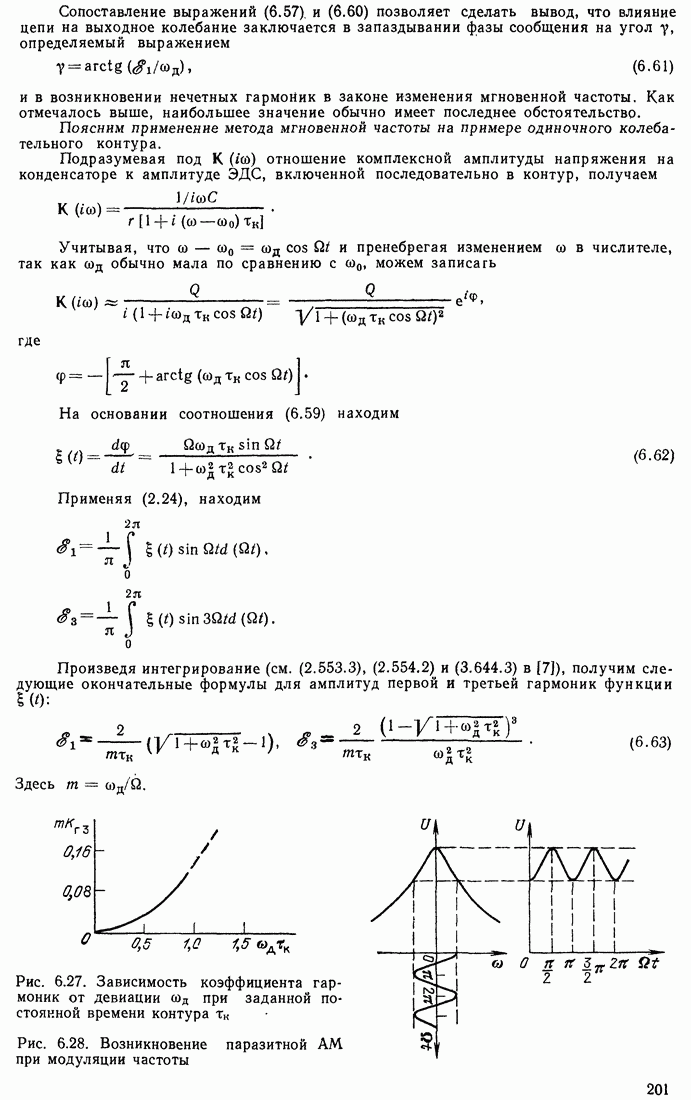
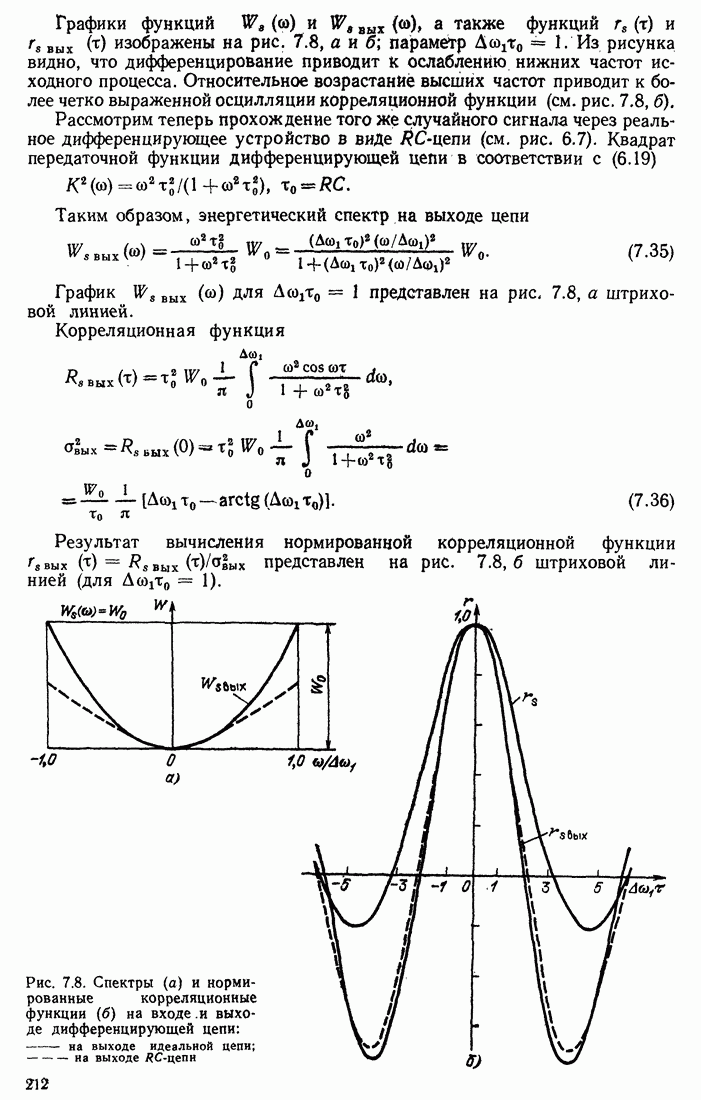
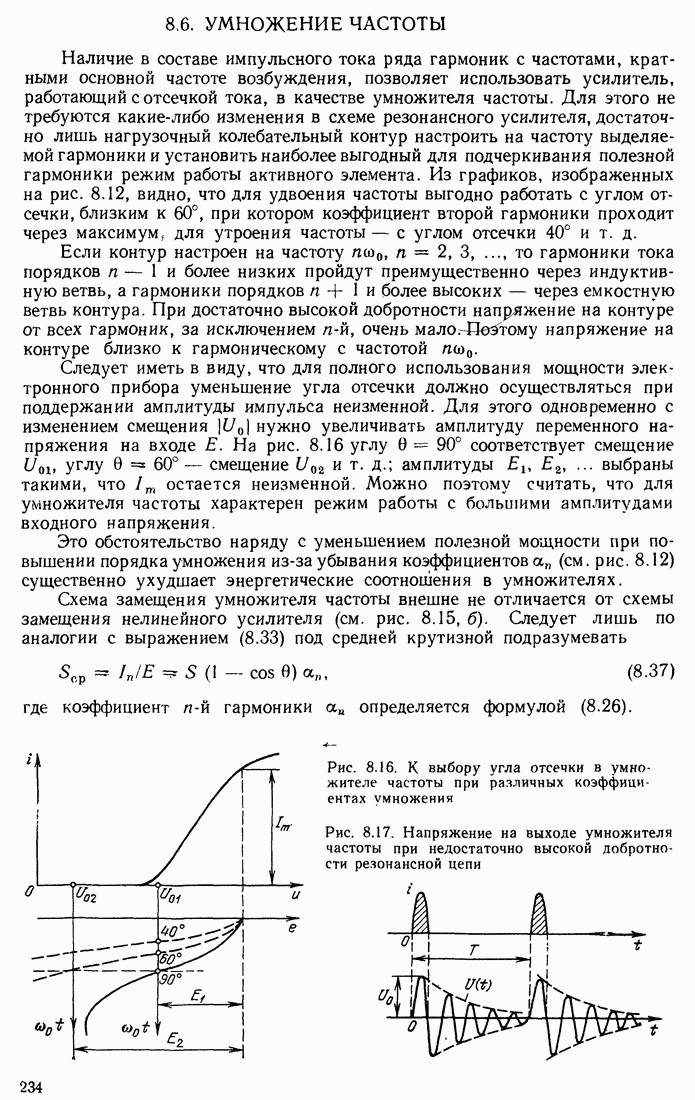
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13.5. ПРИМЕРЫ ПОСТРОЕНИЯ СОГЛАСОВАННЫХ ФИЛЬТРОВ
1. ПРЯМОУГОЛЬНЫЙ ВИДЕОИМПУЛЬС
Зададим сигнал следующей функцией времени:
 (13.27)
(13.27)
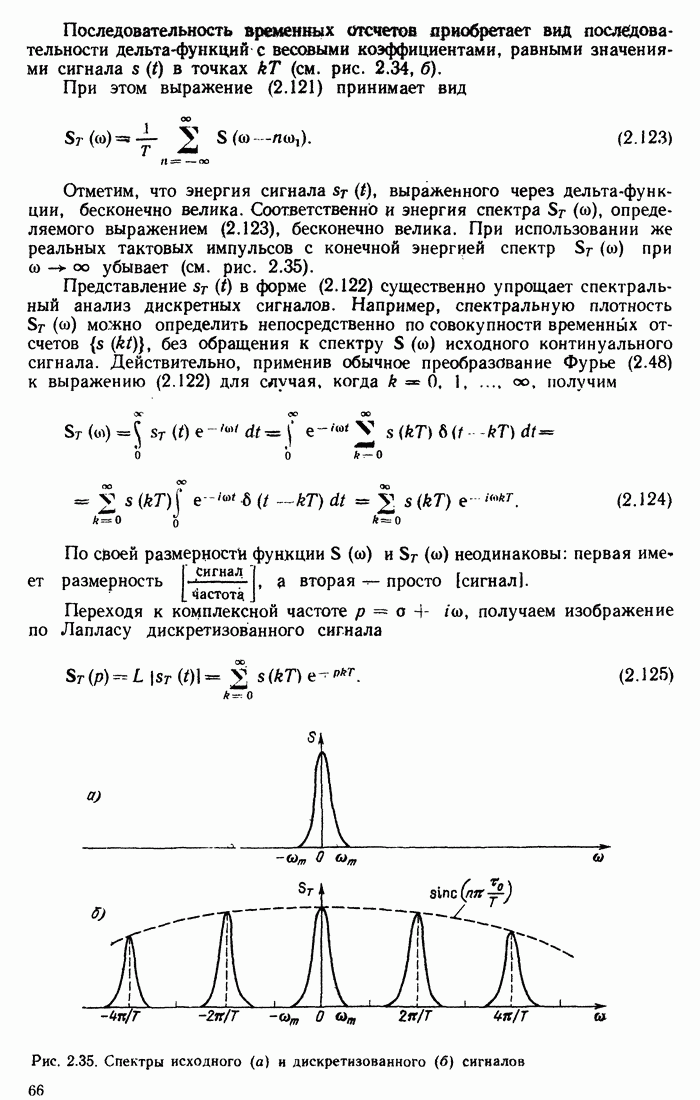
Спектральная плотность такого сигнала, как известно,
 (13.28)
(13.28)
По формуле (13.8), в которой  приравниваем длительности импульса
приравниваем длительности импульса  находим передаточную функцию согласованного фильтра
находим передаточную функцию согласованного фильтра
 (13.29)
(13.29)
Рассматриваемый пример характерен тем, что  отличается от спектра сигнала
отличается от спектра сигнала  лишь постоянным коэффициентом. Ясно, что и импульсная характеристика фильтра
лишь постоянным коэффициентом. Ясно, что и импульсная характеристика фильтра  совпадает по форме с самим сигналом
совпадает по форме с самим сигналом  действительно, из соотношения (13.15) следует, что
действительно, из соотношения (13.15) следует, что
 (13.30)
(13.30)
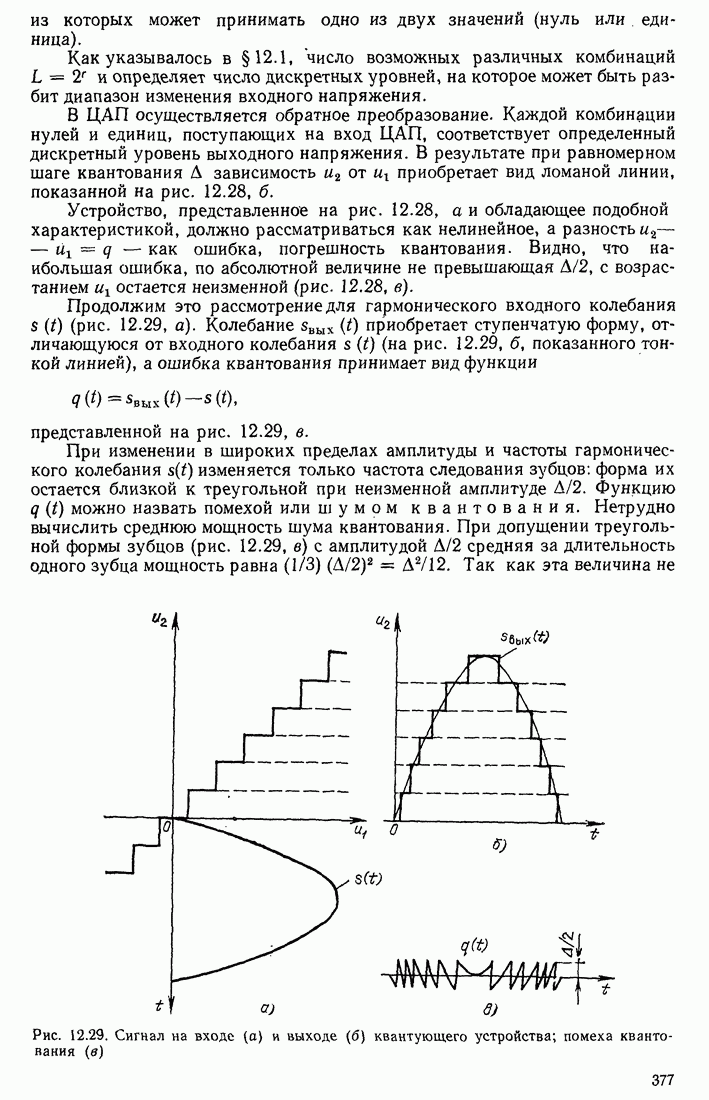
График  (рис. 13.6) по форме полностью совпадает с входным импульсом
(рис. 13.6) по форме полностью совпадает с входным импульсом 
Дальнейшая задача сводится к отысканию структуры физической цепи, обладающей импульсной характеристикой, изображенной на рис. 13.6, и передаточной функцией, определяемой формулой (13.29).
Простейший сигнал (13.27) удобен для иллюстрации основных положений синтеза четырехполюсника по заданной импульсной характеристике  или, что то же, по комплексной передаточной функции
или, что то же, по комплексной передаточной функции  являющейся преобразованием Фурье от
являющейся преобразованием Фурье от 
Прежде всего отметим, что интеграл

т. е. интеграл сходится, так что в рассматриваемом примере функция  не противоречит критерию Пэли — Винера (13.16).
не противоречит критерию Пэли — Винера (13.16).
Показанную на рис. 13.7 структурную схему фильтра можно наметить непосредственно по передаточной функции (13.29). Входящий в эту функцию множитель  реализуется интегрирующим звеном, а второй множитель
реализуется интегрирующим звеном, а второй множитель  — устройством вычитания, к которому сигнал попадает без задержки и с задержкой
— устройством вычитания, к которому сигнал попадает без задержки и с задержкой  Передаточная функция идеальной линии задержки (без потерь) равна
Передаточная функция идеальной линии задержки (без потерь) равна  .
.

Рис. 13.6. Импульсная характеристика фильтра, согласованного с прямоугольным импульсом

Рис. 13.7. Структурная схема фильтра, согласованного с прямоугольным импульсом

Рис. 13.8. Формирование импульсной характеристики в идеальном (а) и физическом (б) фильтрах
Объяснить работу этой схемы можно также на основании временных представлений: при подаче на вход единичного импульса ЭДС [дельта-функции  ] на выходе идеального интегратора появляется скачок напряжения в момент
] на выходе идеального интегратора появляется скачок напряжения в момент  На выходе устройства получается напряжение в виде разности двух единичных скачков, сдвинутых относительно друг друга на время
На выходе устройства получается напряжение в виде разности двух единичных скачков, сдвинутых относительно друг друга на время  (рис. 13.8, а).
(рис. 13.8, а).
Реализация изображенного на рис. 13.7 устройства, которое обеспечивало бы точное интегрирование, а также задержку входного сигнала без искажения его формы (в пределах бесконечно широкого спектра единичного импульса), практически неосуществима. Можно, однако, получить достаточно хорошее приближение при использовании реальной интегрирующей RC-цепи, если обеспечить постоянную времени этой цепи, достаточно большую по сравнению с  . При этом на выходе вычитающего устройства импульс напряжения, являющийся разностью двух экспонент (рис. 13.8, б), может быть реализован достаточно близким к прямоугольному.
. При этом на выходе вычитающего устройства импульс напряжения, являющийся разностью двух экспонент (рис. 13.8, б), может быть реализован достаточно близким к прямоугольному.
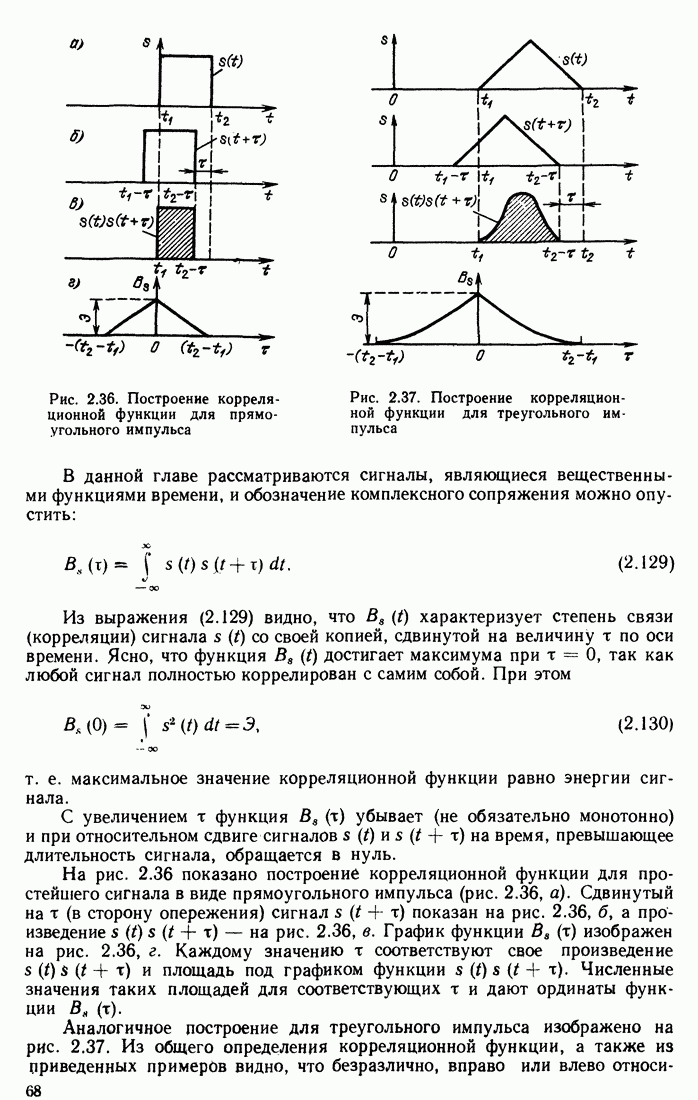
Найдем напряжение на выходе фильтра. Применяя формулу (13.18) и учитывая, что корреляционная функция прямоугольного импульса имеет вид равнобедренного треугольника с основанием  и высотой, равной энергии импульса
и высотой, равной энергии импульса  , получаем
, получаем
 (13.31)
(13.31)
Максимальное значение выходного сигнала, равное  достигается в момент
достигается в момент  т. е. к концу действия входного сигнала (рис. 13.9).
т. е. к концу действия входного сигнала (рис. 13.9).
Отношение сигнал-помеха в соответствии с (13.9)
 (13.32)
(13.32)
Определим теперь пик сжатого сигнала по формуле (13.26). В данном примере  , а
, а

Следовательно,

Таким образом,  .
.
Как будет видно из дальнейших примеров, пик выходного сигнала намного превышает амплитуду входного при согласованной фильтрации сложных сигналов (с большой базой).
2. РАДИОИМПУЛЬС С ЧАСТОТНО-МОДУЛИРОВАННЫМ ЗАПОЛНЕНИЕМ
Рассмотрим сигнал, изображенный на рис. 13.10, а. Огибающая этого сигнала имеет прямоугольную форму, а частота заполнения нарастает по линейному закону (рис. 13.10, б) со скоростью
 (13.33)
(13.33)
где  — длительность импульса;
— длительность импульса;  — полное изменение частоты внутри импульса;
— полное изменение частоты внутри импульса;  — центральная частота заполнения. В дальнейшем исходим из условия, что
— центральная частота заполнения. В дальнейшем исходим из условия, что  . Таким образом,
. Таким образом,
 (13.34)
(13.34)
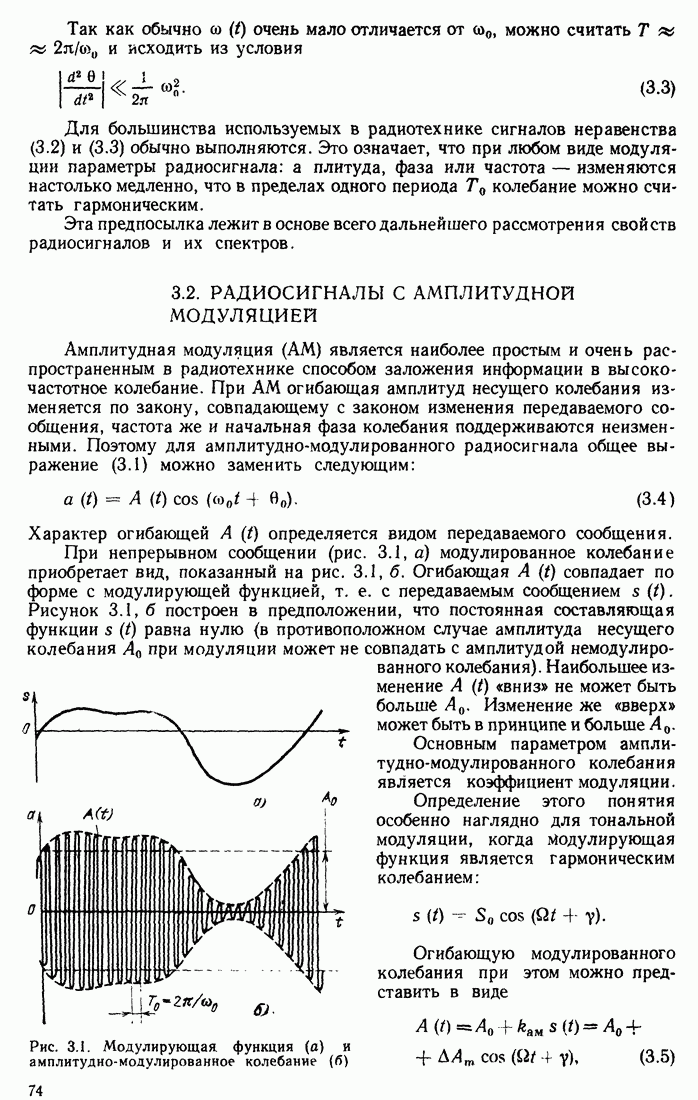
а мгновенное значение сигнала в интервале от  до
до  определяется выражением
определяется выражением
 (13.35)
(13.35)
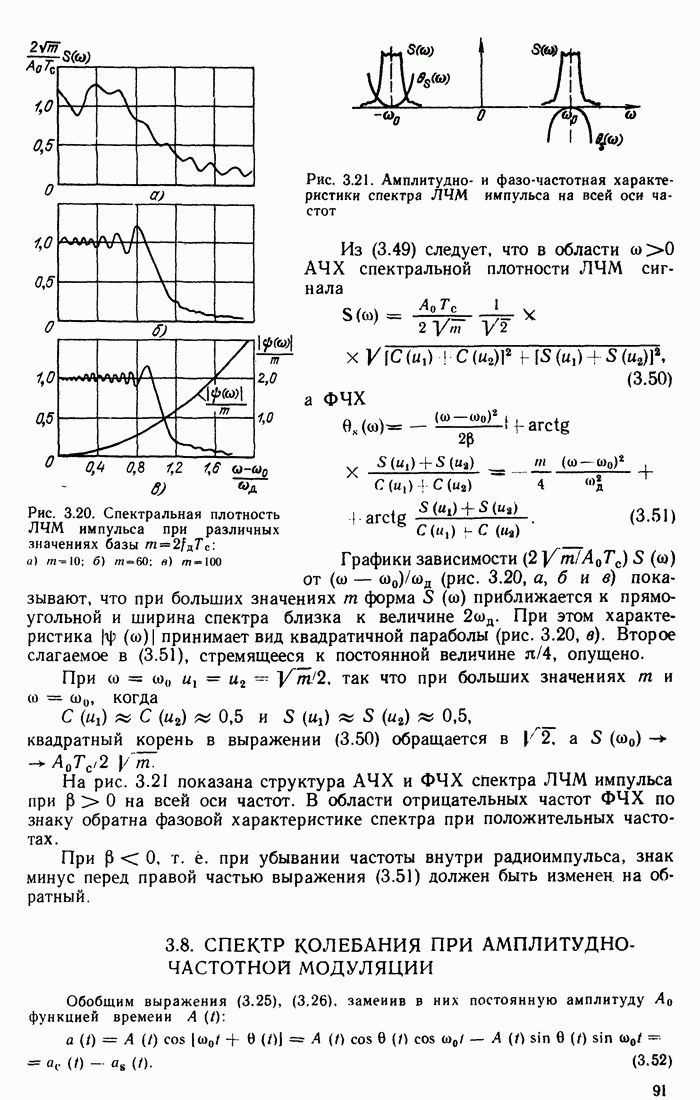
Спектральная плотность подобного импульса была определена в гл. 3. Было установлено, что модуль и фаза спектральной плотности определяются соответственно формулами (3.50) и (3.51).
Эти выражения могут быть в принципе положены в основу синтезирования фильтра, но создание четырехполюсника, точно реализующего столь сложные АЧХ и ФЧХ, представляет собой задачу трудную или даже вообще невыполнимую. Поэтому приходится прибегать к различным приемам аппроксимации АЧХ и ФЧХ. Первым этапом на этом пути является допущение о том, что огибающая спектра сигнала имеет прямоугольную форму, а ФЧХ — форму квадратичной параболы.

Рис. 13.9. Сигнал на выходе фильтра, согласованного с прямоугольным импульсом

Рис. 13.10. ЛЧМ импульс (а) и закон изменения мгновенной частоты (б)
Таким образом, точные выражения заменяются приближенным [см. пояснения к формулам (3.50) и (3.51)]
 (13.36)
(13.36)
В § 3.7 было показано, что такое приближение тем лучше, чем больше  (постоянный фазовый сдвиг
(постоянный фазовый сдвиг  опущен).
опущен).
При отсчете времени t от начала импульса фазовый спектр сигнала запишем в виде
 (13.37)
(13.37)
Для сигнала с подобными амплитудными и фазовыми спектрами согласованный фильтр должен иметь прямоугольную АЧХ и ФЧХ, определяемую выражением
 (13.38)
(13.38)
Строго прямоугольная АЧХ также неосуществима. Поэтому дальнейшее упрощение заключается в замене прямоугольной амплитудной характеристики характеристикой реализуемого полосового фильтра. После этого фильтр может быть осуществлен в виде сочетания двух линейных четырехполюсников: полосового резонансного фильтра (обычный усилитель промежуточной частоты приемника) и специального четырехполюсника с равномерной АЧХ и квадратичной ФЧХ.
Заметим, что фазовой характеристике (13.38) соответствует групповое время запаздывания узкополосного сигнала

В качестве устройства с требуемой ФЧХ может быть использована любая цепь, у которой задержка в некотором частотном диапазоне (вблизи частоты  ) линейно зависит от частоты. Такими свойствами обладают, в частности, дисперсионные ультразвуковые линии задержки.
) линейно зависит от частоты. Такими свойствами обладают, в частности, дисперсионные ультразвуковые линии задержки.
Определим сигнал на выходе фильтра. При этом будем иметь в виду не аппроксимированный, а точно согласованный фильтр, передаточная функция которого отвечает условию (13.8).
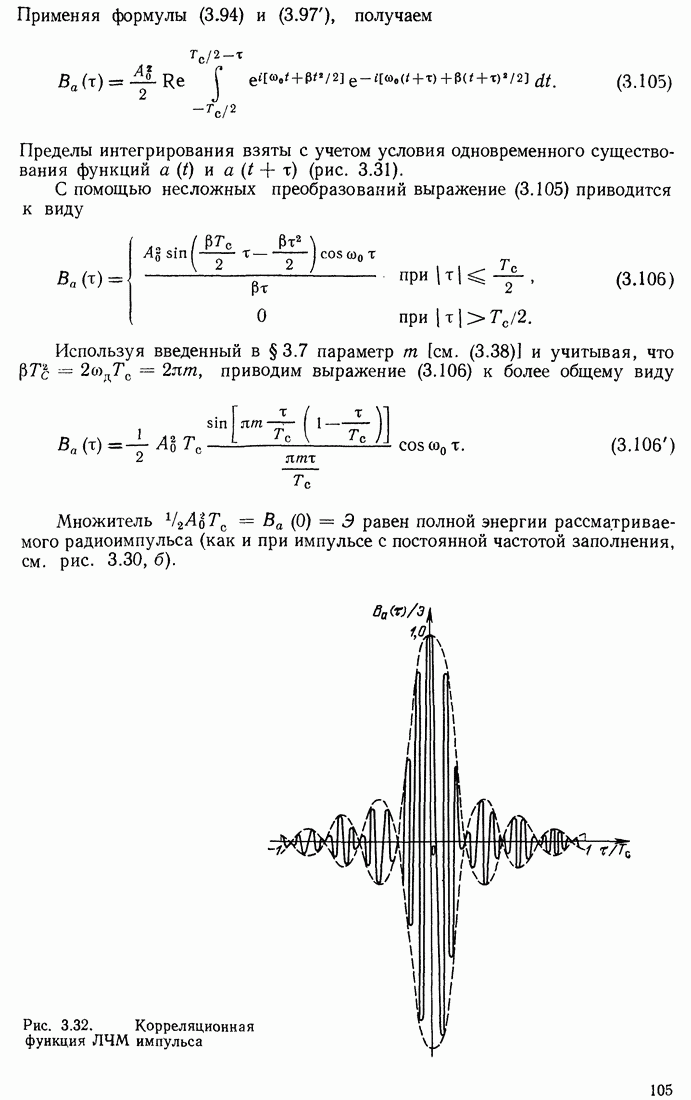
Основываясь на соотношении (13.18) воспользуемся выражением (3.106) для корреляционной функции входного сигнала, введенным в § 3.11:

Заменяя в этом выражении  на
на  и ограничиваясь рассмотрением участка вблизи точки
и ограничиваясь рассмотрением участка вблизи точки  , т. е. в окрестности точки, где выходной сигнал достигает пикового значения, можем считать
, т. е. в окрестности точки, где выходной сигнал достигает пикового значения, можем считать  .
.
Тогда

Учитывая, что  [см. (3.38)], последнее выражение перепишем в несколько иной форме
[см. (3.38)], последнее выражение перепишем в несколько иной форме

Подставляя полученное выражение в (13.18), находим напряжение на выходе согласованного фильтра
 (13.40)
(13.40)
где огибающая

Заметим, что частота заполнения не модулирована и равна  , т. е. средней частоте входного сигнала.
, т. е. средней частоте входного сигнала.
Поясним этот важный результат. ЛЧМ импульсу, определяемому выражением (13.25), при  соответствует амплитудный спектр прямоугольной формы и фазовый спектр в виде квадратичной параболы. После прохождения через согласованный фильтр амплитудный спектр остается прямоугольным, а фазовый спектр принимает вид линейной зависимости
соответствует амплитудный спектр прямоугольной формы и фазовый спектр в виде квадратичной параболы. После прохождения через согласованный фильтр амплитудный спектр остается прямоугольным, а фазовый спектр принимает вид линейной зависимости  в пределах
в пределах  . Тем самым эффект ЧМ снимается и спектр приобретает вид двух лепестков прямоугольной формы (одного в области
. Тем самым эффект ЧМ снимается и спектр приобретает вид двух лепестков прямоугольной формы (одного в области  и другого в области
и другого в области  , симметричных относительно частот
, симметричных относительно частот  линейным фазовым спектром. В соответствии с теоремой о смещении спектра (см. п. 3 § 2.8) подобная структура спектра соответствует функции времени вида
линейным фазовым спектром. В соответствии с теоремой о смещении спектра (см. п. 3 § 2.8) подобная структура спектра соответствует функции времени вида  , где
, где  — медленная функция, имеющая смысл огибающей амплитуд сжатого сигнала. Спектральная плотность функции
— медленная функция, имеющая смысл огибающей амплитуд сжатого сигнала. Спектральная плотность функции  получается сдвигом упомянутых двух лепестков на
получается сдвигом упомянутых двух лепестков на  к нулевой частоте и в рассматриваемом примере (ЛЧМ импульс) имеет форму прямоугольника с основанием, равным
к нулевой частоте и в рассматриваемом примере (ЛЧМ импульс) имеет форму прямоугольника с основанием, равным  с центром в точке
с центром в точке  . По аналогии с п. 4 § 2.10 (см. рис. 2.19), заменив
. По аналогии с п. 4 § 2.10 (см. рис. 2.19), заменив  и
и  придем к
придем к  в виде функции
в виде функции  .
.
Очевидно,что отсутствие модуляции высокочастотного заполнения сигнала на выходе согласованного фильтра имеет место при любом законе ЧМ входного сигнала. При определении же огибающей выходного сигнала необходимо учитывать изменение формы амплитудного спектра сигнала в фильтре (при непрямоугольной форме на входе фильтра).
Определим пик сжатого сигнала при нормировании энергии выходного сигнала к энергии сигнала на входе [см. (13.26)], в данном случае

Поэтому


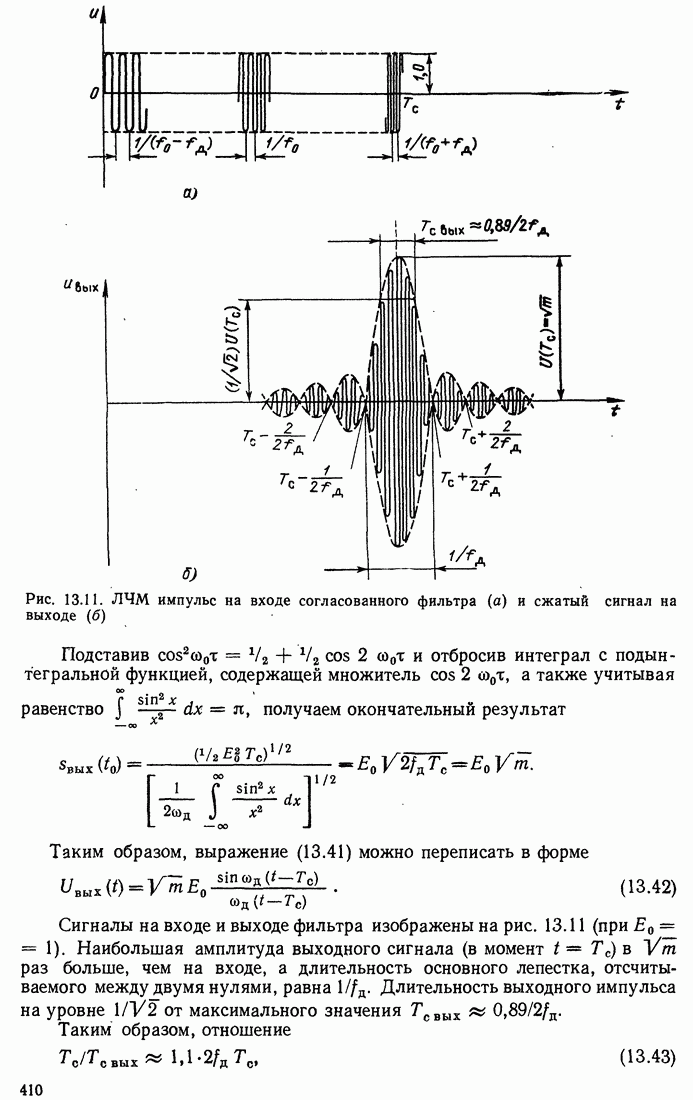
Рис. 13.11. ЛЧМ импульс на входе согласованного фильтра (а) и сжатый сигнал на выходе (б)
Подставив  и отбросив интеграл с подынтегральной функцией, содержащей множитель
и отбросив интеграл с подынтегральной функцией, содержащей множитель  , а также учитывая равенство
, а также учитывая равенство  , получаем окончательный результат
, получаем окончательный результат

Таким образом, выражение (13.41) можно переписать в форме
 (13.42)
(13.42)
Сигналы на входе и выходе фильтра изображены на рис. 13.11 (при  Наибольшая амплитуда выходного сигнала (в момент
Наибольшая амплитуда выходного сигнала (в момент  )
)  раз больше, чем на входе, а длительность основного лепестка, отсчитываемого между двумя нулями, равна
раз больше, чем на входе, а длительность основного лепестка, отсчитываемого между двумя нулями, равна  . Длительность выходного импульса на уровне
. Длительность выходного импульса на уровне  от максимального значения
от максимального значения  .
.
Таким образом, отношение
 (13.43)
(13.43)
близкое по значению к параметру модуляции  можно назвать коэффициентом сжатия ЧМ импульса в согласованном фильтре.
можно назвать коэффициентом сжатия ЧМ импульса в согласованном фильтре.
Из выражения (13.42) видно, что компенсация фаз спектра сигнала — основная операция в согласованном фильтре — приводит к сжатию импульса в  раз при одновременном увеличении пика сигнала в
раз при одновременном увеличении пика сигнала в  раз (при нормировке энергий входного и выходного сигналов).
раз (при нормировке энергий входного и выходного сигналов).
Это весьма ценно для практики, так как позволяет удлинять импульс, генерируемый передатчиком, для увеличения энергии сигнала без потери разрешающей способности, которая определяется длительностью импульса на выходе согласованного фильтра. Техническое преимущество этого метода проявляется особенно в тех случаях, когда увеличение амплитуды импульсов в передатчике ограничивается импульсной мощностью электронных приборов, используемых для генерации колебаний. Значительно проще увеличивать энергию сигнала удлинением импульсов при одновременном наложении ЧМ. При этом параметр модуляции  должен расти пропорционально длительности
должен расти пропорционально длительности  излучаемого сигнала (при заданной длительности
излучаемого сигнала (при заданной длительности  импульса на выходе согласованного фильтра). Иными словами, девиация частоты должна оставаться неизменной, а скорость изменения частоты
импульса на выходе согласованного фильтра). Иными словами, девиация частоты должна оставаться неизменной, а скорость изменения частоты  должна быть обратно пропорциональна
должна быть обратно пропорциональна  (см. (13.39)).
(см. (13.39)).
3. ПАЧКА ОДИНАКОВЫХ ИМПУЛЬСОВ
Рассмотрим сигнал в виде группы из  одинаковых видеоимпульсов (рис. 13.12). Интервалы между импульсами могут быть неодинаковыми. Спектр такого сигнала
одинаковых видеоимпульсов (рис. 13.12). Интервалы между импульсами могут быть неодинаковыми. Спектр такого сигнала
 (13.44)
(13.44)
где  — спектр первого имплульса, начинающегося в момент
— спектр первого имплульса, начинающегося в момент  — спектр второго импульса, начинающегося в момент
— спектр второго импульса, начинающегося в момент  и т. д.
и т. д.
Так как полная длительность изображенного на рис. 13.12 сигнала равна  то в соответствии с выражением (13.8) согласованный со спектром
то в соответствии с выражением (13.8) согласованный со спектром  фильтр должен иметь коэффициент передачи
фильтр должен иметь коэффициент передачи
 (13.45)
(13.45)
В этом выражении  представляет собой коэффициент передачи фильтра, согласованного с одиночным импульсом.
представляет собой коэффициент передачи фильтра, согласованного с одиночным импульсом.
Основываясь на выражении (13.45), нетрудно наметить схему фильтра, согласованного с сигналом, изображенным на рис. 13.12. Подобный фильтр должен содержать звено с передаточной функцией  обеспечивающее оптимальную внутриимпульсную обработку сигнала, и набор линий задержек. Величины этих задержек должны нарастать в порядке, обратном расстановке импульсов в пачке на входе фильтра. Один из возможных вариантов такого устройства показан на рис. 13.13, а.
обеспечивающее оптимальную внутриимпульсную обработку сигнала, и набор линий задержек. Величины этих задержек должны нарастать в порядке, обратном расстановке импульсов в пачке на входе фильтра. Один из возможных вариантов такого устройства показан на рис. 13.13, а.

Рис. 13.12. Сигнал в виде пачки импульсов

Рис. 13.13. Согласованная фильтрация пачки импульсов (к рис. 13.12)
Максимальный импульс на выходе сумматора получается, когда первый импульс входной последовательности, прошедший через задержку  суммируется со вторым импульсом, прошедшим через задержку
суммируется со вторым импульсом, прошедшим через задержку  с третьим импульсом, задержанным на
с третьим импульсом, задержанным на  , и так далее вплоть до последнего импульса проходящего через рассматриваемое устройство без дополнительной задержки. Вместо набора из
, и так далее вплоть до последнего импульса проходящего через рассматриваемое устройство без дополнительной задержки. Вместо набора из  линий задержки конструктивно проще и выгоднее применять одну линию задержки с
линий задержки конструктивно проще и выгоднее применять одну линию задержки с  отводами (рис. 13.13, б). Отводы располагаются таким образом, чтобы соответствующие им задержки нарастали в том же порядке, что и на рис. 13.13, а.
отводами (рис. 13.13, б). Отводы располагаются таким образом, чтобы соответствующие им задержки нарастали в том же порядке, что и на рис. 13.13, а.
Построение согласованного фильтра значительно упрощается, когда входной сигнал представляет собой последовательность равноотстоящих одинаковых импульсов, т. е. когда

Для этого случая выражение (13.45) можно записать так:
 (13.46)
(13.46)
При достаточно большом числе  выражение в квадратных скобках можно свернуть по формуле геометрической прогрессии
выражение в квадратных скобках можно свернуть по формуле геометрической прогрессии
 (13.47)
(13.47)
Структура выражения (13.46) указывает на возможность осуществления согласованного фильтра в виде каскадного соединения двух четырехполюсников: одного с передаточной функцией  , как и в схеме на рис. 13,13, а, согласованного с одиночным импульсом, и другого в виде цепи с обратной связью, содержащей всего лишь одну линию задержки Т (рис. 13.14). Передаточная функция подобной цепи (на рис. 13.14 обведенной штриховой линией) определяется выражением
, как и в схеме на рис. 13,13, а, согласованного с одиночным импульсом, и другого в виде цепи с обратной связью, содержащей всего лишь одну линию задержки Т (рис. 13.14). Передаточная функция подобной цепи (на рис. 13.14 обведенной штриховой линией) определяется выражением
 (13.48)
(13.48)
Символом  обозначен безынерционный четырехполюсник, учитывающий затухание в линии задержки (достигающее десятков децибел) и вклю чающий в себя усилитель, компенсирующий это затухание.
обозначен безынерционный четырехполюсник, учитывающий затухание в линии задержки (достигающее десятков децибел) и вклю чающий в себя усилитель, компенсирующий это затухание.

Рис. 13.14. Гребенчатый фильтр

Рис. 13.15. Амплитудно-частотная- характеристика гребенчатого фильтра
Для устойчивости цепи коэффициент  должен быть меньше единицы. Сама линия задержки при этом может рассматриваться как идеальная с передаточной функцией
должен быть меньше единицы. Сама линия задержки при этом может рассматриваться как идеальная с передаточной функцией 
При частотах, отвечающих условию  обратная связь отрицательна и
обратная связь отрицательна и  . При частотах
. При частотах  обратная связь положительна и
обратная связь положительна и 
Амплитудно-частотная характеристика цепи приобретает вид, показанный на рис. 13.15. Фильтры с подобной характеристикой называются гребенчатыми  . Они эффективны для выделения сигналов в виде периодической последовательности импульсов на фоне белого шума. Чем больше число импульсов в пачке
. Они эффективны для выделения сигналов в виде периодической последовательности импульсов на фоне белого шума. Чем больше число импульсов в пачке  и чем ближе
и чем ближе  к единице, тем лучше приближение цепи к согласованному фильтру.
к единице, тем лучше приближение цепи к согласованному фильтру.
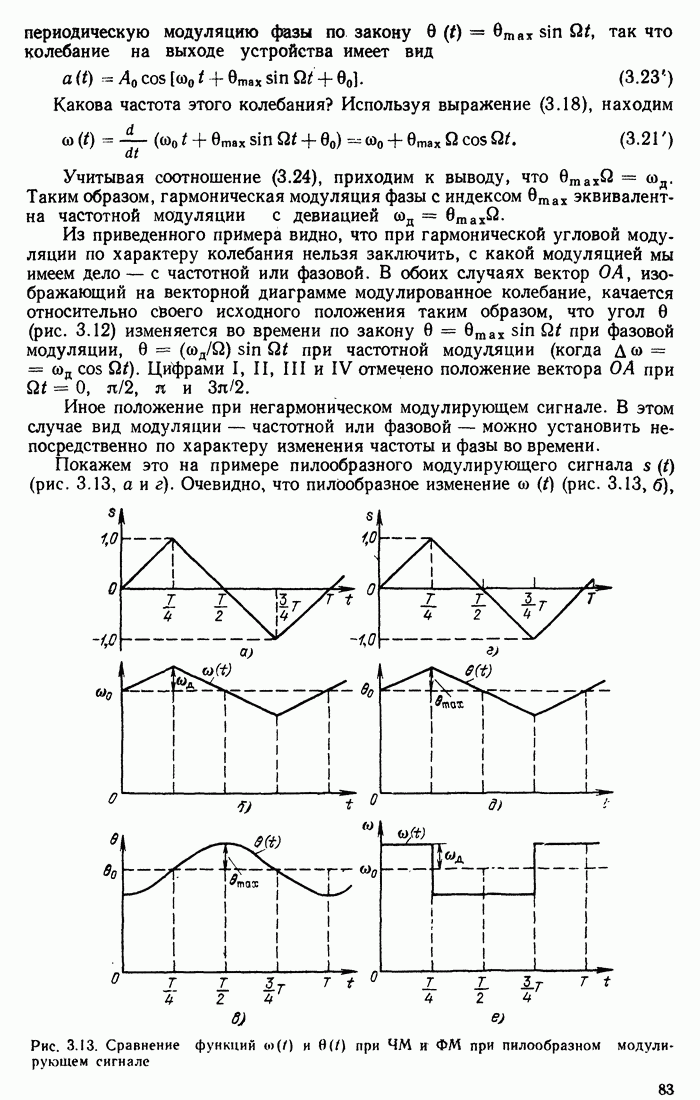
Импульсная характеристика фильтра 

Коэффициенты при единичных импульсах, возникающих на выходе четырехполюсника через интервалы Т, убывают по закону, близкому к экспоненте. Таким образом, импульсная характеристика фильтра имеет вид, показанный на рис. 13.16.
Все приведенные выше рассуждения можно распространить и на фильтрацию последовательности радиоимпульсов. Необходимо лишь под  подразумевать коэффициент передачи фильтра, согласованного с одиночным радиоимпульсом. Кроме того, для обеспечения сложения задержанных радиоимпульсов в фазе требуется введение корректирующих фазовых сдвигов (при
подразумевать коэффициент передачи фильтра, согласованного с одиночным радиоимпульсом. Кроме того, для обеспечения сложения задержанных радиоимпульсов в фазе требуется введение корректирующих фазовых сдвигов (при  ).
).

Рис. 13.16. Импульсная характеристика гребенчатого фильтра

Рис. 13.17. Формирование сигнала, сопряженного с заданным фильтром
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
- Глава 1. ОБЩАЯ ХАРАКТЕРИСТИКА РАДИОТЕХНИЧЕСКИХ ПРОЦЕССОВ, СИГНАЛОВ И ЦЕПЕЙ
- 1.1. ПЕРЕДАЧА СИГНАЛОВ НА РАССТОЯНИЕ И ИСПОЛЬЗУЕМЫЕ В РАДИОТЕХНИКЕ ЧАСТОТЫ
- 1.2. ПРЕОБРАЗОВАНИЕ СИГНАЛОВ В РАДИОТЕХНИЧЕСКИХ СИСТЕМАХ
- 1.3. КЛАССИФИКАЦИЯ СИГНАЛОВ, ИСПОЛЬЗУЕМЫХ В РАДИОТЕХНИКЕ
- 1.4. РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И МЕТОДЫ ИХ АНАЛИЗА
- 1.5. ПРОБЛЕМА ПОМЕХОУСТОЙЧИВОСТИ И ЭЛЕКТРОМАГНИТНОЙ СОВМЕСТИМОСТИ РАДИОТЕХНИЧЕСКИХ СИСТЕМ
- Глава 2. ХАРАКТЕРИСТИКИ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
- 2.2. ПРЕДСТАВЛЕНИЕ ПРОИЗВОЛЬНОГО СИГНАЛА В ВИДЕ СУММЫ ЭЛЕМЕНТАРНЫХ КОЛЕБАНИИ
- 2.3. ГАРМОНИЧЕСКИЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ
- 2.4. СПЕКТРЫ ПРОСТЕЙШИХ ПЕРИОДИЧЕСКИХ СИГНАЛОВ
- 2.5. РАСПРЕДЕЛЕНИЕ МОЩНОСТИ В СПЕКТРЕ ПЕРИОДИЧЕСКОГО СИГНАЛА
- 2.6. ГАРМОНИЧЕСКИЙ АНАЛИЗ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
- 2.7. СООТНОШЕНИЕ МЕЖДУ СПЕКТРАМИ ОДИНОЧНОГО ИМПУЛЬСА И ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ИМПУЛЬСОВ
- 2.8. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 2.9. РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ В СПЕКТРЕ НЕПЕРИОДИЧЕСКОГО СИГНАЛА
- 2.10. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ СПЕКТРОВ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
- 2.11. БЕСКОНЕЧНО КОРОТКИЙ ИМПУЛЬС С ЕДИНИЧНОЙ ПЛОЩАДЬЮ (ДЕЛЬТА-ФУНКЦИЯ)
- 2.12. СООТНОШЕНИЕ МЕЖДУ ДЛИТЕЛЬНОСТЬЮ СИГНАЛА И ШИРИНОЙ ЕГО СПЕКТРА. СКОРОСТЬ УБЫВАНИЯ СПЕКТРА
- 2.13. СПЕКТРЫ НЕКОТОРЫХ НЕИНТЕГРИРУЕМЫХ ФУНКЦИЙ
- 2.14. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ НА ПЛОСКОСТИ КОМПЛЕКСНОЙ ЧАСТОТЫ
- 2.15. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ С ОГРАНИЧЕННОЙ ПОЛОСОЙ ЧАСТОТ В ВИДЕ РЯДА КОТЕЛЬНИКОВА
- 2.16. ТЕОРЕМА ОТСЧЕТОВ В ЧАСТОТНОЙ ОБЛАСТИ
- 2.17. ДИСКРЕТИЗОВАННЫЕ СИГНАЛЫ
- 2.18. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
- 2.19. СООТНОШЕНИЕ МЕЖДУ КОРРЕЛЯЦИОННОЙ ФУНКЦИЕЙ И СПЕКТРАЛЬНОЙ ХАРАКТЕРИСТИКОЙ СИГНАЛА
- Глава 3. МОДУЛИРОВАННЫЕ КОЛЕБАНИЯ
- 3.2. РАДИОСИГНАЛЫ С АМПЛИТУДНОЙ МОДУЛЯЦИЕЙ
- 3.3. СПЕКТР АМПЛИТУДНО-МОДУЛИРОВАННОГО КОЛЕБАНИЯ
- 3.4. УГЛОВАЯ МОДУЛЯЦИЯ. ФАЗА И МГНОВЕННАЯ ЧАСТОТА КОЛЕБАНИЯ
- 3.5. СПЕКТР КОЛЕБАНИЯ ПРИ УГЛОВОЙ МОДУЛЯЦИИ. ОБЩИЕ СООТНОШЕНИЯ
- 3.6. СПЕКТР КОЛЕБАНИЯ ПРИ ГАРМОНИЧЕСКОЙ УГЛОВОЙ МОДУЛЯЦИИ
- 3.7. СПЕКТР РАДИОИМПУЛЬСА С ЧАСТОТНО-МОДУЛИРОВАННЫМ ЗАПОЛНЕНИЕМ
- 3.8. СПЕКТР КОЛЕБАНИЯ ПРИ АМПЛИТУДНО-ЧАСТОТНОЙ МОДУЛЯЦИИ
- 3.9. ОГИБАЮЩАЯ, ФАЗА И ЧАСТОТА УЗКОПОЛОСНОГО СИГНАЛА
- 3.10. АНАЛИТИЧЕСКИЙ СИГНАЛ
- 3.11. КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ МОДУЛИРОВАННОГО КОЛЕБАНИЯ
- 3.12. ДИСКРЕТИЗАЦИЯ УЗКОПОЛОСНОГО СИГНАЛА
- Глава 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ СИГНАЛОВ
- 4.2. ВИДЫ СЛУЧАЙНЫХ ПРОЦЕССОВ. ПРИМЕРЫ
- 4.3. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ МОЩНОСТИ СЛУЧАЙНОГО ПРОЦЕССА
- 4.4. СООТНОШЕНИЕ МЕЖДУ СПЕКТРАЛЬНОЙ ПЛОТНОСТЬЮ И КОВАРИАЦИОННОЙ ФУНКЦИЕЙ СЛУЧАЙНОГО ПРОЦЕССА
- 4.5. ВЗАИМНАЯ КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ И ВЗАИМНАЯ СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ДВУХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 4.6. УЗКОПОЛОСНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- 4.7. КОМПЛЕКСНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- 4.8. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ. ПРОСТРАНСТВО СИГНАЛОВ
- 4.9. ПРОСТРАНСТВО СЛУЧАЙНЫХ СИГНАЛОВ
- Глава 5. ЛИНЕЙНЫЕ РАДИОТЕХНИЧЕСКИЕ ЦЕПИ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
- 5.1. ОПРЕДЕЛЕНИЯ И СВОЙСТВА АКТИВНЫХ ЦЕПЕЙ
- 5.2. АКТИВНЫЙ ЧЕТЫРЕХПОЛЮСНИК КАК ЛИНЕЙНЫЙ УСИЛИТЕЛЬ
- 5.3. ЧАСТОТНЫЕ И ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ РАДИОЭЛЕКТРОННЫХ ЦЕПЕЙ
- 5.4. АПЕРИОДИЧЕСКИЙ УСИЛИТЕЛЬ
- 5.5. КАСКАДНОЕ СОЕДИНЕНИЕ ИДЕНТИЧНЫХ АПЕРИОДИЧЕСКИХ УСИЛИТЕЛЕЙ
- 5.6. РЕЗОНАНСНЫЙ УСИЛИТЕЛЬ
- 5.7. ОБРАТНАЯ СВЯЗЬ В АКТИВНОМ ЧЕТЫРЕХПОЛЮСНИКЕ
- 5.8. ПРИМЕНЕНИЕ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗИ ДЛЯ УЛУЧШЕНИЯ ХАРАКТЕРИСТИК УСИЛИТЕЛЯ
- 5.9. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АКТИВНЫХ ЦЕПЕЙ С ОБРАТНОЙ СВЯЗЬЮ. АЛГЕБРАИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
- 5.10. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- Глава 6. ПРОХОЖДЕНИЕ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
- 6.2. СПЕКТРАЛЬНЫЙ МЕТОД
- 6.3. МЕТОД ИНТЕГРАЛА НАЛОЖЕНИЯ
- 6.4. ПРОХОЖДЕНИЕ ДИСКРЕТНЫХ СИГНАЛОВ ЧЕРЕЗ АПЕРИОДИЧЕСКИЙ УСИЛИТЕЛЬ
- 6.5. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ СИГНАЛОВ
- 6.6. АНАЛИЗ РАДИОСИГНАЛОВ В ИЗБИРАТЕЛЬНЫХ ЦЕПЯХ. МЕТОД ОГИБАЮЩЕЙ
- 6.7. ПРОХОЖДЕНИЕ РАДИОИМПУЛЬСА ЧЕРЕЗ РЕЗОНАНСНЫЙ УСИЛИТЕЛЬ
- 6.8. ЛИНЕЙНЫЕ ИСКАЖЕНИЯ АМПЛИТУДНО-МОДУЛИРОВАННОГО КОЛЕБАНИЯ В РЕЗОНАНСНОМ УСИЛИТЕЛЕ
- 6.9. ПРОХОЖДЕНИЕ ФАЗОМАНИПУЛИРОВАННОГО КОЛЕБАНИЯ ЧЕРЕЗ РЕЗОНАНСНУЮ ЦЕПЬ
- 6.10. ПРОХОЖДЕНИЕ ЧАСТОТНО-МАНИПУЛИРОВАННОГО КОЛЕБАНИЯ ЧЕРЕЗ ИЗБИРАТЕЛЬНУЮ ЦЕПЬ
- 6.11. ПРОХОЖДЕНИЕ ЧАСТОТНО-МОДУЛИРОВАННОГО КОЛЕБАНИЯ ЧЕРЕЗ ИЗБИРАТЕЛЬНЫЕ ЦЕПИ
- Глава 7. ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
- 7.1. ПРЕОБРАЗОВАНИЕ ХАРАКТЕРИСТИК СЛУЧАЙНОГО ПРОЦЕССА В ЛИНЕЙНЫХ ЦЕПЯХ
- 7.2. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ МОЩНОСТИ И КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ СЛУЧАЙНОГО ПРОЦЕССА НА ВЫХОДЕ ЦЕПИ
- 7.3. ХАРАКТЕРИСТИКИ СОБСТВЕННЫХ ШУМОВ В РАДИОЭЛЕКТРОННЫХ ЦЕПЯХ
- 7.4. ДИФФЕРЕНЦИРОВАНИЕ СЛУЧАЙНОЙ ФУНКЦИИ
- 7.5. ИНТЕГРИРОВАНИЕ СЛУЧАЙНОЙ ФУНКЦИИ
- 7.6. ПАРАМЕТРЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОГО ПРОЦЕССА НА ВЫХОДЕ ЛИНЕЙНОЙ ЦЕПИ. ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ
- 7.7. НОРМАЛИЗАЦИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ В УЗКОПОЛОСНЫХ ЛИНЕЙНЫХ ЦЕПЯХ
- Глава 8. НЕЛИНЕЙНЫЕ ЦЕПИ И МЕТОДЫ ИХ АНАЛИЗА
- 8.2. АППРОКСИМАЦИЯ НЕЛИНЕЙНЫХ ХАРАКТЕРИСТИК
- 8.3. ВОЗДЕЙСТВИЕ УЗКОПОЛОСНОГО РАДИОСИГНАЛА НА БЕЗЫНЕРЦИОННЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ
- 8.4. ВОЗДЕЙСТВИЕ БИГАРМОНИЧЕСКОГО КОЛЕБАНИЯ НА НЕЛИНЕЙНЫЙ РЕЗИСТИВНЫЙ ЭЛЕМЕНТ
- 8.5. НЕЛИНЕЙНОЕ РЕЗОНАНСНОЕ УСИЛЕНИЕ
- 8.6. УМНОЖЕНИЕ ЧАСТОТЫ
- 8.7. АМПЛИТУДНОЕ ОГРАНИЧЕНИЕ
- 8.8. НЕЛИНЕЙНАЯ ЦЕПЬ С ФИЛЬТРАЦИЕЙ ПОСТОЯННОГО ТОКА (ВЫПРЯМЛЕНИЕ)
- 8.9. АМПЛИТУДНОЕ ДЕТЕКТИРОВАНИЕ
- 8.10. ЧАСТОТНОЕ И ФАЗОВОЕ ДЕТЕКТИРОВАНИЕ
- 8.11. ПРЕОБРАЗОВАНИЕ ЧАСТОТЫ СИГНАЛА
- 8.12. СИНХРОННОЕ ДЕТЕКТИРОВАНИЕ
- 8.13. ПОЛУЧЕНИЕ АМПЛИТУДНО-МОДУЛИРОВАННЫХ КОЛЕБАНИИ
- 8.14. РЕЗОНАНС В КОЛЕБАТЕЛЬНОМ КОНТУРЕ С НЕЛИНЕЙНОЙ ЕМКОСТЬЮ
- 8.15. ВОЗДЕЙСТВИЕ ГАРМОНИЧЕСКОГО СИГНАЛА НА НЕЛИНЕЙНУЮ ЕМКОСТЬ. УМНОЖИТЕЛЬ ЧАСТОТЫ НА ВАРАКТОРЕ
- 8.16. ВОЗДЕЙСТВИЕ ДВУХ ГАРМОНИЧЕСКИХ КОЛЕБАНИИ НА ЦЕПЬ С НЕЛИНЕЙНЫМ ЭНЕРГОЕМКИМ ЭЛЕМЕНТОМ
- 8.17. ТЕОРЕМА МЭНЛИ—РОУ
- 8.18. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ ЦЕПЯХ ПО ЗАДАННОМУ ДИФФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ
- Глава 9. ГЕНЕРИРОВАНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- 9.1. АВТОКОЛЕБАТЕЛЬНАЯ СИСТЕМА
- 9.2. ВОЗНИКНОВЕНИЕ КОЛЕБАНИЯ В АВТОГЕНЕРАТОРЕ
- 9.3. СТАЦИОНАРНЫЙ РЕЖИМ АВТОГЕНЕРАТОРА
- 9.4. МЯГКИЙ И ЖЕСТКИЙ РЕЖИМЫ САМОВОЗБУЖДЕНИЯ
- 9.5. ПРИМЕРЫ СХЕМ АВТОГЕНЕРАТОРОВ
- 9.6. НЕЛИНЕЙНОЕ УРАВНЕНИЕ АВТОГЕНЕРАТОРА
- 9.7. МЕТОД ФАЗОВОЙ ПЛОСКОСТИ
- 9.8. ФАЗОВЫЕ ПОРТРЕТЫ АВТОГЕНЕРАТОРА
- 9.9. АВТОГЕНЕРАТОРЫ С ВНУТРЕННЕЙ ОБРАТНОЙ СВЯЗЬЮ
- 9.10. АВТОГЕНЕРАТОР С ЛИНИЕЙ ЗАДЕРЖКИ В ЦЕПИ ОБРАТНОЙ СВЯЗИ
- 9.11. RC-ГЕНЕРАТОРЫ
- 9.12. ДЕЙСТВИЕ ГАРМОНИЧЕСКОЙ ЭДС НА ЦЕПИ С ПОЛОЖИТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ. РЕГЕНЕРАЦИЯ
- 9.13. ДЕЙСТВИЕ ГАРМОНИЧЕСКОЙ ЭДС НА АВТОГЕНЕРАТОР. ЗАХВАТЫВАНИЕ ЧАСТОТЫ
- 9.14. УГЛОВАЯ МОДУЛЯЦИЯ В АВТОГЕНЕРАТОРЕ
- Глава 10. ЦЕПИ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10.1. ОБЩИЕ ХАРАКТЕРИСТИКИ ЦЕПЕЙ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10.2. ПРОХОЖДЕНИЕ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- 10.3. ПРИМЕР ОПРЕДЕЛЕНИЯ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ ПАРАМЕТРИЧЕСКОЙ ЦЕПИ
- 10.4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЦЕПИ С ПЕРИОДИЧЕСКИ ИЗМЕНЯЮЩИМСЯ ПАРАМЕТРОМ
- 10.5. ПРИНЦИП ПАРАМЕТРИЧЕСКОГО УСИЛЕНИЯ СИГНАЛОВ
- 10.6. ОДНОКОНТУРНЫЙ ПАРАМЕТРИЧЕСКИЙ УСИЛИТЕЛЬ
- 10.7. ДВУХКОНТУРНЫЙ ПАРАМЕТРИЧЕСКИЙ УСИЛИТЕЛЬ
- 10.8. ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИИ
- 10.9. СОПОСТАВЛЕНИЕ ПАРАМЕТРИЧЕСКИХ И НЕЛИНЕЙНЫХ ПРЕОБРАЗОВАНИИ СИГНАЛОВ
- Глава 11. ВОЗДЕЙСТВИЕ СЛУЧАЙНЫХ КОЛЕБАНИЙ НА НЕЛИНЕЙНЫЕ И ПАРАМЕТРИЧЕСКИЕ ЦЕПИ
- 11.2. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА В БЕЗЫНЕРЦИОННЫХ НЕЛИНЕЙНЫХ ЦЕПЯХ
- 11.3. ПРЕОБРАЗОВАНИЕ СПЕКТРА СЛУЧАЙНОГО ПРОЦЕССА В БЕЗЫНЕРЦИОННОМ НЕЛИНЕЙНОМ ЭЛЕМЕНТЕ
- 11.4. ВОЗДЕЙСТВИЕ УЗКОПОЛОСНОГО ШУМА НА АМПЛИТУДНЫЙ ДЕТЕКТОР
- 11.6. СОВМЕСТНОЕ ВОЗДЕЙСТВИЕ ГАРМОНИЧЕСКОГО СИГНАЛА И ГАУССОВСКОГО ШУМА НА АМПЛИТУДНЫЙ ДЕТЕКТОР
- 11.6. СОВМЕСТНОЕ ВОЗДЕЙСТВИЕ ГАРМОНИЧЕСКОГО СИГНАЛА И ГАУССОВСКОГО ШУМА НА ЧАСТОТНЫЙ ДЕТЕКТОР
- 11.7. ВЗАИМОДЕЙСТВИЕ ГАРМОНИЧЕСКОГО СИГНАЛА И ГАУССОВСКОГО ШУМА В АМПЛИТУДНОМ ОГРАНИЧИТЕЛЕ С РЕЗОНАНСНОЙ НАГРУЗКОЙ
- 11.8. КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ И СПЕКТР СЛУЧАЙНОГО ПРОЦЕССА В ЛИНЕЙНОЙ ПАРАМЕТРИЧЕСКОЙ ЦЕПИ
- 11.9. ВЛИЯНИЕ МУЛЬТИПЛИКАТИВНОЙ ПОМЕХИ НА ЗАКОН РАСПРЕДЕЛЕНИЯ СИГНАЛА
- Глава 12. ДИСКРЕТНАЯ ОБРАБОТКА СИГНАЛОВ. ЦИФРОВЫЕ ФИЛЬТРЫ
- 12.2. ПРИНЦИП ДИСКРЕТНОЙ ФИЛЬТРАЦИИ
- 12.3. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЦИФРОВОГО ФИЛЬТРА
- 12.4. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СИГНАЛОВ
- 12.5. ПРИМЕНЕНИЕ МЕТОДА Z-ПРЕОБРАЗОВАНИЯ ДЛЯ АНАЛИЗА ДИСКРЕТНЫХ СИГНАЛОВ И ЦЕПЕЙ
- 12.6. Z-ПРЕОБРАЗОВАНИЕ BPEMEHHЫХ ФУНКЦИЙ
- 12.7. z-ПРЕОБРАЗОВАНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ДИСКРЕТНЫХ ЦЕПЕЙ
- 12.8. ПРИМЕРЫ АНАЛИЗА ЦИФРОВЫХ ФИЛЬТРОВ
- 12.9. ЦИФРОВЫЕ ФИЛЬТРЫ С КОМПЛЕКСНЫМИ ВЕСОВЫМИ КОЭФФИЦИЕНТАМИ
- 12.10. ПРЕОБРАЗОВАНИЕ АНАЛОГ—ЦИФРА. ШУМЫ КВАНТОВАНИЯ
- 12.11. ПРЕОБРАЗОВАНИЕ ЦИФРА—АНАЛОГ И ВОССТАНОВЛЕНИЕ КОНТИНУАЛЬНОГО СИГНАЛА
- 12.12. БЫСТРОДЕЙСТВИЕ АРИФМЕТИЧЕСКОГО УСТРОЙСТВА ЦИФРОВОГО ФИЛЬТРА
- 12.13. АЛГОРИТМ ЦИФРОВОЙ ФИЛЬТРАЦИИ ВО ВРЕМЕННОЙ И ЧАСТОТНОЙ ОБЛАСТЯХ
- 12.14. БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 12.15. СПЕКТРАЛЬНЫЙ АНАЛИЗ НА БАЗЕ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 12.16. ПРИМЕНЕНИЕ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ В УСТРОЙСТВАХ ОБРАБОТКИ СИГНАЛОВ
- Глава 13. ПРИНЦИПЫ ОПТИМАЛЬНОЙ ЛИНЕЙНОИ ФИЛЬТРАЦИИ СИГНАЛА НА ФОНЕ ПОМЕХ
- 13.2. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ОПТИМАЛЬНОГО ФИЛЬТРА
- 13.3. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА СОГЛАСОВАННОГО ФИЛЬТРА. ФИЗИЧЕСКАЯ ОСУЩЕСТВИМОСТЬ
- 13.4. СИГНАЛ И ПОМЕХА НА ВЫХОДЕ СОГЛАСОВАННОГО ФИЛЬТРА
- 13.5. ПРИМЕРЫ ПОСТРОЕНИЯ СОГЛАСОВАННЫХ ФИЛЬТРОВ
- 13.6. ФОРМИРОВАНИЕ СИГНАЛА, СОПРЯЖЕННОГО С ЗАДАННЫМ ФИЛЬТРОМ
- 13.7. ФИЛЬТРАЦИЯ ЗАДАННОГО СИГНАЛА ПРИ НЕБЕЛОМ ШУМЕ
- 13.8. ФИЛЬТРАЦИЯ СИГНАЛА С НЕИЗВЕСТНОЙ НАЧАЛЬНОЙ ФАЗОЙ
- 13.9. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ КОМПЛЕКСНОГО СИГНАЛА. КВАДРАТУРНАЯ ОБРАБОТКА
- 13.10. ЦИФРОВОЙ СОГЛАСОВАННЫЙ ФИЛЬТР
- Глава 14. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ НЕКОТОРЫМИ СПЕЦИАЛЬНЫМИ ФУНКЦИЯМИ
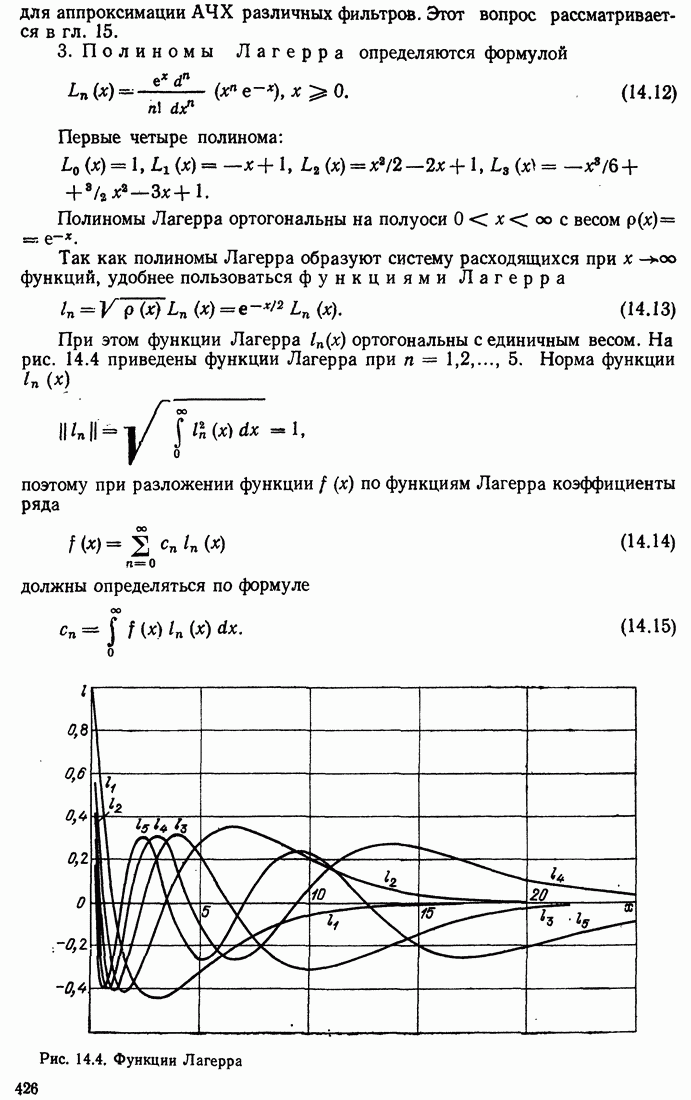
- 14.2. ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ И ФУНКЦИИ НЕПРЕРЫВНОГО ТИПА
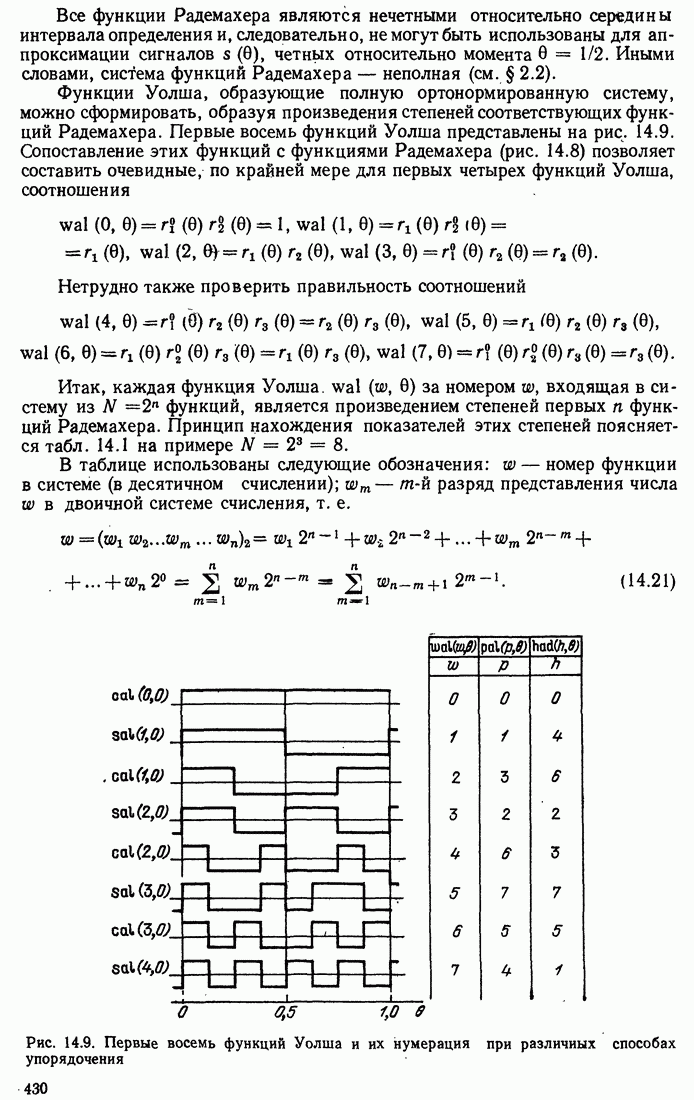
- 14.3. ФУНКЦИИ УОЛША
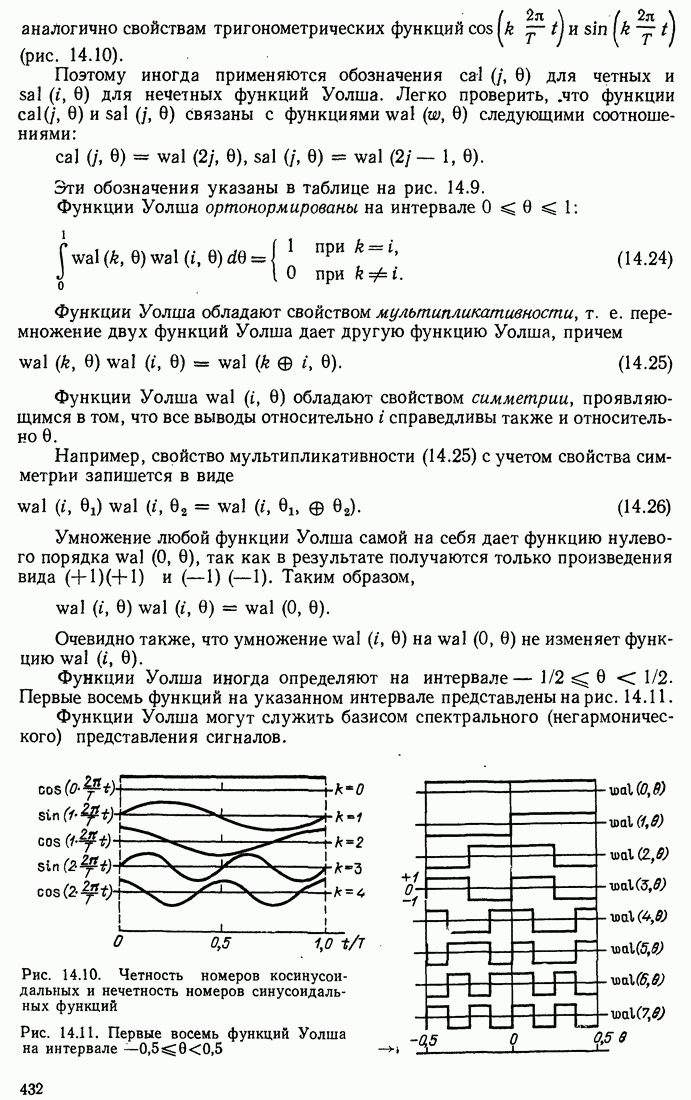
- 14.4. РАЗЛИЧНЫЕ СПОСОБЫ НУМЕРАЦИИ ФУНКЦИЙ УОЛША
- 14.5. ПРИМЕРЫ ПРИМЕНЕНИЯ ФУНКЦИЙ УОЛША
- 14.6. ДИСКРЕТНЫЕ ФУНКЦИИ УОЛША
- Глава 15. ЭЛЕМЕНТЫ СИНТЕЗА ЛИНЕЙНЫХ РАДИОЦЕПЕЙ
- 15.2. ПРЕДСТАВЛЕНИЕ АНАЛОГОВОГО ЧЕТЫРЕХПОЛЮСНИКА КАСКАДНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТАРНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ
- 15.3. РЕАЛИЗАЦИЯ БЕЗЫНДУКТИВНОСТНОИ ЦЕПИ ВТОРОГО ПОРЯДКА
- 15.4. ОСОБЕННОСТИ СИНТЕЗА ЧЕТЫРЕХПОЛЮСНИКА ПО ЗАДАННОЙ АМПЛИТУДНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ
- 15.5. СИНТЕЗ ФИЛЬТРА НИЖНИХ ЧАСТОТ. ФИЛЬТР БАТТЕРВОРТА
- 15.6. ПРИМЕР СИНТЕЗА ФИЛЬТРА БАТТЕРВОРТА ВТОРОГО ПОРЯДКА
- 15.7. ФИЛЬТР ЧЕБЫШЕВА (НИЖНИХ ЧАСТОТ)
- 15.8. СИНТЕЗ РАЗЛИЧНЫХ ФИЛЬТРОВ НА ОСНОВЕ ФИЛЬТРА НИЖНИХ ЧАСТОТ
- 15.9. СВЯЗЬ МЕЖДУ АМПЛИТУДНО- И ФАЗОЧАСТОТНОЙ ХАРАКТЕРИСТИКАМИ В ЦИФРОВЫХ ЦЕПЯХ
- 15.10. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ФЧХ ЦИФРОВОГО ФИЛЬТРА ПО ЗАДАННОЙ АЧХ
- 15.11. СИНТЕЗ ЦИФРОВЫХ ФИЛЬТРОВ. ОБЩИЕ ЗАМЕЧАНИЯ
- 15.12. СИНТЕЗ ЦИФРОВЫХ ФИЛЬТРОВ ПО АНАЛОГОВОМУ ПРОТОТИПУ
- 15.13. МЕТОД ИНВАРИАНТНЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- Глава 16. ОБОБЩЕННАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ СИГНАЛОВ. КЕПСТРАЛЬНЫЙ АНАЛИЗ
- 16.1. ОБОБЩЕННЫЙ ПРИНЦИП СУПЕРПОЗИЦИИ
- 16.2. ОБОБЩЕННАЯ СХЕМА ГОМОМОРФНОЙ ОБРАБОТКИ СИГНАЛОВ
- 16.3. ГОМОМОРФНАЯ ОБРАБОТКА МУЛЬТИПЛИКАТИВНОГО СИГНАЛА
- 16.4. ГОМОМОРФНАЯ ОБРАБОТКА СВЕРНУТОГО СИГНАЛА
- 16.5. КЕПСТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ. КЕПСТР МОЩНОСТИ
- 16.6. ОПРЕДЕЛЕНИЕ ЗАДЕРЖКИ СИГНАЛА
- 16.7. ПРИМЕР ОПРЕДЕЛЕНИЯ ЗАДЕРЖКИ СИГНАЛА
- 16.8. ВЛИЯНИЕ ПОМЕХ
- 16.9. КОМПЛЕКСНЫЙ КЕПСТР
- 16.10. СВОЙСТВА КОМПЛЕКСНОГО КЕПСТРА
- 16.11. НЕКОТОРЫЕ СВОЙСТВА КЕПСТРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ
- Приложение 1. ПРАВИЛА ПЕРЕХОДА ОТ ИЗОБРАЖЕНИЯ ПО ЛАПЛАСУ Ls(p) К СПЕКТРАЛЬНОЙ ПЛОТНОСТИ S(w)
- Приложение 2. ПРАВИЛО ПРЕОБРАЗОВАНИЯ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ ПРИ ИНТЕГРИРОВАНИИ СИГНАЛА
- Приложение 3. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ УЗКОПОЛОСНОГО СИГНАЛА С НЕИЗВЕСТНОЙ НАЧАЛЬНОЙ ФАЗОЙ
- Приложение 4. СОГЛАСОВАННАЯ ФИЛЬТРАЦИЯ КОМПЛЕКСНОГО СИГНАЛА
- Приложение 5. О НЕОДНОЗНАЧНОСТИ ОПРЕДЕЛЕНИЯ ФАЗОЧАСТОТНОЙ ХАРАКТЕРИСТИКИ СПЕКТРА СИГНАЛА
- СПИСОК ЛИТЕРАТУРЫ