| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Распределение интенсивности в дифракционной картине и в спектре
2.1. Решение электромагнитной краекой задачи
Чтобы решить произвольную задачу дифракции электромагнитных волн в однородной диэлектрической среде, достаточно использовать уравнения Максвелла и задать граничные условия,
которым должно удовлетворять полное поле (падающее плюс дифрагированное). Если бы получение строгого решения уравнений Максвелла в каждом практическом случае было бы достаточно простой задачей, то все проблемы оптической дифракции и образования изображения формулировались и решались бы при помощи этих уравнений.
Если электрический вектор падающей волны обозначить через  а рассеянной волны — через
а рассеянной волны — через  то вектор рассеянного поля, равный
то вектор рассеянного поля, равный

где вектор полного поля

должен удовлетворять соответствующим граничным условиям на рассеивающей поверхности или же на границах отверстия. Простейшей границей является, очевидно, бесконечно протяженная плоскость идеального проводника, действующего как отражатель.

Рис. 1. Схема, поясняющая граничные условия (4).
В этом случае одно из граничных условий сводится к тому, что на поверхности проводника должна исчезать тангенциальная составляющая полного поля  Из этого требования с помощью уравнений Максвелла сразу же получаются законы отражения электромагнитных волн.
Из этого требования с помощью уравнений Максвелла сразу же получаются законы отражения электромагнитных волн.
Уравнения Максвелла для свободного пространства, записанные в дифференциальной форме, имеют вид

Эти уравнения всегда должны дополняться соответствующими граничными условиями, которые для нормальных составляющих  (рис. 1) имеют вид
(рис. 1) имеют вид

где  поверхностная плотность заряда, а для тангенциальных составляющих
поверхностная плотность заряда, а для тангенциальных составляющих

где К — поверхностная плотность тока.
Если уравнения Максвелла записать в интегральной форме, то граничные условия войдут в них неявно (рис. 2);

где  вектор плотности тока. Уравнения Максвелла в дифференциальной форме вместе с граничными условиями особенно удобны для решения задач дифракции электромагнитных волн (света) на границах простой формы, которые допускают раздельное решение уравнений.
вектор плотности тока. Уравнения Максвелла в дифференциальной форме вместе с граничными условиями особенно удобны для решения задач дифракции электромагнитных волн (света) на границах простой формы, которые допускают раздельное решение уравнений.

Рис. 2. Схема, поясняющая уравнение (6).
К таким границам относятся границы, имеющие форму цилиндра или развернутой цилиндрической поверхности бесконечной протяженности (например, дифракционная решетка) или же форму сферы, эллипсоида, набора цилиндров, сфер и т. д. Решения становятся особенно простыми для двумерных поверхностей, которые являются функциями только двух координат (цилиндры, дифракционные решетки).
Однако строгое решение электромагнитной краевой задачи было найдено до сих пор только в очень малом числе случаев (край, щель, клин, сфера, решетка с синусоидальным профилем и т. д.). В действительности математические трудности, возникающие при решении электромагнитных краевых задач, весьма велики и сравнимы с трудностями решения краевых задач в других разделах физики (например, в квантовой теории).
Обычно интересуются дифракцией волн, имеющих вид простых гармоник

или же их суперпозиций, где  амплитуда вектора, не зависимая от времени. Известно, что в этом случае векторы
амплитуда вектора, не зависимая от времени. Известно, что в этом случае векторы  удовлетворяют волновым уравнениям
удовлетворяют волновым уравнениям

где  Частота
Частота  и длина волны X связаны соотношением
и длина волны X связаны соотношением

где с — скорость света. Для случая монохроматической волны имеем

а на границах

Внутри идеального проводника  где поля
где поля  соотношение (5) приобретает вид
соотношение (5) приобретает вид

т. е. ранее указанные граничные условия на поверхности проводника принимают форму

Граничное условие для поля  является особенно простым на двумерных поверхностях, когда одна из координат исключается. Проиллюстрируем с помощью этого метода некоторые этапы решения дифракционной задачи. Рассмотрим плоскополяризованную волну
является особенно простым на двумерных поверхностях, когда одна из координат исключается. Проиллюстрируем с помощью этого метода некоторые этапы решения дифракционной задачи. Рассмотрим плоскополяризованную волну  падающую вдоль оси
падающую вдоль оси  из вакуума (среда 1) на поверхность
из вакуума (среда 1) на поверхность  не зависимую от
не зависимую от  Пусть
Пусть  параллельна Вследствие симметрии условий дифрагированное поле также будет иметь одну компоненту магнитного поля
параллельна Вследствие симметрии условий дифрагированное поле также будет иметь одну компоненту магнитного поля  Пусть полная
Пусть полная  -компонента магнитного поля в среде 1 равна — Для полного поля в среде 1 имеем
-компонента магнитного поля в среде 1 равна — Для полного поля в среде 1 имеем

а на поверхности

что следует из уравнения (12). Развертывая уравнение  по отдельным компонентам и замечая, что
по отдельным компонентам и замечая, что 
 , для полного ноля имеем
, для полного ноля имеем

Поскольку

то получаем граничное условие

Мы установили, что граничное условие для поля  сводится к следующему: производная по нормали от
сводится к следующему: производная по нормали от  -компоненты полного магнитного поля должна равняться нулю на поверхности идеального проводника, если эта поверхность не зависит от координаты
-компоненты полного магнитного поля должна равняться нулю на поверхности идеального проводника, если эта поверхность не зависит от координаты  параллельно которой направлен вектор магнитного поля в падающей волне. В общем случае можно показать, что все производные по нормали от ковариантных компонент магнитного поля должны равняться нулю на поверхности идеального проводника, если форма его поверхности совпадает с координатной поверхностью криволинейной ортогональной системы координат.
параллельно которой направлен вектор магнитного поля в падающей волне. В общем случае можно показать, что все производные по нормали от ковариантных компонент магнитного поля должны равняться нулю на поверхности идеального проводника, если форма его поверхности совпадает с координатной поверхностью криволинейной ортогональной системы координат.
Чтобы решить краевую задачу электромагнитной дифракции, кроме использования уравнений Максвелла и граничных условий, необходимо удовлетворить также некоторым дополнительным условиям. Одно из них — это «принцип излучения на бесконечности» Зоммерфельда, согласно которому количество энергии от источников, проходящей через конечную площадку, находящуюся на бесконечном удалении от этих источников, стремится к нулю. (На самом деле этот принцип несколько более сильный; он утверждает, что источники должны излучать, а не поглощать энергию.) Второе условие следует из закона сохранения энергии и теоремы Пойнтинга. Третье условие возникает в процессе разложения поля в ряд Фурье по плоским волнам и требует включения волн не только с действительными волновыми числами, но и с мнимыми. Для волн с мнимыми волновыми числами, т. е. затухающих волн, или же в общем случае неоднородных волн с комплексными волновыми числами, поверхность равной амплитуды не совпадает с поверхностью равной фазы. Например, в двумерном случае обычной цилиндрической линзы, вариации толщины которой создают изменения в поглощении света в линзе, поверхности равных фаз и равных амплитуд ортогональны друг другу. В оптике чаще всего встречаются именно неоднородные водны.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора русского издания
- Глава 1. ВВЕДЕНИЕ
- 1. Современная оптика — раздел радиоалектроники
- 2. Теория — основа радиооптики
- 3. Математические методы современной оптики
- 4. Краевая задача дифракции электромагнитных волн в оптике и некоторые ограничения операционного метода
- 5. Решение краевой задачи на примере дифракционной решетки [5]
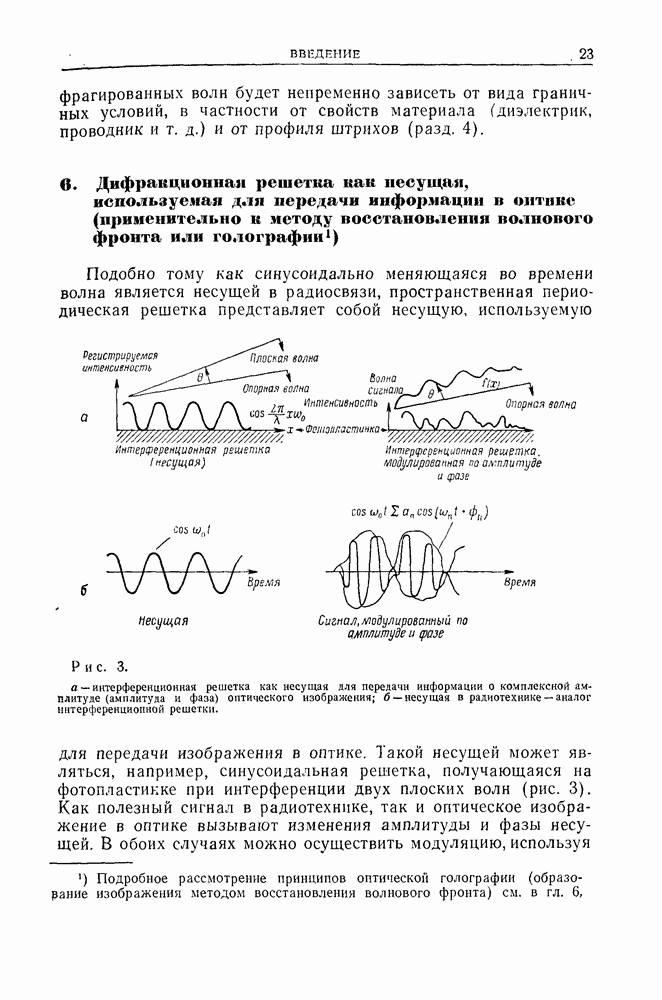
- 6. Дифракционная решетка как несущая, используемая для передачи информации в онтикс (применительно к методу восстановления волнового фронта или голографии
- 7. Оптика и теория связи Исторический обзор
- Глава 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФРАКЦИИ
- 1. Две стороны дифракции света
- 2. Распределение интенсивности в дифракционной картине и в спектре
- 2.2. Проблема образования изображения и принцип Гюйгенса
- 3. Теория образования изображения и обработка оптических сигналов при помощи преобразования Фурье
- Глава 3. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Сложение света, падающего из нескольких точек источника на отдельную точку изображения
- 6. Анализ процесса образования изображения в пространстве фурье-координат
- 7. Физический смысл функции разброса и анализ процесса образования изображения в плоскости фурье-координат
- 7.2. Синусоидальный по интенсивности предмет имеет функцию пространстненно-частотного отклика, совпадающую с фурье-образом дифракционной картины
- 8. Использование фурье-координат для синтеза предметных функций
- Глава 4. КОГЕРЕНТНОСТЬ СВЕТА (ЭКСПЕРИМЕНТАЛЬНЫЕ ХАРАКТЕРИСТИКИ)
- 2. Определение когерентности
- 2.2. Интерференционный анализ временной когерентности
- 2.3. Сравнение корреляционного и интерференционного методов
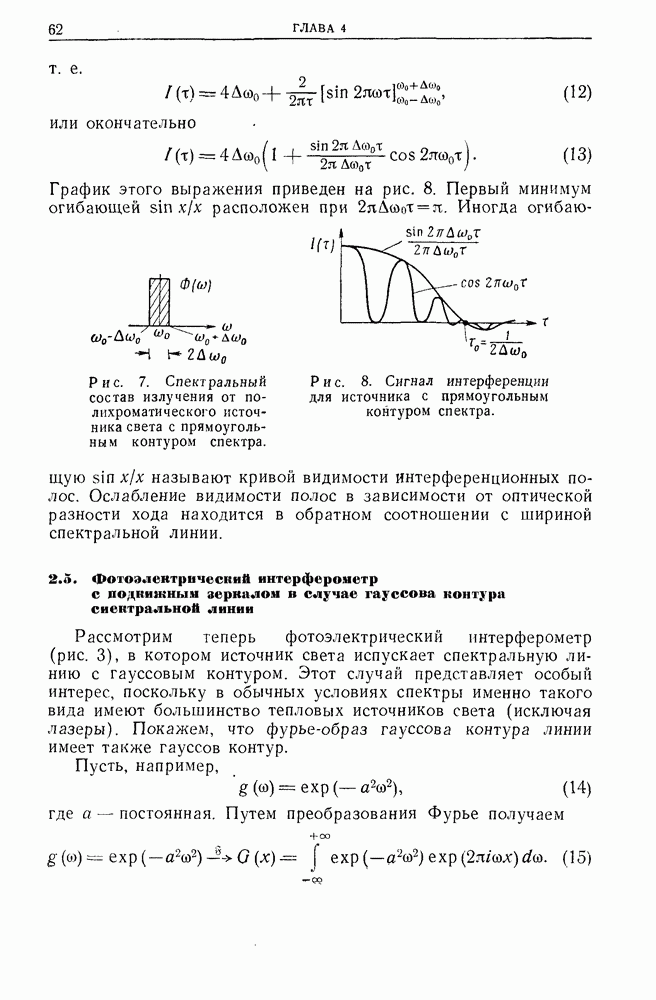
- 2.4. Узкий спектр с прямоугольным контуром
- 2.5. Фотоэлектрический интерферометр с поднижным зеркалом в случае гауссова контура спектральной линии
- 2.6. Физический смысл спектра мощности
- 2.7. Гетеродинный анализ сигналов и биений
- 2.8. Пространственная когерентность
- 2.9. Частичная когерентность света от протяженного некогерентного источника
- 2.10. Корреляция интенсивности при частичной когерентности
- 2.11. Интерферометр интенсивности
- Глава 5. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ КОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Когерентное освещение
- 3. Образование изображения при когерентном освещении как процесс двойной дифракции
- 4. Критерии разрешения Аббе и Релея
- 5. Передаточная функция при когерентном и некогерентном освещении
- 6. Фазовый контраст
- 7. Оптическая фильтрация с помощью голограммы согласованного фильтра
- 7.1. Процедура изготовления согласованного фильтра и операция фильтрации
- 8. Оптическая обработка информации, корреляционный анализ и оптические корреляторы
- 8.2. Оптический кросс-коррелятор
- 9. Интерферометрия и оптический синтез изображения (сложение комплексных амплитуд) методом последовательного наложения голографических картин на одну голограмму [5]
- Глава 6. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ОПТИЧЕСКОЙ ГОЛОГРАФИИ
- 2.1. Процесс получевия голограммы
- 2.2. Процесс восстановления изображения
- 2.3. Физические принципы голографии
- 2.4. Геометрическое увеличение
- 2.5. Разрешающая способность
- 3. Голография Фурье с высоким разрешением
- 3.2. Физические основы безлинзовой голографии Фурье высокого разрешения
- 3.3. Теория безлинзовой голографии Фурье
- 3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
- 4. Компенсация протяженности источника в голографии
- 5. Требование к когерентности в голографии
- 6. Сводка основных результатов
- 7. Электронный микроскоп и рентгеновский голографический микроскоп
- 8. Заключение
- 9. Голография при некогерентном освещении
- 9.2. Голография при пространственно-некогерентном освещении
- Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
- 1. Преобразование Фурье
- 2. Свертка
- 3. Функция корреляции
- 4. Распределения, или обобщенные функции
- 4.2. Импульсный отклик линейной системы
- 4.3. Отклик линейной системы на произвольную входную функцию
- 5. Спектральный анализ
- Дополнение автора к русскому изданию. ВОССТАНОВЛЕНИЕ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ В БЕЛОМ СВЕТЕ С ИСПОЛЬЗОВАНИЕМ ДИФРАКЦИОННОГО ЭФФЕКТА ЛИППМАНА — БРЭГГА
- ПРИЛОЖЕНИЕ 1. МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА
- Принцип восстановления волнового фронта
- Освещение сферической волной
- Восстановление при освещении точечным источником
- Побочная часть волны при восстановлении с помощью точечного источника
- Ухучшенне разделения изобрашений с помощью масок и других методов
- Освещающие волны с астигматизмом и сферической аберрацией
- Восстановление при наличии сферической аберрации и астигматизма
- Критерии когерентности
- Восстановление в оптическом диапазоне
- Экспериментальная проверка
- Заключение
- МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА, II
- 2. Принцип восстановления волнового фронта
- 3. Теория образования изображения при использовании метода пропускания
- 4. Восстановление
- 5. Критерии когерентности
- 6. Условия, необходимые для получения голограмм
- 7. Восстановление по методу темного поля
- ПРИЛОЖЕНИЕ 2. ПРИМЕНЕНИЯ ГОЛОГРАФИИ
- 2. Трехмерная фотография
- 3. Распознавание образов
- 4. Иитерференционная память
- 5. Интерферометрия
- 6. Голография в технологии
- 7. Голографический метод в интроскопии
- 8. Голографическая микроскопия
- 9. Голографическое кино
- 10. Голографическое телевидение
- 11. Голографическая оптика