| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Освещающие волны с астигматизмом и сферической аберрацией
Следуя методу, впервые предложенному Дебаем, построим общую когерентную освещающую волну из плоских элементарных волн, нормальных к направлению  и с амплитудой
и с амплитудой  в бесконечно малом телесном углу
в бесконечно малом телесном углу  т. е.
т. е.

Амплитуда А предполагается действительной, фазовый множи тель  выражает опережение фазы относительно прямого луча, проходящего через источник О, расположенный в начале координат. Пусть О совпадает со «средним параксиальным фокусом» пучка, а фазу положим равной
выражает опережение фазы относительно прямого луча, проходящего через источник О, расположенный в начале координат. Пусть О совпадает со «средним параксиальным фокусом» пучка, а фазу положим равной

Первый член соответствует опережению фазы вследствие астигматизма, второй определяется «эллиптической» сферической аберрацией. Для упрощения здесь предполагалось, что эллиптические ошибки второго и четвертого порядка имеют одни и те же главные оси х, у.
Введем полярные углы  , связанные с
, связанные с  следующими соотношениями:
следующими соотношениями:

Функция  может быть записана в виде
может быть записана в виде 

Член четвертого порядка теперь равен сумме, в состав которой входят такие слагаемые: член, связанный со сферической аберрацией, и два члена, обусловленные астигматизмом, один из которых эллиптический, а второй — с учетверенной периодичностью. Если линза круглая, то

и член с астигматизмом четвертого порядка исчезает. Здесь С — постоянная сферической аберрации. Ее смысл иллюстрирует
схема распределения лучей в пучке, приведенная на рис. 8. В большей части практически важных приложений разрабатываемой здесь теории хорошо оправдано приближение геометрической оптики, так как предполагается применять пучки с апертурами, примерно в 10 раз большими, чем в обычной электронной микроскопии, где дифракционный диск имеет тот же порядок Величины, что и геометрические аберрации. Поскольку минимальное сечение пучка растет как третья степень апертуры, а дифракционный эффект обратно пропорционален первой степени, то он представляет лишь малую поправку — порядка  геометрических размеров.
геометрических размеров.

Рис. 8. Конфигурация пучка в фокусе при наличии сферической аберрации 
Если апертурный угол равен  то все лучи пересекают ось аксиальной каустики, представляющей собой линию длиной за параксиальным фокусом О. Диаметр пучка в гауссовой плоскости
то все лучи пересекают ось аксиальной каустики, представляющей собой линию длиной за параксиальным фокусом О. Диаметр пучка в гауссовой плоскости  равен однако диаметр минимального сечения, расположенного в плоскости
равен однако диаметр минимального сечения, расположенного в плоскости  в 4 раза меньще. Минимальное сечение определяется пересечением огибающей каустики, которая является поверхностью вращения, описываемой уравнением
в 4 раза меньще. Минимальное сечение определяется пересечением огибающей каустики, которая является поверхностью вращения, описываемой уравнением  с конусом максимального раскрытия, определяемого уравнением
с конусом максимального раскрытия, определяемого уравнением 
Этот конус и внсщияя каустика делят пучок на четыре области различного характера, две из которых, выделенные на рис. 8 точками, содержат интерференционные полосы. Первая из них лежит внутри огибающей, но вне конуса. Лучи пересекаются в каждой точке этой области. Вторая область окружает аксиальную каустику. Она ограничена огибающей и конусом максимального раскрытия, и в каждой ее точке пересекаются три луча. Интерференционные полосы в обеих областях настолько резки и контрастны, что делают помещенные в них предметы почти невидимыми; таким образом, весь отмеченный точками объем не является подходящим местом для
размещения предметов, В двух остающихся областях, справа и слева, каждую точку пересекает лищь один луч. Они представляют собой области с плавным изменением интенсивности фона, пригодные для расположения микроскопических предметов. В области слева самая большая плотность освещенности — вблизи края; во второй области, справа, плотность максимальна на оси.
Если в добавление ко всему пучок также астигматичен, как это всегда бывает в электронной оптике, то рис. 8 все еще может служить полезной иллюстрацией, но теперь лишь для главных сечений пучка, причем они должны быть изображены смещенными вдоль оси на  Следовательно, точка О будет теперь находиться посередине между двумя фокальными линиями, ориентированными под прямыми углами друг к другу, а также к оси пучка и разделенными расстоянием
Следовательно, точка О будет теперь находиться посередине между двумя фокальными линиями, ориентированными под прямыми углами друг к другу, а также к оси пучка и разделенными расстоянием 
Возвращаясь к представлениям волновой оптики, просуммируем элементарные волны (31), в результате чего получим следующее выражение для комплексной амплитуды в точке 

Мы используем здесь упрощения, вытекающие из уравнения (35); они будут применяться также для упрощения обсуждения во всех последующих формулах, но результаты будут таковы, что позволят без труда распространить их также и на более общий случай, описываемый уравнениями (32) и (34).
Введем под знаком интеграла в выражение (36) фурье-координаты

Точные уравнения преобразования имеют вид 

Мы снова предполагаем, что пучок достаточно узкий, что позволяет нам пренебречь выражением  в знаменателе последнего выражения. Однако в фазовом множителе мы должны учесть все члены вплоть до четвертого порядка по
в знаменателе последнего выражения. Однако в фазовом множителе мы должны учесть все члены вплоть до четвертого порядка по  и написать
и написать

в этом приближении получаем

Значение этого интеграла, как и значение точного выражения (36), может быть легко оценено при больших расстояниях  от источника в направлении
от источника в направлении  Эта оценка дает
Эта оценка дает

где функция  задается уравнением (32) или (34). Множитель
задается уравнением (32) или (34). Множитель  выражающий сдвиг волнового фронта на
выражающий сдвиг волнового фронта на  по сравнению с компонентами (31), возникает вследствие перехода от плоских волн к сферическим и обычен для дифракционной теории. Уравнение (36.2) представляет фон в области физической тени предмета, которую мы должны теперь рассчитать.
по сравнению с компонентами (31), возникает вследствие перехода от плоских волн к сферическим и обычен для дифракционной теории. Уравнение (36.2) представляет фон в области физической тени предмета, которую мы должны теперь рассчитать.
Предмет, расположенный в плоскости  может быть охарактеризован, как и прежде, комплексной функцией пропускания
может быть охарактеризован, как и прежде, комплексной функцией пропускания  Используя основную предпосылку дифракционной теории Френеля — Кирхгофа, будем считать, что амплитуда непосредственно перед предметом равна амплитуде невозмущенной освещающей волны
Используя основную предпосылку дифракционной теории Френеля — Кирхгофа, будем считать, что амплитуда непосредственно перед предметом равна амплитуде невозмущенной освещающей волны  и непосредственно за предметом отличается от нее в
и непосредственно за предметом отличается от нее в  раз. Теперь переменные
раз. Теперь переменные  в выражении для освещающей волны нужно обозначить индексом
в выражении для освещающей волны нужно обозначить индексом  т. е. «исходный»), чтобы отличить их от переменных без индекса, описывающих волну, рассеянную предметом и распространяющуюся от него.
т. е. «исходный»), чтобы отличить их от переменных без индекса, описывающих волну, рассеянную предметом и распространяющуюся от него.
Задача заключается в том, чтобы из выражений, описывающих продифрагировавшие плоские элементарные волны, составляющие начальную волну, построить выражение для рассеянной волны. Для этого снова можно применить формулу Френеля—Кирхгофа в упрощенном виде (7.1), но только волну  необходимо заменить суммой элементарных волн (34). Величина
необходимо заменить суммой элементарных волн (34). Величина  по-прежнему означает расстояние точки наблюдения
по-прежнему означает расстояние точки наблюдения  от точки предмета
от точки предмета  Следовательно, формула Френеля — Кирхгофа теперь примет вид
Следовательно, формула Френеля — Кирхгофа теперь примет вид

где

Выражая углы через фурье-координаты  и
и  мы получим в том же самом приближении, как и в (36.1), что
мы получим в том же самом приближении, как и в (36.1), что

(38)
Симметрия этого выражения нарушается двумя последними членами, но она сразу же восстанавливается, если мы переходим к физической тени путем деления амплитуды  на фон
на фон  определяемый уравнением (36.2):
определяемый уравнением (36.2):

Эта формула определяет физическую тень на бесконечности от предмета, расположенного в плоскости  и освещенного пучком, сформированным системой с аберрациями четвертого порядка. Очевидно, что она может быть распространена на аберрации любого порядка. Она является эквивалентом формулы преобразования (14) для освещения точечным источником, но ее нельзя записать в форме интеграла по плоскости предмета, так как интегрирование по углам нельзя здесь выполнить в трансцендентных функциях, обычно используемых в анализе. С другой стороны, этот интеграл можно без труда свести к двойному интегралу по переменным углам с помощью фурье-образа
и освещенного пучком, сформированным системой с аберрациями четвертого порядка. Очевидно, что она может быть распространена на аберрации любого порядка. Она является эквивалентом формулы преобразования (14) для освещения точечным источником, но ее нельзя записать в форме интеграла по плоскости предмета, так как интегрирование по углам нельзя здесь выполнить в трансцендентных функциях, обычно используемых в анализе. С другой стороны, этот интеграл можно без труда свести к двойному интегралу по переменным углам с помощью фурье-образа  функции
функции  который равен
который равен

Уравнение (39) принимает тогда вид 

Это преобразование можно проиллюстрировать несколькими простыми примерами. Если  т. е. нет никакого предмета, то
т. е. нет никакого предмета, то  является дельта-функцией
является дельта-функцией

Это означает, что интеграл (40) равен значению подынтегрального выражения при  как и прежде, единице.
как и прежде, единице.
Если  -гармоническая функция х, у с периодами
-гармоническая функция х, у с периодами 

то  снова дельта-функция, но смещенная в точку
снова дельта-функция, но смещенная в точку 

и интеграл снова равен знач-ению подынтегрального выражения, но на этот раз в точке  Физическая тень определяется уравнением
Физическая тень определяется уравнением

Первый множитель в показателе экспоненты мы уже встречали в теневом преобразовании при освещении точечным источником. Но период в тени более не остается постоянной величиной; другими словами, тень синусоидальной решетки не копирует исходного предмета. Если, например,  т. е. решетка параллельна оси у, то расстояние между двумя максимумами равно
т. е. решетка параллельна оси у, то расстояние между двумя максимумами равно

Первый множитель представляет собой геометрическую тень с периодом  второй является поправкой, возникающей вследствие астигматизма и сферической аберрации, а также обусловленной наличием члена четвертого порядка, выражающего отклонение сферического волнового фронта от параболоида. Во всех практических приложениях
второй является поправкой, возникающей вследствие астигматизма и сферической аберрации, а также обусловленной наличием члена четвертого порядка, выражающего отклонение сферического волнового фронта от параболоида. Во всех практических приложениях  будет порядка величины
будет порядка величины  причем
причем  всегда пренебрежимо мало по сравнению с
всегда пренебрежимо мало по сравнению с  Таким образом, астигматизм и сферическую аберрацию пучка можно определить по двум голограммам синусоидальной решетки, полученным при двух взаимно перпендикулярных положениях. Однако этот метод не очень чувствителен. Вблизи края освещенного поля, где расстояние между двумя соседними максимумами будет в
Таким образом, астигматизм и сферическую аберрацию пучка можно определить по двум голограммам синусоидальной решетки, полученным при двух взаимно перпендикулярных положениях. Однако этот метод не очень чувствителен. Вблизи края освещенного поля, где расстояние между двумя соседними максимумами будет в  раз меньше геометрического расстояния. Если же нужно получить хорошие фотографии, то
раз меньше геометрического расстояния. Если же нужно получить хорошие фотографии, то  должно быть порядка
должно быть порядка  множитель будет порядка единицы. Отсюда видно, что синусоидальная
множитель будет порядка единицы. Отсюда видно, что синусоидальная
решетка является не очень подходяшим тест-объектом. Сферическую аберрацию можно намного лучше определить по физической тени тонкой проволоки, но обсуждение этого случая не может быть проведено на основе использования элементарных выражений и рассматриваться здесь не будет.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора русского издания
- Глава 1. ВВЕДЕНИЕ
- 1. Современная оптика — раздел радиоалектроники
- 2. Теория — основа радиооптики
- 3. Математические методы современной оптики
- 4. Краевая задача дифракции электромагнитных волн в оптике и некоторые ограничения операционного метода
- 5. Решение краевой задачи на примере дифракционной решетки [5]
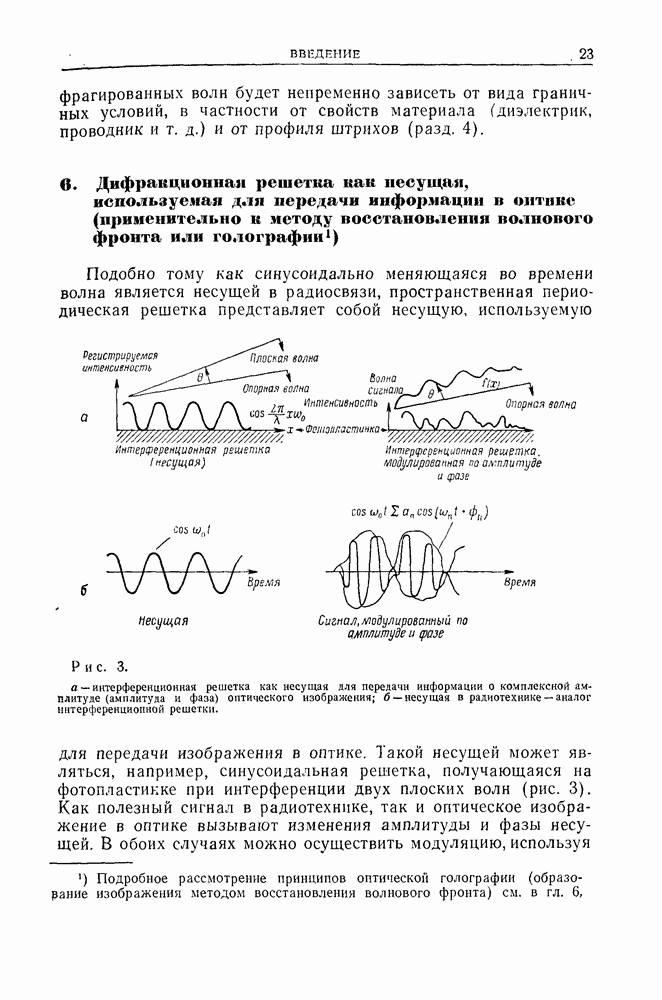
- 6. Дифракционная решетка как несущая, используемая для передачи информации в онтикс (применительно к методу восстановления волнового фронта или голографии
- 7. Оптика и теория связи Исторический обзор
- Глава 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФРАКЦИИ
- 1. Две стороны дифракции света
- 2. Распределение интенсивности в дифракционной картине и в спектре
- 2.2. Проблема образования изображения и принцип Гюйгенса
- 3. Теория образования изображения и обработка оптических сигналов при помощи преобразования Фурье
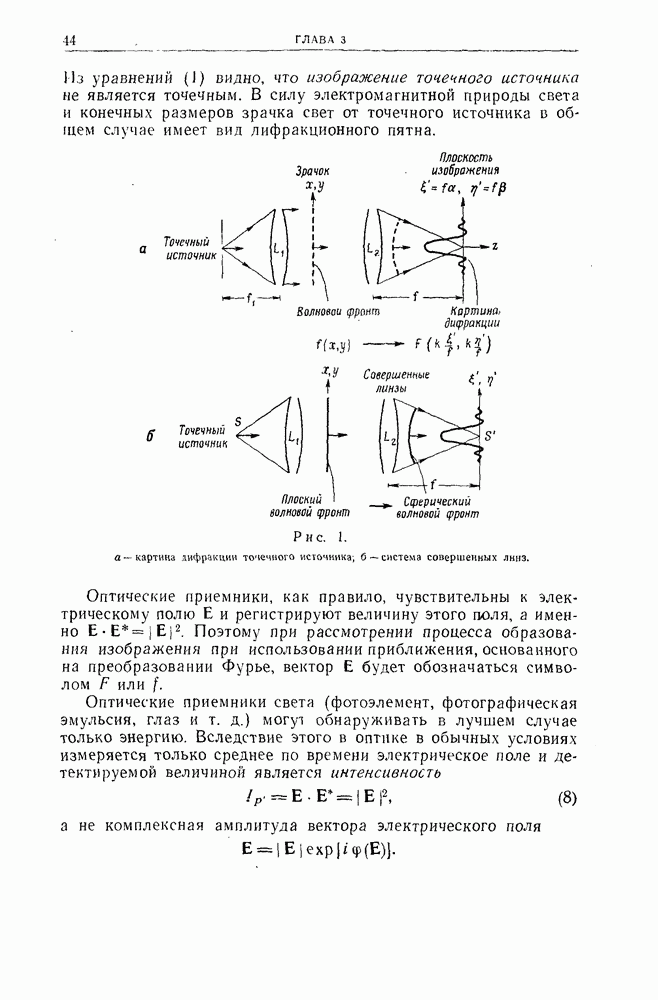
- Глава 3. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Сложение света, падающего из нескольких точек источника на отдельную точку изображения
- 6. Анализ процесса образования изображения в пространстве фурье-координат
- 7. Физический смысл функции разброса и анализ процесса образования изображения в плоскости фурье-координат
- 7.2. Синусоидальный по интенсивности предмет имеет функцию пространстненно-частотного отклика, совпадающую с фурье-образом дифракционной картины
- 8. Использование фурье-координат для синтеза предметных функций
- Глава 4. КОГЕРЕНТНОСТЬ СВЕТА (ЭКСПЕРИМЕНТАЛЬНЫЕ ХАРАКТЕРИСТИКИ)
- 2. Определение когерентности
- 2.2. Интерференционный анализ временной когерентности
- 2.3. Сравнение корреляционного и интерференционного методов
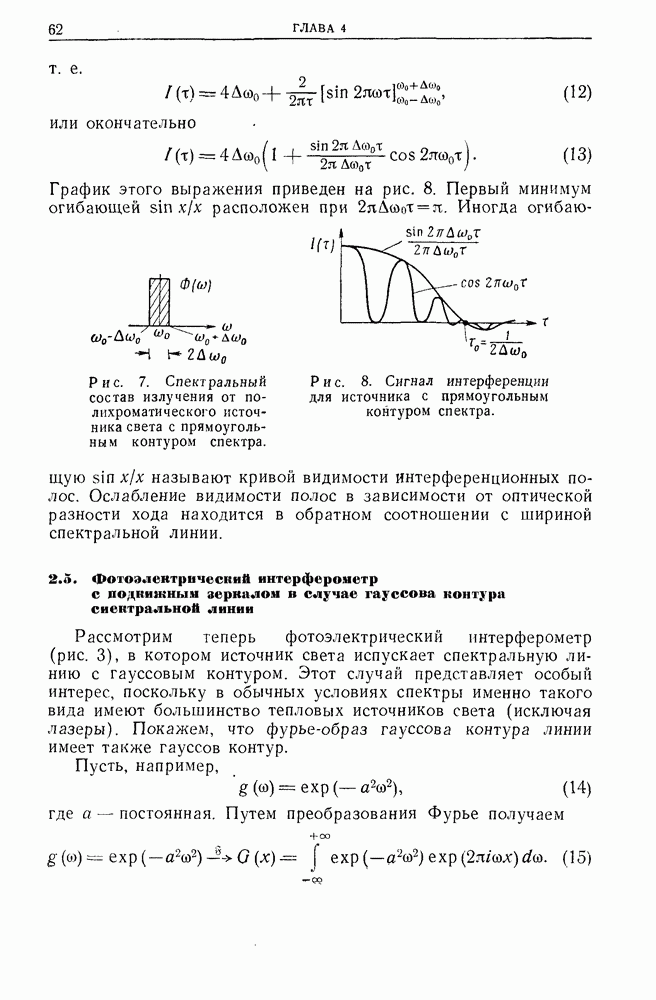
- 2.4. Узкий спектр с прямоугольным контуром
- 2.5. Фотоэлектрический интерферометр с поднижным зеркалом в случае гауссова контура спектральной линии
- 2.6. Физический смысл спектра мощности
- 2.7. Гетеродинный анализ сигналов и биений
- 2.8. Пространственная когерентность
- 2.9. Частичная когерентность света от протяженного некогерентного источника
- 2.10. Корреляция интенсивности при частичной когерентности
- 2.11. Интерферометр интенсивности
- Глава 5. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ КОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Когерентное освещение
- 3. Образование изображения при когерентном освещении как процесс двойной дифракции
- 4. Критерии разрешения Аббе и Релея
- 5. Передаточная функция при когерентном и некогерентном освещении
- 6. Фазовый контраст
- 7. Оптическая фильтрация с помощью голограммы согласованного фильтра
- 7.1. Процедура изготовления согласованного фильтра и операция фильтрации
- 8. Оптическая обработка информации, корреляционный анализ и оптические корреляторы
- 8.2. Оптический кросс-коррелятор
- 9. Интерферометрия и оптический синтез изображения (сложение комплексных амплитуд) методом последовательного наложения голографических картин на одну голограмму [5]
- Глава 6. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ОПТИЧЕСКОЙ ГОЛОГРАФИИ
- 2.1. Процесс получевия голограммы
- 2.2. Процесс восстановления изображения
- 2.3. Физические принципы голографии
- 2.4. Геометрическое увеличение
- 2.5. Разрешающая способность
- 3. Голография Фурье с высоким разрешением
- 3.2. Физические основы безлинзовой голографии Фурье высокого разрешения
- 3.3. Теория безлинзовой голографии Фурье
- 3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
- 4. Компенсация протяженности источника в голографии
- 5. Требование к когерентности в голографии
- 6. Сводка основных результатов
- 7. Электронный микроскоп и рентгеновский голографический микроскоп
- 8. Заключение
- 9. Голография при некогерентном освещении
- 9.2. Голография при пространственно-некогерентном освещении
- Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
- 1. Преобразование Фурье
- 2. Свертка
- 3. Функция корреляции
- 4. Распределения, или обобщенные функции
- 4.2. Импульсный отклик линейной системы
- 4.3. Отклик линейной системы на произвольную входную функцию
- 5. Спектральный анализ
- Дополнение автора к русскому изданию. ВОССТАНОВЛЕНИЕ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ В БЕЛОМ СВЕТЕ С ИСПОЛЬЗОВАНИЕМ ДИФРАКЦИОННОГО ЭФФЕКТА ЛИППМАНА — БРЭГГА
- ПРИЛОЖЕНИЕ 1. МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА
- Принцип восстановления волнового фронта
- Освещение сферической волной
- Восстановление при освещении точечным источником
- Побочная часть волны при восстановлении с помощью точечного источника
- Ухучшенне разделения изобрашений с помощью масок и других методов
- Освещающие волны с астигматизмом и сферической аберрацией
- Восстановление при наличии сферической аберрации и астигматизма
- Критерии когерентности
- Восстановление в оптическом диапазоне
- Экспериментальная проверка
- Заключение
- МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА, II
- 2. Принцип восстановления волнового фронта
- 3. Теория образования изображения при использовании метода пропускания
- 4. Восстановление
- 5. Критерии когерентности
- 6. Условия, необходимые для получения голограмм
- 7. Восстановление по методу темного поля
- ПРИЛОЖЕНИЕ 2. ПРИМЕНЕНИЯ ГОЛОГРАФИИ
- 2. Трехмерная фотография
- 3. Распознавание образов
- 4. Иитерференционная память
- 5. Интерферометрия
- 6. Голография в технологии
- 7. Голографический метод в интроскопии
- 8. Голографическая микроскопия
- 9. Голографическое кино
- 10. Голографическое телевидение
- 11. Голографическая оптика