| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
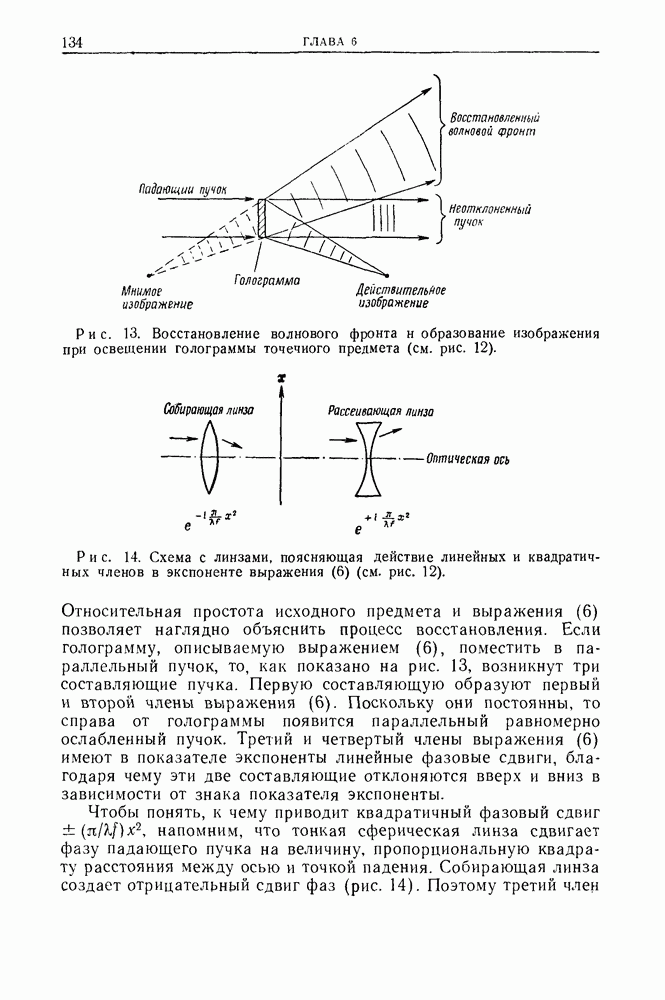
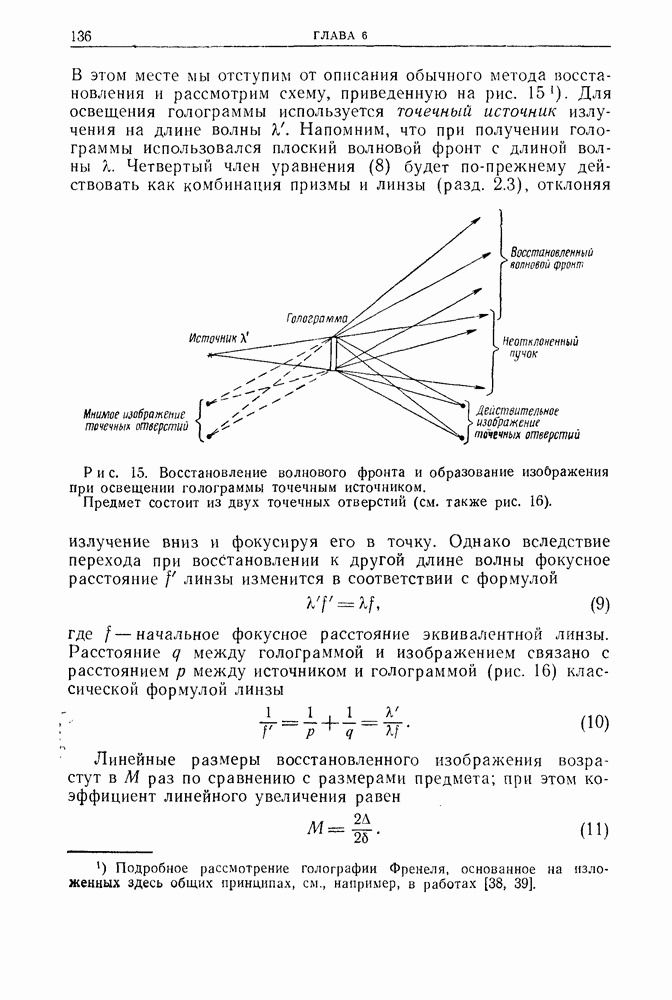
Побочная часть волны при восстановлении с помощью точечного источника
Простота преобразований (16.1) и (16.2) наводит на мысль о построении произвольных плоских предметов из гауссовых пятен (интенсивность в пятне распределена по нормальному закону). В пределе они переходят в двумерные дельта-функции, которые могут представлять любую функцию  однако нет никакой необходимости переходить к этому пределу, более того, это было бы физически неоправдано. Оптические образы создаются не точками, а элементарными областями, размер которых соответствует пределу разрешения. В пределах такой малой плошади значения функции
однако нет никакой необходимости переходить к этому пределу, более того, это было бы физически неоправдано. Оптические образы создаются не точками, а элементарными областями, размер которых соответствует пределу разрешения. В пределах такой малой плошади значения функции  описывающей восстановленный предмет, не являются не зависимыми друг от друга.
описывающей восстановленный предмет, не являются не зависимыми друг от друга.
Сначала мы осуществим процесс восстановления для единичного гауссова пятна. Пусть функция пропускания в плоскости предмета имеет вид

где  означает расстояние от центра пятна
означает расстояние от центра пятна  амплитуда волны, прошедшей в центре пятна; когерентный фон принят за единицу. В случае только поглощающего предмета
амплитуда волны, прошедшей в центре пятна; когерентный фон принят за единицу. В случае только поглощающего предмета  - действительное положительное число, меньшее 1. Если
- действительное положительное число, меньшее 1. Если
предмет имеет чисто фазовый контраст, то  и 1/41 лежит в пределах от О до 2.
и 1/41 лежит в пределах от О до 2.
Физическая тень функции (20) в соответствии с уравнениями (16.1) и (16.2) может быть описана следующей функцией:

где

и

причем точки  являются геометрической тенью
являются геометрической тенью  Дифракционная картина (21) сосредоточена около этой точки. Ее вид определяется безразмерным параметром
Дифракционная картина (21) сосредоточена около этой точки. Ее вид определяется безразмерным параметром  Если
Если  велико, то
велико, то  приближается к геометрической тени функции
приближается к геометрической тени функции 
В более важном случае, которому соответствует  выражение (21) можно упростить:
выражение (21) можно упростить:

Чем меньше исходное пятно, тем больше его физическая тень.
Фотография заменяет комплексную физическую тень (21.1) действительной функцией пропускания

Это приближение справедливо при 
Обратное преобразование (15), примененное к первым двум членам в правой части выражения (22), восстанавливает исходный предмет (20), но контраст восстановленного предмета отличается от контраста исходного в  раз. Это же самое преобразование, примененное к последнему члену правой части выражения (22), дает побочный член, характеризующий ошибку:
раз. Это же самое преобразование, примененное к последнему члену правой части выражения (22), дает побочный член, характеризующий ошибку:

Он равен амплитуде (при единичном когерентном фоне), создаваемой изображением-«двойником» в плоскости исходного предмета. Побочное изображение сосредоточено около точки  но его характер совершенно отличается от характера исходного предмета. Амплитуда
но его характер совершенно отличается от характера исходного предмета. Амплитуда  медленно уменьшается по мере роста расстояния
медленно уменьшается по мере роста расстояния  от центра, причем тем медленнее, чем меньше радиус а исходного пятна, в то время как фаза
от центра, причем тем медленнее, чем меньше радиус а исходного пятна, в то время как фаза
изменяется быстро в соответствии с последним множителем в выражении (23), и это изменение не зависит от размеров пятна. Таким образом, влияние побочного изображения будет проявляться в образовании системы частых и слабых интерференционных полос, наложенных на восстановленное изображение.
Для справок можно привести также точное значение восстановленной функции пропускания  в случае
в случае 

Первые два члена соответствуют точно восстановленному изображению, последние два — побочной амплитуде. Они отличаются от выражения (23) лишь членами порядка  или выше.
или выше.
На рис. 5 показан процесс восстановления в случае  на примере гауссова пятна с абсолютно черным центром. Необходимо соблюдать осторожность в случае контрастного предмета и не увеличивать контраст выше
на примере гауссова пятна с абсолютно черным центром. Необходимо соблюдать осторожность в случае контрастного предмета и не увеличивать контраст выше  Как показано на рис. 6, это приводит к появлению более светлого центра внутри черного кольца, а черные линии будут казаться двойными.
Как показано на рис. 6, это приводит к появлению более светлого центра внутри черного кольца, а черные линии будут казаться двойными.
До сих пор размер отверстия мы считали неограниченным; следовательно, не было нижнего предела размеров пятна а, которое можно было бы точно воспроизвести. Влияние ограниченного разрешения можно просто учесть, если предположить, что при получении голограммы была использована маска с амплитудным пропусканием

Маска такого вида предпочтительнее отверстий с резкими краями не только с точки зрения математической простоты, но также и потому, что такая маска ослабляет до минимума «ложные детали», возникаюшие от резких краев апертуры. Они широко применяются в структурном анализе ([8, стр. 350]).
Если маска применяется дважды, как при фотографировании, так и в процессе восстановления, то ее полное действие определяется выражением

Чтобы получить теперь правильный контраст в процессе восстановления, положим  Пусть также
Пусть также  Мы должны теперь восстановить предмет, т. е. гауссово пятно (20), с помощью физической тени
Мы должны теперь восстановить предмет, т. е. гауссово пятно (20), с помощью физической тени


(кликните для просмотра скана)
которая отличается от функции нронускания (22) только множителем, обусловленным маской. Вводя малый безразмерный параметр

и пренебрегая степенями  выше первой, с помощью преобразования (15) получим
выше первой, с помощью преобразования (15) получим

Первый член этого выражения описывает фон. За исключением очень малых дифракционных эффектов (порядка а), он представляет собой геометрическую тень маски, спроектированную на плоскость предмета. Второй член описывает «правильно» восстановленный предмет. Основное различие заключается в том, что протяженность восстановленного пятна равна  вместо а. Следовательно,
вместо а. Следовательно,  имеет смысл предела разрешения (с точностью до некоторого численного множителя, который будет определен позже). Множитель
имеет смысл предела разрешения (с точностью до некоторого численного множителя, который будет определен позже). Множитель  перед амплитудой отражает то обстоятельство, что амплитуда уменьшается в том же самом отношении, в каком увеличивается площадь пятна. Уменьшение контраста в изображении очень малых предметов кажется более сильным, чем в случае обычной микроскопии, где амплитуда убывает как корень квадратный из площади, однако результат получается тот же самый, поскольку контраст в передаче интенсивности при наличии сильного когерентного фона является линейной функцией амплитуды.
перед амплитудой отражает то обстоятельство, что амплитуда уменьшается в том же самом отношении, в каком увеличивается площадь пятна. Уменьшение контраста в изображении очень малых предметов кажется более сильным, чем в случае обычной микроскопии, где амплитуда убывает как корень квадратный из площади, однако результат получается тот же самый, поскольку контраст в передаче интенсивности при наличии сильного когерентного фона является линейной функцией амплитуды.
Член, характеризующий ошибку, во второй строке имеет структуру, отличающуюся от структуры, описываемой выражением (23); он больше не сосредоточен точно в исходном пятне, а содержит множитель, сосредоточенный в зеркальном изображении пятна  С помощью подстановки
С помощью подстановки  мы можем записать этот член в другой, очень удобной форме:
мы можем записать этот член в другой, очень удобной форме:

Это выражение особенно удобно в случае, когда  так как в этом случае амплитуда в системе полос 4 не зависит от
так как в этом случае амплитуда в системе полос 4 не зависит от  Амплитуда (но не фаза) сосредоточена в точке
Амплитуда (но не фаза) сосредоточена в точке 
Этот результат можно положить в основу теории побочной части волны при восстановлении произвольных предметов с целью формулирования требований, предъявляемых к предметам в двухступенчатой микроскопии.
Микроскоп, как и любая другая оптическая система, может передавать лишь конечное количество информации. Описание предмета с помощью непрерывной функции пропускания становится поэтому нежелательной идеализацией, поскольку такая функция содержит бесконечное количество невоспроизводимых деталей.

Рис. 7. Разбивка предмета на независимые элементы.
Мы подойдем ближе к адекватному описанию, если разделим предмет на ячейки размером порядка предела разрешения, свяжем с каждой ячейкой некоторый комплекс информации и исследуем прохождение этой информации через оптическую систему.
Уравнение (25.1) наводит на мысль, что если мы представим предмет в виде решетки двумерных гауссовых пятен с размерами  то получим особенно простые результаты. Как показано на рис. 7, мы располагаем эти пятна в виде гексагональной решетки с расстоянием
то получим особенно простые результаты. Как показано на рис. 7, мы располагаем эти пятна в виде гексагональной решетки с расстоянием  между соседними центрами, где
между соседними центрами, где  предел разрешения, который мы определим немного по-другому, чем обычно, а именно постулируем, что три (а не два) равных гауссовых пятна с размерами
предел разрешения, который мы определим немного по-другому, чем обычно, а именно постулируем, что три (а не два) равных гауссовых пятна с размерами  находятся на пределе разрешения, если их центры удалены один от другого на расстояние
находятся на пределе разрешения, если их центры удалены один от другого на расстояние  т. е. минимум между ними исчезает как раз при этом расстоянии. Если
т. е. минимум между ними исчезает как раз при этом расстоянии. Если  то, согласно уравнению (25), амплитуда в члене, описывающем правильно восстановленный предмет, следует закону
то, согласно уравнению (25), амплитуда в члене, описывающем правильно восстановленный предмет, следует закону  точке, находящейся
точке, находящейся
посередине между тремя центрами  следовательно,
следовательно,  определяется из условия
определяется из условия

откуда получаем

Это выражение находится в хорошем согласии с обычным определением предела разрешения

если мы определим  такой угол, при котором амплитуда фона уменьшается в
такой угол, при котором амплитуда фона уменьшается в  раз, т. е. интенсивность фона составляет из его максимального значения. Обозначая соответствуюший радиус в плоскости предмета как
раз, т. е. интенсивность фона составляет из его максимального значения. Обозначая соответствуюший радиус в плоскости предмета как  мы получим
мы получим

откуда следует

Пусть  число независимых элементов в пределах освешенного поля, т. е. число ячеек, содержащихся в диске радиусом
число независимых элементов в пределах освешенного поля, т. е. число ячеек, содержащихся в диске радиусом  Каждая ячейка занимает площадь
Каждая ячейка занимает площадь

следовательно, число  равно
равно

Число  легко может быть сделано очень большим, порядка
легко может быть сделано очень большим, порядка  Это показывает возможность статистической оценки побочной части воспроизводимого изображения на основе предположения о случайном распределении амплитуды по независимым элементам предмета. Понятно, конечно, что в особых случаях это может привести к большим ошибкам, но тем не менее это, бесспорно, приемлемое предположение, если рассматривается ббльшое число разнообразных предметов.
Это показывает возможность статистической оценки побочной части воспроизводимого изображения на основе предположения о случайном распределении амплитуды по независимым элементам предмета. Понятно, конечно, что в особых случаях это может привести к большим ошибкам, но тем не менее это, бесспорно, приемлемое предположение, если рассматривается ббльшое число разнообразных предметов.
Присвоим элементам номера от 1 до  Побочная амплитуда в восстановленном изображении в точке х, у возникает как результат суперпозиции членов вида (25.1), описывающих ошибку, по одному от каждой ячейки с центром
Побочная амплитуда в восстановленном изображении в точке х, у возникает как результат суперпозиции членов вида (25.1), описывающих ошибку, по одному от каждой ячейки с центром  Обозначим
Обозначим  расстояние от точки
расстояние от точки  до точки х, у. С учетом
до точки х, у. С учетом
 вытекающих из условия
вытекающих из условия  результирующая амплитуда ошибки равна
результирующая амплитуда ошибки равна

где через  обозначено расстояние от точки
обозначено расстояние от точки  до точки
до точки 
Относительное расстояние  между точками
между точками  входит здесь только в фазовый множитель
входит здесь только в фазовый множитель  Два множителя, характеризующих спад вероятности, уменьшаются медленно. Первый из них, стоящий перед суммой, соответствует корню квадратному из ослабления фона, т. е. он уменьшается со скоростью, вдвое меньшей, чем амплитуда фона. Второй множитель сосредоточен в точке
Два множителя, характеризующих спад вероятности, уменьшаются медленно. Первый из них, стоящий перед суммой, соответствует корню квадратному из ослабления фона, т. е. он уменьшается со скоростью, вдвое меньшей, чем амплитуда фона. Второй множитель сосредоточен в точке  и спадает с той же скоростью, что и первый множитель. Таким образом, в качестве первого приближения допустимо положить оба множителя равными единице и заменить уравнение (27) упрощенным выражением
и спадает с той же скоростью, что и первый множитель. Таким образом, в качестве первого приближения допустимо положить оба множителя равными единице и заменить уравнение (27) упрощенным выражением

Другими словами, чтобы получить в точке х, у амплитуду ошибки, мы должны в этой точке осуществить суперпозицию большого числа,  незатухающих волн с длинами
незатухающих волн с длинами  исходящих из всех точек изображения
исходящих из всех точек изображения  Эти длины волны всегда больше предела разрешения
Эти длины волны всегда больше предела разрешения  Их наименьшее значение, достигаемое при
Их наименьшее значение, достигаемое при  равно
равно  в то время как предел разрешения равен
в то время как предел разрешения равен 
Введем теперь гипотезу, что между фазами этих волн нет никакой корреляции. В этом предположении среднее значение квадрата компоненты синфазной с фоном, которое обозначим эффз равно половине суммы абсолютных значений квадратов членов, стоящих в правой части:

Здесь мы через Лэфф обозначим среднее значение квадрата вторичных амплитуд  усредненное по всему полю. Понятно, что средний уровень пропускания предмета должен рассматриваться как часть фона, и
усредненное по всему полю. Понятно, что средний уровень пропускания предмета должен рассматриваться как часть фона, и  есть мера отклонения от равномерности. Объединяя уравнения (26) и (28), получим
есть мера отклонения от равномерности. Объединяя уравнения (26) и (28), получим

Уравнение (29) дает нам возможность сформулировать критерий отбора подходящих предметов. Фон можно рассматривать
как практически равномерный, если контраст в интенсивности не превышает около 5%, т. е. если амплитуда контраста меньше 2,5%. Это означает, что в среднем по всему полю подходящие предметы должны удовлетворять условию

Рассмотрим в качестве примера черно-белый предмет, в котором черная часть, где  покрывает
покрывает  часть освещенного поля, в то время как для остальной части
часть освещенного поля, в то время как для остальной части  В этом случае
В этом случае  и мы получаем простое правило, что черными точками или линиями должно быть покрыто не более 1% освещенного поля. Если, например, в качестве предмета взять диск, наполовину черный и наполовину белый, его диаметр не должен превышать
и мы получаем простое правило, что черными точками или линиями должно быть покрыто не более 1% освещенного поля. Если, например, в качестве предмета взять диск, наполовину черный и наполовину белый, его диаметр не должен превышать  диаметра поля.
диаметра поля.
В качестве второго примера рассмотрим предмет с чисто фазовым контрастом, но со случайным распределением фазовых сдвигов. Мы должны определять это условием, которое должно быть удовлетворено в случае каждого применения теории Френеля — Кирхгофа; между точками, отстоящими друг от друга меньше чем на длину волны, фаза не должна заметно изменяться. Другими словами, если предмет резко сфокусирован, он должен казаться однородным и прозрачным. В обычной микроскопии этому условию будут удовлетворять покрытый «морщинами» лист целлулоида или даже покрытая сеткой желатина. Однако слой коллоидной дисперсии на молочном стекле этому условию не удовлетворяет. Помня это ограничение, мы можем применить теперь уравнение (29). Можно показать, что значение Лэфф снова равно единице. В случае чисто фазового контраста конец комплексного вектора пропускания  движется по единичной окружности, причем все ориентации
движется по единичной окружности, причем все ориентации  равновероятны. Следовательно,
равновероятны. Следовательно,  что дает
что дает  и
и

Это означает, что если фазовый предмет такого тина перекрывает все поле, то он создает очень серьезные искажения, так как  Этот результат показывает, что неравномерно прозрачная подложка, на которой находится предмет, даже если она невидима в обычный микроскоп, сделает самые контрастные или регулярно повторяющиеся детали предмета почти невидимыми. Поскольку кажется сомнительным, что в электронной микроскопии Можно будет найти либо «оптически плоскую», либо по крайней мере приемлемую поддерживающую мембрану периодической структуры, то желательно применять такие мембраны, которые занимают лишь малую часть освещенного поля, либо обходиться вообще без них.
Этот результат показывает, что неравномерно прозрачная подложка, на которой находится предмет, даже если она невидима в обычный микроскоп, сделает самые контрастные или регулярно повторяющиеся детали предмета почти невидимыми. Поскольку кажется сомнительным, что в электронной микроскопии Можно будет найти либо «оптически плоскую», либо по крайней мере приемлемую поддерживающую мембрану периодической структуры, то желательно применять такие мембраны, которые занимают лишь малую часть освещенного поля, либо обходиться вообще без них.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора русского издания
- Глава 1. ВВЕДЕНИЕ
- 1. Современная оптика — раздел радиоалектроники
- 2. Теория — основа радиооптики
- 3. Математические методы современной оптики
- 4. Краевая задача дифракции электромагнитных волн в оптике и некоторые ограничения операционного метода
- 5. Решение краевой задачи на примере дифракционной решетки [5]
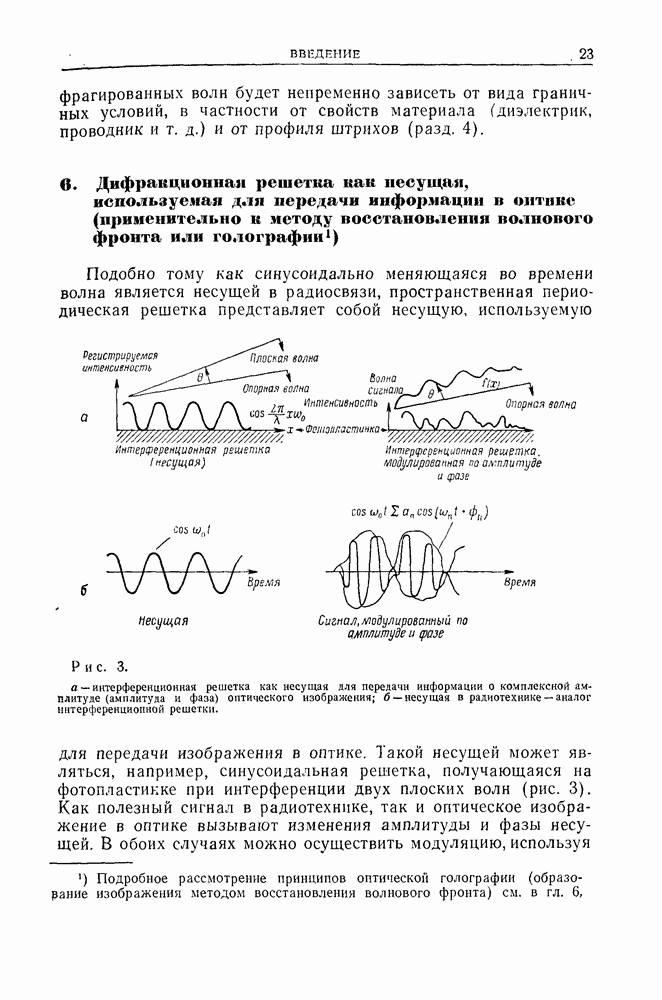
- 6. Дифракционная решетка как несущая, используемая для передачи информации в онтикс (применительно к методу восстановления волнового фронта или голографии
- 7. Оптика и теория связи Исторический обзор
- Глава 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФРАКЦИИ
- 1. Две стороны дифракции света
- 2. Распределение интенсивности в дифракционной картине и в спектре
- 2.2. Проблема образования изображения и принцип Гюйгенса
- 3. Теория образования изображения и обработка оптических сигналов при помощи преобразования Фурье
- Глава 3. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Сложение света, падающего из нескольких точек источника на отдельную точку изображения
- 6. Анализ процесса образования изображения в пространстве фурье-координат
- 7. Физический смысл функции разброса и анализ процесса образования изображения в плоскости фурье-координат
- 7.2. Синусоидальный по интенсивности предмет имеет функцию пространстненно-частотного отклика, совпадающую с фурье-образом дифракционной картины
- 8. Использование фурье-координат для синтеза предметных функций
- Глава 4. КОГЕРЕНТНОСТЬ СВЕТА (ЭКСПЕРИМЕНТАЛЬНЫЕ ХАРАКТЕРИСТИКИ)
- 2. Определение когерентности
- 2.2. Интерференционный анализ временной когерентности
- 2.3. Сравнение корреляционного и интерференционного методов
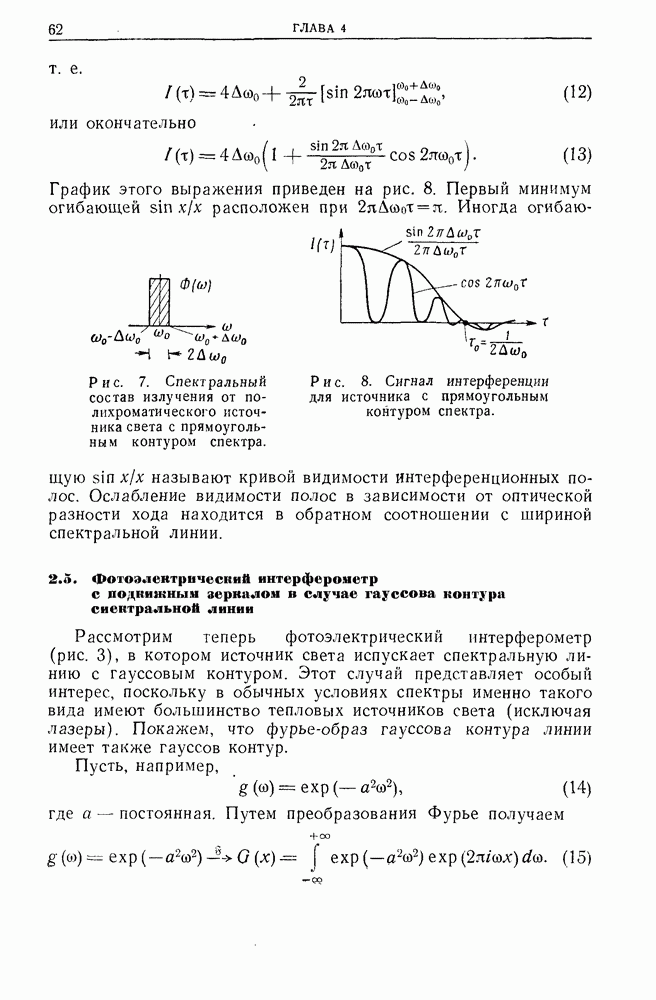
- 2.4. Узкий спектр с прямоугольным контуром
- 2.5. Фотоэлектрический интерферометр с поднижным зеркалом в случае гауссова контура спектральной линии
- 2.6. Физический смысл спектра мощности
- 2.7. Гетеродинный анализ сигналов и биений
- 2.8. Пространственная когерентность
- 2.9. Частичная когерентность света от протяженного некогерентного источника
- 2.10. Корреляция интенсивности при частичной когерентности
- 2.11. Интерферометр интенсивности
- Глава 5. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ КОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Когерентное освещение
- 3. Образование изображения при когерентном освещении как процесс двойной дифракции
- 4. Критерии разрешения Аббе и Релея
- 5. Передаточная функция при когерентном и некогерентном освещении
- 6. Фазовый контраст
- 7. Оптическая фильтрация с помощью голограммы согласованного фильтра
- 7.1. Процедура изготовления согласованного фильтра и операция фильтрации
- 8. Оптическая обработка информации, корреляционный анализ и оптические корреляторы
- 8.2. Оптический кросс-коррелятор
- 9. Интерферометрия и оптический синтез изображения (сложение комплексных амплитуд) методом последовательного наложения голографических картин на одну голограмму [5]
- Глава 6. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ОПТИЧЕСКОЙ ГОЛОГРАФИИ
- 2.1. Процесс получевия голограммы
- 2.2. Процесс восстановления изображения
- 2.3. Физические принципы голографии
- 2.4. Геометрическое увеличение
- 2.5. Разрешающая способность
- 3. Голография Фурье с высоким разрешением
- 3.2. Физические основы безлинзовой голографии Фурье высокого разрешения
- 3.3. Теория безлинзовой голографии Фурье
- 3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
- 4. Компенсация протяженности источника в голографии
- 5. Требование к когерентности в голографии
- 6. Сводка основных результатов
- 7. Электронный микроскоп и рентгеновский голографический микроскоп
- 8. Заключение
- 9. Голография при некогерентном освещении
- 9.2. Голография при пространственно-некогерентном освещении
- Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
- 1. Преобразование Фурье
- 2. Свертка
- 3. Функция корреляции
- 4. Распределения, или обобщенные функции
- 4.2. Импульсный отклик линейной системы
- 4.3. Отклик линейной системы на произвольную входную функцию
- 5. Спектральный анализ
- Дополнение автора к русскому изданию. ВОССТАНОВЛЕНИЕ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ В БЕЛОМ СВЕТЕ С ИСПОЛЬЗОВАНИЕМ ДИФРАКЦИОННОГО ЭФФЕКТА ЛИППМАНА — БРЭГГА
- ПРИЛОЖЕНИЕ 1. МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА
- Принцип восстановления волнового фронта
- Освещение сферической волной
- Восстановление при освещении точечным источником
- Побочная часть волны при восстановлении с помощью точечного источника
- Ухучшенне разделения изобрашений с помощью масок и других методов
- Освещающие волны с астигматизмом и сферической аберрацией
- Восстановление при наличии сферической аберрации и астигматизма
- Критерии когерентности
- Восстановление в оптическом диапазоне
- Экспериментальная проверка
- Заключение
- МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА, II
- 2. Принцип восстановления волнового фронта
- 3. Теория образования изображения при использовании метода пропускания
- 4. Восстановление
- 5. Критерии когерентности
- 6. Условия, необходимые для получения голограмм
- 7. Восстановление по методу темного поля
- ПРИЛОЖЕНИЕ 2. ПРИМЕНЕНИЯ ГОЛОГРАФИИ
- 2. Трехмерная фотография
- 3. Распознавание образов
- 4. Иитерференционная память
- 5. Интерферометрия
- 6. Голография в технологии
- 7. Голографический метод в интроскопии
- 8. Голографическая микроскопия
- 9. Голографическое кино
- 10. Голографическое телевидение
- 11. Голографическая оптика