| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.1. Процесс получевия голограммы
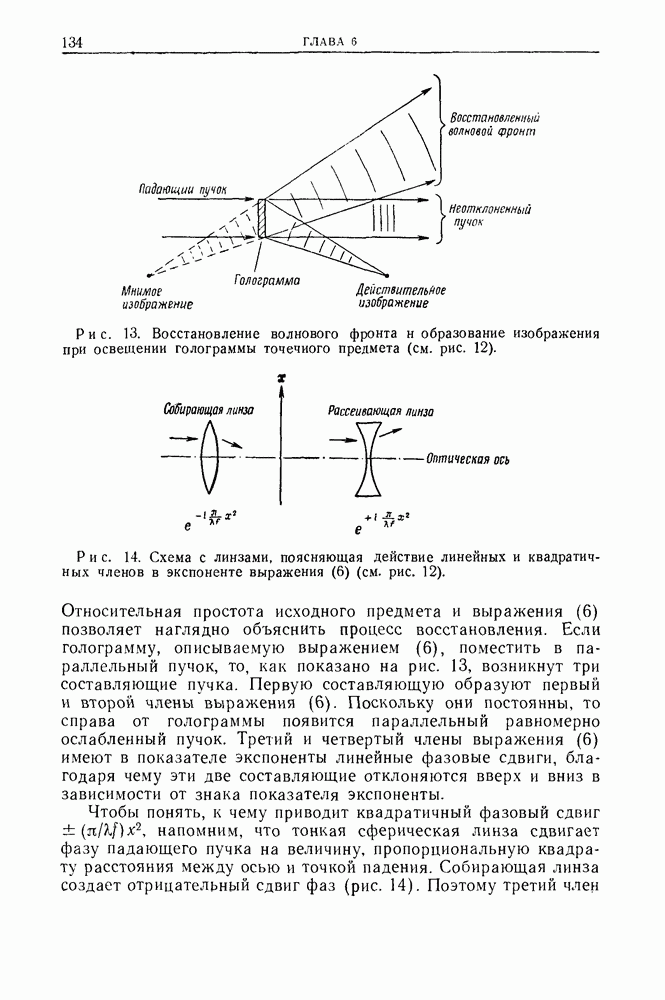
Амплитуду и фазу рассеянной волны можно зарегистрировать фотографически, если к рассеянной волне, падающей на фотопластинку, добавить когерентный опорный пучок. Простейшая схема осуществления такой суперпозиции световых волн показана на рис. 3 и 9. Широкая плоская волна освещает одновременно предмет и плоское зеркало [11] или треугольную призму [16]. Излучение, рассеянное предметом, создает вблизи фотопластинки поле с амплитудой  и фазой
и фазой  Призма, поворачивая пучок на малый угол
Призма, поворачивая пучок на малый угол  создает там же поле с постоянной амплитудой
создает там же поле с постоянной амплитудой  и линейно меняющейся фазой
и линейно меняющейся фазой  где а —
где а —

Рис. 9. Схема получения голограммы (см. также рис. 2 и 3).
постоянная, определяемая углом 6 и длиной волны Я (при малых углах

Полная амплитуда поля на фотопластинке равна

Фотоэмульсия зарегистрирует интенсивность

Мы видим, что благодаря наличию опорного пучка  удалось сохранить фазу
удалось сохранить фазу  рассеянной волны.
рассеянной волны.
Фотографическая эмульсия регистрирует интенсивность света, возведенную в некоторую степень, определяемую коэффициентом контрастности у. Если работать на линейном участке характеристической кривой фотоэмульсии, то амплитудное пропускание ее  пропорционально выражению
пропорционально выражению

где у — коэффициент контрастности. При выводе мы предполагали, что интенсивность опорного пучка намного выше, чем интенсивность света, рассеянного предметом. Это позволяет сохранить в разложении бинома только члены первого порядка. Выражение (4) Габор [1, 2] назвал уравнением голограммы.
Следует отметить две особенности этого уравнения. Во-первых, коснемся роли коэффициента контрастности у. В отличие от требований, возникающих при осуществлении аналогичных процессов, ни точная величина у, ни ее знак не влияют на процесс получения голограммы. Например, если изготовить контрастный отпечаток с голограммы и этим изменить знак у на обратный, то это приведет к изменению фазы переменной составляющей пропускания на 180°. Небольшое изменение абсолютной величины коэффициента контрастности у приведет к усилению или ослаблению амплитуды этой переменной составляющей.
Вторая особенность затрагивает взаимосвязь амплитуды  и фазы
и фазы  Легко заметить, что амплитуда
Легко заметить, что амплитуда  и фаза
и фаза  рассеянной волны входят в уравнение голограммы естественным образом, т. е. как
рассеянной волны входят в уравнение голограммы естественным образом, т. е. как  в третий член (4) и
в третий член (4) и  в четвертый. Недавно Кэйзи [32] и Пеннингтон [33] доказали, что распределение интенсивности света можно превратить в вариации толщины эмульсии, пропорциональные (при определенных условиях [34]) экспозиции, и путем фотохимического отбеливания получить рельефно-фазовую голограмму. В этом случае, если экспозиции не слишком велики, комплексная амплитуда пропускания голограммы имеет вид
в четвертый. Недавно Кэйзи [32] и Пеннингтон [33] доказали, что распределение интенсивности света можно превратить в вариации толщины эмульсии, пропорциональные (при определенных условиях [34]) экспозиции, и путем фотохимического отбеливания получить рельефно-фазовую голограмму. В этом случае, если экспозиции не слишком велики, комплексная амплитуда пропускания голограммы имеет вид

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора русского издания
- Глава 1. ВВЕДЕНИЕ
- 1. Современная оптика — раздел радиоалектроники
- 2. Теория — основа радиооптики
- 3. Математические методы современной оптики
- 4. Краевая задача дифракции электромагнитных волн в оптике и некоторые ограничения операционного метода
- 5. Решение краевой задачи на примере дифракционной решетки [5]
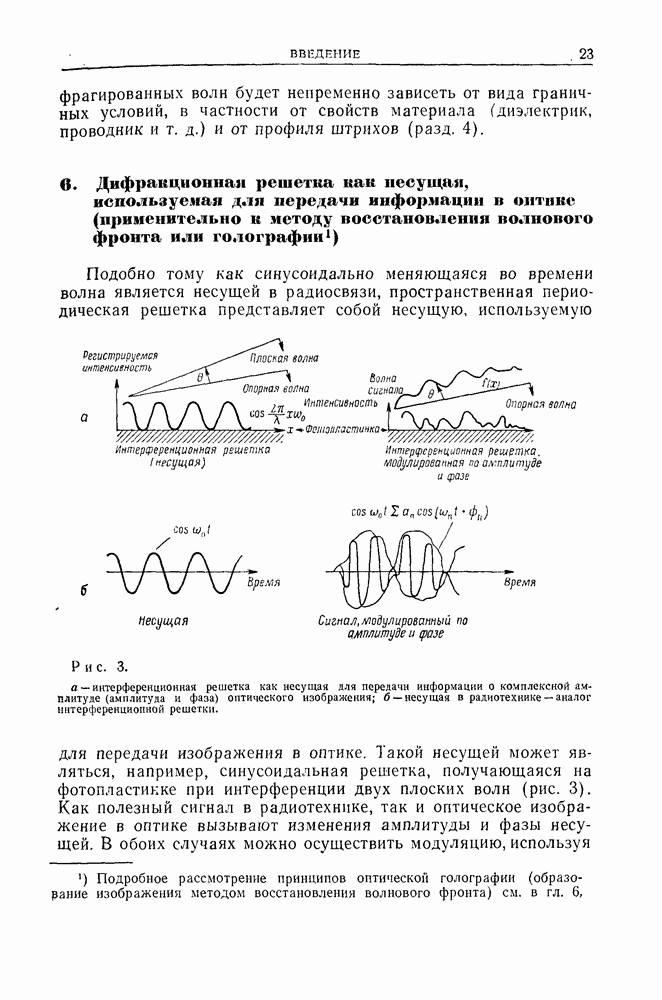
- 6. Дифракционная решетка как несущая, используемая для передачи информации в онтикс (применительно к методу восстановления волнового фронта или голографии
- 7. Оптика и теория связи Исторический обзор
- Глава 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФРАКЦИИ
- 1. Две стороны дифракции света
- 2. Распределение интенсивности в дифракционной картине и в спектре
- 2.2. Проблема образования изображения и принцип Гюйгенса
- 3. Теория образования изображения и обработка оптических сигналов при помощи преобразования Фурье
- Глава 3. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Сложение света, падающего из нескольких точек источника на отдельную точку изображения
- 6. Анализ процесса образования изображения в пространстве фурье-координат
- 7. Физический смысл функции разброса и анализ процесса образования изображения в плоскости фурье-координат
- 7.2. Синусоидальный по интенсивности предмет имеет функцию пространстненно-частотного отклика, совпадающую с фурье-образом дифракционной картины
- 8. Использование фурье-координат для синтеза предметных функций
- Глава 4. КОГЕРЕНТНОСТЬ СВЕТА (ЭКСПЕРИМЕНТАЛЬНЫЕ ХАРАКТЕРИСТИКИ)
- 2. Определение когерентности
- 2.2. Интерференционный анализ временной когерентности
- 2.3. Сравнение корреляционного и интерференционного методов
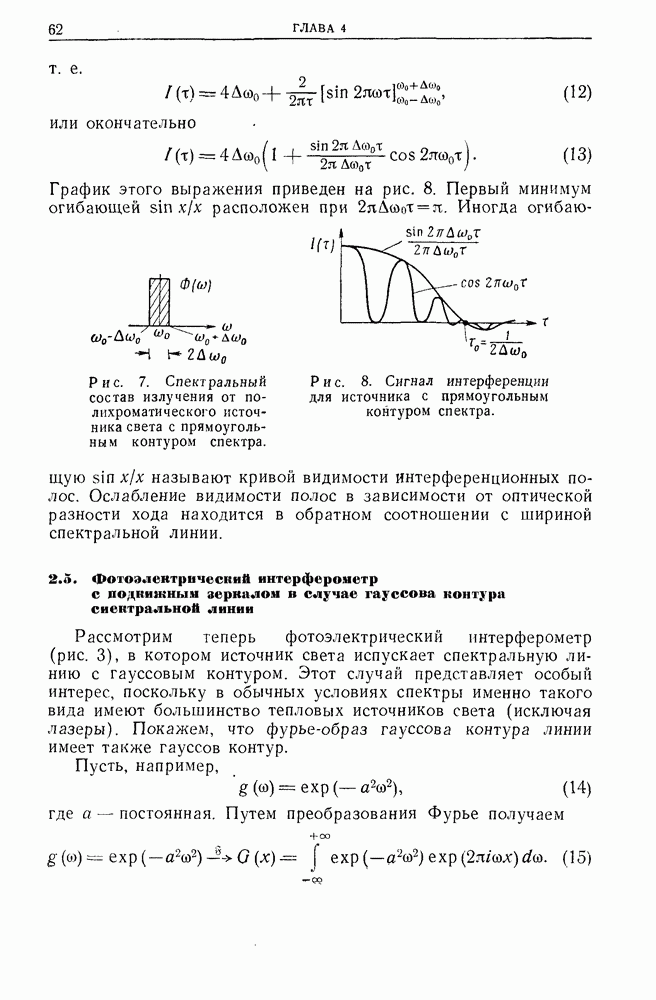
- 2.4. Узкий спектр с прямоугольным контуром
- 2.5. Фотоэлектрический интерферометр с поднижным зеркалом в случае гауссова контура спектральной линии
- 2.6. Физический смысл спектра мощности
- 2.7. Гетеродинный анализ сигналов и биений
- 2.8. Пространственная когерентность
- 2.9. Частичная когерентность света от протяженного некогерентного источника
- 2.10. Корреляция интенсивности при частичной когерентности
- 2.11. Интерферометр интенсивности
- Глава 5. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ КОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Когерентное освещение
- 3. Образование изображения при когерентном освещении как процесс двойной дифракции
- 4. Критерии разрешения Аббе и Релея
- 5. Передаточная функция при когерентном и некогерентном освещении
- 6. Фазовый контраст
- 7. Оптическая фильтрация с помощью голограммы согласованного фильтра
- 7.1. Процедура изготовления согласованного фильтра и операция фильтрации
- 8. Оптическая обработка информации, корреляционный анализ и оптические корреляторы
- 8.2. Оптический кросс-коррелятор
- 9. Интерферометрия и оптический синтез изображения (сложение комплексных амплитуд) методом последовательного наложения голографических картин на одну голограмму [5]
- Глава 6. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ОПТИЧЕСКОЙ ГОЛОГРАФИИ
- 2.1. Процесс получевия голограммы
- 2.2. Процесс восстановления изображения
- 2.3. Физические принципы голографии
- 2.4. Геометрическое увеличение
- 2.5. Разрешающая способность
- 3. Голография Фурье с высоким разрешением
- 3.2. Физические основы безлинзовой голографии Фурье высокого разрешения
- 3.3. Теория безлинзовой голографии Фурье
- 3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
- 4. Компенсация протяженности источника в голографии
- 5. Требование к когерентности в голографии
- 6. Сводка основных результатов
- 7. Электронный микроскоп и рентгеновский голографический микроскоп
- 8. Заключение
- 9. Голография при некогерентном освещении
- 9.2. Голография при пространственно-некогерентном освещении
- Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
- 1. Преобразование Фурье
- 2. Свертка
- 3. Функция корреляции
- 4. Распределения, или обобщенные функции
- 4.2. Импульсный отклик линейной системы
- 4.3. Отклик линейной системы на произвольную входную функцию
- 5. Спектральный анализ
- Дополнение автора к русскому изданию. ВОССТАНОВЛЕНИЕ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ В БЕЛОМ СВЕТЕ С ИСПОЛЬЗОВАНИЕМ ДИФРАКЦИОННОГО ЭФФЕКТА ЛИППМАНА — БРЭГГА
- ПРИЛОЖЕНИЕ 1. МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА
- Принцип восстановления волнового фронта
- Освещение сферической волной
- Восстановление при освещении точечным источником
- Побочная часть волны при восстановлении с помощью точечного источника
- Ухучшенне разделения изобрашений с помощью масок и других методов
- Освещающие волны с астигматизмом и сферической аберрацией
- Восстановление при наличии сферической аберрации и астигматизма
- Критерии когерентности
- Восстановление в оптическом диапазоне
- Экспериментальная проверка
- Заключение
- МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА, II
- 2. Принцип восстановления волнового фронта
- 3. Теория образования изображения при использовании метода пропускания
- 4. Восстановление
- 5. Критерии когерентности
- 6. Условия, необходимые для получения голограмм
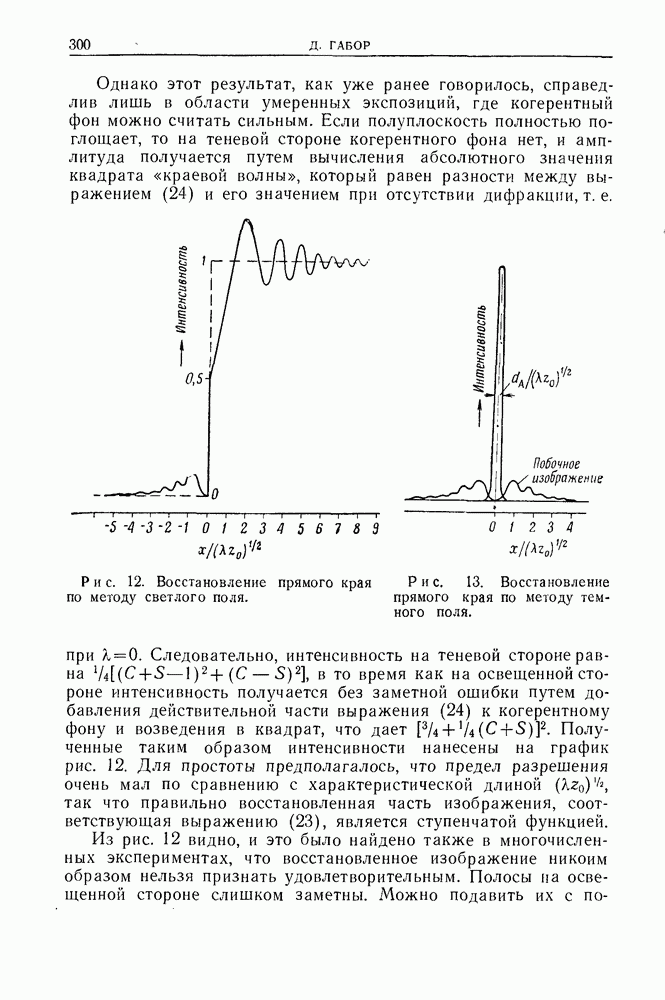
- 7. Восстановление по методу темного поля
- ПРИЛОЖЕНИЕ 2. ПРИМЕНЕНИЯ ГОЛОГРАФИИ
- 2. Трехмерная фотография
- 3. Распознавание образов
- 4. Иитерференционная память
- 5. Интерферометрия
- 6. Голография в технологии
- 7. Голографический метод в интроскопии
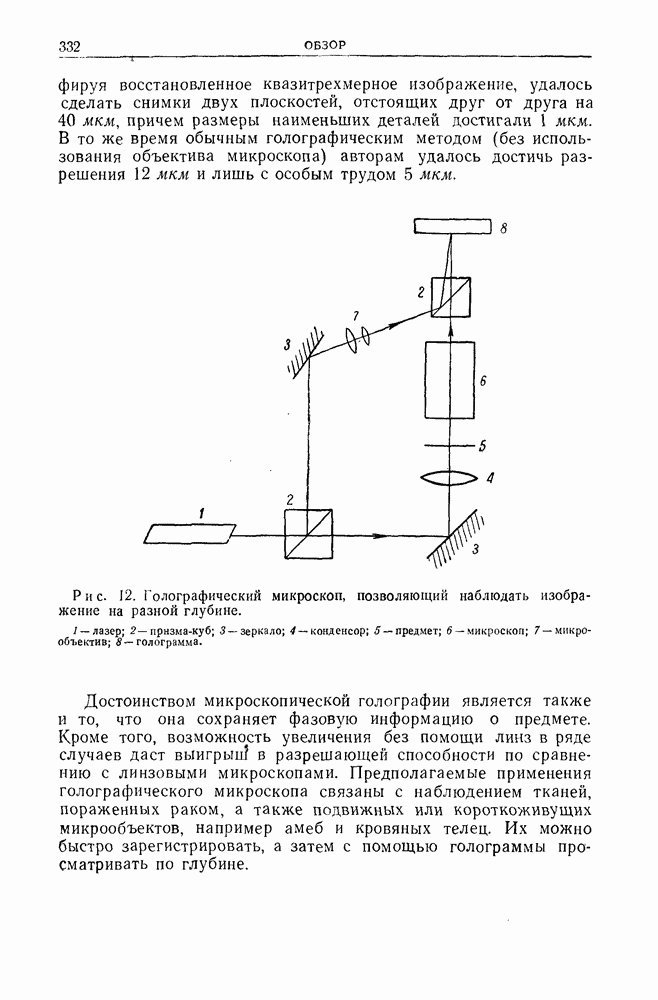
- 8. Голографическая микроскопия
- 9. Голографическое кино
- 10. Голографическое телевидение
- 11. Голографическая оптика