| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
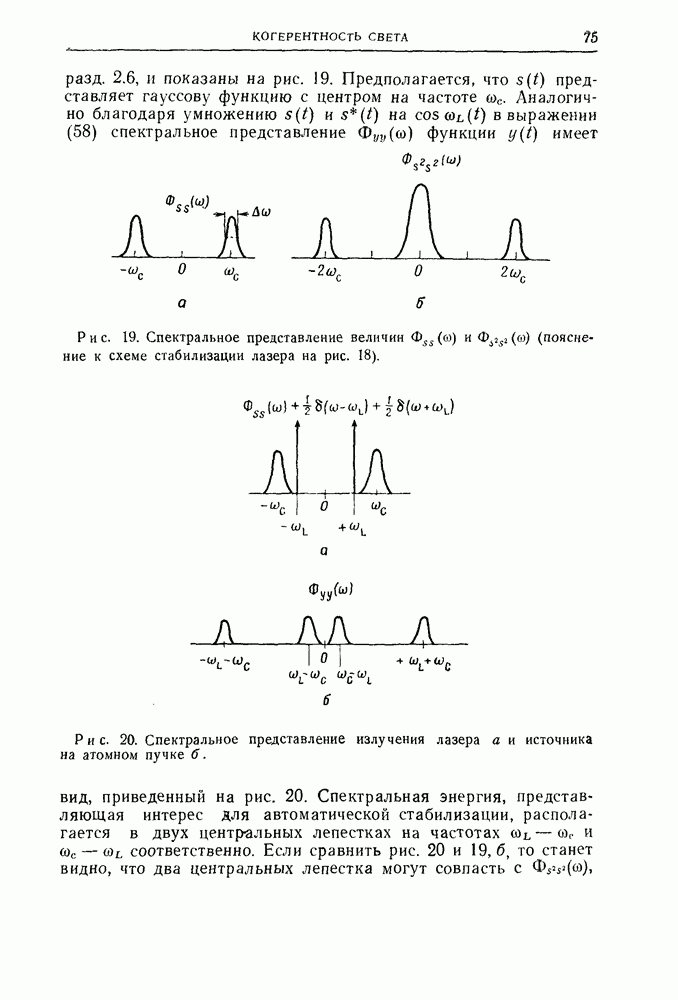
2.3. Физические принципы голографии
Для выяснения физических принципов голографии рассмотрим метод регистрации и восстановления волнового фронта для образцов исчезающе малых размеров. Первоначальный вариант этого метода применительно к точечным образцам был предложен Табором [2], а позднее был развит Роджерсом [13, 35—37] и Эль-Самом [14].

Рис. 12. Голограмма точечного предмета. Схема используется при обсуждении коэффициента увеличения, определяемого выражением (6).
По аналогии с этими работами выберем в качестве образца непрозрачную пластинку с точечным отверстием. Если такое отверстие осветить плоской волной, то, согласно принципу Гюйгенса, оно будет действовать как источник сферической волны. На фотопластинку упадет волна с амплитудой

где  -некоторая постоянная. А, — длина волны света,
-некоторая постоянная. А, — длина волны света,  расстояние между точечным отверстием и фотографической пластинкой (рис. 12). Согласно уравнению (4), пропускание голограммы для точечного предмета равно
расстояние между точечным отверстием и фотографической пластинкой (рис. 12). Согласно уравнению (4), пропускание голограммы для точечного предмета равно


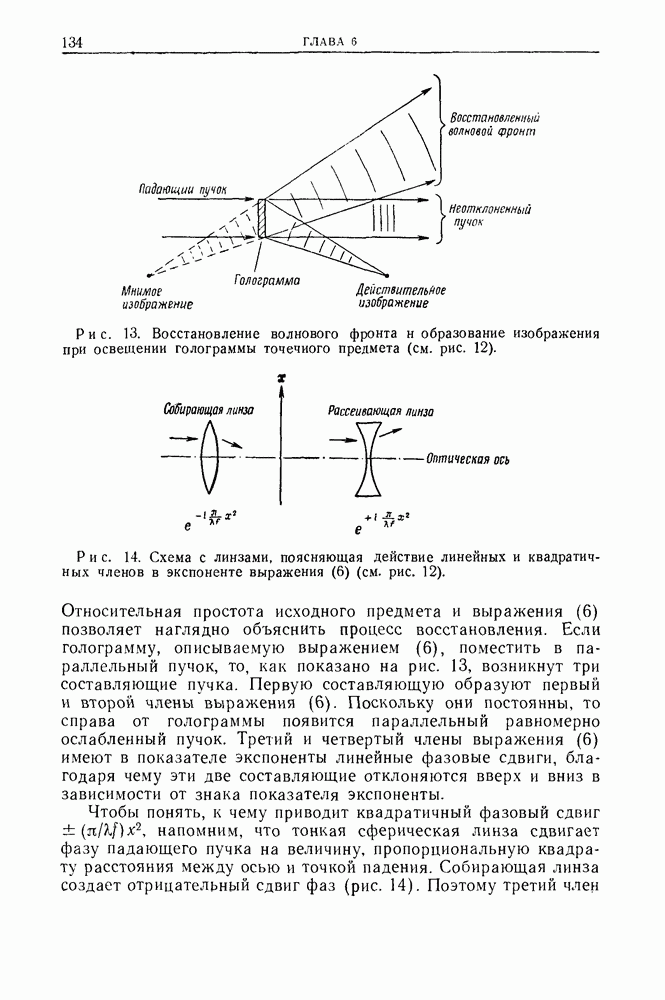
Рис. 13. Восстановление волнового фронта и образование изображения при освещении голограммы точечного предмета (см. рис. 12).

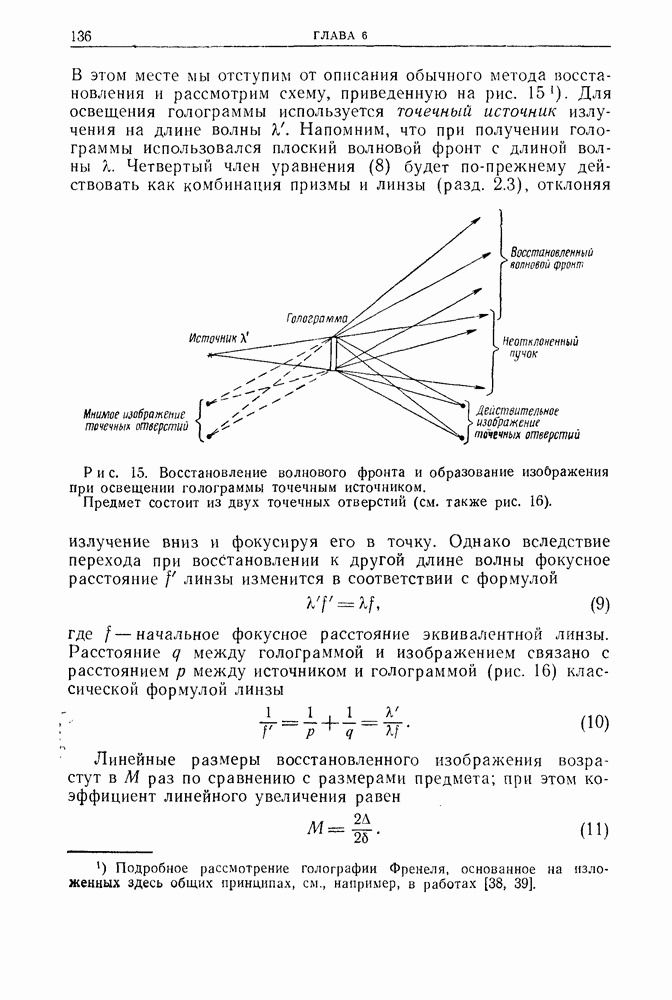
Рис. 14. Схема с линзами, поясняющая действие линейных и квадратичных членов в экспоненте выражения (6) (см. рис. 12).
Относительная простота исходного предмета и выражения (6) позволяет наглядно объяснить процесс восстановления. Если голограмму, описываемую выражением (6), поместить в параллельный пучок, то, как показано на рис. 13, возникнут три составляющие пучка. Первую составляющую образуют первый и второй члены выражения (6). Поскольку они постоянны, то справа от голограммы появится параллельный равномерно ослабленный пучок. Третий и четвертый члены выражения (6) имеют в показателе экспоненты линейные фазовые сдвиги, благодаря чему эти две составляющие отклоняются вверх и вниз в зависимости от знака показателя экспоненты.
Чтобы понять, к чему приводит квадратичный фазовый сдвиг  напомним, что тонкая сферическая линза сдвигает фазу падающего пучка на величину, пропорциональную квадрату расстояния между осью и точкой падения. Собирающая линза создает отрицательный сдвиг фаз (рис. 14). Поэтому третий член
напомним, что тонкая сферическая линза сдвигает фазу падающего пучка на величину, пропорциональную квадрату расстояния между осью и точкой падения. Собирающая линза создает отрицательный сдвиг фаз (рис. 14). Поэтому третий член
выражения (6) не только отклоняет пучок вверх, но и действует как рассеивающая линза. Падающая плоская волна повернет вверх и превратится в расходящуюся сферическую волну. Эта волна идентична волне, которая освещала голограмму при экспозиции. Аналогично четвертый член выражения (6) действует на плоский пучок не только как отклоняющая вниз призма, но и как собирающая линза. Повернутый вниз пучок превращается в сходящуюся сферическую волну. Эта волна сфокусируется в точку на расстоянии  от голограммы. Таким образом при освещении голограммы плоской волной мы получаем не только восстановленный исходный волновой фронт рассеянной волны, но также и сфокусированное изображение предмета, в данном случае — точечный источник. В разд. 2.4 рассматриваются система освещения нредмета точечным источником и свойственная голографии возможность получения больших геометрических увеличений.
от голограммы. Таким образом при освещении голограммы плоской волной мы получаем не только восстановленный исходный волновой фронт рассеянной волны, но также и сфокусированное изображение предмета, в данном случае — точечный источник. В разд. 2.4 рассматриваются система освещения нредмета точечным источником и свойственная голографии возможность получения больших геометрических увеличений.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора русского издания
- Глава 1. ВВЕДЕНИЕ
- 1. Современная оптика — раздел радиоалектроники
- 2. Теория — основа радиооптики
- 3. Математические методы современной оптики
- 4. Краевая задача дифракции электромагнитных волн в оптике и некоторые ограничения операционного метода
- 5. Решение краевой задачи на примере дифракционной решетки [5]
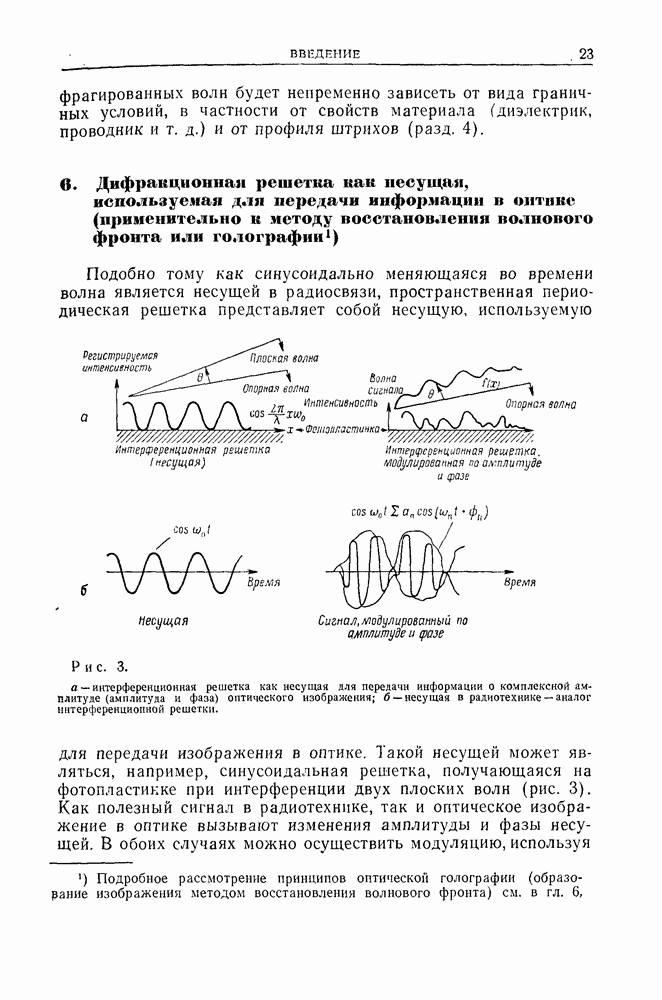
- 6. Дифракционная решетка как несущая, используемая для передачи информации в онтикс (применительно к методу восстановления волнового фронта или голографии
- 7. Оптика и теория связи Исторический обзор
- Глава 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФРАКЦИИ
- 1. Две стороны дифракции света
- 2. Распределение интенсивности в дифракционной картине и в спектре
- 2.2. Проблема образования изображения и принцип Гюйгенса
- 3. Теория образования изображения и обработка оптических сигналов при помощи преобразования Фурье
- Глава 3. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Сложение света, падающего из нескольких точек источника на отдельную точку изображения
- 6. Анализ процесса образования изображения в пространстве фурье-координат
- 7. Физический смысл функции разброса и анализ процесса образования изображения в плоскости фурье-координат
- 7.2. Синусоидальный по интенсивности предмет имеет функцию пространстненно-частотного отклика, совпадающую с фурье-образом дифракционной картины
- 8. Использование фурье-координат для синтеза предметных функций
- Глава 4. КОГЕРЕНТНОСТЬ СВЕТА (ЭКСПЕРИМЕНТАЛЬНЫЕ ХАРАКТЕРИСТИКИ)
- 2. Определение когерентности
- 2.2. Интерференционный анализ временной когерентности
- 2.3. Сравнение корреляционного и интерференционного методов
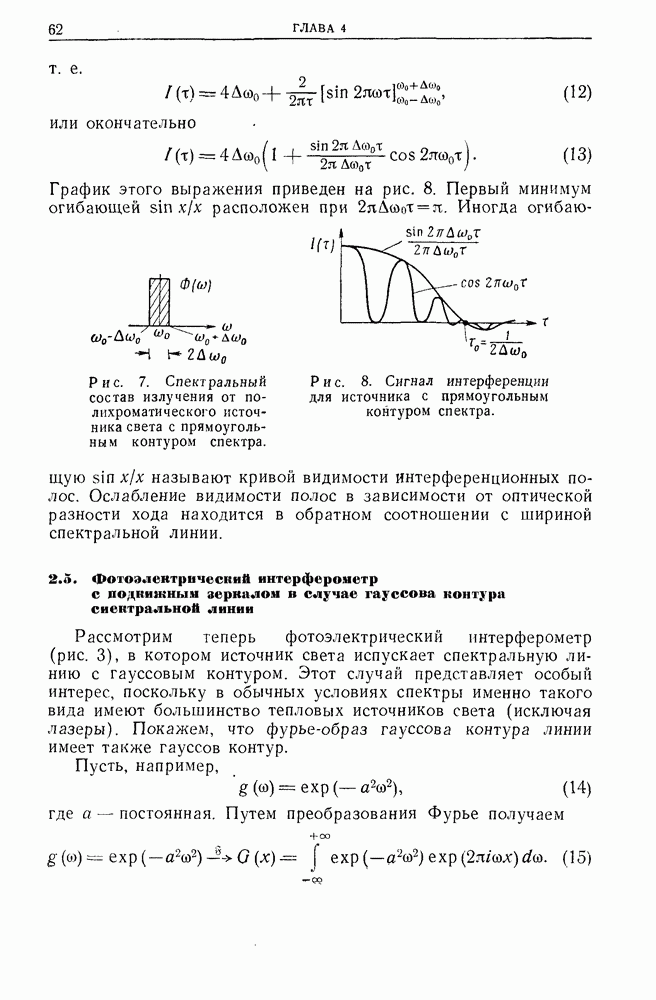
- 2.4. Узкий спектр с прямоугольным контуром
- 2.5. Фотоэлектрический интерферометр с поднижным зеркалом в случае гауссова контура спектральной линии
- 2.6. Физический смысл спектра мощности
- 2.7. Гетеродинный анализ сигналов и биений
- 2.8. Пространственная когерентность
- 2.9. Частичная когерентность света от протяженного некогерентного источника
- 2.10. Корреляция интенсивности при частичной когерентности
- 2.11. Интерферометр интенсивности
- Глава 5. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ КОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Когерентное освещение
- 3. Образование изображения при когерентном освещении как процесс двойной дифракции
- 4. Критерии разрешения Аббе и Релея
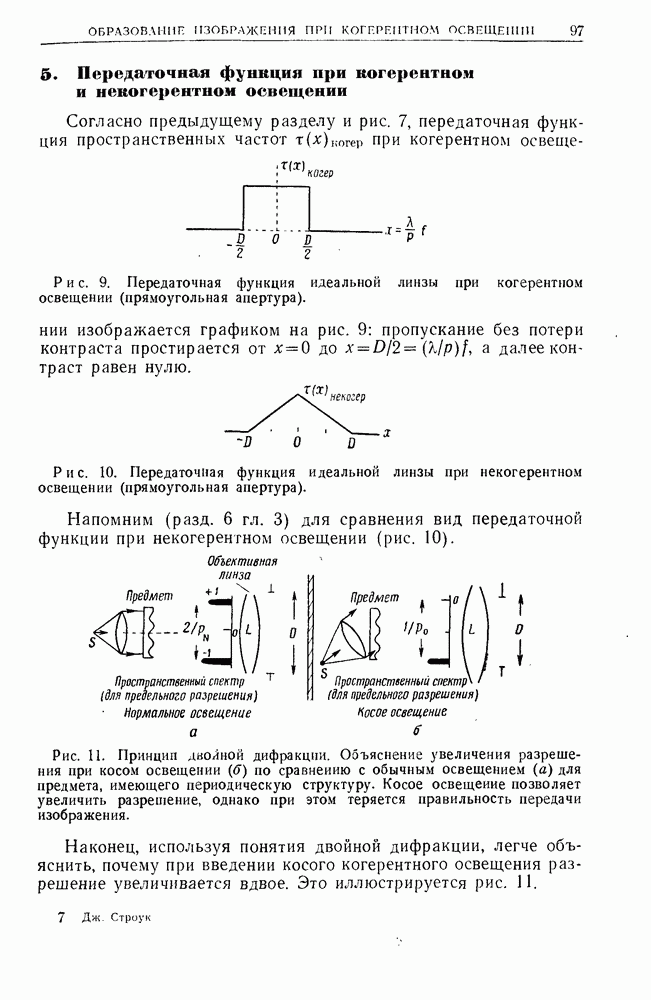
- 5. Передаточная функция при когерентном и некогерентном освещении
- 6. Фазовый контраст
- 7. Оптическая фильтрация с помощью голограммы согласованного фильтра
- 7.1. Процедура изготовления согласованного фильтра и операция фильтрации
- 8. Оптическая обработка информации, корреляционный анализ и оптические корреляторы
- 8.2. Оптический кросс-коррелятор
- 9. Интерферометрия и оптический синтез изображения (сложение комплексных амплитуд) методом последовательного наложения голографических картин на одну голограмму [5]
- Глава 6. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ОПТИЧЕСКОЙ ГОЛОГРАФИИ
- 2.1. Процесс получевия голограммы
- 2.2. Процесс восстановления изображения
- 2.3. Физические принципы голографии
- 2.4. Геометрическое увеличение
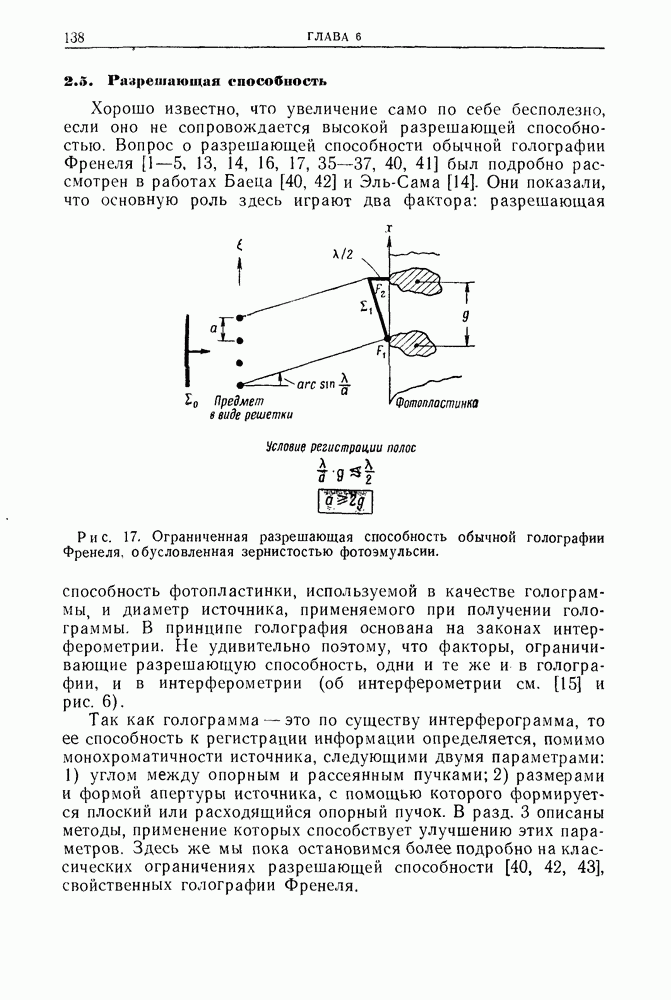
- 2.5. Разрешающая способность
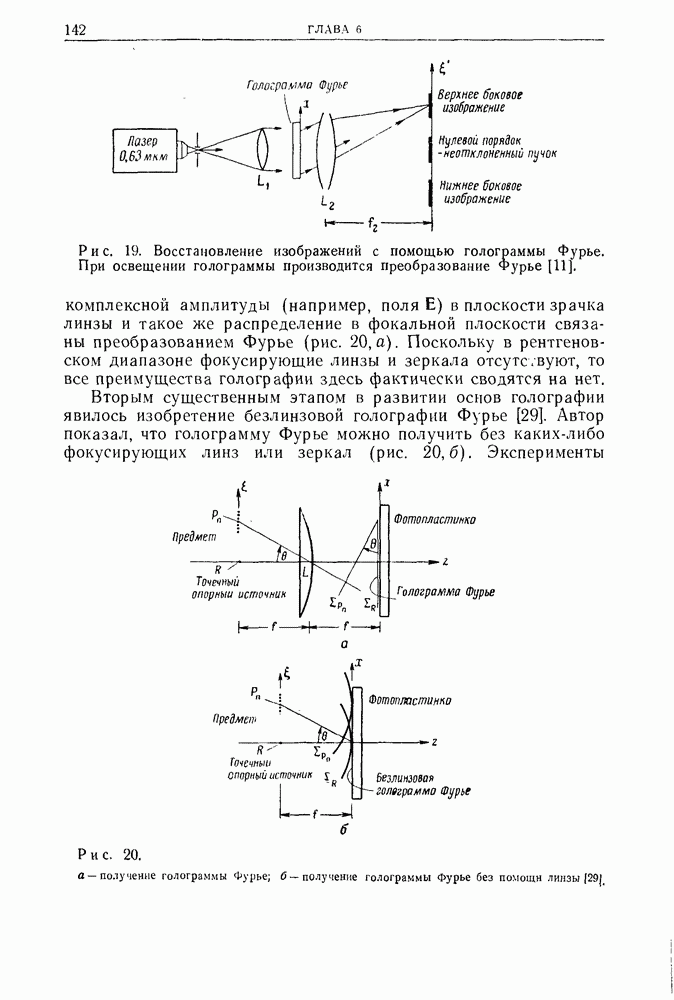
- 3. Голография Фурье с высоким разрешением
- 3.2. Физические основы безлинзовой голографии Фурье высокого разрешения
- 3.3. Теория безлинзовой голографии Фурье
- 3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
- 4. Компенсация протяженности источника в голографии
- 5. Требование к когерентности в голографии
- 6. Сводка основных результатов
- 7. Электронный микроскоп и рентгеновский голографический микроскоп
- 8. Заключение
- 9. Голография при некогерентном освещении
- 9.2. Голография при пространственно-некогерентном освещении
- Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
- 1. Преобразование Фурье
- 2. Свертка
- 3. Функция корреляции
- 4. Распределения, или обобщенные функции
- 4.2. Импульсный отклик линейной системы
- 4.3. Отклик линейной системы на произвольную входную функцию
- 5. Спектральный анализ
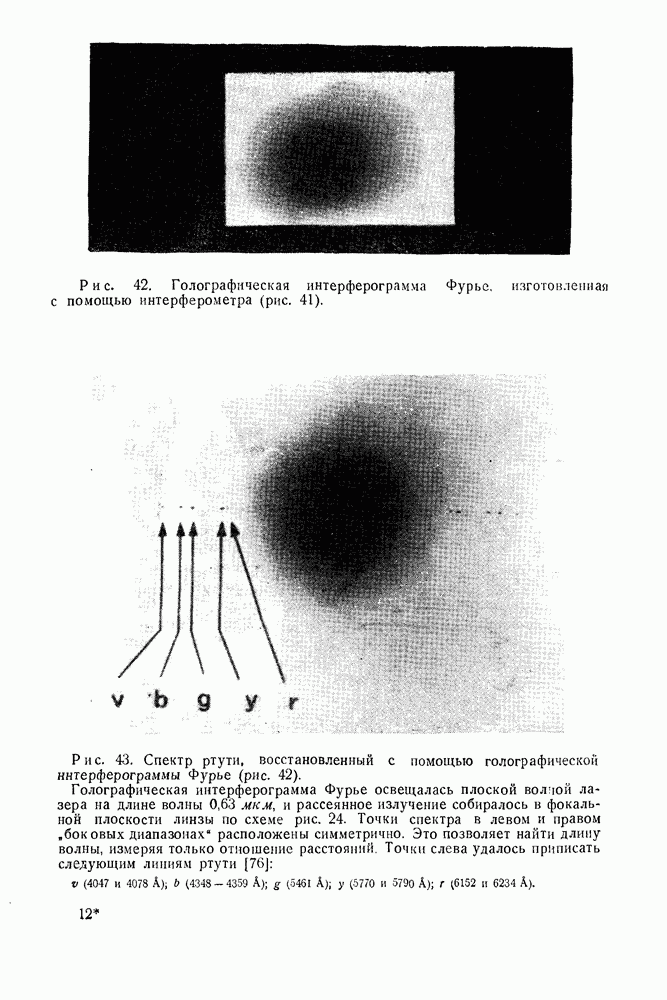
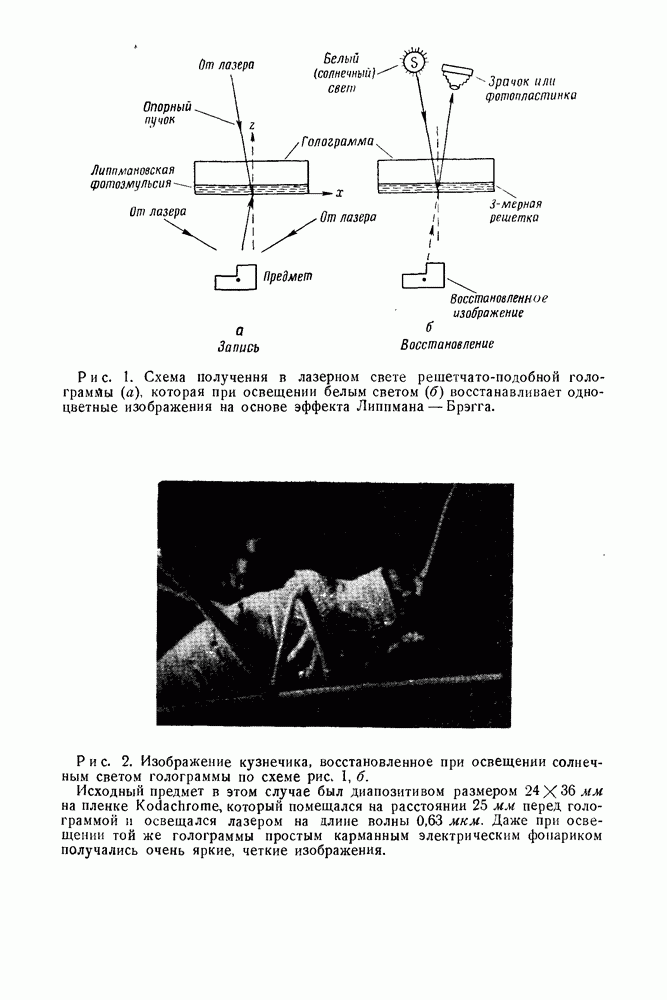
- Дополнение автора к русскому изданию. ВОССТАНОВЛЕНИЕ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ В БЕЛОМ СВЕТЕ С ИСПОЛЬЗОВАНИЕМ ДИФРАКЦИОННОГО ЭФФЕКТА ЛИППМАНА — БРЭГГА
- ПРИЛОЖЕНИЕ 1. МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА
- Принцип восстановления волнового фронта
- Освещение сферической волной
- Восстановление при освещении точечным источником
- Побочная часть волны при восстановлении с помощью точечного источника
- Ухучшенне разделения изобрашений с помощью масок и других методов
- Освещающие волны с астигматизмом и сферической аберрацией
- Восстановление при наличии сферической аберрации и астигматизма
- Критерии когерентности
- Восстановление в оптическом диапазоне
- Экспериментальная проверка
- Заключение
- МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА, II
- 2. Принцип восстановления волнового фронта
- 3. Теория образования изображения при использовании метода пропускания
- 4. Восстановление
- 5. Критерии когерентности
- 6. Условия, необходимые для получения голограмм
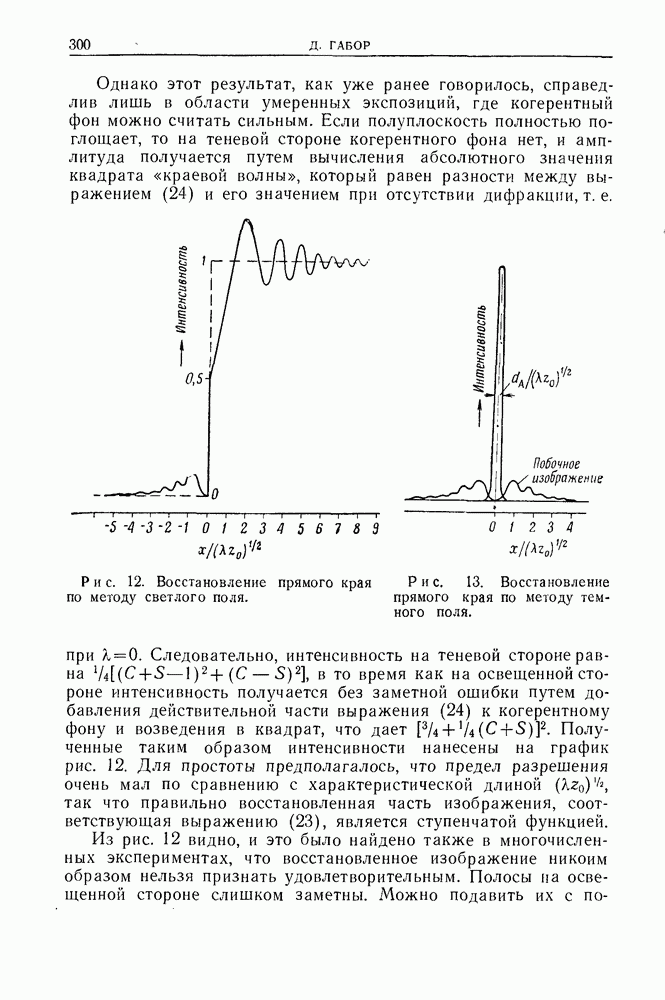
- 7. Восстановление по методу темного поля
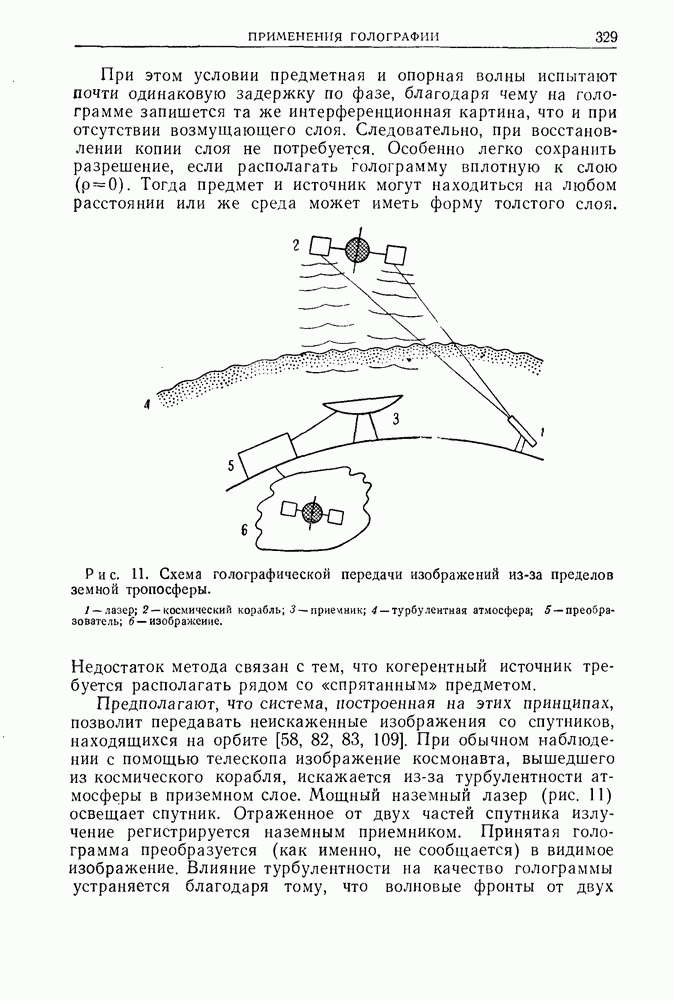
- ПРИЛОЖЕНИЕ 2. ПРИМЕНЕНИЯ ГОЛОГРАФИИ
- 2. Трехмерная фотография
- 3. Распознавание образов
- 4. Иитерференционная память
- 5. Интерферометрия
- 6. Голография в технологии
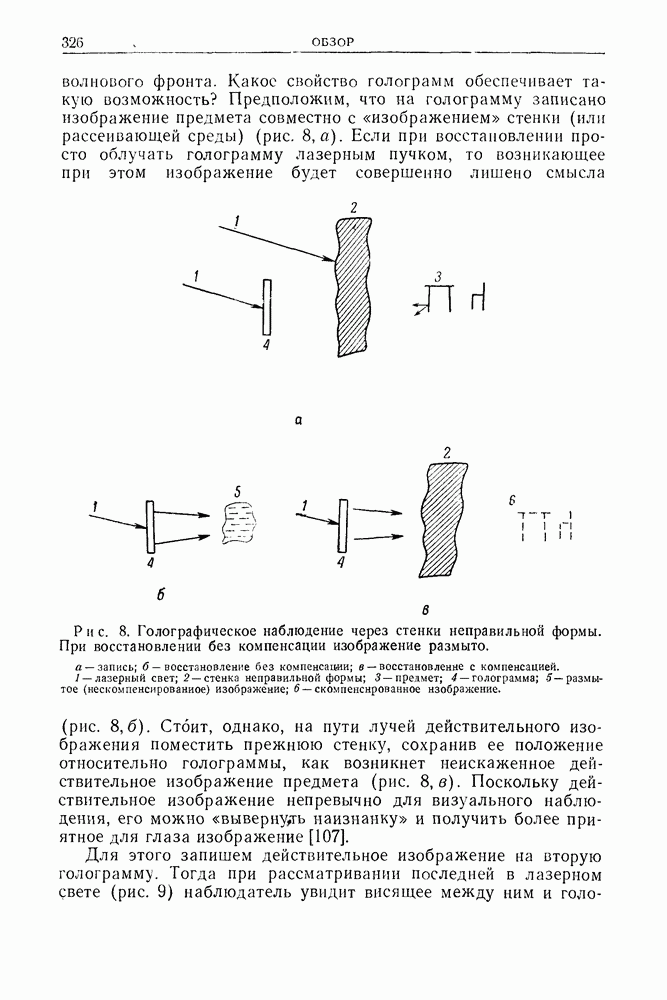
- 7. Голографический метод в интроскопии
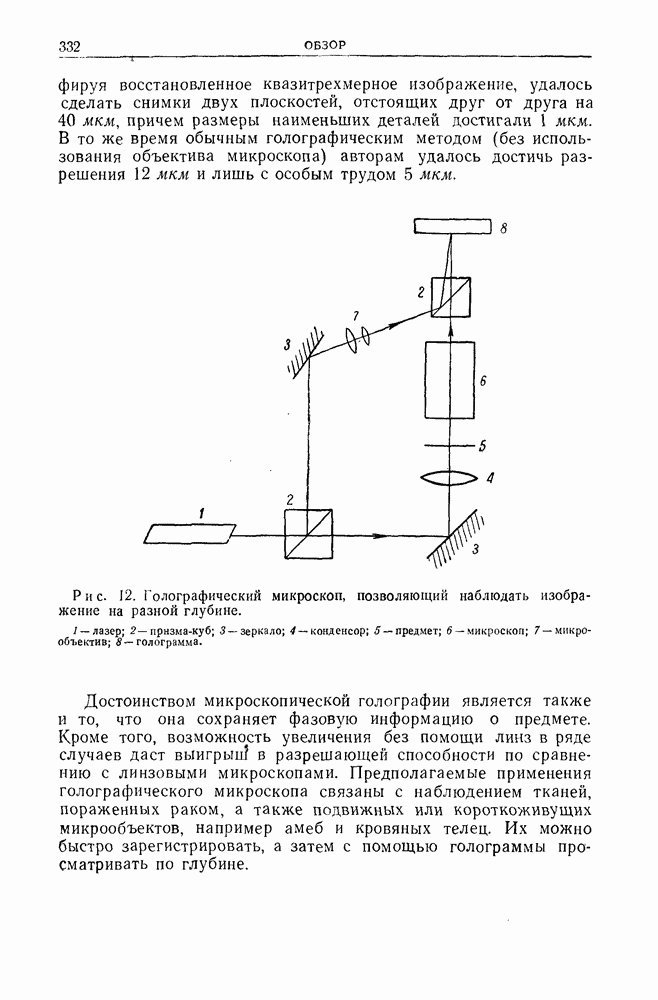
- 8. Голографическая микроскопия
- 9. Голографическое кино
- 10. Голографическое телевидение
- 11. Голографическая оптика