| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.9. Частичная когерентность света от протяженного некогерентного источника
Пусть источник  освещает две щели
освещает две щели  как показано на рис. 24. Центр источника расположен на оси
как показано на рис. 24. Центр источника расположен на оси  перпендикулярной плоскости
перпендикулярной плоскости  и проходящей через щель
и проходящей через щель 

Рис. 24. Получение пространственной когерентности в плоскости  при освещении щелей протяженным пространственно некогерентным источником.
при освещении щелей протяженным пространственно некогерентным источником.
Согласно предыдущему разделу, источник является совершенно некогерентным. Это означает, что если две щели поместить в плоскости источника, то интерференционные полосы не возникнут. Однако можно доказать, что если удалить эти щели достаточно далеко от некогерентного источника, то можно получить интерференционные полосы с хорошим и даже очень хорошим контрастом.
Рассмотрим две волны  покидающие излучатель вдоль направления, которое определяется единичным вектором
покидающие излучатель вдоль направления, которое определяется единичным вектором  идущим из центра
идущим из центра  (рис. 25):
(рис. 25):

где  направляющие конусы, а
направляющие конусы, а  — единичные векторы, направленные вдоль соответствующих осей. Пусть вектор
— единичные векторы, направленные вдоль соответствующих осей. Пусть вектор

определяет положение  относительно
относительно  Разность хода волн
Разность хода волн  испущенных в точке А, до точек
испущенных в точке А, до точек  равна
равна

Следовательно, излучатель А создает в точках  электрические поля (см. рис. 24)
электрические поля (см. рис. 24)

где 
Если в точке А имеется много излучателей, например атомов, то получаем

Мы предполагаем, что свет является монохроматичным.

Рис. 25. Схема получения пространственной когерентности в плоскости ту (см. рис. 24).
На практике для наблюдения полос в двухщелевом интерферометре требуется не особенно высокая монохроматичность, если только разность времен х, за которые два луча пройдут расстояние от источника до плоскости наблюдения, достаточно мала. В случае полихроматического источника можно использовать светофильтры.
Для оценки контраста полос необходимо найти выражение для

Имеем

где  оптические разности хода, определяемые выражением (76). Получаем
оптические разности хода, определяемые выражением (76). Получаем

Однако вследствие некогерентности источника все перекрестные члены при усреднении обратятся в нуль. Оставшиеся члены дадут

Если число излучателей стремится к бесконечности, то, переходя к пределу, получаем

где

есть интенсивность, приходящаяся на единицу телесного угла с заданными угловыми координатами  Другими словами,
Другими словами,  соответствует распределению интенсивности по источнику при его наблюдении из точки
соответствует распределению интенсивности по источнику при его наблюдении из точки 
С помощью выражений (82) и (83) сразу же находим, что коэффициент частичной когерентности у, который описывает интерференцию света, идущего от  при освещении самих щелей протяженным некогерентным источником равен
при освещении самих щелей протяженным некогерентным источником равен

Уравнение (84) весьма примечательно. Оно показывает, что степень частичной когерентности между точками  освещенными протяженным некогерентным источником, является фурье-образом распределения интенсивности
освещенными протяженным некогерентным источником, является фурье-образом распределения интенсивности  источника, наблюдаемого из плоскости, где расположены щели
источника, наблюдаемого из плоскости, где расположены щели  При этом важно помнить, что центр источника расположен на одной оси с
При этом важно помнить, что центр источника расположен на одной оси с  Детали можно уяснить на следующем примере.
Детали можно уяснить на следующем примере.
а. Двухщелевой интерферометр Юнга и звездный интерферометр Майкельсона
Свойства интерферометров Юнга и Майкельсона позволяют уяснить понятие коэффициента частичной когерентности, определяемого выражением (70), и содержание соотношения между этим коэффициентом и распределением интенсивности по источнику, выражаемое с помощью преобразования Фурье. Рассмотрим сначала  двухщелевого интерферометра, приведенную на рис. 26. Пусть
двухщелевого интерферометра, приведенную на рис. 26. Пусть  постоянная величина.
постоянная величина.

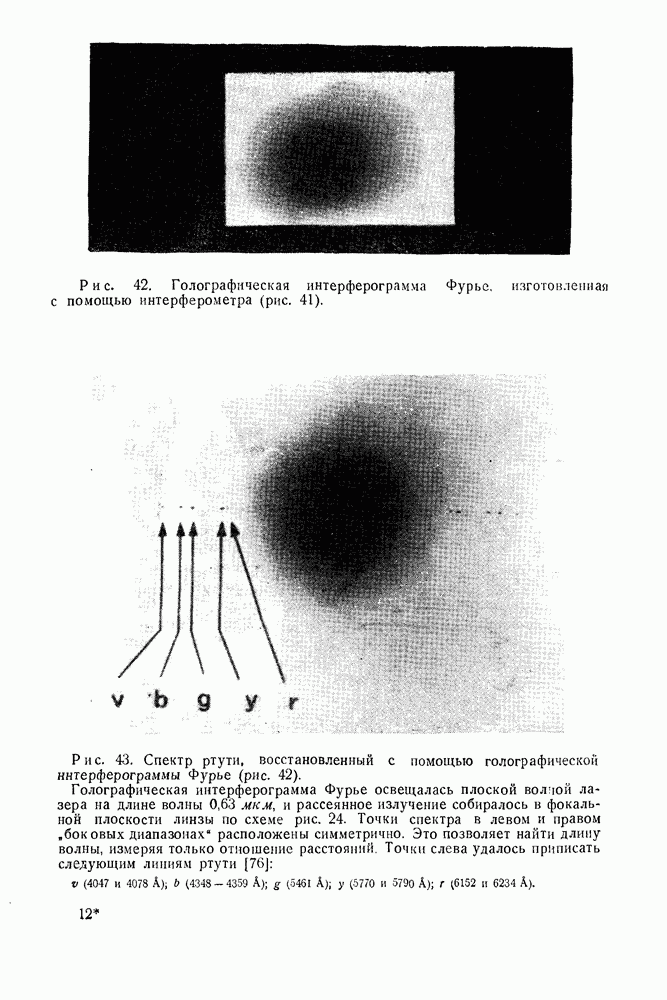
Рис. 26. Интерференционные полосы в интерферометре Юнга при наблюдении звезды — протяженного, пространственно-некогерентного источника света.
Эксперимент показывает, что при некоторых условиях в плоскости  возникает система интерференционных полос.
возникает система интерференционных полос.
Физические свойства системы полос легко описать с помощью понятий, встречающихся в теории преобразования Фурье [выражения (1а) и (18) гл. 3]. Действительно [выражение (12) гл. 7], если

то

Следовательно,

и наблюдаемая интенсивность (рис. 27) описывается выражением

т. е.

где  - огибающая, которая модулирует амплитуду полос, определяемая с помощью выражения
- огибающая, которая модулирует амплитуду полос, определяемая с помощью выражения

и

Контраст системы интерференционных полос равен 

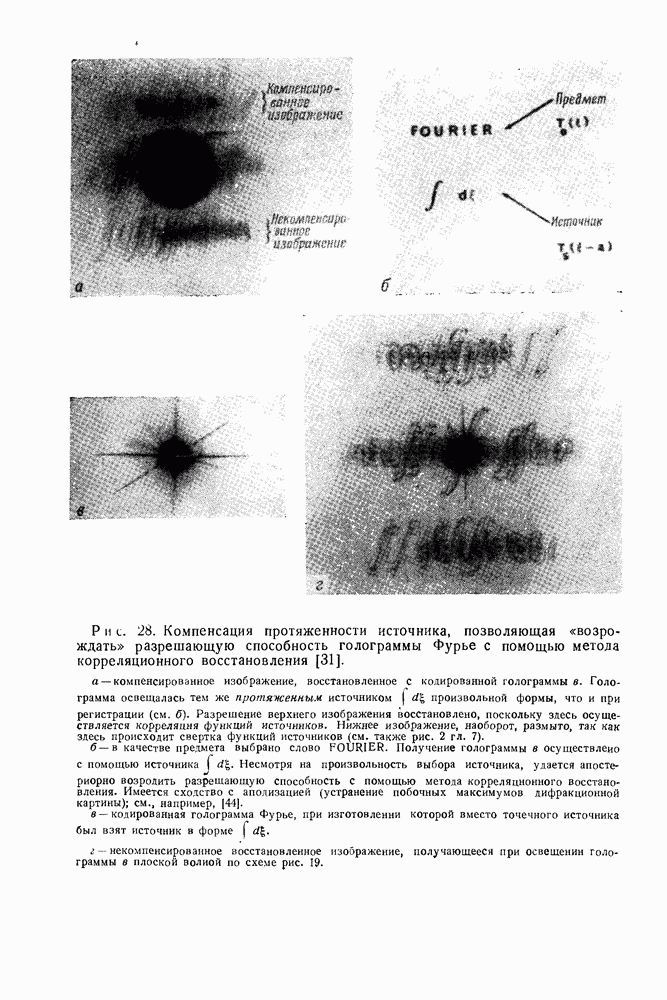
Если двухщелевой интерферометр использовать для измерения диаметра звезд, то кривая видимости полос определяется функцией  график которой изображен на рис. 28.
график которой изображен на рис. 28.

Рис. 27. Образование интерференционных полос в звездном интерферометре (см. рис. 26).
Очень важно заметить, что кривая  на рис. 28 подразумевает, что одна из шмелей находится в центре максимума кривой
на рис. 28 подразумевает, что одна из шмелей находится в центре максимума кривой 

Рис. 28. Коэффициент пространственной когерентности  в плоскости щелей при освещении плоскости удаленным, пространственно-некогерентным источником.
в плоскости щелей при освещении плоскости удаленным, пространственно-некогерентным источником.
Очевидно, что видимый угловой диаметр звезды можно получить непосредственно путем измерения расстояния  вдоль оси х между щелями
вдоль оси х между щелями  когда интерференционные полосы исчезают.
когда интерференционные полосы исчезают.
Интересная особенность заключается  что всегда имеется такое расстояние между
что всегда имеется такое расстояние между  при котором интерференционные полосы от протяженного некогерентного источника получаются с хорошим контрастом. Это замечание можно использовать для оценки условий, при которых с помощью обычного теплового источника света, например, миниатюрной импульсной лампы, можно сформировать пространственно когерентную сферическую (или плоскую) волну. Если такую лампу расположить за достаточно узким красным светофильтром, то ее излучение можно сделать до такой степени когерентным, что удастся наблюдать восстановленное изображение с помощью голограммы, например голограммы Фурье. Для этого голограмму необходимо держать перед глазом, а лампу удалить на расстояние вытянутой руки.
при котором интерференционные полосы от протяженного некогерентного источника получаются с хорошим контрастом. Это замечание можно использовать для оценки условий, при которых с помощью обычного теплового источника света, например, миниатюрной импульсной лампы, можно сформировать пространственно когерентную сферическую (или плоскую) волну. Если такую лампу расположить за достаточно узким красным светофильтром, то ее излучение можно сделать до такой степени когерентным, что удастся наблюдать восстановленное изображение с помощью голограммы, например голограммы Фурье. Для этого голограмму необходимо держать перед глазом, а лампу удалить на расстояние вытянутой руки.
Для примера рассмотрим лампу диаметром  удаленную от глаза на расстояние
удаленную от глаза на расстояние  Найдем то расстояние
Найдем то расстояние  при котором график
при котором график  на рис. 28 имеет первый минимум:
на рис. 28 имеет первый минимум:

Таким образом, пространственная когерентность будет достаточно хорошей на площадке размером  Зрачок глаза имеет те же размеры. Следовательно, мы можем наблюдать изображение, восстановленное с помощью голограммы Фурье!
Зрачок глаза имеет те же размеры. Следовательно, мы можем наблюдать изображение, восстановленное с помощью голограммы Фурье!
Часто говорят, что когерентность световых пучков улучшается с расстоянием только благодаря самому процессу распространения. В действительности дело просто в том, что при неизменных размерах источника и неизменном расстоянии между щелями расстояние  становится относительно малым, в частности малым по сравнению с эффективной шириной кривой
становится относительно малым, в частности малым по сравнению с эффективной шириной кривой  по мере увеличения расстояния между источником и щелями.
по мере увеличения расстояния между источником и щелями.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора русского издания
- Глава 1. ВВЕДЕНИЕ
- 1. Современная оптика — раздел радиоалектроники
- 2. Теория — основа радиооптики
- 3. Математические методы современной оптики
- 4. Краевая задача дифракции электромагнитных волн в оптике и некоторые ограничения операционного метода
- 5. Решение краевой задачи на примере дифракционной решетки [5]
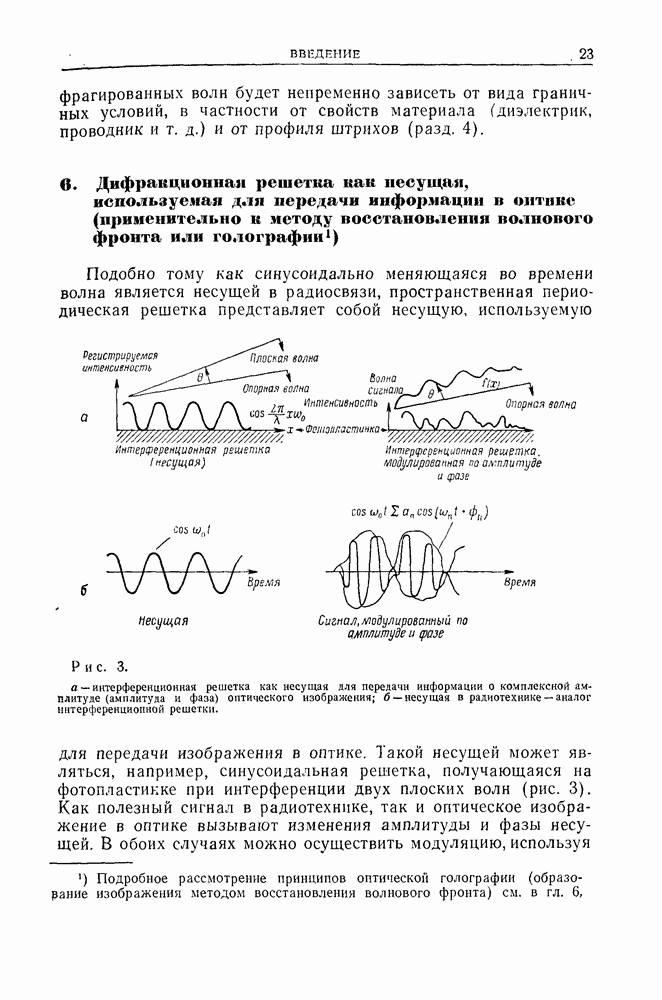
- 6. Дифракционная решетка как несущая, используемая для передачи информации в онтикс (применительно к методу восстановления волнового фронта или голографии
- 7. Оптика и теория связи Исторический обзор
- Глава 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФРАКЦИИ
- 1. Две стороны дифракции света
- 2. Распределение интенсивности в дифракционной картине и в спектре
- 2.2. Проблема образования изображения и принцип Гюйгенса
- 3. Теория образования изображения и обработка оптических сигналов при помощи преобразования Фурье
- Глава 3. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Сложение света, падающего из нескольких точек источника на отдельную точку изображения
- 6. Анализ процесса образования изображения в пространстве фурье-координат
- 7. Физический смысл функции разброса и анализ процесса образования изображения в плоскости фурье-координат
- 7.2. Синусоидальный по интенсивности предмет имеет функцию пространстненно-частотного отклика, совпадающую с фурье-образом дифракционной картины
- 8. Использование фурье-координат для синтеза предметных функций
- Глава 4. КОГЕРЕНТНОСТЬ СВЕТА (ЭКСПЕРИМЕНТАЛЬНЫЕ ХАРАКТЕРИСТИКИ)
- 2. Определение когерентности
- 2.2. Интерференционный анализ временной когерентности
- 2.3. Сравнение корреляционного и интерференционного методов
- 2.4. Узкий спектр с прямоугольным контуром
- 2.5. Фотоэлектрический интерферометр с поднижным зеркалом в случае гауссова контура спектральной линии
- 2.6. Физический смысл спектра мощности
- 2.7. Гетеродинный анализ сигналов и биений
- 2.8. Пространственная когерентность
- 2.9. Частичная когерентность света от протяженного некогерентного источника
- 2.10. Корреляция интенсивности при частичной когерентности
- 2.11. Интерферометр интенсивности
- Глава 5. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ КОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Когерентное освещение
- 3. Образование изображения при когерентном освещении как процесс двойной дифракции
- 4. Критерии разрешения Аббе и Релея
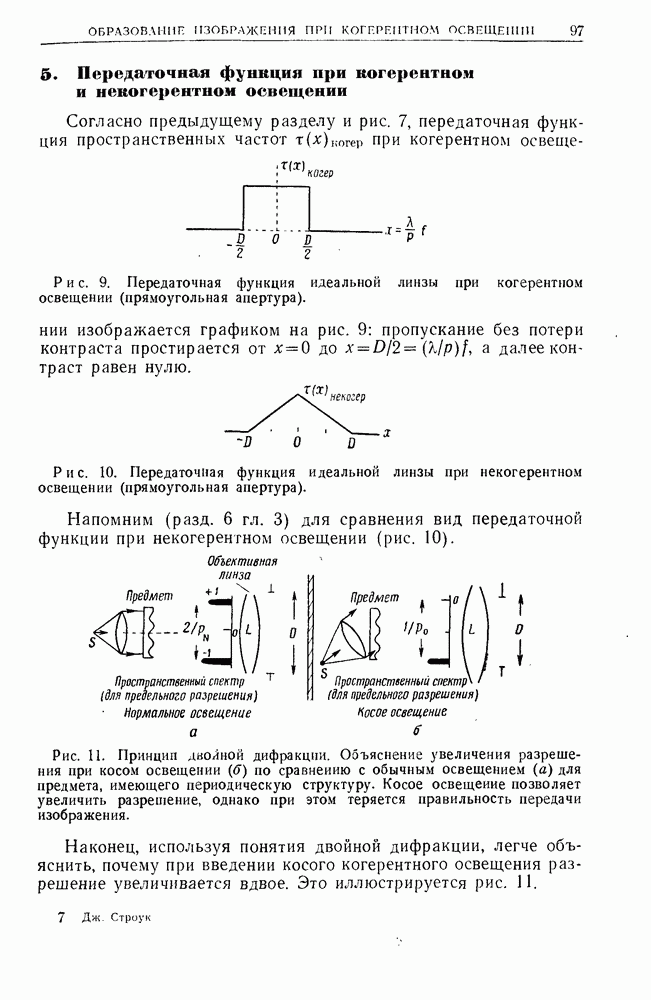
- 5. Передаточная функция при когерентном и некогерентном освещении
- 6. Фазовый контраст
- 7. Оптическая фильтрация с помощью голограммы согласованного фильтра
- 7.1. Процедура изготовления согласованного фильтра и операция фильтрации
- 8. Оптическая обработка информации, корреляционный анализ и оптические корреляторы
- 8.2. Оптический кросс-коррелятор
- 9. Интерферометрия и оптический синтез изображения (сложение комплексных амплитуд) методом последовательного наложения голографических картин на одну голограмму [5]
- Глава 6. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ОПТИЧЕСКОЙ ГОЛОГРАФИИ
- 2.1. Процесс получевия голограммы
- 2.2. Процесс восстановления изображения
- 2.3. Физические принципы голографии
- 2.4. Геометрическое увеличение
- 2.5. Разрешающая способность
- 3. Голография Фурье с высоким разрешением
- 3.2. Физические основы безлинзовой голографии Фурье высокого разрешения
- 3.3. Теория безлинзовой голографии Фурье
- 3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
- 4. Компенсация протяженности источника в голографии
- 5. Требование к когерентности в голографии
- 6. Сводка основных результатов
- 7. Электронный микроскоп и рентгеновский голографический микроскоп
- 8. Заключение
- 9. Голография при некогерентном освещении
- 9.2. Голография при пространственно-некогерентном освещении
- Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
- 1. Преобразование Фурье
- 2. Свертка
- 3. Функция корреляции
- 4. Распределения, или обобщенные функции
- 4.2. Импульсный отклик линейной системы
- 4.3. Отклик линейной системы на произвольную входную функцию
- 5. Спектральный анализ
- Дополнение автора к русскому изданию. ВОССТАНОВЛЕНИЕ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ В БЕЛОМ СВЕТЕ С ИСПОЛЬЗОВАНИЕМ ДИФРАКЦИОННОГО ЭФФЕКТА ЛИППМАНА — БРЭГГА
- ПРИЛОЖЕНИЕ 1. МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА
- Принцип восстановления волнового фронта
- Освещение сферической волной
- Восстановление при освещении точечным источником
- Побочная часть волны при восстановлении с помощью точечного источника
- Ухучшенне разделения изобрашений с помощью масок и других методов
- Освещающие волны с астигматизмом и сферической аберрацией
- Восстановление при наличии сферической аберрации и астигматизма
- Критерии когерентности
- Восстановление в оптическом диапазоне
- Экспериментальная проверка
- Заключение
- МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА, II
- 2. Принцип восстановления волнового фронта
- 3. Теория образования изображения при использовании метода пропускания
- 4. Восстановление
- 5. Критерии когерентности
- 6. Условия, необходимые для получения голограмм
- 7. Восстановление по методу темного поля
- ПРИЛОЖЕНИЕ 2. ПРИМЕНЕНИЯ ГОЛОГРАФИИ
- 2. Трехмерная фотография
- 3. Распознавание образов
- 4. Иитерференционная память
- 5. Интерферометрия
- 6. Голография в технологии
- 7. Голографический метод в интроскопии
- 8. Голографическая микроскопия
- 9. Голографическое кино
- 10. Голографическое телевидение
- 11. Голографическая оптика