| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2. Проблема образования изображения и принцип Гюйгенса
Используя некоторые существенные приближения, можно, как правило, показать, что гюйгенсовское решение в оптике (как, например, ее «строгая» векторная форма в формулировке преобразования Фурье) выводится из уравнений Максвелла. Одно из главных приближений состоит в том, что принцип Гюйгенса применим только вблизи центра квазисферического волнового фронта, образующего изображение. При рассмотрении проблем дифракции 11 образования изображений необходимо отдавать себе отчет в приближенном характере принципа Гюйгенса. И во всяком случае кажущаяся простота принципа Гюйгенса даже в той его приемлемой форме, которая получена эвристически на базе принципа суперпозиции и спектрального разложения по плоским волнам, не должна служить оправданием для его использования в качестве основы «строгого» решения, получаемого путем добавления к первоначальному приближению членов более высоких порядков. Однако, если правильно использовать принцип Гюйгенса, выраженный с помощью преобразования Фурье, то он становится достаточно универсальным средством для рассмотрения проблем образования изображений. В частности, его применяют для отыскания распределения интенсивности в пределах дифракционной картины, образуемой волновым фронтом конечного размера при отражении, преломлении и дифракции света в оптических элементах (зеркалах, линзах, призмах, решетках).
Точное выражение принципа Гюйгенса, которое получается из уравнений Максвелла, имеет следующий вид;

где  комплексная амплитуда вектора электрического поля в точке
комплексная амплитуда вектора электрического поля в точке  Плоскости изображения вблизи центра квазисферического волнового фронта радиусом
Плоскости изображения вблизи центра квазисферического волнового фронта радиусом  направляющие косинусы, определяющие положение точки
направляющие косинусы, определяющие положение точки  если наблюдатель находится на апертуре с центром в точке О квазисферического волнового фронта;
если наблюдатель находится на апертуре с центром в точке О квазисферического волнового фронта;  координаты, определяющие точку на апертуре; А(х, у) — отклонение волнового фронта от сферичности;
координаты, определяющие точку на апертуре; А(х, у) — отклонение волнового фронта от сферичности;  а
а  амплитуда
амплитуда  на волновом
на волновом
фронте. Направляющие косинусы  а также координаты х и у относятся к квазиплоскому участку волнового фронта в совершенной фокусирующей системе (зеркало или линза). В такой фокусирующей системе плоская волна преобразуется в сферическую. Совершенная система преобразует квазиплоскую волну в квазисферическую. Кроме того, если учесть сделанные приближения, аберрации плоской волны тождественны аберрациям сферической волны.
а также координаты х и у относятся к квазиплоскому участку волнового фронта в совершенной фокусирующей системе (зеркало или линза). В такой фокусирующей системе плоская волна преобразуется в сферическую. Совершенная система преобразует квазиплоскую волну в квазисферическую. Кроме того, если учесть сделанные приближения, аберрации плоской волны тождественны аберрациям сферической волны.
Уравнение (18) имеет вид преобразования Фурье и выражает следующее: комплексная амплитуда вектора электрического поля в точке на плоскости изображения равна фурье-образу распределения комплексной амплитуды электрического поля в пределах апертуры, образующей изображение. При этом, очевидно, электрические векторы в пределах апертуры и плоскости изображения параллельны самой плоскости изображения. Преобразование Фурье необходимо выполнить для каждой точки дифракционной картины. Например, для совершенно однородной плоской волны в пределах прямоугольной апертуры шириной А вдоль оси  и мы имеем
и мы имеем

или, интегрируя,

Таким образом, комплексная амплитуда  изменяется в плоскости изображения как известная функция
изменяется в плоскости изображения как известная функция  которая имеет первый минимум при
которая имеет первый минимум при

где фокусное расстояние оптической системы. Все приемники (фотоэлектрические, фотографические и т. п.) регистрируют только интенсивность

Зйездочка здесь означает «комплексное сопряжение». Интенсивность  изменяется как
изменяется как  и первый минимум ее, естественно, расположен на расстоянии от центрального максимума. Обычно
и первый минимум ее, естественно, расположен на расстоянии от центрального максимума. Обычно  называют дифракционной картиной, соответствующей апертуре А.
называют дифракционной картиной, соответствующей апертуре А.
Уравнение (18), которое описывает дифракцию на бесконечности, обусловленную апертурой, может быть доказано эвристически на основе принципа суперпозиции и принципа Гюйгенса, если вкладывать в него обычный смысл. Рассмотрим зрачок в плоскости  и точку
и точку  в центре элемента поверхности
в центре элемента поверхности  этой плоскости. Элемент поверхности с центром
этой плоскости. Элемент поверхности с центром  испускает элементарную волну
испускает элементарную волну  где
где  скалярная компонента вектора
скалярная компонента вектора  в зрачке. В направлении, определяемом направляющими косинусами
в зрачке. В направлении, определяемом направляющими косинусами  волна из
волна из  имеет сдвиг по фазе
имеет сдвиг по фазе  по отношению к фазе элементарной волны, испущенной из центра зрачка О. Благодаря суперпозиции волна в направлении
по отношению к фазе элементарной волны, испущенной из центра зрачка О. Благодаря суперпозиции волна в направлении  равняется сумме этих волн
равняется сумме этих волн 

Все элементарные волны, посылаемые или пропускаемые зрачком в направлении а  фокусируются совершенной фокусирующей системой в одну точку
фокусируются совершенной фокусирующей системой в одну точку  фокальной плоскости, так что
фокальной плоскости, так что

Поскольку  то для координат изображения в фокальной плоскости фокусирующей системы
то для координат изображения в фокальной плоскости фокусирующей системы

и

где  фокусное расстояние. Дифракционную картину описывают следующие уравнения:
фокусное расстояние. Дифракционную картину описывают следующие уравнения:

и

которые совпадают с выражениями для дифракционной картины, полученными из уравнений Максвелла (18) с использованием указанных там приближений.
Таким образом, задание распределения комплексной ампли туды (по амплитуде и фазе) электромагнитного поля в пределах апертуры независимо от того, как образовалось это поле,
позволяет нам рассчитать дифракционную картину, соответствующую данному распределению поля в пределах данной апертуры. Однозначное соотношение, существующее при указанных приближениях между распределением поля в апертуре и распределением света в дифракционной картине, имеет вид преобразования Фурье. Широкое использование операторного метода расчета при решении проблем образования изображения уже дало плодотворные результаты. В частности, была выявлена фундаментальная аналогия между задачами радиосвязи и задачами образования изображения и спектроскопии, для решения которых в равной мере подходят и принцип суперпозиции и операторный метод. Один из методов, с помощью которого можно воссоздать распределение комплексной амплитуды  в плоскости апертуры линзы, сводится к тому, чтобы поместить в апертуру голограмму и дополнительно осветить ее плоской или сферической волной.
в плоскости апертуры линзы, сводится к тому, чтобы поместить в апертуру голограмму и дополнительно осветить ее плоской или сферической волной.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора русского издания
- Глава 1. ВВЕДЕНИЕ
- 1. Современная оптика — раздел радиоалектроники
- 2. Теория — основа радиооптики
- 3. Математические методы современной оптики
- 4. Краевая задача дифракции электромагнитных волн в оптике и некоторые ограничения операционного метода
- 5. Решение краевой задачи на примере дифракционной решетки [5]
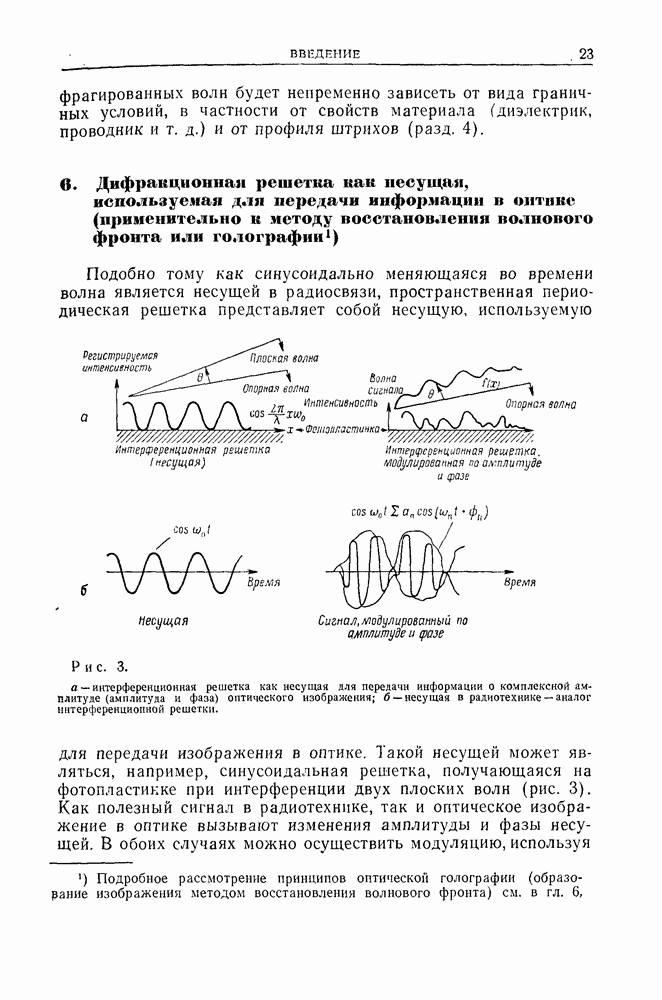
- 6. Дифракционная решетка как несущая, используемая для передачи информации в онтикс (применительно к методу восстановления волнового фронта или голографии
- 7. Оптика и теория связи Исторический обзор
- Глава 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФРАКЦИИ
- 1. Две стороны дифракции света
- 2. Распределение интенсивности в дифракционной картине и в спектре
- 2.2. Проблема образования изображения и принцип Гюйгенса
- 3. Теория образования изображения и обработка оптических сигналов при помощи преобразования Фурье
- Глава 3. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Сложение света, падающего из нескольких точек источника на отдельную точку изображения
- 6. Анализ процесса образования изображения в пространстве фурье-координат
- 7. Физический смысл функции разброса и анализ процесса образования изображения в плоскости фурье-координат
- 7.2. Синусоидальный по интенсивности предмет имеет функцию пространстненно-частотного отклика, совпадающую с фурье-образом дифракционной картины
- 8. Использование фурье-координат для синтеза предметных функций
- Глава 4. КОГЕРЕНТНОСТЬ СВЕТА (ЭКСПЕРИМЕНТАЛЬНЫЕ ХАРАКТЕРИСТИКИ)
- 2. Определение когерентности
- 2.2. Интерференционный анализ временной когерентности
- 2.3. Сравнение корреляционного и интерференционного методов
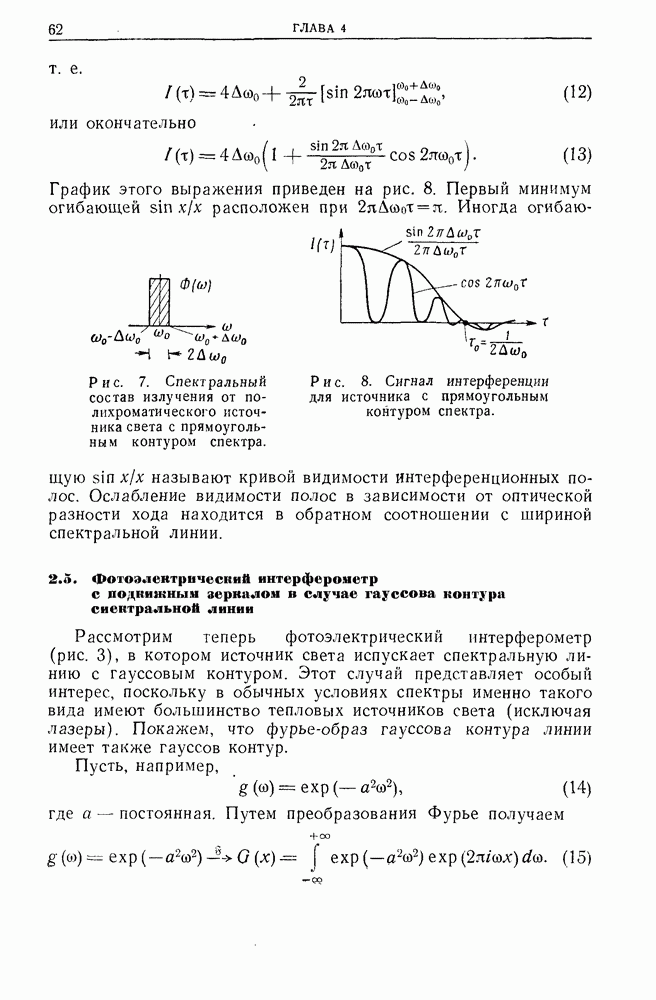
- 2.4. Узкий спектр с прямоугольным контуром
- 2.5. Фотоэлектрический интерферометр с поднижным зеркалом в случае гауссова контура спектральной линии
- 2.6. Физический смысл спектра мощности
- 2.7. Гетеродинный анализ сигналов и биений
- 2.8. Пространственная когерентность
- 2.9. Частичная когерентность света от протяженного некогерентного источника
- 2.10. Корреляция интенсивности при частичной когерентности
- 2.11. Интерферометр интенсивности
- Глава 5. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ КОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Когерентное освещение
- 3. Образование изображения при когерентном освещении как процесс двойной дифракции
- 4. Критерии разрешения Аббе и Релея
- 5. Передаточная функция при когерентном и некогерентном освещении
- 6. Фазовый контраст
- 7. Оптическая фильтрация с помощью голограммы согласованного фильтра
- 7.1. Процедура изготовления согласованного фильтра и операция фильтрации
- 8. Оптическая обработка информации, корреляционный анализ и оптические корреляторы
- 8.2. Оптический кросс-коррелятор
- 9. Интерферометрия и оптический синтез изображения (сложение комплексных амплитуд) методом последовательного наложения голографических картин на одну голограмму [5]
- Глава 6. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ОПТИЧЕСКОЙ ГОЛОГРАФИИ
- 2.1. Процесс получевия голограммы
- 2.2. Процесс восстановления изображения
- 2.3. Физические принципы голографии
- 2.4. Геометрическое увеличение
- 2.5. Разрешающая способность
- 3. Голография Фурье с высоким разрешением
- 3.2. Физические основы безлинзовой голографии Фурье высокого разрешения
- 3.3. Теория безлинзовой голографии Фурье
- 3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
- 4. Компенсация протяженности источника в голографии
- 5. Требование к когерентности в голографии
- 6. Сводка основных результатов
- 7. Электронный микроскоп и рентгеновский голографический микроскоп
- 8. Заключение
- 9. Голография при некогерентном освещении
- 9.2. Голография при пространственно-некогерентном освещении
- Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
- 1. Преобразование Фурье
- 2. Свертка
- 3. Функция корреляции
- 4. Распределения, или обобщенные функции
- 4.2. Импульсный отклик линейной системы
- 4.3. Отклик линейной системы на произвольную входную функцию
- 5. Спектральный анализ
- Дополнение автора к русскому изданию. ВОССТАНОВЛЕНИЕ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ В БЕЛОМ СВЕТЕ С ИСПОЛЬЗОВАНИЕМ ДИФРАКЦИОННОГО ЭФФЕКТА ЛИППМАНА — БРЭГГА
- ПРИЛОЖЕНИЕ 1. МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА
- Принцип восстановления волнового фронта
- Освещение сферической волной
- Восстановление при освещении точечным источником
- Побочная часть волны при восстановлении с помощью точечного источника
- Ухучшенне разделения изобрашений с помощью масок и других методов
- Освещающие волны с астигматизмом и сферической аберрацией
- Восстановление при наличии сферической аберрации и астигматизма
- Критерии когерентности
- Восстановление в оптическом диапазоне
- Экспериментальная проверка
- Заключение
- МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА, II
- 2. Принцип восстановления волнового фронта
- 3. Теория образования изображения при использовании метода пропускания
- 4. Восстановление
- 5. Критерии когерентности
- 6. Условия, необходимые для получения голограмм
- 7. Восстановление по методу темного поля
- ПРИЛОЖЕНИЕ 2. ПРИМЕНЕНИЯ ГОЛОГРАФИИ
- 2. Трехмерная фотография
- 3. Распознавание образов
- 4. Иитерференционная память
- 5. Интерферометрия
- 6. Голография в технологии
- 7. Голографический метод в интроскопии
- 8. Голографическая микроскопия
- 9. Голографическое кино
- 10. Голографическое телевидение
- 11. Голографическая оптика