| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
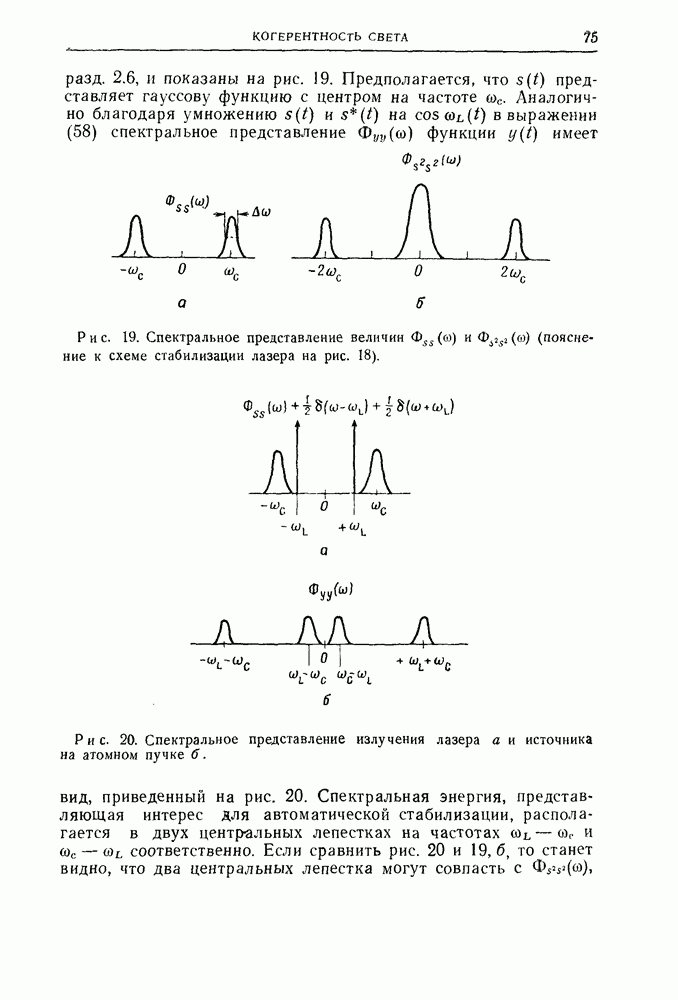
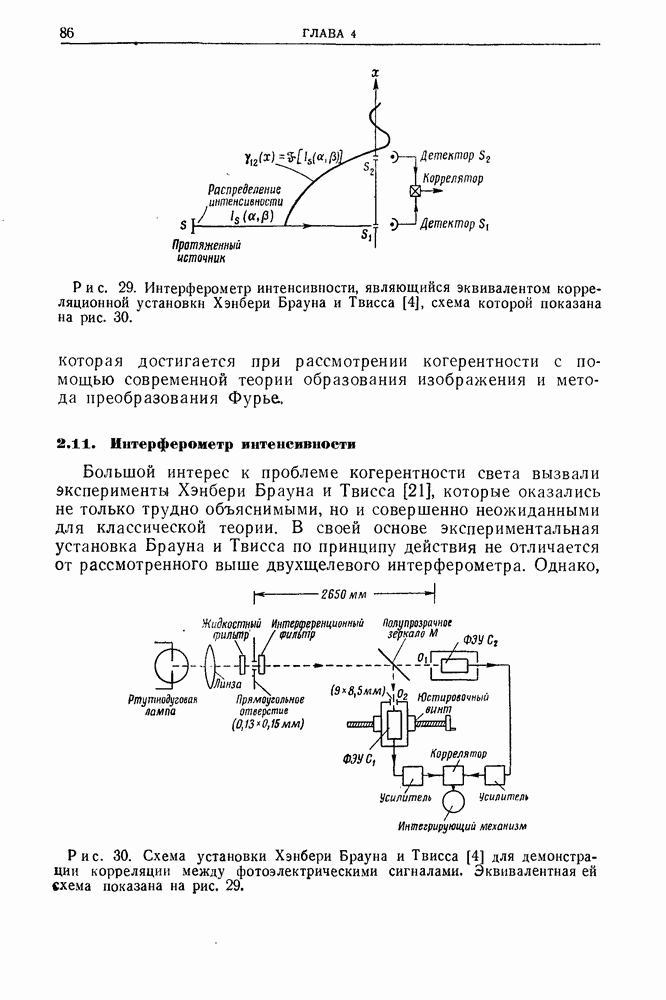
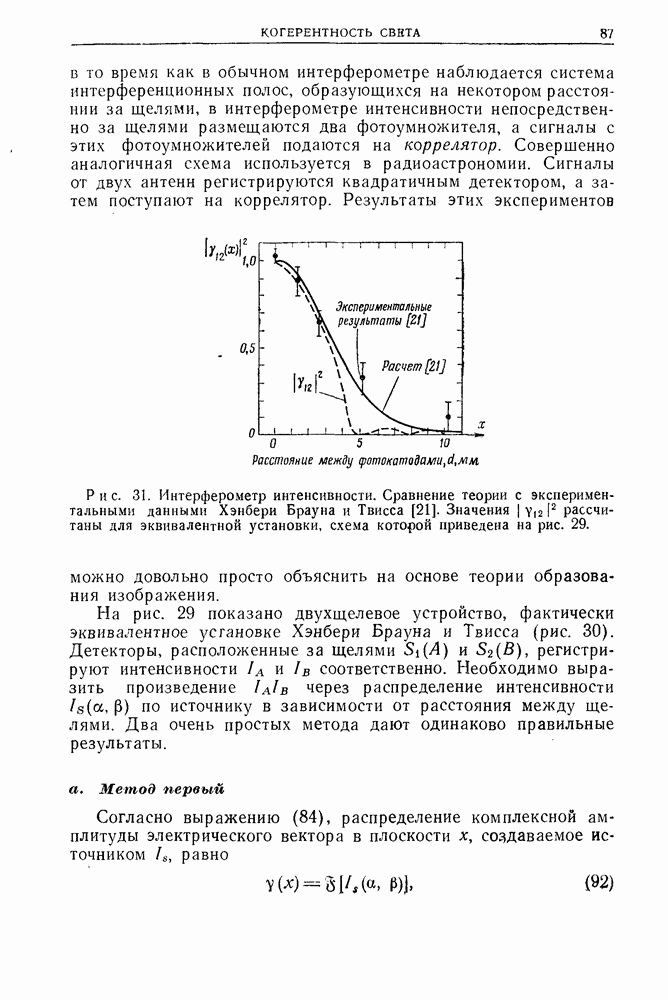
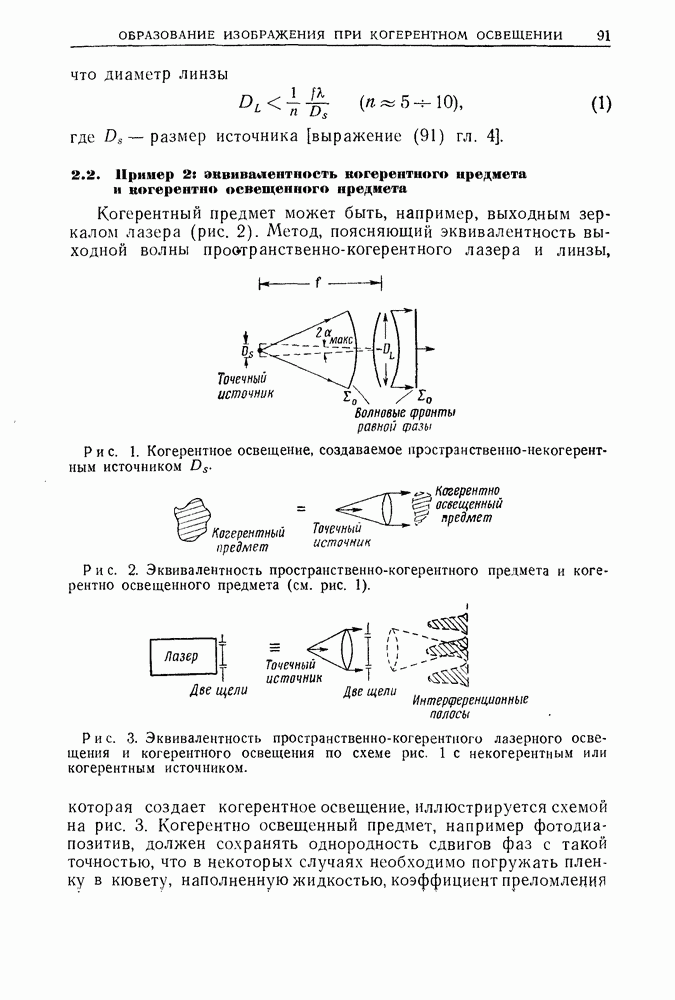
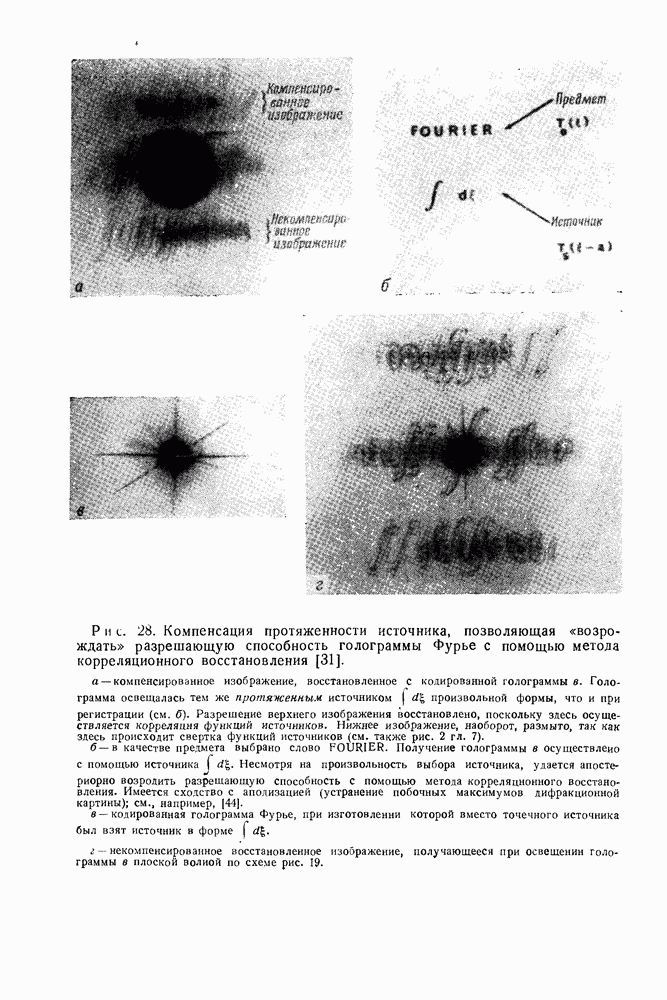
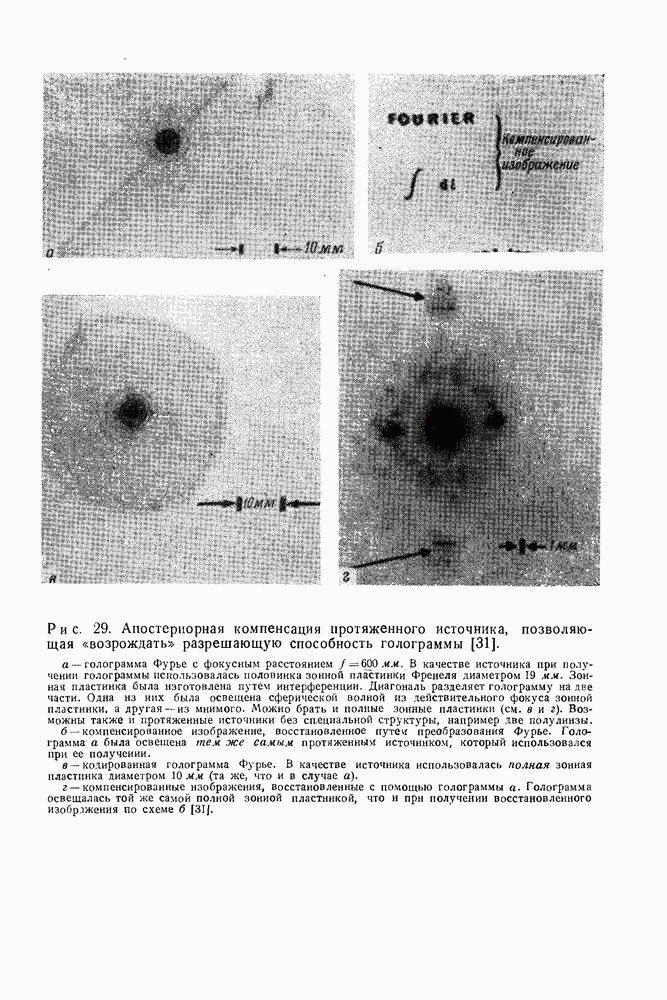
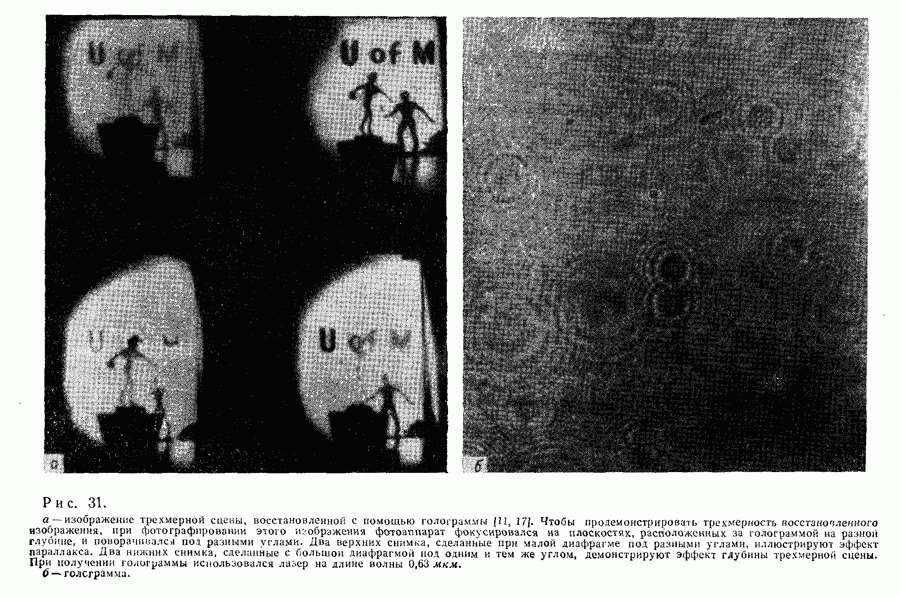
3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
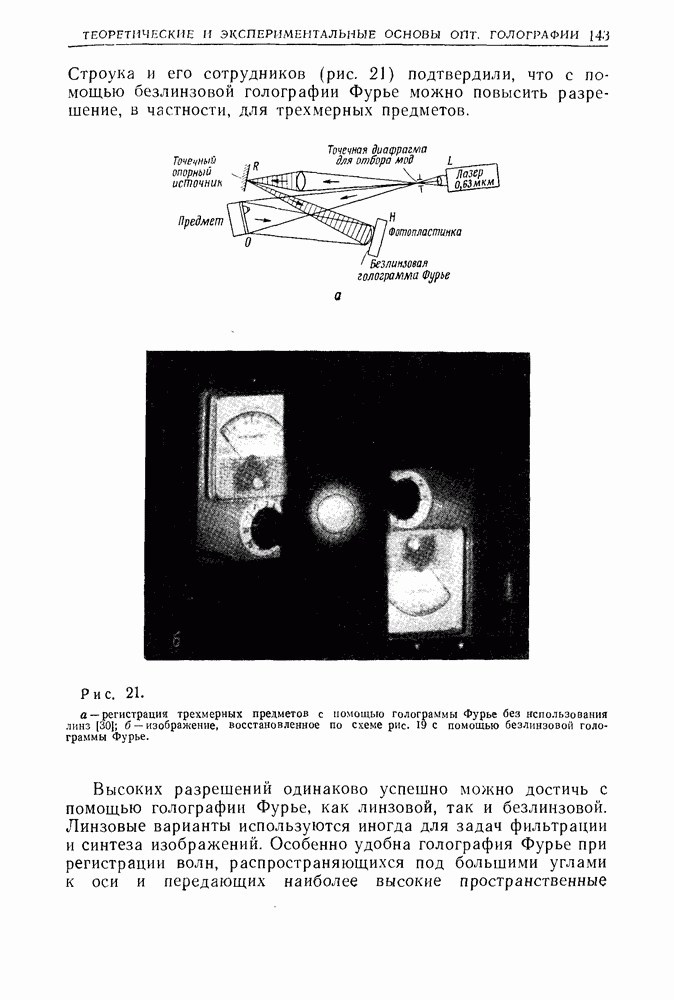
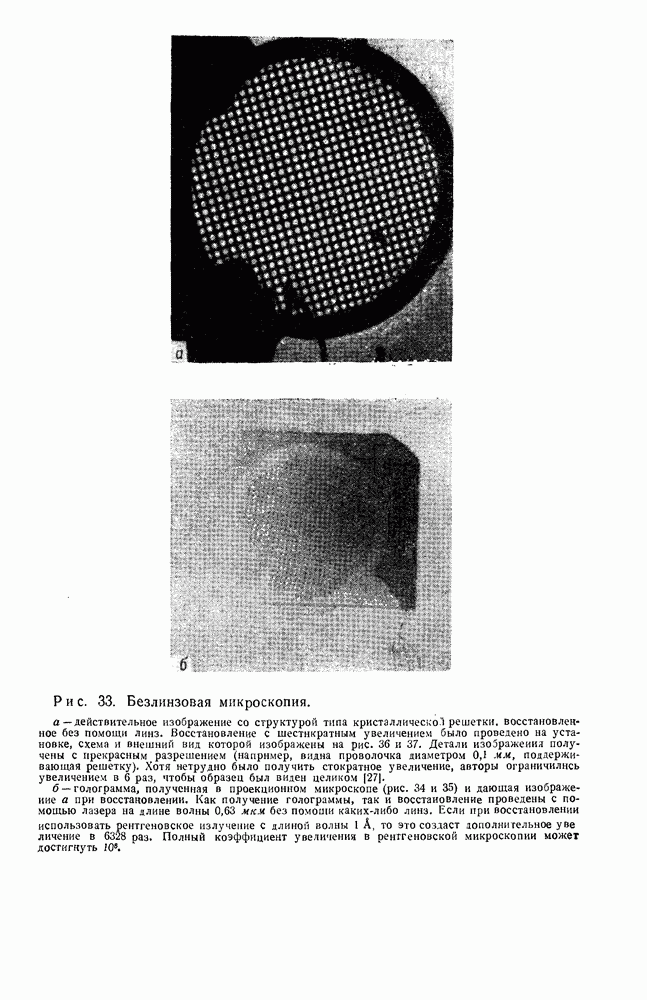
Голография Фурье, особенно ее безлинзовый вариант, вызывает к себе больший интерес, так как она дает высокое пространственное разрешение но предмету, особенно при захвате света, дифрагированного под большими углами.
Рассмотрим в качестве предмета двумерную дифракционную решетку, характеризуемую постоянной решетки а. Углы падения  и дифракции
и дифракции  связаны уравнением решетки [выражение (1) гл. 1].
связаны уравнением решетки [выражение (1) гл. 1].

Если излучение падает нормально к поверхности решетки  то
то

Отсюда видно, что если разрешение достигает величины порядка длины волны X, то угол дифракции составляет примерно 
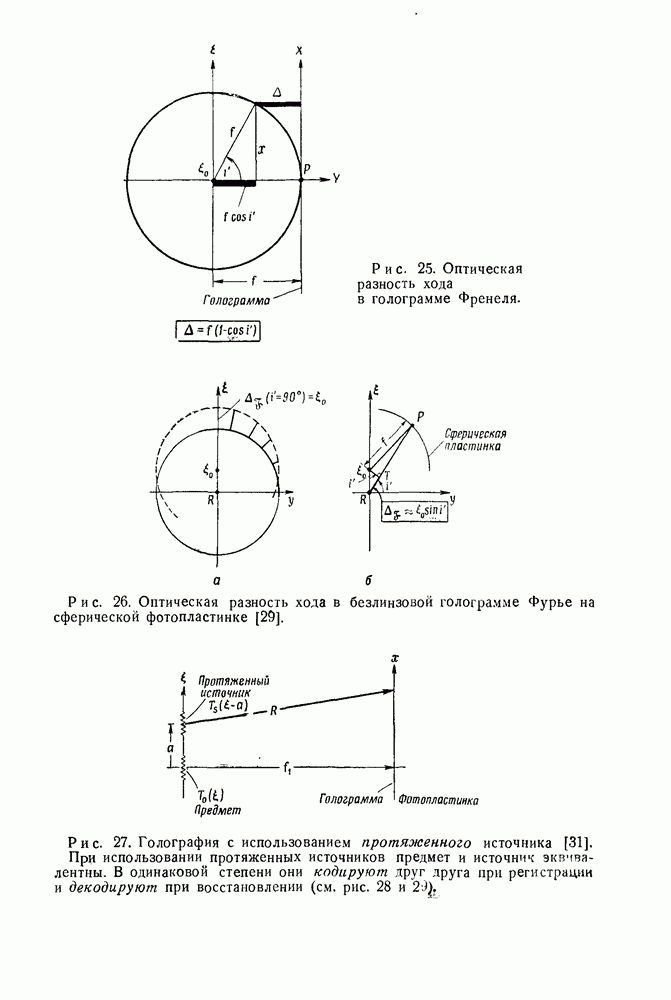
Если дифракция происходит под большими углами, то голограмма Френеля уже больше не описывается приближенными выражениями (24). Используя схему на рис. 25, можно показать, что оптическая разность хода равна

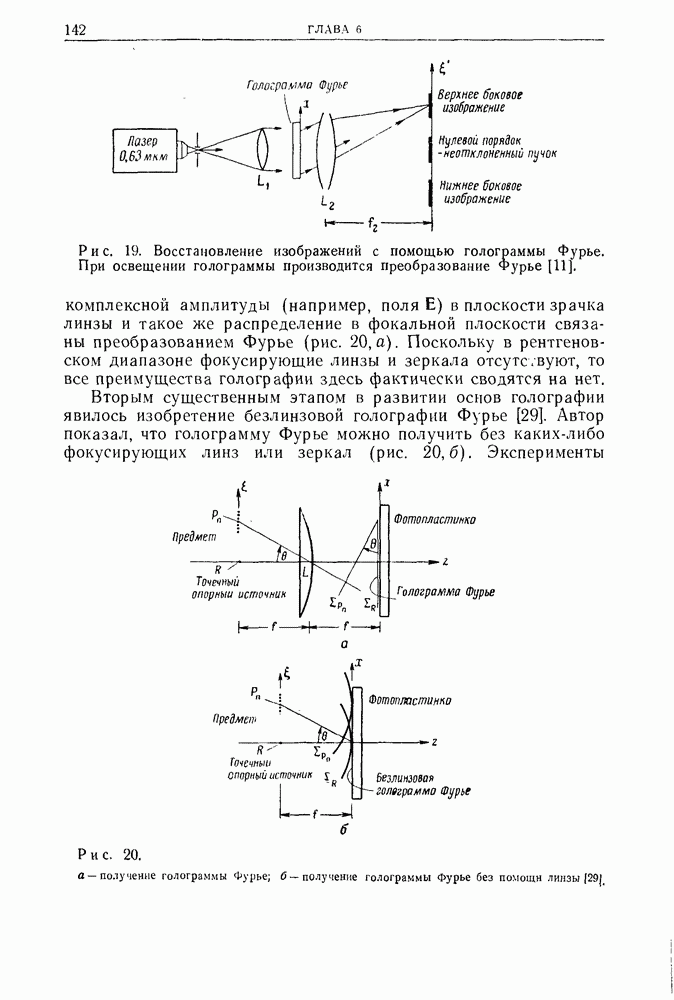
В безлинзовой голографии Фурье оптическая разность хода определяется совсем другим выражением (рис. 26)

Это выражение справедливо для любых углов, если только голограмма Фурье регистрируется на сферической фотопластинке. Для малых углов пластинка может оставаться плоской 
Сравнивая выражения (40) и (41), можно сделать вывод, что коэффициент «выигрыша» в разрешающей способности составит

Мы видим, что преимущества голографии Фурье по разрешающей способности по сравнению с голографией Френеля особенно заметны при больших углах дифракции и при малых расстояниях Если  (например,
(например,  то коэффициент «выигрыша»
то коэффициент «выигрыша»  в этом случае равен
в этом случае равен

Из таблицы видно, что даже при углах дифракции  голография Фурье дает выигрыш в 100 раз по сравнению с голографией Френеля для типичных в рентгеновской микроскопии
голография Фурье дает выигрыш в 100 раз по сравнению с голографией Френеля для типичных в рентгеновской микроскопии

(кликните для просмотра скана)
значений  а фактически этот выигрыш в разрешении может достигать трех порядков величины.
а фактически этот выигрыш в разрешении может достигать трех порядков величины.
Приведем также таблицу значений параметра  т. е. величины, которая в уравнении (42) заключена в квадратные скобки
т. е. величины, которая в уравнении (42) заключена в квадратные скобки

с величиной  она связана соотношением
она связана соотношением

Даже в микроскопии видимого или ультрафиолетового диапазона голография Фурье дает ощутимые преимущества, например при  выигрыш составляет 10, а при
выигрыш составляет 10, а при  выигрыш в разрешении превышает 30.
выигрыш в разрешении превышает 30.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора русского издания
- Глава 1. ВВЕДЕНИЕ
- 1. Современная оптика — раздел радиоалектроники
- 2. Теория — основа радиооптики
- 3. Математические методы современной оптики
- 4. Краевая задача дифракции электромагнитных волн в оптике и некоторые ограничения операционного метода
- 5. Решение краевой задачи на примере дифракционной решетки [5]
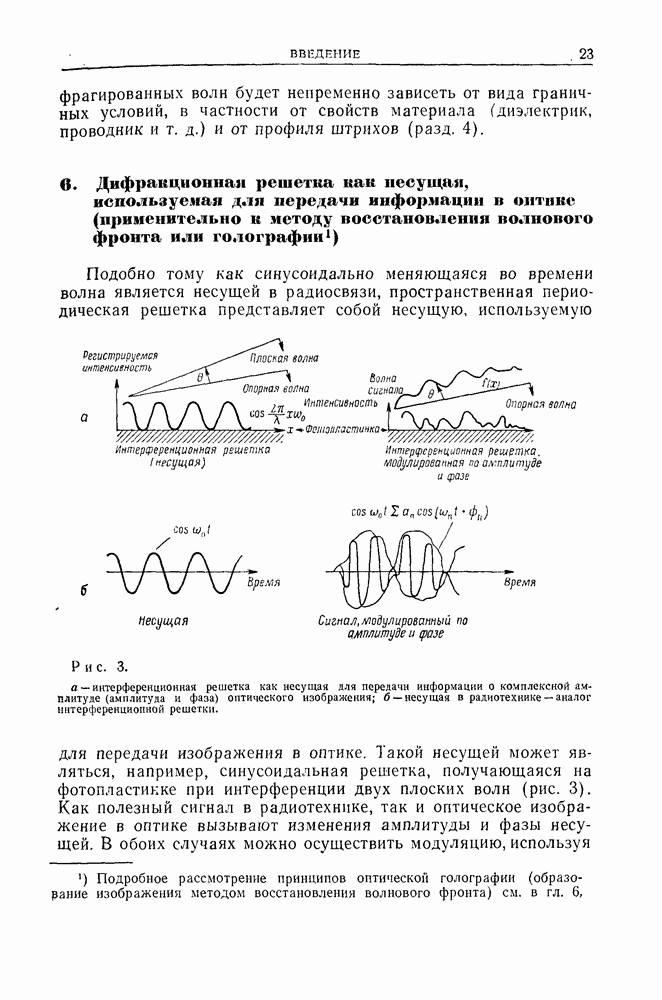
- 6. Дифракционная решетка как несущая, используемая для передачи информации в онтикс (применительно к методу восстановления волнового фронта или голографии
- 7. Оптика и теория связи Исторический обзор
- Глава 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФРАКЦИИ
- 1. Две стороны дифракции света
- 2. Распределение интенсивности в дифракционной картине и в спектре
- 2.2. Проблема образования изображения и принцип Гюйгенса
- 3. Теория образования изображения и обработка оптических сигналов при помощи преобразования Фурье
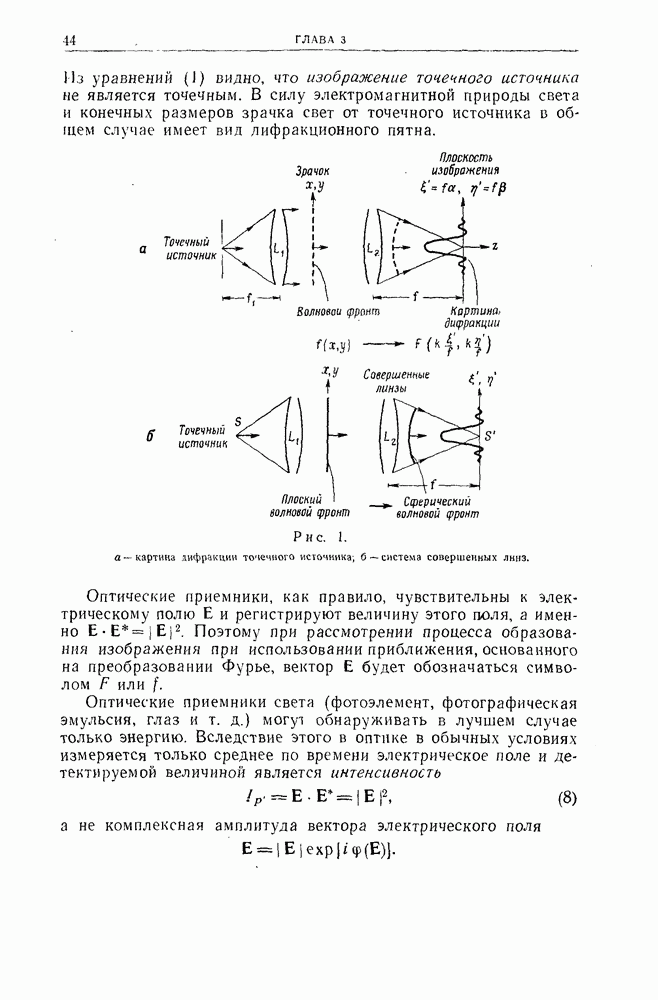
- Глава 3. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Сложение света, падающего из нескольких точек источника на отдельную точку изображения
- 6. Анализ процесса образования изображения в пространстве фурье-координат
- 7. Физический смысл функции разброса и анализ процесса образования изображения в плоскости фурье-координат
- 7.2. Синусоидальный по интенсивности предмет имеет функцию пространстненно-частотного отклика, совпадающую с фурье-образом дифракционной картины
- 8. Использование фурье-координат для синтеза предметных функций
- Глава 4. КОГЕРЕНТНОСТЬ СВЕТА (ЭКСПЕРИМЕНТАЛЬНЫЕ ХАРАКТЕРИСТИКИ)
- 2. Определение когерентности
- 2.2. Интерференционный анализ временной когерентности
- 2.3. Сравнение корреляционного и интерференционного методов
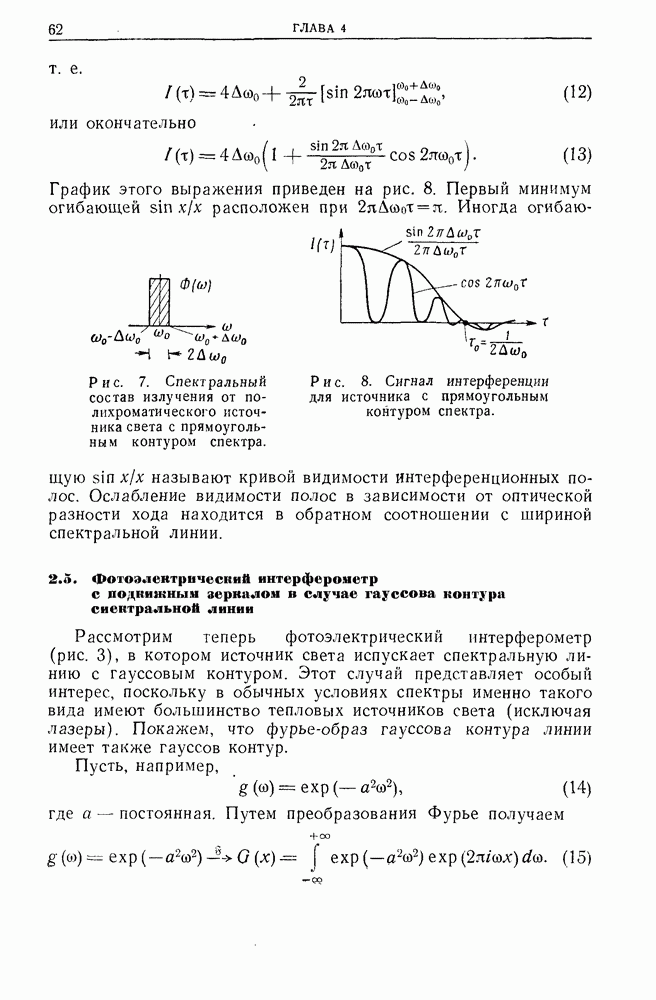
- 2.4. Узкий спектр с прямоугольным контуром
- 2.5. Фотоэлектрический интерферометр с поднижным зеркалом в случае гауссова контура спектральной линии
- 2.6. Физический смысл спектра мощности
- 2.7. Гетеродинный анализ сигналов и биений
- 2.8. Пространственная когерентность
- 2.9. Частичная когерентность света от протяженного некогерентного источника
- 2.10. Корреляция интенсивности при частичной когерентности
- 2.11. Интерферометр интенсивности
- Глава 5. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ КОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Когерентное освещение
- 3. Образование изображения при когерентном освещении как процесс двойной дифракции
- 4. Критерии разрешения Аббе и Релея
- 5. Передаточная функция при когерентном и некогерентном освещении
- 6. Фазовый контраст
- 7. Оптическая фильтрация с помощью голограммы согласованного фильтра
- 7.1. Процедура изготовления согласованного фильтра и операция фильтрации
- 8. Оптическая обработка информации, корреляционный анализ и оптические корреляторы
- 8.2. Оптический кросс-коррелятор
- 9. Интерферометрия и оптический синтез изображения (сложение комплексных амплитуд) методом последовательного наложения голографических картин на одну голограмму [5]
- Глава 6. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ОПТИЧЕСКОЙ ГОЛОГРАФИИ
- 2.1. Процесс получевия голограммы
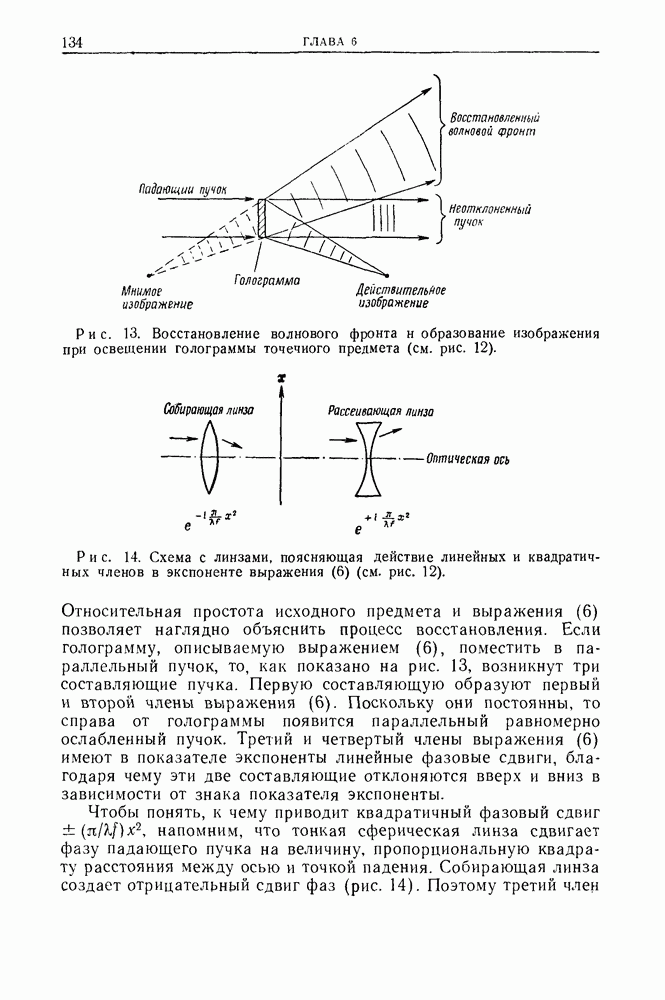
- 2.2. Процесс восстановления изображения
- 2.3. Физические принципы голографии
- 2.4. Геометрическое увеличение
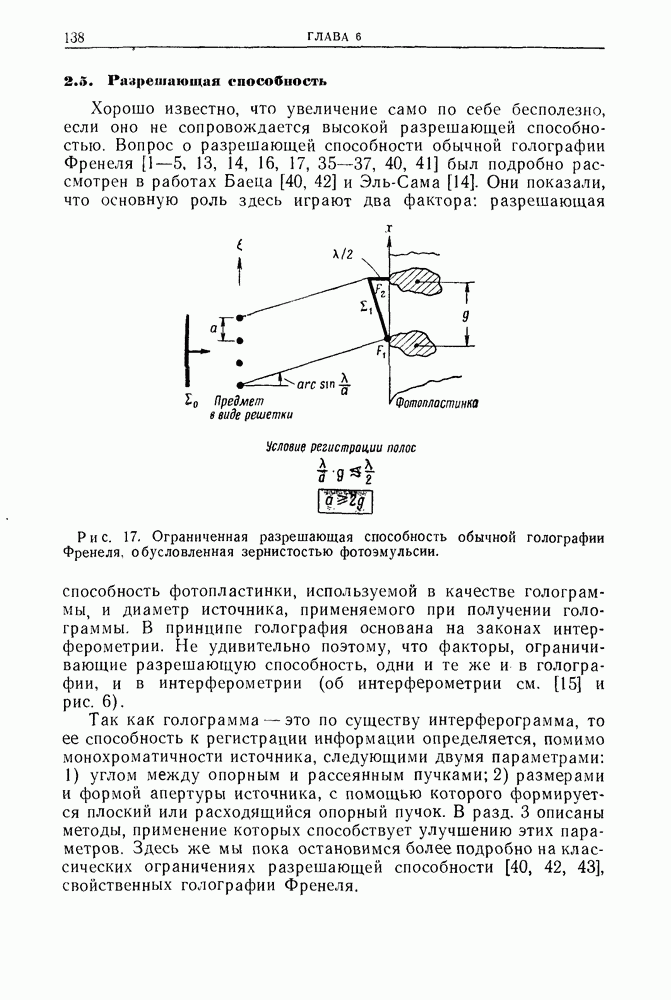
- 2.5. Разрешающая способность
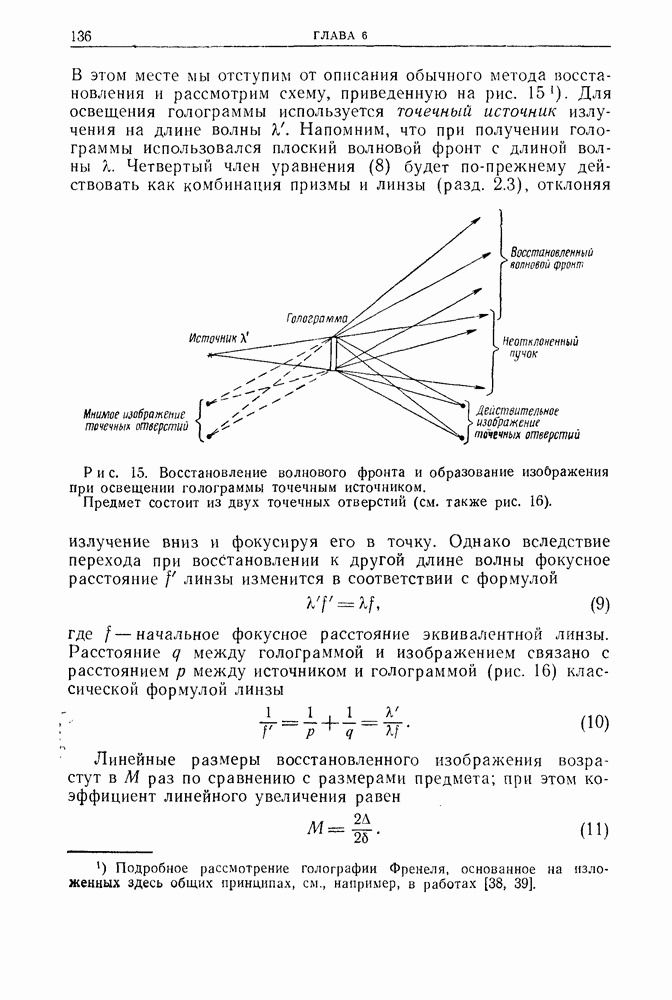
- 3. Голография Фурье с высоким разрешением
- 3.2. Физические основы безлинзовой голографии Фурье высокого разрешения
- 3.3. Теория безлинзовой голографии Фурье
- 3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
- 4. Компенсация протяженности источника в голографии
- 5. Требование к когерентности в голографии
- 6. Сводка основных результатов
- 7. Электронный микроскоп и рентгеновский голографический микроскоп
- 8. Заключение
- 9. Голография при некогерентном освещении
- 9.2. Голография при пространственно-некогерентном освещении
- Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
- 1. Преобразование Фурье
- 2. Свертка
- 3. Функция корреляции
- 4. Распределения, или обобщенные функции
- 4.2. Импульсный отклик линейной системы
- 4.3. Отклик линейной системы на произвольную входную функцию
- 5. Спектральный анализ
- Дополнение автора к русскому изданию. ВОССТАНОВЛЕНИЕ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ В БЕЛОМ СВЕТЕ С ИСПОЛЬЗОВАНИЕМ ДИФРАКЦИОННОГО ЭФФЕКТА ЛИППМАНА — БРЭГГА
- ПРИЛОЖЕНИЕ 1. МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА
- Принцип восстановления волнового фронта
- Освещение сферической волной
- Восстановление при освещении точечным источником
- Побочная часть волны при восстановлении с помощью точечного источника
- Ухучшенне разделения изобрашений с помощью масок и других методов
- Освещающие волны с астигматизмом и сферической аберрацией
- Восстановление при наличии сферической аберрации и астигматизма
- Критерии когерентности
- Восстановление в оптическом диапазоне
- Экспериментальная проверка
- Заключение
- МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА, II
- 2. Принцип восстановления волнового фронта
- 3. Теория образования изображения при использовании метода пропускания
- 4. Восстановление
- 5. Критерии когерентности
- 6. Условия, необходимые для получения голограмм
- 7. Восстановление по методу темного поля
- ПРИЛОЖЕНИЕ 2. ПРИМЕНЕНИЯ ГОЛОГРАФИИ
- 2. Трехмерная фотография
- 3. Распознавание образов
- 4. Иитерференционная память
- 5. Интерферометрия
- 6. Голография в технологии
- 7. Голографический метод в интроскопии
- 8. Голографическая микроскопия
- 9. Голографическое кино
- 10. Голографическое телевидение
- 11. Голографическая оптика