| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
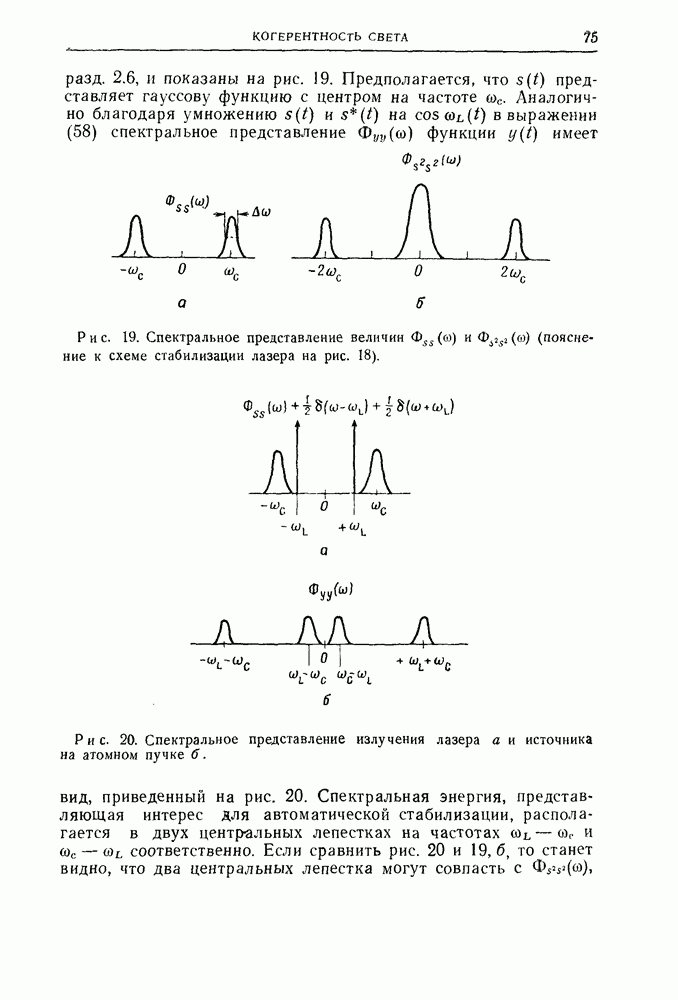
Преобразование Фурье и его различные приложения к операциям свертки, корреляции и распределениям в настоящее время уже вошли в арсенал теоретической оптики и стали ее неотъемлемым инструментом. Это видно на примерах теории образования изображения, интерферометрии, спектроскопии и, наконец, голографии. Даже элементарное рассмотрение теории преобразования Фурье, приведенное ниже, дает исследователям универсальное средство для анализа различных задач физической оптики, теории дифракции и интерферометрии. А во многих случаях использование только таких теорем, как теоремы смещения или теоремы свертки, которые будут даны в следующих разделах, позволяет быстро находить решения целого ряда задач, которые в прошлом требовали применения специально разработанных и часто весьма громоздких методов.
1. Преобразование Фурье
Если задана действительная или комплексная функция  действительного переменного х, меняющегося в пределах от
действительного переменного х, меняющегося в пределах от  до
до  такая, что существует интеграл
такая, что существует интеграл

т. е. функция  принадлежит к классу
принадлежит к классу  то фурье-образ
то фурье-образ  этой функции
этой функции  определяется выражением
определяется выражением

Часто выражение (2) записывается сокращенно в виде

или

где символ  обозначает преобразование Фурье, или фурье-образ функции, а стрелка обозначает сам процесс преобразования.
обозначает преобразование Фурье, или фурье-образ функции, а стрелка обозначает сам процесс преобразования.
Аналогично можно представить обратное преобразование Фурье, которое получается, если в экспоненте взять знак минус: 
Если функция  принадлежит к классу
принадлежит к классу  то
то

или в сокращенном виде

или, наконец,

где символ  означает обратное преобразование Фурье, или инверсный фурье-образ.
означает обратное преобразование Фурье, или инверсный фурье-образ.
1.1. Некоторые свойства преобразования Фурье
Приведем, как правило, без доказательства те свойства, которые очень часто используются в оптике.
1.2. Линейность
Пусть  комплексные постоянные. Из определения (2) непосредственно следует, что если
комплексные постоянные. Из определения (2) непосредственно следует, что если

то

1.3. Теорема смещения
Это наиболее важное свойство выражается соотношением, которое нетрудно доказать. Свойство смещения фурье-образа состоит в следующем.
Если

то

где  постоянная. Функция
постоянная. Функция  получена из первоначальной функции
получена из первоначальной функции  путем смещения начала отсчета в точку
путем смещения начала отсчета в точку  Действительно,
Действительно,

Если произвести замену переменных

то

преобразуется в

что и требовалось доказать.
1.4. Обратная теорема смещения
Это свойство является симметричным предыдущему, и его тоже легко доказать. Если

то

где  постоянная.
постоянная.
Если фурье-образ существует, то выражения (9) и (10) можно записать в следующем виде:

далее

и

Легко убедиться в целесообразности следующих обозначений (рис. 1):

где, например, выражение  соответствует функции
соответствует функции  если начало координат перенесено из точки
если начало координат перенесено из точки  в точку
в точку 

Рис. 1. Теорема смещения фурье-образа, вытекающая из (9).
С помощью выражений  мы можем записать систему (9) и (10) в такой форме
мы можем записать систему (9) и (10) в такой форме

Наконец, следует обратить внимание на то, что различие между фурье-образом, который содержит  и инверсным фурье-образом, содержащим
и инверсным фурье-образом, содержащим  имеет существенное значение, когда производят сложение или вычитание двух фурье-образов (96) и (9в). Соответствующим примером служат соотношения (58) — (64).
имеет существенное значение, когда производят сложение или вычитание двух фурье-образов (96) и (9в). Соответствующим примером служат соотношения (58) — (64).
1.5. Таблица свойств преобразования Фурье
Таблица свойств преобразования Фурье, приводимая без доказательств, дана здесь ввиду значимости этих свойств для многих оптических задач. Большинство необходимых доказательств легко выполнить по схеме, использованной в предыдущем разделе. Если  постоянные величины, то
постоянные величины, то

1.6. Двумерное и многомерное преобразования Фурье
Если учесть очевидное ограничение [как и в случае соотношения (1)], то вместо  можно использовать переменные
можно использовать переменные  а также
а также  и соответствующие кратные интегралы в формулах преобразования.
и соответствующие кратные интегралы в формулах преобразования.
1.7. Изменение масштаба и преобразование Фурье
Докажем, что если

то

где а — комплексная постоянная с модулем  Нам требуется доказать
Нам требуется доказать

Пусть  Рассмотрим сначма
Рассмотрим сначма  Если
Если  то
то  и
и

Теперь пусть  Если
Если  то
то  и
и

В общем случае  имеем
имеем

что и требовалось доказать.
Особый случай изменения масштаба возникает при 

Важный класс преобразования комплексно-сопряженной функции рассматривается в следующем разделе.
1.8. Фурье-образ комплексно-сопряженной функции
Этот важный класс преобразований встречается в оптике очень часто. Пусть  комплексно-сопряженная функция к
комплексно-сопряженная функция к  Иначе говоря,
Иначе говоря,  получается из
получается из  путем замены всех
путем замены всех  на
на  Учитывая это, найдем, что
Учитывая это, найдем, что

Действительпо, сразу получаем

что и требовалось доказать.
1.9. Тригонометрическая форма преобразования Фурье
Часто используется следующая тригонометрическая форма преобразования Фурье:

1.10. Свойства симметрии
Используя предыдущие уравнения, легко доказать следующие важные соотнощения.
Если  действительна, т. е.
действительна, т. е.

то

или

Если  действительна и четна, т. е.
действительна и четна, т. е.

то

Если  действительна и нечетна, т. е.
действительна и нечетна, т. е.

то

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора русского издания
- Глава 1. ВВЕДЕНИЕ
- 1. Современная оптика — раздел радиоалектроники
- 2. Теория — основа радиооптики
- 3. Математические методы современной оптики
- 4. Краевая задача дифракции электромагнитных волн в оптике и некоторые ограничения операционного метода
- 5. Решение краевой задачи на примере дифракционной решетки [5]
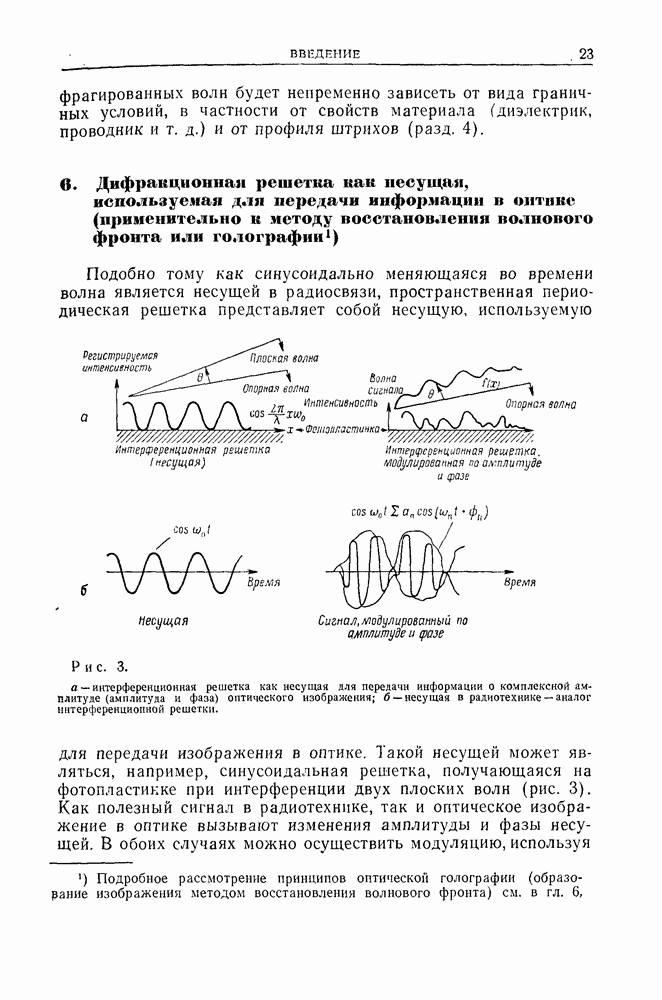
- 6. Дифракционная решетка как несущая, используемая для передачи информации в онтикс (применительно к методу восстановления волнового фронта или голографии
- 7. Оптика и теория связи Исторический обзор
- Глава 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФРАКЦИИ
- 1. Две стороны дифракции света
- 2. Распределение интенсивности в дифракционной картине и в спектре
- 2.2. Проблема образования изображения и принцип Гюйгенса
- 3. Теория образования изображения и обработка оптических сигналов при помощи преобразования Фурье
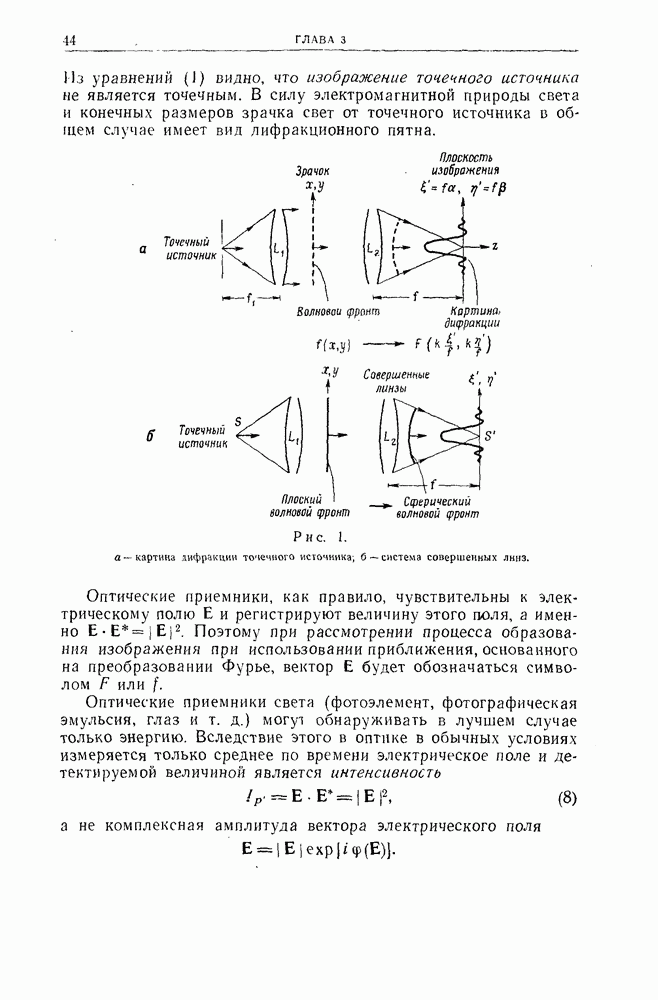
- Глава 3. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Сложение света, падающего из нескольких точек источника на отдельную точку изображения
- 6. Анализ процесса образования изображения в пространстве фурье-координат
- 7. Физический смысл функции разброса и анализ процесса образования изображения в плоскости фурье-координат
- 7.2. Синусоидальный по интенсивности предмет имеет функцию пространстненно-частотного отклика, совпадающую с фурье-образом дифракционной картины
- 8. Использование фурье-координат для синтеза предметных функций
- Глава 4. КОГЕРЕНТНОСТЬ СВЕТА (ЭКСПЕРИМЕНТАЛЬНЫЕ ХАРАКТЕРИСТИКИ)
- 2. Определение когерентности
- 2.2. Интерференционный анализ временной когерентности
- 2.3. Сравнение корреляционного и интерференционного методов
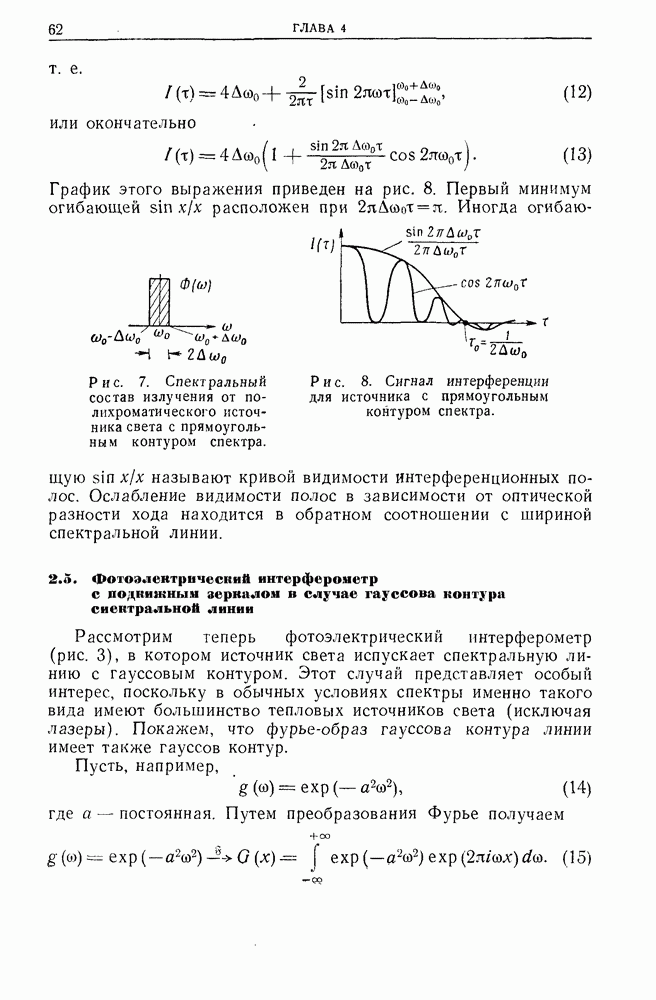
- 2.4. Узкий спектр с прямоугольным контуром
- 2.5. Фотоэлектрический интерферометр с поднижным зеркалом в случае гауссова контура спектральной линии
- 2.6. Физический смысл спектра мощности
- 2.7. Гетеродинный анализ сигналов и биений
- 2.8. Пространственная когерентность
- 2.9. Частичная когерентность света от протяженного некогерентного источника
- 2.10. Корреляция интенсивности при частичной когерентности
- 2.11. Интерферометр интенсивности
- Глава 5. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ КОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Когерентное освещение
- 3. Образование изображения при когерентном освещении как процесс двойной дифракции
- 4. Критерии разрешения Аббе и Релея
- 5. Передаточная функция при когерентном и некогерентном освещении
- 6. Фазовый контраст
- 7. Оптическая фильтрация с помощью голограммы согласованного фильтра
- 7.1. Процедура изготовления согласованного фильтра и операция фильтрации
- 8. Оптическая обработка информации, корреляционный анализ и оптические корреляторы
- 8.2. Оптический кросс-коррелятор
- 9. Интерферометрия и оптический синтез изображения (сложение комплексных амплитуд) методом последовательного наложения голографических картин на одну голограмму [5]
- Глава 6. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ОПТИЧЕСКОЙ ГОЛОГРАФИИ
- 2.1. Процесс получевия голограммы
- 2.2. Процесс восстановления изображения
- 2.3. Физические принципы голографии
- 2.4. Геометрическое увеличение
- 2.5. Разрешающая способность
- 3. Голография Фурье с высоким разрешением
- 3.2. Физические основы безлинзовой голографии Фурье высокого разрешения
- 3.3. Теория безлинзовой голографии Фурье
- 3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
- 4. Компенсация протяженности источника в голографии
- 5. Требование к когерентности в голографии
- 6. Сводка основных результатов
- 7. Электронный микроскоп и рентгеновский голографический микроскоп
- 8. Заключение
- 9. Голография при некогерентном освещении
- 9.2. Голография при пространственно-некогерентном освещении
- Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
- 1. Преобразование Фурье
- 2. Свертка
- 3. Функция корреляции
- 4. Распределения, или обобщенные функции
- 4.2. Импульсный отклик линейной системы
- 4.3. Отклик линейной системы на произвольную входную функцию
- 5. Спектральный анализ
- Дополнение автора к русскому изданию. ВОССТАНОВЛЕНИЕ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ В БЕЛОМ СВЕТЕ С ИСПОЛЬЗОВАНИЕМ ДИФРАКЦИОННОГО ЭФФЕКТА ЛИППМАНА — БРЭГГА
- ПРИЛОЖЕНИЕ 1. МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА
- Принцип восстановления волнового фронта
- Освещение сферической волной
- Восстановление при освещении точечным источником
- Побочная часть волны при восстановлении с помощью точечного источника
- Ухучшенне разделения изобрашений с помощью масок и других методов
- Освещающие волны с астигматизмом и сферической аберрацией
- Восстановление при наличии сферической аберрации и астигматизма
- Критерии когерентности
- Восстановление в оптическом диапазоне
- Экспериментальная проверка
- Заключение
- МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА, II
- 2. Принцип восстановления волнового фронта
- 3. Теория образования изображения при использовании метода пропускания
- 4. Восстановление
- 5. Критерии когерентности
- 6. Условия, необходимые для получения голограмм
- 7. Восстановление по методу темного поля
- ПРИЛОЖЕНИЕ 2. ПРИМЕНЕНИЯ ГОЛОГРАФИИ
- 2. Трехмерная фотография
- 3. Распознавание образов
- 4. Иитерференционная память
- 5. Интерферометрия
- 6. Голография в технологии
- 7. Голографический метод в интроскопии
- 8. Голографическая микроскопия
- 9. Голографическое кино
- 10. Голографическое телевидение
- 11. Голографическая оптика