| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Освещение сферической волной
Чтобы более подробно изучить процесс восстановления, будет полезно начать с простого случая освещения точечным источником. Такое освещение может быть в первом приближении осуществлено с помощью достаточно малого отверстия, используемого в качестве источника света. Вначале будет удобно ограничить обсуждение двумерными предметами, занимающими часть замкнутой поверхности  которая включает точечный источник О. Предмет в точке
которая включает точечный источник О. Предмет в точке  поверхности
поверхности  может быть охарактеризован коэффициентом пропускания амплитуды
может быть охарактеризован коэффициентом пропускания амплитуды  который равен отношению комплексных амплитуд по обе стороны от
который равен отношению комплексных амплитуд по обе стороны от  в окрестности точки
в окрестности точки  Коэффициент
Коэффициент  вообще говоря, комплексный; он действителен лишь в случае чисто поглощающих предметов. Вполне очевидно, что понятие коэффициента пропускания (действительного или комплексного) не применимо к предмету, который является двумерным в математическом смысле. Что же касается физического предмета, к которому это понятие применимо, то мы должны предположить, что его толщина равна по крайней мере нескольким длинам волн. Более того, мы должны предположить, что вдоль поверхности
вообще говоря, комплексный; он действителен лишь в случае чисто поглощающих предметов. Вполне очевидно, что понятие коэффициента пропускания (действительного или комплексного) не применимо к предмету, который является двумерным в математическом смысле. Что же касается физического предмета, к которому это понятие применимо, то мы должны предположить, что его толщина равна по крайней мере нескольким длинам волн. Более того, мы должны предположить, что вдоль поверхности  функция
функция  не изменяется заметно в пределах длины волны. Таковы условия применимости теории дифракции Френеля — Кирхгофа. В электронной оптике при использовании быстрых электронов с длиной волны около 0,05 А эти условия всегда выполняются, так как не существует предметов (исключая атомные ядра), чьи физические свойства изменялись бы значительно в пределах расстояния около десяти длин волн,
не изменяется заметно в пределах длины волны. Таковы условия применимости теории дифракции Френеля — Кирхгофа. В электронной оптике при использовании быстрых электронов с длиной волны около 0,05 А эти условия всегда выполняются, так как не существует предметов (исключая атомные ядра), чьи физические свойства изменялись бы значительно в пределах расстояния около десяти длин волн,
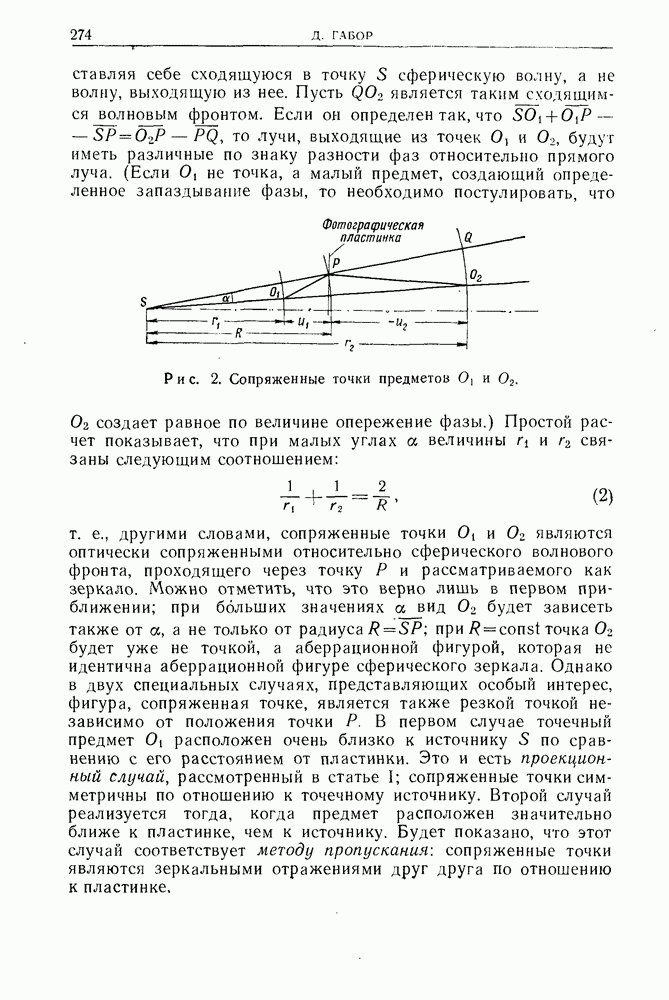
С учетом этих ограничении мы можем применить дифракционную формулу Френеля — Кирхгофа (ср., например, [6, стр. 73]). Обозначения пояснены на рис. 2.

Рис. 2. Схема, поясняющая дифракционную формулу Френеля — Кирхгофа.
Если в точке  положен источник монохроматического излучения единичной интенсивности, то амплитуда освещающей волны равна
положен источник монохроматического излучения единичной интенсивности, то амплитуда освещающей волны равна

где  расстояние, отсчитываемое от точки
расстояние, отсчитываемое от точки  Наличие предмета на поверхности 2 приводит к изменению амплитуды за точкой
Наличие предмета на поверхности 2 приводит к изменению амплитуды за точкой  до значения
до значения

Применим теперь эту формулу для того, чтобы рассчитать «физическую тень» плоского предмета на бесконечности. Физическая тень включает дифракционные эффекты, и ее необходимо отличать от «геометрической тени», в которую она переходит при неограниченном уменьшении длины волны.
Поскольку используемые на практике пучки имеют углы расходимости порядка 0,05 или меньше, мы можем положить  и считать множитель
и считать множитель  постоянной величиной. Мы также опустим постоянный множитель
постоянной величиной. Мы также опустим постоянный множитель  и запишем уравнение (7) в упрощенной форме
и запишем уравнение (7) в упрощенной форме

Используя обозначения, которые поясняются на рис. 3, получаем следующее выражение для расстояния  от начала отсчета до некоторой точки
от начала отсчета до некоторой точки  в плоскости предмета
в плоскости предмета 

В этом разделе мы будем использовать лишь два первых члена разложения.
Точка наблюдения  может быть расположена в направлении оси
может быть расположена в направлении оси  на некотором расстоянии
на некотором расстоянии  очень большом по сравнению с
очень большом по сравнению с  (практически на бесконечности), так что мы можем написать
(практически на бесконечности), так что мы можем написать

Первые члены в выражениях для  определяют постоянные фазовые множители, не зависящие от х и у, которые могут быть опущены.
определяют постоянные фазовые множители, не зависящие от х и у, которые могут быть опущены.

Рис. 3. Схема для пояснения обозначений.
Остающаяся существенная часть (7.1) может быть названа «амплитудой волны, распространяющейся в направлении  и равна
и равна

Если пределы интегрирования не указаны, то в этой статье далее всегда будет подразумеваться, что интегрирование производится в бесконечных пределах. Так как фаза в подынтегральном выражении справедлива лишь для малых углов, уравнение (8) имеет физический смысл только в том случае, если  быстро убывает до исчезающе малых значений вне малой центральной области.
быстро убывает до исчезающе малых значений вне малой центральной области.
Теперь вместо направляющих косинусов удобно ввести «фурье-координаты»  с помощью соотношений
с помощью соотношений

Связь этих переменных с координатами  в плоскости, расположенной на большом расстоянии
в плоскости, расположенной на большом расстоянии  определяется выражениями
определяется выражениями

Если угол расходимости освешаюшего пучка достаточно мал, то  можно рассматривать как координаты в плоскости физической тени. Геометрическая тень точки
можно рассматривать как координаты в плоскости физической тени. Геометрическая тень точки  имеет фурье-координаты
имеет фурье-координаты  Величина
Величина

является единственным параметром дифракционной задачи. Квадратный корень из нее можно рассматривать как характеристическую длину. Далее будет показано, что детали с размерами, большими имеют тени, более или менее подобные самим деталям, однако тени более мелких деталей при дифракции теряют всякое сходство с самими деталями.
Используя обозначения (9) и (10), а также подстановку  уравнение (8) можно записать в виде
уравнение (8) можно записать в виде

Таким образом, амплитуда волны, распространяющейся в направлении  равна, согласно стандартным обозначениям [7], фурье-образу функции
равна, согласно стандартным обозначениям [7], фурье-образу функции

Мы можем сразу же написать выражение и для обратного преобразования

Полезно исследовать эти преобразования чисто математически, временно пренебрегая условиями, которые должны быть наложены на функцию  чтобы придать ей физический смысл. Прежде всего мы представим их в более симметричной форме. Предположим, что амплитуда
чтобы придать ей физический смысл. Прежде всего мы представим их в более симметричной форме. Предположим, что амплитуда  получается при прохождении освещающей волны
получается при прохождении освещающей волны  через «тень предмета» в плоскости
через «тень предмета» в плоскости  обладающую пропусканием
обладающую пропусканием  (Можно отметить, что
(Можно отметить, что  вообще говоря, комплексная величина; следовательно, тень предмета не может быть заменена фотографическим негативом.) Другими словами, пусть
вообще говоря, комплексная величина; следовательно, тень предмета не может быть заменена фотографическим негативом.) Другими словами, пусть

Фон  можно получить непосредственно из уравнения (11), положив
можно получить непосредственно из уравнения (11), положив  и обозначив
и обозначив 

Окончательно фурье-образ и прообраз описываются симметричными формулами

Их можно назвать прямым и обратным «теневыми преобразованиями», а функции  -парой «теневых образов». Они, конечно, тесно связаны с фурье-образами, хотя в некоторых отношениях и проще их.
-парой «теневых образов». Они, конечно, тесно связаны с фурье-образами, хотя в некоторых отношениях и проще их.
Преобразования (14) и (15) можно получить одно из другого с помощью следуюпдего правила. Заменим  на х на у на
на х на у на  т. е. латинские символы греческими, а также заменим
т. е. латинские символы греческими, а также заменим  на
на  на
на  Два последовательных преобразования восстанавливают исходный предмет. Физически это означает, что если бы вместо фотографии мы могли бы получить «тень предмета», поглощение и преломление в которой определяются функцией
Два последовательных преобразования восстанавливают исходный предмет. Физически это означает, что если бы вместо фотографии мы могли бы получить «тень предмета», поглощение и преломление в которой определяются функцией  и осветили бы ее когерентным фоном, то мы должны были бы в точности восстановить предмет
и осветили бы ее когерентным фоном, то мы должны были бы в точности восстановить предмет  в его первоначальном положении. Так как фотография не может передать мнимую часть функции
в его первоначальном положении. Так как фотография не может передать мнимую часть функции  то при освещении ее когерентным фоном возникает определенная остаточная волна, которую мы рассмотрим в следующем разделе. Но сначала полезно рассмотреть несколько примеров теневых преобразований.
то при освещении ее когерентным фоном возникает определенная остаточная волна, которую мы рассмотрим в следующем разделе. Но сначала полезно рассмотреть несколько примеров теневых преобразований.
Как и в случае интегралов Фурье, образы экспоненциальных функций от квадратичных форм особенно просты и поучительны. Удобно записать их в следующем виде:

Это - произведение множителя, зависящего от х, на множитель, зависящий от у, а так как образ в свою очередь равен произведению сомножителей, зависящих от  , то достаточно найти образ функции
, то достаточно найти образ функции

который равен

Следовательно, теневой образ экспоненциальной функции от квадратичной формы является функцией того же самого типа,
что и фурье-образ экспоненты, но соотношение между параметрами будет другим. Например, если  постоянная величина, то
постоянная величина, то  будет равно той же самой постоянной, в то время как фурье-образ постоянной величины есть дельта-функция, которая обрашается в нуль всюду, кроме точки, где аргумент равен нулю. Далее теневой образ гармонической функции
будет равно той же самой постоянной, в то время как фурье-образ постоянной величины есть дельта-функция, которая обрашается в нуль всюду, кроме точки, где аргумент равен нулю. Далее теневой образ гармонической функции

снова является гармонической функцией

Период тени равен  что совпадает с геометрической тенью периода
что совпадает с геометрической тенью периода  Единственное отличие заключается в фазовом множителе
Единственное отличие заключается в фазовом множителе  -Если период
-Если период  велик по сравнению с характеристической длиной то фазовый множитель стремится к единице. Это означает, что если предмет не содержит более мелких деталей, нежели то физическая тень стремится к геометрической:
велик по сравнению с характеристической длиной то фазовый множитель стремится к единице. Это означает, что если предмет не содержит более мелких деталей, нежели то физическая тень стремится к геометрической:

Уравнения (16.3) и (16.4) указывают простое правило построения теневого образа предмета путем разложения функции  в интеграл Фурье с периодами
в интеграл Фурье с периодами  Фурье-коэффициенты образа будут отличаться от оригинала только фазовым множителем
Фурье-коэффициенты образа будут отличаться от оригинала только фазовым множителем

Для практических целей этот метод следует использовать осторожно, так как бесконечные цуги периодических функций не очень пригодны для описания малых предметов и так как применимость уравнений (14) и (15) к физическим процессам, строго говоря, ограничена предметами, которые заметно пропускают свет лишь в области 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора русского издания
- Глава 1. ВВЕДЕНИЕ
- 1. Современная оптика — раздел радиоалектроники
- 2. Теория — основа радиооптики
- 3. Математические методы современной оптики
- 4. Краевая задача дифракции электромагнитных волн в оптике и некоторые ограничения операционного метода
- 5. Решение краевой задачи на примере дифракционной решетки [5]
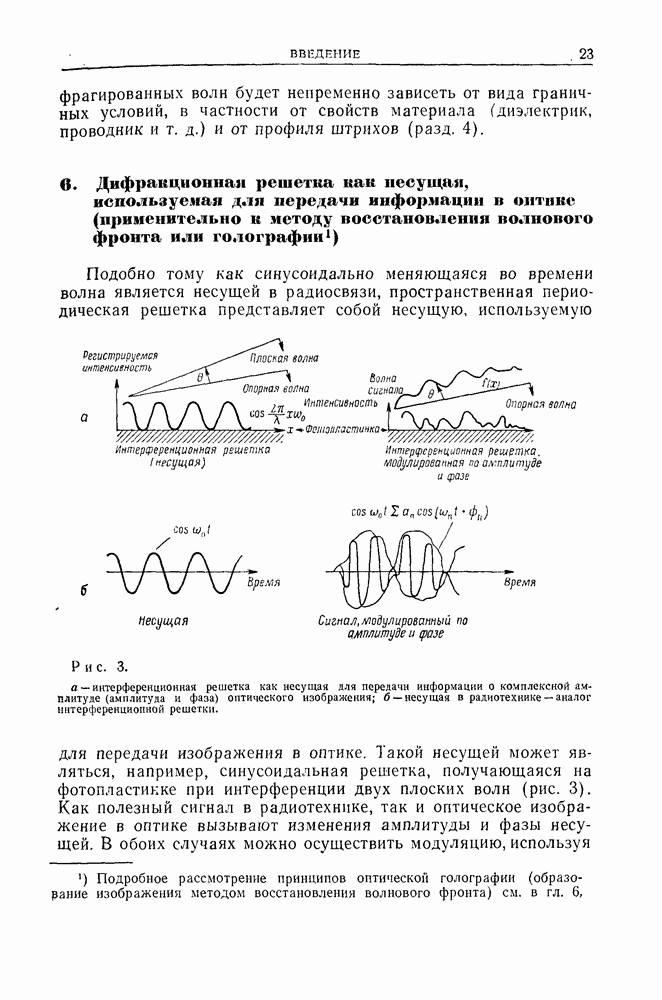
- 6. Дифракционная решетка как несущая, используемая для передачи информации в онтикс (применительно к методу восстановления волнового фронта или голографии
- 7. Оптика и теория связи Исторический обзор
- Глава 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФРАКЦИИ
- 1. Две стороны дифракции света
- 2. Распределение интенсивности в дифракционной картине и в спектре
- 2.2. Проблема образования изображения и принцип Гюйгенса
- 3. Теория образования изображения и обработка оптических сигналов при помощи преобразования Фурье
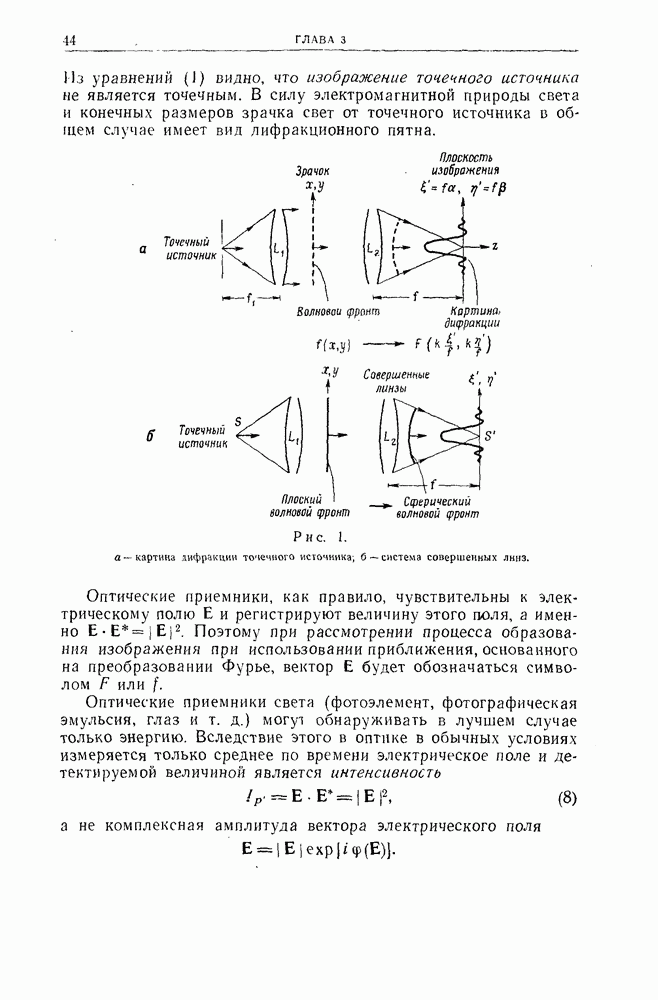
- Глава 3. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Сложение света, падающего из нескольких точек источника на отдельную точку изображения
- 6. Анализ процесса образования изображения в пространстве фурье-координат
- 7. Физический смысл функции разброса и анализ процесса образования изображения в плоскости фурье-координат
- 7.2. Синусоидальный по интенсивности предмет имеет функцию пространстненно-частотного отклика, совпадающую с фурье-образом дифракционной картины
- 8. Использование фурье-координат для синтеза предметных функций
- Глава 4. КОГЕРЕНТНОСТЬ СВЕТА (ЭКСПЕРИМЕНТАЛЬНЫЕ ХАРАКТЕРИСТИКИ)
- 2. Определение когерентности
- 2.2. Интерференционный анализ временной когерентности
- 2.3. Сравнение корреляционного и интерференционного методов
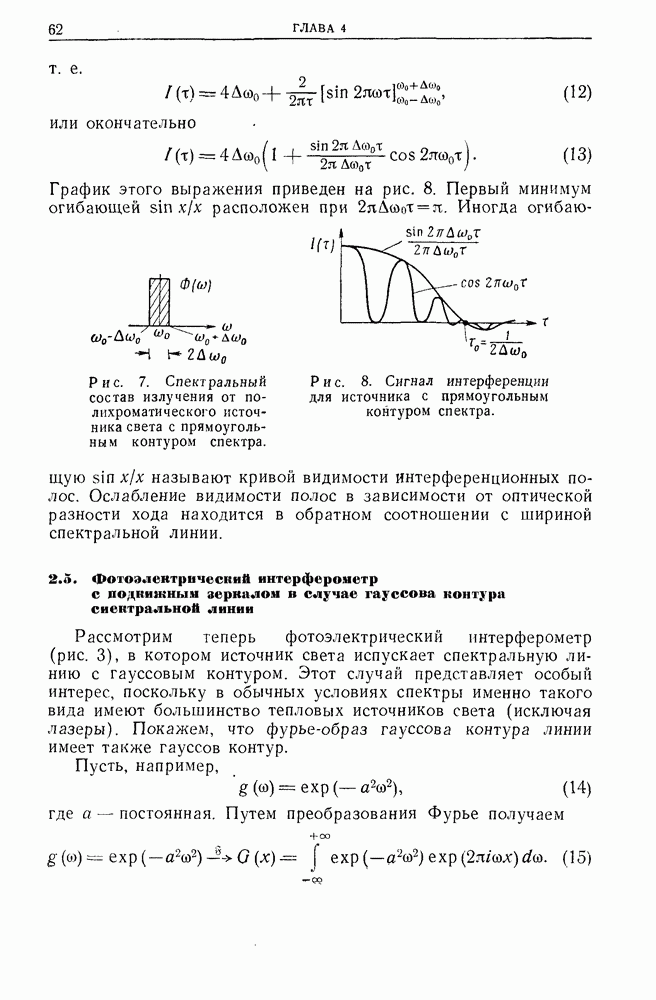
- 2.4. Узкий спектр с прямоугольным контуром
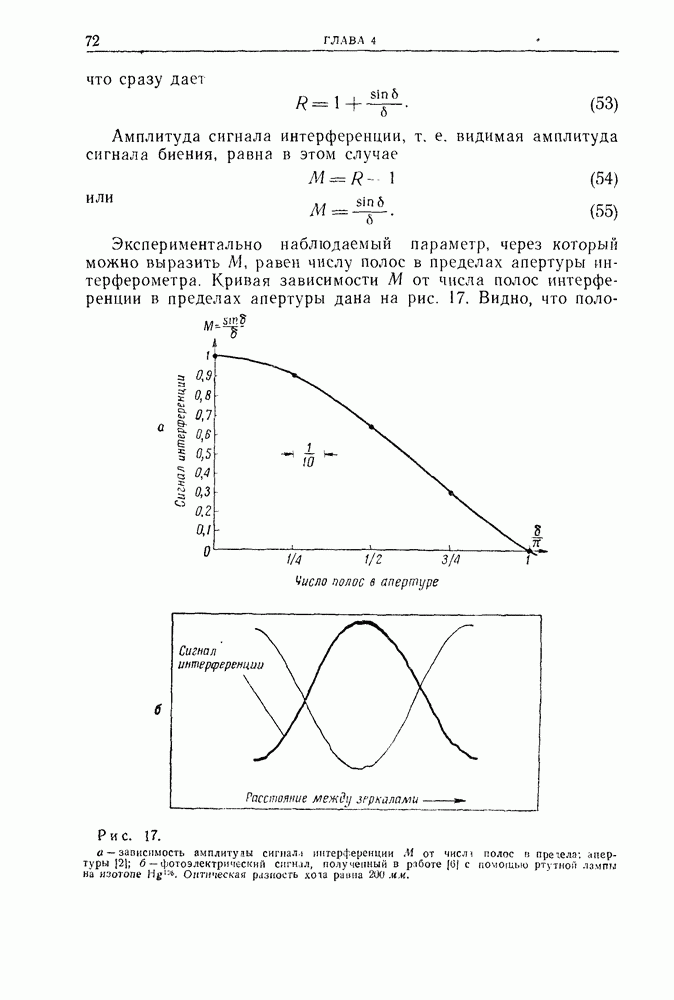
- 2.5. Фотоэлектрический интерферометр с поднижным зеркалом в случае гауссова контура спектральной линии
- 2.6. Физический смысл спектра мощности
- 2.7. Гетеродинный анализ сигналов и биений
- 2.8. Пространственная когерентность
- 2.9. Частичная когерентность света от протяженного некогерентного источника
- 2.10. Корреляция интенсивности при частичной когерентности
- 2.11. Интерферометр интенсивности
- Глава 5. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ КОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Когерентное освещение
- 3. Образование изображения при когерентном освещении как процесс двойной дифракции
- 4. Критерии разрешения Аббе и Релея
- 5. Передаточная функция при когерентном и некогерентном освещении
- 6. Фазовый контраст
- 7. Оптическая фильтрация с помощью голограммы согласованного фильтра
- 7.1. Процедура изготовления согласованного фильтра и операция фильтрации
- 8. Оптическая обработка информации, корреляционный анализ и оптические корреляторы
- 8.2. Оптический кросс-коррелятор
- 9. Интерферометрия и оптический синтез изображения (сложение комплексных амплитуд) методом последовательного наложения голографических картин на одну голограмму [5]
- Глава 6. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ОПТИЧЕСКОЙ ГОЛОГРАФИИ
- 2.1. Процесс получевия голограммы
- 2.2. Процесс восстановления изображения
- 2.3. Физические принципы голографии
- 2.4. Геометрическое увеличение
- 2.5. Разрешающая способность
- 3. Голография Фурье с высоким разрешением
- 3.2. Физические основы безлинзовой голографии Фурье высокого разрешения
- 3.3. Теория безлинзовой голографии Фурье
- 3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
- 4. Компенсация протяженности источника в голографии
- 5. Требование к когерентности в голографии
- 6. Сводка основных результатов
- 7. Электронный микроскоп и рентгеновский голографический микроскоп
- 8. Заключение
- 9. Голография при некогерентном освещении
- 9.2. Голография при пространственно-некогерентном освещении
- Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
- 1. Преобразование Фурье
- 2. Свертка
- 3. Функция корреляции
- 4. Распределения, или обобщенные функции
- 4.2. Импульсный отклик линейной системы
- 4.3. Отклик линейной системы на произвольную входную функцию
- 5. Спектральный анализ
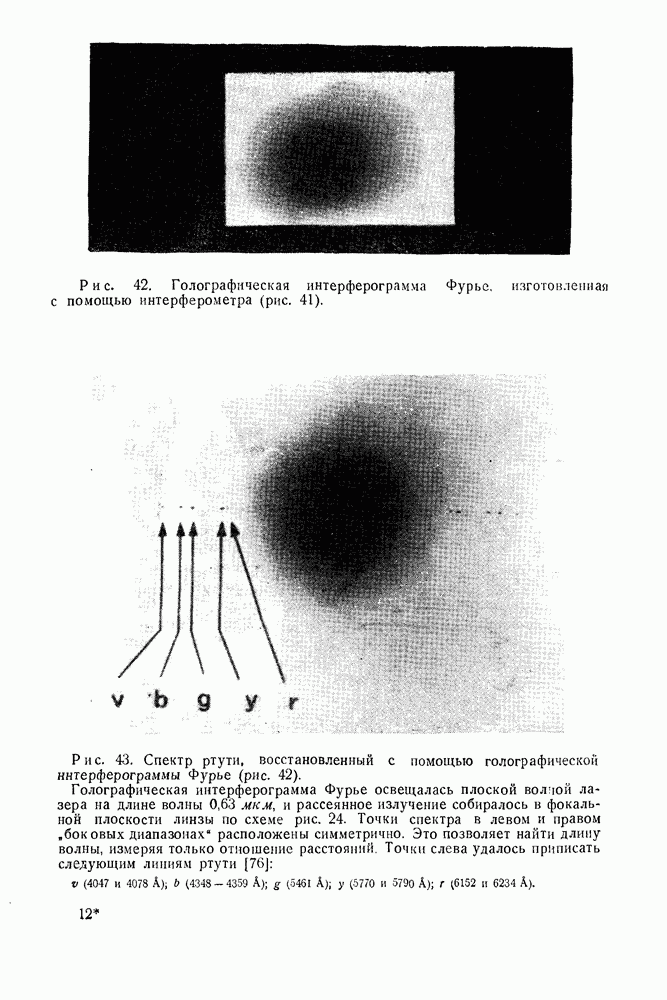
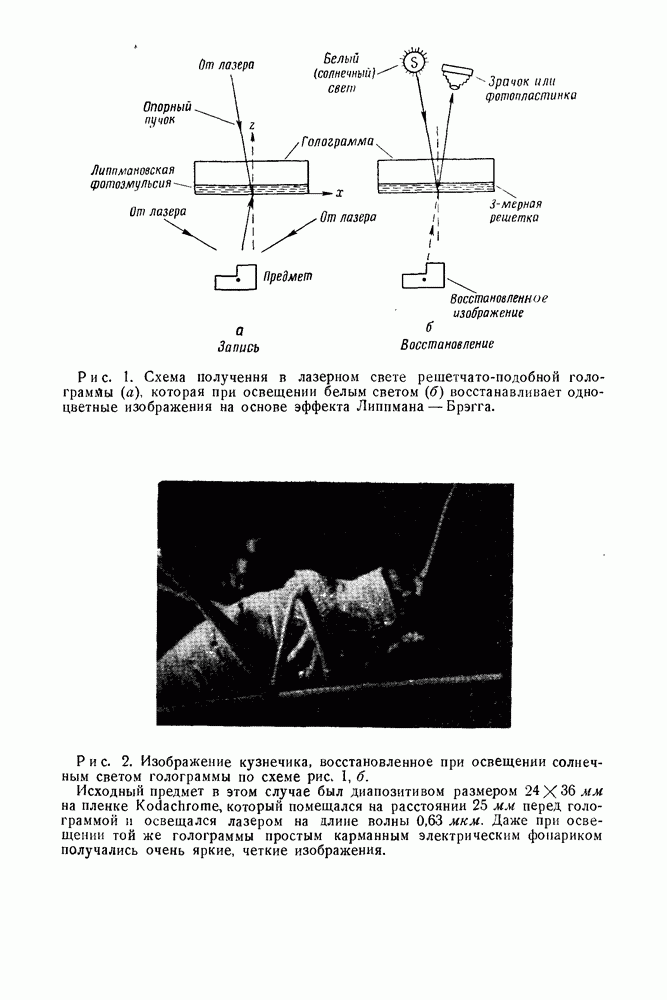
- Дополнение автора к русскому изданию. ВОССТАНОВЛЕНИЕ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ В БЕЛОМ СВЕТЕ С ИСПОЛЬЗОВАНИЕМ ДИФРАКЦИОННОГО ЭФФЕКТА ЛИППМАНА — БРЭГГА
- ПРИЛОЖЕНИЕ 1. МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА
- Принцип восстановления волнового фронта
- Освещение сферической волной
- Восстановление при освещении точечным источником
- Побочная часть волны при восстановлении с помощью точечного источника
- Ухучшенне разделения изобрашений с помощью масок и других методов
- Освещающие волны с астигматизмом и сферической аберрацией
- Восстановление при наличии сферической аберрации и астигматизма
- Критерии когерентности
- Восстановление в оптическом диапазоне
- Экспериментальная проверка
- Заключение
- МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА, II
- 2. Принцип восстановления волнового фронта
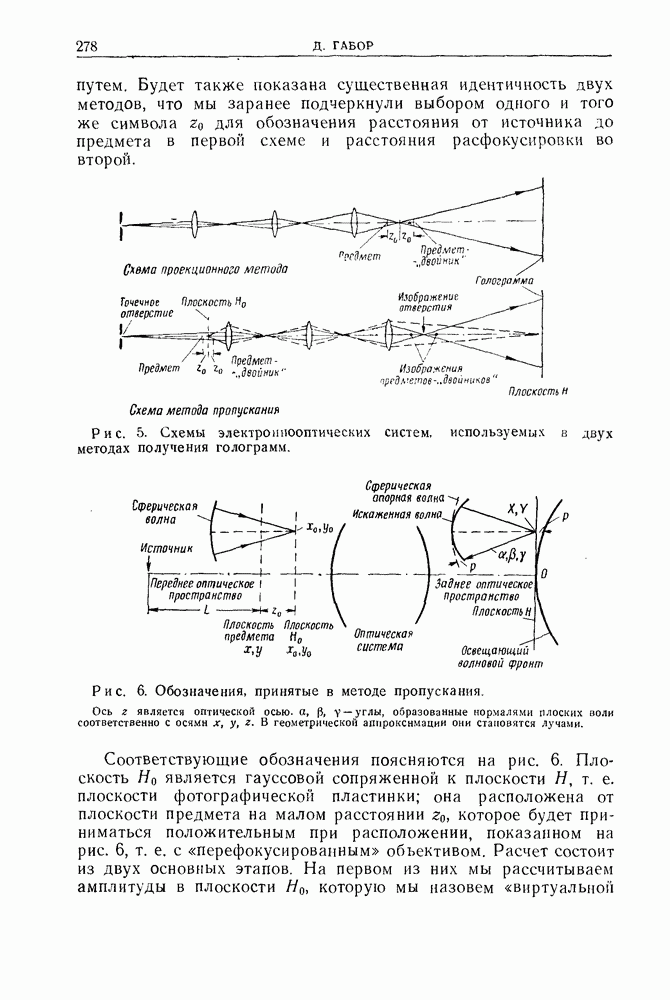
- 3. Теория образования изображения при использовании метода пропускания
- 4. Восстановление
- 5. Критерии когерентности
- 6. Условия, необходимые для получения голограмм
- 7. Восстановление по методу темного поля
- ПРИЛОЖЕНИЕ 2. ПРИМЕНЕНИЯ ГОЛОГРАФИИ
- 2. Трехмерная фотография
- 3. Распознавание образов
- 4. Иитерференционная память
- 5. Интерферометрия
- 6. Голография в технологии
- 7. Голографический метод в интроскопии
- 8. Голографическая микроскопия
- 9. Голографическое кино
- 10. Голографическое телевидение
- 11. Голографическая оптика