| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5. Требование к когерентности в голографии
Строго говоря, для получения голограммы при пространственно-когерентном освещении требуется выполнить только одно условие когерентности, которое состоит в том, чтобы излучение от каждой точки предмета могло интерферировать с излучением от любой точки источника.
Условие когерентности удовлетворяется при выполнении следующих требований. Во-первых, рассеивающий предмет  и источник
и источник  должны испускать свет одной и той же частоты. Во-вторых, необходимо, чтобы предмет и источник были стационарными в поле, которое падает на голограмму. Это условие не нарушается для диффузно рассеивающего предмета. Кроме того, и сам предмет можно освещать диффузным светом. При этом условие стационарности нарушено не будет. Наконец, в предыдущем разделе было доказано, что различие между предметом и источником фактически отсутствует. Таким образом, как источник, так и предмет могут образовывать диффузную волну при условии, конечно, что источник
должны испускать свет одной и той же частоты. Во-вторых, необходимо, чтобы предмет и источник были стационарными в поле, которое падает на голограмму. Это условие не нарушается для диффузно рассеивающего предмета. Кроме того, и сам предмет можно освещать диффузным светом. При этом условие стационарности нарушено не будет. Наконец, в предыдущем разделе было доказано, что различие между предметом и источником фактически отсутствует. Таким образом, как источник, так и предмет могут образовывать диффузную волну при условии, конечно, что источник  используемый при восстановлении, дает кросс-корреляцию
используемый при восстановлении, дает кросс-корреляцию  которая равна дельта-функции, как это было показано в разд. 4.
которая равна дельта-функции, как это было показано в разд. 4.
Метод получения голограммы (рис. 38) при освещении предмета рассеивателем, движущимся во время экспозиции, был успешно продемонстрирован в работе [28] Результаты ее можно
легко понять, если привлечь теорию наложения интенсивностей в скрытом изображении при последовательных экспозициях [45] одной и той же голограммы (разд. 9 гл. 5).
Если для регистрации голограммы вместо лазеров используются обычные источники света, область, на которой может возникнуть интерференция, ограничивается шириной спектральной линии. Когерентная длина  определяет размеры и глубину предмета или сцены, голограмму которой можно получить путем интерференции с плоской или сферической волной, формируемой с помощью зеркала, располагаемого иногда вблизи предмета.
определяет размеры и глубину предмета или сцены, голограмму которой можно получить путем интерференции с плоской или сферической волной, формируемой с помощью зеркала, располагаемого иногда вблизи предмета.
Рассмотрим две волны света, одну с частотой  а другую с частотой
а другую с частотой  Пусть с — скорость света в вакууме,
Пусть с — скорость света в вакууме,  длина волны, соответствующая частоте
длина волны, соответствующая частоте  Тогда
Тогда

Круговая частота

а фаза  входящая в уравнение волны, равна
входящая в уравнение волны, равна

Пусть в момент  две волны с частотами
две волны с частотами  находятся в одинаковой фазе. Через некоторый промежуток времени
находятся в одинаковой фазе. Через некоторый промежуток времени  которому соответствует длина
которому соответствует длина  определяемая как
определяемая как

две волны разойдутся по фазе на величину

Отсюда, дифференцируя соотношения (86) и (84), из выражения (88) получим

где  разность длин волн, соответствующая разности частот
разность длин волн, соответствующая разности частот 
Определим длину когерентности  как расстояние, на котором разность фаз между двумя волнами составит
как расстояние, на котором разность фаз между двумя волнами составит  Сравнивая выражения (89) и (87), получаем следующее значение когерентной длины;
Сравнивая выражения (89) и (87), получаем следующее значение когерентной длины;

Это уравнение используется для определения размеров, в пределах которых можно сохранить когерентность, когда задана определенная геометрия, а спектр излучения состоит из двух линий.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора русского издания
- Глава 1. ВВЕДЕНИЕ
- 1. Современная оптика — раздел радиоалектроники
- 2. Теория — основа радиооптики
- 3. Математические методы современной оптики
- 4. Краевая задача дифракции электромагнитных волн в оптике и некоторые ограничения операционного метода
- 5. Решение краевой задачи на примере дифракционной решетки [5]
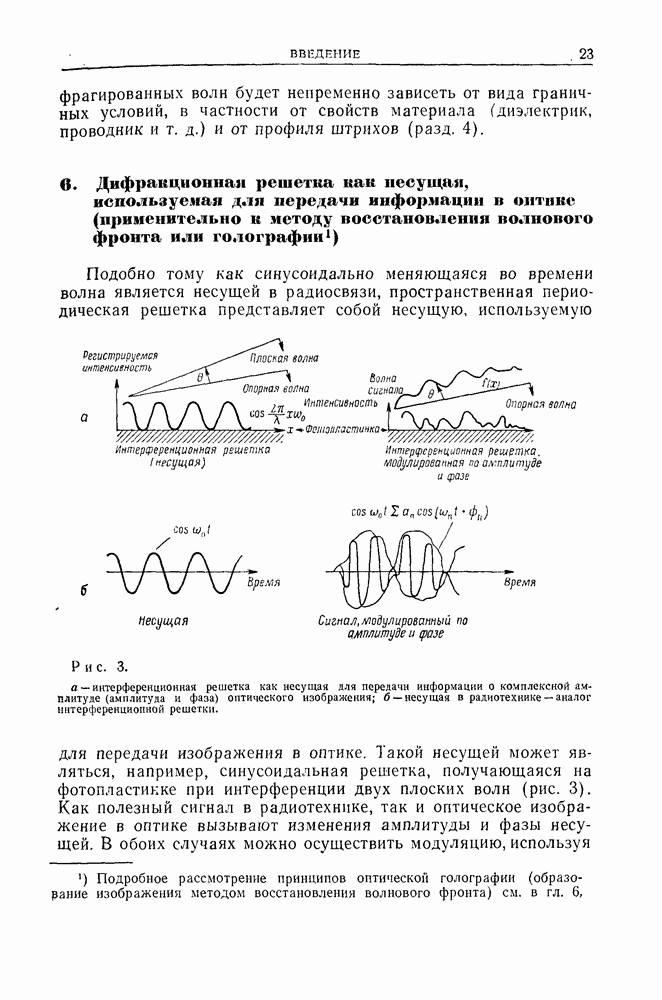
- 6. Дифракционная решетка как несущая, используемая для передачи информации в онтикс (применительно к методу восстановления волнового фронта или голографии
- 7. Оптика и теория связи Исторический обзор
- Глава 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФРАКЦИИ
- 1. Две стороны дифракции света
- 2. Распределение интенсивности в дифракционной картине и в спектре
- 2.2. Проблема образования изображения и принцип Гюйгенса
- 3. Теория образования изображения и обработка оптических сигналов при помощи преобразования Фурье
- Глава 3. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Сложение света, падающего из нескольких точек источника на отдельную точку изображения
- 6. Анализ процесса образования изображения в пространстве фурье-координат
- 7. Физический смысл функции разброса и анализ процесса образования изображения в плоскости фурье-координат
- 7.2. Синусоидальный по интенсивности предмет имеет функцию пространстненно-частотного отклика, совпадающую с фурье-образом дифракционной картины
- 8. Использование фурье-координат для синтеза предметных функций
- Глава 4. КОГЕРЕНТНОСТЬ СВЕТА (ЭКСПЕРИМЕНТАЛЬНЫЕ ХАРАКТЕРИСТИКИ)
- 2. Определение когерентности
- 2.2. Интерференционный анализ временной когерентности
- 2.3. Сравнение корреляционного и интерференционного методов
- 2.4. Узкий спектр с прямоугольным контуром
- 2.5. Фотоэлектрический интерферометр с поднижным зеркалом в случае гауссова контура спектральной линии
- 2.6. Физический смысл спектра мощности
- 2.7. Гетеродинный анализ сигналов и биений
- 2.8. Пространственная когерентность
- 2.9. Частичная когерентность света от протяженного некогерентного источника
- 2.10. Корреляция интенсивности при частичной когерентности
- 2.11. Интерферометр интенсивности
- Глава 5. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ КОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Когерентное освещение
- 3. Образование изображения при когерентном освещении как процесс двойной дифракции
- 4. Критерии разрешения Аббе и Релея
- 5. Передаточная функция при когерентном и некогерентном освещении
- 6. Фазовый контраст
- 7. Оптическая фильтрация с помощью голограммы согласованного фильтра
- 7.1. Процедура изготовления согласованного фильтра и операция фильтрации
- 8. Оптическая обработка информации, корреляционный анализ и оптические корреляторы
- 8.2. Оптический кросс-коррелятор
- 9. Интерферометрия и оптический синтез изображения (сложение комплексных амплитуд) методом последовательного наложения голографических картин на одну голограмму [5]
- Глава 6. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ОПТИЧЕСКОЙ ГОЛОГРАФИИ
- 2.1. Процесс получевия голограммы
- 2.2. Процесс восстановления изображения
- 2.3. Физические принципы голографии
- 2.4. Геометрическое увеличение
- 2.5. Разрешающая способность
- 3. Голография Фурье с высоким разрешением
- 3.2. Физические основы безлинзовой голографии Фурье высокого разрешения
- 3.3. Теория безлинзовой голографии Фурье
- 3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
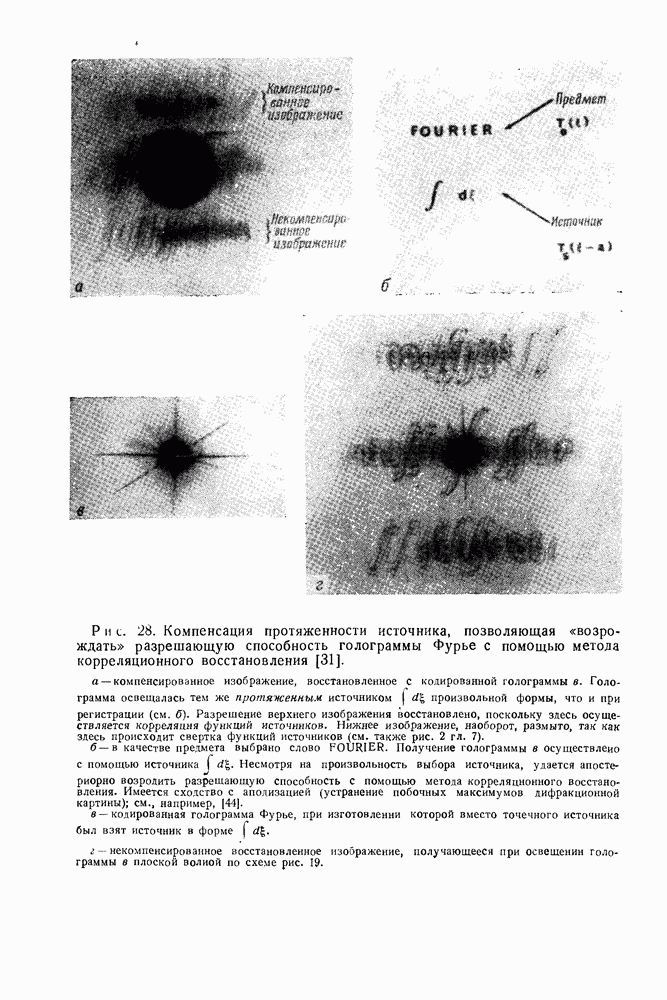
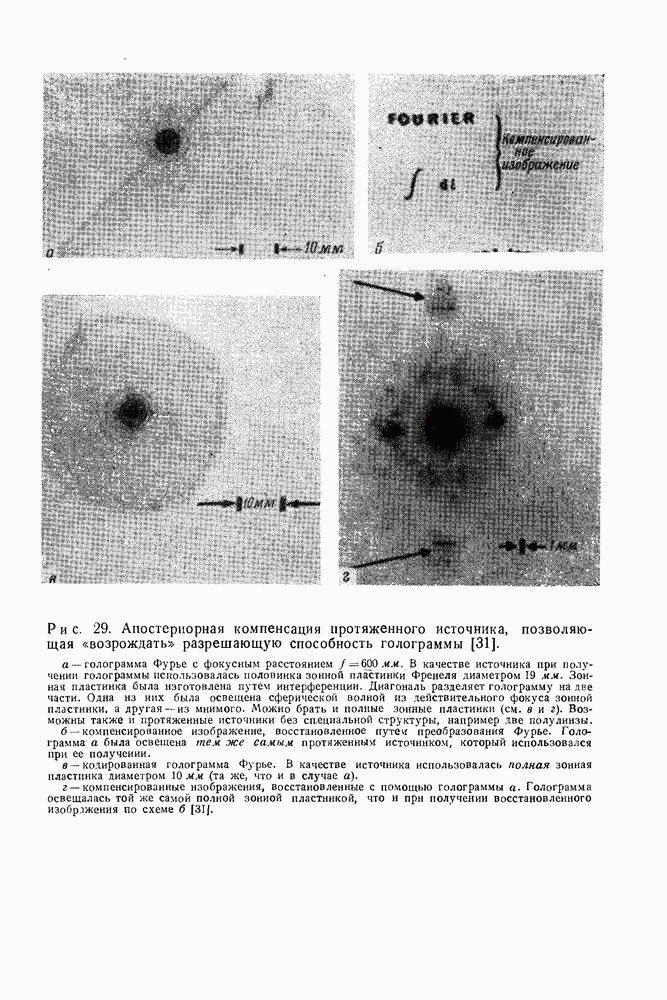
- 4. Компенсация протяженности источника в голографии
- 5. Требование к когерентности в голографии
- 6. Сводка основных результатов
- 7. Электронный микроскоп и рентгеновский голографический микроскоп
- 8. Заключение
- 9. Голография при некогерентном освещении
- 9.2. Голография при пространственно-некогерентном освещении
- Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
- 1. Преобразование Фурье
- 2. Свертка
- 3. Функция корреляции
- 4. Распределения, или обобщенные функции
- 4.2. Импульсный отклик линейной системы
- 4.3. Отклик линейной системы на произвольную входную функцию
- 5. Спектральный анализ
- Дополнение автора к русскому изданию. ВОССТАНОВЛЕНИЕ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ В БЕЛОМ СВЕТЕ С ИСПОЛЬЗОВАНИЕМ ДИФРАКЦИОННОГО ЭФФЕКТА ЛИППМАНА — БРЭГГА
- ПРИЛОЖЕНИЕ 1. МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА
- Принцип восстановления волнового фронта
- Освещение сферической волной
- Восстановление при освещении точечным источником
- Побочная часть волны при восстановлении с помощью точечного источника
- Ухучшенне разделения изобрашений с помощью масок и других методов
- Освещающие волны с астигматизмом и сферической аберрацией
- Восстановление при наличии сферической аберрации и астигматизма
- Критерии когерентности
- Восстановление в оптическом диапазоне
- Экспериментальная проверка
- Заключение
- МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА, II
- 2. Принцип восстановления волнового фронта
- 3. Теория образования изображения при использовании метода пропускания
- 4. Восстановление
- 5. Критерии когерентности
- 6. Условия, необходимые для получения голограмм
- 7. Восстановление по методу темного поля
- ПРИЛОЖЕНИЕ 2. ПРИМЕНЕНИЯ ГОЛОГРАФИИ
- 2. Трехмерная фотография
- 3. Распознавание образов
- 4. Иитерференционная память
- 5. Интерферометрия
- 6. Голография в технологии
- 7. Голографический метод в интроскопии
- 8. Голографическая микроскопия
- 9. Голографическое кино
- 10. Голографическое телевидение
- 11. Голографическая оптика