| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
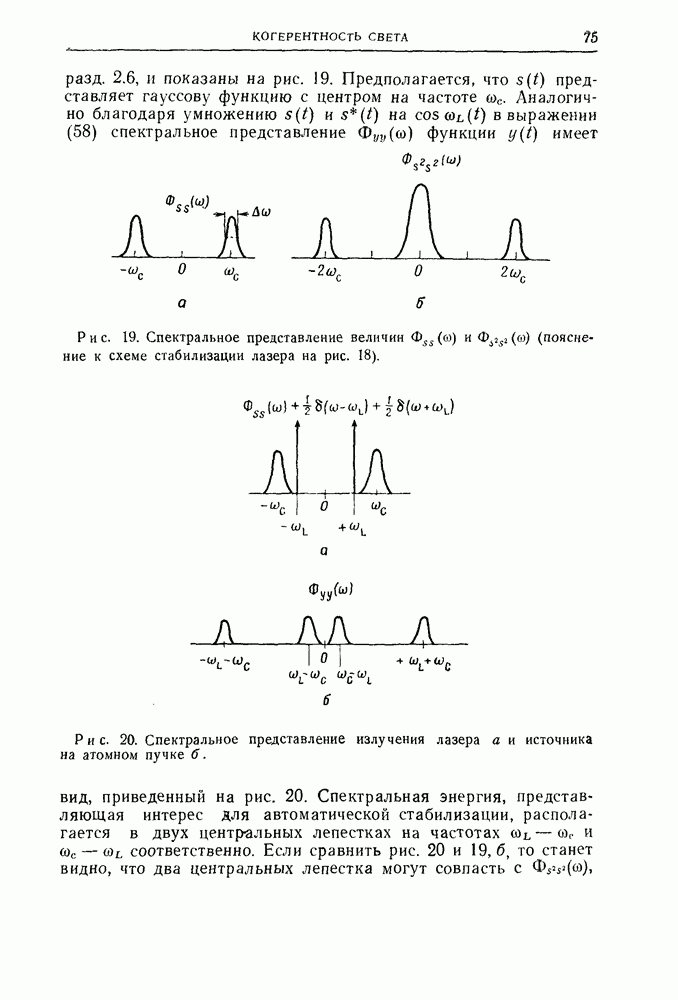
2. Принцип восстановления волнового фронта
Рассмотрим монохроматическую, когерентную волну с амплитудой  падающую на фотографическую пластинку. Предположим, что пластинка проявлена с обращением или же с негатива отпечатан позитив, так что результирующий коэффициент контрастности равен
падающую на фотографическую пластинку. Предположим, что пластинка проявлена с обращением или же с негатива отпечатан позитив, так что результирующий коэффициент контрастности равен  На линейном участке
На линейном участке
кривой почернения коэффициент пропускания амплитуды  для обработанной фотографической пластинки определяется выражением
для обработанной фотографической пластинки определяется выражением  где К — постоянная величина. Представим теперь, что
где К — постоянная величина. Представим теперь, что  состоит из когерентного фона, или освещающей волны
состоит из когерентного фона, или освещающей волны  и возмущения, или вторичной волны
и возмущения, или вторичной волны  рассеянной предметом:
рассеянной предметом:

С другой стороны, если мы осветим фотографию-голограмму одним лишь когерентным фоном, то мы тотчас за эмульсией получим волну  В простейшем, а также наиболее благоприятном случае коэффициент контрастности
В простейшем, а также наиболее благоприятном случае коэффициент контрастности  При этом значении контраста
При этом значении контраста

Для простоты предположим, что когерентный фон однороден по интенсивности, т. е.  и сопоставим два последних уравнения. Выражения перед скобками с точностью до постоянного множителя равны. Внутри скобок мы видим, что вместо амплитуды когерентного фона
и сопоставим два последних уравнения. Выражения перед скобками с точностью до постоянного множителя равны. Внутри скобок мы видим, что вместо амплитуды когерентного фона  в уравнение (1) входит
в уравнение (1) входит  Если мы предположим — и это очень существенное условие, — что амплитуда когерентного фона намного больше амплитуд, рассеянных предметом, то членом
Если мы предположим — и это очень существенное условие, — что амплитуда когерентного фона намного больше амплитуд, рассеянных предметом, то членом  можно пренебречь. Следующие члены
можно пренебречь. Следующие члены  идентичны в обоих выражениях. Это означает, что восстановлена подлинная вторичная волна с правильной фазой, и если пренебречь малым членом
идентичны в обоих выражениях. Это означает, что восстановлена подлинная вторичная волна с правильной фазой, и если пренебречь малым членом  то и с правильной относительной амплитудой. Но последний член в выражении (1) новый: он представляет волну с той же самой амплитудой, как и вторичная волна
то и с правильной относительной амплитудой. Но последний член в выражении (1) новый: он представляет волну с той же самой амплитудой, как и вторичная волна  но со знаком фазы, отличным от знака когерентного фона.
но со знаком фазы, отличным от знака когерентного фона.
Это можно пояснить с помощью диаграммы, показанной на рис. 1. Если рассеянная волна относителыго слаба, то полная амплитуда волны очень близка к вектору  равному амплитуде когерентного фона, сложенной с синфазной компонентой рассеянной волны. В случае фотографической пластинки с коэффициентом контрастности
равному амплитуде когерентного фона, сложенной с синфазной компонентой рассеянной волны. В случае фотографической пластинки с коэффициентом контрастности  эта амплитуда, возведенная в квадрат, характеризует пропускание, показанное на нижней диаграмме. Чтобы обе диаграммы привести к одному масштабу.
эта амплитуда, возведенная в квадрат, характеризует пропускание, показанное на нижней диаграмме. Чтобы обе диаграммы привести к одному масштабу.
амплитуда когерентного фона полагается равной единице. Амплитуда прошедшей волны теперь очень близка к амплитуде когерентного фона, сложенной с удвоенной синфазной компонентой рассеянной волны. Этот результат можно интерпретировать, как показано на диаграмме, таким образом, что восстановленная волна отличается от исходной лишь «сопряженной амплитудой», синфазная компонента которой равна, а квадратурная компонента противоположна соответствующим компонентам амплитуды рассеянной волны. Может показаться, что эта интерпретация произвольна, поскольку квадратурная компонента подавляется, однако ниже будет показано, что это очень близко соответствует восприятию амплитуды рассеянной волны глазом, а именно как волны, идущей от предмета-«двойника».

Рис. 1. Векторная диаграмма, объясняющая принцип восстановления для коэффициента контрастности 
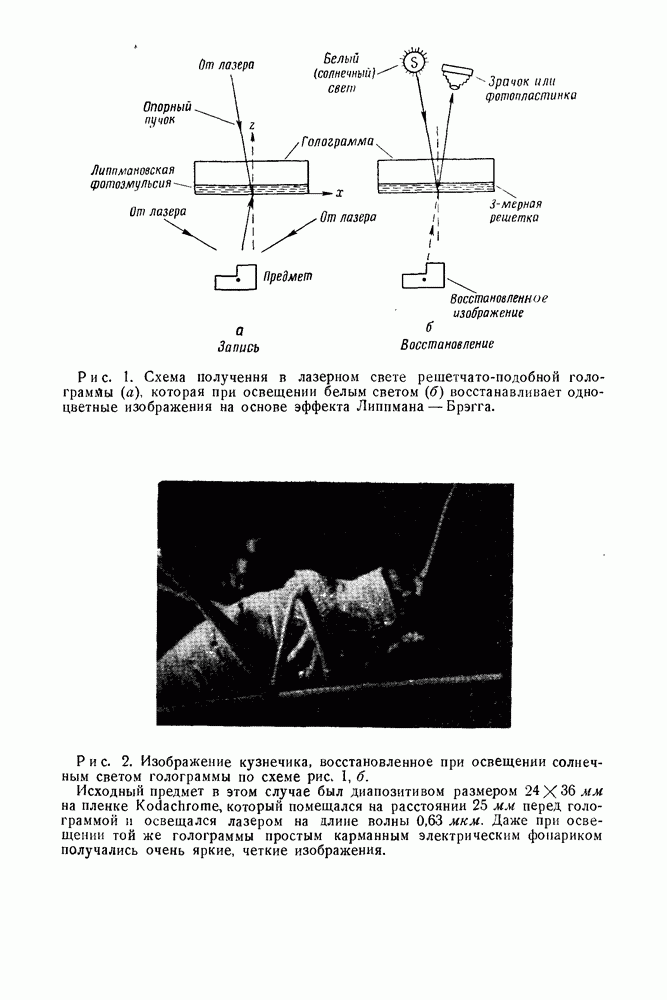
Для того чтобы показать это, мы можем продолжить в несколько более общей форме рассуждения, начатые в статье I, По-прежнему будем предполагать, что освещающая волна выходит из точечного источника, но опустим предположение, сделанное в статье I, что фотографическая пластинка находится на бесконечности. Переход к освещающим волнам, отличным от сферических, легко может быть осуществлен на последней стадии.
Рассмотрим точечный источник  точечный предмет
точечный предмет  и точку
и точку  фотографической пластинки (рис. 2). В точку
фотографической пластинки (рис. 2). В точку  падают прямой луч
падают прямой луч  и непрямой
и непрямой  Разность фаз между ними равна сумме двух компонент: одна из них пропорциональна разности длин прямой и ломаной линий, а вторая равна некоторому скачку фазы, который луч может испытать при рассеянии на предмете. Интерференция этих лучей дает в точке
Разность фаз между ними равна сумме двух компонент: одна из них пропорциональна разности длин прямой и ломаной линий, а вторая равна некоторому скачку фазы, который луч может испытать при рассеянии на предмете. Интерференция этих лучей дает в точке  полную амплитуду. Но в точности та же самая амплитуда получилась бы при другом знаке разности фаз двух лучей. Мы можем построить два таких луча с другим знаком разности фаз, прежде всего обращая направление распространения, т. е.
полную амплитуду. Но в точности та же самая амплитуда получилась бы при другом знаке разности фаз двух лучей. Мы можем построить два таких луча с другим знаком разности фаз, прежде всего обращая направление распространения, т. е.
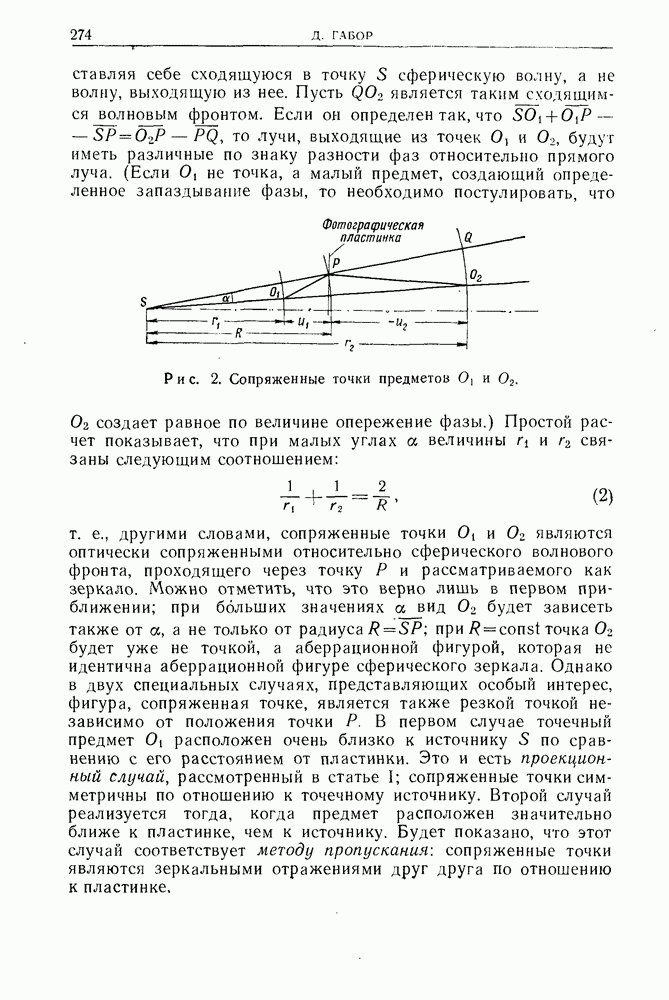
представляя себе сходящуюся в точку  сферическую волну, а не волну, выходящую из нее. Пусть
сферическую волну, а не волну, выходящую из нее. Пусть  является таким сходящимся волновым фронтом. Если он определен так, что
является таким сходящимся волновым фронтом. Если он определен так, что  то лучи, выходящие из точек
то лучи, выходящие из точек  будут иметь различные по знаку разности фаз относительно прямого луча. (Если О, не точка, а малый предмет, создающий определенное запаздывание фазы, то необходимо постулировать, что
будут иметь различные по знаку разности фаз относительно прямого луча. (Если О, не точка, а малый предмет, создающий определенное запаздывание фазы, то необходимо постулировать, что  создает равное по величине опережение фазы.)
создает равное по величине опережение фазы.)

Рис. 2. Сопряженные точки предметов  .
.
Простой расчет показывает, что при малых углах а величины и  связаны следующим соотношением:
связаны следующим соотношением:

т. е., другими словами, сопряженные точки  являются оптически сопряженными относительно сферического волнового фронта, проходящего через точку
являются оптически сопряженными относительно сферического волнового фронта, проходящего через точку  и рассматриваемого как зеркало. Можно отметить, что это верно лишь в первом приближении; при больших значениях а вид
и рассматриваемого как зеркало. Можно отметить, что это верно лишь в первом приближении; при больших значениях а вид  будет зависеть также от а, а не только от радиуса
будет зависеть также от а, а не только от радиуса  при
при  точка
точка  будет уже не точкой, а аберрационной фигурой, которая не идентична аберрационной фигуре сферического зеркала. Однако в двух специальных случаях, представляющих особый интерес, фигура, сопряженная точке, является также резкой точкой независимо от положения точки
будет уже не точкой, а аберрационной фигурой, которая не идентична аберрационной фигуре сферического зеркала. Однако в двух специальных случаях, представляющих особый интерес, фигура, сопряженная точке, является также резкой точкой независимо от положения точки  В первом случае точечный предмет О, расположен очень близко к источнику
В первом случае точечный предмет О, расположен очень близко к источнику  по сравнению с его расстоянием от пластинки. Это и есть проекционный случай, рассмотренный в статье
по сравнению с его расстоянием от пластинки. Это и есть проекционный случай, рассмотренный в статье  сопряженные точки симметричны по отношению к точечному источнику. Второй случай реализуется тогда, когда предмет расположен значительно ближе к пластинке, чем к источнику. Будет показано, что этот случай соответствует методу пропускания, сопряженные точки являются зеркальными отражениями друг друга по отношению к пластинке.
сопряженные точки симметричны по отношению к точечному источнику. Второй случай реализуется тогда, когда предмет расположен значительно ближе к пластинке, чем к источнику. Будет показано, что этот случай соответствует методу пропускания, сопряженные точки являются зеркальными отражениями друг друга по отношению к пластинке.
Могут спросить, нельзя ли получить какое-то преимущество при промежуточном расположении, помещая предмет, например, посередине между источником и пластинкой так, что сопряженный предмет отодвигается в бесконечность. Однако никаких преимуществ это не дает, поскольку, как видно из уравнения (2), две сопряженнные амплитуды в точке  всегда равны. От сопряженного предмета избавиться нельзя; он является неизбежным следствием «нечувствительности к фазе» фотографической пластинки [2].
всегда равны. От сопряженного предмета избавиться нельзя; он является неизбежным следствием «нечувствительности к фазе» фотографической пластинки [2].
Используя обозначения рис. 2, запищем уравнение (2) в виде


Рис. 3. Использование различных освещающих волн при восстановлении дает тот же эффект, что и оптическое преобразование.
Это соотнощение является оптически инвариантным, т. е., другими словами, если в процессе восстановления отображают оптическое пространство источника и голограммы таким образом, что сферическая волна, идущая от источника к пластинке, имеет некоторую другую кривизну, то две сопряженные амплитуды остаются зеркальными изображениями относительно преобразованного сферического волнового фронта.
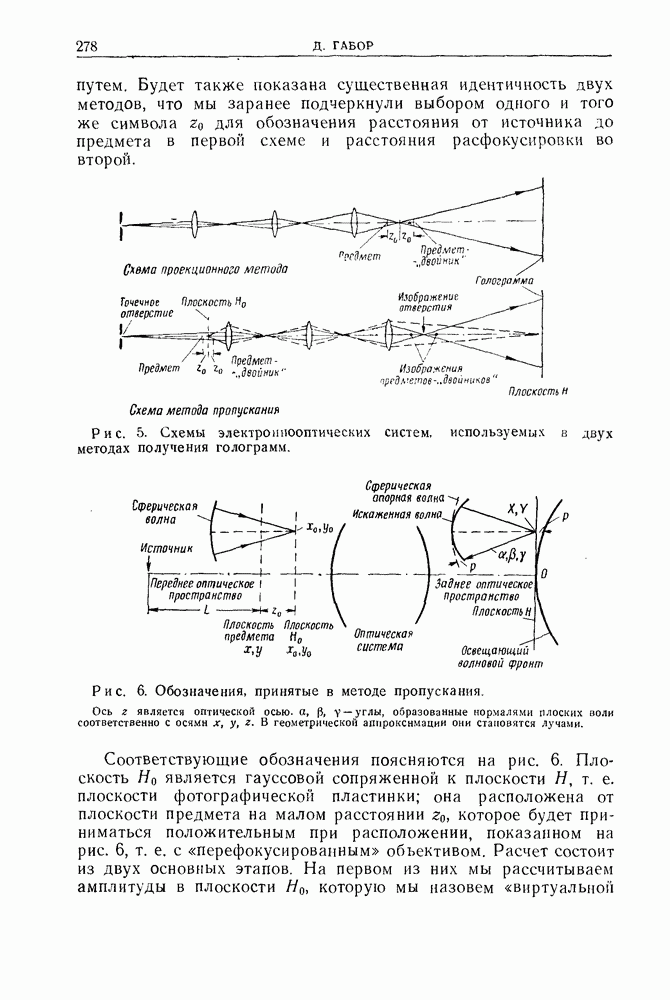
При выводе уравнения (1) предполагалось, что волна, использованная в процессе восстановления, характеризуется теми же самыми разностями фаз между различными точками фотографической пластинки, как и волна, использованная для получения голограммы. Теперь мы опустим это предположение и покажем, что по крайней мере в этом приближении замена одной освещающей волны другой дает тот же самый эффект, что и оптическое преобразование. Предположим, как показано на рис. 3, что пластинка первоначально была освещена из точки  удаленной от нее на расстояние в то время как в процессе восстановления это расстояние равняется
удаленной от нее на расстояние в то время как в процессе восстановления это расстояние равняется 

(кликните для просмотра скана)
Представим теперь, что перед голограммой мы помещаем тонкую отрицательную линзу с фокусным расстоянием, определяемым соотношением  а за ней — положительную линзу с равным по величине, но положительным фокусным расстоянием. Таким образом, полный эффект равен нулю, но поскольку отрицательная линза восстановила первоначальную кривизну волнового фронта, отсюда сразу же вытекает, что в оптическом пространстве между двумя линзами сопряженные изображения занимают свои первоначальные положения
а за ней — положительную линзу с равным по величине, но положительным фокусным расстоянием. Таким образом, полный эффект равен нулю, но поскольку отрицательная линза восстановила первоначальную кривизну волнового фронта, отсюда сразу же вытекает, что в оптическом пространстве между двумя линзами сопряженные изображения занимают свои первоначальные положения  Следовательно, замена волнового фронта дает тот же самый эффект, что и положительная линза, помещенная за голограммой. Мы получаем, например, для первой точки уравнение преобразования
Следовательно, замена волнового фронта дает тот же самый эффект, что и положительная линза, помещенная за голограммой. Мы получаем, например, для первой точки уравнение преобразования

В частности, если новая освещающая волна плоская, то в преобразовании начального положения предмета действие голограммы аналогично действию линзы с фокусным расстоянием  Это свойство, а также некоторые другие интересные оптические свойства голограмм были недавно отмечены Роджерсом [3].
Это свойство, а также некоторые другие интересные оптические свойства голограмм были недавно отмечены Роджерсом [3].
Если освещающая волна не сферическая, то сопряженный предмет более не будет резким, а исказится аберрациями двойной волны, обусловленными отклонениями волнового фронта от сферы. Это проиллюстрировано на рис. 4. Соответствующая теория развита в статье 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора русского издания
- Глава 1. ВВЕДЕНИЕ
- 1. Современная оптика — раздел радиоалектроники
- 2. Теория — основа радиооптики
- 3. Математические методы современной оптики
- 4. Краевая задача дифракции электромагнитных волн в оптике и некоторые ограничения операционного метода
- 5. Решение краевой задачи на примере дифракционной решетки [5]
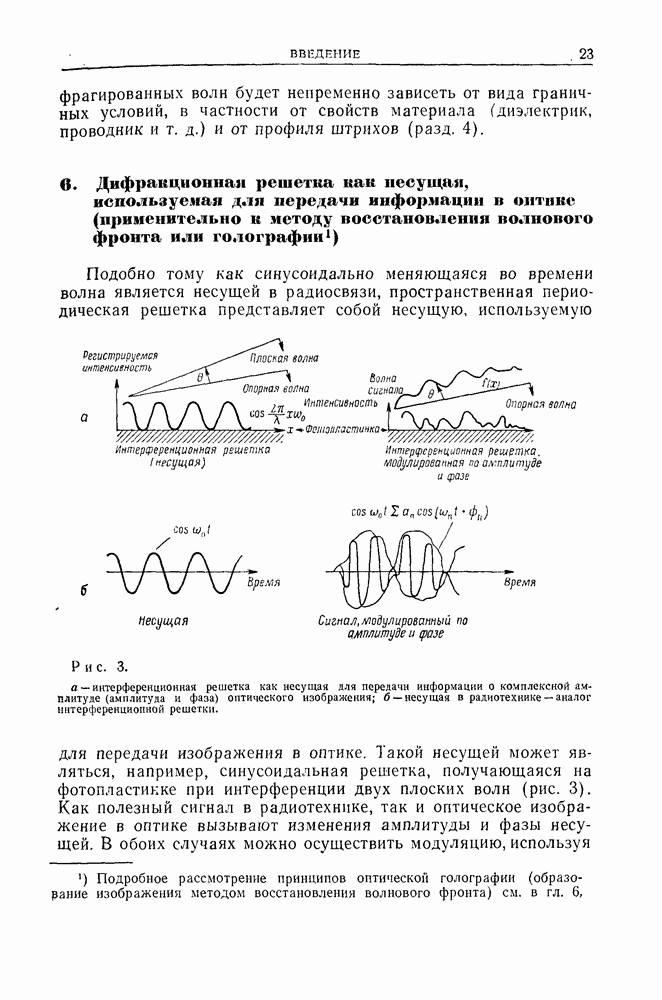
- 6. Дифракционная решетка как несущая, используемая для передачи информации в онтикс (применительно к методу восстановления волнового фронта или голографии
- 7. Оптика и теория связи Исторический обзор
- Глава 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФРАКЦИИ
- 1. Две стороны дифракции света
- 2. Распределение интенсивности в дифракционной картине и в спектре
- 2.2. Проблема образования изображения и принцип Гюйгенса
- 3. Теория образования изображения и обработка оптических сигналов при помощи преобразования Фурье
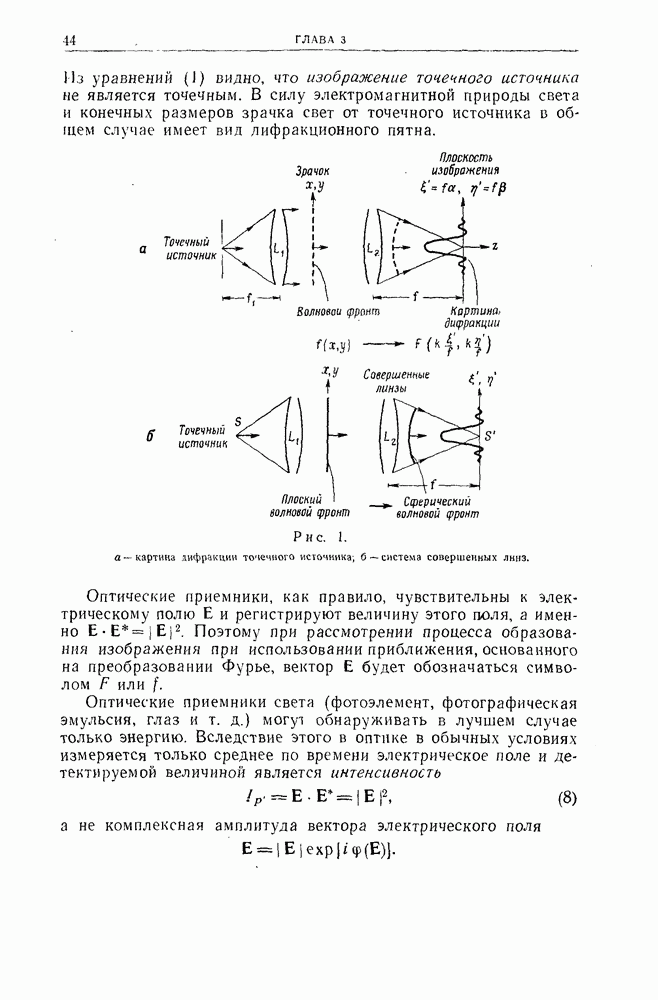
- Глава 3. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Сложение света, падающего из нескольких точек источника на отдельную точку изображения
- 6. Анализ процесса образования изображения в пространстве фурье-координат
- 7. Физический смысл функции разброса и анализ процесса образования изображения в плоскости фурье-координат
- 7.2. Синусоидальный по интенсивности предмет имеет функцию пространстненно-частотного отклика, совпадающую с фурье-образом дифракционной картины
- 8. Использование фурье-координат для синтеза предметных функций
- Глава 4. КОГЕРЕНТНОСТЬ СВЕТА (ЭКСПЕРИМЕНТАЛЬНЫЕ ХАРАКТЕРИСТИКИ)
- 2. Определение когерентности
- 2.2. Интерференционный анализ временной когерентности
- 2.3. Сравнение корреляционного и интерференционного методов
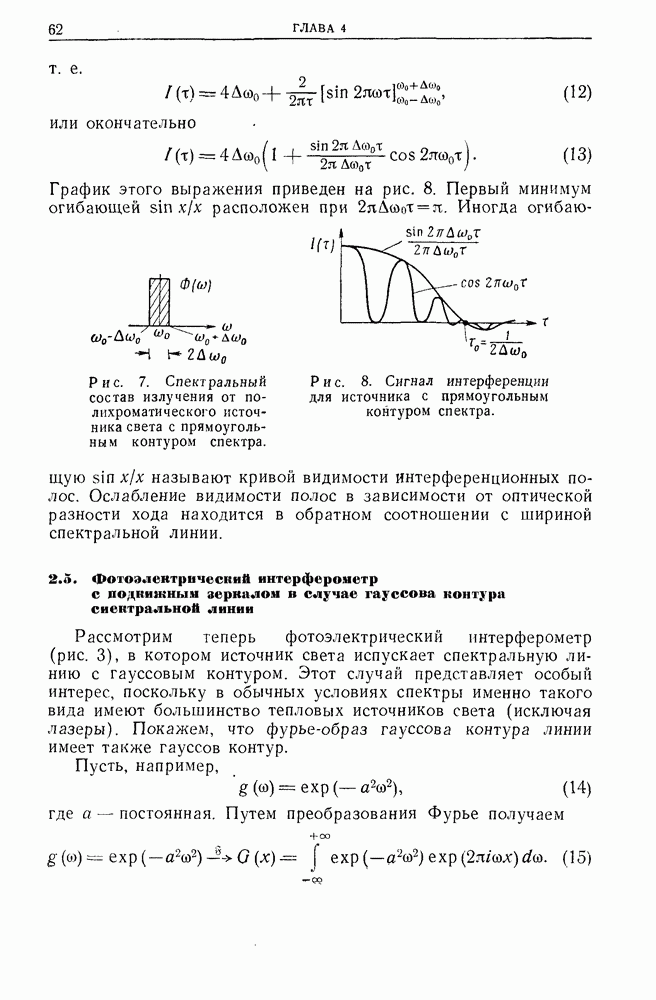
- 2.4. Узкий спектр с прямоугольным контуром
- 2.5. Фотоэлектрический интерферометр с поднижным зеркалом в случае гауссова контура спектральной линии
- 2.6. Физический смысл спектра мощности
- 2.7. Гетеродинный анализ сигналов и биений
- 2.8. Пространственная когерентность
- 2.9. Частичная когерентность света от протяженного некогерентного источника
- 2.10. Корреляция интенсивности при частичной когерентности
- 2.11. Интерферометр интенсивности
- Глава 5. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ КОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Когерентное освещение
- 3. Образование изображения при когерентном освещении как процесс двойной дифракции
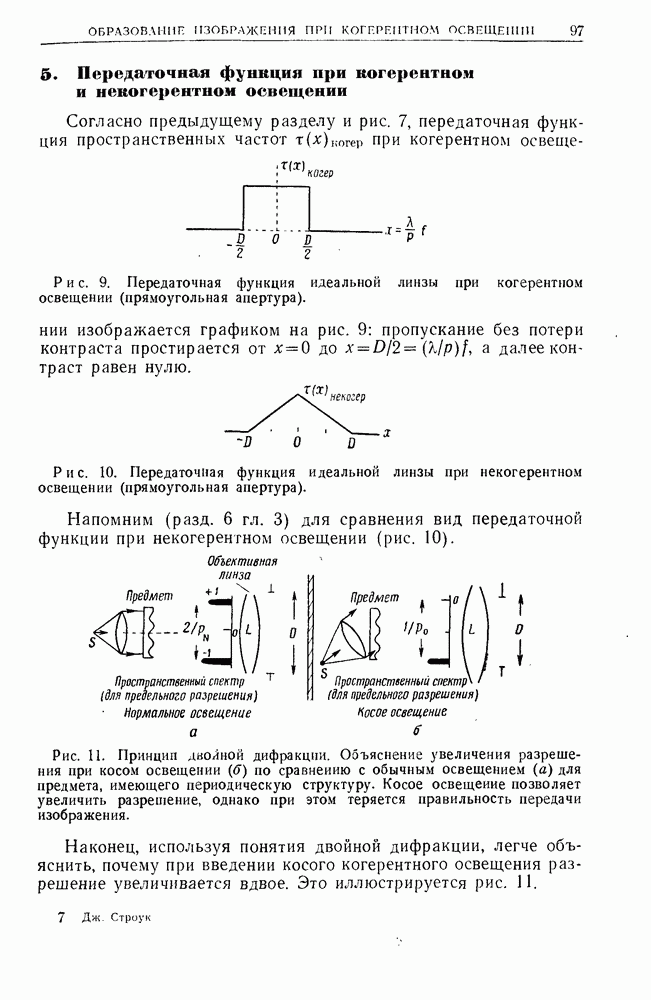
- 4. Критерии разрешения Аббе и Релея
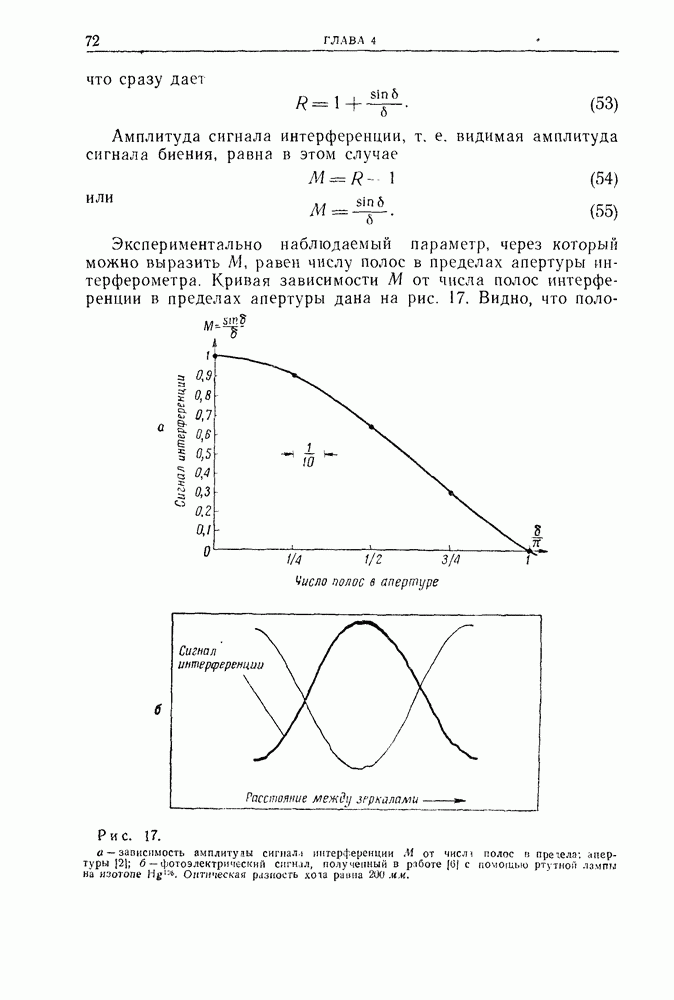
- 5. Передаточная функция при когерентном и некогерентном освещении
- 6. Фазовый контраст
- 7. Оптическая фильтрация с помощью голограммы согласованного фильтра
- 7.1. Процедура изготовления согласованного фильтра и операция фильтрации
- 8. Оптическая обработка информации, корреляционный анализ и оптические корреляторы
- 8.2. Оптический кросс-коррелятор
- 9. Интерферометрия и оптический синтез изображения (сложение комплексных амплитуд) методом последовательного наложения голографических картин на одну голограмму [5]
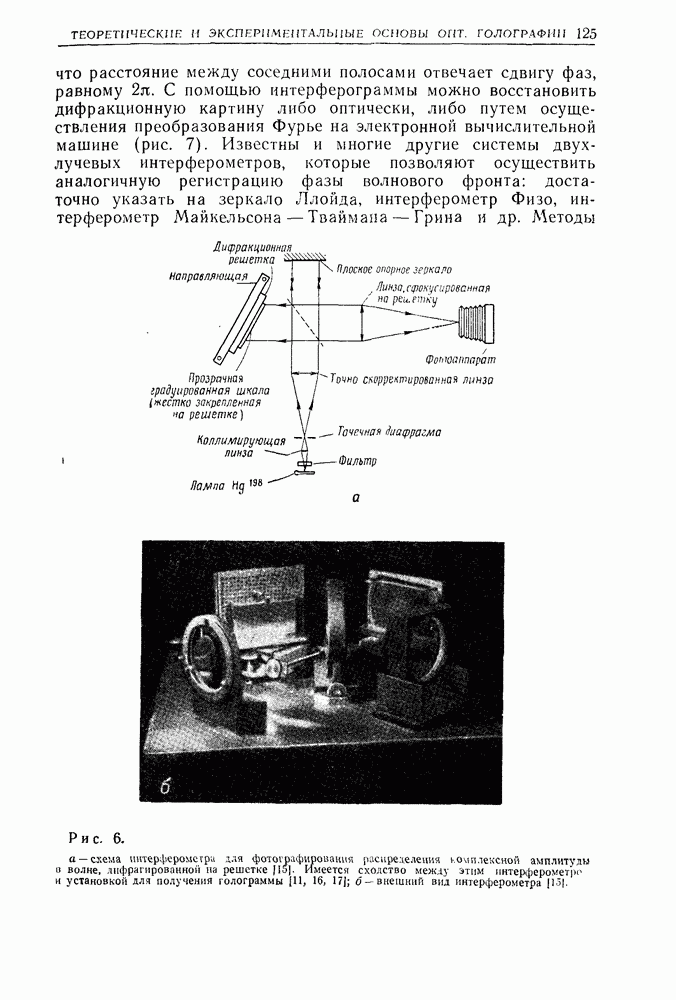
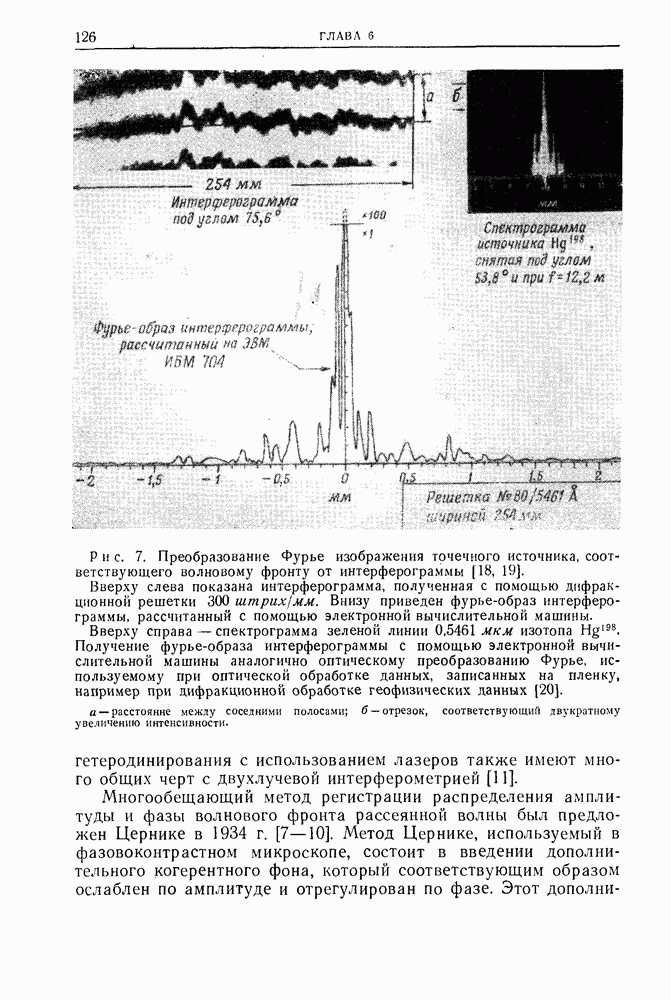
- Глава 6. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ОПТИЧЕСКОЙ ГОЛОГРАФИИ
- 2.1. Процесс получевия голограммы
- 2.2. Процесс восстановления изображения
- 2.3. Физические принципы голографии
- 2.4. Геометрическое увеличение
- 2.5. Разрешающая способность
- 3. Голография Фурье с высоким разрешением
- 3.2. Физические основы безлинзовой голографии Фурье высокого разрешения
- 3.3. Теория безлинзовой голографии Фурье
- 3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
- 4. Компенсация протяженности источника в голографии
- 5. Требование к когерентности в голографии
- 6. Сводка основных результатов
- 7. Электронный микроскоп и рентгеновский голографический микроскоп
- 8. Заключение
- 9. Голография при некогерентном освещении
- 9.2. Голография при пространственно-некогерентном освещении
- Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
- 1. Преобразование Фурье
- 2. Свертка
- 3. Функция корреляции
- 4. Распределения, или обобщенные функции
- 4.2. Импульсный отклик линейной системы
- 4.3. Отклик линейной системы на произвольную входную функцию
- 5. Спектральный анализ
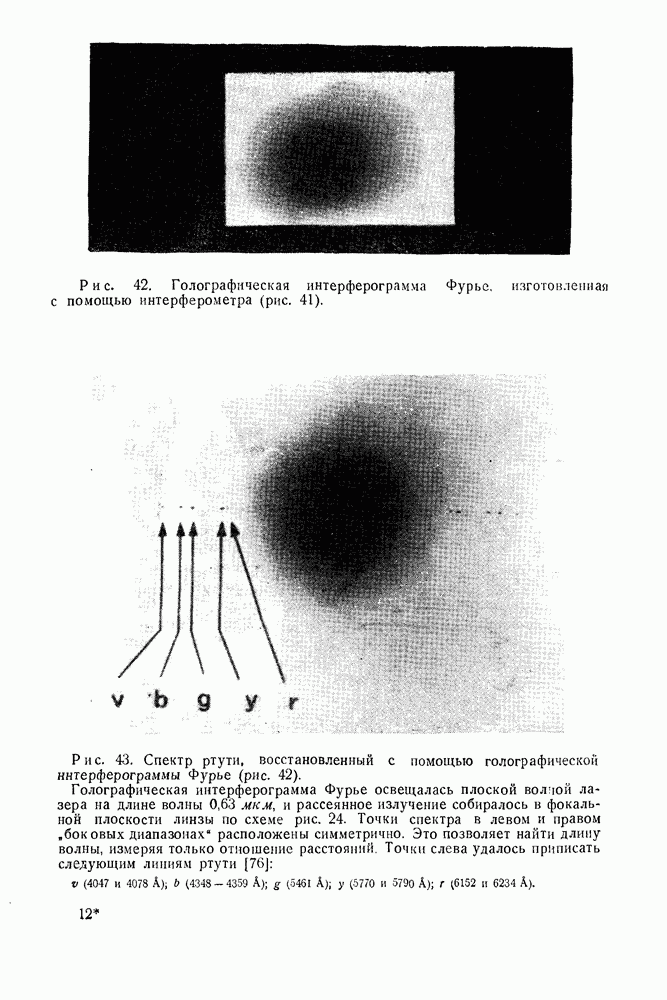
- Дополнение автора к русскому изданию. ВОССТАНОВЛЕНИЕ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ В БЕЛОМ СВЕТЕ С ИСПОЛЬЗОВАНИЕМ ДИФРАКЦИОННОГО ЭФФЕКТА ЛИППМАНА — БРЭГГА
- ПРИЛОЖЕНИЕ 1. МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА
- Принцип восстановления волнового фронта
- Освещение сферической волной
- Восстановление при освещении точечным источником
- Побочная часть волны при восстановлении с помощью точечного источника
- Ухучшенне разделения изобрашений с помощью масок и других методов
- Освещающие волны с астигматизмом и сферической аберрацией
- Восстановление при наличии сферической аберрации и астигматизма
- Критерии когерентности
- Восстановление в оптическом диапазоне
- Экспериментальная проверка
- Заключение
- МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА, II
- 2. Принцип восстановления волнового фронта
- 3. Теория образования изображения при использовании метода пропускания
- 4. Восстановление
- 5. Критерии когерентности
- 6. Условия, необходимые для получения голограмм
- 7. Восстановление по методу темного поля
- ПРИЛОЖЕНИЕ 2. ПРИМЕНЕНИЯ ГОЛОГРАФИИ
- 2. Трехмерная фотография
- 3. Распознавание образов
- 4. Иитерференционная память
- 5. Интерферометрия
- 6. Голография в технологии
- 7. Голографический метод в интроскопии
- 8. Голографическая микроскопия
- 9. Голографическое кино
- 10. Голографическое телевидение
- 11. Голографическая оптика