| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Решение краевой задачи на примере дифракционной решетки [5]
Дифракция света на решетке лучше всего описывается так называемым уравнением решетки

где  углы, образованные со средней плоскостью решетки падающим и дифрагированным волновыми фронтами соответственно; а — постоянная решетки.
углы, образованные со средней плоскостью решетки падающим и дифрагированным волновыми фронтами соответственно; а — постоянная решетки.
В учебниках это уравнение обычно весьма просто выводится с помощью принципа Гюйгенса. Однако, применяя гюйгенсовское решение, делают неправильное заключение, что плоская дифрагированная волна получается как огибающая многих маленьких сферических волн.
На практике же просто предполагают, что если на плоскую решетку падает плоская волна, то дифрагированные волны также являются плоскими, образуя дискретную совокупность. Фактически существование плоских дифрагированных волн есть следствие всего лишь периодической структуры решетки.
Доказательство существования дискретной совокупности плоских дифрагированных волн, удовлетворяющих уравнению решетки (1), когда на решетку падает плоская волна, сводится к следующему.
Линованные решетки имеют по существу двумерную структуру. Их поверхность описывается функцией  которая не зависит от координаты
которая не зависит от координаты  и является периодической функцией х:
и является периодической функцией х:

Штрихи решетки направлены вдоль оси  Вспомним класс двумерных задач (не зависимых от 2). По своей природе двумерные
Вспомним класс двумерных задач (не зависимых от 2). По своей природе двумерные
задачи являются в сущности скалярными. Однако это не означает, что их можно идентифицировать с неэлектромагнитными задачами, например с акустическими. Двумерную задачу можно сформулировать, используя лишь одну компоненту электромагнитного поля, например  или
или 

Рис. 2, Схема, поясняющая уравнение решетки 
Кроме того, можно показать, что компоненты  или
или  в подобных задачах удовлетворяют волновому уравнению
в подобных задачах удовлетворяют волновому уравнению

написанному в качестве примера для компоненты  где
где  Множитель
Множитель  опущен.
опущен.
Частное решение уравнения (3), имеющее вид

представляет собой выражение плоской волны, где 9 — угол дифракции (не ограниченный в данном случае одним значением  которое удовлетворяет уравнению решетки). Если 9 не является действительным значением, то выражение (4) представляет собой затухающую волну [5, 6].
которое удовлетворяет уравнению решетки). Если 9 не является действительным значением, то выражение (4) представляет собой затухающую волну [5, 6].
Общее решение уравнения (3) состоит из совокупности плоских волн различных направлений и может быть записано в виде интеграла Фурье

где  амплитуда плоской волны. Функция
амплитуда плоской волны. Функция  в общем виде является комплексной, и чтобы ее найти, требуется решить уже конкретную задачу.
в общем виде является комплексной, и чтобы ее найти, требуется решить уже конкретную задачу.
В случае оптической решетки необходимо рассматривать дифракцию поляризованных волн и векторы  или
или  в падающей волне выбрать параллельными штрихам,
в падающей волне выбрать параллельными штрихам,  вдоль оси
вдоль оси  Пусть
Пусть  или
или  компоненты поля впадающей волне для этих двух случаев поляризации. Тогда можно написать
компоненты поля впадающей волне для этих двух случаев поляризации. Тогда можно написать

Пусть далее  - дифрагированное поле. Поскольку суммарное поле
- дифрагированное поле. Поскольку суммарное поле  удовлетворяет волновому уравнению и поскольку поле в падающей волне удовлетворяет тому же уравнению, то дифрагированное поле
удовлетворяет волновому уравнению и поскольку поле в падающей волне удовлетворяет тому же уравнению, то дифрагированное поле  также должно удовлетворять волновому уравнению. В самой общей форме дифрагированное поле
также должно удовлетворять волновому уравнению. В самой общей форме дифрагированное поле  можно представить в виде суммы плоских волн различных направлений
можно представить в виде суммы плоских волн различных направлений

Здесь  амплитуда плоской дифрагированной волны, соответствующей углу распространения
амплитуда плоской дифрагированной волны, соответствующей углу распространения  Согласно уравнению (7), существует бесконечная совокупность дифрагированных волн, непрерывно распределенных по углу.
Согласно уравнению (7), существует бесконечная совокупность дифрагированных волн, непрерывно распределенных по углу.
Докажем, что периодическая структура решетки и то обстоятельство, что граничные условия на поверхности решетки относятся к суммарному полю  приводят к уравнению решетки
приводят к уравнению решетки  которому удовлетворяет только дискретная совокупность волн, взятая из непрерывного углового распределения.
которому удовлетворяет только дискретная совокупность волн, взятая из непрерывного углового распределения.
Фактически на поверхности решетки необходимо иметь

Если в уравнение (8) подставить соотношения (6) и (7), то получим

Разделив результат на  и вынеся за скобку
и вынеся за скобку  получим
получим

Для любых заданных  любого угла у множитель
любого угла у множитель  постоянен. Поэтому, чтобы уравнение (10) удовлетворялось, необходимо положить
постоянен. Поэтому, чтобы уравнение (10) удовлетворялось, необходимо положить

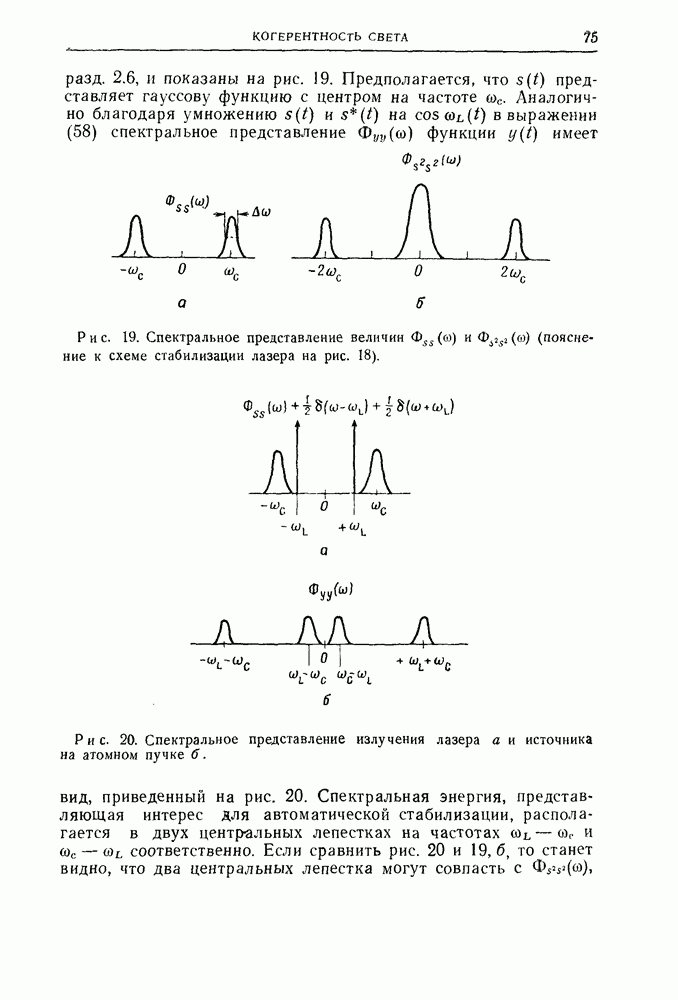
т. е.

Заметим, что  также целое число вследствие того, что
также целое число вследствие того, что  является периодом решетки. Вспоминая, что
является периодом решетки. Вспоминая, что  из соотношения (12) получаем уравнение решетки в окончательном виде
из соотношения (12) получаем уравнение решетки в окончательном виде

Мы доказали таким образом, что плоская волна

падающая на регулярную поверхность с периодом а, создает дифрагированное поле  состоящее из дискретной совокупности плоских волн:
состоящее из дискретной совокупности плоских волн:

Следует обратить внимание на то, что дифракция света на решетке в основном обусловлена граничными условиями и периодичностью структуры решетки. Удивительно то, что точное выражение граничных условий не входит явным образом в то решение, которое было нами получено при доказательстве существования плоских дифрагированных волн, удовлетворяющих уравнению решетки. Очевидно, однако, что амплитуда 
фрагированных волн будет непременно зависеть от вида граничных условий, в частности от свойств материала (диэлектрик, проводник и т. д.) и от профиля штрихов (разд. 4).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора русского издания
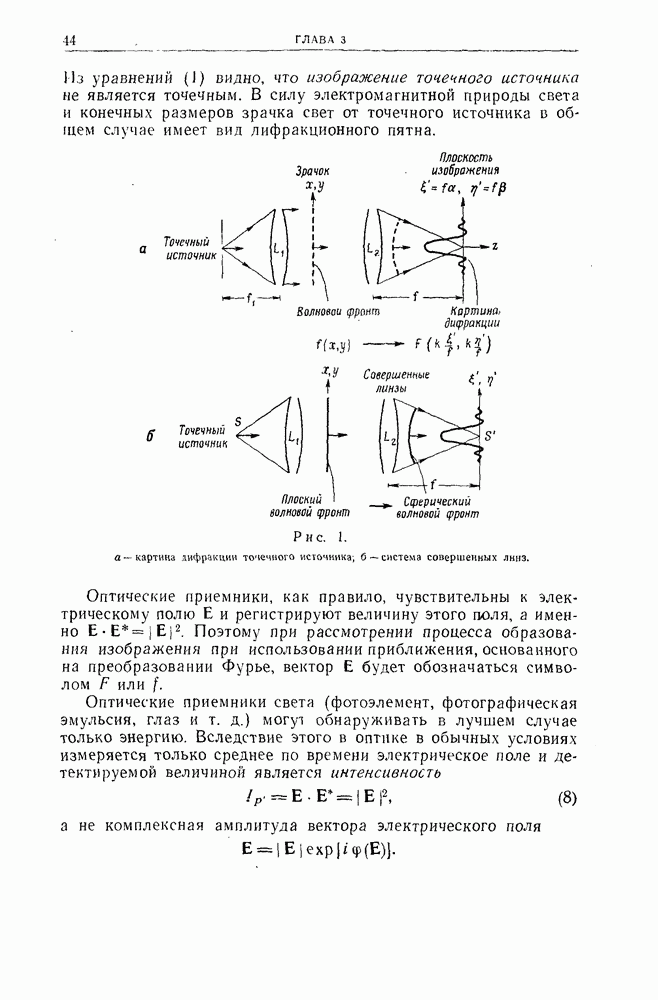
- Глава 1. ВВЕДЕНИЕ
- 1. Современная оптика — раздел радиоалектроники
- 2. Теория — основа радиооптики
- 3. Математические методы современной оптики
- 4. Краевая задача дифракции электромагнитных волн в оптике и некоторые ограничения операционного метода
- 5. Решение краевой задачи на примере дифракционной решетки [5]
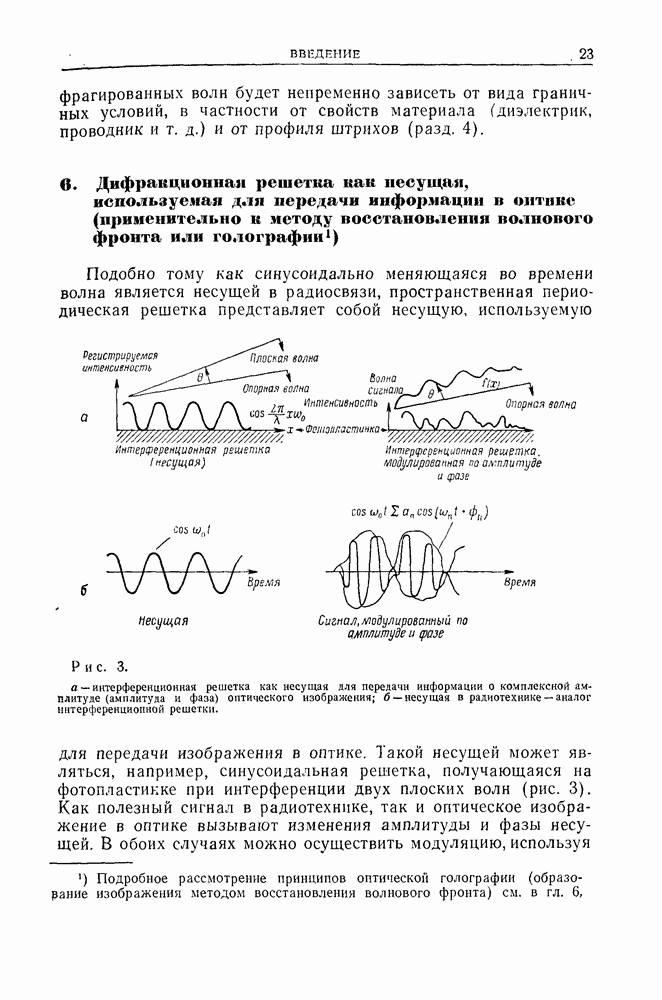
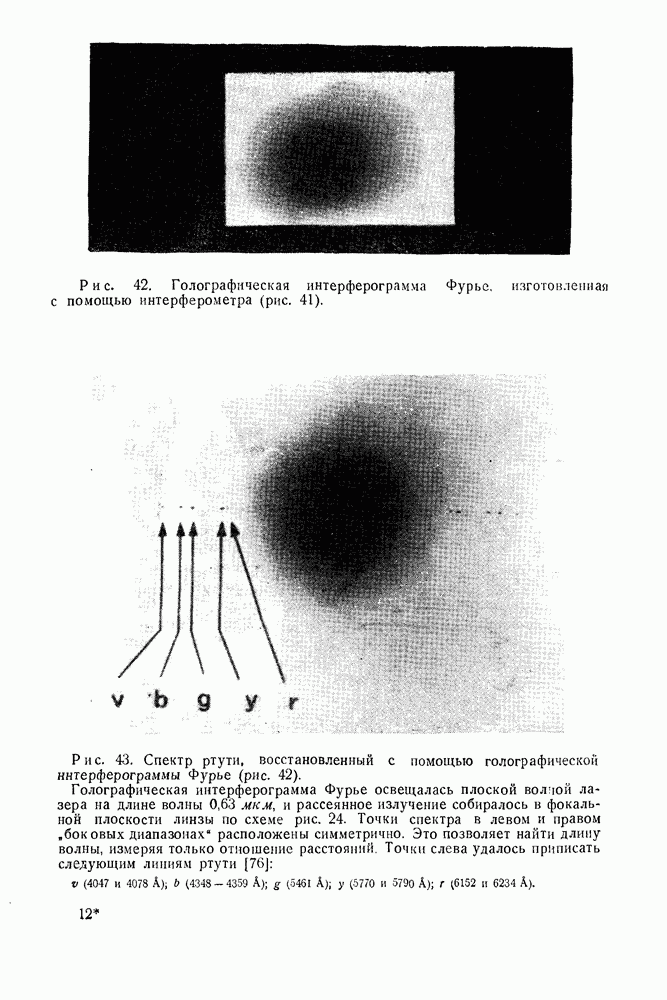
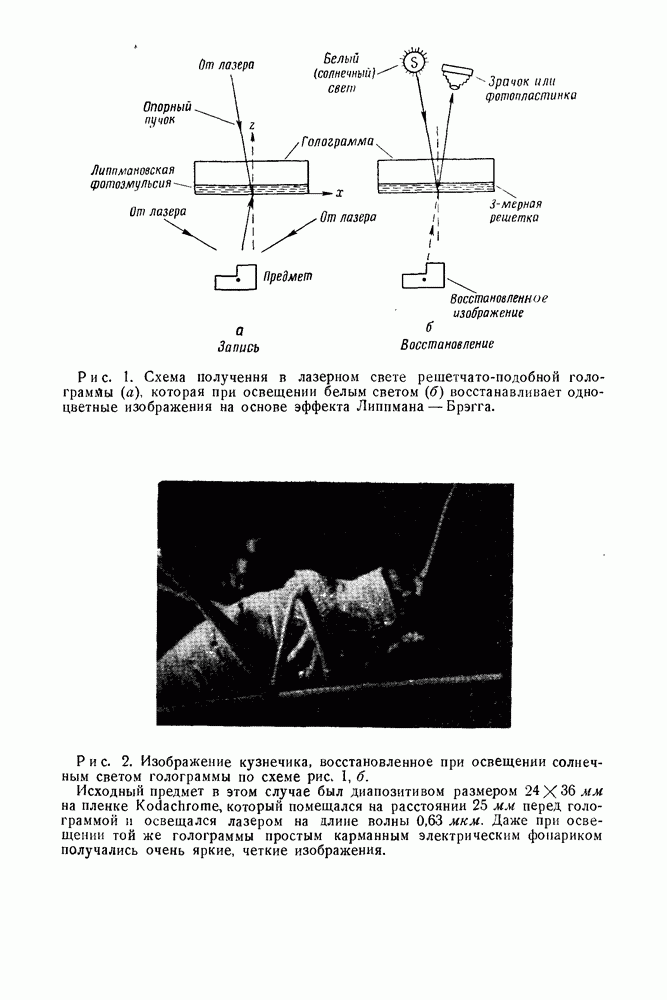
- 6. Дифракционная решетка как несущая, используемая для передачи информации в онтикс (применительно к методу восстановления волнового фронта или голографии
- 7. Оптика и теория связи Исторический обзор
- Глава 2. КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФРАКЦИИ
- 1. Две стороны дифракции света
- 2. Распределение интенсивности в дифракционной картине и в спектре
- 2.2. Проблема образования изображения и принцип Гюйгенса
- 3. Теория образования изображения и обработка оптических сигналов при помощи преобразования Фурье
- Глава 3. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 2. Сложение света, падающего из нескольких точек источника на отдельную точку изображения
- 6. Анализ процесса образования изображения в пространстве фурье-координат
- 7. Физический смысл функции разброса и анализ процесса образования изображения в плоскости фурье-координат
- 7.2. Синусоидальный по интенсивности предмет имеет функцию пространстненно-частотного отклика, совпадающую с фурье-образом дифракционной картины
- 8. Использование фурье-координат для синтеза предметных функций
- Глава 4. КОГЕРЕНТНОСТЬ СВЕТА (ЭКСПЕРИМЕНТАЛЬНЫЕ ХАРАКТЕРИСТИКИ)
- 2. Определение когерентности
- 2.2. Интерференционный анализ временной когерентности
- 2.3. Сравнение корреляционного и интерференционного методов
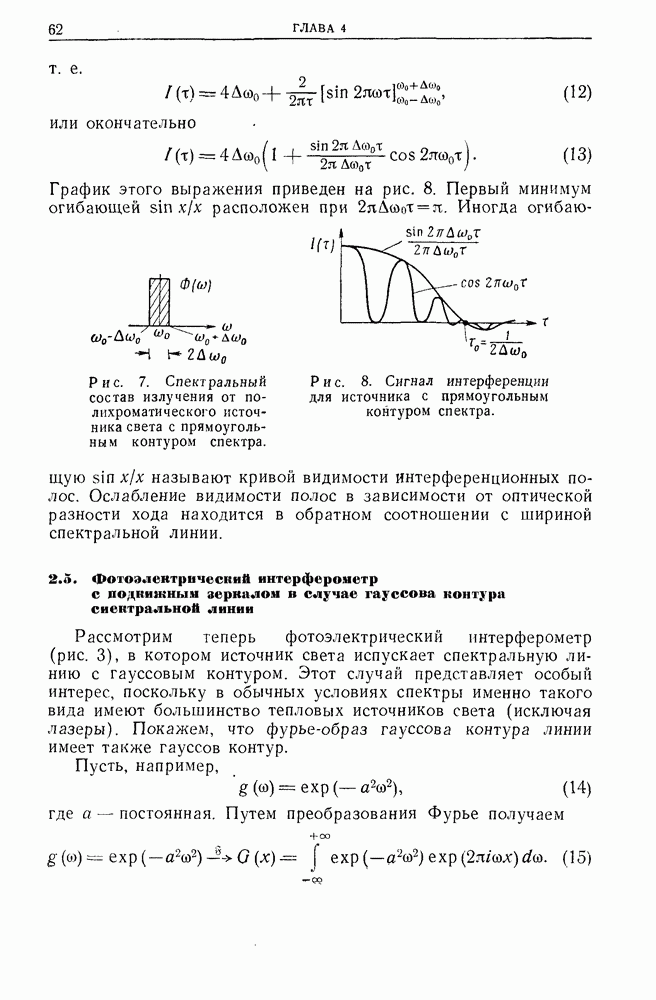
- 2.4. Узкий спектр с прямоугольным контуром
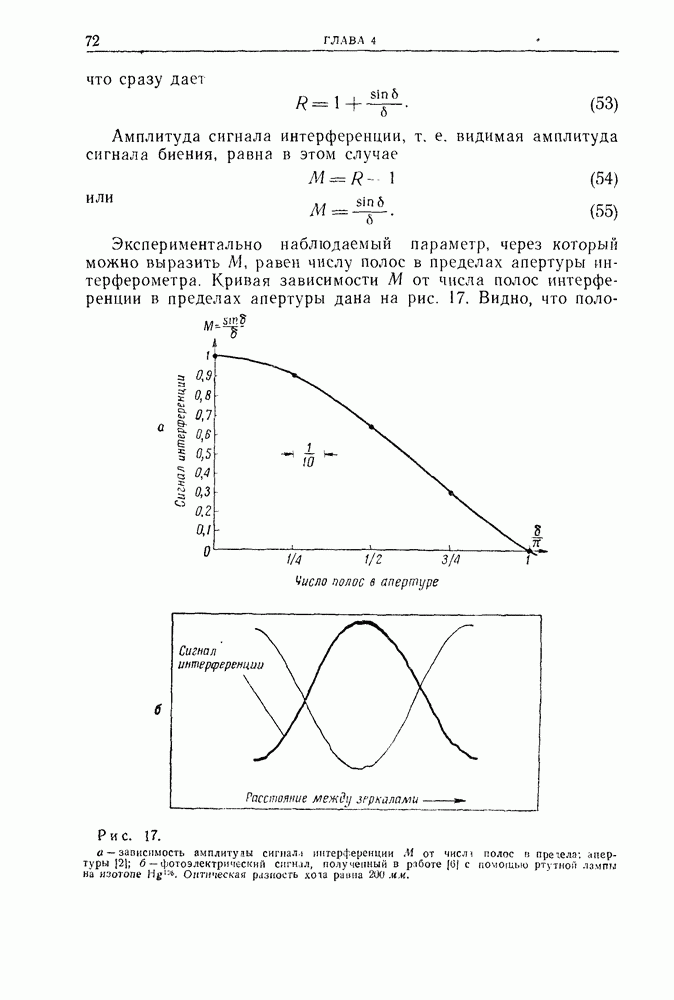
- 2.5. Фотоэлектрический интерферометр с поднижным зеркалом в случае гауссова контура спектральной линии
- 2.6. Физический смысл спектра мощности
- 2.7. Гетеродинный анализ сигналов и биений
- 2.8. Пространственная когерентность
- 2.9. Частичная когерентность света от протяженного некогерентного источника
- 2.10. Корреляция интенсивности при частичной когерентности
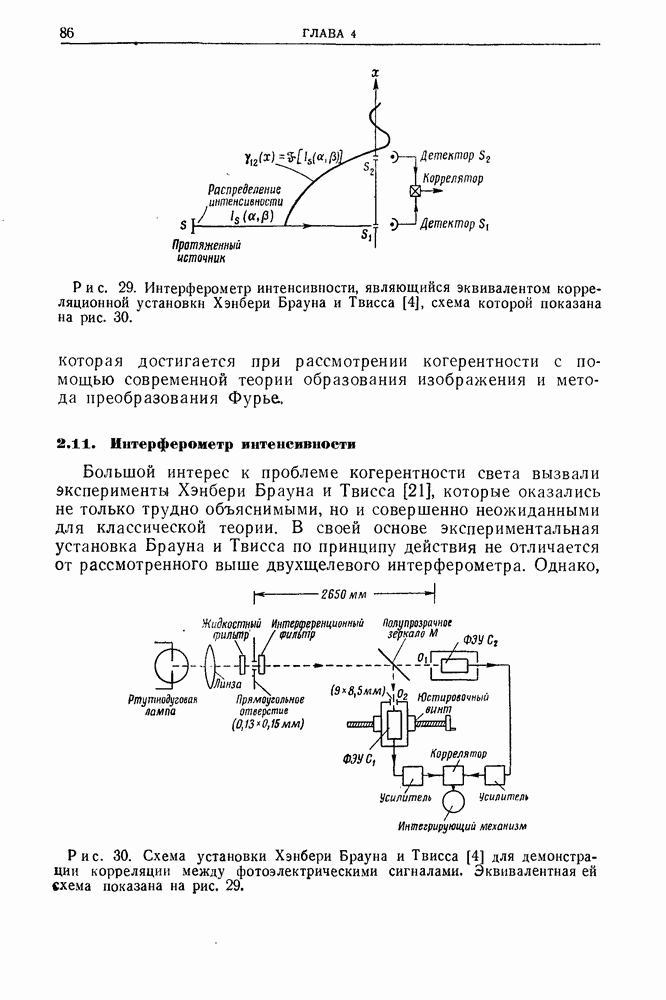
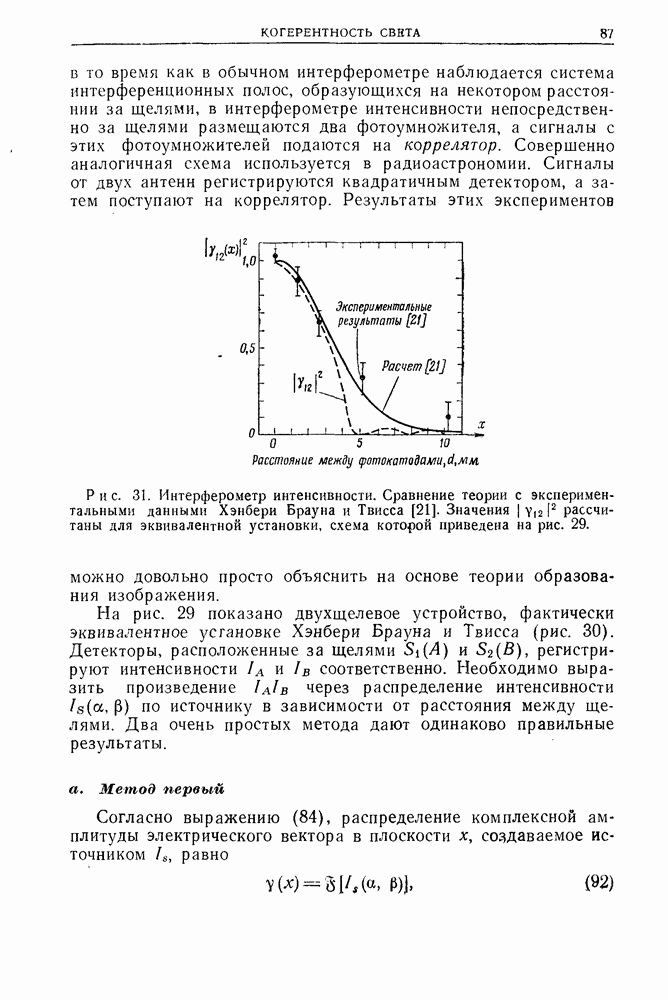
- 2.11. Интерферометр интенсивности
- Глава 5. ОБРАЗОВАНИЕ ИЗОБРАЖЕНИЯ ПРИ КОГЕРЕНТНОМ ОСВЕЩЕНИИ
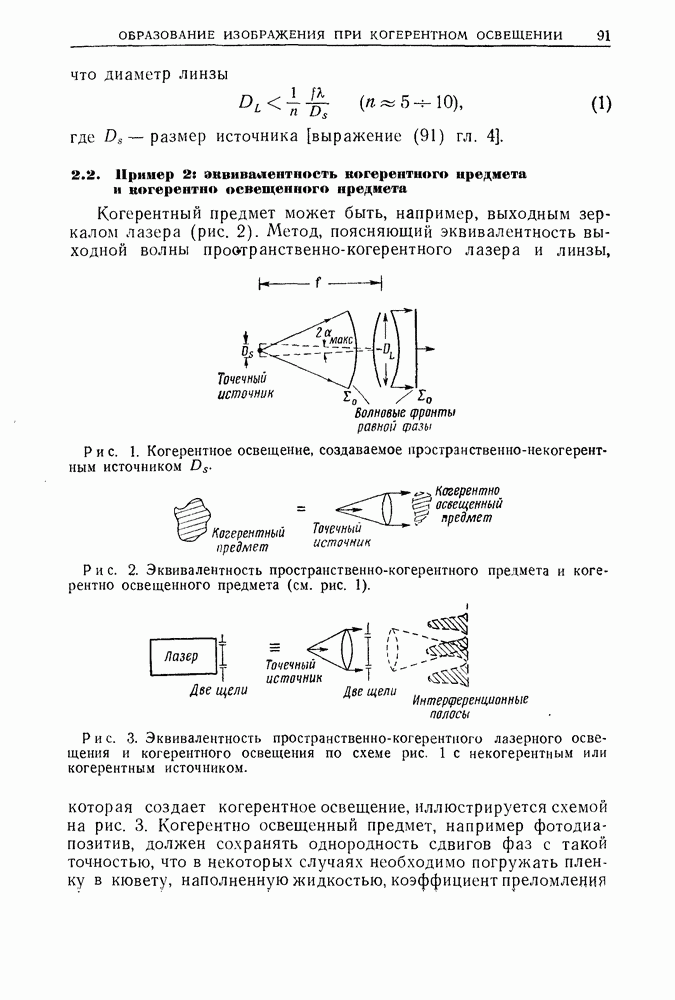
- 2. Когерентное освещение
- 3. Образование изображения при когерентном освещении как процесс двойной дифракции
- 4. Критерии разрешения Аббе и Релея
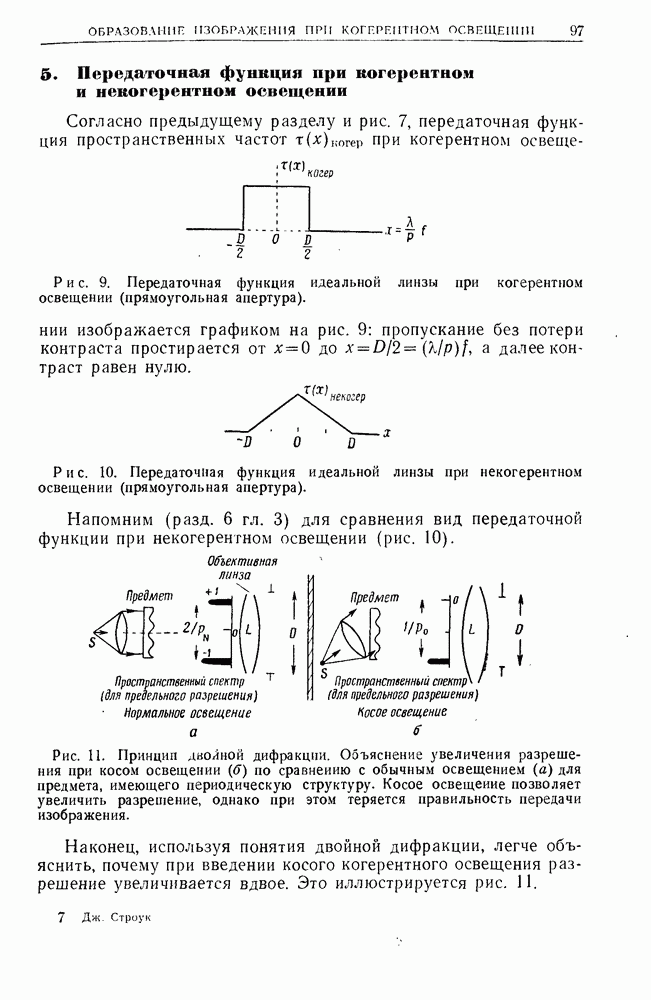
- 5. Передаточная функция при когерентном и некогерентном освещении
- 6. Фазовый контраст
- 7. Оптическая фильтрация с помощью голограммы согласованного фильтра
- 7.1. Процедура изготовления согласованного фильтра и операция фильтрации
- 8. Оптическая обработка информации, корреляционный анализ и оптические корреляторы
- 8.2. Оптический кросс-коррелятор
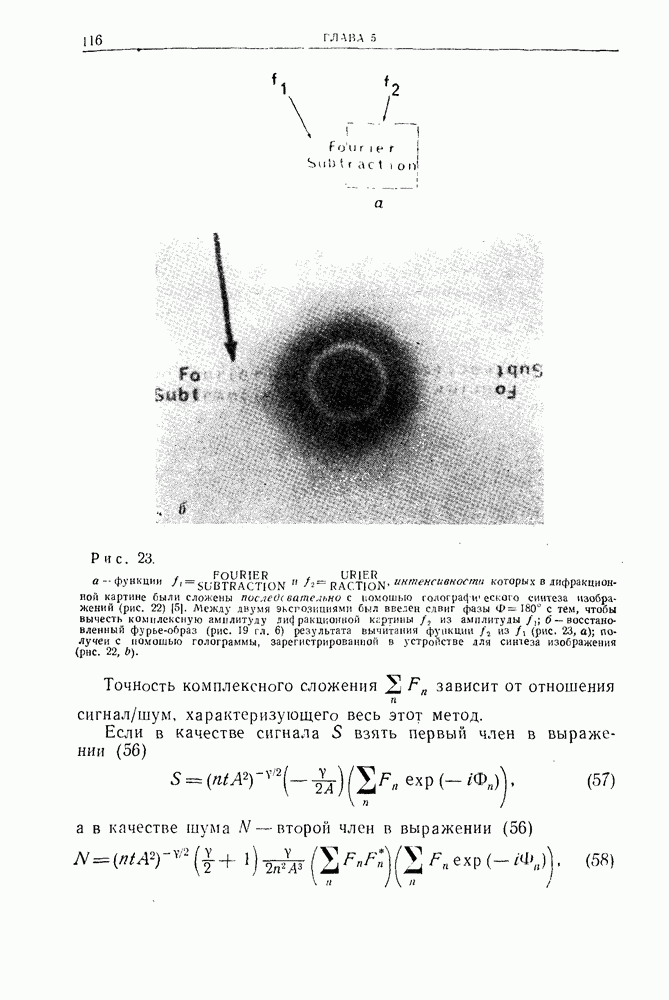
- 9. Интерферометрия и оптический синтез изображения (сложение комплексных амплитуд) методом последовательного наложения голографических картин на одну голограмму [5]
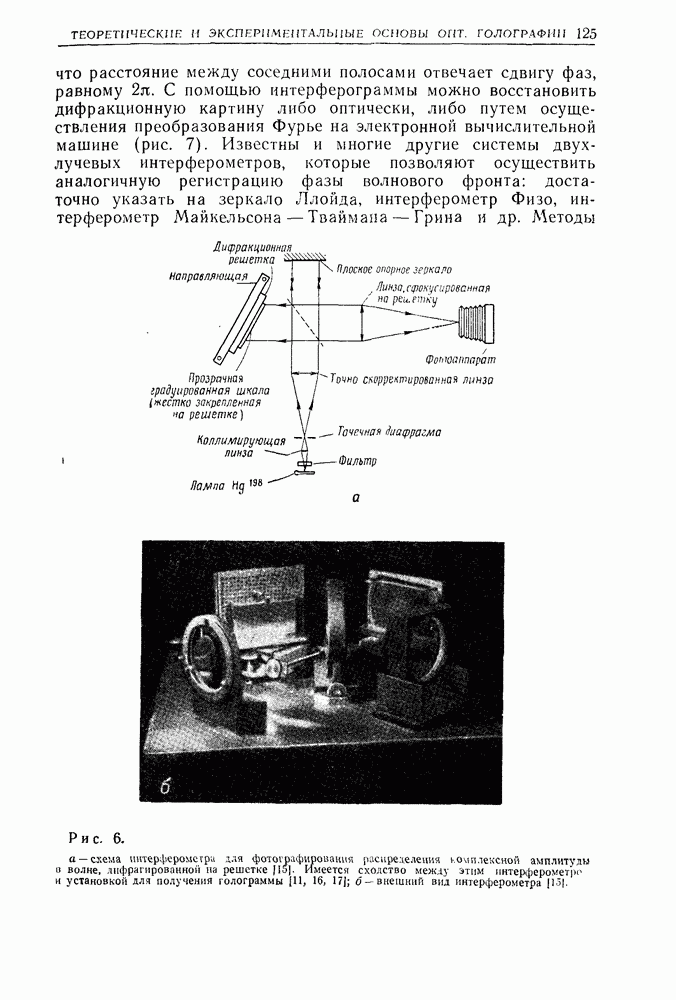
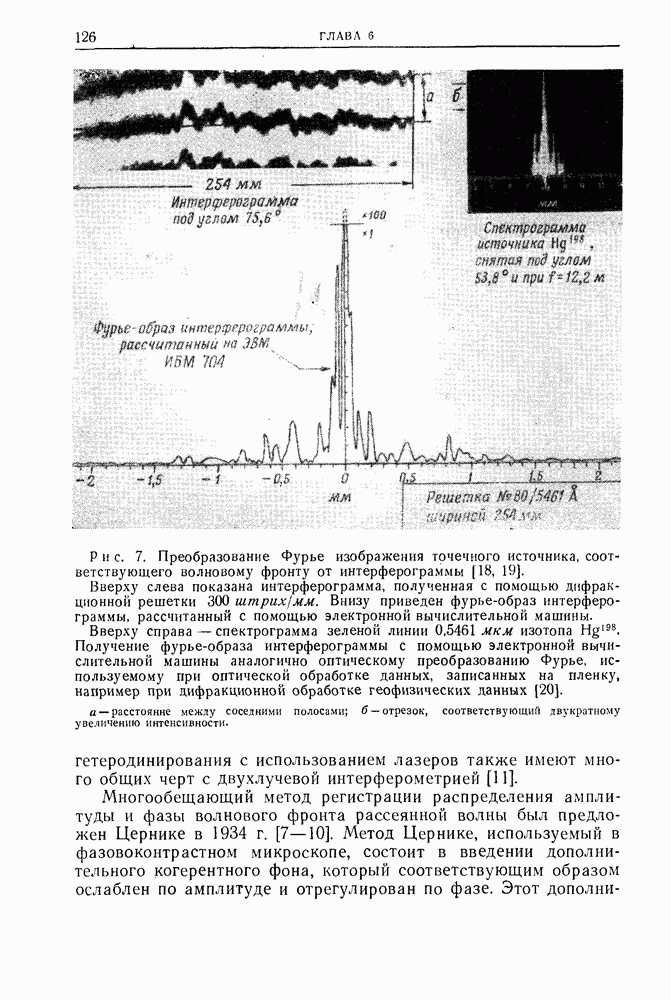
- Глава 6. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ОПТИЧЕСКОЙ ГОЛОГРАФИИ
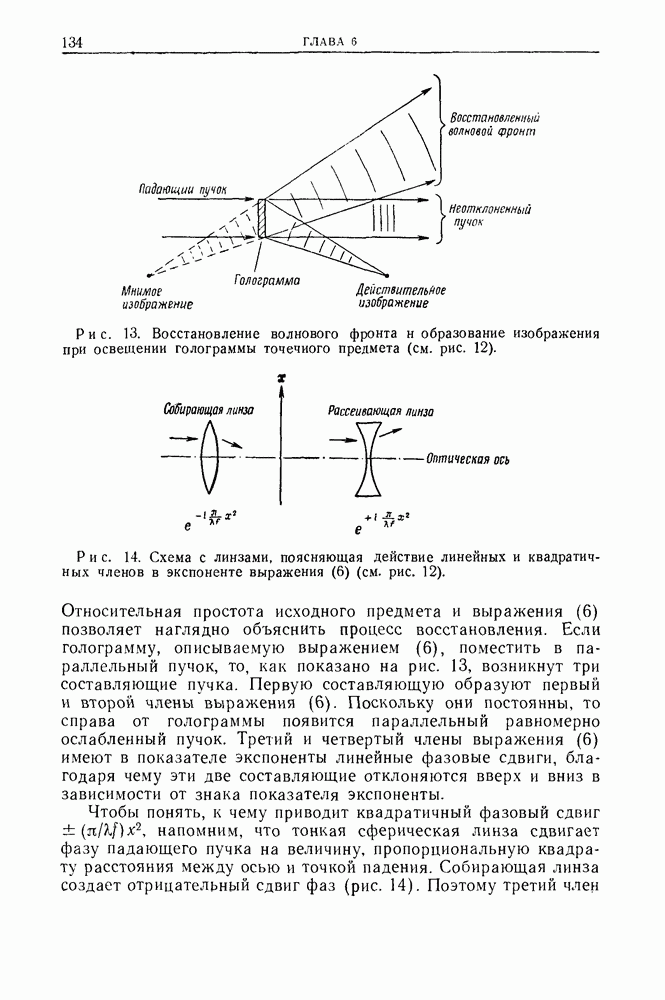
- 2.1. Процесс получевия голограммы
- 2.2. Процесс восстановления изображения
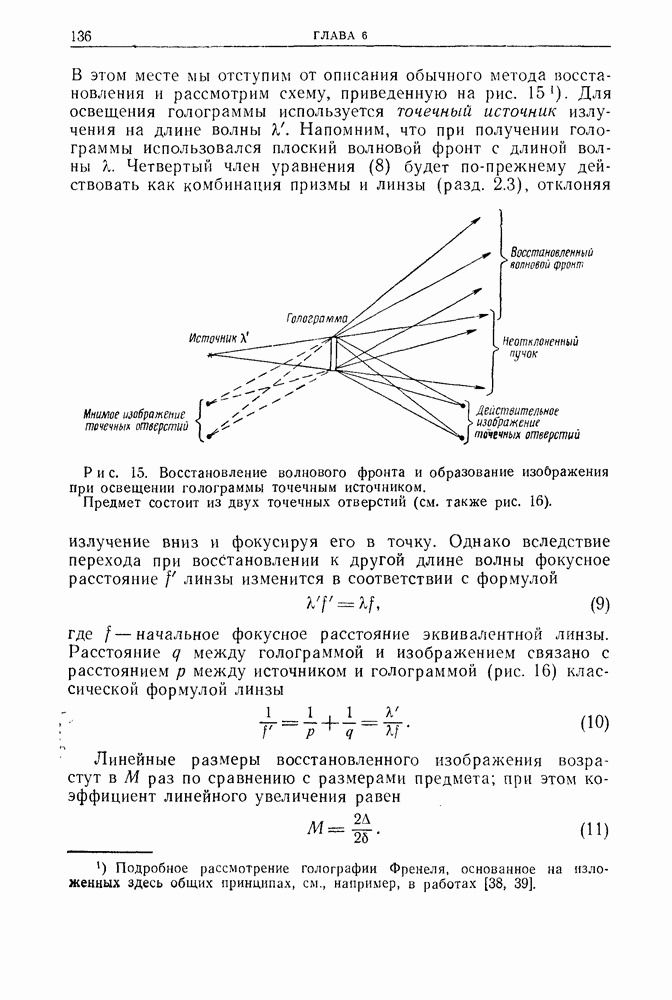
- 2.3. Физические принципы голографии
- 2.4. Геометрическое увеличение
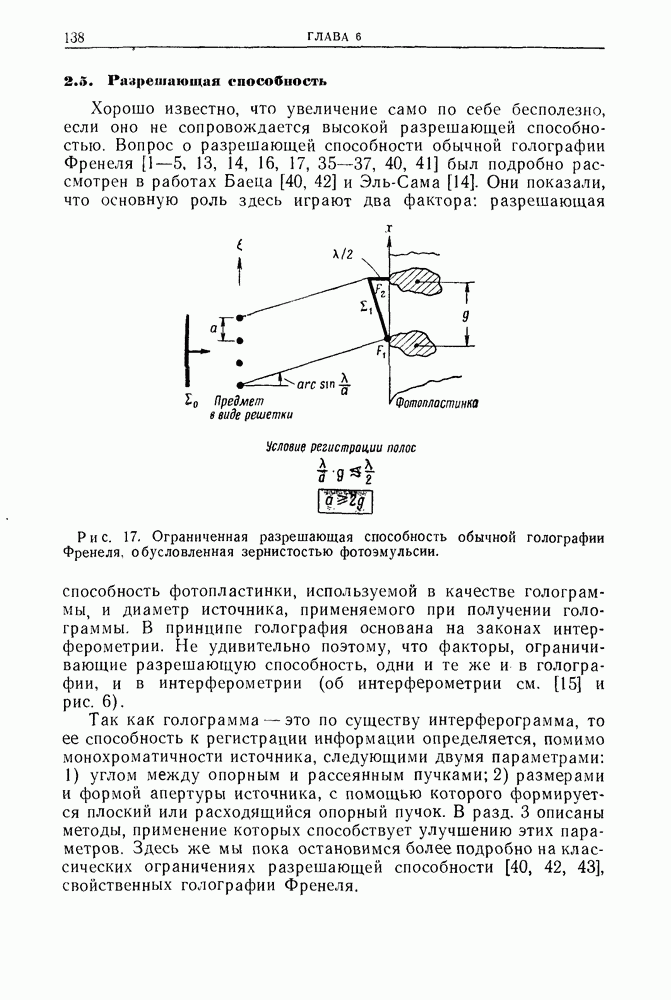
- 2.5. Разрешающая способность
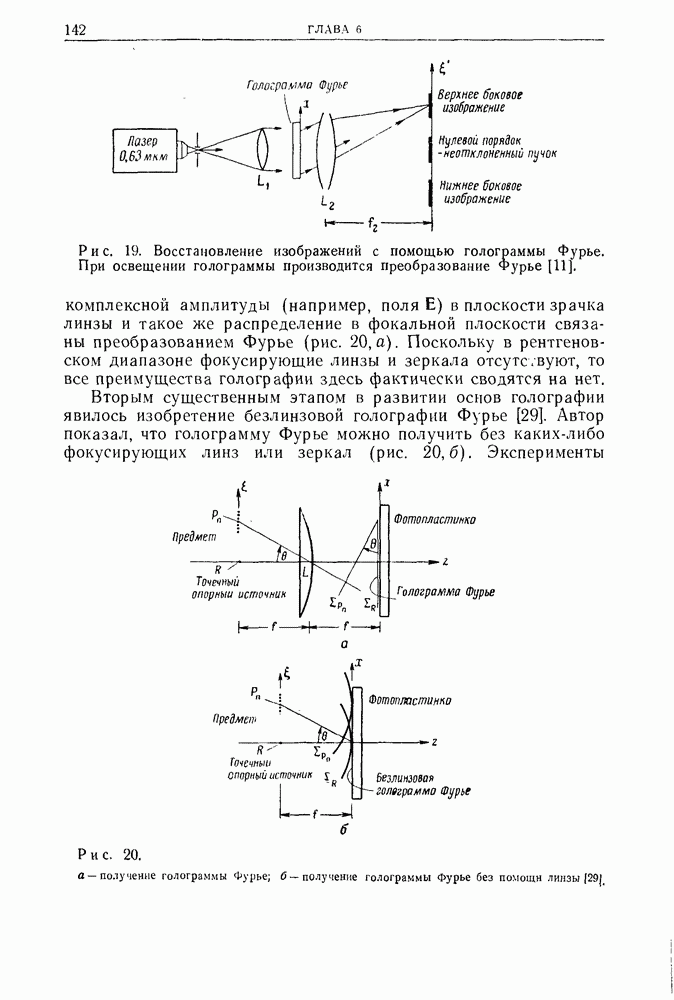
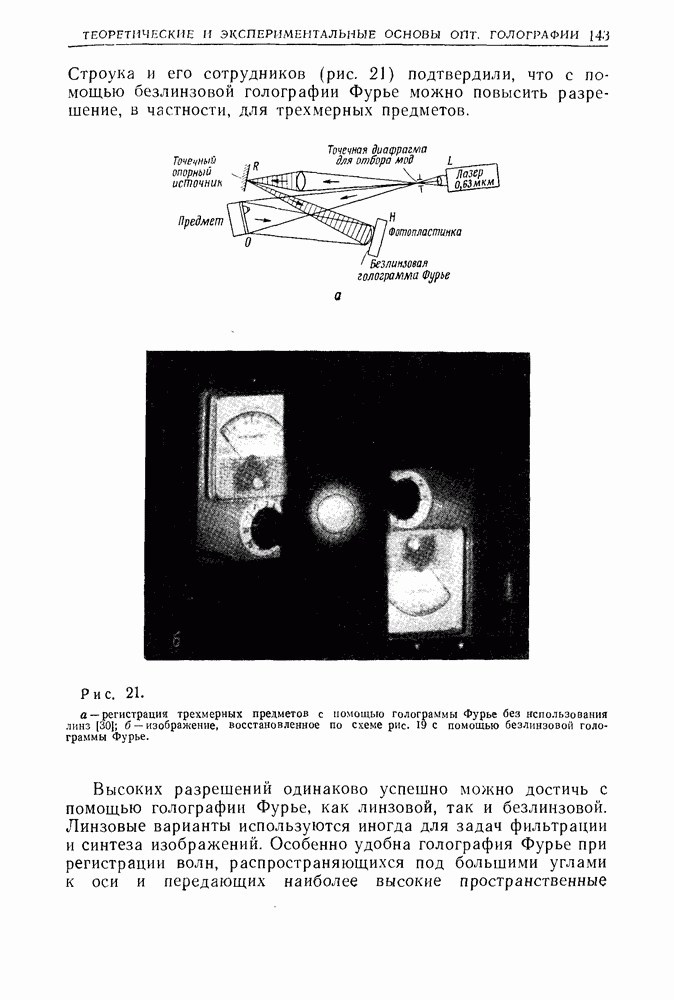
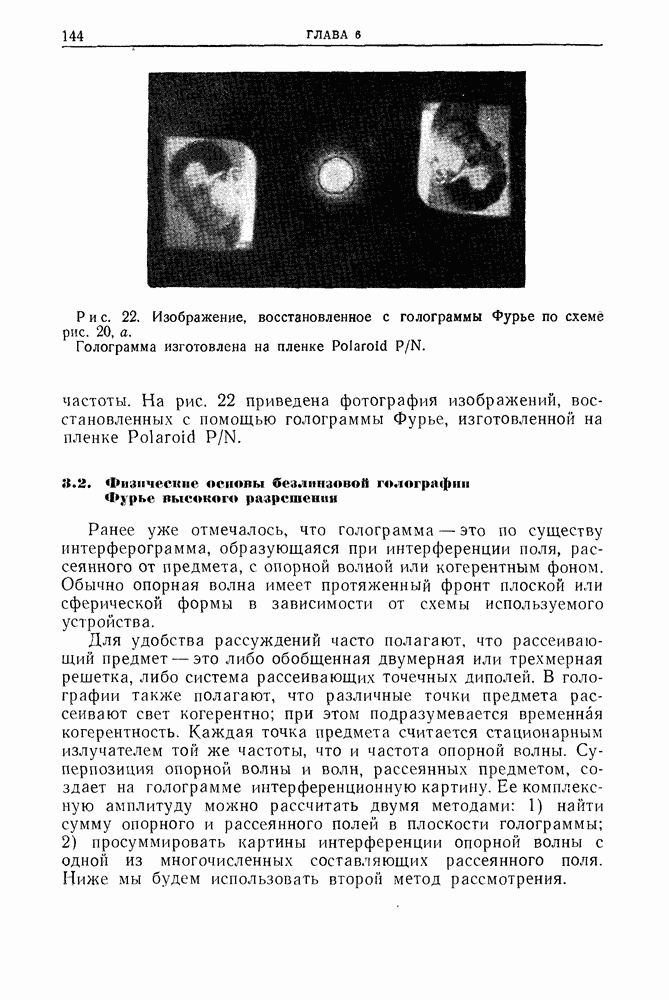
- 3. Голография Фурье с высоким разрешением
- 3.2. Физические основы безлинзовой голографии Фурье высокого разрешения
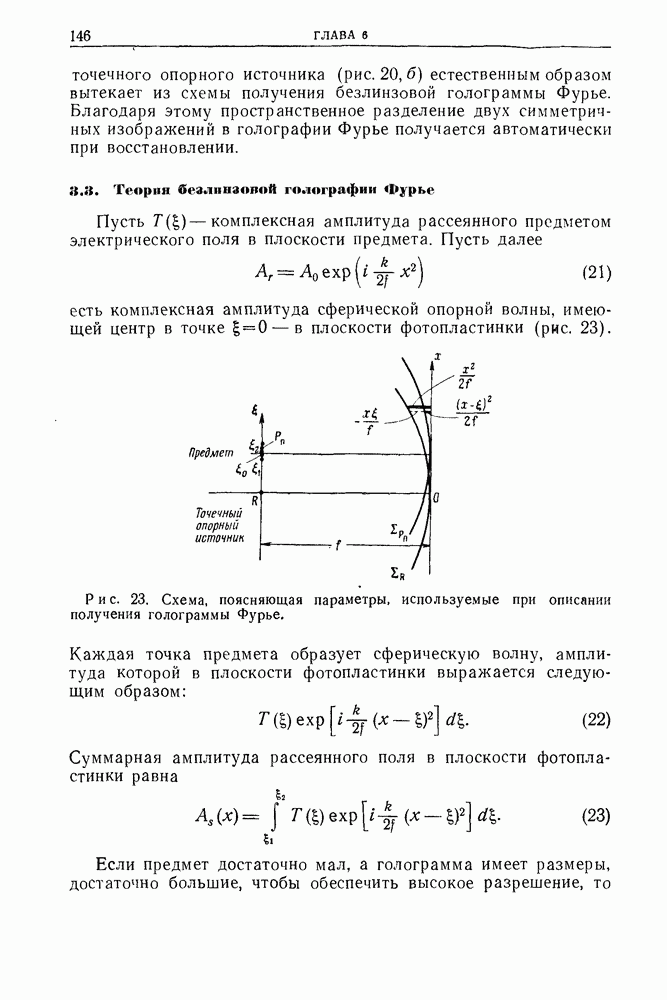
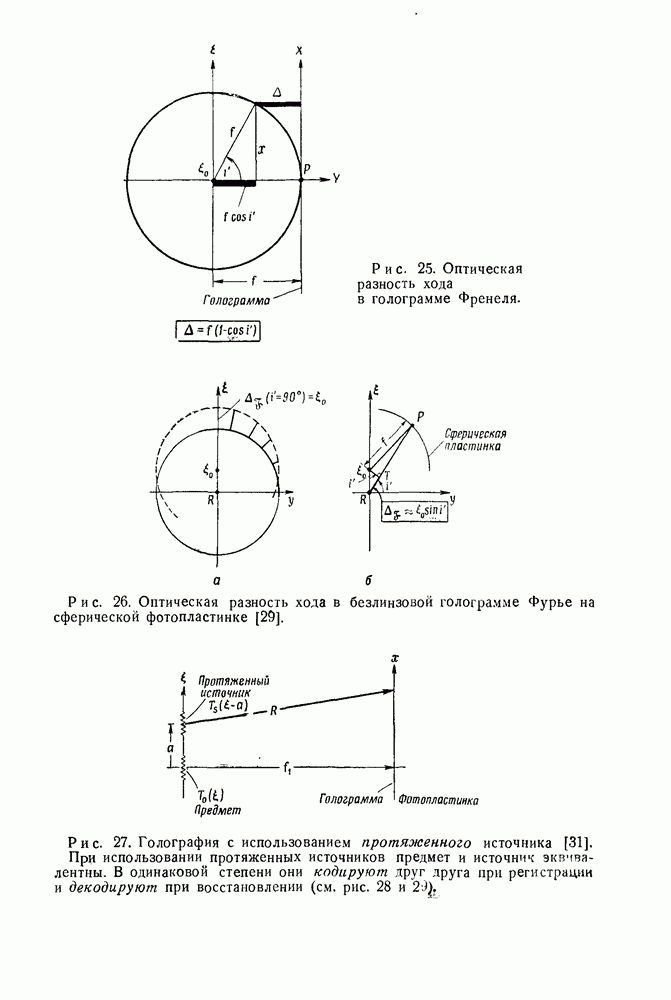
- 3.3. Теория безлинзовой голографии Фурье
- 3.4. Сопоставление разрешающих способностей голографии Фурье в голографии Френеля
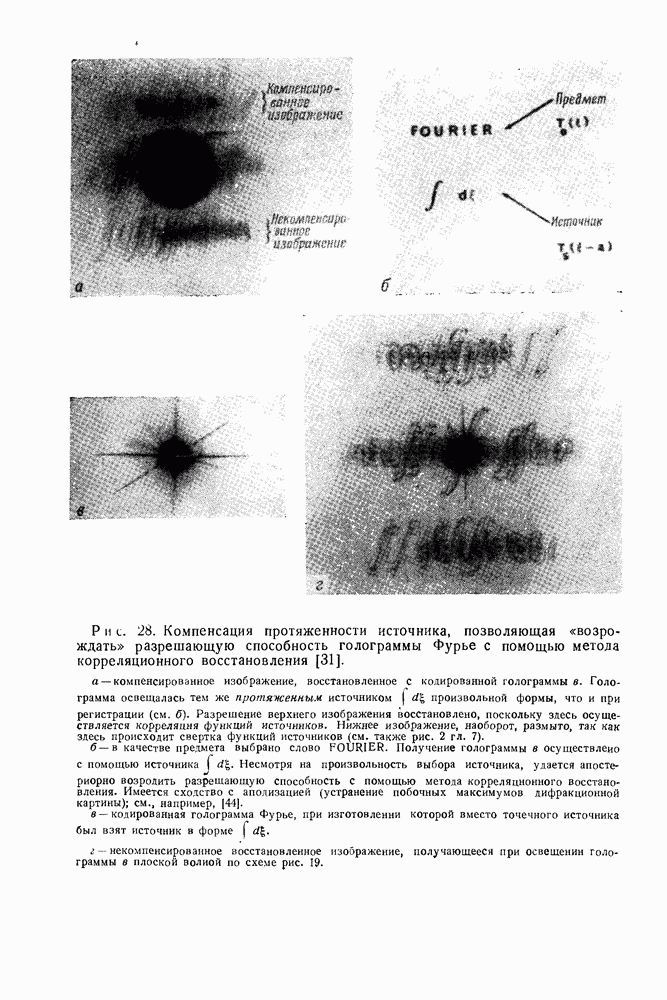
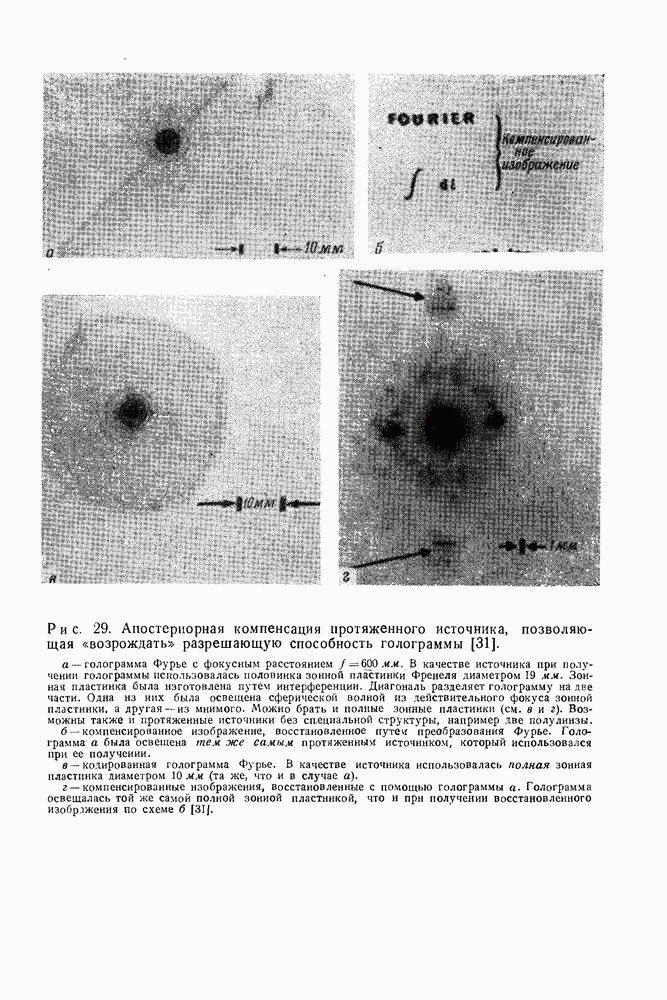
- 4. Компенсация протяженности источника в голографии
- 5. Требование к когерентности в голографии
- 6. Сводка основных результатов
- 7. Электронный микроскоп и рентгеновский голографический микроскоп
- 8. Заключение
- 9. Голография при некогерентном освещении
- 9.2. Голография при пространственно-некогерентном освещении
- Глава 7. ПРЕОБРАЗОВАНИЕ ФУРЬЕ. ОПЕРАЦИИ СВЕРТКИ И КОРРЕЛЯЦИИ. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ТЕОРИЯ РАСПРЕДЕЛЕНИЙ, ИЛИ ОБОБЩЕННЫХ ФУНКЦИЙ
- 1. Преобразование Фурье
- 2. Свертка
- 3. Функция корреляции
- 4. Распределения, или обобщенные функции
- 4.2. Импульсный отклик линейной системы
- 4.3. Отклик линейной системы на произвольную входную функцию
- 5. Спектральный анализ
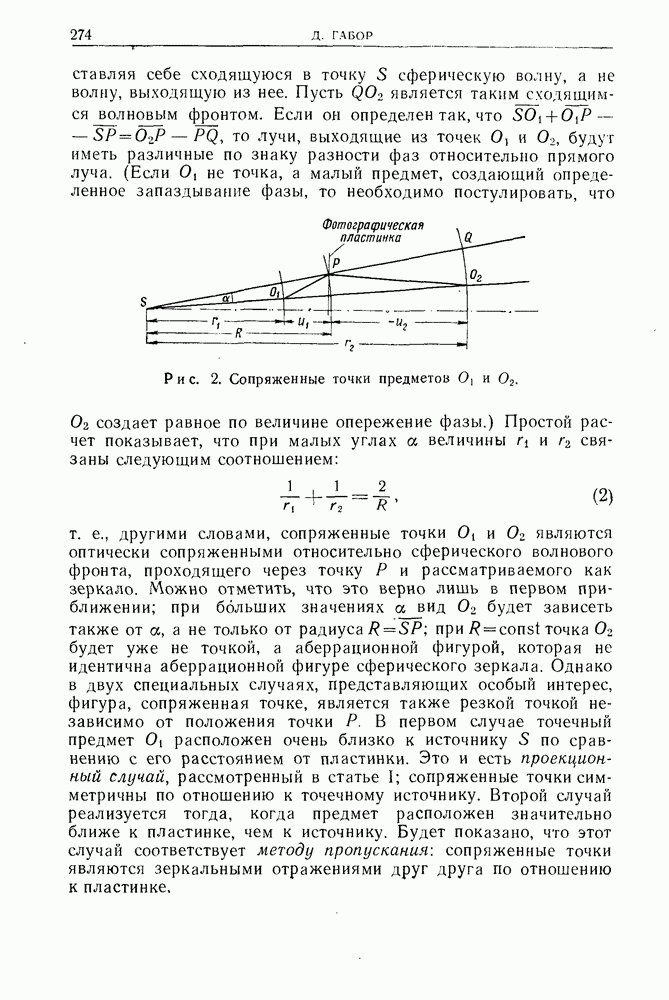
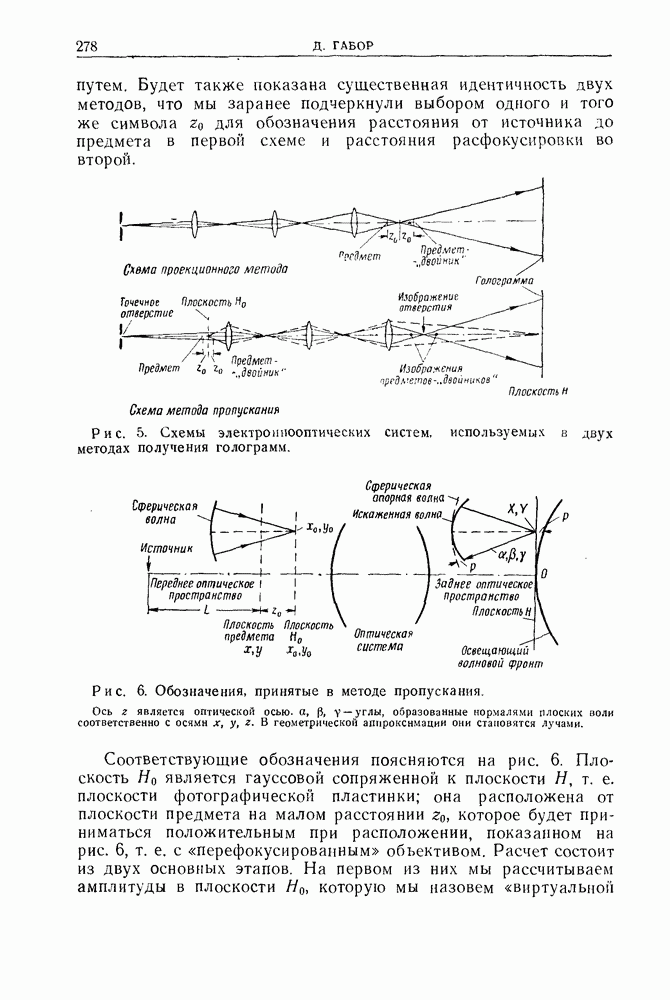
- Дополнение автора к русскому изданию. ВОССТАНОВЛЕНИЕ ГОЛОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ В БЕЛОМ СВЕТЕ С ИСПОЛЬЗОВАНИЕМ ДИФРАКЦИОННОГО ЭФФЕКТА ЛИППМАНА — БРЭГГА
- ПРИЛОЖЕНИЕ 1. МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА
- Принцип восстановления волнового фронта
- Освещение сферической волной
- Восстановление при освещении точечным источником
- Побочная часть волны при восстановлении с помощью точечного источника
- Ухучшенне разделения изобрашений с помощью масок и других методов
- Освещающие волны с астигматизмом и сферической аберрацией
- Восстановление при наличии сферической аберрации и астигматизма
- Критерии когерентности
- Восстановление в оптическом диапазоне
- Экспериментальная проверка
- Заключение
- МИКРОСКОПИЯ НА ОСНОВЕ МЕТОДА ВОССТАНОВЛЕНИЯ ВОЛНОВОГО ФРОНТА, II
- 2. Принцип восстановления волнового фронта
- 3. Теория образования изображения при использовании метода пропускания
- 4. Восстановление
- 5. Критерии когерентности
- 6. Условия, необходимые для получения голограмм
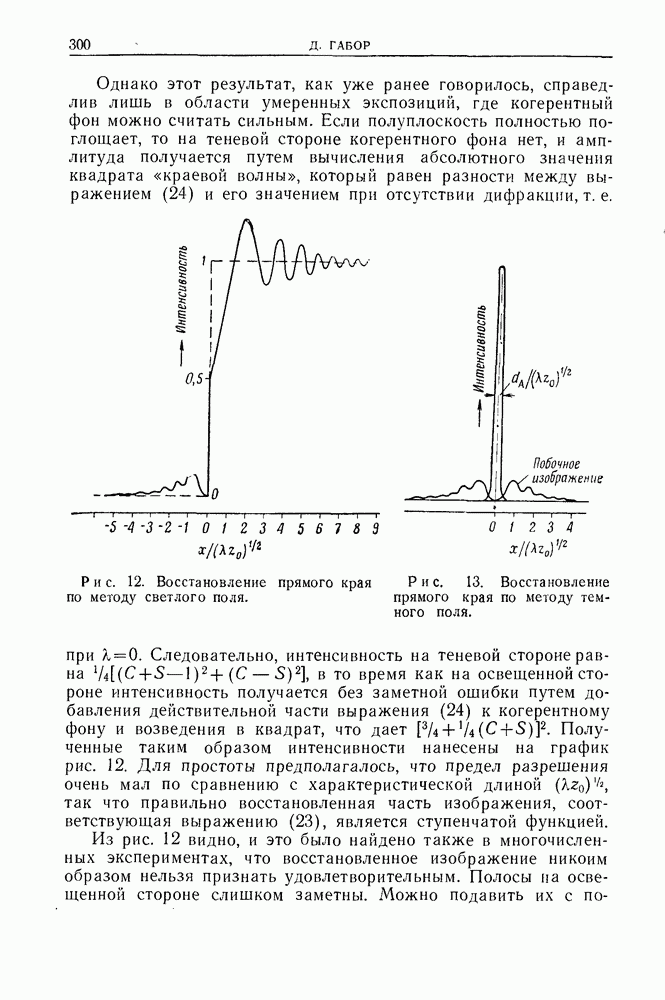
- 7. Восстановление по методу темного поля
- ПРИЛОЖЕНИЕ 2. ПРИМЕНЕНИЯ ГОЛОГРАФИИ
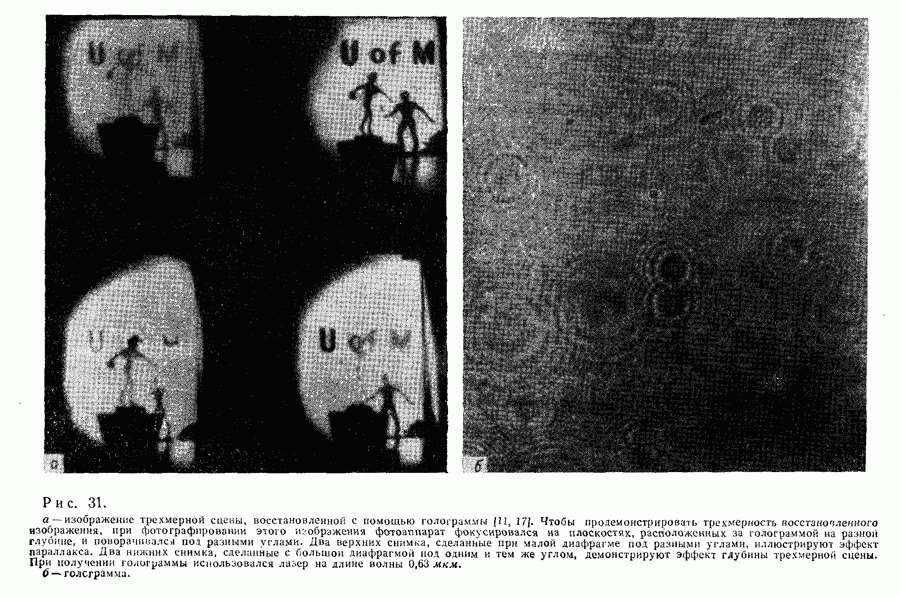
- 2. Трехмерная фотография
- 3. Распознавание образов
- 4. Иитерференционная память
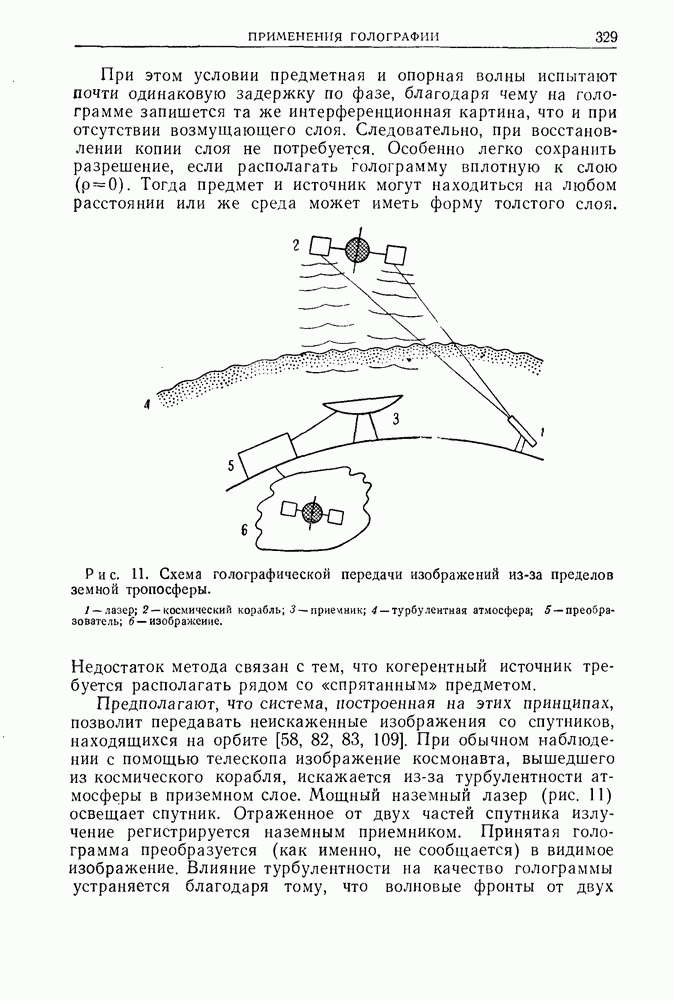
- 5. Интерферометрия
- 6. Голография в технологии
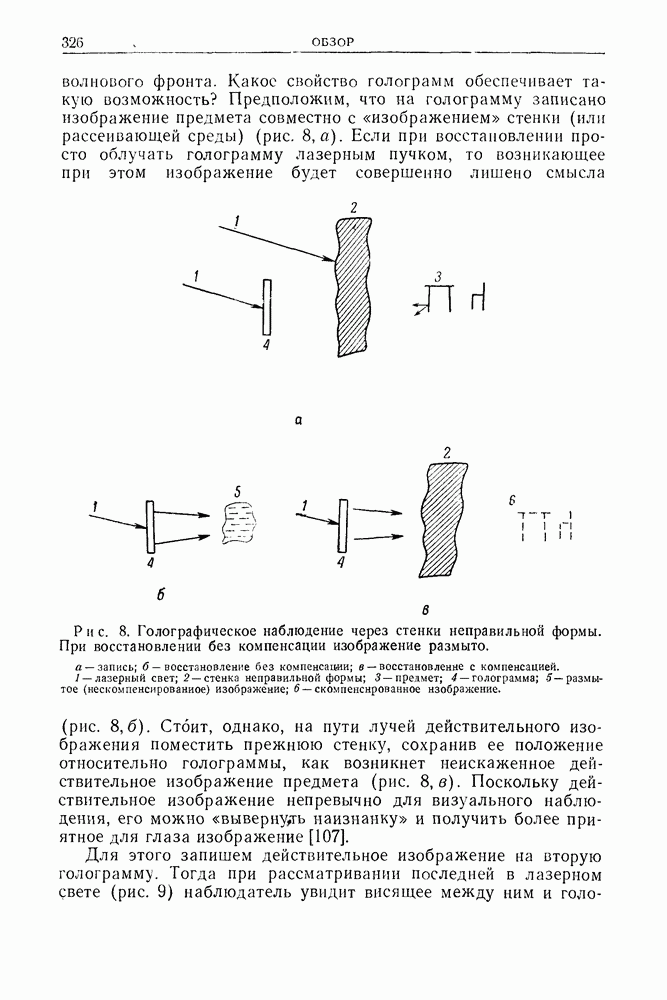
- 7. Голографический метод в интроскопии
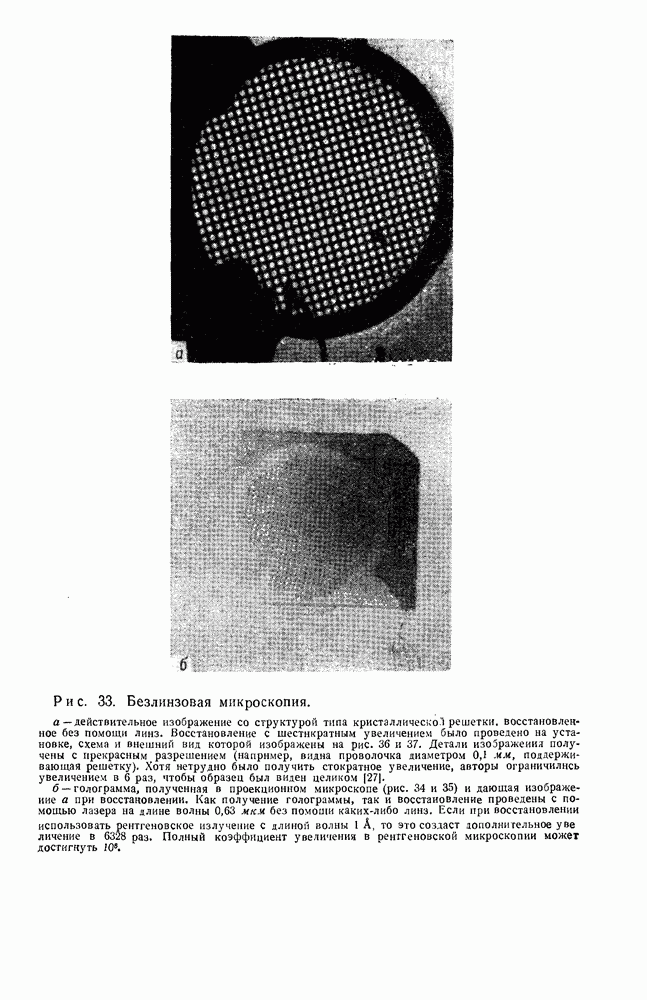
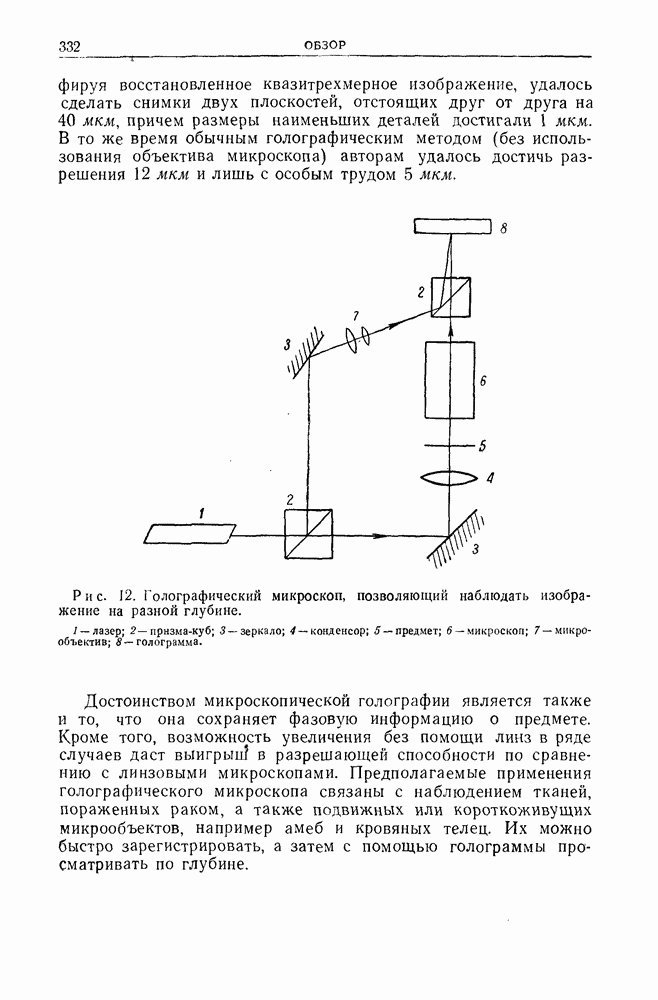
- 8. Голографическая микроскопия
- 9. Голографическое кино
- 10. Голографическое телевидение
- 11. Голографическая оптика