| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 5. Восстановление значений характеристической функции в классе линейных решающих правил
Пусть дана полная выборка

На полной выборке множество решающих правил распадается на конечное число  классов эквивалентности
классов эквивалентности  Два решающих правила
Два решающих правила  попадают в один класс эквивалентности, если они одинаково делят выборку (10.24) на две подвыборки.
попадают в один класс эквивалентности, если они одинаково делят выборку (10.24) на две подвыборки.
Всего возможно  разделений выборки (10.24) на два класса с помощью правил
разделений выборки (10.24) на два класса с помощью правил  и, следовательно, существует
и, следовательно, существует  классов эквивалентности.
классов эквивалентности.
Согласно определению (см. § 7 гл. VI)

Для линейных решающих правил в пространстве размерности  справедлива оценка (см. § 8 гл. VI)
справедлива оценка (см. § 8 гл. VI)

Таким образом, на полной выборке (10.24) множество линейных решающих правил  распадается на
распадается на  классов эквивалентности
классов эквивалентности 
Заметим, что классы эквивалентности не равнозначны по объему. Одни из них содержат «больше» решающих правил, другие — «меньше». Поставим в соответствие каждому классу эквивалентности величину, характеризующую долю линейных решающих правил, принадлежащих этому классу по отношению ко всем линейным решающим правилам. Такую величину можно сконструировать. Действительно, поставим в соответствие каждой функции

направляющий вектор (рис. 19)

Тогда множеству всех гиперплоскостей соответствует в пространстве параметров а единичная сфера, каждому классу эквивалентности  соответствует на поверхности сферы своя область. (Множество из
соответствует на поверхности сферы своя область. (Множество из  классов эквивалентности разбивают сферу на
классов эквивалентности разбивают сферу на  областей.) Отношение площади, соответствующей области к площади сферы X и характеризует долю функций из класса эквивалентности
областей.) Отношение площади, соответствующей области к площади сферы X и характеризует долю функций из класса эквивалентности  отношению ко всем возможным линейным решающим правилам.
отношению ко всем возможным линейным решающим правилам.

Рис. 19.
Упорядочим теперь классы эквивалентности по убыванию величин  и введем следующую структуру:
и введем следующую структуру:

где элементу  принадлежат лишь те классы эквивалентности, для которых
принадлежат лишь те классы эквивалентности, для которых

Таким образом, мы построили структуру, каждый элемент  которой обладает экстремальным свойством: для данного числа классов эквивалентности он содержит максимальную долю всех решающих правил. Однако на практике вычислить величину
которой обладает экстремальным свойством: для данного числа классов эквивалентности он содержит максимальную долю всех решающих правил. Однако на практике вычислить величину  и, следовательно, построить структуру (10.25) трудно. Поэтому мы рассмотрим другую характеристику объема класса эквивалентности, которая близка по смыслу к и может быть найдена на практике.
и, следовательно, построить структуру (10.25) трудно. Поэтому мы рассмотрим другую характеристику объема класса эквивалентности, которая близка по смыслу к и может быть найдена на практике.
Обозначим через  величину расстояния между выпуклыми оболочками векторов полной выборки, отнесенных решающими правилами из
величину расстояния между выпуклыми оболочками векторов полной выборки, отнесенных решающими правилами из  к разным классам, и поставим в соответствие классу эквивалентности
к разным классам, и поставим в соответствие классу эквивалентности  число
число

где  радиус минимальной сферы, содержащей множество (10.24), т. е.
радиус минимальной сферы, содержащей множество (10.24), т. е.

Зададим на множестве классов эквивалентности структуру

где в  включены лишь такие классы эквивалентности
включены лишь такие классы эквивалентности  для которых
для которых

Множество  в (10.27) пусто.
в (10.27) пусто.
Для того чтобы построить метод упорядоченной минимизации суммарного риска на структуре (10.27), оценим число  классов эквивалентности, принадлежащих элементу структуры
классов эквивалентности, принадлежащих элементу структуры 
Справедлива
Лемма. Число  классов эквивалентности в
классов эквивалентности в  оценивается величиной
оценивается величиной

где  — минимум двух величин:
— минимум двух величин:

 размерность пространства,
размерность пространства,  целая часть числа а.
целая часть числа а.
Доказательство. Заметим, что число  равно максимальному числу разбиений выборки
равно максимальному числу разбиений выборки

на два таких класса, что расстояние между их выпуклыми оболочками больше  т. е.
т. е.

Число таких решающих правил не превосходит

где  максимальное число точек выборки, для которых любое разбиение на два класса удовлетворяет условию (10.31). Заметим, что если условие (10.31)
максимальное число точек выборки, для которых любое разбиение на два класса удовлетворяет условию (10.31). Заметим, что если условие (10.31)
выполняется, то разбиение заведомо осуществляется с помощью гиперплоскости, поэтому заведомо

где  размерность пространства.
размерность пространства.
Пусть теперь задано  точек
точек

 всевозможных разбиений этих точек на два подмножества
всевозможных разбиений этих точек на два подмножества

Обозначим через  расстояние между выпуклыми оболочками векторов, принадлежащих разным подмножествам при разбиении
расстояние между выпуклыми оболочками векторов, принадлежащих разным подмножествам при разбиении 
Тот факт, что условие (10.31) выполняется для всякого  можно записать как
можно записать как

Тогда число  не превосходит максимального числа векторов, при котором еще выполняется неравенство
не превосходит максимального числа векторов, при котором еще выполняется неравенство

Из соображений симметрии следует, что максимум  достигается, когда векторы
достигается, когда векторы  располагаются в вершинах правильного
располагаются в вершинах правильного  -мерного симплекса, вписанного в шар радиуса
-мерного симплекса, вписанного в шар радиуса  разбиение на два подсимплекса размерности
разбиение на два подсимплекса размерности  для четных
для четных  и два подсимплекса размерности
и два подсимплекса размерности  для нечетных
для нечетных  При этом путем элементарных расчетов может быть найдено, что
При этом путем элементарных расчетов может быть найдено, что

Для  величины
величины

близки (различаются менее чем на 0,001). Поэтому примем

(Оценкой сверху  было бы выражение
было бы выражение

Из неравенств (10.32) и (10.33) следует, что для целых 

Окончательно, учитывая, что разбиение осуществляется гиперплоскостью, т. е.  получаем
получаем

И следовательно, согласно теореме 6.6

Лемма доказана.
Из теоремы 10.2 и леммы следует, что с вероятностью 1—г] одновременно для всех решающих правил из  будет выполнено неравенство
будет выполнено неравенство

где k — наименьшее решение неравенства

Метод упорядоченной минимизации суммарного риска состоит в том, чтобы индексировать рабочую выборку с помощью правила  которое минимизирует по
которое минимизирует по  и а функционал (10.35). Пусть минимум равен
и а функционал (10.35). Пусть минимум равен  Для такой индексации справедливо утверждение
Для такой индексации справедливо утверждение

В главе XI мы приведем описание алгоритмов, минимизирующих суммарный риск в классе линейных решающих
правил. Здесь же рассмотрим пример, иллюстрирующий разницу в решении задачи классификации векторов рабочей выборки методом минимизации суммарного риска и с помощью решающего правила минимизирующего эмпирический риск на обучающей последовательности.
На рис. 20 векторы первого класса обучающей последовательности обозначены крестиками, векторы второго класса — кружочками. Черными точками показаны векторы экзаменационной выборки.

Рис. 20.
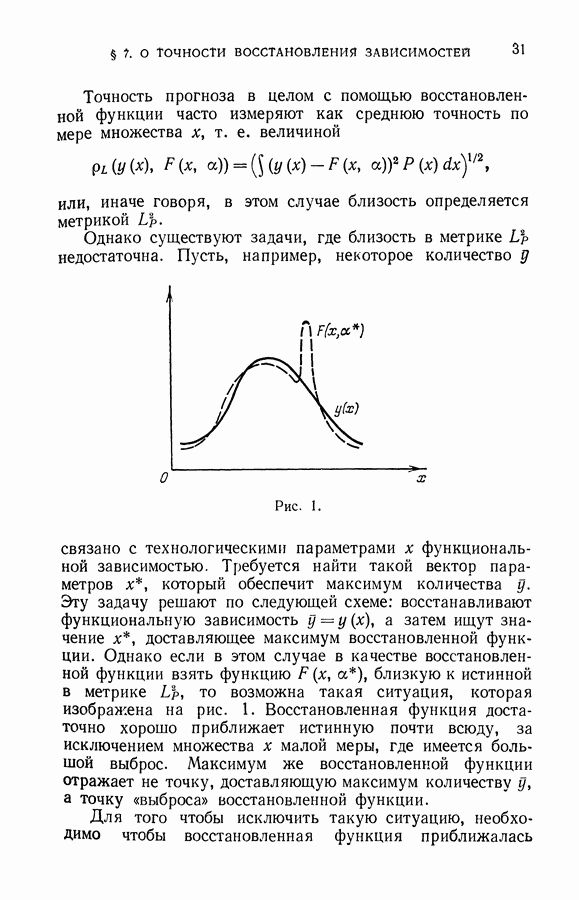
Решение этой задачи в схеме минимизации среднего риска заключается в том, чтобы построить разделяющую гиперплоскость, гарантирующую минимальную вероятность ошибки. Пусть решение выбирается среди гиперплоскостей, безошибочно делящих векторы обучающей последовательности. В этом случае минимальную гарантированную вероятность ошибок обеспечит оптимальная разделяющая гиперплоскость (такая, которая наиболее удалена от элементов обучающей последовательности). Те векторы, которые лежат по разные стороны гиперплоскости  относятся к различным классам. Таково решение задачи методом минимизации среднего риска. Решение задачи методом минимизации суммарного риска
относятся к различным классам. Таково решение задачи методом минимизации среднего риска. Решение задачи методом минимизации суммарного риска
определяется гиперплоскостью  максимизирующей расстояние между выпуклыми оболочками разделяемых множеств. Векторы, находящиеся по одну сторону гиперплоскости, относятся к первому классу, а по другую сторону гиперплоскости — ко второму классу.
максимизирующей расстояние между выпуклыми оболочками разделяемых множеств. Векторы, находящиеся по одну сторону гиперплоскости, относятся к первому классу, а по другую сторону гиперплоскости — ко второму классу.
На рисунке выделены (заштрихованы) точки рабочей выборки, которые классифицируются гиперплоскостями  по-разному.
по-разному.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ЗАДАЧА ВОССТАНОВЛЕНИЯ ЗАВИСИМОСТЕЙ ПО ЭМПИРИЧЕСКИМ ДАННЫМ
- § 2. Задача обучения распознаванию образов
- § 3. Задача восстановления регрессии
- § 4. Задача интерпретации результатов косвенных экспериментов
- § 5. Некорректно поставленные задачи
- § 6. О точности и надежности минимизации риска по эмпирическим данным
- § 7. О точности восстановления зависимостей по эмпирическим данным
- § 8. Особенности задач восстановления зависимостей
- Основные утверждения главы 1
- ПРИЛОЖЕНИЕ К ГЛАВЕ I. МЕТОДЫ РЕШЕНИЯ НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ
- § П2. Задачи, корректные по Тихонову
- § П3. Метод регуляризации
- § П4. Метод квазирешений
- ГЛАВА II. МЕТОДЫ МИНИМИЗАЦИИ СРЕДНЕГО РИСКА
- § 2. Проблема больших выбросов
- § 3. Априорная информация в задачах восстановления зависимостей по эмпирическим данным
- § 4. Два механизма минимизации среднего риска
- § 5. Задача восстановления плотности распределения вероятностей
- § 6. Равномерная близость эмпирических средних к математическим ожиданиям
- § 7. Обобщение теоремы Гливенко — Кантелли и задача распознавания образов
- § 8. Замечания о двух механизмах минимизации среднего риска по эмпирическим данным
- Основные утверждения главы II
- ГЛАВА III. МЕТОДЫ ПАРАМЕТРИЧЕСКОЙ СТАТИСТИКИ В ЗАДАЧЕ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ
- § 2. Задача дискриминантного анализа
- § 3. Решающие правила в задаче распознавания образов
- § 4. Об оценке качества алгоритмов восстановления плотности вероятностей
- § 5. Байесов алгоритм восстановления плотности
- § 6. Байесова оценка распределения вероятностей дискретных независимых признаков
- § 7. Байесовы приближения плотности нормального закона
- § 8. Несмещенные оценки
- § 9. Достаточные статистики
- § 10. Вычисление наилучшей несмещенной оценки
- § 11. Задача оценивания параметров плотности
- § 12. Метод максимума правдоподобия
- § 13. Оценивание параметров плотности вероятностей методом максимума правдоподобия
- § 14. Замечания о различных методах приближения плотности
- Основные утверждения главы III
- ГЛАВА IV. МЕТОДЫ ПАРАМЕТРИЧЕСКОЙ СТАТИСТИКИ В ЗАДАЧЕ ВОССТАНОВЛЕНИЯ РЕГРЕССИИ
- § 2. Замечание о постановке задачи интерпретации результатов прямых экспериментов
- § 3. Ошибки измерений
- § 4. Экстремальные свойства законов Гаусса и Лапласа
- § 5. Об устойчивых методах оценивания параметра сдвига
- § 6. Устойчивое оценивание параметров регрессии
- § 7. Устойчивость законов Гаусса и Лапласа
- § 8. Класс плотностей, образованных смесью плотностей
- § 9. Плотности, сосредоточенные на отрезке
- § 10. Устойчивые методы восстановления регрессии
- Основные утверждения главы IV
- ГЛАВА V. ОЦЕНИВАНИЕ ПАРАМЕТРОВ РЕГРЕССИИ
- § 2. Теория нормальной регрессии
- § 3. Методы восстановления нормальной регрессии, равномерно лучшие метода наименьших квадратов
- § 4. Теорема об оценивании вектора средних многомерного нормального закона
- § 5. Теорема Гаусса — Маркова
- § 6. Наилучшие линейные оценки
- § 7. Критерии качества оценок
- § 8. Вычисление наилучших линейных оценок
- § 9. Использование априорной информации
- Основные утверждения главы V
- ГЛАВА VI. МЕТОД МИНИМИЗАЦИИ ЭМПИРИЧЕСКОГО РИСКА В ЗАДАЧЕ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ
- § 2. Равномерная сходимость частот появления событий к их вероятностям
- § 3. Частный случай
- § 4. Детерминистская постановка задачи
- § 5. Верхние оценки вероятности ошибок
- § 6. e-сеть множества
- § 7. Необходимые и достаточные условия равномерной сходимости частот к вероятностям
- § 8. Свойства функции роста
- § 9. Оценка уклонения эмпирически оптимального решающего правила
- § 10. Замечания об оценке скорости равномерной сходимости частот к вероятностям
- Основные утверждения главы VI
- ПРИЛОЖЕНИЕ К ГЛАВЕ VI. ТЕОРИЯ РАВНОМЕРНОЙ СХОДИМОСТИ ЧАСТОТ К ВЕРОЯТНОСТЯМ
- § П.2. Функция роста
- § П.3. Основная лемма
- § П.4. Вывод достаточных условий
- § П.5. Оценка величины Г
- § П.6. Оценка вероятности равномерного относительного уклонения
- ГЛАВА VII. МЕТОД МИНИМИЗАЦИИ ЭМПИРИЧЕСКОГО РИСКА В ЗАДАЧЕ ВОССТАНОВЛЕНИЯ РЕГРЕССИИ
- § 2. Частный случай
- § 3. Обобщение на класс с бесконечным числом элементов
- § 4. Емкость множества произвольных функций
- § 5. Равномерная ограниченность отношения моментов
- § 6. Две теоремы о равномерной сходимости
- § 7. Теорема о равномерном относительном уклонении
- § 8. Замечания о теории равномерной сходимости
- Основные утверждения главы VII
- ГЛАВА VIII. МЕТОД УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА В ЗАДАЧАХ ВОССТАНОВЛЕНИЯ ЗАВИСИМОСТЕЙ
- § 2. Оценка «скользящий контроль»
- § 3. Оценка «скользящий контроль» в задаче восстановления регрессии
- § 4. Восстановление характеристической функции в классе линейных решающих правил
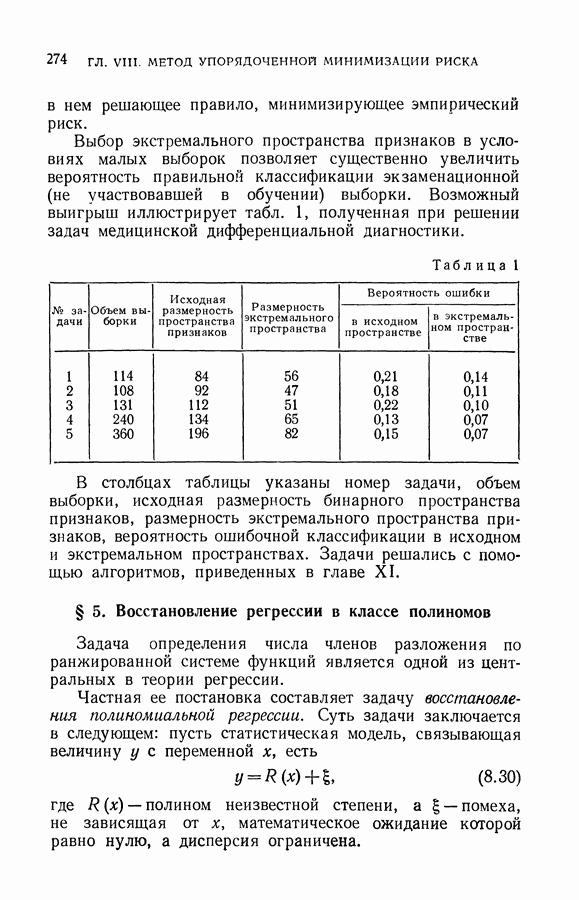
- § 5. Восстановление регрессии в классе полиномов
- § 6. Восстановление регрессии в классе линейных по параметрам функций
- § 7. Восстановление регрессии в классе линейных по параметрам функций (продолжение)
- § 8. Селекция обучающей последовательности
- § 9. Несколько общих замечаний
- Основные утверждения главы VIII
- ГЛАВА IX. РЕШЕНИЕ НЕКОРРЕКТНЫХ ЗАДАЧ ИНТЕРПРЕТАЦИИ ИЗМЕРЕНИЙ МЕТОДОМ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
- § 2. Определение понятия сходимость
- § 3. Теоремы об интерпретации результатов косвенных экспериментов
- § 4. Доказательство теорем
- § 5. Методы полиномиального и кусочно-полиномиального приближений
- § 6. Методы решения некорректных задач измерения
- § 7. Проблема восстановления плотности распределения вероятностей
- § 8. Восстановление плотности методом Парзена
- § 9. Восстановление плотности методом упорядоченной минимизации риска
- Основные утверждения главы IX
- ПРИЛОЖЕНИЕ К ГЛАВЕ IX. СТАТИСТИЧЕСКАЯ ТЕОРИЯ РЕГУЛЯРИЗАЦИИ
- ГЛАВА X. ВОССТАНОВЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИИ В ЗАДАННЫХ ТОЧКАХ
- § 2. Метод упорядоченной минимизации суммарного риска
- § 3. Оценка равномерного относительного уклонения частот в двух подвыборках
- § 4. Оценка равномерного относительного уклонения средних в двух подвыборках
- § 5. Восстановление значений характеристической функции в классе линейных решающих правил
- § 6. Селекция выборки для восстановления значений характеристической функции
- § 7. Восстановление значений произвольной функции в классе линейных по параметрам функций
- § 8. Селекция выборки для восстановления значений произвольной функции
- § 9. Восстановление значений характеристической функции в классе кусочно-линейных решающих правил
- § 10. Восстановление значений произвольной функции в классе кусочно-линейных функций
- § 11. Локальные алгоритмы восстановления значений характеристической функции
- § 12. Локальные алгоритмы восстановления значений произвольной функции
- § 13. Замечания о восстановлении значений функции
- Основные утверждения главы X
- ПРИЛОЖЕНИЕ К ГЛАВЕ X. ЗАДАЧА ТАКСОНОМИИ
- § П.2. Алгоритмы таксономии
- ГЛАВА XI. АЛГОРИТМЫ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ
- § 2. Построение разделяющих гиперплоскостей
- § 3. Алгоритмы максимизации квадратичной формы
- § 4. Методы построения оптимальной разделяющей гиперплоскости
- § 5. Алгоритм экстремального разбиения значений признака на градации
- § 6. Алгоритмы построения разделяющей гиперплоскости
- § 7. Построение разделяющей гиперплоскости в экстремальном пространстве признаков
- § 8. Построение кусочно-линейной разделяющей поверхности
- § 9. Алгоритмы восстановления значений функции в классе линейных решающих правил
- § 10. Алгоритмы восстановления значений функции в классе кусочно-линейных решающих правил
- ГЛАВА XII. АЛГОРИТМЫ ВОССТАНОВЛЕНИЯ НЕХАРАКТЕРИСТИЧЕСКИХ ФУНКЦИЙ
- § 2. Алгоритм восстановления регрессии в классе полиномов
- § 3. Фундаментальные сплайны
- § 4. Алгоритмы восстановления функции в классе сплайнов
- § 5. Алгоритмы решения некорректных задач интерпретации измерений
- § 6. Алгоритмы восстановления многомерной регрессии в классе линейных функций
- § 7. Алгоритмы восстановления значений произвольной функции в классе линейных по параметрам функций
- § 8. Алгоритмы восстановления регрессии в классе кусочно-линейных функций
- § 9. Алгоритмы восстановления значений произвольной функции в классе кусочно-линейных функций
- ПОСЛЕСЛОВИЕ
- КОММЕНТАРИИ
- ЛИТЕРАТУРА