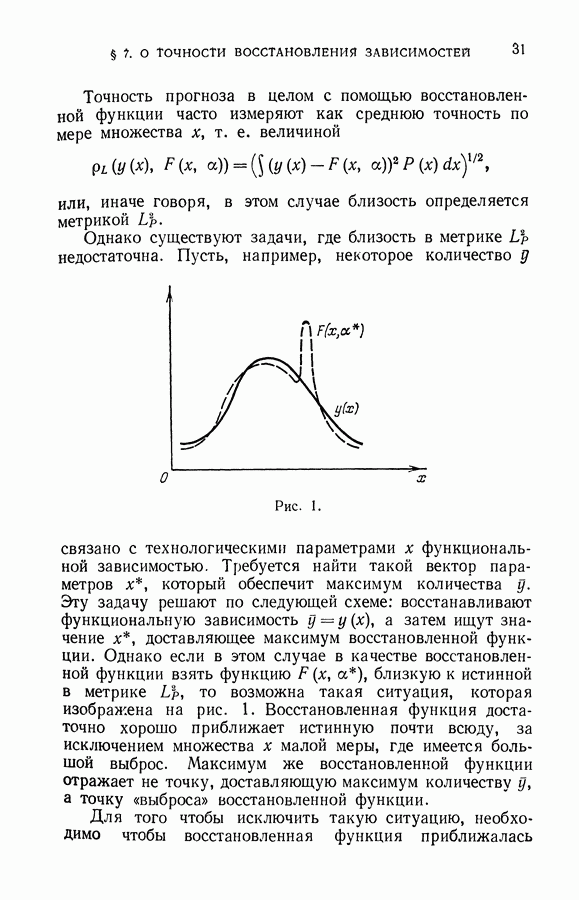
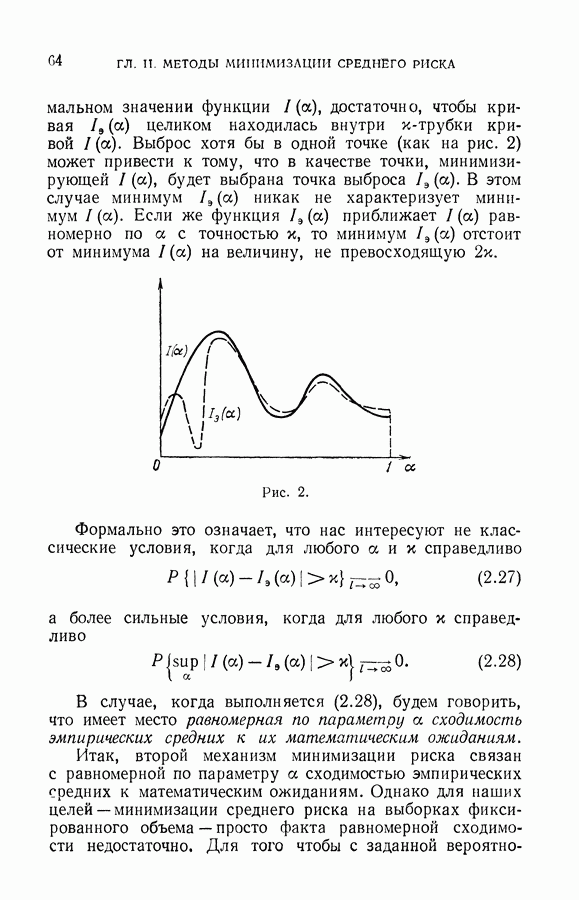
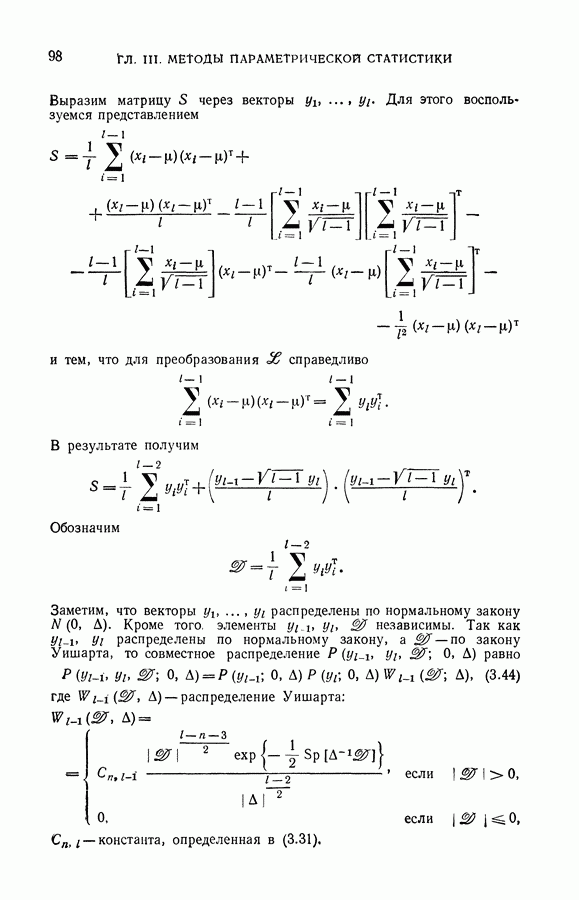
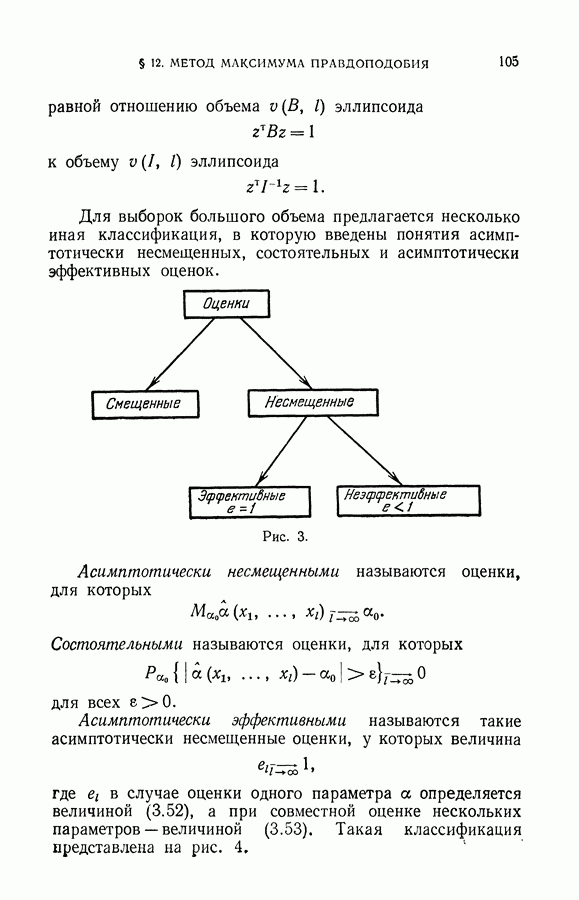
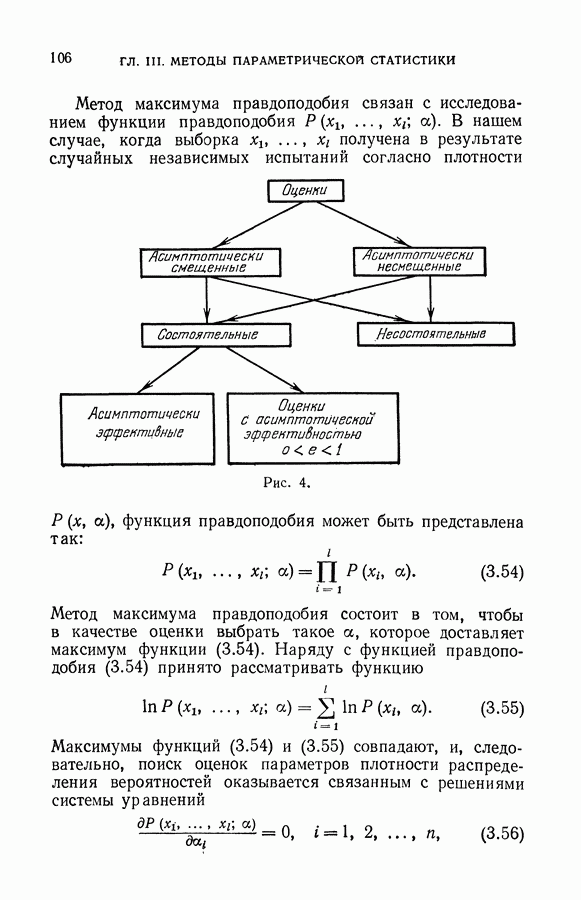
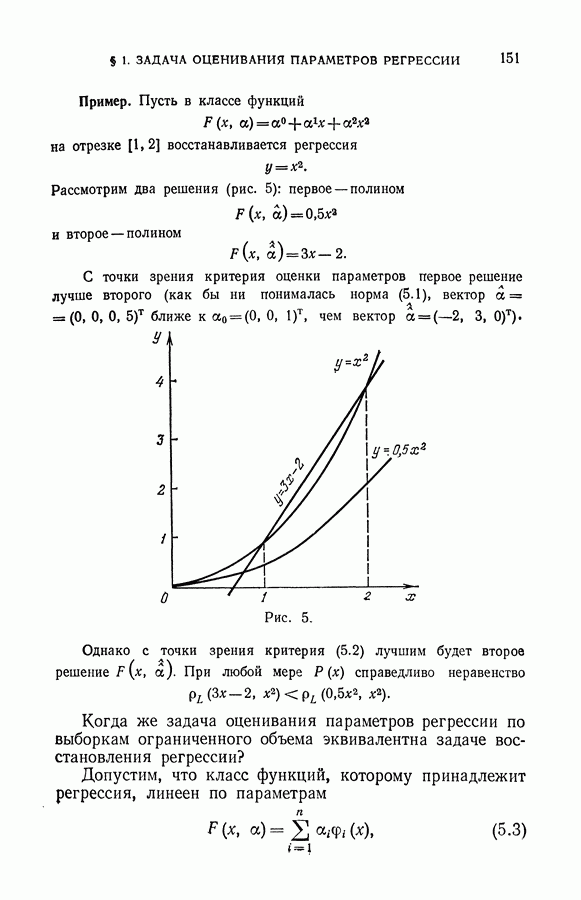
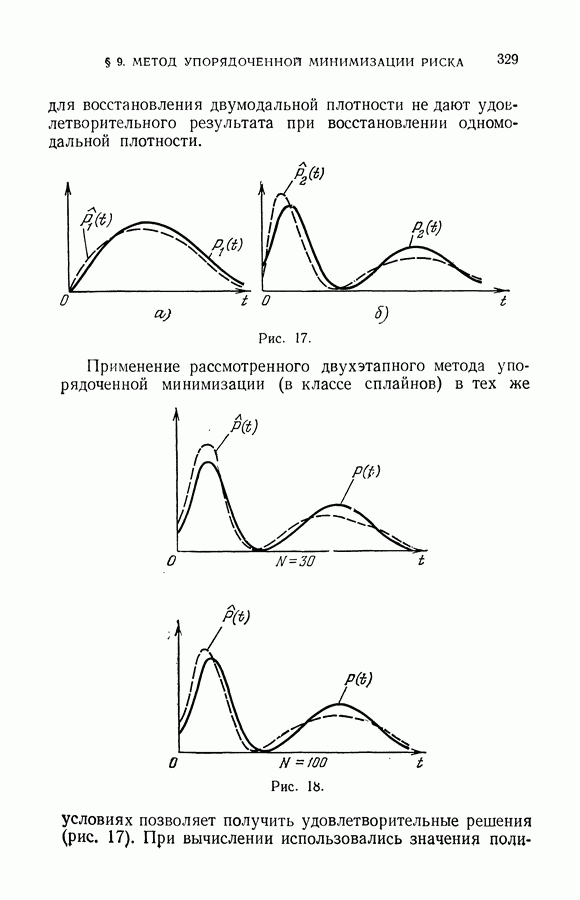
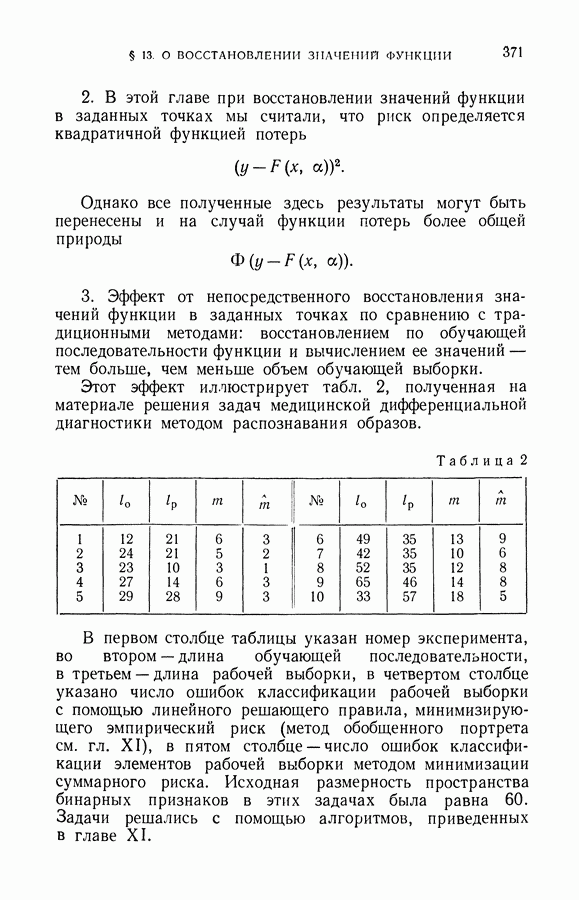
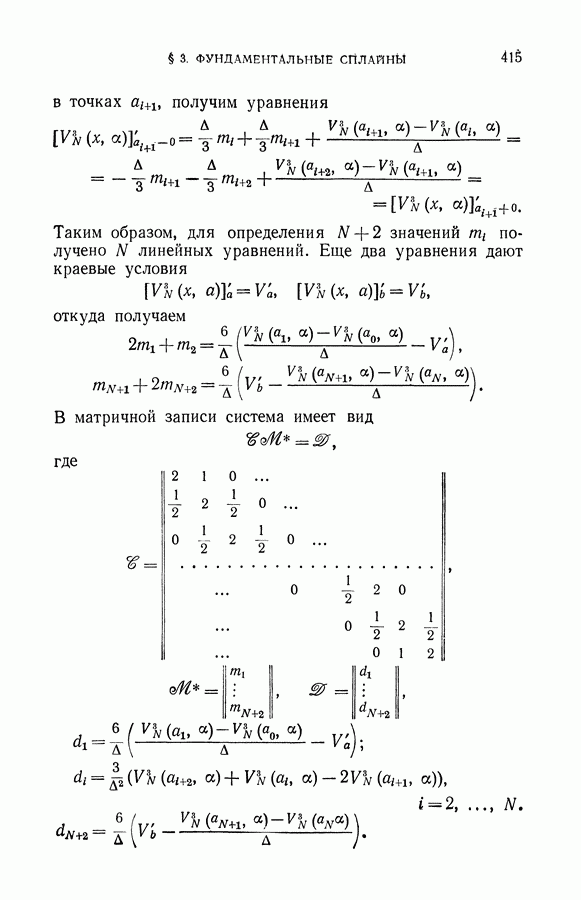
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ П3. Метод регуляризации
Метод регуляризации был предложен А. Н. Тихоновым в 1963 г.
Пусть необходимо решить операторное уравнение

заданное непрерывным взаимно однозначным из  оператором
оператором  И пусть решение
И пусть решение  существует.
существует.
Введем в рассмотрение непрерывный функционал  который назовем стабилизатором и который обладает следующими тремя свойствами:
который назовем стабилизатором и который обладает следующими тремя свойствами:
1) решение операторного уравнения принадлежит области определения  функционала
функционала 
2) на области определения функционал  принимает вещественные неотрицательные значения;
принимает вещественные неотрицательные значения;
3) все множества

являются компактами.
Идея метода регуляризации состоит в том, чтобы найти решение  как элемент, минимизирующий некоторый функционал, но не функционал
как элемент, минимизирующий некоторый функционал, но не функционал

(такая задача была бы эквивалентна решению уравнения  и потому тоже некорректна), а «исправленный» функционал
и потому тоже некорректна), а «исправленный» функционал

с параметром регуляризации  Задача минимизации функционала
Задача минимизации функционала  устойчива, т. е. близким функциям
устойчива, т. е. близким функциям  соответствуют близкие элементы
соответствуют близкие элементы  и минимизирующие функционалы
и минимизирующие функционалы  Проблема состоит в том, чтобы установить, в каком соотношении должны находиться величины
Проблема состоит в том, чтобы установить, в каком соотношении должны находиться величины  чтобы последовательность решений
чтобы последовательность решений  регуляризованных задач
регуляризованных задач  сходилась при 8-0 к решению операторного уравнения
сходилась при 8-0 к решению операторного уравнения  Эти соотношения устанавливает следующая теорема.
Эти соотношения устанавливает следующая теорема.
Теорема П. 1. Пусть  метрические пространства, и пусть для
метрические пространства, и пусть для  существует решение уравнения
существует решение уравнения  Тогда, если вместо точной правой части
Тогда, если вместо точной правой части  уравнения
уравнения  известны приближения
известны приближения  такие, что
такие, что  а значения параметра у выбираются так, что
а значения параметра у выбираются так, что

то элементы минимизирующие функционалы  на
на  сходятся к точному решению
сходятся к точному решению  при
при 
Доказательство теоремы использует следующий факт: для всякого фиксированного  и любого
и любого  существует элемент
существует элемент  минимизирующий на
минимизирующий на  функционал
функционал 
Пусть у и S удовлетворяют соотношению  Рассмотрим последовательность элементов
Рассмотрим последовательность элементов  минимизирующих
минимизирующих  и покажем, что имеет место сходимость
и покажем, что имеет место сходимость

По определению имеем

Учитывая, что

заключаем

Так как выполнены условия  то все элементы ряда
то все элементы ряда  для достаточно малых
для достаточно малых  принадлежат компакту где
принадлежат компакту где  а их образы
а их образы  сходятся:
сходятся:

Отсюда на основании леммы заключаем, что сходятся и прообразы

что и требовалось доказать.
В гильбертовом пространстве для линейного оператора А функционал  может быть взят равным
может быть взят равным  И хотя множества
И хотя множества  при этом оказываются слабо компактными, сходимость регуляризованных решений в силу свойств гильбертова пространства, как будет показано ниже, оказывается сильной. Такой выбор регуляризующего функционала удобен еще и тем, что область его определения
при этом оказываются слабо компактными, сходимость регуляризованных решений в силу свойств гильбертова пространства, как будет показано ниже, оказывается сильной. Такой выбор регуляризующего функционала удобен еще и тем, что область его определения  совпадает со всем пространством
совпадает со всем пространством  Однако в этом случае условия на параметр у более жесткие, чем в теореме
Однако в этом случае условия на параметр у более жесткие, чем в теореме  у должно стремиться к нулю медленнее, чем
у должно стремиться к нулю медленнее, чем  Итак, справедлива теорема.
Итак, справедлива теорема.
Теорема П.2. Пусть  гильбертово пространство и
гильбертово пространство и  Тогда при
Тогда при  удовлетворяющем соотношениям
удовлетворяющем соотношениям  регуляризованные элементы
регуляризованные элементы  сходятся при
сходятся при  к точному решению
к точному решению  в метрике пространства
в метрике пространства 
Доказательство. Из геометрии гильбертовых про странств известно, что сфера  является слабым компактом и что из свойств слабой сходимости элементов
является слабым компактом и что из свойств слабой сходимости элементов  к элементу
к элементу  и сходимости норм
и сходимости норм  вытекает сильная сходимость
вытекает сильная сходимость

Кроме того, из слабой сходимости  вытекает
вытекает

Используя эти свойства гильбертова пространства, докажем теорему. Для этого заметим, что для слабой сходимости в пространстве  справедлива предыдущая теорема:
справедлива предыдущая теорема:  слабо сходятся к
слабо сходятся к  при
при 
Поэтому, согласно  , справедливо неравенство
, справедливо неравенство

С другой стороны, учитывая то, что  и то, что
и то, что  получаем
получаем

Следовательно, имеет место сходимость норм

а это вместе с фактом существования слабой сходимости влечет в силу свойств гильбертова пространства сильную сходимость

что и требовалось доказать.
Приведенные теоремы являются центральными в теории регуляризации. С их помощью устанавливается
принципиальная возможность решения некорректных задач. Однако при решении практических задач вопросы сходимости последовательности регуляризованных решений не являются наиболее актуальными. Обычно правая часть операторного уравнения задана с конечной точностью  и проблема заключается в том, чтобы определить величину константы регуляризации
и проблема заключается в том, чтобы определить величину константы регуляризации  при которой будет обеспечено наилучшее приближение к искомому решению. Для этой ситуации утверждения теорем
при которой будет обеспечено наилучшее приближение к искомому решению. Для этой ситуации утверждения теорем  где величина у определяется с точностью до константы
где величина у определяется с точностью до константы  и то при достаточно малых б), являются явно недостаточными.
и то при достаточно малых б), являются явно недостаточными.
В настоящее время нет сколько-нибудь надежных методов выбора константы регуляризации. Однако имеются многочисленные примеры того, что при надлежащем выборе константы у могут быть получены достаточно хорошие приближения к решению некорректных задач.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ЗАДАЧА ВОССТАНОВЛЕНИЯ ЗАВИСИМОСТЕЙ ПО ЭМПИРИЧЕСКИМ ДАННЫМ
- § 2. Задача обучения распознаванию образов
- § 3. Задача восстановления регрессии
- § 4. Задача интерпретации результатов косвенных экспериментов
- § 5. Некорректно поставленные задачи
- § 6. О точности и надежности минимизации риска по эмпирическим данным
- § 7. О точности восстановления зависимостей по эмпирическим данным
- § 8. Особенности задач восстановления зависимостей
- Основные утверждения главы 1
- ПРИЛОЖЕНИЕ К ГЛАВЕ I. МЕТОДЫ РЕШЕНИЯ НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ
- § П2. Задачи, корректные по Тихонову
- § П3. Метод регуляризации
- § П4. Метод квазирешений
- ГЛАВА II. МЕТОДЫ МИНИМИЗАЦИИ СРЕДНЕГО РИСКА
- § 2. Проблема больших выбросов
- § 3. Априорная информация в задачах восстановления зависимостей по эмпирическим данным
- § 4. Два механизма минимизации среднего риска
- § 5. Задача восстановления плотности распределения вероятностей
- § 6. Равномерная близость эмпирических средних к математическим ожиданиям
- § 7. Обобщение теоремы Гливенко — Кантелли и задача распознавания образов
- § 8. Замечания о двух механизмах минимизации среднего риска по эмпирическим данным
- Основные утверждения главы II
- ГЛАВА III. МЕТОДЫ ПАРАМЕТРИЧЕСКОЙ СТАТИСТИКИ В ЗАДАЧЕ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ
- § 2. Задача дискриминантного анализа
- § 3. Решающие правила в задаче распознавания образов
- § 4. Об оценке качества алгоритмов восстановления плотности вероятностей
- § 5. Байесов алгоритм восстановления плотности
- § 6. Байесова оценка распределения вероятностей дискретных независимых признаков
- § 7. Байесовы приближения плотности нормального закона
- § 8. Несмещенные оценки
- § 9. Достаточные статистики
- § 10. Вычисление наилучшей несмещенной оценки
- § 11. Задача оценивания параметров плотности
- § 12. Метод максимума правдоподобия
- § 13. Оценивание параметров плотности вероятностей методом максимума правдоподобия
- § 14. Замечания о различных методах приближения плотности
- Основные утверждения главы III
- ГЛАВА IV. МЕТОДЫ ПАРАМЕТРИЧЕСКОЙ СТАТИСТИКИ В ЗАДАЧЕ ВОССТАНОВЛЕНИЯ РЕГРЕССИИ
- § 2. Замечание о постановке задачи интерпретации результатов прямых экспериментов
- § 3. Ошибки измерений
- § 4. Экстремальные свойства законов Гаусса и Лапласа
- § 5. Об устойчивых методах оценивания параметра сдвига
- § 6. Устойчивое оценивание параметров регрессии
- § 7. Устойчивость законов Гаусса и Лапласа
- § 8. Класс плотностей, образованных смесью плотностей
- § 9. Плотности, сосредоточенные на отрезке
- § 10. Устойчивые методы восстановления регрессии
- Основные утверждения главы IV
- ГЛАВА V. ОЦЕНИВАНИЕ ПАРАМЕТРОВ РЕГРЕССИИ
- § 2. Теория нормальной регрессии
- § 3. Методы восстановления нормальной регрессии, равномерно лучшие метода наименьших квадратов
- § 4. Теорема об оценивании вектора средних многомерного нормального закона
- § 5. Теорема Гаусса — Маркова
- § 6. Наилучшие линейные оценки
- § 7. Критерии качества оценок
- § 8. Вычисление наилучших линейных оценок
- § 9. Использование априорной информации
- Основные утверждения главы V
- ГЛАВА VI. МЕТОД МИНИМИЗАЦИИ ЭМПИРИЧЕСКОГО РИСКА В ЗАДАЧЕ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ
- § 2. Равномерная сходимость частот появления событий к их вероятностям
- § 3. Частный случай
- § 4. Детерминистская постановка задачи
- § 5. Верхние оценки вероятности ошибок
- § 6. e-сеть множества
- § 7. Необходимые и достаточные условия равномерной сходимости частот к вероятностям
- § 8. Свойства функции роста
- § 9. Оценка уклонения эмпирически оптимального решающего правила
- § 10. Замечания об оценке скорости равномерной сходимости частот к вероятностям
- Основные утверждения главы VI
- ПРИЛОЖЕНИЕ К ГЛАВЕ VI. ТЕОРИЯ РАВНОМЕРНОЙ СХОДИМОСТИ ЧАСТОТ К ВЕРОЯТНОСТЯМ
- § П.2. Функция роста
- § П.3. Основная лемма
- § П.4. Вывод достаточных условий
- § П.5. Оценка величины Г
- § П.6. Оценка вероятности равномерного относительного уклонения
- ГЛАВА VII. МЕТОД МИНИМИЗАЦИИ ЭМПИРИЧЕСКОГО РИСКА В ЗАДАЧЕ ВОССТАНОВЛЕНИЯ РЕГРЕССИИ
- § 2. Частный случай
- § 3. Обобщение на класс с бесконечным числом элементов
- § 4. Емкость множества произвольных функций
- § 5. Равномерная ограниченность отношения моментов
- § 6. Две теоремы о равномерной сходимости
- § 7. Теорема о равномерном относительном уклонении
- § 8. Замечания о теории равномерной сходимости
- Основные утверждения главы VII
- ГЛАВА VIII. МЕТОД УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА В ЗАДАЧАХ ВОССТАНОВЛЕНИЯ ЗАВИСИМОСТЕЙ
- § 2. Оценка «скользящий контроль»
- § 3. Оценка «скользящий контроль» в задаче восстановления регрессии
- § 4. Восстановление характеристической функции в классе линейных решающих правил
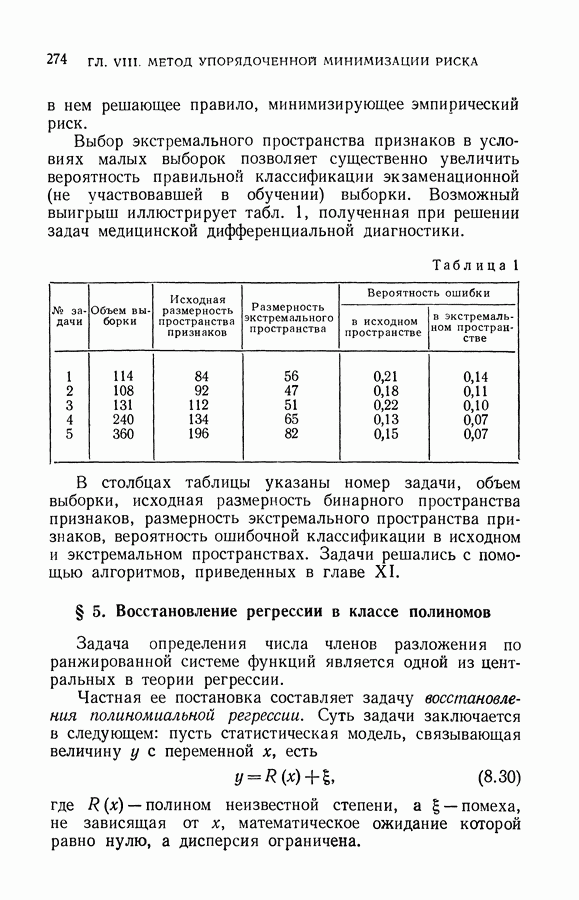
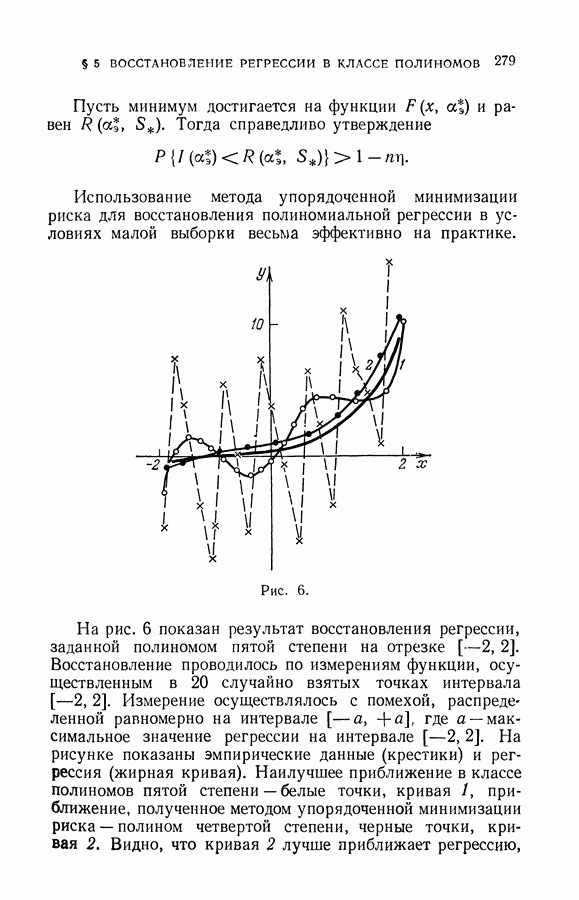
- § 5. Восстановление регрессии в классе полиномов
- § 6. Восстановление регрессии в классе линейных по параметрам функций
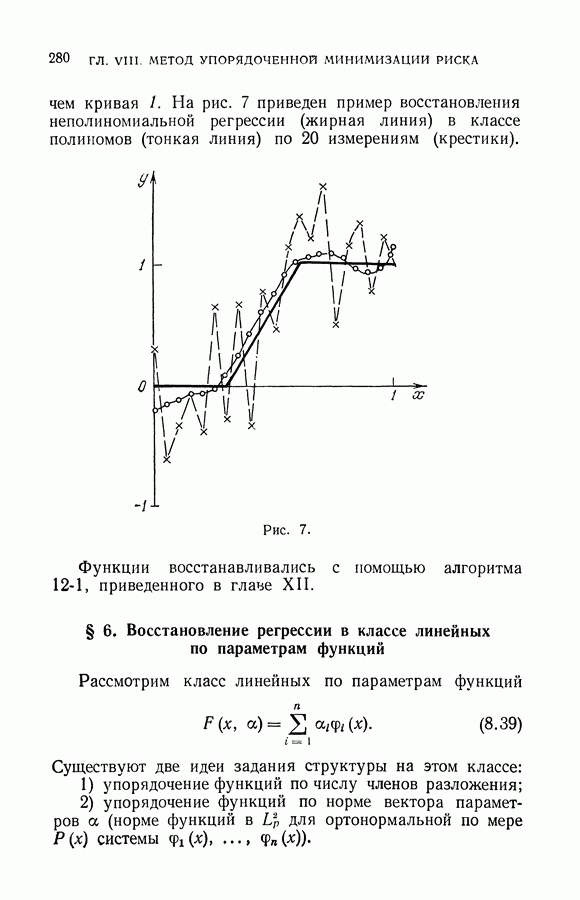
- § 7. Восстановление регрессии в классе линейных по параметрам функций (продолжение)
- § 8. Селекция обучающей последовательности
- § 9. Несколько общих замечаний
- Основные утверждения главы VIII
- ГЛАВА IX. РЕШЕНИЕ НЕКОРРЕКТНЫХ ЗАДАЧ ИНТЕРПРЕТАЦИИ ИЗМЕРЕНИЙ МЕТОДОМ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
- § 2. Определение понятия сходимость
- § 3. Теоремы об интерпретации результатов косвенных экспериментов
- § 4. Доказательство теорем
- § 5. Методы полиномиального и кусочно-полиномиального приближений
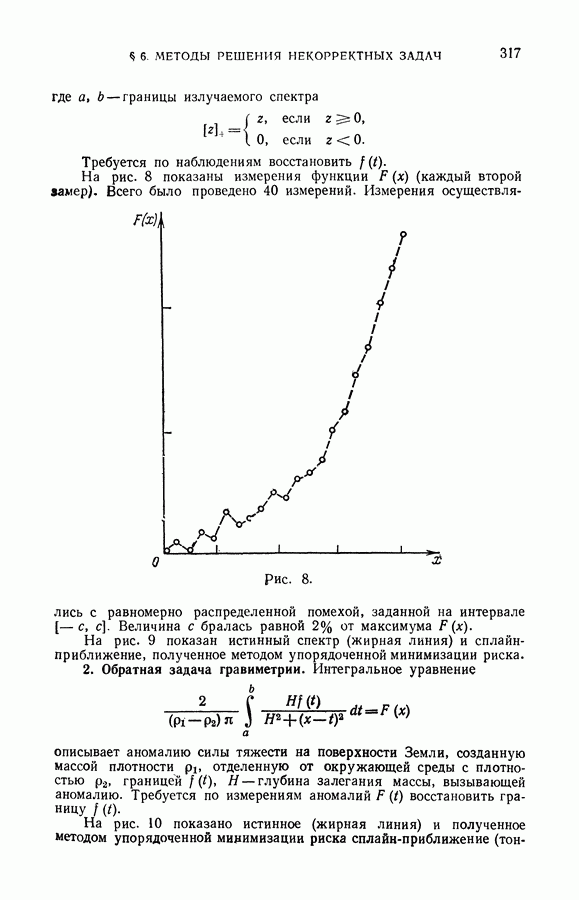
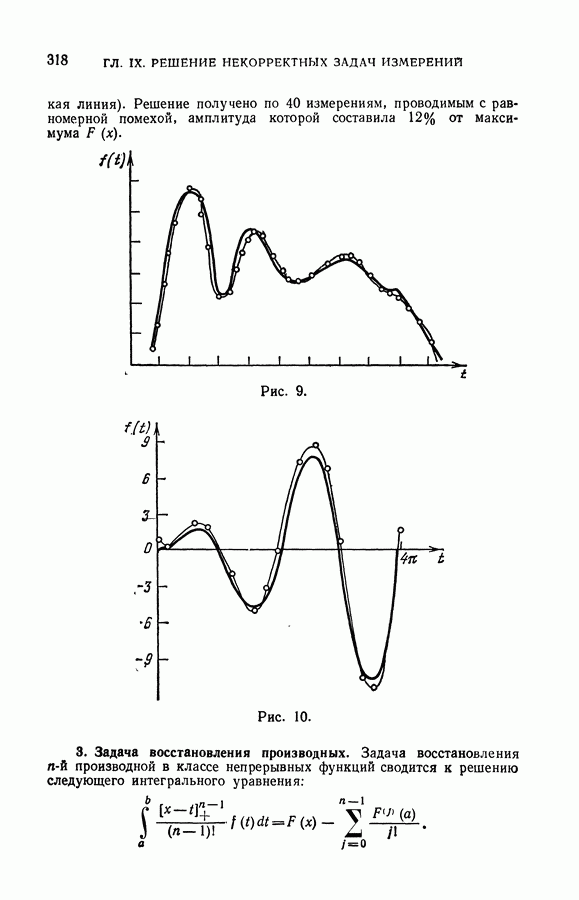
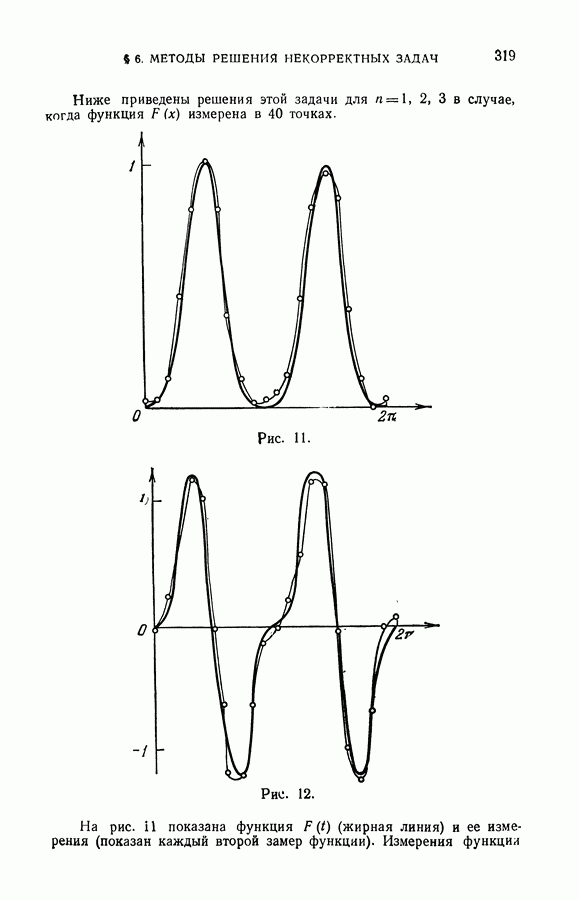
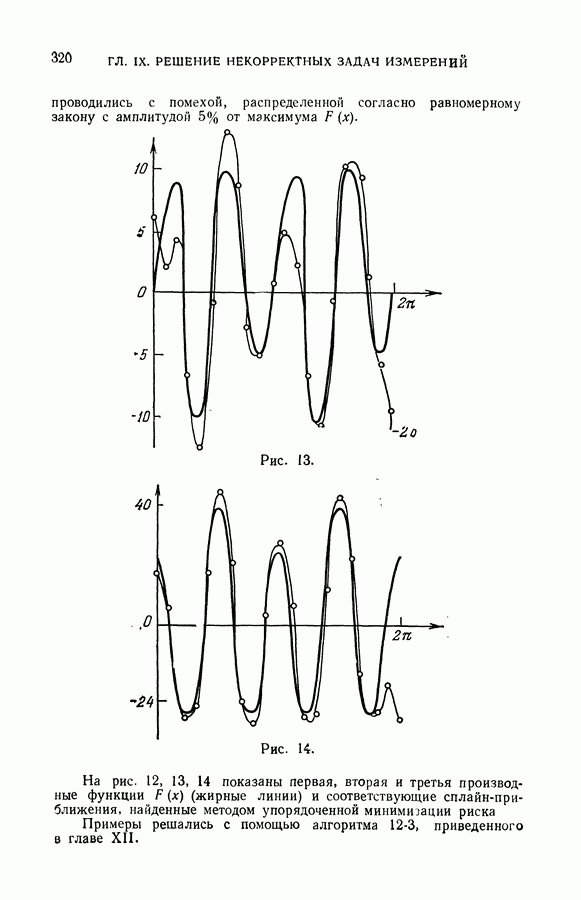
- § 6. Методы решения некорректных задач измерения
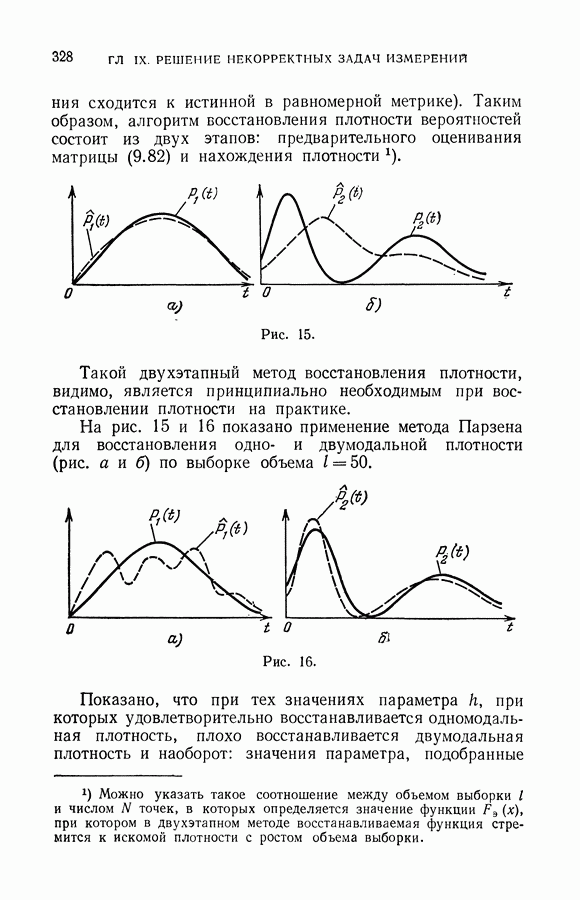
- § 7. Проблема восстановления плотности распределения вероятностей
- § 8. Восстановление плотности методом Парзена
- § 9. Восстановление плотности методом упорядоченной минимизации риска
- Основные утверждения главы IX
- ПРИЛОЖЕНИЕ К ГЛАВЕ IX. СТАТИСТИЧЕСКАЯ ТЕОРИЯ РЕГУЛЯРИЗАЦИИ
- ГЛАВА X. ВОССТАНОВЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИИ В ЗАДАННЫХ ТОЧКАХ
- § 2. Метод упорядоченной минимизации суммарного риска
- § 3. Оценка равномерного относительного уклонения частот в двух подвыборках
- § 4. Оценка равномерного относительного уклонения средних в двух подвыборках
- § 5. Восстановление значений характеристической функции в классе линейных решающих правил
- § 6. Селекция выборки для восстановления значений характеристической функции
- § 7. Восстановление значений произвольной функции в классе линейных по параметрам функций
- § 8. Селекция выборки для восстановления значений произвольной функции
- § 9. Восстановление значений характеристической функции в классе кусочно-линейных решающих правил
- § 10. Восстановление значений произвольной функции в классе кусочно-линейных функций
- § 11. Локальные алгоритмы восстановления значений характеристической функции
- § 12. Локальные алгоритмы восстановления значений произвольной функции
- § 13. Замечания о восстановлении значений функции
- Основные утверждения главы X
- ПРИЛОЖЕНИЕ К ГЛАВЕ X. ЗАДАЧА ТАКСОНОМИИ
- § П.2. Алгоритмы таксономии
- ГЛАВА XI. АЛГОРИТМЫ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ
- § 2. Построение разделяющих гиперплоскостей
- § 3. Алгоритмы максимизации квадратичной формы
- § 4. Методы построения оптимальной разделяющей гиперплоскости
- § 5. Алгоритм экстремального разбиения значений признака на градации
- § 6. Алгоритмы построения разделяющей гиперплоскости
- § 7. Построение разделяющей гиперплоскости в экстремальном пространстве признаков
- § 8. Построение кусочно-линейной разделяющей поверхности
- § 9. Алгоритмы восстановления значений функции в классе линейных решающих правил
- § 10. Алгоритмы восстановления значений функции в классе кусочно-линейных решающих правил
- ГЛАВА XII. АЛГОРИТМЫ ВОССТАНОВЛЕНИЯ НЕХАРАКТЕРИСТИЧЕСКИХ ФУНКЦИЙ
- § 2. Алгоритм восстановления регрессии в классе полиномов
- § 3. Фундаментальные сплайны
- § 4. Алгоритмы восстановления функции в классе сплайнов
- § 5. Алгоритмы решения некорректных задач интерпретации измерений
- § 6. Алгоритмы восстановления многомерной регрессии в классе линейных функций
- § 7. Алгоритмы восстановления значений произвольной функции в классе линейных по параметрам функций
- § 8. Алгоритмы восстановления регрессии в классе кусочно-линейных функций
- § 9. Алгоритмы восстановления значений произвольной функции в классе кусочно-линейных функций
- ПОСЛЕСЛОВИЕ
- КОММЕНТАРИИ
- ЛИТЕРАТУРА