| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 8. Алгоритмы восстановления регрессии в классе кусочно-линейных функций
Алгоритмы восстановления кусочно-линейных функций, рассматриваемые в этом параграфе, построены по той же схеме, по которой реализованы алгоритмы построения кусочно-линейных решающих правил (см. § 8 гл. XI).
Определяется таксонная структура обучающей последовательности  элемент которой
элемент которой  задает разделение обучающей выборки на
задает разделение обучающей выборки на  подмножеств. В соответствии с полученным разбиением выборки на таксоны исходное пространство X делится на
подмножеств. В соответствии с полученным разбиением выборки на таксоны исходное пространство X делится на  подпространств
подпространств  по правилу: вектор х относится к области
по правилу: вектор х относится к области 
если из  чисел
чисел

число  наименьшее. Величина
наименьшее. Величина  есть расстояние от точки х до множества
есть расстояние от точки х до множества 
Для каждой области строится своя линейная функция, минимизирующая эмпирический риск. Таким образом, в соответствии  элементу таксонной структуры ставится кусочно-линейная функция.
элементу таксонной структуры ставится кусочно-линейная функция.
С помощью алгоритма 12-7 определяется такая кусочнолинейная функция (т. е. такой элемент таксонной структуры  множества
множества  обучающей последовательности), для которой достигает минимума функционал
обучающей последовательности), для которой достигает минимума функционал

Реализуется алгоритм 12-7 по схеме:
1. С помощью алгоритма таксономии, описанного в § 8 гл. XI, задается таксонная структура множества X обучающей последовательности.
2. Перебором по элементам таксонной структуры строятся кусочно-линейные функции, состоящие из одного, двух, трех и т. д. кусков плоскостей.
3. Выбирается такая кусочно-линейная функция, для которой оценка (12.35) минимальная.
Алгоритм 12-7 может быть усилен за счет селекции векторов обучающей последовательности. В этом случае минимизируется функционал

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ЗАДАЧА ВОССТАНОВЛЕНИЯ ЗАВИСИМОСТЕЙ ПО ЭМПИРИЧЕСКИМ ДАННЫМ
- § 2. Задача обучения распознаванию образов
- § 3. Задача восстановления регрессии
- § 4. Задача интерпретации результатов косвенных экспериментов
- § 5. Некорректно поставленные задачи
- § 6. О точности и надежности минимизации риска по эмпирическим данным
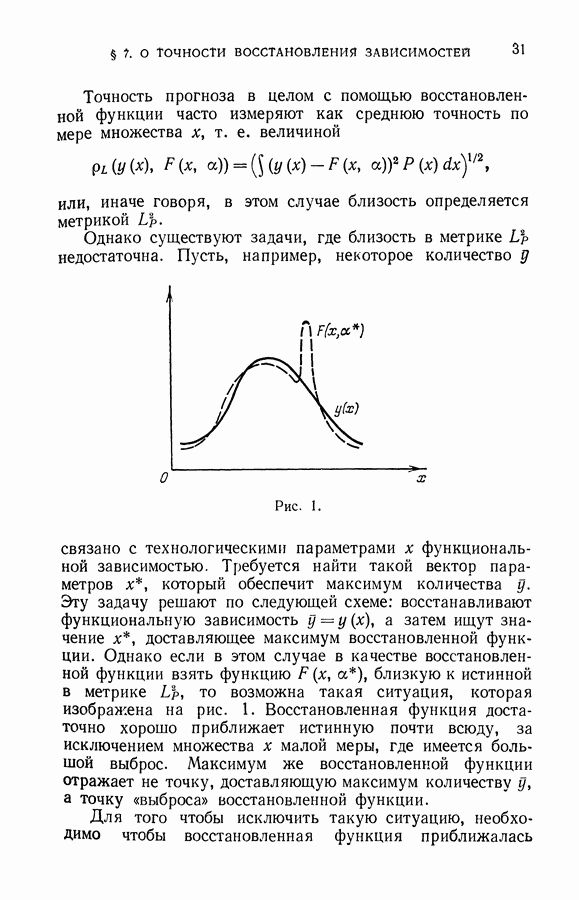
- § 7. О точности восстановления зависимостей по эмпирическим данным
- § 8. Особенности задач восстановления зависимостей
- Основные утверждения главы 1
- ПРИЛОЖЕНИЕ К ГЛАВЕ I. МЕТОДЫ РЕШЕНИЯ НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ
- § П2. Задачи, корректные по Тихонову
- § П3. Метод регуляризации
- § П4. Метод квазирешений
- ГЛАВА II. МЕТОДЫ МИНИМИЗАЦИИ СРЕДНЕГО РИСКА
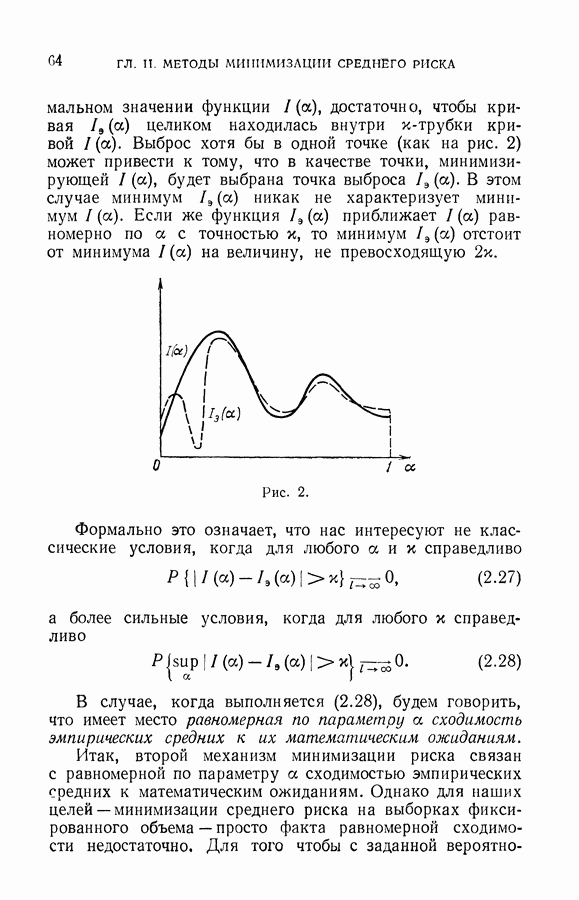
- § 2. Проблема больших выбросов
- § 3. Априорная информация в задачах восстановления зависимостей по эмпирическим данным
- § 4. Два механизма минимизации среднего риска
- § 5. Задача восстановления плотности распределения вероятностей
- § 6. Равномерная близость эмпирических средних к математическим ожиданиям
- § 7. Обобщение теоремы Гливенко — Кантелли и задача распознавания образов
- § 8. Замечания о двух механизмах минимизации среднего риска по эмпирическим данным
- Основные утверждения главы II
- ГЛАВА III. МЕТОДЫ ПАРАМЕТРИЧЕСКОЙ СТАТИСТИКИ В ЗАДАЧЕ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ
- § 2. Задача дискриминантного анализа
- § 3. Решающие правила в задаче распознавания образов
- § 4. Об оценке качества алгоритмов восстановления плотности вероятностей
- § 5. Байесов алгоритм восстановления плотности
- § 6. Байесова оценка распределения вероятностей дискретных независимых признаков
- § 7. Байесовы приближения плотности нормального закона
- § 8. Несмещенные оценки
- § 9. Достаточные статистики
- § 10. Вычисление наилучшей несмещенной оценки
- § 11. Задача оценивания параметров плотности
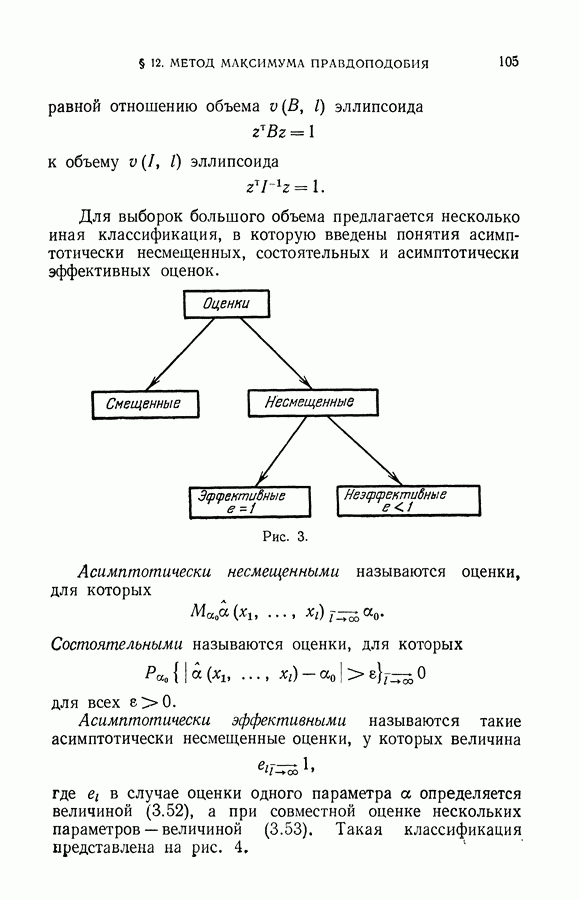
- § 12. Метод максимума правдоподобия
- § 13. Оценивание параметров плотности вероятностей методом максимума правдоподобия
- § 14. Замечания о различных методах приближения плотности
- Основные утверждения главы III
- ГЛАВА IV. МЕТОДЫ ПАРАМЕТРИЧЕСКОЙ СТАТИСТИКИ В ЗАДАЧЕ ВОССТАНОВЛЕНИЯ РЕГРЕССИИ
- § 2. Замечание о постановке задачи интерпретации результатов прямых экспериментов
- § 3. Ошибки измерений
- § 4. Экстремальные свойства законов Гаусса и Лапласа
- § 5. Об устойчивых методах оценивания параметра сдвига
- § 6. Устойчивое оценивание параметров регрессии
- § 7. Устойчивость законов Гаусса и Лапласа
- § 8. Класс плотностей, образованных смесью плотностей
- § 9. Плотности, сосредоточенные на отрезке
- § 10. Устойчивые методы восстановления регрессии
- Основные утверждения главы IV
- ГЛАВА V. ОЦЕНИВАНИЕ ПАРАМЕТРОВ РЕГРЕССИИ
- § 2. Теория нормальной регрессии
- § 3. Методы восстановления нормальной регрессии, равномерно лучшие метода наименьших квадратов
- § 4. Теорема об оценивании вектора средних многомерного нормального закона
- § 5. Теорема Гаусса — Маркова
- § 6. Наилучшие линейные оценки
- § 7. Критерии качества оценок
- § 8. Вычисление наилучших линейных оценок
- § 9. Использование априорной информации
- Основные утверждения главы V
- ГЛАВА VI. МЕТОД МИНИМИЗАЦИИ ЭМПИРИЧЕСКОГО РИСКА В ЗАДАЧЕ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ
- § 2. Равномерная сходимость частот появления событий к их вероятностям
- § 3. Частный случай
- § 4. Детерминистская постановка задачи
- § 5. Верхние оценки вероятности ошибок
- § 6. e-сеть множества
- § 7. Необходимые и достаточные условия равномерной сходимости частот к вероятностям
- § 8. Свойства функции роста
- § 9. Оценка уклонения эмпирически оптимального решающего правила
- § 10. Замечания об оценке скорости равномерной сходимости частот к вероятностям
- Основные утверждения главы VI
- ПРИЛОЖЕНИЕ К ГЛАВЕ VI. ТЕОРИЯ РАВНОМЕРНОЙ СХОДИМОСТИ ЧАСТОТ К ВЕРОЯТНОСТЯМ
- § П.2. Функция роста
- § П.3. Основная лемма
- § П.4. Вывод достаточных условий
- § П.5. Оценка величины Г
- § П.6. Оценка вероятности равномерного относительного уклонения
- ГЛАВА VII. МЕТОД МИНИМИЗАЦИИ ЭМПИРИЧЕСКОГО РИСКА В ЗАДАЧЕ ВОССТАНОВЛЕНИЯ РЕГРЕССИИ
- § 2. Частный случай
- § 3. Обобщение на класс с бесконечным числом элементов
- § 4. Емкость множества произвольных функций
- § 5. Равномерная ограниченность отношения моментов
- § 6. Две теоремы о равномерной сходимости
- § 7. Теорема о равномерном относительном уклонении
- § 8. Замечания о теории равномерной сходимости
- Основные утверждения главы VII
- ГЛАВА VIII. МЕТОД УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА В ЗАДАЧАХ ВОССТАНОВЛЕНИЯ ЗАВИСИМОСТЕЙ
- § 2. Оценка «скользящий контроль»
- § 3. Оценка «скользящий контроль» в задаче восстановления регрессии
- § 4. Восстановление характеристической функции в классе линейных решающих правил
- § 5. Восстановление регрессии в классе полиномов
- § 6. Восстановление регрессии в классе линейных по параметрам функций
- § 7. Восстановление регрессии в классе линейных по параметрам функций (продолжение)
- § 8. Селекция обучающей последовательности
- § 9. Несколько общих замечаний
- Основные утверждения главы VIII
- ГЛАВА IX. РЕШЕНИЕ НЕКОРРЕКТНЫХ ЗАДАЧ ИНТЕРПРЕТАЦИИ ИЗМЕРЕНИЙ МЕТОДОМ УПОРЯДОЧЕННОЙ МИНИМИЗАЦИИ РИСКА
- § 2. Определение понятия сходимость
- § 3. Теоремы об интерпретации результатов косвенных экспериментов
- § 4. Доказательство теорем
- § 5. Методы полиномиального и кусочно-полиномиального приближений
- § 6. Методы решения некорректных задач измерения
- § 7. Проблема восстановления плотности распределения вероятностей
- § 8. Восстановление плотности методом Парзена
- § 9. Восстановление плотности методом упорядоченной минимизации риска
- Основные утверждения главы IX
- ПРИЛОЖЕНИЕ К ГЛАВЕ IX. СТАТИСТИЧЕСКАЯ ТЕОРИЯ РЕГУЛЯРИЗАЦИИ
- ГЛАВА X. ВОССТАНОВЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИИ В ЗАДАННЫХ ТОЧКАХ
- § 2. Метод упорядоченной минимизации суммарного риска
- § 3. Оценка равномерного относительного уклонения частот в двух подвыборках
- § 4. Оценка равномерного относительного уклонения средних в двух подвыборках
- § 5. Восстановление значений характеристической функции в классе линейных решающих правил
- § 6. Селекция выборки для восстановления значений характеристической функции
- § 7. Восстановление значений произвольной функции в классе линейных по параметрам функций
- § 8. Селекция выборки для восстановления значений произвольной функции
- § 9. Восстановление значений характеристической функции в классе кусочно-линейных решающих правил
- § 10. Восстановление значений произвольной функции в классе кусочно-линейных функций
- § 11. Локальные алгоритмы восстановления значений характеристической функции
- § 12. Локальные алгоритмы восстановления значений произвольной функции
- § 13. Замечания о восстановлении значений функции
- Основные утверждения главы X
- ПРИЛОЖЕНИЕ К ГЛАВЕ X. ЗАДАЧА ТАКСОНОМИИ
- § П.2. Алгоритмы таксономии
- ГЛАВА XI. АЛГОРИТМЫ ОБУЧЕНИЯ РАСПОЗНАВАНИЮ ОБРАЗОВ
- § 2. Построение разделяющих гиперплоскостей
- § 3. Алгоритмы максимизации квадратичной формы
- § 4. Методы построения оптимальной разделяющей гиперплоскости
- § 5. Алгоритм экстремального разбиения значений признака на градации
- § 6. Алгоритмы построения разделяющей гиперплоскости
- § 7. Построение разделяющей гиперплоскости в экстремальном пространстве признаков
- § 8. Построение кусочно-линейной разделяющей поверхности
- § 9. Алгоритмы восстановления значений функции в классе линейных решающих правил
- § 10. Алгоритмы восстановления значений функции в классе кусочно-линейных решающих правил
- ГЛАВА XII. АЛГОРИТМЫ ВОССТАНОВЛЕНИЯ НЕХАРАКТЕРИСТИЧЕСКИХ ФУНКЦИЙ
- § 2. Алгоритм восстановления регрессии в классе полиномов
- § 3. Фундаментальные сплайны
- § 4. Алгоритмы восстановления функции в классе сплайнов
- § 5. Алгоритмы решения некорректных задач интерпретации измерений
- § 6. Алгоритмы восстановления многомерной регрессии в классе линейных функций
- § 7. Алгоритмы восстановления значений произвольной функции в классе линейных по параметрам функций
- § 8. Алгоритмы восстановления регрессии в классе кусочно-линейных функций
- § 9. Алгоритмы восстановления значений произвольной функции в классе кусочно-линейных функций
- ПОСЛЕСЛОВИЕ
- КОММЕНТАРИИ
- ЛИТЕРАТУРА