1.4.1. МОДЕЛЬ ФАЗИРОВАННОЙ РЕШЕТКИ

Попытаемся теперь показать применимость вышеописанных положений к конкретной задаче: созданию математической модели

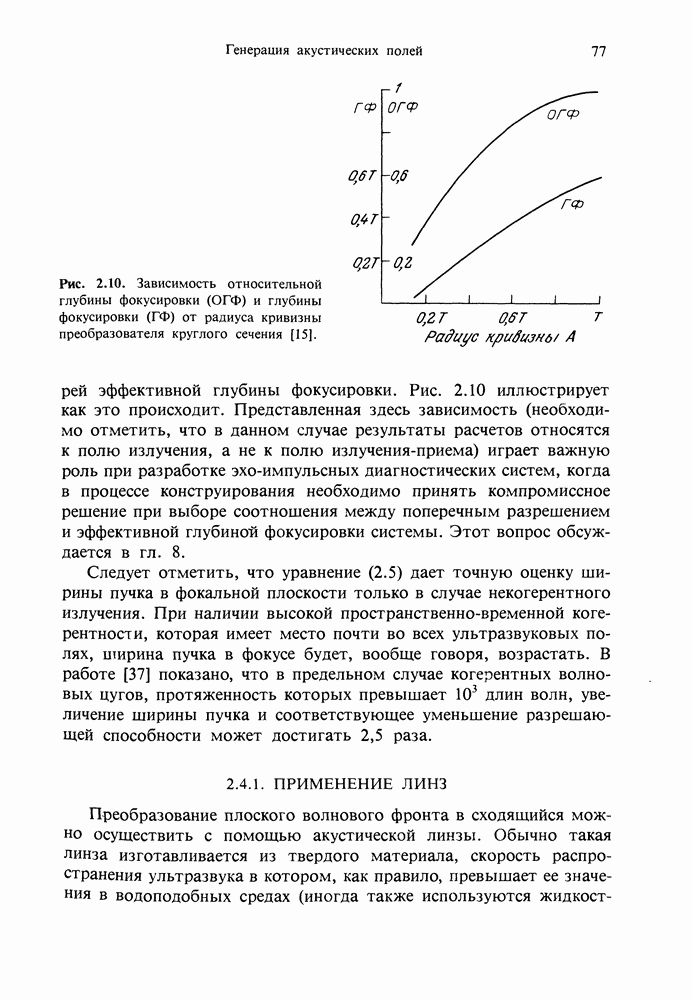
Рис. 1.1. Линейная решетка сферических источников: обозначения системы координат.

решетки, состоящей из соосных сферических акустических источников. Практическая важность таких решеток источников будет показана в гл. 2 и 8. На рис. 1.1 представлены обозначения системы координат для этой модели. Предполагается, что источники излучают одинаковые импульсы давления и располагаются симметрично по обе стороны от центра решетки в положительном и отрицательном направлениях х. Предположим, что поле давления источника задается следующим выражением:

где

На рис. 1.2 показана осциллограмма такого импульса при (М—длина импульса в единицах длины волны). Радиус источника, который обозначался в предыдущих разделах как считается пренебрежимо малым. Задержки возбуждения сферических источников представлены в уравнении (1.83) как Параметр расстояние от центра решетки до произвольной точки поля; расстояние от источника до этой же точки; координата источника; X — длина волны в импульсе.

Рис. 1.2. Форма импульса при Ордината описывается выражением

Предоставим читателю самостоятельно найти условия, при которых уравнение (1.49) упрощается до

Эти условия обсуждались в разд. 1.4. Из уравнения (1.49) видно, что выражение (1.85) с ростом расстояния становится все более точным.

Использование уравнений (1.82) — (1.85) зависит от понимания пространственных и временных соотношений между импульсами, излученными различными сферическими источниками. При акустических мощностях, применяемых в медицинском диагностическом оборудовании, можно считать, что принцип суперпозиции полей давления источников выполняется.

Можно представить две концентрические сферические поверхности с постоянным радиальным зазором распространяющиеся от одиночного сферического источника со скоростью звука. Через время от начала возбуждения первого источника акустический импульс от элемента удалится на В своей ближайшей к источнику точке акустическое возмущение удалено от него на Обозначим эти расстояния и назовем их расстояниями от источника соответственно до переднего и заднего фронтов импульса. Если нарисовать двумерную диаграмму для

этих фронтов в полярных координатах с началом в центре решетки (как в уравнении (1.84)), то можно вывести уравнения для в такой системе координат. При этом можно связать импульсы от отдельных сферических источников в решетке. Затем различные определения расстояний приравниваются и решаются квадратные уравнения относительно Эти рассуждения поясняются рис. 1.3.

Например, оказывается, что

Если считать все другие величины под корнем малыми по сравнению с то множитель выносится из-под корня и для упрощения (1.86) и (1.87) используется разложение в ряд Тейлора.

Рис. 1.3. Геометрия импульса, излученного отдельным элементом, в системе координат, связанной с центром решетки .

Границы импульса в направлении в приблизительно равны

и

Проверяя расстояние между фронтами импульса, получаем

Как видно, с точностью до разумных приближений можно считать, что импульсы от отдельных элементов имеют толщину в направлении в, что очень упрощает сложение возмущений давления от разных источников.

Рассмотрим теперь расстояние между передним и задним фронтами импульсов от разных источников. Вычитание (1.88) из (1.89) дает

Разность (1.89) для двух различных источников дает другое полезное выражение:

Прежде чем рассмотреть общую модель решетки, необходимо выяснить лишь задержки возбуждения различных источников Однако, если задержки и расположение элементов определены, этой информации достаточно, чтобы на ЭВМ построить диаграмму направленности. В конце вычислений суммируются вклады отдельных источников в произвольной точке поля в соответствии с принципом суперпозиции.

Для создания линейных решеток с электронным сканированием апертуры вдоль оси преобразователя важна фокусировка. Для создания фазированных решеток важны как фокусировка, так и управление пучком акустического излучения. Оба этих процесса можно ввести в уравнения с помощью задержек возбуждения источников Далее мы определим выражения для этих задержек.

Произвольная нормаль, пересекающая линейную решетку источников в ее центре, и ось решетки определяют плоскость, в которой рассматриваются фокусировка и управление. Двумерные графики, поясняющие предыдущие уравнения, справедливы только вблизи

этой плоскости. На практике это достаточно реальная модель, так как можно использовать статическую фокусировку, чтобы с точностью до дифракционных поправок ограничить акустическое излучение этой областью. В указанной плоскости излучение решетки будет сфокусировано на расстоянии от ее центра. Угловое отклонение фокуса от нормали к решетке в ее центре обозначим через С помощью геометрических построений можно показать, что для точечной фокусировки на расстоянии с углом

Рис. 1.4 может помочь в объяснении связи между параметрами в уравнении (1.93). Постоянную можно определить, налагая условие, что внешний элемент (с координатой обладает нулевой задержкой для максимального угла сканирования

Рис. 1.4. Обозначения координат для сканирования луча с точечным фокусом.

Уравнение (1.93) можно привести к виду, удобному для оценки уравнений (1.91) и (1.92):

где членом в знаменателе пренебрегают как малым.

Тогда для сканируемой фокальной точки хорошим приближением (1.91) и (1.92) служат (1.96) и (1.97):

Из уравнения (1.96) видно, что толщина огибающей результирующего возмущения давления в направлении в зависит от угла сканирования

Теперь можно получить выражения для диаграммы направленности линейной решетки. Во-первых, необходимо определить систему координат, связанную с возмущениями давления. Для этого определим параметры, сведенные в рис. 1.5. Для заданного угла

Рис. 1.5. Геометрия огибающей результирующего импульса. Показаны координаты, применяемые при описании внутренней структуры импульса.

сканирования расстояние в направлении в между передним фронтом результирующего импульса и вкладом сферического источника есть

Если на переднем фронте результирующего импульса и нарастает к центру решетки, то

Тогда выражения давления и радиальной компоненты скорости частиц для сферических источников имеют вид

Здесь, как обычно,

Вклад сферического источника можно представить в виде гармонического ряда Фурье на интервале (

где ширина импульса в направлении в единицах полуволн

Коэффициенты входящие в уравнение (1.102), согласно теории преобразования Фурье, имеют вид

а интегрирование дает

Все зависимости от апертуры, длины волны и угла заключены в параметре — длине импульса в полуволнах.

Суммирование по всем элементам и изменение порядка суммирования дают

где

Азимутальная зависимость радиальной компоненты интенсивности определяется выражением

Уравнение (1.107) в виде ряда Фурье имеет вид

Радиальное сжатие информации в импульсе в направлении в можно получить, усредняя радиальную компоненту интенсивности по всему импульсу:

Для упрощения можно использовать свойство ортогональности -функции Кронекера (здесь это

Параметр

представляет собой удобную характеристику азимутальной структуры импульса.

Уравнения (1.104) и (1.111) — основной результат этого раздела. Их можно эффективно применять на малых компьютерах для расчета диаграммы направленности линейных решеток. Этот подход служит для иллюстрации аналитических методов, которые можно

использовать совместно с решениями для простых источников, чтобы определить диаграммы направленности более сложных излучателей. Уравнения (1.104) и (1.111) являются исходными для оптимизации решетки, если требуется сканируемый точечный фокус.