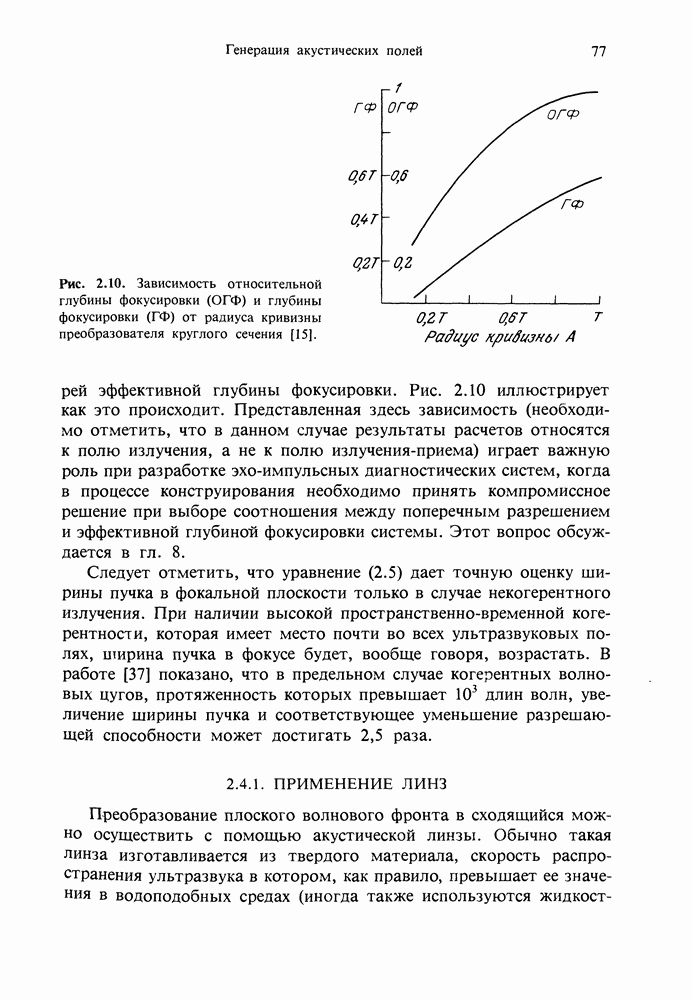
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
11.5.2. СПЕКТР ИМПУЛЬСНО-ДОПЛЕРОВСКОГО СИГНАЛА
При анализе характеристик импульсно-доплеровских приборов необходимо вначале сделать некоторые упрощения, а затем обсудить влияние возможных отклонений от них. Как было показано выше (см., например, (11.63)), мощность рассеянного эритроцитами сигнала пропорциональна четвертой степени модуля волнового вектора (частоты). Здесь мы будем предполагать, что спектр излученного импульса достаточно узок, т. е. импульс имеет достаточную длительность, так что в пределах ширины спектра рассеяние не зависит от частоты. Будем предполагать, что любой участок импульса рассеивается так же, как и непрерывное излучение, но амплитуда сигнала зависит от времени. Предположим также, что вне оси пучка форма импульса нигде не меняется, т. е. поведение импульса описывается функцией расстояния вдоль оси пучка. В этом случае
для импульсно-доплеровского прибора формулу (11.42) можно переписать так:

где  период следования импульсов,
период следования импульсов,  расстояние вдоль оси пучка от преобразователя до точки
расстояние вдоль оси пучка от преобразователя до точки  огибающая излученного импульса с учетом искажений, вносимых приемным трактом.
огибающая излученного импульса с учетом искажений, вносимых приемным трактом.
Существует множество различных демодуляторов для импульсно-доплеровских приборов. Все они чувствительны к принимаемому сигналу лишь в течение короткого отрезка времени после каждого излученного импульса. Найдем спектр доплеровского сигнала, получаемого при использовании одного из таких демодуляторрв (для других демодуляторов спектры получаются аналогично).
Устройство рассматриваемого демодулятора показано на рис. 11.7. Принятый сигнал  перемножается с опорным сигналом
перемножается с опорным сигналом  и после прохождения фильтра низких частот с импульсным откликом
и после прохождения фильтра низких частот с импульсным откликом  (или передаточной функцией
(или передаточной функцией  стробируется по времени с задержкой
стробируется по времени с задержкой  относительно каждого момента излучения импульса (длительность строба
относительно каждого момента излучения импульса (длительность строба  выбирают много меньше характерного времени изменения
выбирают много меньше характерного времени изменения  Затем сигнал поступает на НЧ-фильтр с импульсным откликом
Затем сигнал поступает на НЧ-фильтр с импульсным откликом  (или передаточной функцией
(или передаточной функцией  Тогда с учетом (11.83) сигнал на выходе демодулятора можно представить в виде
Тогда с учетом (11.83) сигнал на выходе демодулятора можно представить в виде


Рис. 11.7. Демодулятор для импульсно-доплеровского прибора.
где  дельта-функция Дирака. Так как
дельта-функция Дирака. Так как  медленно меняющиеся функции, а характерные времена изменения функций
медленно меняющиеся функции, а характерные времена изменения функций  сравнимы
сравнимы  фильтр после перемножителя будет существенно сказываться лишь на
фильтр после перемножителя будет существенно сказываться лишь на  Полагая
Полагая

и используя фильтрующее свойство дельта-функции, получаем ел 

где

Из сравнения со случаем сигнала в ДПНИ (уравнение (11.44)) видно, что импульсно-доплеровский сигнал также содержит множитель вида

В случае импульсного сигнала функция распределения чувствительности по полю (уравнение (11.86)) включает сомножитель  описывающий изменение чувствительности вдоль пучка (рис. 11.8). Действие остальных сомножителей в уравнении (11.85) можно проследить, подставляя в него выражение (11.87) и
описывающий изменение чувствительности вдоль пучка (рис. 11.8). Действие остальных сомножителей в уравнении (11.85) можно проследить, подставляя в него выражение (11.87) и

Рис. 11.8. Измерительный объем и изменение чувствительности вдоль оси пучка в импульсно-доплеровском приборе.
выполняя преобразование Фурье:

здесь  обозначают фурье-образы функций
обозначают фурье-образы функций  использованы также основные свойства преобразования Фурье [25]. Свертка
использованы также основные свойства преобразования Фурье [25]. Свертка  с периодической
с периодической  -функцией приводит к периодическому повторению спектра
-функцией приводит к периодическому повторению спектра  вдоль оси со (рис. 11.9). Чтобы устранить этот эффект, применяют фильтр, пропускающий сигналы только в полосе угловых частот от
вдоль оси со (рис. 11.9). Чтобы устранить этот эффект, применяют фильтр, пропускающий сигналы только в полосе угловых частот от  до
до  Идеальная передаточная функция
Идеальная передаточная функция  показана на рис. 11.9. Однако реализуемая на практике характеристика фильтра будет иметь более пологие скаты на границах диапазона.
показана на рис. 11.9. Однако реализуемая на практике характеристика фильтра будет иметь более пологие скаты на границах диапазона.
Следует отметить, что полоса однозначно определяемых частот сигналов ограничена диапазоном  , т. е. величиной
, т. е. величиной  частота повторения импульсов). Если спектр выходит за эти пределы, то его «внешняя» часть все же попадает в тот же диапазон, но уже с частотами другого знака. Это общее для всех сигналов с периодической выборкой явление называется маскировкой. При заданной частоте повторения импульсов единственный способ согласовать доплеровскую частоту с рабочим диапазоном — увеличить угол между осью пучка и вектором скорости. На частоту повторения импульсов накладывается ограничение: импульс должен пройти расстояние до исследуемого сосуда и назад до момента излучения следующего импульса. Таким образом,
частота повторения импульсов). Если спектр выходит за эти пределы, то его «внешняя» часть все же попадает в тот же диапазон, но уже с частотами другого знака. Это общее для всех сигналов с периодической выборкой явление называется маскировкой. При заданной частоте повторения импульсов единственный способ согласовать доплеровскую частоту с рабочим диапазоном — увеличить угол между осью пучка и вектором скорости. На частоту повторения импульсов накладывается ограничение: импульс должен пройти расстояние до исследуемого сосуда и назад до момента излучения следующего импульса. Таким образом,

Рис. 11.9. Огибающая спектра доплеровских частот на выходе демодулятора импульсно-доплеровского прибора до НЧ-фильтра  и частотная характеристика идеального фильтра, включаемого после демодуляции
и частотная характеристика идеального фильтра, включаемого после демодуляции 
максимальная глубина локации равна

Ограничение на доплеровскую частоту  приводит к ограничению максимальной измеряемой скорости кровотока (см. (11.6)):
приводит к ограничению максимальной измеряемой скорости кровотока (см. (11.6)):

Исключая Т из (11.89) и (11.90), получаем наибольшую величину произведения скорости на дальности»:

Из (11.88) получаем спектр мощности

где  спектр ДПНИ, функция чувствительности которого модифицирована согласно (11.86). Так как обычно
спектр ДПНИ, функция чувствительности которого модифицирована согласно (11.86). Так как обычно  показатель
показатель  может быть очень малым, поэтому обычно для поддержания достаточного уровня сигнала на выходе фильтра, следующего за перемножителем, вместо устройства выборки используют устройство выборки-хранения. При этом
может быть очень малым, поэтому обычно для поддержания достаточного уровня сигнала на выходе фильтра, следующего за перемножителем, вместо устройства выборки используют устройство выборки-хранения. При этом

Выполняя преобразование Фурье над  и учитывая, что
и учитывая, что  подавляет повторения
подавляет повторения  и устраняет неоднозначность, получаем спектр сигнала
и устраняет неоднозначность, получаем спектр сигнала

и спектр мощности

где  функция выборки. Параметр
функция выборки. Параметр  существенно влияет на частотную характеристику, так как он равен 1 при
существенно влияет на частотную характеристику, так как он равен 1 при
 и спадает до 0,41 на максимально возможной доплеровской частоте
и спадает до 0,41 на максимально возможной доплеровской частоте  Для сохранения равномерности характеристик необходимо подобрать такой вид функции
Для сохранения равномерности характеристик необходимо подобрать такой вид функции  чтобы произведение
чтобы произведение  было постоянным вплоть до максимальной ожидаемой доплеровской частоты.
было постоянным вплоть до максимальной ожидаемой доплеровской частоты.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редакторов перевода
- Часть I. Физические основы
- ГЛАВА 1. Теоретические основы акустики
- 1.2. Основные соотношения и определения линейной акустики
- 1.3. Простейшие виды бегущих волн
- 1.3.1. ПЛОСКИЕ БЕГУЩИЕ ВОЛНЫ
- 1.3.2. СФЕРИЧЕСКИЕ БЕГУЩИЕ ВОЛНЫ
- 1.3.3. ЦИЛИНДРИЧЕСКАЯ СИММЕТРИЯ
- 1.3.4. СРЕДНЯЯ ИНТЕНСИВНОСТЬ
- 1.4. Приближения и модели
- 1.4.1. МОДЕЛЬ ФАЗИРОВАННОЙ РЕШЕТКИ
- 1.5. Распределенные гармонические источники и угловой спектр плоских волн
- 1.5.1. ОПРЕДЕЛЕНИЕ УГЛОВОГО СПЕКТРА ПЛОСКИХ ВОЛН
- 1.5.2. СРЕДНЯЯ ПО ВРЕМЕНИ МОЩНОСТЬ ИЗЛУЧЕНИЯ РАСПРЕДЕЛЕННОГО ГАРМОНИЧЕСКОГО ИСТОЧНИКА
- 1.5.3. СВЯЗЬ С ДИАГРАММОЙ НАПРАВЛЕННОСТИ В ДАЛЬНЕЙ ЗОНЕ
- 1.6. Нестационарные поля излучения распределенных источников
- 1.7. Одномерное волновое движение
- 1.7.2. ОТРАЖЕНИЕ И ПРОХОЖДЕНИЕ ПРИ НОРМАЛЬНОМ ПАДЕНИИ
- 1.7.3. НАКЛОННОЕ ПАДЕНИЕ
- 1.7.4. ПРОХОЖДЕНИЕ ЧЕРЕЗ ПЛАСТИНКУ (НОРМАЛЬНОЕ ПАДЕНИЕ)
- 1.8. Нелинейные эффекты в жидких средах без потерь
- ГЛАВА 2. Генерация акустических полей и их структура
- 2.2. Пьезоэлектрические преобразователи
- 2.3. Импульсные акустические поля
- 2.4. Фокусированные поля
- 2.4.1. ПРИМЕНЕНИЕ ЛИНЗ
- 2.4.2. ПОЛЯ ПРЕОБРАЗОВАТЕЛЕЙ КРАЕВЫХ ВОЛН И АКСИКОНОВ
- 2.5. Формирование пучков с помощью решеток преобразователей
- 2.6. Акустическое поле гибридной системы «Торонто»
- 2.7. Генерация акустических полей для терапии
- 2.8. Заключение
- ГЛАВА 3. Прием и измерение ультразвука
- 3.2. Пьезоэлектрические устройства
- 3.2.1. КАЛИБРОВКА ГИДРОФОНА МЕТОДОМ ВЗАИМНОСТИ
- 3.2.2. МЕТОДЫ ПРОВЕДЕНИЯ ИЗМЕРЕНИЙ В ТОЧКЕ
- 3.3. Детекторы смещения
- 3.4. Измерения радиационного давления
- 3.4.1. ИЗМЕРЕНИЯ С БОЛЬШОЙ МИШЕНЬЮ
- 3.4.2. ИЗМЕРЕНИЯ С МАЛОЙ МИШЕНЬЮ
- 3.5. Калориметрия
- 3.6. Методы оптической дифракции
- 3.7. Другие методы приема и измерения звука
- 3.8. Измерение биологически эффективных экспозиций и доз
- ГЛАВА 4. Затухание и поглощение ультразвука
- 4.2. Сечения взаимодействия ультразвуковой волны с биологической тканью
- 4.3. Анализ механизмов поглощения продольных ультразвуковых волн
- 4.3.2. ВЯЗКОУПРУГИЕ СВОЙСТВА КВАЗИТВЕРДЫХ СРЕД
- 4.3.3. НЕОДНОРОДНЫЕ СРЕДЫ
- 4.3.5. ЗАВИСИМОСТЬ ЗАТУХАНИЯ ОТ ТЕМПЕРАТУРЫ
- 4.3.6. ВЛИЯНИЕ ВНЕШНЕГО ДАВЛЕНИЯ
- 4.3.7. ВЗАИМОСВЯЗЬ ЯВЛЕНИЙ ПОГЛОЩЕНИЯ, ДИСПЕРСИИ, ЗАТУХАНИЯ И РАССЕЯНИЯ ЗВУКА
- 4.3.8. НЕЛИНЕЙНЫЕ ЭФФЕКТЫ
- 4.3.9. ВЛИЯНИЕ КАВИТАЦИИ
- 4.4. Измерение коэффициентов затухания и поглощения в биологических тканях
- 4.4.1.1. Поглощение звука в биологических тканях
- 4.4.1.2. Затухание в биологических тканях
- 4.4.1.3. Измерения in vivo
- 4.4.2. ПРОБЛЕМЫ, СВЯЗАННЫЕ С АРТЕФАКТАМИ И ПОГРЕШНОСТЯМИ ИЗМЕРЕНИЙ
- 4.4.2.3. Влияние неоднородностей
- 4.4.2.4. Контрольные измерения на стандартных материалах
- 4.4.2.5. Влияние условий измерений
- 4.5. Обзор литературных данных о коэффициентах затухания и поглощения
- 4.5.1.1. Внутримолекулярное поглощение
- 4.5.1.2. Межмолекулярное поглощение
- 4.5.2. БИОЛОГИЧЕСКИЕ ТКАНИ
- 4.5.2.2. Вклад рассеяния в затухание звука
- 4.5.2.3. Вклад структурных неоднородностей в поглощение
- 4.5.2.4. Частотная зависимость
- 4.5.2.5. Температурная зависимость
- 4.5.2.6. Влияние структурных компонентов ткани
- 4.6. Заключение
- ГЛАВА 5. Скорость звука
- 5.2.1. МЕТОДЫ ИЗМЕРЕНИЙ
- 5.2.1.3. Акустическая микроскопия
- 5.2.1.4. Измерения in vivo
- 5.2.2. ПРОБЛЕМЫ, АРТЕФАКТЫ И ПОГРЕШНОСТИ
- 5.2.2.2. Влияние неоднородностей на время прихода сигнала
- 5.2.2.3. Испытания на стандартных материалах
- 5.2.2.4. Влияние условий измерения
- 5.3. Анализ опубликованных данных о скорости звука
- 5.3.2. ЗАВИСИМОСТЬ СКОРОСТИ ЗВУКА ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- 5.3.3. ВЛИЯНИЕ СТРУКТУРНЫХ КОМПОНЕНТОВ ТКАНИ
- 5.4. Заключение
- ГЛАВА 6. Отражение и рассеяние ультразвука
- 6.2. Основы теории рассеяния
- 6.2.2. СЕЧЕНИЕ РАССЕЯНИЯ
- 6.2.3. РЕШЕНИЕ ДЛЯ ОДИНОЧНОГО ПРЕПЯТСТВИЯ
- 6.2.4. ДИФРАКЦИОННАЯ ТЕОРИЯ ДЛЯ СОВОКУПНОСТИ РАССЕИВАТЕЛЕЙ
- 6.3. Рассеяние в случайно-неоднородных средах
- 6.4. Экспериментальное исследование рассеяния
- 6.4.2. ВЗАИМОСВЯЗЬ МЕЖДУ ПОЛНЫМ СЕЧЕНИЕМ РАССЕЯНИЯ И ЗАТУХАНИЕМ
- 6.4.3. ЗАВИСИМОСТЬ СЕЧЕНИЯ РАССЕЯНИЯ ОТ ЧАСТОТЫ
- 6.4.4. УГЛОВАЯ ЗАВИСИМОСТЬ КОЭФФИЦИЕНТОВ РАССЕЯНИЯ
- 6.4.5. ВЛИЯНИЕ РАЗЛИЧНЫХ КОМПОНЕНТОВ ТКАНЕЙ
- 6.5. Рассеяние импульсных сигналов
- 6.5.2. СВОЙСТВА ИЗОБРАЖЕНИЙ, ПОЛУЧАЕМЫХ ПРИ В-СКАНИРОВАНИИ
- 6.5.3. ПРОСТРАНСТВЕННО-ВРЕМЕННАЯ КОРРЕЛЯЦИЯ ЭХО-СИГНАЛОВ
- 6.6. Импедиография
- 6.7. Заключение
- Часть II. Методы визуализации и исследования
- ГЛАВА 7. Визуализация в медицине
- 7.2. Количественные описания при получении и восприятии изображения
- 7.2.2. МЕРЫ ПРОСТРАНСТВЕННЫХ ХАРАКТЕРИСТИК СИСТЕМ ВИЗУАЛИЗАЦИИ
- 7.3. Характеристики зрительного восприятия человека
- 7.3.1. ОСТРОТА ЗРЕНИЯ И ВОСПРИЯТИЕ ЯРКОСТНОГО КОНТРАСТА
- 7.3.2. ФАКТОР ВРЕМЕНИ В ЗРИТЕЛЬНОМ ВОСПРИЯТИИ
- 7.4. Место ультразвука в медицинской визуализации
- 7.5. Систематика интерпретации изображений
- ГЛАВА 8. Эхо-импульсные методы визуализации и измерений
- 8.2. Режимы представления эхо-импульсной информации
- 8.3. Передаточная функция
- 8.4. Сложное сканирование и некогерентность изображения
- 8.5. Влияние среды распространения
- 8.6. Обработка сигнала
- 8.7. Ограничение скорости сканирования и частоты кадров
- 8.8. Испытания и оценка характеристик систем
- 8.9. Области применения эхо-импульсных методов
- 8.9.3. ИССЛЕДОВАНИЕ ВНУТРЕННИХ ОРГАНОВ
- 8.9.4. ПРИПОВЕРХНОСТНЫЕ И НАРУЖНЫЕ ОРГАНЫ
- 8.9.5. КАРДИОЛОГИЯ
- 8.9.6. НЕВРОЛОГИЯ
- 8.10. Заключение
- ГЛАВА 9. Прочие методы визуализации
- 9.2. Двумерная регистрация акустического изображения
- 9.3. Трансмиссионная визуализация
- 9.4. Трансмиссионная реконструктивная визуализация полей затухания и скорости звука
- 9.5. Визуализация в режиме обратного рассеяния с реконструкцией по двум параметрам
- 9.6. Акустическая голография
- 9.7. Акустическая микроскопия
- ГЛАВА 10. Телегистология
- 10.2. Использование объемных характеристик исследуемой ткани
- 10.3. Использование признаков эхограммы
- 10.4. Использование характеристик рассеяния на тканях
- 10.4.2. ОРИЕНТАЦИОННЫЙ АНАЛИЗ
- 10.5. Использование параметров движения тканей
- 10.6. Заключение
- ГЛАВА 11. Доплеровские методы
- 11.2. Эффект Доплера
- 11.3. Доплеровский прибор непрерывного излучения
- 11.4. Импульсно-доплеровский измеритель скорости кровотока
- 11.5. Анализ спектра доплеровского сигнала
- 11.5.2. СПЕКТР ИМПУЛЬСНО-ДОПЛЕРОВСКОГО СИГНАЛА
- 11.5.3. ФОРМА СПЕКТРА ДОПЛЕРОВСКОГО СИГНАЛА
- 11.6. Средняя скорость
- 11.7. Пульсирующий поток
- 11.8. Ограничения теории
- Часть III. Биофизика ультразвуковых эффектов и их применение
- 12.1. Тепловые механизмы
- 12.1.2. ЭКСПЕРИМЕНТАЛЬНЫЕ НАБЛЮДЕНИЯ ТЕМПЕРАТУРНЫХ РАСПРЕДЕЛЕНИЙ
- 12.2. Кавитация
- 12.2.3. ПОРОГ КАВИТАЦИИ
- 12.2.4. КОНТРОЛЬ КАВИТАЦИИ
- 12.2.4.3. Сонолюминесценция
- 12.2.4.4. Звукохимия
- 12.2.4.5. Методы прямого наблюдения
- 12.2.4.6. Сравнение различных методов контроля кавитации
- 12.2.5. ЭКСПЕРИМЕНТАЛЬНО ИЗМЕРЕННЫЕ ПОРОГИ КАВИТАЦИИ
- 12.3. Радиационное давление, акустические течения и другие нетепловые механизмы
- 12.3.2. АКУСТИЧЕСКИЕ ТЕЧЕНИЯ
- 12.3.3. СДВИГОВЫЕ НАПРЯЖЕНИЯ
- 12.3.4. АКУСТИЧЕСКИЕ МИКРОПОТОКИ ВОКРУГ ПУЗЫРЬКА
- 12.3.5. ДРУГИЕ НЕТЕПЛОВЫЕ ЭФФЕКТЫ
- 12.3.6. СИЛЫ ВЗАИМОДЕЙСТВИЯ ЧАСТИЦ
- 12.3.7. БИОЛОГИЧЕСКИЕ ЭФФЕКТЫ
- 12.4. Некавитационные источники сдвиговых напряжений
- 12.5. Наблюдения эффектов нетепловой природы в структурированных тканях
- 12.5.2. ТКАНИ МЛЕКОПИТАЮЩИХ
- 12.6. Выводы
- ГЛАВА 13. Применение ультразвука в терапии и хирургии
- 13.2. Физиологические основы ультразвуковой терапии
- 13.2.2. НЕТЕПЛОВЫЕ ЭФФЕКТЫ
- 13.3. Физиотерапия
- 13.3.2. ИСПОЛЬЗОВАНИЕ УЛЬТРАЗВУКА В ФИЗИОТЕРАПИИ
- 13.4. Хирургия
- 13.4.1. ХИРУРГИЯ С ПОМОЩЬЮ ФОКУСИРОВАННОГО УЛЬТРАЗВУКА
- 13.4.2. БОЛЕЗНЬ МЕНЬЕРА
- 13.4.3. ИНСТРУМЕНТАЛЬНАЯ УЛЬТРАЗВУКОВАЯ ХИРУРГИЯ
- 13.4.4. СТОМАТОЛОГИЯ
- 13.5. Ультразвук при лечении рака
- ГЛАВА 14. Оценка безопасности применения ультразвука в медицине
- 14.3. Исследования на изолированных клетках
- 14.4. Исследования на многоклеточных организмах
- 14.4.4. УЛЬТРАЗВУК В ОНКОЛОГИИ
- 14.5. Исследования эмбрионов человека
- 14.6. Краткие рекомендации и указания по режимам облучения
- 14.7. Заключение