2.4. Фокусированные поля

До сих пор рассматривались акустические поля излучателей «плоских волн», т. е. таких излучателей, у которых фаза возбуждающего сигнала постоянна в пределах апертурной плоскости. Такие излучатели образуют особую группу и интерес к ним вызван достаточно тривиальными причинами. Во-первых, плоские преобразователи легко изготовить (отметим, что при изготовлении пьезоэлектрических преобразователей из кварца предварительно необходимо выделить заданную кристаллографическую плоскость). Во-вторых, теоретические результаты, полученные для плоских преобразователей, легче трактовать по сравнению со случаем искривленных поверхностей. Однако в общем случае поля оптимальной для практических приложений конфигурации отличаются от полей, создаваемых плоскими излучателями с равномерным возбуждением.

Целенаправленное отклонение от пространственной однородности либо функции возбуждения, либо функции отклика (либо их

обе их вместе) в пределах апертуры преобразователя — аподизация — уже упоминалась как метод подавления краевых волн. В непрерывном режиме возбуждение краевых волн приводит к появлению паразитных боковых лепестков в структуре волнового пучка. Аподизация позволяет видоизменять структуру поля и в этом смысле может рассматриваться как метод обеспечения некоторой фокусировки. Такая возможность часто не учитывается при анализе методов фокусирования ультразвука. Естественно, что характер влияния аподизации источника на структуру поля будет зависеть от конкретного вида аподизирующей функции. Некоторые наглядные примеры этого представлены на рис. 2.3.

Более традиционным и более эффективным методом фокусирования является метод фазирования, состоящий во введении заданного закона распределения фазы возбуждающего сигнала в пределах апертуры излучателя. На практике такой метод реализуется с помощью различных способов. Прежде всего это достигается путем придания определенной формы активному элементу излучателя, например при использовании пьезокерамики или пьезопластических материалов. Второй способ состоит во введении соответствующих фазовых сдвигов между электрическими сигналами, подаваемыми на отдельные элементы многоэлементного преобразователя. Используются также акустические зеркала и линзы, которые, вообще говоря, дополнительно обеспечивают определенную степень аподизации за счет затухания в материале линзы. В дальнейшем будет показано, что между этими четырьмя способами существуют важные различия.

По аналогии с оптикой обычно принято считать, что сферическая поверхность является наиболее «естественной» формой фокусирующей поверхности. Однако не следует забывать, что широкое использование сферических преобразователей часто обусловлено простотой их изготовления, а вовсе не тем, что они во всех случаях имеют преимущества по сравнению с поверхностями другого профиля. Следует также отметить, что на практике многие фокусирующие системы характеризуются сравнительно небольшими значениями отношения диаметра излучателя к длине волны, при этом различие между «идеальной» и сферической поверхностями становится несущественным. Исключение составляют широкоугольные линзовые фокусирующие системы (типа тех, которые используются в акустических микроскопах, см. гл. 9), зеркальные системы, в которых применяются комбинации эллипсоидальных и гиперболоидных зеркал [22], а также аксиконовые системы, которые будут рассмотрены в разд. 2.4.2.

Рис. 2.8. Геометрические параметры, используемые при анализе фокусировки [15].

Фокусирующие свойства круглых преобразователей, выполненных в виде части сферы (без аподизации), рассмотрел Коссофф [15]. Соответствующая конфигурация показана на рис. 2.8. Анализ работы таких преобразователей наиболее удобно проводить на основе сравнения с поведением «эквивалентного плоского преобразователя», т. е. плоского круглого преобразователя радиуса а, для которого френелевское расстояние есть

В качестве практической безразмерной величины, характеризующей фокусирующие свойства такой системы, Коссофф использовал параметр, который он назвал степенью фокусировки, именно параметр

где радиус кривизны активного элемента преобразователя. Используя этот параметр, Коссофф выделяет три различных случая:

Следует отметить, что существуют разные (и неэквивалентные) определения фокуса акустического пучка. Так, например, согласно одному из них фокусом называется точка на оси, соответствующая минимальной ширине пучка. По другому определению фокус связывают с положением на оси максимума интенсивности акустического поля. Коссофф использовал последнее определение. На рис. 2.9

Рис. 2.9. Осевое распределение интенсивности в случае сферических фокусирующих преобразователей с различными коэффициентами эффективности

Здесь А — радиус кривизны преобразователя,

показаны полученные им результаты расчетов зависимости интенсивности от расстояния до излучателя вдоль оси для ряда преобразователей с различными степенями фокусировки. Интенсивность нормирована на максимальное значение интенсивности, создаваемой эквивалентным плоским преобразователем. Из представленных данных непосредственно следует, что а) невозможно получить фокусировку в дальнем поле эквивалентного плоского преобразователя и б) акустический фокус всегда локализован в точке, сдвинутой относительно центра кривизны в сторону преобразователя, причем фокус будет приближаться к центру кривизны по мере возрастания степени фокусировки.

На фокусном расстоянии ширина ультразвукового пучка, определяемая интервалом между первыми минимумами распределения интенсивности в поперечном направлении, дается выражением (см. гл. 8)

Выигрыш в поперечной разрешающей способности при возрастании степени фокусировки или соответственно величины относительного отверстия [1] неизбежно сопровождается

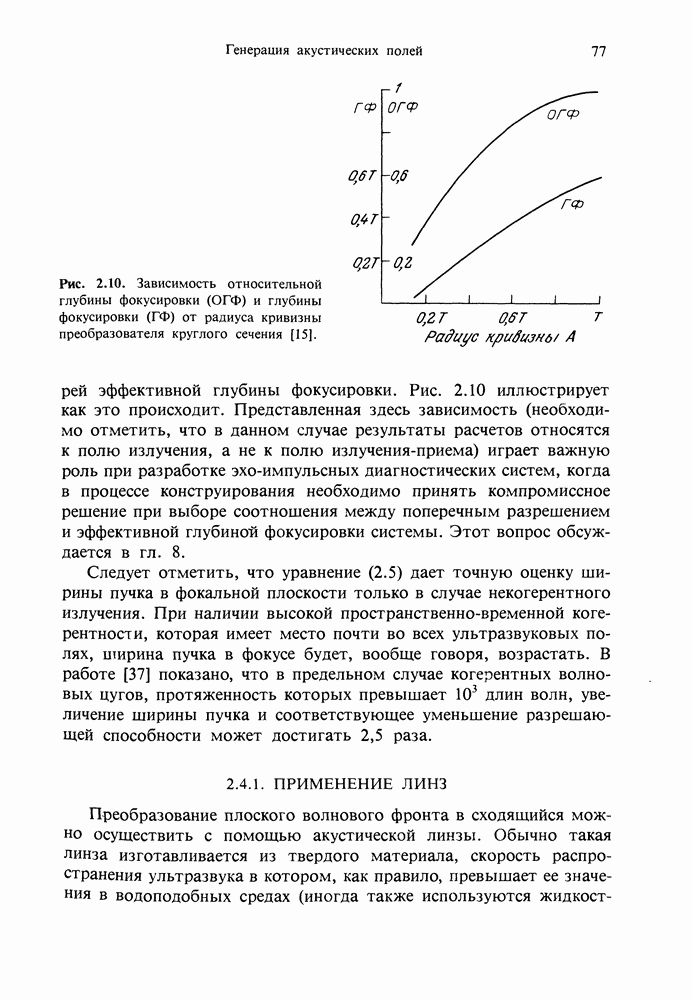
Рис. 2.10. Зависимость относительной глубины фокусировки (ОГФ) и глубины фокусировки (ГФ) от радиуса кривизны преобразователя круглого сечения [15].

потерей эффективной глубины фокусировки. Рис. 2.10 иллюстрирует как это происходит. Представленная здесь зависимость (необходимо отметить, что в данном случае результаты расчетов относятся к полю излучения, а не к полю излучения-приема) играет важную роль при разработке эхо-импульсных диагностических систем, когда в процессе конструирования необходимо принять компромиссное решение при выборе соотношения между поперечным разрешением и эффективной глубиной фокусировки системы. Этот вопрос обсуждается в гл. 8.

Следует отметить, что уравнение (2.5) дает точную оценку ширины пучка в фокальной плоскости только в случае некогерентного излучения. При наличии высокой пространственно-временной когерентности, которая имеет место почти во всех ультразвуковых полях, ширина пучка в фокусе будет, вообще говоря, возрастать. В работе [37] показано, что в предельном случае когерентных волновых цугов, протяженность которых превышает 103 длин волн, увеличение ширины пучка и соответствующее уменьшение разрешающей способности может достигать 2,5 раза.