4.3.8. НЕЛИНЕЙНЫЕ ЭФФЕКТЫ

До сих пор анализ механизмов потерь проводился в предположении, что реакция исследуемой среды на механические напряжения, вызванные акустической волной, линейна. В действительности такое предположение справедливо только в тех случаях, когда амплитуда волны очень мала. В данном разделе мы рассмотрим условия, при которых распространение акустических волн в жидкостях и мягких биологических тканях должно быть заметно нелинейным. Будет рассмотрено также влияние нелинейного распространения волн на реальные значения затухания в среде.

Некоторые аспекты нелинейного распространения акустических волн рассмотрены в упоминавшихся ранее работах Фрая и Данна [75], а также Данна и др. [53]. Теоретические основы были кратко изложены в гл. 1 данной книги применительно к средам без затухания. К сожалению, одна из наиболее исчерпывающих работ по данной тематике, а именно работа Бейера [18], практически недоступна. Однако и более ранние работы [19, 20] не утратили своей ценности и до сих пор представляют большой интерес. Совсем недавно были опубликованы статьи целого ряда авторов, исследовавших нелинейные эффекты при условиях, характерных для медицинских применений ультразвука [33, 85, 127, 128, 158] (см. также разд. 2.7 настоящей книги).

В разд. 1.8 было показано, что в общем случае нелинейного распространения решение волнового уравнения можно получить на основе его разложения в ряд по малым параметрам, характеризующим свойства среды. Учет только двух первых членов разложения в ряд Тейлора приводит к линейной теории или теории первого порядка. Нелинейная теория или теория второго порядка базируется на учете квадратичного члена разложения. При этом без учета потерь взаимосвязь между акустическим давлением и флуктуациями плотности среды описывается уравнением (1.195)

где обозначения те же, что и в гл. 1.

Из квадратичной зависимости акустического давления от плотности среды непосредственно следует, что волна будет распространяться с фазовой скоростью, зависящей от локальных значений колебательной скорости или давления

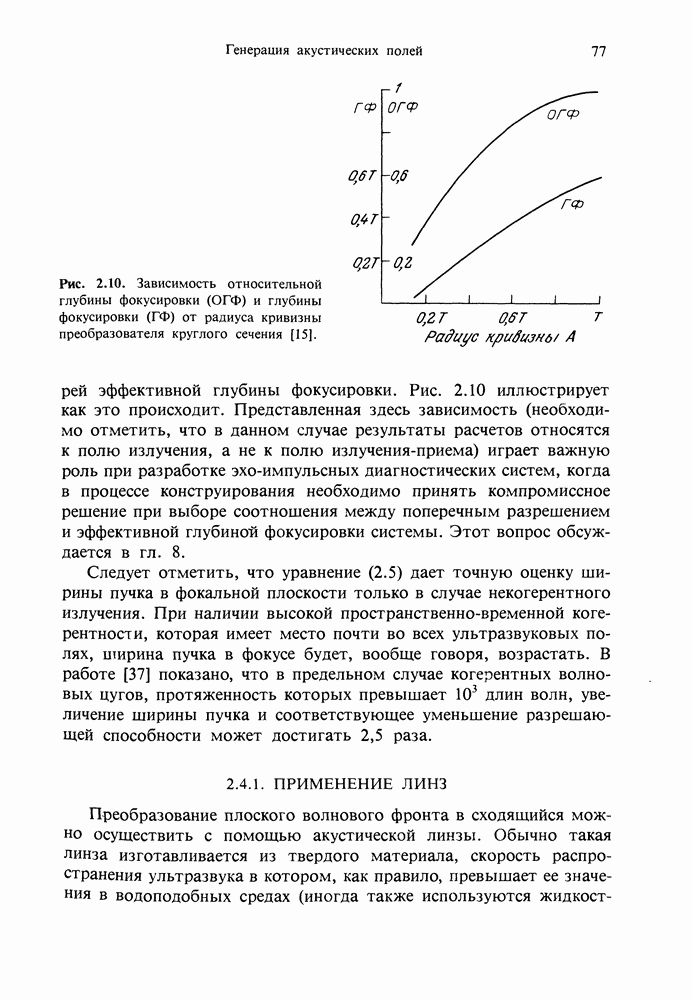
где колебательная скорость частиц, со — скорость звука в линейном приближении, и отношение В/А называется нелинейным параметром среды. Это означает, что области сжатия, или гребни, волны распространяются с несколько большей, а области разряжения, или впадины, — с несколько меньшей скоростью по сравнению со скоростью со, предсказываемой линейной теорией. В результате по мере распространения накапливается искажение профиля волны, который становится постепенно все круче, и волна первоначально синусоидальной формы преобразуется в пилообразную волну, если только затухание не нарушает этой картины (рис. 4.3,а-в). Соответствующее изменение формы волны, которая первоначально имела вид описывается следующим решением волнового уравнения второго порядка, полученным Фубини (см. [20]):

Это выражение можно разложить в ряд Фурье

где - константа, зависящая от нелинейных свойств среды. Хотя данное решение справедливо только для значений из уравнения (4.46) непосредственно следует, что по мере распространения волны происходит уменьшение амплитуды основной гармоники, энергия которой передается в высшие гармоники.

Расстояние от излучателя до точки называется расстоянием до разрыва и определяется как

Это расстояние, на котором в отсутствие затухания производная становится отрицательно бесконечной, т. е. в волне Появляется разрыв, представляющий собой ударный фронт. При волна

приобретает все более пилообразную форму и ударный фронт нарастает. Хотя представленный анализ справедлив при отсутствии в среде диссипативных потерь, он позволяет получить ряд основных закономерностей нелинейного распространения.

Во-первых, чем больше нелинейный параметр тем раньше происходит формирование ударного фронта и тем больше искажается профиль волны на заданном расстоянии от излучателя. Отметим, что в линейном приближении параметр В/А обращается в нуль. Экспериментальные методы определения нелинейного

Рис. 4.3. Эволюция синусоидальной волны по мере распространения в нелинейной среде с малым затуханием и дисперсией. Волна возбуждается в точке в момент времени а — Генерация исходной синусоидальной волны на излучателе; б - образование ударного фронта в результате накопления нелинейных искажений; в — нарастание ударного фронта (образование пилообразной волны); г - обеднение спектра волны высокочастотными гармониками (область стабилизации); д - затухание и возврат к синусоидальной форме волны на больших расстояниях от излучателя [18].

параметра В/А основаны либо на измерении зависимости скорости звука от температуры и давления [128, 140], либо на регистрации спектрального состава волны [128]. Значения В/А для газов лежат в интервале от 0 до 1, для жидкостей и твердых тел этот параметр может изменяться от 2 до 13. Нелинейный параметр слабо растет при повышении температуры или давления. В табл. 4.1 представлены значения В/А для ряда веществ, в том числе и для некоторых биологических тканей.

Таблица 4.1 Значение нелинейного параметра В/А ряда жидкостей и биологических тканей при атмосферном давлении и температуре 20 °С

Предварительные исследования, выполненные Лоу и др. [127, 128], показывают, что нелинейный параметр линейно зависит от концентрации макромолекул и не зависит от молекулярного веса. Эти результаты позволяют предположить, что межмолекулярные и внутримолекулярные взаимодействия в растворенных веществах практически не влияют на величину В/А. Наиболее вероятным источником нелинейности следует считать взаимодействия между молекулами растворенного вещества и растворителя. Из данных, приведенных для цельной и

гомогенизированной печени, видно также, что на значение В/А оказывает влияние макроструктура ткани.

Во-вторых, нелинейные эффекты развиваются скорее на высоких частотах по сравнению с низкими. Это обусловлено накапливающимся характером этих эффектов по мере распространения волны, и при фиксированном расстоянии нелинейные эффекты будут проявляться тем сильнее, чем большее число длин волн укладывается в пределах данного расстояния.

В-третьих, чем больше начальная амплитуда волны, тем короче расстояние до разрыва. И наоборот, если стремится к нулю, то стремится к бесконечности, что соответствует переходу к линейной теории.

И наконец, чем меньше скорость звука в среде, тем короче становится расстояние до разрыва и тем большее искажение профиля волны наблюдается на фиксированном расстоянии от излучателя. Бейер [18], а также Мадгоски и др. [140] показали, что в однородных средах небиологического происхождения параметр В/А в первом приближении линейно зависит от обратной величины скорости звука. В общем случае наблюдаемое нелинейное искажение может изменяться в различных средах в более широких пределах, чем это следовало бы исключительно из различий в значении нелинейного параметра В/А. Следует отметить, что, по данным Лоу и др. [127] величина В/А растет с ростом скорости звука в воде (в интервале температур 0-60 °С) и в водных растворах биологических макромолекул. В тех биологических средах, которые были исследованы до настоящего времени, скорость звука не слишком заметно влияла на наблюдаемые нелинейные искажения акустических волн.

Разумная оценка наиболее вероятной пиковой интенсивности акустических импульсов на выходе диагностической эхо-импульсной аппаратуры медицинского назначеия составляет примерно . В водоподобных средах это соответствует начальной амплитуде колебательной скорости приблизительно равной или амплитуде звукового давления около 8 атм. В табл. 4.2 для ряда сред приведены расчетные значения расстояния до разрыва соответствующие указанной величине амплитуды колебательной скорости. По этим значениям можно судить, насколько быстро могут накапливаться нелинейные искажения при отсутствии затухания звука.

Как видно из рис. 4.3, г и д, наличие в среде зависящего от частоты затухания приводит к постепенному уменьшению амплитуды

(кликните для просмотра скана)

волны и обеднению ее гармониками, причем гармоники высших порядков исчезают первыми. В результате на некотором расстоянии от излучателя в волне останется лишь составляющая основной частоты и дальнейшее распространение волны подчиняется линейной теории. Для каждой гармонической составляющей существует определенный интервал расстояний (называемый областью стабилизации), в пределах которого скорость передачи энергии в данную гармонику приблизительно равна скорости уменьшения ее энергии за счет затухания. Именно в этой области каждая гармоника достигает максимума и затем начинает спадать по амплитуде. Некоторые авторы пытались применить различные приближенные методы с целью введения затухания в выражения, описывающие зависимость амплитуд основной гармоники и гармонических составляющих высших порядков от расстояния [18, 20]. Анализ проводился только для непрерывных волн. В этом плане следует отметить работу Фрая и Данна [75], которые учитывали только передачу энергии из основной частоты во вторую гармонику и пренебрегали всеми остальными процессами обмена энергией между различными гармониками. Строго говоря, их анализ применим только для области однако полученное ими выражение для интенсивности основной гармоники

действительно дает интенсивность при а при стремится к величине

Из этого выражения можно оценить отношение (интенсивности основной гармоники в приближении линейной теории) к а именно

В табл. 4.2 приведены некоторые расчетные величины, полученные в соответствии с выражениями (4.48) и (4.49). Последний столбец таблицы характеризует относительное увеличение (в процентах) среднего значения коэффициента затухания звука за счет нелинейных эффектов при прохождении волны от излучателя до точки 21 в предположении, что наблюдается только основная частота. Эти значения рассчитаны по формуле

где коэффициент затухания при нелинейном распространении. Представленные данные показывают, что при определенных условиях наличие нелинейных эффектов может привести к существенным погрешностям при измерениях затухания и поглощения [21, 85].

Очевидно, что погрешности измерения затухания звука, связанные с нелинейным характером распространения волны, зависят от множества параметров, включая не только уже рассмотренные ранее величины но также и расстояние от излучателя до той области, где проводятся измерения. В общем случае можно утверждать, что неэкспоненциальный характер затухания волн конечной амплитуды приводит к пространственному изменению коэффициента затухания. В частности, на расстояниях, очень близких и очень далеких от излучателя, он приблизительно равен коэффициенту затухания для волн бесконечно малой амплитуды, а в области стабилизации волны его значение достигает максимума. Ситуация осложняется еще тем, что на практике для подобных измерений применяются самые разнообразные методы (см. разд. 4.4). Используются как непрерывный, так и импульсный режимы излучения, при этом регистрируется либо пиковая амплитуда сигнала, либо спектральное распределение энергии. Одни приемники акустических волн могут регистрировать энергию сигнала и поэтому воспринимать все гармонические составляющие спектра непрерывного излучения источника. Другие могут обладать резонансными свойствами и быть чувствительными только к гармоникам нечетных порядков. Кроме того, одни приемники могут регистрировать сигналы в широкой, хотя и ограниченной, полосе частот, другие же являются узкополосными и воспринимают только сигнал основной частоты. В каждом конкретном случае методы теоретического анализа будут различными. Некоторые из них уже рассматривались [20], однако следует подчеркнуть, что наиболее общими и перспективными представляются компьютерные методы численного анализа [95]. Напомним, что пример нелинейного распространения акустических волн уже был рассмотрен в разд. 2.7.