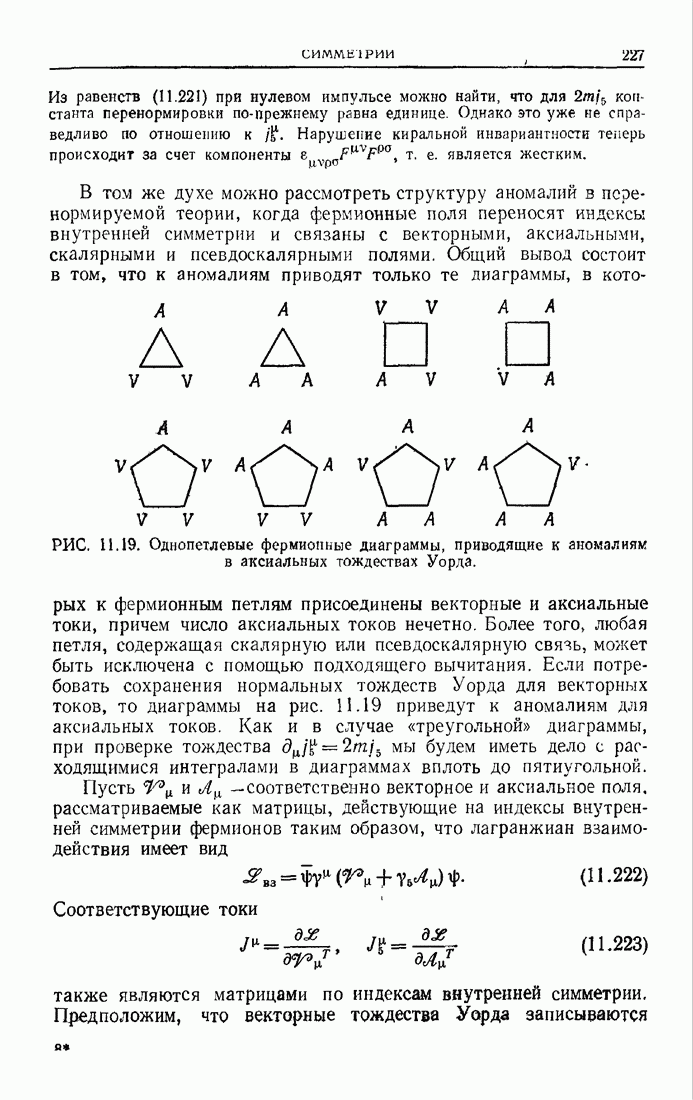
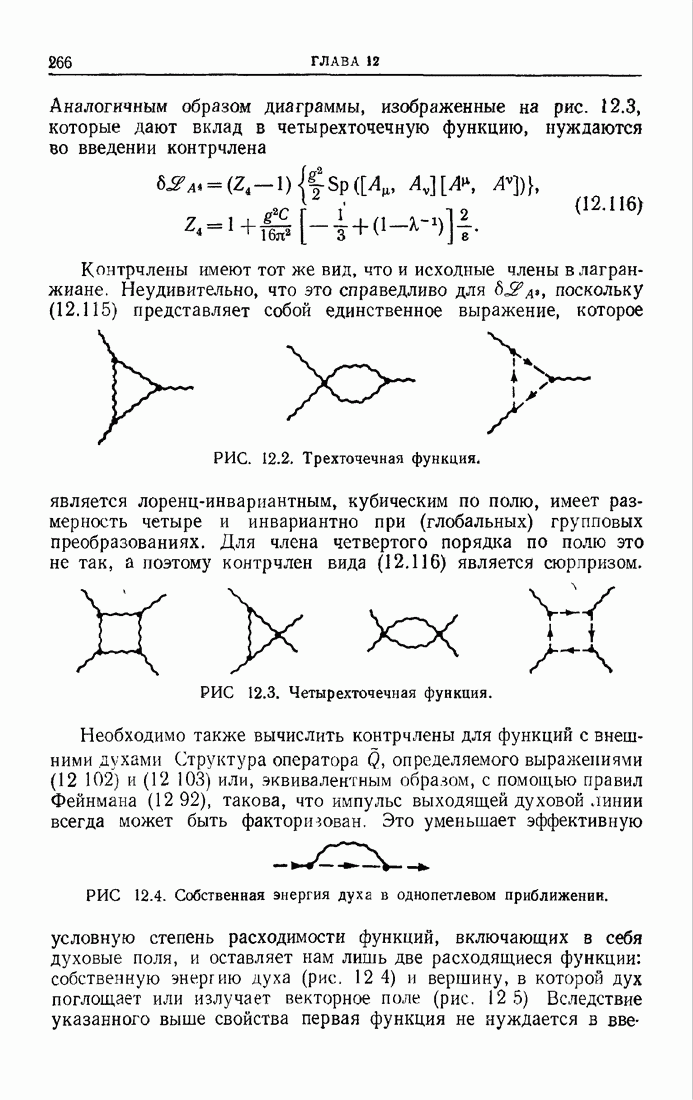
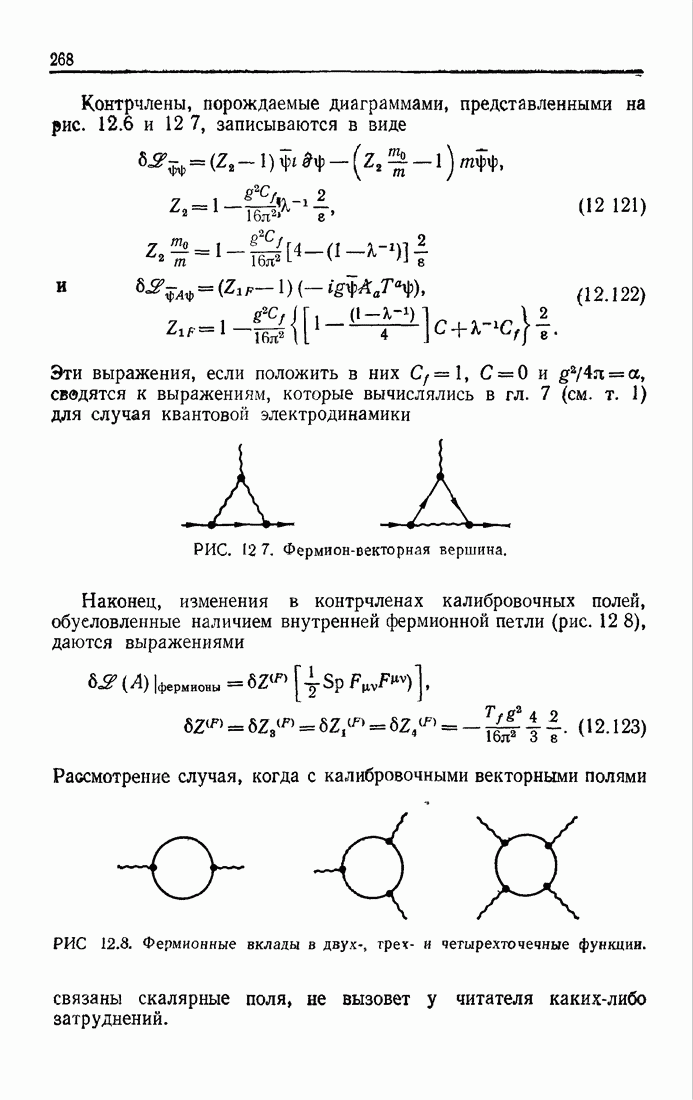
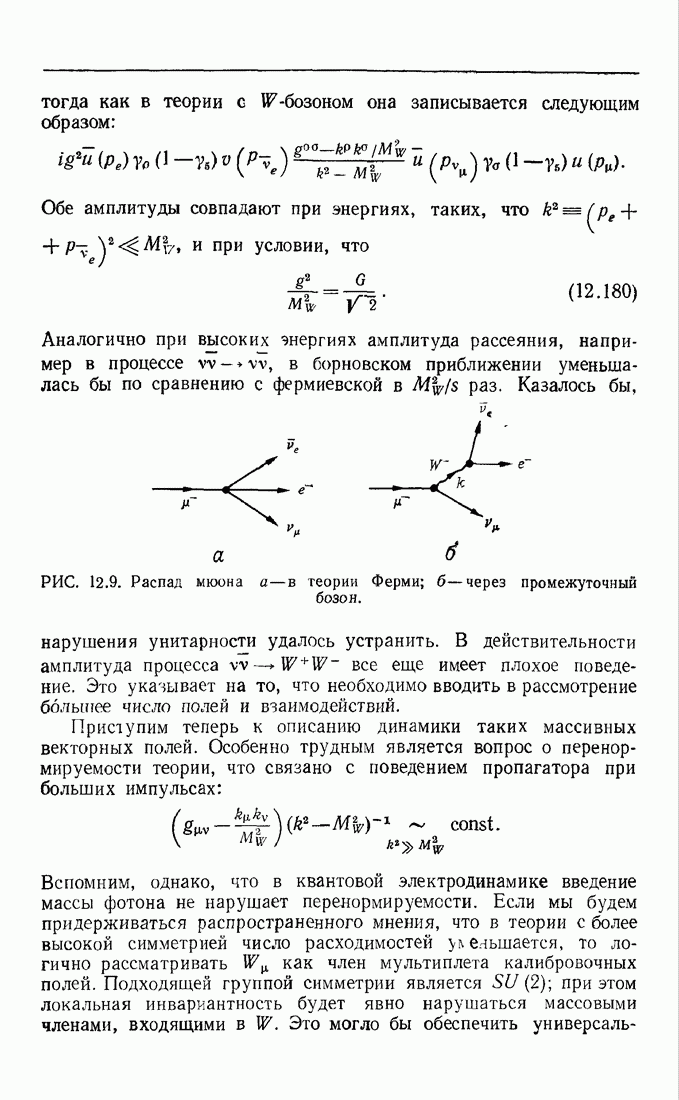
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
13.5. ОПЕРАТОРНЫЕ РАЗЛОЖЕНИЯ
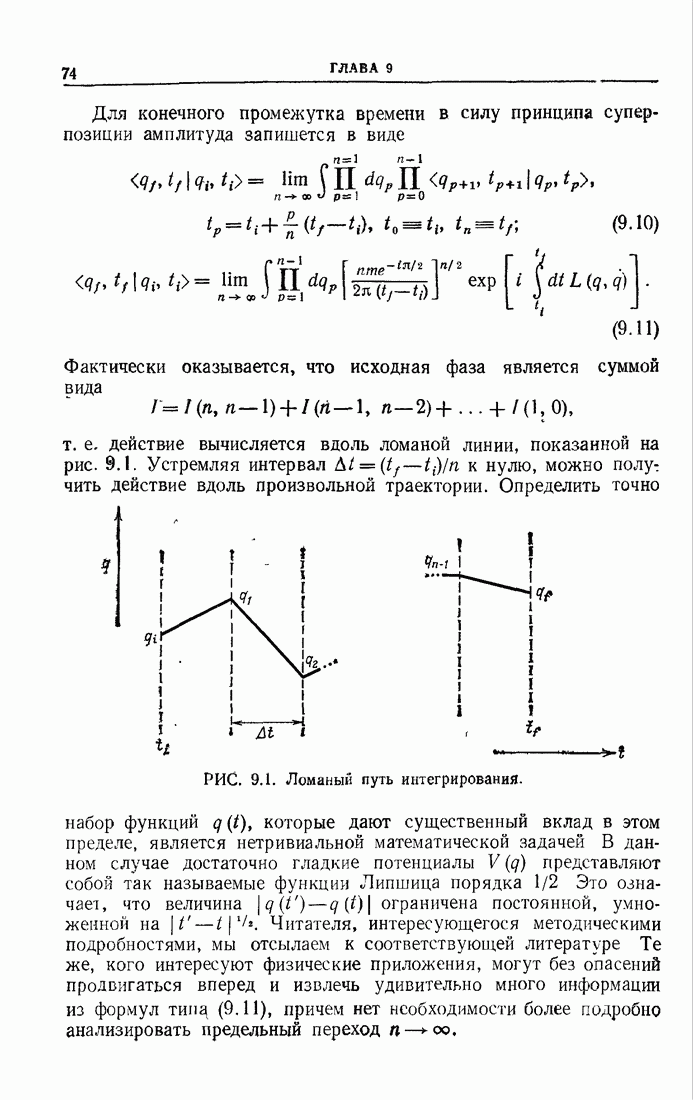
Проведенное выше рассмотрение иллюстрирует интерес к изучению поведения матричных элементов произведений составных операторов в некоторых хорошо определенных предельных случаях. Этими случаями являются следующие:
1. Пространственно-подобный интервал стремится к нулю (евклидов случай).
2 Времениподобный интервал стремится к нулю (метрика Минковского).
3. Величина стремится к нулю (свегоподобный предел).
Случаи 2 и 3 характерны для физики частиц. Вообще говоря, рассматриваемые операторы являются сохраняющимися или частично сохраняющимися токами Случай 1 можно проанализировать наиболее полно. Полученные результаты непосредственно применимы в статистической механике. Основополагающие работы в этой области были сделаны Вилсоном и Циммерманом.
13.5.1. Разложение на малых расстояниях
Рассмотрим произведение двух локальных операторов. В целях упрощения будем указывать только их зависимость от конфигурационных переменных. Для этого произведения Вилсон предложил разложение на малых расстояниях в виде
 (13.131)
(13.131)
Здесь через  обозначена последовательность локальных регулярных операторов, в то время как с-числовые коэффициенты
обозначена последовательность локальных регулярных операторов, в то время как с-числовые коэффициенты  в пределе
в пределе  сингулярны. В рамках теории возмущений их поведение с точностью до логарифмов определяется канонической размерностью соответствующих операторов:
сингулярны. В рамках теории возмущений их поведение с точностью до логарифмов определяется канонической размерностью соответствующих операторов:
 (13.132)
(13.132)
Чем выше размерность величины  тем быстрее С стремится к нулю. Очевидно, что ренормгрупповые эффекты приводят к некоторой модификации этих соображений.
тем быстрее С стремится к нулю. Очевидно, что ренормгрупповые эффекты приводят к некоторой модификации этих соображений.
Когда имеют дело с евклидовой теорией, слово «оператор» несколько дезориентирует. В действительности мы подразумеваем возможность построить обобщенные функции Грина  , в которых
, в которых  аргументов
аргументов  относятся к фундаментальным полям, а оставшиеся два — к А и В. Смысл выражения (13.131) состоит в том, что если упорядочить операторы О в соответствии с их размерностью, то
относятся к фундаментальным полям, а оставшиеся два — к А и В. Смысл выражения (13.131) состоит в том, что если упорядочить операторы О в соответствии с их размерностью, то

Разложение Вилсона обладает тем свойством, что сингулярности, возникающие в пределе  содержатся в с-числовых коэффициентах
содержатся в с-числовых коэффициентах  независимо от числа аргументов и типов элементарных полей, входящих в функции Грина. В пространстве Минковского равенство (13.133) понимается, как асимптотический ряд (в слабом смысле) матричных элементов между физическими состояниями. Очевидно, это является обобщением случая, рассмотренного выше, когда все разности координат одновременно устремлялись к нулю. Мы покажем, что для коэффициентов
независимо от числа аргументов и типов элементарных полей, входящих в функции Грина. В пространстве Минковского равенство (13.133) понимается, как асимптотический ряд (в слабом смысле) матричных элементов между физическими состояниями. Очевидно, это является обобщением случая, рассмотренного выше, когда все разности координат одновременно устремлялись к нулю. Мы покажем, что для коэффициентов  можно написать ренормгрупповые уравнения
можно написать ренормгрупповые уравнения
Вместо того чтобы приводить громоздкое общее доказательство, удовлетворимся рассмотрением простого примера из теории скалярного поля Будем считать операторы А и В элементарными полями и найдем главный коэффициент
 (13.134)
(13.134)
Из (13.132) можно ожидать, что  ведет себя в данном порядке как полином по
ведет себя в данном порядке как полином по  с точностью до членов порядка
с точностью до членов порядка  . Чтобы доказать это, рассмотрим два набора связных функций Грина
. Чтобы доказать это, рассмотрим два набора связных функций Грина  и изучим дополнительные вычитания, необходимые для построения в сравнении с теми, что необходимы для построения
и изучим дополнительные вычитания, необходимые для построения в сравнении с теми, что необходимы для построения  . На рис. 13.13 иллюстрируется пример, включающии G и
. На рис. 13.13 иллюстрируется пример, включающии G и 
Подынтегральное выражение в фейнмановском интеграле, относящемся к G, можно получить, если отождествить две внешние вершины, принадлежащие  (рассматривая их далее как одну), и соответствующим образом подправить симметрийиый коэффициент. Но вычитания, которые необходимо произвести,
(рассматривая их далее как одну), и соответствующим образом подправить симметрийиый коэффициент. Но вычитания, которые необходимо произвести,
будут иными. Для анализа перенормировочной процедуры достаточно рассмотреть одночастичпо-неприводимые функции  . Однако не следует удалять из
. Однако не следует удалять из  две внешние линии, которые должны «склеиться» при переходе к
две внешние линии, которые должны «склеиться» при переходе к 

РИС. 13.13. Связные функции Грина 
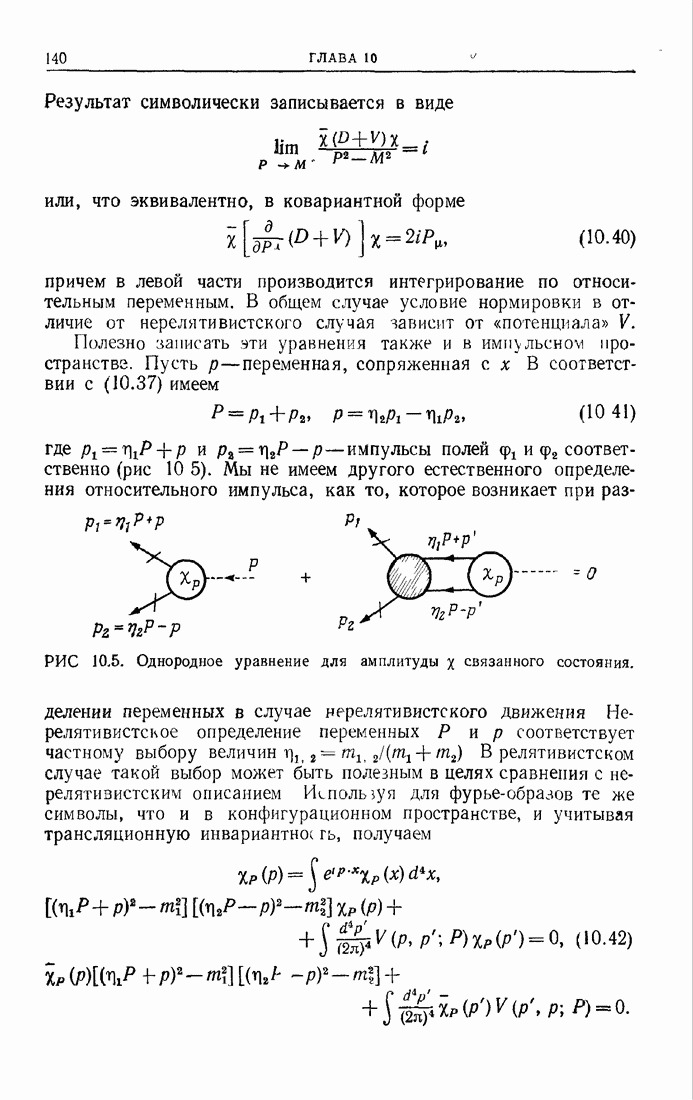
Обозначим через одночастично-неприводимую  -точечную функцию с полными пропагаторами на внешних линиях, по которым протекают импульсы и
-точечную функцию с полными пропагаторами на внешних линиях, по которым протекают импульсы и  . Пусть
. Пусть  и
и  -перенормированные подынтегральные выражения соответственно для
-перенормированные подынтегральные выражения соответственно для  . Они связаны соотношением
. Они связаны соотношением
 (13.135)
(13.135)
где  обусловлено вычитаниями расходимостей из подграфов, содержащих вершину V, сопоставляемую оператору
обусловлено вычитаниями расходимостей из подграфов, содержащих вершину V, сопоставляемую оператору  Эти подграфы соответствуют неприводимым функциям Грина с двумя внешними ф-линиями и имеют нулевую условную степень расходимости, если считать, что размерность
Эти подграфы соответствуют неприводимым функциям Грина с двумя внешними ф-линиями и имеют нулевую условную степень расходимости, если считать, что размерность  равна двум. Как и в гл. 8, обозначим через
равна двум. Как и в гл. 8, обозначим через  множество всех лесов расходящихся подграфов, причем один из них содержит v. Если
множество всех лесов расходящихся подграфов, причем один из них содержит v. Если  является наименьшим расходящимся подграфом множества
является наименьшим расходящимся подграфом множества  содержащим вершину V, то можно написать
содержащим вершину V, то можно написать
 (13.136)
(13.136)
где  -множество расходящихся подграфов, принадлежащих
-множество расходящихся подграфов, принадлежащих  , a
, a  -множество расходящихся подграфов, которые либо целиком содержат
-множество расходящихся подграфов, которые либо целиком содержат  , либо вообще не пересекаются с
, либо вообще не пересекаются с  . Пусть
. Пусть  — подынтегральное выражение до вычитаний, общее для
— подынтегральное выражение до вычитаний, общее для  явное выражение для
явное выражение для  имеет вид
имеет вид
 (13.137)
(13.137)
Суммирование можно выполнить следующим образом Сначала учтем подграф  , содержащий v, затем просуммируем по лесам
, содержащий v, затем просуммируем по лесам
 принадлежащим
принадлежащим  (исключая при этом само
(исключая при этом само  ), и далее — по лесам
), и далее — по лесам  редуцированной диаграммы
редуцированной диаграммы  Последняя представляет собой одну из диаграмм, дающих вклад в функцию
Последняя представляет собой одну из диаграмм, дающих вклад в функцию  Для диаграммы, дающей вклад в функцию
Для диаграммы, дающей вклад в функцию  обозначим через а подграф, соответствующий
обозначим через а подграф, соответствующий  . Если отвлечься от пропагаторов (и возможных собственно-энергетических вставок в них) двух линий, которые (для
. Если отвлечься от пропагаторов (и возможных собственно-энергетических вставок в них) двух линий, которые (для  ) соединяются в вершине v, то а представляет собой неприводимую четырехточечную функцию. Назовем ее
) соединяются в вершине v, то а представляет собой неприводимую четырехточечную функцию. Назовем ее 
Для любого  подынтегральное выражение I факторизуется следующим образом:
подынтегральное выражение I факторизуется следующим образом:  При промежуточной перенормировке операторы
При промежуточной перенормировке операторы  сводятся к ряду Тейлора при нулевом импульсе. Леса
сводятся к ряду Тейлора при нулевом импульсе. Леса  относятся к
относятся к  являются лесами
являются лесами  сводится к замене величины
сводится к замене величины  ее постоянным членом (а).
ее постоянным членом (а).

РИС. 13.14. Вычитания при нулевом импульсе в 
Эта операция иллюстрируется на рис. 13.14, на котором показан некоторый вклад в  Соответствующая диаграмма содержит две линии, которые можно будет затем соединить в вершине V. Под действием операции
Соответствующая диаграмма содержит две линии, которые можно будет затем соединить в вершине V. Под действием операции  все внешние импульсы полагаются равными нулю, за исключением импульса k, как бы циркулирующего по подграфу
все внешние импульсы полагаются равными нулю, за исключением импульса k, как бы циркулирующего по подграфу  . Математически это можно записать следующим образом:
. Математически это можно записать следующим образом:
 (13.138)
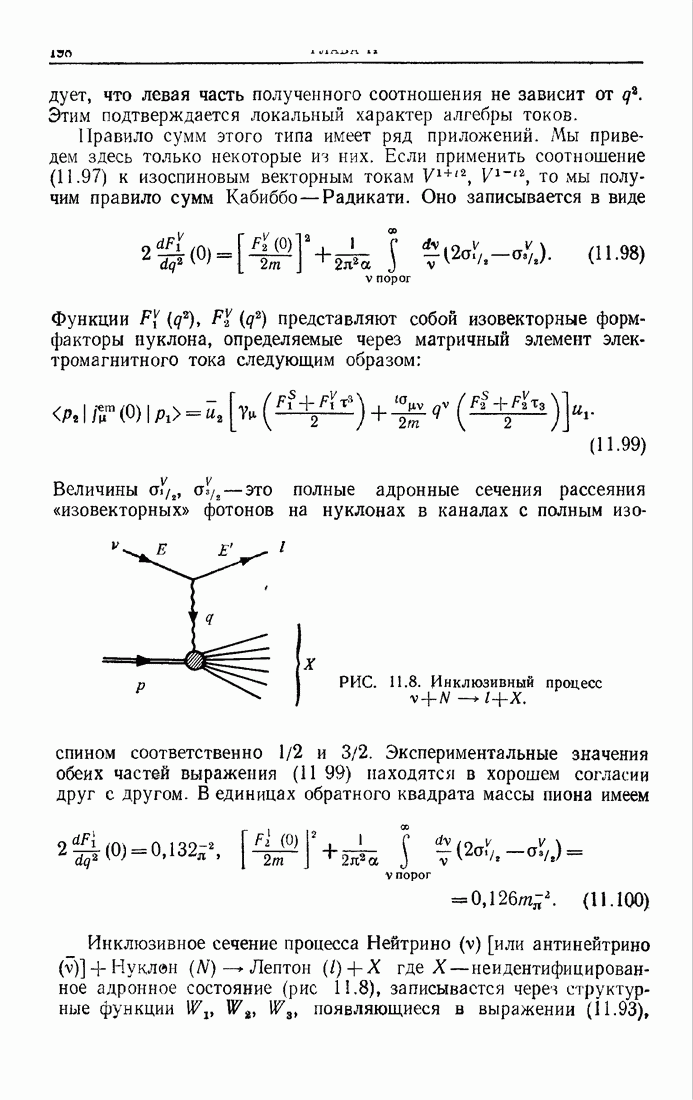
(13.138)
откуда с учетом соотношения (13.135) имеем
 (13.139)
(13.139)
Перенормированное подынтегральное выражение для  записано в таком виде, что вычитания, связанные с V, фигурируют явно, хотя они, безусловно, компенсируются вторым членом в правой части этого соотношения. В данном случае обозначение
записано в таком виде, что вычитания, связанные с V, фигурируют явно, хотя они, безусловно, компенсируются вторым членом в правой части этого соотношения. В данном случае обозначение  является несколько двусмысленным, поскольку число аргументов все еще равно
является несколько двусмысленным, поскольку число аргументов все еще равно  и операция
и операция  действует на функцию Грина, которую будем обозначать как
действует на функцию Грина, которую будем обозначать как

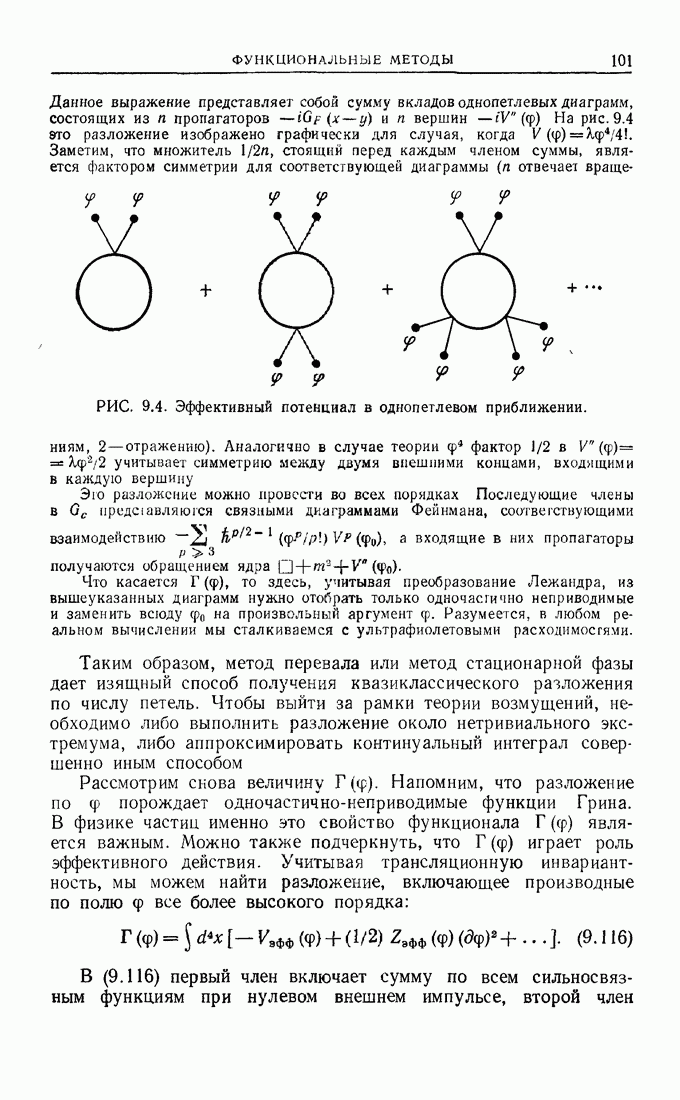
После интегрирования по импульсам петель и суммирования по диаграммам функцию Грина можно записать следующим образом:

Определим величины

Обозначение  напоминает, что оператору, заключенному в скобки, приписывается размерность, равная двум. Для упрощения обозначений мы воспользовались символами Г-произведения в пространстве Минковского. Полагая
напоминает, что оператору, заключенному в скобки, приписывается размерность, равная двум. Для упрощения обозначений мы воспользовались символами Г-произведения в пространстве Минковского. Полагая
 (13.141)
(13.141)
для фурье-образа при Нулевом импульсе и учитывая равенство (13.139), приходим к заключению, что
 (13.142)
(13.142)
Индекс Р указывает на то, что рассматриваемая величина получена из неприводимой функции Грина  добавлением полных пропагаторов на двух внешних линиях. Мы рекомендуем читателю проверить описанные выше операции на каком-либо примере, чтобы убедиться в необходимости наличия симметрийного фактора (1/2) в (13.142).
добавлением полных пропагаторов на двух внешних линиях. Мы рекомендуем читателю проверить описанные выше операции на каком-либо примере, чтобы убедиться в необходимости наличия симметрийного фактора (1/2) в (13.142).
Эта алгебраическая конструкция хорошо приспособлена для изучения предела  Действительно, исходя из теории перенормировок, можно считать, что после вычитаний интеграл сходится. В частности, функции Грина, включающие
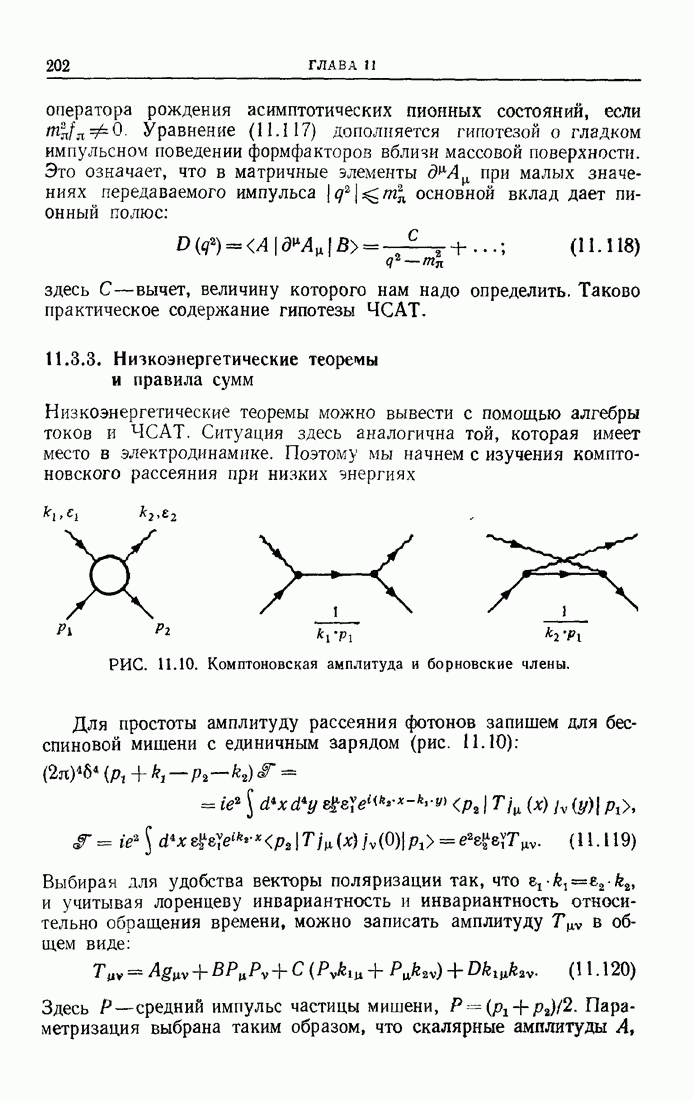
Действительно, исходя из теории перенормировок, можно считать, что после вычитаний интеграл сходится. В частности, функции Грина, включающие  в каждом порядке теории возмущений, при
в каждом порядке теории возмущений, при  стремятся к функциям Грина, содержащим
стремятся к функциям Грина, содержащим  с точностью до поправок вида
с точностью до поправок вида  по крайней мере в евклидовой области.
по крайней мере в евклидовой области.
Следовательно, равенство (13.142) позволяет выделить следующую наиболее сингулярную часть функции  :
:
 (13.143)
(13.143)
В каждом порядке теории возмущений  ведет себя как полином по
ведет себя как полином по  Например, в низшем порядке функция
Например, в низшем порядке функция  пропорциональна
пропорциональна

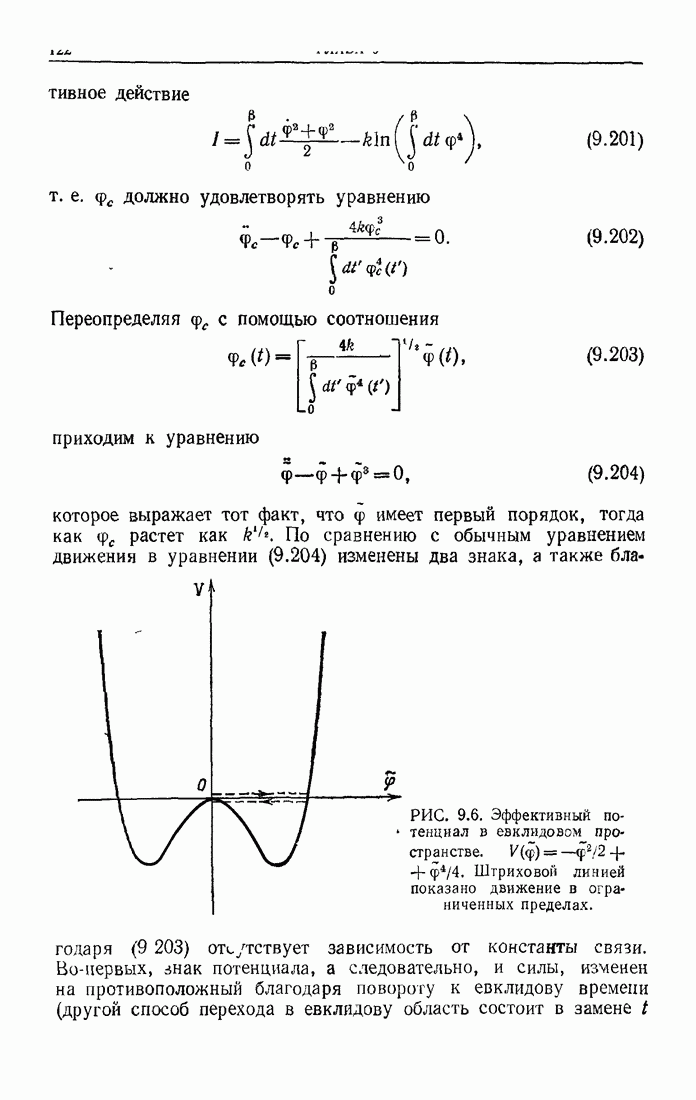
Вышеприведенному выводу можно придать более рафинированную форму, с тем чтобы продемонстрировать построение последующих членов разложения Вилсона. Мы опустим обсуждение этого довольно скучного вопроса и, предполагая, что окончательный результат правилен, займемся изучением следствий, вытекающих из применения ренермализационной группы к коэффициенту С. Согласно (13 143), при этом потребуется анализировать функции Грина при исключительных импульсах.
Из примера, данного выше, ясно, что в теории возмущений функция  может содержать и субдоминантные члены Поэтому мы должны сделать выбор, следовать ли нам первоначальному методу Каллана—Симанзика, в котором вводится массовая вставка при нулевом импульсе, или подходу Вайнберга, основанному на использовании не зависящих от массы условий нормировки. Для определенности выберем первую возможность и обозначим через
может содержать и субдоминантные члены Поэтому мы должны сделать выбор, следовать ли нам первоначальному методу Каллана—Симанзика, в котором вводится массовая вставка при нулевом импульсе, или подходу Вайнберга, основанному на использовании не зависящих от массы условий нормировки. Для определенности выберем первую возможность и обозначим через  асимптотическую форму функции
асимптотическую форму функции  получающуюся в результате отбрасывания членов, которые в рамках теории возмущений являются недоминирующими. Покажем, что
получающуюся в результате отбрасывания членов, которые в рамках теории возмущений являются недоминирующими. Покажем, что  удовлетворяет уравнению вида
удовлетворяет уравнению вида
 (13.145)
(13.145)
Связные функции Грина удовлетворяют уравнению
 (13.146)
(13.146)
Заметим, что всегда можно определить А таким образом, что множитель  [см. (13.70)] будет отсутствовать.
[см. (13.70)] будет отсутствовать.
Подставим в (13.146) разложение Вилсона при  и удержим только доминирующий член. В данном пределе левую часть этого выражения можно записать в виде
и удержим только доминирующий член. В данном пределе левую часть этого выражения можно записать в виде

Уравнение Каллана—Симанзика выполняется также и для 
 (13.147)
(13.147)
Отсюда уже следует желаемый результат при условии, что в пределе  правую часть выражения (13 146) можно отождествить с
правую часть выражения (13 146) можно отождествить с 
 (13.148)
(13.148)
Справедливость этого соотношения следует из рассмотрения, аналогичного тому, который мы провели кратко выше — необходимо только обобщить его на функции Грина, содержащие массовую вставку А. Заметим, что последняя находится вне подграфа  , дающего вклад в
, дающего вклад в  поскольку единственной расходящейся функцией с двумя
поскольку единственной расходящейся функцией с двумя  -вставками является амплитуда вакуум-вакуумного перехода Отсюда следует, что соотношение (13 148) выполняется, и таким образом мы доказали, что
-вставками является амплитуда вакуум-вакуумного перехода Отсюда следует, что соотношение (13 148) выполняется, и таким образом мы доказали, что  удовлетворяет уравнению ренормализационной группы (13 145).
удовлетворяет уравнению ренормализационной группы (13 145).
Все это распространяется и на последующие члены операторного разложения. Возвращаясь к общему случаю, когда рассматривается произведение  , видим, что (13.132) необходимо исправить на
, видим, что (13.132) необходимо исправить на
 (13.149)
(13.149)
где  — канонические, а
— канонические, а  аномальные размерности соответствующих операторов. Предполагается, что последние являются мультипликативна перенормируемыми.
аномальные размерности соответствующих операторов. Предполагается, что последние являются мультипликативна перенормируемыми.
Строго говоря, уравнения (13.145) и (13.149) справедливы только в евклидовой области. Они выполняются и в метрике Минковского
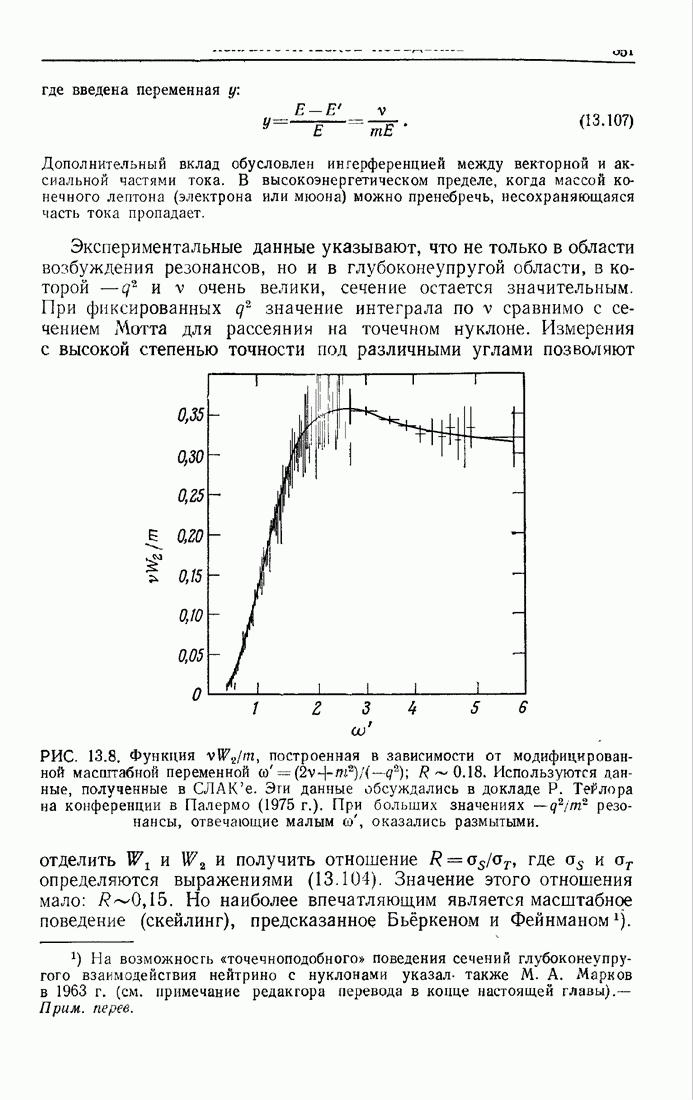
при условии, что фейнмановские добавки h остаются конечными. Предельный переход к реальному пространству Минковского, необходимый при анализе  -аннигиляции, требует детального рассмотрения возможных осцилляций при больших импульсах.
-аннигиляции, требует детального рассмотрения возможных осцилляций при больших импульсах.
Разложение Вилсона установлено только в смысле слабой сходимости. К примеру, оно выполняется для любой функции GB, содержащей  элементарных полей
элементарных полей  и операторы
и операторы  . Однако нет никакой гарантии, что (13 131) можно непосредственно применить к другим функциям Грина, включающим дополнительно еще какие-то составные операторы. Например, равенство
. Однако нет никакой гарантии, что (13 131) можно непосредственно применить к другим функциям Грина, включающим дополнительно еще какие-то составные операторы. Например, равенство

является неверным. В этом случае, поскольку функция как целое является примитивно расходящейся, существуют дополнительные вклады в поведение на малых расстояниях, кроме тех, что обусловлены двумя полями ( генерирующими коэффициент
генерирующими коэффициент  ). В частности, необходимо учитывать вычитание для всей диаграммы как целого, которое дает новую функцию
). В частности, необходимо учитывать вычитание для всей диаграммы как целого, которое дает новую функцию  не зависящую от
не зависящую от  :
:
 (13.150)
(13.150)
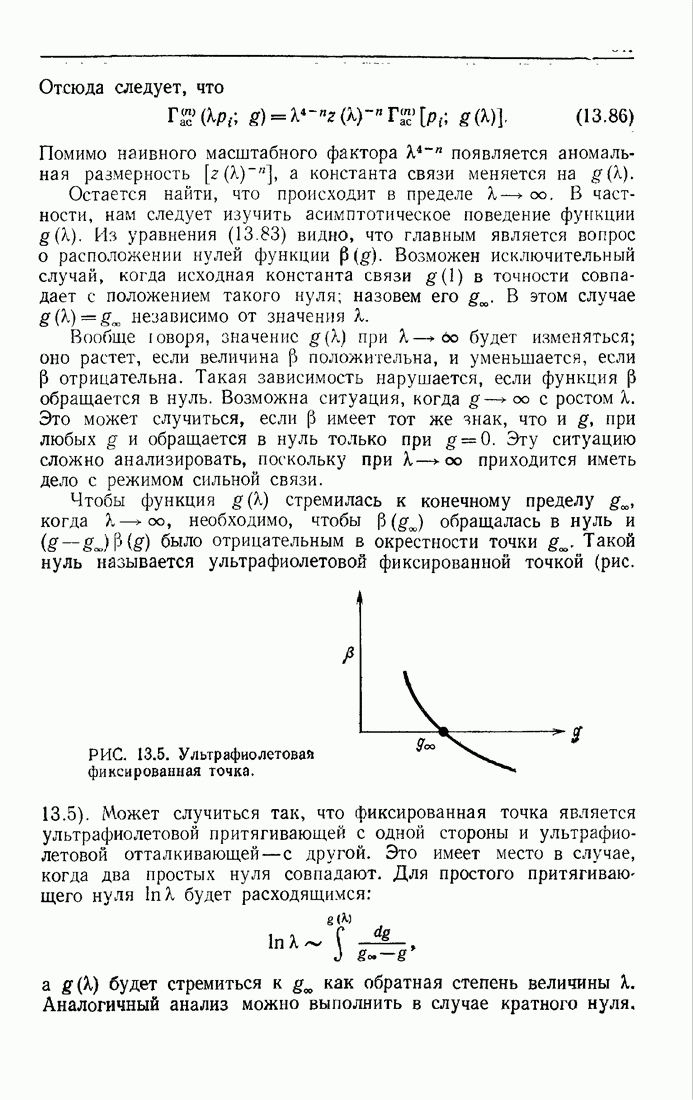
Характер следствий, вытекающих из операторного разложения, зависит от того, имеются ли в действительности (т. е. вне рамок теории возмущений) ультрафиолетовые фиксированные точки Если такая точка существует, то мы получаем результаты с помощью модифицированного анализа размерностей, причем

В асимптотически свободной теории, в которой функции  имеют порядок
имеют порядок  можно записать, как в разд. 13.3,
можно записать, как в разд. 13.3,

Интегрируя (13.149), получаем
 (13.153)
(13.153)
Таким образом, мы видим, что отклонения от канонического масштабного поведения имеют логарифмический характер.
Чтобы применить описанные выше методы к изучению конкретных примеров, необходимо указать вид соответствующих операторов, исследовать связанные с ними законы сохранения и обобщить анализ на случай светоподобных интервалов.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 8. ПЕРЕНОРМИРОВКА
- 8.1.2. Регуляризация
- 8.1.3. Подсчет степени расходимости
- 8.1.4. Теорема о сходимости
- 8.2. ПЕРЕНОРМИРОВКА
- 8.2.2. Рекуррентная формула Боголюбова
- 8.2.3. Явное решение Циммермана
- 8.2.4. Перенормировка в параметрическом представлении
- 8.2.5. Конечные перенормировки
- 8.2.6. Составные операторы
- 8.3. ПРЕДЕЛ НУЛЕВОЙ МАССЫ, АСИМПТОТИЧЕСКОЕ ПОВЕДЕНИЕ И ТЕОРЕМА ВАЙНБЕРГА
- 8.3.2. Поведение в ультрафиолетовой области и теорема Вайнберга
- 8.4. СЛУЧАЙ КВАНТОВОЙ ЭЛЕКТРОДИНАМИКИ
- 8.4.2. Регуляризация Паули — Вилларса во всех порядках
- 8.4.3. Перенормировка
- 8.4.4. Поляризация вакуума в двухпетлевом приближении
- ПРИМЕЧАНИЯ
- Глава 9. ФУНКЦИОНАЛЬНЫЕ МЕТОДЫ
- 9.1. КОНТИНУАЛЬНЫЕ ИНТЕГРАЛЫ
- 9.1.2. Траектории в пространстве Баргмана — Фока
- 9.1.3. Фермионные системы
- 9.2. РЕЛЯТИВИСТСКАЯ ФОРМУЛИРОВКА
- 9.2.1. Запись S-матрицы и функций Грина через континуальные интегралы
- 9.2.2. Эффективное действие и метод перевала
- 9.3. СИСТЕМЫ СО СВЯЗЯМИ
- 9.3.2. Электромагнитное поле как пример
- 9.4. ВЫСОКИЕ ПОРЯДКИ ТЕОРИИ ВОЗМУЩЕНИЙ
- 9.4.2. Ангармонический осциллятор
- ПРИМЕЧАНИЯ
- Глава 10. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ И ПРОБЛЕМА СВЯЗАННЫХ СОСТОЯНИЙ
- 10.1. УРАВНЕНИЯ ДАЙСОНА—ШВИНГЕРА
- 10.1.2. Перенормировка
- 10.2. РЕЛЯТИВИСТСКИЕ СВЯЗАННЫЕ СОСТОЯНИЯ
- 10.2.2. Поворот Вика
- 10.2.3. Обмен скалярными безмассовыми частицами в лестничном приближении
- 10.3. СВЕРХТОНКОЕ РАСЩЕПЛЕНИЕ В ПОЗИТРОНИИ
- 10.3.1. Общая постановка задачи
- 10.3.2. Вычисление в порядке а
- ПРИМЕЧАНИЯ
- Глава II. СИММЕТРИИ
- 11.1. РЕАЛИЗАЦИЯ СИММЕТРИЙ В КВАНТОВОЙ ТЕОРИИ
- 11.1.2. Основное состояние
- 11.2. СПЕКТР МАСС, МУЛЬТИПЛЕТЫ И ГОЛДСТОУНОВСКИЕ БОЗОНЫ
- 11.2.2. Спонтанное нарушение симметрии
- 11.3. АЛГЕБРА ТОКОВ
- 11.3.2. Частичное сохранение аксиального тока и киральная симметрия
- 11.3.3. Низкоэнергетические теоремы и правила сумм
- 11.4. сигма-МОДЕЛЬ
- 11.4.2. Перенормировка
- 11.5. АНОМАЛИИ
- 11.5.2. Аксиальная аномалия в сигма-модели
- 11.5.3. Общие свойства
- ПРИМЕЧАНИЯ
- Глава 12. НЕАБЕЛЕВЫ КАЛИБРОВОЧНЫЕ ПОЛЯ
- 12.1.2. Классическая динамика
- 12.1.3. Решения классических уравнений движения в евклидовой области
- 12.1.4. Калибровочная инвариантность и дополнительные связи
- 12.2. КВАНТОВАНИЕ КАЛИБРОВОЧНЫХ ПОЛЕЙ
- 12.2.2. Интегрирование по калибровочной группе
- 12.2.3. Правила Фейнмана
- 12.3. ЭФФЕКТИВНОЕ ДЕЙСТВИЕ В ОДНОПЕТЛЕВОМ ПРИБЛИЖЕНИИ
- 12.3.2. Двухточечная функция
- 12.3.3. Другие функции
- 12.3.4. Перенормировка однопетлевых диаграмм
- 12.4. ПЕРЕНОРМИРОВКА
- 12.4.1. Тождества Славнова — Тейлора
- 12.4.2. Тождества для сильносвязных функций
- 12.4.3. Рекурсивный метод построения контрчленов
- 12.4.4. Зависимость функций Грина от калибровки
- 12.4.5. Аномалии
- 12.5. МАССИВНЫЕ КАЛИБРОВОЧНЫЕ ПОЛЯ
- 12.5.2. Массивная калибровочная теория
- 12.5.3. Спонтанное нарушение симметрии
- 12.5.4. Перенормировка спонтанно нарушенных калибровочных теорий
- 12.5.5. Калибровочная независимость и унитарность S-матрицы
- 12.6. МОДЕЛЬ ВАЙНБЕРГА — САЛАМА
- 12.6.2. Электрон-нейтринные сечения
- 12.6.3. Поправки высших порядков
- 12.6.4. Включение адронов
- ПРИМЕЧАНИЯ
- Глава 13. АСИМПТОТИЧЕСКОЕ ПОВЕДЕНИЕ
- 13.1. ЭФФЕКТИВНЫЙ ЗАРЯД В ЭЛЕКТРОДИНАМИКЕ
- 13.12. Уравнение Каллана — Симанзика
- 13.2. НАРУШЕННАЯ МАСШТАБНАЯ ИНВАРИАНТНОСТЬ
- 13.2.1. Масштабная и конформная инвариантность
- 13.2.2. Модифицированные тождества Уорда
- 13.2.3. Коэффициенты Каллана — Симанзика в низших порядках
- 13.3. ВОССТАНОВЛЕННАЯ МАСШТАБНАЯ ИНВАРИАНТНОСТЬ
- 13.3.2. Асимптотическая свобода
- 13.3.3. Массовые поправки
- 13.4. ГЛУБОКОНЕУПРУГОЕ ЛЕПТОН-АДРОННОЕ РАССЕЯНИЕ И ЭЛЕКТРОН-ПОЗИТРОННАЯ АННИГИЛЯЦИЯ В АДРОНЫ
- 13.4.2. Динамика на световом конусе
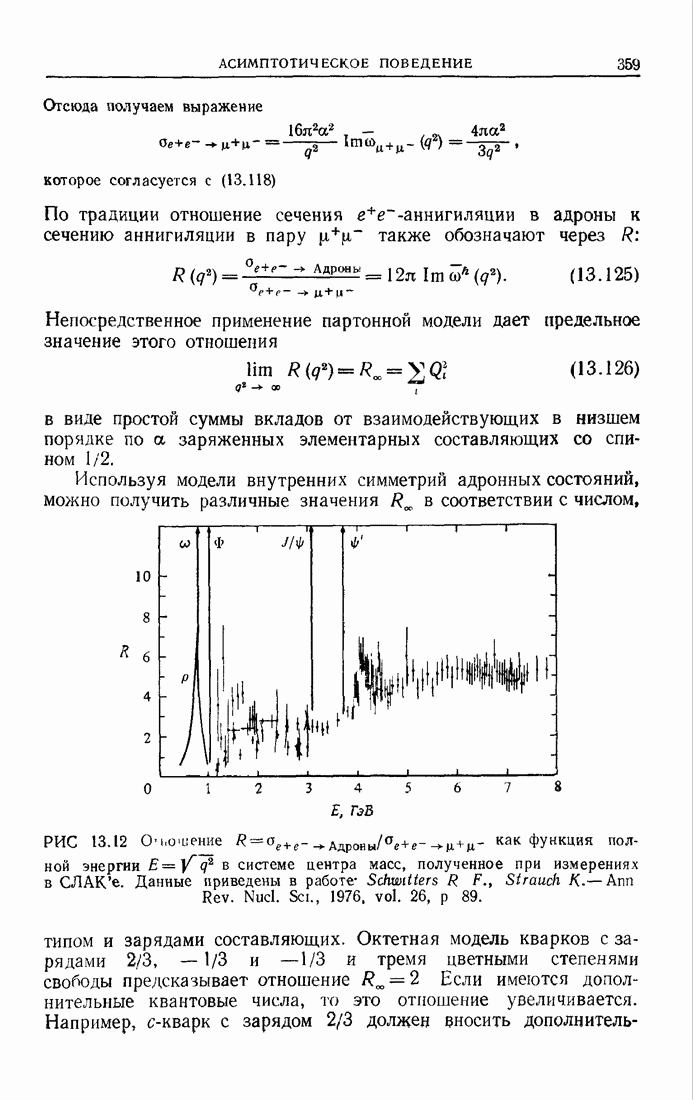
- 13.4.3. Электрон-позитронная аннигиляция
- 13.5. ОПЕРАТОРНЫЕ РАЗЛОЖЕНИЯ
- 13.5.2. Доминирующие и субдоминантные операторы, смешивание операторов и законы сохранения
- 13.5.3. Разложение на световом конусе
- ПРИМЕЧАНИЯ
- ПРИЛОЖЕНИЕ