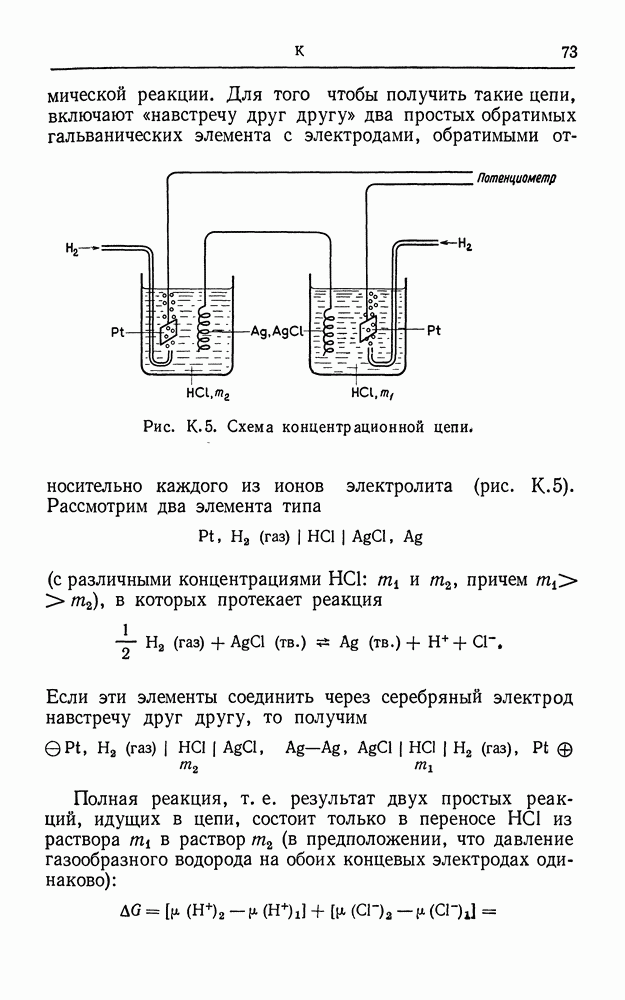
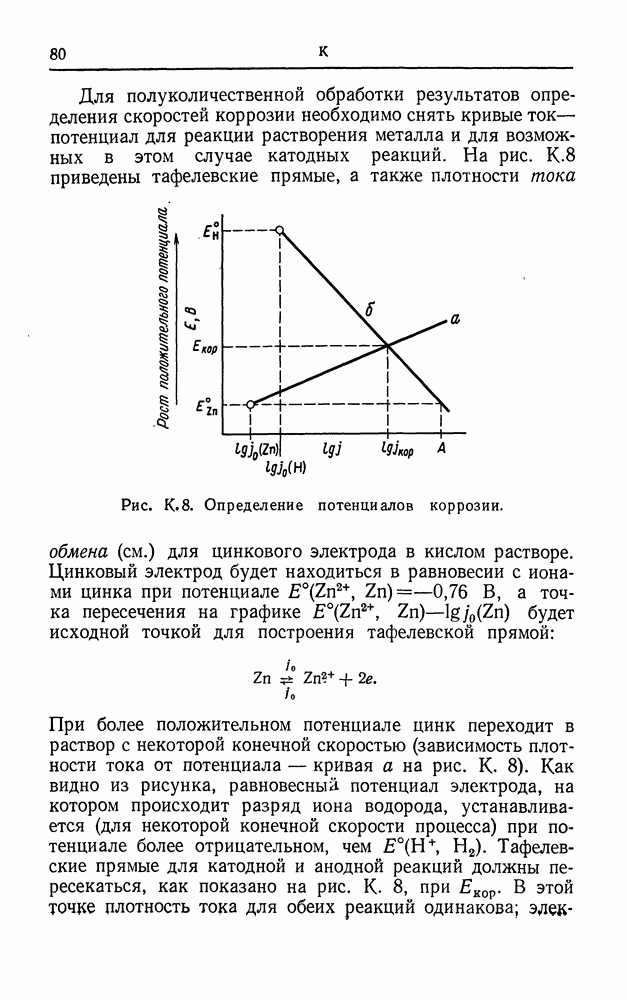
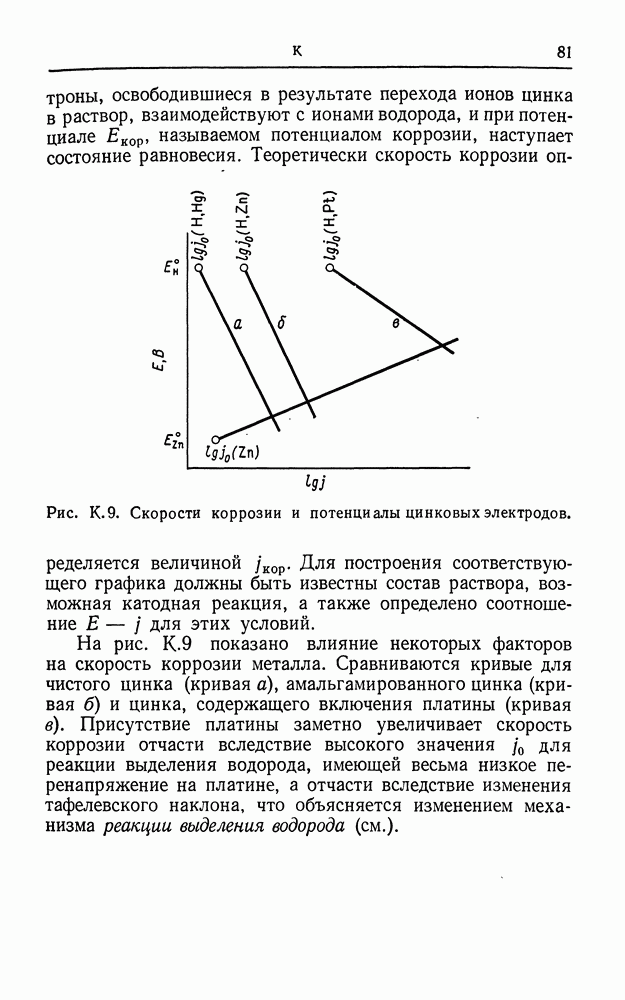
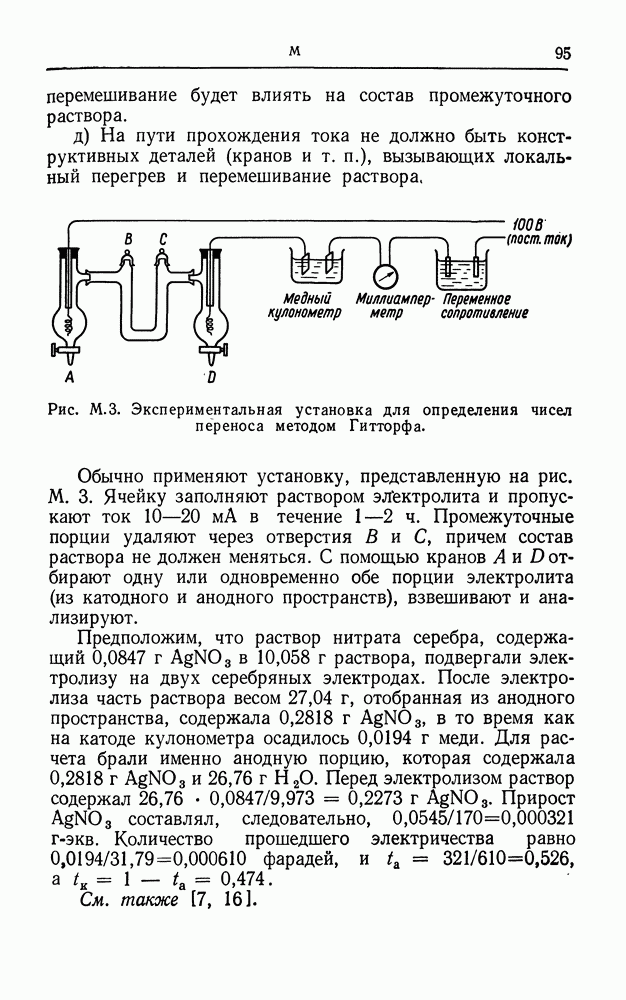
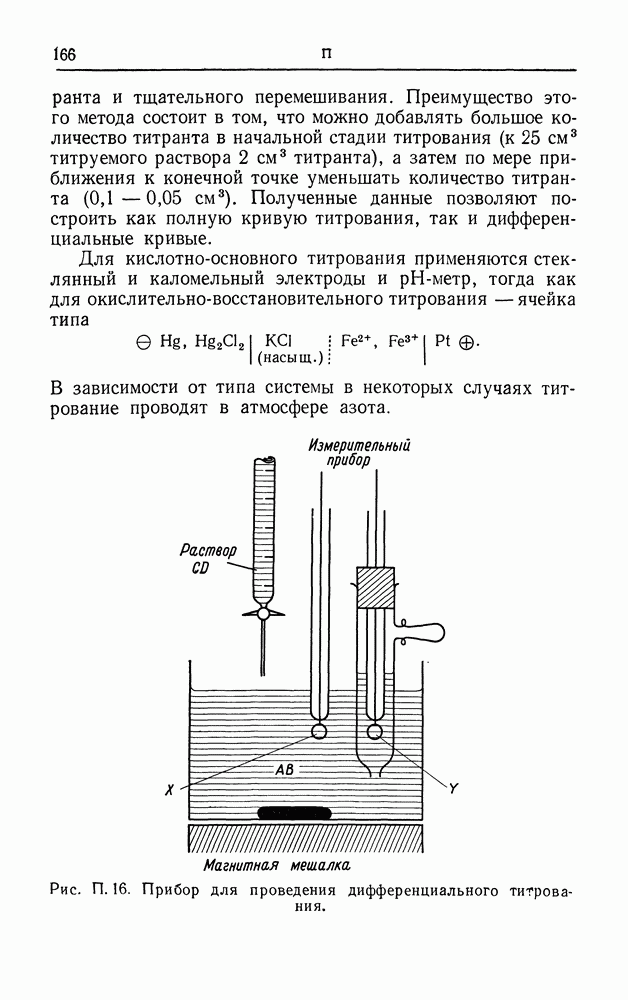
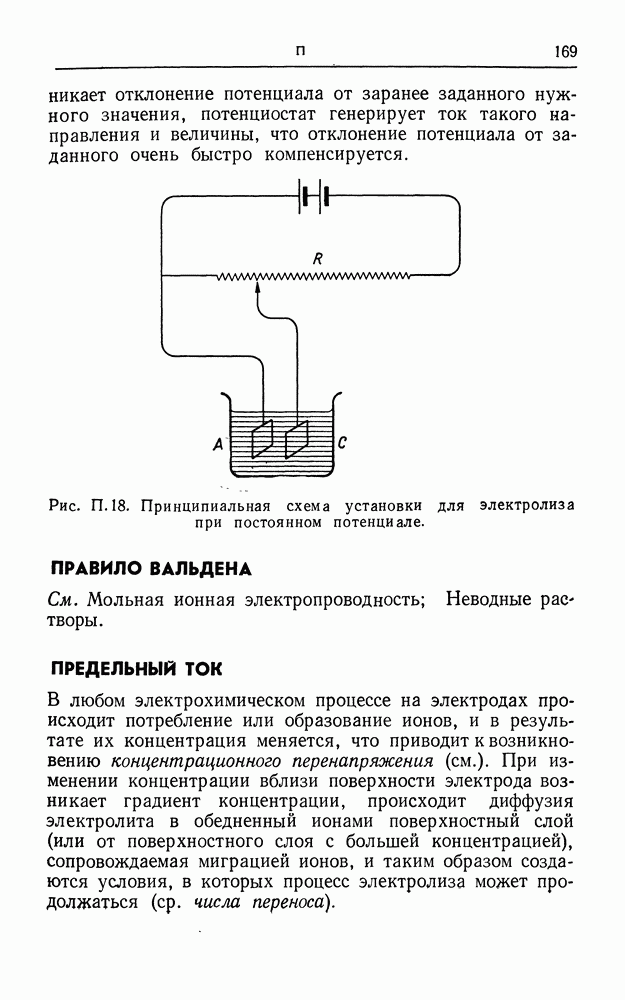
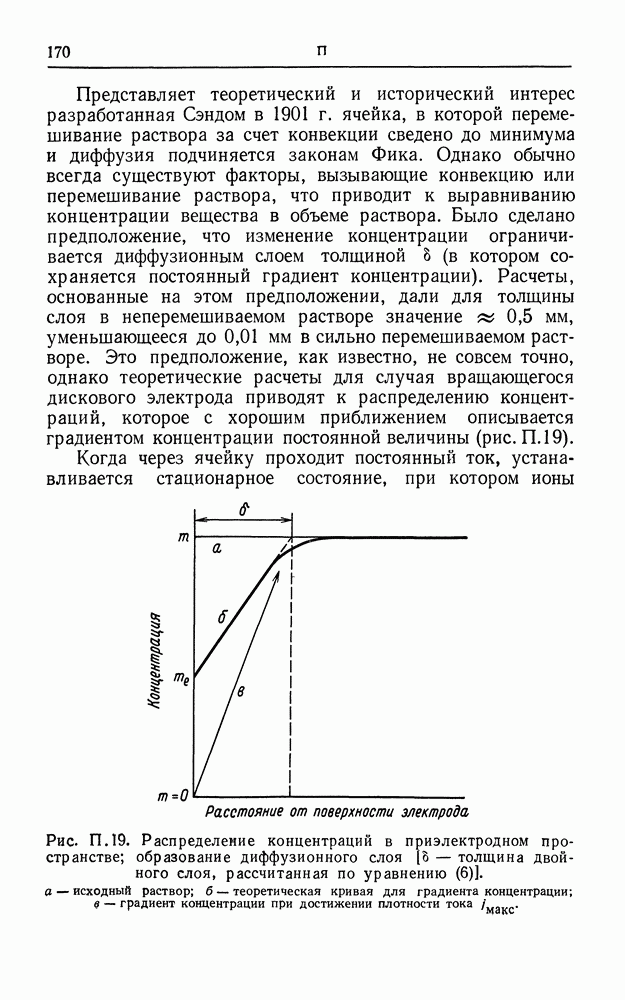
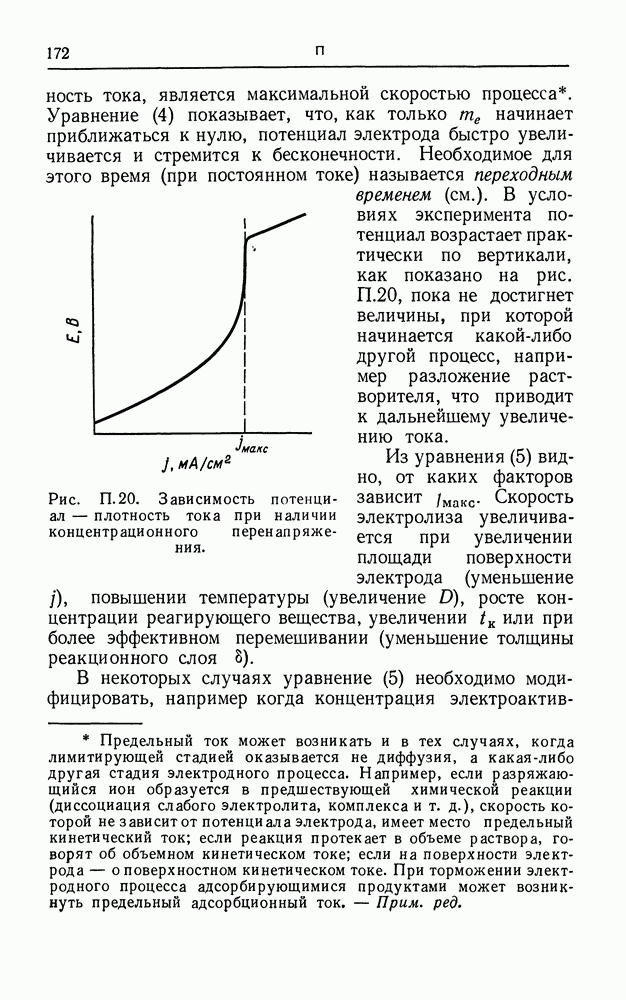
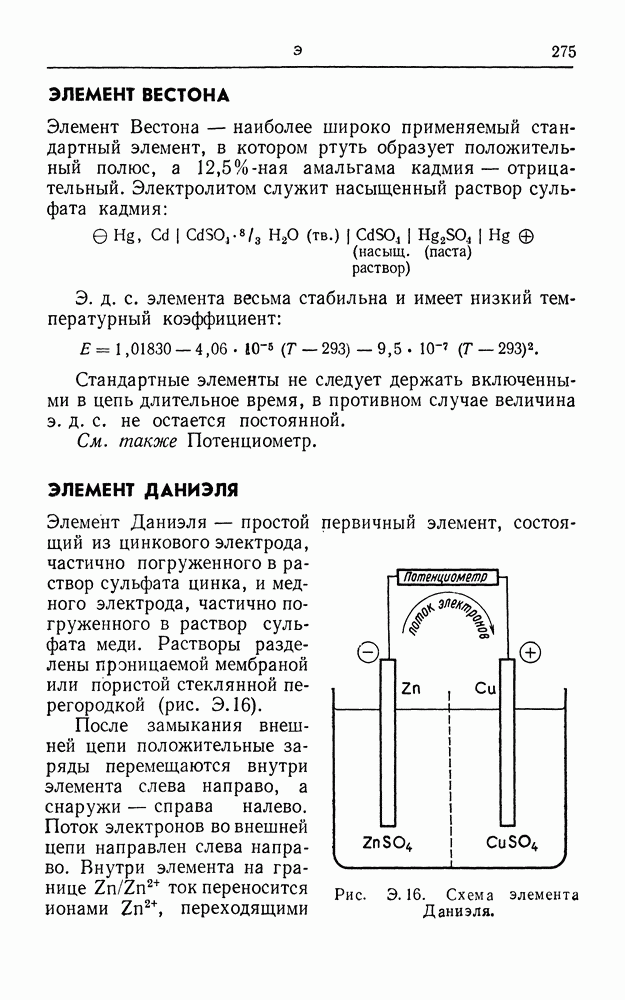
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ДИФФУЗИЯ В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
Рассмотрим диффузию полностью диссоциированного 1:1-электролита. Катионы и анионы в нем будут двигаться независимо друг от друга в направлении градиента концентрации, но если их подвижности неодинаковы, то более подвижный ион будет опережать другой, менее подвижный. Это приведет к возникновению электрического поля, которое будет ускорять движение медленного иона и замедлять движение быстрого иона, в результате скорости движения разноименных ионов выравниваются и условие электронейтральности сохранится. Таким образом, скорость диффузии электролита определяется подвижностями катионов и анионов. Для бесконечно разбавленного раствора электролита коэффициент диффузии описывается уравнением Нернста

где  — эквивалентные электропроводности катиона и аниона при бесконечном разбавлении (в
— эквивалентные электропроводности катиона и аниона при бесконечном разбавлении (в  ).
).
Для растворов с конечной концентрацией уравнение Нернста необходимо модифицировать двояким образом. Во-первых, диффузия определяется градиентом осмотического давления, или химического потенциала (не обязательно только градиентом концентрации), и поэтому необходимо принимать во внимание средний коэффициент активности электролита. Во-вторых, следует учитывать влияние ионной атмосферы. В отличие от того, что происходит в явлении электропроводности, при диффузии катионы и анионы движутся в одном и том же направлении, и поэтому симметрия ионных атмосфер не нарушается. В этом случае релаксационный эффект отсутствует, но существует небольшой электрофоретический эффект, который для разбавленных растворов был рассчитан Онзагером. Самые точные измерения подтверждают справедливость уравнения Нернста с указанными поправками.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- О ПОЛЬЗОВАНИИ СЛОВАРЕМ
- СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
- АККУМУЛЯТОР
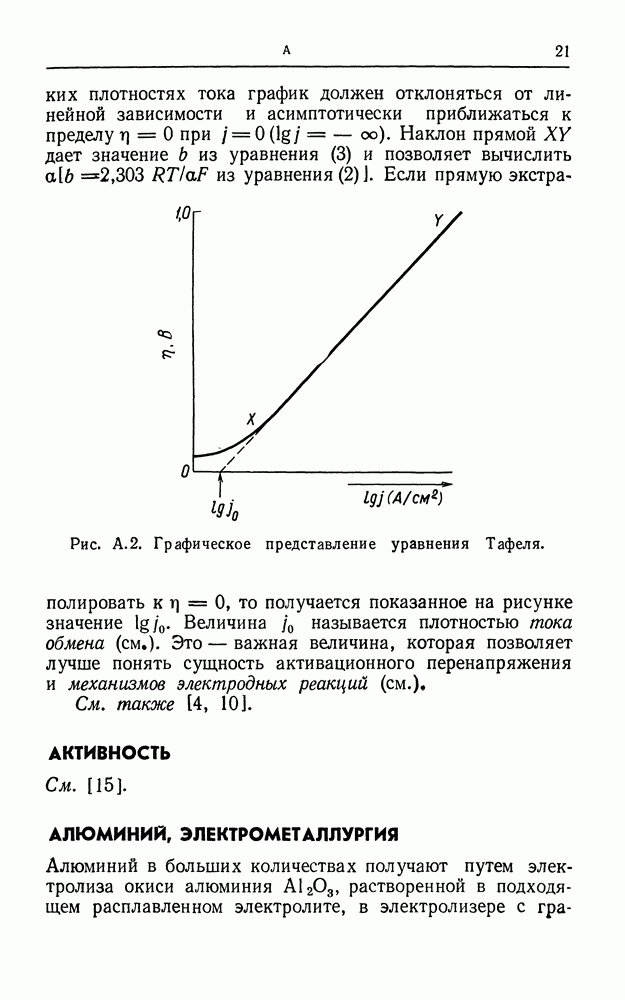
- АКТИВАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- АКТИВНОСТЬ
- АЛЮМИНИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- АМАЛЬГАМНЫЙ ЭЛЕКТРОД
- АМПЕР
- АМПЕРОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- АМПЕРОСТАТ
- АНИОН
- АНОД
- АНОДИРОВАНИЕ
- БАТАРЕЯ
- БЕРИЛЛИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- БИПОЛЯРНЫЙ ЭЛЕКТРОД
- БЛЕСКООБРАЗОВАТЕЛИ
- БУФЕРНЫЙ РАСТВОР
- ВАГНЕРОВСКОЕ ЗАЗЕМЛЕНИЕ
- ВНУТРЕННИЙ ЭЛЕКТРОЛИЗ
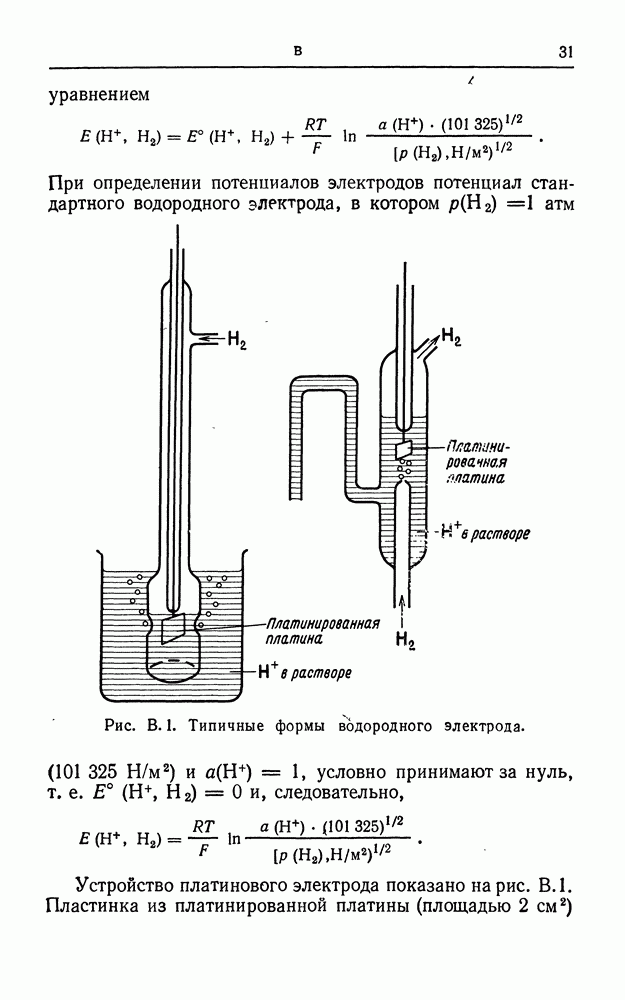
- ВОДОРОДНЫЙ ЭЛЕКТРОД
- ВОЛЬТ
- ВОЛЬФРАМОВЫЙ ЭЛЕКТРОД
- ВЫХОД ПО ТОКУ
- ГАЗОВЫЙ ЭЛЕКТРОД
- ГАЛЬВАНИЧЕСКИЙ ЭЛЕМЕНТ
- ГАЛЬВАНОПЛАСТИКА
- ГАЛЬВАНОСТАТ
- ГАЛЬВАНОСТЕГИЯ
- ГИДРАТАЦИЯ ИОНОВ
- ДАТЧИК АММИАКА
- ДАТЧИК СЕРНИСТОГО ГАЗА
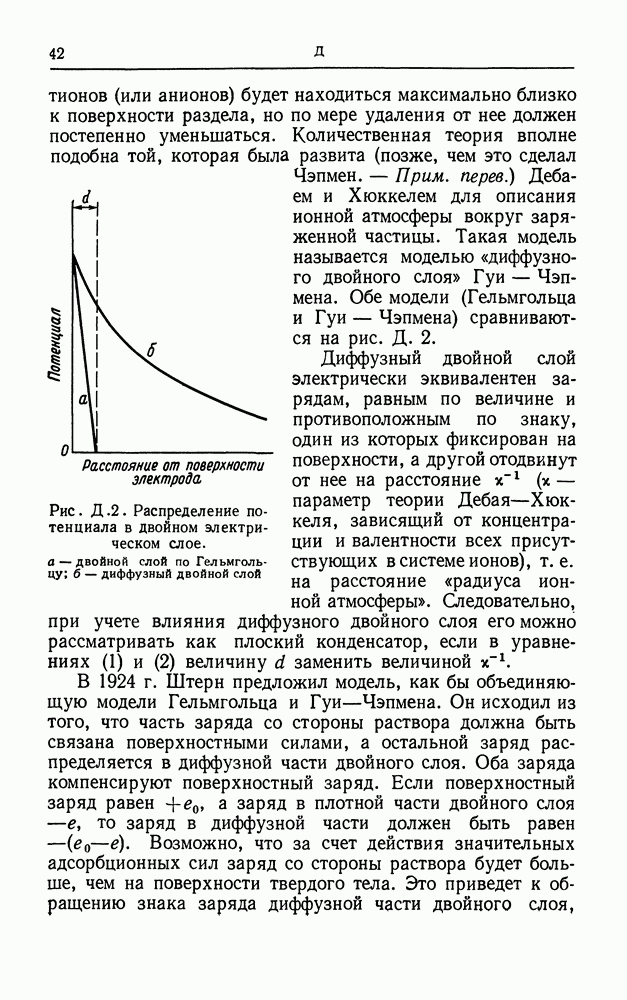
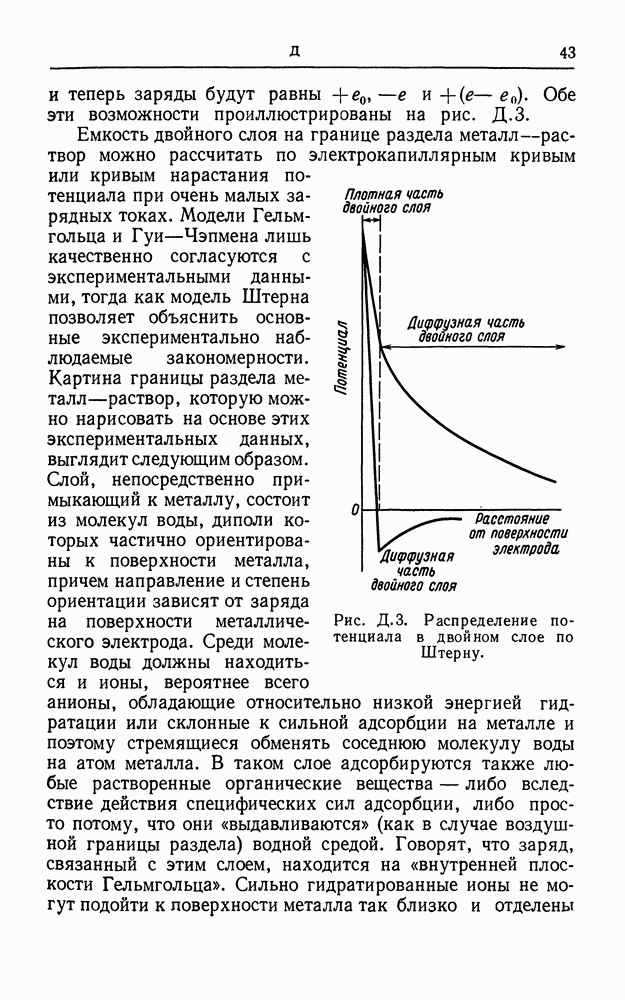
- ДВОЙНОЙ СЛОЙ
- ДВОЙНОЙ ЭЛЕКТРИЧЕСКИЙ СЛОЙ
- ДЗЕТА-ПОТЕНЦИАЛ
- ДИФФУЗИОННЫЙ ПОТЕНЦИАЛ
- ДИФФУЗИЯ В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
- ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ
- ЗАКОН КОЛЬРАУША
- ЗАКОН РАЗВЕДЕНИЯ ОСТВАЛЬДА
- ЗАКОНЫ ФАРАДЕЯ
- ИНДИКАТОР
- ИНДИКАТОРНЫЙ ЭЛЕКТРОД
- ИНДИФФЕРЕНТНЫЙ (ФОНОВЫЙ) ЭЛЕКТРОЛИТ
- ИОДНЫЙ КУЛОНОМЕТР
- ИОННАЯ АТМОСФЕРА
- ИОННЫЕ ПАРЫ
- ИОННЫЕ РАСПЛАВЫ
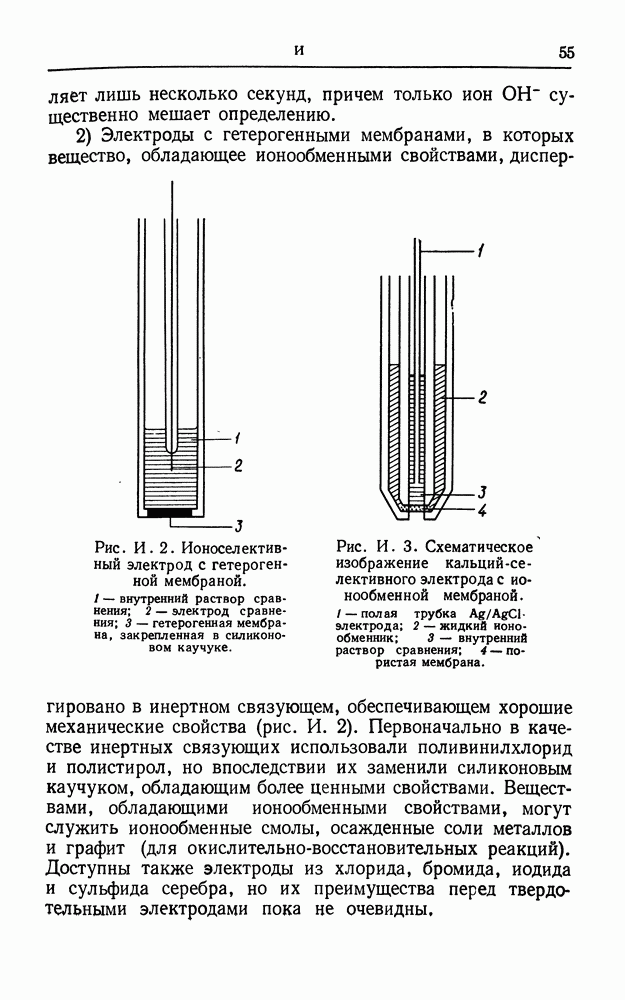
- ИОНОСЕЛЕКТИВНЫЕ ЭЛЕКТРОДЫ
- КАДМИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- КАЛОМЕЛЬНЫЙ ЭЛЕКТРОД
- КАЛЬЦИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- КАПИЛЛЯР ЛУГГИНА
- КАТИОН
- КАТИОНОСЕЛЕКТИВНЫЙ ЭЛЕКТРОД
- КАТОД
- КАТОДНАЯ ЗАЩИТА
- КИСЛОРОДНОЕ ПЕРЕНАПРЯЖЕНИЕ
- КИСЛОРОДНЫЙ ЭЛЕКТРОД (КИСЛОРОДНЫЙ ЗОНД)
- КОМПЛЕКСНЫЕ ИОНЫ
- КОНВЕНЦИЯ О ЗНАКАХ
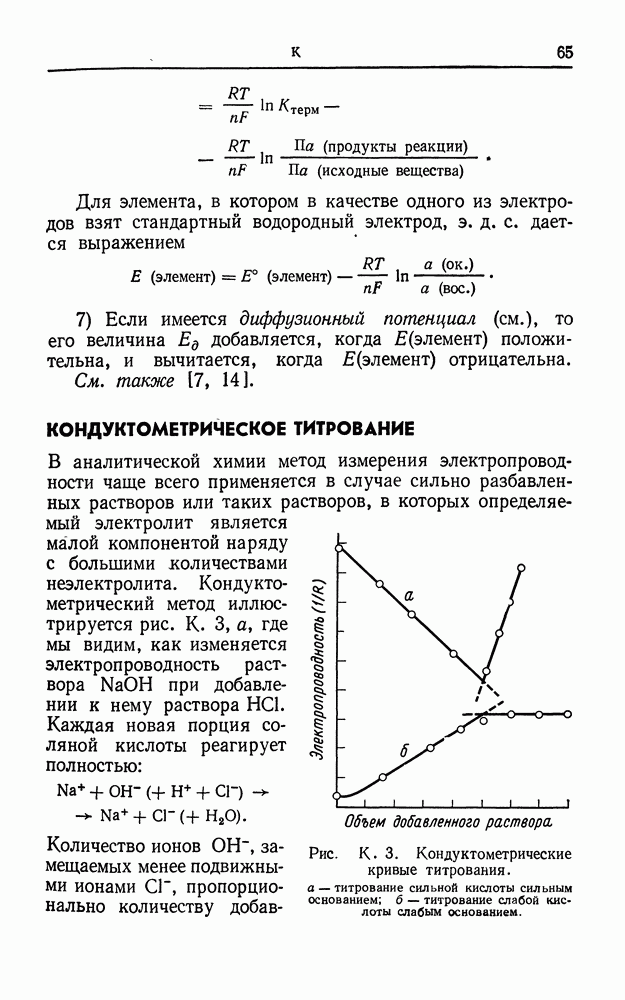
- КОНДУКТОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- КОНСТАНТА ДИССОЦИАЦИИ
- КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
- КОНЦЕНТРАЦИОННАЯ ЦЕПЬ
- КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- КОРРОЗИЯ
- КОЭФФИЦИЕНТ АКТИВНОСТИ
- КУЛОН
- КУЛОНОМЕТР
- КУЛОНОМЕТРИЯ
- ЛИТИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- МАГНИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- МЕДНООКИСНЫЙ ЭЛЕМЕНТ
- МЕДНЫЙ КУЛОНОМЕТР
- МЕДЬ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- МЕМБРАННЫЙ ЭЛЕКТРОД
- МЕТАЛЛИЧЕСКИЙ ЭЛЕКТРОД
- МЕТАЛЛООКИСНЫЙ ЭЛЕКТРОД
- МЕТОД ГИТТОРФА
- МЕТОД ДВИЖУЩЕЙСЯ ГРАНИЦЫ
- МЕХАНИЗМЫ ЭЛЕКТРОДНЫХ РЕАКЦИЙ
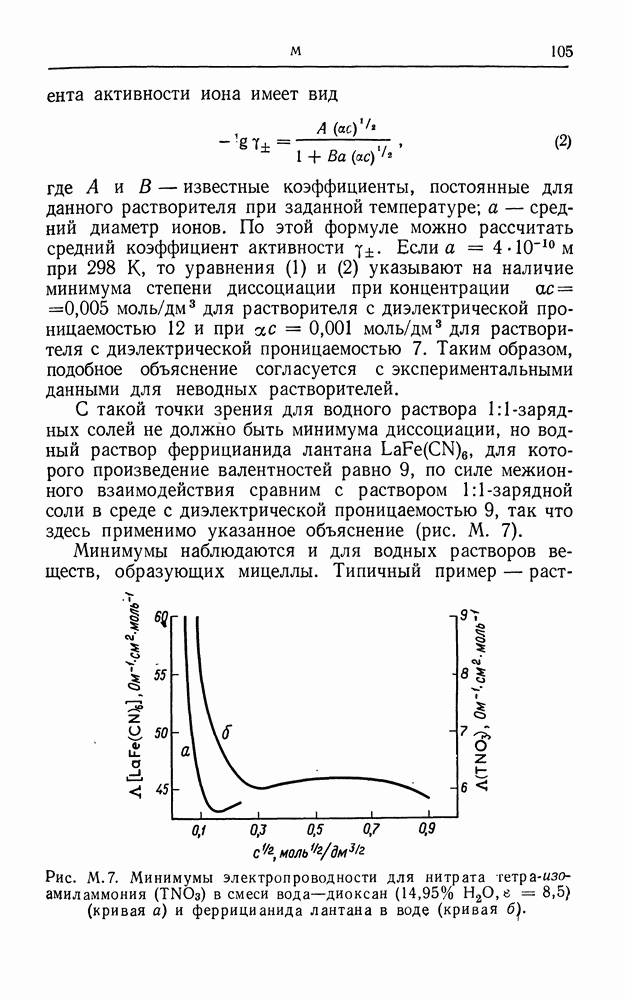
- МИНИМУМЫ ЭЛЕКТРОПРОВОДНОСТИ
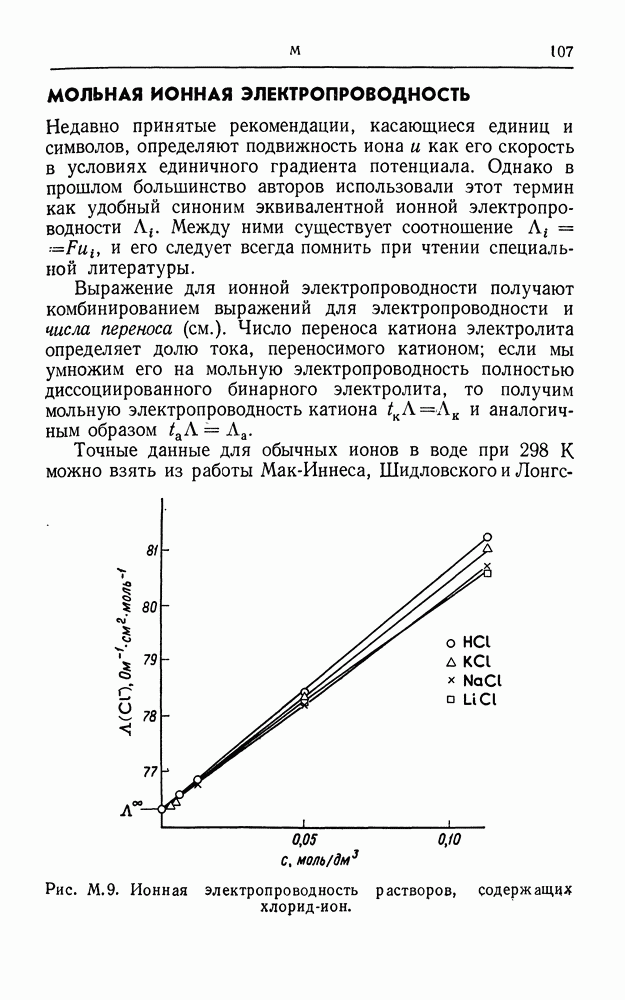
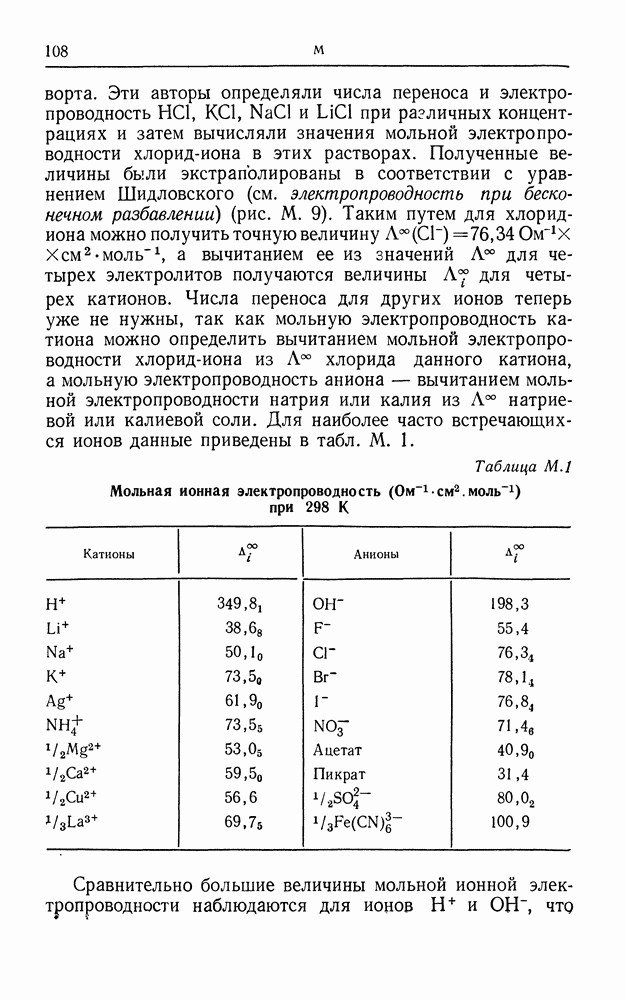
- МОЛЬНАЯ ИОННАЯ ЭЛЕКТРОПРОВОДНОСТЬ
- МОСТ УИТСТОНА
- НАПРЯЖЕНИЕ РАЗЛОЖЕНИЯ
- НЕВОДНЫЕ РАСТВОРЫ
- НИКЕЛЬ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
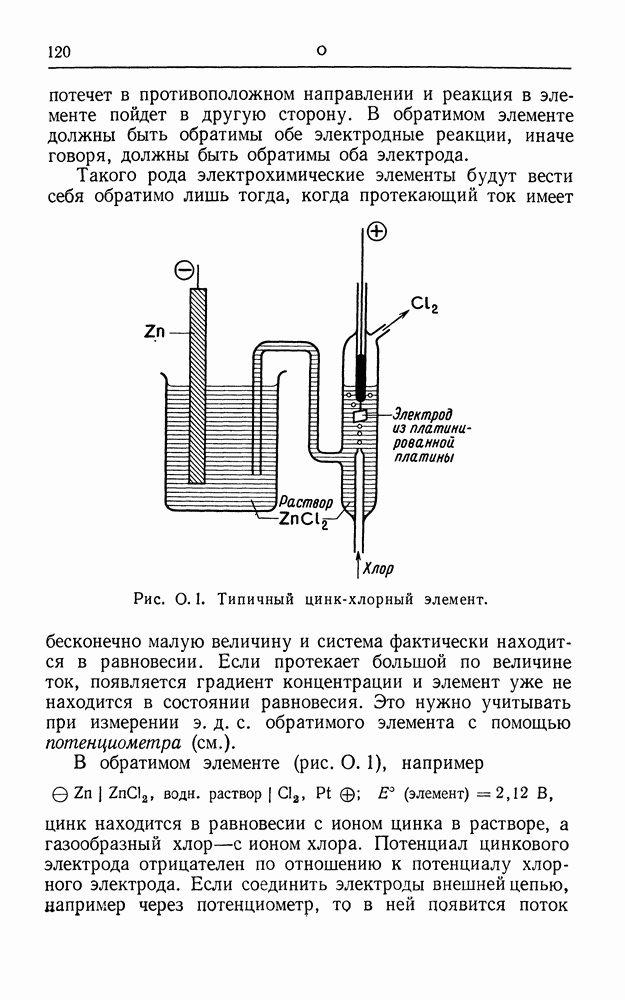
- ОБРАТИМЫЙ ГАЛЬВАНИЧЕСКИЙ ЭЛЕМЕНТ
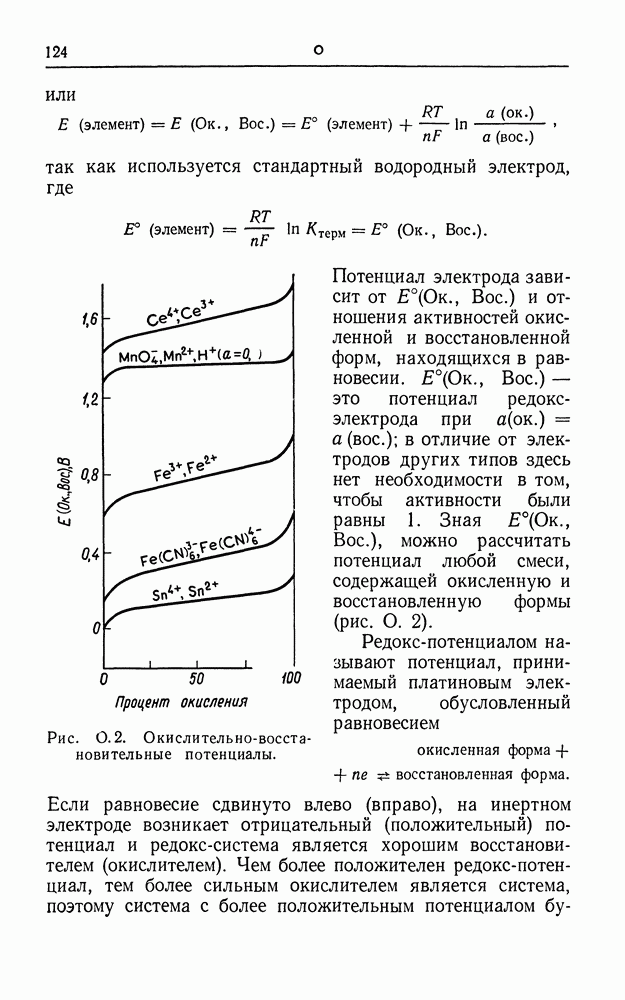
- ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНАЯ (РЕДОКС) ЭЛЕКТРОДНАЯ СИСТЕМА
- ОМ
- ОПРЕСНЕНИЕ ВОДЫ
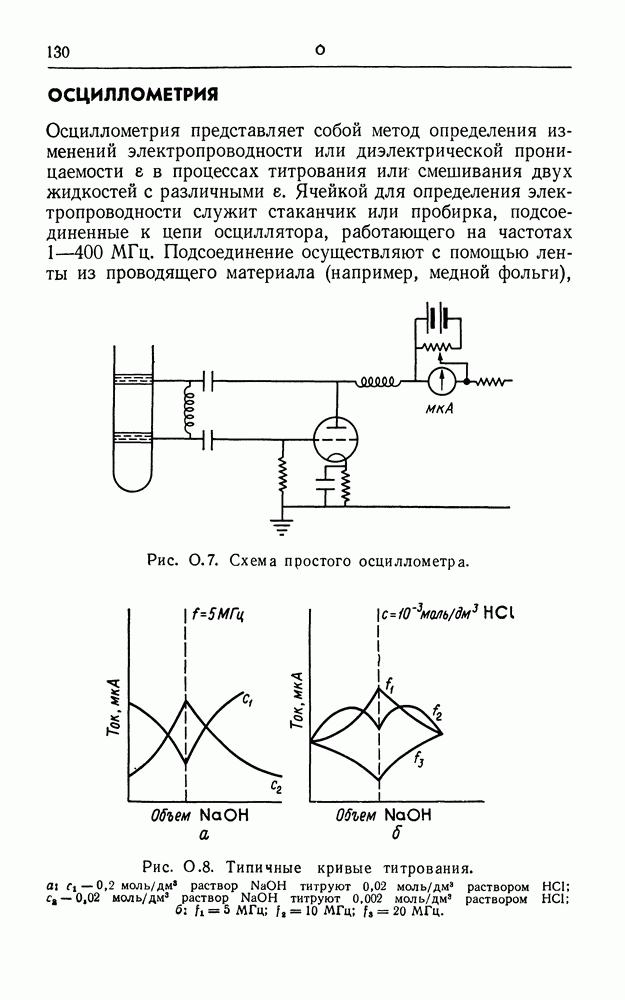
- ОСЦИЛЛОМЕТРИЯ
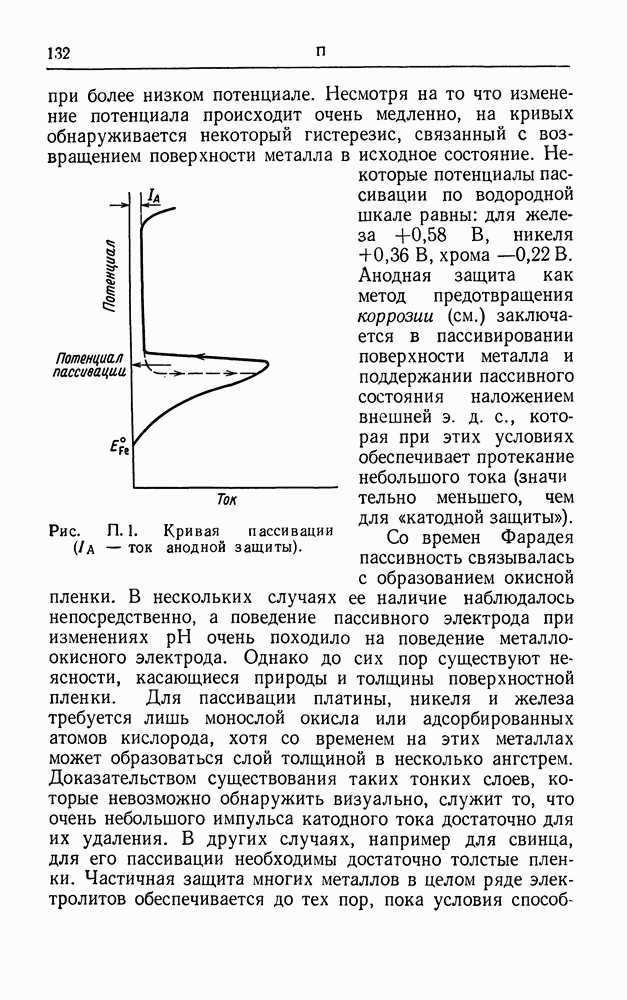
- ПАССИВНОСТЬ
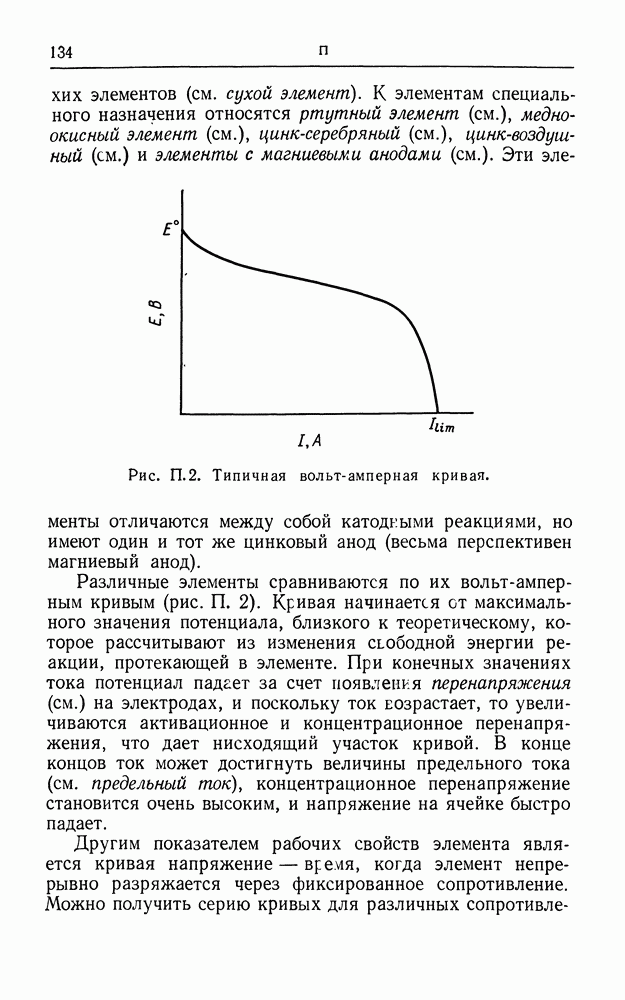
- ПЕРВИЧНЫЙ ГАЛЬВАНИЧЕСКИЙ ЭЛЕМЕНТ
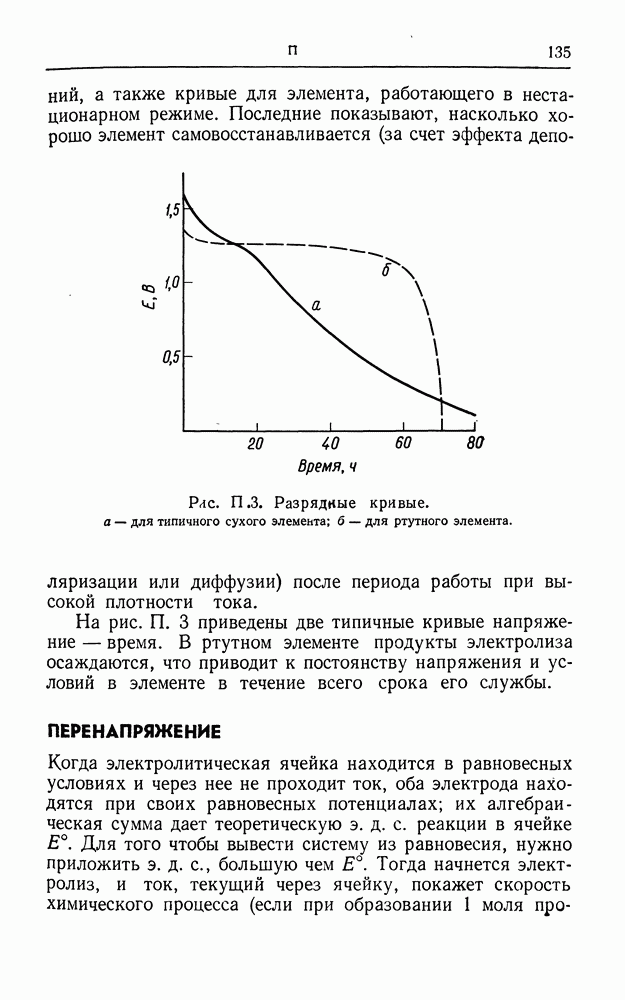
- ПЕРЕНАПРЯЖЕНИЕ
- ПЕРЕНАПРЯЖЕНИЕ ВОДОРОДА
- ПЕРЕХОДНОЕ ВРЕМЯ
- ПЕРСОЛИ
- ПЛАТИНОВЫЕ И ЗОЛОТЫЕ ЭЛЕКТРОДЫ
- рН-МЕТР
- ПОДВИЖНОСТЬ
- ПОДВИЖНОСТЬ ИОНОВ
- ПОЛУЭЛЕМЕНТ
- ПОЛЯРИЗАЦИОННЫЕ КРИВЫЕ
- ПОЛЯРИЗАЦИЯ
- ПОЛЯРИЗУЕМЫЕ ЭЛЕКТРОДЫ
- ПОЛЯРОГРАФИЯ
- ПОПРАВКА НА ЭЛЕКТРОПРОВОДНОСТЬ РАСТВОРИТЕЛЯ
- ПОСТОЯННАЯ ЯЧЕЙКИ
- ПОТЕНЦИАЛ, ОБРАТИМЫЕ ЭЛЕКТРОДЫ
- ПОТЕНЦИАЛ ПОЛУВОЛНЫ
- ПОТЕНЦИАЛ СЕДИМЕНТАЦИИ
- ПОТЕНЦИАЛ ТЕЧЕНИЯ
- ПОТЕНЦИОМЕТР
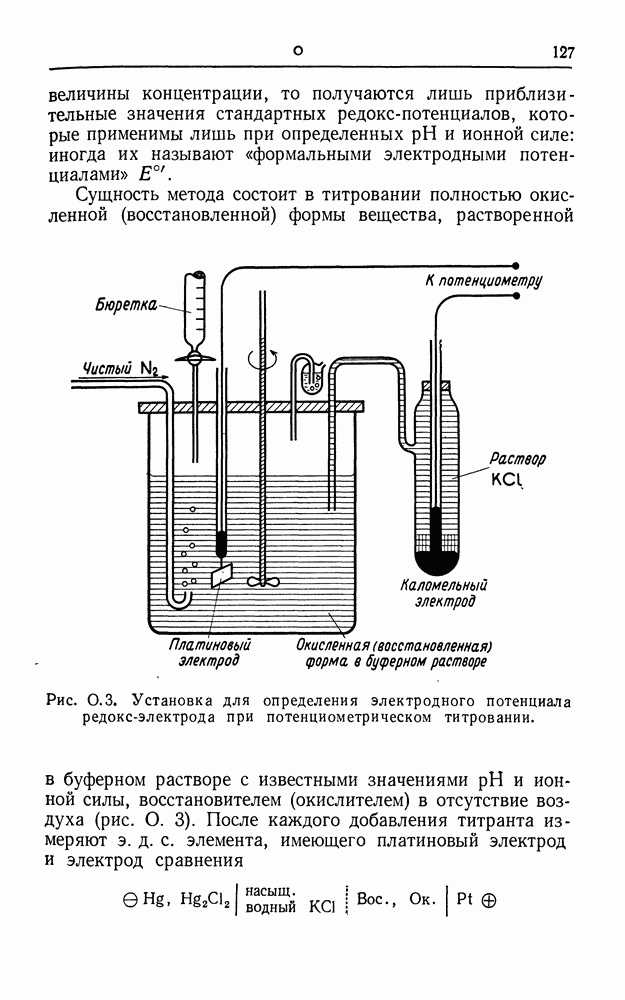
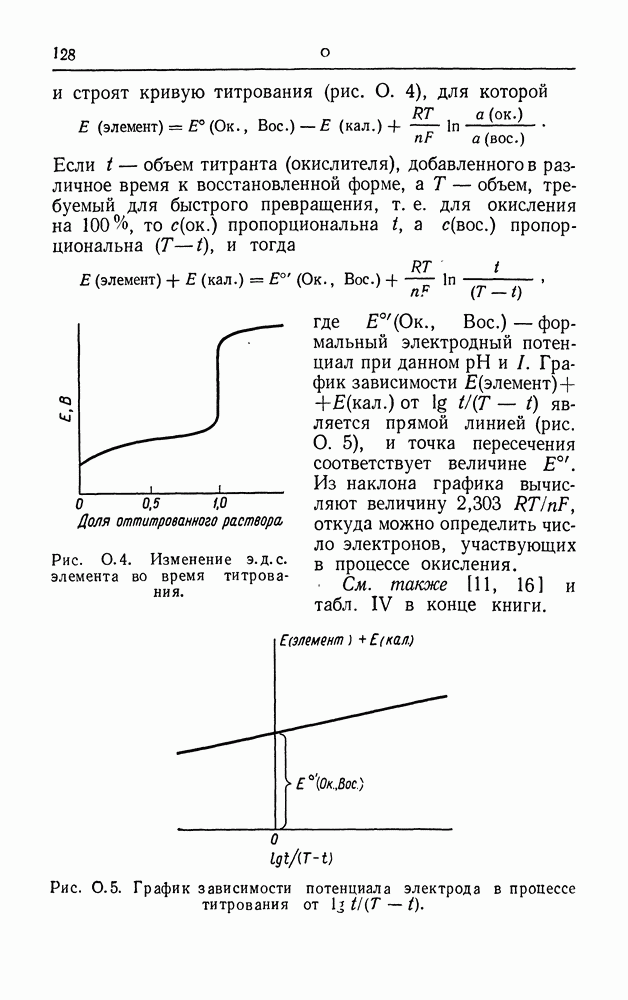
- ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- ПОТЕНЦИОСТАТ
- ПРАВИЛО ВАЛЬДЕНА
- ПРЕДЕЛЬНЫЙ ТОК
- ПРОТЕКТОРНАЯ ЗАЩИТА
- РАСПЛАВЫ СОЛЕЙ
- РЕАКЦИЯ ВЫДЕЛЕНИЯ ВОДОРОДА
- РТУТНЫЙ ЭЛЕМЕНТ
- РЯД ПОТЕНЦИАЛОВ
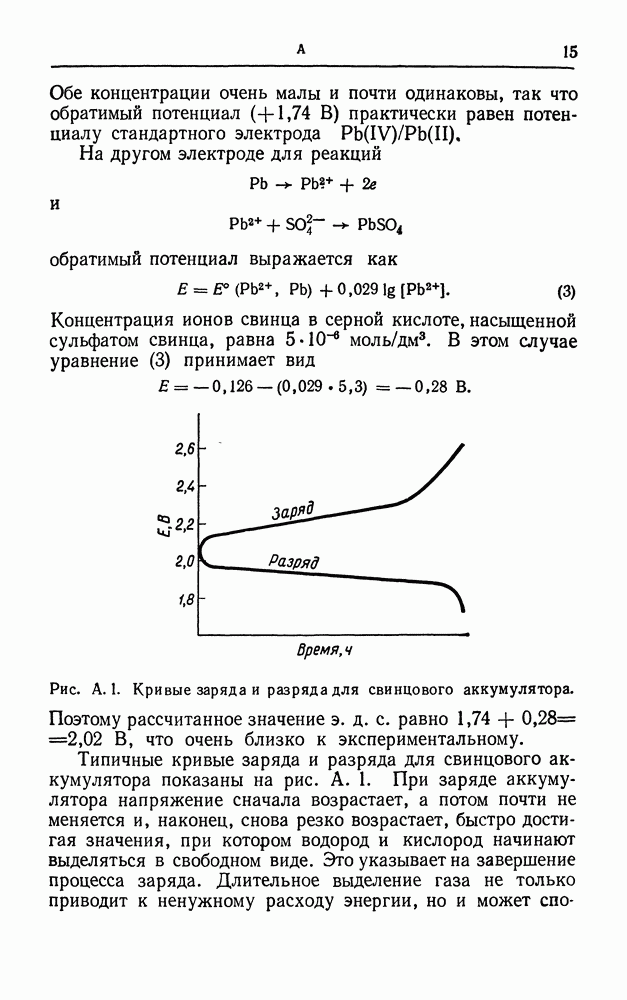
- СВИНЦОВЫЙ АККУМУЛЯТОР
- СЕРЕБРЯНЫЙ КУЛОНОМЕТР
- СЕРЕБРЯНЫЙ ЭЛЕКТРОД
- СЛОЙ ГЕЛЬМГОЛЬЦА
- СЛОЙ ГУИ
- СОЛЕВОЙ МОСТИК
- СТАНДАРТНЫЕ РАСТВОРЫ ДЛЯ ЭЛЕКТРОПРОВОДНОСТИ
- СТАНДАРТНЫЙ ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ
- СТАНДАРТНЫЙ ЭЛЕМЕНТ
- СТЕКЛЯННЫЙ ЭЛЕКТРОД
- СУРЬМЯНЫЙ ЭЛЕКТРОД
- СУХОЙ ЭЛЕМЕНТ
- ТЕОРИЯ ИОННОЙ АССОЦИАЦИИ БЬЕРРУМА
- ТЕОРИЯ ЭЛЕКТРОЛИТИЧЕСКОЙ ДИССОЦИАЦИИ АРРЕНИУСА
- ТЕРМОДИНАМИКА ГАЛЬВАНИЧЕСКИХ ЭЛЕМЕНТОВ
- ТОК ОБМЕНА
- ТОПЛИВНЫЙ ЭЛЕМЕНТ
- УРАВНЕНИЕ БРЕНСТЕДА—БЬЕРРУМА
- УРАВНЕНИЕ ДЕБАЯ — ХЮККЕЛЯ
- УРАВНЕНИЕ ИЛЬКОВИЧА
- УРАВНЕНИЕ НЕРНСТА
- УРАВНЕНИЕ ОНЗАГЕРА
- УРАВНЕНИЕ ТАФЕЛЯ
- УРАВНЕНИЕ ЭЛЕКТРОПРОВОДНОСТИ ПИТТСА
- УРАВНЕНИЕ ЭЛЕКТРОПРОВОДНОСТИ ФУОССА
- УРАВНЕНИЯ ЭЛЕКТРОПРОВОДНОСТИ
- ХЕМОТРОНЫ
- ХИНГИДРОННЫЙ ЭЛЕКТРОД
- ХЛОРНЫЙ ЭЛЕКТРОД
- ХЛОРСЕРЕБРЯНЫЙ ЭЛЕКТРОД
- ХРОНОАМПЕРОМЕТРИЯ
- ХРОНОПОТЕНЦИОМЕТРИЯ
- ЦИНК-ВОЗДУШНЫЙ ЭЛЕМЕНТ
- ЦИНК-СЕРЕБРЯНЫЙ ЭЛЕМЕНТ
- ЦИНК, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- ЦИФРОВОЙ ВОЛЬТМЕТР
- ЧАСТОТНАЯ ЗАВИСИМОСТЬ ЭЛЕКТРОПРОВОДНОСТИ
- ЧИСЛА ПЕРЕНОСА
- ЧИСЛО ФАРАДЕЯ
- ЩЕЛОЧНЫЕ АККУМУЛЯТОРЫ
- ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ
- ЭЛЕКТРИЧЕСКИЕ ЕДИНИЦЫ ИЗМЕРЕНИЯ
- ЭЛЕКТРОВЕСОВОЙ АНАЛИЗ
- ЭЛЕКТРОД
- ЭЛЕКТРОДВИЖУЩАЯ СИЛА (Э.Д.С.)
- ЭЛЕКТРОДИАЛИЗ
- ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ
- ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- ЭЛЕКТРОЛИЗ ВОДЫ
- ЭЛЕКТРОЛИЗЕР
- ЭЛЕКТРОЛИЗ РАСТВОРА ПОВАРЕННОЙ СОЛИ
- ЭЛЕКТРОЛИТИЧЕСКАЯ ОЧИСТКА (РАФИНИРОВАНИЕ)
- ЭЛЕКТРОЛИТИЧЕСКОЕ ВОССТАНОВЛЕНИЕ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
- ЭЛЕКТРОЛИТИЧЕСКОЕ ОКИСЛЕНИЕ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
- ЭЛЕКТРОЛИТИЧЕСКОЕ ПОЛИРОВАНИЕ
- ЭЛЕКТРОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- ЭЛЕКТРООСАЖДЕНИЕ МЕТАЛЛОВ
- ЭЛЕКТРООСАЖДЕНИЕ СПЛАВОВ
- ЭЛЕКТРООСМОС
- ЭЛЕКТРОПРОВОДНОСТЬ
- ЭЛЕКТРОПРОВОДНОСТЬ ВОДНЫХ РАСТВОРОВ
- ЭЛЕКТРОПРОВОДНОСТЬ НА ВЫСОКИХ ЧАСТОТАХ
- ЭЛЕКТРОПРОВОДНОСТЬ НЕВОДНЫХ РАСТВОРОВ
- ЭЛЕКТРОПРОВОДНОСТЬ ПРИ БЕСКОНЕЧНОМ РАЗБАВЛЕНИИ
- ЭЛЕКТРОПРОВОДНОСТЬ ПРИ ВЫСОКИХ НАПРЯЖЕННОСТЯХ ПОЛЯ
- ЭЛЕКТРОПРОВОДНОСТЬ РАСПЛАВОВ СОЛЕЙ
- ЭЛЕКТРОФОРЕЗ
- ЭЛЕКТРОХИМИЧЕСКАЯ РАЗМЕРНАЯ ОБРАБОТКА МЕТАЛЛОВ
- ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ИНФОРМАЦИИ
- ЭЛЕКТРОХИМИЧЕСКИЙ ЭКВИВАЛЕНТ
- ЭЛЕМЕНТ ВЕСТОНА
- ЭЛЕМЕНТ ДАНИЭЛЯ
- ЭЛЕМЕНТ КЛАРКА
- ЭЛЕМЕНТЫ С МАГНИЕВЫМИ АНОДАМИ
- ЭФФЕКТ ВИНА
- ЭФФЕКТ ДОРНА
- ЭФФЕКТ ФАЛЬКЕНГАГЕНА
- СПИСОК ЛИТЕРАТУРЫ