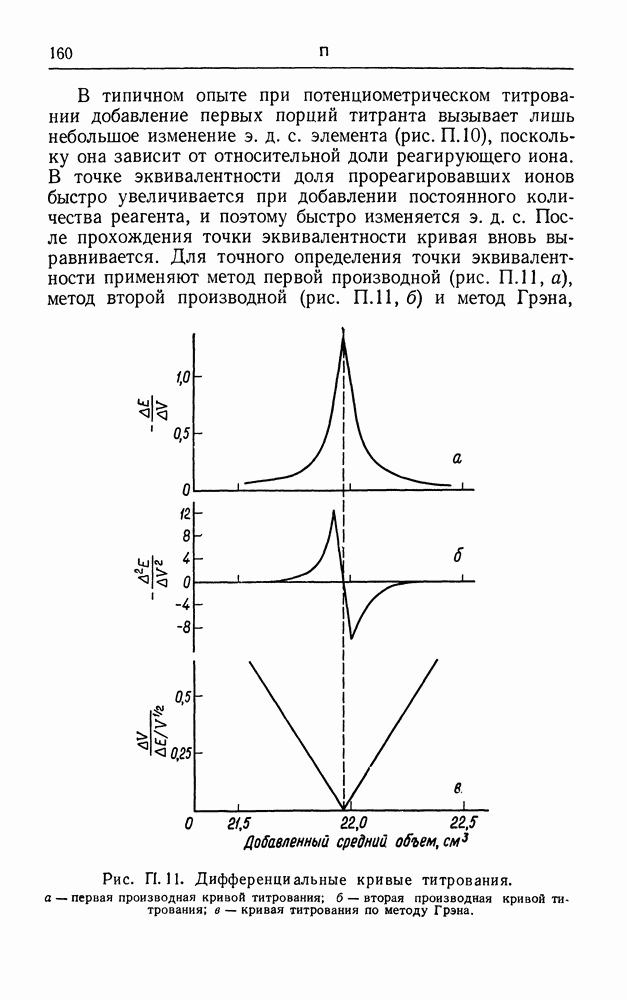
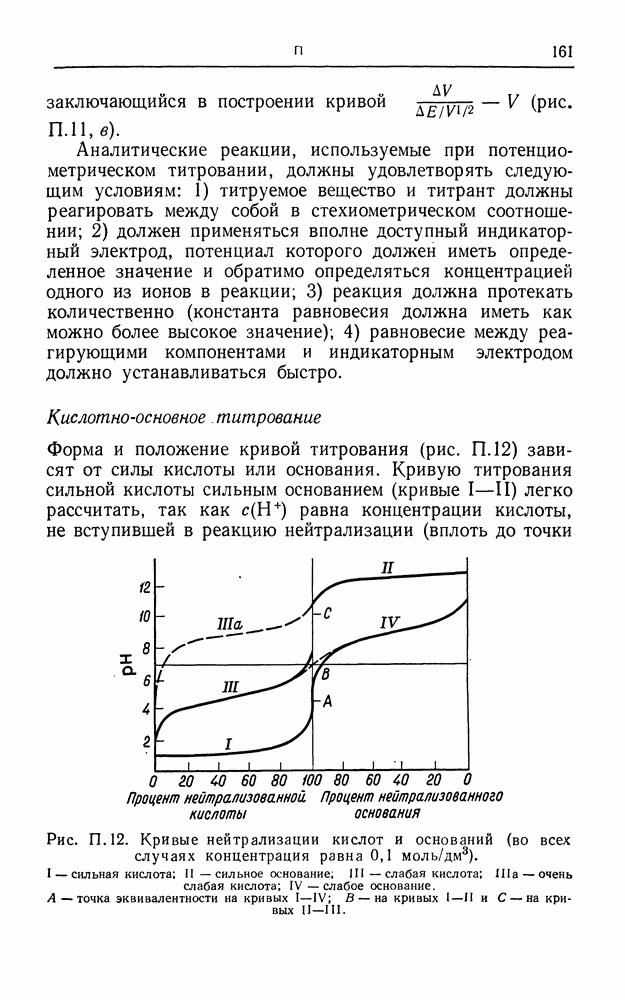
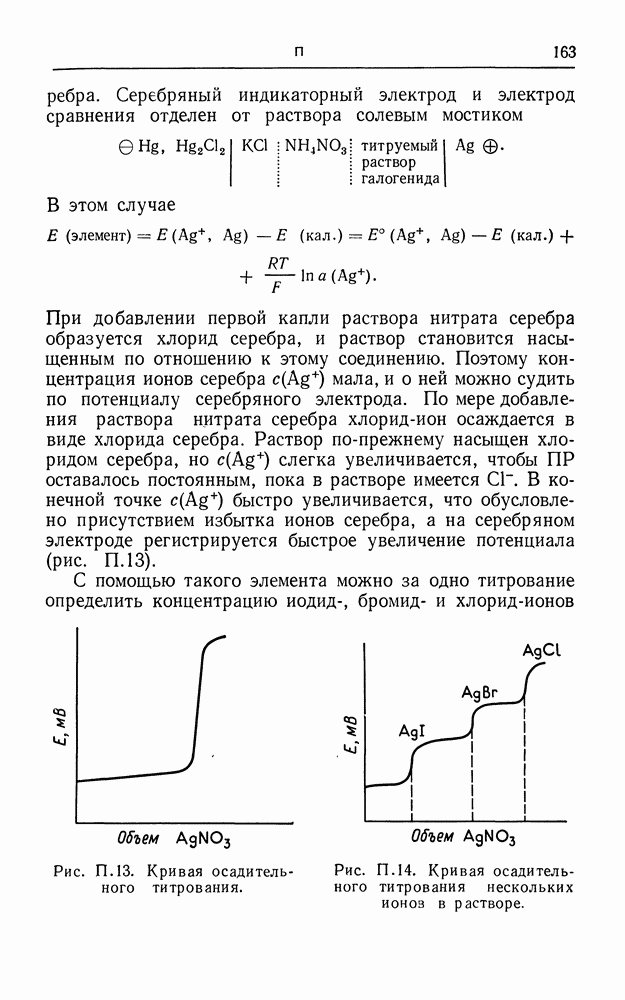
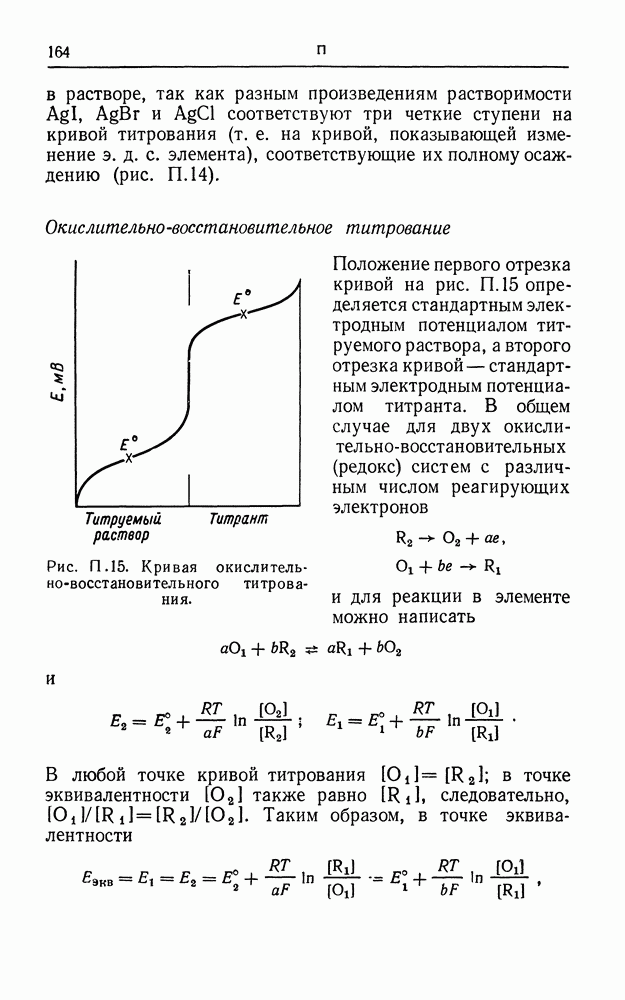
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
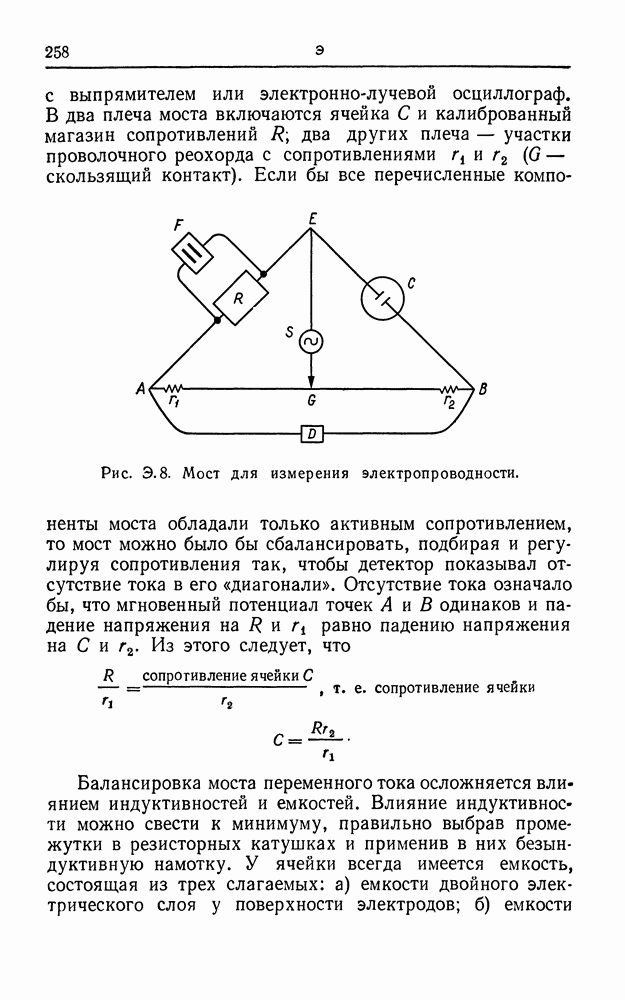
АКТИВАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
Во всяком электролитическом процессе часть потребляемой энергии затрачивается на преодоление внутреннего сопротивления элемента. Если это сопротивление обозначить через  а ток — через
а ток — через  то соответствующее падение напряжения в растворе будет равно
то соответствующее падение напряжения в растворе будет равно  В. Кроме
В. Кроме
того, на каждом электроде возникает концентрационное перенапряжение (см.).
Остальная часть разности между внешним напряжением и равновесной  для реакции в элементе называется активационным перенапряжением. Оно также складывается из отдельных величин для двух электродных процессов:
для реакции в элементе называется активационным перенапряжением. Оно также складывается из отдельных величин для двух электродных процессов:

Можно рассматривать отдельно два электродных потенциала (см. напряжение разложения), опуская член  и тогда для катода можно написать
и тогда для катода можно написать

Если концентрационное перенапряжение можно не принимать во внимание, то  . То же самое относится и к аноду.
. То же самое относится и к аноду.
Измеренные таким путем значения электродных потенциалов изменяются в широком диапазоне. В случае быстрых реакций, например для осаждения многих металлов, ток велик, даже если катодный потенциал лишь незначительно превышает свое равновесное значение. В случае же других реакций, особенно таких, в которых выделяются газы, чтобы получить достаточно большие токи, требуются высокие перенапряжения. По-видимому, в таких случаях в механизме разряда существует медленная стадия, которая обусловливает накопление электронов на катоде в стационарных условиях (постоянный ток).
Перенапряжение водорода
Перенапряжение водорода (или водородное перенапряжение) было предметом интенсивных исследований. При разряде водорода в растворах  при плотности тока
при плотности тока  измерения перенапряжения показали, что оно изменяется от
измерения перенапряжения показали, что оно изменяется от  на платинированной платине до
на платинированной платине до  на ртути — «металле с высоким перенапряжением». Это указывает на то, что сам электрод играет очень важную роль в процессе.
на ртути — «металле с высоким перенапряжением». Это указывает на то, что сам электрод играет очень важную роль в процессе.
Общее соотношение между плотностью тока и электродным потенциалом было выведено Тафелем в 1905 г. (уравнение Тафеля):

где А — константа. Если вспомнить, что величина  представляет собой скорость реакции, то налицо поразительное сходство с уравнением Аррениуса
представляет собой скорость реакции, то налицо поразительное сходство с уравнением Аррениуса  Кроме того, Тафель показал, что в случае разряда водорода на ртутном электроде множитель А равен
Кроме того, Тафель показал, что в случае разряда водорода на ртутном электроде множитель А равен  поэтому для данного процесса уравнение Тафеля можно записать в виде
поэтому для данного процесса уравнение Тафеля можно записать в виде

где величина с размерностью энергии  Дж соответствует энергии активации Е в теории скоростей термохимических реакций и представляет собой энергию на один моль, необходимую для преодоления энергетического барьера на пути реакции, т. е. для образования переходного состояния. Однако множитель
Дж соответствует энергии активации Е в теории скоростей термохимических реакций и представляет собой энергию на один моль, необходимую для преодоления энергетического барьера на пути реакции, т. е. для образования переходного состояния. Однако множитель  введенный Тафелем, не имел ясного смысла; как было показано позднее, в других случаях множитель может быть иным. Поэтому уравнение Тафеля в общем виде записывается как
введенный Тафелем, не имел ясного смысла; как было показано позднее, в других случаях множитель может быть иным. Поэтому уравнение Тафеля в общем виде записывается как
 (1)
(1)
где а — так называемый коэффициент переноса. Прологарифмируем уравнение (1):

Таким образом, результаты измерения  можно выразить простой формулой
можно выразить простой формулой

где а и b — константы (тафелевские постоянные), а  — положительная величина, т. е. для катодного процесса
— положительная величина, т. е. для катодного процесса 
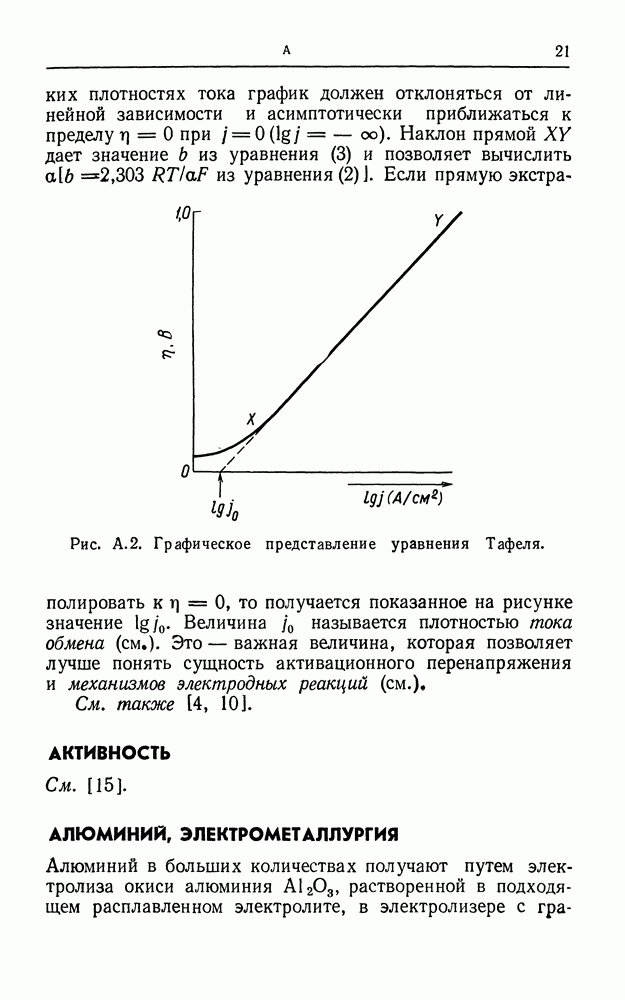
Типичный тафелевский график показан на рис.  Между X и Y выполняется соотношение Тафеля. Если не допустить возникновения концентрационного перенапряжения, то эта линейная зависимость может сохраняться до очень высоких плотностей тока. Однако при очень низких
Между X и Y выполняется соотношение Тафеля. Если не допустить возникновения концентрационного перенапряжения, то эта линейная зависимость может сохраняться до очень высоких плотностей тока. Однако при очень низких
них плотностях тока график должен отклоняться от линейной зависимости и асимптотически приближаться к пределу  при
при  . Наклон прямой XY дает значение b из уравнения (3) и позволяет вычислить
. Наклон прямой XY дает значение b из уравнения (3) и позволяет вычислить  из уравнения (2) J. Если прямую экстраполировать к
из уравнения (2) J. Если прямую экстраполировать к  то получается показанное на рисунке значение
то получается показанное на рисунке значение 

Рис. А.2. Графическое представление уравнения Тафеля.
Величина  называется плотностью тока обмена (см.). Это — важная величина, которая позволяет лучше понять сущность активационного перенапряжения и механизмов электродных реакций (см.)
называется плотностью тока обмена (см.). Это — важная величина, которая позволяет лучше понять сущность активационного перенапряжения и механизмов электродных реакций (см.)
См. также [4, 10].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- О ПОЛЬЗОВАНИИ СЛОВАРЕМ
- СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
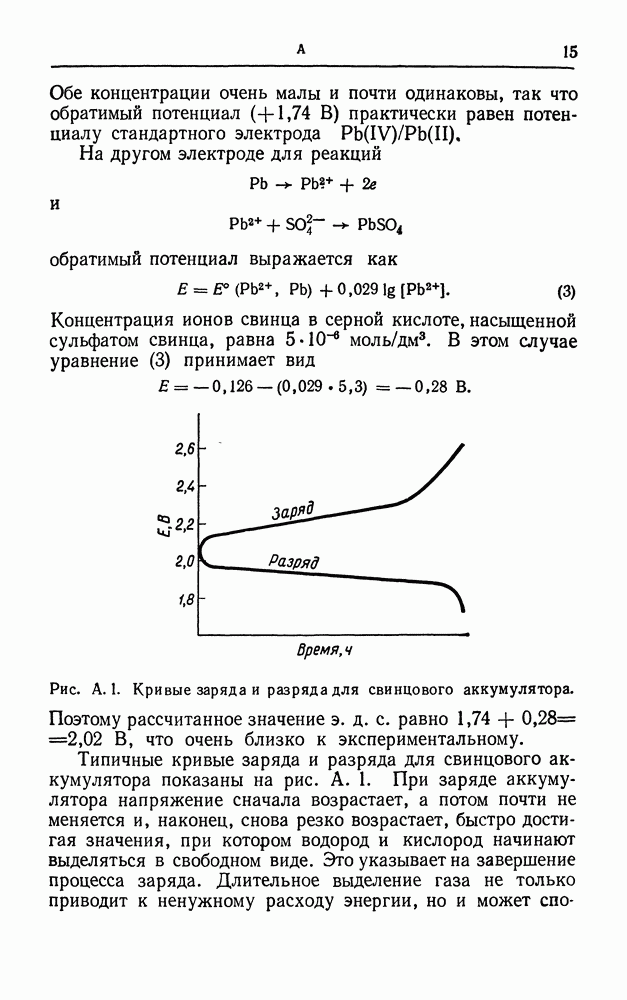
- АККУМУЛЯТОР
- АКТИВАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- АКТИВНОСТЬ
- АЛЮМИНИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- АМАЛЬГАМНЫЙ ЭЛЕКТРОД
- АМПЕР
- АМПЕРОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- АМПЕРОСТАТ
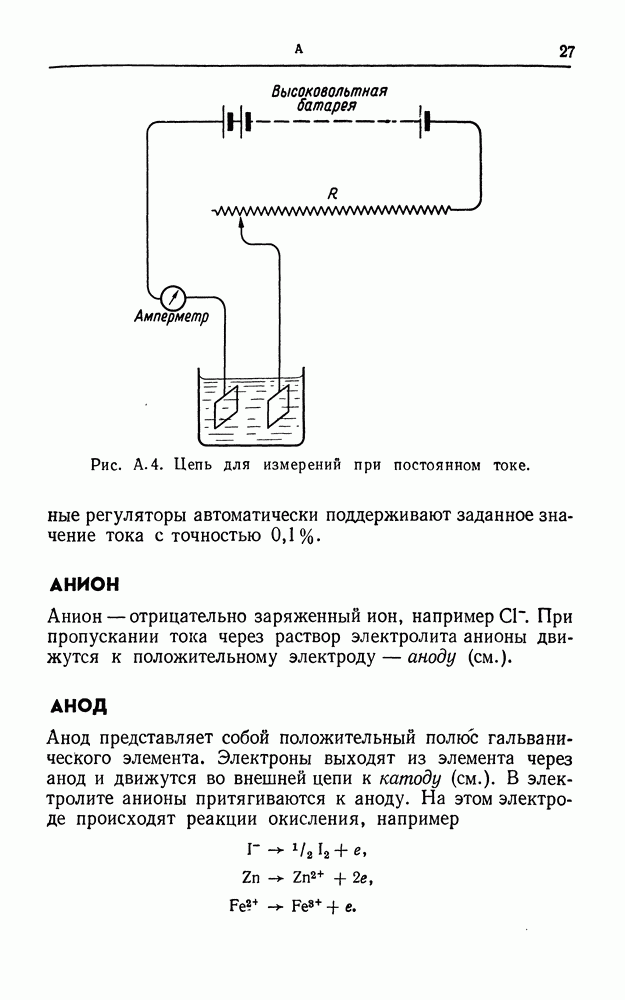
- АНИОН
- АНОД
- АНОДИРОВАНИЕ
- БАТАРЕЯ
- БЕРИЛЛИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- БИПОЛЯРНЫЙ ЭЛЕКТРОД
- БЛЕСКООБРАЗОВАТЕЛИ
- БУФЕРНЫЙ РАСТВОР
- ВАГНЕРОВСКОЕ ЗАЗЕМЛЕНИЕ
- ВНУТРЕННИЙ ЭЛЕКТРОЛИЗ
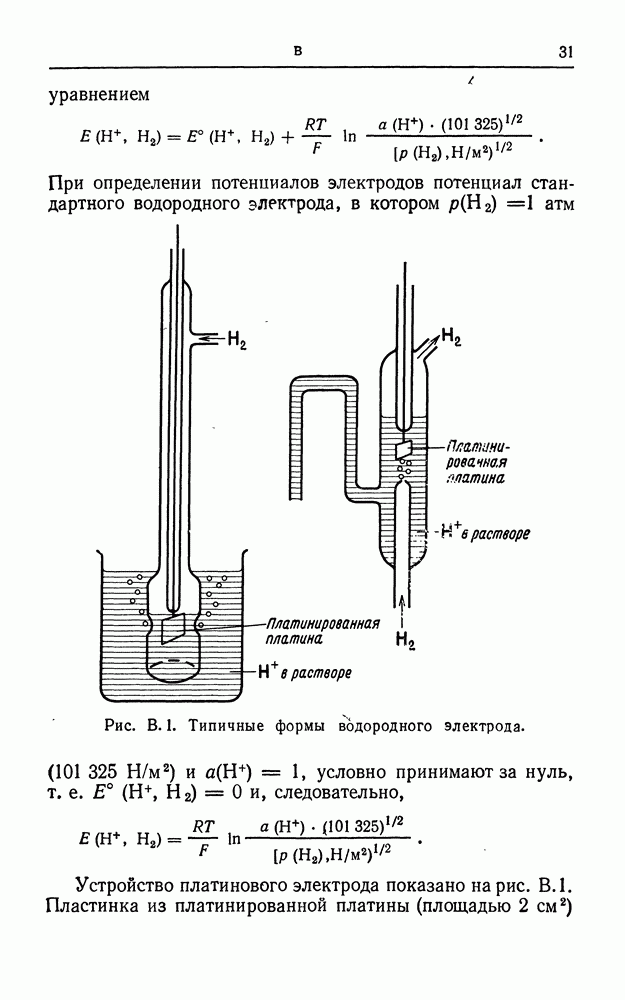
- ВОДОРОДНЫЙ ЭЛЕКТРОД
- ВОЛЬТ
- ВОЛЬФРАМОВЫЙ ЭЛЕКТРОД
- ВЫХОД ПО ТОКУ
- ГАЗОВЫЙ ЭЛЕКТРОД
- ГАЛЬВАНИЧЕСКИЙ ЭЛЕМЕНТ
- ГАЛЬВАНОПЛАСТИКА
- ГАЛЬВАНОСТАТ
- ГАЛЬВАНОСТЕГИЯ
- ГИДРАТАЦИЯ ИОНОВ
- ДАТЧИК АММИАКА
- ДАТЧИК СЕРНИСТОГО ГАЗА
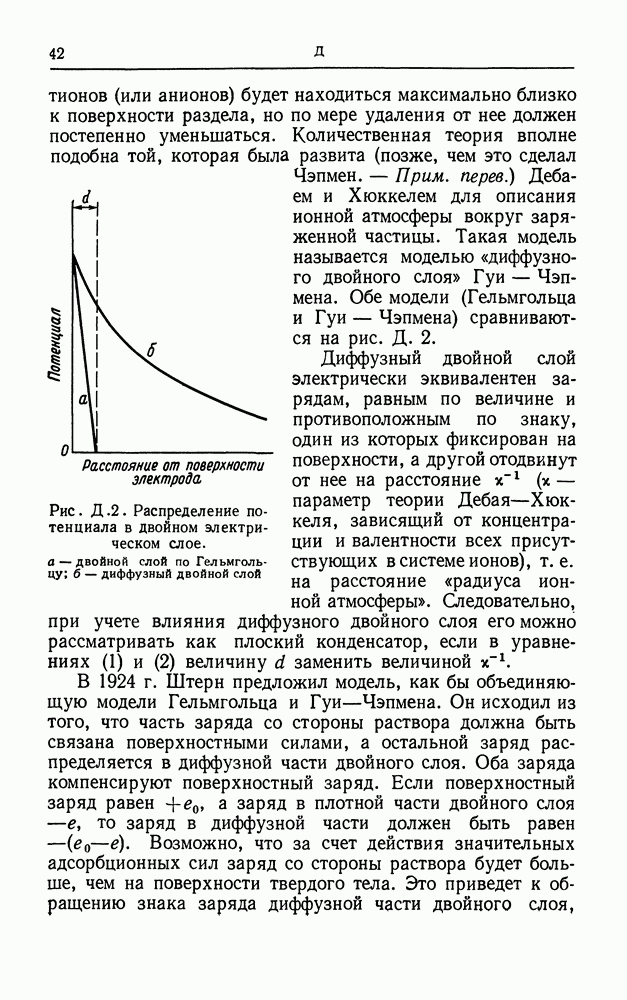
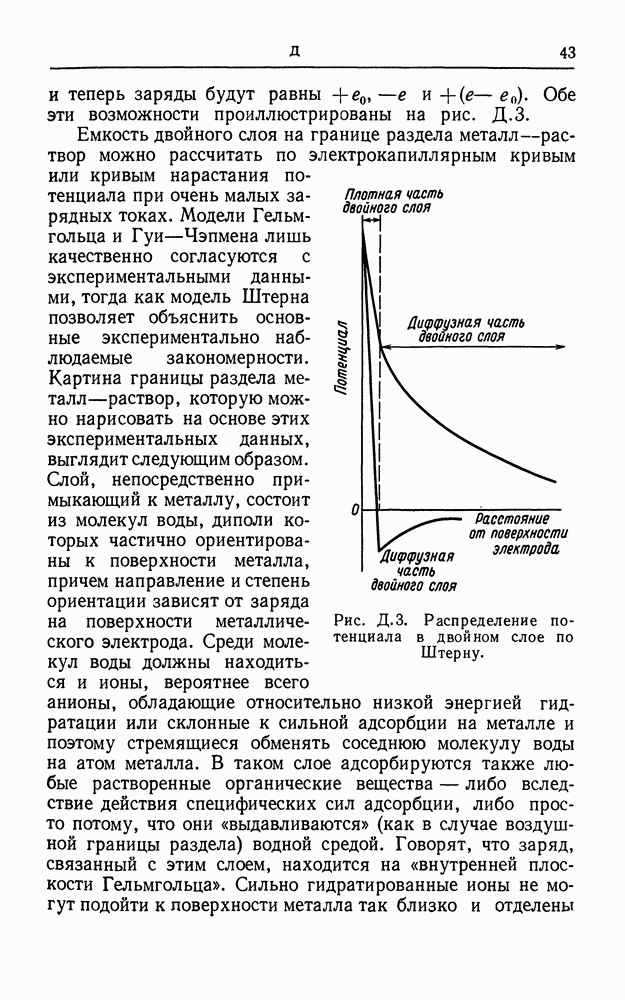
- ДВОЙНОЙ СЛОЙ
- ДВОЙНОЙ ЭЛЕКТРИЧЕСКИЙ СЛОЙ
- ДЗЕТА-ПОТЕНЦИАЛ
- ДИФФУЗИОННЫЙ ПОТЕНЦИАЛ
- ДИФФУЗИЯ В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
- ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ
- ЗАКОН КОЛЬРАУША
- ЗАКОН РАЗВЕДЕНИЯ ОСТВАЛЬДА
- ЗАКОНЫ ФАРАДЕЯ
- ИНДИКАТОР
- ИНДИКАТОРНЫЙ ЭЛЕКТРОД
- ИНДИФФЕРЕНТНЫЙ (ФОНОВЫЙ) ЭЛЕКТРОЛИТ
- ИОДНЫЙ КУЛОНОМЕТР
- ИОННАЯ АТМОСФЕРА
- ИОННЫЕ ПАРЫ
- ИОННЫЕ РАСПЛАВЫ
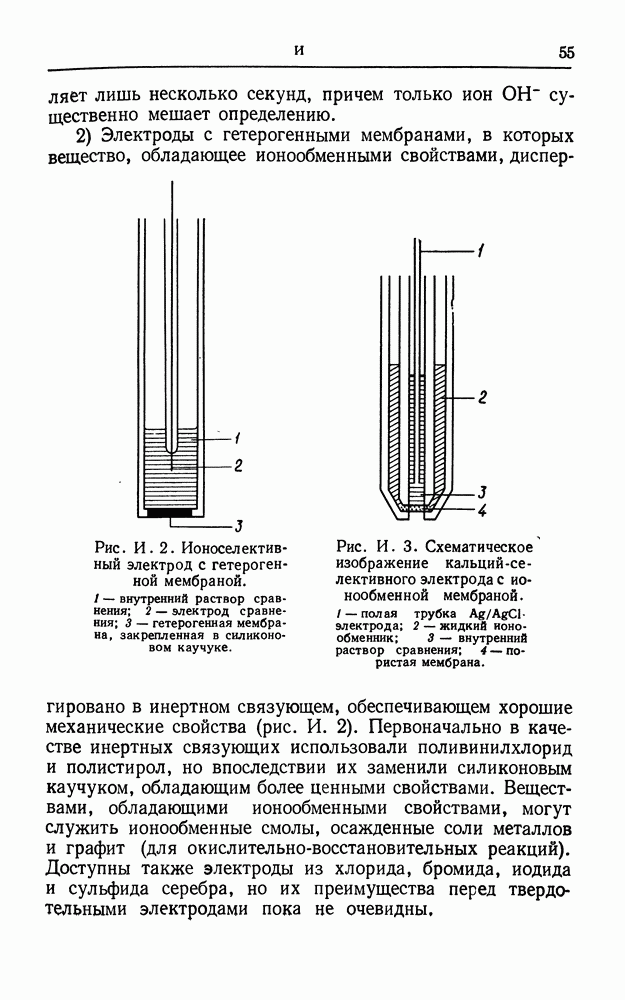
- ИОНОСЕЛЕКТИВНЫЕ ЭЛЕКТРОДЫ
- КАДМИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- КАЛОМЕЛЬНЫЙ ЭЛЕКТРОД
- КАЛЬЦИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- КАПИЛЛЯР ЛУГГИНА
- КАТИОН
- КАТИОНОСЕЛЕКТИВНЫЙ ЭЛЕКТРОД
- КАТОД
- КАТОДНАЯ ЗАЩИТА
- КИСЛОРОДНОЕ ПЕРЕНАПРЯЖЕНИЕ
- КИСЛОРОДНЫЙ ЭЛЕКТРОД (КИСЛОРОДНЫЙ ЗОНД)
- КОМПЛЕКСНЫЕ ИОНЫ
- КОНВЕНЦИЯ О ЗНАКАХ
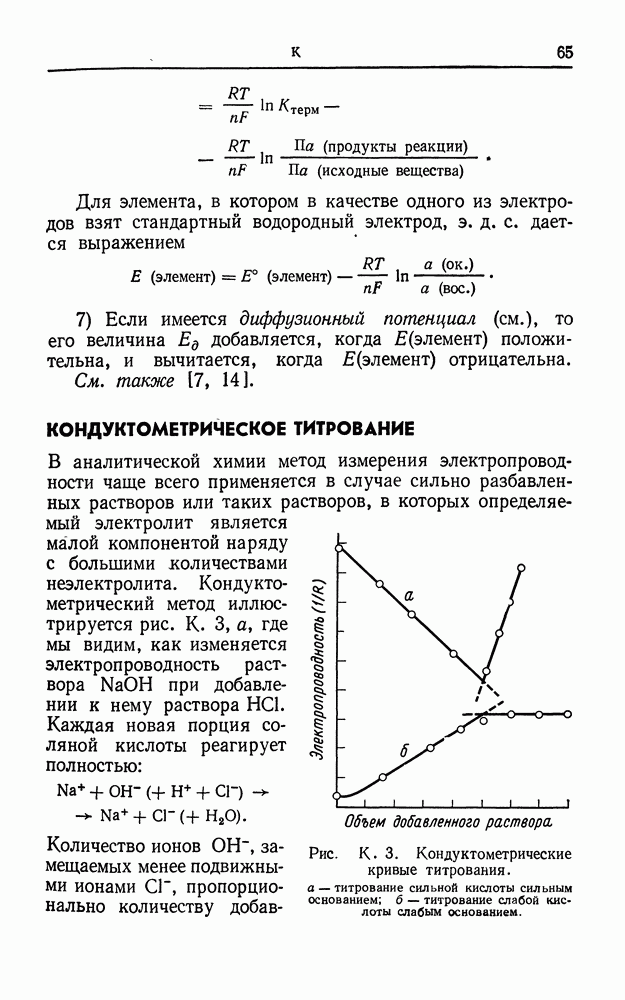
- КОНДУКТОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- КОНСТАНТА ДИССОЦИАЦИИ
- КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
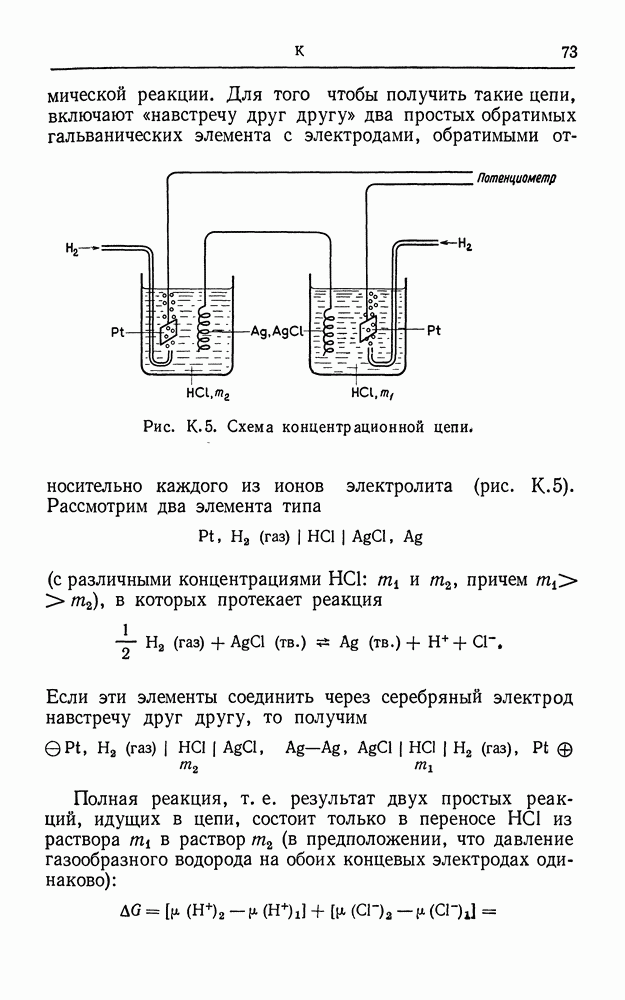
- КОНЦЕНТРАЦИОННАЯ ЦЕПЬ
- КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
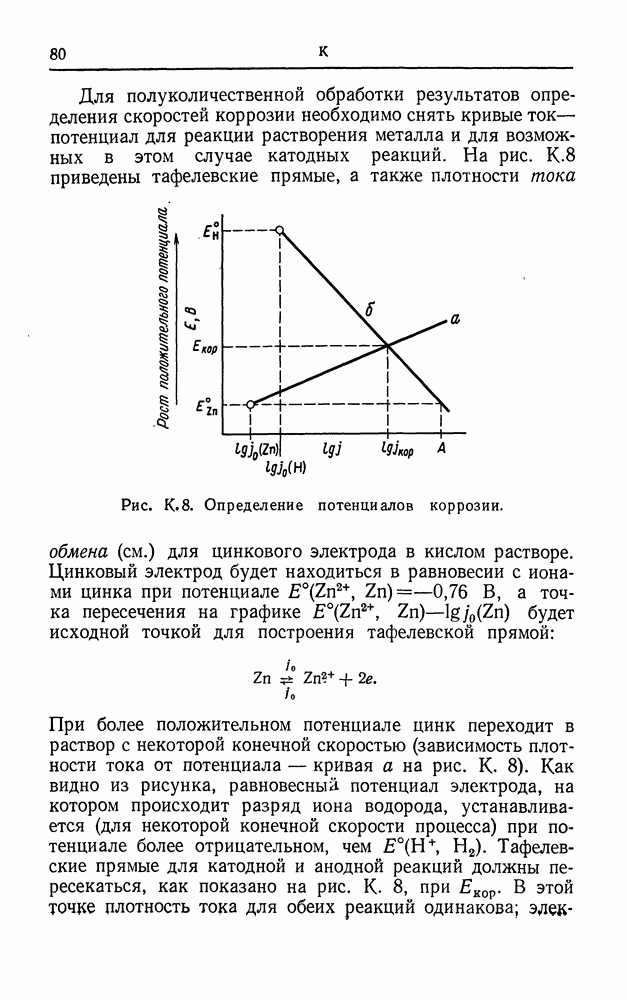
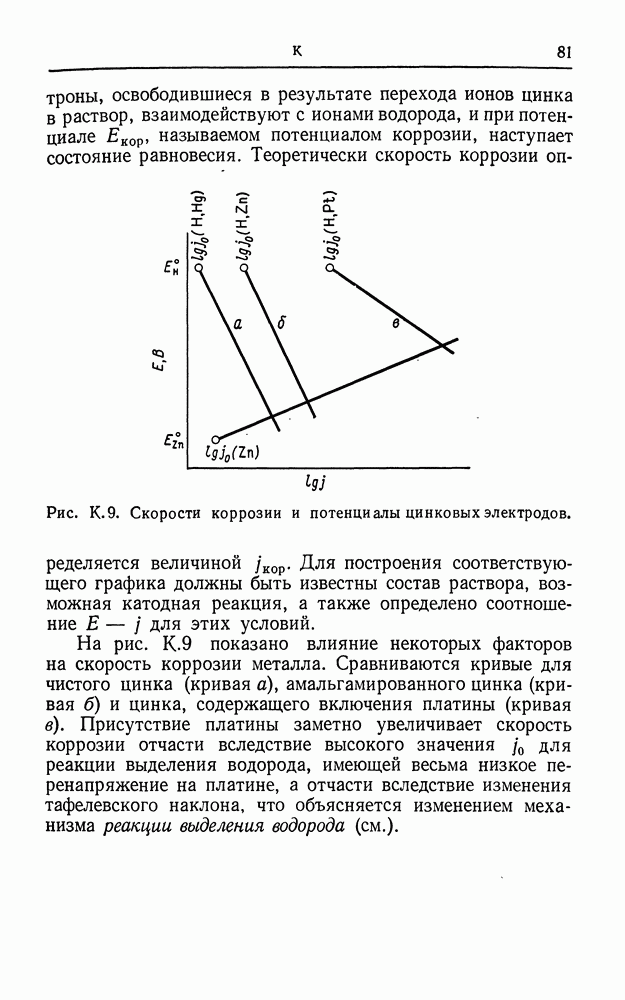
- КОРРОЗИЯ
- КОЭФФИЦИЕНТ АКТИВНОСТИ
- КУЛОН
- КУЛОНОМЕТР
- КУЛОНОМЕТРИЯ
- ЛИТИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- МАГНИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- МЕДНООКИСНЫЙ ЭЛЕМЕНТ
- МЕДНЫЙ КУЛОНОМЕТР
- МЕДЬ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- МЕМБРАННЫЙ ЭЛЕКТРОД
- МЕТАЛЛИЧЕСКИЙ ЭЛЕКТРОД
- МЕТАЛЛООКИСНЫЙ ЭЛЕКТРОД
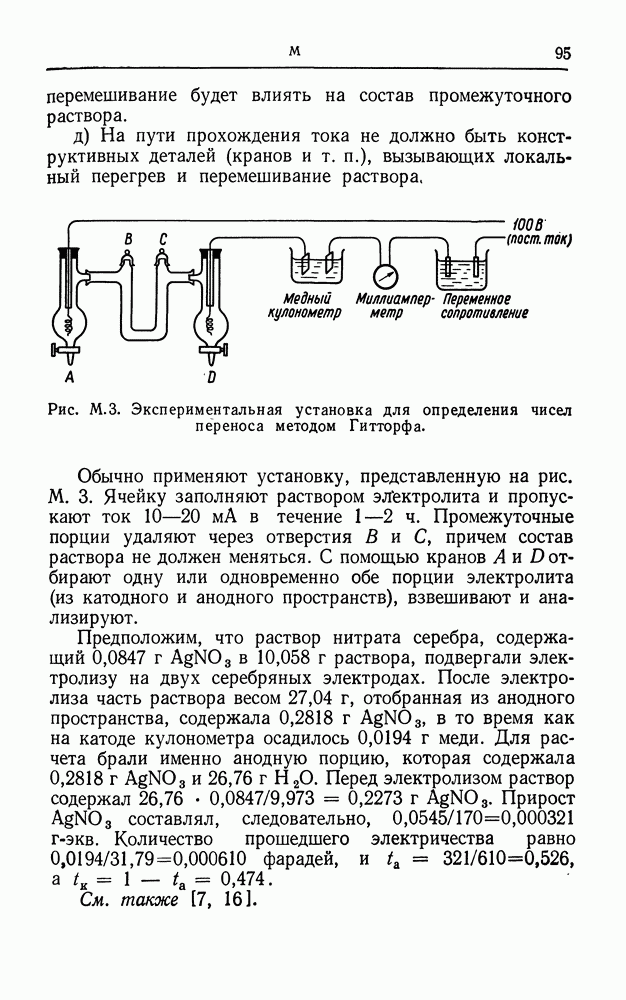
- МЕТОД ГИТТОРФА
- МЕТОД ДВИЖУЩЕЙСЯ ГРАНИЦЫ
- МЕХАНИЗМЫ ЭЛЕКТРОДНЫХ РЕАКЦИЙ
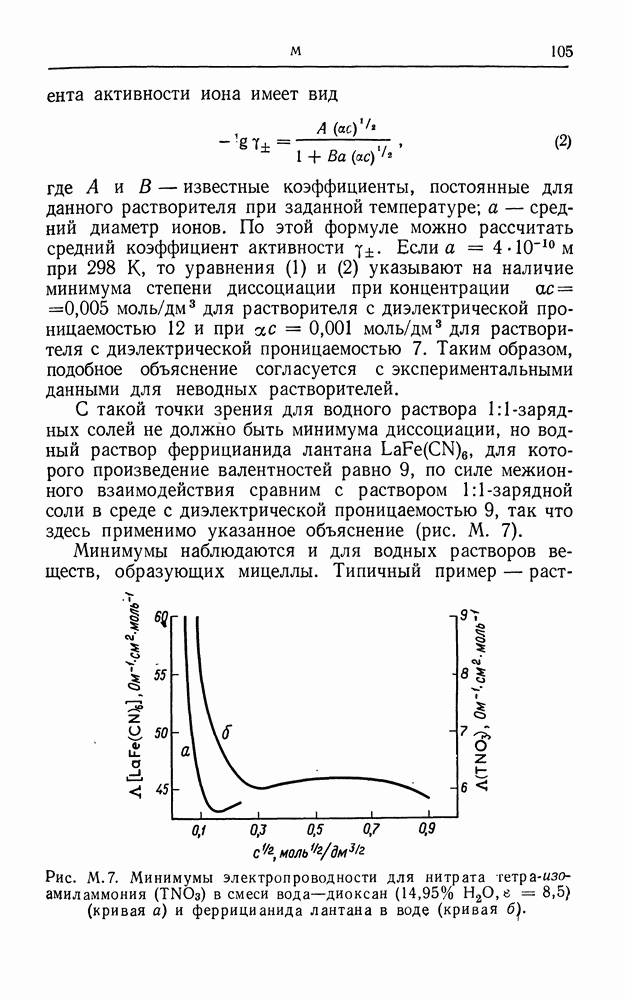
- МИНИМУМЫ ЭЛЕКТРОПРОВОДНОСТИ
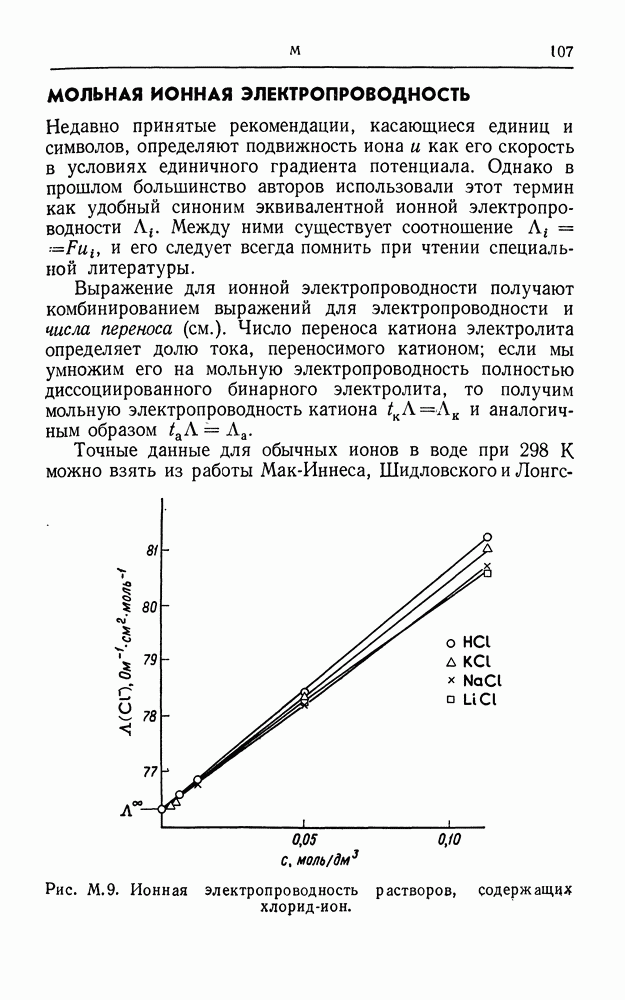
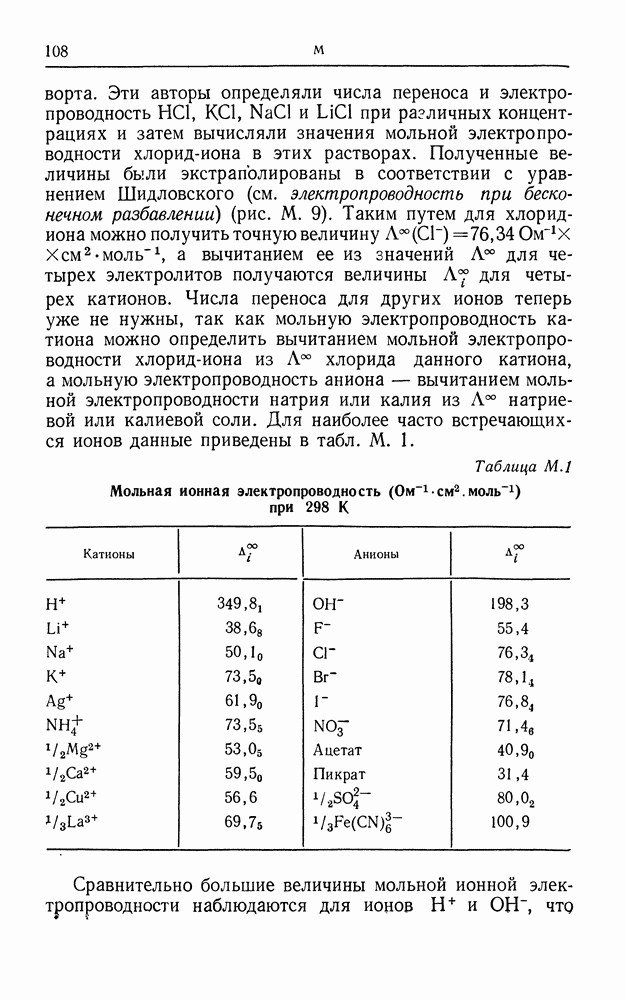
- МОЛЬНАЯ ИОННАЯ ЭЛЕКТРОПРОВОДНОСТЬ
- МОСТ УИТСТОНА
- НАПРЯЖЕНИЕ РАЗЛОЖЕНИЯ
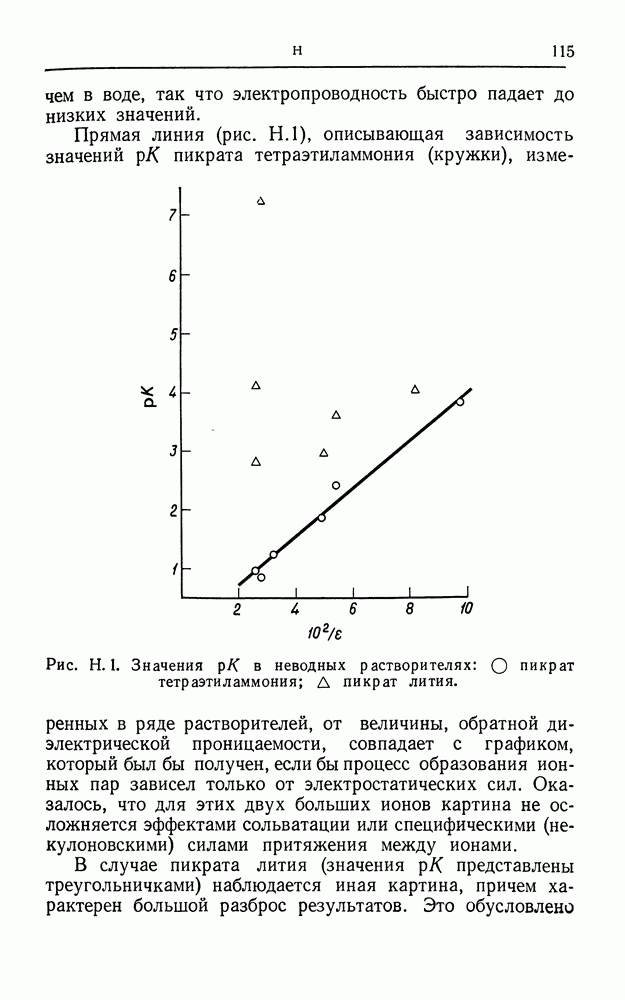
- НЕВОДНЫЕ РАСТВОРЫ
- НИКЕЛЬ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- ОБРАТИМЫЙ ГАЛЬВАНИЧЕСКИЙ ЭЛЕМЕНТ
- ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНАЯ (РЕДОКС) ЭЛЕКТРОДНАЯ СИСТЕМА
- ОМ
- ОПРЕСНЕНИЕ ВОДЫ
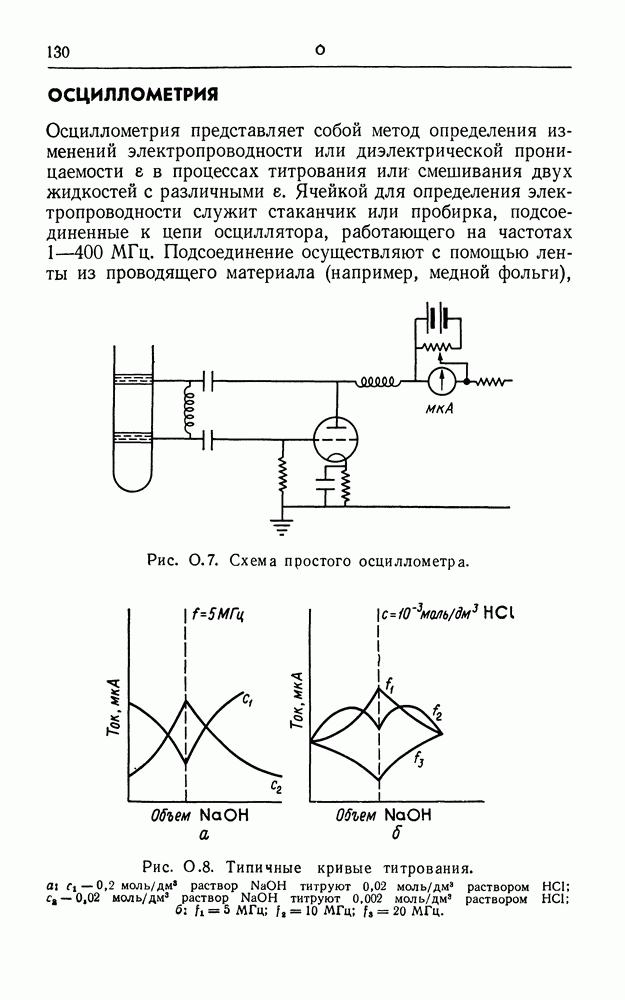
- ОСЦИЛЛОМЕТРИЯ
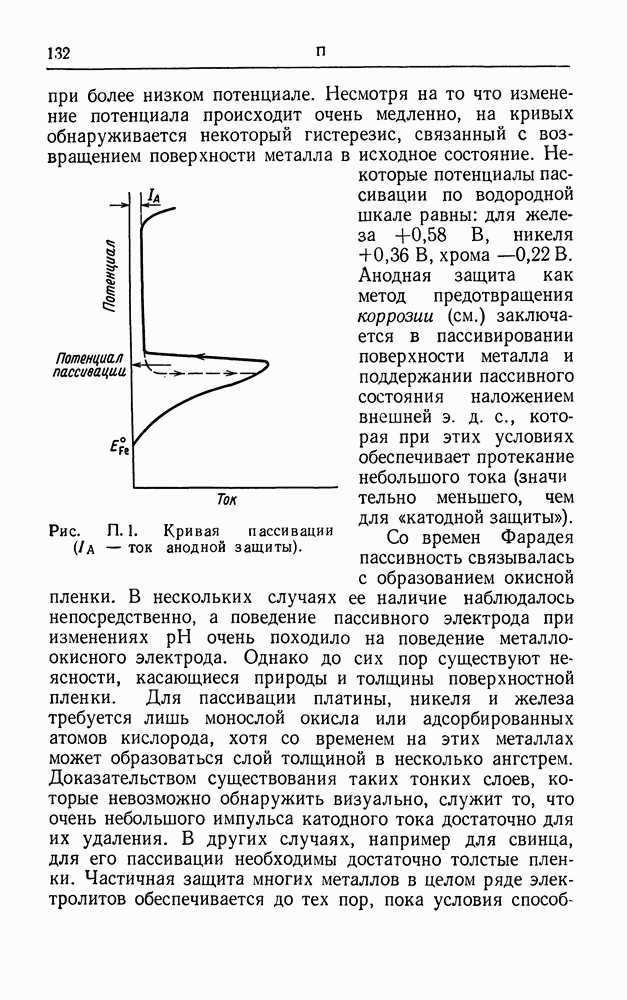
- ПАССИВНОСТЬ
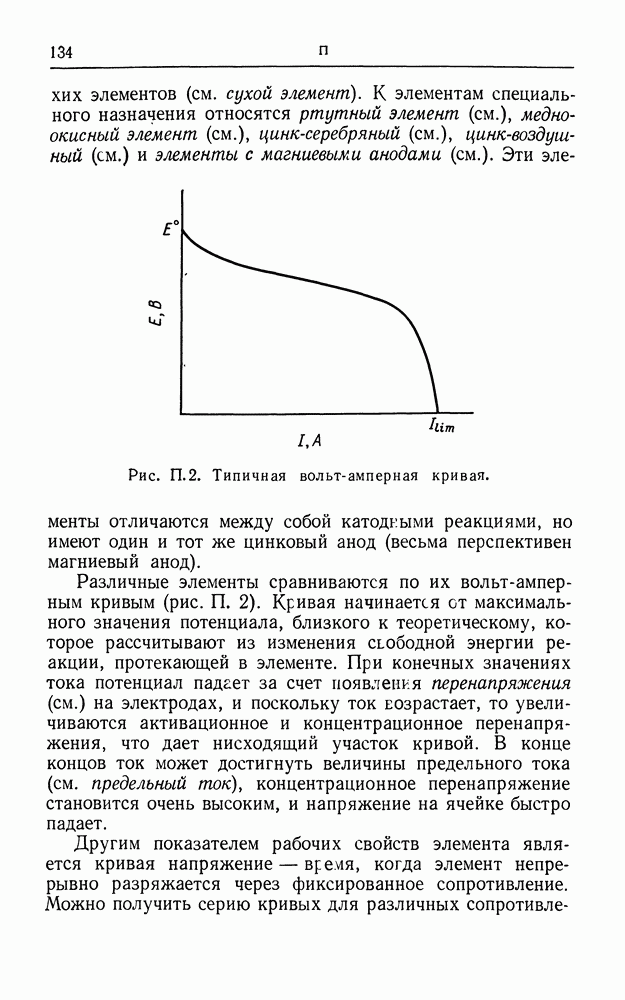
- ПЕРВИЧНЫЙ ГАЛЬВАНИЧЕСКИЙ ЭЛЕМЕНТ
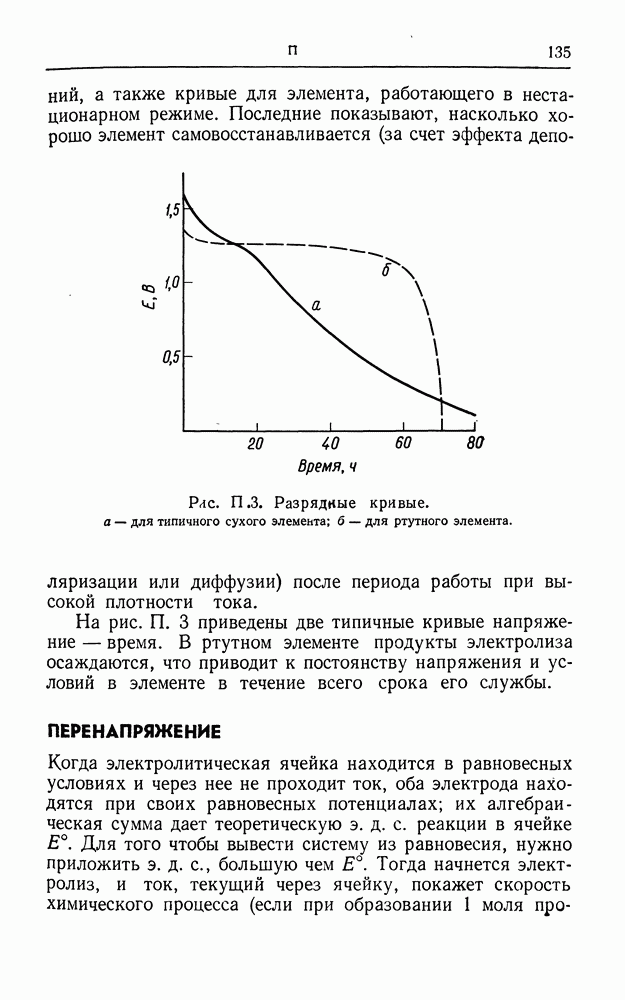
- ПЕРЕНАПРЯЖЕНИЕ
- ПЕРЕНАПРЯЖЕНИЕ ВОДОРОДА
- ПЕРЕХОДНОЕ ВРЕМЯ
- ПЕРСОЛИ
- ПЛАТИНОВЫЕ И ЗОЛОТЫЕ ЭЛЕКТРОДЫ
- рН-МЕТР
- ПОДВИЖНОСТЬ
- ПОДВИЖНОСТЬ ИОНОВ
- ПОЛУЭЛЕМЕНТ
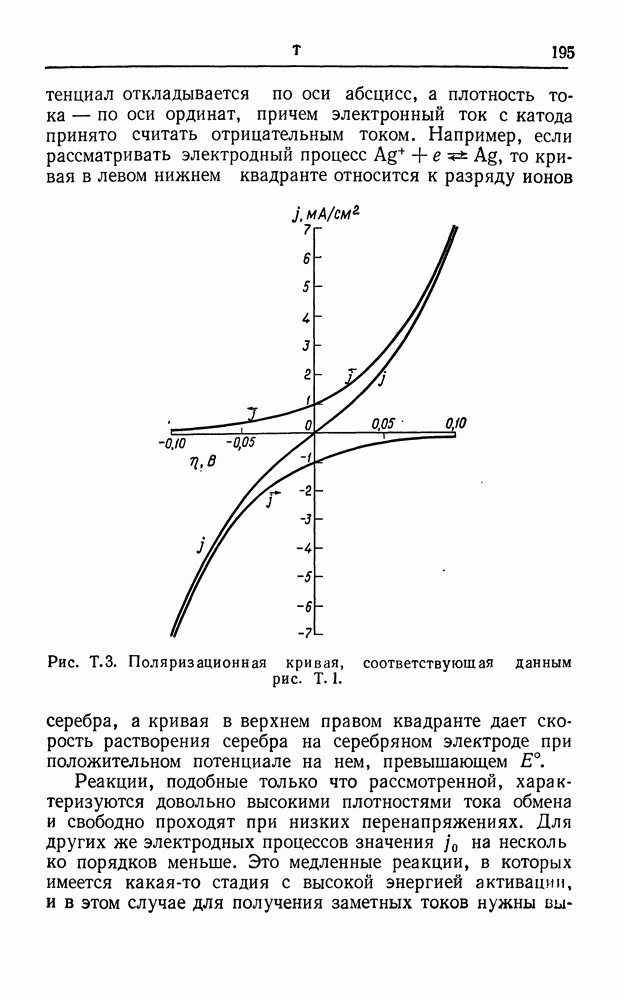
- ПОЛЯРИЗАЦИОННЫЕ КРИВЫЕ
- ПОЛЯРИЗАЦИЯ
- ПОЛЯРИЗУЕМЫЕ ЭЛЕКТРОДЫ
- ПОЛЯРОГРАФИЯ
- ПОПРАВКА НА ЭЛЕКТРОПРОВОДНОСТЬ РАСТВОРИТЕЛЯ
- ПОСТОЯННАЯ ЯЧЕЙКИ
- ПОТЕНЦИАЛ, ОБРАТИМЫЕ ЭЛЕКТРОДЫ
- ПОТЕНЦИАЛ ПОЛУВОЛНЫ
- ПОТЕНЦИАЛ СЕДИМЕНТАЦИИ
- ПОТЕНЦИАЛ ТЕЧЕНИЯ
- ПОТЕНЦИОМЕТР
- ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- ПОТЕНЦИОСТАТ
- ПРАВИЛО ВАЛЬДЕНА
- ПРЕДЕЛЬНЫЙ ТОК
- ПРОТЕКТОРНАЯ ЗАЩИТА
- РАСПЛАВЫ СОЛЕЙ
- РЕАКЦИЯ ВЫДЕЛЕНИЯ ВОДОРОДА
- РТУТНЫЙ ЭЛЕМЕНТ
- РЯД ПОТЕНЦИАЛОВ
- СВИНЦОВЫЙ АККУМУЛЯТОР
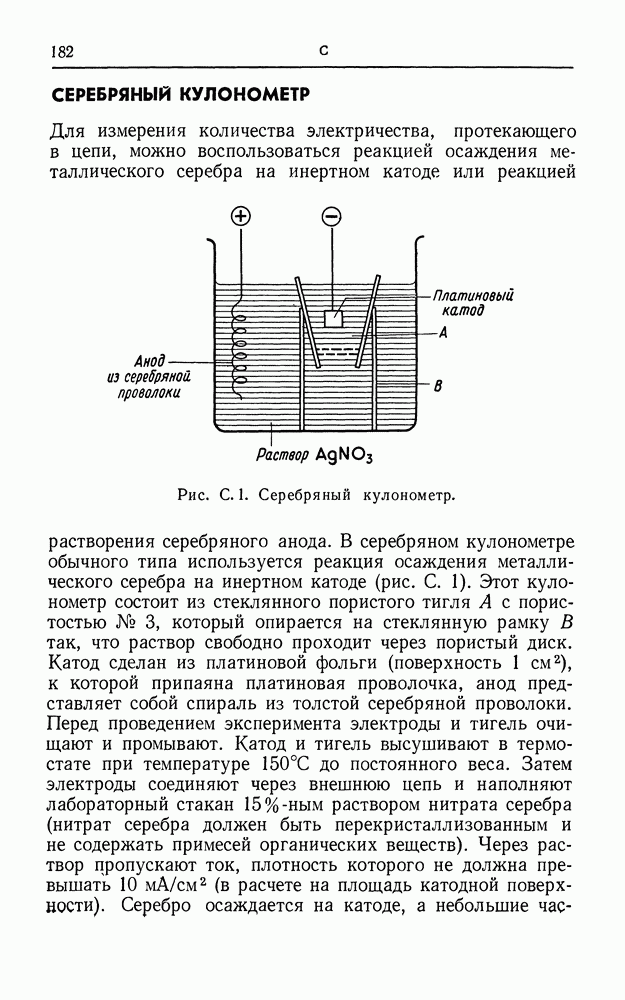
- СЕРЕБРЯНЫЙ КУЛОНОМЕТР
- СЕРЕБРЯНЫЙ ЭЛЕКТРОД
- СЛОЙ ГЕЛЬМГОЛЬЦА
- СЛОЙ ГУИ
- СОЛЕВОЙ МОСТИК
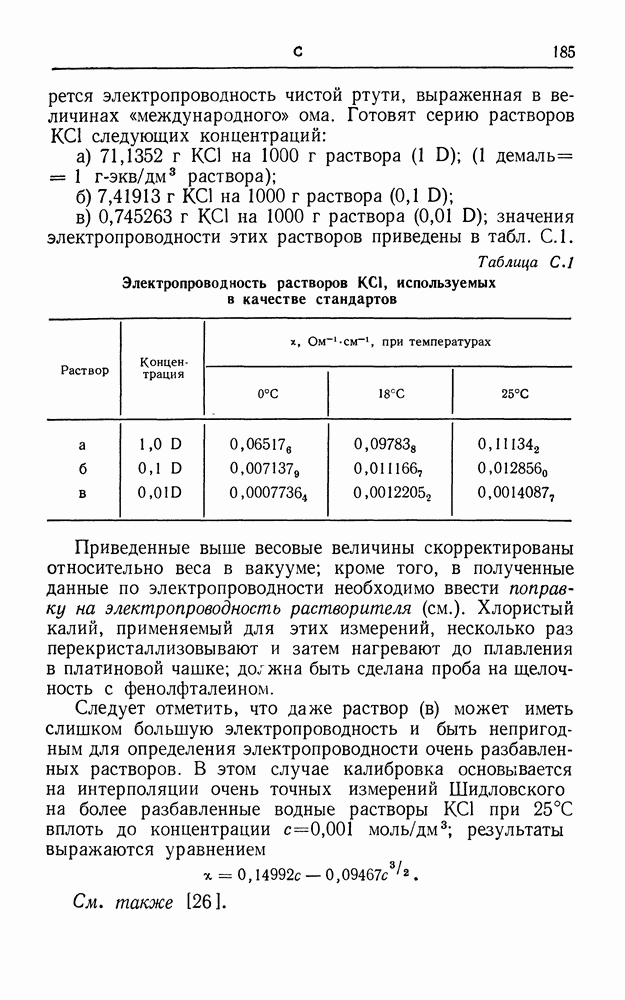
- СТАНДАРТНЫЕ РАСТВОРЫ ДЛЯ ЭЛЕКТРОПРОВОДНОСТИ
- СТАНДАРТНЫЙ ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ
- СТАНДАРТНЫЙ ЭЛЕМЕНТ
- СТЕКЛЯННЫЙ ЭЛЕКТРОД
- СУРЬМЯНЫЙ ЭЛЕКТРОД
- СУХОЙ ЭЛЕМЕНТ
- ТЕОРИЯ ИОННОЙ АССОЦИАЦИИ БЬЕРРУМА
- ТЕОРИЯ ЭЛЕКТРОЛИТИЧЕСКОЙ ДИССОЦИАЦИИ АРРЕНИУСА
- ТЕРМОДИНАМИКА ГАЛЬВАНИЧЕСКИХ ЭЛЕМЕНТОВ
- ТОК ОБМЕНА
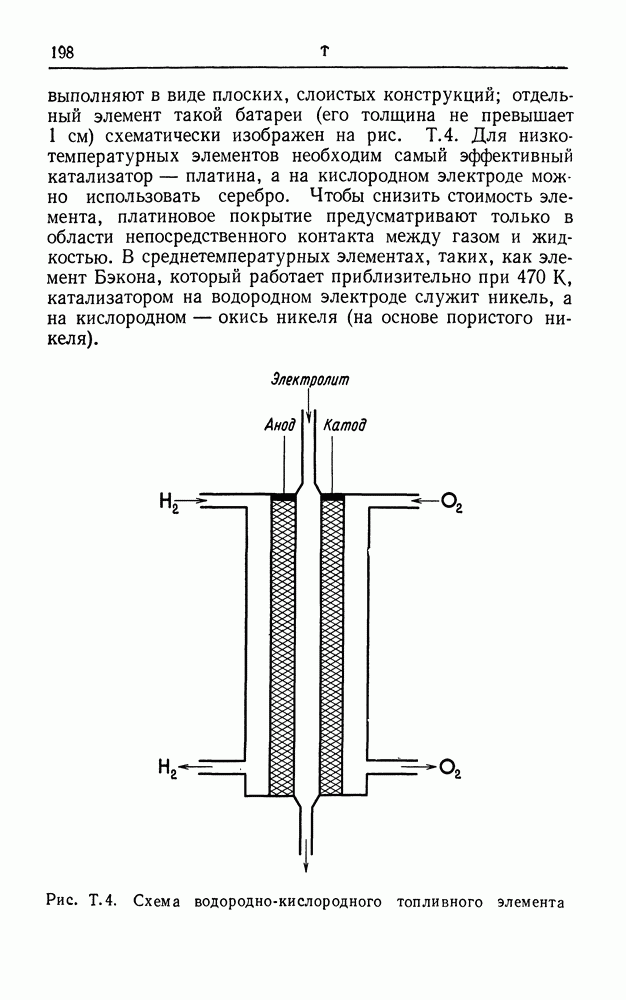
- ТОПЛИВНЫЙ ЭЛЕМЕНТ
- УРАВНЕНИЕ БРЕНСТЕДА—БЬЕРРУМА
- УРАВНЕНИЕ ДЕБАЯ — ХЮККЕЛЯ
- УРАВНЕНИЕ ИЛЬКОВИЧА
- УРАВНЕНИЕ НЕРНСТА
- УРАВНЕНИЕ ОНЗАГЕРА
- УРАВНЕНИЕ ТАФЕЛЯ
- УРАВНЕНИЕ ЭЛЕКТРОПРОВОДНОСТИ ПИТТСА
- УРАВНЕНИЕ ЭЛЕКТРОПРОВОДНОСТИ ФУОССА
- УРАВНЕНИЯ ЭЛЕКТРОПРОВОДНОСТИ
- ХЕМОТРОНЫ
- ХИНГИДРОННЫЙ ЭЛЕКТРОД
- ХЛОРНЫЙ ЭЛЕКТРОД
- ХЛОРСЕРЕБРЯНЫЙ ЭЛЕКТРОД
- ХРОНОАМПЕРОМЕТРИЯ
- ХРОНОПОТЕНЦИОМЕТРИЯ
- ЦИНК-ВОЗДУШНЫЙ ЭЛЕМЕНТ
- ЦИНК-СЕРЕБРЯНЫЙ ЭЛЕМЕНТ
- ЦИНК, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- ЦИФРОВОЙ ВОЛЬТМЕТР
- ЧАСТОТНАЯ ЗАВИСИМОСТЬ ЭЛЕКТРОПРОВОДНОСТИ
- ЧИСЛА ПЕРЕНОСА
- ЧИСЛО ФАРАДЕЯ
- ЩЕЛОЧНЫЕ АККУМУЛЯТОРЫ
- ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ
- ЭЛЕКТРИЧЕСКИЕ ЕДИНИЦЫ ИЗМЕРЕНИЯ
- ЭЛЕКТРОВЕСОВОЙ АНАЛИЗ
- ЭЛЕКТРОД
- ЭЛЕКТРОДВИЖУЩАЯ СИЛА (Э.Д.С.)
- ЭЛЕКТРОДИАЛИЗ
- ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ
- ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- ЭЛЕКТРОЛИЗ ВОДЫ
- ЭЛЕКТРОЛИЗЕР
- ЭЛЕКТРОЛИЗ РАСТВОРА ПОВАРЕННОЙ СОЛИ
- ЭЛЕКТРОЛИТИЧЕСКАЯ ОЧИСТКА (РАФИНИРОВАНИЕ)
- ЭЛЕКТРОЛИТИЧЕСКОЕ ВОССТАНОВЛЕНИЕ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
- ЭЛЕКТРОЛИТИЧЕСКОЕ ОКИСЛЕНИЕ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
- ЭЛЕКТРОЛИТИЧЕСКОЕ ПОЛИРОВАНИЕ
- ЭЛЕКТРОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- ЭЛЕКТРООСАЖДЕНИЕ МЕТАЛЛОВ
- ЭЛЕКТРООСАЖДЕНИЕ СПЛАВОВ
- ЭЛЕКТРООСМОС
- ЭЛЕКТРОПРОВОДНОСТЬ
- ЭЛЕКТРОПРОВОДНОСТЬ ВОДНЫХ РАСТВОРОВ
- ЭЛЕКТРОПРОВОДНОСТЬ НА ВЫСОКИХ ЧАСТОТАХ
- ЭЛЕКТРОПРОВОДНОСТЬ НЕВОДНЫХ РАСТВОРОВ
- ЭЛЕКТРОПРОВОДНОСТЬ ПРИ БЕСКОНЕЧНОМ РАЗБАВЛЕНИИ
- ЭЛЕКТРОПРОВОДНОСТЬ ПРИ ВЫСОКИХ НАПРЯЖЕННОСТЯХ ПОЛЯ
- ЭЛЕКТРОПРОВОДНОСТЬ РАСПЛАВОВ СОЛЕЙ
- ЭЛЕКТРОФОРЕЗ
- ЭЛЕКТРОХИМИЧЕСКАЯ РАЗМЕРНАЯ ОБРАБОТКА МЕТАЛЛОВ
- ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ИНФОРМАЦИИ
- ЭЛЕКТРОХИМИЧЕСКИЙ ЭКВИВАЛЕНТ
- ЭЛЕМЕНТ ВЕСТОНА
- ЭЛЕМЕНТ ДАНИЭЛЯ
- ЭЛЕМЕНТ КЛАРКА
- ЭЛЕМЕНТЫ С МАГНИЕВЫМИ АНОДАМИ
- ЭФФЕКТ ВИНА
- ЭФФЕКТ ДОРНА
- ЭФФЕКТ ФАЛЬКЕНГАГЕНА
- СПИСОК ЛИТЕРАТУРЫ