| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
МЕХАНИЗМЫ ЭЛЕКТРОДНЫХ РЕАКЦИЙ
Как и для обычных химических реакций, большую часть сведений о механизме электролитических процессов получают, измеряя их скорости, о которых в данном случае удобно судить по силе тока. При этом основной переменной является не температура, а потенциал электрода, и отправной точкой для теоретического анализа служат такие соотношения, как уравнение Тафеля (см.). Но здесь могут встретиться такие же трудности, как и при исследовании обычной кинетики реакций в растворах. Реакция протекает по наилегчайшему пути, который обычно включает несколько последовательных стадий, и задача состоит в том, чтобы выявить эти стадии и установить, какая из них —
скорость определяющая. Кроме того, электродные процессы являются гетерогенными реакциями, и поэтому необходимо учитывать каталитические свойства электрода и его адсорбционную способность по отношению к различным присутствующим веществам.
В отличие от химической реакции электрохимическая реакция включает хотя бы одну стадию, связанную с переходом электронов через границу раздела электрод — раствор.

Рис. М. 6. Кривая потенциальной энергии.
Рассмотрим катодный процесс, в котором происходит разряд однозарядного гидратированного катиона. Разряжаться будут лишь те катионы, которые ближе всего находятся к электроду, т. е. катионы во внешней плоскости Гельмгольца (см. двойной электрический слой). Разряд этих катионов графически можно представить в виде энергетической диаграммы, изображенной на рис. М. 6. Катионы должны обладать такой энергией, чтобы достигнуть вершины энергетического барьера, — эта дополнительная энергия идет на растяжение связей и разрыхление структуры гидратной оболочки иона. На вершине барьера катионы присоединяют электроны соответствующей энергии и переходят в устойчивое состояние на поверхности электрода. В отсутствие электрического поля скорость реакции может быть записана в виде

где Е — химическая энергия активации. Если концентрацию ионов  на границе раздела выразить в моль/см2, то для сбудем иметь размерность
на границе раздела выразить в моль/см2, то для сбудем иметь размерность  . Умножая обе части равенства (1) на число Фарадея, для плотности тока получим следующее выражение:
. Умножая обе части равенства (1) на число Фарадея, для плотности тока получим следующее выражение:

Однако в действительности, как только составлена электродная система, на границе раздела сразу же возникает потенциал, который возрастает до тех пор, пока не уравняются скорости обоих противоположных процессов  и не установится равновесие. В этом случае возникает равновесная разность потенциалов
и не установится равновесие. В этом случае возникает равновесная разность потенциалов  и нужно учитывать соответствующий электрический вклад в энергию системы. На левой части приведенного уравнения окислительно-восстановительной реакции это сказывается слабо, поскольку в ней фигурируют нейтральные компоненты. Энергия же электрона изменяется на
и нужно учитывать соответствующий электрический вклад в энергию системы. На левой части приведенного уравнения окислительно-восстановительной реакции это сказывается слабо, поскольку в ней фигурируют нейтральные компоненты. Энергия же электрона изменяется на  (или на
(или на  в пересчете на один моль). Эту энергию необходимо добавить к энергии частиц, фигурирующих в правой части уравнения реакции. Если принять приближенно, что при переходе через двойной слой энергия изменяется линейно с расстоянием, то линия А В на рис. М. 6 должна сместиться вверх на расстояние, соответствующее величине
в пересчете на один моль). Эту энергию необходимо добавить к энергии частиц, фигурирующих в правой части уравнения реакции. Если принять приближенно, что при переходе через двойной слой энергия изменяется линейно с расстоянием, то линия А В на рис. М. 6 должна сместиться вверх на расстояние, соответствующее величине  и занять положение CD. Таким образом, энергия активации изменится на величину, соответствующую разности высот BF и CG. Эта величина меньше
и занять положение CD. Таким образом, энергия активации изменится на величину, соответствующую разности высот BF и CG. Эта величина меньше  и изменение энергии активации можно записать в виде
и изменение энергии активации можно записать в виде  где множитель
где множитель  называется коэффициентом симметрии. Анализ диаграммы показывает, что (3 зависит от величины углов между линиями А В и HD и горизонталью. Если эти углы равны, то
называется коэффициентом симметрии. Анализ диаграммы показывает, что (3 зависит от величины углов между линиями А В и HD и горизонталью. Если эти углы равны, то  и экспериментально полученные данные весьма близки к этому значению. Естественно, что в понижении энергии активации участвует не вся разность потенциалов, а лишь часть ее, причем именно та, которую
и экспериментально полученные данные весьма близки к этому значению. Естественно, что в понижении энергии активации участвует не вся разность потенциалов, а лишь часть ее, причем именно та, которую
ион должен преодолеть, чтобы достичь промежуточного состояния. Если же рассматривать обратную реакцию, в которой положительный ион должен покинуть поверхность и двигаться против поля, то на него будет влиять лишь доля полной разности потенциалов, равная  так что энергия активации возрастет на величину
так что энергия активации возрастет на величину 
Чтобы учесть эти эффекты, уравнение (1) следует видоизменить. Для реакции ионизации

а для реакции разряда

Но при равновесном потенциале  суммарный (результирующий) ток равен нулю, т. е.
суммарный (результирующий) ток равен нулю, т. е.  » где
» где  — плотность тока обмена (см.).
— плотность тока обмена (см.).
При любом другом электродном потенциале это равенство не выполняется и суммарный ток будет отличаться от нуля. Предположим, что электродный потенциал становится более отрицательным из-за наличия перенапряжения (см.)  . Рассуждая так же, как и раньше, приходим к выводу, что энергия активации процесса разряда катиона уменьшается на
. Рассуждая так же, как и раньше, приходим к выводу, что энергия активации процесса разряда катиона уменьшается на  а энергия активации реакции ионизации увеличивается на
а энергия активации реакции ионизации увеличивается на  . Поэтому вместо уравнений (2) и (3) можно написать
. Поэтому вместо уравнений (2) и (3) можно написать

Однако нет необходимости пользоваться этими полными выражениями, поскольку уравнения (2) и (3) дают плотность тока обмена  при стандартном равновесном потенциале. Подставляя величину
при стандартном равновесном потенциале. Подставляя величину  в уравнения (4) и (5), получаем токи, обусловленные приложенным перенапряжением:
в уравнения (4) и (5), получаем токи, обусловленные приложенным перенапряжением:

и

Для суммарного тока имеем

При больших катодных перенапряжениях  становится пренебрежимо малым, и поэтому можно написать
становится пренебрежимо малым, и поэтому можно написать

или

Это соотношение эквивалентно уравнению Тафеля, чем и подтверждается правильность изложенной теории. Аналогичный результат можно получить для тока ионизации, когда потенциал электрода намного положительнее равновесного.
При небольшом перенапряжении  ни одним из противоположных процессов нельзя пренебрегать и следует учитывать оба процесса. Однако при малых
ни одним из противоположных процессов нельзя пренебрегать и следует учитывать оба процесса. Однако при малых  уравнение (6) можно упростить, заменив каждую экспоненту в нем первым членом разложения ее в степенной ряд. Тогда при
уравнение (6) можно упростить, заменив каждую экспоненту в нем первым членом разложения ее в степенной ряд. Тогда при 

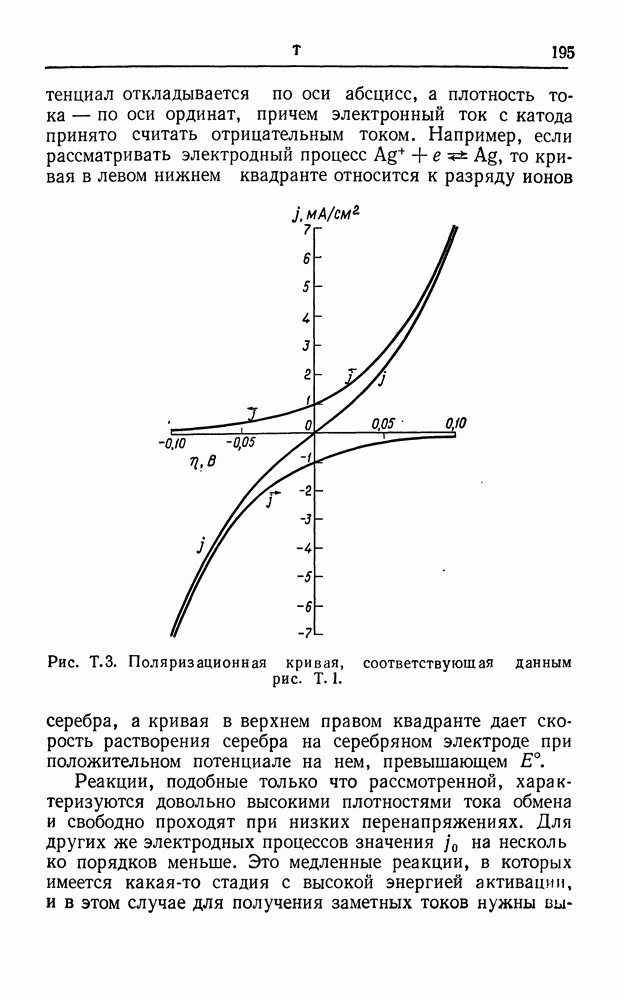
Таким образом, при малых перенапряжениях суммарный ток прямо пропорционален перенапряжению. Линейный участок кривой  показан на рис. Т. 1 и Т. 2 (см. ток обмена), причем в каждом конкретном случае наклон кривой определяется величиной
показан на рис. Т. 1 и Т. 2 (см. ток обмена), причем в каждом конкретном случае наклон кривой определяется величиной  для рассматриваемого электродного процесса.
для рассматриваемого электродного процесса.
Если эти результаты для одноэлектронного процесса переноса, соответствующие уравнению (7) в случае больших перенапряжений и уравнению (8) в случае малых перенапряжений, применяются при выводе выражения для тока суммарной электролитической реакции, то при этом необходимо учитывать упрощения, используемые при выводе уравнений (7) и (8). В частности, предполагалось, что эффективная поверхность электрода постоянна и влияние адсорбции на эту поверхность незначительно. Кроме того,
если  в уравнениях представляют собой соответственно концентрацию ионов в объеме раствора и разность потенциалов между раствором и электродом, то в эти величины необходимо ввести поправку, связанную с потенциалом диффузной части двойного слоя. К тому же в принятом приближении о существовании линейной зависимости энергии от расстояния величина
в уравнениях представляют собой соответственно концентрацию ионов в объеме раствора и разность потенциалов между раствором и электродом, то в эти величины необходимо ввести поправку, связанную с потенциалом диффузной части двойного слоя. К тому же в принятом приближении о существовании линейной зависимости энергии от расстояния величина  постоянна, однако нелинейный участок, всегда имеющийся вблизи вершины барьера, приводит к уменьшению
постоянна, однако нелинейный участок, всегда имеющийся вблизи вершины барьера, приводит к уменьшению  с ростом
с ростом  в тех случаях, когда энергия активации мала и перенапряжение велико.
в тех случаях, когда энергия активации мала и перенапряжение велико.
Чтобы объяснить механизм электродной реакции, необходимо, во-первых, знать химические особенности реакции, число участвующих в ней электронов и состав раствора. Во-вторых, из тафелевского наклона (см. активационное перенапряжение) следует определить коэффициент переноса а. Для простого электронного переноса он равен коэффициенту симметрии (3, но в более общем случае коэффициент а равен коэффициенту (3, умноженному на число электронов, участвующих в реакции, и зависит от других параметров суммарного процесса. Для определения порядка реакции по каждому компоненту раствора изменяют поочередно концентрацию каждого компонента и наблюдают за изменением плотности тока при постоянном потенциале. Кроме того, чтобы идентифицировать стадии суммарного электродного процесса, можно рассматривать, как и при изучении кинетики обычных химических реакций, изотопные
эффекты, изменение pH и влияние добавок. Наконец, точно так же, как в обычной кинетике используются релаксационные методы, здесь можно изучать переходные процессы при импульсном или переменном токе с целью выявления промежуточных стадий реакций и получения информации об адсорбционных явлениях на поверхности электрода. Некоторые примеры исследования таких механизмов приведены в статье реакция выделения водорода (см.).
См. также [4]; Thirsk Н. /., Harrison J. A., Guide to the Study of Electrochemical Kinetics, Academic Press, 1972.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- О ПОЛЬЗОВАНИИ СЛОВАРЕМ
- СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
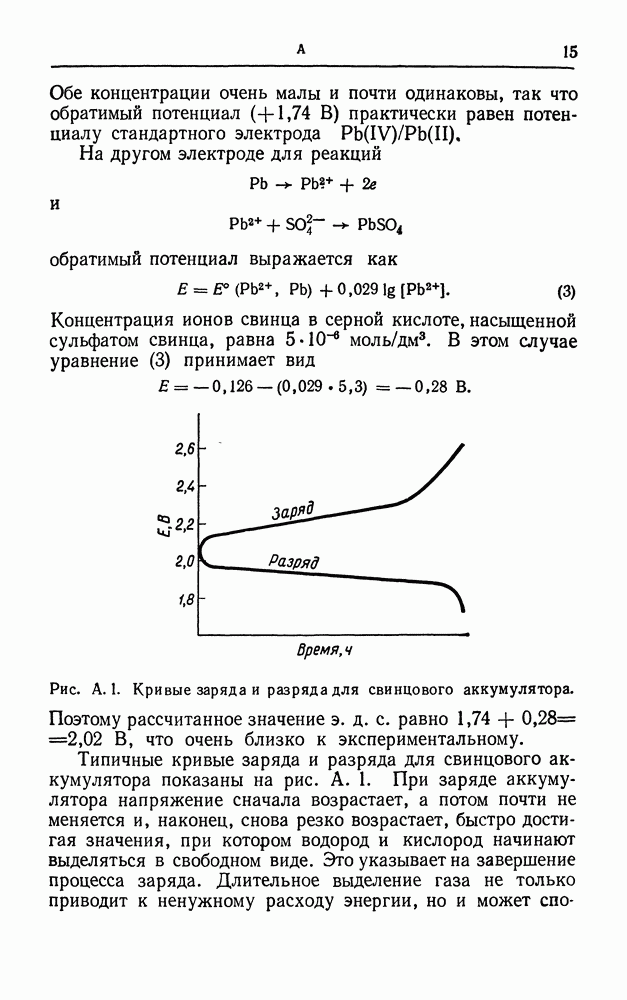
- АККУМУЛЯТОР
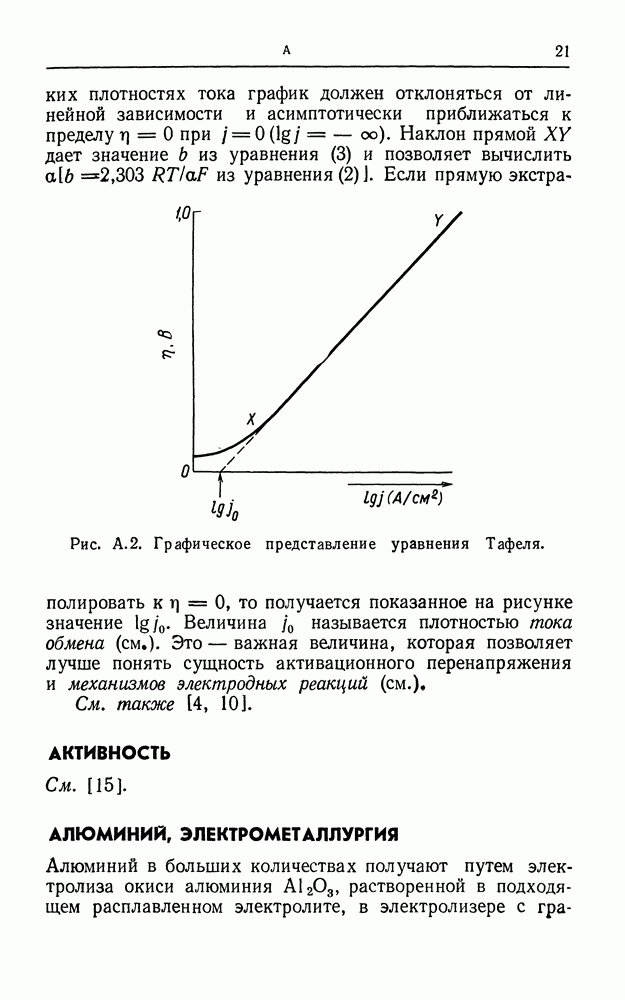
- АКТИВАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- АКТИВНОСТЬ
- АЛЮМИНИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- АМАЛЬГАМНЫЙ ЭЛЕКТРОД
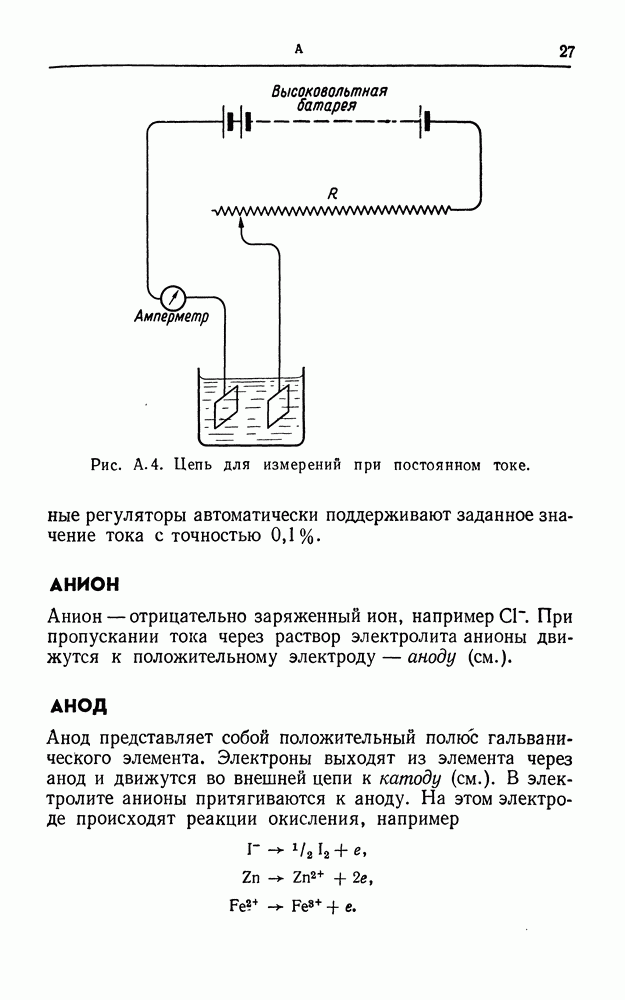
- АМПЕР
- АМПЕРОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- АМПЕРОСТАТ
- АНИОН
- АНОД
- АНОДИРОВАНИЕ
- БАТАРЕЯ
- БЕРИЛЛИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- БИПОЛЯРНЫЙ ЭЛЕКТРОД
- БЛЕСКООБРАЗОВАТЕЛИ
- БУФЕРНЫЙ РАСТВОР
- ВАГНЕРОВСКОЕ ЗАЗЕМЛЕНИЕ
- ВНУТРЕННИЙ ЭЛЕКТРОЛИЗ
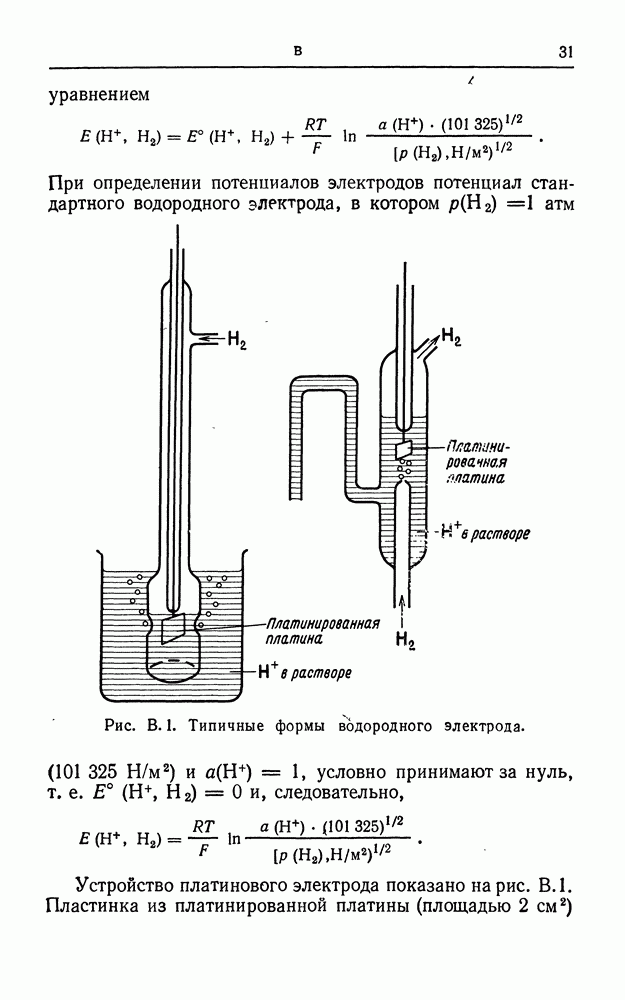
- ВОДОРОДНЫЙ ЭЛЕКТРОД
- ВОЛЬТ
- ВОЛЬФРАМОВЫЙ ЭЛЕКТРОД
- ВЫХОД ПО ТОКУ
- ГАЗОВЫЙ ЭЛЕКТРОД
- ГАЛЬВАНИЧЕСКИЙ ЭЛЕМЕНТ
- ГАЛЬВАНОПЛАСТИКА
- ГАЛЬВАНОСТАТ
- ГАЛЬВАНОСТЕГИЯ
- ГИДРАТАЦИЯ ИОНОВ
- ДАТЧИК АММИАКА
- ДАТЧИК СЕРНИСТОГО ГАЗА
- ДВОЙНОЙ СЛОЙ
- ДВОЙНОЙ ЭЛЕКТРИЧЕСКИЙ СЛОЙ
- ДЗЕТА-ПОТЕНЦИАЛ
- ДИФФУЗИОННЫЙ ПОТЕНЦИАЛ
- ДИФФУЗИЯ В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
- ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ
- ЗАКОН КОЛЬРАУША
- ЗАКОН РАЗВЕДЕНИЯ ОСТВАЛЬДА
- ЗАКОНЫ ФАРАДЕЯ
- ИНДИКАТОР
- ИНДИКАТОРНЫЙ ЭЛЕКТРОД
- ИНДИФФЕРЕНТНЫЙ (ФОНОВЫЙ) ЭЛЕКТРОЛИТ
- ИОДНЫЙ КУЛОНОМЕТР
- ИОННАЯ АТМОСФЕРА
- ИОННЫЕ ПАРЫ
- ИОННЫЕ РАСПЛАВЫ
- ИОНОСЕЛЕКТИВНЫЕ ЭЛЕКТРОДЫ
- КАДМИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- КАЛОМЕЛЬНЫЙ ЭЛЕКТРОД
- КАЛЬЦИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- КАПИЛЛЯР ЛУГГИНА
- КАТИОН
- КАТИОНОСЕЛЕКТИВНЫЙ ЭЛЕКТРОД
- КАТОД
- КАТОДНАЯ ЗАЩИТА
- КИСЛОРОДНОЕ ПЕРЕНАПРЯЖЕНИЕ
- КИСЛОРОДНЫЙ ЭЛЕКТРОД (КИСЛОРОДНЫЙ ЗОНД)
- КОМПЛЕКСНЫЕ ИОНЫ
- КОНВЕНЦИЯ О ЗНАКАХ
- КОНДУКТОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- КОНСТАНТА ДИССОЦИАЦИИ
- КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
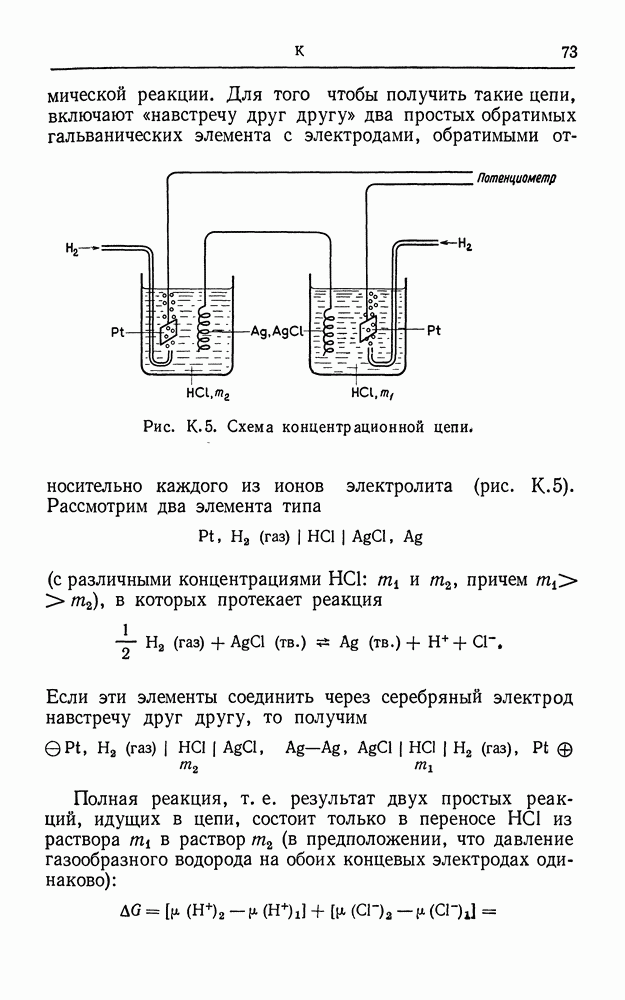
- КОНЦЕНТРАЦИОННАЯ ЦЕПЬ
- КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
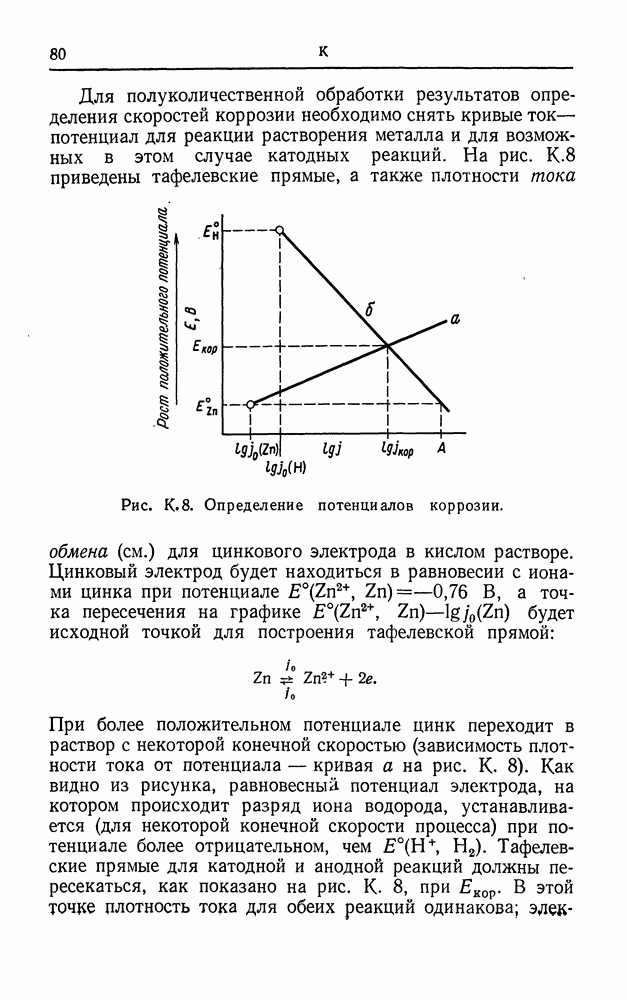
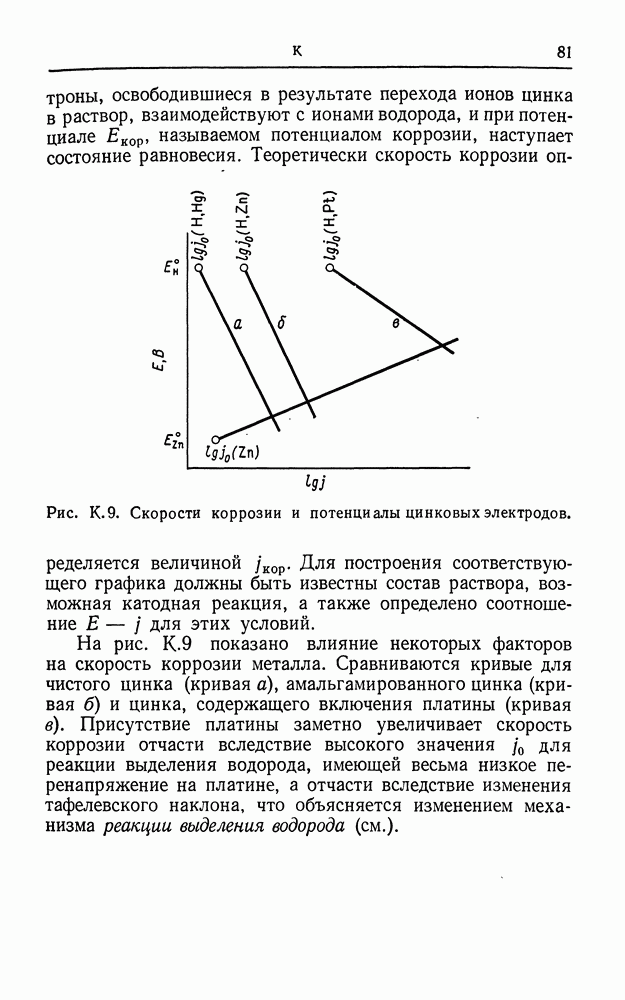
- КОРРОЗИЯ
- КОЭФФИЦИЕНТ АКТИВНОСТИ
- КУЛОН
- КУЛОНОМЕТР
- КУЛОНОМЕТРИЯ
- ЛИТИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- МАГНИЙ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- МЕДНООКИСНЫЙ ЭЛЕМЕНТ
- МЕДНЫЙ КУЛОНОМЕТР
- МЕДЬ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- МЕМБРАННЫЙ ЭЛЕКТРОД
- МЕТАЛЛИЧЕСКИЙ ЭЛЕКТРОД
- МЕТАЛЛООКИСНЫЙ ЭЛЕКТРОД
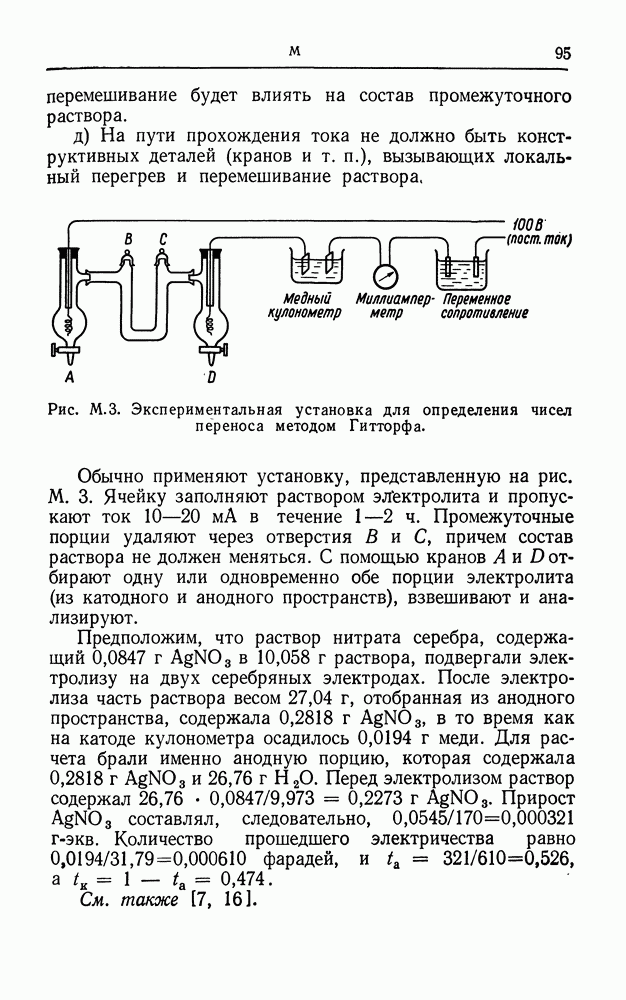
- МЕТОД ГИТТОРФА
- МЕТОД ДВИЖУЩЕЙСЯ ГРАНИЦЫ
- МЕХАНИЗМЫ ЭЛЕКТРОДНЫХ РЕАКЦИЙ
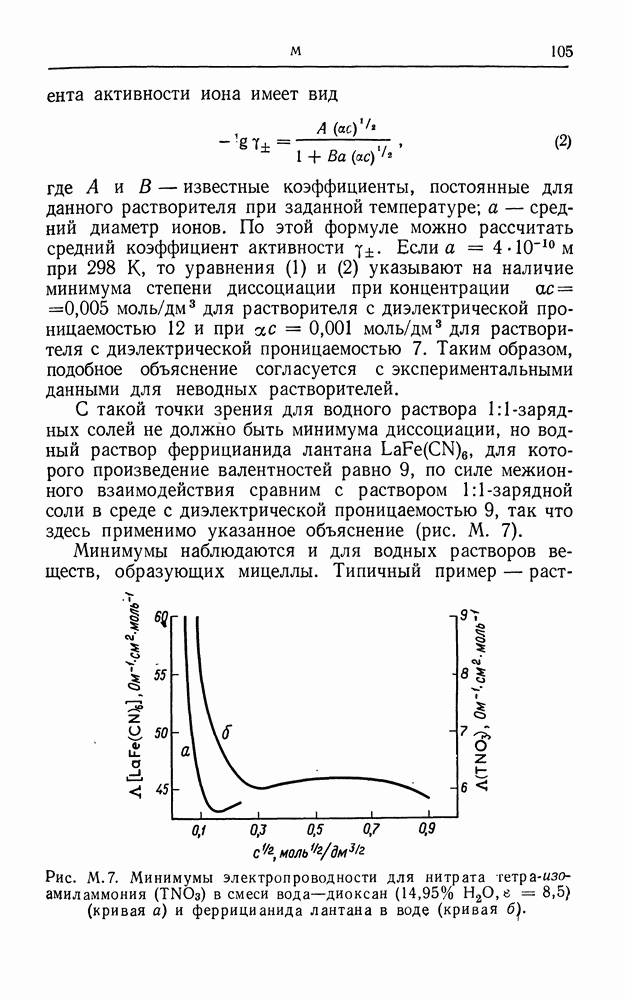
- МИНИМУМЫ ЭЛЕКТРОПРОВОДНОСТИ
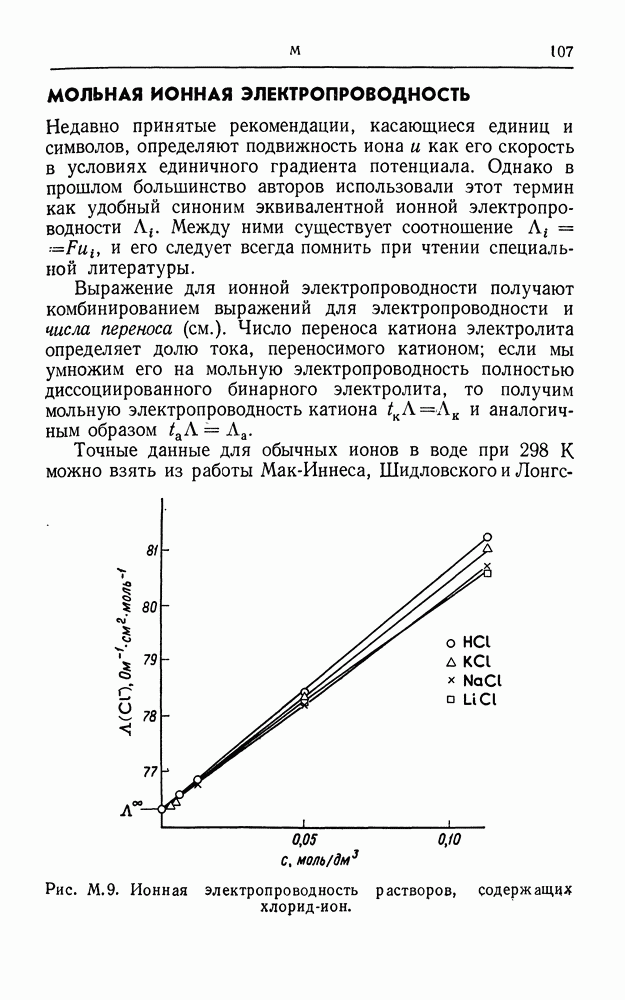
- МОЛЬНАЯ ИОННАЯ ЭЛЕКТРОПРОВОДНОСТЬ
- МОСТ УИТСТОНА
- НАПРЯЖЕНИЕ РАЗЛОЖЕНИЯ
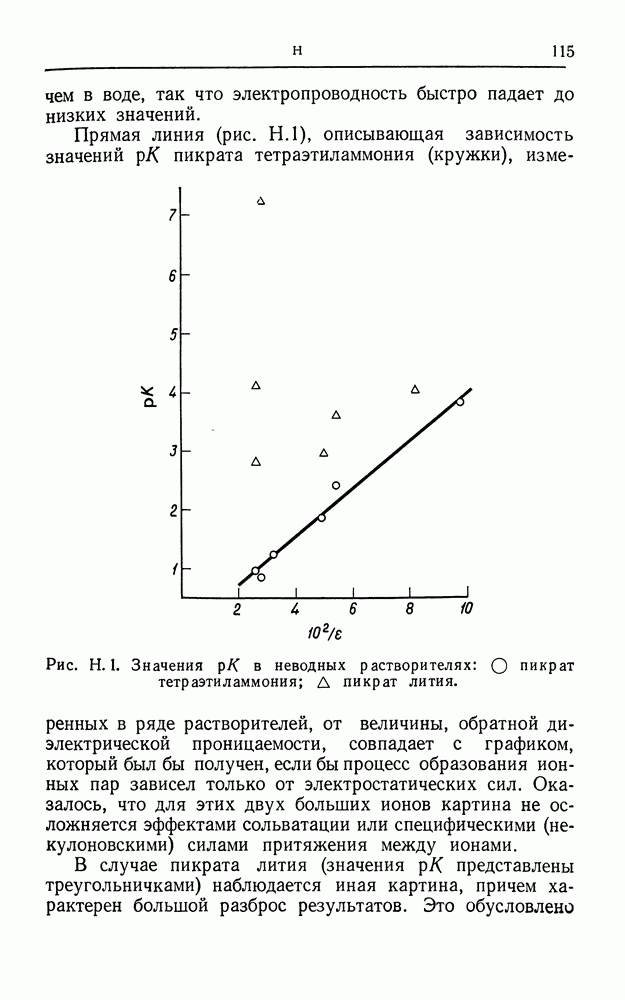
- НЕВОДНЫЕ РАСТВОРЫ
- НИКЕЛЬ, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- ОБРАТИМЫЙ ГАЛЬВАНИЧЕСКИЙ ЭЛЕМЕНТ
- ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНАЯ (РЕДОКС) ЭЛЕКТРОДНАЯ СИСТЕМА
- ОМ
- ОПРЕСНЕНИЕ ВОДЫ
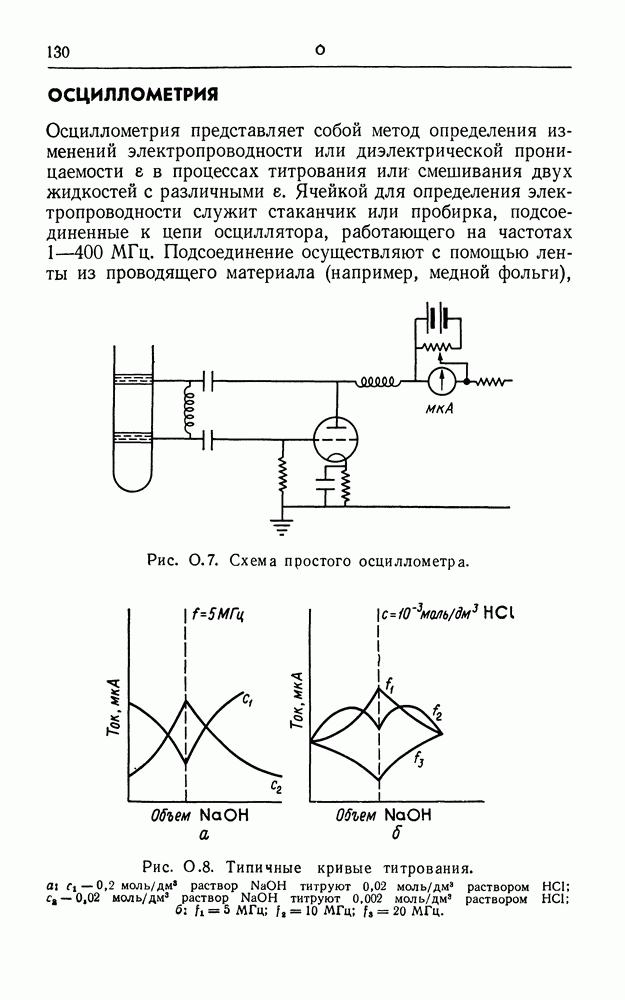
- ОСЦИЛЛОМЕТРИЯ
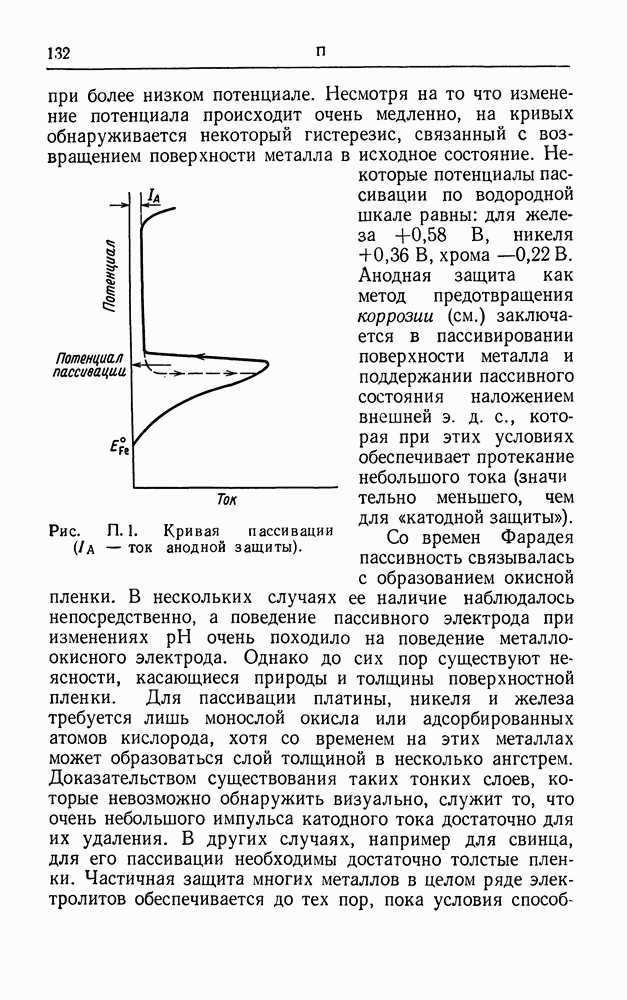
- ПАССИВНОСТЬ
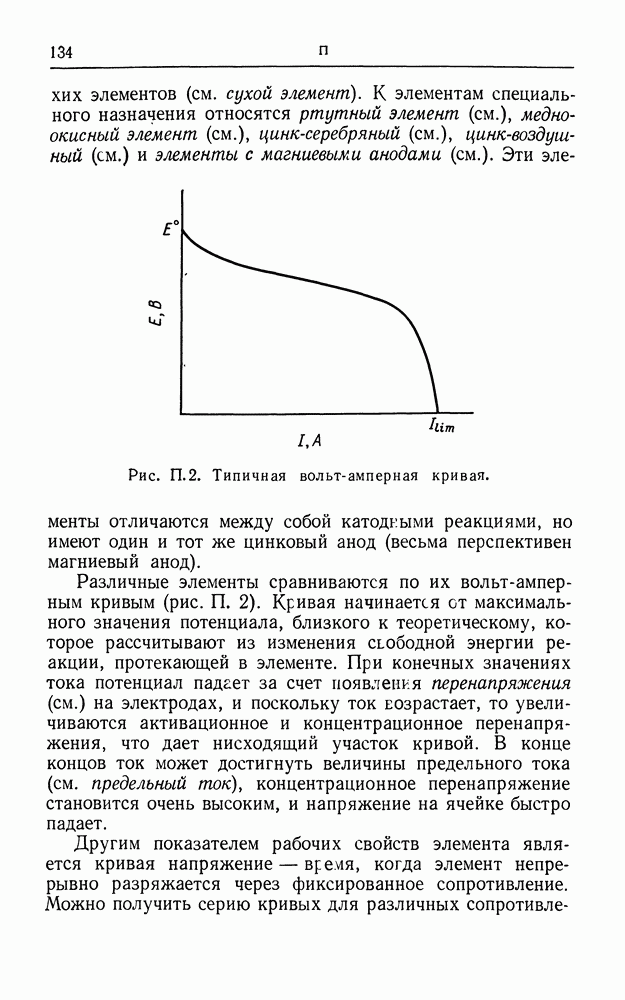
- ПЕРВИЧНЫЙ ГАЛЬВАНИЧЕСКИЙ ЭЛЕМЕНТ
- ПЕРЕНАПРЯЖЕНИЕ
- ПЕРЕНАПРЯЖЕНИЕ ВОДОРОДА
- ПЕРЕХОДНОЕ ВРЕМЯ
- ПЕРСОЛИ
- ПЛАТИНОВЫЕ И ЗОЛОТЫЕ ЭЛЕКТРОДЫ
- рН-МЕТР
- ПОДВИЖНОСТЬ
- ПОДВИЖНОСТЬ ИОНОВ
- ПОЛУЭЛЕМЕНТ
- ПОЛЯРИЗАЦИОННЫЕ КРИВЫЕ
- ПОЛЯРИЗАЦИЯ
- ПОЛЯРИЗУЕМЫЕ ЭЛЕКТРОДЫ
- ПОЛЯРОГРАФИЯ
- ПОПРАВКА НА ЭЛЕКТРОПРОВОДНОСТЬ РАСТВОРИТЕЛЯ
- ПОСТОЯННАЯ ЯЧЕЙКИ
- ПОТЕНЦИАЛ, ОБРАТИМЫЕ ЭЛЕКТРОДЫ
- ПОТЕНЦИАЛ ПОЛУВОЛНЫ
- ПОТЕНЦИАЛ СЕДИМЕНТАЦИИ
- ПОТЕНЦИАЛ ТЕЧЕНИЯ
- ПОТЕНЦИОМЕТР
- ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- ПОТЕНЦИОСТАТ
- ПРАВИЛО ВАЛЬДЕНА
- ПРЕДЕЛЬНЫЙ ТОК
- ПРОТЕКТОРНАЯ ЗАЩИТА
- РАСПЛАВЫ СОЛЕЙ
- РЕАКЦИЯ ВЫДЕЛЕНИЯ ВОДОРОДА
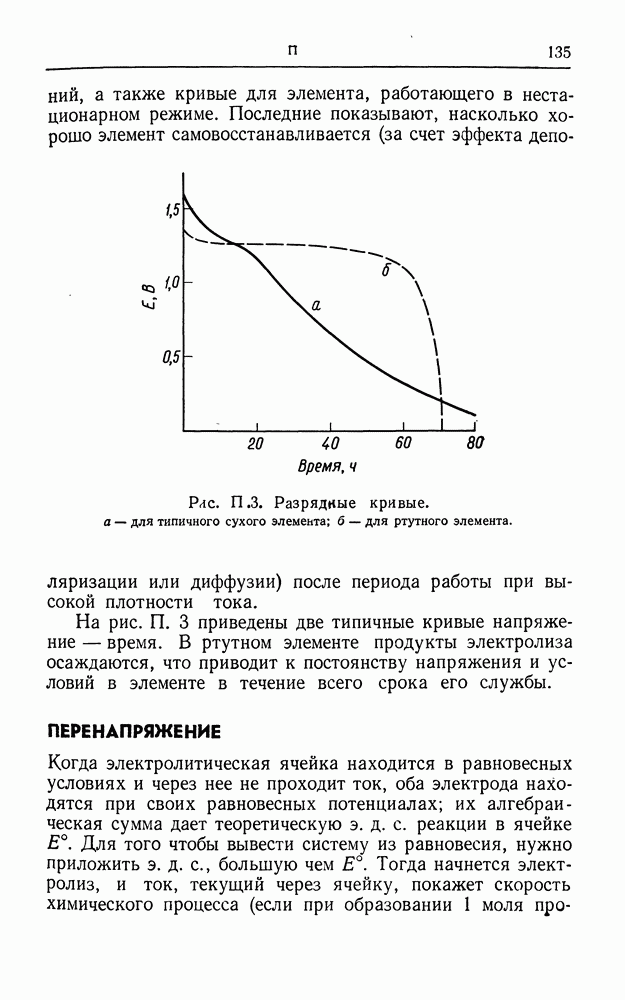
- РТУТНЫЙ ЭЛЕМЕНТ
- РЯД ПОТЕНЦИАЛОВ
- СВИНЦОВЫЙ АККУМУЛЯТОР
- СЕРЕБРЯНЫЙ КУЛОНОМЕТР
- СЕРЕБРЯНЫЙ ЭЛЕКТРОД
- СЛОЙ ГЕЛЬМГОЛЬЦА
- СЛОЙ ГУИ
- СОЛЕВОЙ МОСТИК
- СТАНДАРТНЫЕ РАСТВОРЫ ДЛЯ ЭЛЕКТРОПРОВОДНОСТИ
- СТАНДАРТНЫЙ ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ
- СТАНДАРТНЫЙ ЭЛЕМЕНТ
- СТЕКЛЯННЫЙ ЭЛЕКТРОД
- СУРЬМЯНЫЙ ЭЛЕКТРОД
- СУХОЙ ЭЛЕМЕНТ
- ТЕОРИЯ ИОННОЙ АССОЦИАЦИИ БЬЕРРУМА
- ТЕОРИЯ ЭЛЕКТРОЛИТИЧЕСКОЙ ДИССОЦИАЦИИ АРРЕНИУСА
- ТЕРМОДИНАМИКА ГАЛЬВАНИЧЕСКИХ ЭЛЕМЕНТОВ
- ТОК ОБМЕНА
- ТОПЛИВНЫЙ ЭЛЕМЕНТ
- УРАВНЕНИЕ БРЕНСТЕДА—БЬЕРРУМА
- УРАВНЕНИЕ ДЕБАЯ — ХЮККЕЛЯ
- УРАВНЕНИЕ ИЛЬКОВИЧА
- УРАВНЕНИЕ НЕРНСТА
- УРАВНЕНИЕ ОНЗАГЕРА
- УРАВНЕНИЕ ТАФЕЛЯ
- УРАВНЕНИЕ ЭЛЕКТРОПРОВОДНОСТИ ПИТТСА
- УРАВНЕНИЕ ЭЛЕКТРОПРОВОДНОСТИ ФУОССА
- УРАВНЕНИЯ ЭЛЕКТРОПРОВОДНОСТИ
- ХЕМОТРОНЫ
- ХИНГИДРОННЫЙ ЭЛЕКТРОД
- ХЛОРНЫЙ ЭЛЕКТРОД
- ХЛОРСЕРЕБРЯНЫЙ ЭЛЕКТРОД
- ХРОНОАМПЕРОМЕТРИЯ
- ХРОНОПОТЕНЦИОМЕТРИЯ
- ЦИНК-ВОЗДУШНЫЙ ЭЛЕМЕНТ
- ЦИНК-СЕРЕБРЯНЫЙ ЭЛЕМЕНТ
- ЦИНК, ЭЛЕКТРОМЕТАЛЛУРГИЯ
- ЦИФРОВОЙ ВОЛЬТМЕТР
- ЧАСТОТНАЯ ЗАВИСИМОСТЬ ЭЛЕКТРОПРОВОДНОСТИ
- ЧИСЛА ПЕРЕНОСА
- ЧИСЛО ФАРАДЕЯ
- ЩЕЛОЧНЫЕ АККУМУЛЯТОРЫ
- ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ
- ЭЛЕКТРИЧЕСКИЕ ЕДИНИЦЫ ИЗМЕРЕНИЯ
- ЭЛЕКТРОВЕСОВОЙ АНАЛИЗ
- ЭЛЕКТРОД
- ЭЛЕКТРОДВИЖУЩАЯ СИЛА (Э.Д.С.)
- ЭЛЕКТРОДИАЛИЗ
- ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ
- ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- ЭЛЕКТРОЛИЗ ВОДЫ
- ЭЛЕКТРОЛИЗЕР
- ЭЛЕКТРОЛИЗ РАСТВОРА ПОВАРЕННОЙ СОЛИ
- ЭЛЕКТРОЛИТИЧЕСКАЯ ОЧИСТКА (РАФИНИРОВАНИЕ)
- ЭЛЕКТРОЛИТИЧЕСКОЕ ВОССТАНОВЛЕНИЕ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
- ЭЛЕКТРОЛИТИЧЕСКОЕ ОКИСЛЕНИЕ ОРГАНИЧЕСКИХ СОЕДИНЕНИЙ
- ЭЛЕКТРОЛИТИЧЕСКОЕ ПОЛИРОВАНИЕ
- ЭЛЕКТРОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- ЭЛЕКТРООСАЖДЕНИЕ МЕТАЛЛОВ
- ЭЛЕКТРООСАЖДЕНИЕ СПЛАВОВ
- ЭЛЕКТРООСМОС
- ЭЛЕКТРОПРОВОДНОСТЬ
- ЭЛЕКТРОПРОВОДНОСТЬ ВОДНЫХ РАСТВОРОВ
- ЭЛЕКТРОПРОВОДНОСТЬ НА ВЫСОКИХ ЧАСТОТАХ
- ЭЛЕКТРОПРОВОДНОСТЬ НЕВОДНЫХ РАСТВОРОВ
- ЭЛЕКТРОПРОВОДНОСТЬ ПРИ БЕСКОНЕЧНОМ РАЗБАВЛЕНИИ
- ЭЛЕКТРОПРОВОДНОСТЬ ПРИ ВЫСОКИХ НАПРЯЖЕННОСТЯХ ПОЛЯ
- ЭЛЕКТРОПРОВОДНОСТЬ РАСПЛАВОВ СОЛЕЙ
- ЭЛЕКТРОФОРЕЗ
- ЭЛЕКТРОХИМИЧЕСКАЯ РАЗМЕРНАЯ ОБРАБОТКА МЕТАЛЛОВ
- ЭЛЕКТРОХИМИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ИНФОРМАЦИИ
- ЭЛЕКТРОХИМИЧЕСКИЙ ЭКВИВАЛЕНТ
- ЭЛЕМЕНТ ВЕСТОНА
- ЭЛЕМЕНТ ДАНИЭЛЯ
- ЭЛЕМЕНТ КЛАРКА
- ЭЛЕМЕНТЫ С МАГНИЕВЫМИ АНОДАМИ
- ЭФФЕКТ ВИНА
- ЭФФЕКТ ДОРНА
- ЭФФЕКТ ФАЛЬКЕНГАГЕНА
- СПИСОК ЛИТЕРАТУРЫ