| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.10. Обратимая реакция смешанного (первого и второго) порядка
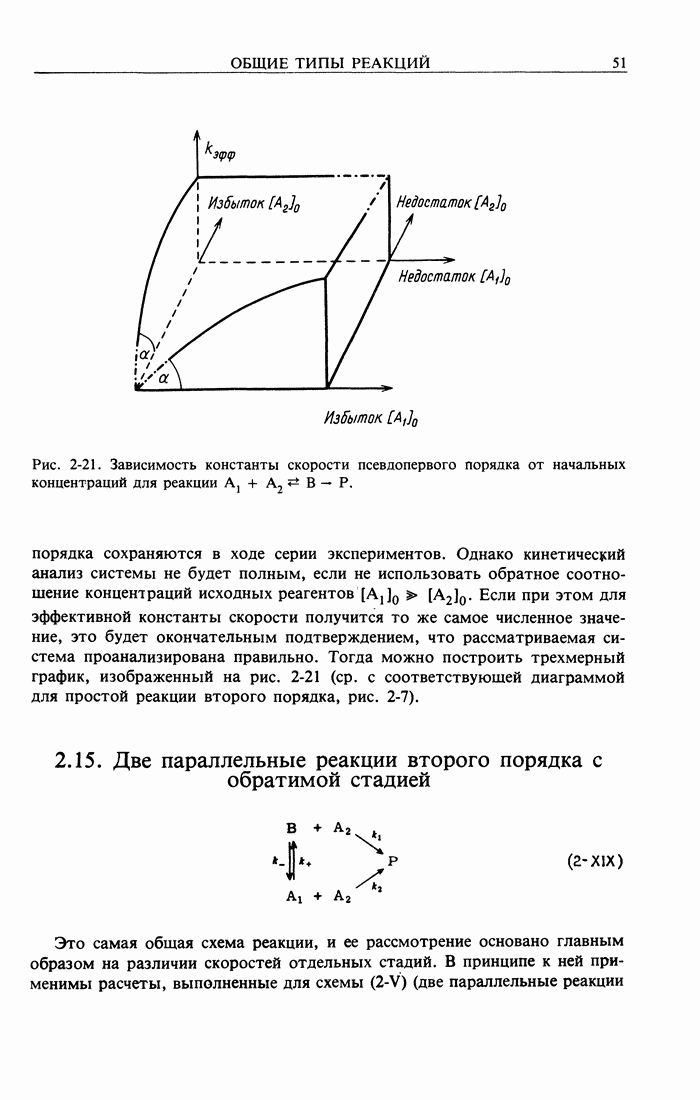
К этим реакциям относятся два случая:  Для первого случая достаточно дать интегральное уравнение скорости. Второй случай очень распространен и известен как обратимое образование комплекса, поэтому мы рассмотрим его подробнее. Оба типа реакций можно считать одинаковой системой, реагирующей в противоположных направлениях.
Для первого случая достаточно дать интегральное уравнение скорости. Второй случай очень распространен и известен как обратимое образование комплекса, поэтому мы рассмотрим его подробнее. Оба типа реакций можно считать одинаковой системой, реагирующей в противоположных направлениях.

Скорость образования продукта выражается уравнением

Учитывая, что при равновесии

уравнение (2-89) можно проинтегрировать и получить выражение, аналогичное (2-80):

Для этой реакции

или

Учитывая, что при равновесии

уравнение (2-93) можно проинтегрировать и получить

Система упрощается, если одно из исходных веществ взять в большом избытке. Так, при 

где  Последнее уравнение соответствует дифференциальному уравнению (2-64) для обратимой реакции первого порядка. Поэтому здесь можно применить описанные ранее методы. Например, график зависимости
Последнее уравнение соответствует дифференциальному уравнению (2-64) для обратимой реакции первого порядка. Поэтому здесь можно применить описанные ранее методы. Например, график зависимости  от времени дает сумму
от времени дает сумму  как эффективную константу скорости
как эффективную константу скорости  Во второй серии экспериментов измеряют концентрацию избыточного реагента, поддерживая постоянной концентрацию
Во второй серии экспериментов измеряют концентрацию избыточного реагента, поддерживая постоянной концентрацию  Это позволяет построить график зависимости
Это позволяет построить график зависимости  от
от  представляющий собой прямую с угловым коэффициентом к
представляющий собой прямую с угловым коэффициентом к  которая отсекает на ординатеотрезок, равный
которая отсекает на ординатеотрезок, равный  Тот факт, что прямая не проходит через начало координат, свидетельствует о наличии обратной реакции. В случае простой кинетики второго порядка или в том случае, когда обратной реакцией можно пренебречь, прямая проходит через начало координат. Уравнение
Тот факт, что прямая не проходит через начало координат, свидетельствует о наличии обратной реакции. В случае простой кинетики второго порядка или в том случае, когда обратной реакцией можно пренебречь, прямая проходит через начало координат. Уравнение

удобно использовать для расчета К с помощью графика зависимости  от
от  График представляет собой прямую, проходящую через начало координат, с угловым коэффициентом, равным К. Дальнейшим подтверждением обратимости реакции является то, что
График представляет собой прямую, проходящую через начало координат, с угловым коэффициентом, равным К. Дальнейшим подтверждением обратимости реакции является то, что  возрастает при увеличении
возрастает при увеличении  или, иными словами, что
или, иными словами, что  не достигает величины
не достигает величины 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
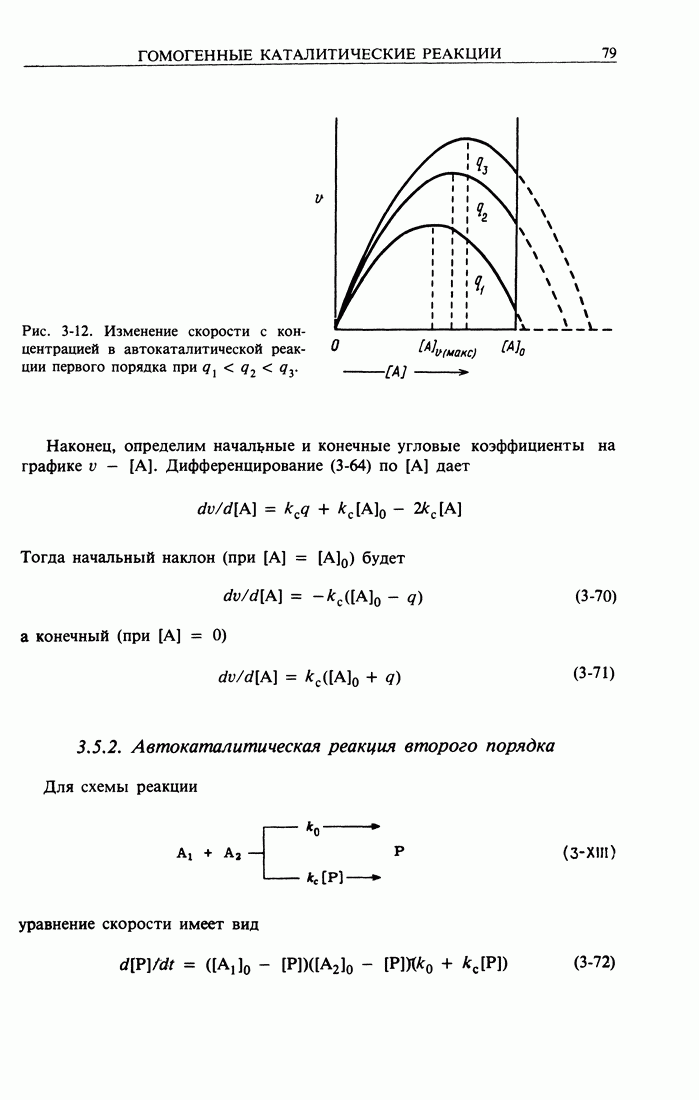
- 3.5. Автокаталитические реакции
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
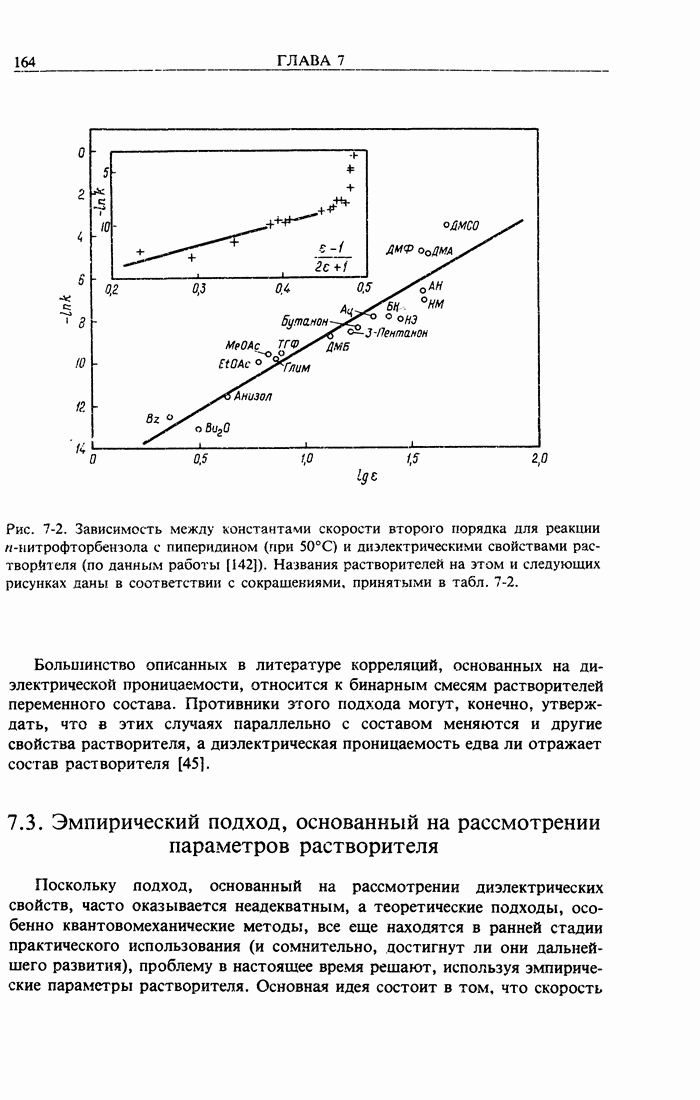
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
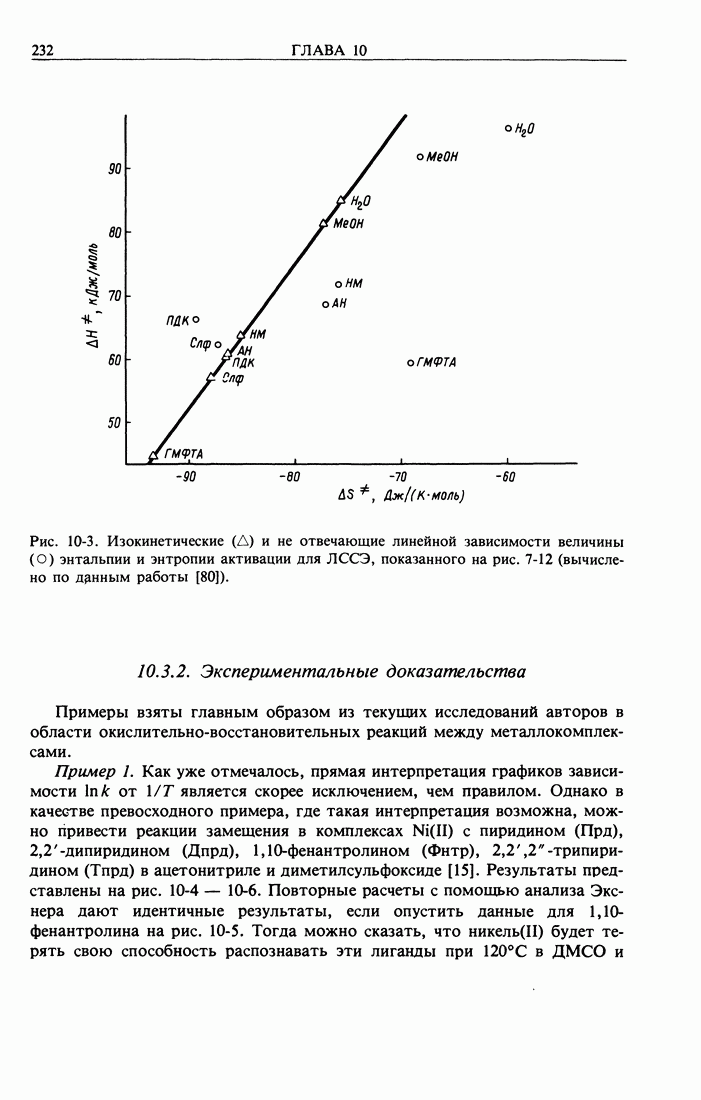
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений