| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.5.2. Из второй серии опытов
В этой серии эксперименты повторяют при различных концентрациях одной из переменных, которая в первой серии рассматривалась как параметр, а концентрацию реагента, взятого в недостатке, поддерживают постоянной. Поэтому число серий опытов, которые нужно провести, соответствует числу параметров концентрации. Этими параметрами могут быть реагенты, взятые в избытке, и/или катализатор. Цель опытов — найти вид функции  в избытке
в избытке  и затем построить полную математическую модель. Методика будет рассмотрена на примере опытов с избыточным реагентом
и затем построить полную математическую модель. Методика будет рассмотрена на примере опытов с избыточным реагентом  По существу, уравнения скорости можно разделить на два типа в зависимости от того, можно или нельзя выделить
По существу, уравнения скорости можно разделить на два типа в зависимости от того, можно или нельзя выделить  или в общем виде
или в общем виде  из
из  Основания для такого разделения получают с помощью метода трансформации (см. разд. 4.3.3).
Основания для такого разделения получают с помощью метода трансформации (см. разд. 4.3.3).
4.5.2.1. Возможность выделения  из
из  существует. В этом случае скорость можно выразить как произведение двух функций:
существует. В этом случае скорость можно выразить как произведение двух функций:

Другими словами,  является множителем функции концентрации реагента, находящегося в недостатке. В простейшем случае реакция обнаруживает какой-либо простой порядок по А (как показано в первой серии опытов). Тогда коэффициент в уравнении
является множителем функции концентрации реагента, находящегося в недостатке. В простейшем случае реакция обнаруживает какой-либо простой порядок по А (как показано в первой серии опытов). Тогда коэффициент в уравнении  называют эффективной константой скорости
называют эффективной константой скорости  Рассмотрим, например, следующее выражение скорости: —
Рассмотрим, например, следующее выражение скорости: —  откуда
откуда

Величины  лучше всего получить методом интегрирования; затем строят их графические зависимости от
лучше всего получить методом интегрирования; затем строят их графические зависимости от  Эти графики служат основой для определения
Эти графики служат основой для определения  . С другой стороны, если реакция не проявляет простого порядка по А, вместо к в качестве критерия используется коэффициент трансформации
. С другой стороны, если реакция не проявляет простого порядка по А, вместо к в качестве критерия используется коэффициент трансформации 

И наконец, можно использовать начальные скорости и построить графические зависимости  от
от  от
от  которые могут дать вид функции
которые могут дать вид функции 
Рис. 4-20 иллюстрирует различные формы графиков, полученные при использовании кэфф. Следует отметить, что пересечение кривых с осями

Рис. 4-20. Изменение константы скорости псевдопервого порядка при изменении концентрации избыточного реагента.
координат только экстраполируется, как показано стрелками, поскольку  должно присутствовать в большом избытке по сравнению с
должно присутствовать в большом избытке по сравнению с  в ходе всей серии опытов; поэтому малые значения
в ходе всей серии опытов; поэтому малые значения  недоступны. Если кривые не проходят через начало координат, это указывает на то, что
недоступны. Если кривые не проходят через начало координат, это указывает на то, что  состоит по крайней мере из двух членов, один из которых не зависит от
состоит по крайней мере из двух членов, один из которых не зависит от 

Следовательно, нетрудно показать, что реакция должна также происходить и в отсутствие  Тогда соответствующая константа скорости должна совпадать с
Тогда соответствующая константа скорости должна совпадать с  из уравнения (4-75). Линейные зависимости на рис. 4-20, а легко интерпретируются:
из уравнения (4-75). Линейные зависимости на рис. 4-20, а легко интерпретируются:

Нелинейные зависимости указывают на то, что формальный порядок по  должен быть меньше единицы (кривая 5) или больше единицы (кривая 4). Наконец, кривые
должен быть меньше единицы (кривая 5) или больше единицы (кривая 4). Наконец, кривые  и 7 отличаются от кривых 4 и 5 только на константу [ср. с уравнением (4-75)]. Ход нелинейных графиков
и 7 отличаются от кривых 4 и 5 только на константу [ср. с уравнением (4-75)]. Ход нелинейных графиков  полностью соответствует ходу нелинейных графиков
полностью соответствует ходу нелинейных графиков  из подразд. 4.5.1.4. Кривую 4 можно привести к линейному виду, построив графическую зависимость
из подразд. 4.5.1.4. Кривую 4 можно привести к линейному виду, построив графическую зависимость  от
от 

Можно также применить полиномиальное приближение. Таким образом, если  линейно меняется с
линейно меняется с  то
то

Что касается кривой 5, то графики зависимостей  от
от  или, наоборот,
или, наоборот,  от
от  могут оказаться линейными. В этом случае уравнение для кэимеет вид
могут оказаться линейными. В этом случае уравнение для кэимеет вид

4.5.2.2. Выделение  из
из  невыполнимо. Если кривые из данной серии опытов нельзя совместить друг с другом, то влияние
невыполнимо. Если кривые из данной серии опытов нельзя совместить друг с другом, то влияние  на разные члены
на разные члены  неодинаково, и, следовательно,
неодинаково, и, следовательно,  нельзя выделить из
нельзя выделить из  В таком случае применяют общий дифференциальный метод (ср. с подразд. 4.5.1.4, случай 2). Следует ожидать, что изменение
В таком случае применяют общий дифференциальный метод (ср. с подразд. 4.5.1.4, случай 2). Следует ожидать, что изменение  сказывается только на численных константах, входящих
сказывается только на численных константах, входящих  а не на виде функции. Поэтому влияние
а не на виде функции. Поэтому влияние  на
на  определяют с помощью отдельных графиков зависимости
определяют с помощью отдельных графиков зависимости  от
от  Рассмотрим вымышленный пример, представленный графически на рис. 4-21.
Рассмотрим вымышленный пример, представленный графически на рис. 4-21.

Рис. 4-21. Пример для случая, когда  нельзя выделить из
нельзя выделить из 
Линейная зависимость  от
от  рис. 4-21,а описывается уравнением
рис. 4-21,а описывается уравнением

Повышение избытка  не нарушает линейной зависимости, но приводит к увеличению как тангенса угла наклона
не нарушает линейной зависимости, но приводит к увеличению как тангенса угла наклона  так и отрезка, отсекаемого прямой на оси ординат
так и отрезка, отсекаемого прямой на оси ординат  Нелинейные зависимости
Нелинейные зависимости  и
и  от
от  приводят к линейному виду, если по оси абсцисс откладывать величины, обратные концентрации
приводят к линейному виду, если по оси абсцисс откладывать величины, обратные концентрации  Двум последним графикам на рис. 4-21 соответствуют уравнения
Двум последним графикам на рис. 4-21 соответствуют уравнения

Теперь уравнение (4-82), выведенное из первой серии опытов, принимает вид

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
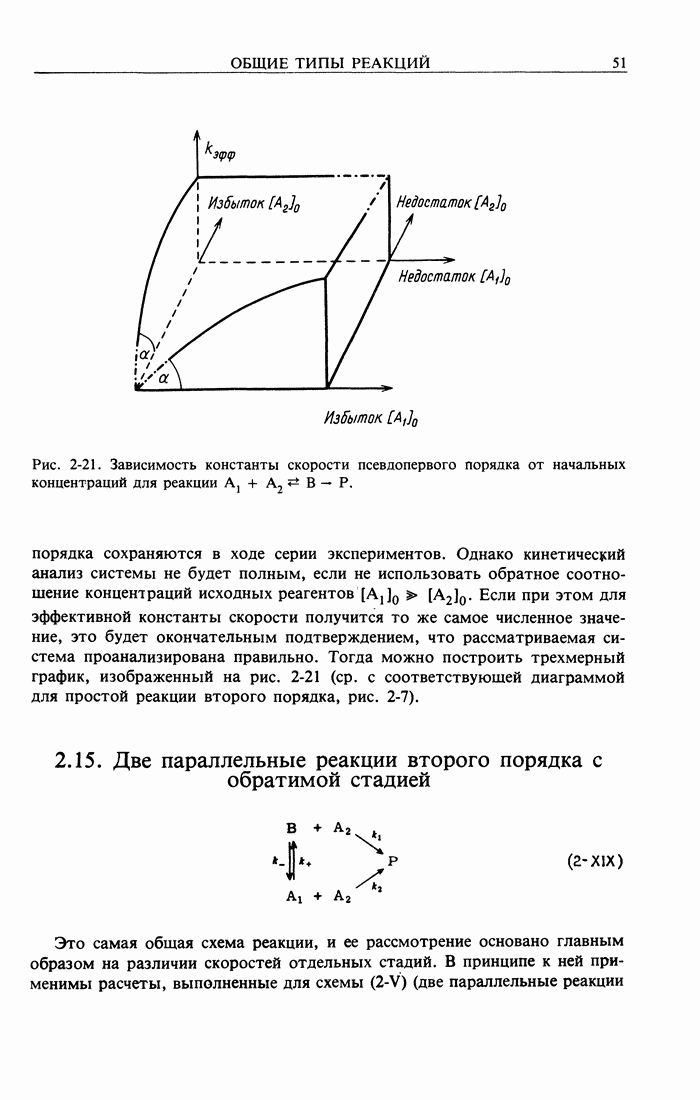
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
- 3.5. Автокаталитические реакции
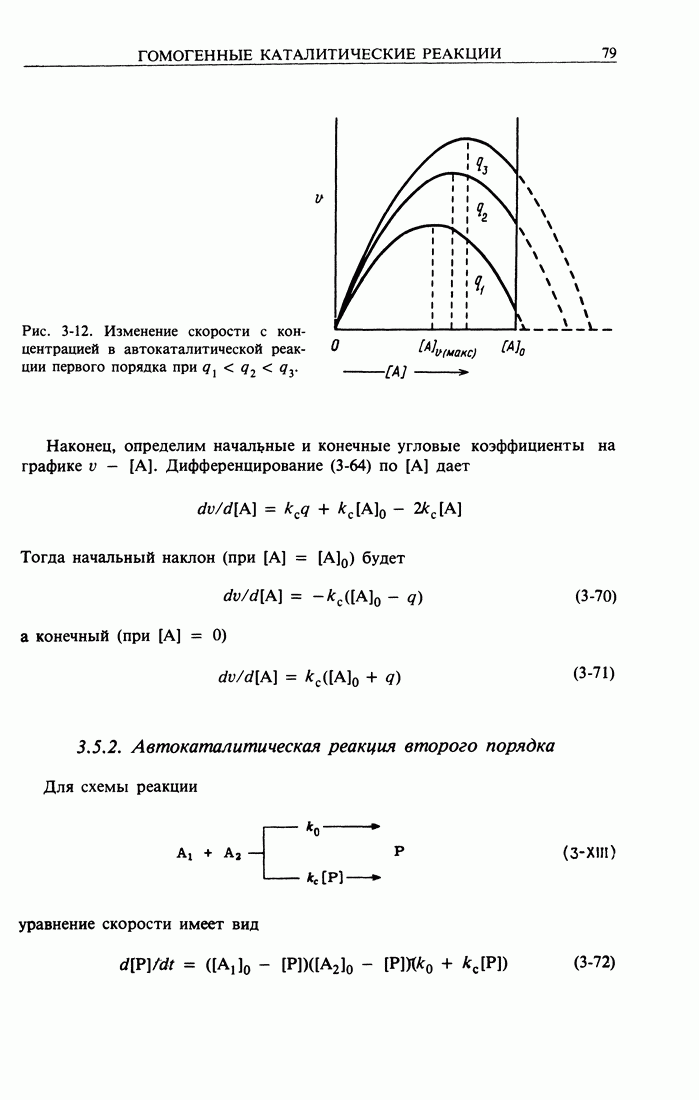
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
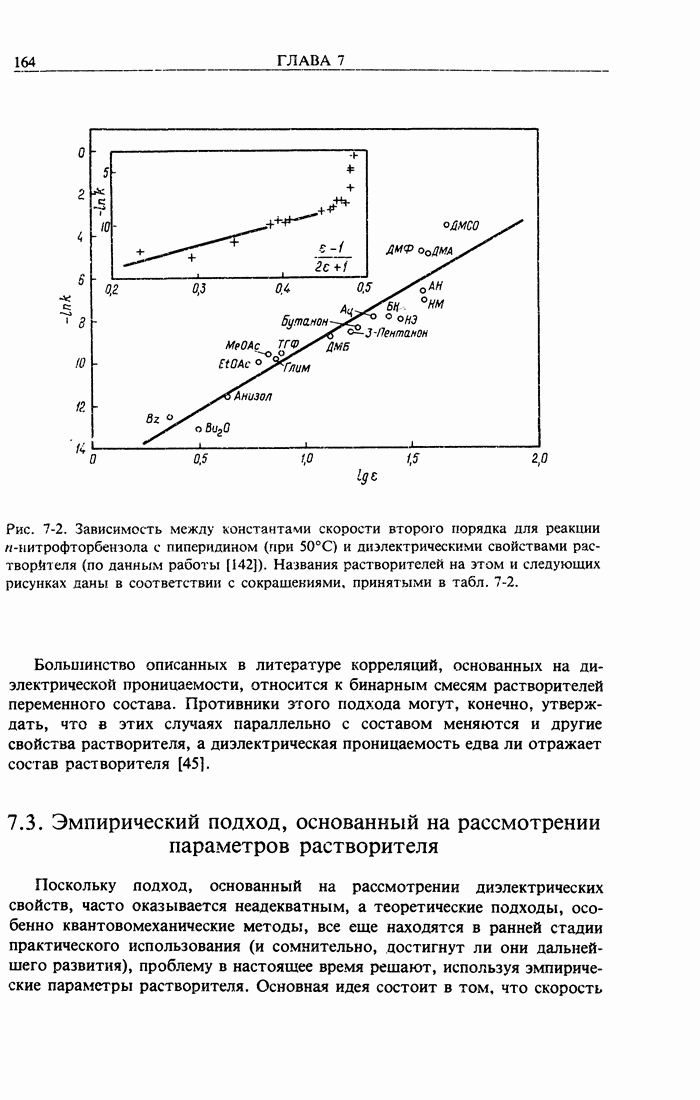
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
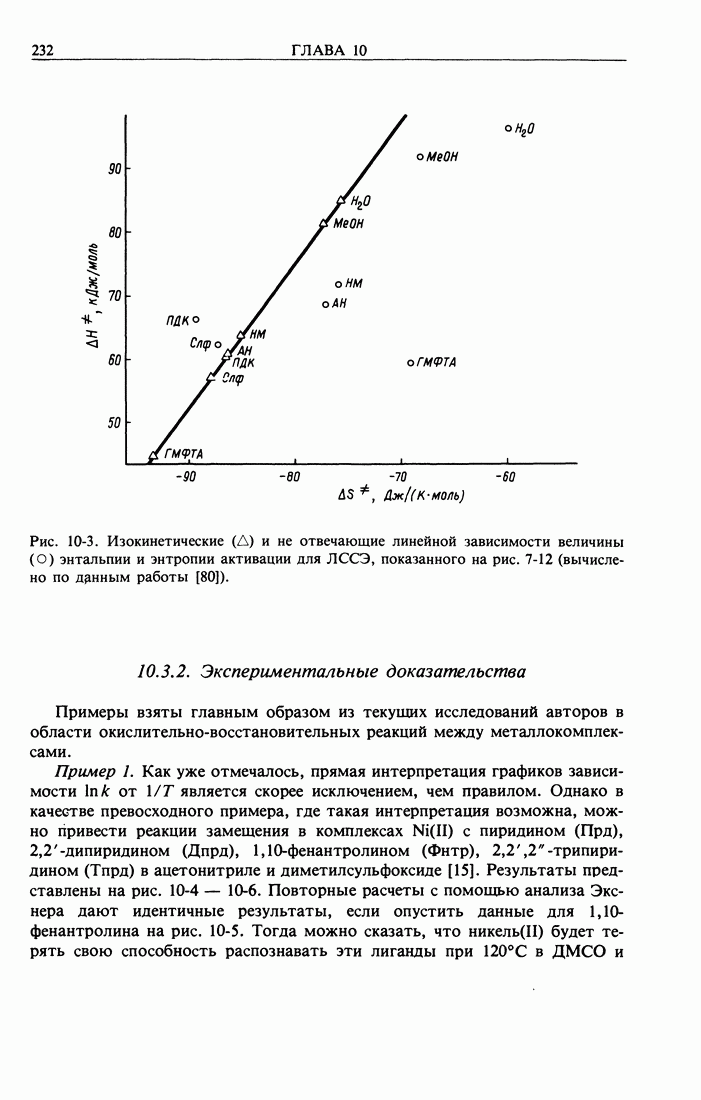
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений