| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. Выбор условий эксперимента
Основная цель анализа кривых  состоит в том, чтобы найти математическое уравнение, которое описывает формы кривых, т.е. уравнение скорости. Основой для вывода такого уравнения служит сравнение кривых
состоит в том, чтобы найти математическое уравнение, которое описывает формы кривых, т.е. уравнение скорости. Основой для вывода такого уравнения служит сравнение кривых  полученных из серии экспериментов при разных начальных концентрациях реагентов, так называемых экспериментальных серий. Число их зависит от числа компонентов реакции. На скорость реакции могут влиять исходные реагенты, продукты реакции (включая интермедиаты), катализатор, растворитель и т.д. Если в реакции участвует несколько реагентов, то условия подбирают таким образом, чтобы все они, кроме одного, находились в большом избытке (ср. с разд. 4.4). Во время реакции концентрации этих избыточных реагентов остаются практически постоянными. Таким образом, уменьшение концентрации реагента, присутствующего в недостатке, изучается как бы изолированно. Этот метод известен как метод изоляции; он преследует цель выделить элементарный процесс или какую-то простую реакцию из всего процесса в целом. За таким взятым в недостатке реагентом или за продуктом реакции удобно следить кинетически. В тех случаях, когда в реакции отсутствует интермедиат или присутствующий интермедиат очень реакционноспособен, уменьшение концентрации реагента во времени соответствует увеличению концентрации продукта (при условии равенства стехиометрических коэффициентов). В любом случае очень полезно, хотя бы в нескольких сериях измерений, проверить, соответствуют ли кинетические кривые расходования реагента кинетическим кривым накопления продукта. Однако следует отметить, что
полученных из серии экспериментов при разных начальных концентрациях реагентов, так называемых экспериментальных серий. Число их зависит от числа компонентов реакции. На скорость реакции могут влиять исходные реагенты, продукты реакции (включая интермедиаты), катализатор, растворитель и т.д. Если в реакции участвует несколько реагентов, то условия подбирают таким образом, чтобы все они, кроме одного, находились в большом избытке (ср. с разд. 4.4). Во время реакции концентрации этих избыточных реагентов остаются практически постоянными. Таким образом, уменьшение концентрации реагента, присутствующего в недостатке, изучается как бы изолированно. Этот метод известен как метод изоляции; он преследует цель выделить элементарный процесс или какую-то простую реакцию из всего процесса в целом. За таким взятым в недостатке реагентом или за продуктом реакции удобно следить кинетически. В тех случаях, когда в реакции отсутствует интермедиат или присутствующий интермедиат очень реакционноспособен, уменьшение концентрации реагента во времени соответствует увеличению концентрации продукта (при условии равенства стехиометрических коэффициентов). В любом случае очень полезно, хотя бы в нескольких сериях измерений, проверить, соответствуют ли кинетические кривые расходования реагента кинетическим кривым накопления продукта. Однако следует отметить, что
согласованность между  сама по себе не является доказательством отсутствия интермедиата. Так, в случае, когда свойства интермедиата лишь незначительно отличаются от свойств исходного реагента, на практике оба вещества измеряют вместе. Получающаяся зависимость от времени, естественно, будет соответствовать зависимости для образования продукта. Таким образом, несогласованность между
сама по себе не является доказательством отсутствия интермедиата. Так, в случае, когда свойства интермедиата лишь незначительно отличаются от свойств исходного реагента, на практике оба вещества измеряют вместе. Получающаяся зависимость от времени, естественно, будет соответствовать зависимости для образования продукта. Таким образом, несогласованность между  ясно указывает на наличие интермедиата. В этом случае для получения полной кинетической информации изменения во времени как для реагента, так и для продукта должны быть измерены в отдельных экспериментальных сериях. В целях экономии времени и реактивов в эксперимент следует включать ровно столько компонентов, сколько необходимо для однозначной характеристики системы.
ясно указывает на наличие интермедиата. В этом случае для получения полной кинетической информации изменения во времени как для реагента, так и для продукта должны быть измерены в отдельных экспериментальных сериях. В целях экономии времени и реактивов в эксперимент следует включать ровно столько компонентов, сколько необходимо для однозначной характеристики системы.
В первой серии экспериментов варьируют только реагент, находящийся в недостатке, скажем  В последующих разделах для указания хода реакции будет употребляться
В последующих разделах для указания хода реакции будет употребляться  В этих условиях
В этих условиях

где  переменная, а остальные величины — постоянные или, говоря математическим языком, рассматриваются как параметры (С обозначает катализатор). Влияние температуры
переменная, а остальные величины — постоянные или, говоря математическим языком, рассматриваются как параметры (С обозначает катализатор). Влияние температуры  и растворителя на скорость реакции будет рассмотрено позже в отдельных главах. Здесь мы обсудим влияние концентрации на скорость реакции. С помощью упомянутого выше метода часто удается искусственно отделить влияние изменения концентрации
и растворителя на скорость реакции будет рассмотрено позже в отдельных главах. Здесь мы обсудим влияние концентрации на скорость реакции. С помощью упомянутого выше метода часто удается искусственно отделить влияние изменения концентрации  на скорость реакции от влияния других компонентов и таким образом показать вид функции
на скорость реакции от влияния других компонентов и таким образом показать вид функции 

В последующих сериях эксперимент повторяют при различных концентрациях одного из избыточных реагентов, сохраняя постоянными остальные параметры и концентрацию реагента, взятого в недостатке. При этом получают

Наконец, найденное уравнение должно быть проверено при обратном соотношении концентраций, т.е. реагент, который был в недостатке, берется теперь в избытке и наоборот. Таким образом, для весьма распространенного случая, включающего два исходных вещества, как правило, требуется провести не менее четырех серий экспериментов. Часто предполагают, что уравнение скорости не зависит от того, какой из реагентов берется в избытке, но это не всегда так.
Следует, однако, особо отметить, что в условиях первой серии экспериментов меняется не только концентрация А (для обобщения мы опускаем подстрочный индекс), но также и концентрации продуктов и возможных интермедиатов. И наконец, изменяется время. Эти обстоятельства могут привести к следующим осложнениям.
Случай а. Продукт ускоряет или тормозит реакцию. В отсутствие интермедиата справедливо соотношение  Таким образом, искомая функция включает еще переменную
Таким образом, искомая функция включает еще переменную  которая в действительности постоянна в пределах одного измерения, так как пропорциональна
которая в действительности постоянна в пределах одного измерения, так как пропорциональна  Поэтому
Поэтому

Случай  Интермедиат влияет на скорость. Поскольку его зависимость от времени отличается от зависимости для исходного реагента, функция включает еще одну переменную. К этому случаю относится, например, каталитическая, реакция, в ходе которой меняется активность катализатора. Случай
Интермедиат влияет на скорость. Поскольку его зависимость от времени отличается от зависимости для исходного реагента, функция включает еще одну переменную. К этому случаю относится, например, каталитическая, реакция, в ходе которой меняется активность катализатора. Случай  обычно описывается уравнением
обычно описывается уравнением

где  некоторая частица, влияющая на скорость, зависимость концентрации которой от времени отличается от зависимости для
некоторая частица, влияющая на скорость, зависимость концентрации которой от времени отличается от зависимости для  что показано подстрочным индексом
что показано подстрочным индексом 
Случай в. Довольно распространен случай, когда продукт реакции меняет активность катализатора. Тогда функция содержит две переменные и параметр  , таким образом, оказывается комбинацией функций для случаев
, таким образом, оказывается комбинацией функций для случаев 

Опишем теперь процедуру, которую используют для распознавания различных видов функций. Напомним, что концентрации избыточного реагента  всегда намного больше любой начальной концентрации
всегда намного больше любой начальной концентрации  реагента, взятого в недостатке.
реагента, взятого в недостатке.
Рассмотрим графики с - относящиеся к двум различным концентрациям А (рис. 4-1,а). Отличие точек 1 и 2 состоит в том, что реагирующая система в точке 2 уже содержит продукты реакций и соответствует промежутку времени  прошедшему с момента
прошедшему с момента  Если кривые совмещаются при сдвиге, указанном стрелками, то это свидетельствует о том, что на скорость не влияют ни продукты, ни какие-либо другие вещества, концентрация которых меняется во времени. Другими словами, скорость является функцией только
Если кривые совмещаются при сдвиге, указанном стрелками, то это свидетельствует о том, что на скорость не влияют ни продукты, ни какие-либо другие вещества, концентрация которых меняется во времени. Другими словами, скорость является функцией только  т.е.
т.е.  Это означает, что серия экспериментов даст одну кинетическую кривую.
Это означает, что серия экспериментов даст одну кинетическую кривую.

Рис. 4-1. Нахождение уравнений скорости вида 
Если же кривые нельзя совместить, то мы имеем случай, показанный на рис. 4-1,6: готовят реакционную смесь с более низкой концентрацией А, чем  затем к ней добавляют свежую порцию этого находящегося в недостатке реагента
затем к ней добавляют свежую порцию этого находящегося в недостатке реагента  так чтобы
так чтобы  Кривую, полученную для последующего уменьшения
Кривую, полученную для последующего уменьшения  снова сравнивают с кривой, относящейся к
снова сравнивают с кривой, относящейся к  Экспериментальные условия, представленные точками 1 и 2 на рис. 4-1,б, различаются только периодом времени
Экспериментальные условия, представленные точками 1 и 2 на рис. 4-1,б, различаются только периодом времени  в течение которого готовилась смесь, тогда как концентрация продуктов одинакова. Если кривые совмещаются при сдвиге, указанном стрелками, то скорость определяется как функция
в течение которого готовилась смесь, тогда как концентрация продуктов одинакова. Если кривые совмещаются при сдвиге, указанном стрелками, то скорость определяется как функция  т.е.
т.е.  В противном случае, если кривые не совмещаются, скорость зависит от частицы
В противном случае, если кривые не совмещаются, скорость зависит от частицы  концентрация которой меняется в ходе реакции иначе, чем концентрация реагента, взятого в недостатке, и тогда может быть справедлива либо функция
концентрация которой меняется в ходе реакции иначе, чем концентрация реагента, взятого в недостатке, и тогда может быть справедлива либо функция  либо
либо 
Следующая стадия исследования заключается в том, чтобы найти функциональную зависимость

С этой целью условия эксперимента подбирают таким образом, чтобы единственной переменной был промежуток времени от начала реакции до момента добавления дополнительной порции вещества А, а все остальные величины — концентрации других реагентов, продуктов, катализатора — оставались бы постоянными. Это достигается с помощью процедуры, показанной на верхней диаграмме рис. 4-2. Проводят серии экспериментов, фиксируя в них определенную начальную концентрацию  каждую новую порцию
каждую новую порцию  добавляют в разные промежутки времени
добавляют в разные промежутки времени  от начала первой реакции, проведенной при определенной концентрации
от начала первой реакции, проведенной при определенной концентрации

Рис. 4-2. Нахождение вида функции  а — интермедиат влияет на скорость реакции; б - активность катализатора меняется во времени: 1 — необратимое ингибирование (ср. с разд. 3.4.2); 2,3 — образуется новое устойчивое каталитическое вещество, активность которого отличается от активности исходного катализатора (пунктирная линия).
а — интермедиат влияет на скорость реакции; б - активность катализатора меняется во времени: 1 — необратимое ингибирование (ср. с разд. 3.4.2); 2,3 — образуется новое устойчивое каталитическое вещество, активность которого отличается от активности исходного катализатора (пунктирная линия).
реагента  и завершают реакцию. Соответствующие начальные скорости
и завершают реакцию. Соответствующие начальные скорости  выражают численно и строят графики их зависимости от
выражают численно и строят графики их зависимости от  (вместо
(вместо  можно также использовать относительные величины
можно также использовать относительные величины  где
где  начальная скорость первой реакции). Если изменение
начальная скорость первой реакции). Если изменение  во времени соизмеримо с изменением реагента, то не следует ожидать окончания реакции, а нужно вводить в систему новые порции
во времени соизмеримо с изменением реагента, то не следует ожидать окончания реакции, а нужно вводить в систему новые порции  при разных значениях времени по ходу реакции. Добавленное количество
при разных значениях времени по ходу реакции. Добавленное количество  должно компенсировать расходование первоначально введенного
должно компенсировать расходование первоначально введенного  так, чтобы соблюдалось равенство
так, чтобы соблюдалось равенство  Однако, поскольку
Однако, поскольку  часто оказывается менее реакционноспособным, чем исходный реагент, рис. 4-2 правильно отражает рассматриваемую процедуру.
часто оказывается менее реакционноспособным, чем исходный реагент, рис. 4-2 правильно отражает рассматриваемую процедуру.
Полученные таким путем графики  представляют собой новое поколение кривых
представляют собой новое поколение кривых  при условии, что
при условии, что  пропорционально
пропорционально  (в противном случае следует использовать калибровочную кривую). Затем можно найти вид функции
(в противном случае следует использовать калибровочную кривую). Затем можно найти вид функции  обрабатывая эти кривые аналогично «нормальным» кинетическим кривым по методике, которая будет обсуждаться в следующих разделах. Две ситуации схематически представлены на рис. 4-2,а и б. Если интермедиат (а затем и
обрабатывая эти кривые аналогично «нормальным» кинетическим кривым по методике, которая будет обсуждаться в следующих разделах. Две ситуации схематически представлены на рис. 4-2,а и б. Если интермедиат (а затем и  влияет на скорость, то начальные скорости проходят через максимум или минимум в зависимости от
влияет на скорость, то начальные скорости проходят через максимум или минимум в зависимости от
того, какой эффект проявляется — ускоряющий или тормозящий (рис. 4-2,а), при условии, конечно, что исследуемый интервал времени соизмерим с периодом полупревращения интермедиата. Это, естественно, служит лишь косвенным доказательством влияния интермедиата. Можно получить и прямое доказательство, добавляя сначала определенные порции выделенного интермедиата и оценивая соответствующие начальные скорости. Таким образом получают калибровочную кривую.
С другой стороны, рис.  показывает возможные усложнения в реакциях, катализируемых комплексами металлов. Влияние продуктов на активность катализатора становится явным, когда катализатор устойчив как в чистом растворителе, так и в растворах, содержащих тот или иной реагент (надо учитывать, что старые растворы вряд ли дадут идентичные результаты). В этом случае удобно вводить в систему разные порции продукта при постоянстве остальных параметров и определять начальные скорости в зависимости от
показывает возможные усложнения в реакциях, катализируемых комплексами металлов. Влияние продуктов на активность катализатора становится явным, когда катализатор устойчив как в чистом растворителе, так и в растворах, содержащих тот или иной реагент (надо учитывать, что старые растворы вряд ли дадут идентичные результаты). В этом случае удобно вводить в систему разные порции продукта при постоянстве остальных параметров и определять начальные скорости в зависимости от 
Последнее (хотя и тривиальное) замечание касается того факта, что приведенный выше метод совмещения применим только тогда, когда реагент присутствует в очень большом избытке. Рассмотрим для примера простую реакцию второго порядка, включающую два реагента. При  (условия псевдопервого порядка не выполняются) кривые
(условия псевдопервого порядка не выполняются) кривые  полученные для разных начальных концентраций
полученные для разных начальных концентраций  не совмещаются при простом сдвиге, как на рис. 4-1,а. Причина заключается в том, что точки 1 и 2 будут различаться по концентрации
не совмещаются при простом сдвиге, как на рис. 4-1,а. Причина заключается в том, что точки 1 и 2 будут различаться по концентрации  которая также влияет на скорость [ср. с уравнением (2-20)].
которая также влияет на скорость [ср. с уравнением (2-20)].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
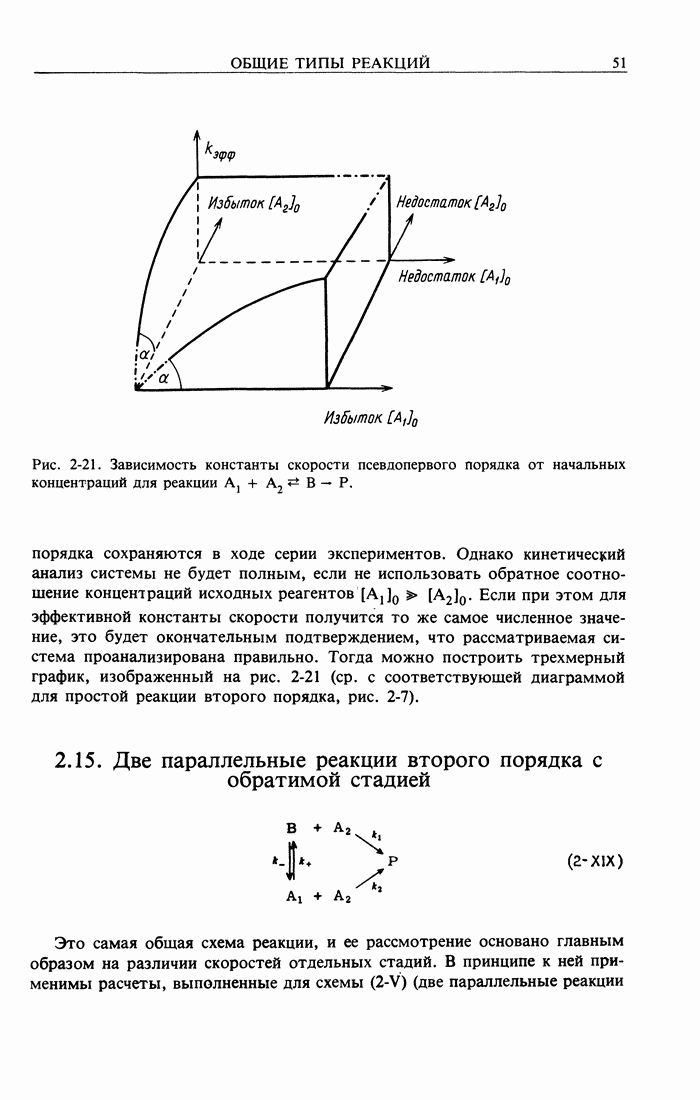
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
- 3.5. Автокаталитические реакции
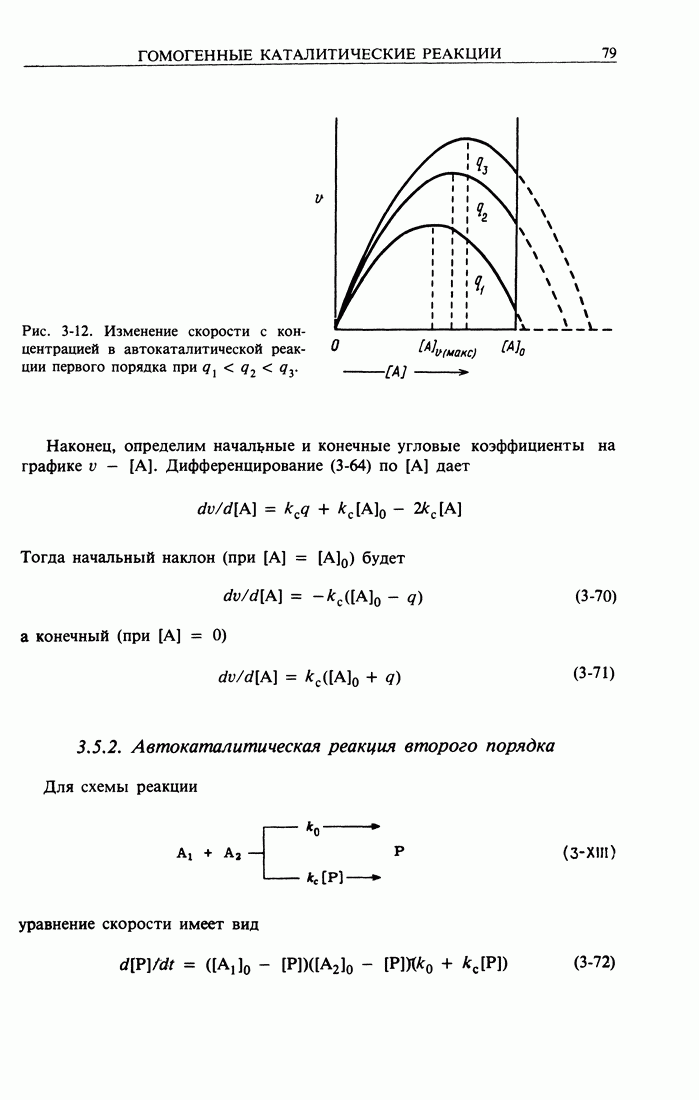
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
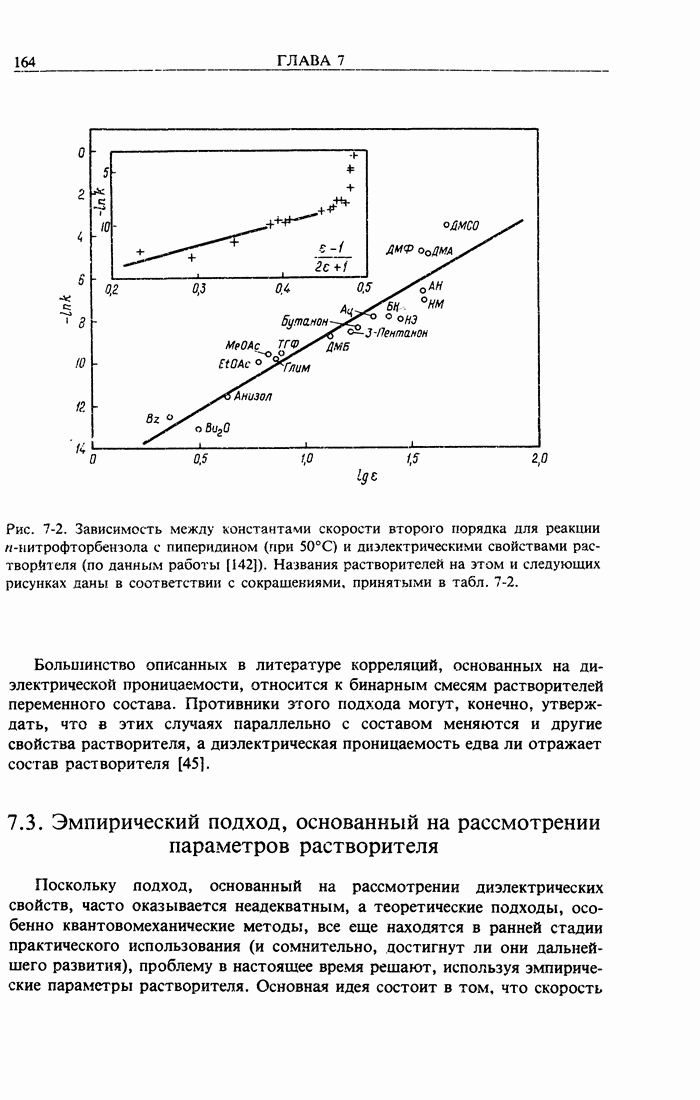
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
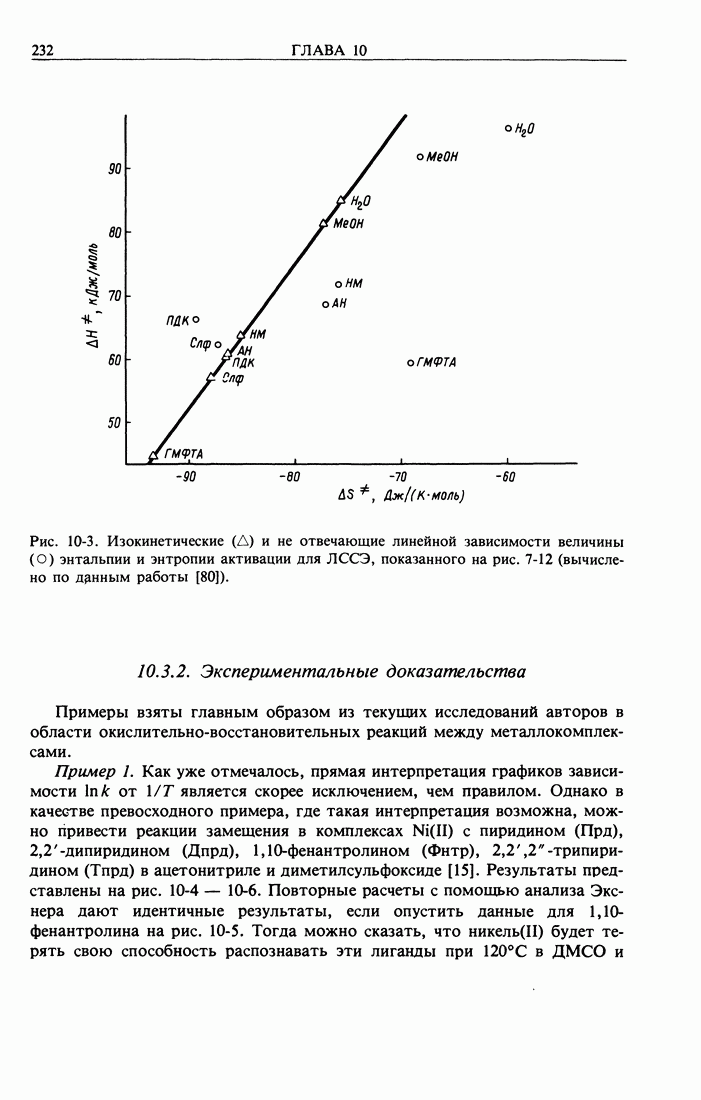
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений