| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
2.1. Простая реакция первого порядка

Скорость пропорциональна концентрации А:

Интегрирование

дает

или

где  начальная концентрация А. Уравнение
начальная концентрация А. Уравнение  показывает, что в реакции первого порядка расходование реагента во времени происходит экспоненциально. Поэтому математические свойства кинетики первого порядка основаны на свойствах экспоненциальной функции. Следующие моменты представляют практический интерес.
показывает, что в реакции первого порядка расходование реагента во времени происходит экспоненциально. Поэтому математические свойства кинетики первого порядка основаны на свойствах экспоненциальной функции. Следующие моменты представляют практический интерес.
Но уравнению  зависимость
зависимость  от
от  является линейной с наклоном, равным - к (знак «минус» указывает на уменьшение
является линейной с наклоном, равным - к (знак «минус» указывает на уменьшение  во времени). Это означает, что для разных
во времени). Это означает, что для разных  мы получим параллельные прямые в полулогарифмических координатах (рис. 2-1).
мы получим параллельные прямые в полулогарифмических координатах (рис. 2-1).
Единицей измерения константы скорости первого порядка является (время), обычно выражаемое в  Вычитание двух уравнений
Вычитание двух уравнений  для разных наборов
для разных наборов  дает
дает


Рис. 2-1. График реакции первого порядка.
Таким образом, для оценки к необязательно знать начальную концентрацию.
Далее, кинетическая кривая первого порядка инвариантна при линейном преобразовании концентрации. Это видно из простой операции замещения  на пропорциональную величину
на пропорциональную величину  в уравнении
в уравнении  :
:

Поскольку величина  постоянна, ее можно вынести за знак дифференциала:
постоянна, ее можно вынести за знак дифференциала:

и затем сократить. Это означает, что кинетическое уравнение остается неизменным при умножении  на какую-либо постоянную величину. Из этого свойства вытекают важные следствия, а именно:
на какую-либо постоянную величину. Из этого свойства вытекают важные следствия, а именно:
а) Для оценки к вместо концентрации можно использовать любую другую, пропорциональную ей величину, например спектральную поглощательную способность, электропроводность, объем раствора, пошедшего на титрование, и т.п. Логарифм такой величины также меняется линейно во времени, и наклон прямой соответствует - k.
б) Согласно уравнению  относительные скорости реакции не зависят от концентрации; они выражаются через время достижения концентрации реагента, соответствующей некоторой доле первоначальной величины, т.е. через время относительного превращения. Например, период полупревращения
относительные скорости реакции не зависят от концентрации; они выражаются через время достижения концентрации реагента, соответствующей некоторой доле первоначальной величины, т.е. через время относительного превращения. Например, период полупревращения  это время, за которое концентрация реагента снизилась до половины первоначальной величины:
это время, за которое концентрация реагента снизилась до половины первоначальной величины:

в) Кинетические кривые, полученные для различных начальных концентраций  можно совместить с произвольно выбранной стандартной
можно совместить с произвольно выбранной стандартной

Рис. 2-2. Иллюстрация процедуры линейного преобразования. Вертикальные и горизонтальные стрелки означают соответственно изменение масштаба концентрации и сдвиг кривых.
кривой, полученной для  путем умножения ординат кривых на соответствующее отношение
путем умножения ординат кривых на соответствующее отношение  Например, деление пополам ординат кривой, полученной для удвоенной начальной концентрации, дает исходную кривую (рис. 2-2,а). С другой стороны, увеличение масштаба концентрации на последних участках отдельной кривой приводит к новой кривой, совпадающей с первоначальной при сдвиге влево (рис. 2-2,б). Рассматриваемое свойство называют инвариантом I (ср. с разд. 4.3.3).
Например, деление пополам ординат кривой, полученной для удвоенной начальной концентрации, дает исходную кривую (рис. 2-2,а). С другой стороны, увеличение масштаба концентрации на последних участках отдельной кривой приводит к новой кривой, совпадающей с первоначальной при сдвиге влево (рис. 2-2,б). Рассматриваемое свойство называют инвариантом I (ср. с разд. 4.3.3).
г) Касательное к кривым зависимости  в точках, соответствующих разным значениям начальных концентраций, пересекаются в одной точке
в точках, соответствующих разным значениям начальных концентраций, пересекаются в одной точке  на абсциссе
на абсциссе  (рис. 2-3). Касательная в точке начальной концентрации представляет начальную скорость
(рис. 2-3). Касательная в точке начальной концентрации представляет начальную скорость 

Отсюда

и, таким образом, величина  не зависит от начальной концентрации. Рассмотрим теперь увеличение во времени концентрации продукта:
не зависит от начальной концентрации. Рассмотрим теперь увеличение во времени концентрации продукта:


Рис. 2-3. Касательные к кривым зависимости  первого порядка в точках, соответствующих начальным концентрациям.
первого порядка в точках, соответствующих начальным концентрациям.

Рис. 2-4. Изменение во времени концентраций  в реакции первого порядка.
в реакции первого порядка.
Интегральнее уравнение нетрудно получить из уравнения  замещением
замещением  на
на 

или

Очевидно, для того чтобы получить линейную зависимость измеряемого значения  от времени, нужно на графике вместо
от времени, нужно на графике вместо  откладывать
откладывать  Это иллюстрируется на рис. 2-4.
Это иллюстрируется на рис. 2-4.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
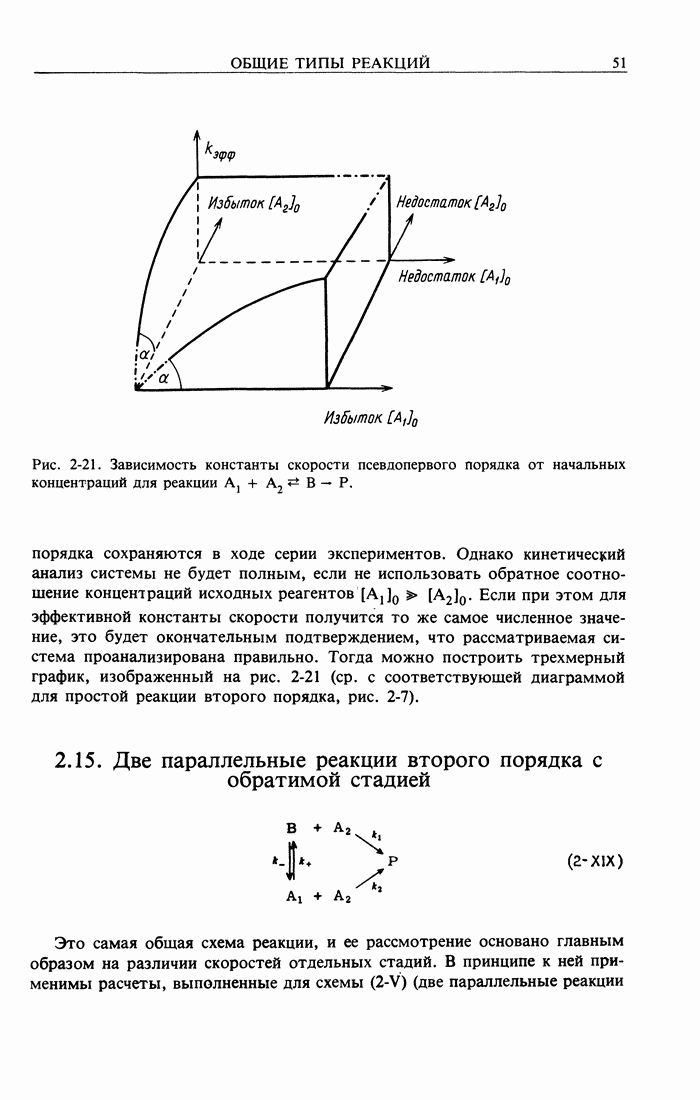
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
- 3.5. Автокаталитические реакции
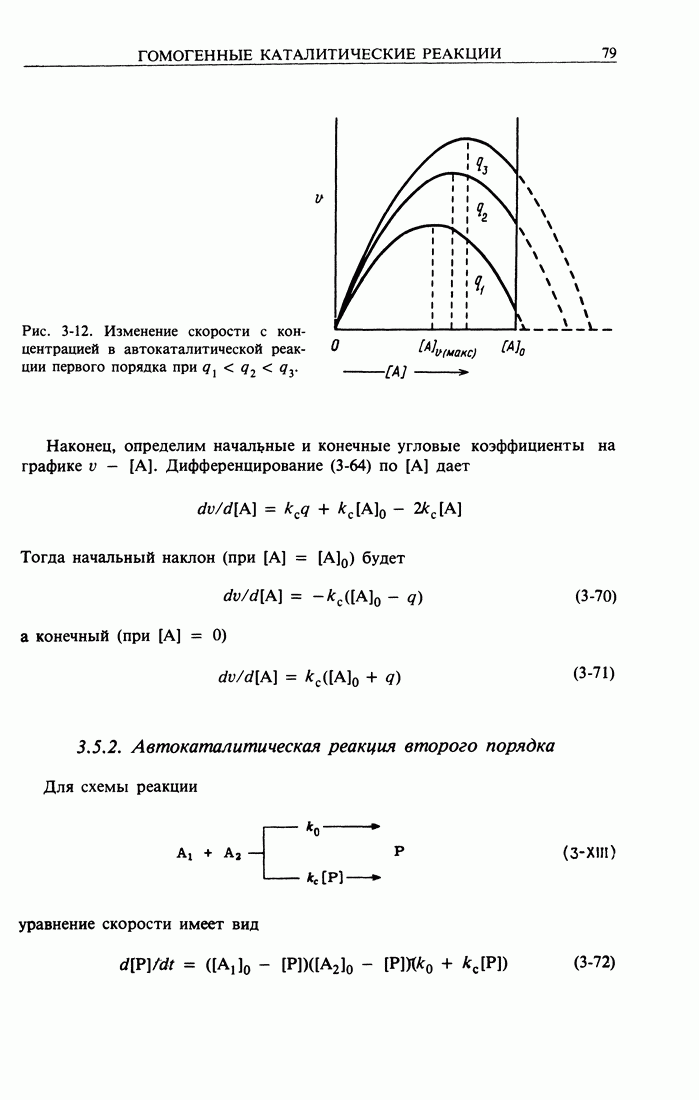
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
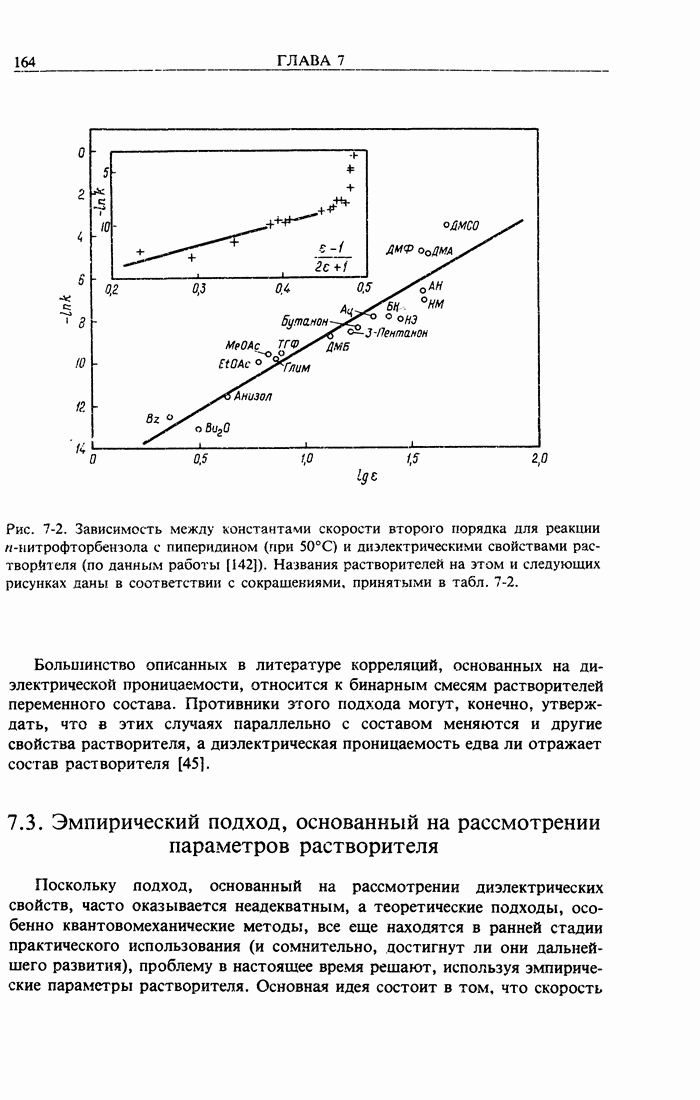
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
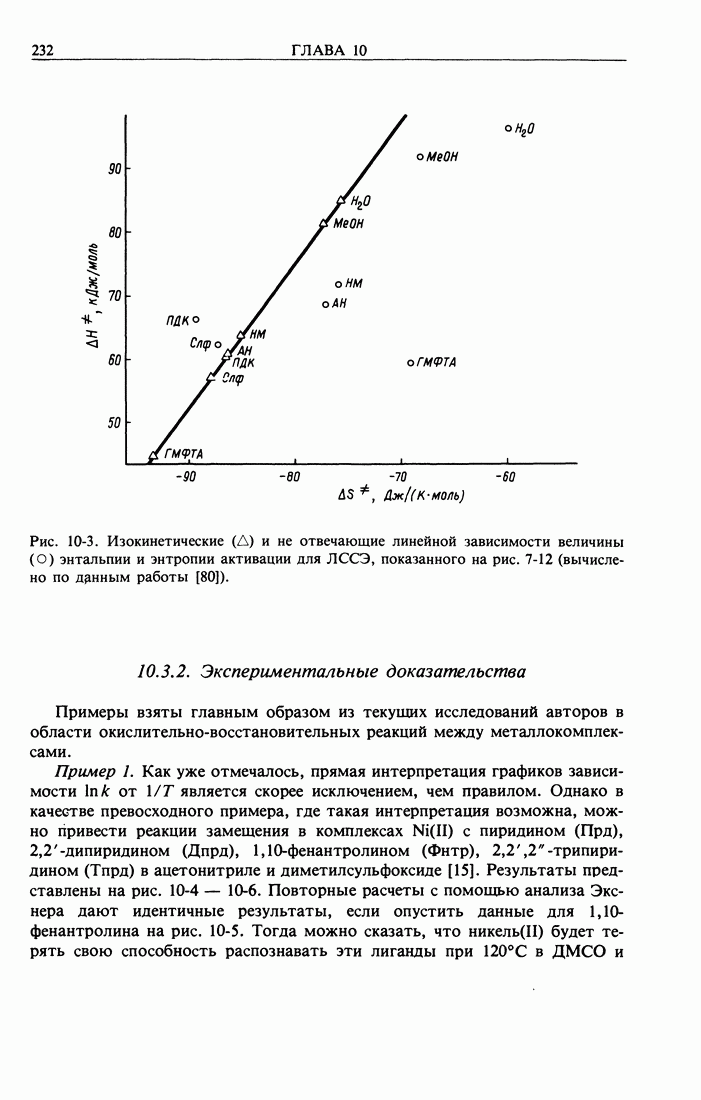
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений