| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.8. Обратимая реакция первого порядка

В этой схеме к  означают константы скорости прямой и обратной реакций соответственно. Уравнение скорости
означают константы скорости прямой и обратной реакций соответственно. Уравнение скорости

при достижении равновесия, т.е. при  принимает вид
принимает вид

Вводя константу равновесия К, получаем

Отсюда с учетом  следует, что
следует, что

Теперь заменим  в уравнении (2-64) на
в уравнении (2-64) на  и после преобразования получим
и после преобразования получим

Второй член в фигурных скобках, согласно уравнению (2-67), просто равен  Следовательно,
Следовательно,


Рис. 2-15. График полулогарифмической зависимости для обратимой реакции первого порядка в случае, когда равновесная концентрация точно не известна.
Это уравнение легко проинтегрировать:

или

График зависимости  от времени дает прямую с угловым коэффициентом, равным —
от времени дает прямую с угловым коэффициентом, равным —  В случае медленных реакций бывает трудно точно определить равновесную концентрацию, и доступной оказывается только концентрация в интервале
В случае медленных реакций бывает трудно точно определить равновесную концентрацию, и доступной оказывается только концентрация в интервале  Тогда эффективную константу скорости можно найти с помощью касательной к кривым
Тогда эффективную константу скорости можно найти с помощью касательной к кривым  в точках, соответствующих
в точках, соответствующих  (рис. 2-15).
(рис. 2-15).
Следует особо отметить, что, хотя измеряют уменьшение  получают сумму констант скоростей прямого и обратного процессов. Разделение этих констант достигается с помощью константы равновесия.
получают сумму констант скоростей прямого и обратного процессов. Разделение этих констант достигается с помощью константы равновесия.
Теперь рассмотрим начальные скорости. Значение абсциссы для точки пересечения касательных в начальном и конечном участках кривой находят по выражению

откуда

Касательная к начальному участку кривой при  пересекает абсциссу в точке
пересекает абсциссу в точке 


Рис. 2-16. Касательные к кривым зависимости с  для обратимой реакции первого порядка.
для обратимой реакции первого порядка.
Поскольку в начале реакции присутствует только А, второе произведение равно нулю и

Очевидно, ни ни  не зависят от начальной концентрации; это хорошо видно из рис. 2-16. В особом случае, когда константы к равны,
не зависят от начальной концентрации; это хорошо видно из рис. 2-16. В особом случае, когда константы к равны,  отсюда
отсюда 
На рис. 2-17 показана зависимость скорости от концентрации для различных начальных концентраций. Угловые коэффициенты прямых, проходящих через абсциссу, равны сумме  Линия, соединяющая точки начальных скоростей, представляет собой проходящую через начало координат прямую с угловым коэффициентом к
Линия, соединяющая точки начальных скоростей, представляет собой проходящую через начало координат прямую с угловым коэффициентом к 

Рис. 2-17. Зависимость скорости от концентрации для обратимой реакции первого порядка.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
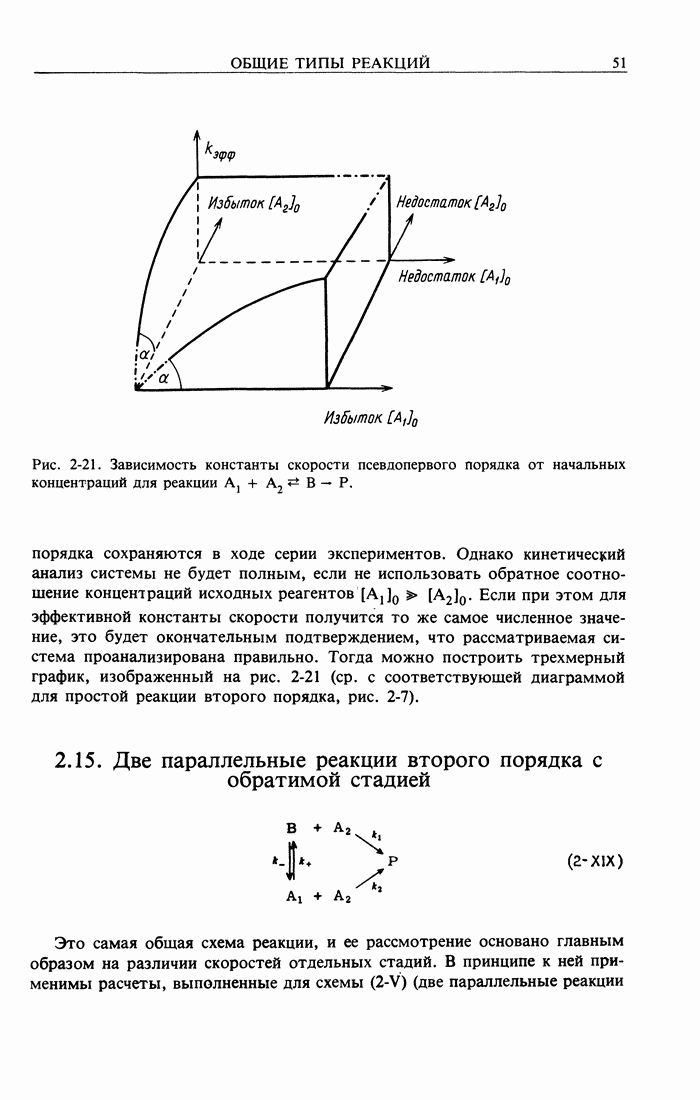
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
- 3.5. Автокаталитические реакции
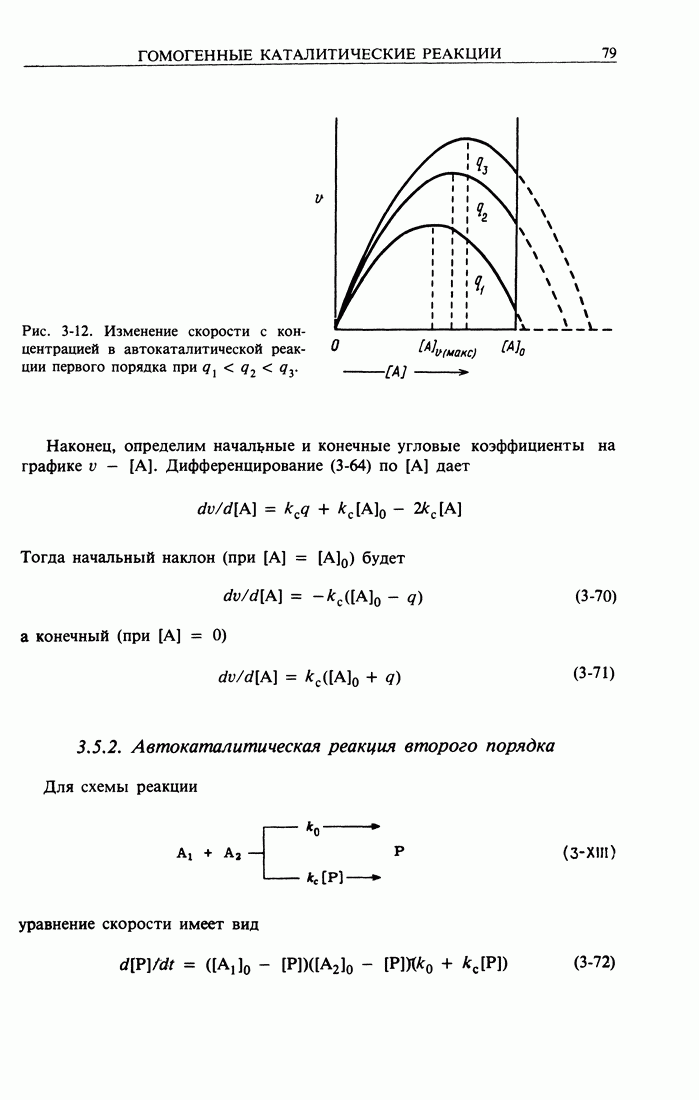
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
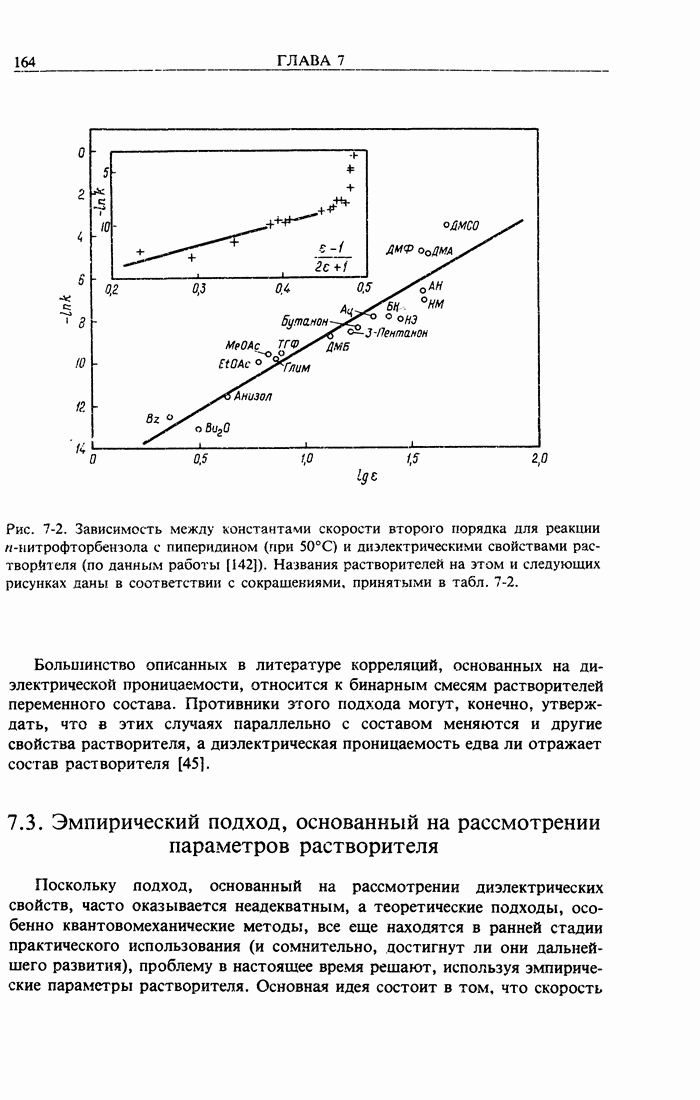
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
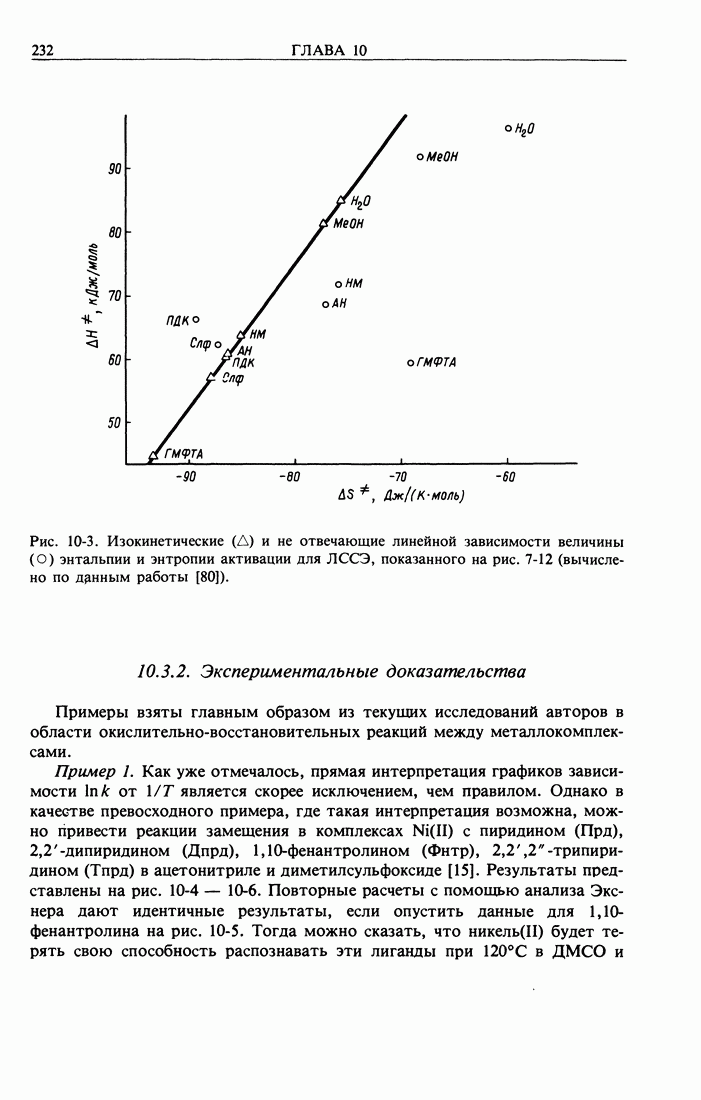
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений