| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.2. Электронные эффекты
Для описания электронных эффектов заместителей используются два основных уравнения — уравнение Гаммета и уравнение Тафта. Первоначально уравнение Гаммета было выведено для реакционной способности ароматических соединений, и в качестве эталонной серии реакций использовалась диссоциация мета- и пара-замещенных бензойных кислот. Здесь заместители расположены достаточно далеко от реакционного центра, и их стерические свойства не должны оказывать влияния на реакцию. Константы заместителя  определяются уравнением
определяются уравнением

где  — соответственно константы диссоциации бензойной кислоты и ее монозамещенных производных в воде при 25°С. Параметр о служит мерой способности заместителя по сравнению с водородом изменять электрический заряд у реакционного центра. Заместители, оттягивающие электроны (мы будем называть их акцепторными заместителями по аналогии с акцепторными растворителями), имеют положительную константу а, так как увеличивают ионизацию кислот. Отрицательные константы относятся к заместителям, отдающим электроны, которые мы будем называть донорными заместителями (по аналогии с донорными растворителями). Поскольку оказалось, что изменение реакционной способности зависит от положения заместителей, стали различать величины от и
— соответственно константы диссоциации бензойной кислоты и ее монозамещенных производных в воде при 25°С. Параметр о служит мерой способности заместителя по сравнению с водородом изменять электрический заряд у реакционного центра. Заместители, оттягивающие электроны (мы будем называть их акцепторными заместителями по аналогии с акцепторными растворителями), имеют положительную константу а, так как увеличивают ионизацию кислот. Отрицательные константы относятся к заместителям, отдающим электроны, которые мы будем называть донорными заместителями (по аналогии с донорными растворителями). Поскольку оказалось, что изменение реакционной способности зависит от положения заместителей, стали различать величины от и  для мета- и пара-замещенных соединений соответственно. Разницу в константах объясняют двумя различными путями влияния замещающей группы на плотность заряда у реакционного центра. Помимо чисто индуктивного эффекта, состоящего в том, что заряд оттягивается
для мета- и пара-замещенных соединений соответственно. Разницу в константах объясняют двумя различными путями влияния замещающей группы на плотность заряда у реакционного центра. Помимо чисто индуктивного эффекта, состоящего в том, что заряд оттягивается  -эффект) или подается
-эффект) или подается  от
от  -связей к ароматическому кольцу, пара-заместители могут также вызывать
-связей к ароматическому кольцу, пара-заместители могут также вызывать  -резонансное взаимодействие между заместителем и реакционным центром. Такое взаимодействие называют мезомерным, или резонансным у эффектом, и по аналогии с индуктивным эффектом различают
-резонансное взаимодействие между заместителем и реакционным центром. Такое взаимодействие называют мезомерным, или резонансным у эффектом, и по аналогии с индуктивным эффектом различают  Считается, что мета-заместители могут вызывать только вторичные резонансные эффекты, которые намного слабее. Предпринимались попытки разделить
Считается, что мета-заместители могут вызывать только вторичные резонансные эффекты, которые намного слабее. Предпринимались попытки разделить  -константы на индуктивные
-константы на индуктивные  и резонансные
и резонансные  компоненты [28, 98]:
компоненты [28, 98]:

Естественно допустить, что индуктивные эффекты почти одинаковы в мета- и  -положениях. Известны различные методы, позволяющие достаточно точно оценить величины
-положениях. Известны различные методы, позволяющие достаточно точно оценить величины  Эти величины практически не зависят от метода определения и выбранной системы, так что индуктивный эффект является свойством только заместителя и не зависит от остальных молекул. Таким образом, по величинам
Эти величины практически не зависят от метода определения и выбранной системы, так что индуктивный эффект является свойством только заместителя и не зависит от остальных молекул. Таким образом, по величинам  можно судить об электроотрицательности заместителей. С другой стороны, установление надежных значений
можно судить об электроотрицательности заместителей. С другой стороны, установление надежных значений  довольно проблематично, поскольку резонансный эффект заместителя нельзя рассматривать вне связи его с партнером по сопряжению, т.е. он зависит от остальных молекул.
довольно проблематично, поскольку резонансный эффект заместителя нельзя рассматривать вне связи его с партнером по сопряжению, т.е. он зависит от остальных молекул.
Усиленные эффекты заместителей наблюдаются в тех случаях, когда заместители вносят заметный вклад в стабилизацию неподеленной электронной пары или положительных зарядов путем резонанса или непосредственно в нем участвуя, т.е. когда резонансный эффект легко передается от одного конца молекулы к другому. Очевидно, что такой эффект могут проявлять только заместители в пара- и орто-положениях. Например, кислотность ионов  -нитрофенола или
-нитрофенола или  -нитроанилина намного выше, чем можно
-нитроанилина намного выше, чем можно
было бы предсказать по обычным константам  Это объясняется дополнительной стабилизацией:
Это объясняется дополнительной стабилизацией:

Аналогично может стабилизироваться положительный заряд:

Поэтому, например, доноры в пара-положении способствуют  -реакциям кумилгалогенидов в большей степени, чем это можно было бы предположить на основании величин
-реакциям кумилгалогенидов в большей степени, чем это можно было бы предположить на основании величин  Были предприняты попытки учесть оба усиленных резонансных эффекта с помощью новых констант: константы
Были предприняты попытки учесть оба усиленных резонансных эффекта с помощью новых констант: константы  для акцепторных заместителей, сопряженных с боковыми цепями, несущими неподеленные электронные пары по соседству с ароматическим кольцом, и константы
для акцепторных заместителей, сопряженных с боковыми цепями, несущими неподеленные электронные пары по соседству с ароматическим кольцом, и константы  для донорных заместителей, сопряженных с электронодефицитными боковыми цепями. Найдено, что величины
для донорных заместителей, сопряженных с электронодефицитными боковыми цепями. Найдено, что величины  и нужно использовать для корреляции скоростей реакций нуклео-фильного и электрофильного замещения ароматических соединений. Поэтому
и нужно использовать для корреляции скоростей реакций нуклео-фильного и электрофильного замещения ароматических соединений. Поэтому  правильно обозначить как константу нуклеофилъного замещения, а — как константу электрофильного замещения. Из изложенного выше очевидно, что эти две шкалы относятся к пара-заместителям; действительно, соответствующие величины для мета-заместителей близки к обычным значениям
правильно обозначить как константу нуклеофилъного замещения, а — как константу электрофильного замещения. Из изложенного выше очевидно, что эти две шкалы относятся к пара-заместителям; действительно, соответствующие величины для мета-заместителей близки к обычным значениям  Как видно из табл. 8-1, для акцепторов величина
Как видно из табл. 8-1, для акцепторов величина  больше, чем
больше, чем  а для доноров
а для доноров  равна
равна  Поэтому разность
Поэтому разность  может служить мерой способности данного акцептора к сопряжению. Аналогично для доноров величина больше, чем
может служить мерой способности данного акцептора к сопряжению. Аналогично для доноров величина больше, чем  а для акцепторов а
а для акцепторов а  равна
равна  следовательно, разность
следовательно, разность  является мерой способности данного до нора к сопряжению. Конечно, прямое сопряжение также имеет значение для ионизации пара-замещенных бензойных кислот. На основании изучения серий реакций, в которых запрещено прямое сопряжение, были предложены «нормальные», т.е. свободные от эффектов прямого сопряжения, шкалы заместителей, практически идентичные обычным величинам Гаммета для мета-замесгителей.
является мерой способности данного до нора к сопряжению. Конечно, прямое сопряжение также имеет значение для ионизации пара-замещенных бензойных кислот. На основании изучения серий реакций, в которых запрещено прямое сопряжение, были предложены «нормальные», т.е. свободные от эффектов прямого сопряжения, шкалы заместителей, практически идентичные обычным величинам Гаммета для мета-замесгителей.
В целом шкалы заместителей по величинам а  как правило, оказываются удовлетворительными для корреляции реакционной
как правило, оказываются удовлетворительными для корреляции реакционной
Таблица 8-1. (см. скан) Электронные константы заместителей
способности ароматических соединений. Некоторые константы заместителей приведены в табл. 8-1 [98].
Влияние заместителя на константы скорости или константы равновесия для аналогичных реакций ароматических соединений с другими боковыми цепями можно теперь выразить как функцию величины о с помощью известного уравнения Гаммета

где  — константы скорости (или равновесия) для реакций мета- и пара-замещенных и незамещенных ароматических соединений соответственно. Величины
— константы скорости (или равновесия) для реакций мета- и пара-замещенных и незамещенных ароматических соединений соответственно. Величины  берут из шкалы заместителей, которую подбирают так, чтобы получить линейную зависимость. Во многих случаях оказывается возможным сделать выводы о природе переходных состояний; эти выводы основываются на свойствах, выражаемых определенным набором
берут из шкалы заместителей, которую подбирают так, чтобы получить линейную зависимость. Во многих случаях оказывается возможным сделать выводы о природе переходных состояний; эти выводы основываются на свойствах, выражаемых определенным набором  -величин. Так, необходимость использовать константы
-величин. Так, необходимость использовать константы  указывает на то, что реакционный центр в переходном состоянии электронодефицитный, т.е. реакция идет через карбониевый ион. Аналогичным образом, необходимость использовать величину
указывает на то, что реакционный центр в переходном состоянии электронодефицитный, т.е. реакция идет через карбониевый ион. Аналогичным образом, необходимость использовать величину  показывает, что реакционный центр
показывает, что реакционный центр
электронообогащенный. Определенные выводы о механизме реакции можно сделать и из того факта, что нет необходимости использовать величину  или
или 
Константа реакции  служит мерой чувствительности исследуемой реакции к изменениям, вызванным замещением; она может быть положительной или отрицательной и либо больше, либо меньше единицы. Однако физический смысл наклона графика Гаммета (как и любого другого эмпирического графика) не совсем ясен, так как зависит от температуры (см. разд. 10.3). Из определения величин о следует, что положительные значения
служит мерой чувствительности исследуемой реакции к изменениям, вызванным замещением; она может быть положительной или отрицательной и либо больше, либо меньше единицы. Однако физический смысл наклона графика Гаммета (как и любого другого эмпирического графика) не совсем ясен, так как зависит от температуры (см. разд. 10.3). Из определения величин о следует, что положительные значения  относятся к реакциям, которые облегчаются акцепторными заместителями; при этом подразумевается, что реакционный центр действует как акцептора Аналогично отрицательные значения
относятся к реакциям, которые облегчаются акцепторными заместителями; при этом подразумевается, что реакционный центр действует как акцептора Аналогично отрицательные значения  соответствуют реакциям, которые ингибируются акцепторными заместителями; это означает, что реакционный центр действует как донор. Интересно проследить взаимосвязь этих эффектов с влиянием акцепторных и донорных растворителей на скорость реакции (ср. с разд. 7.5).
соответствуют реакциям, которые ингибируются акцепторными заместителями; это означает, что реакционный центр действует как донор. Интересно проследить взаимосвязь этих эффектов с влиянием акцепторных и донорных растворителей на скорость реакции (ср. с разд. 7.5).
Уравнение Гаммета может быть расширено путем разделения индуктивного и резонансного эффектов и записано в виде приближения по двум параметрам:

По таким уравнениям можно судить об относительных вкладах индуктивного и рездкансного эффектов в суммарный эффект заместителя. В частности, они применимы в тех случаях, когда непригодно простое соотношение Гаммета с величинами от и  например, уравнение
например, уравнение  можно применить к серии реакций, для которых ни
можно применить к серии реакций, для которых ни  ни
ни  не дают приемлемого согласования. Поскольку очень часто в распоряжении экспериментатора имеется только несколько точек, особенно большое значение придается правильной интерпретации множественной регрессии, т.е. при рассмотрении коэффициента корреляции нельзя пренебрегать уменьшением степеней свободы.
не дают приемлемого согласования. Поскольку очень часто в распоряжении экспериментатора имеется только несколько точек, особенно большое значение придается правильной интерпретации множественной регрессии, т.е. при рассмотрении коэффициента корреляции нельзя пренебрегать уменьшением степеней свободы.
Обратимся теперь к реакционной способности алифатических соединений. Естественно, что в отсутствие стерических (и резонансных) эффектов реакционная способность алифатических соединений должна коррелировать со шкалой  -величин. Например, это имеет место для величин
-величин. Например, это имеет место для величин  замещенных уксусных кислот, что выражается уравнением, выведенным Гамметом [49] и Шортером [133]:
замещенных уксусных кислот, что выражается уравнением, выведенным Гамметом [49] и Шортером [133]:

где  константа кислотности водной уксусной кислоты при
константа кислотности водной уксусной кислоты при  константа кислотности соответствующих монозамещенных кислот.
константа кислотности соответствующих монозамещенных кислот.
Однако лучше известна более ранняя работа Тафта [145], который пытался выделить индуктивные эффекты, сравнивая катализируемый кислотой и основанием гидролиз замещенных ацетатов. Он исходил из допущения, что относительная скорость кислотного гидролиза  контролируется только резонансным и стерическим эффектами, тогда как соответствующая величина
контролируется только резонансным и стерическим эффектами, тогда как соответствующая величина  для щелочного гидролиза зависит от индуктивного эффекта и от тех же резонансного и стерического эффектов, которые проявляются при кислотном гидролизе. Поэтому разность между этими двумя величинами должна быть мерой индуктивного эффекта заместителя; ее обозначают а и относят к группе
для щелочного гидролиза зависит от индуктивного эффекта и от тех же резонансного и стерического эффектов, которые проявляются при кислотном гидролизе. Поэтому разность между этими двумя величинами должна быть мерой индуктивного эффекта заместителя; ее обозначают а и относят к группе  в соединениях
в соединениях 

где k — константа скорости гидролиза  -замещенного сложного эфира,
-замещенного сложного эфира,  соответствующая константа скорости для эфира с
соответствующая константа скорости для эфира с  а коэффициент
а коэффициент  произвольно выбранная величина, с помощью которой величины а можно поместить на ту же шкалу, что и величины Гаммета. Несмотря на некоторую неясность допущений Тафта, величину о можно успешно использовать, гак как она связана со шкалой
произвольно выбранная величина, с помощью которой величины а можно поместить на ту же шкалу, что и величины Гаммета. Несмотря на некоторую неясность допущений Тафта, величину о можно успешно использовать, гак как она связана со шкалой  простым соотношением
простым соотношением

Таким образом, оказывается возможным использовать шкалу  для корреляции реакционной способности алифатических соединений в тех случаях, когда стерические эффекты отсутствуют или являются постоянными для данной серии реакций. Тогда первоначальное уравнение Тафта
для корреляции реакционной способности алифатических соединений в тех случаях, когда стерические эффекты отсутствуют или являются постоянными для данной серии реакций. Тогда первоначальное уравнение Тафта  принимает вид
принимает вид

что аналогично уравнению Гаммета. Некоторые величины  приведены в табл. 8-1.
приведены в табл. 8-1.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
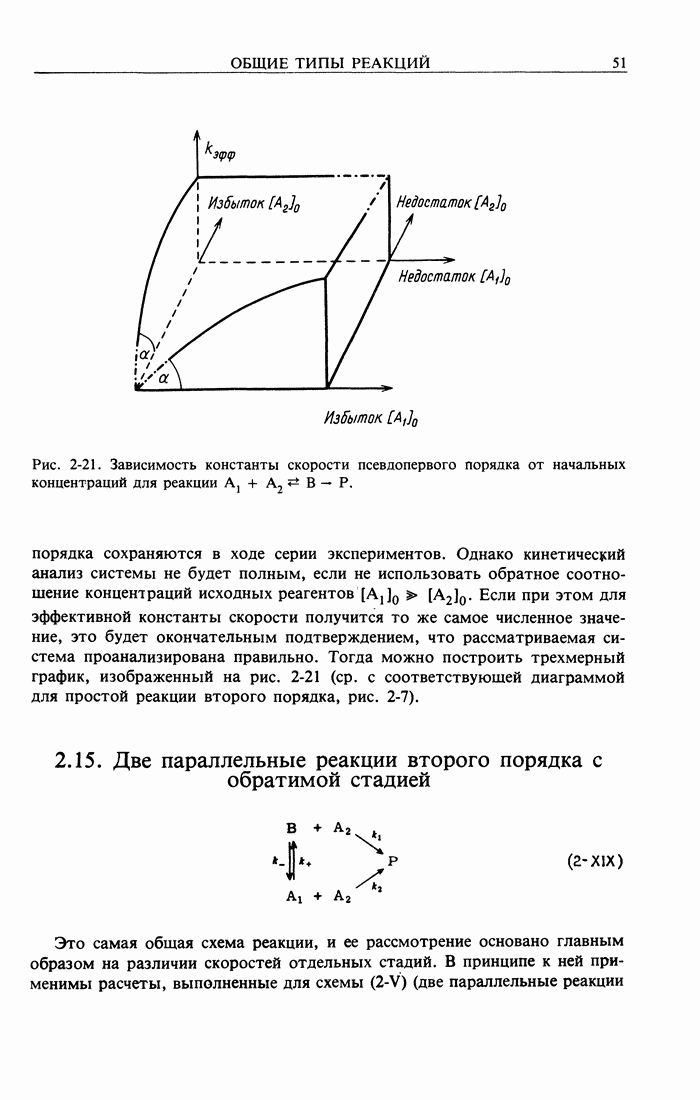
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
- 3.5. Автокаталитические реакции
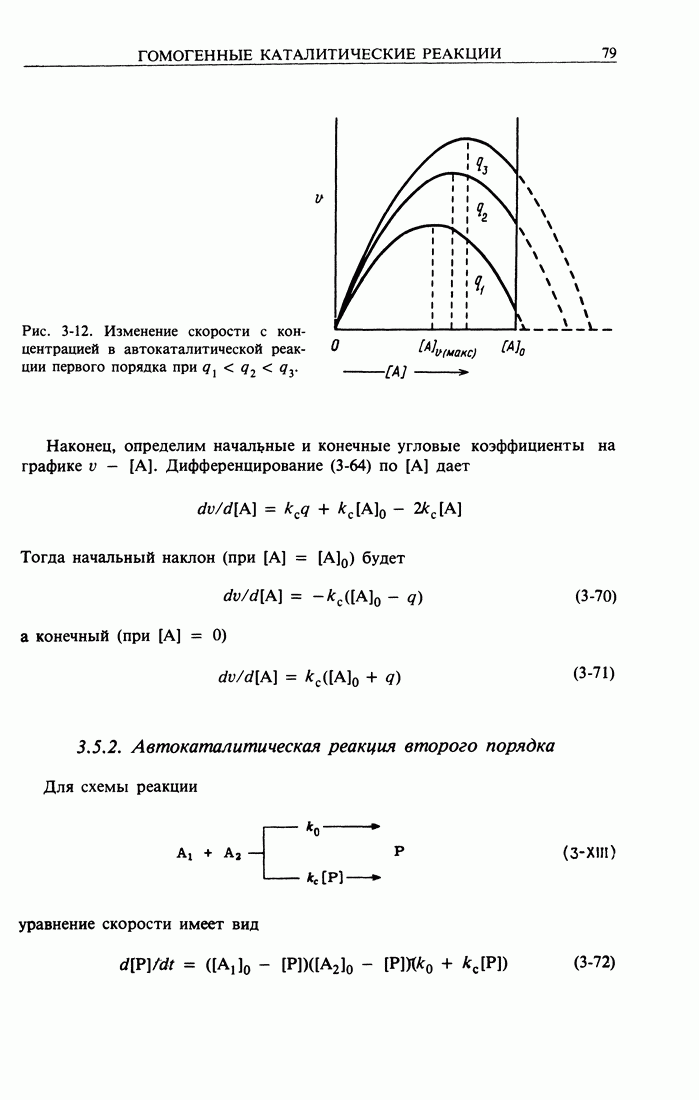
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
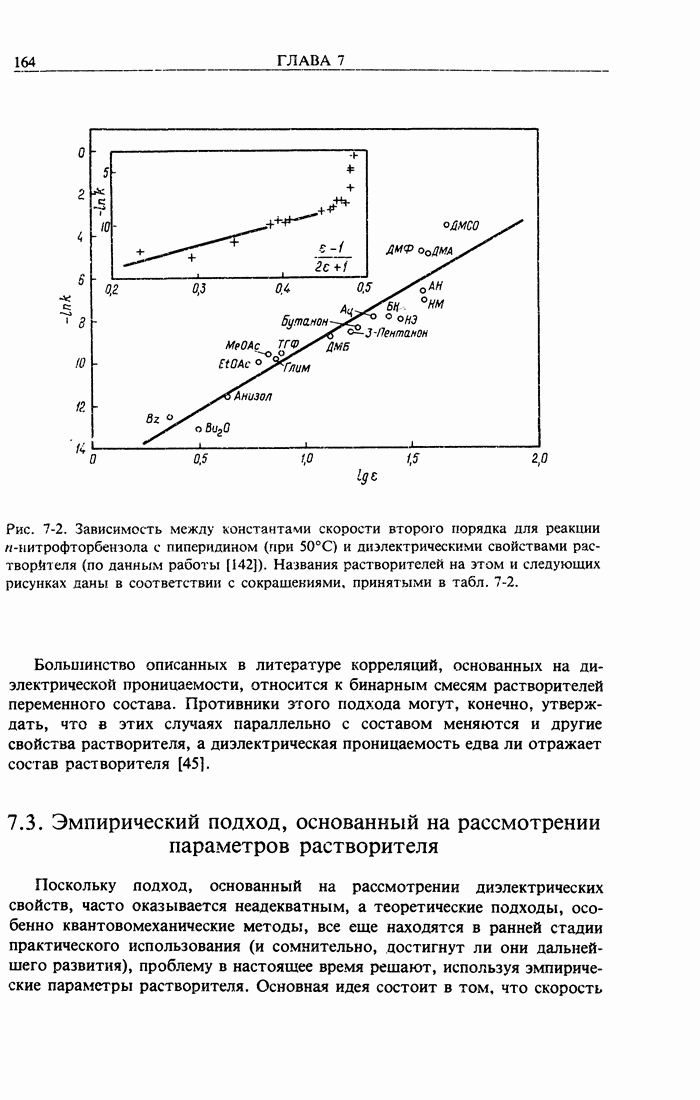
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
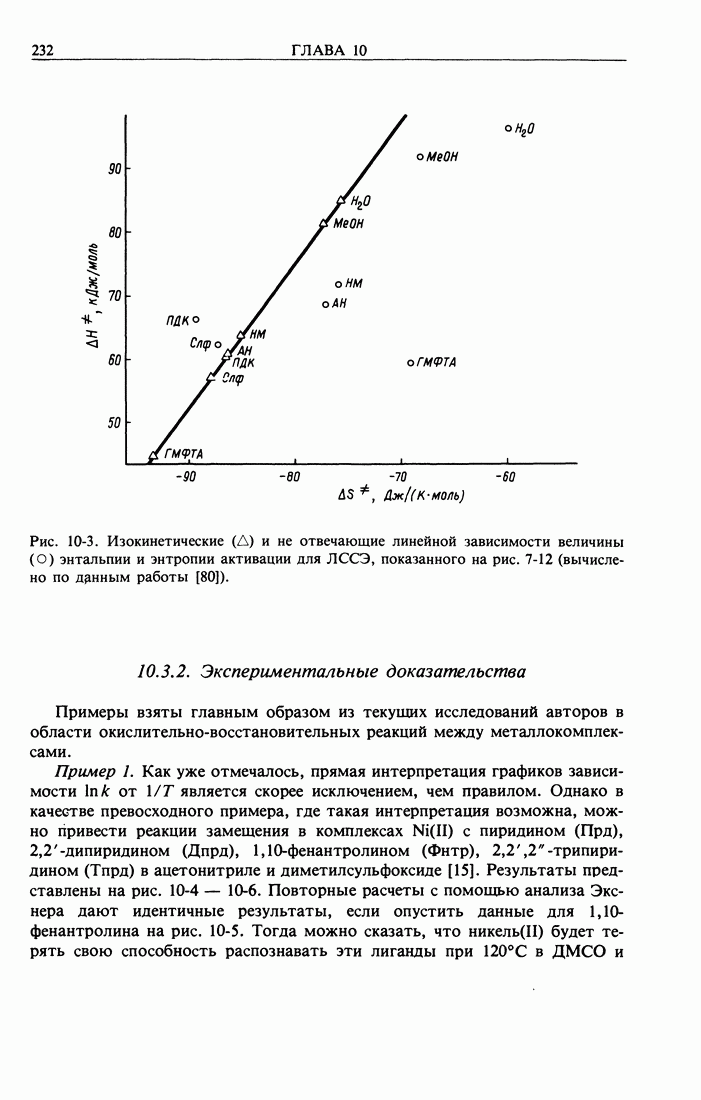
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений