| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.7. Выводы
Уравнения скорости, представляющие физическую модель реакции, можно разделить на три категории, содержащие а) одцн член, б) алгебраическую сумму членов и в) частное (дробно-линейная функция).
Каждый член типа «а», «б» или член знаменателя типа «в» является произведением физических констант и концентраций и имеет размерность
концентрация/время, обычно выражаемую в  Произведение константы скорости первого порядка и одной концентрации представляет элементарную реакцию первого порядка или элементарную реакцию второго порядка, где одним из реагентов является растворитель. Произведение константы скорости второго порядка и двух концентраций (или квадрата концентрации одного реагента или концентраций двух разных реагентов) указывает на элементарную реакцию второго порядка. Как уже говорилось во введении, элементарные реакции имеют или первый, или второй порядок. Однако наряду с константами скорости, константами равновесия или константами псевдоравновесия, такими, как константа Михаэлиса, в кинетическом уравнении может быть член, степень которого выше двух. Эта увеличенная степень означает, что в эффективную константу скорости или равновесия включена еще одна константа равновесия, размерность которой
Произведение константы скорости первого порядка и одной концентрации представляет элементарную реакцию первого порядка или элементарную реакцию второго порядка, где одним из реагентов является растворитель. Произведение константы скорости второго порядка и двух концентраций (или квадрата концентрации одного реагента или концентраций двух разных реагентов) указывает на элементарную реакцию второго порядка. Как уже говорилось во введении, элементарные реакции имеют или первый, или второй порядок. Однако наряду с константами скорости, константами равновесия или константами псевдоравновесия, такими, как константа Михаэлиса, в кинетическом уравнении может быть член, степень которого выше двух. Эта увеличенная степень означает, что в эффективную константу скорости или равновесия включена еще одна константа равновесия, размерность которой  Например, обсуждая уравнение (3-11), мы видели, что константу скорости третьего порядка следует рассматривать как произведение константы скорости второго порядка и константы равновесия. Это указывает на элементарную реакцию второго порядка, которой предшествует быстрое равновесие.
Например, обсуждая уравнение (3-11), мы видели, что константу скорости третьего порядка следует рассматривать как произведение константы скорости второго порядка и константы равновесия. Это указывает на элементарную реакцию второго порядка, которой предшествует быстрое равновесие.
Вернемся к рассмотренному во введении уравнению  для бензидиновой перегруппировки. Второй из двух членов этого уравнения имеет второй порядок. Получены экспериментальные доказательства, что стадиям перегруппировки предшествует быстрый и равновесный перенос протона:
для бензидиновой перегруппировки. Второй из двух членов этого уравнения имеет второй порядок. Получены экспериментальные доказательства, что стадиям перегруппировки предшествует быстрый и равновесный перенос протона:

Учитывая это, уравнение  можно записать в виде
можно записать в виде

Однако и это уравнение все еще остается упрощенной формой физической модели, и к этому вопросу мы скоро вернемся. Тем не менее последнее уравнение показывает, что член второй степени может представлять элементарную стадию первого порядка, которой предшествует быстрое равновесие.
Если уравнение скорости состоит более чем из одного члена (тип «б» или знаменатель в уравнении типа «в»), это говорит о том, что один компонент участвует в нескольких реакциях, которые происходят независимо. Члены с положительным знаком указывают на прямые и параллельные реакции, а члены с отрицательным знаком — на обратные реакции.
Наконец, дробно-линейное уравненение скорости (тип «в») показывает, что реакция протекает через образование интермедиата Боденштейна или/и что компонент числителя включен в побочное равновесие, а это приводит к снижению эффективной концентрации. Знаменатель, который удобно представить в виде  и т.д., состоит из членов, каждый из которых (кроме единицы естественно) является произведением констант равновесия или псевдоравновесия и концентраций, так что эти члены безразмерны. Число членов в знаменателе, кроме членов
и т.д., состоит из членов, каждый из которых (кроме единицы естественно) является произведением констант равновесия или псевдоравновесия и концентраций, так что эти члены безразмерны. Число членов в знаменателе, кроме членов  соответствует числу побочных равновесий, в которых участвует ключевое вещество. Это означает, что любое кинетическое уравнение скорости реакции, включающее константы равновесия, должно также иметь знаменатель. Это относится и к уравнению (4-113), но здесь знаменатель имеет очень сложный вид из-за квадратичной зависимости уравнения материального баланса
соответствует числу побочных равновесий, в которых участвует ключевое вещество. Это означает, что любое кинетическое уравнение скорости реакции, включающее константы равновесия, должно также иметь знаменатель. Это относится и к уравнению (4-113), но здесь знаменатель имеет очень сложный вид из-за квадратичной зависимости уравнения материального баланса

Однако для малых значений К физическая модель сводится к (4-113). С другой стороны, если мало только значение  квадратичный член в (4-114) пренебрежимо мал и уравнение (4-113) принимает вид
квадратичный член в (4-114) пренебрежимо мал и уравнение (4-113) принимает вид

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
- 3.5. Автокаталитические реакции
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
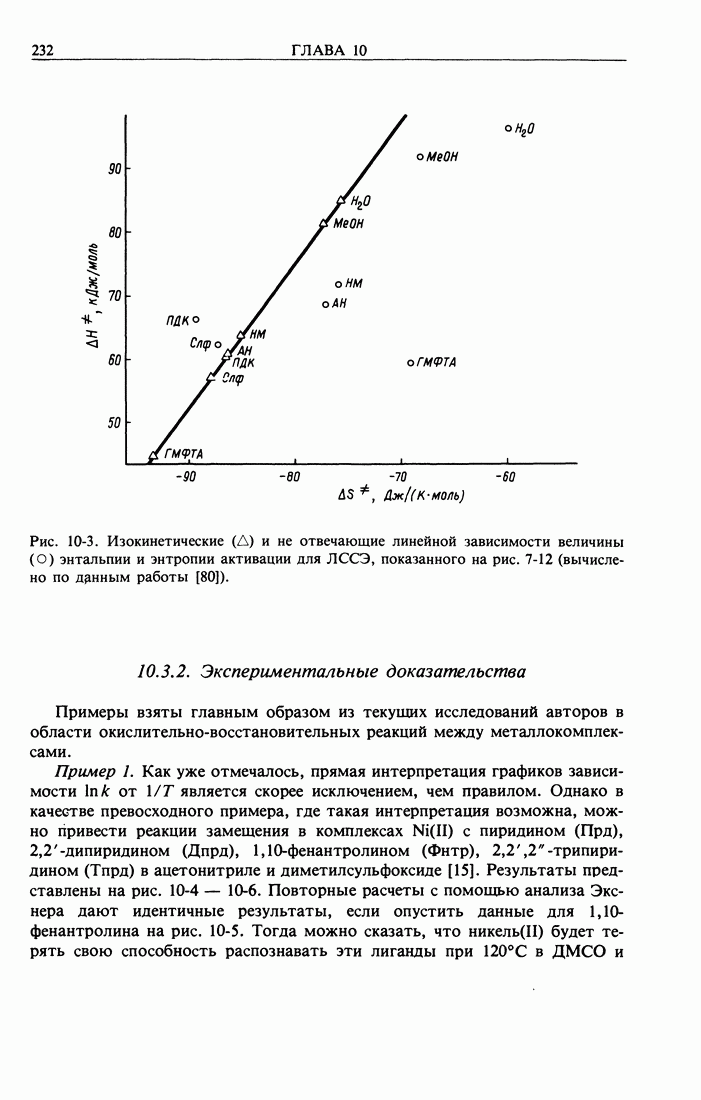
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений