| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.3. Методы анализа кривых зависимости концентрации от времени
В настоящее время имеются три метода анализа кинетических кривых. Два из них  дифференциальный и интегральный
дифференциальный и интегральный  основаны соответственно на двух типах уравнений скорости
основаны соответственно на двух типах уравнений скорости  и
и  Третьим является метод трансформации, который менее известен, но часто оказывается очень удобным.
Третьим является метод трансформации, который менее известен, но часто оказывается очень удобным.
4.3.1. Дифференциальный метод
Этот метод связан с рассмотрением скоростей реакций. Кривые  дифференцируют графически и получают наклоны
дифференцируют графически и получают наклоны  касательных к различным точкам кривой (т.е. разные концентрации при разных значениях времени). Наиболее подходящим является зеркальный метод. Зеркало помещают в точке кривой, к которой нужно провести касательную, так чтобы
касательных к различным точкам кривой (т.е. разные концентрации при разных значениях времени). Наиболее подходящим является зеркальный метод. Зеркало помещают в точке кривой, к которой нужно провести касательную, так чтобы
бы было видно отражение кривой. Затем зеркало поворачивают вокруг точки до тех пор, пока не получится отражение кривой без изгиба. Тогда перпендикуляр к этой зеркальной плоскости будет касательной к кривой в данной точке. Наклон касательной является частной производной и связывает определенную концентрацию со скоростью реакции:

Затем строят зависимость  от
от  т.е. получают графическую форму уравнения
т.е. получают графическую форму уравнения

Вид этого графика дает прямую информацию об уравнении скорости.
Вариантом дифференциального метода является метод начальных скоростей, который ограничивается оценкой наклона кривых  полученных для различных начальных концентраций в точках, соответствующих
полученных для различных начальных концентраций в точках, соответствующих  Найденное этим путем уравнение скорости справедливо тсщько для начальной стадии реакции, однако, если продукты не влияют на скорость, оно пригодно и для описания процесса в целом. Действительно, разница между графиками
Найденное этим путем уравнение скорости справедливо тсщько для начальной стадии реакции, однако, если продукты не влияют на скорость, оно пригодно и для описания процесса в целом. Действительно, разница между графиками  свидетельствует о том, что продукт влияет на скорость реакции, в том числе и на активность катализатора.
свидетельствует о том, что продукт влияет на скорость реакции, в том числе и на активность катализатора.
Следует, однако, отметить, что методом начальных скоростей можно найти вид функции  даже в том случае, когда продукт влияет на скорость. Методика иллюстрирована на рис.
даже в том случае, когда продукт влияет на скорость. Методика иллюстрирована на рис.  и заключается в следующем. Прежде всего оценивают начальную скорость при относительно высокой начальной концентрации
и заключается в следующем. Прежде всего оценивают начальную скорость при относительно высокой начальной концентрации  Затем измерение повторяют при несколько более низкой концентрации
Затем измерение повторяют при несколько более низкой концентрации  и получают
и получают  Когда последняя смесь прореагировала полностью, добавляют свежую порцию
Когда последняя смесь прореагировала полностью, добавляют свежую порцию  точно равную разности
точно равную разности  Новое значение начальной скорости
Новое значение начальной скорости  которое при этом получится, есть не что иное, как скорость
которое при этом получится, есть не что иное, как скорость

Рис. 4-3. Определение  методом начальных скоростей.
методом начальных скоростей.
первоначальной реакции, т.е. реакции, начинающейся с  при достижении концентрации
при достижении концентрации  Эта методика представлена на рис. 4-3: повторные измерения при разных концентрациях
Эта методика представлена на рис. 4-3: повторные измерения при разных концентрациях  дают
дают  и в результате
и в результате 

Графики зависимостей  от
от  от
от  идентичны, если отсутствует влияние продукта, Этот интересный метод может оказаться особенно полезным в некоторых ситуациях, например если реакционный сосуд так мал, что количество образца, которое можно взять на анализ, недостаточно для получения полной кривой
идентичны, если отсутствует влияние продукта, Этот интересный метод может оказаться особенно полезным в некоторых ситуациях, например если реакционный сосуд так мал, что количество образца, которое можно взять на анализ, недостаточно для получения полной кривой 
Главное преимущество дифференциального метода перед интегральным состоит в том, что не требуется априори никаких соображений по поводу порядка и механизма реакции. Дифференциальное уравнение скорости выводится непосредственно из эксперимента. Главный недостаток метода заключается в том, что исходные данные  нужно сначала перевести в данные
нужно сначала перевести в данные  («второе поколение» экспериментальных данных), а также в том, что довольно трудно точно построить касательную. Особенно это играет роль в тех случаях, когда экспериментальные графики
(«второе поколение» экспериментальных данных), а также в том, что довольно трудно точно построить касательную. Особенно это играет роль в тех случаях, когда экспериментальные графики  не записываются непрерывно, а строятся по отдельным точкам. Значительных улучшений можно добиться выравниванием, или «сглаживанием», данных, т.е. аппроксимировать точки какой-либо кривой, а затем построить касательные к этой плавной кривой.
не записываются непрерывно, а строятся по отдельным точкам. Значительных улучшений можно добиться выравниванием, или «сглаживанием», данных, т.е. аппроксимировать точки какой-либо кривой, а затем построить касательные к этой плавной кривой.
4.3.2. Интегральный метод
Метод основан на использовании прямой функциональной зависимости между концентрацией и временем:

Это означает, что кривые  можно обрабатывать без предварительного преобразования, и поэтому можно получить более точные кинетические константы. Главный недостаток метода связан с тем, что нужно сначала предположить вид интегрального уравнения скорости, а затем проверить, описывает ли это уравнение экспериментальные кривые. Если нет, то следует принять другое уравнение. Эта процедура повторяется до тех пор, пока не будет найдено хорошее согласование. Метод очень удобен для простых реакций, а также и для более сложных реакций, если к ним применимы условия псевдопервого порядка (ср. с разнообразными примерами в предыдущей главе).
можно обрабатывать без предварительного преобразования, и поэтому можно получить более точные кинетические константы. Главный недостаток метода связан с тем, что нужно сначала предположить вид интегрального уравнения скорости, а затем проверить, описывает ли это уравнение экспериментальные кривые. Если нет, то следует принять другое уравнение. Эта процедура повторяется до тех пор, пока не будет найдено хорошее согласование. Метод очень удобен для простых реакций, а также и для более сложных реакций, если к ним применимы условия псевдопервого порядка (ср. с разнообразными примерами в предыдущей главе).
Следует, однако, подчеркнуть, что в случае сложных реакций интегральный метод может привести к ошибочным выводам. Как правило, линейное соотношение в классических координатах, использующее интегральные
уравнения, а именно зависимости  от t (псевдонулевой порядок),
от t (псевдонулевой порядок),  от
от  [(псевдо)первый порядок] и
[(псевдо)первый порядок] и  от t [(псевдо)второй порядок], является в действительности необходимым условием, но не достаточным доказательством предполагаемого порядка реакции. Необходимо исследовать как можно больший интервал начальных концентраций. Только параллельные прямые в соответствующих координатах служат ясным доказательством наблюдаемого порядка. Это всегда следует иметь в виду, поскольку порядок реакции может оказаться простым, если какие-либо неизвестные эффекты стремятся компенсировать друг друга. Примером служит конкурентное ингибирование продуктом, компенсирующее действие катализатора: если 1 приблизительно равна
от t [(псевдо)второй порядок], является в действительности необходимым условием, но не достаточным доказательством предполагаемого порядка реакции. Необходимо исследовать как можно больший интервал начальных концентраций. Только параллельные прямые в соответствующих координатах служат ясным доказательством наблюдаемого порядка. Это всегда следует иметь в виду, поскольку порядок реакции может оказаться простым, если какие-либо неизвестные эффекты стремятся компенсировать друг друга. Примером служит конкурентное ингибирование продуктом, компенсирующее действие катализатора: если 1 приблизительно равна  то сложная функция образования катализатора [схема (3-VI)]
то сложная функция образования катализатора [схема (3-VI)]

сводится к

Тогда убыль  выражается как
выражается как

Несмотря на  что это закон скорости псевдопервого порядка, графики зависимости
что это закон скорости псевдопервого порядка, графики зависимости  полученные при разных начальных концентрациях, не дадут набора параллельных прямых, поскольку кэявляется функцией
полученные при разных начальных концентрациях, не дадут набора параллельных прямых, поскольку кэявляется функцией  Напомним также, что уравнение (2-86) справедливо для обратимой реакции второго порядка, в которой константа равновесия равна единице.
Напомним также, что уравнение (2-86) справедливо для обратимой реакции второго порядка, в которой константа равновесия равна единице.
Другая ситуация, которая может привести к ложным выводам, возникает, например, в случае, если в ходе реакции меняется ее порядок, иными словами, если лимитирующая стадия сдвигается. Теперь вспомним график на рис. 3-2, относящийся к реакции нулевого порядка на ранней стадии и первого порядка на конечных стадиях. Если степень превращения составляет 60—70%, то при использовании одной относительно высокой начальной концентрации должно получиться линейное уменьшение  т.е.
т.е.

Однако это лишь грубое приближение реального уравнения скорости 

и оно не дает достаточной информации о реакции. Неточных выводов можно избежать, если проводить реакцию при различных начальных
концентрациях до глубины превращения -70%. В экстремальном случае, когда  реакция первого порядка действительно имеет место.
реакция первого порядка действительно имеет место.
С другой стороны, отсутствие строгой параллельности прямых в любых классических координатах может быть следствием ошибочного предположения о порядке реакции. Если предположить другой порядок, то можно получить лучшее согласование.
В настоящее время интегральный метод приобрел определенные преимущества в связи с тем, что численное интегрирование даже сложных дифференциальных уравнений стало доступным с помощью ЭВМ. Таким образом, можно уточнить кинетические константы, полученные дифференциальными методами, и рассчитать их наиболее правильные значения.
4.3.3. Метод трансформации
Информацию об уравнении скорости можно также получить, проводя исследование в таких условиях, при которых кинетические кривые из серии опытов становятся конгруэнтными. В таких исследованиях используется метод трансформации. Он особенно удобен для обработки сложных кинетических кривых, т.е. таких кривых, которые нельзя привести к линейному виду с помощью классических координат. Как будет показано в дальнейшем, этот метод позволяет отличить однородные уравнения скорости от других уравнений.
Суть метода заключается в следующем. Сначала выбирают так называемую стандартную кривую. Затем определяют соотношение ординат (рис. 4-4, тип а) или абсцисс (рис. 4-4, тип б) остальных кривых в данной серии опытов, которые должны совместиться со стандартной кривой. Эти соотношения называют коэффициентами трансформации  причем различают
причем различают

Рис. 4-4. Метод трансформации. Тип а: меняется концентрация реагента, находящегося в недостатке. Тип б: меняется параметр, например концентрация избыточного реагента.
величины  (Далее проверяют, постоянны ли эти соотношения по всему ходу кинетических кривых, другими словами, не зависят ли они от глубины протекания реакции. Чаще всего соотношение не зависит от степени превращения, и это означает, что одну кинетическую кривую можно совместить с другими путем подходящего изменения масштаба этой кривой по соответствующей оси координат. Такое изменение обычно называют отображением по данной оси, а упомянутые выше соотношения называют коэффициентами отображения. Они определяются отношением координаты стандартной кривой к соответствующей координате кривых, которые должны быть преобразованы. Таким образом, коэффициент отображения показывает, на сколько нужно умножить координату преобразуемой кривой, чтобы эта кривая совместилась со стандартной кривой. Может оказаться необходимым изменить масштаб обеих координат.
(Далее проверяют, постоянны ли эти соотношения по всему ходу кинетических кривых, другими словами, не зависят ли они от глубины протекания реакции. Чаще всего соотношение не зависит от степени превращения, и это означает, что одну кинетическую кривую можно совместить с другими путем подходящего изменения масштаба этой кривой по соответствующей оси координат. Такое изменение обычно называют отображением по данной оси, а упомянутые выше соотношения называют коэффициентами отображения. Они определяются отношением координаты стандартной кривой к соответствующей координате кривых, которые должны быть преобразованы. Таким образом, коэффициент отображения показывает, на сколько нужно умножить координату преобразуемой кривой, чтобы эта кривая совместилась со стандартной кривой. Может оказаться необходимым изменить масштаб обеих координат.
Следующий вопрос касается установления соотношения между коэффициентами отображения и начальными концентрациями, меняющимися в данной серии опытов. Если это соотношение линейно, то его рассматривают  алее в терминах инвариантности (ср. с
алее в терминах инвариантности (ср. с  в разд. 2.1 и типом 1 в разд. 2,2) В сущности метод трансформации лежит в основе процедуры, используемой для установления свойств инвариантов 1 или II. Поэтому, как отмечалось ранее, следует рассмотреть, концентрации каких реагентов должны меняться.
в разд. 2.1 и типом 1 в разд. 2,2) В сущности метод трансформации лежит в основе процедуры, используемой для установления свойств инвариантов 1 или II. Поэтому, как отмечалось ранее, следует рассмотреть, концентрации каких реагентов должны меняться.
Первая серия опытов: меняется концентрация реагента, находящегося в недостатке.
Инвариант  Серия опытов обнаруживает свойство инварианта I, если при линейном уменьшении масштаба по оси с в соответствии с начальными концентрациями получается единственная кривая, т.е. математически
Серия опытов обнаруживает свойство инварианта I, если при линейном уменьшении масштаба по оси с в соответствии с начальными концентрациями получается единственная кривая, т.е. математически

Это соотношение указывает на однородное уравнение скорости первой степени:

где каждый член линейно зависит от 

С точки зрения механизма реакции мы имеем здесь дело с реакционной системой, состоящей только  отдельных реакций первого порядка (или обычно псевдопервого порядка), например из параллельных реакций или последовательности обратимой
отдельных реакций первого порядка (или обычно псевдопервого порядка), например из параллельных реакций или последовательности обратимой  необратимой реакций. В простейшем случае это просто реакция первого порядка, рассмотренная в самом начале книги.
необратимой реакций. В простейшем случае это просто реакция первого порядка, рассмотренная в самом начале книги.
Инвариант II. Кривые могут быть отображены на произвольно выбранную стандартную кривую при уменьшении и увеличении масштабов по осям  соответственно линейно с начальной концентрацией [ср. с уравнением (2-19)]:
соответственно линейно с начальной концентрацией [ср. с уравнением (2-19)]:

Это указывает на однородное уравнение скорости второй степени

где снова  В простейшем случае это относится к реакции второго порядка. Кроме того, эта система использовалась для характеристики чисто автокаталитического процесса первого порядка (ср. с разд.
В простейшем случае это относится к реакции второго порядка. Кроме того, эта система использовалась для характеристики чисто автокаталитического процесса первого порядка (ср. с разд. 
Вторая серия опытов: меняется концентрация Избыточного реагента (или катализатора).
Инвариант  Кинетические кривые, обнаруживающие это свойство, могут быть преобразованы по оси
Кинетические кривые, обнаруживающие это свойство, могут быть преобразованы по оси  с коэффициентом отображения, который линейно связан с начальной концентрацией. Это указывает на то, что меняющаяся концентрация избыточного реагента не входит в
с коэффициентом отображения, который линейно связан с начальной концентрацией. Это указывает на то, что меняющаяся концентрация избыточного реагента не входит в  а скорее появляется в виде множителя в уравнении скорости, т.е. является частью эффективной константы скорости:
а скорее появляется в виде множителя в уравнении скорости, т.е. является частью эффективной константы скорости:

где  Чтобы найти вид этой функции, строят зависимость коэффициента отображения от концентрации избыточного реагента. Обработка таких графиков будет рассмотрена в разд. 4.5.2. Здесь заметим только, что коэффициенты отображения можно использовать аналогичным образом для оценки зависимости скорости от температуры, растворителя и т.д. (что будет обсуждаться в соответствующих главах).
Чтобы найти вид этой функции, строят зависимость коэффициента отображения от концентрации избыточного реагента. Обработка таких графиков будет рассмотрена в разд. 4.5.2. Здесь заметим только, что коэффициенты отображения можно использовать аналогичным образом для оценки зависимости скорости от температуры, растворителя и т.д. (что будет обсуждаться в соответствующих главах).
Инвариант II. Для рассматриваемого случая инвариант II встречается Редко и точно так же дает уравнение

Следует отметить, что помимо информации о механизме реакции свойства инвариантности обладают еще и тем преимуществом, что все кривые данной серии опытов можно свести к единственной кривой для Дальнейшей обработки. Таким образом, результирующая кривая имеет
более точную форму, чем отдельные кривые. Это особенно удобно, если экспериментальные кривые получают только по нескольким точкам.
Теперь остается прокомментировать практические аспекты проверки свойств инвариантности, в особенности инварианта I, представляющего наибольшую практическую ценность. Легко видеть, что первоначальная процедура, основанная на рассмотрении рис. 4-4, довольно трудоемка. «Более того, она может оказаться неточной, особенно при наличии только нескольких экспериментальных точек, поскольку трудно определить систематические отклонения. При автоматической и непрерывной записи кривых  их обработка не вызывает осложнений. В этом случае стандартную кривую можно скопировать на кусок кальки и затем совмещать с другими кривыми, вычерченными при соответствующих изменениях развертки по оси времени и чувствительности. Пример показан на рис. 3-11.
их обработка не вызывает осложнений. В этом случае стандартную кривую можно скопировать на кусок кальки и затем совмещать с другими кривыми, вычерченными при соответствующих изменениях развертки по оси времени и чувствительности. Пример показан на рис. 3-11.
Известен и другой доступный графический метод, который можно использовать следующим образом. Рассмотрим две кривые, которые отличаются только параметром, не входящим в  и не зависят от времени:
и не зависят от времени:

Введем коэффициент 

и проинтегрируем:

или, в логарифмической форме,

Для данных значений  т.е. при одинаковой степени превращения, левые части последних двух уравнений идентичны, а правые различаются только на член
т.е. при одинаковой степени превращения, левые части последних двух уравнений идентичны, а правые различаются только на член  (промежутки времени
(промежутки времени  необходимы для израсходования одного и того же количества А). Так как этот анализ не дает вида
необходимы для израсходования одного и того же количества А). Так как этот анализ не дает вида

Рис. 4-5. Проверка свойства инварианта 
функции  то ее можно аппроксимировать в левые части уравнений соответствующей величиной
то ее можно аппроксимировать в левые части уравнений соответствующей величиной  Это допустимо, поскольку
Это допустимо, поскольку  являются однозначными функциями
являются однозначными функциями  (математически первые производные от
(математически первые производные от  не имеют нулевых значений). Построение зависимости
не имеют нулевых значений). Построение зависимости  от
от  для серии опытов даст набор кривых, которые будут различаться только соответствующей (постоянной) величиной
для серии опытов даст набор кривых, которые будут различаться только соответствующей (постоянной) величиной  таким образом, могут быть совмещены простым сдвигом в одном измерении (рис. 4-5). На практике это означает, что совместимость по оси времени кривых данной серии опытов в координатах
таким образом, могут быть совмещены простым сдвигом в одном измерении (рис. 4-5). На практике это означает, что совместимость по оси времени кривых данной серии опытов в координатах  свидетельствует о том, что влияние меняющейся концентрации избыточного реагента в уравнении скорости выражается просто множителем и не зависит от времени»
свидетельствует о том, что влияние меняющейся концентрации избыточного реагента в уравнении скорости выражается просто множителем и не зависит от времени»
Аналогично данные  из серии опытов, в которой меняли концентрацию реагента, находящегося в недостатке, могут быть представлены в координатах
из серии опытов, в которой меняли концентрацию реагента, находящегося в недостатке, могут быть представлены в координатах  том случае, когда полученные таким путем линии совместимы при сдвиге (без поворота) вдоль оси ординат, уравнение скорости является однородным и линейным. В простейшем случае получаются параллельные прямые. На этой стадии совершенно очевидна связь метода трансформации с интегральным методом.
том случае, когда полученные таким путем линии совместимы при сдвиге (без поворота) вдоль оси ординат, уравнение скорости является однородным и линейным. В простейшем случае получаются параллельные прямые. На этой стадии совершенно очевидна связь метода трансформации с интегральным методом.
4.3.4. Применение трех методов
Как мы видели, каждый из рассмотренных методов имеет свои преимущества и недостатки, которые можно обобщить следующим образом. Использование дифференциального метода не требует допущений, касающихся гипотез о схеме реакции. Однако этот метод использует не первичные экспериментальные данные, а второе поколение данных, которые трудно определить с достаточной точностью. Для интегрального метода мы наблюдаем обратную ситуацию. В расчете непосредственно используются данные  но обработку кинетических данных начинают с предположения
но обработку кинетических данных начинают с предположения
о зависимости между концентрацией и временем, которая проверяется по экспериментальным данным. Наконец, метод трансформации объединяет преимущества обоих предыдущих методов. Но его главным недостатком является то, что он, как правило, не дает численных значений констант скоростей, а дает только ключ к виду уравнения скорости.
Как будет видно из дальнейшего изложения, систематический кинетический анализ позволяет использовать преимущества всех трех методов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
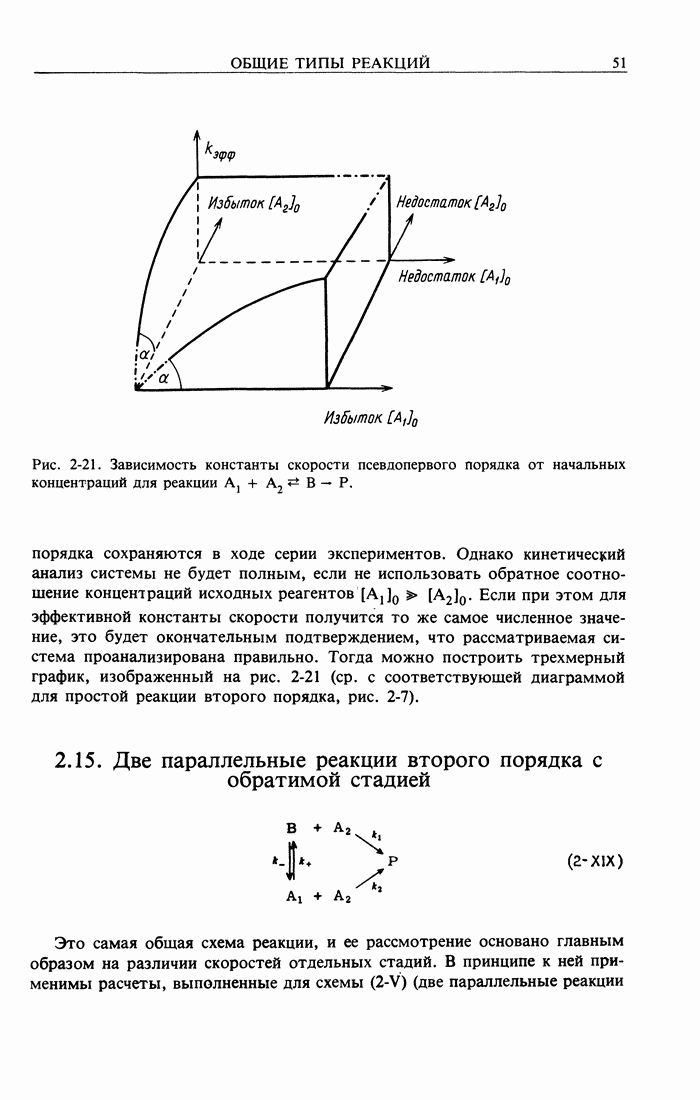
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
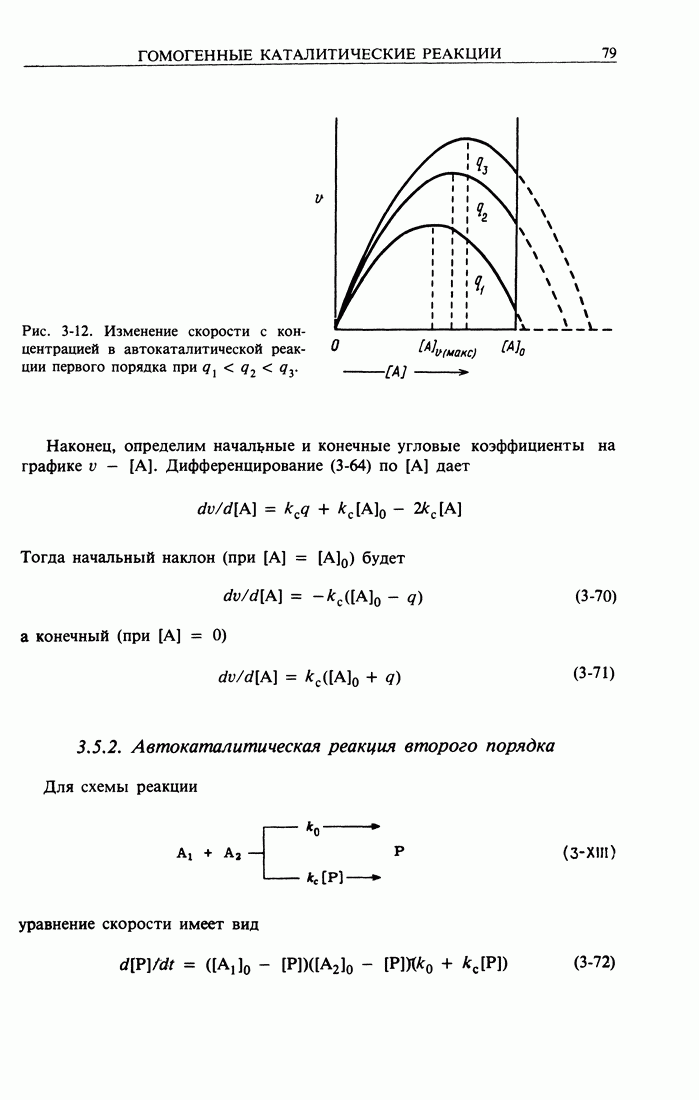
- 3.5. Автокаталитические реакции
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
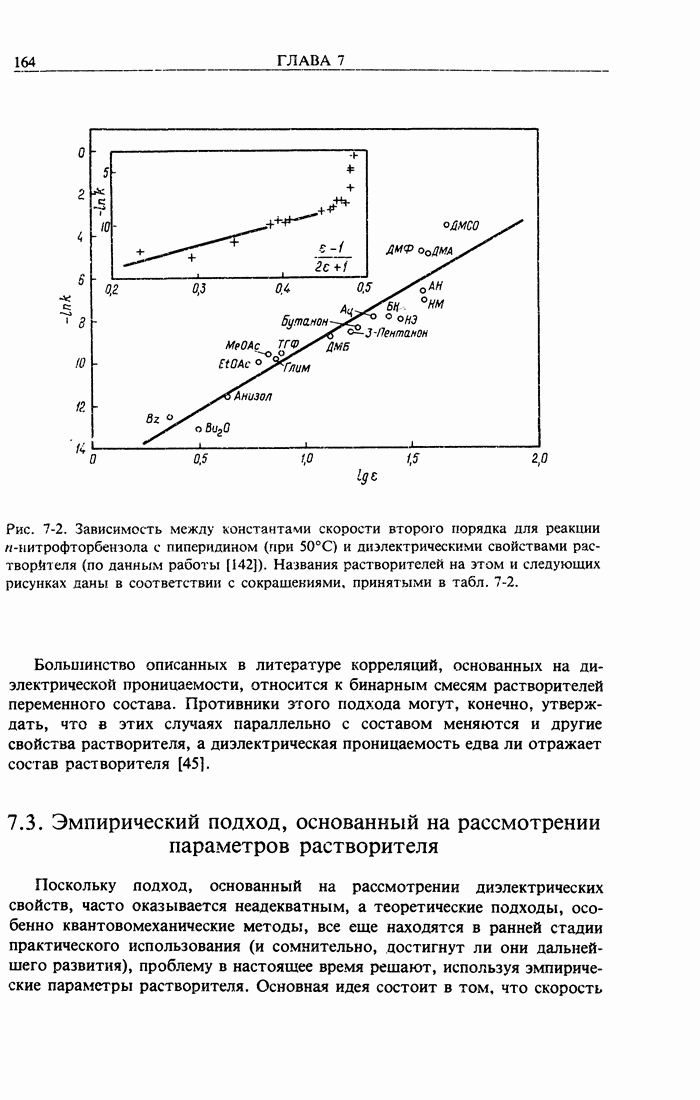
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
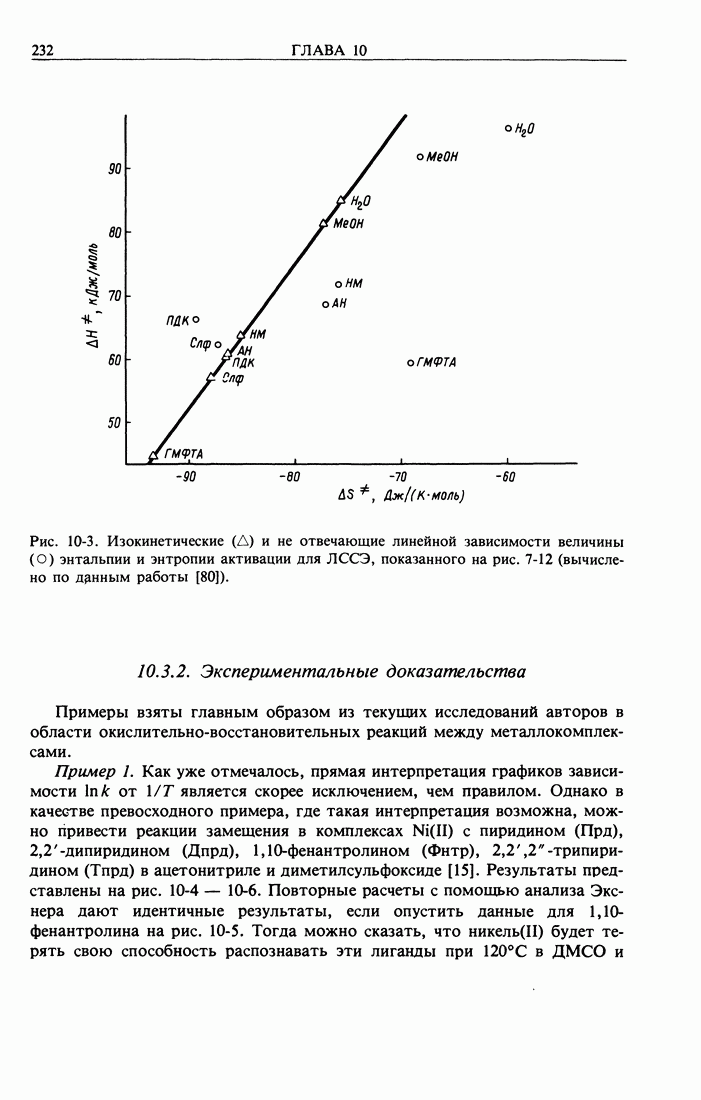
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений