| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.3. Две параллельные реакции первого порядка

Дифференциальные уравнения для реагентов и продуктов имеют вид

Первое уравнение можно прямо записать в интегральной форме по аналогии с (2-4):

Деление (2-25) на (2-26) дает

Поскольку изначально в реакции присутствовал только реагент А, то  и поэтому можно записать
и поэтому можно записать

Таким образом, отношение концентраций продуктов зависит только от отношения констант скоростей. Подставляя (2-27) в уравнение материального баланса  получаем
получаем

Комбинируя два последних уравнения, находим

К тем же самым уравнениям можно прийти, подставляя выражение  из (2-27) соответственно в (2-25) и (2-26) и затем интегрируя. На рис. 2-8 показано изменение концентрации реагента и продуктов для произвольных значений
из (2-27) соответственно в (2-25) и (2-26) и затем интегрируя. На рис. 2-8 показано изменение концентрации реагента и продуктов для произвольных значений 
Суть рассмотренного случая состоит в том, что как расходование реагента, так и образование продукта подчиняются закону скорости первого порядка. Поэтому все методы, описанные для последнего, применимы и здесь для получения в любой момент времени суммы констант скоростей двух стадий. Так, графики зависимости  или
или  от времени дают прямую, тангенс угла наклона которой равен
от времени дают прямую, тангенс угла наклона которой равен 
Для определения каждой из констант нужно исключить из (2-31) выражение в круглых скобках, использовав (2-27):


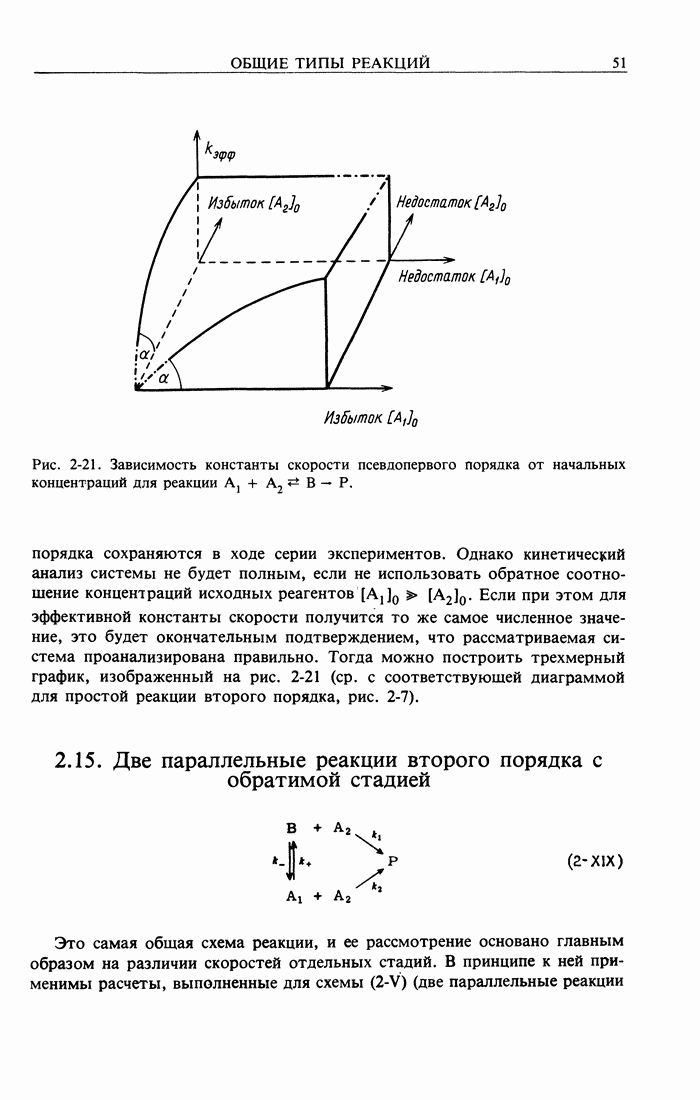
Рис. 2-8. Кривые зависимости концентрации от времени для двух параллельных реакций первого порядка.
Аналогично из (2-32) имеем

График зависимости  и
и  от
от  представляет собой прямую, проходящую через начало координат, с угловыми коэффициентами, равными
представляет собой прямую, проходящую через начало координат, с угловыми коэффициентами, равными  соответственно. Далее, как видно из уравнения (2-29), график зависимости
соответственно. Далее, как видно из уравнения (2-29), график зависимости  от
от  также является прямой, проходящей через начало координат, с угловым коэффициентом
также является прямой, проходящей через начало координат, с угловым коэффициентом  Последние два графика могут служить признаком параллельных реакций первого порядка. Аналогичным образом такие же методы применимы и к большему числу параллельных реакций.
Последние два графика могут служить признаком параллельных реакций первого порядка. Аналогичным образом такие же методы применимы и к большему числу параллельных реакций.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
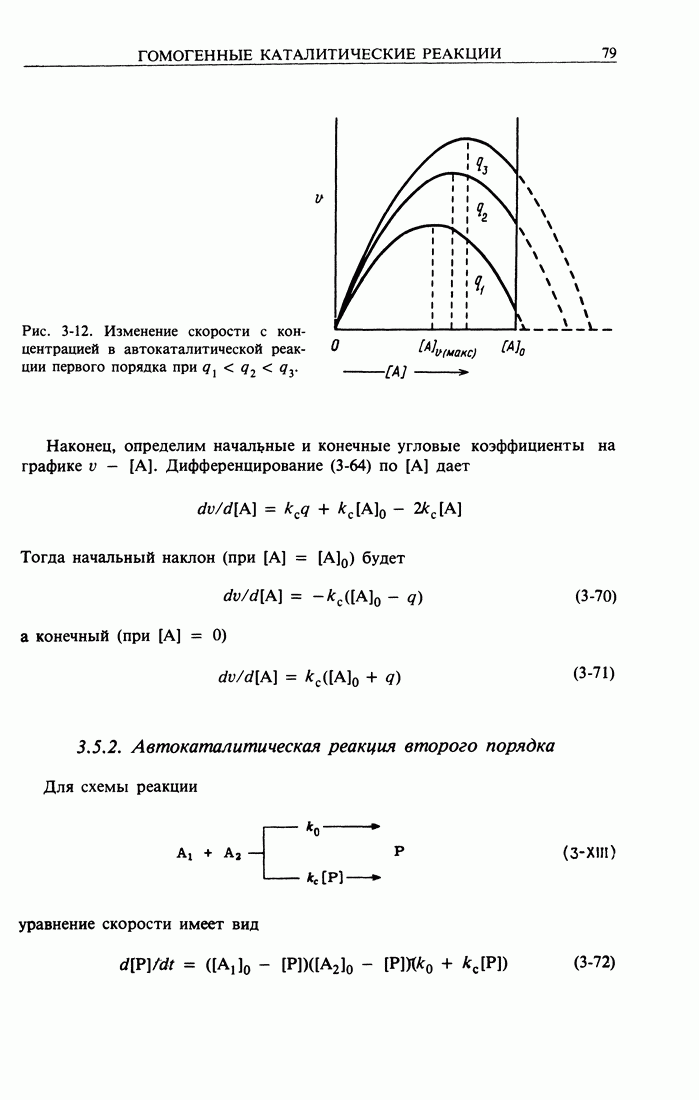
- 3.5. Автокаталитические реакции
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
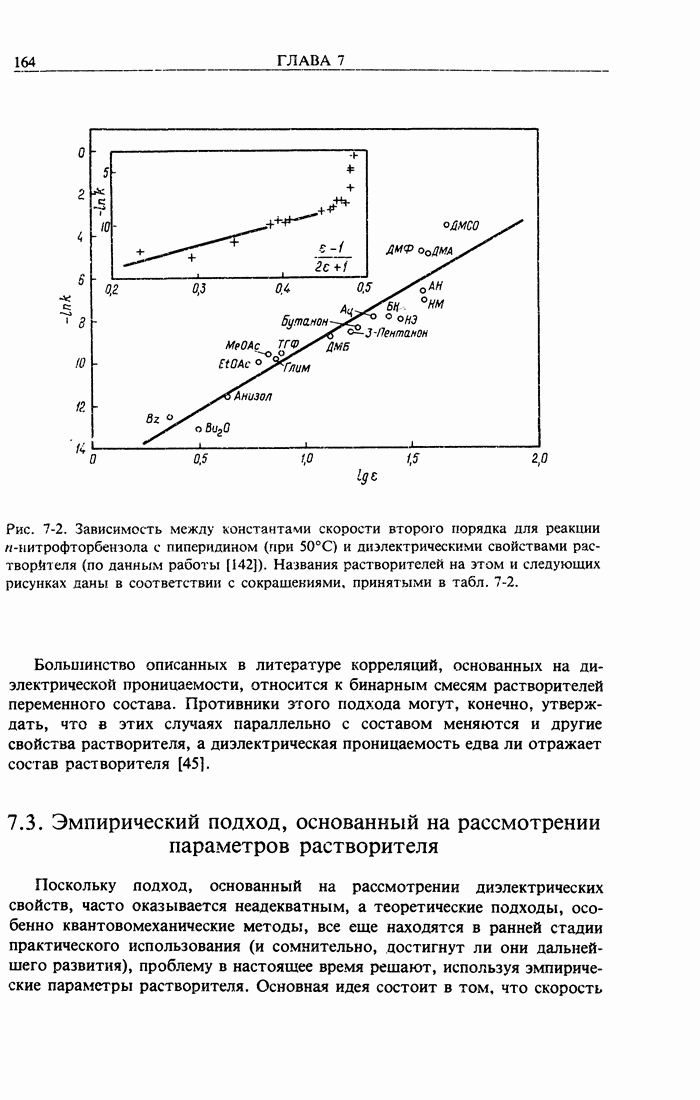
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
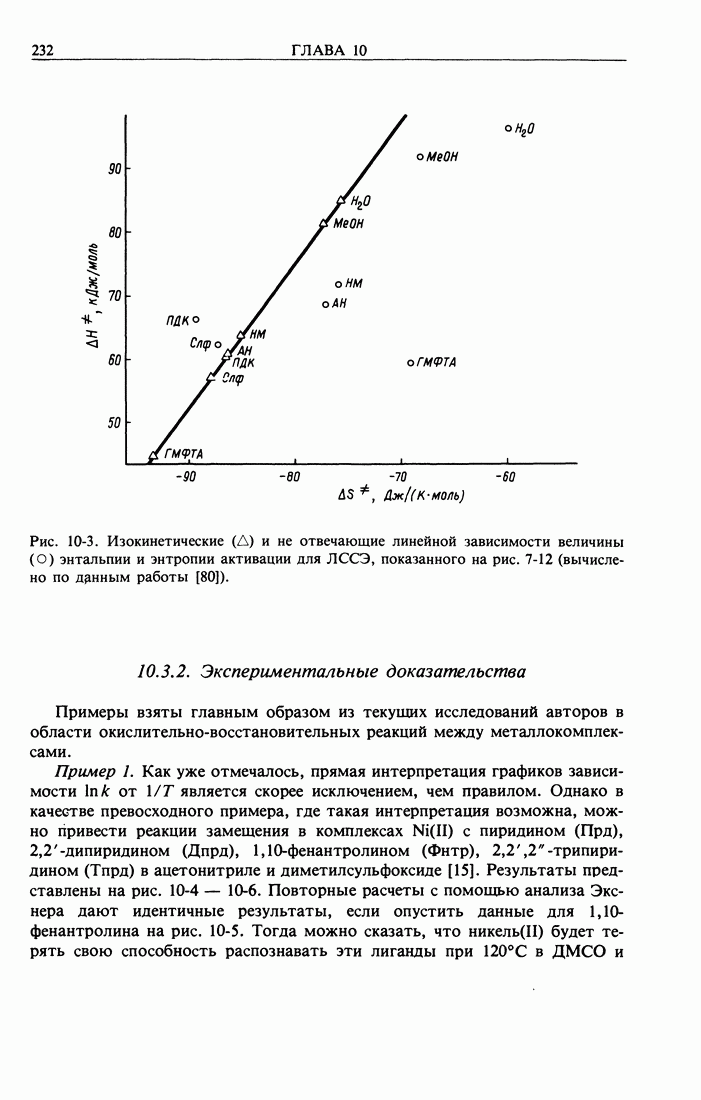
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений