| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.6. Физическая модель реакции
Как уже говорилось, схема реакции однозначно характеризуется набором дифференциальных уравнений, каждое из которых представляет скорость изменения концентрации одного из участвующих в реакции веществ. Поэтому в предыдущих главах описание каждого типа реакции начиналось с записи соответствующего набора уравнений. С другой стороны, математическая модель реакции выражается одним определенным уравнением скорости, соответствующим кинетически измеряемым частицам. Следующей стадией анализа является физическая интерпретация математической модели. Это означает отнесение элементарных реакций к каждому члену выражения скорости, посредством чего математические константы преобразуют в физические величины, т.е. в константы скорости, константы равновесия и их произведения. Затем остается проверить, можно ли объединить элементарные стадии, на которые указывает математическая модель, таким образом, чтобы получить на молекулярном уровне непрерывное описание всего пути реакции, от начального до конечного состояния. Если это удается сделать, то полученное уравнение скорости представляет физическую модель реакции. Иногда математическая модель оказывается сокращенной формой физической модели. Это случается, когда выбранные экспериментальные условия скрывают некоторые элементарные стадии. Чтобы выявить эти стадии, необходимо подходящим образом модифицировать условия. Если математическая модель допускает более чем одну физическую интерпретацию, то необходимы дальнейшие кинетические исследования. Из-за огромного числа комбинаций уравнений, выводимых из первой и второй серий экспериментов, мы не будем обсуждать полные математические модели, а остановимся на физических обоснованиях некоторых примеров, полученных из ранее выведенных уравнений.
4.6.1. Физический смысл некоторых математически выведенных уравнений
Из уравнения 
Константы этого уравнения непосредственно дают константы сокрости двух параллельных реакций, одна из которых некаталитическая  а другая — автокаталитическая
а другая — автокаталитическая 

См. схему (3-XI) в разд. 3.5.1.
Из уравнения 

Рис. 4-22. Иллюстрация того, что уравнение  является упрощением физической модели.
является упрощением физической модели.
Это уравнение является упрощением физической модели и справедливо только для тех случаев, когда исследуют область концентраций, отмеченную на рис. 4-22 сплошной линией. Чтобы проследить за остальной частью кривой (изображенной пунктиром), необходимо повторить измерения при более низких значениях  В любом случае полная кривая описывается уравнением (4-36), которое здесь принимает вид
В любом случае полная кривая описывается уравнением (4-36), которое здесь принимает вид

При условии  уравнение (4-91) сводится к уравнению
уравнение (4-91) сводится к уравнению  в котором
в котором  равна
равна  Физический смысл уравнения
Физический смысл уравнения  заключается в том, что А не участвует в лимитирующей стадии. Такое поведение типично для реакций, катализируемых комплексами металлов, и встречается в двух следующих ситуациях.
заключается в том, что А не участвует в лимитирующей стадии. Такое поведение типично для реакций, катализируемых комплексами металлов, и встречается в двух следующих ситуациях.
а) Катализатор быстро реагирует с А, давая комплекс  который медленно превращается в продукты. В ходе всей реакции катализатор практически насыщен веществом А, которое поэтому не влияет на скорость:
который медленно превращается в продукты. В ходе всей реакции катализатор практически насыщен веществом А, которое поэтому не влияет на скорость:

Если в реакции участвует один реагент, то коэффициенты в (4-91), исходя из (3-22), имеют вид

Если в реакции участвуют два реагента ( то из (3-13) следует, что
то из (3-13) следует, что

См. схемы (3-II) и  в разд. 3.1 и 3.2.
в разд. 3.1 и 3.2.
б) Лимитирующей стадией является взаимодействие катализатора с  По сравнению с этим взаимодействием
По сравнению с этим взаимодействием  быстро реагирует с А:
быстро реагирует с А:

Если комплекс с катализатором образуется медленно и применимо условие  то (3-13) сводится к уравнению
то (3-13) сводится к уравнению

(отметьте изменение подстрочных индексов по сравнению с гл. 3) или в иной форме:

После деления числителя и знаменателя на к  получаем уравнение
получаем уравнение

позволяющее сделать отнесение математических констант уравнения (4-91):

Конечно, уравнение  может также относиться и к некаталитическим реакциям, и случай, когда А реагирует с активной частицей
может также относиться и к некаталитическим реакциям, и случай, когда А реагирует с активной частицей  образующейся из
образующейся из  в лимитирующей стадии, эквивалентен схеме (4-II):
в лимитирующей стадии, эквивалентен схеме (4-II):

Согласно (2-109), константы выражаются как

Для каждой из трех последних схем реакции расходование А соответствует нулевому порядку до тех пор, пока содержание А в реакционной смеси не уменьшится настолько, что больше не будет выполняться условие лимитирующей стадии. Поэтому графики зависимости  от
от  не имеют резкого обрыва, а характеризуются более или менее выраженной кривизной на конечных стадиях. См. случай 1 в разд. 2.11 и случай 1 в разд. 3.1.
не имеют резкого обрыва, а характеризуются более или менее выраженной кривизной на конечных стадиях. См. случай 1 в разд. 2.11 и случай 1 в разд. 3.1.
Из уравнения (4-10): 
Случай, когда уменьшение  описывается простой кривой первого порядка, наблюдается для разных типов реакций, которые мы теперь рассмотрим более подробно.
описывается простой кривой первого порядка, наблюдается для разных типов реакций, которые мы теперь рассмотрим более подробно.
Тип 1:  Это реакция
Это реакция  (см. разд. 2.1), которая встречается редко, например при внутримолекулярных перегруппировках. Одновременно уравнение (4-10) часто встречается как выражение для математической модели реакции, включающей два реагента
(см. разд. 2.1), которая встречается редко, например при внутримолекулярных перегруппировках. Одновременно уравнение (4-10) часто встречается как выражение для математической модели реакции, включающей два реагента  в условиях псевдопервого порядка
в условиях псевдопервого порядка  и
и  в (4-10) является константой скорости псевдопервого порядка k. Если Агэфф
в (4-10) является константой скорости псевдопервого порядка k. Если Агэфф  то
то

При обратном соотношении концентраций

где к та же самая. Тогда мы имеем дело с простой реакцией второго порядка

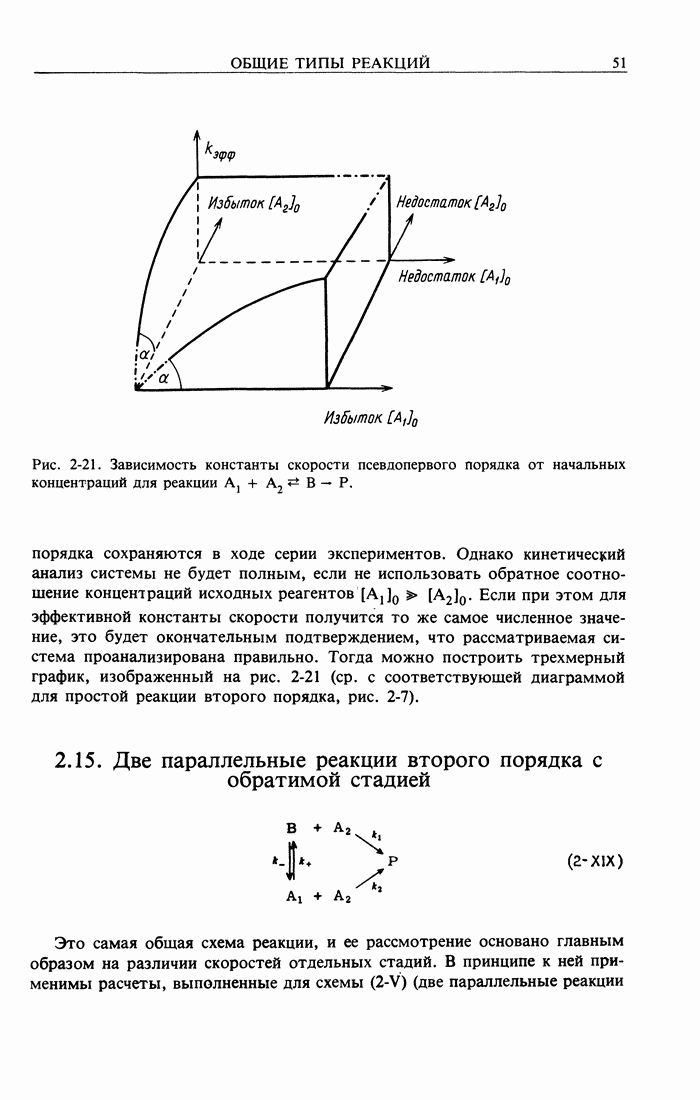
См. схему (2-III) и рис. 2-7. Иногда уравнение (4-10) может выражать закон скорости псрвдопервого порядка, например для реакций сольволиза, где  растворитель, присутствующий обычно в большом избытке.
растворитель, присутствующий обычно в большом избытке.
Довольно часто к стремится к предельному значению при возрастании  Комбинируя (4-10) и (4-81), получаем
Комбинируя (4-10) и (4-81), получаем

Характер насыщения к указывает на то, что реакция происходит через образование интермедиата. При большом избытке А уравнение скорости имеет вид


Рис. 4-23. Некоторые сложные случаи для реакций псевдопервого порядка.
(Заметим, что численные значения констант здесь те же, что и в приведенных выше уравнениях.) Это подтверждает схему (2-XVIII). См. разд. 2.14 и рис. 2-21. В этом случае константы выражаются как

Кроме этих двух простых ситуаций для реакции псевдопервого порядка может возникнуть и сложная ситуация, когда численные значения  зависят от того, какой из реагентов берется в избытке. Некоторые сложные случаи показаны на рис. 4-23.
зависят от того, какой из реагентов берется в избытке. Некоторые сложные случаи показаны на рис. 4-23.
Рис. 4-239а. Прямые 1 и 2 не пересекаются. Если исключены ошибки эксперимента (например, ошибки в определении концентраций), то здесь мы имеем дело с простой реакцией второго порядка, в которой реагент  загрязнен настолько, что его истинная концентрация маньше предполагаемой. Возможно и другое осложнение, связанное с тем, что в данных
загрязнен настолько, что его истинная концентрация маньше предполагаемой. Возможно и другое осложнение, связанное с тем, что в данных
условиях только часть вещества  активна, и поэтому его относительное количество всегда пропорционально его абсолютной концентрации. В этом случае в рассматриваемом интервале времени не успевает установиться равновесие между активными и неактивными компонентами
активна, и поэтому его относительное количество всегда пропорционально его абсолютной концентрации. В этом случае в рассматриваемом интервале времени не успевает установиться равновесие между активными и неактивными компонентами 
Рис. 4-23,6. Несмотря на то что  возрастает при увеличении избытка
возрастает при увеличении избытка  (линия
(линия  при высоких значениях
при высоких значениях  кривая стремится к насыщению (линия 2). Это может быть вызвано двумя причинами: либо реакция протекает через образование интермедиата, распад которого сильно ускоряется под действием А, либо это простая реакция второго порядка, в которой вещество
кривая стремится к насыщению (линия 2). Это может быть вызвано двумя причинами: либо реакция протекает через образование интермедиата, распад которого сильно ускоряется под действием А, либо это простая реакция второго порядка, в которой вещество  состоит из частиц неодинаковой активности, и относительная концентрация активной формы уменьшается с ростом
состоит из частиц неодинаковой активности, и относительная концентрация активной формы уменьшается с ростом  Чтобы различить эти случаи, следует сфокусировать внимание на двух других сериях опытов. Когда концентрация реагента
Чтобы различить эти случаи, следует сфокусировать внимание на двух других сериях опытов. Когда концентрация реагента  находящегося в недостатке, меняется при постоянном избытке А (линия 5), в последнем случае (т.е. при неодинаковой активности частиц
находящегося в недостатке, меняется при постоянном избытке А (линия 5), в последнем случае (т.е. при неодинаковой активности частиц  уравнение
уравнение  должно быть справедливо только при низких значениях
должно быть справедливо только при низких значениях  так как при более высоких значениях не может наблюдаться псевдопервый порядок. В этой области концентраций эффективная константа скорости, определенная по отношению
так как при более высоких значениях не может наблюдаться псевдопервый порядок. В этой области концентраций эффективная константа скорости, определенная по отношению  (ср. с заключительным замечанием в разд. 4.5.3), должна уменьшаться таким образом, чтобы линия 3 пересеклась с линией 4, параллельной оси
(ср. с заключительным замечанием в разд. 4.5.3), должна уменьшаться таким образом, чтобы линия 3 пересеклась с линией 4, параллельной оси  т.е. скорость не меняется при изменении
т.е. скорость не меняется при изменении  С другой стороны, если в реакции участвует интермедиат, линия 3 должна идти параллельно оси
С другой стороны, если в реакции участвует интермедиат, линия 3 должна идти параллельно оси  а линия 4 — линейно уменьшаться при возрастании
а линия 4 — линейно уменьшаться при возрастании  Таким образом, очевидно, что рис.
Таким образом, очевидно, что рис.  относится к реакции, в которой реагент
относится к реакции, в которой реагент  состоит из частиц разной активности. Это можно определить и другими физическими методами. Если трехмерный график строят, используя величины истинных концентраций активных частиц вместо общей концентрации
состоит из частиц разной активности. Это можно определить и другими физическими методами. Если трехмерный график строят, используя величины истинных концентраций активных частиц вместо общей концентрации  то должен получиться график, изображенный на рис. 2-7.
то должен получиться график, изображенный на рис. 2-7.
Рис. 4-23В соответствии с высказанными выше соображениями данный график иллюстрирует образование интермедиата, распад которого сильно ускоряется веществом А. Этот случай типичен для каталитических реакций второго порядка, в ходе которых катализатор предварительно связывается с реагентом А.
Рис. 4-23,г. Насыщение происходит либо при высоких значениях  либо при высоких значениях
либо при высоких значениях  но предельная величина
но предельная величина  при этом различается. Это наблюдение должно соответствовать реакции, происходящей через образование интермедиата, распад которого катализируется А, хотя такой эффект и менее выражен, чем в случае рис. 4-23,в.
при этом различается. Это наблюдение должно соответствовать реакции, происходящей через образование интермедиата, распад которого катализируется А, хотя такой эффект и менее выражен, чем в случае рис. 4-23,в.
Тип 2: образуется более чем один продукт. Если отношение концентраций продуктов не меняется во времени, это указывает на то, что происходят параллельные реакции первого или псевдопервого порядка. См. схему (2-IV) в разд. 2.3. Важно убедиться, что отношение продуктов постоянно в любой момент времени, так как в двух последовательных реакциях первого
порядка  тоже линейно меняется во времени, поскольку существует вероятность того, что интермедиат с очень низкой реакционной способностью имитирует конечный продукт. Но в таком случае отношение
тоже линейно меняется во времени, поскольку существует вероятность того, что интермедиат с очень низкой реакционной способностью имитирует конечный продукт. Но в таком случае отношение  не может быть постоянным.
не может быть постоянным.
Тип 3: изменение  во времени выражается
во времени выражается  -образной кривой. Это свидетельствует о последовательности реакций (псевдо)первого порядка. См. схему (2-VI) в разд. 2.5.
-образной кривой. Это свидетельствует о последовательности реакций (псевдо)первого порядка. См. схему (2-VI) в разд. 2.5.
Тип 4: из зависимости  от
от  явствует, что
явствует, что  при
при  отличается от истинной начальной концентрации. Этому случаю соответствуют схемы (2-XIV) или (2-XVIII), см. разд. 2.11 и 2.14. Уменьшение
отличается от истинной начальной концентрации. Этому случаю соответствуют схемы (2-XIV) или (2-XVIII), см. разд. 2.11 и 2.14. Уменьшение  начали измерять после того, как установилось равновесие А В, поэтому
начали измерять после того, как установилось равновесие А В, поэтому  графике полулогарифмической зависимости при
графике полулогарифмической зависимости при  появляется не
появляется не  (ср. с рис. 2-18).
(ср. с рис. 2-18).
Из уравнения (4-16): 
Это уравнение описывает обратимую реакцию первого порядка. См. схему  в разд. 2.8. Следует, однако, подчеркнуть, что неполное расходование А необязательно указывает на равновесную реакцию. Возможно, что А состоит из частиц неодинаковой активности, как описывается уравнением (4-18). Чтобы различить эти два случая, можно повторить кинетические измерения при более высокой температуре. Возможные изменения графйка с показанные на рис. 4-24, очень информативны. Другой способ заключается в том, чтобы начать измерения реакции со стороны продукта при условии, что в распоряжении имеются чистые продукты.
в разд. 2.8. Следует, однако, подчеркнуть, что неполное расходование А необязательно указывает на равновесную реакцию. Возможно, что А состоит из частиц неодинаковой активности, как описывается уравнением (4-18). Чтобы различить эти два случая, можно повторить кинетические измерения при более высокой температуре. Возможные изменения графйка с показанные на рис. 4-24, очень информативны. Другой способ заключается в том, чтобы начать измерения реакции со стороны продукта при условии, что в распоряжении имеются чистые продукты.
Кривые на рис. 4-24 интерпретируют следующим образом:
(см. скан)

Рис. 4-24. Изменение формы основной полулогарифмической кривой (0) при повышении температуры.
(см. скан)
Все эти типы реакций являются предельными случаями общей схемы (2-Х1Х),см. разд. 2.15. Как уже отмечалось, особенности обработки данных в значительной степени зависят от разности скоростей отдельных стадий. Кривая 4 на приведенном выше рисунке соответствует уравнению (4-23), в котором  и
и  относятся соответственно к константам скорости реакций
относятся соответственно к константам скорости реакций  См. схему
См. схему  в разд. 2.4.
в разд. 2.4.
Из уравнения (4-24): 
Это уравнение соответствует обратимой реакции второго порядка

См. схему (2-XI) в разд. 2.9. Как и в предыдущем примфе, здесь существует вероятность того, что неполное расходование А связано с наличием частиц разной активности. Чтобы выяснить это, либо повторяют измерения при другой температуре, либо строят графическую зависимость  от времени. Линейный характер этой зависимости свидетельствует о том, что имеет место реакция
от времени. Линейный характер этой зависимости свидетельствует о том, что имеет место реакция

Из уравнений (4-28), (4-31) и (4-33): степенные ряды по  Уравнение общего вида
Уравнение общего вида

представляет параллельные реакции с различным порядком по А. Если в уравнении имеется член, не содержащий  то сталкиваются с сокращенной формой уравнения
то сталкиваются с сокращенной формой уравнения  Тогда требуются дальнейшие измерения при низких значениях
Тогда требуются дальнейшие измерения при низких значениях 
Из  (4-36), (4-38), (4-40) и
(4-36), (4-38), (4-40) и  дробно-линейные уравнения скорости типичны для каталитических реакций, хотя и не ограничиваются ими. Вид знаменателя дает определенное
дробно-линейные уравнения скорости типичны для каталитических реакций, хотя и не ограничиваются ими. Вид знаменателя дает определенное
представление о реакции, если иметь в виду различные типы ингибирования, которые обсуждались в разд. 3.4. Рассмотрим обоснование дробно-линейных уравнений скорости.
Возвращаясь к рассуждениям, приведенным в гл. 2 и 3, мы видим, что дробно-линейные уравнения скорости выводятся для реакций, идущих через интермедиат, который образуется в обратимой стадии и который настолько реакционноспособен, что можно применить приближение Боденштейна. Поэтому такой интермедиат называют интермедиатом Боденштейна. Его стационарная концентрация связана с отношением скорости его образования к скорости прямой реакции, включающей обратную реакцию до исходных реагентов. Если скорость реакции зависит от концентрации интермедиата Боденштейна, то в уравнении появляется знаменатель. В качестве примера рассмотрим схему (2-XV):

для которой выражение скорости имеет вид [см. уравнение (2-109)]

Это уравнение может относиться и к каталитическим, и к некаталитическим реакциям. В первом случае, однако, условия становятся более сложными. С учетом катализатора схема (2-XV) преобразуется в схему (3-II), для которой

Если в уравнение материального баланса включить катализатор и вместо  подставить
подставить  то в знаменателе появится сомножитель, соответствующий знаменателю уравнения
то в знаменателе появится сомножитель, соответствующий знаменателю уравнения  и тогда уравнение скорости примет вид
и тогда уравнение скорости примет вид

или, через функцию Михаэлиса,

что тождественно уравнению (3-13).
Что касается реакций, катализируемых комплексами металлов, то, как уже говорилось, в таких реакциях может установиться равновесие между катализатором и другими компонентами реакции; это приводит к дальнейшему уменьшению концентрации свободного катализатора, а значит, и к понижению его активности. Меру такого ингибирования отражает член  в выражении скорости. Согласно уравнению (3-30),
в выражении скорости. Согласно уравнению (3-30),

Каждый член  относится к обратимой побочной реакции с участием катализатора. Он выражается произведением концентраций и констант равновесия и является безразмерной величиной. Если интермедиат Боденштейна сам вовлечен в дополнительное равновесие, то соответствующий член узнают по наличию константы Михаэлиса (или функции Михаэлиса). Существенной особенностью знаменателя в уравнении скорости, представляющем физическую модель, является то, что все входящие в него члены должны быть безразмерными. Конечно, знаменатель можно записать по-разному, но наиболее общепринятая форма записи — это та, что приведена в последнем уравнении, где первый член — единица. При такой форме записи выявляется функция образования комплекса между катализатором и другими компонентами реакционной смеси, т.е. функция закомплексованности. Если знаменатель равен единице, это означает, что весь катализатор находится в свободном состоянии, т.е.
относится к обратимой побочной реакции с участием катализатора. Он выражается произведением концентраций и констант равновесия и является безразмерной величиной. Если интермедиат Боденштейна сам вовлечен в дополнительное равновесие, то соответствующий член узнают по наличию константы Михаэлиса (или функции Михаэлиса). Существенной особенностью знаменателя в уравнении скорости, представляющем физическую модель, является то, что все входящие в него члены должны быть безразмерными. Конечно, знаменатель можно записать по-разному, но наиболее общепринятая форма записи — это та, что приведена в последнем уравнении, где первый член — единица. При такой форме записи выявляется функция образования комплекса между катализатором и другими компонентами реакционной смеси, т.е. функция закомплексованности. Если знаменатель равен единице, это означает, что весь катализатор находится в свободном состоянии, т.е.  Очень важен, конечно, второй член
Очень важен, конечно, второй член  являющийся неотъемлемой характеристикой каталитического процесса поскольку он описывает образование активного комплекса между катализатором и одним из исходных реагентов. Каждый следующий член соответствует обратимой побочной реакции катализатора, в результате чего снижается действующая конценгграция катализатора.
являющийся неотъемлемой характеристикой каталитического процесса поскольку он описывает образование активного комплекса между катализатором и одним из исходных реагентов. Каждый следующий член соответствует обратимой побочной реакции катализатора, в результате чего снижается действующая конценгграция катализатора.
Для получения знаменателя вида  и т.д. необходимо, чтобы один из членов знаменателя в математической модели был численной константой: в противном случае модель неточна, и нужно провести дополнительные эксперименты при низких значениях
и т.д. необходимо, чтобы один из членов знаменателя в математической модели был численной константой: в противном случае модель неточна, и нужно провести дополнительные эксперименты при низких значениях  Чем точнее эта константа, тем меньше ошибка в определении физических констант. Это положение будет продемонстрировано ниже. С другой стороны, если в математической модели нельзя выделить численную константу, то тогда можно получить только относительные величины физических констант.
Чем точнее эта константа, тем меньше ошибка в определении физических констант. Это положение будет продемонстрировано ниже. С другой стороны, если в математической модели нельзя выделить численную константу, то тогда можно получить только относительные величины физических констант.
Теперь рассмотрим два примера преобразования математической модели в физическую.
а) Пусть математическая модель каталитической реакции имеет вид

Деление на  приводит к знаменателю желаемого вида:
приводит к знаменателю желаемого вида:

откуда

Необходимо, чтобы член  имел размерность константы скорости третьего порядка, т.е. произведения константы скорости второго порядка и константы равновесия [ср. с уравнением (3-11)]. Интермедиатами Боденштейна могут быть
имел размерность константы скорости третьего порядка, т.е. произведения константы скорости второго порядка и константы равновесия [ср. с уравнением (3-11)]. Интермедиатами Боденштейна могут быть  или
или  Поскольку реакция имеет первый порядок и по
Поскольку реакция имеет первый порядок и по  и по С, справедлива схема (3-11):
и по С, справедлива схема (3-11):

 Следует напомнить, что
Следует напомнить, что  является функцией
является функцией  Поэтому, чтобы можно было пренебречь влиянием
Поэтому, чтобы можно было пренебречь влиянием  необходимо убедиться в том, что коэффициент трансформации
необходимо убедиться в том, что коэффициент трансформации  линейно зависит от
линейно зависит от  Каждый член знаменателя в уравнении (4-107) относится к реакции, включающей катализатор:
Каждый член знаменателя в уравнении (4-107) относится к реакции, включающей катализатор:

или, наоборот,


Последний член указывает на обратимую реакцию, связанную и говорит в пользу уравнения (4-110) по сравнению с (4-109). Отсюда следует, что в математической модели опущен член вида  Тогда либо повторяют измерения, используя высокую концентрацию предварительно добавляемого продукта, либо определяют
Тогда либо повторяют измерения, используя высокую концентрацию предварительно добавляемого продукта, либо определяют  что возможно сделать, так как известна
что возможно сделать, так как известна  Совершенно очевидно, что число неизвестных превышает число имеющихся уравнений, поэтому необходимы дополнительные данные, которые можно получить методом начальных скоростей. Поучительным примером сложной реакции, проанализированной описанным здесь методом, является эпоксидирование циклогексена гидропероксидом этилбензола в присутствии молибденового катализатора [116, 119].
Совершенно очевидно, что число неизвестных превышает число имеющихся уравнений, поэтому необходимы дополнительные данные, которые можно получить методом начальных скоростей. Поучительным примером сложной реакции, проанализированной описанным здесь методом, является эпоксидирование циклогексена гидропероксидом этилбензола в присутствии молибденового катализатора [116, 119].
б) Хорошим примером дробно-линейного уравнения скорости, описывающего неаталитическую реакцию, служит уравнение (4-88):

Каждый член в знаменателе относится к реакции интермедиата Боденштейна. Поскольку ни  ни
ни  не связаны с
не связаны с  первый член знаменателя представляет величину, обратную константе реакции интермедиата с образованием исходных веществ. Второй член
первый член знаменателя представляет величину, обратную константе реакции интермедиата с образованием исходных веществ. Второй член  соответствует прямой реакции с
соответствует прямой реакции с  приводящей к конечным продуктам. Константы выражаются как
приводящей к конечным продуктам. Константы выражаются как

См. схему (2-XV) в разд. 2.11.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
- 3.5. Автокаталитические реакции
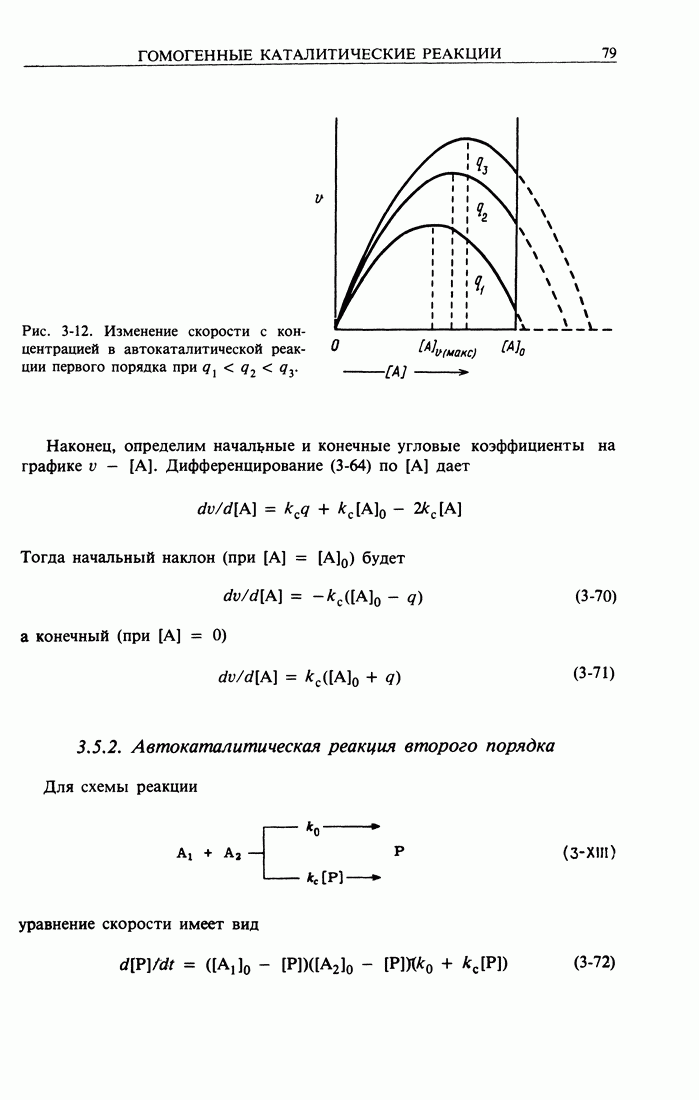
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
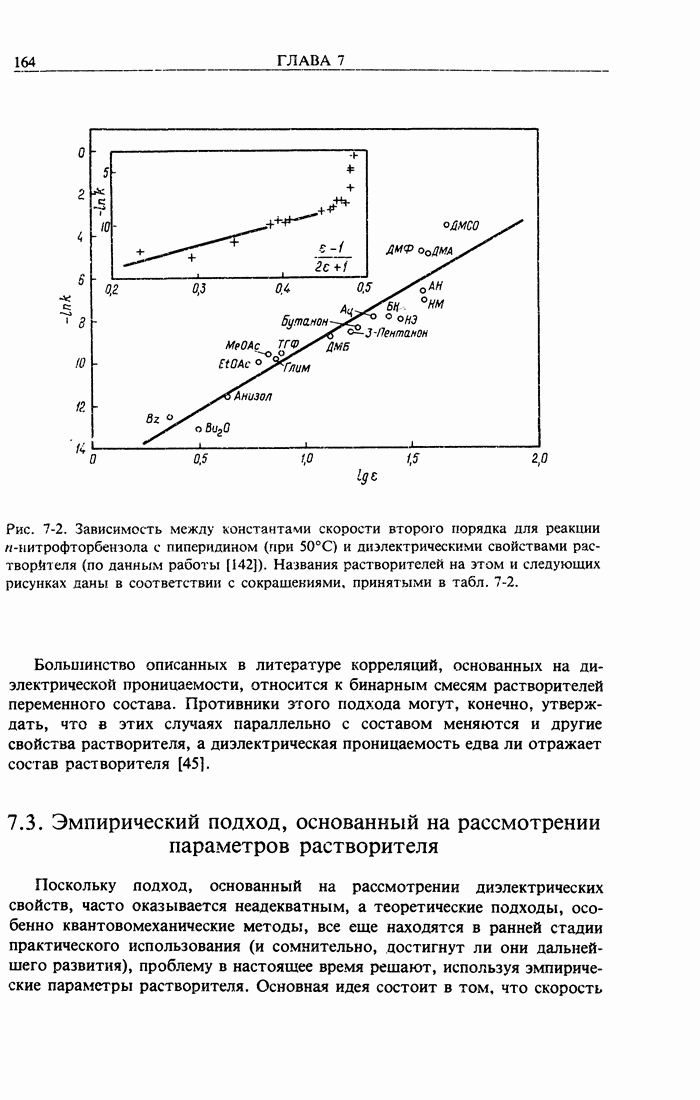
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
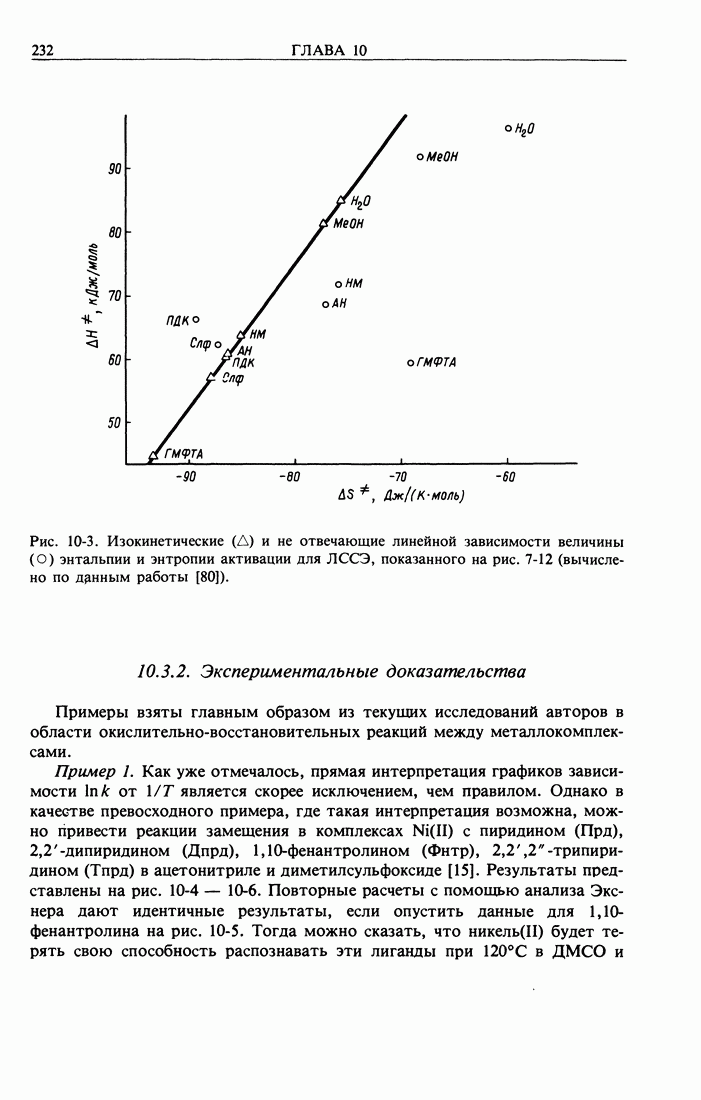
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений