| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.5.3. Из последующих серий опытов
Наконец, нужно убедиться в том, что математическая модель, выведенная из предыдущих серий опытов, представляет общее уравнение скорости рассматриваемой реакции. Такое уравнение должно быть справедливо для любого соотношения концентраций и поэтому не может содержать концентрации избыточных реагентов. Чтобы осуществить такую проверку, берут обратное отношение начальных концентраций реагентов и смотрят, приведет ли это к такому же, как и раньше, выражению скорости. Обычно это удается. Например, при условии 

Тогда при обратном соотношении реагентов, т.е. при  получаем
получаем

где  и
и  тождественны соответствующим константам уравнения (4-86). Поэтому уравнение можно обобщить, опустив подстрочные индексы, отмечающие избыточные концентрации:
тождественны соответствующим константам уравнения (4-86). Поэтому уравнение можно обобщить, опустив подстрочные индексы, отмечающие избыточные концентрации:

Очевидно, последнее выражение скорости дает такую же информацию, что и два предыдущих уравнения, а именно при  реакция подчиняется закону скорости псевдопервого порядка, тогда как при
реакция подчиняется закону скорости псевдопервого порядка, тогда как при  порядок реакции меняется от нуля до единицы.
порядок реакции меняется от нуля до единицы.
Однако уравнение скорости может измениться при замене избыточного реагента на реагент, находящийся в недостатке. В экстремальных случаях могут меняться стехиометрические коэффициенты или даже может пойти совершенно другая реакция. Но помимо этих осложнений в выведенных выражениях скорости могут появиться менее резкие различия, заключающие в себе полезную информацию о ходе реакции. Для примера снова возьмем уравнение (4-86) и обратные концентрации. Тогда вместо (4-87) получается выражение

Это уравнение несовместимо с уравнением (4-86), несмотря на то, что оба уравнения имеют одинаковую математическую форму и даже совпадающие по численным значениям константы. В таком случае напрашивается очевидный вывод, что оба уравнения являются лишь сокращенными формами истинной математической модели. Для того чтобы физически интерпретировать наблюдаемые расхождения, необходимы дальнейшие исследования. Это будет продемонстрировано позднее.
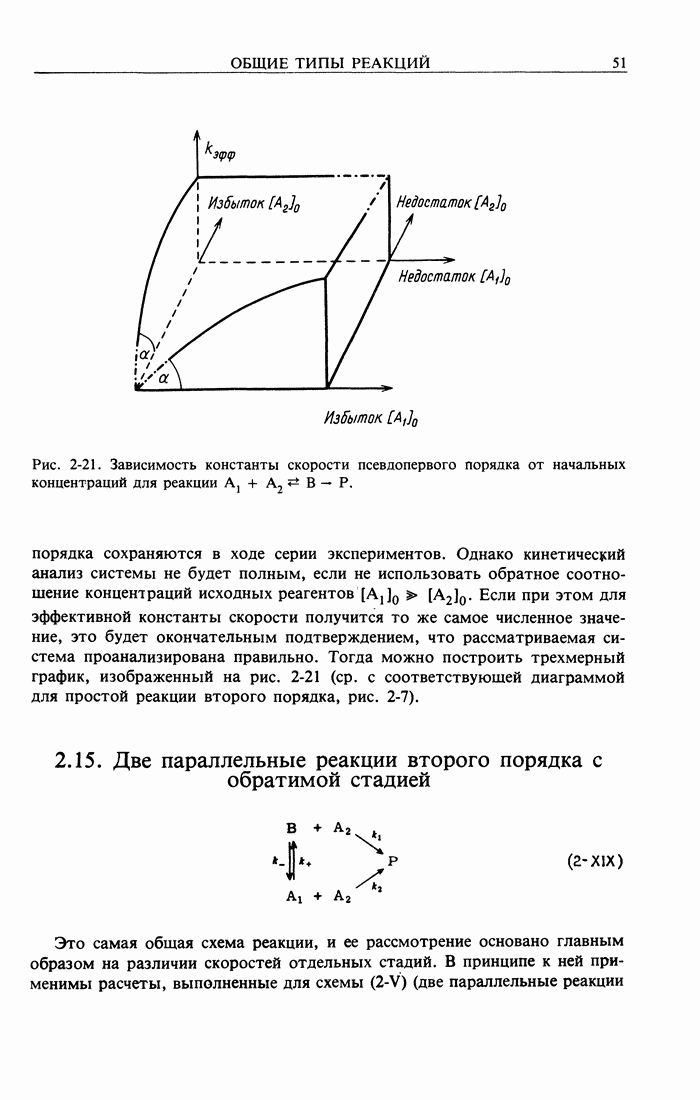
Наконец, численные значения эффективных констант скоростей могут зависеть от того, какой из реагентов берут в избытке. Окончательную разницу можно установить с помощью трехмерных графиков. Такие графики дают также свидетельство надежности значений  полученных из четырех серий опытов: экспериментальные линии на графиках стремятся к общей точке, как показано для простых случаев на рис. 2-7 и 2-21 или для более сложных случаев на рис.
полученных из четырех серий опытов: экспериментальные линии на графиках стремятся к общей точке, как показано для простых случаев на рис. 2-7 и 2-21 или для более сложных случаев на рис.  При необходимости значения к можно также получить в области концентраций, для которой не выполняются условия псевдопервого порядка. Это достигается с помощью метода начальных скоростей. Исходя из уравнения
При необходимости значения к можно также получить в области концентраций, для которой не выполняются условия псевдопервого порядка. Это достигается с помощью метода начальных скоростей. Исходя из уравнения  величину к выражают отношением
величину к выражают отношением  [находящийся в недостатке реагент
[находящийся в недостатке реагент  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 2. ОБЩИЕ ТИПЫ РЕАКЦИЙ
- 2.1. Простая реакция первого порядка
- 2.2. Простая реакция второго порядка
- 2.3. Две параллельные реакции первого порядка
- 2.4. Две параллельные реакции первого порядка с общим продуктом
- 2.5. Последовательность двух реакций первого порядка
- 2.6. Последовательность трех реакций первого порядка
- 2.7. Последовательность реакций смешанного (второго и первого) порядка
- 2.8. Обратимая реакция первого порядка
- 2.9. Обратимая реакция второго порядка
- 2.10. Обратимая реакция смешанного (первого и второго) порядка
- 2.11. Последовательность двух реакций первого порядка с обратимой первой стадией
- 2.12. Последовательность двух обратимых реакций первого порядка
- 2.13. Две параллельные обратимые реакции первого порядка с общим продуктом
- 2.14. Последовательность двух реакций второго и первого порядков с обратимой первой стадией
- 2.15. Две параллельные реакции второго порядка с обратимой стадией
- 3. ГОМОГЕННЫЕ КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
- 3.2. Каталитическая реакция первого порядка
- 3.3. Реакция нулевого порядка
- 3.4. Ингибирование катализатора
- 3.4.1. Обратимое ингибирование
- 3.4.2. Необратимое ингибирование
- 3.5. Автокаталитические реакции
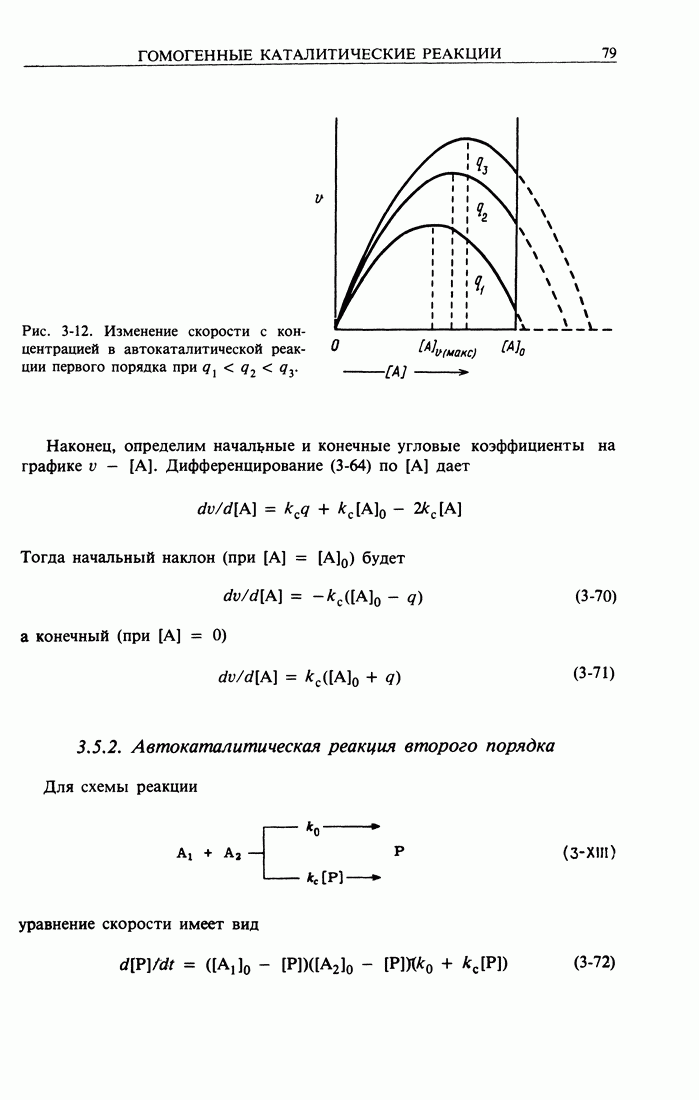
- 3.5.2. Автокаталитическая реакция второго порядка
- 4. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ: СИСТЕМАТИЧЕСКИЙ КИНЕТИЧЕСКИЙ АНАЛИЗ
- 4.2. Выбор условий эксперимента
- 4.3. Методы анализа кривых зависимости концентрации от времени
- 4.4. Порядок реакции и его значение
- 4.5. Математическая модель реакции
- 4.5.2. Из второй серии опытов
- 4.5.3. Из последующих серий опытов
- 4.6. Физическая модель реакции
- 4.7. Выводы
- 4.8. Схема и механизм реакции
- 5. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 5.1. Уравнение Аррениуса
- 5.2. Теория активированного комплекса
- 5.3. Теория столкновений
- 5.4. Сравнение выведенных уравнений
- 5.5. Физический смысл энтропии активации
- 5.6. Физический смысл энергии активации
- 5.7. Формы аррениусовских графиков
- 6. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
- 7. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ РАСТВОРИТЕЛЯ
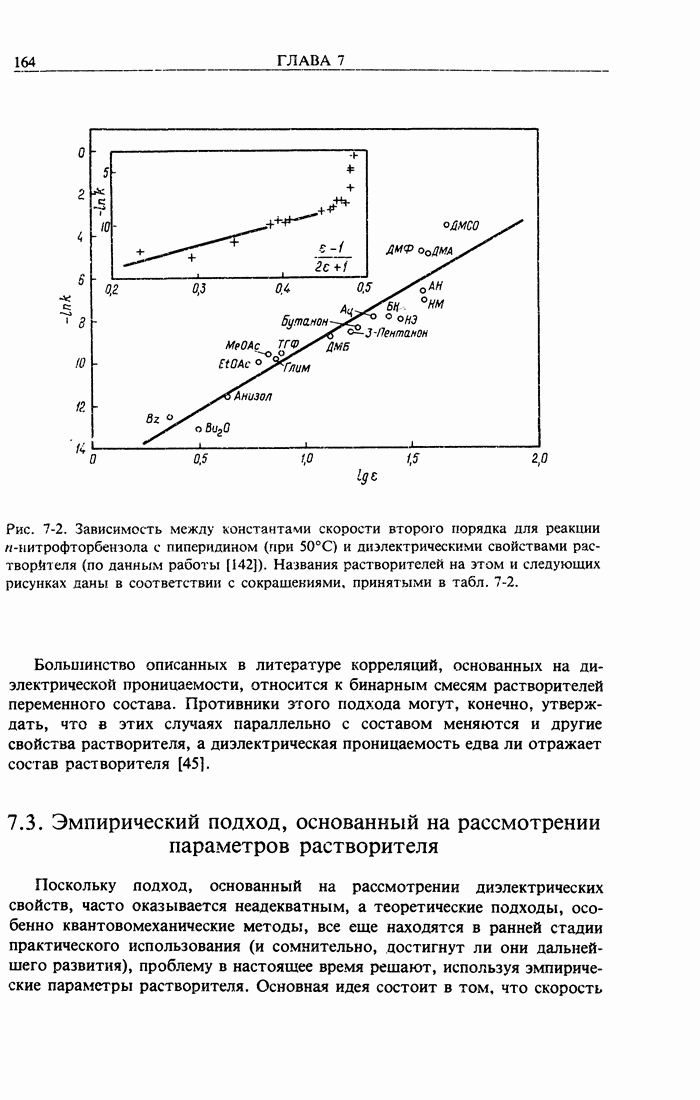
- 7.2. Подход, основанный на рассмотрении диэлектрической проницаемости
- 7.3. Эмпирический подход, основанный на рассмотрении параметров растворителя
- 7.5.2. Корреляции между донорными числами и другими шкалами
- 7.3.3. Корреляции между акцепторными числами и другими шкалами
- 7.3.4. Выводы
- 7.4. Согласование двух подходов
- 7.5. Современная ситуация
- 7.6. Экспериментальные доказательства
- 7.7. Влияние ионной силы растворителя
- 7.8. Сравнительная шкала донорной и акцепторной способности
- 8. ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
- 8.2. Электронные эффекты
- 8.3. Стерические эффекты
- 8.4. Сведения о механизмах реакций
- 9. ПРИЛОЖЕНИЕ К ГЛАВАМ 7 И 8
- 10. ФИЗИЧЕСКОЕ ОБОСНОВАНИЕ ЭМПИРИЧЕСКИХ КОРРЕЛЯЦИЙ
- 10.2. Принцип линейности свободных энергий (принцип ЛСЭ)
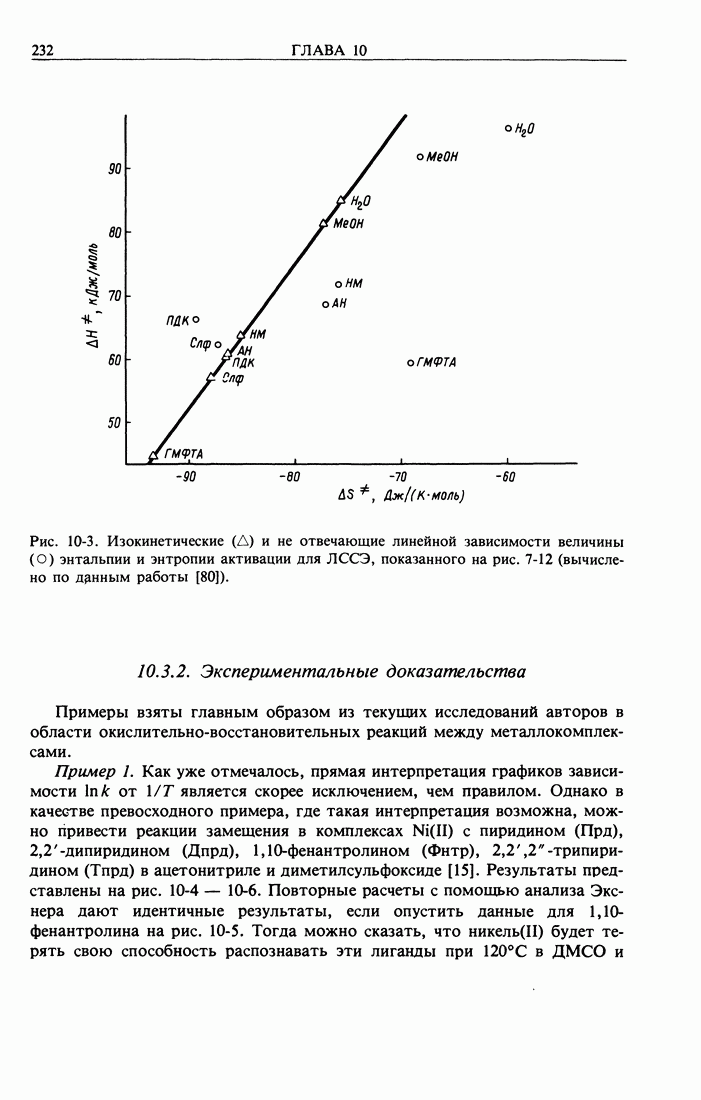
- 10.3. Изокинетическое соотношение (ИКС)
- 10.3.1. Метод Экснера для установления ИКС
- 10.3.2. Экспериментальные доказательства
- 10.3.3. Практические следствия из изокинетических соотношений